1 Introduction

Rock thermal cracking plays a major role in the development and utilization of underground energy sources such as oil, natural gas, and geothermal energy (Ghassemi 2012). Thermal cracking technology can change the macroscopic fracture structure of the rock, such as the length and width of the crack, and generate a large number of macroscopic secondary thermal cracks, forming an effective water flow crack network. The crack network can activate the characteristics of fluid migration in the rock. Therefore, the rock thermal cracking mechanism has been highly valued by experts and scholars at home and abroad for many years.

To study the growth behavior of rock cracks considering the temperature effect, experts and scholars have carried out a large number of laboratory tests and numerical simulation of the thermal fracture process of rock. Zuo et al. (2008) conducted laboratory tests on the deformation and damage characteristics of sandstone under different temperature conditions. The test results showed that sandstone gradually changed from brittle fracture to ductile fracture with the increase of temperature. Deng et al. (1997) found through tests that with the increase of the applied pressure load on the rock, the temperature of rock increases significantly, and the difference is significantly affected by the lithology and the particle size of rock. Simpson (1985) studied the effect of heating rate on the thermal fracture behavior of rocks through laboratory experiments.

In recent years, meshless methods, such as discrete element method (DEM) (Cundall and Strack 1979; Itasca Consulting Group 2004; Potyondy and Cundall 2004; Zhao et al. 2012; Zhao 2013), smooth particle hydrodynamics (SPH) method (Gingold and Monaghan 1977; Lucy 1977), and peridynamical (PD) method (Silling 2000), have been rapidly developed in the numerical calculation of rock thermal cracking. Discrete element method is more used to solve mechanical problems and heat conduction problems of materials (Feng et al. 2008; Shimizu 2006; Vargas and McCarthy 2001), and it is less applied to rock thermal cracking simulation. Smooth particle hydrodynamics is a meshless method in Lagrangian form, originally proposed by Lucy (1997), and Ginold and Monaghan (1997) to solve astrophysics problems. Over the years, it has been widely used, such as fluid flow (Benz and Asphaug 1995; Monaghan 1994; Morris et al. 1997; Takeda et al. 1994; Xu and Deng 2016), heat conduction problems (Clear and Monaghan 1999; Zhou and Bi 2018), and the dynamic response of solid materials (Benz and Asphaug 1995; Libersky et al. 1993). However, the application of SPH method in the heat conduction problem is not yet mature. The traditional SPH method first solves the stress rate, and then integrates the stress rate to solve the stress. For the thermo-solid coupling problem, the time scale of temperature integration is much larger than that of stress integration, so it is difficult to directly introduce the temperature change rate into the constitutive equation of the stress rate. In addition, the tensile instability of traditional SPH algorithm is determined by the Euler kernel function calculated by the spatial coordinates of the current configuration, and this inherent defect has not been fundamentally solved. Fortunately, in the work of Belytschko et al. (2000), it has been proved that the Lagrangian kernel approximation using material coordinates can eliminate the tensile instability phenomenon. Peridynamic (PD) theory was first proposed by Silling (2000). The motion control equation of PD theory is an integral–differential form without spatial derivatives, which can be used to solve fracture problems such as crack propagation. The bond-based peridynamic theory is based on the assumption of paired interaction forces of the same size, which results in the Poisson's ratio of the two-dimensional isotropic material solution problem being limited to 1/4. Aiming at the problem that Poisson's ratio in the bond-based peridynamical theory is limited, Zhou and Shou (2017) introduced the tangential bond in the existing peridynamical theory, which effectively solved the problem. Although the PD method has achieved good simulation results in the numerical calculation of rock fracture, it also has some shortcomings and is still in the development stage.

Although scholars at home and abroad have carried out a large number of laboratory tests and numerical analysis on the thermal cracking process of rocks, frictional contact problems between heterogeneous particles during the thermal crack propagation of rocks are rarely considered. Especially for the Finite-Element Method (FEM) commonly used in engineering, such as the Extended Finite-Element method (XFEM) (Paluszny and Matthai 2009), the Generalized Finite-Element Method (GFEM) (Strouboulis et al. 2000a, b), and the Particle Finite-Element Method (PFEM) (Aubry et al. 2005; Pin et al. 2007), when implementing frictional contact algorithms, it is very difficult for these methods to consider slippage and separation along the defect direction. Numerical Manifold Method (NMM) is a combination of Discontinuous Deformation Analysis (DDA) (Shi and Goodman 1989) and Finite-Element Method (FEM). It is commonly used to solve static cracks and discontinuities in crack propagation (Tsay et al. 1999). However, when the crack tip is just inside the element, the accuracy of this method will be reduced, and a regular mathematical overlay system (Zhang et al. 2010) is needed to accurately evaluate the stress intensity factors (SIFs).

In most geotechnical engineering problems, the SPH algorithm itself is troubled by the “boundary defects”. In fluid and solid mechanics, the SPH interpolation near the boundary is usually inaccurate and needs to be handled appropriately. Monaghan generally simulates the boundary of a rigid body using virtual particles, fluid particles, normalization conditions, and boundary particle forces (Monaghan and Kajtar 2009), and has achieved good results. More information can be found from the work in (Bonet and Kulasegaram 2000; Feldman and Bonet 2007; Libersky et al. 1993; Monaghan 1989, 1992, 1994; Takeda et al. 1994). In addition, particle–surface contact and particle–particle contact based on the momentum equation are also used to describe the contact behavior between particles, where the contact force is applied along the direction of the center line of interacting particles or along the normal direction of the boundary (Campbell et al. 2000; Kulasegaram et al. 2004; Seo and Min 2006). However, the above methods are only suitable for completely smooth or non-slip boundaries, and are not suitable for common friction and sliding contact problems in geotechnical engineering.

Existing studies have shown that the only algorithm that can handle the frictional contact problem in the SPH framework is proposed by Gutfraind and Savage (1997), in which the frictional Coulomb boundary is realized by applying the normal repulsive force and the tangential force proportional to the normal force on the particles by the solid wall. However, this algorithm also has some shortcomings: ① When the friction force is not fully mobilized, the assumption that the tangential force is proportional to the normal force is inaccurate; ② articles may pass through the solid wall and cannot be pulled back; ③ In engineering practice, the movement and rotation of configuration are not considered; ④ More importantly, this algorithm is not suitable for deformed structures. Wang and Chen (2014) proposed a particle–segment friction contact method for two-dimensional simulation of soil–structure interaction and obtained accurate results, but this algorithm is only suitable for the contact between solid particles and structural surface particles.

The purpose of this study is to propose an accurate and stable thermo-mechanical coupling numerical algorithm considering friction effect based on MATLAB software, namely, a new coupled thermo-mechanical bond-based TLF_SPH (TM-BB-TLF_SPH) method. To overcome the shortcomings of SPH method in solving the thermal–mechanical coupling problem, first, the TLF_SPH method is described in detail based on total Lagrangian formula. Then, a pairwise force function is embedded in TLF_SPH to describe the thermoelasticity of the virtual bond. In addition, a hybrid contact friction (HFC) algorithm is embedded in the thermal–mechanical coupling model to study the influence of friction on the initiation, propagation, and coalescence of thermal cracks. The HFC algorithm under the TLF_SPH framework overcomes some shortcomings of the friction algorithm based on SPH particle–segment contact. It not only eliminates the numerical instability caused by the penalty factor in the contact force calculation formula, but also improves the convergence of the numerical model using the particle–particle contact algorithm to smooth the contact force of the structural particles at the corners. When the virtual bond breaks, there is no interaction between the particles except the contact force, which is only related to the contact state between the contact pairs. Numerical examples show that the thermal–mechanical coupling model can accurately predict the initiation and propagation of thermal cracks under the action of frictional contact, and the numerical results agree well with the previous experimental observations.

This paper is organized as follows: In Sect. 2, the main process of TLF_SPH model establishment is briefly summarized. In Sect. 3, the frictional contact algorithm between particles is illustrated. In Sect. 4, the thermal mechanical coupling model considering friction effect is derived, and the damage mechanism of the virtual bond is revealed. In Sect. 5, three numerical examples are given, which not only illustrate the accuracy and stability of the HFC algorithm embedded in TLF_SPH, but also verify the reliability of the proposed thermal–mechanical coupling model considering the friction effect. Finally, conclusions are drawn in Sect. 6, and the influence of thermal expansion coefficient on the thermal fracture mode of rock disc is discussed.

2 Establishment of TLF_SPH Model

The stability of the meshless method based on Euler kernel function and Lagrangian kernel function is analyzed in detail by Belytschko et al. (2000). The research results show that tensile instability is an inherent defect of Euler's formula, and the use of Lagrangian kernel can effectively avoid the tension instability, which provides the possibility for the stability analysis of nonlinear dynamics of elastomer. Therefore, this paper introduces the idea of Lagrangian kernel algorithm in continuum mechanics, and derives and establishes the TLF_SPH model based on total Lagrangian formula suitable for geometric nonlinear analysis, and the traditional SPH solution method for solid materials is redescribed. In TLF_SPH, kernel gradient only needs to be calculated once from the initial position of the particle, and there is no need to calculate the continuity equation, which significantly improves the calculation efficiency of the program.

Suppose there is an ith particle with a position vector of \({\varvec{X}}_{i}\) in the reference coordinate system, which deforms under the action of external force, and its position vector is \({\varvec{x}}_{i}\),then the displacement vector of the ith particle is:\({\varvec{u}}_{i} { = }{\varvec{x}}_{i} - {\varvec{X}}_{i}\), as shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of deformation process of interacting the ith particle in configuration

Full size image

According to the SPH particle approximation method, the deformation gradient tensor and displacement gradient tensor of the ith particle under the Lagrangian framework can be discretized into the following forms:

$$\left\{ \begin{gathered} {\varvec{F}}_{i} = \left( {\frac{{{\text{d}}{\varvec{x}}}}{{{\text{d}}{\varvec{X}}}}} \right)_{i} = \sum\limits_{j}^{N} {\frac{{m_{j} }}{{\rho_{0j} }}({\varvec{x}}_{j} - {\varvec{x}}_{i} )\nabla_{i} W_{ij} } \hfill \\ {\varvec{L}}_{i} = \left( {\frac{{{\text{d}}{\varvec{u}}}}{{{\text{d}}{\varvec{X}}}}} \right)_{i} = \sum\limits_{j}^{N} {\frac{{m_{j} }}{{\rho_{0j} }}({\varvec{u}}_{j} - {\varvec{u}}_{i} )\nabla_{i} W_{ij} } \hfill \\ \end{gathered} \right.,$$
(1)

where u = x-X is the displacement vector of particles; x is the position vector of particles; X is the initial position vector of particles;\(\rho_{0}\) is the initial density of particles; and \(\nabla_{i}^{C} W_{ij}\) is the modified kernel gradient. It is important to note that the density of the particles remains unchanged, during the entire calculation process, and kernel gradient \(\nabla_{i} W_{ij}\) only needs to be calculated once from the initial position of particles.

According to continuum mechanics, the Green–Lagrangian strain tensor at the ith particle can be expressed by the displacement gradient tensor (\({\varvec{L}}_{i}\)) as follows:

$${\varvec{E}}_{i} = ({\varvec{L}}_{i}^{T} + {\varvec{L}}_{i} + {\varvec{L}}_{i}^{T} {\varvec{L}}_{i} ).$$
(2)

Therefore, the Euler strain tensor of the ith particle in the deformed configuration can be obtained from the deformation gradient tensor and the Green–Lagrangian strain tensor as

$${\varvec{\varepsilon}}_{i} { = {\bf F}}_{i}^{ - T} {\varvec{E}}_{i} {\varvec{F}}_{i}^{T} ,$$
(3)

where \({\varvec{F}}_{i}^{ - T}\) indicates that matrix \({\varvec{F}}_{i}\) is first inverted and then transposed.

According to elastic mechanics, for the plane stress problem, the Cauchy stress tensor and Euler strain have the following relationship:

$$\left[ \begin{gathered} ({\varvec{\sigma}}_{x} )_{i} \hfill \\ ({\varvec{\sigma}}_{y} )_{i} \hfill \\ ({\varvec{\sigma}}_{xy} )_{i} \hfill \\ \end{gathered} \right]{ = }\frac{E}{(1 + v)(1 - 2v)}\left[ \begin{gathered} 1 - v\;\;\;\;v\;\;\;\;\;\;\;\;0 \hfill \\ \;\;v\;\;\;\;1 - v\;\;\;\;\;\;0 \hfill \\ \;\;0\;\;\;\;\;\;{0}\;\;\;\;{1/2} - v \hfill \\ \end{gathered} \right]\left[ \begin{gathered} ({\varvec{\varepsilon}}_{x} )_{i} \hfill \\ ({\varvec{\varepsilon}}_{y} )_{i} \hfill \\ ({\varvec{\varepsilon}}_{xy} )_{i} \hfill \\ \end{gathered} \right].$$
(4)

Then, the first type of Piola–Kirchhoff stress tensor can be obtained from the Cauchy stress tensor

$${\varvec{P}}_{i} = J_{i} {\varvec{\sigma}}_{i} {\varvec{F}}_{i}^{ - T} ,$$
(5)

where \(J_{i} { = }\det ({\varvec{F}}_{i} )\) is the determinant of the deformation gradient tensor (\({\varvec{F}}_{i}\)).

In the Lagrangian frame, the governing equation for continuum mechanics are given by (Chakraborty and Shaw 2013; Libersky et al. 1993; Shaw and Reid 2009a, b; Weibull 1951)

$$\left\{ \begin{gathered} \frac{{{\text{d}}{\varvec{v}}^{\alpha } }}{{{\text{d}}t}} = \frac{1}{\rho }\frac{{\partial {\varvec{\sigma}}^{\alpha \beta } }}{{\partial {\varvec{x}}^{\beta } }} \hfill \\ {\varvec{v}}^{\alpha } = \frac{{{\text{d}}{\varvec{x}}^{\alpha } }}{{{\text{d}}t}} \hfill \\ \end{gathered} \right.,$$
(6)

where ρ is solid density;\({\varvec{v}}^{\beta }\) is the βth component of the solid velocity;\({\varvec{x}}^{\beta }\) is the βth component of the spatial coordinate; and \({\varvec{\sigma}}^{\alpha \beta }\) is the (α, β) th component of the total stress tensor, and the superscripts α, β = 1, 2 are used to denote the two spatial directions.

Following the research of Libersky et al. (1993), the momentum equation of the TLF_SPH model without external force can be converted to discretized weak form as

$$\frac{{{\text{d}}{\varvec{v}}_{i}^{\alpha } }}{{{\text{d}}t}} = \sum\limits_{j = 1}^{U} {m_{j} } \left( {\frac{{{\varvec{P}}_{i}^{\alpha \beta } }}{{\rho_{0i}^{2} }} + \frac{{{\varvec{P}}_{j}^{\alpha \beta } }}{{\rho_{0j}^{2} }}} \right)\frac{{\partial W_{ij} }}{{\partial {\varvec{x}}_{i}^{\beta } }}.$$
(7)

An artificial viscosity term \(\Pi_{ij}\) is added to Eq. (7) to stabilize SPH computation, get rid of numerical oscillations and improve calculation accuracy. There are several forms of artificial viscosity (Monaghan 1988). In this study, the form consisting of a combination of linear and quadratic (Neumann and Richtmyer 1950) viscosity as prescribed by Monaghan and Gingold (1983) is used

$$\Pi_{ij} { = }\left\{ {\begin{array}{*{20}c} {\frac{{ - \alpha_{1} \overline{C}_{ij} u_{ij} + \alpha_{2} u_{ij}^{2} }}{{\overline{\rho }_{ij} }},} & {if\;{\varvec{v}}_{ij} \cdot {\varvec{x}}_{ij} < \;0} \\ {0,} & {{\text{otherwise}}} \\ \end{array} } \right.,$$
(8)

where α and β are the artificial viscosity parameters and ε is a small number, generally taken as 0.01.\(\overline{c}_{ij} = (c_{i} + c_{j} )/2\) and \(\overline{\rho }_{ij} = (\rho_{i} + \rho_{j} )/2\) indicate sound speed (\(c = \sqrt {4G/3\rho_{0} }\))and density of the solid, both averaged at the ith and jth particles, respectively (Hallquist 1998).\({\varvec{v}}_{ij} = {\varvec{v}}_{i} - {\varvec{v}}_{j}\) is the relative velocity of ith and jth particles. Similarly,\({\varvec{x}}_{ij} = {\varvec{x}}_{i} - {\varvec{x}}_{j}\) is the relative distance of ith and jth particles. The term \(u_{ij}\) is defined as \(u_{ij} { = }h{\varvec{v}}_{ij} {\varvec{x}}_{ij} /({\varvec{x}}_{ij}^{2} + \varepsilon h^{2} )\).

3 Friction Contact Algorithm Between Particles

3.1 Modification of Contact Boundary Governing Equation

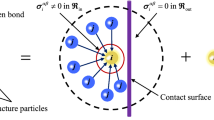
As shown in Fig. 2, when dealing with the contact between solid particles and deformed structures, the support domain of particles close to the contact surface is only limited to one side of the interface, that is, the support domain of the ith solid particle cannot contain any structural particles, and vice versa. Therefore, if the influence of contact is considered, the momentum equation of the ith solid particle in contact with the structured particles can be written as follows:

$$\frac{{{\text{d}}{\varvec{v}}_{i}^{\alpha } }}{{{\text{d}}t}} = \frac{1}{\rho }\frac{{\partial {\varvec{\sigma}}_{i}^{\alpha \beta } }}{{\partial {\varvec{x}}_{i}^{\beta } }} + \frac{{{\varvec{F}}_{i}^{\alpha } }}{{m_{i} }}{ + }{\varvec{b}}_{i}^{\alpha } ,$$
(9)

where \({\varvec{F}}^{\alpha }\) is the contact force in α coordinate direction; ρ is the density of particles;\({\varvec{b}}^{\alpha }\) is the acceleration caused by physical force in the α coordinate direction.

Fig. 2
figure 2

Decomposition of acceleration for the ith particle

Full size image

It can be seen from Fig. 2 that the supporting domain \(\Re_{{{\text{in}}}}\) of the ith solid particle in contact with structural particles is missing. Therefore, the first term \((\partial {\varvec{\sigma}}^{\alpha \beta } /\partial {\varvec{x}}^{\beta } )\) on the right side of the momentum equation cannot be discretized. To make the ith solid particle have a complete influence domain, an outer domain \(\Re_{{{\text{out}}}}\) is added outside the contact surface, and the stress of the particles in the outer domain \(\Re_{{{\text{out}}}}\) is set to zero. Then, Eq. (9) can be discretized as:

$$\frac{{{\text{d}}{\varvec{v}}_{i}^{\alpha } }}{{{\text{d}}t}} = \sum\limits_{{j \in \Re_{in} }} {m_{j} \left( {\frac{{{\varvec{P}}_{i}^{\alpha \beta } }}{{\rho_{i}^{2} }} + \frac{{{\varvec{P}}_{j}^{\alpha \beta } }}{{\rho_{j}^{2} }} + \Pi_{ij} } \right)\frac{{\partial W_{ij} }}{{\partial {\varvec{x}}_{i}^{\beta } }}} + \sum\limits_{{j \in \Re_{out} }} {\frac{{{\varvec{F}}_{i}^{\alpha } }}{{m_{i} }}} + {\varvec{b}}^{\alpha } .$$
(10)

3.2 Hybrid friction contact (HFC) algorithm for contact boundary

The traditional particle–particle contact algorithm has significant advantages in contact detection (Campbell et al. 2000). When the penetration between two particles is detected, the contact occurs between particles. The penetration state between the ith and jth particles is defined as

$$p{ = }\frac{{h_{i} + h_{j} }}{2} - {\mathbf{||}}{\varvec{x}}_{ij} {\mathbf{||,}}$$
(11)

where hi and hj are the smooth lengths of particles;\({\varvec{x}}_{ij}\) is the relative position vector between the ith and jth particles. When p > 0, particles penetrate; p < 0, particles do not penetrate, as shown in Fig. 3. However, this algorithm only calculates the contact force between particles along the normal direction, ignoring the influence of tangential deformation between particles. Therefore, the contact force calculated by this method does not follow the deformation law of the actual contact surface, and cannot accurately simulate the friction force between the contact surfaces.

Fig. 3
figure 3

Schematic diagram of particle-to-particle contact

Full size image

As shown in Fig. 4, Wang et al. (2013) proposed a particle–segment contact algorithm in the SPH framework, and introduced a penalty factor \(\eta\) to “weaken the intensity of penalty parameter”, which improved the accuracy of numerical calculations. The algorithm was finally successfully applied to the two-dimensional simulation of the local deformation behavior of the material around the contact surface under the soil–structure interaction.

Fig. 4
figure 4

Schematic diagram of particle-to-segment contact

Full size image

The particle–segment contact algorithm calculates the contact force based on the relative position between the ith and jth particles. Suppose the contact force of the ith particle is \({\varvec{F}}_{i}^{\alpha }\). If the ith and the jth particles come into contact, the acceleration of the ith particle due to the contact force is \({\varvec{a}}_{i}^{\alpha } { = {\bf F}}_{i}^{\alpha } /m_{i}\), as shown in Fig. 5.

Fig. 5
figure 5

Schematic diagram of particle-to-segment contact

Full size image

In this algorithm, the boundary and the surface of structure are discrete in sections, and the contact force \({\varvec{F}}_{n}\) along the normal direction of the structure surface is represented by the residual penetration

$${\varvec{F}}_{n} { = }\left( {1 - \eta } \right)\frac{{2m_{i} }}{{\Delta t^{2} }}\Delta d_{n} { = }\left( {1 - \eta } \right)\frac{{2m_{i} }}{{\Delta t^{2} }}\left( {d_{0} - d_{ip} } \right) \cdot {\bf{n},}$$
(12)
$$d_{ip} = - ({\varvec{x}}_{i} - {\varvec{x}}_{p} ) \cdot {\bf{n},}$$
(13)

where \(\Delta t\) is the time step; mi is the mass of the ith solid particle;\(\eta\) is a penalty factor reflecting the allowable degree of residual penetration (\(\eta\) = 0 indicates that the particle has not penetrated). The introduction of \(\eta\) effectively reduces the stress oscillation during the contact simulation process and improves the stability of the numerical calculation.\(d_{ip}\) is the real-time distance between the ith particle and the contact point p;\({\varvec{n}}\) is the out-of-unit normal vector at the contact point p on the structural surface;\(d_{0}\) is the threshold of contact detection (when \(d_{ip}\) < \(d_{0}\), particles come into contact). In particular, for rigid structures,\(d_{0} { = }{{\Delta x} \mathord{\left/ {\vphantom {{\Delta x} 2}} \right. \kern-\nulldelimiterspace} 2}\); for deformed structures \(d_{0} { = }\Delta x\).

Although the accuracy of the particle–segment contact algorithm proposed by Wang et al. (2013) in the SPH framework has achieved good results, it is difficult to determine the penalty factor \(\eta\), which is determined by SPH's Euler kernel function idea. The TLF_SPH model established in this article is based on the idea of Lagrangian kernel function. Therefore, after the particle–segment contact algorithm is embedded in the TLF_SPH model, the penalty factor term (1–\(\eta\)) can be completely removed, which not only achieves good numerical accuracy, but also further improves the numerical stability of the contact calculation. Then, the normal contact force acting on solid particles can be expressed in the following form:

$${\varvec{F}}_{n} { = }\frac{{2m_{i} }}{{\Delta t^{2} }}\left( {d_{0} - d_{ip} } \right) \cdot {\varvec{n}}{.}$$
(14)

Assuming that the structure surface is completely rough and there is no relative sliding between solid particles and structure surface particles, the contact force \({\varvec{F}}_{\tau }\) of solid particles along the tangential direction is static friction, which can be calculated as follows:

$${\varvec{F}}_{\tau } { = }\frac{{2m_{i} }}{{\Delta t^{2} }}\Delta \hat{\bf{x}}_{pi}^{\tau } ,$$
(15)

where \(\Delta \hat{\bf{x}}_{pi}^{\tau }\) is the total relative position vector of the contact point p and the ith solid particle along the unit tangent vector direction of the contact surface

$$\Delta {\varvec{x}}_{pi} { = }({\varvec{v}}_{p} - {\varvec{v}}_{i} )\Delta t,$$
(16)
$$\Delta {\varvec{x}}_{pi}^{n} = (\Delta {\varvec{x}}_{pi} \cdot {\varvec{n}}) \cdot {\varvec{n}},$$
(17)
$$\Delta \hat{\bf{x}}_{pi}^{\tau } = \sum\limits_{n = 1}^{{N_{t} }} {(\Delta {\varvec{x}}_{pi} - \Delta {\varvec{x}}_{pi}^{n} )} ,$$
(18)

where \(\Delta {\varvec{x}}_{pi}\) is the relative position vector of the contact point p and the ith solid particle in the current time step;\(\Delta {\varvec{x}}_{pi}^{n}\) is the relative position vector of the contact point p and the ith solid particle along the out-of-unit normal vector direction of contact surface in the current time step; Nt is the total number of time steps;\({\varvec{v}}_{p}\) is the velocity vector at the contact point p. It should be noted that for rigid structures, the velocity at the contact point p can be obtained by the following formula:

$${\varvec{v}}_{p} = {\varvec{v}}_{t} + {\varvec{\omega}} \otimes {\varvec{L}},$$
(19)

where \({\varvec{v}}_{t}\) is the traction speed of rigid structure;\({\varvec{\omega}}\) is the rotation speed of rigid structure;\({\varvec{L}}\) is the position vector from the rotation reference point to the contact point.

For a deformed structure, the velocity at the contact point p can be obtained by linear interpolation of the velocity of adjacent structure particles \(b1\) and \(b2\)

$${\varvec{v}}_{p} = \frac{{{\varvec{v}}_{b1} {\mathbf{||}}{\varvec{x}}_{p} {\mathbf{ - }}{\varvec{x}}_{b2} {\mathbf{||}}{ + }{\varvec{v}}_{b2} {\mathbf{||}}{\varvec{x}}_{p} {\mathbf{ - }}{\varvec{x}}_{b1} {\mathbf{||}}}}{{{\mathbf{||}}{\varvec{x}}_{b2} {\mathbf{ - }}{\varvec{x}}_{b1} {\mathbf{||}}}},$$
(20)

where \({\varvec{x}}_{p}\) is the position vector of the contact point p on the structure surface; \({\varvec{x}}_{b1}\) and \({\varvec{x}}_{b2}\) is the position vector of the adjacent particles on both sides of the contact point p.

When the solid particles and the structural surface particles slide relatively, there is \({\mathbf{||}}{\varvec{F}}_{\tau } {\mathbf{||}}\; > \mu {\mathbf{||}}{\varvec{F}}_{n} {\mathbf{||}}\). Then, the contact force of solid particles along the tangential direction is sliding friction force, which is recorded as \(\hat{\bf{F}}_{\tau }\), and its expression is as follows:

$$\hat{\bf{F}}_{\tau } { = }\mu {\mathbf{||}}{\varvec{F}}_{n} {\mathbf{||}} \cdot \frac{{{\varvec{F}}_{\tau } }}{{{\mathbf{ ||}}{\varvec{F}}_{\tau } {\mathbf{||}}\;}},$$
(21)

where \({\varvec{F}}_{n}\) is the normal contact force at the contact point p on the structural surface; u is the dynamic friction coefficient;\({\varvec{F}}_{\tau }\) is the static friction force generated when the solid particles and the contact surface have no relative sliding.

Therefore, the total contact force of the contact surface acting on the ith solid particle is

$${\varvec{F}}_{i} { = }\left\{ \begin{gathered} {\varvec{F}}_{n} + {\varvec{F}}_{\tau } ,\quad {\mathbf{||}}{\varvec{F}}_{\tau } {\mathbf{||}}\; \le \mu {\mathbf{||}}{\varvec{F}}_{n} {\mathbf{||}} \hfill \\ {\varvec{F}}_{n} + \hat{\bf{F}}_{\tau } {\mathbf{,}}\quad {\mathbf{||}}{\varvec{F}}_{\tau } {\mathbf{||}}\; > \mu {\mathbf{||}}{\varvec{F}}_{n} {\mathbf{||}} \hfill \\ \end{gathered} \right..$$
(22)

After the contact force of the ith solid particle is determined, for a rigid structure, the total contact reaction force of rigid structure is as follows:

$${\varvec{F}}_{{{\text{sum}}}} { = } - \sum\limits_{i = 1}^{{N_{F} }} {{\varvec{F}}_{i} } ,$$
(23)

where \(N_{F}\) is the number of solid particles interacting with contact surface.

For a deformed structure, the reaction force of the structure particles \(b_{1}\) and \(b_{2}\) adjacent to the contact point p can be obtained by linear interpolation of the ith solid particle interacting with them

$$\left\{ \begin{gathered} {\varvec{F}}_{b1} = - \frac{{{\mathbf{||}}{\varvec{x}}_{p} {\mathbf{ - }}{\varvec{x}}_{b2} {\mathbf{||}}}}{{{\mathbf{||}}{\varvec{x}}_{b2} {\mathbf{ - }}{\varvec{x}}_{b1} {\mathbf{||}}}}{\varvec{F}}_{i} \hfill \\ {\varvec{F}}_{b2} = - \frac{{{\mathbf{||}}{\varvec{x}}_{p} {\mathbf{ - }}{\varvec{x}}_{b1} {\mathbf{||}}}}{{{\mathbf{||}}{\varvec{x}}_{b2} {\mathbf{ - }}{\varvec{x}}_{b1} {\mathbf{||}}}}{\varvec{F}}_{i} \hfill \\ \end{gathered} \right..$$
(24)

It should be noted that when the structured particles are on the contact surface, there is only one contact section for the ith solid particle. Therefore, the above algorithm is only applicable to the contact between the solid particles and the structured surface particles. When the structural particles are located in the corners, the ith solid particle may have multiple contact segments, and the above algorithm is no longer applicable. In response to this situation, a hybrid friction contact algorithm of master and slave contact surfaces proposed by Zhan et al. (2020) greatly simplifies the calculation and implementation of the program. However, when the structural surfaces are curved or irregular, the accuracy of numerical calculation will be disturbed.

The hybrid friction contact (HFC) algorithm proposed in this paper is simpler and more effective to deal with corner particles. First, the TLF_SPH program searches for the corner particles on the structure surface within the influence domain of the ith solid particle. If the ith solid particle has multiple contact segments, the structure particle nearest to the ith solid particle is selected and denoted as the pth particle. Then, based on the partial penetration algorithm, the normal contact force and tangential contact force between the ith and pth particles are calculated using Eqs. (25) and (26), respectively. According to the adaptive characteristics of SPH, when there are enough corner particles on the structural surface, the numerical accuracy of the contact force can fully meet the calculation requirements. In particular, the above method is more effective in dealing with the numerical singularity problem caused by the missing contact segment at the tip of the pre-existing defects.

If the structure particle is in the corner, the normal contact force acting on the ith solid particle can be expressed in the following form:

$${\varvec{F}}_{n}^{{{\text{corner}}}} { = }\frac{{2m_{i} }}{{\Delta t^{2} }}\left( {d_{0} - d_{ip} } \right) \cdot {\varvec{n}}_{ip} ,$$
(25)

where \(d_{ip}\) is the real-time distance between the ith and pth particles;\({\varvec{n}}_{ip}\) is the unit vector of the line between the ith and pth particles, whose direction is from the pth particle to the ith particle.

Assuming that there is no relative sliding between the ith solid particle and the pth corner particle, the tangential contact force of the ith solid particle is static friction force, which can be calculated as follows:

$${\varvec{F}}_{\tau }^{{{\text{corner}}}} = \frac{{2m_{i} }}{{\Delta t^{2} }}\sum\limits_{n = 1}^{{N_{t} }} {\left\{ {({\varvec{v}}_{p} - {\varvec{v}}_{i} )\Delta t - \left[ {({\varvec{v}}_{p} - {\varvec{v}}_{i} )\Delta t \cdot {\varvec{n}}_{ip} } \right] \cdot {\varvec{n}}_{ip} } \right\}} ,$$
(26)

where \(m_{i}\) is the mass of the ith solid particle; Nt is the total number of time steps;\({\varvec{v}}_{p}\) is the velocity vector of the pth corner particle;\({\varvec{v}}_{i}\) is the velocity vector of the ith solid particle.

To better illustrate the calculation process of the algorithm, the calculation flowchart of the contact algorithm is given in Fig. 6.

Fig. 6
figure 6

Calculation flowchart of contact force algorithm

Full size image

4 TLF_SPH Thermo-mechanical Coupling Model Considering Friction Effect

4.1 Heat Conduction Control Equation and Its Discretization

In the process of heat conduction, assuming that each ith particle can be regarded as a heat storage to store heat, the virtual bonds formed between the ith and jth particles in the non-local influence domain is also called “thermal bond” by Bobaru and Duangpanya (2010, 2012). As shown in Fig. 7, “thermal bond” can be used as a thermal conductor between the interacting ith and jth particles to transfer heat, and heat storage and heat conductors together constitute heat conduction in a thermal system. According to the theory of continuum, the differential equation of transient heat conduction in a two-dimensional rectangular coordinate system is

$$\lambda \left( {\frac{{\partial^{2} \Theta }}{{\partial x^{2} }}{ + }\frac{{\partial^{2} \Theta }}{{\partial y^{2} }}} \right){ = }\rho c_{v} \frac{\partial \Theta }{{\partial t}}.$$
(27)
Fig. 7
figure 7

Heat conduction model between interacting particles and schematic diagram of heat flux flowing through ith particle

Full size image

The rate of temperature change can be obtained by Eq. (27) as follows:

$$\frac{\partial \Theta }{{\partial t}}{ = }\frac{1}{\rho c}\sum\limits_{\beta } {\frac{\partial }{{\partial {\varvec{x}}^{\beta } }}\left( {{\varvec{\kappa}}^{\beta } \frac{\partial \Theta }{{\partial {\varvec{x}}^{\beta } }}} \right)} ,$$
(28)

where, ρ is the density of the material, kg/m3; c is the specific heat capacity of the material, J/(kg °C);\({\varvec{x}}^{\beta }\) is a two-dimensional space coordinate element, β = 1, 2;\({\varvec{\kappa}}^{\beta }\) is the heat conduction coefficient along the β direction, and \(\Theta\) is the instantaneous temperature, °C.

According to Fourier's law, the heat flux can be obtained from the temperature gradient as

$${\varvec{q}}^{\beta } = - {\varvec{\kappa}}^{\beta } \left( {\frac{{\partial\Theta }}{{\partial {\varvec{x}}^{\beta } }}} \right).$$
(29)

Substituting Eq. (29) into Eq. (28), the rate of temperature change can be obtained as follows:

$$\frac{{\partial\Theta }}{\partial t} = - \frac{1}{\rho c}\nabla \cdot {\varvec{q}}^{\beta } ,$$
(30)

where, \({\varvec{q}}^{\beta }\) is the heat flux along the direction of heat conduction, and the superscript β = 1, 2.

According to the approximation method of SPH particles, Eqs. (29) and (30) can be discretized into the following forms:

$$\left\{ \begin{gathered} {\varvec{q}}_{i}^{\beta } = {\varvec{\kappa}}_{i}^{\beta } \sum\limits_{j = 1}^{N} {\frac{{m_{j} }}{{\rho_{j} }}(\Theta _{i} -\Theta _{j} )\frac{{\partial W_{ij} }}{{\partial {\varvec{x}}_{i}^{\beta } }}} \hfill \\ \frac{{\partial\Theta _{i} }}{\partial t} = \frac{1}{{\rho_{i} c_{i} }}\sum\limits_{j = 1}^{N} {\frac{{m_{j} }}{{\rho_{j} }}({\varvec{q}}_{i}^{\beta } - {\varvec{q}}_{j}^{\beta } )\frac{{\partial W_{ij} }}{{\partial {\varvec{x}}_{i}^{\beta } }}} \hfill \\ \end{gathered} \right.,$$
(31)

where \(\partial W_{ij} /\partial {\varvec{x}}_{i}^{\beta }\) is the gradient of the kernel function;\(\Theta _{i}\) and \(\Theta _{j}\) are the temperature of the ith and jth particles, respectively;\({\varvec{q}}_{i}^{\beta }\) and \({\varvec{q}}_{j}^{\beta }\) are the heat flux of the ith and jth particles along the β direction, respectively.

In the numerical simulation of heat conduction, the kernel function is truncated due to the absence of boundary particles. To improve the numerical accuracy of boundary particles, the kernel gradient is modified. Then, the discrete model of the transient heat conduction equation after the kernel function gradient is modified is as follows:

$$\left\{ \begin{gathered} {\varvec{q}}_{i}^{\beta } = {\varvec{\kappa}}_{i}^{\beta } \sum\limits_{j = 1}^{N} {\frac{{m_{j} }}{{\rho_{j} }}(\Theta _{i} -\Theta _{j} ) \otimes M_{i}^{ - 1} \frac{{\partial W_{ij} }}{{\partial {\varvec{x}}_{i}^{\beta } }}} \hfill \\ \frac{{\partial\Theta _{i} }}{\partial t} = \frac{1}{{\rho_{i} c_{i} }}\sum\limits_{j = 1}^{N} {\frac{{m_{j} }}{{\rho_{j} }}({\varvec{q}}_{i}^{\beta } - {\varvec{q}}_{j}^{\beta } ) \otimes M_{i}^{ - 1} \frac{{\partial W_{ij} }}{{\partial {\varvec{x}}_{i}^{\beta } }}} \hfill \\ M_{i} { = }\sum\limits_{j}^{N} {\frac{{m_{j} }}{{\rho_{j} }}\nabla_{i} W_{ij} \otimes ({\varvec{x}}_{j} - {\varvec{x}}_{i} )} \hfill \\ \end{gathered} \right.,$$
(32)

where \(\rho_{i}\) and \(\rho_{j}\) are the density of the ith and jth particles, respectively; mi and mj are the masses of the ith and jth particles, respectively;\(M_{i}^{ - 1}\) is the inverse of matrix \(M_{i}\), which is used to modify kernel gradient.

4.2 Boundary Conditions for Heat Conduction

In the process of heat conduction, three types of thermal diffusion boundary conditions can be applied, namely, the first type of non-local boundary conditions, the second type of non-local boundary conditions, and the third type of non-local boundary conditions. The specific implementation strategy of the first type of non-local boundary conditions, called Dirichlet boundary conditions, is to impose a given temperature \(\tilde{\theta }(\hat{x},t)\) on the boundary of the computational domain \(\Re\), namely

$$\Theta |_{\Re } = \tilde{\theta }(\hat{x},t),$$
(33)

where \(\hat{\bf{x}}\) is the particle position on the boundary of the computational domain \(\Re\).

According to the classical continuum theory, the second type of non-local boundary conditions called Neumann boundary conditions can be expressed as

$$\left( {\kappa_{x} n_{x} \frac{{\partial \Theta (\hat{\bf{x}},t)}}{\partial x}{ + }\kappa_{y} n_{y} \frac{{\partial \Theta (\hat{\bf{x}},t)}}{\partial y}} \right){ = } - \hat{\bf{q}}^{\beta } \cdot \bf{n,}$$
(34)

where \(\hat{\bf{x}}\) is the particle position on the boundary of the computational domain \(\Re\);\(\Theta (\hat{\bf{x}},t)\) and \(\hat{\bf{q}}^{\beta }\) are the temperature and heat flux given on the boundary of the computational domain \(\Re\), respectively;\(\kappa_{x}\) and \(\kappa_{y}\) are the thermal conductivity coefficients of materials along the x direction and y direction, respectively. n is the out-of-unit normal vector on the boundary;\(n_{x}\) and \(n_{y}\) are the x and y components of n, respectively.

The third type of non-local boundary conditions is also called Robin boundary conditions. This boundary condition is implemented when heat transfer occurs between the surface of the object and the surrounding medium. According to the classical continuum theory, the third type of non-local boundary conditions can be expressed as

$$\left( {\kappa_{x} n_{x} \frac{{\partial \Theta (\hat{\bf{x}},t)}}{\partial x}{ + }\kappa_{y} n_{y} \frac{{\partial \Theta (\hat{\bf{x}},t)}}{\partial y}} \right){ = } - h\left[ {\Theta (\hat{\bf{x}},t) - \Theta_{0} )} \right],$$
(35)

where \(\hat{\bf{x}}\) is the particle position on the boundary of the computational domain \(\Re\);\(\Theta (\hat{\bf{x}},t)\) is the temperature given on the boundary of the computational domain \(\Re\);\(\Theta_{0}\) is the temperature of the surrounding medium; h is the heat convection coefficient between the solid and the surrounding medium.

4.3 Non-local Thermal Stress in the TLF_SPH Model

In the theory of continuum mechanics, it is believed that there is a force between the ith and jth particles in the non-local influence domain. To describe the force state between the ith and jth particles, the initial relative position vector and relative displacement vector between the ith and jth particles are defined as \({\varvec{\xi}}{ = }{\varvec{X}}_{i} - {\varvec{X}}_{j}\) and \({\varvec{\eta}}{ = }{\varvec{u}}_{i} - {\varvec{u}}_{j}\), respectively, as shown in Fig. 8. Then, the relative position vector between the ith and the jth particles in the deformed configuration can be expressed as

$$\tilde{\varvec{\xi }} = ({\varvec{X}}_{j} + {\varvec{u}}_{j} ) - {(}{\varvec{X}}_{i} + {\varvec{u}}_{i} ) = ({\varvec{X}}_{j} - {\varvec{X}}_{i} ) + ({\varvec{u}}_{j} - {\varvec{u}}_{i} ) = {\varvec{\xi}}{ + }{\varvec{\eta}}.$$
(36)
Fig. 8
figure 8

Schematic diagram of deformation process of interacting the ith and jth particles in configuration

Full size image

According to Newton’s third law, the pairwise force acting on the ith and jth particles is equal, and the direction is reversed along the action bond, as shown in Fig. 9. Then, based on thermoelasticity, a pairwise force function of the ith particle can be expressed as

$${\varvec{f}}({\varvec{x}}_{i} - {\varvec{x}}_{j} ,\Theta ,t){ = }\frac{{c_{m} \left( {\alpha_{j} (\Theta _{j} -\Theta _{0} ) - \alpha_{i} (\Theta _{i} -\Theta _{0} )} \right)}}{1 - v} \cdot \bf{e,}$$
(37)

where \(\Theta _{0}\) is the initial temperature of particles;\(\Theta\) is the instantaneous temperature of particles; E is the modulus of elasticity; α is the thermal expansion coefficient; v is the Poisson's ratio;\({\varvec{e}}\) is the unit direction vector of virtual bonds in the deformed coordinate system, and its expression is as follows:

$${\varvec{e}} = \frac{{{\varvec{x}}_{j} - {\varvec{x}}_{i} }}{{{\mathbf{||}}{\varvec{x}}_{j} - {\varvec{x}}_{i} {\mathbf{||}}}} = \frac{{{\varvec{\xi}}{ + }{\varvec{\eta}}}}{{{\mathbf{||}}{\varvec{\xi}}{ + }{\varvec{\eta}}{\mathbf{||}}}}.$$
(38)
Fig. 9
figure 9

Schematic diagram of thermoelastic interaction between the ith and jth particles in the non-local influence domain

Full size image

For the two-dimensional plane strain problem, the expression of the micro-elastic modulus is as follows (Shou 2017):

$$c_{m} { = }\frac{6E}{{\pi \delta^{3} (1 - v)}}.$$
(39)

To eliminate the unbalanced force between particles, this paper adopts the concept of dual influence domain with fixed horizon proposed by Ren et al. (2017). The horizon of the ith particle in the DH-PD model is defined as

$${\mathbf{\Re }}_{{{\varvec{x}}_{i} }} { = }\left\{ {{\varvec{x}}_{j} {\mathbf{/ ||}}{\varvec{x}}_{j} - {\varvec{x}}_{i} {\mathbf{||}}\; \le \delta_{{{\varvec{x}}_{i} }} } \right\},$$

where \({\mathbf{||}}{\varvec{x}}_{j} - {\varvec{x}}_{i} {\mathbf{||}}\) is the distance between the ith and jth particles;\(\delta_{i}\) is the horizon radius of the ith particles in \({\mathbf{\Re }}_{{{\varvec{x}}_{i} }}\). In a sense, the horizon \({\mathbf{\Re }}_{{{\varvec{x}}_{i} }}\) is the union of all the bonds starting from the ith particles. The double horizon of the ith particles is defined as

$${\mathbf{\Re }}_{{{\varvec{x}}_{i} }} { = }\left\{ {{\varvec{x}}_{j} {\mathbf{/}}{\varvec{x}}_{i} {\mathbf{ \in \Re }}_{{{\varvec{x}}_{i} }} } \right\}.$$

Any particle in \({\mathbf{\Re }}_{{{\varvec{x}}_{i} }}\) will form a double-bond \({\varvec{x}}_{j} {\varvec{x}}_{i}\). In other words, the horizon \({\mathbf{\Re }}_{{{\varvec{x}}_{i} }}\) is the union of all bonds starting from the jth particle. That is, any virtual bond in the horizon \({\mathbf{\Re }}_{{{\varvec{x}}_{i} }}\) is also a particle bond with the interacting particle in the double horizon \({\mathbf{\Re }}_{{{\varvec{x}}_{i} }}\). Then, if other external forces are not considered in the dual-horizon \({\mathbf{\Re }}_{{{\varvec{x}}_{i} }}\), the momentum equation of the ith particle can be discretized into the following form:

$$\frac{{{\text{d}}{\varvec{v}}_{i}^{\alpha } }}{{{\text{d}}t}} = \frac{1}{{\rho_{i} }}\int\limits_{{{\mathbf{\Re }}_{{{\varvec{x}}_{i} }} }} {{\varvec{f}}({\varvec{x}}_{i} - {\varvec{x}}_{j} ,\Theta ,t)V_{j} } { = }\frac{1}{{\rho_{i} }}\sum\limits_{j = 1}^{N} {\frac{{m_{j} }}{{\rho_{j} }}} \left( {{\varvec{f}}({\varvec{x}}_{i} - {\varvec{x}}_{j} ,\Theta ,t) - {\varvec{f}}({\varvec{x}}_{j} - {\varvec{x}}_{i} ,\Theta ,t)} \right)W_{ij} ,$$
(40)

where \(\rho_{i}\) and \(\rho_{j}\) are the densities of the ith and jth particles, respectively;\(m_{j}\) is the mass of the ith particle;\({\varvec{f}}({\varvec{x}}_{i} - {\varvec{x}}_{j} ,\Theta ,t)\) and \({\varvec{f}}({\varvec{x}}_{j} - {\varvec{x}}_{i} ,\Theta ,t)\) are the point force function of the ith and jth particles, respectively;\(W({\mathbf{||}}{\varvec{x}}_{j} - {\varvec{x}}_{i} {\mathbf{||}}\;,h)\) represents the interpolation kernel function, and h is the smoothing length;\({\varvec{v}}_{i}^{\alpha }\) the velocity of the ith particle and the superscript α = 1, 2 are integer indices for the two spatial directions.

4.4 Damage Mechanism of Virtual Bonds in TLF_SPH

Rock materials are mainly brittle failure. Therefore, the selection of failure criteria is particularly important, which determines the initiation, propagation and bonding mode of rock cracks. In peridynamic theory, when the material is deformed, there is an interaction between adjacent material points in the influence domain, and the interaction between any two adjacent material points is established through virtual bonds (Zhou and Shou 2017). Then, the virtual bonds of a given material point in the influence domain together constitute a complete network unit, as shown in Fig. 10a. In this paper, the Hoek–Brown strength criterion is applied to determine the initiation and propagation of cracks. When the stress on the particle bond satisfies the Hoek–Brown strength criterion, the particle bond breaks, and no force transmission is carried out, and micro-cracks gradually initiate from here, as shown in Fig. 10b. The f in the Fig. 10 is the interaction factor, which will be explained in detail later.

Fig. 10
figure 10

Discretization of 2D particles with virtual bonds: (a) the influence domain without damage virtual bonds; (b) the influence domain with damage virtual bonds

Full size image

The Hoek–Brown strength criterion commonly used in tunnel engineering can be defined as the following form (Hoek and Brown 1980; Hoek 1983):

$${\varvec{\sigma}}_{1} = {\varvec{\sigma}}_{3} { + }\sqrt {m{\varvec{\sigma}}_{3} {\varvec{\sigma}}_{c} + s{\varvec{\sigma}}_{c}^{2} } ,$$
(41)

where the strength parameters m and s can be determined by the parameter GSI, which depends on the structure and surface state of the rock joints and cracks;\({\varvec{\sigma}}_{c}\) is the uniaxial compressive strength of the intact rock. The intensity parameters m and s are defined by Hoek et al. (Hoek 1990; Hoek and Brown 1997) as

$$m = m_{i} \;{\text{exp}}\left( {\frac{{{\text{GSI}} - 100}}{28 - 14D}} \right),$$
(42)
$$s = {\text{exp}}\left( {\frac{{{\text{GSI}} - 100}}{9 - 3D}} \right),$$
(43)

where GSI reflects the degree of weakening of rock mass strength caused by complex geological conditions, which varies from 0 to 100. The value of GSI is determined by the structural characteristics and joint surface state in the GSI chart of rock mass. D is the disturbance coefficient, which varies from 0 for undisturbed rock masses to 1 for strongly disturbed rock masses. mi is the value of m for intact rock, which varies from 4 to 33, which can be obtained by experiment.

The Cauchy stress on the virtual bond is approximately taken as the average value of the two particle stresses

$${\varvec{\sigma}}({\varvec{\xi}},t) = ({\varvec{\sigma}}_{i} + {\varvec{\sigma}}_{j} )/2.$$
(44)

In the TLF_SPH model, the compressive stress is defined as negative, and the stress and strain of particles in the program calculation process conform to the elastic–brittle constitutive relationship, as shown in Fig. 11. To describe the fracture state of particle bonds, a parameter called interaction factor f is introduced to reflect whether the particle bonds are broken or not (Chakraborty and Shaw 2013). The model initially has f = 1. As the load increases, when the stress on the virtual bond reaches the maximum bearing capacity, the virtual bond breaks and its stiffness drops to zero with f = 0. Then, the number of broken "bonds" of the ith particle in the non-local influence domain is counted, and the damage coefficient Df is constructed to quantify describe the damage degree of particles. The damage coefficient is defined as

$$D_{f} = N_{{{\text{damaged}}\;{\text{bonds}}}} /N_{{{\text{total}}\;{\text{bonds}}}} ,$$
(45)

where \(N_{{{\text{damaged}}\;{\text{bonds}}}}\) is the number of damaged bonds of any particle in the influence domain;\(N_{{{\text{total}}\;{\text{bonds}}}}\) is the total number of virtual bonds of any particle in the influence domain.

Fig. 11
figure 11

The law of linear elasticity used in the numerical model

Full size image

It is well known that the accuracy of the SPH method is closely related to particles distribution, Kernel function selection, and smoothing length evolution. It is obvious from the definition of immediate neighborhood, the kernel may not be always zero at cut-off boundary or if the kernel support is not entirely contained within the problem domain. In this case, different approaches have been proposed to improve the consistency and accuracy of the SPH method (Liu et al. 1995; Shao et al. 2012). In this paper, to avoid the discontinuity of the kernel function of the particles near the crack caused by the fracture of virtual bonds, a kernel gradient correction (KGC) technique is applied to improve the approximation accuracy with a correction included when computing the gradients of the kernel as Chen et al. (1999)

$$\nabla_{i}^{C} W_{ij,\beta } = L(r_{i} )\nabla_{i} W_{ij,\beta } ,$$
(46)
$$L(r_{i} ){ = } - \left( {\sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left( \begin{gathered} x_{ij} \frac{{\partial W_{ij} }}{{\partial x_{i} }}\;\;\;x_{ij} \frac{{\partial W_{ij} }}{{\partial y_{i} }} \hfill \\ y_{ij} \frac{{\partial W_{ij} }}{{\partial x_{i} }}\;\;\;y_{ij} \frac{{\partial W_{ij} }}{{\partial y_{i} }} \hfill \\ \end{gathered} \right)} } \right)^{ - 1} ,$$
(47)

where \(x_{ij} = x_{i} - x_{j}\), \(y_{ij} = y_{i} - y_{j}\),\(W_{ij,\beta } = \partial W(x_{i} - x_{j} ,h)/\partial {\varvec{x}}_{i}^{\beta }\).

Ultimately, considering the damage-thermo-mechanical coupling effect, the TLF_SPH momentum equation of the ith particle in the non-local influence domain can finally be discretized into the following form:

$$\frac{{{\text{d}}(v_{i}^{\alpha } )^{\Theta } }}{{{\text{d}}t}} = \sum\limits_{{j \in \Re_{in} }} {f \cdot m_{j} \left( {\frac{{{\varvec{P}}_{i}^{\alpha \beta } }}{{\rho_{0i}^{2} }} + \frac{{{\varvec{P}}_{j}^{\alpha \beta } }}{{\rho_{0j}^{2} }} + \Pi_{ij} } \right)\frac{{\partial^{C} W_{ij} }}{{\partial x_{i}^{\beta } }}} + \frac{1}{{\rho_{0i} }}\sum\limits_{{j \in \Re_{in} }} {f \cdot \frac{{m_{j} }}{{\rho_{0j} }}\left( {f(x_{i} - x_{j} ,\Theta ,t) - f(x_{j} - x_{i} ,\Theta ,t)} \right)W_{ij} } + \sum\limits_{{j \in \Re_{out} }} {\frac{{F_{i}^{\alpha } }}{{m_{i} }}} + b^{\alpha } .$$
(48)

To more clearly describe the implementation strategy of the thermo-mechanical-damage coupling model bond-based TLF_SPH, the calculation flowchart of TLF_SPH under thermo-mechanical coupling conditions is given in Fig. 12.

Fig. 12
figure 12

The calculation flowchart of TLF_SPH under thermo-mechanical coupling conditions

Full size image

5 Numerical Results and Discussion

In this section, a numerical example is used to prove the stability and accuracy of the particle penetration algorithm in the TLF_SPH model, so as to provide strong support for the successful embedding of the later thermo-mechanical coupling model. To study the fracture modes of rock specimens under different thermodynamic conditions, Cruz and Gillen (1980), Golterman (1995), and Zhou et al. (2001) conducted laboratory experiments to study the thermal fracture process of granite specimens with embedded materials with different thermal expansion coefficients placed in the center of borehole. In this paper, two examples are used to verify the effectiveness of the thermo-mechanical coupling model considering the frictional contact between the contact surface and particles in predicting the crack initiation and propagation modes under thermodynamic conditions. The numerical results obtained are more consistent with the above experimental results.

5.1 Frictional Sliding Along a Slope

The numerical model is a square sample of 0.1 m × 0.1 m. The Young's modulus of the sample is 10 MPa, the Poisson's ratio is 0.2, and the density is 1000 kg/m3. The four sides of the specimen are in contact with rigid surface. Among the four rigid surfaces from B1 to B4, only B4 is rough, with a friction coefficient of 0.3, and the remaining three rigid surfaces are smooth, as shown in Fig. 13. When B1 moves vertically downward at speed v1, the sample undergoes uniaxial unconfined compression. To reduce the stress oscillation in the specimen, v1 first linearly increases from 0 m/s to 1.0 × 10–2 m/s in the initial 0.2 s, and then, B1 moves vertically downward at a constant speed of 1.0 × 10–2 m/s. After 0.6 s, v1 uniformly decreases from 1.0 × 10–2 m/s to 0 at 1.0 s, as shown in Fig. 14. Then, B4 moves to the left at the horizontal velocity of v2 with an acceleration of 5.0 × 10–2 m/s until the horizontal velocity increases to 1.0 × 10–2 m/s at 1.2 s and v2 remains unchanged. Therefore, there is a slip between the sample and B4, and a friction effect is generated during the sliding process. This paper uses 100 uniformly distributed particles to simulate the frictional contact problem. Each particle has a mass of 0.1 kg. In addition, it is assumed that the sample is a linear elastic material to compare the numerical results with the analytical solution.

Fig. 13
figure 13

Numerical model description

Full size image
Fig. 14
figure 14

The velocity of rigid surface

Full size image

The advantage of this improved algorithm, proposed by Wang and Chan (2014), is that it can handle the frictional contact problem in a simple and accurate way. However, the numerical results are overly dependent on the selection of penalty factors \(\eta\), and the value of \(\eta\) is difficult to be consistent in different cases, as shown in Fig. 15a. In addition, under the framework of general particle dynamics (GPD), Bi and Zhou (2017) have carried out a numerical simulation of dynamic friction function in the process of rock rupture. This contact algorithm carried out a flexible calculation of the contact force of any crack surface, but the stability of numerical result is too poor with a large frictional fluctuation amplitude. Therefore, it is difficult to accurately describe the friction behavior of particle contact, as shown in Fig. 15b.

Fig.15
figure 15

The magnitude of contact force acting on the B4 rigid surface: a vertical stress; b frictional force

Full size image

The vertical stress and frictional force of B4 surface are given in Fig. 15a, b, respectively. It can be seen from Fig. 15a that with the increase of the penalty factor \(\eta\), the numerical precision of SPH contact algorithm first increases and then decreases. When \(\eta\) = 0.82, the numerical accuracy is the highest, which is basically consistent with the analytical solution. The TLF_SPH contact algorithm proposed in this paper modifies the normal contact force function in the SPH contact algorithm. In particular, the algorithm removes the penalty factor term \((1 - \eta )\), and its numerical accuracy and stability are obviously improved, and the numerical results are in better agreement with the analytical solutions, as shown in Fig. 15.

The friction and horizontal velocity distribution of the particles at the bottom of the sample are shown in Fig. 16. In the initial stage of calculation, the particles at the bottom of the sample gradually moves to the left under the push of static friction, of which the contact force shows a relatively obvious gradient growth from right to left. With the passage of time, the increasing range of contact force of the particles at the bottom of the sample decreases gradually. As the horizontal deformation of the bottom particles continues to increase, the contact force of B2 rigid surface acting on the particles at the bottom of the sample gradually increases, causing the horizontal movement of the bottom particles to be strongly inhibited. When t = 1.4 s, the static friction force of the particles at the bottom of the sample reaches 25 KN, which is close to the sliding friction force, as shown in Fig. 16d. When t = 1.5 s, the contact force of the particles at the bottom of the sample increases sharply, from 25 to 35 KN. It shows that the tangential contact force of the bottom particles has reached the basic condition of sliding friction, and the static friction force acting on the bottom particles of the sample becomes sliding friction, and the sample began to slide relative to the rigid surface of B4.

Fig. 16
figure 16

The friction and velocity distribution of the particles at the bottom of the sample. a–e Friction; f horizontal velocity

Full size image

When t = 1.5 s, it can be seen from Eq. (23) that the friction force of the particles at the bottom of the sample acting on the B2 rigid surface is 27.4 KN, which is in good agreement with the theoretical value of 27.8 KN of sliding friction, as shown in Fig. 15b. In addition, it can be seen from Fig. 16f that when t = 1.5 s, the movement of the particles at the bottom of the sample has stabilized with the same speed as the rigid surface of B4. After that, only dynamic friction occurred between the B4 rigid surface and the sample.

5.2 Rock Thermal Fracture Mode Without Considering the Effect of Frictional Contact

The rock thermal–mechanical coupling geometric model contains an outer cylinder with a radius of R and an inner disc with a radius of r. The outer cylinder and inner disc are composed of matrix material and embedded material, respectively, as shown in Fig. 17. The size and mechanical parameters of this numerical rock sample are basically consistent with those of used by Tang (2006) in the numerical simulation calculation, as shown in Table 1.

Fig. 17
figure 17

Geometric model for thermal–mechanical coupling calculation of rock disc

Full size image
Table 1 Thermal–mechanical coupling numerical calculation parameters of rock sample
Full size table

In present numerical model, the rock disc is discretized into 9059 particles with the particle spacing \(\Delta x\) = 1.0 mm and the radius of influence domain \(\delta\) = 3.015 mm. The initial temperature of the model is set to 0 °C, and the first type of temperature boundary condition is adopted to uniformly heat up the whole model. That is, the temperature increases by 0.02 °C for each calculation step until the temperature of the model rises to 260 °C. To make the simulation calculation result closer to the real indoor experiment, the Weibull distribution function is used to randomly assign the compressive strength of rock particles in the model to describe the non-uniform characteristics of the compressive strength of real rock samples (Bi et al. 2016, 2017; Zhou et al. 2015). The probability density function of Weibull distribution used in this paper is (Weibull 1951)

$$W(x) = \frac{\omega }{{\lambda_{0} }}\left( {\frac{\lambda }{{\lambda_{0} }}} \right)^{\omega - 1} \exp \left[ { - \left( {\frac{\lambda }{{\lambda_{0} }}} \right)^{\omega } } \right],$$
(49)

where \(\omega\) is the homogeneity of the material, and the smaller the value of \(\omega\), the higher the dispersion of the mechanical properties of particles;\(\lambda\) is the mechanical parameter of the particle;\(\lambda_{0}\) is the expected value. In this numerical model, the non-uniformity index \(\omega\) = 10, as shown in Fig. 18.

Fig. 18
figure 18

The uniaxial compressive strength distribution of the particles in the numerical model (unit: Pa)

Full size image

Figure 19 shows the thermal crack evolution process of the disc under the thermal and mechanical coupling when the thermal expansion coefficient of the embedded material is greater than that of the matrix material. As the temperature increases, the embedded material is under hydrostatic pressure. Under the expansion and extrusion of the embedded material, the matrix material is in the state of compressive stress along the radial direction and tensile stress along the hoop direction.

Fig. 19
figure 19

The damage evolution process of matrix particles at different temperatures under thermal mechanical coupling without considering frictional contact: a damage; b horizontal velocity; c vertical velocity

Full size image

When the temperature rises to 120 °C, micro-cracks begin to appear in the inner ring of the matrix, and a small amount of macro-cracks appear at the upper end of the inner ring. The propagation speed of the particles near the radial cracks at the upper and lower ends of the inner ring is obviously higher than that near the radial cracks at the left and right ends, as shown in Fig. 19a1–c1. When the temperature rises to 160 °C, the cracks propagate rapidly along the radial direction of the matrix, and macro-cracks appear at the upper, lower, left, and right ends of the inner ring. The number of macroscopic cracks at the left and right ends of the inner ring is relatively large with a relatively fast propagation speed, as shown in Fig. 19a2–c2. As time goes on, the macro-cracks continue to propagate along the radial direction toward the outer boundary of the matrix material, and the number of micro-cracks increases slowly. When the temperature rises to 230 °C, the number of micro-cracks increases sharply, and three obvious macroscopic radial cracks are found at the upper and lower ends and left end of the inner ring expand into three obvious macroscopic radial cracks, while no obvious propagation phenomenon is found at the right end of the inner ring.

As shown in Fig. 19a4, when the temperature rises to 260 °C, the strain energy stored in the matrix in the early stage is suddenly released, and the radial macroscopic crack growth speed at the upper and lower ends and the left end of the inner ring of the matrix increases. The macroscopic cracks penetrate radially outwards to the boundary of the matrix material along the radial direction, which eventually leads to thermal cracking. However, the horizontal macroscopic cracks at the right end of the inner ring of the matrix did not expand obviously. This phenomenon is roughly consistent with the previous experimental observations, which is determined by the temperature gradient cracking mechanism of anisotropic brittle rock material (Golterman 1995; Zhou et al. 2001). As shown in Fig. 19c4, the vertical velocity of the crack at the upper end of the inner ring is concentrated, which is caused by the asymmetry of the horizontal macro-radial crack propagation. In addition, the radial macroscopic tensile cracks indicate that the strong tensile stress of the inner ring of the matrix along the hoop direction is the driving force for the tensile failure of the material (Ali and Bradshaw 2011), as shown in Fig. 20.

Fig. 20
figure 20

The previous experimental observations by Tang et al. (2006)

Full size image

To further verify the reliability of the thermal–mechanical coupling algorithm, the numerical calculation results of the particle stress field are compared with theoretical data, as shown in Fig. 21. It can be seen from Fig. 21 that the numerical solution of the model stress field is in good agreement with the theoretical value.

Fig. 21
figure 21

Comparison between numerical results and theoretical solutions of thermal stress

Full size image

5.3 Rock Thermal Fracture Mode Considering Frictional Contact Effect

The initiation of micro-cracks is caused by the relative motion between two adjacent rock particles. The displacement mode between two adjacent particles can accurately describe the propagation of rock cracks. Combined with the previous experimental observations, the displacement modes that may occur tensile failure between adjacent particles are determined to be two types, namely, T-type displacement and X-type displacement. As shown in Fig. 22, the line segment with arrows represents the displacement vector of rock particles. It should be noted that the direction along the two adjacent particles is defined as the normal direction, and the direction perpendicular to the line connecting the two adjacent particles is the hoop direction.

Fig. 22
figure 22

Comparison between numerical results and theoretical solutions of thermal stress

Full size image

T-type displacement mode: There is a relative displacement along the normal direction between two adjacent particles, and there is no relative displacement along the hoop direction. According to the direction of normal displacement vector of adjacent particles, T-type displacement is divided into T I-type displacement with opposite normal displacement vector direction and T II-type displacement with same normal displacement vector direction, as shown in Fig. 22a, b. This displacement mode is mainly tensile failure, which promotes the initiation of micro-cracks and the expansion of macro-cracks in rock mass.

X-type displacement mode: There is not only a relative displacement in the hoop direction between two adjacent particles, but also a relative displacement in the normal direction. According to the direction of normal displacement vector and tangential displacement vector of adjacent particles, X-type displacement is divided into X I-type displacement, X II-type displacement, and X III-type displacement, as shown in Fig. 22c–e. This displacement mode is mainly tension–shear failure. Driven by this displacement mode, both tension failure and shear failure can occur between two adjacent particles, forming tension and shear cracks.

For the second sample, the material geometry, thermodynamic parameters, and heating process are exactly the same as those of the first sample. The only difference is that the second sample considers the frictional contact between the embedded particles and the matrix particles. When the thermal expansion coefficient of the embedded particles is greater than that of the matrix particles, with the increase of temperature, the matrix particles are subjected to the expansion and extrusion of the embedded particles, so there will be a frictional contact effect between the contact surfaces of heterogeneous particles.

Figure 23 shows the damage evolution process of the matrix particles at different temperatures under the thermal and mechanical coupling considering frictional contact. Before the temperature rises to 160 °C, the initiation of micro-cracks and the growth of macroscopic cracks in the inner ring of the matrix are basically the same as those without considering the frictional contact. When the temperature rises to 230 °C, the propagation of the radial macroscopic cracks at the left end of the inner ring of the matrix is significantly inhibited by frictional contact, and the length of the macro crack is obviously shorter than that without considering the frictional contact, as shown in Figs. 19a3 and 23a3. However, the propagation of horizontal macroscopic cracks at the right end of the inner ring is promoted by frictional contact. This is because the strain energy stored in the matrix at this temperature cannot be completely released from the left end of the inner ring, and the remaining strain energy is transferred to the right end of the inner ring along the horizontal direction for partial release.

Fig. 23
figure 23

The damage evolution process of matrix particles at different temperatures under thermal mechanical coupling considering frictional contact: a damage; b horizontal displacement; c vertical displacement

Full size image

When the temperature rises to 260 °C, the strain energy stored in the matrix is completely released, and the radial macroscopic cracks at the upper and lower ends of the inner ring of the matrix rapidly propagate and penetrate to the boundary of the matrix material along the radial direction, while the macro-cracks at the left and right ends of the inner ring of the matrix no longer propagate. The macroscopic thermal crack propagation mode under this algorithm and that without considering the frictional contact are compared with the previous experimental observations (Tang et al. 2006). The results show that the thermal crack propagation mode considering the frictional contact effect is more consistent with the experimental observations, and the propagation mode of thermal cracks is smoother, as shown in Figs. 19a4, 20 and 23a4.

In addition, it can be seen from Fig. 23b, c that the displacement mode near the matrix crack is TI type displacement, as shown in Fig. 22a. Driven by this displacement field, the matrix particles are mainly tensile failure, forming tensile micro-cracks, and macroscopic cracks. Therefore, the thermal fracture mode of the rock disc is tensile failure along the hoop direction, with the thermal expansion coefficient of the matrix material smaller than that of the embedded material.

At the end of this section, the effect of the thermal expansion coefficient on the rock thermal fracture mode is discussed. In the present model, the thermal expansion coefficient of matrix material and the thermal expansion coefficient of embedded material in this example are taken as 1.5 × 10–5 and 1.0 × 10–5, respectively. The boundary conditions and other thermodynamic parameters of the model are the same as before, as shown in Table 1.

The numerical and experimental results of rock thermal fracture are shown in Fig. 24. It can be seen from Fig. 24a, b that the displacement of the matrix particles at the material interface is much larger than that of the embedded particles at the material interface, with the same displacement vector direction. It can be seen that the displacement mode near the circumferential crack belongs to the T II-type displacement, as shown in Fig. 22b. During the entire thermal cracking process, the matrix particles move outward along the radial direction, and the radial strong tensile stress at the material interface is the driving force. The matrix is in a state of tensile stress along the radial direction and is in a state of compressive stress along the hoop direction. Therefore, the thermal fracture mode of the rock disc is tensile failure along the hoop direction, with the thermal expansion coefficient of the matrix material greater than that of the embedded material. Moreover, numerical simulation results are in good agreement with the previous experimental observations (Tang et al. 2006), as shown in Fig. 24c, d.

Fig. 24
figure 24

Numerical and experimental results of rock thermal fracture: a horizontal displacement at 90 °C; b vertical displacement at 90 °C; c damage at 200 °C; d the previous experimental observations by Tang et al. (2006)

Full size image

6 Conclusions

In this paper, under the framework of smooth particle hydrodynamics based on total Lagrangian formula (TLF_SPH), a new thermal–mechanical coupling numerical algorithm considering frictional contact is proposed. In the TLF-SPH program, the force between the interacting particles is transmitted through virtual bonds. The complete virtual bonds can withstand the tensile and compressive stress, shear stress, and frictional contact force between the interacting particles. According to Hoek–Brown strength criterion, the fracture of virtual bonds between particles is determined, and the fractured virtual bonds can only withstand the compressive stress and frictional contact force between the interacting particles.

The shear slip numerical tests of soil samples show that the calculation results of TLF_SPH contact algorithm are more stable and accurate than those of traditional SPH contact algorithm, which are in good agreement with the theoretical solution. The contact algorithm proposed in this paper can better simulate the frictional contact behavior of specimen during shearing and sliding, and fully reveal the frictional contact mechanism between the object and the contact surface. To further strengthen the connection of TLF_SPH and engineering practice, it is necessary to extend the frictional contact algorithm to more general situations, such as efficiently and accurately simulating geotechnical problems such as static pressure piles, shield tunnels, and seismic landslides.

Several examples are used to verify the effectiveness of the proposed thermal cracking algorithm, and the influence of frictional contact on the propagation mode of rock thermal cracks is discussed. For sample 1, the thermal expansion coefficient of the matrix material is smaller than that of the embedded material. The matrix material is in a state of tensile stress along the hoop direction and compressive stress along the radial direction. The displacement mode near the radial macroscopic cracks of the matrix is T I-type, and the strong tensile stress of the matrix along the hoop direction is the driving force for tensile failure. In addition, the numerical results of thermal stress are in good agreement with theoretical data. For sample 2, on the basis of sample 1, the effect of frictional contact on the thermal cracking of the rock disc is considered. Numerical results show that the propagation mode of rock thermal cracks considering frictional contact is smoother, and the propagation path of macroscopic cracks is in better agreement with the previous experimental observations. For sample 3, the thermal expansion coefficient of the matrix material is greater than that of the embedded material. The matrix material is in a state of tensile stress along the radial direction and compressive stress along the hoop direction. The displacement mode of the matrix near the circumferential macroscopic cracks is T II-type, and the strong tensile stress of the matrix along the radial direction is the driving force for tensile failure.