1 Introduction

Numerical modelling is essential for studying the fundamental processes occurring in geological bodies and for geotechnical engineering design. Generally, there are mainly three categories of numerical modelling methods in geomechanics (Jing 2003): (1) continuum-based methods, including finite element method (FEM) (Zienkiewicz and Taylor 2000), finite difference method (FDM) (Perrone and Kao 1975), boundary element methods (BEM) (Beskos 1987, 1997); (2) discontinuum-based methods, including the discrete element method (DEM) (Cundall 1971), DDA (Shi 1988); and (3) hybrid discontinuum–continuum methods, including the hybrid finite discrete element method (FDEM) (Munjiza 2004) and the numerical manifold method (NMM) (Shi 1997). Geomechanics studies alway involve various discontinuities, such as joints, faults, weak intercalated layer, and the sliding along discontinuities results in the instability of geological bodies (Chen et al. 2017; Jiang and Zhou 2017). Therefore, the latter two categories of numerical methods have attracted much attention, especially with the increasing computational power. However, the treatment of contact interactions between bodies is still one of the most important and challenging tasks for these numerical methods (Jing 2003).

As the typical discontinuum-based methods, all contacts of UDEC (Itasca Consulting Group Inc. 2013) and DDA can be classified into three types (Jing 2003): the corner-to-corner contact, the corner-to-edge contact and the edge-to-edge contact. Among them, the corner-to-edge contact is the fundamental contact, as the other two contact types can be converted to this type. Moreover, the penalty method is adopted to calculate contact force, and Coulomb’s friction law is used to determine the tangential contact states (He and Ma 2010). For UDEC, the contact state is determined at the end of each time step. On the other hand, the contact state in DDA (the implicit method) is determined through open–close iterations, namely, adding or removing contact springs repeatedly in each time step, which may not always convergent (Doolin and Sitar 2004). Furthermore, the simulation results are sensitive to the stiffness of contact springs which requires iterative calibration (Tsesarsky and Hatzor 2006). Despite those difficulties in solving contact problems when using implicit methods, many improvements to the contact algorithm have been established (Shi. 2015; Bao and Zhao 2010; Cai et al. 2000). To overcome the shortcomings of the penalty method, the augmented Lagrange multiplier method (Bao et al. 2014) and the Lagrange multiplier method (Cai et al. 2000) were proposed. Nevertheless, the open-close iteration is still needed to reach the correct contact state. Besides, rank deficiency of the Jaccobian matrix (Jiang and Zheng 2011) may lead to a breakdown of numerical simulation.

In many cases of geotechnical engineering applications, the transition from continua to discontinuum need to be studied, namely, the process of failure, fracture or fragmentation of a solid. The FDEM, proposed by Munjiza (2004), is one of the more powerful and widely applied tools to model this problem, especially for problem related to rock fracturing (Rougier et al. 2014; Grasselli et al. 2015; Lisjak and Grasselli 2014; Yan et al. 2016; Yan and Zheng 2016). The FDEM is based on the discretization of the modeling domain with triangular elements together with four-noded cohesive elements embedded between the edges of all adjacent triangle pairs. For the contact algorithm, a potential function method is used and allows contacting triangular elements to penetrate into each other, generating distributed contact forces. However, since the contact algorithm is proposed based on the contacting triangular blocks, it is not suitable to be extended to other numerical methods (Lisjak et al. 2016).

The numerical manifold method (NMM), which was initially proposed by Shi (1992a, b), is another continuum–discontinuum method for geotechnical engineering. One of the main attractive advantages of NMM over other numerical methods is its ability to solve continuous and discontinuous problems in a unified approach without inserting virtual cracks. Over the past few decades, NMM has been extensively studied and applied to various fields, such as anchored rock mass (Wei et al. 2017), progressive failure analyses of rock slopes (Ning et al. 2011; An et al. 2014; Wong and Wu 2014), seepage analysis (Jiang et al. 2010; Zheng et al. 2014; Hu et al. 2015), transient heat conduction of rock material (He et al. 2017; Zhang et al. 2018), large deformation analysis (Fan et al. 2016; Wei and Jiang 2017) and seismic response analysis of geomechanics problems (Wei et al. 2018). The contact algorithm of NMM was inherited from the DDA method, thus, it confronts the abovementioned difficulties. In an effort to deal with the contact problems of NMM, Yang and Zheng (2016) proposed a direct approach for contact problem to avoid the introduction of penalty parameters. However, this approach inevitably leads to solving a nonsymmetric system. Zheng and Jiang (2009) and Zheng and Li (2015) removed the penalty parameter and the open-close iteration by considering discontinuous system as a nonlinear mixed complementarity problem in which the contact conditions are expressed by the complementarity equations. Due to the adoption of contact forces as the independent variables and rank deficiency of the Jacobi matrix, the solution would become inefficient. By taking the contact forces as the basic variables, Zheng et al. (2016) proposed a dual form of DDA, called DDA-d, in which the displacements can be expressed in terms of contact force. This improvement discards the artificial springs and has an efficiency comparable with DDA. However, when this improvement is extended to NMM, the solution efficiency would be sacrificed considerably because a great deal of computation time has to be spent on the inverse of numerous matrices of large dimensions (Yang and Zheng 2016).

In the present study, a new contact formulation for large frictional sliding is proposed and implemented in the explicit NMM. In the proposed contact algorithm, the contact force is calculated based on the overlapped contact area without determination of contact types during the simulation. To avoid the difficulties caused by open–close iterations, the explicit method is adopted. Although this new contact algorithm is implemented in the context of NMM, it could undoubtedly be employed by other numerical methods, such as FEM, DEM, DDA. The analysis results of some interesting and challenging examples suggest that the proposed algorithm to simulate contact problems involving large frictional sliding is promising.

2 Fundamental of Explicit NMM

2.1 Problem Description

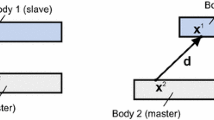
Figure 1 shows the deformed configuration of two 2D bodies in contact at a given time \(t_{n}\). The two bodies are denoted as master \(\varOmega^{(1),n}\) and slave \(\varOmega^{(2),n}\). Note that we use super index n for variables defined at time \(t_{n}\). Each body (i) has a boundary with prescribed displacements \(\varGamma_{\text{u}}^{\left( i \right)}\) and tractions \(\varGamma_{\sigma }^{\left( i \right)}\). There is also a portion of the boundary \(\varGamma_{\text{c}}^{\left( i \right)}\) where the body is in contact, and \(\varGamma_{\text{c}}^{\left( 1 \right)}\) and \(\varGamma_{\text{c}}^{\left( 2 \right)}\) denote the contact portion on the slave and master surfaces, respectively.

Fig. 1
figure 1

Deformed configuration of two contacting bodies and the definition of penetration \(g_{\text{N}}\)

Full size image

The governing equations formulated with respect to the current configuration in combination with the displacement and traction boundary conditions define the boundary value problem:

$${\mathbf{\nabla }} \cdot {\varvec{\upsigma}}^{\left( i \right)} + \rho^{\left( i \right)} {\mathbf{b}}^{\left( i \right)} = \rho^{\left( i \right)} {\mathbf{\ddot{u}}}^{\left( i \right)} \;{\text{in}}\;\varOmega^{\left( i \right)}$$
(1)
$$\left( {\frac{{D\widehat{{\varvec{\upsigma}}}}}{Dt}} \right)^{\left( i \right)} = {\mathbf{D}}^{\left( i \right)} { \sim }\widehat{{{\dot{\mathbf{\varepsilon }}}}}^{\left( i \right)}$$
(2)
$${\dot{\mathbf{\varepsilon }}}^{\left( i \right)} = {\text{sym}}\left( {{\mathbf{\nabla }} \cdot {\dot{\mathbf{u}}}^{\left( i \right)} } \right)$$
(3)
$${\mathbf{u}}^{\left( i \right)} = \overline{{\mathbf{u}}}^{\left( i \right)} \;{\text{on}}\;\varGamma_{\text{u}}^{\left( i \right)}$$
(4)
$${\mathbf{t}}^{\left( i \right)} = \overline{{\mathbf{t}}}^{\left( i \right)} \;{\text{on}}\;\varGamma_{t}^{\left( i \right)}$$
(5)
$${\mathbf{t}}_{\text{c}}^{\left( 1 \right)} = - \, {\mathbf{t}}_{\text{c}}^{\left( 2 \right)} \;{\text{on}}\;\varGamma_{\text{c}}^{\left( i \right)}$$
(6)

where, \({\mathbf{\nabla }}\) is the gradient operator, \({\varvec{\upsigma}}\) is the Cauchy stress, \(\rho\) is the density of material, \({\mathbf{b}}\) is the body force vector, \({\mathbf{u}}\), \({\dot{\mathbf{u}}}\), \({\mathbf{\ddot{u}}}\) are the displacement, velocity and acceleration vectors. \({\mathbf{D}}\) is the constitutive equation and the linear elastic material is assumed in this study. \({\dot{\mathbf{\varepsilon }}}\) is the rate of deformation.\(\overline{{\mathbf{u}}}^{\left( i \right)}\) and \(\overline{{\mathbf{t}}}^{\left( i \right)}\) are the given displacement and traction vectors, respectively. \({\mathbf{t}}_{\text{c}}^{\left( i \right)}\) is the contact traction Prescribed values marked with a hat (\(\widehat{ \cdot }\)) in Eq. (2) are corotational values in a coordinate system that rotates with the material. In fact, the NMM was mainly applied to solve problems in rock mechanics and rock engineering field, which are often known as small-strain, large-rotation problem. Therefore, the corotational approach is suitable.

In the corotational approach, the corotational Cauchy stress \(\widehat{{\varvec{\upsigma}}}\) and the corotational rate-of-deformation \(\widehat{{{\dot{\mathbf{\varepsilon }}}}}\) are obtained by

$$\widehat{{{{\varvec{\upsigma }}}}} = {\mathbf{R}}^{\text{T}} \cdot {\varvec{\upsigma}} \cdot {\mathbf{R}},\;\widehat{{{\dot{\mathbf{\varepsilon }}}}} = {\mathbf{R}}^{\text{T}} \cdot {\dot{\mathbf{\varepsilon }}} \cdot {\mathbf{R}}$$
(7)

where R is the rotation matrix. Note that the corotational Cauchy stress tensor is the same tensor as the Cauchy stress, it is just expressed in terms of components in a coordinate system that rotates with the material.

2.2 Approximation of NMM

In the NMM, the approximation to the problem domain is constructed using a dual cover system, i.e. the mathematical cover (MC) and physical cover (PC), which makes the NMM capable of solving continuous and discontinuous problems in a unified framework. A distinct feature of the NMM, which differentiate it from other numerical methods, is that the MC is not required to be compatible with the external boundaries and the possible internal discontinuities of the problem domain. As illustrated in Fig. 2, the MC is composed of a set of overlapped small patches. Each small patch, denoted by MI (I = 1, 2, 3), can span discontinues and the boundary of problem domain. The union of these small patches completely covers the problem domain. In addition, the shape of the MC patch can be arbitrary, though the regular polygonal cover is commonly adopted. The intersection of MC patches and problem domain generates the PC patches. Similarly, the PC is the union of PC patches.

Fig. 2
figure 2

Cover system generation procedures

Full size image

Figure 3 presents the process of generating manifold element using the dual cover system in the NMM. The problem domain, denoted as Ω, is covered by three MC patches, i.e. the yellow trapezoid MC patch M1, the red circle MC patch M2 and the blue square MC patch M3. It can be seen from Fig. 1 that the shapes are totally different from each other. The PC patches are generated from the intersection of the problem domain and the MC patches. For example, the intersecting M1 with the problem domain generates \(P_{1}^{1}\). Similarly, the M2 generates \(P_{2}^{1}\) and \(P_{2}^{2}\).and M3 generates \(P_{3}^{1}\) and \(P_{3}^{2}\). Then, those PC patches overlap each other to form the manifold elements. For convenience, a single index i is adopted to denote two indices of the physical patch, namely

$$i\left( {I,j} \right) = \mathop \sum \limits_{l = 1}^{I - 1} m_{l} + j$$
(8)

where, \(m_{l}\) is the number of the physical patches formed in mathematical patch l.

Fig. 3
figure 3

The generation of manifold elements

Full size image

After the generation of the cover system, a local displacement approximation reflecting the local characteristic of the field is defined on each PC patch. Usually, the polynomial functions of PC patch Pi are adopted as the local approximation

$${\mathbf{u}}_{i} \left( {{\mathbf{x}},t} \right) = {\mathbf{a}}^{\text{T}} \left( {\mathbf{x}} \right) \cdot {\mathbf{d}}_{i} \left( t \right)$$
(9)

where, \({\mathbf{d}}_{i}\) is the vector of unknowns to be calculated of Pi, and \({\mathbf{a}}^{\text{T}}\) is the matrix of polynomial base which may be constant, linear- or higher-order terms. The general form of \({\mathbf{a}}^{\text{T}}\) is expressed as

$${\mathbf{a}}^{\text{T}} \left( {\mathbf{x}} \right) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & 0 & x \\ \end{array} } & {\begin{array}{*{20}c} 0 & y & 0 \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {y^{p} } & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } & {\begin{array}{*{20}c} x & 0 & y \\ \end{array} } & {\begin{array}{*{20}c} \cdots & 0 & {y^{p} } \\ \end{array} } \\ \end{array} } \right]$$
(10)

However, high-order terms adopted in NMM may result in linear dependence problem, which have been discussed by An et al.(2011), Ghasemzadeh et al. (2015), and Tian and Wen (2015). Therefore, the 0th order polynomial is selected as the local approximation for the PC patches in this study.

Then, the local approximation for the PC patches is pasted together through the weight functions \(w_{i} \left( {\mathbf{x}} \right)\) to obtain the global approximation for one manifold element E as follow:

$${\mathbf{u}}^{h} \left( {{\mathbf{x}},t} \right) = \mathop \sum \limits_{i = 1}^{n} w_{i} \left( {\mathbf{x}} \right) \cdot {\mathbf{u}}_{i} \left( {{\mathbf{x}},t} \right) = {\mathbf{Td}}$$
(11)

with

$${\mathbf{T}} = \left[ {\begin{array}{*{20}l} {w_{1} } \hfill & 0 \hfill & {w_{2} } \hfill & 0 \hfill & \cdots \hfill & {w_{n} } \hfill & 0 \hfill \\ 0 \hfill & {w_{1} } \hfill & 0 \hfill & {w_{2} } \hfill & \cdots \hfill & 0 \hfill & {w_{n} } \hfill \\ \end{array} } \right]$$
(12)
$${\mathbf{d}} = \left[ {\begin{array}{*{20}c} {{\mathbf{d}}_{1} } & {{\mathbf{d}}_{2} } & {\begin{array}{*{20}c} \cdots & {{\mathbf{d}}_{n} } \\ \end{array} } \\ \end{array} } \right]^{\text{T}} ,\;{\mathbf{d}}_{i} = \left[ {\begin{array}{*{20}c} {d_{i1} } & {d_{i2} } \\ \end{array} } \right]$$
(13)

where n is the number of physical covers sharing manifold element E.

The weight function \(w_{i} \left( {\mathbf{x}} \right)\) of physical patch Pi is inherited from that of the corresponding MC patches MI on which the weight function \(w_{I} \left( {\mathbf{x}} \right)\) satisfy that

$$w_{\text{I}} \left( {\mathbf{x}} \right) > 0\quad {\text{for}}\;{\mathbf{x}} \in M_{I}$$
(14a)
$$w_{\text{I}} \left( {\mathbf{x}} \right) = 0\quad {\text{for}}\;{\mathbf{x}} \notin M_{I}$$
(14b)
$$\mathop \sum \limits_{I = 1}^{{N_{\text{M}} }} w_{\text{I}} \left( {\mathbf{x}} \right) = 1\quad {\text{for}}\;{\mathbf{x}} \in M_{I}$$
(14c)

where Eqs. (14a) and (14b) indicate that the weight function has non-zero values only on its corresponding mathematical patches, and zero elsewhere; while Eq. (14c) is the partition of unity property to assure a conforming approximation. Obviously, The PU function depends on the shape of the MC patches.

In this study, the regular hexagonal MC is adopted to construct the PU function and each manifold element is shared by three hexagonal MC patches. Moreover, the regular hexagon is made of six regular triangles in which the \(w_{\text{I}} \left( {\mathbf{x}} \right)\) in Eqs. (14a–14c) is identical to the shape function of three-node triangular finite element.

2.3 Iteration Equations of Explicit NMM

In this section, the iteration equations of explicit NMM is derived. In the NMM, finite-dimensional subspaces, \(V^{\text{h}} \subset V\) and \(V_{0}^{\text{h}} \subset V_{0}\), are used as the approximating trial and test space. Using the Galerkin method, the weak form for momentum Eq. (1) can be stated as:

Find \({\mathbf{u}}^{\text{h}} \in {\text{V}}^{\text{h}} \subset {\text{V}}\) such that

$$\begin{aligned} & \int\limits_{{\varOmega^{\text{e}} }} {\delta {\varvec{\upvarepsilon}}^{\varvec{T}} \left( {{\mathbf{u}}^{\text{h}} } \right)\sigma \left( {{\mathbf{u}}^{\text{h}} } \right){\text{d}}\varOmega } + \int\limits_{{\varOmega^{\text{e}} }} {\left( {\delta {\mathbf{u}}^{\text{h}} } \right)^{\text{T}} \rho {\mathbf{\ddot{u}}}^{\text{h}} {\text{d}}\varOmega } + {\varvec{\uplambda}}\int\limits_{{\varGamma_{\text{u}}^{\text{e}} }} {\left( {\delta {\mathbf{u}}^{\text{h}} } \right)^{\text{T}} \left( {{\mathbf{u}}^{\text{h}} - \overline{{\mathbf{u}}} } \right){\text{d}}\varGamma } \\ & \quad = \int\limits_{{\varGamma_{\text{t}}^{\text{e}} }} {\left( {\delta {\mathbf{u}}^{\text{h}} } \right)^{\text{T}} \overline{{\mathbf{t}}} {\text{d}}\varGamma } + \int\limits_{{\varOmega^{\text{e}} }} {\left( {\delta {\mathbf{u}}^{\text{h}} } \right)^{\text{T}} {\mathbf{b}}{\text{d}}\varGamma } + \int\limits_{{\varGamma_{\text{c}}^{\text{e}} }} {\left( {\delta {\mathbf{u}}^{\text{h}} } \right)^{\text{T}} {\mathbf{t}}_{\text{c}} {\text{d}}\varGamma } \\ \end{aligned}$$
(15)

Considering the arbitrariness of test function \(\delta {\mathbf{u}}^{\text{h}}\), the discrete approximation to the weak form (15), the semidiscrete momentum equations are obtained:

$${\mathbf{M\ddot{d}}} = {\mathbf{f}}$$
(16a)
$${\mathbf{f}} = {\mathbf{f}}_{\text{ext}} + {\mathbf{f}}_{\lambda } + {\mathbf{f}}_{\text{c}} - {\mathbf{f}}_{\text{int}}$$
(16b)

where

$${\mathbf{M}} = \sum\limits_{e = 1}^{{N_{el} }} {\rho \int\limits_{{\varOmega^{e} }} {{\mathbf{T}}_{\varvec{e}}^{\text{T}} {\mathbf{T}}_{e} {\text{d}}\varOmega } }$$
(17)
$${\mathbf{f}}_{\text{int}} = \mathop \sum \limits_{e = 1}^{{N_{el} }} \left( {\int\limits_{{\varOmega^{e} }} {{\mathbf{B}}_{e}^{\text{T}} {\mathbf{DB}}_{e} {\text{d}}\varOmega } + {\varvec{\uplambda}}\int\limits_{{\varGamma_{u}^{e} }} {{\mathbf{T}}_{\varvec{e}}^{\text{T}} {\mathbf{T}}_{e} {\text{d}}\varGamma } } \right)$$
(18)
$${\mathbf{f}}_{\text{ext}} = \mathop \sum \limits_{e = 1}^{{N_{el} }} \left( {\int\limits_{{\varOmega^{e} }} {{\mathbf{T}}_{\varvec{e}}^{\text{T}} {\mathbf{b}}{\text{d}}\varOmega } + \int\limits_{{\varGamma_{t}^{e} }} {{\mathbf{T}}_{\varvec{e}}^{\text{T}} \overline{{\mathbf{t}}} {\text{d}}\varGamma } } \right)$$
(19)
$${\mathbf{f}}_{\lambda } = \mathop \sum \limits_{e = 1}^{{N_{u} }} \left( {{\varvec{\uplambda}}\int\limits_{{\varGamma_{u}^{e} }} {{\mathbf{T}}_{\varvec{e}}^{\text{T}} \overline{{\mathbf{u}}} {\text{d}}\varGamma } } \right)$$
(20)
$${\mathbf{f}}_{\text{c}} = \mathop \sum \limits_{e = 1}^{{N_{c} }} \left( {\int\limits_{{\varGamma_{c}^{e} }} {{\mathbf{T}}_{\varvec{e}}^{\text{T}} {\mathbf{t}}_{c} {\text{d}}\varGamma } } \right)$$
(21)

where \(N_{\text{el}}\) denote the total number of elements. \(N_{\text{u}}\) and \(N_{\text{c}}\) denote the number of elements on the boundary and elements in contact, respectively. \({\mathbf{f}}_{\text{int}}\), \({\mathbf{f}}_{\text{ext}}\), \({\mathbf{f}}_{\lambda }\), \({\mathbf{f}}_{\text{c}}\) are internal nodal force, external nodal force, boundary constraint nodal force and contact nodal forces, respectively. \({\mathbf{B}}_{\varvec{e}}\) is the strain–displacement matrix.

To solve Eqs. (16a, 16b), the explicit time integration scheme is adopted. The major advantage of explicit algorithm for solving contact problems is that in each time step, the bodies are first integrated completely independently as if they were not in contact. This uncoupled update correctly indicates which parts of the body will be in contact at the end of the time step and then the contact conditions are imposed. Therefore, neither linearization nor a Newton solver is needed, so the deleterious effects of discontinuities on Newton solvers are avoided. In other words, there are no iterations when establishing the contact interface. Moreover, the time steps are small because of stability requirements, so the discontinuities due to contact wreak less havoc.

In this study, the central difference formula is adopted and the velocity, acceleration are denoted as

$${\dot{\mathbf{d}}}^{{n + \frac{1}{2}}} = \frac{{\left( {{\mathbf{d}}^{n + 1} - {\mathbf{d}}^{n} } \right)}}{{\Delta t^{{n + \frac{1}{2}}} }}$$
(22)
$${\mathbf{\ddot{d}}}^{n} = \frac{{\left( {{\dot{\mathbf{d}}}^{{n + \frac{1}{2}}} - {\dot{\mathbf{d}}}^{{n - \frac{1}{2}}} } \right)}}{{\Delta t^{n} }}.$$
(23)

We now consider the semidiscrete momentum Eqs. (16a, 16b) at time step n. The equations for updating the nodal velocities and displacements are obtained by substituting Eq. (23) into Eqs. (16a, 16b), namely,

$${\dot{\mathbf{d}}}^{{n + \frac{1}{2}}} = {\dot{\mathbf{d}}}^{{n - \frac{1}{2}}} + \Delta t^{n} {\mathbf{M}}^{ - 1} {\mathbf{f}}^{n}$$
(24)

At any time step n, the displacements \({\mathbf{d}}^{n}\) are known. The nodal forces \({\mathbf{f}}^{n}\) can be determined by sequentially evaluating equations from (16b). Then, the displacements \({\mathbf{d}}^{n + 1}\) at time step n + 1 can be determined by Eq. (22).

3 A New Contact Formulation

There are two aspects to contact in the numerical methods, namely, the contact detection and contact interaction. Contact detection is aimed at detecting couples of blocks or bodies close to each other, i.e. eliminating couples of blocks that far from each other and cannot possibly be in contact. In other words, the role of contact detection is to avoid processing contact interaction when there is no contact. In this study, the algorithm of contact detection is similar to the other numerical (Beskos 1997; Cai et al. 2000; Chen et al. 2017; Cundall 1971) methods and will not be discussed. Therefore, the following sections will focus on the new algorithm of contact interaction. Different from most of numerical method that adopt the concentrated contact force approach, the distributed contact force approach is adopted, and the contact force is calculated directly based on the overlapped area of bodies in contact and the contact states.

3.1 General Description of Contact Interaction

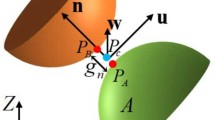
As shown in Fig. 1, The master and the slave bodies overlap each other over area S, boundary by boundary. In order to solve contact interactions, a correspondence between points in the slave and master surfaces must be defined. For every point in slave surface \({\mathbf{x}}^{\left( 2 \right)}\), a corresponding contact point on the master surface \(\overline{{\mathbf{x}}}^{\left( 1 \right)}\) can be obtained as the intersection of the surface \(\varGamma_{\text{c}}^{\left( 1 \right)}\) with the line in the direction of the normal vector \({\mathbf{n}}^{\left( 1 \right)}\), as depicted in Fig. 1. Vector \({\mathbf{n}}^{\left( 1 \right)}\) is the unit normal to the master surface. Therefore, penetration at a given point \({\mathbf{x}}^{\left( 2 \right)}\) on the slave surface into master body can be defined as

$$g_{\text{N}} \left( {{\mathbf{x}}^{(2)} } \right) = \left( {\overline{{\mathbf{x}}}^{(1)} - {\mathbf{x}}^{(2)} } \right) \cdot {\mathbf{n}}^{(1)}$$
(25)

Note that within this definition, the penetration \(g_{\text{N}} \left( {{\mathbf{x}}^{(2)} } \right)\) is negative if the contact is open and positive when there is penetration of the bodies.

When the bodies penetrate each other, there is contact traction \({\mathbf{t}}_{\text{c}}^{\left( i \right)}\) occurs on the contact surfaces \(\varGamma_{\text{c}}^{\left( i \right)}\), which can be separated into normal and tangential components:

$${\mathbf{t}}_{\text{c}}^{\left( i \right)} = {\mathbf{p}}^{\left( i \right)} + {\mathbf{t}}^{\left( i \right)} = p_{\text{N}}^{\left( i \right)} {\mathbf{n}} + t_{\text{T}}^{\left( i \right)} {\mathbf{s}}$$
(26)

where, \(p_{\text{N}}^{\left( i \right)}\) and \(t_{\text{T}}^{\left( i \right)}\) are the normal contact force and tangential contact force acted on \(\varGamma_{\text{c}}^{\left( i \right)}\), respectively.

The contact interface must verify the classical Kuhn–Tucker conditions

$$g_{\text{N}} \le 0,\quad p_{\text{N}} \ge 0,\;p_{\text{N}} g_{\text{N}} = 0$$
(27)

The first term is the impenetrability condition, the second on implies that only compressive interaction is allowed and the third term ensures that if there is contact (\(p_{\text{N}} > 0\), the gap is zero.

In this study, the penalty method is adopted to solve the contact interaction. Therefore, the excessive interpenetration between the two bodies are permitted. Generally, the normal traction of contact force can be defined as a function of the interpenetration. For simplicity, a linear function is adopted to evaluate the normal contact force. For the slave surface \(\varGamma_{\text{c}}^{{\left( {21} \right)}}\), the normal contact force can be expressed as

$$p_{\text{N}} \left( {{\mathbf{x}}^{\left( 2 \right)} } \right) = \alpha_{\text{N}} g_{\text{N}} \left( {{\mathbf{x}}^{\left( 2 \right)} } \right)$$
(28)

where, \(\alpha_{\text{N}}\) is the normal penalty coefficient.

3.2 Discretization of the Contact Problem

3.2.1 Normal Contact Force

Figure 4 shows the bodies in contact which are discretized using two-dimensional mathematical cover. In the discretized bodies, the slave and master contact surfaces are divided into a number of connected segments. The position of a given point \({\mathbf{x}}_{\text{g}}^{\left( 2 \right)}\) in a slave segment \(c_{k}^{\left( 2 \right)}\) is interpolated from the slave vertex k − 1 and k. The corresponding contact point in the master surface \(c_{k}^{\left( 1 \right)}\) is defined by the current position \(\overline{{\mathbf{x}}}_{\text{g}}^{\left( 1 \right)}\). This point is obtained as the intersection of the master segment and the line emanating from the slave point in direction \(\overline{{\mathbf{n}}}_{\text{g}}^{\left( 1 \right)}\). Note that the direction \(\overline{{\mathbf{n}}}_{\text{g}}^{\left( 1 \right)}\) is equal to the unit normal vector \({\mathbf{n}}_{k}^{\left( 1 \right)}\) of the master segment \(c_{k}^{\left( 1 \right)}\).

Fig. 4
figure 4

The discretization of overlapped area for two bodies in contact

Full size image

According to Eq. (25), the penetration of given point \({\mathbf{x}}_{g}^{\left( 2 \right)}\) into the master body can be given as

$$g_{\text{N}} \left( {{\mathbf{x}}_{\text{g}}^{\left( 2 \right)} } \right) = \left( {\overline{{\mathbf{x}}}_{\text{g}}^{\left( 1 \right)} - {\mathbf{x}}_{\text{g}}^{\left( 2 \right)} } \right) \cdot \overline{{\mathbf{n}}}_{\text{g}}^{\left( 1 \right)}$$
(29)

As illustrated in Fig. 4, the overlapped area is divided into several domains according to the number of master segments in contact. The division lines are inner angular bisector at the vertex of master body. As can be seen from Fig. 4 that one slave segment may be divided into several sub segments by the division lines. Using this approach, the penetration \(g_{\text{N}}\) of any point on the slave segment to the master surface can be calculated in the corresponding domain.

One arbitrary domain, as shown in Fig. 5, is selected to demonstrate the procedure to calculate normal contact force. The normal contact force acted on the slave segment \(c_{k}^{\left( 2 \right)}\) is denoted by \({\mathbf{p}}_{k}^{\left( 2 \right)}\) which is in blue in Fig. 5. Accordingly, the distributed normal contact force acted on sub-segment \(c_{k,j}^{\left( 2 \right)}\) is denoted by \({\mathbf{p}}_{k,j}^{\left( 2 \right)}\). The equivalent point load \({\mathbf{P}}_{k,j}^{\left( 2 \right)}\) of \({\mathbf{p}}_{k,j}^{\left( 2 \right)}\) and its point of force application \({\mathbf{x}}_{k,j}^{\left( 2 \right)}\) are calculated by

$${\mathbf{P}}_{k,j}^{\left( 2 \right)} = \frac{{\left( {{}_{1}{\mathbf{p}}_{k,j}^{\left( 2 \right)} + {}_{2}{\mathbf{p}}_{k,j}^{\left( 2 \right)} } \right)}}{2}l_{k,j}^{\left( 2 \right)}$$
(30)
$${\mathbf{x}}_{k,j}^{\left( 2 \right)} = \frac{{{}_{1}{\mathbf{p}}_{k,j}^{\left( 2 \right)} \left( {2{}_{1}{\mathbf{x}}_{k,j}^{\left( 2 \right)} + {}_{2}{\mathbf{x}}_{k,j}^{\left( 2 \right)} } \right) + {}_{2}{\mathbf{p}}_{k,j}^{\left( 2 \right)} \left( {{}_{1}{\mathbf{x}}_{k,j}^{\left( 2 \right)} + 2{}_{2}{\mathbf{x}}_{k,j}^{\left( 2 \right)} } \right)}}{{\left( {{}_{1}{\mathbf{p}}_{k,j}^{\left( 2 \right)} + {}_{2}{\mathbf{p}}_{k,j}^{\left( 2 \right)} } \right)}}$$
(31)
$${}_{1}{\mathbf{p}}_{k,j}^{\left( 2 \right)} = {\mathbf{p}}_{k,j}^{\left( 2 \right)} \left( {{}_{1}\varvec{x}_{k,j}^{\left( 2 \right)} } \right),{}_{2}{\mathbf{p}}_{k,j}^{\left( 2 \right)} = {\mathbf{p}}_{k,j}^{\left( 2 \right)} \left( {{}_{2}{\mathbf{x}}_{k,j}^{\left( 2 \right)} } \right)$$
(32)

where \(l_{k,j}^{\left( 2 \right)}\) is the length of sub segment \(c_{k,j}^{\left( 2 \right)}\). \({}_{1}{\mathbf{x}}_{k,j}^{\left( 2 \right)}\) and \({}_{2}{\mathbf{x}}_{k,j}^{\left( 2 \right)}\) are two ends of sub segment \(c_{k,j}^{\left( 2 \right)}\).\({}_{1}{\mathbf{p}}_{k,j}^{\left( 2 \right)}\) and \({}_{2}{\mathbf{p}}_{k,j}^{\left( 2 \right)} \varvec{ }\) the normal contact force at \({}_{1}{\mathbf{x}}_{k,j}^{\left( 2 \right)}\) and \({}_{2}{\mathbf{x}}_{k,j}^{\left( 2 \right)}\), respectively.

Fig. 5
figure 5

Force diagrams in one typical domain

Full size image

To calculate the normal contact force of master segment \(c_{k}^{\left( 1 \right)}\), the ‘virtual’ distributed force \({\mathbf{p}}_{\text{div}}\) acted on the division lines, which is in red in Fig. 5a, also need to be calculated by the same approach as the slave segments. So is the equivalent point load \({\mathbf{p}}_{\text{div}}\) and its point of the force application \({\mathbf{x}}_{\text{div}}\).

Based on the equilibrium of force and moment of the domain, the equivalent point load \({\mathbf{P}}_{k}^{\left( 1 \right)}\) of normal contact force acted on the master segment and its point of force application \({\mathbf{x}}_{k}^{\left( 1 \right)}\) are obtained (as depicted in Fig. 5b),

$${\mathbf{P}}_{k}^{\left( 1 \right)} = \sum\limits_{j = 1}^{n} {{\mathbf{P}}_{k,j}^{\left( 2 \right)} } + \sum\limits_{j = 1}^{2} {{\mathbf{P}}_{{{\text{div}},j}} }$$
(33)
$${\mathbf{P}}_{k}^{\left( 1 \right)} \times {\mathbf{x}}_{k}^{\left( 1 \right)} = \sum\limits_{j = 1}^{n} {{\mathbf{P}}_{k,j}^{\left( 2 \right)} \times {\mathbf{x}}_{k,j}^{\left( 2 \right)} } + \sum\limits_{j = 1}^{2} {{\mathbf{P}}_{{{\text{div}},j}} \times {\mathbf{x}}_{{{\text{div}},j}} }$$
(34)

where ‘×’ represents the cross product of vectors. n is the number of slave segments or sub-segments of the domain.

It should be noted that \({\mathbf{P}}_{k}^{\left( 1 \right)}\) is obviously not equal to the sum of \({\mathbf{P}}_{k,j}^{\left( 2 \right)}\) in the domain. However, the sum of contact forces \({\mathbf{P}}^{\left( i \right)}\) acted on the bodies in contact are equal (as shown in Fig. 6), namely

$${\mathbf{P}}^{\left( 1 \right)} = - \, {\mathbf{P}}^{\left( 2 \right)}$$
(35)
$${\mathbf{P}}^{\left( 1 \right)} = \sum\limits_{k = 1}^{{N^{\left( 1 \right)} }} {{\mathbf{P}}_{k}^{\left( 1 \right)} } ,\;{\mathbf{P}}^{\left( 2 \right)} = \sum\limits_{k = 1}^{{N^{\left( 2 \right)} }} {\sum\limits_{j = 1}^{n} {{\mathbf{P}}_{k,j}^{\left( 2 \right)} } }$$
(36)

where, \(N^{\left( i \right)}\) is the number of contact segments of body i.

Fig. 6
figure 6

Determination of direction of total equivalent normal contact force

Full size image

3.2.2 Tangential Contact Force

Based on the above derivation, the normal direction \({\mathbf{n}}_{\text{c}}\) of the overlapped contact area can be defined as the unit vector of \({\mathbf{P}}^{\left( 1 \right)}\), as shown in Fig. 6. Correspondingly, the tangential direction \({\mathbf{s}}_{\text{c}}\) of the whole contact area is perpendicular to \({\mathbf{n}}_{\text{c}}\). It should be noted that if any of the two contact surfaces is a straight line, \({\mathbf{n}}_{\text{c}}\) is equal to the normal vector of that contact surface.

In this study, the cumulative tangential displacement \(V^{n}\) of the contact overlapped area at time step n is defined and calculated by

$$V^{n} = V^{n - 1} + \Delta V$$
(37)
$$\begin{aligned} \Delta V & = \int\limits_{{\varGamma_{\text{c}}^{\left( 1 \right)} }} {\Delta v^{\left( 1 \right)} {\text{d}}l} - \int\limits_{{\varGamma_{\text{c}}^{\left( 2 \right)} }} {\Delta v^{\left( 2 \right)} {\text{d}}l} \\ & = \sum\limits_{i = 1}^{{N^{\left( 1 \right)} }} {\frac{{\left( {\Delta v_{i}^{\left( 1 \right)} + \Delta v_{i + 1}^{\left( 1 \right)} } \right)\Delta l_{j}^{\left( 1 \right)} }}{2}} - \sum\limits_{j = 1}^{{N^{\left( 2 \right)} }} {\frac{{\left( {\Delta v_{j}^{\left( 2 \right)} + \Delta v_{j + 1}^{\left( 2 \right)} } \right)\Delta l_{j}^{\left( 2 \right)} }}{2}} \\ \end{aligned}$$
(38)
$$\Delta v^{\left( i \right)} = \Delta {\mathbf{u}}^{\left( i \right)} \cdot {\mathbf{s}}_{\text{c}}$$
(39)
$$\Delta {\mathbf{u}}^{\left( i \right)} = {\mathbf{u}}^{\left( i \right)} \left( {t_{n} } \right) - {\mathbf{u}}^{\left( i \right)} \left( {t_{n - 1} } \right)$$
(40)

where,\(\Delta {\mathbf{u}}^{\left( i \right)}\) denotes the displacement increment of contact surface \(\varGamma_{\text{c}}^{\left( i \right)}\) at time step n. \(\Delta v_{j}^{\left( i \right)}\) is the tangential displacement at vertexes or intersections j of contact surface \(\varGamma_{\text{c}}^{\left( i \right)}\). \(N^{\left( j \right)}\) is the number of the vertexes and intersections of contact surface \(\varGamma_{\text{c}}^{\left( i \right)}\). \(\Delta l_{j}^{\left( i \right)}\) is the length of segment or sub segment j.

Based on the definition, the total tangential contact forces \({\mathbf{T}}^{\left( i \right)}\) of the contact area is calculated as

$${\mathbf{T}}^{\left( 1 \right)} = - {\mathbf{T}}^{\left( 2 \right)} ,\;{\mathbf{T}}^{\left( 1 \right)} = T{\mathbf{s}}_{\text{c}} ,\;T = \alpha_{\text{T}} V^{n}$$
(41)

where \(\alpha_{\text{T}}\) is the tangential penalty parameter.

Then, the Mohr–Coulomb criterion is adopted to determine the contact state. For the contact in stick, if \(\left| T \right| < \left| {\mu_{\text{f}} P} \right|\) (P is the normal of \({\mathbf{P}}^{\left( i \right)}\)), the contact is in stick. Otherwise, the contact state changes to be in slip. When the contact is to be in slip or open, the cumulative tangential displacement \(V^{n}\) is set to be zero. For the contact in slip if the \(\Delta V\) changes the sign, the contact state changes to be in stick.

To calculate the tangential contact force in a unified framework for contact in stick and contact in slip, an equivalent frictional coefficient \(\mu_{\text{eq}}\) is introduced and defined as,

$$\mu_{\text{eq}} = \left\{ {\begin{array}{*{20}c} {\left| {\frac{T}{P}} \right|\quad {\text{in}}\;{\text{stick}}\;\left( {\left| T \right| < \left| {\mu_{\text{f}} P} \right|} \right)} \\ {\mu_{\text{f}} \quad {\rm in} \; {\rm slip} \;\left( {\left| T \right| > \left| {\mu_{\text{f}} P} \right|} \right)} \\ \end{array} } \right.$$
(42)

Then, the tangential frictional force \({\mathbf{t}}_{\text{k}}^{{\left( {\text{i}} \right)}}\) on the contact segment \(c_{k}^{\left( i \right)}\) can be obtained by

$${\mathbf{t}}_{k}^{\left( i \right)} = {\text{sgn}}\left( {V_{n} } \right)\mu_{\text{eq}} p_{\text{N}}^{\left( i \right)} {\mathbf{s}}_{k}^{\left( i \right)}$$
(43)
$${\mathbf{s}}_{k}^{\left( i \right)} = \frac{{{\mathbf{x}}_{k}^{\left( i \right)} - {\mathbf{x}}_{k - 1}^{\left( i \right)} }}{{\left| {{\mathbf{x}}_{k}^{\left( i \right)} - {\mathbf{x}}_{k - 1}^{\left( i \right)} } \right|}}$$
(44)

where \({\mathbf{x}}_{k}^{\left( i \right)}\) is the coordinate of the vertex k of the contact surface \(\varGamma_{\text{c}}^{\left( i \right)}\). \({\mathbf{s}}_{k}^{\left( i \right)}\) is the tangential unit vector along the segment \(c_{k}^{\left( i \right)}\).

3.3 Contribution to the Global Equations

According to Eq. (15), the virtual energy contributed by the contact force acted on the contact boundaries is expressed as

$$\varPi_{\text{c}}^{\left( i \right)} = \int\limits_{{\varGamma_{\text{c}}^{\left( i \right)} }} {\left( {\delta {\mathbf{u}}^{\text{h}} } \right)^{\text{T}} {\mathbf{t}}_{\text{c}}^{\left( i \right)} {\text{d}}\varGamma } = \left( {\delta {\mathbf{d}}} \right)^{\text{T}} {\mathbf{f}}_{\text{c}}^{\left( i \right)} = \left( {\delta {\mathbf{d}}} \right)^{\text{T}} \sum\limits_{k = 1}^{n} {{\mathbf{f}}_{c,k}^{\left( i \right)} }$$
(45)
$${\mathbf{f}}_{c,k}^{\left( i \right)} = \mathop \int \limits_{{c_{k}^{\left( i \right)} }} {\mathbf{T}}_{\varvec{e}}^{\text{T}} {\mathbf{t}}_{c,k}^{\left( i \right)} {\text{d}}\varGamma$$
(46)

where, n denotes the number of contact segment or sub segment of body \(\varOmega^{\left( i \right)}\), \({\mathbf{f}}_{c,k}^{\left( i \right)}\) is the nodal force of contact force acted on the segment or sub segment \(c_{k}^{\left( i \right)}\).

In the proposed contact interaction algorithm, the distributed contact forces \({\mathbf{t}}_{c,k}^{\left( i \right)} = {\mathbf{p}}_{k}^{\left( i \right)} + {\mathbf{t}}_{k}^{\left( i \right)} \varvec{ }\) are converted to equivalent point load \({\mathbf{T}}_{c,k}^{\left( i \right)} = {\mathbf{P}}_{k}^{\left( i \right)} + {\mathbf{T}}_{k}^{\left( i \right)} \varvec{ }\) and its point of force application \({\mathbf{x}}_{k}^{\left( i \right)}\).

Therefore, Eq. (46) can be written as

$${\mathbf{f}}_{c,k}^{\left( i \right)} = {\mathbf{T}}_{\varvec{e}}^{\text{T}} \left( {{}_{d}{\mathbf{x}}_{k}^{\left( i \right)} } \right)\left( {{\mathbf{P}}_{k}^{\left( i \right)} + {\mathbf{T}}_{k}^{\left( i \right)} } \right)$$
(47)

Substituting Eqs. (45), (46) and (47) into (16b), the contribution of the contact force acted on the contact segment \(c_{k}^{\left( i \right)}\) to the global equation is obtained,

$$\sum\limits_{k = 1}^{n} {{\mathbf{f}}_{c,k}^{\left( i \right)} } \to {\mathbf{f}}_{c}$$
(48)

3.4 Implementation of Contact Algorithm

The contact algorithm for calculating the contact nodal forces is presented in Table 1. The first step is contact detection, which is aimed at detecting couples of blocks or bodies close to each other and eliminating couples of blocks that far from each other and cannot possible be in contact. In this step, overlapped contact areas (diagrammatic figures shown in Fig. 4) are obtained. After the contact detection, a loop to calculate contact force and its contributions to the global load vectors is presented. In this loop, the normal contact force \(p_{\text{N}}\) of one overlapped contact area is firstly calculated. Then, based on the contact state in time step n − 1, the trail tangential contact force \(T\) is calculated using Eq. (41). It is noted that if the overlapped contact area is a new contact, a sticking condition is assumed and the corresponding cumulative tangential displacement \(V^{n - 1} = 0\). Next, the contact states at \(t_{n}\) are checked. The sticking contact become slipping if the normal contact force is greater than the limit of friction. Similarly, the slipping contact become stick if there is a change in the sign of the average slip increment. Based on the checked contact state, the tangential contact force \(\varvec{t}\) is calculated. Finally, the contributions of contact force to the global load vector are obtained.

Table 1 The algorithm for calculating contact nodal force \({\mathbf{f}}_{\text{c}}\)
Full size table

4 Numerical Examples

4.1 Momentum Conservation Test

This example is aimed to validate the correctness of new contact formulation involving frictionless contact. As shown in Fig. 7, there are two blocks on a rectangular table. The left-side block slides with no friction toward the right-side stationary block at a constant velocity \(v_{0}\) = 0.5 m/s. The material properties of the two blocks are the same: density ρ = 2800 kg/m3, Young’s modulus E = 2000 MPa, and Poisson’s ratio v = 0.25. To reduce the oscillation of result after block collision, the normal contact stiffness is taken as one tenth of E, namely, kn = 200 MPa/m. The discretization of this problem using NMM is shown in Fig. 7. The time span of the simulation is 3.0 s with a time step increment of 10−4 s.

Fig. 7
figure 7

Collison of two blocks and its discretization (unit: m)

Full size image

Theoretically, the two blocks system should satisfy the momentum conservation, i.e., the total momentum of the two blocks system always keep constant during the collision process. Figure 8 illustrates the velocity histories of Block A, Block B only and the sum of both blocks. It can be seen that the Block A collides with Block B at t = 1 s and completes energy exchange in less than 0.01 s. Then, Block B slides toward right at a constant velocity v = 0.5 m/s. The values of total horizontal momentum are identical to the theoretical values, which confirms that the proposed algorithm for frictionless contact problem is working correctly.

Fig. 8
figure 8

Moment histories of Block 1, Block 2 only and the sum of both blocks

Full size image

4.2 A Block Slides Along an Inclined Slope

The second example is a benchmark to validate the accuracy of new contact formulation in friction case. As shown in Fig. 9, a rectangle block is sliding down a ramp with a slope at an angle of 30° to the horizontal. The material parameters of the block and the ramp are the same: Young’s modulus E = 10 GPa, Poisson’s ratio v = 0.25 and the mass density ρ = 2300 kg/m3. The normal stiffness of contact \(k_{\text{n}}\) and \(k_{\text{s}}\) are set to 10 GPa/m and 10 GPa/m, respectively.

Fig. 9
figure 9

A block slides along an inclined slope with two different frictional segments (unit: m)

Full size image

To investigate the correctness of contact state transition from sticking to slipping, the surface of the ramp is divided into two different frictional segments, namely, AB and BC. The frictional angle of the two segments are \(\varphi_{1} = 20^\circ\) and \(\varphi_{2} = 38.3^\circ\), respectively. The ramp is fixed and the block is under gravitational acceleration of 10 m/s2. The time span of the simulation is 7.0 s with a time step increment of 10−4 s. Theoretically, the acceleration of the block sliding along the two inclined segments are 1.85 m/s2 and − 1.85 m/s2, respectively. However, the acceleration \(a_{j}\) at the junction of the two inclined segments is non-uniform. For this example, considering the normal contact force acted on the bottom of the block is triangular distributed and the value at the heel of the block is approximately zero, the acceleration \(a_{j}\) can be expressed as

$$a_{j} \left( t \right) = \sin \theta - \tan \varphi_{2} \cos \theta + \alpha^{2} \left( {\tan \varphi_{2} - \tan \varphi_{1} } \right)\cos \theta$$
(49)
$$\alpha \left( t \right) = {{\left( {L - \int\limits_{0}^{t} {v\left( T \right){\text{d}}T} } \right)} \mathord{\left/ {\vphantom {{\left( {L - \int\limits_{0}^{t} {v\left( T \right){\text{d}}T} } \right)} L}} \right. \kern-0pt} L},\;v\left( t \right) = v_{0} + \int\limits_{0}^{t} {a_{j} \left( T \right){\text{d}}T}$$
(50)

where, v is the velocity of the block and \(v_{0}\) is the velocity of the block when its toe reach point B. L is the length of the block, \(\alpha\) is the ratio of the block bottom sliding on segment AB.

Figure 10 shows the velocity history of the sliding block during the whole sliding process obtained by improved explicit NMM, original NMM and analytical solution. It is observed obviously from Fig. 10 that the block is in uniformly acceleration motion along the segment AB. The toe of block reach point B at t = 2.8 s. Then, the block sliding along both of segments AB and BC. The velocity history at this stage is shown in detail in Fig. 10b. As can be seen that the block in this stage is in nonuniform acceleration motion and the peak velocity is 5.28 m/s2 at t = 2.91 s. At t = 3.85 s, the block changes to uniformly deceleration motion along segment BC and stops on the slope at 5.9 s. The movement of the block obtained by improved explicit NMM agrees with the analytical solution.

Fig. 10
figure 10

The velocity history of the sliding block: a the whole sliding process; b the stage of the block sliding through point B

Full size image

Although the results obtained by original NMM seems to agree with the analytical solution (shown in Fig. 10a), the velocity history deviates from the analytical solution when the toe of block reach point B at t = 2.8 s. Due to the vertex-to-edge contact type adopted in the original NMM, the contact forces acted on the bottom of block are point forces rather than distributed forces. Moreover, the point force acted on the toe of block is maximum force and so is the corresponding frictional force. Therefore, the velocity obtained by original NMM decreases faster than that by analytical solution or improved explicit NMM.

The results indicate that the proposed new contact formulation work correctly and is capable of simulating the contact state transition from slipping to sticking, which confirms that the proposed algorithm for frictional contact problem is better than original algorithm.

4.3 Two Elastic Beams

The purpose of this example, chosen according to Popp et al. (2010), is to demonstrate the performance and robustness of the proposed algorithm to simulate large sliding contact. Since this example is large rotation and small strain problem, the constitutive equations described in the corotational system is suitable and the hypoelastic material behavior is assumed here. As illustrated in Fig. 11, two curved beams (E = 10,000 Pa, v = 0.32, ρ = 2.3) come into frictional contact due to the upper beam being subjected to a horizontal velocity (v = 1 m/s) at its two top ends. The normal stiffness of contact \(k_{\text{n}}\) and \(k_{\text{s}}\) are set to 100,000 Pa/m and 100,000 Pa/m, respectively. The discretization of this problem using NMM is shown in Fig. 11 and there are 345 mathematical covers and 506 manifold elements

Fig. 11
figure 11

Large deformation contact of two elastic beams and its NMM discretization (unit: m)

Full size image

Due to the fact that no damping is introduced in this study, the deformation of the two beams is reversible and a snap through phenomenon occurs when the upper beam moves around 15 m in the frictionless case. Therefore, the frictional contact force should be considered in this simulation. In this case, frictional angle φ = 10° for the contact is adopted. The evolution of deformation is illustrated by some characteristics stages in Fig. 12. As can be seen, the two curve beams undergo large deformation during the simulation. Different from the frictionless case, the snap through phenomenon occurs when the upper beam moves to approximately u = 16 m. Then, the two contacting beams come to stability quickly through friction between beams, as shown in Fig. 12d. The results agree very well with that in Zheng et al. (2016), which confirms that the proposed algorithm for large sliding problem involving large deformation is working correctly.

Fig. 12
figure 12

Deformed configurations for large deformation contact problem: au = 8; bu = 12; cu = 16; and du = 20. (unit: m)

Full size image

4.4 Multi-blocks Contact Interaction

This example (Bao and Zhao 2010) is designed to investigate the ability of proposed contact formulation to deal with vertex-to-vertex contact, which is the most challenging contact type in conventional NMM. As shown in Fig. 13, a four-blocks system on a fixed table is present. A point load F (− 4 × 107 kN, − 3 × 107 kN) is applied on Block A and the gravity is not taken into consideration. The material properties of all blocks are the same: mass density ρ = 2300 kg/m3; Young’s Modulus E = 10 GPa, Poisson’s ratio v = 0.3, friction angle between blocks is 15°, and the cohesion is 0. The computational control parameters are as follow: time step size \(\Delta t = 10^{ - 5} \;{\text{s}}\) and 600,000 time steps. The normal and shear contact spring stiffness are kn = 10 GPa/m and ks = 10 GPa/m.

Fig. 13
figure 13

the model of multi-blocks contact and its NMM discretization (unit: m)

Full size image

Since that the horizontal force |Fx| is greater than the vertical force |Fy|, the displacement along the horizontal direction should be larger than that along the vertical direction. Therefore, block A should move horizontally along the top edge of block C, rather than vertically along the side edge. Figure 14 presents the final configurations by original NMM and explicit NMM, colored with the resultant displacements. As can be seen that the solution by explicit NMM is correct. It should be noted that due to the adoption of penalty method to solve this example, Block A penetrates the other three blocks at an initial stage of simulation. Therefore, Block B moves towards right in the simulation, but its displacement is far less than the upward displacement of Block D, as shown in Fig. 14b.

Fig. 14
figure 14

Final configuration of multi-blocks contact interaction together with resultant displacement contours: a original NMM; b explicit NMM with proposed contact algorithm (unit: m)

Full size image

5 Preliminary Simulation of Vaiont Landslide

In this example, the Vaiont landslide (Maclaughlin 1997) which occurred in northern Italy on October 1963, is chosen to investigate the ability and robustness of proposed contact formulation to deal with numerous singular contacts. Figure 15 shows the profile of the Vaiont landslide before and after the occurrence of slide. In this simulation, based on the shape of failure surface and the character of slope topography, the whole slope is divided into rock base and sliding mass. Then the sliding masses are divided into the smaller discrete deformable blocks by pre-existing discontinuities, as shown in Fig. 16. The NMM model is also depicted in Fig. 16. As we can see that since the landslide mass consists of several triangle blocks and quadrangle blocks, it is convenient to define the manifold mesh for each block. Therefore, the NMM discretization for this example consists of two parts, namely, rock base and landslide mass. Each block in landslide mass is covered by three regular hexagonal physical patches denoted by red point. The overlap of these three patches is the equilateral triangle circumscribed the characteristic circle of the block. The radius of this circle is defined as the maximum distance from the centroid to the vertexes of the block. In this NMM model, there are 504 blocks in landslide mass and more than 2000 contact-pairs. Since most of contacts are vertex–vertex contact, the problem is extremely singular for the conventional NMM.

Fig. 15
figure 15

The typical cross-section of the Voiant landslide before and after sliding

Full size image
Fig. 16
figure 16

The NMM discretization for the landslide mass and rock base. Note that the NMM discretization for this example consists of two parts, namely, rock base and landslide mass. Each block in landslide mass is covered by three regular hexagonal physical patches denoted by red point. The overlap of these three patches is the equilateral triangle circumscribed the characteristic circle of the block. The radius of this circle is defined as the maximum distance from the centroid to the vertexes of the block (color figure online)

Full size image

According to Zheng et al. (2014), the property of landslide mass and bed rock are as follow mass density ρ = 2300 kg/m3, Young’s modulus E = 10 GPa, Poisson’s ratio v = 0.3. The frictional angle of the blocks is 8.5° and the cohesion is 0. The computational control parameters are as follow: time step size \(\Delta t = 10^{ - 5} \;{\text{s}}\) and the time span T = 35 s. The normal and shear contact spring stiffness are kn = 10 GPa/m and ks = 10 GPa/m as shown in Fig. 16, three blocks located at different parts of the sliding mass are selected to investigate the dynamical behavior of the sliding mass in the landslide process.

Figure 17 shows the velocity and displacement time histories of monitoring blocks. Figure 18 presents the landslide process of Vaiont landslide simulated by the explicit NMM, with the configurations at different time. As shown in Fig. 16, the landslide mass looks like a “chair” and can be divided into two parts. One is the landslide mass stacked along the inclined slide surface, called “back of chair”. The other is the landslide mass stacked on the horizontal slide surface, called “seat of chair”. The resistance force along the inclined slide surface is insufficient to keep “back of chair” stability. Therefore, “back of chair” slide down gradually, and pushes “seat of chair” move forward. It can be seen from Fig. 17 that the velocity of three blocks located at different parts of landslide mass is similar, suggesting that the landslide mass move forward as a whole. At the initial stage, the velocity of three blocks increases gradually. When the landslide mass hits the opposite bank at t = 14.2 s, the whole landslide decelerate rapidly and accumulated in the valley. The duration of landslide process is around 30 s, which agree with the description in Zheng et al. (2014). After overlapping the final step of NMM calculation with the topographic cross-section at the Vaiont landslide, the deposit pattern of the simulated Vaiont landslide coincides well with the local topography.

Fig. 17
figure 17

The resultant velocity histories of three monitoring blocks

Full size image
Fig. 18
figure 18

Simulation results of Vaiont landslide: at = 8 s; bt = 15 s; ct = 23 s and dt = 30 s (unit: m)

Full size image

6 Conclusions

In this study, a new contact formulation for large frictional sliding, in which the contact force is calculated directly based on the overlapped area of bodies in contact and the contact states, is proposed and implemented in the explicit NMM. Due to the elimination of the contact type judgement and open-close iteration, the proposed contact algorithm is robust and very easy to be implemented.

Five numerical examples are presented to verify the proposed contact algorithm. The first two examples are benchmarks used to validate the proposed contact algorithm in the case of frictionless and friction cases, respectively. The third example is used to demonstrate the ability of the proposed algorithm to simulate large sliding contact involving large deformation. The fourth example is used to validate the correctness of solving corner-to-corner contact problem, which is a difficulty in discontinuum-based numerical methods. The last example, containing a large number of corner-to-corner contacts, is presented to test the ability of the new algorithm in solving the extremely singular problem. All the simulation results obtained in this study agree well with the analytical solution or reference results, indicating that the proposed contact algorithm has reached a practical level in accuracy, robustness and effectiveness.

Note that the contact algorithm proposed in this study is derived base on explicit methods. The weaknesses of explicit methods are also applicable to this study. Therefore, the derivation of the proposed contact algorithm based on the implicit method is one of our future works. In addition, our future work includes.

  1. (1)

    Investigating the effect of mechanical damping on contact interactions in the explicit NMM.

  2. (2)

    Implementing the proposed contact algorithm to other numerical methods, such as FEM, DEM, DDA.

  3. (3)

    Developing parallel computing technology. The explicit methods are easy to be highly parallelized and the solution efficiency will be enhanced considerably.