Determine In-Situ Stress and Characterize Complex Fractures in Naturally Fractured Reservoirs from Diagnostic Fracture Injection Tests

Abstract

Estimation of in-situ stresses has significant applications in earth sciences and subsurface engineering, such as fault zone studies, underground CO₂ sequestration, nuclear waste repositories, oil and gas reservoir development, and geothermal energy exploitation. Over the past few decades, Diagnostic Fracture Injection Tests (DFIT), which have also been referred to as Injection-Falloff Tests, Fracture Calibration Tests, and Mini-Frac Tests, have evolved into a commonly used and reliable technique to obtain in-situ stress. Simplifying assumptions used in traditional methods often lead to inaccurate estimation of the in-situ stress, even for a planar fracture geometry. When a DFIT is conducted in naturally fractured reservoirs, the stimulated natural fractures can either alter the effective reservoir permeability within the distance of investigation or interact with the hydraulic fracture to form a complex fracture geometry, this further complicates stress estimation. In this study, we present a new pressure transient model for DFIT analysis in naturally fractured reservoirs. By analyzing synthetic, laboratory and field cases, we found that fracture complexity and permeability evolution can be detected from DFIT data. Most importantly, it is shown that using established methods to pick minimum in-situ stress often lead to over or underestimates, regardless of whether the reservoir is heavily fractured or sparsely fractured. Our proposed “variable compliance method” gives a much more accurate and reliable estimation of in-situ stress in both homogenous and naturally fractured reservoirs. By combining the unique pressure signatures associated with the closure of natural fractures, a lower bound on the horizontal stress anisotropy can be estimated.

1 Introduction

A quantitative estimation of in-situ stress is crucial for many applications in earth sciences and subsurface engineering, such as fault zone studies (Scholz 2002), underground CO₂ sequestration (Iding and Ringrose 2009), nuclear waste repositories (Witherspoon 2004), wellbore stability (Wang and Samuel 2016) and geothermal energy exploitation (Evans et al. 1992). In hydrocarbon reservoirs, the magnitude of in-situ stress plays a vital role in hydraulic fracture design (Singh et al. 2019; Liu et al. 2017; Fu et al. 2019; Wang 2016), transport capacity of propped and un-propped fractures (Guo et al. 2017; Zhang et al. 2017; Wang and Sharma 2018a, b), sand production (Vardoulakis et al. 1996), reservoir compaction and subsidence (Fredrich et al. 2000). Currently, the most reliable method to estimate minimum in-situ stress is through diagnostic fracture injection tests (DFIT).

In most parts of the world, at depths within reach of the drill bit, that the stress acting vertically on a horizontal plane is a principal stress. This requires that the other two principal stresses act in a horizontal direction. Stress regime is often used to categorize the relative magnitudes of the principal stresses. A normal faulting regime is one in which the vertical stress is the greatest stress. When the vertical stress is the intermediate stress, a strike-slip regime is indicated. If the vertical stress is the least stress the regime is defined to be reversed. The horizontal stresses at a given depth will be smallest in a normal faulting regime, larger in a strike-slip regime, and greatest in a reverse faulting regime. In a normal faulting regime, vertical in-situ stress is estimated via integrating density logs along the true vertical depth (TVD) of a wellbore, and once the minimum horizontal stress is determined from DFIT (except for very shallow depth where vertical stress is the minimum in-situ stress), the maximum horizontal stress can be estimated through stress-induced wellbore breakouts (Zoback 2007).

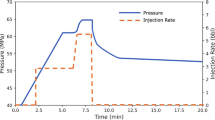
Diagnostic fracture injection tests involve pumping a fluid (typically water) for a short period of time, creating a relatively small hydraulic fracture before the well is shut-in. The pressure transient data after shut-in is analyzed to obtain fracture closure pressure or closure stress (equivalent to minimum in-situ stress). A typical pressure trend during DFIT in a homogeneous reservoir (i.e., absent of natural fractures and weak planes) is qualitatively shown in Fig. 1. Besides in-situ stress determination, reservoir pore pressure and flow capacity can also be estimated from DFIT analysis.

Fig. 1

Diagram showing sequence of events observed in a typical DFIT with planar fracture geometry

Estimating minimum in-situ stress by creating small hydraulic fractures has become standard practice for stress determination because of its simplicity and reliability (Haimson and Fairhurst 1969; Haimson and Cornet 2003). The fracture closure pressure/stress is often interpreted as equivalent to the minimum in-situ stress. In addition to stress determination, estimating reservoir flow capacity is also of paramount importance when analyzing pressure fall-off data. The advent of fracturing pressure decline analysis was pioneered by the work of Nolte (1979, 1986), where the leak-off behavior was introduced into DFIT analysis for the first time. With the assumptions of power-law fracture growth, negligible spurt loss, constant fracture surface area after shut-in and Carter’s leak-off model (one-dimensional leak-off of fluid from a constant pressure boundary, the solution to the diffusivity equation predicts that the leak-off rate will scale with the inverse of the square root of time), a remarkably simple and useful equation for the pressure decline can be obtained:

$${P_{\text{f}}}\left( {\Delta {t_{\text{D}}}} \right)={\text{ISIP}} - \frac{{\pi {r_{\text{p}}}{C_{\text{L}}}{S_{\text{f}}}\sqrt {{t_{\text{p}}}} }}{2}G\left( {\Delta {t_{\text{D}}}} \right)$$

(1)

Here, ${\text{ISIP}}$ is the instantaneous shut-in pressure at the end of pumping, ${P_{\text{f}}}$ is the fracture pressure at the dimensionless time $\Delta {{\text{t}}_{\text{D}}} , ~{t_{\text{p}}}$ is the total pumping time. ${r_{\text{p}}}$ is the productive fracture ratio, which is the ratio of fracture surface area that is subject to leak-off to the total fracture surface area. For low permeability, unconventional reservoirs, ${r_{\text{p}}} \approx$1. ${C_{\text{L}}}$ is Carter’s leak-off coefficient which is a constant. ${S_{\text{f}}}$ is the fracture stiffness (the reciprocal of fracture compliance), which can be calculated using Table 1 for different fracture geometries when the fracture is fully open. It is assumed that ${S_{\text{f}}}$ is a constant until the fracture closes instantaneously when the fluid pressure in the fracture drops to the minimum in-situ stress.

Table 1 Fracture stiffness expressions for different fracture geometry models

$E^{\prime}$ is the plane strain Young’s modulus and can be calculated using Young’s Modulus, $E$, and Poisson’s Ratio, $\upsilon$:

$$E^{\prime} =\frac{E}{{1 - {\upsilon ^2}}}~$$

(2)

The dimensionless time $\Delta {t_{\text{D}}}$ is defined by:

$$\Delta {t_{\text{D}}}=\frac{{\Delta t}}{{{t_{\text{p}}}}}$$

(3)

where $~\Delta t$ is the shut-in time. G-function is defined as

$$G\left( {\Delta {t_{\text{D}}}} \right)=\frac{4}{\pi }\left[ {g\left( {\Delta {t_{\text{D}}}} \right) - g\left( 0 \right)} \right]$$

(4)

Where the g-function of time is approximated by,

$$g\left( {\Delta {t_{\text{D}}}} \right)=\left\{ {\begin{array}{*{20}{l}} {(1+\Delta {t_{\text{D}}}){{\sin }^{ - 1}}{{(1+\Delta {t_{\text{D}}})}^{ - 1/2}}+\Delta t_{{\text{D}}}^{{1/2}}}&{{\text{for~low~fluid~efficiency}}} \\ {\frac{4}{3}\left[ {{{(1+\Delta {t_{\text{D}}})}^{1.5}} - \Delta t_{{\text{D}}}^{{1.5}}} \right]}&{{\text{for~high~fluid~efficiency}}} \end{array}} \right.$$

(5)

Castillo (1987) used Nolte’s G-function for modeling the pressure decline behavior and developed the straight-line plot of the G-function vs pressure. Any departure from this straight-line is interpreted as the closure of the fracture. Unfortunately, plots of pressure vs G-function often yield curves with multiple points of inflection that have been attributed to abnormal leak-off behavior, which makes it difficult to interpret the changes in slope and identify fracture closure. So identification of fracture closure pressure is usually done using plots of pressure and GdP/dG vs G-function (Barree et al. 2009), where the closure is picked at the tangential point between a straight line that passes the origin and the GdP/dG curve. This prevailing method of determining minimum in-situ stress using the “tangent line method” (it also has been referred to as the “holistic approach”) although has been widely accepted as a standard practice, but has never been theoretically justified. Liu et al. (2016) and Marongiu-Porcu et al. (2014) proposed a log–log plot of pressure derivatives, where the fracture closure pressure is picked at the end of the 3/2 slope. Their method yields identical in-situ stress estimates as the “tangent line method” because both methods are based on the same assumptions, and the 3/2 slope just arises from a spatial integration of Carter’s leak-off assumption (i.e., constant fracturing fluid pressure), which has nothing to do with closure stress at all (McClure 2017; Van den Hoek 2017). Carter’s leak-off assumption is clearly violated during a DFIT because the pressure is continuously declining with time. McClure et al. (2016) modeled fracture closure behavior using a fully coupled numerical simulator and found that the “tangent line method” can severely underestimate closure pressure. Based on simulation results, they proposed a “compliance method” for picking closure pressure on the G-function plot, where closure pressure is picked at the point where the fracture stiffness starts to increase (pressure derivative deviates upward from a straight line on G-function or square-root-of-time plot). Wang and Sharma (2017b, 2018b) presented a “variable compliance method” to estimate fracture closure pressure, fracture surface roughness and un-propped fracture conductivity, where the effect of fracture-pressure-dependent-leakoff (FPDL) and variable fracture compliance (due to progressive fracture closure from its edges to the center) are included. They found that the conventional “tangent line method” underestimates the minimum in-situ stress, especially in depleted reservoirs, while the “compliance method” picks the mechanical closure pressure but overestimates the minimum in-situ stress, especially when height recession occurs. Their subsequent work (Wang and Sharma 2019) also found that traditional well-test solutions that are based on a constant injection rate assumption are inappropriate for DFIT analysis.

Pre-existing planes of weakness are a common feature in geological formations. It is well-understood that rocks containing interlocked or weakly bonded planes are weaker than intact rock since the plane serves as a preferential plane of failure. Typical forms of weak planes are the joints, faults, veins, dikes, and bedding planes. DFIT analysis does not distinguish between these different kinds of weak planes, rather, it is the final fracture geometry, leak-off and complex fracture closure process that determines the pressure fall-off response. In this article, we investigate how the final fracture complexity and its hydraulic conductivity impact DFIT analysis. For the purpose of clarity, “natural fracture” is used herein as a generalized term representing all types of pre-existing weak planes in the subsurface.

Previous researchers have been mainly focused on planar fractures in homogeneous reservoirs, and little work has been done to interpret DFIT data as regards to stress determination and fracture characterization in naturally fractured reservoirs with FPDL and variable fracture compliance. In this study, we extend our previous work to investigate pressure transient behavior in naturally fractured reservoirs and compare the estimated in-situ stress from different methods using synthetic and laboratory data. In addition, unique signatures of fracture complexity on diagnostic plots are also discussed and compared with field observations.

2 Mathematical Modeling of DFIT

2.1 Fracture-Pressure-Dependent-Leak-off with Variable Compliance

The transient pressure response during fracture closure is derived using the following assumptions:

• 1. The reservoir is isotropic and homogeneous and contains a single slightly compressible fluid.

• 2. The fluid viscosity, formation porosity, and total compressibility are independent of pressure.

• 3. Reservoir permeability is low so that poroelastic effects caused by fluid leak-off are negligible

• 4. Gravity effects are negligible and pressure gradients are small thorough out the reservoir.

• 5. Mechanically closed fracture has residual fracture width so it is still subject to leak-off and the fracture leak-off surface area remains unchanged.

• 6. Pressure gradient inside the fracture is negligible after shut-in. This assumption of infinite conductivity after closure means that a channel of relatively high permeability (compared to surrounding rock matrix) remains where the fracture occurred. This could be caused by erosion or distortion of the fracture walls. As long as after-closure linear flow occurs, the closed fracture can be treated as having infinite conductivity.

• 7. The pore pressure disturbance caused by fracture propagation is negligible. This means that fluid leak-off during pumping is very small and the duration of injection is very short when compared to the shut-in period.

• 8. Leak-off is linear and perpendicular to the fracture surface and pressure interference among fractures and late time radial flow has not yet developed.

Assuming 1D linear Darcy flow and a slightly compressible, single-phase fluid in the reservoir, the differential form of the mass balance can be written as:

$$\frac{{\partial P}}{{\partial t}}=\frac{1}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{\partial }{{\partial x}}\left( {k\frac{{\partial P}}{{\partial x}}} \right)$$

(6)

where ${\text{P}}$ is the pressure, ${\text{k}}$ is formation permeability, which can be a function of P. $~{\mu _{\text{f}}}$ is fluid viscosity, $\phi$ is formation porosity and ${c_{\text{t}}}$ is total formation compressibility and x is the distance to fracture surface. From a material balance perspective (fluid compressibility is negligible compared to that of the fracture), the total rate of fluid leak-off into the formation, ${q_{\text{f}}}$, after shut-in equals the rate of shrinkage of total fracture volume, ${V_{\text{f}}}$, as pressure declines:

$${q_{\text{f}}}= - ~\frac{{{\text{d}}{V_{\text{f}}}}}{{{\text{d}}t}}$$

(7)

Fracture stiffness, which is the reciprocal of fracture compliance, is defined as:

$${S_{\text{f}}}=\frac{{{A_{\text{f}}}{\text{d}}{P_{\text{f}}}}}{{{\text{d}}{V_{\text{f}}}}}$$

(8)

where ${P_{\text{f}}}$ is pressure inside fracture and ${A_{\text{f}}}$ is half of the total fracture surface area (only account for 1 wall). Physically speaking, fracture stiffness or fracture compliance delineates fracture system compressibility that is normalized by fracture surface area. Substituting Eq. (8) into Eq. (7), we have

$${q_{\text{f}}}= - {\text{~}}\frac{{{A_{\text{f}}}{\text{d}}{P_{\text{f}}}}}{{{S_{\text{f}}}{\text{d}}t}}$$

(9)

At the boundary of the fracture surface, both Darcy’s law and material balance have to be honored:

$${q_{\text{f}}}= - {\text{~}}2{A_{\text{f}}}\frac{k}{{{\mu _{\text{f}}}}}~\frac{{{\text{d}}P}}{{{\text{d}}x}}= - ~{\text{~}}\frac{{{A_{\text{f}}}{\text{d}}{P_{\text{f}}}}}{{{S_{\text{f}}}{\text{d}}t}}\quad {\text{at~}}x=0$$

(10)

Rearranging Eq. (10), we get the boundary condition at the fracture surface:

$$\frac{k}{{{\mu _{\text{f}}}}}~\frac{{{\text{d}}P}}{{{\text{d}}x}}=\frac{1}{{2{S_{\text{f}}}}}\frac{{{\text{d}}{P_{\text{f}}}}}{{{\text{d}}t}}~{\text{at}}\quad x=0$$

(11)

With initial condition (disregarding the pressure disturbance during the short injection period)

$$~~P={P_0}\quad ~{\text{at}}\;t=0,~\quad x>0$$

(12)

$$~~P={\text{ISIP}}\quad {\text{at}}~t=0,~\quad x=0$$

(13)

where ${P_0}$ is the initial pore pressure and ${\text{ISIP}}$ is the instant shut-in pressure. The governing equation Eqs. (6), plus the initial condition Eqs. (12), (13) and boundary condition Eq. (11) uniquely describe the pressure transient behavior during DFIT. To account for wellbore storage effects, the fracture stiffness ${S_{\text{f}}}~$ needs to be replaced by the fracture-wellbore system stiffness, which is defined as:

$${S_{\text{s}}}=\,\frac{{{A_{\text{f}}}}}{{{C_{\text{s}}}}}=\frac{{{A_{\text{f}}}}}{{\frac{{{A_{\text{f}}}}}{{{S_{\text{f}}}}}+{C_{\text{w}}}}} \approx \frac{{{A_{\text{f}}}}}{{\frac{{{A_{\text{f}}}}}{{{S_{\text{f}}}}}+{V_{\text{w}}}~{c_{\text{w}}}}}=\frac{{{S_{\text{f}}}{A_{\text{f}}}}}{{{A_{\text{f}}}+{S_{\text{f}}}{V_{\text{w}}}~{c_{\text{w}}}}}$$

(14)

where ${V_{\text{w}}}$ is the wellbore volume and ${c_{\text{w}}}$ is the water (i.e., injection fluid that stored in the wellbore) compressibility, ${c_{\text{w}}}$ is the wellbore storage coefficient and ${C_{\text{s}}}$ is the fracture-wellbore system storage coefficient. The fracture-wellbore system stiffness reflects the overall compressibility of the fracture and wellbore system normalized by the fracture surface area. Note that in the above derivation, both ${S_{\text{f}}}$ and $k$ are not limited to a constant value. The above equations are solved simultaneously using the method of lines (MOL), and the detailed formula for numerical discretization is presented in the Appendix.

2.2 Fracture Stiffness of Complex Fracture Geometry

In essence, fracture stiffness (or compliance) represents a surface area normalized compressibility of a fracture system, and for a fracture with complex fracture geometry, the total fracture stiffness is controlled by the stiffness of multiple individual fracture segments, as illustrated in Fig. 2.

Fig. 2

Illustration of complex fracture geometry

The complex fracture is formed by individual segments with different orientations and fracture surface area. Let the ith fracture surface area of one wall denoted as ${A_{{\text{f}},i}}$ and its pressure-dependent stiffness denoted as ${S_{{\text{f}},i}}$, the total fracture stiffness can be determined from the stiffness of each individual fracture segment (analogous to capacitors in parallel):

$${S_{\text{f}}}=\frac{{{A_{\text{f}}}}}{{\frac{{{A_{{\text{f}},1}}}}{{{S_{{\text{f}},1}}}}+\frac{{{A_{{\text{f}},2}}}}{{{S_{{\text{f}},2}}}}+ \cdots +\frac{{{A_{{\text{f}},n}}}}{{{S_{{\text{f}},n}}}}}}$$

(15)

where,

$${A_{\text{f}}}={A_{{\text{f}},1}}+{A_{{\text{f}},2}}+ \cdots +{A_{{\text{f}},n}}$$

(16)

2.3 Pressure Dependent Permeability

In previous literature (Barree et al. 2009), the phenomenon of pressure-dependent permeability is often referred to as pressure-dependent leak-off (PDL), however, this is not an appropriate term, because leak-off is always pressure-dependent, even if the permeability is constant (Wang and Sharma 2017b). There are many equations that can be used to express the formation of effective permeability as a function of pressure, such as a linear, power law or hyperbolic relationship. To make a general case and use as few free parameters as possible, we adopt a general formula to relate formation permeability and pressure:

$$k\left( P \right)=\left( {{k_{\text{e}}} - {k_0}} \right)\frac{{{{\text{e}}^{\text{c}}} - {{\text{e}}^{\frac{{{\text{ISIP}} - P}}{{{\text{ISIP}} - {P_{{\text{original}}}}}}c}}}}{{{{\text{e}}^c} - 1}}+{k_0}$$

(17)

where ${k_{\text{e}}}$ is the effective reservoir matrix permeability in the vicinity of the fracture at the end of pumping and ${k_0}$ is the original reservoir permeability. ${P_{{\text{original}}}}$ is the pressure where reservoir permeability drops to its original value ${k_0}$and c a free parameter controls the evolution of permeability. ${k_{\text{e}}}$ is larger than ${k_0}$ because the surrounding permeability is enhanced by stimulated fracture networks during pumping. After the pressure drops to or below ${P_{{\text{original}}}}$, the conductivity of the stimulated fracture network is reduced to a point where its effect on the overall effective permeability becomes negligible. Figure 3 demonstrates the pressure-dependent permeability for different values of c.

Fig. 3

Illustration of pressure-dependent permeability with different values of c

2.4 Pressure Dependent Fracture Compliance

Fracture closure is a gradual process with increasing fracture stiffness (or decreasing fracture compliance) as fracture closes from tip to wellbore or closes from a higher stress region to a lower stress region in layered formations. A method to obtain a pressure-dependent fracture stiffness based on fracture geometry, rock properties, and surface roughness has been well discussed by Wang and Sharma (2017b) and Wang et al. (2018b). The influence of surface roughness on fracture stiffness is described by a contact law relating the fracture width to the net closure stress for fractured rocks (Willis-Richards et al. 1996):

$${\sigma _{\text{c}}}=\frac{{{\sigma _{{\text{ref}}}}}}{9}\left( {\frac{{{w_0}}}{{{w_{\text{f}}}}} - 1} \right)\quad {\text{for~}}~{w_{\text{f}}} \leq {w_0}$$

(18)

where ${w_{\text{f}}}$ is the fracture aperture and, ${w_0}$ is the contact width, which represents the fracture aperture when the contact normal stress is equal to zero, ${\sigma _{\text{c}}}$ is the contact normal stress on the fracture, and ${\sigma _{{\text{ref}}}}$ is a contact reference stress, which denotes the effective normal stress at which the aperture is reduced by 90%. The contact width ${w_0}$ is determined by the tallest asperities, and the strength, spatial and height distribution of asperities are reflected by the contact reference stress ${\sigma _{{\text{ref}}}}$. Equation (18) indicates that as residual fracture width becomes smaller, more stress is required to further close the fracture and the fracture becomes stiffer.

3 DFIT in Natural Fractured Reservoirs

All reservoirs are naturally fractured to some degree. Depending on the density and dimensions of natural fractures and the location where the DFIT is done, the natural fractures can impact hydraulic fracture propagation and the adjacent flow capacity. If the reservoir is heavily fractured and these natural fractures are well-connected, as shown in Fig. 4a, then the formation can be considered as homogenous within the distance of investigation and the effective permeability is controlled by both fracture and matrix. High-pressure fluid injection during the pumping period enhances the local effective permeability because it widens the natural fractures. However, as pressure declines during shut-in, the effective permeability will gradually decline until it reaches the original value. The original effective permeability does not necessarily represent the matrix permeability, because the existence of natural fractures may already have enhanced the permeability. Such cases are often observed in coalbed methane (CBM) and naturally fractured carbonate reservoirs. If the reservoir is sparsely or moderately fractured, and the stimulated natural fractures are discrete and not well-connected, then these natural fractures or isolated fracture networks will not change the overall flow capacity in the reservoir (Wang 2017), but they can interact with hydraulic fractures, and generate a complex fracture geometry, as shown in Fig. 4b. Under this scenario, the fracture stiffness/compliance and leak-off surface area are impacted by the sequential closure of individual fracture segments or branches, where the branches with the highest normal stress perpendicular to local fracture orientation will close first, and the fracture segments that open against the minimum principal stress will be the last to close. If the hydraulic fracture does not initiate along the maximum principal stress direction because of the local hoop stress around perforations, non-planar fractures can also be formed. In this section, we are going to investigate the pressure transient behavior under these scenarios and discuss the implications of estimating minimum in-situ stress using different methods.

Fig. 4

Illustration of the impact of natural fractures

3.1 Base Case: Planar Fracture Geometry in Homogeneous Reservoir

Before we embark on investigating the pressure transient behavior with closing fractures in fractured reservoirs, we will first examine pressure decline behavior for a planar fracture and discuss the causes for the discrepancy for estimated closure stress using established methods. Table 2 shows the input parameters for the Base Case Scenario.

Table 2 Input parameters for the Base Case scenario

With the known fracture geometry, rock modulus, minimum in-situ stress and surface roughness (represented by two contact parameters ${w_0}$ and ${\sigma _{{\text{ref}}}}$), the fracture stiffness and volume evolution can be uniquely determined at different fluid pressures (Wang and Sharma 2017a; Wang et al. 2018), the results are shown in Fig. 5. As can be seen, when the fluid pressure inside the fracture is relatively high, the fracture volume declines linearly with pressure (fracture stiffness/compliance is constant). However, as the pressure declines to a certain level the fracture volume and pressure depart from a linear relationship, and fracture stiffness starts to increase noticeably. In the end, when the fluid pressure drops to a sufficient low level, the residual fracture volume (supported by asperities) becomes more or less insensitive to pressure drop with extremely high fracture stiffness (low compliance). This fracture stiffness curve can be explained by the fact that when the pressure inside the fracture is relatively high, it is still wide open and its stiffness is a constant. However, as pressure continues to drop, the fracture will gradually close from its edges to its center, which increases the fracture stiffness gradually.

Fig. 5

Simulated fracture stiffness and fracture volume evolution during fracture closure

Figure 6 shows the normalized tiltmeter response (It measures the fracture surface displacement and its slope is proportional to fracture compliance or the reciprocal of fracture stiffness. The changes in tiltmeter measurement are proportional to the changes of fracture volume for a constant fracture surface area) plotted against wellbore pressure during the shut-in period of 2B well at three different stations from the GRI/DOE M-site. The tiltmeter demonstrates that soon after shut-in, the measured displacement declines linearly with pressure (roughly constant fracture stiffness). After the pressure declines to a certain level, the measured displacement vs pressure departs from a linear relationship. As pressure continues declining, more and more fracture surface area comes into contact with the rough fracture surfaces and asperities, and the fracture stiffness increases gradually. This field measurement is consistent with the general trend from our modeling results shown in Fig. 5 (i.e. the evolution of simulated fracture volume is consistent with the measured normalized tilt). It is challenging to estimate closure stress based on mechanical closure from tiltmeter measurement. If we pick the closure stress using the “tangent line method” on tiltmeter measurement (Craig et al. 2017), the closure stress is 15 MPa, and if we pick the closure stress using the “compliance method”, the closure stress is 21 MPa. There is a 6 MPa discrepancy between these two methods. As discussed by Wang and Sharma (2017b), the “tangent line method” only marks the end of fracture storage dominated flow, so it always underestimates closure stress while the “compliance method” can overestimate closure stress because it only marks the beginning fracture closure on edges or tips. The “variable compliance method” proposed by Wang and Sharma (2017b) provides an alternative way to estimate closure stress that not only accounts for the difference between two endpoints (fracture compliance start to change and fracture compliance become small enough to be considered as negligible), but also compensates for the impact of leak-off, which is reflected on G-function time or the square root of time.

Fig. 6

Tiltmeter measurement from 2B well of GRI/DOE M-site project

To illustrate the benefit of the “variable compliance method” and compare the estimated closure stress from different methods, the pressure-dependent fracture stiffness from Fig. 5 is used as a boundary condition for Eq. (11) to simulate the pressure decline response, all other parameters are provided in Table 2. Figure 7 shows the pressure decline and its derivatives on the G-function and square root of time plots. Compared to the input closure stress of 35 MPa, the estimated closure stress by the “tangent line method” is 32.2 MPa (− 2.8 MPa error), the estimated closure stress by the “compliance method” is 36.8 MPa (1.8 MPa error), and the estimated closure stress by the “variable compliance method” is 35.2 MPa (0.2 MPa error). It clearly indicates that the closure stress estimated by the “variable compliance method” is more reliable. Detailed comparisons with different fracture geometry, surface roughness, reservoir properties, and wellbore storage effects have been presented by Wang and Sharma (2017b), and hence will not be discussed further. But one thing that should be emphasized here is that the curvature of pressure derivative, before it reaches the peak value, is determined by the competing effect of the evolution of fracture stiffness and the deviation from Carter’s leak-off (i.e., the difference between the true leak-off rate and that predicted by Carter’s leak-off model). In some special cases, the pressure derivative can happen to be a straight line before it reaches the peak, under this scenario, both “compliance method” and “variable compliance method” is not applicable and only then, “tangent line method” is appropriate to use (Wang and Sharma 2017b). Figure 8 shows the pressure profiles in the formation away from the fracture surface at different shut-in times. Together with Fig. 7, we can notice that the closure time is around 8.85 h when fluid pressure drops to the close stress, and the corresponding distance of investigation is less than 7 m at the time of closure. This is very typical in low permeability formations.

Fig. 7

Pressure decline and its derivatives of Base Case scenario

Fig. 8

Pressure profile and distance of investigation for the Base Case scenario

Figure 9 shows the simulated $\Delta t\frac{{{\text{d}}\Delta {P_{\text{f}}}}}{{{\text{d}}\Delta t}}$ vs $\Delta t$ on a log–log plot $(\Delta {P_{\text{f}}}={P_{\text{f}}} - {\text{ISIP}})$, from which different flow regimes (i.e., ½ slope indicates formation linear-flow, ¾ slope indicates formation bilinear flow and a unit slope indicates formation radial flow) can be detected. From the results, we can observe that before-closure linear flow with ½ slope is apparent during fracture closure and after-closure linear flow with − 1/2 slope also emerges in late time. The formation linear flow only occurs when fluid diffusion inside reservoir dominates the pressure transient behavior, not the dynamic fracture closure process. During the early-time when pressure is relatively high, the fracture is wide open and its stiffness is constant, the leak-off process dictates pressure decline behavior. However, as progressive fracture closure begins, the pressure derivatives deviate from the ½ slope and the dynamic fracture closure behavior dominates the pressure decline behavior. At the late-time, when fracture stiffness become so high and its compressibility becomes so low, the fracture becomes essentially static, and leak-off process re-established as the dominant mechanism for pressure decline and after-closure formation linear flow emerges. If formation permeability is large enough, after-closure radial will develop at the end.

Fig. 9

Log–log plot of pressure derivative for the Base Case scenario

Figures 7 and 9 are text-book cases under ideal scenarios where only one single planar hydraulic fracture is created in a homogenous reservoir. Unfortunately, many field DFIT cases demonstrate non-ideal behavior in naturally fracture reservoirs that are difficult to interpret. Now the question remains: what unique features will emerge from DFIT data in naturally fractured reservoirs and how do we reliably estimate in-situ stress and characterize fracture complexity under these contexts? Are these established methods reliable ways to estimate closure stress? In the following sections, we will examine these cases and discuss how to interpret the associated pressure transient behavior.

3.2 Heavily Fractured Reservoir

3.2.1 Pressure Dependent Permeability during Before-Closure

First, let us investigate the case where the reservoir is heavily fractured and all the stimulated fractures form well-connected networks that alter the effective permeability around the hydraulic fracture. The effective permeability is highest at the end of pumping and gradually declines as pressure drops and fluid leaks off into the formation. Assuming that the effective permeability follows Eq. (17), with c = 3 and P_original is 0.5 MPa above the minimum in-situ stress, all the other input parameters are the same as the base case. Figure 10 shows the pressure decline and its derivatives with different values of enhanced effective permeability k_e at the end of pumping. From the results, we can clearly observe that there exists a “bump” on the pressure derivative during fracture closure before it reaches its final peak. In all cases, the pressure derivatives “bump” at a fracturing pressure that is 4.5 MPa below the ISIP, which is the exact value of P_original. So the values of P_original can be readily obtained from field DFIT data if it exhibits this pressure-dependent permeability signature. We can also observe that the higher the k_e, the large the initial slope of pressure derivatives.

Fig. 10

Pressure decline and its derivatives with before-closure pressure-dependent permeability

Under these circumstances, the effect of pressure-dependent permeability masks the initial phase of fracture closure and the moment when the fracture stiffness starts to change cannot be identified. In such cases, the “compliance method” is hard to apply. We can, however, modify our “variable compliance method” approach as follows: first, we identify the dimensionless G-time or the square root of time at the end of the first pressure derivative “bump” (i.e., end of pressure-dependent permeability) and at the intersection of pressure derivative and a tangent line passing through the origin (i.e., the closure point picked by the “tangent line method”). Then average the values of this two dimensionless G-time or the square-root-of-time and extrapolate back to the pressure curve that corresponds to the averaged G-time or the square root of time. Table 3 shows the estimated closures by the “tangent line method” and the “variable compliance method”. As can be seen, the “tangent line method” consistently underestimates the closure stress. This stems from the fact that the “tangent line method” assumes constant fracture stiffness and Carter’s leak-off during fracture closure, but these two assumptions are not valid during fracture closure (Wang and Sharma 2017b). The closure stress estimated by the “variable compliance method” gives significantly lower errors.

Table 3 Comparison of estimated closure stress from different methods with before-closure pressure-dependent permeability

3.2.2 Pressure Dependent Permeability Extends to After-Closure

The above cases are well-known as the so-called PDL cases (Barree et al. 2009) where pressure-dependent-permeability only occurs during the before-closure period. However, depending on the contrast between the matrix permeability and the natural fracture conductivity, natural fracture orientation, and the strength of asperities on the fracture walls, the residual conductivity of stimulated natural fracture may still enhance the overall flow capacity even after the fracture fluid pressure drops below the minimum in-situ stress. Let’s modify the above cases by assuming ${P_{{\text{original}}}}$= 25 MPa (10 MPa below minimum in-situ stress) and ${k_{\text{e}}}=20{k_0}$, Fig. 11 shows the simulated pressure decline and its derivatives with different values of c. Figure 3 shows that the parameter c controls how the effective permeability evolves as pressure declines. When c is positive and large, the permeability decline more sharply when the pressure approaches P_original. When c is negative, the smaller the c is, more reduction in permeability occurs during the early shut-in time. From the results, we can observe that when c = − 8, the pressure decline behavior is very similar to the Base Case, the early-time pressure-dependent-permeability is overshadowed by the dynamic fracture closure process and the changes in permeability in late-time is too small to be noticed on a diagnostic plot. However, in all other cases, we can see a clear defection on the pressure derivative curve after closure when the slope of pressure derivatives start to increase. On closer examination, we can notice that all the deflection points occur when the pressure drops to 25 MPa, which is exactly P_original where the effective permeability drops to a constant value.

Fig. 11

Pressure decline and its derivatives when pressure-dependent-permeability extend to after-closure

What is more interesting is how the pressure-dependent-permeability manifests itself on the log–log plot, as shown in Fig. 12. When c = − 8, the pressure derivative behavior resembles the Base Case except for the fact that after-closure linear flow does not emerge until the very end. In all other cases, we observe a pressure derivative “valley” or “dip” during the after-closure period. Relate to Fig. 11, it is found that the bottoms of these derivative valleys occur when the effective permeability drops to a constant value. It is surprising that all the pressure derivative curves finally converge into single − 1/2 slope regardless of their individual permeability evolution history, as long as their final constant permeability is the same. Unfortunately, in most field cases, the shut-in time is not long enough to observe the final linear flow period. The results also indicate that before the pressure dip occurs, it still possible to observe a short transient period of after-closure linear-flow. However, if the reduction in the effective permeability dominates the pressure transient behavior, instead of the diffusion process, then the transient after-closure linear may completely disappear and we can even observe a false radial flow. This is because the more sensitive the permeability is to pressure drop, the larger the pressure derivative slope will be distorted towards a smaller value. For example, when c = 8, the pressure derivative before the dip is even smaller than − 1, which can possibly be wrongly interpreted as spherical flow.

Fig. 12

Log–log plot of pressure derivative for different values of c

Table 4 shows the estimated closures by different methods. As can be seen, the “tangent line method” underestimates the closure stress and “compliance method” overestimates the closure stress, while the “variable compliance method” gives the least error.

Table 4 Comparison of estimated closure stress from different methods when pressure- dependent-permeability extends to after-closure

Figure 13 shows an example of field data where the signature of pressure-dependent-permeability emerges during the after-closure period (the late-time data on the square-root-time plot is truncated to better illustrate closure data). Because the pressure is measured at the surface, the early-time distortion of excessive pressure drop is caused by tip extension and reduction of friction in the wellbore and the near-wellbore region. At late-time, the fluctuation in pressure derivatives is caused by the thermal contraction and expansion of fluid and metal near the wellhead because of the cyclic fluctuation in the ambient temperature. This noisy derivative is often apparent when pressure changes are low in late-time. The before-closure data does not show any sign of pressure-dependent-permeability because of the dominant influence of dynamic fracture closure behavior with increasing fracture stiffness, however, a pressure derivative dip occurs after a few days of shut-in time. This indicates that there are well-connected and stimulated natural fractures within the distance of investigation (DOI) of this DFIT and the − 1 slope on the log–log plot before the pressure derivative tip is most likely caused by pressure dependent permeability, rather than real radial flow.

Fig. 13

Example of field case A when pressure-dependent-permeability extend to after-closure

Figure 14 shows another example of field data where the signature of pressure-dependent-permeability appears on both before and after-closure data. Previously, the occurrence of a pressure derivative tip in the after-closure data has been explained by using the dual-porosity model (Chipperfield 2006; Soliman et al. 2010). This is a possible explanation in some naturally fractured carbonate and coalbed methane (CBM) reservoirs. But increasingly, after-closure pressure derivative tip has been observed in many discretely fractured reservoirs, where the dual-porosity model is not applicable, as is evident in rate transient analysis (Anderson et al. 2010), pressure transient analysis (Kuchuk and Biryukov 2015) and cross-field studies (Raterman et al. 2017). It is also difficult to imagine that the diffusion process inside the well-connected natural fractures would take days to complete before the diffusion into matrix takes over as the dominant process if a dual-porosity assumption is made.

Fig. 14

Example of field case B with pressure-dependent permeability signature on both before and after closure data

The changes in effective permeability become more complicated if there are multiple natural fracture sets with different orientations and connectivity. Each fracture set has its individual influence on the effective permeability as pressure declines (e.g., some may be more pressure sensitive at a higher pressure while others at lower pressure) and the final effective permeability-pressure curve needs to be generated from up-scaling. Under these scenarios, Eq. (17) may not be adequate to delineate this more complicated permeability evolution.

3.3 Discretely Fractured Reservoir

in the case of sparsely or moderately fractured reservoirs, even though the stimulated natural fractures are discrete and not well-connected, they can interact with propagating hydraulic fracture and generate a complex fracture geometry. to make modeling and analysis tractable, we’ll first investigate a simplified version of a complex fracture geometry that only consists of two sets of vertical fractures with different orientations and fracture surface area, as shown in Fig. 15, and then more general scenarios will be discussed. In Fig. 15, we can see that the main hydraulic fracture (i.e., fracture set 1) is perpendicular to the minimum in-situ stress, while the natural fractures (i.e., fracture set 2) are perpendicular to the maximum in-situ stress. As pressure declines inside the fracture after shut-in, the natural fracture that opens against the maximum principal stress will close first, and the hydraulic fracture that opens against the minimum principal stress will be the last to close. here, there are two possible scenarios that are likely to happen during this sequential closure process: (1) the closed natural fracture maintains its hydraulic connectivity to the main hydraulic fracture. (2) The closed natural fracture loses its hydraulic connectivity to the main hydraulic fracture. We’ll discuss these two scenarios and their implications in interpreting DFIT data separately.

Fig. 15

Top view of complex fracture geometry with two sets of vertical fractures

3.3.1 Closed Fracture Maintains Its Hydraulic Connectivity to the Main Fracture

If the intersection of fractures are well aligned (not skewed) and supported by asperities and tortuous walls, then it is likely that the closed natural fractures can maintain hydraulic connectivity to the open fracture. In this case, the sequential closure of natural fractures or branches of a complex fracture will not alter the total leak-off surface area but will change the overall fracture stiffness evolution. Assume a complex fracture that consists of two sets of fractures, as shown in Fig. 15. The total surface areas are ${A_{{\text{f}}1}}~$and ${A_{{\text{f}}2}}~$for fracture set 1 and fracture set 2, respectively. The maximum horizontal in-situ stress is 38 MPa and the minimum horizontal in-situ stress is 33 MPa. We further assume that all fractures close like a PKN fracture. Figure 16 shows the fracture stiffness evolution with different surface area ratio. As can be seen, if we only have fracture set 2 (i.e., natural fractures), the fracture stiffness will increase at 39.5 MPa, and if we only have fracture set 1 (i.e., hydraulic fractures), the fracture stiffness will increase around 34.5 MPa. The overall fracture stiffness evolution is calculated using Eq. (15) with different surface area ratios. For such a complex fracture geometry, the overall fracture stiffness behaves like a parallel system of capacitors, so the changes in fracture stiffness are not directly proportional to the surface area ratio, but are mostly influenced by the fracture set that has the highest ratio of surface area to stiffness.

Fig. 16

Fracture stiffness evolution for complex fracture geometry if closed fracture maintains hydraulic connectivity

Figure 17 shows the pressure decline and its derivatives for a complex fracture geometry when closed natural fractures maintain their hydraulic connectivity to the main hydraulic fracture. Due to the fact that the fracture stiffness evolution is smooth and gradual, the closure of the natural fracture is undetectable on a G-function or the square root of time plot. But from the pressure derivatives, we can notice that the larger the surface area of the natural fracture, the sooner the pressure derivatives curve upward and the faster the pressure decline during fracture closure.

Fig. 17

Pressure decline and its derivatives of complex fracture geometry if closed fracture maintains hydraulic connectivity

Table 5 summarizes the estimated closure stress by different methods. As always, the “tangent line method” underestimates the closure stress, while “compliance method” overestimates closure stress. The “compliance method” gives a much larger error if the surface area of natural fracture is large. This is because the “compliance method” picks the pressure when natural fracture edges or tips start to closure, which can be much higher than the minimum in-situ stress, because of different orientation of natural fractures. The “variable compliance method” yields the least error.

Table 5 Comparison of estimated closure stress of complex fracture geometry if closed fracture maintains hydraulic connectivity

In fact, the information on fracture complexity can’t be detected under such cases, and compared to a single hydraulic fracture scenario (i.e., only fracture set 1 in Fig. 16), the impact of natural fractures on overall fractures stiffness evolution can be substituted by “rougher” fracture walls with larger contact width and higher contact reference stress (Wang and Sharma 2017b) to obtain an earlier and steeper increase in fracture stiffness as pressure declines. In addition, height recession can also lead to an earlier and steeper increase in fracture stiffness (Wang and Sharma 2017b). So based on “before-closure” DFIT data alone, we may not be able to distinguish the causes of the increase in fracture stiffness (fracture complexity or surface roughness or recession in barrier layers). Nevertheless, as discussed by Wang and Sharma (2017b), the “variable compliance method” is insensitive to fracture geometry, surface roughness, reservoir properties, and stiffness evolution, and from the above results, we see that it is also much less sensitive to the existence of natural fractures, so the “variable compliance method” is a more reliable way of estimate closure stress, especially when it is unclear whether the created fracture geometry is complex or planar.

3.3.2 Closed Fracture Loses Its Hydraulic Connectivity to the Main Fracture

If the intersections of fractures are skewed and not well-aligned (such as a T-shaped fracture), then it is likely that the closed fracture will lose its hydraulic connectivity to the main fracture. In such cases, the sequential closure of natural fractures or branches of a complex fracture will alter both the total leak-off surface area and the overall fracture stiffness evolution. Assume the same complex fracture as discussed in the previous section. The maximum horizontal in-situ stress is 37 MPa and the minimum horizontal in-situ stress is 33 MPa. We further assume the natural fractures will gradually lose their hydraulic connectivity to the open hydraulic fracture when fluid pressure drops around 37 MPa (i.e., the closure stress of natural fracture). Figure 18 shows the fracture stiffness evolution with different surface area ratio when natural fractures lose their hydraulic connectivity after closure. Compared to Fig. 16, we can notice that the overall fracture stiffness evolution is not monotonically increasing with declining pressure anymore. The surface area ratio will shape the fracture stiffness evolution before the closure of natural fractures, but once the pressure drops to a certain level and disconnect all the natural fractures, the overall fracture stiffness becomes the fracture stiffness of the remaining hydraulic fracture.

Fig. 18

Pressure decline and its derivatives of complex fracture geometry if closed fracture loses hydraulic connectivity

Figure 19 shows the pressure decline and its derivatives of complex fracture geometry when closed fractures lose hydraulic connectivity. It can be clearly observed that there are two peaks on pressure derivatives curve, the first one is associated with the closure process of natural fractures, and the second one is associated with the closure process of the hydraulic fracture.

Fig. 19

Pressure decline and its derivatives of complex fracture geometry if closed fracture loses hydraulic connectivity

If we only analyzed the portion of data after the first peak of pressure derivatives and use it to estimate the closure stress associated with the closure of the hydraulic fracture, we can compare the results from different methods, as shown in Table 6. Again, we can notice that the “tangent line method” underestimates closure stress while the “compliance method” overestimates closure stress. The “variable compliance method” is more reliable and gives the least error.

Table 6 Comparison of estimated closure stress of complex fracture geometry if closed fracture loses hydraulic connectivity

In reality, a complex fracture can consist of many fracture sets with different orientations and surface areas. The approach and analysis presented for our simplified cases are still valid for these more general scenarios. Assuming that a complex fracture has four sets of fractures with equal surface area, but open against different in-situ normal stresses (37 MPa, 35 MPa, 33 MPa, and 31 MPa) because of their orientations, Fig. 20 shows the evolution of fracture stiffness as a function of fracturing pressure. As can be seen, if natural fractures gradually lose their hydraulic connectivity when fluid pressure drops to the normal stress that is perpendicular to that fracture surface, the overall fracture stiffness will exhibit three peaks before it finally reflects the fracture stiffness of the last open fracture.

Fig. 20

Fracture stiffness evolution of complex fracture geometry with four sets of fracture

Figure 21 shows the corresponding pressure decline and its derivatives. As expected, four peaks emerge on the pressure derivatives and if we only analyze the portion of data after the third peak to estimate closure stress, the “tangent line method” underestimates the closure stress by around 1 MPa. The “variable compliance method” gives a closer value. In general, the estimated closure stress by the “tangent line method” can be regarded as the lower bound of closure stress and the closure stress estimated by the “compliance method” can be viewed as the upper bound of closure stress.

Fig. 21

Pressure decline and its derivatives of complex fracture geometry with four sets of fracture

It should be emphasized that the closure pressure of natural fractures does not necessarily equal the pressure where the natural fractures lose their hydraulic connectivity to the main fracture. At what pressure these hydraulic disconnections occur depends on the tortuosity, roughness properties of fracture walls and geometry at the intersection. It is very likely that some of the closed natural fractures still maintain their hydraulic connectivity to the main hydraulic fracture until the pressure drops below the minimum in-situ stress. In such cases, the fracture complexity can manifest itself in both before-closure and after-closure data. Figure 22 shows a good example of such a scenario. As can be seen, multiple pressure derivative peaks span the entire duration of the test.

Fig. 22

Field example of multiple pressure derivative peaks on the G-function plot (Wallace et al. 2014)

4 Comparison with Experiment

Craig et al. (2017) compared and discussed fracture closure stress estimated by the “Compliance Method” and the “Tangent Line Method” using tiltmeter measurements and laboratory experiments. Figure 23 shows the G-function plots using data extracted from laboratory experiments from their study. As expected the pressure decline is affected by tip extension and fluid transient behavior along the fracture soon after shut-in, so a brief pressure derivative spike often immediately follows shut-in. In many cases, this pressure derivative spike may mask the “open fracture period” (when fracture stiffness is still constant) and make it difficult to locate the moment when the fracture stiffness starts to increase. If the closure time is not long enough, this early-time abnormal pressure (large pressure drop during a short time interval) can’t be distinguished from the signature of pressure-dependent permeability, which is normal in the case in laboratory experiments where the fracture closes in less than 1 min. In the soft rock case of Fig. 23a the imposed closure stress is 7 MPa, but the closure stress estimated by the “Tangent Line Method” is only 3 MPa, which is significantly lower. It can be observed that the early-time pressure derivative spike masks a large portion of before closure data, the “compliance method” and “variable compliance method” are not applicable. In the moderately hard rock case of Fig. 23b, the imposed closure stress is 16 MPa, the closure stress estimated by the “Tangent Line Method” is 14.32 MPa and the closure stress estimated by “compliance method” is 20.16 MPa. The closure stress estimated by the “variable compliance method” is 17 MPa at the averaged G-function time of 1.745. This result is consistent with our simulated synthetic cases presented in this study and our previous study (Wang and Sharma 2017b). Laboratory experiments also show that the “variable compliance method” gives the least error and “Tangent Line Method” normally underestimates closure stress.

Fig. 23

Laboratory fracture closure experiment for soft (a) and moderately hard rock (b) (Craig et al. 2017)

5 Discussion

Examining Eqs. (6)–(14) closely, it is evident that the pressure decline is governed by a linear partial differential equation (PDE) system in the formation that is coupled with an ordinary differential equation (ODE) at the fracture surface. The minimum in-situ stress is just one of many implicit factors that shape the evolution of the fracture pressure in the boundary ODE. the primary cause of the error associated with the “tangent line method” stems from the traditional G-function plot analysis, where the assumptions of carter’s leak-off (i.e., constant pressure boundary condition in the fracture) and constant fracture stiffness during closure (changes abruptly to infinite at closure stress) are violated during fracture closure. the primary cause for the error associated with the “compliance method” is the fact that the increase in fracture system stiffness can happen even before the fracture pressure drops to the minimum in-situ stress (as the tips of the fracture come into contact or sequential closure of fracture branches).

For planar fracture geometry, the fracture closes progressively from its edges to the center with a gradual increase in stiffness (or decrease in compliance). Both numerical modeling (as shown in Fig. 5) and tiltmeter measurements (as shown in Fig. 6) show smooth curves without a sharp indication of closure stress. The pressure decline signature that reflects the combined effects of pressure-dependent leak-off and fractures stiffness evolution is not going to yield additional information on closure stress. The “variable compliance method”, provides an alternative way to estimate the minimum in-situ stress. By history matching the DFIT data, using properties of fracture surface roughness and formation flow capacity, the range of un-propped fracture conductivity and formation permeability can be obtained for various fracture dimensions (Wang and Sharma 2018b).

In naturally fractured reservoirs, it is difficult to quantify such information through a history match. In the case of pressure-dependent permeability, the pressure response is affected by the declining effective permeability within the distance of investigation and the increase of fracture stiffness. Those two independent mechanisms are intertwined and cannot be separated from the DFIT data, especially in the case where the period of pressure-dependent permeability spans a large portion of before-closure data. In other words, the information on the individual evolution of fracture stiffness and effective permeability is lost and cannot be recovered quantitatively from DFIT data. In some heavily fractured reservoirs where permeability is extremely sensitive to pressure, the fracture-wellbore system stiffness evolution can be completely masked by pressure-dependent leak-off behavior, and thus, it becomes particularly challenging to identify closure stress. Under these circumstances, forced fracture closure via flow back at a constant rate would be a better option, because it ensures that the information on fracture stiffness evolution can be recovered by plotting pressure vs cumulative flow back volume, as long as flow back rate is much larger than the leak-off rate and becomes the dominating force for pressure decline during the period of fracture closure.

Besides the G-function or square-root-of-time plot, the log–log plot is an extremely useful tool to identify flow regimes and aid in interpretation when the effective permeability is pressure-dependent. The traditional method of using variable Carter’s leak-off coefficient to account for pressure-dependent permeability not only invalidates the very assumptions of Carter’s leak-off model but also fails to depict leak-off behavior when pressure-dependent permeability continues to exist during the after-closure period.

In the case of complex fractures, if the closed fracture segments retain their hydraulic connectivity to the main hydraulic fracture, we will get a smooth pressure decline response like a planar fracture. In such cases, we do not know what the topology of the complex fracture is and we will not be able to constrain the fracture dimensions using a simple material balance calculation. Without a good estimation of the initial fracture geometry to start with, a meaningful history match and uncertainty analysis are difficult to achieve. If the closed fracture segments lose hydraulic connectivity to the main hydraulic fracture, we will observe multiple pressure derivative peaks on G-function or square-root-of-time plots. In such cases, we can discern, how many sets of fractures (with different orientations), are intercepted by the main hydraulic fracture. However, we still cannot recover the fracture topology, because the information on the individual fracture surface area, orientations, and their stiffness evolution are smeared together as a compound effect and cannot be separated. The situation can get more complicated if some of the closed fracture segments retain their hydraulic connectivity to the main fracture while others do not. Similar to the rate transient analysis (RTA) in naturally fractured reservoirs (Wang 2018), the nature of non-unique interpretation of pressure transient response requires additional independent data to constrain our quantitative analysis. Nevertheless, our proposed “variable compliance method” provides an alternative way to estimate in-situ stress, which is more reliable than established methods, even in naturally fractured reservoirs.

Even though it is challenging to analyze DFIT data quantitatively in naturally fractured reservoirs, valuable information can be obtained from such an analysis and this can have substantial implications for reservoir stimulation and geomechanical modeling. For example, our field experience indicates that wells that exhibit multiple pressure derivative peaks in diagnostic plots of DFIT data is normally a poor producer after hydraulic fracturing, and often encounters premature screen-out during stimulation. This is because if the stimulated natural fracture losses its connectivity to the main hydraulic fracture during fracture closure, then it is less likely to have enough capacity to transport fluid to the wellbore through the main hydraulic fracture during production. It also signals poor connectivity at fracture intersections, which poses difficulties for proppant transport. In addition, DFIT analysis is also extremely useful in constraining horizontal stress anisotropy. If pressure-dependent-permeability does appear on before-closure data, then the endpoint can be interpreted as a lower bound of the closure stress on the secondary fracture set. Thus, it can be interpreted as a lower bound for the maximum horizontal stress. If the stimulated natural fractures are poorly-connected with multiple pressure derivative peaks, then the first peak of pressure derivative, which signals the hydraulic closure of a fracture branch, can be interpreted as the lower bound of the maximum horizontal stress (i.e., the first peak of pressure derivative does not guarantee its association with the first closed fracture branch or the mechanical closure of the fracture, it only reflects the first occurrence of the loss of hydraulic connectivity at a fracture intersection).

In general, the approaches and methods used in DFIT analysis can also be applied to any pressure fall-off data with closing fractures, such as the shut-in period of multi-stage hydraulic fracturing and water injection process with induced fractures. Similar to rate transient analysis, the outcome of the quantitative analysis of DFIT data may not be unique, and more often than not, other independent data are needed to constrain/calibrate our interpretation and perform a reasonable sensitivity analysis. Despite the fact that there are other techniques to characterize subsurface fracture systems, such as using seismic surveys to detect large scale fractures/faults, running image logs to detect natural fractures that intersect the wellbore, they cannot provide any information on the stress-dependent connectivity and flow capacity of the stimulated fractures because they are measured under static conditions. On the contrary, DFIT is a dynamic process where both pressure transients in the reservoir and fracture closing behavior can manifest themselves on different diagnostic plots. This provides us with critical information to characterize fractured reservoirs that cannot be obtained by any other means.

6 Conclusions

During the past decade, DFIT has evolved into an indispensable tool for estimating in-situ stress, calibrating hydraulic fracture models and characterizing reservoir flow capacity and fracture complexity/connectivity. In this study, we present a new pressure transient model for DFIT analysis in naturally fractured reservoirs, which not only preserves the physics of unsteady-state reservoir flow behavior, elastic fracture mechanics, material balance, variable fracture compliance during fracture closure, but also incorporates pressure-dependent effective permeability and sequential closure of complex fracture branches and natural fractures. We show that the results from our model agree well with laboratory and field data, and the unique signatures associated with natural fracture closure can now be interpreted in a meaningful manner. Conclusions reached from the analysis presented in this paper include the following:

• 1. Square-root-of-time and G function plots yield the same quantitative information in both homogenous and naturally fractured reservoirs.

• 2. If the stimulated natural fractures are well-connected, the pressure-dependent-permeability may or may not appear on before-closure data, depending on the competing effect of decreasing permeability and increasing fracture stiffness.

• 3. If pressure-dependent permeability occurs during the before-closure time period, it can partly mask some information on fracture stiffness (or compliance) evolution and the associated mechanical closure process.

• 4. If pressure-dependent permeability continues into the after-closure period, a pressure derivative dip may occur at the moment when the effective permeability drops to a constant value. Depending on how sensitive the permeability is to pressure, a false radial flow or spherical flow might emerge during the after-closure period.

• 5. In sparsely fractured reservoirs with complex fracture geometry, if the closed fracture maintains its hydraulic connectivity to the open fracture, then fracture complexity cannot be detected from DFIT before-closure data because the pressure derivative response resembles a fracture with “rougher” walls or height recession from a planar fracture. However, if the closed fracture loses its hydraulic connectivity to the main hydraulic fracture, then fracture complexity can be detected qualitatively where multiple peaks on the pressure derivative plot are observed.

• 6. The lower bound of horizontal stress anisotropy can be estimated from DFIT data if pressure-dependent permeability or multiple pressure derivative peaks occur on diagnostic plots during the before-closure period.

• 7. In naturally fractured reservoirs, the conventional “tangent line method” consistently underestimates closure stress; it only can be interpreted as the lower bound of minimum in-situ stress. The “compliance method” tends to only reflect the onset of fracture closure (i.e., closure on fracture edges or closure of fracture branches). Our proposed “variable compliance method” gives a much more accurate and reliable estimation of minimum in-situ stress in both homogenous and naturally fractured reservoirs.

Appendix: Modeling Pressure Transient Behavior during DFIT using Method of Lines (MOL)

In essence, DFIT analysis is a pressure transient analysis. However, unlike pressure transient analysis of tradition well-testing techniques, the fracture cannot be treated as a static and the leak-off rate does not follow Carter’s leak-off assumption (i.e., constant fracturing pressure), but rather coupled with variable fracture-wellbore system compliance/stiffness during fracture closure. Classic well-test solutions normally assume a constant injection rate, but in reality, “constant injection rate” does not equal “constant leak-off rate into formation”, because over 90% of injected fluid stay inside fracture at the end of pumping, instead of leaking into formation, thus, make DFIT violate the required boundary condition for using existing well-test solutions. That’s why G-function and classic well-test solution based models can lead to incorrect interpretation and are not capable of bridging both before and after closure data coherently. Figure 24 illustrates a linear leak-off from fracture surface into the formation.

Fig. 24

Illustration of one-dimensional leak-off

As discussed in Sect. 2.1, the pressure transient behavior during DFIT is uniquely described by the following equations:

$$\frac{{\partial P}}{{\partial t}}=\frac{1}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{\partial }{{\partial x}}\left( {k\frac{{\partial P}}{{\partial x}}} \right)$$

(19)

$$\frac{k}{{{\mu _{\text{f}}}}}~\frac{{{\text{d}}P}}{{{\text{d}}x}}=\frac{1}{{2{S_{\text{f}}}}}\frac{{{\text{d}}{P_{\text{f}}}}}{{{\text{d}}t}}~\quad {\text{at}}~x=0$$

(20)

$$P={P_0}~\quad {\text{at}}\;t=0,~\quad x>0$$

(21)

$$~~P={\text{ISIP~}}\quad {\text{at}}\;t=0,~\quad x=0$$

(22)

Since the permeability k in the partial differential equation (PDE) of Eq. (19) is not limited to a constant value and the boundary condition at the fracture surface (i.e., x = 0) is an ordinary differential equation (ODE) by itself, the analytical solution does not exist. To solve this system of PDE with ODE boundary condition, the concept of method of lines (MOL) is used, to replace the spatial derivative in the PDE with algebraic approximations, and then the PDE system can be transformed into a system of ODEs, which can be solved simultaneously and efficiently by well-established numerical methods. Since the MOL essentially replaces the problem PDEs with systems of approximating ODEs, the addition of other ODEs is easily accomplished.

Let divide the reservoir domain in the x-direction into a number of M points with uniform spacing of $\varDelta x$. Using the finite difference method, Eq. (19) can be represented in a discretized manner as:

$$\frac{{{\text{d}}{P_{\text{i}}}}}{{{\text{dt}}}}=\frac{1}{{{{{{\upmu}}}_{\text{f}}}\phi {{\text{c}}_{\text{t}}}}}\frac{{\left( {{k_{\text{i}}}+{k_{{\text{i}}+1}}} \right)\left( {{P_{{\text{i}}+1}} - {P_{\text{i}}}} \right) - \left( {{k_{\text{i}}}+{k_{{\text{i}} - 1}}} \right)\left( {{P_{\text{i}}} - {P_{{\text{i}} - 1}}} \right)}}{{2\Delta {x^2}}},{\text{~}}2 \leq {\text{i}} \leq {\text{M}} - 1$$

(23)

where i is an index designating a position along a grid in the x-direction. The initial condition can be written as:

$$~{P_i}=\left\{ {\begin{array}{*{20}{c}} {{\text{ISIP}},~~~~~~~~~i=1} \\ {{P_0},~~~~~~~~~~~~~i \geq 2} \end{array}} \right.~\quad {\text{at}}~t=0$$

(24)

At the boundary of the fracture surface, we can have

$$\frac{{{\text{d}}{P_1}}}{{{\text{d}}t}}=\frac{{2{S_{\text{f}}}{k_1}}}{{{\mu _{\text{f}}}}}~\frac{{{P_2} - {P_1}}}{{\Delta x}}$$

(25)

If the simulation domain is large enough compared to the simulated time scale, then pressure transient front will not reach the boundary and it can be treated as infinite acting boundary condition where$P={P_{0~}}\;{\text{as}}\;x \to \infty$. Just for the purpose of completing the ODE system, here we assume no flux boundary condition (it is also a symmetric condition where at a fictitious point M + 1 outside the grid in x satisfying$~{P_{M+1}}={P_{M - 1}}$) at the M point:

$$\frac{{{\text{d}}{P_M}}}{{{\text{d}}t}}=\frac{{{k_M}}}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{{P_{M - 1}} - 2{P_M}+{P_{M - 1}}}}{{\Delta {x^2}}}$$

(26)

Combine Eqs. (22), (24) and (25), a system ODE for initial value problem can be assembled:

$$\left[ {\begin{array}{*{20}{c}} {\frac{{{\text{d}}{P_1}}}{{{\text{d}}t}}} \\ {\frac{{{\text{d}}{P_2}}}{{{\text{d}}t}}} \\ {\begin{array}{*{20}{c}} \vdots \\ {\frac{{{\text{d}}{P_{M - 1}}}}{{{\text{d}}t}}} \\ {\frac{{{\text{d}}{P_M}}}{{{\text{d}}t}}} \end{array}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\frac{{2{S_{\text{f}}}{k_1}}}{{{\mu _{\text{f}}}}}~\frac{{{P_2} - {P_1}}}{{\Delta x}}} \\ {\frac{1}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{\left( {{k_2}+{k_3}} \right)\left( {{P_3} - {P_2}} \right) - \left( {{k_2}+{k_1}} \right)\left( {{P_2} - {P_1}} \right)}}{{2\Delta {x^2}}}} \\ {\begin{array}{*{20}{c}} \vdots \\ {\frac{1}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{\left( {{k_{M - 1}}+{k_M}} \right)\left( {{P_M} - {P_{M - 1}}} \right) - \left( {{k_{M - 1}}+{k_{M - 2}}} \right)\left( {{P_{M - 1}} - {P_{M - 2}}} \right)}}{{2\Delta {x^2}}}} \\ {\frac{{{k_M}}}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{{P_{M - 1}} - 2{P_M}+{P_{M - 1}}}}{{\Delta {x^2}}}} \end{array}} \end{array}} \right]$$

(27)

The first order time derivative can be approximated using a backward finite difference:

$$\frac{{\partial {P_i}}}{{\partial t}}~ \approx \frac{{P_{i}^{n} - P_{i}^{{n - 1}}}}{{\Delta t}}+O(\Delta t)$$

(28)

where t moves forward in steps that indexed by n. Substitute Eq. (25) into Eq. (26) we can get

$$\left[ {\begin{array}{*{20}{c}} {\frac{{P_{1}^{n} - P_{1}^{{n - 1}}}}{{\Delta t}}} \\ {\frac{{P_{2}^{n} - P_{2}^{{n - 1}}}}{{\Delta t}}} \\ {\begin{array}{*{20}{c}} \vdots \\ {\frac{{P_{{M - 1}}^{n} - P_{{M - 1}}^{{n - 1}}}}{{\Delta t}}} \\ {\frac{{P_{M}^{n} - P_{M}^{{n - 1}}}}{{\Delta t}}} \end{array}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\frac{{2{S_{\text{f}}}{k_1}}}{{{\mu _{\text{f}}}}}~\frac{{P_{2}^{n} - P_{1}^{n}}}{{\Delta x}}} \\ {\frac{1}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{\left( {k_{2}^{n}+k_{3}^{n}} \right)\left( {P_{3}^{n} - P_{2}^{n}} \right) - \left( {k_{2}^{n}+k_{1}^{n}} \right)\left( {P_{2}^{n} - P_{1}^{n}} \right)}}{{2\Delta {x^2}}}} \\ {\begin{array}{*{20}{c}} \vdots \\ {\frac{1}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{\left( {k_{{M - 1}}^{n}+k_{M}^{n}} \right)\left( {P_{M}^{n} - P_{{M - 1}}^{n}} \right) - \left( {k_{{M - 1}}^{n}+k_{{M - 2}}^{n}} \right)\left( {P_{{M - 1}}^{n} - P_{{M - 2}}^{n}} \right)}}{{2\Delta {x^2}}}} \\ {\frac{{{k_M}}}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{P_{{M - 1}}^{n} - 2P_{M}^{n}+P_{{M - 1}}^{n}}}{{\Delta {x^2}}}} \end{array}} \end{array}} \right]$$

(29)

Now we can solve Eq. (29) explicitly for the solution at an advanced time step $P_{i}^{n}$ in terms of the solution of the previous time step $P_{i}^{{n - 1}}$. However, since $P_{{i - 1}}^{n}$ is unknown so Eq. (29) is implicit in $P_{i}^{n}$. For each grid point, the full set of algebraic equations has to be solved simultaneously.