1 Introduction

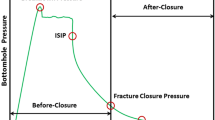
The exploitation of low-permeability unconventional reservoirs has become more and more important in the energy supply chain. Hydraulic fracturing is the main technology for developing these shale gas and shale oil resources. Hydraulic fracturing like many other subsurface activities is governed by rock mechanics parameters, among them in situ stress plays a critical role on the outcome of hydraulic fracturing treatments. Diagnostic fracture injection tests (DFIT) are widely used to estimate formation properties such as initial pore pressure, formation permeability (Wang and Sharma 2019; Cai et al. 2020), and closure pressure (Barree et al. 2007) in these low-permeability reservoirs. The aforementioned properties play an essential role in hydraulic fracturing design and long-term production forecasting. During a DFIT, untreated water is usually injected for a short period of time at a low rate to create a small fracture, although some authors have recommended a high injection rate (Craig 2014). After injection, the well is shut-in for an extended period of time. Pressure decline after shut-in is then collected and analyzed to obtain the reservoir properties. A typical DFIT test procedure is illustrated in Fig. 1.

Fig. 1
figure 1

Example of an ideal DFIT test procedure showing the pressure increase and falloff during injection and the shut-in period

Full size image

Traditional DFIT analyses to determine closure stress are based on G-function and its derivatives (Nolte 1979). Embedded within the G-function’s derivation are few assumptions: a constant leakoff coefficient, constant fracture stiffness, uniform fracture closure, and planar fracture geometry. Following these assumptions, fracture pressure linearly declines with the G-function as

$$\Delta P\left(\Delta {t}_{\mathrm{D}}\right)=\frac{C{H}_{\text{p}}{E}{^{\prime}}\sqrt{{t}_\text{inj}}}{{H}^{2}{\beta }_{\text{s}}}G\left(\Delta {t}_\text{D}\right),$$
(1)

where \(C\) is the fluid-loss coefficient; \({H}_{\text{p}}\) is fluid-loss height; H is fracture height; E′ is the plane strain Young’s modulus, \(\Delta {t}_{\text{D}}=\Delta t/{t}_{\text{inj}}\); \(\Delta t\) is the time after shut-in; \({t}_{\text{inj}}\) is the duration of the injection; and \({\beta }_{\text{s}}\) is the ratio of average and wellbore pressure while shut-in (Nolte 1979). The G-function is given by

$$G\left(\Delta {t}_{\text{D}}\right)=\frac{4}{\pi }\left[g\left(\Delta {t}_{\text{D}}, \alpha \right)-g\left(0, \alpha \right)\right],$$
(2)

The G-function is only weakly dependent on α ranging from 0.5 to 1.0 (McClure et al. 2016). If the leakoff rate along the fracture is assumed to be uniform, G-function reduces to the square root of time. The square root of time is also widely used (Zoback 2007). When α = 1, \(g\left( \Delta {t}_{\text{D}}\right)\) is given by

$$g\left(\Delta {t}_{\text{D}}\right)=\frac{4}{3}\left[{\left(1+\Delta {t}_{\text{D}}\right)}^{1.5}-\Delta {t}_{\text{D}}^{1.5}\right],$$
(3)

and \(\Delta {t}_{\text{D}}\), which is the elapsed time normalized by the injection time, is defined as

$$\Delta {t}_{\text{D}}=\frac{t-{t}_\text{inj}}{{t}_\text{inj}},$$
(4)

where \(t\) is the elapsed time since the beginning of pumping. From Eq. (1), the plot of pressure versus G-function is expected to be a straight line and the deviation from the straight line indicates the occurrence of the fracture closure that can be used to identify the minimum horizontal stress (Castillo 1987). The slope of this straight line can also be used for calculating the pressure-independent leakoff coefficient. By overserving Eq. (1), \(G\times {\text{d}}P/{\text{d}}G\) forms a straight line that can be used to determine the fracture closure as well (Barree and Mukherjee 1996). However, in reality, plots of pressure vs. G-time often show non-linear behaviors. The nonideal observations are mostly contributed by wellbore and near-wellbore pressure drops, pressure-dependent leakoff, fracture height recession, the closing of secondary transverse fractures, and fracture tip-extension (Nolte 1991; Barree et al. 2007; Jung et al. 2016). The typical pressure decline behaviors are summarized in Fig. 2. According to Barree et al. (2007), the closure pressure can be determined by the tangential point between a straight line that passes the origin and the plot when the \(G\times {\text{d}}P/{\text{d}}G\) curve is concave upward. When the curve is concaving downward, the fracture closure time is picked when the curve stops increasing. Instead of using the tangent line method suggested by Barree et al. (2007), McClure et al. (2016) propose the fracture compliance method and advocate for picking the closure pressure at the initial deviation from linearity of \(G\times {\text{d}}P/{\text{d}}G\). The authors suggest that in most cases, \(G\times {\text{d}}P/{\text{d}}G\) curves upward due to the change in fracture stiffness during fracture closure rather than a more traditional interpretation such as fracture height recession or the storage effect driven by the closure of activated natural fractures. Wang and Sharma (2017) suggest that the fracture compliance method overestimates the closure pressure, and the traditional G-function analysis underestimates the closure pressure. They propose combining the tangential method with the compliance method to provide a more accurate assessment of the closure pressure.

Fig. 2
figure 2

Schematics of ideal and nonideal behaviors in the \(G\times {\text{d}}P/{\text{d}}G\) plot

Full size image

In addition to methods based on G-function plots, there are other efforts to analyze DFIT data using different types of plots. Bourdet plots (Bourdet et al. 2004) show the change in pressure \(\Delta p\) and \(\Delta t\times {\text{d}}\Delta p/{\text{d}}\Delta t\) vs. shut-in time \(\Delta t\) in log–log scale during fracture closure. Mohamed et al. (2011), Marongiu-Porcu et al. (2011) and Marongiu-Porcu and Retnanto 2017) modify Bourdet plots by taking the derivative with respect to superposition time \(\tau \) to account for the injection period. Superposition time \(\tau \) is defined as

$$\tau =\frac{\Delta t+{t}_{\text{inj}}}{\Delta t}.$$
(5)

Craig and Blasingame (2006) advocate for using the effective pressure response to interpret DFIT data. The effective pressure response is defined as

$$I\left(\Delta p\right)= {\int }_{0}^{{t}_{\text{inj}}+\Delta t}\Delta p {\text{d}}t,$$
(6)

i.e., the Bourdet plot is modified from plotting \(\Delta p\) and \(\Delta t\times {\text{d}}\Delta p/{\text{d}}\Delta t\) to the effective pressure response, \(I\). The wellbore storage period on the Bourdet plot of the effective pressure is long due to low formation permeability and the storage effect associated to the wellbore and the fracture. Craig and Blasingame (2006) suggest identifying the fracture closure at the point where the fracture/wellbore storage changes (which is caused by the changing fracture stiffness at closure). This corresponds to the time during the wellbore storage period that a deflection can be identified in the Bourdet plot with respect to effective pressure.

The existing DFIT analyses investigate the effect of pressure-dependent leakoff, transverse storage, and fracture height recession on the pressure decline. However, there is an important practical issue that has not yet received sufficient attention. Due to excessive frictions and flow restrictions at the perforations, axial fractures may develop along the wellbore to accommodate fluid flow into the transverse fractures (Weijers et al. 1994), as shown in Fig. 3a. This phenomenon differs from the nonplanar fracture problem due to the activation of natural fractures, as both the axial fracture and the transverse fracture are directly and separately connected to the wellbore. Due to the geometry of horizontal wells, an increase in the bottomhole pressure will generate tensile tangential stresses that may overcome the tensile strength of the axial fracture and trigger its initiation (Abbas et al. 2013). In the field, the initiation of an axial fracture is more favorable if the injection rate is high enough. A schematic diagram of axial and transverse fractures from a horizontal borehole is shown in Fig. 3b. However, axial fractures may not extend quite as far from the wellbore since tectonic stress and stress shadowing favor the propagation of transverse fractures. Nevertheless, the closure of the axial fracture during DFIT adds complexity to the analysis and causes traditional analysis to result in significant inaccuracy when determining the closure stress. Jung et al. (2016) present a case study using a 2D hydraulic fracture simulation where a small axial fracture forms initially parallel to the wellbore and then reorients in the direction perpendicular to the minimum horizontal stress. However, the competition between the axial fractures and the transverse fractures can be complicated, which is primarily determined by the initial defect length and the stress field (Lecampion et al. 2013). The axial fractures and the transverse fractures may also initiate at the same time depending on their energy requirement. In addition, due to the short injection period during DFITs, the size of the axial fractures is comparable to the transverse fractures (see Fig. 3a). Sherman et al. (2015) simulate initiations of the axial fractures and the transverse fractures using a fully coupled 3D finite element hyraulic fracturing model. The study shows that after the initial development of an axial fracture, the transverse fracture forms as a branch of the axial fracture immediately (around 0.5 s after starting injection). The branching location is close to the wellbore instead of the tip of the axial fracture. Ugueto et al. (2019) also report the simultaneous occurrences of the axial fractures and the transverse fractures using distributed temperature sensing (DTS). The observations are consistent with the numerical study from Sherman et al. (2015). More recently, Daneshy (2020) documented initiation of axial fractures during injection in closely spaced clusters in horizontal wells. Hence in this study, we presumed simultaneous initiation of the axial and transverse fractures. Modelling this phenomenon requires detailed modelling of perforation holes (Wang and Dahi Taleghani 2014), which has no impact on the result of the DFIT, hence we skip this part of the problem and mainly focus on how presence of axial fractures may impact DFIT data and its interpretations.

Fig. 3
figure 3

(a) Experimental result showing axial and transverse fractures initiating at the same time (Weijers et al. 1994). (b) Schematic diagram of axial and transverse fractures from the horizontal borehole

Full size image

In this work, we simulate the DFIT using a coupled geomechanics and fluid flow model and demonstrate that the estimation of minimum horizontal stress (\({s}_\text{h}\)) can be inaccurate in presence of axial fractures. In addition, residual fracture width from fracture surface roughness can lead to the overestimation of \({s}_\text{h}\). Therefore, we propose a calibration method to correct the closure stress from DFIT. Since the axial fracture is perpendicular to the maximum horizontal stress (\({s}_\text{H})\), we can also infer \({S}_\text{H}\) from the proposed analysis. We propose what we call the reflection point method to determine \({S}_\text{H}\). Based on our analysis, if there is an indication of the presence of an axial fracture, one can consider the maximum horizontal stress to be at the first reflection point where the pressure-dependent leakoff (PDL) effect dominates the transverse storage effect. Transverse storage occurs when the main fracture intercepts a secondary fracture. The secondary fracture can provide pressure support to the main fracture rather than PDL effect. While “transverse fracture” refers to the secondary fracture in DFIT, it refers to the main fracture in the literature on the initiation of axial fractures (Weijers et al. 1994; Abbas et al. 2013). To avoid confusion, in this paper, we use “transverse fracture” to refer to the fracture that propagates perpendicular to the wellbore (or the minimum horizontal stress), which stands in contrast to the axial fracture (or longitude fracture). We also use the term “fracture storage effect” to represent pressure support from the axial fracture instead of relying on the transverse fracture storage effect commonly used in the DFIT literature.

2 Methodology

In this study, a fully three-dimensional model is created to simulate DFIT in horizontal wells. To fully understand the fracture closure process during DFIT, a realistic description of induced transverse fractures and potential axial fractures is required. Thus, the modeling consists of two steps: the injection stage and the well shut-in stage. The cohesive zone method (CZM) is adopted to simulate the initiation and propagation of fractures. In the CZM, cohesive elements are pre-inserted as potential paths of fracture propagation and these paths can be adjusted to align with evolving fracture paths. During injection, the fluid pressure in the cohesive elements increases, which causes the interfaces of the cohesive elements to begin separating. The process is governed by the traction–separation law (TSL; for more details, see Yu et al. (2018). For fluids, we presumed single-phase Newtonian fluid with constant viscosity and compressibility. The effect of gravity on the fluid flow is neglected here, as the length of the fracture and injection time are too short to realize this effect. During fracture propagation, two sets of fractures may form: main fracture, which is perpendicular to the minimum horizontal stress, and axial fractures, which are parallel to the well and form due to frictions at perforations (Weijers et al. 1994). Figure 4a shows the configuration of cohesive elements representing potential paths for axial and transverse fractures with respect to the wellbore. In the cohesive elements, pressure nodes for the fluid mass balance equation are located in the middle of the elements. To ensure fluid flow continuity at the fractures’ intersection points, we link the pressure nodes of the main fracture to the corresponding pressure nodes of the axial fracture, as illustrated in Fig. 4b. This method is described in more detail in Dahi Taleghani et al. (2018). Upon shut-in, pressure starts to decline due to fluid leakoff into the formation and let the fracture to close under closing stresses. However, due to the connectivity of two fractures through the wellbore, further complications are expected.

Fig. 4
figure 4

(a) Sketch showing the arrangement of the cohesive elements at the intersection of a growing hydraulic fracture and an axial fracture (b) linking nodes at the intersection of an axial fracture and a main fracture to ensure fluid flow continuity

Full size image

While most prevailing DFIT studies neglect the effect of geomechanics and only solve pore pressure equation, this approach may not properly simulate stress shadowing and the interactions between axial and transverse fractures. Our proposed DFIT model simultaneously solves both rock stress and fluid flow, thereby illustrating a more realistic fracture closure process. The governing equation coupling rock matrix deformation and fluid flow via linear poroelasticity is

$${\sigma }_{ij}-{\sigma }_{ij}^{0}=\frac{E}{1+\nu }\left({\varepsilon }_{ij}+\frac{\nu }{1-2\nu }{\varepsilon }_{kk}{\delta }_{ij}\right)-\alpha \left(p-{p}_{0}\right){\delta }_{ij},$$
(7)

where \({\sigma }_{ij}\) are the stress components; \({\sigma }_{ij}^{0}\) are the initial stress components; \(E,\) \(\nu \) are Young’s modulus and Poisson’s ratio of the formation, respectively; \({\varepsilon }_{ij}\) is the strain tensor; \(\alpha \) is Biot's constant; \(p\) is fluid pressure; and \({p}_{0}\) is initial fluid pressure in the formation. The fluid mass balance equation inside the fracture is given by

$$\frac{\partial {w}_{\text{f}}}{\partial t}+\nabla \cdot q+{q}_{\text{leak}}={q}_{\text{well}},$$
(8)

where \({q}_{\text{well}}\) is the injection rate at the wellbore. \({q}_{\text{leak}}\) is the fluid leakoff rate. Unlike the commonly used 1D Carter’s model, our model incorporates non-uniform leakoff rate, which is calculated as

$${q}_{\text{leak}}={c}_{\text{leak}}({p}_{\text{m}}-{p}_{\text{s}}),$$
(9)

where \({c}_{\text{leak}}\) is leakoff coefficient, \({p}_{\text{m}}\) is pressure at the cohesive element mid node and \({p}_{\text{s}}\) is the pressure at the cohesive element surface. \(q\) is the flowrate inside the fracture, which is calculated using the cubic law as

$$q=-{C}_{1}\frac{{{w}_{\text{f}}}^{2}}{12\mu }\frac{{\text{d}}{p}_{\text{f}}}{{\text{d}}x},$$
(10)

where \({C}_{1}\) is a factor accounting for the effects of fracture surface roughness that cause deviations from the ideal parallel plate; in this study, \({C}_{1}\) is assumed to be 0.8. The governing equations for coupling fluid flow and geomechanics that are used in the model can also be found in Cai and Dahi Taleghani (2019).

In addition to the aforementioned equations, a contact model for fracture surfaces that accounts for residual fracture width is needed. Due to the roughness of the fracture walls, the fractures may not close to zero aperture. Their inherent roughness begins to resist closure. To model the mechanical response of fracture closure on rough walls, this study adopts the Barton-Bandis fracture closure model, which is given by

$${\sigma }_{n}=\frac{{w}_{0}-{w}_{\text{f}}}{{C}_{2}-\frac{{C}_{2}}{{w}_{0}}({w}_{0}-{w}_{\text{f}})},$$
(11)

where \({\sigma }_{n}\) is the contact stress to resist fracture closure and \({w}_{0}\) is the critical aperture at which the fracture walls begin to contact each other, i.e. when \({w}_{\text{f}}\) > \({w}_{0}\), \({\sigma }_{n}=0\). \({C}_{2}\) is a parameter that represents the compressibility of the residual fracture. McClure et al. (2016) showed that due to the fracture closure on rough surfaces, the closure stress determined by the \(G\times {\text{d}}P/{\text{d}}G\) analysis may be much larger than \({s}_\text{h}\). The magnitude of the overestimation varies from case to case depending on the roughness of the fracture walls. Here, we propose calibrating the DFIT analysis based on the residual fracture width fraction. The minimum horizontal stress is calibrated as

$${S}_\text{h}={p}_{\text{c}}-{{f}_{\text{r}}p}_\text{net},$$
(12)

where \({p}_{\text{net}}\) is the net pressure, and is defined as

$${p}_{\text{net}}={p}_{\text{si}}-{S}_\text{h}.$$
(13)

\({p}_{\text{si}}\) is the bottomhole pressure at the beginning of shut-in. Combining Eqs. (12) and (13), we have

$${S}_\text{h}=\frac{{p}_{\text{c}}-{f}_{\text{r}}{p}_{\text{si}}}{1-{f}_{\text{r}}}.$$
(14)

Since this study focuses on conducting DFIT analysis rather than determining the residual fracture width during fracture closure, \({f}_{\text{r}}\), which is used to calibrate the DFIT analysis from the simulation results, is calculated based on the average fracture width as

$${f}_{\text{r}}=\frac{{w}_{\text{r}}}{\overline{w} },$$
(15)

where \(\overline{w }\) is the average fracture width calculated from the simulation results and \({w}_{\text{r}}\) is the residual fracture width. The fraction of the residual width depends on the rock fabric and in situ stress (Ahmadi et al. 2016; Van Dam and de Pater 1999). The downhole tiltmeter array has been found useful for accurately measuring the residual width of unpropped fractures (Warpinski et al. 1997). However, a tiltmeter measurement is not often available. In such cases, we can calibrate \({s}_\text{h}\) using the average fraction of residual volume based on available studies. Warpinski (2010) used a downhole tiltmeter array, finding that the fracture closure often leaves 20–30% residual fracture width. Van Dam et al. (2000) observed up to a 15% residual aperture (compared to the maximum aperture during fracture propagation) long after shut-in. In the DFIT test, the residual fracture volume fraction can be higher in comparison with that in the hydraulic fracturing since a lower injection rate is used. Thus, we recommend calculating the residual volume fraction using the typical residual fracture width observed in lab studies if a tiltmeter measurement is not available. Sakaguchi et al. (2008) measured the asperity height and distribution of tensile fractures on large rock blocks. The authors show that the residual width when the two fracture surfaces are in contact is around 2 mm. Bhide et al. (2014) created X-ray microtomographic images to estimate the residual fracture width, which varied from 1.8 to 1.95 mm. Zou et al. (2015) conducted experiments on 20 fractured shale samples and found the average fracture width to be 1.88 mm. Thus, we recommend using 1.9 mm as the \({w}_{\text{r}}\) value in Eq. (15). The average fracture width \(\overline{w }\) can be calculated as

$$\overline{w }=\frac{2H}{E}{p}_{\text{net}}.$$
(16)

The last component to be considered in the numerical model is the near-wellbore pressure drop. During the shut-in period of a DFIT test, the fracture fluid pressure measurement is lower than the bottomhole pressure measurement due to the near-wellbore pressure drop. Pokalai et al. (2015) show that the near-wellbore pressure drop introduced by the wellbore tortuosity is very high when there is a preexisting natural fracture. During the well shut-in period, we not only incorporate a pressure drop at the perforation but also an additional pressure drop due to the wellbore tortuosity. The total pressure drop is calculated using an empirical relationship (Pokalai et al. 2015) such that

$$\Delta {p}_{\text{w}}={C}_{3}{q}_{\text{exp}}^{2}+{C}_{4}{q}_{\text{exp}}^{0.5}.$$
(17)

where \({q}_{\text{exp}}\) is the flow rate from the wellbore to the formation. The constant \({C}_{3}\) combines the effect of friction in the wellbore and the perforations. Friction in the wellbore is related to the wellbore diameter and the wellbore roughness (Moody 1944). \({C}_{4}\) is a parameter that depends on the pressure-dependent fracture opening and far-field stresses (Hildek and Weijers 2007). Ignoring the change in wellbore volume, \({q}_{\text{exp}}\) is given by

$${q}_{\text{exp}}=\frac{{\text{d}}{V}_{\text{exp}}}{{\text{d}}t},$$
(18)

where \({V}_{\text{exp}}\) is the cumulative expanded fluid volume from the well to the formation that is given by

$${V}_{\text{exp}}={V}_{\text{well}}{C}_{\text{w}}\Delta {p}_{\text{si}} ,$$
(19)

where \(\Delta {p}_{\text{si}}\) is the pressure drop after the well shut-in.

3 Results and Discussion

In the following sections, different DFIT cases are presented and discussed to be understand the role of the aforementioned parameters. Simulation results are provided in the form of two types of figures: G-function plots (\(G\times {\text{d}}P/{\text{d}}G\) plot and \({\text{d}}P/{\text{d}}G\) plot) and screenshots of fracture openings that show fracture closure behaviors. In the beginning, we present a base case study to show how pressure decline behavior is different when an axial fracture is present. The input parameters of the base case scenario are shown in Table 1.

Table 1 Input parameters of case studies
Full size table

The inputs of other case studies are modified based on the base case. In Case 1, the injection time is reduced from 3 to 2 min. Thus, the fluid pressure is not high enough to initiate an axial fracture. In Case 1, we demonstrate how the initiation of an axial fracture can affect the pressure decline and DFIT analysis. In Case 2, the axial fracture is smaller (around 0.6 of the main fracture size). We show that the effect of the axial fracture closure is slightly more difficult to spot in the \(G\times {\text{d}}P/{\text{d}}G\) plot. However, combining the \(G\times {\text{d}}P/{\text{d}}G\) plot with the \({\text{d}}P/{\text{d}}G\) plot makes this effect noticeable. Case 3 and Case 4 investigate the effects of different parameters in the contact models. In Case 3, the induced fracture is less compliant in comparison to the base case. The residual fracture compressibility is reduced to 2e−4 MPa−1. Case 4 has a higher residual fracture width of 2.8 mm. We show that the proposed calibration method works well regardless of the parameters of the contact model. In Case 5, we study the effect when the formation has lower permeability. The permeability is lowered to 0.01 md. In Case 6, we study the pressure characteristic when there is no horizontal stress contrast. In Case 7, the horizontal stress contrast is smaller: 3 MPa compared to 5 MPa in the base case. These modifications to the base case model are summarized in Table 2. For each case, we apply three commonly used interpretation methods: the tangent line method (Barree and Mukherjee 1996; Barree et al. 2007), fracture compliance method (McClure et al. 2016) and variable fracture compliance method (Wang and Sharma 2017) to determine the closure stress. We first utilize these methods without the proposed calibration method and then correct the results using the proposed calibration procedure to realize the difference.

Table 2 Modifications to base case model for all other case studies
Full size table

3.1 Base Case

In the base case, the axial fracture is assumed to have the same size as the transverse fracture. This allows us to investigate the effect of the axial fracture more clearly. In Fig. 5, we show the initial fracture opening at the end of the injection period. Note that the axial fracture has an obvious bottleneck in comparison to the transverse fracture. This is for two reasons. First, the transverse fracture is much easier to open in comparison to the axial fracture. The fracture mouth of the axial fracture supplies the transverse fracture, which causes the non-uniform opening after the injection. Second, in situ stress is increased due to the opening of the transverse fracture. The effect is largest near the mouth of the transverse fracture. In fact, the transverse fracture has a slight bottleneck shape as well due to the stress increase near the fracture mouth region introduced by the axial fracture initiation. The effect is less significant in comparison to the axial fracture. This is because the axial fracture has a smaller opening; thus, the stress increase only slightly affects the transverse fracture. During the fracture closure process, the fracture at the mouth may close first (Dahi Taleghani et al. 2020). Due to the non-uniform initial opening, a non-uniform fracture closure is very likely to happen during the shut-in period, as shown in the snapshots of the numerical simulation. The wellbore and the perforation are only shown in the base case to illustrate the model. In all other cases, we have chosen not to show the wellbore and the perforation so that the reader is able to better visualize the fracture width of the axial fracture.

Fig. 5
figure 5

Base case: snapshot of the numerical simulation showing the initial fracture opening after the fracture propagation

Full size image

The pressure decline shows fracture closure in different stages (the numbered arrows shown in Fig. 6. At the beginning, the \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 6a) shows the effect of the fracture storage, which can be identified by a concave upward trend until G-time reaches about 5 (Arrow 1). The concave upward trend suggests that the fracture storage effect dominates the pressure-dependent leakoff (PDL) effect for two reasons. First, the axial fracture is well connected to the transverse fracture through the wellbore, which makes the pressure support effect more significant than the PDL effect. Second, the smaller PDL effect is also because that the effective leakoff area is smaller in the presence of the axial fracture is present than the case where the transverse fracture intersects and activates the natural fracture.

Fig. 6
figure 6

Base case: closure stress estimation from the analysis of (a) the \(G\times {\text{d}}P/{\text{d}}G\) plot and (b) the \({\text{d}}P/{\text{d}}G\) plot

Full size image

When G-time reaches 5 (Arrow 1), the effect of fracture storage ceases as the pressure decline rate stops increasing. The lack of further increase in the pressure decline rate is caused by the complete closure of the axial fracture, as indicated both in the \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 6a) and the \({\text{d}}P/{\text{d}}G\) plot (Fig. 6b). Figure 7 also suggests that the axial fracture is fully closed. The maximum width of the axial fracture becomes lower than the residual width input of the simulation, 1.5 mm. The axial fracture does not close uniformly due to its initial non-uniform opening (Fig. 5) as well as its flow into the transverse fracture from the fracture mouth. We advocate picking the maximum horizontal stress \({S}_\text{H}\) at this reflection point as confirmed by simulation results. The reflection point is easier to spot in the \({\text{d}}P/{\text{d}}G\) plot at the peak of the first hump than it is in the \(G \times {\text{d}}P/{\text{d}}G\) plot.

Fig.7
figure 7

Base case: snapshot of the numerical simulation showing that the axial fracture fully closes non-uniformly at G-time = 5

Full size image

When the transverse fracture losses pressure support from the axial fracture, it starts to close at the fracture mouth and the fracture tip. While the fracture tip receding is common during the shut-in period if the leakoff rate is high (Dahi Taleghani et al. 2020), the mouth closure is rarely observed when no production operation is performed. When the axial fracture is open, it provides pressure support to the transverse fracture. After the axial fracture closes, the transverse fracture can have reverse fluid leakoff into the axial fracture. This phenomenon only happens under these particular circumstances. Using the \(G\times {\text{d}}P/{\text{d}}G\) plot alone, it can be hard to observe the change in the pressure decline rate as well as the reflection point. Combining the \(G\times {\text{d}}P/{\text{d}}G\) plot and the \({\text{d}}P/{\text{d}}G\) plot can help with interpretation. The PDL effect is indicated more clearly in the \({\text{d}}P/{\text{d}}G\) plot (Fig. 6b). The pressure decline rate decreases after the axial fracture closes and before the fracture surfaces of the transverse fracture come into contact (from Arrow 1 to Arrow 2). At Arrow 2, \(G\times {\text{d}}P/{\text{d}}G\) curves upward again, which indicates the transverse fracture starts to close partially, as shown in Fig. 8 at G-time = 5.6.

Fig. 8
figure 8

Base case: snapshot of the numerical simulation showing the transverse fracture starts to close at G-time = 5.6

Full size image

According to the tangent line method, the closure stress should be picked at Arrow 3 at G-time = 6.8, which is 42.7 MPa. Using the fracture compliance method, the closure point is picked at the green arrow when G-time is equal to 6.35 and the fracture compliance starts to change significantly. We found the complete closure of the transverse fracture happens neither at the closure time determined using the tangent line method nor that identified using the fracture compliance method. As shown in Fig. 9, the maximum fracture aperture of the transverse fracture reduces to the input residual fracture width of − 1.5 mm, which indicates its full closure at G-time = 6.6. Pressure found at the complete closure time is 43 MPa. The variable compliance method suggests that the fracture compliance method overestimates \({s}_\text{h}\), while the traditional tangential line method underestimates \({s}_\text{h}\). Thus, the variable compliance method calculates the average of the tangent line method and the fracture compliance method, which is 43.4 MPa. In addition to determining closure stress, it is possible to determine the maximum horizontal stress from the plot using the reflection point method. At Arrow 1, when the G-function is around 5, the concave upward trend stops and the pressure decline rate slightly decreases, which together indicate that the PDL dominates over the fracture storage effect due to closure of the axial fracture. \({s}_\text{H}\) is picked to be 48.1 MPa at that moment.

Fig. 9
figure 9

Base case: snapshot of the numerical simulation showing the transverse fracture fully closes at G-time = 6.6

Full size image

A comparison of these different methods for determining closure stress is summarized in Table 3. Note that all the \({s}_\text{h}\) estimation methods and the proposed reflection point method for estimating \({s}_\text{H}\) significantly overestimate \({s}_\text{h}\) and \({s}_\text{H}\). This is because the roughness surfaces of the fracture can prevent the fracture from closing completely; in other words, some residual fracture volume remains after shut-in. Thus, we applied the proposed calibration method to improve the accuracy in estimating \({s}_\text{h}\) and \({S}_\text{h}\). To test the calibration procedure, the calibration factor \({f}_{\text{r}}\) is calculated from the residual aperture input divided by the average fracture aperture calculated from the simulation outputs. After the calibration, the tangential line method produces an \({s}_\text{h}\) estimation of 40.4 MPa, only 1.0% higher than the input value of 40 MPa. The fracture compliance method has an \({s}_\text{h}\) estimation of 41.9 MPa, 4.7% higher than the \({s}_\text{h}\) input value. The variable compliance method provides an \({s}_\text{h}\) estimation of 41.1 MPa, 2.8% higher than the \({s}_\text{h}\) input value. The DFIT analysis methods based on fracture compliance all tend to overestimate \({s}_\text{h}\). This is due to the fact the closed axial fracture provides an extra path for fluid leakoff at the mouth of the transverse fracture. The transverse fracture first closes at the mouth and the \(G\times {\text{d}}P/{\text{d}}G\) and \({\text{d}}P/{\text{d}}G\) plot curves upward even though a large portion of the fracture has not closed yet. Stress in the region close to the fracture mouth is slightly increased due to the initiation of both the axial and transverse fractures so that the closure stress picked from the fracture mouth closure cannot represent \({s}_\text{h}\) in other regions. Thus, when the axial fracture is present, \({s}_\text{h}\) can be significantly overestimated when using methods based on fracture compliance. Although the tangent line method can slightly overestimate closure time, it provides the most reasonable \({s}_\text{h}\) estimation. The simulation results show the complete fracture closure happens later than the time determined from the fracture compliance method. The reflection point method provides an \({S}_\text{H}\) estimation of 45.4 MPa with 0.9% overestimation.

Table 3 Results of DFIT interpretations (base case)
Full size table

3.2 Case 1 (Planar Fracture Only)

In Case 1, only a planar fracture is formed after injecting the fluid. There is an initial short preexisting axial fracture intersecting the wellbore that is oriented perpendicular to the maximum horizontal stress. However, there was not enough induced stress to open it. The initial opening of the fracture is shown in Fig. 10. Unlike the base case, Case 1 features a planar fracture with a very uniform opening due to the stress distribution near the fracture mouth that is not further increased by the initiation of the axial fracture.

Fig. 10
figure 10

Case 1: snapshots of the numerical simulation showing the uniform initial fracture opening after fracture propagation

Full size image

No closure of the axial fracture is identified in the \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 11a). \(G\times {\text{d}}P/{\text{d}}G\) is almost linearly increasing until G-time is around 8.5 (Arrow 1) when the transverse fracture begins to close. Upon fracture closure, \(G\times {\text{d}}P/{\text{d}}G\) reaches its peak at G-time = 9.4 (Arrow 2). Although the \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 11a) seems linear in the early stage, from the \({\text{d}}P/{\text{d}}G\) plot (Fig. 11b), we can see that the pressure decline rate is slightly increasing over time. This may be due to a slight change in fracture compliance. McClure et al. (2016) suggest fracture compliance is not a constant during fracture closure. Wang and Sharma (2018) also show fracture stiffness remains constant only when the fluid pressure is very high. Jung et al. (2016) suggest the concave upward \(G\times {\text{d}}P/{\text{d}}G\) plot may be caused by the changing fracture stiffness rather than the fracture storage effect considered in traditional DFIT analysis (Nolte 1991; Barree et al. 2007). However, the effect of the changing fracture compliance is not as large as the fracture storage effect. Note that compared with the base case, for a planar fracture that does not intersect a secondary fracture, the concave upward trend can only be observed from the \({\text{d}}P/{\text{d}}G\) plot. In the \(G\times {\text{d}}P/{\text{d}}G\) plot, the pressure decline appears to be linear. However, when an axial fracture is present, the concave upward trend of the \(G\times {\text{d}}P/{\text{d}}G\) plot is more obvious, and it is followed by a PDL-dominant period. The two different concave upward behaviors thus can be distinguished easily.

Fig. 11
figure 11

Case 1: closure stress estimation based on an analysis of (a) the \(G\times {\text{d}}P/{\text{d}}G\) plot and (b) the \({\text{d}}P/{\text{d}}G\) plot

Full size image

Using the tangent line method, we pick the closure stress at Arrow 2, which is 41.0 MPa. Using the fracture compliance method, we pick the closure stress to be 43.6 MPa at Arrow 1 when G-time equals 8.5. The variable compliance method gives the average of the tangent line method and the fracture compliance method, which is 42.3 MPa. After the calibration, the tangent line method produces an \({s}_\text{h}\) estimation of 38.8 MPa, 3.0% lower than the input value. The fracture compliance method has an \({s}_\text{h}\) estimation of 42.0 MPa, 5.0% higher than the \({s}_\text{h}\) input value. The variable compliance method provides an \({s}_\text{h}\) estimation of 40.4 MPa, only 1.0% higher than the \({s}_\text{h}\) input value. Before calibrating the interpretation results with the residual fracture width, the tangent line method provides the most accurate \({s}_\text{h}\) because it identifies a fracture closure time later than the true fracture closure time, thereby offsetting the overestimation introduced by the fracture roughness. The fracture aperture is reduced to less than the residual fracture width at G-time = 9. The closure time is later than the closure time determined based on the fracture compliance method and earlier than the value determined based on the tangent line method. By averaging the results from the tangent line method and the fracture compliance method, the variable fracture compliance method can determine the most accurate closure time, and it performs best after calibration with an error of 1.0%, which is consistent with the findings in Wang and Sharma (2017). Thus, when the \(G\times {\text{d}}P/{\text{d}}G\) plot shows the characteristic of a planar fracture, we recommend using the variable compliance method. We are not able to analyze the \({s}_\text{H}\) for this case since no axial fracture is formed; that is, a reflecting point is not available. A comparison of the different methods used to determine closure stress is provided in Table 4.

Table 4 Results of DFIT interpretations (Case 1)
Full size table

3.3 Case 2 (Smaller Axial Fracture)

In Case 2, the axial fracture has a smaller size (about 0.6 of the transverse fracture). The \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 12a) seems slightly concave upward until G-time is around 4.5. This stands in contrast to the base case in which the effect of the transverse fracture storage is more significant because of a larger axial fracture. When G-time reaches 4.5, the pressure decline rate starts to decrease. From the \(G\times {\text{d}}P/{\text{d}}G\) plot alone, we cannot see the reflection point very clearly. However, from the \({\text{d}}P/{\text{d}}G\) plot (Fig. 12b), we can observe that the pressure decline rate is slightly decreasing from Arrow 1 to Arrow 2 due to the PDL effect, similar to the base case. At G-time = 6 (Arrow 2), the transverse fracture starts to close at the fracture mouth and the fracture tip, as shown in Fig. 13. At G-time = 7.8, \(G\times {\text{d}}P/{\text{d}}G\) reaches its peak (Arrow 3).

Fig. 12
figure 12

Case 2: closure stress estimation from an analysis of (a) the \(G\times {\text{d}}P/{\text{d}}G\) plot and (b) the \({\text{d}}P/{\text{d}}G\) plot

Full size image
Fig. 13
figure 13

Case 2: snapshot of the numerical simulation showing the transverse fracture starts to close at G-time = 6

Full size image

Based on the tangent line method, the closure stress should be picked at G-time = 7.8, which is 42.3 MPa. Using the fracture compliance method, the closure point is picked to be 44.2 MPa at G-time = 7, when the fracture compliance starts to change significantly. The variable compliance method gives the average of the tangent line method and the fracture compliance method, which is 43.3 MPa. After the calibration, the tangential line method produces an \({s}_\text{h}\) estimation of 40.15 MPa, only 0.4% higher than the input value of 40 MPa. The fracture compliance method has an \({s}_\text{h}\) estimation of 42.4 MPa, 6.0% higher than the \({s}_\text{h}\) input. The variable compliance method provides an \({s}_\text{h}\) estimation of 41.3 MPa, 3.3% higher than the \({s}_\text{h}\) input. The reflection point method provides an \({S}_\text{H}\) estimation of 45.4 MPa with an error of + 0.9%. A comparison of different methods to determine \({s}_\text{h}\) and \({S}_\text{h}\) can be found in Table 5. Similar to the base case, in Case 2, complete fracture closure happens later than the time determined by the fracture compliance method and earlier than the time determined by the tangent line method. In this case, when the axial fracture is much smaller than the transverse fracture, the tangent line method still provides the most accurate \({s}_\text{h}\) estimation. Comparing the results from the base case and Case 2, we conclude that when an axial fracture is present, the DFIT analysis based on the fracture compliance significantly overestimates \({s}_\text{h}\) regardless of the size of the axial fracture. However, when the size of the axial fracture is small, the dP/dG plot must be used to observe the reflection point more clearly.

Table 5 Results of DFIT interpretations (Case 2)
Full size table

3.4 Case 3 (Less Compliant Fracture)

In Case 3, the axial fracture is less compliant than it is in the base case. Fracture compressibility is reduced to 2e−4 MPa−1. At the beginning, the \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 14a) is concave upward until G-time is around 5 due to the fracture storage effect. When G-time reaches 5, the pressure decline rate starts to decrease. We can see that similar to the base case, in Case 3, the pressure decline rate is slightly decreasing from Arrow 1 to Arrow 2 due to the PDL effect. \({S}_\text{H}\) can be picked from either the \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 14a) or the \({\text{d}}P/{\text{d}}G\) plot (Fig. 14b). At G-time = 5.6 (Arrow 2), when the pressure decline rate rises again, the transverse fracture starts to close at the fracture mouth and the fracture tip. The time the transverse fracture starts to close is the same as in the base case since the change in fracture compliance does not affect the time of closure.

Fig. 14
figure 14

Case 3: closure stress estimation from an analysis of (a) the \(G\times {\text{d}}P/{\text{d}}G\) plot and (b) the dP/dG plot

Full size image

Based on the tangent line method, the closure stress should be picked to be 42.5 MPa (Arrow 3). Using the fracture compliance method, the closure point is picked to be 44.2 MPa at the green arrow when G-time equal to 7, where the fracture compliance starts to change significantly. The variable compliance method gives the average of the tangent line method and the fracture compliance method, which is 43.3 MPa. After the calibration, the tangential line method produces an \({s}_\text{h}\) estimation of 40.2 MPa, 0.5% higher than the \({s}_\text{h}\) input value. The fracture compliance method has a \({s}_\text{h}\) estimation of 42.1 MPa, 5.2% higher than the \({s}_\text{h}\) input value. The variable compliance method provides an \({s}_\text{h}\) estimation of 41.1 MPa, 2.8% higher than the \({s}_\text{h}\) input value. Similar to the base case, in Case 4, complete fracture closure happens later than the time determined by the fracture compliance method and earlier than the time determined by the tangent line method. After calibration, the tangent line method provides the most accurate \({s}_\text{h}\) estimation. The reflection point method provides an \({S}_\text{H}\) estimation of 45.6 MPa with an error of + 1.7%. A comparison of different methods to determine closure stress is provided in Table 6. Comparing the results from the base case to those of Case 4, we can see that the performance of the three \({s}_\text{h}\) estimation approaches is independent of the fracture compliance.

Table 6 Results of DFIT interpretations (Case 3)
Full size table

3.5 Case 4 (Higher Residual Fracture Width)

Rough walls can provide resistance to the fracture closing process. Additionally, plastic deformations of rocks due to pressurization during fracturing may induce residual openings. To study the effect of residual fracture width during DFIT, we use an extreme large residual width fraction of 35%—a fracture residual of 2.7 mm. The \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 15a) shows the significant effect of the transverse fracture storage till G-time = 3.4. Then the pressure decline rate decreases slightly for a short period of time due to the PDL effect. This period is very short in comparison to that of the base case. Due to the large residual aperture in Case 4, the transverse fracture closes faster, which conceals the effect of PDL. The decrease in the pressure decline rate is more visible in the \({\text{d}}P/{\text{d}}G\) plot (Fig. 15b) than it is in the \(G \times {\text{d}}P/{\text{d}}G\) plot. Thus, the reflection point method relies on the \({\text{d}}P/{\text{d}}G\) plot when the residual width is high. At Arrow 2, the pressure decline rate rises again due to the closure of the transverse fracture.

Fig. 15
figure 15

Case 4: closure stress estimation from an analysis of (a) the \(G\times {\text{d}}P/{\text{d}}G\) plot and (b) the dP/dG plot

Full size image

Based on the tangent line method, the closure stress should be picked at G-time = 4.6 (Arrow 3), which is 47 MPa. Using the fracture compliance method, the closure point is determined to be 50.5 MPa at G-time = 3.6, when the fracture compliance starts to change significantly. The true fracture closure time is G-time = 4.5, as shown in the snapshot of the numerical simulation (Fig. 16). Similar to other case studies, in this case, the fracture compliance method significantly underestimates fracture closure time, while the tangent line method slightly overestimates fracture closure time. The variable compliance method gives the average of the tangent line method and the fracture compliance method, which is 48.25 MPa. After the calibration, the tangential line method produces an \({s}_\text{h}\) estimation of 39.35 MPa, − 1.6% lower than the \({s}_\text{h}\) input value. The fracture compliance method has an \({s}_\text{h}\) estimation of 45.1 MPa, 12.8% higher than the \({s}_\text{h}\) input value. The variable compliance method provides an \({s}_\text{h}\) estimation of 42.2 MPa, with an error of 5.5%. The reflection point method provides an \({S}_\text{H}\) estimation of 44.0 MPa with an error of − 2.0%. A comparison of different methods to determine closure stress is provided in Table 7. Similar to the other case studies, in this case, we recommend using the tangent line method when an axial fracture is present because it has the most accurate fracture closure identification. Note that the residual width used in this case study is extremely high to investigate the accuracy of the proposed calibration method. After the calibrations, despite all the methods produce slightly higher errors in comparison with the previous case studies, we can consider the proposed calibration works well for estimating horizontal stresses regardless of different contact models.

Fig. 16
figure 16

Case 4: snapshot of the numerical simulation showing complete fracture closure at G-time = 4.5

Full size image
Table 7 Results of DFIT interpretations (Case 4)
Full size table

3.6 Case 5 (Lower Permeability Reservoir)

In Case 5, the formation has a lower permeability of 0.01 md. We can see that at the beginning of shut-in, the pressure decline rate is decreasing, as shown in the \(G\times {\text{d}}P/{\text{d}}G\) plot and the \({\text{d}}P/{\text{d}}G\) plot (Fig. 17). The decrease in the pressure decline rate, which is due to a lower permeability reservoir results in a very slow leakoff rate. An additional leakoff path provided by the axial fracture that can significantly increase the leakoff rate. The PDL effect dominates the fracture storage effect during the early shut-in period until there is substantial leakoff volume. At G-time = 10, the \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 17a) starts to concave upward until G-time is around 11 due to the fracture storage effect. We advocate picking \({S}_\text{H}\) at the reflection point. It can be picked from either the \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 17a) or the \({\text{d}}P/{\text{d}}G\) plot (Fig. 17b). We can see that similar to the base case, the pressure decline rate is slightly decreasing from Arrow 1 to Arrow 2, which is due to the PDL effect. Around G-time = 14 (Arrow 2), when the pressure decline rate rises again, the transverse fracture starts to close at the fracture mouth and the fracture tip. The time that the transverse fracture starts to close in Case 5 is the same as in the base case since the change in fracture compliance does not affect the time of closure.

Fig. 17
figure 17

Case 5: closure stress estimation from an analysis of (a) the \(G\times {\text{d}}P/{\text{d}}G\) plot and (b) the \({\text{d}}P/{\text{d}}G\) plot

Full size image

Based on the tangent line method, the closure stress should be picked to be 42.9 MPa (Arrow 3). Using the fracture compliance method, the closure point is picked to be 43.9 MPa at G-time = 16, when the fracture compliance starts to change significantly. The variable compliance method gives an average of the tangent line method and the fracture compliance method, which is 42.4 MPa. After the calibration, the tangential line method leads to an \({s}_\text{h}\) estimation of 40.8 MPa, 2% higher than the input value. The fracture compliance method has an estimation for \({s}_\text{h}\) of 41.9 MPa, 4.8% higher than the \({s}_\text{h}\) input value. The variable compliance method provides an estimation for \({s}_\text{h}\) of 41.4 MPa, 3.4% higher than the \({s}_\text{h}\) input value. Complete fracture closure happens later than the time determined by the fracture compliance method and earlier than the time determined by the tangent line method. Compared to the results of the base case, the performance of three \({s}_\text{h}\) estimation approaches in Case 5 is independent of the fracture compliance. After calibration, the tangent line method provides the most accurate \({s}_\text{h}\) estimation when an axial fracture is present. The reflection point method provides an \({S}_\text{H}\) estimation of 46.2 MPa with an error of 2.7%. The comparison of different methods to determine closure stress is provided in Table 6.

3.7 Case 6 (\({{{S}}}_{{\text{H}}}={{{S}}}_{{\text{h}}}\))

In Case 6, the maximum horizontal stress is set to be the same as the minimum horizontal stress, i.e. 40 MPa. In other words, the dimensions of the transverse fracture will be the same as the dimensions of the axial fracture due to symmetry of the model. The initial bottleneck of the fracture is due to the stress concentration around the fracture mouth region, as shown in Fig. 18. Although no closure of the axial fracture can be identified from the \(G\times {\text{d}}P/{\text{d}}G\) plot, the axial fracture and the transverse fracture are closing simultaneously. As indicated in the \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 19a) the pressure is almost linearly increasing until G-time is around 6.5 (Arrow 1). Although there is a small fluctuation in the pressure decline curve, as revealed in the \({\text{d}}P/{\text{d}}G\) plot (Fig. 19b), the effect of the change in fracture compliance is not very large in comparison to that of the base case where the fracture storage effect and the PDL effect change the pressure decline rate more significantly. The comparison of different methods to determine closure stress is provided in Table 8.

Fig. 18
figure 18

Case 6: snapshot of the numerical simulation showing the non-uniform axial fracture closure during shut-in (at G-time = 4.5)

Full size image
Fig. 19
figure 19

Case 6: closure stress estimation from an analysis of (a) the \(G\times {\text{d}}P/{\text{d}}G\) plot and (b) the \({\text{d}}P/{\text{d}}G\) plot

Full size image
Table 8 Results of DFIT interpretations (Case 5)
Full size table

Using the tangent line method, we pick the closure stress at the moment of 43 MPa at G-time = 7 (Arrow 2). Using the fracture compliance method, the closure stress would be 44.5 MPa at Arrow 1 at G-time = 6.5. The variable compliance method gives the average of the tangent line method and the fracture compliance method, which is 43.7 MPa. After the calibration, the tangential line method produces the most accurate \({s}_\text{h}\) estimation—40.1 MPa, 0.3% higher than the input value. The fracture compliance method has an \({s}_\text{h}\) estimation of 42.2 MPa, 5.6% higher than the \({s}_\text{h}\) input value. The variable compliance method provides an \({s}_\text{h}\) estimation of 41.2 MPa, 3.0% higher than the input value for \({s}_\text{h}\). The comparison of different methods to determine closure stress is provided in Table 9. The calibration method significantly improves the accuracy of the DFIT analysis. When there is no difference in horizontal stresses, the reflection point cannot be identified even though the axial fracture is initiated. Thus, \({s}_\text{H}\) cannot be found in this case. The two fractures are still closing at the same time.

Table 9 Results of DFITs interpretations (Case 6)
Full size table

3.8 Case 7 (Less Horizontal Differential Stress)

In Case 7, the maximum horizontal stress is set to be lower: 43 MPa. At the beginning of shut-in, the \(G\times {\text{d}}P/{\text{d}}G\) plot (Fig. 20a) shows the effect of transverse fracture storage, which is identified by a concave upward trend until G-time = 5.7 (Arrow 1). The concave upward trend suggests that the fracture storage effect dominates the PDL. Then, the effect of fracture storage ceases as the pressure decline rate stops increasing, which is caused by full closure of the axial fracture as indicated both in the \(G\times \mathrm{d}P/\mathrm{d}G\) plot (Fig. 20a) and the \({\text{d}}P/{\text{d}}G\) plot (Fig. 20b). As shown in the \({\text{d}}P/{\text{d}}G\) plot, after the axial fracture fully closes, the pressure decline rate continues increases with a slower rate. This is different from the base case where after the axial fracture closes, PDL dominates which causes decrease of pressure decline. This is due to the fact that when the horizontal differential stress is smaller, the difference of width between the axial fracture and the transverse fracture is also smaller. Part of the transverse fracture starts to close before the axial fracture completely closes. Screenshot of the numerical simulation in Fig. 21 confirms this phenomenon. At G-time = 5.7, when the maximum aperture of axial fracture is reduced to less than the residual fracture width—1.5 mm, width of transverse fracture mouth and fracture tip also falls below the residual fracture width. After the axial fracture closure, whether the pressure decline rate decrease, or continue increasing depends on the competence between the PDL effect and closure of the transverse fracture. In this case, when the transverse fracture closes a lot at the fracture mouth and the fracture tip, the closure of the transverse fracture dominates the PDL effect which results in increasing of the pressure decline rate.

Fig. 20
figure 20

Case 7: closure stress estimation from analysis of (a) \(G\times {\text{d}}P/{\text{d}}G\) and (b) \({\text{d}}P/{\text{d}}G\) plot

Full size image
Fig. 21
figure 21

Case 7: snapshot of the numerical simulation showing complete axial fracture closure during shut-in (at G-time 5.7)

Full size image

From the tangent line method, the closure stress should be picked to be 42.5 MPa at Arrow 3. Using the fracture compliance method, the closure pressure is picked to be 44.3 MPa at G-time = 6.5, when the fracture compliance starts to change significantly. The variable compliance method calculates the average of the tangent line method and the fracture compliance method and provides a value of 43.4 MPa. After the calibration, the tangent line method provides a \({s}_\text{h}\) estimation of 40.3 MPa, 0.1% lower than the input value. The fracture compliance method has a \({s}_\text{h}\) estimation of 42.4 MPa, 6.0% higher than the \({s}_\text{h}\) input. The variable compliance method provides a \({s}_\text{h}\) estimation of 41.3 MPa, 3.3% higher than the \({s}_\text{h}\) input. Like the other cases with the presence of the axial fracture, complete fracture closure happens later than the time determined by the fracture compliance method and earlier than the time determined by the tangent line method. Comparing the results (Table 10), the tangent line method provides the most accurate \({s}_\text{h}\) estimation in Case 8. The reflection point method provides an estimated \({S}_\text{H}\) of 43.8 MPa with an error of + 1.8%.

Table 10 Results of DFIT interpretations (Case 7)
Full size table

4 Conclusion

This work presents a fully coupled geomechanics and fluid flow model for DFIT. While available DFIT analyses investigate the effect of pressure-dependent leakoff, transverse fracture storage, and fracture height recession on shut-in behavior, there is little discussion of the effect of the initiation and closure of axial fractures. Thus, we proposed a coupled geomechanics and fluid flow model to investigate this effect. Our modeling results show that stress changes in the matrix around the fracture can cause the initial non-uniform opening of both the axial fracture and transverse fracture and their closure behavior. The results also show that the presence of an axial fracture can have a unique effect on the G-function plots (\(G\times {\text{d}}P/{\text{d}}G\) plot and \({\text{d}}P/{\text{d}}G\) plot). When an axial fracture is formed, the \(G\times {\text{d}}P/{\text{d}}G\) plot initially has a concave upward trend, which shows the fracture storage effect at the beginning of shut-in. This fracture storage effect ceases when the axial fracture fully closes. Since the closed axial fracture can be an extra leakoff path for the transverse fracture, the PDL effect can be found in the G-function plot as the pressure decline rate starts to decrease. When formation permeability is extremely low, the PDL effect can initially dominate the fracture storage effect.

The simulation results suggest that when an axial fracture is present, the DFIT analysis based on fracture compliance indicates an earlier fracture closure due to the non-uniform fracture closure of the transverse fracture. Therefore, these methods should be used when there is no indication of the initiation of the axial fracture (fracture storage behavior followed by PDL). In addition to examining the performance of available DFIT interpretation schools, we propose a method that we call the reflection point method to identify the closure of the axial fracture. From the reflection point in the \(G\)-function plots, it is possible to determine the maximum horizontal stress \({s}_\text{H}\) in addition to \({s}_\text{h}\). We show that using the \(G\times {\text{d}}P/{\text{d}}G\) plot alone can make it hard to observe the reflection point or a change in the pressure decline rate. Combining the \(G\times {\text{d}}P/{\text{d}}G\) plot and the \({\text{d}}P/{\text{d}}G\) plot can aid in DFIT interpretation. We also found that the overestimation of the horizontal stresses introduced by fracture surface roughness is huge but can be calibrated using the method proposed in this study. The calibration method can be applied successfully to all DFIT analyses based on the \(G\) function plot. When the downhole tiltmeter test is available at the DFIT site, we recommend calculating \({f}_{\text{r}}\) using the fracture residual width obtained from the inclinometer array. When the test is not available, we recommend assuming the fracture residual width to be 1.9 mm based on available experimental studies.