1 Introduction

The reinforcement of rock masses by untensioned fully grouted bolts, due to its efficacy and low cost, is widely used to restrain deformation of rock masses and to support the stability of engineering works in civil and mining engineering. Since Freeman (1978) investigated the behavior of fully grouted rock bolts in the Kieder experimental tunnel, various means including field monitoring, laboratory tests, analytical analysis and numerical modeling are adopted to reveal the distributions of the axial stress in the bolt and the shear stress at the bolt–grout interface and to develop bolting theories and bolting approaches for engineering design (Gaziev and Lapin 1983; Dight 1983a, b; Sun 1984; Tao and Chen 1984; Indraratna and Kaiser 1990; Stillborg 1994; Hyett et al. 1996; Li and Stillborg 1999; Oreste 2008; Bobet and Einstein 2011; Cao et al. 2013; Martín et al. 2013; He et al. 2014; Cai et al. 2015; Das et al. 2015; Aziz et al. 2016; Tan 2016; Oliveira and Diederichs 2017). However, most of researches focus on the reinforcement behavior of bolts by considering only the axial force acting in the bolts. In practice, as we know, fully grouted bolts are considered as pure tension elements to support the stability of rock slopes. By taking the components of the axial force of the bolt on the potential sliding plane (joint plane) and establishing limit equilibria, one can evaluate the stability of a rock slope reinforced with bolts. However, for a fully grouted bolt, movements are necessary to activate the resistant force in the bolt. Jointed or stratified rock masses have a potential to move along two directions, respectively, perpendicular to and parallel to the joint plane. The bolt activates an axial force due to the opening of the joint and a shear force resulted from the transverse displacement of the joint. As that the increase in the strength provided by a passive reinforcing system is a function of the displacement along the discontinuity surface, axial and transverse interactions between a single reinforcement element and the surrounding rock should be considered, and hence, the reinforcement mechanism of a passive reinforcing system is more complex than an active one (Oreste and Cravero 2008). Therefore, the approaches considering only the axial force are not accurate. To accurately understand the behavior of a bolted rock joint, the shear force mobilized at the cross section of the bolt must be taken into account.

Some investigations have been performed to study the mechanical behavior of jointed rock bolts under shearing (Ge and Liu 1988; Yang 1994; Ferrero 1995; Li and Zhu 1999; Wu et al. 2003; Jalalifar and Aziz 2010; Li et al. 2016). Experimental results indicate that the angle between the bolt axis and the joint plane, the strength of the surrounding rock mass and the friction angle of the joint have significant influence on the contribution to the stiffness and strength of the bolted rock joint subjected to shearing (Haas 1981; Spang and Egger 1990; Egger and Zabuski 1991; Chen and Li 2015). Dight (1983a, b) developed an analytical expression to predict the maximum force mobilized in the bolt and pointed out that the failure of the bolt is determined by the combination of the axial and shear forces. Holmberg (1991) further proposed a method which gives a prediction on the maximum bolting contribution when the bolt is inclined to the joint. Pellet and Egger (1996) advised a new analysis model for evaluating the contribution of a bolt to the shear strength of a rock joint. The main characteristics of this model consider the interaction of the axial and shear forces mobilized in the bolt, as well as the large plastic displacements of the bolt occurring during the loading process. Grasselli (2005) investigated the behavior of a bolted rock joint subjected to shearing without considering the dilatancy of the joint, and presented that the bolt which is slightly inclined to the joint is in a state of pure traction while the bolt with a steep inclination to the joint behaviors in a mixed situation of shear and traction, and that the contribution of traction reduces with increasing the angle between the bolt and the joint but at the same time the contribution of shear rises. Oreste and Cravero (2008) proposed a method named block reinforcement procedure for the design of a passive reinforcing system, which is capable to stabilize potentially unstable rock blocks. This method takes a dowel or a passive element as a beam, and the element–rock interaction is characterized by a series of Winkler springs. Dowel effect is assumed to be only activated by a small displacement; in other words, only elastic state is considered in the method. The induced forces acting in a dowel, therefore, can be expressed as functions of the rock block displacement. Wang et al. (2014) proposed a mechanical model by taking the deflect length of the bolt as a statically indeterminate beam and discussed the relationship of the axial and shear stresses acting in the bolt. Maiolino and Pellet (2015) carried out full-scale shear tests performed on bolted joint and found that bolt ultimate contribution increases linearly with respect to the bolt diameter.

Although above works contributed to the understanding of mechanical behaviors of bolted rock joints, present knowledge cannot provide a widely accepted theoretical system. Most of researches focus on laboratory tests aiming to investigate bolting mechanism of fully grouted bolts under shearing on the one hand, and on the other hand, the existing theoretical models developed on the basis of the elastic foundation beam theory are much complex and fail to be applied in practice. Besides, the design method of rock slope bolting, taking into account only the tension force acting in the bolt, disagrees to the bolting mechanism and hence is not accurate. Therefore, investigations are necessary to develop a robust reinforcement model to be used in the design of fully grouted bolts in jointed rock slopes.

The strength of the steel bar is one major parameter for determining the reinforcement capacity of a fully grouted bolt. According to Grasselli (2005), before the steel bar reaches its yield stress, the bolt mobilizes 85% of its resistant contribution associated with a small displacement of 1.8 mm. For engineering design, in fact, the yield stress rather than the ultimate strength is adopted as the allowable strength of the steel bar for safety margin. That is to say, the bolt is limited to behavior in the elastic stage, or failure will occur. This fundamental principle is widely accepted in different bolting design methods including the block reinforcement procedure proposed by Oreste and Cravero (2008), which takes the axial, shear and bending stresses as linear functions of a small dislocation displacement of a potentially unstable block. This paper focuses on bolting mechanisms of slope engineering, and therefore, the reinforcement capacity of a fully grouted bolt is discussed in the elastic stage of the steel bar. The aim is to investigate the relationship between the shear and axial forces acting at the intersection of the bolt and the rock joint and then to propose an applicable analytical model to assess the resistant contribution by the combination of the shear and axial forces mobilized in the bolt for bolting design of slope engineering.

2 Mechanical Model

When a bolted rock joint is subjected to a shear displacement, the bolt deflects and at the same time, the host rock provides a reaction. For bedding rock slopes, bolting can enhance the shear strength of the joint and restrain the deformation of the rock mass by the combination of the axial and shear forces acting at the intersection between the bolt and the joint. Reinforcement mechanisms of a fully grouted bolt in bedding rock slopes include three aspects as follows:

  1. (1)

    a component of the axial force resulted from the opening of the joint, perpendicular to the joint plane, provides a friction resistance at the joint,

  2. (2)

    the axial force provides a component parallel to the joint which directly enhances the resistance,

  3. (3)

    and dowel effect restraints the movement along the joint.

Dowel effect provides a transverse shear resistance against shear movement of the rock joint and hence significantly influences the resistant contribution of a fully grouted bolt in bedding rock slopes. Generally, the following should be satisfied for the transverse shear resistance of a bolt to take action.

  1. (1)

    there exists shear deformation in the bolted rock mass which is perpendicular to the bolt axis,

  2. (2)

    the bolt is closely in contact with the surrounding rock mass so that, once shear deformation occurs, the rock mass immediately applies a transverse load on the bolt,

  3. (3)

    and the bolt should have proper shear strength and stiffness.

Obviously, for fully grouted bolts in bedding rock slopes, the above three items are satisfied. Therefore, transverse shear resistance will be mobilized while shear deformation at the joint plane occurs.

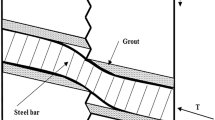
As depicted in Fig. 1, when a bolted rock joint is subjected to shearing, the bolt deflects antisymmetrically with respect to the joint plane. Along the deflecting length, the host rock applies compressive and tension loads on both sides of the bolt, respectively. As the adhesive strength between the steel bar and the grout is very low, the tension load is neglectable in the following presentation.

Fig. 1
figure 1

Separation of a bolted rock joint subjected to shearing

Full size image

According to Grasselli (2005), after the bolt reaches its yield strength, two plastic hinges occur at the deflecting section and the distance between these two plastic hinges is about one or two bolt diameters. Ge and Liu (1988) also pointed out that the deflecting length of a fully grouted bolt is 3–4 the steel bar diameters. These observations indicate that the deflecting length is far less than the anchorage section, which ranges from tens of centimeters to several meters. Besides, at the deflecting length, the bolt–grout interface will decouple under the combination of the shear and traction loads, and hence, the cohesion at the bolt–grout interface, which is the main contribution to the shear force at the interface, decreases to zero. Therefore, the friction force at the bolt–grout interface of the deflecting section is much less than the axial force (equal to the global shear force at the bolt–grout interface of the anchorage section) and hence can be ignored. For simplicity, the friction force at the bolt–grout interface of the deflecting section is assumed to be zero in the following discussions (Pellet and Egger 1996).

Distribution of the compressive load provided by the grout depends on the compressive strength of the grout and the shear displacement at the joint, and several distribution forms including trapezoid, parabola and triangle were proposed (Pellet 1994; Ferrero 1995; Wang et al. 2014). For simplicity, the compressive load is assumed as a triangular distribution in this study.

According to above presentations, the deflecting section of a fully grouted bolt can be taken as a statically indeterminate beam with two fixed ends (Wang et al. 2014), and the corresponding mechanical model is depicted in Fig. 2.

Fig. 2
figure 2

Beam model of the deflecting length

Full size image

3 Analytical Method

3.1 Structural Mechanical Analysis

By releasing the restraint of one end of the beam in Fig. 2, we get a statically determinate beam model as shown in Fig. 3. Denoting the axial force, shear force and bending moment acting at end B as \(X_{1}\), \(X_{2}\) and \(X_{3}\), respectively, and the axial displacement, the deflection and the rotation angle at end B as \(\Delta_{1}\), \(\Delta_{2}\) and \(\Delta_{3}\), respectively, force method equations based on structural mechanics (Long and Bao 2006) can be written as:

$$\left. {\begin{array}{*{20}c} {\delta_{11} X_{1} + \delta_{12} X_{2} + \delta_{13} X_{3} + \Delta_{1q} = \Delta_{1} } \\ {\delta_{21} X_{1} + \delta_{22} X_{2} + \delta_{23} X_{3} + \Delta_{2q} = \Delta_{2} } \\ {\delta_{31} X_{1} + \delta_{32} X_{2} + \delta_{33} X_{3} + \Delta_{3q} = \Delta_{3} } \\ \end{array} } \right\}$$
(1)

where \(\delta_{ij}\) and \(\Delta_{iq}\) are, respectively, the displacements along the direction of \(X_{i}\) resulted from \(X_{j} = 1\) and the compressive load q. \(\delta_{ij}\) and \(\Delta_{iq}\) can be determined by the graph multiplication method of structural mechanics (Long and Bao 2006), with the forms:

$$\delta_{ij} = \left[ {\begin{array}{*{20}c} {\frac{l}{EA}} & 0 & 0 \\ 0 & {\frac{{l^{3} }}{3EI} + \frac{kl}{GA}} & {\frac{{l^{2} }}{2EI}} \\ 0 & {\frac{{l^{2} }}{2EI}} & {\frac{l}{EI}} \\ \end{array} } \right]$$
(2)
$$\Delta_{iq} = \left[ {\begin{array}{*{20}c} 0 & {\frac{29}{960EI}q_{0} l^{4} + \frac{k}{12GA}q_{0} l^{2} } & {\frac{{q_{0} l^{3} }}{24EI}} \\ \end{array} } \right]$$
(3)

where E and G are, respectively, the elastic modulus and the shear modulus of the bolt, A and I are, respectively, the area and the moment of inertia of the bolt section, k is a non-uniformity coefficient of distribution of the shear stress at the bolt section, which is equal to 10/9 for a solid circular section (Long and Bao 2006; Hibbeler 2012), \(q_{0}\) is the maximal collection degree of the compressive load and l is the deflecting length of the bolt.

Fig. 3
figure 3

Forces acting at the determinate beam

Full size image

Forces of the deflecting length of the bolt as shown in Fig. 3 are antisymmetric with respect to the intersection between the bolt and the joint (Grasselli 2005). According to above presentations, it is reasonable to assume \(X_{2} = 0\) and \(\Delta_{3} = 0\). Substituting Eqs. (2) and (3) into Eq. (1) results in:

$$\left. {\begin{array}{*{20}c} {\frac{l}{EA}X_{1} = \Delta_{1} } \\ {\frac{{l^{2} }}{2EI}X_{3} + \frac{29}{960EI}q_{o} l^{4} + \frac{k}{12GA}q_{o} l^{2} = \Delta_{2} } \\ {\frac{l}{EI}X_{3} + \frac{{q_{o} l^{3} }}{24EI} = 0} \\ \end{array} } \right\}$$
(4)

From Eq. (4), we can obtain:

$$\left. {\begin{array}{*{20}c} {X_{1} = \frac{EA}{l}\Delta_{1} } \\ {q_{o} = \frac{{\Delta_{2} }}{{\frac{{kl^{2} }}{12GA} + \frac{{3l^{4} }}{320EI}}}} \\ \end{array} } \right\}$$
(5)

An orthogonal coordinate system, as shown in Fig. 3, is established such that the x- and y-axes are, respectively, parallel to and perpendicular to the bolt axis. The internal forces in the bolt subjected to only the compressive load q are, respectively, calculated by

$$Q_{q} (x) = \left\{ {\begin{array}{*{20}l} {\frac{{q_{o} }}{l}x^{2} \qquad\qquad\qquad\,{ (}{l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0pt} 2} \ge x \ge 0)} \hfill \\ {\frac{{q_{o} }}{l}x^{2} - 2q_{o} x + q_{o}\quad l { (}l \ge x > {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0pt} 2})} \hfill \\ \end{array} } \right.$$
(6)
$$M_{q} (x) = \left\{ {\begin{array}{*{20}l} {\frac{{q_{o} }}{3l}x^{3}\qquad\qquad\qquad\qquad\quad\quad { (}{l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0pt} 2} \ge x \ge 0)} \hfill \\ {\frac{{q_{o} }}{3l}x^{3} - q_{o} x^{2} + q_{o} lx - \frac{{q_{o} l^{2} }}{4}\qquad{ (}l \ge x > {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0pt} 2})} \hfill \\ \end{array} } \right.$$
(7)
$$N_{q} (x) = 0$$
(8)

where \(Q_{q} (x)\), \(M_{q} (x)\) and \(N_{q} (x)\) are, respectively, the shear force, the bending moment and the axial force of the bolt subjected to only the compressive load q.

Then, according to structural mechanics, the shear force, \(Q_{o}\), and the axial force, \(N_{o}\), which act in the bolt at the intersection between the bolt and the joint plane, can be calculated as:

$$Q_{o} = \frac{{q_{o} l}}{4} = \frac{{\Delta_{2} }}{{\frac{kl}{3GA} + \frac{{3l^{3} }}{80EI}}}$$
(9)
$$N_{o} = X_{1} = \frac{EA}{l}\Delta_{1}$$
(10)

In Fig. 4, the expression of deformation compatibility at end B can be written as:

$$\left. {\begin{array}{*{20}c} {\Delta_{1} = u\sin \alpha + v\cos \alpha } \\ {\Delta_{2} = v\sin \alpha - u\cos \alpha } \\ \end{array} } \right\}$$
(11)

where u and v are, respectively, the opening and shear displacements of the rock joint, and \(\alpha\) is the angle of the bolt with respect to the joint plane.

Fig. 4
figure 4

Deformation compatibility conditions at end B

Full size image

Denoting the dilation angle of the joint as β, we have:

$$u = v\tan \beta$$
(12)

Combining Eqs. (11) and (12) results in:

$$\frac{{\Delta_{2} }}{{\Delta_{1} }} = \tan (\alpha - \beta )$$
(13)

An expression describing the relationship of \(Q_{o}\) and \(N_{o}\) is then obtained by substituting Eqs. (9) and (10) into Eq. (13), with the form:

$$\frac{{Q_{o} }}{{N_{o} }} = K\tan (\alpha - \beta )$$
(14)

where K is a constant determined by the deflecting length, the geometric and mechanical parameters of the bolt, with the form of \(K = \frac{1}{{\frac{kE}{3G} + \frac{{3l^{2} A}}{80I}}}\).

The contributions to the support force against sliding along the joint plane, \(R_{Q}\) and \(R_{N}\), respectively, provided by \(Q_{o}\) and \(N_{o}\), as shown in Fig. 5, have the following forms:

$$R_{Q} = Q_{o} \sin \alpha - Q_{o} \cos \alpha \tan \varphi$$
(15)
$$R_{N} = N_{o} \cos \alpha + N_{o} \sin \alpha \tan \varphi$$
(16)

where \(\varphi\) is the friction angle of the joint plane.

Fig. 5
figure 5

Contributions of the internal forces acting in the bolt at the intersection

Full size image

By combining Eqs. (14)–(16), we have:

$$\frac{{R_{Q} }}{{R_{N} }} = K\tan (\alpha - \beta )\tan (\alpha - \varphi )$$
(17)

It is indicated from Eqs. (14) and (17) that the shear and axial forces acting at the intersection between the bolt and the joint plane contribute simultaneously to the support force against sliding of a bedding rock slope and that the contributions are linearly related to each other. The ratio of \(R_{Q}\) to \(R_{N}\) increases with increasing the angle of the bolt with respect to the joint plane, but descends with rising the dilation angle and the friction angle at the joint plane.

3.2 Calculation of the Bolt Contribution

To determine the contribution of a bolt to the stability of a slope, it is necessary to deduce the expression of the axial and shear forces in the bolt. It is proposed that failure occurs in point O (Dight 1983a, b; Pellet and Egger 1996).

In this presentation, we discuss the contribution of the bolt to the stability of a bedding rock slope, so the bolt is assumed to fail once section O yields. According to Tresca criterion, an expression describing the relation of the shear and axial forces acting at the section O is given as:

$$Q_{o} = \frac{1}{2}\sqrt {(Af_{y} )^{2} - N_{o}^{2} }$$
(18)

where \(f_{y}\) is the yielding stress of the bolt.

Combining Eqs. (14) and (18), the axial and shear forces are, respectively, expressed by

$$N_{o} = \frac{1}{{\sqrt {4K^{2} \tan^{2} (\alpha - \beta ) + 1} }}Af_{y}$$
(19)
$$Q_{o} = \frac{K\tan (\alpha - \beta )}{{\sqrt {4K^{2} \tan^{2} (\alpha - \beta ) + 1} }}Af_{y}$$
(20)

Then, the design support force provided by a fully grouted bolt against sliding of a bedding slope can be expressed as:

$$R = \frac{(\cos \alpha + \sin \alpha \tan \varphi ) + K\tan (\alpha - \beta )(\sin \alpha - \cos \alpha \tan \varphi )}{{\sqrt {4K^{2} \tan^{2} (\alpha - \beta ) + 1} }}Af_{y}$$
(21)

4 Influence of Relevant Parameters

It can be seen from above presentations that the angle of the bolt with respect to the joint plane, \(\alpha\), the dilation angle, \(\beta\), and the friction angle, \(\varphi\), significantly influence the resistant force of a fully grouted bolt against sliding of bedding rock slopes. For slope bolting design, however,\(\beta\) and \(\varphi\) are determinate and hence impossible to change. Therefore, the following mainly focuses on the influence of \(\alpha\) on the contribution of the rock bolt.

In this section, a scenario in which \(E = 206\) GPa, \(G = 79\) GPa, \(f_{y} = 600\) MPa,\(D = 25\) mm and \(l = 3D\) is analyzed to assess the influence of \(\alpha\) on the behavior of the bolt.

Figures 6 and 7, with different \(\varphi\) and \(\beta\), respectively, show the relationships between the ratio of \(R_{Q}\) to \(R_{N}\) and \(\alpha\). Figures 6 and 7 show that the inclination of the bolt significantly influences the ratio of the contributions.

Fig. 6
figure 6

Influence of the angle, \(\alpha\), on the ratio, \({{R_{Q} } \mathord{\left/ {\vphantom {{R_{Q} } {R_{N} }}} \right. \kern-0pt} {R_{N} }}\), for different values of \(\phi\) with \(\beta = 5^{ \circ }\)

Full size image
Fig. 7
figure 7

Influence of the angle, \(\alpha\), on the ratio, \({{R_{Q} } \mathord{\left/ {\vphantom {{R_{Q} } {R_{N} }}} \right. \kern-0pt} {R_{N} }}\), for different values of \(\beta\) with \(\phi = 30^{ \circ }\)

Full size image

The curves depicted in Fig. 6 consist of two parts, which are, respectively, related to two cases. The first case corresponds to an inclination varying from zero to the friction angle of the joint. In this case, the ratio of the contributions is very close to zero. This indicates that the contribution of the bolt is almost provided by the axial force in the bolt and that the contribution of the shear force acting in the bolt, namely the dowel effect, can be neglectable. In other words, the bolt can be taken as a pure tension element, while the angle of the bolt with respect to the joint plane is less than the friction angle of the joint.

In case two, the inclination has a range from the friction angle to 90°. It can be seen that the ratio increases with the inclination of the bolt rising, which means that, in this case, the contribution of the bolt is provided by the combination of the axial and shear forces in the bolt and that the contribution of the shear force becomes more and more important with the inclination increasing. When the bolt is steeply inclined to the joint plane, the dowel effect plays a dominant role to support the stability of a bedding rock slope.

Figure 6 also shows that the ratio is influenced by the friction angle. The smaller the friction angle, the larger the ratio is. According to Eqs. (15) and (16), the contribution of the shear force increases with the friction angle decreasing but at the same time, the contribution of the axial force diminishes.

Figure 7 shows that the dilation angle has no significant effect on the ratio when the inclination of the bolt is less than 70°. However, when the inclination reaches 70°, the ratio descends with the dilation angle rising and especially, in the case that the bolt is normal to the joint, small increment of the dilation angle will result in marked decrement of the ratio. Therefore, it should be pointed out that, when the bolt is steeply inclined to the joint plane, the dilation angle of the joint must be taken into account, or much inaccuracy occurs.

5 Experimental Investigations

In order to verify the proposed model, preliminary laboratory shear tests of bolted joints were conducted. The testing device can, respectively, apply normal and shear loads, and eight dial gages are used to monitor the displacements, respectively, normal to and parallel to the joint during shearing. The specimens consist of two concrete blocks (each of 40 cm × 40 cm × 20 cm) with a bolt installed through the center of the joint, as depicted in Fig. 8. In this study, different angles between the bolt and the joint such as 90°, 75°, 60° and 45° are selected for shear testing.

Fig. 8
figure 8

Arrangement adopted for the shear tests of bolted joint

Full size image

The bolts are hot rolled round bars with a diameter of 8 mm, and the mechanical properties obtained from the uniaxial tensile tests of the bolt are reported in Table 1. The friction angles of the joint are determined through direct shear tests on unbolted blocks. The mechanical parameters of the concrete blocks, cement mortar and joints are listed in Table 2. The water-to-cement ratio of the cement mortar was 0.45, and the borehole diameter is 20 mm.

Table 1 Mechanical parameters of the steel bar
Full size table
Table 2 Mechanical parameters of materials
Full size table

The curves of shear load and shear deformation of bolting joints with different inclinations are presented in Fig. 9. It can be observed that the curves with different inclinations have similar shapes. For a clear understanding, the curve of shear load and shear deformation with an inclination of 60° is separately drawn in Fig. 10. Obviously, there are four stages including elastic, yielding, plastic hardening and failure stages during shearing. When the joint displacement is small, the shear load increases linearly with the shear displacement, which corresponds to the elastic state of the steel bar. At the second stage, the shear displacement increases but the shear load keeps almost constant. This case is in line with the yielding stage of the steel bar. For the third stage, the shear load rises with the shear displacement increasing, which indicates that the bolt is in the plastic hardening stage. At last, the shear load decreases sharply with the shear displacement increasing, which indicates that failure occurs. Similar phenomenon was observed by others (Grasselli 2005; Jalalifar and Aziz 2010).

Fig. 9
figure 9

Shear displacement versus shear load of the rock bolts with different inclinations

Full size image
Fig. 10
figure 10

Typical shear displacement versus shear load curve of a bolt with an inclination of 60°

Full size image

Figure 11 shows the failure of the rock bolts with different inclination angles. The following phenomena are clearly shown in Fig. 11:

Fig. 11
figure 11

Failure photographs of rock bolts with different inclinations

Full size image
  1. (1)

    the failure of the bolt occurs at the cross point of the joint and the bolt, and except for the cross point there is no other plastic hinge observed, which is different from the result depicted by Grasselli (2005).

  2. (2)

    distinct bending deformation of the bolt near the joint is observed to be antisymmetrical with respect to the joint plane, and the length of the transverse shear deformation section of the bolt is about 2~3 times of the bolt diameter.

  3. (3)

    and when failure occurs, the bending angle of the bolt is marked. The bigger the inclination, the greater the bending angle.

The contribution of the bolt can be calculated by the shear and normal loads as:

$$R = T_{s} - T_{n} \tan \varphi$$
(22)

where \(T_{s}\), \(T_{n}\) are, respectively, the shear and normal loads.

To compare the ultimate resistances calculated by the model and from the test results, multiplying the design support force R calculated by Eq. (21) with the ratio of \(R_{u}\) to \(R_{y}\) which are, respectively, the contributions calculated from tests in cases of yielding and failure states of the bolt, results in the theory value of the ultimate resistance. The test and calculation results are depicted in Fig. 12.

Fig. 12
figure 12

Comparisons between the developed approach and the test results

Full size image

Figure 12 shows that the theoretical calculations coincide with the shear test results. As the inclination increases from 45° to 90°, both the bolt contributions obtained by the developed model and the experimental test descend. Specifically, when the inclination is 45°, 60°, 75° and 90°, the differences between the experimental results and calculation results are 3.3, 5.8, 5.9 and 1.3%, respectively, which indicates that the developed model can accurately predict the contribution of the bolt.

6 Comparisons and Discussions

In practice, as previously mentioned, only the axial force acting in the bolt is considered to contribute to the stability of rock slopes in bolting design. The support force provided only by the axial force is calculated by (GB 50330-2013, China 2013)

$$R = [\cos \alpha + \sin \alpha \tan \varphi ]Af_{y}$$
(23)

Figure 13 describes the influence of the inclination of the bolt on the support forces computed by Eqs. (21) and (23), respectively, where the support forces are divided by the yielding tensile force of the bolt, Af y . Figure 13 shows that the curves of the two cases have similar shapes. The support forces for both cases increase with the inclination increasing to about 40°, which is equal to the friction angle and then descend. That is to say, to obtain a maximum value of the support force, the design inclination should be set as large as the friction angle. Besides, when the inclination varies in the range from zero to 60° the support force calculated by the approach developed in the paper is slightly smaller than that by the proposed method in the code (GB 50330-2013, China 2013), and however, while the inclination is larger than 60°, the former is markedly less than the latter and the ratio of the latter to the former increases with the inclination rising.

Fig. 13
figure 13

Contributions in cases of with and without the consideration of the dowel effect with \(\phi = 40^{ \circ }\)

Full size image

The dowel effect always exists regardless of the size of the inclination of the bolt to the joint. Figure 13 indicates clearly that the design method suggested by the code overestimates the resistance of the bolt, especially for the case of steep inclination of the bolt to the joint and hence needs to be improved. Although an analytical approach was developed and verified with experimental results, the deflecting length, \(l\), incorporated in Eq. (21), about 2–3 times of the bolt diameter according to experimental observations, is influenced by other factors such as the strength and diameter of the bolt, the strengths of the grout and rock and the inclination of the bolt to the joint, and needs further investigations to be formulized.

7 Conclusions

This presentation proposes a new approach for evaluating the contribution of a fully grouted bolt to the stability of bedding rock slopes, by taking the deflecting section of the bolt as a statically indeterminate beam and adopting force method equations and deformation compatibility relationships. This model is helpful to understand the reinforcement mechanism of fully grouted bolts and to improve bolting design.

The present bolting design method takes into account only the axial force acting in the bolt. For bedding rock slopes, however, deformation of the bolt perpendicular to the bolt axis is strongly restricted by the host rock, and hence, a shear force, which is proved to have an important contribution on the shear strength of the rock joint, is activated in the bolt. In other words, the dowel effect should be considered for bolting design.

The contributions of the shear and axial forces acting at the intersection between the bolt and the joint plane have a linear relationship, which is determined by the angle of the bolt with respect to the joint plane, the dilation angle and the friction angle at the joint plane as well as other geometric and mechanical parameters. The ratio of the contributions resulted from the shear and axial forces increases with the angle of the bolt with respect to the joint plane increasing but decreases with both the dilation angle and the friction angle rising.

A scenario is adopted to illustrate the influence of relevant parameters on the contribution. The results show that, when the inclination of the bolt is less than the friction angle of the joint, the ratio of the contributions is almost zero, and hence, the dowel effect cannot be considered. However, the ratio increases markedly with the inclination increasing in the range from the friction angle to 90°, which means that the global contribution of the bolt is provided by the combination of the shear and axial forces and that the contribution of the shear force plays a more and more important role. It is also observed that, when the bolt steeply inclines to the joint plane (larger than 70° for example), the ratio is greatly influenced by the dilation angle.

Laboratory tests results show that the bolt near the joint deflects antisymmetrically with respect to the joint plane, that the deflecting length of the bolt is about 2~3 times of the bolt diameter and that failure occurs at the cross point of the joint and the bolt. The steeper the inclination, the more distinct the dowel effect. The test data are in good agreement with the results calculated by the developed method.

The comparisons between the developed method and the design approach suggested in the code (GB 50330-2013, China 2013) were made. The results show that the design method overestimates the resistance of the bolt, especially for the case of steep inclination of the bolt to the joint, which would result in security issues of projects.