1 Introduction

The effects of three-body baryon forces on baryon multi-systems are becoming more important in many physics categories. In particular, in the current situation called “hyperon puzzle”, the difficulty to reconcile the measured masses of neutron stars with the presence of hyperons in their interiors, the three-body baryon force seems to be a promising candidate for the origin of the extra repulsive effect.

Several approaches to the three-body baryon force using the quark model, that is, the 9-quark 3-baryon system, have been reported so far. In other words, the effect of the interaction between the nine quarks through antisymmetry may be the appearance of a kind of three-body effect over the three baryons. In this sense, the quark model seems to be a promising approach.

There are two main advantages of the quark model. The first is that it is possible to describe from one baryon system to several baryon systems in a unified framework. This allows us to extend the framework we have used for two-baryon interactions directly to a three-baryon system. The second is that it is possible to evaluate the effect of each quark-Hamiltonian component. This not only allows us to consider the kinematical and dynamical parts of the quark separately, but also allows us to evaluate each component of the interaction. We explore the possibility of solving the hyperon puzzle by applying the three-body baryon force derived from the quark model.

We will examine in the next section whether the quark-Pauli effect has a special repulsive effect on various three-baryon systems. In Sect. 3, we examine what kind of three-body effect the color-magnetic term, known to produce a strong short-range repulsion in a two-baryon system, gives in various three-baryon systems under the flavor-SU(3) approximation. A summary is drawn in Sect. 4.

2 Quark-Pauli Effect in Three-Baryon Systems

Just as white dwarfs are interpreted as being supported by electron-induced degeneracy, namely Pauli effect by electrons, neutron stars are also considered to be supported by neutron-induced degeneracy. If the neutron Pauli effect and the repulsive force originating from the two-baryon interaction cannot support the neutron star, it may be supported by the quark degeneracy pressure, namely the quark-Pauli effect.

The quark-Pauli effect is evaluated by solving the eigenvalue problem of the resonating group method (RGM) norm kernel in the three-baryon systems [1]. This method may be intuitively interpreted as follows. Let us consider a two-baryon wave function,

$$\begin{aligned} \varPhi _{B_1B_2}(1;2)=\frac{1}{\sqrt{2}}\left[ \phi _{B_1}(1)\phi _{B_2}(2)-\phi _{B_1}(2)\phi _{B_2}(1)\right] , \end{aligned}$$
(1)

which is normalized, \(\left\langle \varPhi _{B_1B_2}\right| \left. \varPhi _{B_1B_2}\right\rangle =1\). When this two-baryon wave function is re-expressed as a six-quark wave function, it becomes as follows using the quark antisymmetrizer \(\mathcal{A}\):

$$\begin{aligned}&\varPsi _{(3q)_1(3q)_2}(123;456) \nonumber \\&\quad =\mathcal{A}\left\{ \frac{1}{\sqrt{2}} \left[ \psi _{(3q)_1}(123)\psi _{(3q)_2}(456)-\psi _{(3q)_1}(456)\psi _{(3q)_2}(123) \right] \right\} , \end{aligned}$$
(2)

which is not normalized, \(\left\langle \varPsi _{(3q)_1(3q)_2}\right| \left. \varPsi _{(3q)_1(3q)_2}\right\rangle =\mu \) with \(\mu \ne 1\), due to the effect of antisymmetry under the exchange of quarks among the baryons. Namely, this is the quark-Pauli effect. If \(\mu \) is explicitly zero, such a two-baryon system means that the existence probability is zero from the viewpoint of six-quark configuration, that is, the Pauli-forbidden state. Even if \(\mu \) is not explicitly zero, the configuration of a two-baryon system with a value of \(\mu \) near zero also has a small existence probability, so that a system should be difficult to realize. Since such a state, called an almost Pauli-forbidden state, resembles the characteristics of the wave function of a system with a strong repulsive potential, it can be considered as a structural repulsive effect due to the quark-Pauli effect. Studies of two-baryon interactions have shown that the structural repulsive effect of the quark-Pauli effect is dominant with or without attraction in the interaction potential.

The 9-quark 3-baryon wave function is given by \(\varPsi _{{\textit{SYI}}}((0s)^9;B_1B_2B_3) =\varPsi ^{({\textit{orb}})}\varPsi ^{({\textit{SF}})}_{{\textit{SYI}}}\varPsi ^{({\textit{color}})},\) where \(\varPsi ^{({\textit{orb}})}\) denotes the orbital part with the \((0s)^9\) configuration, \(\varPsi ^{({\textit{SF}})}_{{\textit{SYI}}}\) the spin-flavor part with the spin value S, the hypercharge Y, and the isospin I, and \(\varPsi ^{({\textit{color}})}\) the color part assuming a color singlet in each baryon. Assuming the eigenfunction of \(\mathcal{A}\) to be

$$\begin{aligned} \sum _{B_1B_2B_3}C({\textit{SYI}};B_1B_2B_3)\varPsi _{{\textit{SYI}}}\left( (0s)^9;B_1B_2B_3\right) , \end{aligned}$$
(3)

we solve the eigenvalue problem

$$\begin{aligned}&\sum _{B_1^\prime B_2^\prime B_3^\prime } \left\langle \varPsi _{{\textit{SYI}}}\left( (0s)^9;B_1B_2B_3\right) \left| \mathcal{A}\right| \varPsi _{SYI}\left( (0s)^9;B_1^\prime B_2^\prime B_3^\prime \right) \right\rangle C({\textit{SYI}};B_1^\prime B_2^\prime B_3^\prime ) \nonumber \\&\quad =\mu _{{\textit{SYI}}}C({\textit{SYI}};B_1B_2B_3)\ . \end{aligned}$$
(4)

Table 1 shows the almost Pauli-forbidden states in the three-baryon system. We can find in this table the feature that many systems have large isospin-value with \(\varSigma \), namely systems containing \(\varSigma ^-\) particle. This is due to the inclusion of the strong quark-Pauli repulsive effect on the \(\varSigma ^-n\ ^3S_1\) state, as is well known in the study of the two-baryon system [2, 3]. We find that the \(\varLambda {\textit{NN}}\) system, which has the lowest threshold of the three baryon systems containing hyperons, is not in a almost Pauli-forbidden state. Therefore, the quark-Pauli effect is not a candidate for solving the hyperon puzzle.

Table 1 Almost Pauli-forbidden states in the three-baryon systems
Full size table

3 Behavior of Color-Magnetic Term in Three-Baryon Systems

Since the solution of the hyperon puzzle cannot be expected by the structural repulsive effect, we next aim at the solution by the three-body baryon force generated from the quark-quark interaction.

We use the RGM formalism for this purpose. The RGM wave function for the nine-quark \(B_1B_2B_3\) system can be expressed by

$$\begin{aligned} \psi =\mathcal{A}\left[ \phi ({\textit{SYI}};B_1B_2B_3)\chi \left( {\varvec{R}}_{12},{\varvec{R}}_{12-3}\right) \right] . \end{aligned}$$
(5)

For a definition of \(\phi ({\textit{SYI}};B_1B_2B_3)\) see Ref. [4]. The wave function \(\chi \) is assumed to satisfy the following RGM equation

$$\begin{aligned}&\left[ \frac{\hbar ^2}{2\mu _1}\varDelta _{R_{12}}-\frac{\hbar ^2}{2\mu _2}\varDelta _{R_{12-3}} \right] \,\chi \left( {\varvec{R}}_{12},{\varvec{R}}_{12-3}\right) \nonumber \\&\qquad +\displaystyle \int K^{(E)}\left( {\varvec{R}}_{12},{\varvec{R}}_{12-3};\,{\varvec{R}}_{12}^\prime ,{\varvec{R}}_{12-3}^\prime \right) \chi \left( {\varvec{R}}_{12}^\prime ,{\varvec{R}}_{12-3}^\prime \right) \,d{\varvec{R}}_{12}^\prime \,d{\varvec{R}}_{12-3}^\prime \nonumber \\&\quad =\varepsilon \,\chi \left( {\varvec{R}}_{12},{\varvec{R}}_{12-3}\right) , \end{aligned}$$
(6)

where \(\mu _1\) and \(\mu _2\) are the appropriate reduced masses, and \(\varepsilon \) is the total energy minus three baryon masses. The quark exchange kernel in Eq. (6),

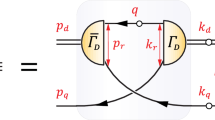
$$\begin{aligned} K^{(E)}=K^{(E)}_T+K^{(E)}_V-(\varepsilon +\varepsilon _{B_1}+\varepsilon _{B_2}+\varepsilon _{B_3})K^{(E)}_1\,, \end{aligned}$$
(7)

gains contributions from the translationally invariant nine-quark kinetic energy operator, T, from the quark-quark interaction, \(V=\sum _{i>j}v_{ij}\), and the norm kernel. In Eq. (7) \(\varepsilon _{B_i}\) is the internal energy of the ith baryon. The separation into two-body and three-body terms can be made through the specific construction of the antisymmetrizer, \(\mathcal{A}\), of Eq. (5) which can be expanded in terms of the permutations \(P_{ij}\) and \(P_{ijk}\) by using double coset generators [5] as

$$\begin{aligned} \mathcal{A}&=\frac{1}{6}\Bigg \{\left[ 1-9\left( P_{36}+P_{69}+P_{93}\right) +27\left( P_{369}+P_{396}\right) \right. \nonumber \\&\left. \left. +54\left( P_{36}P_{59}+P_{69}P_{83}+P_{93}P_{26}\right) \right] \left[ \sum _{\mathcal{P}=1}^6(-1)^{\pi (\mathcal{P})}\mathcal{P} \right] -216P_{26}P_{59}P_{83}\right\} . \end{aligned}$$
(8)

The six \(\mathcal{P}\) include those quark exchanges which are equivalent to baryon exchanges. Of the five basic types of terms in \(\mathcal{A}\), the third to fifth category involve the exchange of quark pairs between different baryon pairs and give rise to nonlocal three-body forces in the baryon–baryon interaction [6]. With these terms, the three-body exchange kernel \(K^{(E)}_{\varTheta 3}\) for the operator \(\varTheta (=T,V,1)\) can be evaluated in terms of the baryon-separation parameters \({\varvec{R}}_a\), \({\varvec{R}}_b\), \({\varvec{R}}_a^\prime \), \({\varvec{R}}_b^\prime \) through

$$\begin{aligned}&K^{(E)}_{\varTheta 3}({\varvec{R}}_a,{\varvec{R}}_b;{\varvec{R}}_a^\prime ,{\varvec{R}}_b^\prime ) \nonumber \\&\quad =\left\langle \phi ({\textit{SYI}};B_1B_2B_3)\delta ({\varvec{R}}_{B_1B_2}-{\varvec{R}}_a)\delta ({\varvec{R}}_{B_1B_2-B_3}-{\varvec{R}}_b)\right. \nonumber \\&\qquad \left. \times \left| \varTheta \mathcal{A}_3 \right| \phi ({\textit{SYI}};B_1B_2B_3)\delta ({\varvec{R}}_{B_1B_2}-{\varvec{R}}_a^\prime )\delta ({\varvec{R}}_{B_1B_2-B_3}-{\varvec{R}}_b^\prime ) \right\rangle , \end{aligned}$$
(9)

where \(\mathcal{A}_3\) represents the third to fifth terms of the Eq. (8).

Here we focus on the three-baryon three-body effect originating from the color-magnetic term \(\varTheta =-\frac{\alpha _S\pi \hbar ^3}{6m^2c} \lambda ^c_i\cdot \lambda ^c_j{\varvec{\sigma }}_i\cdot {\varvec{\sigma }}_j\delta (r)\)(or \(\varTheta =cm\)), which is well known for giving short-range repulsion between two baryons, as the quark potential, where \(\lambda ^c_i\) denotes the color-SU(3) generator, \({\varvec{\sigma }}_i\) the spin-SU(2) generator, \(\alpha _S\) the strong quark–gluon coupling constant, m quark mass. We consider the flavor-SU(3) limit in this work. We adopt a value that seems reasonable as a quark-parameter set; \(mc^2=313\) MeV, \(\alpha _S=1\) and the oscillator length parameter for the quark wave functions in the baryon \(b=0.6\) fm.

We evaluate the following integral amount to evaluate the nonlocal three-body color-magnetic exchange kernel, \(K^{(E)}_{cm3}\), as a localized:

$$\begin{aligned}&V_{cm3}\left( {\varvec{R}}_a,{\varvec{R}}_b\right) =\displaystyle \int K^{(E)}_{cm}\left( {\varvec{R}}_a,{\varvec{R}}_b; {\varvec{R}}_a^\prime ,{\varvec{R}}_b^\prime \right) \chi \left( {\varvec{R}}_a^\prime ,{\varvec{R}}_b^\prime \right) \,d{\varvec{R}}_a^\prime \,d{\varvec{R}}_b^\prime , \end{aligned}$$
(10)
$$\begin{aligned}&K^{(E)}_{cm}\left( {\varvec{R}}_a,{\varvec{R}}_b; {\varvec{R}}_a^\prime ,{\varvec{R}}_b^\prime \right) =K^{(E)}_{cm3}\left( {\varvec{R}}_a,{\varvec{R}}_b; {\varvec{R}}_a^\prime ,{\varvec{R}}_b^\prime \right) -\left( \varepsilon _{B_1}^{cm}+\varepsilon _{B_2}^{cm}+\varepsilon _{B_3}^{cm}\right) K^{(E)}_1,\end{aligned}$$
(11)
$$\begin{aligned}&\chi \left( {\varvec{R}}_a^\prime ,{\varvec{R}}_b^\prime \right) \exp \left( -\frac{3}{4\nu _1^2}{\varvec{R}}_a^{\prime \,2}-\frac{1}{\nu _2^2}{\varvec{R}}_b^{\prime \,2}\right) \,, \end{aligned}$$
(12)

where \(\nu _1\) and \(\nu _2\) are two types of width parameters in Jacobian coordinates composed of three baryons. we assume \(\nu _1=\nu _2=b\) in this report for simplicity.

Figure 1 shows \(V_{cm3}\) in Eq. (10) for the case where the three baryons form the equilateral triangle configurations. From the figure, we can find the following behavior of the three-body effect, which is highly flavor-dependent; it is a repulsive force in the \({\textit{NNN}}\) system with the isospin \(I=1/2\), a strong repulsive force in the \(\varLambda {\textit{NN}}\) system, an attractive force in the \(\varSigma {\textit{NN}}\) system with \(I=2\), and a weak repulsive force in the \(\varXi {\textit{NN}}\) system with \(I=3/2\). In particular, the strength of the repulsive force in the \(\varLambda {\textit{NN}}\) system contributes as much as the two-body effect generated from the second term in Eq. (8). Considering the consistency with the binding energy of hyper-triton, such a strong \(\varLambda {\textit{NN}}\) three-body repulsive force is not realistic. This may be due to the use of the same values as the oscillator length parameter b for the two width parameters \(\nu _1\) and \(\nu _2\). The relatively strong repulsive three-body effect in the \(\varLambda {\textit{NN}}\) system of color-magnetic terms may be a promising candidate for the extra repulsive effect needed to solve the hyperon puzzle.

Fig. 1
figure 1

\(V_{cm3}\) in Eq. (10) for the case where the three baryons form the equilateral triangle configurations with a side length of r(fm). the bold line denotes \({\textit{NNN}}\) (the total isospin \(I=\frac{1}{2}\)) system, the dashed-line \(\varLambda {\textit{NN}}(0)\), the solid line \(\varLambda {\textit{NN}}(1)\), the bold dashed-line \(\varSigma {\textit{NN}}(2)\), and the dotted line \(\varXi {\textit{NN}}\left( \frac{3}{2}\right) \). The small dotted-line denotes the two-body contribution in the second term in Eq. (8) for the \(\varLambda {\textit{NN}}(1)\). Total spin is \(\frac{1}{2}\) in all channels

Full size image

4 Summary

We evaluated the three-body baryon effect in the quark model to solve the ‘hyperon puzzle’. As candidates for the extra repulsive effect required to solve the hyperon puzzle, we focused on the structural repulsive core caused by the quark-Pauli effect and the color-magnetic term, which is a promising interaction between quarks. The result is that in the lowest threshold \(\varLambda {\textit{NN}}\) system, no significant structural repulsive core is obtained, but a strong repulsive three-body effect is obtained from the color-magnetic term. This result is inconsistent with the conclusions of Ref. [7], which the intrinsic three-baryon interaction at short distance vanishes for all quantum numbers. Further research is needed to investigate the cause.