1 Introduction

Tunnel field effect transistors (TFET) (Bhuwalka et al. 2005; Bhuwalka et al. 2006) with Subthreshold Slope (SS) below 60 have become the adroit candidate for low power applications. However, with shrinking device dimension, the fabrication of semiconductor based devices with abrupt junctions became increasingly complex (Pratap et al. 2016). Thus, Junctionless TFET (JL-TFET) were proposed (Ghosh and Akram 2013) with uniform doping throughout the device and no abrupt junction, thereby reducing fabrication complexity (Damrongplasit et al. 2013; Gundapaneni et al. 2012). The JLTFET combines the concept of JLFET and TFET, where an N + N+N + structure can be converted into a PIN structure by effectively controlling the polar gate work function (Ghosh and Akram 2013). This work incorporates the concept of JLTFET with triple material gate (TMG) (Bagga et al. 2015; Vanitha et al. 2015; Dewan et al. 2016) along with the use of asymmetric hetero-dielectric in a Si based structure. The proposed structure is found to improve the current ratio, SS and comparatively involves less fabrication complexity (Toh et al. 2007). The use of asymmetric dual k is known to improve the electric field across the junction (Raushan et al. 2018) and thereby increasing the ON current. Although, a number of models have been proposed for JLTFET (Ghosh and Akram 2013; Bal et al. 2014; Akram et al. 2014), but the analytical model for TMG AHD JLTFET is introduced for the first time in this work. The proposed structure is analytically solved for the expression of surface potential. The derived expression is then used as a tool to optimize the structure. The sole theory is to amalgamate the above three concept in a single device and study its impact. However, state of art techniques in semiconductor design involves rigorous process of tuning the design parameters and re-simulating the structure to achieve the specified target. Thus, these empirical techniques have become a bottleneck for semiconductor device designers. Therefore, this paper highlights the use of optimization algorithms to tune the device parameters. The surface potential model incorporates all physical effects even in downscaled devices. Thus, surface potential based model for the proposed device is derived and is used to optimize the structure. The traditional optimization approaches such as numerical based approaches (Pinnau 2007), derivative based techniques (Lian et al. 2018) are known to suffer from local optima stagnation, poor convergence and are not suitable for complex quantum model analysis. This paper uses various modern optimization approaches (Zhang et al. 2009; Talukder 2011; Kameyama 2009; Liu et al. 2014; Storn and Price 1995; Mirjalili and Lewis 2016a, b) to design the structure. However, a hybrid combination of PSO and DE i.e. DEPSO provides the best accuracy as well as computational efficiency for the proposed model. All device simulations are performed in Synopsis TCAD tool (S.I. Association 2015). The optimization algorithms are implemented in MATLAB 2015 version to achieve the target design parameters. This paper has been structured as follows: Sect. 2 describes the device architecture, Sect. 3 illustrates the optimization process, Sect. 4 explains the model derivation, Sect. 5 discusses the results and finally Sect. 6 draws the conclusion.

2 Device Structure

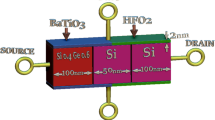
This section illustrates the proposed structure shown in Fig. 1. The structure depicts an n-type Si channel hetero-dielectric double gate Junctionless TFET. A uniform doping concentration of 1 × 1019 cm−3 is used throughout the device, thus making a Junctionless TFET easier to fabricate (Bal et al. 2014). The device structure consists of two isolated gates: Polar gate nearer to the source for generating P + region and control gate in middle to create channel.

Fig. 1
figure 1

Proposed structure for AHD-TMG-JLTFET

Full size image

The polar gate is biased at 0 V (Bal et al. 2014). A triple material configuration is used for controlling the gate with different metal M1 (auxiliary), M2 (control), and M3 (tunnel). Each metal gate has different work function \(\Phi_{1} ,\Phi_{2}\ and\ \Phi_{3}\) and length L1, L2 and L3. Proper tuning of control gate work function will result in better current ratio. The inclusion of spacer between two gates helps in reducing the coupling between the two gates (Akram et al. 2014). The dielectric of both polar and control gates is of two different types: high-k (HfO2) near the source and low-k (SiO2) near the drain in two different layers. The use of asymmetric HD layer across front and back gate resulted in improved current characteristics. The effective oxide thickness is calculated as in (Bentrcia et al. 2012). All simulations are performed in Synopsis TCAD tool.

3 Optimization problem formulation

The main concern associated with TFET design is to improve the current ratio and this opens to many novel device structures. A structure can provide its best performance if properly optimized. Thus, optimizing the structure plays a crucial role. This paper makes use of various evolutionary computational algorithms. The algorithms are chosen in such a way that they improve computational efficiency as well as accuracy without compromising the device inherent characteristics. This technique of device optimization requires an objective function. The model for surface potential is derived for the proposed structure. Since, the surface potential based model is quite close to physical prototype and takes into account various physical effects occurring in TFET, it is used as an objective function. Thereby, improving surface potential across the junction will help improving the electric field and, in turn, the ON current also increases. The optimization process is divided into three steps:

3.1 Preprocess

The sensitivity analysis is performed in this process so that the parameters which significantly affect device performance can be sorted. As the device model consists of a large number of parameters, it becomes difficult to handle significant amount of variables. Thus, preprocess aids in data reduction and thereby in limiting the computational complexity. The selection of design variables is divided into certain sections and is done by performing sensitivity analysis. The sensitivity analysis can facilitate understanding the impact of various parameters on the device performance. A set of parameters (say, L1, L2, and L3), are adjusted while others are fixed at certain values to assess the impact on device performance. The device parameters are divided into certain groups and the sensitivity analysis is performed. The parameters which significantly influence the device performance are then selected as design variables and the other least significant parameters are considered as constant. Tables 1 and 2 list out the various design constants and variables used in the optimization process. The choice of material and doping concentrations are kept fixed.

Table 1 Design constants
Full size table
Table 2 Design variables
Full size table

3.2 Parameter extraction/algorithm parameters

A number of modern optimization algorithms such as DEPSO, human behavior based particle swarm optimization (HBPSO) (Liu et al. 2014), particle swarm optimization (PSO) and Whale Optimization Algorithm (WOA) are used to optimize the structure. The effectiveness of different optimization algorithms are evaluated by performing 20 independent runs of each algorithm. This technique is used to evaluate the robustness of the algorithms by considering the best achieved value of the objective function. A comparative analysis reflects that the performance of DEPSO is superior in terms of efficiency and accuracy. The working principle of DEPSO algorithm is explained in the subsequent section.

Hybrid DEPSO: The DEPSO algorithm (Zhang et al. 2009) is the hybrid version of the DE and PSO algorithm. The DE has some pros, and it includes its capacity to preserve the diversity of the population and the ability to explore local search. But the algorithm has no means to memorize the preceding process and utilize the global information regarding the search space. Therefore, there will be wastage of computing power and there is a risk for the algorithm to be trapped in local optima. The differential information can be useful for the search ability, but it also leads to instability in some solutions. To get the advantages of both PSO and DE, the hybrid DEPSO algorithm has been designed. Here the PSO algorithm is integrated into DE and thus it results in fast convergence and higher population diversity (Zhang et al. 2009). The algorithm parameters are listed in Table 3 (Fig. 2).

Table 3 Optimization algorithm parameters
Full size table
Fig. 2
figure 2

The DEPSO algorithm

Full size image

3.3 Post process

Post process involves the validation of the results obtained by optimization algorithm by simulating the results in TCAD simulator.

4 Mathematical Model for the proposed structure

The 2-D Poisson’s equation for potential distribution of channel can be represented as

$$\frac{{\partial^{2} \phi \left( {x,y} \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} \phi \left( {x,y} \right)}}{{\partial y^{2} }} = \frac{{ - qN_{ch} }}{{\varepsilon_{si} }}\quad (0 \le x \le L ;0 \le y \le t_{si} )$$
(1)

where, \(N_{ch}\) is the channel doping concentration, \(\varepsilon_{si}\) represents the dielectric constant of Si, L represents the total length of the control gate, \(\phi (x,y)\) is the potential at any point in the channel, q is the charge of electron, and \(t_{si}\) is the thickness of the device.

A parabolic function by Young’s approximation is used to represent potential profile across the channel with \(A_{0}\) being the surface potential which is a function of x and,\(A_{1} \left( x \right),\) \(A_{2} \left( x \right)\) are arbitrary constants:

$$\phi \left( {x,y} \right) = A_{0} + A_{1} \left( x \right)y + A_{2} \left( x \right)y^{2} .$$
(2)

As three different metals are used M1, M2, M3, thus, the surface potential under each metal can be expressed as

$$\phi_{j} \left( {x,y} \right) = A_{0j} + A_{j1} \left( x \right)y + A_{j2} \left( x \right)y^{2} .$$
(3)

For \(L_{j - 1} \le x \le L_{j}\) and \(0 \le y \le t_{si}\), where j = 1, 2, 3 for M1, M2, M3 and \(\phi_{j}\) is the corresponding potential. \(L_{0}\) is the starting point of the channel i.e. \(L_{0} = 0.\)

As three different materials were used in the gate, they will have different work function and subsequently different flat band where, \(\chi\) is the electron affinity, \(E_{g}\) is the band gap of Silicon at room temperature and \({{\Phi }}_{{\begin{array}{*{20}c} B \\ { } \\ \end{array} }}\) is the bulk potential voltage:

$$\begin{aligned} & V_{FB,L1} = {{\Phi }}_{{{\text{M}}1 }} - {{\Phi }}_{\text{Si }} ,\quad V_{FB,L2} = {{\Phi }}_{{{\text{M}}2 }} - {{\Phi }}_{\text{Si }} , \\ & V_{FB,L3} = {{\Phi }}_{{{\text{M}}3 }} - {{\Phi }}_{\text{Si }} \\ \end{aligned}$$
(4)

\({{\Phi }}_{{{\text{M}}1}} ,{{\Phi }}_{{{\text{M}}2}} ,{{\Phi }}_{{{\text{M}}3}}\) are the work function of M1, M2, M3 and \({{\Phi }}_{\text{Si }}\) is the silicon work function:

$${{\Phi }}_{\text{Si }} = \chi + \frac{{E_{g} }}{2q} + {{\Phi }}_{{\begin{array}{*{20}c} B \\ { } \\ \end{array} }}$$
(5)
$${{\Phi }}_{{\begin{array}{*{20}c} B \\ { } \\ \end{array} }} = {\text{V}}_{\text{T}} \ln \left( {\frac{{{\text{N}}_{\text{ch}} }}{{{\text{n}}_{\text{i}} }}} \right),$$
(6)

where, thermal voltage, \(V_{T} = \frac{{kT}}{q}\) and \({\text{n}}_{\text{i}}\) is the intrinsic concentration of silicon.

  1. 1.

    In case of TMG the electric field at the front and back gate is continuous

$$\begin{aligned} & \left. {\frac{{d\phi_{1} \left( {x,y} \right)}}{dy}} \right|_{y = 0} = - \frac{{C_{ox1f} }}{{C_{s} }}\frac{{V_{gs1} - A_{01\left( x \right)} }}{{t_{si} }}, \\ & V_{gs1} = V_{gs} - V_{FB,L1} ,\quad C_{s} = \frac{{\varepsilon_{Si} }}{{t_{Si} }} \\ \end{aligned}$$
(7)
$$\begin{aligned} & \left. {\frac{{d\phi_{2} \left( {x,y} \right)}}{dy}} \right|_{y = 0} = - \frac{{C_{ox2f} }}{{C_{s} }}\frac{{V_{gs2} - A_{02\left( x \right)} }}{{t_{si} }},\quad V_{gs2} = V_{gs} - V_{FB,L2} \\ & \left. {\frac{{d\phi_{3} \left( {x,y} \right)}}{dy}} \right|_{y = 0} = - \frac{{C_{ox3f} }}{{C_{s} }}\frac{{V_{gs3} - A_{03\left( x \right)} }}{{t_{si} }},\quad V_{gs3} = V_{gs} - V_{FB,L3} . \\ \end{aligned}$$

Again for metal M1, the dielectric layer 1 consists of HfO2 and layer 2 consists of SiO2, so the equivalent capacitance can be calculated as

$$C_{ox1f} = \frac{{ C_{oxH} .C_{oxs} }}{{ C_{oxH} + C_{oxs} }},{\text{ where layer 1}}, C_{oxH} = \frac{{\varepsilon_{{HfO_{2} }} }}{{t_{oxf} }}{\text{ and layer 2}}, C_{oxs} = \frac{{\varepsilon_{{SiO_{2} }} }}{{t_{oxf} }}.$$

Similarly, for M2, the dielectric layer 1 consists of HfO2 and SiO2 and layer 2 consists of HfO2 only, so the equivalent capacitance can be calculated as

$$C_{ox2f} = \frac{{ C_{ox2} .C_{ox22} }}{{ C_{ox2} + C_{ox22} }},$$
$${\text{where layer 1}}, \quad C_{ox2} = \frac{{\varepsilon_{{HfO_{2} + \varepsilon_{{SiO_{2} }} }} }}{{t_{oxf} }}$$
$${\text{and layer 2}}, \quad C_{ox22} = \frac{{\varepsilon_{{HfO_{2} }} }}{{t_{oxf} }}.$$

For M3, the entire dielectric layer consists of HfO2

$$C_{ox3f} = \frac{{\varepsilon_{{HfO_{2} }} }}{{2t_{oxf} }}$$

where, \(t_{oxf }\), is the front oxide layer thickness and is equal to layer 2 thickness. Also \(\varepsilon_{{HfO_{2} }} \, and \, \varepsilon_{{SiO_{2} }}\) are permittivity of HfO2 and SiO2.

  1. 2.

    Electric field at the back gate is also continuous at \(y = t_{si}\),

$$\left. {\frac{{d\phi_{1} \left( {x,y} \right)}}{dy}} \right|_{{y = t_{si} }} = - \frac{{C_{oxb} }}{{C_{s} }}\frac{{\phi_{B1} \left( x \right) - V_{gs1} }}{{t_{si} }}$$
(8)
$$\begin{aligned} & \left. {\frac{{d\phi_{2} \left( {x,y} \right)}}{dy}} \right|_{{y = t_{si} }} = - \frac{{C_{oxb} }}{{C_{s} }}\frac{{\phi_{B2} \left( x \right) - V_{gs2} }}{{t_{si} }} \\ & \left. {\frac{{d\phi_{3} \left( {x,y} \right)}}{dy}} \right|_{{y = t_{si} }} = - \frac{{C_{oxb} }}{{C_{s} }}\frac{{\phi_{B3} \left( x \right) - V_{gs3} }}{{t_{si} }} \\ \end{aligned}$$

\(C_{oxb} = \frac{{\varepsilon_{{HfO_{2} }} }}{{t_{oxb} }}\), \(\phi_{B}\) is the potential along the back gate oxide, which is same as front gate potential. \(\phi_{B} \left( {x,y} \right) = \left. {\phi \left( {x,y} \right)} \right|_{{y = t_{si} }} .\)

\(\phi_{Bj} \left( {x,y} \right)\) is the corresponding back gate potential and can be expressed as

$$\phi_{Bj} \left( {x,y} \right) = A_{0j} \left( x \right) + A_{j1} \left( x \right)t_{Si} + A_{j2} \left( x \right)t_{Si}^{2} ,\quad {\text{for M1}},{\text{M2}},{\text{M3}}$$

\(\phi_{j} \left( {x,y = 0} \right) = A_{0j}\), the potential of the channel is the surface potential.

  1. 3.

    Surface potential is similar and continuous at interface

    $$\begin{aligned} & \phi_{1} \left( {L_{1} ,0} \right) = \phi_{2} \left( {L_{1} ,0} \right) \\ & \phi_{2} \left( {L_{2} ,0} \right) = \phi_{3} \left( {L_{2} ,0} \right). \\ \end{aligned}$$
    (9)
  2. 4.

    Electric field is similar and continuous at interface

    $$\begin{aligned} & \left. {\frac{{d\phi_{1} \left( {x,y} \right)}}{dy}} \right|_{{x = L_{1} }} = \left. {\frac{{d\phi_{2} \left( {x,y} \right)}}{dy}} \right|_{{x = L_{1} }} \\ & \left. {\frac{{d\phi_{2} \left( {x,y} \right)}}{dy}} \right|_{{x = L_{2} }} = \left. {\frac{{d\phi_{3} \left( {x,y} \right)}}{dy}} \right|_{{x = L_{2} }} . \\ \end{aligned}$$
    (10)
  3. 5.

    \(\phi _{1} \left( {0,0} \right) = V_{{bipot}} = V_{T} \ln \left( {\frac{{N_{a} N_{{ch}} }}{{n_{i}^{2} }}} \right)\), where, \({\text{V}}_{\text{bipot}}\) is the built in potential and \({\text{V}}_{\text{DS}}\) is the drain to source voltage. \({\text{N}}_{\text{a}} = {\text{N}}_{\text{d}} = {\text{N}}_{\text{ch}}\) as device is uniformly doped.

  4. 6.
    $$\phi _{3} \left( {L_{3} ,0} \right) = V_{{bipot}} + ~V_{{DS}} = V_{T} \ln \left( {\frac{{N_{d} N_{{ch}} }}{{n_{i}^{2} }}} \right)$$
    (11)

Solving Eq. (3) the constants can be found and are represented below

$$\begin{aligned} & A_{11} \left( x \right) = - \frac{{C_{ox1f} }}{{C_{s} }}\frac{{V_{gs1} - A_{01\left( x \right)} }}{{t_{si} }} \\ & A_{21} \left( x \right) = - \frac{{C_{ox2f} }}{{C_{s} }}\frac{{V_{gs2} - A_{02\left( x \right)} }}{{t_{si} }} \\ & A_{31} \left( x \right) = - \frac{{C_{ox3f} }}{{C_{s} }}\frac{{V_{gs3} - A_{03\left( x \right)} }}{{t_{si} }} \\ & A_{12} \left( x \right) = \frac{{\frac{{C_{oxb} }}{{C_{s} t_{si} }}\left( {1 + \frac{{C_{ox1f} }}{{C_{s} }} + \frac{{C_{ox1f} }}{{C_{oxb} }}} \right)}}{{t_{si} \left( {2 + \frac{{C_{ox1f} }}{{C_{s} }}} \right)}}\left[ {V_{gs1} - A_{01\left( x \right)} } \right] \\ & A_{22} \left( x \right) = \frac{{\frac{{C_{oxb} }}{{C_{s} t_{si} }}\left( {1 + \frac{{C_{ox2f} }}{{C_{s} }} + \frac{{C_{ox2f} }}{{C_{oxb} }}} \right)}}{{t_{si} \left( {2 + \frac{{C_{ox2f} }}{{C_{s} }}} \right)}}\left[ {V_{gs2} - A_{02\left( x \right)} } \right] \\ & A_{12} \left( x \right) = \frac{{\frac{{C_{oxb} }}{{C_{s} t_{si} }}\left( {1 + \frac{{C_{ox3f} }}{{C_{s} }} + \frac{{C_{ox3f} }}{{C_{oxb} }}} \right)}}{{t_{si} \left( {2 + \frac{{C_{ox3f} }}{{C_{s} }}} \right)}}\left[ {V_{gs3} - A_{03\left( x \right)} } \right]. \\ \end{aligned}$$

Putting the values of the above constants in Eq. (3) and comparing with Eq. (1), we get

$$\frac{{\partial^{2} \phi_{j} \left( x \right)}}{{\partial x^{2} }} - m_{j} \phi_{j} \left( x \right) = n_{j}$$

where, \(m_{j} = \frac{{2C_{oxb} }}{{C_{s} t_{si} }}\left( {1 + \frac{{C_{oxfj} }}{{C_{s} }} + \frac{{C_{oxfj} }}{{C_{oxb} }}} \right)\)

$$n_{j} = \frac{{ - qN_{ch} }}{{\varepsilon_{si} }} - \frac{{ 2C_{oxb} }}{{C_{s} t_{si} }}V_{gsj} \left( {1 + \frac{{C_{oxfj} }}{{C_{s} }} + \frac{{C_{oxfj} }}{{C_{oxb} }}} \right).$$
(12)

The surface potential under three regions

$$\phi_{1} \left( x \right) = U\exp \left( {\lambda_{1} x} \right) + V\exp \left( { - \lambda_{1} x} \right) - \frac{{n_{1} }}{{m_{1} }}$$
(13)
$$\phi_{2} \left( x \right) = W\exp \left( {\lambda_{2} \left( {x - L_{1} } \right)} \right) + X\exp \left( { - \lambda_{2} \left( {x - L_{1} } \right)} \right) - \frac{{n_{2} }}{{m_{2} }}$$
(14)
$$\phi_{3} \left( x \right) = Y\exp \left( {\lambda_{3} \left( {x - L_{1} - L_{2} } \right)} \right) + Z\exp \left( { - \lambda_{3} \left( {x - L_{1} - L_{2} } \right)} \right) - \frac{{n_{3} }}{{m_{3} }}$$
(15)

where, \(\lambda_{j } = \sqrt {m_{j} }\), j = 1, 2, 3.

The constants U, V, W, X, Y, and Z can be solved by using boundary conditions (6)–…

$$\begin{aligned} & U = V_{bipot} - V + \frac{{n_{1} }}{{m_{1} }} \\ & W = U\exp \left( {\lambda_{1} L_{1} } \right) + \frac{{n_{2} }}{{m_{2} }} - \frac{{n_{1} }}{{m_{1} }} \\ & X = V\exp \left( { - \lambda_{1} L_{1} } \right) + \frac{{n_{2} }}{{m_{2} }} - \frac{{n_{1} }}{{m_{1} }} \\ & Y = \exp \left( { - \lambda_{3} L_{3} } \right) + ({\text{V}}_{\text{bipot}} + {\text{V}}_{\text{DS}} ) + \frac{{n_{3} }}{{\alpha_{3} }} - {\text{Z exp}}\left( { - \lambda_{3} L_{3} } \right) \\ & P_{1} = - \frac{{n_{1} }}{{m_{1} }},P_{2} = - \frac{{n_{2} }}{{m_{2} }},P_{3} = - \frac{{n_{3} }}{{m_{3} }} \\ & D = \frac{{C_{1} }}{{C_{2} }}, \\ & C_{1} = \exp \left( { - \lambda_{1} L_{1} + 2\lambda_{3} L_{3} } \right) + \exp \left( {\lambda_{1} L_{1} } \right) \\ & C_{2} = \exp \left( { - \lambda_{1} L_{1} + 2\lambda_{3} L_{3} } \right) - \exp \left( {\lambda_{1} L_{1} } \right) \\ & {\text{E}} = 2{\text{D cosh}}\left( {\lambda_{2} L_{2} } \right) - 2\sinh \left( {\lambda_{2} L_{2} } \right) \\ & V = \frac{{ ({\text{V}}_{\text{bipot}} + {\text{V}}_{\text{DS}} ) + \exp \left( { - (\lambda_{1} L_{1} + \lambda_{3} L_{3} } \right)\left( {1 - D} \right)}}{\text{E}} + \frac{{{\text{D}}\left( {P_{3} - P_{2} } \right)}}{\text{E}} \\ & \quad + \frac{{P_{3} \exp \left( { - (\lambda_{1} L_{1} + \lambda_{3} L_{3} } \right)\left( {D - 1} \right) + {\text{V}}_{\text{bipot}} + \exp \left( {\lambda_{2} L_{2} } \right)\left( {1 - D} \right) + P_{1} \exp \left( {\lambda_{2} L_{2} } \right)\left( {1 - D} \right)}}{\text{E}} \\ & \quad + \frac{{\left( {{\text{D}}\left( {P_{1} - P_{2} } \right)\cosh \left( {\lambda_{2} L_{2} - \lambda_{1} L_{1} } \right) - \sinh \left( {\lambda_{2} L_{2} - \lambda_{1} L_{1} } \right)} \right)}}{\text{E}} \\ & Z = \frac{{2{\text{Vsinh}}\left( {\lambda_{2} L_{2} } \right)}}{{C_{2} }} + \frac{{P_{1} \exp \left( {\lambda_{2} L_{2} } \right)}}{{C_{2} }} + \frac{{({\text{V}}_{\text{bipot}} + {\text{V}}_{\text{DS}} ) + \exp \left( { - (\lambda_{1} L_{1} + \lambda_{3} L_{3} } \right)}}{{C_{2} }} \\ & \quad + \frac{{\left( {P_{2} - P_{3} } \right)}}{{C_{2} }} \\ & \quad + \frac{{{\text{V}}_{\text{bipot}} \exp \left( {\lambda_{2} L_{2} } \right) - [\left( {P_{1} - P_{2} } \right)\cosh \left( {\lambda_{2} L_{2} - \lambda_{1} L_{1} } \right)] - P_{3} \exp \left( { - (\lambda_{1} L_{1} + \lambda_{3} L_{3} } \right)}}{{C_{2} }}. \\ \end{aligned}$$

5 Results validation and discussion

5.1 Device characteristics

Figure 3 depicts the characteristics of the projected device. It illustrates that AHD-TMG-JLTEFT can produce higher ON current compared to conventional JLTFET (Ghosh and Akram 2013) and DMGJLTFET (Bal et al. 2014) if proper work function is chosen. Table 4 reflects the comparison among various JL-TFET.

Fig. 3
figure 3

ID − VGS as function of various control gate work function

Full size image
Table 4 Comparison table for various existing work
Full size table

The OFF current and SS value also shows much improvement compared to conventional device. The impact of polar gate work function variation is portrayed in Fig. 4. The transconductance is also an essential parameter to assess the analog performance of devices, which is defined as the first derivative of drain current (Ids) with respect to VGS, the formula of gm is given by Eq. (16): as shown in Fig. 5, the gm of the AHD-TMG-JLTEFT is found to be 1 × 10−3 S/µm which is much higher as compared to other reported JLTFET:

$${\text{g}}_{\text{m}} = \frac{{{\text{dI}}_{\text{D}} }}{{{\text{dV}}_{\text{gs}} }}.$$
(16)
Fig. 4
figure 4

ID − VGS as function of polar gate work function

Full size image
Fig. 5
figure 5

Transconductance plot

Full size image

Figure 6 shows the surface potential plot of simulated and modeled surface potential. The close matching between the plots validates the accuracy of the proposed model. The deviation is little higher in the drain side due to assumption considered while deriving the model. Figure 7 depicts the comparison between the existing structures and the proposed one. The use of triple material gate improves the surface potential across the channel. The use of three gate materials resulted in the step change in surface potential at the metal interface. This increase in surface potential is due to increase in carrier velocity as well as transport efficiency.

Fig. 6
figure 6

Simulated and modeled surface potential

Full size image
Fig. 7
figure 7

Comparison plot of surface potential of various structures

Full size image

5.2 Convergence analysis and optimization results validation

The mathematical model of the proposed structure discussed in Sect. 4 Eq. (15) is optimized using a variety of algorithms such as DEPSO, DE, PSO, HBPSO, and WOA. The main purpose is to maximize the surface potential at the tunnel junction by optimizing the variables in Table 2. All optimization algorithms are implemented in the MATLAB software for obtaining the best values for process parameters and they are listed out in Table 5. The results in Table 5 depict that DEPSO can achieve the most accurate result compared to TCAD simulated result. A comparison plot of surface potential derived from optimization of analytical model by DEPSO algorithm and TCAD simulated model is plotted in Fig. 8. The comparison plot reflects that DEPSO algorithm based optimized structure can achieve higher values of surface potential compared to the values obtained by hit and trail based optimization in TCAD. Thus, use of optimization algorithm can be useful in optimizing device parameters. Further, the convergence plot depicted Fig. 9 reflects that DEPSO algorithm amongst all has better performance with best convergence in surface potential computation. The optimized dimensions achieved via algorithmic technique can be validated by designing the proposed structure with optimized dimension in TCAD software. The small deviation between results obtained from MATLAB and TCAD simulation is due to the rounding of the parameters. The simulated device reports an ON-current of 3 × 10−4 A and OFF-current of 2.4 × 10−14 A.

Table 5 The optimized design variables obtained from different algorithms
Full size table
Fig. 8
figure 8

Surface potential after optimization

Full size image
Fig. 9
figure 9

Sensitivity analysis for fitness evaluation

Full size image

6 Conclusion

This paper provides a fresh concept to accelerate the tuning process parameters and help in benefiting design process of nano-devices. Finally, the validity of the proposed analytical model is compared with numerical solution simulation data results, which are obtained by using TCAD device simulator. In this article, we have successfully used DEPSO algorithm for surface-potential-based model parameter extraction for proposed TFET structure. Comparison reflects that measured surface potential and the optimized values are quite accurate.