1 Introduction

Electrohydrodynamics (EHD) is concerned with the interaction design of electric and flow fields, at which the Ohmic model is extremely an accurate approximation. Such interaction occurs as a result of the influence of the Coulomb force on a medium, subsequently, as a result of the work done by the electric field in the flow of currents. In this case, the movement of the medium gives rise to redistribution of the volume charges, which yields as the change of the electric field. In other words, EHD may be regarded as a divaricate of fluid mechanics concerning the effects of electric forces. Actually, it includes the impacts of the electric field in a moving medium; for instance, see Melcher and Taylor (1969) and Saville (1997). Melcher and Taylor (1969) introduced a review of the mechanism of EHD on the interface shear stress. Saville (1997) introduced a review dealing with the establishment of the leaky dielectric model and experimental tests designed to indicate its usefulness. Several applications of EHD in various fields; ranging from dynamics in a biological system, dielectric phoretic orientation, the expulsion of liquids, to atmospheric and cloud physics. The EHD stability is very essential in the applications spread from electro-kinetic assays to electro-spray ionization. Chen (2011) gave a review on the EHD stability, at which the basic foundations of this topic and introduced some models, were illustrated. Recent works on the nonlinear EHD stability showed some behavior of the system not predicted throughout the linear stability theory. El-Sayed et al. (2014a) studied the phenomenon of the viscous potential theory in nonlinear stability of electro-visco-elastic of two superposed dielectric fluids. Throughout this work, the multiple time scales, technique, were utilized. As a result, a Ginzburg–Landau equation was achieved. Additionally, they concluded that the three-dimensional disturbances are more unstable than the two-dimensional ones, which were occurring for most physical parameters except the kinematic viscosities. El-Sayed et al. (2010) studied a weakly nonlinear theory of wave propagation in two superposed dielectric fluids streaming in the presence of the vertical electric field, and in the absence of surface charges at the interface. They found that the dimensions (two or three) of the system have a dual role (stabilizing as well as destabilizing). El-Sayed et al. (2011) investigated the weakly nonlinear stability analysis of wave propagation in two superposed dielectric fluids streaming in the presence of vertical electric field producing surface charges. The method of multiple scales resulted in a nonlinear Klein–Gordon equation with complex coefficients describing the behavior of the perturbed system at the critical point. Recently, Moatimid et al. (2019) studied the problem of EHD stability of a vertical infinite cylindrical liquid sheet embedded between two dielectric perfect incompressible cylindrical liquids. To relax the mathematical manipulation, they utilized the viscous potential theory. Their analysis reveals coupled Mathieu equations. Away from the symmetric and anti-symmetric modes, they considered a general case for the surface deflections.

A non-Newtonian fluid is a fluid whose viscosity is variable based on applied stress or force. The most common example of a non-Newtonian fluid is cornstarch dissolved in water. The behavior of Newtonian fluids like water can be described exclusively by temperature and pressure. An interesting example of a non-Newtonian fluid is flowing inside the human body, which is the blood. The non-Newtonian fluids have received considerable interest in many physical and technological applications. They are more realistic than the Newtonian fluids. A special class of fluids is known as visco-elastic fluids. The latter exhibits properties of elasticity in addition to viscosity. Therefore, the study of visco-elastic fluids has gained increasing importance in the last decades. Furthermore, they have more and more industrially important. Sharma and Chand (1999) studied the instability of streaming Walters’ B elastico-viscous fluid in porous media. They found that in the special case, when perturbations in the direction of streaming are ignored, the system can be stable or unstable, depending upon the kinematic visco-elasticity, medium porosity and medium permeability. Kumar and Singh (2010) studied the Rayleigh–Taylor instability of two superposed Walters’ B fluids. In the case of the stable stratification, the system seems to be stable under certain conditions. El-Sayed et al. (2014b) studied the nonlinear Kelvin–Helmholtz instability of two superposed semi-infinite of the Walters’ B dielectric fluids in porous media. They considered a normal electric field in the absence of the surface charges. By utilizing the multiple time scale technique, the analyzed the stability criteria in linear as well as the nonlinear approaches. Keeping in mind the importance of the non-Newtonian fluids, Kumar (2017) considered the effect of a suspended particle on the Walters’ B fluids. The fluid is heated from below in porous media, and in the presence of a uniform magnetic field. It was observed that the magnetic field postpones the onset of convection, while the medium permeability and the suspended particles hasten the onset of convection. Recently, Barik et al. (2018) made an attempt to study the effects of elasticity, suction/injection, porous media in the flow of visco-elastic fluids of the Walters’ B type. They entered the flow domain without the boundary layer approximation. Furthermore, they discussed the viscous and non-conducting flow as a special case.

Bau (1982) investigated the stability analysis of a plane interface between two superposed fluid layers saturated in porous media, at which, he derived the neutral stability criteria in the case of Darcian as well as non-Darcian fluids. Additionally, in both cases, the instability happens such that the velocities should exceed some critical value. Zakaria et al. (2008) investigated the stability profile of streaming magnetic fluids saturated in porous media. Their model involved three incompressible magnetic fluid layers. They indicated that the thickness of the middle layer has a destabilizing role. Furthermore, dual roles were obtained in view of the initial streaming and the porosity in the stability configuration. Al-Karashi and Gamiel (2017) investigated the interface stability of three fluid layers, which were fully saturated in porous media. Their linear stability approach leads to two coupled Mathieu equations. They found that the porosity had a dual influence on the stability picture. Recently, Moatimid et al. (2018) investigated the influence of an axial periodic field on streaming flows throughout three coaxial infinite cylinders. The three fluids are saturated in fully saturated porous media. Furthermore, the numerical calculations indicate that the coefficients of mass and heat transfers as well as the streaming have a destabilizing role; in contrast, the porosity had a stabilizing influence. Recently, Moatimid et al. (2019) introduced a few representatives of porous media in the problem of a streaming cylindrical sheet. Their analysis resulted in damped differential equations with complex coefficients. These equations were combined to obtain a single dispersion equation. They concluded that Darcy’s coefficients, as well as the dielectric constants, played a stabilizing influence in the stability configuration.

As well-known from all previous perturbation methods ranging from the traditional, straightforward methods until the multiple-scales method, all of them depend mainly on a small parameter. This parameter must have existed in the given differential equation. Consequently, the problem cannot be solved without the existence of such a parameter. He (1999) is considered as the first author, who overcomes this difficulty by imposing an artificial embedded parameter \(\delta \in \left[ {0,\,1} \right]\) in the given differential equation. The solution may be achieved by classifying the problem into two parts. One of them is termed as the liner, which has an exact solution; simultaneously, the other part defines the nonlinear one. Therefore, the artificial parameter lies between the two previous parts. In this approach, He (1999) introduced a promising and powerful analytical method, which is abbreviated as (HPM). This method is applied to obtain an analytical approximate solution for numerous nonlinear differential equations that arise in sciences and mathematical physics. A comparison with the HPM and the other perturbation methods reveals that HPM resulted in more accurate solutions. El-Dib (2017a) introduced a novelty approach on the HPM to treat the exciting nonlinear differential equations. In other words, modulation on the HPM is done to analyze a nonlinear differential equation with periodic coefficients. His modification may be applied for linear as well as nonlinear differential equations. His approach reveals the transition curves. Therefore, stable/unstable regions are identified. Furthermore, El-Dib (2017b) suggested a modified version of the HPM by exiting the method of multiple scales. He applied his technique to some nonlinear oscillators. Additionally, the stability picture for the parametric resonance is graphed. Moatimid et al. (2018) studied the problem of an infinite cylindrical sheet in the presence of an exciting axial electric field. They obtained a couple of Mathieu equations. To relax the mathematical manipulation, they utilized the matrix concept. In their work, a coupling of the HPM with the multiple time scales method is done. Therefore, their approach does not need a small parameter in the given equation. Moreover, the stability analysis reveals both the resonance and non-resonance cases. Recently, El-Dib and Moatimid (2018) adapted the HPM to obtain exact solutions of linear as well as nonlinear differential equations. The basic idea in their approach is to choose a suitable trial function, usually, in the form of a power series. The cancellation of the first order approximate solution guarantees that all higher orders are, also, canceled. Accordingly, the remaining zero-order solution will be supported to become an accurate one. Recently, Fedorov et al. (2019) demonstrated that the HPM may be utilized to obtain an analytical approximate to their model. They showed that the obtained solutions are in good agreement with the existing numerical methods. In addition, their analysis reveals different HPM operators. More recently, Moatimid et al. (2020) made a coupling of the Laplace transforms and HPM to obtain an approximate analytical solution of the interface profile between two hydro-magnetic Darcian flow, and separated by a cylindrical interface.

The viscous potential theory plays an essential role in simplifying the mathematical analysis when studying the stability problems; for instance, see Joseph (2003, 2006). Joseph (2003) showed how the viscosity of a viscous fluid in the potential flow away from the boundary layers enters the Prandtl’s boundary layer equations. Joseph (2006) introduced an attempt to identify the main events in the history of thought about the rotational flow of viscous fluids. Therefore, throughout the viscous potential flow, the viscosity in the Navier–Stokes, as well as the vorticity, are vanishing. Simultaneously, the viscous stresses are not zero. In the light of this theory, the tangential stresses are not included, whereas, the viscous effects are contributed only in the normal stress balance. Funada and Joseph (2001) analyzed the viscous potential flow of Kelvin–Helmholtz instability. Their analysis resulted in an explicit dispersion relation, at which the effects of surface tension and viscosity on the normal stress are not neglected. Furthermore, the stability criterion for viscous potential flow is expressed by a critical value of the relative velocity. Funada and Joseph (2003) analyzed the linear theory of capillary instability of threads of Maxwell fluids. Their analysis extended the analysis of viscous potential flow, as given by Joseph (2003, 2006), to visco-elastic fluids of Maxwell type. The viscous potential flow has been widely utilized in recent years. It attracts many authors in studying the linear as well as nonlinear stability problems of physical interest. El-Sayed et al. (2014a) investigated the nonlinear EHD Kelvin–Helmholtz instability of two superposed visco-elastic fluids of the Walters’ B type. To relax the mathematical manipulation, they used the viscous potential flow theory. In the light of the viscous potential theory, recently, Moatimid and Mostapha (2019) analyzed the nonlinear instability of the surface waves propagating through two jets of viscoelastic fluids obey the Oldroyd B model. The flow is getting through porous media under the action of a uniform axial electric field. General dispersion relation and neutral curves are addressed and plotted for the different parameters. Awasthi et al. (2012) studied the viscous corrections of the potential flow analysis of Kelvin–Helmholtz instability of two viscous fluids in the presence of a tangential magnetic field. They demonstrated that the irrotational shearing stresses have a stabilizing effect in the presence of heat and mass transfer throughout the interface. Recently, Moatimid et al. (2019) studied the influence of a uniform axial electric field on a cylindrical streaming sheet. To avoid the mathematical manipulation; their analysis was based on the viscous potential theory.

As aforementioned, there is growing importance of non-Newtonian fluids in chemical engineering, modern technology and industry, therefore, the investigation of such fluids is desired. There are many models follow the visco-elastic fluids. Among these fluids, the Walters’ B model exists. Therefore, this paper attempts to investigate a nonlinear stability approach to Walters’ B fluid. To simplify the analysis, the mathematical treatment depends mainly on the viscous potential theory. Because of the instability in porous media meets an interest in geophysics and bio-mechanics, the current paper is considered throughout porous media. Circular vertical cylinders are filled with a Walters’ B fluid, are considered. An axial uniform axial electric field acts on the inner as well as outer the two fluids. The stability criteria are obtained, analytically and numerically confirmed. Furthermore, the profile of the solution of the surface deflection is approximately calculated. To clarify the presentation of the problem; the rest of the paper is organized as follows: Sect. 2 is devoted to introducing the formulation of the problem, it includes the governing equations of motion and the corresponding appropriate nonlinear boundary conditions. Additionally, the method of solution, by means of the normal mode analysis, and the governing nonlinear characteristic equation is given in this section. The linear dispersion relation, and stability analysis are introduced throughout Sect. 3. Furthermore, the linear stability analysis of the linear approach is achieved throughout this section. The nonlinear stability that results in a Ginzburg–Landau equation together with the theoretical and numerical calculations are presented in Sect. 4. In the light of the HPM, with the aid of the expanded frequency concept, a bounded approximate solution of the surface elevation is derived in Sect. 5. Moreover, a numerical estimation of this profile is added to this section. The obtained results are summarized as concluding remarks in Sect. 6. This section is included the main outcomes of the effects of the various including physical parameters in the analysis of linear as well as the nonlinear stability of the problem at hand.

2 Formulation of the problem

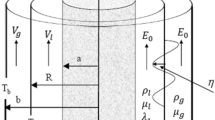
A system consists of two homogeneous, incompressible, dielectric, and streaming visco-elastic Walters’ B fluids, along the axis of the jet, is considered. Throughout the following formulation, the subscripts 1 and 2 symbolize the parameters associated with the inner, and outer fluids, respectively. The dynamic viscosity, and dynamic visco-elasticity are referred to as: \(\mu,\) and \(\mu^{\prime}\), respectively. The uniform density, dielectric constants, are referred to as: \(\rho,\) and \(\varepsilon\), respectively. The flows are saturated throughout porous media, at which Darcy’s coefficient is indicated by the symbol \(\nu\). For simplicity, the porosity may be considered as a unity. Both of the two cylindrical fluids are streaming with a uniform velocities, which are referred by \(U\). The system is scrutinized under the influence of a uniform axial electric field, tangential to the interface between the two media, whose strength is denoted by \(E_{0}\). The gravitational forces \((g)\) that act along the negative z-direction are taken into consideration. For more appropriate, the cylindrical polar coordinate system \((r,\,\theta ,z)\) is utilized. In the equilibrium state, the z-axis is taken along the axis of symmetry of the system. A sketch of the physical model is given in Fig. 1.

Fig. 1
figure 1

Sketch of the model in the undisturbed state

Full size image

Typically, as given throughout the pioneering work of Chandrasekhar (1961), the liquid jet is stable for all the asymmetric mode \(m \ne 0\), but it becomes unstable at the axisymmetric mode \(m = 0\). Consequently, the most interesting mode of disturbance is the axisymmetric mode. Therefore, from now on, the case of \(m = 0\) is only considered. The disturbed cylinder, especially, considering the Fourier component with the wave number \(k\) and the cylindrical symmetry, the inner and outer surfaces, is given by

$$r = R + \eta (z,t),$$
(1)

where \(\eta (z;t)\) is a general unknown function which represents the surface deflection behavior.

Therefore, after a small and finite departure from the equilibrium state, the interface profile may be expressed as:

$$S(r,z;t) = r - R - \eta (z,t).$$
(2)

Therefore, the unit outward normal vector of the interfaces may be written as:

$$\underline{n} = \nabla S/\left| {\nabla S} \right| = (\underline{e}_{r} - \,\eta_{z} \,\underline{e}_{z} )(1 + \eta_{z}^{2} )^{ - 1/2} ,$$
(3)

where \(\underline{e}_{r}\) and \(\underline{e}_{z}\) are unit vectors along the r- and z-directions, respectively.

The governing equations of motion of an incompressible fluid; for instance, see El-Sayed et al. (2014a), may be written as:

$$\rho_{j} \left( {\frac{{\partial \underline{v}_{j} }}{\partial t} + (\underline{v}_{j} .\nabla )\underline{v}_{j} } \right) = - \nabla P_{j} - \nu_{j} \,\underline{v}_{j} - \rho_{j} g\underline{e}_{z} + \left( {\mu_{j} - \mu^{\prime}_{j} \frac{\partial }{\partial t}} \right)\nabla^{2} \underline{v}_{j} ,\,\,\,\,\,\,\,\,\,\,\,\,\,j = 1,2,$$
(4)

where \(v_{j} = v_{j} (r,z;t)\) is the fluid velocity, and \(P_{j}\) represents the pressure.

The zero-order solution of Eq. (4), yields:

$$P_{0j} = - \rho_{j} gz - \nu_{j} \,U_{j} + \lambda_{j} ,$$
(5)

where \(\lambda_{j}\) is an arbitrary integration constant.

As shown in the previous formulation of the problem, the fluids are assuming as perfect flows. Therefore, one may assume that the fluids are being irrotational flows. Simultaneously, the perturbed velocity may be written as:

$$\underline{v}_{j} = U_{j} \underline{e}_{z} + \nabla \phi_{j} = \frac{{\partial \phi_{j} }}{\partial r}\underline{e}_{r} + \left( {U_{j} + \frac{{\partial \phi_{j} }}{\partial z}} \right)\underline{e}_{z} .$$
(6)

Because of the incompressibility condition, the potential function \(\phi_{j} (r,z;t)\) must satisfy the following Laplace equation:

$$\nabla^{2} \phi_{j} = 0\,.\,$$
(7)

Typically, as shown by many researchers, the solutions of governing distribution functions will be based on the normal modes analysis. Therefore, following Chandrasekhar (Chandrasekhar 1961), one may write and

$$\phi_{j} (r,z;t) = \hat{\phi }_{j} (r;t)e^{ikz} + c.c.\,,$$
(8)

where the notation \(c.c.\) represents the complex conjugate of the preceding term.

The finite solutions of the Laplace’s equation are then become

$$\hat{\phi }_{1} (r;t) = A_{1} (t)I_{0} (kr),$$
(9I)

and

$$\hat{\phi }_{2} (r;t) = A_{2} (t)K_{0} (kr),$$
(9II)

where \(A_{1} (t)\) and \(A_{2} (t)\) are arbitrary time-dependent functions to be determined in light of the favorable nonlinear boundary conditions. Moreover \(I_{0} (kr)\) and \(K_{0} (kr)\) represent the modified Bessel functions of the first and second kinds, respectively.

The integration of the linear equation of motion (4) resulted in the Bernoulli’s formula, which gives the distribution function of the pressure as:

$$P_{j} = - \rho_{j} \left( {\frac{{\partial \phi_{j} }}{\partial t} + i\,k\,U_{j} \phi_{j} } \right) - \nu_{j} \,\phi_{j} .$$
(10)

On the other hand, in accordance with the Maxwell equations; for instance, see Melcher (1981), for the quasi-static approximation, on neglecting the influence of the magnetic field, they may be written as:

$$\nabla \cdot \varepsilon_{j} \underline{E}_{j} = 0,$$
(11)

and

$$\,\nabla \times \underline{E}_{j} = \underline{0} .$$
(12)

As given in the formulation of the problem, no surface currents are assumed to be present at the surface of separation. Therefore, the electric field may be expressed in terms of the scalar electro-static potentials \(\,\psi_{j} (r,z;t)\). i.e. \(\underline{E}_{j} = E_{0} - \,\nabla \psi_{j} (r,z;t)\), such that the total perturbed electric fields can be expressed as:

$$\underline{E}_{j} = - \frac{{\partial \psi_{j} }}{\partial r}\underline{e}_{r} + \left( {E_{0\,} - \frac{{\partial \psi_{j} }}{\partial z}} \right)\underline{e}_{z} .$$
(13)

In other words, the electrically insulating fluid justifies the stationary form of the Maxwell equations, which are reduced to the Laplace’s equation for the electric potential \(\,\psi_{j} (r,z;t)\) in each fluid layer. Consequently, the combination of Eqs. (11) and (13) yields

$$\nabla^{2} \psi_{j} = 0.$$
(14)

As expressed previously in Eq. (8), the electric potentials may be written as:

$$\hat{\psi }_{1} (r;t) = B_{1} (t)I_{0} (kr),$$
(15I)

and

$$\hat{\psi }_{2} (r;t) = B_{2} (t)K_{0} (kr),$$
(15II)

where \(B_{1} (t)\) and \(B_{2} (t)\) are arbitrary time-dependent functions to be evaluated by using the appropriate nonlinear boundary conditions.

2.1 Nonlinear boundary conditions

The general solutions of the velocity and electric potential distributions, as given in Eqs. (9I, and 9II) and (15I, and 15II), must satisfy the following convenient nonlinear boundary conditions:

At the free interface \(r = R + \eta (z;t){:}\)

  1. 1.

    The conservation of mass across the interface, which is so-called the kinematic condition, yields

    $$\frac{DS}{Dt} = 0\;{\text{at}}\;r = R + \eta (z;t)\,,$$
    (16)

    where \({D \mathord{\left/ {\vphantom {D {Dt}}} \right. \kern-0pt} {Dt}}\) represents the material derivative operator.

  2. 2.

    The jump of the tangential components of the electric is continuous at the interface, results

    $$\underline{n} \times \,\left\| {\underline{E}_{j} } \right\| = \underline{0} .\quad j = 1,2,$$
    (17)

    where \(\left\| * \right\| = *_{2} - *_{1}\) denotes the jump of the external and internal fluid layers, respectively.

  3. 3.

    The jump of the normal components of the electric displacement is continuous at the interface, requires

    $$\underline{n} \,.\,\left\| {\varepsilon_{j} \,\underline{E}_{j} } \right\| = 0.\quad j = 1,2,$$
    (18)

At this stage, on substituting from Eqs. (9I, and 9II) and (15I, and 15II) into Eqs. (16)–(18), one finds the special solutions which are consistent with the aforementioned nonlinear boundary conditions. They can be written as follows:

$$\phi_{1} = \frac{{\left( {\eta_{t} + U_{1} \,\eta_{z} } \right)I_{0} (kr)}}{{k\,\left( {I_{1} (kR) - iI_{0} (kR)\eta_{z} } \right)}},$$
(19)
$$\phi_{2} = - \frac{{\left( {\eta_{t} + U_{2} \,\eta_{z} } \right)K_{0} (kr)}}{{k\,\left( {K_{1} (kR) + iK_{0} (kR)\eta_{z} } \right)}},$$
(20)
$$\psi_{1} = \frac{{E_{0} \,(\varepsilon_{1} - \varepsilon_{2} )\,I_{0} (kr)\eta_{z} \left( { - i\,K_{0} (kR) + K_{1} (kR)\eta_{z} } \right)}}{\,\varLambda },$$
(21)

and

$$\psi_{2} = \frac{{E_{0} \,(\varepsilon_{1} - \varepsilon_{2} )\,K_{0} (kr)\eta_{z} \left( {i\,I_{0} (kR) + I_{1} (kR)\eta_{z} } \right)}}{\,\varLambda },$$
(22)

where

$$\varLambda = k\left( {\varepsilon_{2} \left( {I_{0} (kR) - iI_{1} (kR)\eta_{z} } \right)\left( {K_{1} (kR) + iK_{0} (kR)\eta_{z} } \right) + \varepsilon_{1} \left( {I_{1} (kR) - iI_{0} (kR)\eta_{z} } \right)\left( {K_{0} (kR) + iK_{1} (kR)\eta_{z} } \right)} \right).$$

The previous distributions of the potential functions \(\phi_{j}\) and \(\psi_{j}\) include the nonlinear terms in the elevation parameter \(\eta\). This nonlinearity is occurring in the light of the nonlinear boundary conditions that are illustrated above. Dropping the nonlinear terms, a linear profile comes out and is equivalent to those obtained in literature by Moatimid and Mostapha (2019) and Moatimid (1995). At this end, the boundary-value problem has been completed solved.

To analyze the stability of the system, the remaining boundary condition arises from the normal component of the stress tensor. In accordance with the presence of the amount of surface tension, this normal component must be discontinuous. The total stress tensor can be formulated as follows; for instance, see El-Sayed et al. (2014a):

$$\sigma_{ij} = - P\delta_{ij} + \varepsilon \,E_{i} E_{j} - \frac{1}{2}\varepsilon \,E^{2} \delta_{ij} + 2(\mu - \mu^{\prime}\frac{\partial }{\partial t})\left( {\underline{n} \, \cdot \left[ {(\underline{n} \, \cdot \,\nabla )\nabla \phi } \right]} \right),$$
(23)

where \(\delta_{ij}\) is the Kronecker delta.

$$\left\| {\underline{n} \, \cdot \,\underline{F} } \right\| = T\,\nabla \cdot \,\underline{n} ,\,$$
(24)

where \(\underline{F}\) is the total force acting on the interface, in view of the two-dimensions disturbances, which is defined as:

$$\underline{F} = \left( {\begin{array}{*{20}c} {\sigma_{rr} } & {\sigma_{rz} } \\ {\sigma_{zr} } & {\sigma_{zz} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {n_{r} } \\ {n_{z} } \\ \end{array} } \right),$$
(25)

where \(n_{r}\), \(n_{z}\) are the components of the unit outward normal vector \(\underline{n}\).

On substituting from the foregoing outcomes in Eq. (25), after lengthy, but straightforward calculation, one gets the following nonlinear characteristic equation:

$$\eta_{tt} + a_{1} \eta_{zt} + a_{2} \eta_{zz} + (b_{1} + ic_{1} )\eta_{t} + (b_{2} + ic_{2} )\eta_{z} = N(\eta ),$$
(26)

where the nonlinear term \(N(\eta )\) represents all the quadratic and cubic terms in the variable \(\eta\), \(a_{i} ,b_{i}\) and \(c_{i}\) are constants. They are all listed in the “Appendix”.

From the zero- order of the normal stress tensor, one gets

$$\lambda_{2} - \lambda_{1} = (\rho_{2} - \rho_{1} )gz + \left( {\nu_{2} \,U_{2} - \nu_{1} \,U_{1} } \right) - \frac{T}{R} + \frac{1}{2}(\varepsilon_{2} - \varepsilon_{1} )E_{0}^{2} .$$
(27)

The stability analysis of the current work, throughout the linear as well as the nonlinear approach, depends mainly on studying the nonlinear characteristic equation as given in (26).

3 Linear stability analysis

Before dealing with the general case, for more convenience, the stability analysis throughout a linear point of view will be analyzed. In the light of this approach, the linearized analysis of the nonlinear equations that are given by Eq. (26) arises when the nonlinear terms of the surface elevation are ignored.

Therefore, the linearized dispersion equations can be written as follows:

$$\eta_{tt} + a_{1} \eta_{zt} + a_{2} \eta_{zz} + (b_{1} + ic_{1} )\eta_{t} + (b_{2} + ic_{2} )\eta_{z} = 0.$$
(28)

For more convenience, assume a uniform monochromatic wave train solution of Eq. (28) in the following form:

$$\eta (z,t) = \gamma \,e^{i(k\,z - \omega \,t)} + c.c.$$
(29)

where \(\gamma\) is the amplitude of the wave train solution.

For a nontrivial solution of \(\gamma\) in Eq. (29), the dispersion relation is then become:

$$\omega^{2} + (\alpha_{1} + i\beta_{1} )\omega + (\alpha_{2} + i\beta_{2} ) = 0,$$
(30)

where the coefficients \(\alpha_{1} ,\alpha_{2} ,\beta_{1}\) and \(\beta_{2}\) are known from the context.

The stability criteria of the dispersion relation (30) are judged by the Routh–Hrutwitz theory (Zahreddine and El-Shehawey 1988). Therefore, the stability criteria may be written as:

$$\alpha_{1} > 0,$$
(31)

and

$$\alpha_{2} \alpha_{1}^{2} + \alpha_{1} \beta_{1} \beta_{2} - \beta_{2}^{2} > 0.$$
(32)

The calculation showed that \(\alpha_{1}\) is independent of the electric field intensity \(E_{0}^{2}\). Simultaneously, the second inequality may be expressed as a form of \(E_{0}^{2}\) in the following:

$$\varGamma \,E_{0}^{2} + {\rm K} > 0,$$
(33)

where \(\varGamma\) and \({\rm K}\) are known from the context.

Before dealing with the numerical calculations, for more convenience, the stability criteria that are given by the inequalities (31) and (32) must be written in a suitable non-dimensional form. This can be done in a number of ways depending primarily on the choice of characteristics of time, length, and mass. For this purpose, consider that the parameters, \(g/\omega^{2}\) and \(T/\omega^{2}\) to symbolize the characteristics of time, length and mass, respectively. The other non-dimensional quantities may be given as:

$$\begin{aligned} &\rho_{1} = \rho \,\rho_{2} ,\;\varepsilon_{1} = \varepsilon \,\varepsilon_{2} ,\nu_{1} = \nu \,\nu_{2} ,\mu_{1} = \mu \,\mu_{2} ,\mu^{\prime}_{1} = \mu^{\prime}\,\mu^{\prime}_{2} , \hfill \\ &\rho_{2} = \rho^{*} T\omega^{4} /\,g^{3} ,\,\,\nu_{2} = \nu^{*} T\omega^{5} /\,g^{3} ,\,k = k^{*} g/\omega^{2} ,R = R^{*} \omega^{2} /g,\, \hfill \\ & V_{2} = V^{*} g/\omega ,\,E_{0}^{2} = E_{0}^{*2} T\omega^{2} /g,\mu_{2} = \mu^{*} T/\omega \,g,\mu_{2}^{\prime } = \mu^{\prime *} T/g\, \hfill \\ \end{aligned}$$

For simplicity, the “*” mark may be ignored in the following analysis.

As stated before, the implication of the inequality (31) must be considered. Therefore, all the following figures are plotted in a certain domain, where this condition is automatically satisfied. Additionally, the calculations indicated that the parameter \(\varGamma \, > 0\) is always of positive significance. This shows the stabilizing influence of the tangential electric field, which is an early result. It is verified by many authors; for instance, Melcher and Taylor (1969), and the references therein.

Our interest is focused on the relation (33). For this purpose, the electric field intensity \(\log \,E_{0}^{2}\) will be plotted versus the wavenumber of the surface waves (\(k\)). In the following figures, the stable region is referred to by the letter \(S\). Meanwhile, the letter \(U\) stands for the unstable region. It is convenient to indicate the influence of the various physical parameters in the stability configuration. Keeping in mind that the considered non-dimensional procedure deals with the ratios of the various physical parameters. For instance; \(\rho\) refers to the ratio between the inner and outer densities, respectively. Therefore, the following figures are plotted for a system having the particulars: \(\rho = 5,\,U = - 0.1,\;R = 0.1,\,\;\varepsilon = 1.5,\,\;\nu = 0.8,\;\mu = 0.3\) and \(\mu^{\prime} = 0.1\). The influence of the ratio of streaming \(U\) on the stability picture is displayed in Fig. 2. All the physical parameters are held fixed except \(U\). As seen, this figure shows that the parameter \(U\) plays a destabilizing influence, especially, for large values of the wave number. This result is in agreement with the result that was already obtained by Moatimid (2003), and others. The influence of the ratio of the Darcy coefficient \(\nu\) is pictured in Fig. 3. The system chosen here was the same as in Fig. 2, but a single value of \((U = - \,0.1)\), and a variation of the Darcy coefficient \(\nu\). As shown from this figure, the increase in the parameter \(\nu\) causes an increase in the instability region. It follows that \(\nu\) has a destabilizing effect, especially, at small values of wavenumber. This is a physical significance, because of the presence of this term in the equation of motion plays a drag force, or resistance to wave motion. This result is in agreement with the result that was already obtained by Moatimid et al. (2019), and others. Figure 4 is depicted to indicate the influences of the ratio of dynamic viscosity \(\mu\). As indicated, all the physical parameters hold fixed, except this parameter. It was observed that \(\mu\) has a destabilizing effect. These effects are enhanced at large values of the wavenumber. This result is in correspondence to the previous results that were achieved by El-Sayed et al. (2014a). Finally, Fig. 5 is depicted to indicate the influences of the ratio of dynamic visco-elasticity \(\mu^{\prime}\). It was observed that \(\mu^{\prime}\) has a destabilizing effect. This influence is enlarged at large values of the wavenumber. This result is in agreement with the result that was already obtained by El-Sayed et al. (2014b).

Fig. 2
figure 2

Plots the linear stability diagram as given in inequalities (33)

Full size image
Fig. 3
figure 3

Plots the linear stability diagram as given in inequalities (33)

Full size image
Fig. 4
figure 4

Plots the linear stability diagram as given in inequalities (33)

Full size image
Fig. 5
figure 5

Plots the linear stability diagram as given in inequalities (33)

Full size image

4 Nonlinear Ginzburg–Landau equation

As given through the linear stability analysis, the interface surface deflection \(\eta = \eta (z,t)\) had a special form which is given in Eq. (29). In this case, the nonlinear characteristic Eq. (2) may be written in an algebraic equation as follows:

$$D(k,\omega )\eta = \gamma (k,\omega )\eta^{2} + \beta (k,\omega )\eta^{3} ,$$
(34)

where \(D\left( {\omega ,\,k} \right)\), \(\gamma \left( {\omega ,\,k} \right)\) and \(\beta \left( {\omega ,\,k} \right)\) are the linear and nonlinear coefficients, respectively.

The following the analysis will be based on the multiple time scale technique (Nayfeh 1976). This technique depends mainly on a small parameter \(\delta\), say. It measures the ratio of a typical wave length, or periodic time, relative to a typical length, or the time scale of modulation. Therefore, one may assume that \(\delta\) is a small parameter that defines the slow modulation. In the light of this approach, the independent variables \(z\) and \(t\), which are measured on the scale of the typical wavelength and period time, can be extended to introduce alternative, independent variables,

$$Z_{n} = \delta^{n} z\;\;{\text{and}}\;\;T_{n} = \delta^{n} t\quad n = 0,1,2, \ldots ,$$
(35)

where

$$L\left( {\frac{\partial }{\partial z},\frac{\partial }{\partial t}} \right)\eta = 0.$$
(36)

Considering \(Z_{0} ,\,\,T_{0}\) as the appropriate variety of fast variations and \(Z_{1} ,\,\,T_{1} ,\,Z_{2} ,\,\,T_{2}\) are referring to the slow ones. The differential operators can now be expressed as the derivative expansions:

$$\frac{\partial }{\partial z} = k\frac{\partial }{\partial \theta } + \delta \frac{\partial }{{\partial Z_{1} }} + \delta^{2} \frac{\partial }{{\partial Z_{2} }} + \cdots \;{\text{and}}\;\frac{\partial }{\partial t} = - \omega \frac{\partial }{\partial \theta } + \delta \frac{\partial }{{\partial T_{1} }} + \delta^{2} \frac{\partial }{{\partial T_{2} }} + \cdots ,$$
(37)

where \(\theta = kZ_{0} - \omega T_{0}\) refers to the lowest order.

It is more favorable to expand the operator \(\tilde{L}\) in the following form:

$$\tilde{L}\left( {ik, - i\omega + i\delta \left( {\frac{\partial }{{\partial Z_{1} }},\frac{\partial }{{\partial T_{1} }}} \right) + i\delta^{2} \left( {\frac{\partial }{{\partial Z_{2} }},\frac{\partial }{{\partial T_{2} }}} \right) + \cdots } \right).$$
(38)

The expression of the operator \(\tilde{L}\) can be expanded in powers of \(\delta\). Using Taylor’s theorem about \((k, - \omega )\), one retains only the terms up to \(O(\delta^{2} )\). On that account,

$$\tilde{L} \to L_{0} + \delta \,L_{1} + \delta^{2} L_{2} + \cdots ,$$
(39)

where

$$L_{0} \equiv (k, - \omega )\frac{\partial }{\partial \theta },$$
(40I)
$$L_{1} \equiv i\left( {\frac{{\partial L_{0} }}{\partial \omega }} \right)\frac{\partial }{{\partial T_{1} }} - i\left( {\frac{{\partial L_{0} }}{\partial k}} \right)\frac{\partial }{{\partial Z_{1} }},$$
(40II)

and

$$L_{2} \equiv i\left( {\frac{{\partial L_{0} }}{\partial \omega }} \right)\frac{\partial }{{\partial T_{2} }} - i\left( {\frac{{\partial L_{0} }}{\partial k}} \right)\frac{\partial }{{\partial Z_{2} }} - \frac{1}{2}\left( {\frac{{\partial^{2} L_{0} }}{{\partial \omega^{2} }}} \right)\frac{{\partial^{2} }}{{\partial T_{1}^{2} }} - \frac{1}{2}\left( {\frac{{\partial^{2} L_{0} }}{{\partial k^{2} }}} \right)\frac{{\partial^{2} }}{{\partial Z_{1}^{2} }} + \frac{1}{2}\left( {\frac{{\partial^{2} L_{0} }}{\partial k\,\partial \omega }} \right)\frac{{\partial^{2} }}{{\partial Z_{1} \partial T_{1} }}.$$
(40III)

Expressing the expansion of the operator (39) into Eq. (29), one finds:

$$\left( {L_{0} + \delta \,L_{1} + \delta^{2} L_{2} } \right)\eta = 0.$$
(41)

The aforementioned analysis follows a perturbation procedure to obtain a uniform valid solution. Indeed, this treatment requires the cancellation of secular terms.

The stability procedure of Eq. (34) was discussed and analyzed in more details throughout our previous works as given in Moatimid and El-Dib (2004), and Moatimid (2006). Therefore, on using similar arguments as given in these references, one obtains the following Ginzburg–Landau equation:

$$i\frac{\partial \gamma }{\partial \tau } + (P_{r} + i\,P_{i} )\frac{{\partial^{2} \gamma }}{{\partial \zeta^{2} }} = (Q_{r} + i\,Q_{i} )\,\gamma^{2} \overline{\gamma } ,$$
(42)

where \(\overline{\gamma }\) is the complex conjugate of \(\gamma\),

$$\begin{aligned} &P_{r} + i\,P_{i} = - \frac{1}{2}\left( {\frac{\partial D}{\partial \omega }} \right)^{ - 1} \left( {V_{g}^{2} \frac{{\partial^{2} D}}{{\partial \omega^{2} }} + 2V_{g} \frac{{\partial^{2} D}}{\partial \omega \,\partial k} + \frac{{\partial^{2} D}}{{\partial k^{2} }}} \right), \hfill \\ &Q_{r} + i\,Q_{i} = \left( {\frac{\partial D}{\partial \omega }} \right)^{ - 1} \left( {\frac{2\gamma }{\varOmega } + 3\beta } \right), \hfill \\ &\zeta = \delta (z - V_{g} t),\quad \tau = \delta^{2} t, \hfill \\ \end{aligned}$$
(43)

and the group velocity may be written as \(V_{g} = - \frac{\partial D}{\partial \,k}\left( {\frac{\partial D}{\partial \omega }} \right)^{ - 1} .\)

Equation (42) addresses the demeanor of modulated waves. Instead of the complex coefficients, the real coefficient of such equation, yields the well-known Schrödinger equation. The latter equation has an exact solution. Whereas, the complex coefficients for making the analysis become more difficult. For simplicity, in the following, an attempt is made to achieve the stability criterion for such an equation. For this purpose, one may express the solution for \(\gamma \left( {\zeta ,\tau } \right)\) in the following form (Liu and Chang 2010):

$$\gamma (\zeta ,\tau ) = \,e^{i(\kappa \,\zeta - \varOmega \,\tau )} + c.c.$$
(44)

Inserting the proposed solution as given in Eq. (44) into Eq. (42), one gets

$$\varOmega = \left( {\kappa^{2} P_{r} + \,Q_{r} } \right) + i\left( {\kappa^{2} P_{i} + Q_{i} } \right).$$
(45)

In the light of this solution, the stability criterion that the imaginary part of the frequency must be greater than zero; therefore, the stability condition would be given by the following inequality:

$$\kappa^{2} P_{i} + Q_{i} < 0.$$
(46)

After lengthy, but straightforward calculations, the transition curve, may be arranged in a fourth-degree polynomial of \(E_{0}^{2}\) as:

$$G_{4} (\,E_{0}^{2} )^{4} + G_{3} (\,E_{0}^{2} )^{3} + G_{2} (\,E_{0}^{2} )^{2} + G_{1} \,E_{0}^{2} + G_{0} = 0.$$
(47)

In order to illustrate the stability criteria throughout the nonlinear stability approach, the transition curves are given in Eq. (47) will be analyzed. Considering a similar procedure as presented in the previous Section to find the non-dimensional quantities of all physical parameters. Therefore, in what follows, numerical calculations for the stability criterion as given in the inequality (46) will be done. In the light of the nonlinear approach, the stability criteria are plotted throughout Figs. 6, 7, 8 and 9. The transition curves are given in Eq. (46). For simplicity, the previous non-dimensional will be taken into account. It should be noted that the numerical calculations showed that the coefficient \(G_{4} \psi\) has always of a negative sign. This shows that the electric field intensity has a stabilizing influence, which is an already result proved by many research studies; for instance, see Moatimid (1995), and reference herein.

Fig. 6
figure 6

Plots the nonlinear stability diagram as given in (47)

Full size image
Fig. 7
figure 7

Depicts the variation of the ratio of the velocity \(U\) of Eq. (47)

Full size image
Fig. 8
figure 8

Depicts the variation of the ratio of the Darcy coefficient \(\nu\) of Eq. (47)

Full size image
Fig. 9
figure 9

Depicts the variation of the ratio of dynamic viscosity \(\mu\) of Eq. (47)

Full size image

Figure 6 is plotted for a system having the particulars:\(\,\rho = 40,\,U = 20,\,R = 1.5,\,\varepsilon = 5,\,\nu = 0.6,\,\mu = 7,\mu^{\prime} = 3\) and \(\kappa = 0.9\). In accordance with this choice of a particular system, the numerical calculation showed that there are two, integrated, positive real roots, whereas, the other two roots are of complex conjugate nature. Actually, this is an algebraic sense. As seen through the linear stability theory, \(\log E_{0}^{2}\) will be plotted versus the wavenumber \(k\). Therefore, Fig. 6 is depicted to indicate the transition curves. As seen from this figure, the nonlinear stability is controlled by, only, two integrated curves. It is verified, in the light of the inequality (46), that the region bounded by these two curves is a stable one. In contrast, the region outside these curves is unstable region. The following figures confirm the previous data. Figure 7 displays the influence of the ratio of the streaming \(U\), for a system having the same particulars as given in Fig. 6. As seen from this figure, this parameter has a destabilizing influence. This result is corresponding to the result that was already verified by El-Sayed et al. (2014a). Figure 8 is depicted to indicate the influences of the ratio of the Darcy coefficient \(\nu\). As indicated, all the physical parameters hold fixed, except the parameter \(\nu\). It was observed that \(\nu\) has a stabilizing effect. This result is in agreement with the result that was already obtained by El-Dib (2003). Finally, Fig. 9 is depicted to indicate the influences of the ratio of dynamic viscosity \(\mu\) on the stability picture. It is observed that \(\mu\) has a stabilizing effect. This result is in agreement with the result that was already obtained by El-Sayed et al. (2014a, b).

5 The nonlinear expanded frequency

The objective of this Section is to accomplish an approximate solution for the surface deflection. As aforementioned, the nonlinear approach resulted in the nonlinear characteristic that is given in Eq. (26). It represents a nonlinear second-order differential equation with complex coefficients of the interface displacement \(\eta (z,t)\,\). Actually, the analysis of this equation, in its present form, is rather difficult. Physically, the nature of the amplitude elevation \(\eta (z,t)\) must be a real function. To facilitate the following calculations, one may consider the time dependent only. In other words, let \(\eta = \eta (0,t) = \gamma (t)\). Therefore, the previous characteristic Eq. (26) may be separated into their real and imaginary parts as follows:

$$\gamma^{\prime\prime} + l_{1} \,\gamma^{\prime} + l_{2} \,\gamma + l_{3\,} \gamma^{2} + l_{4} \,\gamma \,\gamma^{\prime} + l_{5} \,\gamma \,\gamma^{\prime\prime} + l_{6} \,\gamma^{3} + l_{7} \,\gamma^{2} \,\gamma^{\prime} + l_{8} \,\gamma^{2} \,\gamma^{\prime\prime} = 0,$$
(48)

and

$$m_{1} \,\gamma^{\prime} + m_{2} \,\gamma + m_{3\,} \gamma^{2} + m_{4} \,\gamma \,\gamma^{\prime} + m_{5} \,\gamma^{3} + m_{6} \,\gamma^{2} \,\gamma^{\prime} = 0,$$
(49)

where \(l_{i} ,\,m_{i} \,(i = 1,2, \ldots )\) are well-known from the context. To avoid the lengthy of the paper, they will be omitted from the text.

To be more comprehensible, the combination of Eqs. (48) and (49) may be achieved by cancelling the term \(\gamma^{\prime}\) between them, the resulting equation can be written as follows:

$$\gamma^{\prime\prime} + \varpi^{2} \,\gamma + s_{1\,} \gamma^{2} + s_{2} \,\gamma \,\gamma^{\prime\prime} + s_{3} \,\gamma^{3} + s_{4} \,\gamma^{2} \,\gamma^{\prime\prime} = 0,$$
(50)

where \(\varpi^{2} ,s_{i} ,\,(i = 1,2, \ldots )\) is well-known from the context. This coefficient plays the influence of the natural frequency of the problem. Typically, it must be positive. To avoid the lengthy of the paper, they will be omitted.

Now, the nonlinear amplitude Eq. (50) has real coefficients. It represents a generalized cubic nonlinear differential equation. The solution for this equation needed initial conditions. For this purpose, the following initial conditions may be inserted:

$$\gamma \left( 0 \right) = 0;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\gamma^{\prime}(0) = 1.$$
(51)

For this purpose, the homotopy formula of the considered parametric equation becomes:

$$\gamma^{\prime\prime} + \varpi^{2} \,\gamma + \delta \left( {s_{1\,} \gamma^{2} + s_{2} \,\gamma \,\gamma^{\prime\prime} + s_{3} \,\gamma^{3} + s_{4} \,\gamma^{2} \,\gamma^{\prime\prime}} \right) = 0;\,\,\delta \in \left[ {0,\,1} \right].$$
(52)

The following analysis will be based on the expanded of the artificial frequency analysis; see for instance El-Dib and Moatimid (2019). In accordance with this approach, consider an artificial frequency \(\sigma^{2}\), so that it may be expanded as follows:

$$\sigma^{2} = \varpi^{2} + \sum\limits_{j = 1}^{\infty } {\delta^{j} \varpi \, _{j} } .$$
(53)

Combining Eqs. (52) and (53), the homotopy equation of this combination, may be rewritten as:

$$\gamma^{\prime\prime} + \sigma^{2} \,\gamma + \delta \left( { - (\varpi_{1} + \delta \,\varpi_{2} )\gamma + s_{1\,} \gamma^{2} + s_{2} \,\gamma \,\gamma^{\prime\prime} + s_{3} \,\gamma^{3} + s_{4} \,\gamma^{2} \,\gamma^{\prime\prime}} \right) = 0.$$
(54)

Taking the Laplace transform to both sides of Eq. (54), considering the initial conditions that are given in Eq. (51), the result becomes:

$$L_{T} \left\{ {\gamma (t;\,\delta )} \right\} = \frac{S}{{S^{2} + \sigma^{2} }} - \frac{1}{{S^{2} + \sigma^{2} }}L_{T} \left\{ {\delta \left( { - (\varpi_{1} + \delta \,\varpi_{2} )\gamma + s_{1\,} \gamma^{2} + s_{2} \,\gamma \,\gamma^{\prime\prime} + s_{3} \,\gamma^{3} + s_{4} \,\gamma^{2} \,\gamma^{\prime\prime}} \right)} \right\}\,.$$
(55)

Employing the inverse transform of both sides of Eq. (55), one finds:

$$\gamma (t;\,\delta ) = L_{T}^{ - 1} \left( {\frac{S}{{S^{2} + \sigma^{2} }}} \right) - L_{T}^{ - 1} \left[ {\frac{1}{{S^{2} + \sigma^{2} }}L_{T} \left\{ {\delta \left( { - (\varpi_{1} + \delta \,\varpi_{2} )\gamma + s_{1\,} \gamma^{2} + s_{2} \,\gamma \,\gamma^{\prime\prime} + s_{3} \,\gamma^{3} + s_{4} \,\gamma^{2} \,\gamma^{\prime\prime}} \right)} \right\}} \right].$$
(56)

In accordance with the regular HPM, the time-dependent function \(\gamma (t;\delta )\) may be expanded as:

$$\gamma (t;\delta ) = \sum\limits_{n = 0}^{\infty } {\delta^{n} \gamma_{n} (t)} = \gamma_{0} (t) + \delta \gamma (t) + \delta^{2} \gamma_{2} (t) + \cdots$$
(57)

Utilizing the expansion of the dependent parameter \(\gamma (t;\delta )\) as given in Eq. (57), and then equating the coefficients of indicial powers \(\delta\) on both sides, one gets

$$\delta^{0} {:}\,\,\gamma_{0} (t) = \frac{1}{\sigma }\sin (\sigma \,t)\,\,,$$
(58)
$$\delta{:}\,\,\,\gamma_{1} (t) = - L_{T}^{ - 1} \left[ {\frac{1}{{S^{2} + \sigma^{2} }}L_{T} \left\{ { - \varpi_{1} \gamma_{0} + s_{1\,} \gamma_{0}^{2} + s_{2} \,\gamma_{0} \,\gamma^{\prime\prime}_{0} + s_{3} \,\gamma_{0}^{3} + s_{4} \,\gamma_{0}^{2} \,\gamma^{\prime\prime}_{0} } \right\}} \right],$$
(59)

and

$$\delta^{2} {:}\gamma_{2} (t) = - L_{T}^{ - 1} \left[ {\frac{1}{{s^{2} + \sigma^{2} }}L_{T} \left\{ { - \varpi_{2} \gamma_{0} - \varpi_{1} \gamma_{1} + 2s_{1\,} \gamma_{0} \gamma_{1} + s_{2} \,(\gamma_{0} \,\gamma^{\prime\prime}_{1} + \gamma_{1} \,\gamma^{\prime\prime}_{0} ) + 3s_{3} \,\gamma_{0}^{2} \gamma_{1} + s_{4} \,(\gamma_{0}^{2} \,\gamma^{\prime\prime}_{1} + 2\gamma_{0} \gamma_{1} \,\gamma^{\prime\prime}_{0} )} \right\}} \right].\,$$
(60)

On substituting from Eq. (58) into Eq. (59), one finds:

$$\,\gamma_{1} (t) = - L_{T}^{ - 1} \left[ {\frac{1}{{S^{2} + \sigma^{2} }}L_{T} \left\{ \begin{aligned} \frac{1}{{2\sigma^{2} }}\left( {s_{1} - \sigma^{2} s_{2} } \right) + \frac{1}{{4\sigma^{3} }}(3s_{3} - 4\varpi_{1} \sigma^{2} - 3s_{4} \sigma^{2} )\sin (\sigma \,t) + \hfill \\ \frac{1}{{4\sigma^{3} }}( - s_{3} + s_{4} \sigma^{2} )\sin (3\sigma \,t) + \frac{1}{{2\sigma^{2} }}(\sigma^{2} s_{2} - s_{1} )\cos (2\sigma \,t) \hfill \\ \end{aligned} \right\}} \right].$$
(61)

The uniformly valid expansion requires the cancellation of the secular terms. Therefore, the coefficient of the function \(\sin (\sigma \,t)\) must be excluded. Therefore, the parameter \(\varpi_{1}\) is determined as:

$$\varpi_{1} = \frac{3\,}{{4\sigma^{2} }}\left( {s_{3} - s_{4} \sigma^{2} } \right).$$
(62)

It follows that the periodic solution of \(\gamma_{1} (t)\) becoming:

$$\gamma_{1} (t) = \frac{{s_{2} \sigma^{2} - s_{1} }}{{2\sigma^{2} }} + \frac{{2\left( {s_{1} - s_{2} \sigma^{2} } \right)}}{{3\sigma^{4} }}\cos (\sigma \,t) + \frac{{3\left( {s_{3} - s_{4} \sigma^{2} } \right)}}{{32\sigma^{5} }}\sin (\sigma \,t) + \frac{{ - s_{1} + s_{2} \sigma^{2} }}{{6\sigma^{4} }}\cos (2\sigma \,t) + \frac{{ - s_{3} + s_{4} \sigma^{2} }}{{32\sigma^{5} }}\sin (3\sigma \,t).$$
(63)

Again, substituting from Eqs. (58), and (63) into Eq. (60), one finds that the cancellation of the secular terms, requires

$$\varpi_{2} = \frac{{63s_{3}^{2} - \sigma^{2} (150s_{3} s_{4} + 320s_{1}^{2} ) + \sigma^{4} (352s_{1} s_{2} + 87s_{4}^{2} ) - 32s_{2}^{2} \sigma^{6} }}{{384\sigma^{6} }}.$$
(64)

On using similar arguments as given before, after lengthy, but straightforward calculations, one finds the solution \(\gamma_{2} (t)\) is:

$$\gamma_{2} (t) = \frac{ - 1}{{46080\sigma^{9} }}\left( \begin{aligned} \tilde{s}_{1} + \tilde{s}_{2} \sin (\sigma \,t) + \tilde{s}_{3} \cos (\sigma \,t) + \tilde{s}_{4} \sin (2\sigma \,t) + \tilde{s}_{5} \cos (2\sigma \,t) \hfill \\ + \tilde{s}_{6} \sin (3\sigma \,t) + \tilde{s}_{7} \cos (3\sigma \,t) + \tilde{s}_{8} \cos (4\sigma \,t) + \tilde{s}_{9} \sin (5\sigma \,t) \hfill \\ \end{aligned} \right).$$
(65)

As before, the approximate bounded solution of the equation of motion that is given in Eq. (50) may be written as follows:

$$\gamma (t) = \mathop {\lim }\limits_{\delta \to 1} \left( {\gamma_{0} (t) + \delta \gamma_{1} (t) + \delta^{2} \gamma_{2} (t)} \right),$$
(66)

where \(\gamma_{0} (t)\,,\,\,\gamma_{1} (t)\) and \(\gamma_{2} (t)\) are the time-dependent functions as given by Eqs. (58), (63) and (65), respectively.

Actually, the approximate solution in Eq. (68) requires that the arguments of the trigonometric functions must be of real value. For this purpose, combining Eqs. (55), (64) and (66), one finds the following characteristic equation:

$$\sigma^{8} + \alpha_{1} \,\sigma^{6} + \alpha_{2} \,\sigma^{4} + \alpha_{3} \,\sigma^{2} - \alpha_{4} = 0,$$
(67)

where \(\alpha_{1} = \frac{1}{12}\left( { - 12\varpi^{2} + s_{2}^{2} + 9s_{4} } \right),\,\alpha_{2} = \frac{ - 1}{384}\left( {352s_{1} s_{2} + 288s_{3} + 87s_{4}^{2} } \right),\,\alpha_{3} = \frac{5}{6}s_{1}^{2} + \frac{25}{64}s_{3} s_{4}\) and \(\alpha_{4} = \frac{{21s_{3}^{2} }}{128}\,.\)

Substituting about \(\varpi_{1}\), and \(\varpi_{2}\) into Eq. (53), one finds that it represents the equation of fourth degree in \(\sigma^{2}\). The necessary stability requirements need that \(\sigma\) to be real and positive. Equation (67) may be rewritten as follows:

$$\sigma^{2} = \frac{{\alpha_{4} }}{{\alpha_{3} }} - \frac{1}{{\alpha_{3} }}\delta \left( {\,\sigma^{8} + \alpha_{1} \,\sigma^{6} + \alpha_{2} \,\sigma^{4} } \right).$$
(68)

To obtain an approximate value of the artificial frequency \(\sigma\), following the HPM, one may write the homotopy equation as follows:

$$\sigma^{2} = \frac{{\alpha_{4} }}{{\alpha_{3} }} - \frac{\delta }{{\alpha_{3} }}\left( {\,\sigma^{8} + \alpha_{1} \,\sigma^{6} + \alpha_{2} \,\sigma^{4} } \right).$$
(69)

Typically, \(\delta\) is the embedding homotopy parameter.

Furthermore, one assumes that \(\sigma = \sigma_{0} + \delta \sigma_{1} + \delta^{2} \sigma_{2} + \cdots\). Following the same procedure as given previously, one finds the solution \(\sigma_{0}^{2}\) is:

$$\sigma_{0}^{2} = \frac{{\alpha_{4} }}{{\alpha_{3} }},$$
(70)

after lengthy, but straightforward calculations, one finds an approximate value of the artificial frequency as:

$$\sigma = \sqrt {\frac{{\alpha_{4} }}{{8\alpha_{3}^{17} }}} \left( \begin{aligned} 8\alpha_{3}^{8} - 4\alpha_{2} \alpha_{3}^{6} \alpha_{4} + 7\alpha_{2}^{2} \alpha_{3}^{4} \alpha_{4}^{2} - 4\alpha_{1} \alpha_{3}^{5} \alpha_{4}^{2} + 18\alpha_{1} \alpha_{2} \alpha_{3}^{3} \alpha_{4}^{3} \hfill \\ - 4\alpha_{3}^{4} \alpha_{4}^{3} + 11\alpha_{1}^{2} \alpha_{3}^{2} \alpha_{4}^{4} + 22\alpha_{2} \alpha_{3}^{2} \alpha_{4}^{4} + 26\alpha_{1} \alpha_{3} \alpha_{4}^{5} + 15\alpha_{4}^{6} \hfill \\ \end{aligned} \right).$$
(71)

Actually, the distribution of the approximate solution that is obtained by Eq. (71) depends mainly on the value of \(\sigma_{0}\). This requires:

$$\frac{{\alpha_{4} }}{{\alpha_{3} }} > 0,$$
(72)

The inequality (72) may be written in the following form:

$$\tilde{\alpha }_{1} E_{0}^{2} + \tilde{\beta }_{1} > 0\,,$$
(73)

where \(\tilde{\alpha }_{1}\), and \(\tilde{\beta }_{1}\) are known from the context.

Simultaneously, as stated above, the natural frequency \(\varpi^{2}\) must be positive, requires:

$$\tilde{\alpha }_{2} E_{0}^{2} + \tilde{\beta }_{2} > 0\,.$$
(74)

where \(\tilde{\alpha }_{2}\), and \(\tilde{\beta }_{2}\) are known from the context.

Actually, the stability criteria depend, as stated previously, the implication of condition (73), together with the inequality given in (74). Take into account, a similar procedure as presented in Sect. 3 to use the non-dimensional quantities of all physical parameters.

Following the particulars of the system as: \(\,\rho = 2,\,\,U = 3,\,R = 0.02,\,\varepsilon = 4,\,\nu = 0.6,\,\,\mu = 2\) and \(\mu^{\prime} = 9\). The present calculations showed that the parameters, and \(\tilde{\alpha }_{2}\) are always of positive significance. This shows, again, that the electric field intensity has a stabilizing influence. As seen through the linear and nonlinear stability theory, \(\log E_{0}^{2}\) is plotted versus the wave number of the surface waves \(k\).

In what follows, numerical calculations are estimated to confirm the stability criteria in (73), and (74). For more convenience, the two criteria are plotted in one figure, Therefore, Fig. 10 is depicted for this purpose, as follows, the equality of (73) is pictured in a solid curve, meanwhile, the equality of (74) is graphed in a dotted one. Furthermore, the stable region, corresponding to he equality of (73), is referred by the letter \(S_{1}\). Simultaneously, the unstable region is symbolizes by the letter \(U_{1}\). On the other hand, these two regions are referred by the letters \(S_{2}\), and \(U_{2}\), in analogy with the second condition. As indicated from this the stability is judged by the solid curve. Therefore, the remaining curves are plotted in the light of the first condition. Consequently, Figs. 11, 12 and 13. Are displayed in the light of the inequality (73). Figure 11 shows the influence of the ratio of \(U\) on the stability picture. As seen from this figure, this parameter has a destabilizing influence. This influence has, already, seen through as well as the nonlinear theory. Similar influences of the parameters \(\nu\), and \(\mu\) are seen. To avoid the lengthy of the paper, they are excluded. In contrast with the linear stability theory, the ratio of dynamic visco-elasticity \(\mu^{\prime}\), plays a dual ole in the stability picture. This influence has been pictured in Fig. 12. Finally, a numerical calculation of the approximate bounded solution that is given by Eq. (49), together with the criteria (73) and (74) will be plotted at \(z = 0\), in Fig. 13. As shown previously, this solution depends mainly on the expanded frequency \(\sigma\).

Fig. 10
figure 10

Displays the contribution of the two criteria (73) and (74)

Full size image
Fig. 11
figure 11

Depicts the variation of the ratio of the velocity \(U\) of inequality (73)

Full size image
Fig. 12
figure 12

Depicts the variation of the ratio of dynamic visco-elasticity \(\mu^{\prime}\) of inequality (73)

Full size image
Fig. 13
figure 13

Depicts the approximate solution of Eq. (66)

Full size image

6 Concluding remarks

This present paper is concerned with the linear as well as nonlinear stability analysis of a vertical cylindrical interface among two perfect, homogeneous, and incompressible dielectric fluids. The fluids are considered as non-Newtonian visco-elastic fluids of the Walters’ B type. The system is pervaded by a uniform axial electric field. Typically, as given by our foregoing works; for instance, see Melcher (1981), and Moatimid et al. (2020), the nonlinear analysis is conducted from the linear solutions of the governing equations of motion together with the convenient nonlinear boundary conditions. To relax the mathematical manipulation, a simplified formulation of the viscous potential flow theory is adopted. Several specific cases are approved across adequate data information. As a special case, when ignoring the nonlinear terms, the linear stability criterion has been obtained. The numerical calculations, throughout the linear approach, confirmed similar results as that were given by many researchers. Following similar arguments that were given by El-Sayed et al. (2014a), it follows that the stability criteria are judged. Consequently, the nonlinear characteristic equation results in the Ginzburg–Landau equation. This equation controls the nonlinear stability criterion of the system. This criterion is illustrated graphically throughout a set of figures. In the light of the nonlinear characteristic equation, the behavior of the surface elevation is analyzed. Because of the real nature of the surface deflection, the nonlinear characteristic equation is split into real and imaginary parts. The combination of these two equations resulted in a second order nonlinear ordinary differential equation of real coefficients. By coupling the HPM together with Laplace transforms, the concept of the expanded frequency achieved a bounded approximate solution. Again, the HPM is utilized to obtain an approximate solution of the expended artificial frequency. A numerical calculation is utilized to graph the amplitude of the surface waves. The influences of some physical parameters had been shown. The concluding remarks may be drawn along the following points:

The investigation of the linear stability analysis yields the following results:

  • The differential equation throughout the linear stability approach is given by Eq. (28).

  • The linear dispersion relation is given in Eq. (30).

  • The numerical calculations showed that the parameters; \(U,\,\nu ,\,\mu\) and \(\mu^{\prime}\) have destabilizing influences on the stability profile. These results are confirmed by the different authors.

The investigation of the nonlinear stability analysis yields the following results:

  • The nonlinear characteristic equation that controls the stability criteria is conducted in Eq. (27).

  • The nonlinear Ginzburg–Landau equation, which governs the nonlinear stability criterion, is given by Eq. (42).

  • A simplified solution of the previous solution is given in Eq. (44). Actually, this solution facilitates stability conditions. The numerical calculations indicated only two integrated curves. The inner region is stable, whereas, the outer region is unstable.

  • As in the linear approach, the nonlinear strategy confirms the same influence of the parameter \(U\). In contrast, the parameters \(\mu\), and \(\nu\) have a stabilizing impact on the stability picture.

The nonlinear frequency expanded, yields the following results:

  • The combination of the real and imaginary parts of the nonlinear characteristic equation, results in Eq. (50), which represents the distribution function of the surface deflection \(\gamma (t)\).

  • The approximate solution of the distribution function of the interface is given by Eq. (66).

  • The criterion of the real artificial frequency is governed by the inequality (73).

  • The criterion of the real natural frequency is governed by the inequality (74).

  • A set figures are plotted to display the criteria of the positive significance of both the natural and artificial frequencies.