1 Introduction

One of the alternate ways of delivering blood flow is electro-magneto flow driven by externally applied electric and magnetic fields. It involves both magnetic and electro-static collisions between the magnetically charged particles in the ionized solution. Considerable amount of work have been done to identify various blood flow patterns and characteristics in the presence of magnetic field and electric current. Electro-magneto blood flow has been implemented in surgical treatments and cancer (tumor) operations.

The artificial blood velocity was measured experimentally at different magnetic fields strength and it was noticed that the velocities of blood and magnetic particles velocity fell tremendously in the presence of magnetic field (Sharma et al. 2015). Although the behaviors of magnetic particles and blood are quiet similar, the magnetic particles velocity is lower than blood velocity due to the drag force and other resistive forces (Shah et al. 2016a). In micro channels the heat conversion capacity and fluid flow can be regulated in the non-local system (Roslan et al. 2016) as it flow faster. Moreover the channel temperature can be adjusted via manipulating the Joule’s parameter. The temperature profile reported was different as compared to those reported by using other model. There was greater heat transfer rate for the oscillatory movement of the triangular wave form of the temperature profile.

Rubbab et al. (2017) obtained the microscopic results such as the typical material length scale, which is important for one to perceive the fluid characteristics. Moreover, all the classical fluid results can be recovered by setting the typical length scale to zero in the couple-stress fluid. Kumar et al. (2012) found that the blood velocity would was increase upon applying the body acceleration and combining the body acceleration with magnetic field. Their study is helpful for treating cardiovascular, blood borne and hypertension diseases. The study conducted by Singh and Rathee (2011) was limited to certain magnetic field range. They studied the blood flow in hypertensive patients and in arteries having blockages. Also, there are some references which performed in this field (Alsagri et al. 2019; Gul et al. 2019; Ahmad 2019; Souayeh et al. 2016, 2017a, b, 2019; Raju et al. 2019; Ahmad and Khan 2019; Krishna et al. 2019; Ahmed et al. 2018; Hussanan et al. 2019; Bezi et al. 2018; Alarifi et al. 2018, 2019).

Obstructions in water and sewage system pipelines are major concerns nowadays. Patel et al. (2012) modeled the constriction by using sinusoidal model. The axial velocity was then solved using the simple pipeline network model. Santapuri (2016) indicates the practicality and usefulness of his framework through multi-ferrous material of the symmetric hexagonal crystal in which the limitations on the material constants were also specified. Buchukuri et al. (2016) investigated the oscillating singularities by using the potential method and the pseudo-differential equations on 35 manifolds with boundary. The uniqueness and existence of the solutions were then established. Bhatti et al. (2017) have performed both numerical and experimental works on MHD and heat transfer of non-Newtonian flows. By using the nano fluid model, Sher et al. (2017) focused on different types of nano-particles which were platelet, cylinder and brick shape in the study of unsteady, non-uniform and peristaltic flow. The thermal conductivity, temperature and axial velocity profiles of these nano-particles were sequenced as bricks < cylinder < platelets. The size of trapped bolus was the largest for bricks as compared to platelets in the nano-fluid model. Usman et al. (2018) found that the heat transfer and fluid flow results for two-phase, unsteady magnetized flow with nano-particles obtained using the fourth order Runge–Kutta and scheme the differential transform method were quiet similar.

Tripathi et al. (2018) noticed that the axial velocity in the core region was increased the electric field whereas the opposite behavior was observed at micro-channel walls. On the other hand, there was a reduction in the number of trapped boluses. In the model proposed by El-Borhamy (2017), flow parameters affecting the convergence of the numerical solution in the regularization process were reported. At large ratio \(\frac{ \in }{{\tau {}_{s}}}\), bifurcated solutions and secondary vortices were more apparent. Falade et al. (2017) found that by raising the injection/suction parameter affected by thin thermal radiation optics in the Oscillatory MHD flow through permeable medium, parameter such as the flow velocity, fluid temperature and skin friction were elevated thus reducing the heat transfer rate on the heated plate. Heat transfer of MHD couple stress fluid flow had major contributions in maximizing heat transfer and reducing skin frictions (Shah et al. 2016b). Moreover by enhancing parameter such as Hartmann number, porosity, heat source and couple stress parameter of the flow, the heat transfer rate could be enhanced significantly meanwhile, if high heat sink parameter and Prandtl number were employed the heat transfer rate would decrease.

Sharma and Sharma (2014) investigated the effect of relaxation time on both spatial and temporal temperature profiles. The effects of several parameters on the temperature fluctuations were graphically analyzed. Tanveer (2016) solved the velocity distribution model in coronary arteries subjected to external magnetic field and fatty particles. The performed study was 65 is helpful in the treatment of various cardiovascular and arterial diseases. Caputo and Fabrizio (NFDt) (2015) modified the old Caputo fractional order derivative (UFDt) so that is free from singular kernel. In NFDt, fractional order works on both temporal and spatial variable. Temporal variable is more suitable for Laplace transform. While, the spatial variables is more suitable for Fourier transform. Time fractional order derivative model gives a non-local system which is free from the singular kernel, which is able to explain the multifariousness of the medium and the oscillation at different levels, which are not well defined in the classical local system or in the fractional order system with singular kernel. For NFDt at \(\alpha = 1\), the classical local system is recovered. Recently, Morales-Delgado et al. (2019) studied the dynamics of the oxygen diffusion through capillary to tissues using Caputo–Fabrizio and Liouville–Caputo fractional derivatives by using Laplace homotopy method.

The purpose of this paper is to deal with application of Caputo–Fabrizio fractional derivative to solve unsteady viscous flow of blood filled with magnetic particles subject to an oscillating pressure gradient through a cylindrical tube. The flow acted upon by external electric field and magnetic field normal to the flow direction.

2 Mathematical model

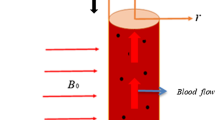
Consider three-dimensional unsteady viscous flow of blood mixed with magnetic particles (iron rich particles) under the action of an oscillating pressure gradient inside the circular cylinder of radius R0. The transport of the blood and magnetic particles in the channel is exposed to the external electric field \(\vec{E}\) and magnetic field \(\vec{B}\) as shown in Fig. 1. The effect of electromagnetic on the velocity profiles of blood flow and magnetic particles flow has been focused in depth.

Fig. 1
figure 1

Electro-magneto blood flow transport model

Full size image

Governing continuity and momentum equations for the electro-magnetic transport of blood mixed with magnetic particles in the cylindrical coordinates \((r,\,\theta ,\,z)\) is given by (Shah et al. 2016a):

$$\frac{{\partial u_{r} }}{\partial r} + \frac{{u_{r} }}{r} + \frac{{\partial u_{z} }}{\partial z} = 0$$
(1)
$$\begin{aligned} \rho \left( {\frac{{\partial u_{r} }}{\partial t} + u_{r} \frac{{\partial u_{r} }}{\partial r} + \frac{{u_{\theta } }}{r}\frac{{\partial u_{r} }}{\partial \theta } - \frac{{u{}_{\theta }^{2} }}{r} + u_{z} \frac{{\partial u_{r} }}{\partial z}} \right) \hfill \\ \quad = - \frac{\partial p}{\partial r} + \rho \,f_{r} + \mu \,\left[ {\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial (ru_{r} )}}{\partial r}} \right)} \right. + \frac{1}{{r^{2} }}\frac{{\partial^{2} u{}_{r}}}{{\partial \theta^{2} }} - \left. {\frac{2}{{r^{2} }}\frac{{\partial u_{\theta } }}{\partial \theta } + \frac{{\partial^{2} u_{r} }}{{\partial z^{2} }}} \right] \hfill \\ \end{aligned}$$
(2)
$$\begin{aligned} \rho \left( {\frac{{\partial u_{\theta } }}{\partial t} + u_{r} \frac{{\partial u_{\theta } }}{\partial r} + \frac{{u_{\theta } }}{r}\frac{{\partial u_{\theta } }}{\partial \theta } + \frac{{u{}_{r}u{}_{\theta }}}{r} + u_{z} \frac{{\partial u_{\theta } }}{\partial z}} \right) \hfill \\ \quad = - \frac{1}{r}\frac{\partial p}{\partial r} + \rho \,f_{\theta } + \mu \,\left[ {\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial (ru_{\theta } )}}{\partial r}} \right)} \right. + \frac{1}{{r^{2} }}\frac{{\partial^{2} u{}_{\theta }}}{{\partial \theta^{2} }} + \left. {\frac{2}{{r^{2} }}\frac{{\partial u_{r} }}{\partial \theta } + \frac{{\partial^{2} u_{\theta } }}{{\partial z^{2} }}} \right] \hfill \\ \end{aligned}$$
(3)
$$\rho \left( {\frac{{\partial u_{z} }}{\partial t} + u_{r} \frac{{\partial u_{z} }}{\partial r} + \frac{{u_{\theta } }}{r}\frac{{\partial u_{z} }}{\partial \theta } + u_{z} \frac{{\partial u_{z} }}{\partial z}} \right) = - \frac{\partial p}{\partial r} + \rho \,f_{z} + \mu \,\left[ {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial u_{z} }}{\partial r}} \right)} \right. + \frac{1}{{r^{2} }}\frac{{\partial^{2} u{}_{z}}}{{\partial \theta^{2} }} + \left. {\frac{{\partial^{2} u_{z} }}{{\partial z^{2} }}} \right].$$
(4)

For the governing continuity and Navier–Stokes equations of the blood flow model in the cylindrical coordinates, we are assuming the following realistic assumptions.

  1. 1.

    Only one velocity component is non-zero i.e.; \(u_{z} = u\) at z-direction. Thus \(u_{r} = 0 = u_{\theta }\)

  2. 2.

    Axial component of the velocity is independent of the angular location, hence \(\frac{{u_{\theta } }}{\partial \theta } = 0\).

The above governing equations from Eqs. (1)–(4) are then reduce to

$$\frac{{\partial u_{z} }}{\partial z} = 0$$
(5)
$$\rho \left( {\frac{{\partial u_{z} }}{\partial z}} \right) = - \frac{\partial p}{\partial z} + \eta \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{{\partial (ru_{z} )}}{\partial r}} \right) + F_{em} + F_{uv} .$$
(6)

2.1 Electro-magnetic field and relative forces

The electro-magnetic field force Fem and the force Fuv due to the motion between blood and magnetic particles can be represented as

$$\begin{aligned} F_{em} = J \times B & = \sigma (E + V \times B) \times B \\ & = - \,\sigma^{2} B^{2} u(r,t)\vec{j} - \rho_{e} E \\ & = - \,\sigma^{2} B^{2} u(r,t)\vec{j} - \rho_{e} E_{z} k \\ \end{aligned}$$
(7)
$$F_{uv} = K{}_{m}\,N\left\{ {v(r,\,t) - u(r,\,t)} \right\}$$
(8)

where B0 and Ez are the magnetic and electric field in axial direction. J is the density of current, \(\vec{j}\) is the unit vector in z-direction, \(u_{z} = u(r,\,t)\,\vec{j}\) is the blood flow velocity component and v(r, t) is the magnetic particles velocity component in z-direction. \(\rho_{e} = - \varepsilon \,\kappa^{2} \,\psi (r)\) is the net charge density. In \(\kappa^{2} \, = \frac{{2z_{0} {}^{2}\,e_{0}^{2} \,n_{0} }}{{\varepsilon \,k_{B} \,T_{a} }}\), \(\varepsilon\) is the dielectric constant, \(\kappa\) is the Debye–Hukel parameter, \(\kappa^{ - 1}\) is the thickness of electrical double layer, \(n_{0}\) is the ionic concentration in the bulk phase, \(e_{0}\) is the electronic charge, \(k_{B}\) is the Boltzmann constant, \(T_{a}\) is the absolute temperature. Km is the stokes constant, N is the number of magnetic particles per unit volume.

2.2 Bio-fluid velocity model

The governing momentum in Eq. (6) is representing the unsteady, axisymmetric transport of the blood flow model in the presence of external pressure gradient and electro-magnetic field:

$$\begin{aligned} \frac{\partial u(r,\,t)}{\partial t} & = \frac{1}{\rho }(A_{0} + A_{1} \cos (\omega \,t)) + \nu \,\,\left( {\frac{{\partial^{2} u(r,\,t)}}{{\partial \,r^{2} }} + \frac{1}{r}\frac{\partial u(r,\,t)}{\partial r}} \right) \\ & \quad + \frac{{K{}_{m}\,N\left\{ {v(r,\,t) - u(r,\,t)} \right\}}}{\rho } - \frac{{\sigma^{2} \,B^{2} u(r,\,t)\,}}{\rho } + \frac{{\varepsilon \,\kappa^{2} \,\psi (r)\,E_{z} }}{\rho },\,\,A_{0} > 0 \\ \end{aligned}$$
(9)

where A0 and A1 are the pulsatile components of the pressure gradient giving rise to the systolic and diastolic pressure. Newton’s second law of motion governs the movement of magnetic particles in the blood flow

$$m\frac{\partial v(r,\,t)}{\partial t} = K{}_{m}\,\left\{ {u(r,\,t) - v(r,\,t)} \right\}$$
(10)

where u(r, t) and v(r, t) are the blood flow and magnetic particles velocity in the axial direction respectively and m is the magnetic particles average mass, \(\rho\) is the fluid density and \(\nu\) is the kinetic viscosity.

Caputo–Fabrizio time fractional order model of Eqs. (9) and (10) is obtained by taking t and multiplying both sides of the equations by \(\frac{\partial }{\partial t} = D_{t}^{(\alpha )}\), which has the dimension of t

$$\begin{aligned} & \lambda^{\alpha } D{}_{t}^{(\alpha )} u(r,\,t) = \frac{\lambda }{\rho }(A_{0} + A_{1} \cos (\omega \,t)) + \lambda \,\nu \,\left( {\frac{{\partial^{2} u(r,\,t)}}{{\partial \,r^{2} }} + \frac{1}{r}\frac{\partial u(r,\,t)}{\partial r}} \right) \\ & \quad + \frac{{K{}_{m}\,N\,\lambda }}{\rho }\left\{ {v(r,\,t) - u(r,\,t)} \right\} - \frac{{\sigma^{2} \,B{}_{0}^{2} u(r,\,t)\,\lambda \,}}{\rho } + \frac{{\varepsilon \,\kappa^{2} \,E_{z} \,\psi (r)\,\lambda }}{\rho },\,A_{0} > 0 \\ \end{aligned}$$
(11)

and

$$\lambda^{\alpha } D{}_{t}^{(\alpha )} \,v(r,\,t) = \frac{{K{}_{m}\,\lambda \,}}{m}\left\{ {u(r,\,t) - v(r,\,t)} \right\}.$$
(12)

The initial and boundary conditions of the blood flow inside circular cylinder of radius R0 are

$$\begin{aligned} & u(r,0) = 0,v(r,0) = 0,r \in [0,R_{0} ] \\ & u(R_{0} ,t) = 0,v(R_{0} ,t) = 0,t > 0. \\ \end{aligned}$$
(13)

To study the non-dimensional model introducing the non-dimensional variables

$$r^{\prime} = \frac{r}{{R_{0} }},\quad t^{\prime} = \frac{t}{\lambda },\quad u^{\prime} = \frac{u}{{u_{0} }},\quad v^{\prime} = \frac{v}{{v_{0} }},\quad \omega = \lambda \omega ,\quad A^{\prime}_{0} = \frac{{\lambda A_{0} }}{{\rho u_{0} }},\quad A^{\prime}_{1} = \frac{{\lambda A_{1} }}{{\rho u_{0} }},\quad \psi^{\prime} = \frac{\psi }{{\psi_{0} }}$$
(14)

where u0 is the characteristic velocity. Equations (11)–(13) becomes (after dropping dashes)

$$\begin{aligned} & D{}_{t}^{(\alpha )} u(r,t) = A_{0} + A_{1} \cos (\omega t) + \frac{1}{\text{Re}}\left( {\frac{{\partial^{2} u(r,t)}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u(r,t)}{\partial r}} \right) \\ & \quad + R\left\{ {v(r,t) - u(r,t)} \right\} - Ha^{2} u(r,t) + K^{2} \psi (r),A_{0} > 0 \\ \end{aligned}$$
(15)
$$G \cdot D_{t}^{(\alpha )} v(r,t) = u(r,t) - v(r,t)$$
(16)
$$\begin{aligned} & u(r,0) = 0,v(r,0) = 0,r \in [0,1] \\ & u(1,t) = 0,v(1,t) = 0,t > 0 \\ \end{aligned}$$
(17)

where \(K^{2} = \frac{{\varepsilon \,\kappa^{2} \,E_{z} \,\lambda }}{\rho }\) is the electro-kinetic width, \(Ha^{2} = \frac{{\sigma^{2} \,B{}_{0}^{2} \lambda \,}}{\rho }\) is the Hartmann number, \(\text{Re} = \frac{{R_{0}^{2} }}{\lambda \,\rho }\) is the Reynolds number, \(R = \frac{{K_{m} \,N\,\lambda }}{\rho }\) is the particles concentration parameter and \(G = \frac{m}{{K_{m} \,\lambda }}\) is the mass parameter of magnetic particles.

2.3 A new definition of fractional derivative without singular kernel NFDt

In 1967 Caputo define fractional time derivative with singular kernel usually denoted as UFDt,

$$D{}_{t}^{(\alpha )} f(t) = \frac{1}{\varGamma (1 - \alpha )}\int\limits_{a}^{t} {\frac{{\dot{f}(\tau )}}{{(t - \tau )^{\alpha } }}} d\tau ,$$
(18)

with \(\alpha \in [0,\,1]\) and \(a \in \left[ { - \infty ,\,t} \right),\,f \in H^{1} (a,\,b),\,b > a\) where H1 is the class of all integrable functions on [a, b]. In Eq. (18) kernel has a singular value at \(t = \tau\). This was further modified by Caputo and Fabrizio (2015) and called as NFDt, by removing the singularity from the definition:

$$D{}_{t}^{(\alpha )} f(t) = \frac{M(\alpha )}{(1 - \alpha )}\int\limits_{a}^{t} {\dot{f}(\tau )} \exp \left( { - \frac{\alpha (t - \tau )}{1 - \alpha }} \right)d\tau ,$$
(19)

where M(0) = M(1) = 1 (condition of the function normalization). In addition to the absence of singularity in the new definition of fractional derivative NFDt, it has another property that it coincides with the old definition UFDt at zero for a constant f(t). Moreover \(f(t) \notin H^{1} (a,\,b)\) can also be operated by NFDt. The equivalent form of the definition in Eq. (19) assumes the form

$$\tilde{D}{}_{t}^{(\sigma )} f(t) = \frac{N(\sigma )}{\sigma }\int\limits_{a}^{t} {\dot{f}(\tau )} \exp \left( { - \frac{(t - \tau )}{\sigma }} \right)d\tau .$$
(20)

One of the property of NFDt is related to the computation of Laplace transform (LT) with variable s, by taking a = 0 in the definition in Eq. (20)

$$LT\,[D_{t}^{(\alpha )} ]f(t) = \frac{s\,LT\,[f(t)] - f(0)}{s + \alpha (1 - s)}.$$
(21)

2.4 Solution to the problem

Laplace transform is most suitable in case of temporal variable t in the blood flow model discussed in Eqs. (15) and (16) and boundary condition in (17). After transformation we have

$$\begin{aligned} & \frac{{s\bar{u}(r,s)}}{s + \alpha (1 - s)} = \frac{1}{s}\left( {A_{0} + K{}^{2}\psi (r)} \right) + \frac{1}{\text{Re}}\left( {\frac{{\partial^{2} \bar{u}(r,s)}}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \bar{u}(r,s)}}{\partial r}} \right) \\ & \quad + R\left\{ {\bar{v}(r,t) - \bar{u}(r,t)} \right\} - Ha^{2} \bar{u}(r,t) + \frac{{A_{1} s}}{{s_{2} + \omega^{2} }},A_{0} > 0 \\ \end{aligned}$$
(22)
$$G\,.\,\frac{{s\,\bar{v}(r,\,s)}}{s + \alpha (1 - s)} = \bar{u}(r,\,s) - \bar{v}(r,\,s)$$
(23)
$$\bar{u}(1,\,s) = 0,\,\bar{v}(1,\,s) = 0.$$
(24)

Substituting \(\bar{v}(r,\,s)\) from Eq. (23) into Eq. (23) and then taking finite Hankel transform with respect to the radial coordinate r along with the boundary condition in Eq. (24),

$$\begin{aligned} & \bar{u}_{H} (\varsigma_{n} ,s)\left( {\frac{s}{s + \alpha (1 - s)} - R\frac{s + \alpha (1 - s)}{s + sG + \alpha (1 - s)} + Ha^{2} + R + \frac{{\varsigma_{n}^{2} }}{\text{Re}}} \right) \\ & \quad = \left( {\frac{1}{s}A_{0} + \frac{{A_{1} s}}{{s^{2} + \omega^{2} }}} \right)\frac{{J_{1} (\varsigma_{n} )}}{{\varsigma_{n} }} + \frac{1}{s}K^{2} \frac{{\varsigma_{n} }}{{\varsigma_{n}^{2} + K^{2} }}J{}_{1}(\varsigma {}_{n}) \\ \end{aligned}$$
(25)

where \(\bar{u}_{H} (\varsigma_{n} ,\,s) = \int\limits_{0}^{1} {r\,u(r,\,s)\,J_{0} (\varsigma_{n} ,\,s)dr}\) is representing the finite Hankel transform of the velocity function \(\bar{u}(r,\,s) = LT\,[u(r,\,t)]\) and \(\varsigma_{n}\), n = 1, 2, … are the positive roots of the equation J0(x)= 0, here J0 is the Bessel function of order zero and belong to the first kind. By simplifying the coefficient of \(\bar{u}_{H} (\varsigma_{n} ,\,s)\) in Eq. (25), we have

$$\bar{u}_{H} (\varsigma_{n} ,\,s) = \frac{{s^{2} \,m_{2n} + s\,m_{3n} + m_{4n} }}{{s^{2} \,m_{5n} + s\,m_{6n} + \alpha^{2} }} \times \left\{ {\left( {\frac{1}{s}A_{0} + \frac{{A_{\,1} \,s}}{{s^{2} + \omega^{2} }}} \right)\,\frac{{J_{1} (\varsigma_{n} )}}{{\varsigma_{n} }} + \frac{1}{s}K^{2} \frac{{\varsigma_{n} }}{{\varsigma_{n}^{2} + K^{2} }}J{}_{1}(\varsigma {}_{n})} \right\}$$
(26)
$$\bar{u}_{H} (\varsigma_{n} ,\,s) = \left\{ {\frac{{m_{9n} }}{{s - m_{7n} }} + \frac{{m_{10n} }}{{s - m_{8n} }}} \right\} \times \left\{ {\left( {\frac{{A_{0} }}{s} + \frac{{A_{\,1} \,s}}{{s^{2} + \omega^{2} }}} \right)\,\frac{{J_{1} (\varsigma_{n} )}}{{\varsigma_{n} }} + \frac{{K^{2} }}{s}\frac{{\varsigma_{n} }}{{\varsigma_{n}^{2} + K^{2} }}J{}_{1}(\varsigma {}_{n})} \right\}$$
(27)

where the parameters introduced in Eqs. (26) and (27) for simplifying the coefficient of \(\bar{u}_{H} (\varsigma_{n} ,\,s)\) in Eq. (25) are as follows

$$\begin{aligned} & m_{1n} = Ha^{2} + R + \frac{{\varsigma_{n} }}{\text{Re}},\quad m_{2n} = 1 + G - \alpha - R - R\alpha^{2} + 2R\alpha + m_{1n} + \alpha^{2} m_{1n} - 2\alpha m_{1n} + Gm_{1n} - G\alpha m_{1n} , \\ & m_{3n} = \alpha + 2R\alpha^{2} - 2R\alpha - 2m_{1n} \alpha^{2} + 2\alpha m_{1n} + G\alpha m_{1n} ,\;m_{4n} = \alpha^{2} m_{1n} - R\alpha^{2} , \\ & m_{5n} = 1 + \alpha^{2} - 2\alpha + G - G\alpha ,\;\;m_{6n} = - 2\,\alpha^{2} + 2\alpha + G\alpha ,\;\;m_{7n} = \frac{{ - m_{3n} + \sqrt {m_{3n}^{2} - 4m_{2n} m_{4n} } }}{{2m_{2n} }}, \\ & m_{8n} = \frac{{ - m_{3n} - \sqrt {m_{3n}^{2} - 4m_{2n} m_{4n} } }}{{2\,m_{2n} }},\;\;m_{9n} = \frac{{m_{7n}^{2} \,m{}_{5n} + m_{7n} \,m_{6n} + \alpha^{2} }}{{m_{7n} - m_{8n} }}, \\ m_{10n} = \frac{{m_{8n}^{2} \,m{}_{5n} + m_{8n} \,m_{6n} + \alpha^{2} }}{{m_{8n} - m_{7n} }}. \\ \end{aligned}$$
(28)

Laplace transform of the image function \(\bar{u}_{H} (\varsigma_{n} ,\,s)\) discussed in Eq. (27) is obtained by using the Robotnov and Hartley’s functions

$$LT^{ - 1} \left[ {\frac{1}{{s^{a} + b}}} \right] = F_{a} ( - b,\,t) = \sum\limits_{n = 0}^{\infty } {\frac{{( - b)^{n} \,t^{(n + 1)a - 1} }}{\varGamma ((n + 1)a)}} ,\,a > 0$$
(29)
$$LT^{ - 1} \left[ {\frac{{s^{c} }}{{s^{a} + b}}} \right] = R_{a,\,c} ( - b,\,t) = \sum\limits_{n = 0}^{\infty } {\frac{{( - b)^{n} \,t^{(n + 1)a - 1 - c} }}{\varGamma ((n + 1)a - c)}} ,\,{\text{Real(}}a - c) > 0$$
(30)
$$u_{H} (\varsigma_{n} ,\,t) = \frac{{J_{1} }}{{\varsigma_{n} }}\left\{ {(e^{{m_{7n} t}} - 1)\left( {\frac{{\varsigma^{2} \,K^{2} \,m_{9n} }}{{m_{7n} (\varsigma^{2} + K^{2} )}} + \frac{{A_{0} \,m_{9n} }}{{m_{7n} }}} \right)} \right. + m_{9n} \,A_{1\,} e^{{m{}_{7n}\,t}} * \cos \,\omega \,t + m_{10n} \,A_{1\,} e^{{m{}_{8n}\,t}} *$$
$$\cos \,\omega \,t + \left. {(e^{{m_{8n} \,t}} - 1)\left( {\frac{{\varsigma^{2} \,K^{2\,} m_{10n} }}{{m_{8n} (\varsigma^{2} + K^{2} )}} + \frac{{A_{0} \,m_{10n} }}{{m_{8n} }}} \right)} \right\}.$$
(31)

2.4.1 Fluid velocity

Bio-fluid flow is obtained by taking the inverse Hankel transform of Eq. (32)

$$u(r,\,t) = 2\sum\limits_{n = 1}^{\infty } {\frac{{J_{0} (r\,\varsigma_{n} )}}{{\varsigma_{n} \,J_{1}^{2} (\varsigma_{n} )}}} \times u_{H} (\varsigma_{n} ,\,t)$$
(32)
$$\begin{aligned} & u(r,t) = 2\sum\limits_{n = 1}^{\infty } {\frac{{J_{0} (r\varsigma_{n} )}}{{\varsigma_{n} J_{1} (\varsigma_{n} )}}} \left\{ {(e^{{m_{7n} t}} - 1)\left( {\frac{{\varsigma_{n}^{2} \,K^{2} \,m_{9n} }}{{m_{7n} (\varsigma_{n}^{2} + K^{2} )}} + \frac{{A_{0} \,m_{9n} }}{{m_{7n} }}} \right)} \right. + m_{9n} A_{1\,} e^{{m{}_{7n}\,t}} * \cos \,\omega \,t \\ & \quad + m_{10n} A_{1\,} e^{{m{}_{8n}\,t}} * \cos \omega t + \left. {(e^{{m_{\,8n} \,t}} - 1)\left( {\frac{{\varsigma_{n}^{2} \,K^{2\,} m_{10n} }}{{m_{\,8n} (\varsigma_{n}^{2} + K^{2} )}} + \frac{{A_{0} \,m_{10n} }}{{m_{\,8n} }}} \right)} \right\},\quad {\text{for}}\,\;0 < \alpha \le 1. \\ \end{aligned}$$
(33)

2.4.2 Magnetic particles velocity

The velocity of the magnetic particles mixed with blood is obtained from Eq. (23)

$$\bar{v}(r,\,s) = \frac{s + \alpha - \alpha \,s}{s + G\,s + \alpha - \alpha \,s}\bar{u}(r,\,s)$$
(34)
$$v(r,t) = m_{12n} (1 - m_{11n} )\left\{ {u(r,t) * e^{{ - m_{12n} \,t}} } \right\},\quad {\text{for}}\;\;0 < \alpha \le 1.$$
(35)

In Eqs. (33) and (35) \(f * g\) represents convolution product of f and g. The parameters introduced in Eq. (12) are as follows

$$m_{11n} = \frac{1 - \alpha }{G - \alpha + 1},\,m_{12n} = \frac{\alpha }{G - \alpha + 1}.$$
(36)

Convolution product between f and g can be calculated as

$$\left( {f * g} \right)(t) = \int\limits_{0}^{t} {f(\tau )} (t - \tau )d\tau .$$
(37)

3 Numerical results and discussion

Our goal was to obtain the blood flow stream parameters from the new definition of Caputo–Fabrizio fractional derivative without singular kernel solved by using both Laplace and finite Hankel transforms. A few numerical modifications were performed using the Mathematica programming. The obtained mathematical forms of u(r, t) and v(r, t) as shown in Eqs. (33) and (35), respectively, were graphically plotted in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11.

Fig. 2
figure 2

Comparison between NFDt and UFDt at \(\alpha = 1\)

Full size image
Fig. 3
figure 3

Velocity profile for K = 0 and at different fractional parameters against r

Full size image
Fig. 4
figure 4

Velocity profile for K = 0.6 and at different fractional parameters against r

Full size image
Fig. 5
figure 5

Velocity profile for K = 1.2 and at different fractional parameters against r

Full size image
Fig. 6
figure 6

Velocity profile for Ha = 0 and at different fractional parameters against r

Full size image
Fig. 7
figure 7

Velocity profile for Ha = 1 and at different fractional parameters against r

Full size image
Fig. 8
figure 8

Velocity profile for Ha = 2 and at different fractional parameters against r

Full size image
Fig. 9
figure 9

Velocity profile for Re = 0.5 and at different fractional parameters against r

Full size image
Fig. 10
figure 10

Velocity profile for Re = 3 and at different fractional parameters against r

Full size image
Fig. 11
figure 11

Velocity profile for Re = 6 and at different fractional parameters against r

Full size image

It was intriguing to isolate the impact of fractional parameter on the velocities of blood and magnetic particles. The effects of electric field, magnetic field and Reynolds number were also presented. The positive root of the Bessel function “J0” was used. For all the graphical plots, the ordinary fluid model was compared with the fractional fluid model by taking \(\alpha \in \{ 0.4,\,0.6,\,0.8,\,1\}\). Other numerical values were \(A_{0} = 0.5,\,A_{1} = 0.6,\,G = 0.5,\,R = 0.5,\,\omega = {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}\;\;{\text{and}}\;\;t = 0.2.\)

Figure 2 compares the velocity profiles for the blood flow and magnetic particles predicted using UFDt and NFDt. The velocity predicted using the local model i.e.; \(\alpha = 1\) agreed well with those reported by Shah et al. (2016a) using theoretical and experimental methods.

The effects of electric field on the velocities of blood flow and magnetic particles at the core region predicted using the ordinary and fractional model were reported in Figs. 3, 4 and 5. At zero electric field, the blood flow velocity was higher than that of magnetic particles due to the drag force. Increasing external electric field would cause a more rapid development in the velocity of magnetic particles due to the collisions between charged particles. However, the fractional fluid velocity was lower than the ordinary fluid velocity.

Figures 6, 7 and 8 show the effect of external magnetic field on the velocity. Apparently, external magnetic field exhibited a significant impact on the velocity profiles predicted using fractional and local models. At high values Ha, the resistive force acting on the blood flow was more intense whereby the velocity of magnetic particles dropped significantly.

The effects of Reynolds number were shown in Figs. 9, 10 and 11. Here, the velocity amplitude in the core region increased at higher Re (Re > 1) and the velocity of magnetic particles was higher than the blood flow velocity. At low Re (Re < 1), the flow behavior of blood and magnetic particles were comparable.

4 Conclusion

The flow of blood mixed with iron-rich particles (magnetic particles) was subjected to the external electro-kinetic energy and magnetic field. The flow was modeled by using the new definition of Caputo–Fabrizio fractional order derivative without singular kernel in the time fractional model. The cylindrical flow domain was considered. The governing nonlinear time fractional order differential equations were solved analytically. The velocities of blood flow and magnetic particles were obtained by taking the Laplace transform with respect to t and finite Hankel transform with respect to r. Graphical plots were generated using the Mathematica software. At high Reynolds number and electro kinetic energy the velocity of magnetic particles was higher than the blood flow velocity. On the other hand, at low Reynolds number and high magnetic field strength, the velocity of magnetic particles dropped tremendously.