Dynamic pull-in of thermal cantilever nanoswitches subjected to dispersion and axial forces using nonlocal elasticity theory

Abstract

Precise analysis of nanoelectromechanical systems has an outstanding contribution in performance improvement of such systems. In this research, the dynamic instability of a cantilever nanobeam connected to a horizontal spring is analyzed. The system is subjected to thermal, electrostatic and molecular (Casimir and van der Waals) forces. By applying the Eringen’s nonlocal elasticity theory, the equilibrium equations are derived. The nonlinear dynamics governing equations of the actuated thermal switch are solved by reduced order method. Finally, the effects of several system parameters on the dynamic behavior of the nanocantilever are examined in detail. It is concluded that considering the nonlocal theory results in increasing the rigidity of cantilever nanobeams, unlike fixed-fixed nanobeams. Furthermore, the nonlocality affects more significantly by increasing the temperature of cantilevers; however, it is completely the opposite for double-clamped beams. The obtained results can be considered for modeling and analysis of several thermal micro and nanosystems.

1 Introduction

Ultra-small structures have attracted much attention due to their potentials for applications in micro/nanoelectromechanical systems (MEMS/NEMS) (Evoy et al. 1999; Lavrik et al. 2004; Craighead 2000; SoltanRezaee et al. 2016; SoltanRezaee and Ghazavi 2017; Farrokhabadi and Tavakolian 2017; Rahmanian et al. 2018; SoltanRezaee et al. 2018; SoltanRezaee and Afrashi 2016). These structures are constructed from a moveable elastic conductive micro/nanobeam suspended over a fixed conductive plane via a dielectric spacer in between (Batra et al. 2006). By applying DC potential difference between the components, the elastic beam deflects toward the ground electrode until at a critical voltage, it adheres the ground. This phenomenon is called the pull-in instability, which should be considered in design, modeling, and analysis of electrostatically actuated systems (Nathanson et al. 1967).

By reducing the dimensions of the beam to the micro/nanoscale, additional forces, including the Casimir or the van der Waals (vdW) force (Farrokhabadi et al. 2016; Tavakolian et al. 2017; Lifshitz 1965; Klimchitskaya et al. 2000), have to be considered. It should be mentioned that considering both the van der Waals and Casimir regimes are physically impossible in ultra-small structures. Beside the intermolecular attractions, miniature systems may be considered under the effects of temperature variations during their operation. Consequently, the thermal load affects significantly on the behavior of such systems, which should be modeled and analyzed (Nakhaie Jazar 2006; Zhu and Espinosa 2004; Rocha et al. 2004; Batra et al. 2008; Zhang et al. 2008).

In order to model and predict the electrostatically behavior of actuated miniature systems, many works have been conducted to survey the vibration response and dynamic pull-in of electrostatically actuated micro/nanobeams. The vibration response of narrow microbeams with electromechanical and electrostatic fringing fields due to both the finite width and thickness were studied by Batra et al. (2008). Chao et al. (2008) investigated the dynamic pull-in instability of microbridges subjected to suddenly applied DC voltage based on a continuous model. In another study, an analytical solution for dynamic response of electrostatically actuated microbeams using homotopy analysis method wad performed by Moghimi Zand and Ahmadian (2009). Chaterjee and Pohit (2009) investigated the static and dynamic pull-in of microcantilevers considering the nonlinearities caused by the large deflection of the cantilever. The nonlinear dynamic pull-in of electrostatically actuated microbeams under DC and AC excitation was studied by Alsaleem et al. (2010) numerically and experimentally. The impact of surface energy on the dynamic response as well as the critical voltage of electrostatic nanobeams is investigated by Fu and Zhang (2011) using the Gurtin and Murdoch’s theory of surface (GMT). Jia et al. (2011) investigated the pull-in instability under the combined electrostatic, intermolecular forces as well as axial residual stress for microbeams with four different boundary conditions (BCs) numerically. Caruntu et al. (2013) applied the reduced order method (ROM) to investigate the nonlinear dynamic response of cantilever MEMS resonators under soft AC voltage of frequency near half of the natural frequency. They concluded that the fringing field significantly affects the treatment of the MEMS resonators. Rahmanian et al. (2018) presented an investigation on nonlinear frequency-response behavior of a viscoelastic double-layred NEMS device. They reported on the effects of surface energy and Casimir regime on superharmonic resonance characteristics of the system. It was observed that, hardening and softening-type behaviors as well as bifurcation point's loci are remarkabely influenced by these parameters. An asymptotic procedure to anticipate the nonlinear vibrational response of classical microbeams subjected to an electric field was presented by Sedighi and Shirazi (2013). They studied the influences of fundamental parameters on the pull-in voltage and natural frequency of MEMS. Rahaeifard et al. (2014) applied the multiple scales method (MSM) for analytical and numerical analysis based on a hybrid finite element/finite difference method on microcantilever beams. The impact of vibrational amplitude on the dynamic pull-in instability and fundamental frequency of microbeam actuators was investigated by Sedighi (2014) based on the strain gradient elasticity theory (SGET). Alipour et al. (2015) studied the influences of intermolecular forces on the response of double clamped nanobeams analytically. To this end, they considered the effects of electrostatic actuation, intermolecular forces, mid-plane stretching, the fringing field as well as residual stress on the dynamic response of beam and solved the obtained governing equation of the system using the Galerkin method.

The literature review reveals that the classical continuum mechanics is not capable to deem the small size effects. The accomplished researches reveal that although the scale effect would not manifest itself for microstructures with length in the order of micrometers, it will be noticeable for the nanostructures response (Wang and Liew 2007). To overcome the problem, the nonlocal theory of Eringen was proposed, which considered the size effects by defining the stress at a reference structural point as a function of the strain field at each point in the bulk (Eringen 1972, 1983).

Applying the theory of the nonlocal elasticity, Wang and Liew (2007) proved that this theory could potentially play a significant role in nanotechnology applications. Reddy (2007) extended an analytical solution for bending, buckling and vibration of beams using Euler–Bernoulli, Timoshenko, Reddy and Levinson beam theories. Roque et al. (2011) applied a meshless method based on collocation with radial basis to study the static bending, buckling and free vibration behaviors of a Timoshenko nanobeam using nonlocal shear deformation beam theory. After that, Thai (2012) studied the bending, buckling and vibration behaviors of an Euler–Bernoulli nanobeam and analytically obtained the solutions of deflection, buckling load and natural frequency for a simply supported beam. In another research, Juntarasaid et al. (2012) developed a model for obtaining the bending deformation due to uniformly distributed load and buckling load of nanowires with various BCs, including the impacts of nonlocality and surface energy. They obtained analytical solutions for static displacement and buckling load of nanowires and compared their results by the finite element method (FEM). Then, Eltaher et al. (2013) obtained the equations of motion (EOM) of a nonlocal Euler–Bernoulli beam based on variational statement and solved the vibration problem of nanobeam using the FEM. Ghorbanpour Arani et al. (2013) investigated the pull-in instability using nonlocal piezoelasticity theory under electrostatic and vdW forces for two cases of cantilever as well as clamped-clamped actuators. The small-scale effects and nonlinear pull-in instability of a nanoswitch subjected to electrostatic and intermolecular forces at different BCs was studied by Mousavi et al. (2013) using DQM. Reddy and El-Borgi (2014) derived the governing equations of Timoshenko beams assuming the Eringen’s nonlocal differential model and modified von Karman nonlinear strains. They also developed the finite element models base on the resulting equations and presented the numerical results for diverse BCs by considering the impact of the nonlocal parameter on the deflection. Aftar that, the static pull-in instability of nanobeams subjected to the combined electrostatic and Casimir forces was studied by Ghorbanpour Arani et al. (2014) employing Euler–Bernoulli Beam and Eringen’s nonlocal elasticity effect. They obtained the nonlinear governing equation of structure applying virtual work principle and solved the obtained equations numerically. Recently, Tavakolian et al. (2017) applied Eringen’s nonlocal elasticity theory along with the nonlocal Euler–Bernoulli beam model to consider the small-scale effects on the static pull-in instability of clamped–clamped microswitches subjected to electrostatic and intermolecular attractions in the presence of thermal and residual stress effects. Moreover, Tavakolian and Farrokhabadi (2017) analyzed the effects of nonlinearity on the behavior of double-clamped nanobeams, where the nonlinear midplane stretching is important. On the other hand, they investigated the accuracy of responses by considering the time increment size and mode shapes number.

It can be concluded from the literature that the behavior of one-dimensional nanostructures has been frequently taken into account by using the classical continuum theories. However, to the best knowledge of the authors, no work has been reported on the thermal force impacts of cantilever nanobeams based on the nonlocal elasticity theory. Hence, investigating the pull-in phenomenon and dynamic behaviors of a novel adjustable cantilever nanoactuator are considered here in the presence of thermal as well as Casimir and vdW effects. In the research, the equations of motion for actuated nanostructure are derived via the nonlocal elasticity theory of Eringen. Finally, an approach of ROM is applied to discuss about the pull-in characteristics and dynamic responses of the cantilever nanosystems quantitatively and qualitatively.

2 Mathematical formulation

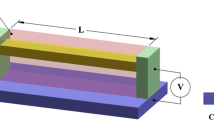
Figure 1 illustrates a cantilever actuator connected to a linear spring under an electric potential of V. The system is simulated via a very thin beam of length L, width b, and uniform thickness of h. The initial gap between the nanobeam and the substrate surface is d. The coordinate system is attached to the neutral axis at the left end of the nanobeam, where x and z refer to the horizontal and vertical coordinates, respectively.

Fig. 1

Schematic of the cantilever nanoactuator connected to a spring

2.1 Nonlocal theory

According to the nonlocal theory, the stress at a point depends not only on the strain of that point but also on the strains of all other points of the body. Neglecting the body force, the nonlocal stress tensor σ at any point x is given by (Eringen 1972)

$${{\upsigma }}_{\text{ij}} ({\text{x}}) = \int_{\text{V}} {{\text{K}}(| {{\text{x}} - {\text{x}^{\prime}}} |,\,{\text{e}}_{0} {\text{a}}/{{\upiota }})} {\text{C}}_{\text{ijkl}} \upvarepsilon_{\text{kl}} ({\text{x}^{\prime}}){\text{dV}}({\text{x}^{\prime}}),$$

(1)

where the terms of σ_ij, and ε_ij are the nonlocal stress and classical strain, respectively, and C_ijkl is the fourth-order elasticity tensors of classical isotropic elasticity. Furthermore, the kernel function of ${\text{K}}(| {{\text{x}} - {\text{x}^{\prime}}}|,{\text{e}}_{0} {\text{a}}/{{\upiota }})$, is the nonlocal modulus. The term $| {{\text{x}} - {\text{x}^{\prime}}} |$ represents the distance in the Euclidean form and e₀ is a constant for calibrating the model with experimental results and other validated models. The terms of a and ${{\upiota }}$ are the internal and external characteristics lengths of the nanostructure. It is worth noting that the term ${\text{e}}_{0} {\text{a}}$ is usually taken as a small-scale parameter. As mentioned, the nonlocal parameter depends on the boundary conditions, chirality, mode shapes, number of walls, and type of motion (Eringen 1983). There is no rigorous study made on estimating the value of the nonlocal parameter. It is suggested that the value of nonlocal parameter can be determined by experiment or by conducting a comparison of dispersion curves from the nonlocal continuum mechanics and molecular dynamics simulation (Arash and Wang 2012). Because of the complexity of using the relationship (1), a simplified constitutive equation in a differential form was proposed by Eringen (1972) as

$$\left( {1 - \, ({\text{e}}_{0} {\text{a}})^{2} {\nabla }^{2} } \right)\upsigma_{\text{ij}} = {\text{t}}_{\text{ij}} ,$$

(2)

where ∇² is the Laplacian operator.

2.2 Nonlocal equations of Euler–Bernoulli beam

For an isotropic material in a one-dimensional case considering the nonlocal parameter ${{\upmu }} = ({\text{e}}_{0} {\text{a}})^{2}$, the nonlocal constitutive relation in Eq. (2) takes the following forms

$${\upsigma}_{\text{x}}- {\upmu}\frac{{\partial^{2} {\upsigma}_{\text{x}} }}{{\partial {\text{x}}^{2} }} = {\text{E}\upvarepsilon}_{\text{x}} ,$$

(3)

where the terms ${{\upsigma }}_{\text{x}}$ and ${{\upvarepsilon }}_{\text{x}}$ are stress and strain components, respectively, and E is Young’s modulus of the beam. For an extracted infinitesimal element of a beam, the equilibrium requirements of forces in the vertical direction and the moments give

$$\begin{aligned} \frac{{\partial {\text{Q}}}}{{\partial {\text{x}}}} = \uprho {\text{A}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{t}}^{2} }} - {\text{q}}, \hfill \\ \frac{{\partial {\text{M}}}}{{\partial {\text{x}}}} = {\text{Q}} + {\text{N}}\frac{{\partial {\text{w}}}}{{\partial {\text{x}}}}, \hfill \\ \end{aligned}$$

(4)

where q is the distributed lateral load per unit length, A is the beam cross section, ρ is the beam density, Q is the transverse shear force, M is the bending moment resultant and N is the applied axial load.

Furthermore, the classical assumption for displacement field in EBT is of

$${\text{u}} = - {\text{z}}\frac{\partial{\text{w}}}{\partial {\text{x}}},$$

(5)

where u is the mid-plane displacements at z = 0 in the transverse direction. The only nonzero strain of an Euler–Bernoulli beam can be related to the deflection w by

$$\upvarepsilon_{\text{x}} = - {\text{z}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }},$$

(6)

Substituting Eq. (6) into the nonlocal constitutive Eq. (3) and considering the bending moment resultant (${\text{M}} = \int\limits{\upsigma_{\text{x}} {\text{zdA}}}$) result in

$${\text{M}} - \upmu \frac{{\partial^{2} {\text{M}}}}{{\partial {\text{x}}^{2} }} = - {\text{EI}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }},$$

(7)

where I is the second inertia moment of the beam cross-sectional area.

Employing the nonlocal constitutive stress–strain relation, the one-dimensional equation of motion of a nonlocal Euler–Bernoulli beam can be written as (Wang 2005)

$$\frac{{\partial^{2} }}{{\partial {\text{x}}^{2} }}\left( {{\text{EI}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }}} \right) + \uprho {\text{A}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{t}}^{2} }} - {\text{N}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }} - \upmu \frac{{\partial^{2} }}{{\partial {\text{x}}^{2} }}\left( {\uprho {\text{A}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{t}}^{2} }} - {\text{N}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }} - {\text{q}}} \right) = {\text{q}}.$$

(8)

Furthermore, the term of q can consist of different distributed loads including the electrostatic, Casimir as well as van der Waals loads.

2.3 Governing forces

The electrostatic force per length of a nanobeam can be given by (Huang et al. 2001)

$${\text{F}}_{\text{{e}}} = \left( {\frac{{\upvarepsilon_{0} \upnu^{2} {\text{b}}}}{{2({\text{d}} -{\text{w}})^{2} }} + \frac{{0.65\upvarepsilon_{0} \upnu^{2} }}{2({\text{d}} -{\text{w}})}} \right),$$

(9)

where $\varepsilon_{0} = 8.854 \times 10^{ - 12} \;{\text{C}}^{2} \,{\text{N}}^{ - 1} \,{\text{m}}^{ - 2}$ is the permittivity of vacuum, v is the applied voltage, b is the beam width and d is the initial gap. Furthermore, the van der Waals force per unit length of the beam is (Israelachvili 1992)

$${\text{F}}_{\text{vdW}} = \frac{\text{Ab}}{{6{{\uppi }}({\text{d}} - {\text{w}})^{3} }}.$$

(10)

where the parameter A = 2.96 × 10⁻¹⁹ J is the Hamaker constant. In addition, the Casimir force per unit length of the beam can be defined as (Lamoreaux 2005)

$${\text{F}}_{\text{c}} = \frac{{{{\uppi }}^{2} {\bar{\text{h}}\text{cb}}}}{{240({\text{d}} - {\text{w}})^{4} }},$$

(11)

where ${\bar{\text{h}}}$ = 1.055 × 10⁻³⁴ J s is the reduced Planck’s constant and c = 2.0998 × 10⁸ m s⁻¹ is the speed of light.

In addition, based on the theory of thermal elasticity mechanics, the thermal force due to the temperature change ${{\uptheta }} = {\text{T}} - {\text{T}}_{0}$ is given by (Kovalenko 1969)

$${\text{N}}_{\text{t}} = - \frac{{\text{EA}}\upalpha \uptheta }{(1 - 2\upnu )},$$

(12)

where ${{\upalpha }}$ denotes the coefficient of thermal expansion in the direction of the x axis, ${{\uptheta }}$ is the temperature change and $\nu$ is the Poisson’s ratio. According to the theory of elasticity, the axial force of the linear spring linked to the free end of cantilever beam is stated as

$${\text{N}}_{\text{sp}} = {\text{K}}_{\text{sp}} .$$

(13)

For the case where the thermal effect and connected spring are taken into account, the term N in Eq. (8) is replaced by summation of N_sp and N_t.

2.4 Dynamic governing equation

Replacing the mentioned distributed and axial loads of previous subsection into the governing Eq. (8) results

$$\begin{aligned} &\frac{{\partial^{2} }}{{\partial {\text{x}}^{2} }}\left( {{\text{EI}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }}} \right) + {{\uprho A}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{t}}^{2} }} + {\text{N}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }} - {{\upmu }}\frac{{\partial^{2} }}{{\partial x^{2} }}\left( {\uprho {\text{A}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{t}}^{2} }} + {\text{N}}\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }}} \right. \hfill \\ &\quad - \left( {\frac{{{{\upvarepsilon }}_{0} {{\upnu }}^{2} {\text{b}}}}{{2({\text{d}} - {\text{w}})^{2} }} + \frac{{0.65{{\upvarepsilon }}_{0} {{\upnu }}^{2} }}{{2({\text{d}} - {\text{w}})}}} \right) - \left. {\left\{ {\begin{array}{*{20}c} {\frac{\text{Aw}}{{6\uppi ({\text{d}} - {\text{w}})^{3} }}} \\ {\frac{{{{\uppi }}^{2} {\bar{\text{h}}\text{cb}}}}{{240({\text{d}} - {\text{w}})^{4} }}} \\ \end{array} } \right.} \right) = \left( {\frac{{{{\upvarepsilon }}_{0} {{\upnu }}^{2} {\text{b}}}}{{2({\text{d}} - {\text{w}})^{2} }} + \frac{{0.65{{\varepsilon }}_{0} {{\upnu }}^{2} }}{{2({\text{d}} - {\text{w}})}}} \right) - \left\{ {\begin{array}{*{20}c} {\frac{\text{Aw}}{{6\uppi ({\text{d}} - {\text{w}})^{3} }}} \\ {\frac{{\uppi^{2} {\bar{\text{h}}\text{cb}}}}{{240({\text{d}} - {\text{w}})^{4} }}} \\ \end{array} } \right.. \hfill \\ \end{aligned}$$

(14-a)

With the BCs for cantilever nanobeam as

$$\begin{aligned}& \left. {\text{w}} \right|_{{\text{x}} = 0} = 0;\quad \left. {\frac{\partial {\text{w}}}{\partial {\text{x}}}} \right|_{{\text{w}} = 0} = 0, \hfill \\ & \left. {\frac{{\partial^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }}} \right|_{{\text{w}} = {\text{L}}} = 0;\quad\left. {\frac{{\partial^{3} {\text{w}}}}{{\partial {\text{x}}^{3} }}} \right|_{{\text{x}} = {\text{L}}} = 0. \hfill \\ \end{aligned}$$

(14-b)

To facilitate theoretical formulations, the following dimensionless quantities are introduced as

$$\begin{aligned} {\text{W}} = \frac{{\text{w}}}{{\text{d}}}; \;\; {\text{X}} = \frac{{\text{x}}}{{\text{L}}}; \;\; {\text{V}} = \sqrt {\frac{{{{\upvarepsilon }}_{0} \upnu ^{2} {\text{L}}^{4} {\text{b}}}}{{2{\text{EId}}^{3} }}} ; \;\; {\text{T}} = {\text{t}}\sqrt {\frac{{{\text{EI}}}}{{\uprho {\text{AL}}^{4} }}} \hfill \\ \uplambda _{3} = \frac{{{\text{AwL}}^{4} }}{{6\uppi {\text{EId}}^{3} }}; \;\; \uplambda _{4} = \frac{{\uppi ^{2} {\text{L}}^{4} {{{\bar{\text{h}}}{\text{cw}}}}}}{{240{\text{EId}}^{5} }};\;\; {\text{N}}^{*} = \frac{{{\text{L}}^{2} }}{{{\text{EI}}}}\left( {\frac{{{\text{EA}}\upalpha \uptheta }}{{1 - 2\upnu }} + {\text{K}}_{{{\text{sp}}}} } \right). \hfill \\ \end{aligned}$$

(15)

Substituting Eqs. (15) into (14-a), one can get

$$\begin{aligned} &\frac{{\partial^{4} {\text{W}}}}{{\partial {\text{X}}^{4} }} + \frac{{\partial^{2} {\text{W}}}}{{\partial {\text{T}}^{2} }} + {\text{N}}^{*} \frac{{\partial^{2} {\text{W}}}}{{\partial {\text{X}}^{2} }} - \upmu \frac{{\partial^{2} }}{{\partial {\text{X}}^{2} }}\left( {{\text{N}}^{*} \frac{{\partial^{2} {\text{W}}}}{{\partial {\text{X}}^{2} }} + \frac{{\partial^{2} {\text{W}}}}{{\partial {\text{T}}^{2} }} - \frac{{\uplambda_{\text{n}} }}{{(1 - {\text{W}})^{\text{n}} }} - \frac{{{\text{V}}^{2} }}{{(1 - {\text{W}})^{2} }}\left(1 + \frac{{0.65{\text{b}}}}{\text{d}}(1 - {\text{W}})\right)} \right) \hfill \\ &= \frac{{\uplambda_{\text{n}} }}{{(1 - {\text{W}})^{\text{n}} }} + \frac{{{\text{V}}^{2} }}{{(1 - {\text{W}})^{2} }}\left( {1 + \frac{{0.65{\text{b}}}}{\text{d}}(1 - {\text{W)}}} \right). \hfill \\ \end{aligned}$$

(16-a)

with the boundary conditions of

$$\left. {\text{W}} \right|_{{{\text{X}} = 0}} = 0,\quad \left. {\frac{{\partial {\text{W}}}}{{\partial {\text{X}}}}} \right|_{{{\text{X}} = 0}} = 0,\quad \left. {\frac{{\partial^{2} {\text{W}}}}{{\partial {\text{X}}^{2} }}} \right|_{{{\text{X}} = 1}} = 0,\quad \left. {\frac{{\partial^{3} {\text{W}}}}{{\partial {\text{X}}^{3} }}} \right|_{{{\text{X}} = 1}} = 0,$$

(16-b)

it is worth noting that the parameter n is considered three and four for van der Waals and Casimir attraction effects, respectively.

In the next section, the reduced order model will be introduced to discretize Eq. (16-a) into a finite-degree of-freedom system consisting of ordinary differential equations in time.

3 Solution method

This is almost impossible to obtain an exact solution for Eq. (16-a), due to high nonlinearity of the problem. Hence, ROM is applied to obtain the response of system and pull-in parameters.

3.1 Reduce order method (ROM)

In this section, using the modal decomposition, the transient behavior study of the nanobeam in presence of electrostatic, intermolecular attraction, thermal force as well as size effects will be investigated. The method of Galerkin decomposition is employed to assess the system equations by a reduced order model composed of a finite number of discrete modal equations (Chaterjee and Pohit 2009). To this end, the solution of governing Eq. (16-a) is expressed as

$${\text{W}}({\text{X,T}}) = \sum\limits_{{\text{i}} = 1}^{{\text{M}}} {{\text{q}}_{\text{i}} } ({\text{X}})\cdot {\text{u}}_{{\text{i}}} ({\text{T}}),$$

(17)

where u_i(T) is an unknown time-dependent and q_i(X) is the ith linear undamped mode shape of the straight cantilever nanobeam. For normalizing the eigenvalue q_i(X), the relation $\int \limits_{0}^{1} {\text{q}}_{{\text{i}}} {\text{q}}_{{\text{j}}} = \updelta_{\text{ij}}$ is applied which is governed in

$${\text{q}}^{{\text{iv}}} = \upomega_{{\text{i}}}^{2} \cdot {\text{q}}.$$

(18)

Here the parameter $\upomega_{i}$ is the ith natural frequency of the nanobeam. It is worth noting that for the first eigenmode, q(x) can be expressed as

$${\text{q}}({\text{X}}) = \left[ {(\cosh\,\uplambda {\text{X}} - \cos\,\uplambda {\text{X}}) - \frac{\cosh\,\uplambda + \cos \,\uplambda }{\sinh \,\uplambda + \sin \,\uplambda }(\sinh \,\uplambda {\text{X}} - \sin \,\uplambda {\text{X}})} \right],$$

(19)

where ${{\uplambda }} = 1.875$ is the root of characteristic equation. The procedure for solving Eq. (16-a) by neglecting the intermolecular forces, involves the multiplying the equation by ${\text{q}}_{\text{n}} (1 - {\text{W}})^{4}$ and using Eq. (18) for eliminating ${\text{q}}^{{\text{iv}}}$ and integrating the outcome from X = 0–1. The coupled nonlinear ODEs of the mentioned system can be written as

$$\begin{aligned} &{\text{u}}^{\prime\prime}_{\text{n}} + \upomega _{\text{n}}^{2} {\text{u}}_{\text{n}} - 4(1 + \upmu {\text{N}}^{*} )\sum\limits_{{{\text{i,j}} = 1}}^{{\text{M}}} \upomega_{\text{i}}^{2} {\text{u}}_{{\text{i}}} {\text{u}}_{\text{j}} \int_{0}^{1} {\text{q}}_{{\text{i}} } {\text{q}}_{{\text{j}}} {\rm{q}}_{{\text{n}}} {\rm{dx}} + 6(1 + \upmu {\text{N}}^{*} )\sum\limits_{{{\text{i,j,k}} = 1}}^{{\text{M}}} \upomega _{\text{i}}^{2} {\text{u}}_{{\text{i}} } {\rm{u}}_{{\text{j}}} {\rm{u}}_{\text{k}} \int_{0}^{1} {\text{q}}_{{\text{i}} } {\rm{q}}_{{\text{j}}} {\rm{q}}_{{\text{k}}} {\rm{q}}_{{\text{n}}} {\rm{dx}} \hfill \\ &\quad - 4(1 + \upmu {\text{N}}^{*} )\sum\limits_{{{\text{i,j,k,l}} = 1}}^{{\text{M}}} {\upomega _{\text{i}}^{2} {\text{u}}_{\text{i}} } {\rm{u}}_{{\text{j}}} {\text{u}}_{{\text{k}}} {\rm{u}}_{\text{l}} \int_{0}^{1} {\text{q}}_{{\text{i}} } {\rm{q}}_{{\text{j}}} {\rm{q}}_{{\text{k}}} {\text{q}}_{{\text{l}}} {\rm{q}}_{{\text{n}}} {\text{dx}} + (1 + \upmu {\text{N}}^{*} )\sum\limits_{{{\text{i,j,k,l,m}} = 1}}^{{\text{M}}} {\upomega _{\text{i}}^{2} {\text{u}}_{\text{i}} } {\rm{u}}_{{\text{j}}} {\text{u}}_{{\text{k}}} {\text{u}}_{{\text{l}}} {\rm{u}}_{\text{m}} \int_{0}^{1} {\text{q}}_{{\text{i}} } {\text{q}}_{{\text{j}}} {\rm{q}}_{{\text{k}}} {\text{q}}_{{\text{l}}} {\rm{q}}_{{\text{m}}} {\text{q}}_{{\text{n}}} {\rm{dx}} \hfill \\ &\quad - 4\sum\limits_{{{\text{i,j}} = 1}}^{{\text{M}}} {\rm{u}}^{\prime\prime}_{{\text{i}} } {\text{u}}_{\text{j}} \int_{0}^{1} {\text{q}}_{{\text{i}} } {\rm{q}}_{{\text{j}}} {\text{q}}_{{\text{n}}} {\rm{dx}} + 6\sum\limits_{{{\text{i,j,k}} = 1}}^{{\text{M}}} {\rm{u}}^{\prime\prime}_{{\text{i}} } {\rm{u}}_{{\text{j}}} {\rm{u}}_{\text{k}} \int_{0}^{1} {\text{q}}_{{\text{i}} } {\rm{q}}_{{\text{j}}} {\text{q}}_{{\text{k}}} {\text{q}}_{{\text{n}}} {\rm{dx}} - 4\sum\limits_{{{\text{i,j,k,l}} = 1}}^{{\text{M}}} {\rm{u}}^{\prime\prime}_{{\text{i}} } {\text{u}}_{{\text{j}}} {\rm{u}}_{{\text{k}}} {\text{u}}_{\text{l}} \int_{0}^{1} {\text{q}}_{{\text{i}} } {\rm{q}}_{{\text{j}}} {\text{q}}_{{\text{k}}} {\rm{q}}_{{\text{l}}} {\text{q}}_{{\text{n}}} {\rm{dx}} \hfill \\ &\quad + \sum\limits_{{{\text{i,j,k,l,m}} = 1}}^{{\text{M}}} {\rm{u}}^{\prime\prime}_{{\text{i}} } {\rm{u}}_{{\text{j}}} {\rm{u}}_{{\text{k}}} {\rm{u}}_{{\text{l}}} {\rm{u}}_{\text{m}} \int_{0}^{1} {\text{q}}_{{\rm{i}} } {\text{q}}_{{\rm{j}}} {\text{q}}_{{\rm{k}}} {\text{q}}_{{\text{l}}} {\rm{q}}_{{\text{m}}} {\rm{q}}_{{\text{n}}} {\rm{dx}} - \upmu \sum\limits_{{{\text{i}} = 1}}^{{\text{M}}} {\text{u}}^{\prime\prime}_{{\text{i}} } \int_{0}^{1} {\ddot{\text{q}}_{\text{i}} } {\rm{q}}_{{\text{n}}} {\rm{dx}} + 4\upmu \sum\limits_{{{\text{i,j}} = 1}}^{{\text{M}}} {\rm{u}}^{\prime\prime}_{{\text{i}} } {\rm{u}}_{\text{j}} \int_{0}^{1} {\ddot{\text{q}}_{{\text{i}}} {\rm{q}}_{{\text{j}}} {\rm{q}}_{{\text{n}}} } {\rm{dx}} \hfill \\ &\quad - 6\upmu \sum\limits_{{{\text{i,j,k}} = 1}}^{{\text{M}}} {{\rm{u}}^{\prime\prime}_{{\text{i}}} } {\rm{u}}_{{\text{j}}} {\rm{u}}_{\text{k}} \int_{0}^{1} {\ddot{\text{q}}_{{\text{i}}} {\rm{q}}_{{\text{j}}} {\text{q}}_{{\text{k}}} {\rm{q}}_{{\text{n}}} } {\text{dx}} + 4\upmu \sum\limits_{{{\text{i,j,k,l}} = 1}}^{{\text{M}}} {\text{u}}^{\prime\prime}_{{\text{i}} } {\rm{u}}_{{\text{j}}} {\rm{u}}_{{\text{k}}} {\rm{u}}_{\text{l}} \int_{0}^{1} {\ddot{\text{q}}_{{\text{i}}} {\rm{q}}_{{\text{j}}} {\rm{q}}_{{\text{k}}} {\rm{q}}_{{\text{l}}} {\rm{q}}_{{\text{n}}} } {\rm{dx}} \hfill \\ &\quad - \upmu \sum\limits_{{{\text{i,j,k,l,m}} = 1}}^{{\text{M}}} {{\rm{u}}^{\prime\prime}_{{\text{i}}} } {\rm{u}}_{{\text{j}}} {\text{u}}_{{\text{k}}} {\text{u}}_{{\text{l}}} {\rm{u}}_{\text{m}} \int_{0}^{1} {\ddot{\text{q}}_{{\text{i}}} {\text{q}}_{{\text{j}}} {\rm{q}}_{{\text{k}}} {\text{q}}_{{\text{l}}} {\rm{q}}_{{\text{m}}} {\text{q}}_{{\text{n}}} } {\text{dx}} + 6\upmu {\text{V}}^{2} \sum\limits_{{{\text{i,j}} = 1}}^{{\text{M}}} {\text{u}}_{{\text{i}} } {\rm{u}}_{\text{j}} \int_{0}^{1} {\dot{\text{q}}_{\text{i}} \dot{\text{q}}_{\text{j}} } {\text{q}}_{{\text{n}}} {\rm{dx}} - {\text{N}}^{*} \sum\limits_{{{\text{i,j,k}} = 1}}^{{\text{M}}} {{\text{u}}_{{\text{i}}} {\rm{u}}_{{\text{j}}} {\text{u}}_{\text{k}} } \int_{0}^{1} {\ddot{\text{q}}_{{\text{i}}} {\text{q}}_{{\text{j}}} {\rm{q}}_{{\text{k}}} {\text{q}}_{{\text{n}}} } {\rm{dx}} \hfill \\ &\quad + (2\upmu {\text{V}}^{2} - {\text{N}}^{*} )\sum\limits_{{{\text{i}} = 1}}^{{\text{M}}} {\text{u}}_{{\text{i}} } \int_{0}^{1} {\ddot{\text{q}}_{{\text{i}}} {\rm{q}}_{\text{n}} } {\text{dx}} - (2\upmu {\text{V}}^{2} - 2{\text{N}}^{*} )\sum\limits_{{{\text{i,j}} = 1}}^{{\text{M}}} {\text{u}}_{{\text{i}} } {\rm{u}}_{\text{j}} \int_{0}^{1} {\ddot{\text{q}}_{{\text{i}}} {\text{q}}_{{\text{j}}} {\text{q}}_{{\text{n}}} } {\text{dx}} + 2\upmu {\text{V}}^{2} \frac{{0.65{\text{d}}}}{\rm{b}}\sum\limits_{{{\text{i,j}} = 1}}^{{\text{M}}} {\text{u}}_{{\text{i}} } {\text{u}}_{\text{j}} \int_{0}^{1} {\dot{\text{q}}_{\text{i}} \dot{\text{q}}_{{\text{j}}} } {\text{q}}_{{\text{n}}} {\text{dx}} \hfill \\ &\quad - 2\upmu {\text{V}}^{2} \frac{{0.65{\text{d}}}}{\rm{b}}\sum\limits_{{{\text{i,j,k}} = 1}}^{{\text{M}}} {\text{u}}_{{\text{i}} } {\text{u}}_{{\text{j}}} {\text{u}}_{\text{k}} \int_{0}^{1} {\dot{\text{q}}_{\text{i}} \dot{\text{q}}_{{\text{j}}} {\text{q}}_{{\text{k}}} } {\text{dx}} + \upmu {\text{V}}^{2} \frac{{0.65{\text{d}}}}{\rm{b}}\sum\limits_{{{\text{i}} = 1}}^{{\text{M}}} {\text{u}}_{{\text{i}} } \int_{0}^{1} {\ddot{\text{q}}_{{\text{i}}} {\text{q}}_{{\text{n}}} } {\text{dx}} - 2\upmu {\text{V}}^{2} \frac{{0.65{\text{d}}}}{\rm{b}}\sum\limits_{{{\text{i,j}} = 1}}^{{\text{M}}} {\text{u}}_{{\text{i}} } {\text{u}}_{{\text{j}}} \int_{0}^{1} {\ddot{\text{q}}_{{\text{i}}}{\rm{q}}_{{\text{j}}} {\text{q}}_{{\text{n}}} } {\text{dx}} \hfill \\ &\quad + \upmu {\text{V}}^{2} \frac{{0.65{\text{d}}}}{\text{b}}\sum\limits_{{{\text{i,j,k}} = 1}}^{{\text{M}}} {\text{u}}_{{\text{i}} } {\rm{u}}_{{\text{j}}} {\rm{u}}_{\text{k}} \int_{0}^{1} {\ddot{\text{q}}_{{\text{i}}} {\rm{q}}_{{\text{j}}} {\rm{q}}_{{\text{k}}} {\text{q}}_{{\text{n}}} } {\rm{dx}} - {\text{V}}^{2} \left(1 + \frac{{0.65{\text{d}}}}{\rm{b}}\right)\int_{0}^{1} {\text{q}}_{{\text{n}} } {\rm{dx}} + {\text{V}}^{2} \left(2 + 3\frac{{0.65{\text{d}}}}{\rm{b}}\right)\sum\limits_{{{\text{i}} = 1}}^{{\text{M}}} {\rm{u}}_{{\text{i}} } \int_{0}^{1} {{\text{q}}_{{\text{i}}} {\rm{q}}_{{\text{n}}} } {\rm{dx}} \hfill \\ &\quad - {\text{V}}^{2} \left(1 + 3\frac{{0.65{\text{d}}}}{\rm{b}}\right)\sum\limits_{{{\text{i,j}} = 1}}^{{\text{M}}} {\text{u}}_{{\text{i}} } {\text{u}}_{{\text{j}}} \int_{0}^{1} {{\text{q}}_{{\text{i}}} {\text{q}}_{{\text{j}}} {\text{q}}_{{\text{n}}} } {\text{dx}} + \frac{{0.65{\text{d}}}}{\rm{b}}{\text{V}}^{2} \sum\limits_{{{\text{i,j,k}} = 1}}^{{\text{M}}} {\text{u}}_{{\text{i}} } {\rm{u}}_{{\text{j}}} {\text{u}}_{\text{k}} \int_{0}^{1} {{\text{q}}_{{\text{i}}} {\rm{q}}_{{\text{j}}} {\rm{q}}_{{\text{k}}} {\rm{q}}_{{\text{n}}} } {\text{dx}} = 0, \quad {\text{n}} = 1,2,\ldots {\text{M}}. \hfill \\ \end{aligned}$$

(20)

Equation (20) is constituted a non-explicit system of second-order nonlinear ordinary-differential equations. To calculate the solutions of these equations, one can use an implicit scheme. In the present study, the authors used the Runge–Kutta method.

It is worth to mention that, solution of Eq. (16-a) by considering the effects of intermolecular forces can be obtained by multiplying the governing equation into ${\text{q}}_{\text{n}} (1 - {\text{W}})^{5}$ and ${\text{q}}_{\text{n}} (1 - {\text{W}})^{6}$ for the van der Waals and Casimir forces, respectively. The expression of obtained nonlinear ODE for vdW and Casimir attractions is presented in Appendix.

4 Results and discussion

In order to verify the results of the numerical simulation, the time history of vibrating a cantilever nanobeam with 300 µm long, 20 µm wide, 2 µm thickness, initial gap d = 2 µm and effective Young’s modulus E = 183.4 GPa in the absence of intermolecular forces and size effects is compared with the results obtained by Rahaeifard et al. (2014) for voltage parameter of V = 0.4 and V = 0.8. It is worth noting that Rahaeifard et al. (2014) obtained their results using the hybrid finite difference method. As it can be seen in Fig. 2, the results of present study exhibit an excellent agreement with the results obtained by Rahaeifard et al. (2014), which have been obtained for the width to the gap ratio of b/d = 5.

Fig. 2

Comparison of the dynamic response of the nanobeam using present study and reported results in Rahaeifard et al. (2014)

In order to investigate the accuracy of the size-dependent model, the impacts of nonlocality on the tip deflection of the cantilever beam are determined and compared with the literature (Ahmadian et al. 2011) by ignoring the molecular effects (Fig. 3). It should be mentioned that, the beam length is L = 20 nm. It is concluded that, acquired results are in a good agreement with those reported by Ahmadian et al. (2011), which have been obtained by DQM method.

Fig. 3

Verification of the presented results by the literature (Ahmadian et al. 2011)

In the following, the results are presented for nanocantilevers, which are made of silicon material with E = 169 GPa and ν = 0.239. The ratio of the width to the gap between the beam and substrate is considered to be b/d = 5, as many previous works (Rahaeifard et al. 2014) and the beam length and width are 20 and 2.5 nm, respectively. In addition, the stiffness of the connected linear spring is equal to 1.1 N/m. Note that the non-dimensional Casimir and van der Waals parameters are assumed to be λ₃ = λ₄ = 0.3 (Sedighi et al. 2014; Tavakolian and Farrokhabadi 2017). The set of nonlinear ODEs is numerically solved for zero initial conditions to obtain the transient response of miniature systems.

The variation of non-dimensional amplitude related to voltage parameter in the presence of electrostatic force in addition to the Casimir attraction (${\uplambda}_{3} = 0.3$) and wan der Waals force (${\uplambda}_{4} = 0.3$) has been illustrated in Fig. 4.

Fig. 4

Variation of the non-dimensional tip deflection with voltage for cantilever beam: a Casimir attraction, b van der Waals force

It can be found that by considering the molecular forces, the pull-in voltage is decreased dramatically. Furthermore, the Casimir attraction accelerates the instability of the nanostructure (V_p = 0.83) in comparison with the van der Waals attraction (V_p = 0.93). The quantitative estimation of the dynamic pull-in parameters can be made from the corresponding phase plots as shown in Fig. 5 for both the Casimir and van der Waals regimes.

Fig. 5

Phase plot of the cantilever nanobeam excited by different applied voltages less and greater than pull-in voltage: a Casimir attraction, b van der Waals force

According to the obtained results, at voltages lower than some critical value, the beam performs periodic motion around an equilibrium position. On this situation, an increase in the applied voltage leads to increase in the amplitude of vibrations and decrease in frequency.

In the following, the impacts of temperature rise and nonlocal parameter on the pull-in behavior of nanosystems are taken into account. In Fig. 6, the impacts of size factor on the deflection of nanocantilevers under the electrostatic force only are studied. In addition, the impacts of Casimir and van der Waals attractions on the system response are examined in detail. It should be mentioned that the non-dimensional voltage parameter has been considered V = 0.8. The acquired results show that enhancing the size factor causes a hardening behavior in cantilever nanobeams, which leads to a dramatic increase in the fundamental frequency of the nanostructure, unlike double-clamped nanobeams (Tavakolian and Farrokhabadi 2017). Furthermore, in Fig. 6b, c depict that in the presence of intermolecular and electrostatic attractions, by increasing the nonlocal effects, the maximum deflection of nanobeam is decreased gradually, unlike double-clamped nanobeams (Tavakolian and Farrokhabadi 2017). It is worth noting that, between two molecular forces, Casimir has more significant impacts on the system behavior at the same nonlocal parameter.

Fig. 6

Effect of nonlocal parameter variation on the time history of nanostructure in the presence of a electrostatic, b electrostatic and Casimir attractions and c electrostatic and van der Waals attractions

Here, the impacts of size factor on the pull-in parameters (critical applied voltage and tip deflection) are displayed in Fig. 7. As illustrated for the cantilever nanobeam, while the presences of electrostatic force and molecular attractions make the structure to behave more soften, the nonlocal effect increases the rigidity of the structure, unlike the clamped-clamped nanobeam (Tavakolian and Farrokhabadi 2017).

Fig. 7

Variation of the non-dimensional tip deflection of the beam with voltage change for different nonlocal parameter: a electrostatic, b electrostatic and Casimir attractions and c electrostatic and van der Waals attractions

Figure 8 shows the impacts of thermal load on the dynamic behavior of the nanocantilever under both electrostatic and molecular forces. Note that the thermal expansion of material is considered ${{\upalpha }} = - \,2.6 \times 10^{ - 6}$. It can be found that increasing the system temperature makes the beam behave more rigid, which increases the critical voltage. As another important point, the freestanding phenomenon due to molecular attractions is obvious in cantilever nanobeams, unlike fixed-fixed nanostructures (Tavakolian and Farrokhabadi 2017).

Fig. 8

Variation of the non-dimensional tip deflection of the beam with voltage change for different temperature: a electrostatic, b electrostatic and Casimir attractions and c electrostatic and van der Waals attractions

Ultimately, the impacts of nonlocality on the critical voltage of actuated nanobeams subjected to molecular forces at different temperatures are shown in Fig. 9. It can be seen that both Casimir and van der Waals regimes decrease the pull-in voltage of the nanosystem, as expected. However, the increase in temperature and size factor causes the hardening behavior of the structure and postpones the instability. Moreover, by increasing the temperature, nonlocality plays a more significant role in cantilever nanobeams, which results in the divergence of pull-in voltages, unlike double-clamped ones (Tavakolian and Farrokhabadi 2017).

Fig. 9

Variation of the non-dimensional pull-in voltage of the cantilever beam with temperature change for different nonlocal parameter: (a) electrostatic, (b) electrostatic and Casimir attractions and (c) electrostatic and van der Waals attractions

5 Conclusion

In this research, the dynamic pull-in behavior of cantilever nanobeams connected to a horizontal spring was investigated according to the nonlocal theory. The presented novel model is useful for determining the pull-in parameters of several types of adjustable nanosystems under the molecular and thermal forces. Here, the nonlinear PDE with variable coefficients were solved numerically by means of the ROM and the results were verified via available numerical results. Furthermore, the impacts of numerous systems parameters on the dynamic responses of nanostructures are analyzed in detail. On the other hand, the effects of the freestanding phenomenon are illustrated in some numerical cases for both the Casimir and vdW attractions. The results demonstrated that considering the intermolecular attractions decreases the beam stability and makes the cantilever nanosystems behave more soften, unlike the temperature increase. Moreover, considering the nonlocal elasticity theory results in increasing the rigidity of cantilever nanobeams, unlike fixed-fixed ones. Finally, the effects of nonlocality become more obvious by increasing the temperature of cantilevers; however, for double-clamped beams is the opposite. The acquired results can be used to design and analysis of different nanostructures in thermal environments.

Appendix 1

1.1 The governing equation of electrostatic and van der Waals attractions

$$\begin{aligned} &{\text{u}}^{\prime\prime}_{\text{n}} + \upomega _{\text{n}}^{2} {\text{u}}_{\text{n}} - 5(1 + \upmu {\text{N}}^{*} )\,\upomega _{1}^{2} {\text{u}}_{1}^{2} \int_{0}^{1} {\text{q}}_{1}^{3} {\text{dx}} + 10(1 + \upmu {\text{N}}^{*} )\upomega _{1}^{2} {\text{u}}_{1}^{3} \int_{0}^{1} {\text{q}}_{1}^{4} {\text{dx}} - 10(1 + \upmu {\text{N}}^{*} )\upomega _{1}^{2} {\text{u}}_{1}^{4} \int_{0}^{1} {\text{q}}_{1}^{5} {\text{dx}} \hfill \\ &\quad + 5(1 + \upmu {\text{N}}^{*} )\upomega _{1}^{2} {\text{u}}_{1}^{5} \int_{0}^{1} {\text{q}}_{1}^{6} {\text{dx}} - (1 + \upmu {\text{N}}^{*} )\upomega _{1}^{2} {\text{u}}_{1}^{6} \int_{0}^{1} {{\text{q}}_{1}^{7} } {\text{dx}} - 5{\text{u}}^{\prime\prime}_{1} {\text{u}}_{1} \int_{0}^{1} {{\text{q}}_{1}^{3} } {\text{dx}} + 10{\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{2} \int_{0}^{1} {\text{q}}_{1}^{4} {\text{dx}} \hfill \\ &\quad - 10{\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{3} \int_{0}^{1} {{\text{q}}_{1}^{5} } {\text{dx}} + 5{\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{4} \int_{0}^{1} {\text{q}}_{1}^{6} {\text{dx}} - {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{5} \int_{0}^{1} {\text{q}}_{1}^{7} {\text{dx}} - \upmu {\text{u}}^{\prime\prime}_{1} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1} } {\text{dx}} + 5\upmu {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{{}} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{2} } {\text{dx}} \hfill \\ &\quad - 10\upmu {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{2} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{3} } {\text{dx}} + 10\upmu {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{3} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{4} } {\text{dx}} - 5\upmu {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{4} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{5} } {\text{dx}} + \upmu {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{5} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{6} } {\text{dx}} \hfill \\ &\quad + \upmu {\text{V}}^{2} \left(6 + 2\frac{{0.65{\text{d}}}}{\text{b}}\right){\text{u}}_{1}^{2} \int_{0}^{1} {\dot{{\text{q}}}_{1}^{2} {\text{q}}_{1} } {\text{dx}} - \upmu {\text{V}}^{2} \left(6 + 4\frac{{0.65{\text{d}}}}{\text{b}}\right){\text{u}}_{1}^{3} \int_{0}^{1} {\dot{{\text{q}}}_{1}^{2} {\text{q}}_{1}^{2} } {\text{dx}} + \left[ {\upmu {\text{V}}^{2} \left(2 + \frac{{0.65{\text{d}}}}{\rm{b}}\right) - {\text{N}}^{*} } \right]{\text{u}}_{1}^{{}} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{2} } {\text{dx}} \hfill \\ &\quad + \left[ {\upmu {\text{V}}^{2} \left(4 + 3\frac{{0.65{\text{d}}}}{\rm{b}}\right) - 5{\text{N}}^{*} } \right]{\text{u}}_{1}^{2} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{2} } {\text{dx}} + \left[ {\upmu {\text{V}}^{2} \left(2 + 3\frac{{0.65{\text{d}}}}{\rm{b}}\right) - 10{\text{N}}^{*} } \right]{\text{u}}_{1}^{3} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{3} } {\text{dx}} \hfill \\ &\quad + 2\upmu {\text{V}}^{2} \frac{{0.65{\text{d}}}}{\rm{b}}{\text{u}}_{1}^{4} \int_{0}^{1} {\dot{{\text{q}}}_{1}^{2} {\text{q}}_{1}^{3} } {\text{dx}} - \left[ {\upmu {\text{V}}^{2} \frac{{0.65{\text{d}}}}{\rm{b}} - 10{\text{N}}^{*} } \right]{\text{u}}_{1}^{4} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{4} } {\text{dx}} + 5{\text{N}}^{*} {\text{u}}_{1}^{5} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{5} } {\text{dx}} + {\text{N}}^{*} {\text{u}}_{1}^{6} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{6} } {\text{dx}} \hfill \\ &\quad + 12\upmu \uplambda _{3} {\text{u}}_{1}^{2} \int_{0}^{1} {\dot{{\text{q}}}_{1}^{2} {\text{q}}_{1}^{{}} } {\text{dx}} + 3\upmu \uplambda _{3} {\text{u}}_{1}^{{}} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{{}} } {\text{dx}} - 3\upmu \uplambda _{3} {\text{u}}_{1}^{2} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{2} } {\text{dx}} - {\text{V}}^{2} \left(1 + \frac{{0.65{\text{d}}}}{\rm{b}}\right)\int_{0}^{1} {{\text{q}}_{1}^{{}} } {\text{dx}} \hfill \\ &\quad + {\text{V}}^{2} \left(3 + 4\frac{{0.65{\text{d}}}}{\rm{b}}\right){\text{u}}_{1}^{{}} \int_{0}^{1} {{\text{q}}_{1}^{2} } {\text{dx}} - {\text{V}}^{2} \left(3 + 6\frac{{0.65{\text{d}}}}{\rm{b}}\right){\text{u}}_{1}^{2} \int_{0}^{1} {{\text{q}}_{1}^{3} } {\text{dx}} + {\text{V}}^{2} \left(1 + 4\frac{{0.65{\text{d}}}}{\rm{b}}\right){\text{u}}_{1}^{3} \int_{0}^{1} {{\text{q}}_{1}^{4} } {\text{dx}} \hfill \\ &\quad - {\text{V}}^{2} \frac{{0.65{\text{d}}}}{\rm{b}}{\text{u}}_{1}^{4} \int_{0}^{1} {{\text{q}}_{1}^{5} } {\text{dx}} - \uplambda _{3} \int_{0}^{1} {{\text{q}}_{1}^{{}} } {\text{dx}} + 2\uplambda _{3} {\text{u}}_{1}^{{}} \int_{0}^{1} {{\text{q}}_{1}^{2} } {\text{dx}} - \uplambda _{3} {\text{u}}_{1}^{2} \int_{0}^{1} {{\text{q}}_{1}^{3} } {\text{dx}} = 0. \hfill \\ \end{aligned}$$

(21)

1.2 The governing equation of electrostatic and Casimir attractions

$$\begin{aligned} &{\text{u}}^{\prime\prime}_{\text{n}} + \upomega_{\text{n}}^{2} {\text{u}}_{\text{n}} - 6(1 + \upmu {\text{N}}^{*} )\,\upomega_{1}^{2} {\text{u}}_{1}^{2} \int_{0}^{1} {{\text{q}}_{1}^{3} } {\text{dx}} + 15(1 + \upmu {\text{N}}^{*} )\upomega_{1}^{2} {\text{u}}_{1}^{3} \int_{0}^{1} {{\text{q}}_{1}^{4} } {\text{dx}} - 20(1 + \upmu {\text{N}}^{*} )\upomega_{1}^{2} {\text{u}}_{1}^{4} \int_{0}^{1} {{\text{q}}_{1}^{5} } {\text{dx}} \hfill \\ &\quad + 15(1 + \upmu {\text{N}}^{*} )\upomega_{1}^{2} {\text{u}}_{1}^{5} \int_{0}^{1} {{\text{q}}_{1}^{6} } {\text{dx}} - 6(1 + \upmu {\text{N}}^{*} )\upomega_{1}^{2} {\text{u}}_{1}^{6} \int_{0}^{1} {{\text{q}}_{1}^{7} } {\text{dx}} + (1 + \upmu {\text{N}}^{*} \upomega_{1}^{2} {\text{u}}_{1}^{7} \int_{0}^{1} {{\text{q}}_{1}^{8} } {\text{dx}} \hfill \\ &\quad- 6{\text{u}}^{\prime\prime}_{1} {\text{u}}_{1} \int_{0}^{1} {{\text{q}}_{1}^{3} } {\text{dx}} + 15{\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{2} \int_{0}^{1} {{\text{q}}_{1}^{4} } {\text{dx}} - 20{\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{3} \int_{0}^{1} {{\text{q}}_{1}^{5} } {\text{dx}} + 15{\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{4} \int_{0}^{1} {{\text{q}}_{1}^{6} } {\text{dx}} - 6{\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{5} \int_{0}^{1} {{\text{q}}_{1}^{7} } {\text{dx}} \hfill \\&\quad + {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{6} \int_{0}^{1} {{\text{q}}_{1}^{8} } {\text{dx}} - \upmu {\text{u}}^{\prime\prime}_{1} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1} } {\text{dx}} + 6\upmu {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{2} } {\text{dx}} - 15\upmu {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{2} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{3} } {\text{dx}} + 20\upmu {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{3} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{4} } {\text{dx}} \hfill \\&\quad - 15\upmu {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{4} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{5} } {\text{dx}} + 6\upmu {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{5} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{6} } {\text{dx}} - \upmu {\text{u}}^{\prime\prime}_{1} {\text{u}}_{1}^{6} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{7} } {\text{dx}} + \upmu {\text{V}}^{2} \left(6 + 2\frac{0.65{\rm{d}}}{\text{b}}\right){\rm{u}}_{1}^{2} \int_{0}^{1} {\dot{{\text{q}}}_{1}^{2} {\text{q}}_{1} } {\text{dx}} \hfill \\&\quad - \upmu {\text{V}}^{2} \left(12 + 6\frac{0.65{\text{d}}}{\rm{b}}\right){\text{u}}_{1}^{3} \int_{0}^{1} {\dot{{\text{q}}}_{1}^{2} {\text{q}}_{1}^{2} } {\text{dx}} + \upmu {\text{V}}^{2} \left(6 + 6\frac{0.65{\text{d}}}{\text{b}}\right){\text{u}}_{1}^{4} \int_{0}^{1} {\dot{{\text{q}}}_{1}^{2} {\text{q}}_{1}^{3} } {\text{dx}} \hfill \\&\quad + \left[ {\upmu {\text{V}}^{2} \left(12 + \frac{0.65{\text{d}}}{\text{b}}\right) - {\text{N}}^{*} } \right]{\text{u}}_{1} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{2} } {\text{dx}} - \left[ {\upmu {\text{V}}^{2} \left(36 + 4\frac{0.65{\text{d}}}{\text{b}}\right) - 6{\text{N}}^{*} } \right]{\text{u}}_{1}^{2} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{2} } {\text{dx}} \hfill \\&\quad + \left[ {\upmu {\text{V}}^{2} \left(6 + 6\frac{0.65{\text{d}}}{\text{b}}\right) - 15{\text{N}}^{*} } \right]{\text{u}}_{1}^{3} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{3} } {\text{dx}} - \left[ {\upmu {\text{V}}^{2} \left(12 + 4\frac{0.65{\text{d}}}{\text{b}}\right) - 20{\text{N}}^{*} } \right]{\text{u}}_{1}^{4} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{4} } {\text{dx}} \hfill \\&\quad - 2\upmu {\text{V}}^{2} \frac{0.65{\text{d}}}{{\text{b}}}{\text{u}}_{1}^{5} \int_{0}^{1} {\dot{{\text{q}}}_{1}^{2} {\text{q}}_{1}^{4} } {\text{dx}} + \left(\upmu {\text{V}}^{2} \frac{0.65{\text{d}}}{\text{b}} - 15{\text{N}}^{*} \right){\text{u}}_{1}^{5} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{5} } {\text{dx}} + 6{\text{N}}^{*} {\text{u}}_{1}^{6} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{6} } {\text{dx}} \hfill \\&\quad - 6{\text{N}}_{\rm {t}}{\text{u}}_{1}^{7} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{7} } {\text{dx}} + 20\upmu \uplambda_{4} {\text{u}}_{1}^{2} \int_{0}^{1} {\dot{{\text{q}}}_{1}^{2} {\text{q}}_{1} } {\text{dx}} + 4\upmu \uplambda_{4} {\text{u}}_{1} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1} } {\text{dx}} - 4\upmu \uplambda_{4} {\text{u}}_{1}^{2} \int_{0}^{1} {\ddot{{\text{q}}}_{1} {\text{q}}_{1}^{2} } {\text{dx}} \hfill \\&\quad - {\text{V}}^{2} \left(1 + \frac{0.65{\rm{d}}}{\text{b}}\right)\int_{0}^{1} {{\text{q}}_{1} } {\text{dx}} + {\text{V}}^{2} \left(4 + 5\frac{0.65{\text{d}}}{\text{b}}\right){\text{u}}_{1} \int_{0}^{1} {{\text{q}}_{1}^{2} } {\text{dx}} - {\text{V}}^{2} \left(6 + 10\frac{0.65{\rm{d}}}{\text{b}}\right){\text{u}}_{1}^{2} \int_{0}^{1} {{\text{q}}_{1}^{3} } {\text{dx}} \hfill \\&\quad + {\text{V}}^{2} \left(4 + 10\frac{0.65{\rm{d}}}{\text{b}}\right){\text{u}}_{1}^{3} \int_{0}^{1} {{\text{q}}_{1}^{4} } {\text{dx}} - {\text{V}}^{2} \left(1 + 5\frac{0.65{\rm{d}}}{\text{b}}\right){\text{u}}_{1}^{4} \int_{0}^{1} {{\text{q}}_{1}^{5} } {\text{dx}} + {\text{V}}^{2} \frac{0.65{\rm{d}}}{\text{b}}{\rm{u}}_{1}^{5} \int_{0}^{1} {{\text{q}}_{1}^{6} } {\text{dx}} \hfill \\&\quad - \uplambda_{4} \int_{0}^{1} {{\text{q}}_{1} } {\text{dx}} + 2\uplambda_{4} {\text{u}}_{1} \int_{0}^{1} {{\text{q}}_{1}^{2} } {\text{dx}} - \uplambda_{4} {\text{u}}_{1}^{2} \int_{0}^{1} {{\text{q}}_{1}^{3} } {\text{dx}} = 0. \hfill \\ \end{aligned}$$

(22)