1 Introduction

Micro- and nanosize mechanical systems are widely used in modern devices. As well known, in the classical continuum theory, only macroscopic effects are taken into consideration; however, some experimental and theoretical studies show that length scale parameters play a major role on the mechanical behavior of micro-/nanostructures (Akgoz and Civalek 2012). The existing size-dependent theories, which include at least one additional or internal material length scale parameter (Akgoz and Civalek 2017), were used in several works to derive the governing equations of nanostructures, including the modified couple stress theory (Krysko et al. 2019; Akgoz and Civalek 2013), the strain gradient theory (Arefia et al. 2018; Akgoz and Civalek 2012), Eringen’s the nonlocal theory (Ebrahimi and Barati 2017b; Ebrahimi et al. 2019; Numanoglu et al. 2018) and the surface elasticity model (Ansari et al. 2013). With the novel manufacturing methods for fabricating small-scale structures, the applications of nanostructures have extended rapidly (Yekrangisendi et al. 2019). Typical cantilever flexoelectric nanobeams thanks to the electromechanical coupling effects are the subject of intensive studies in the field of nano-/microelectromechanical systems (N/MEMS). They have been extensively used as sensors and actuators (Cao et al. 2015). Piezoelectric and flexoelectric materials are also employed for vibration control (Koszewnika 2018), noise control systems (Casadei et al. 2010), data collection (Sumali et al. 2001), actuators (Liu et al. 2015), telecommunication and sensor networks (Hao and Liao 2010), energy harvesting (Managheb et al. 2018; Rojas et al. 2019) and shape control of structures (Donthireddy and Chandrashekhara 1996). However, size-dependent linear electromechanical coupling has been reported in isotropic dielectrics (Mishima et al. 1997; Cross 2006; Baskaran et al. 2011) and the classical piezoelectric theory describes the relation between electric polarization and uniform strain in non-centrosymmetric dielectrics at macroscales. In small scale, when the strain gradient is considered in solids, linear electromechanical coupling arises. This size-dependent electromechanical effect is known as the flexoelectric effect (Maranganti et al. 2006). On the other word, in micro- and nanoscale, the dielectric polarization depends not only on the strain tensor, but also on the curvature tensor. Thus, size-dependent (micro/nano) structures must be analyzed properly in different mechanical aspects and this process cannot be performed using classical continuum theory (Ebrahimia and Barati 2017a). Therefore, it is necessary to employ a size-dependent piezoelectricity, which accounts for the micro- and nanostructures. The first step toward developing size-dependent electromechanical theories is the establishment of the size-dependent continuum mechanics theory (Hadjesfandiari and Dargush 2011). It should be pointed out that many size-dependent theories based on the modified couple stress (Krysko et al. 2019), the strain gradient theory (Arani et al. 2015; Arefia et al. 2018), the nonlocal theory (Ke et al. 2012; Ebrahimi and Barati 2017b) and the surface elasticity model (Ansari et al. 2013) were used in several works to derive the governing equations of piezoelectric nanobeams. For this purpose, some researchers have illustrated the size effect in flexoelectric properties and linear electromechanical coupling in all classes of dielectric materials even for centrosymmetric crystals (Ebnali Samani and Tadi Beni 2018; Baskaran et al. 2011; Rojas et al. 2019). Many studies investigated the mechanical and electrical equations of the micro- and nanostructures by considering flexoelectricity effect (Nateghi et al. 2012). A size-dependent piezoelectricity theory, based on the electromechanical formulation, was developed by Hadjesfandiari (2013). The flexoelectricity theory developed by Hadjesfandiari (2013) introduces a compatible theory for piezoelectric and dielectric materials at the micro- and nanoscale. Most of micro-/nanosystems operate based on vibration of mechanical elements such as micro-/nanobeams, plates and wires; so study of vibration and control of micro-/nanomechanical elements is of great importance (Esmaeili and Beni 2019). On the other hand, mechanical vibrating elements are used in a large number of NEMS, for sensing and actuating. In these systems, it is important to achieve high sensitivity by accurate model. In this field, the most works use the von-Karman strain–displacement relationship for the nonlinear analysis, which leads to the linear equations of motion for the clamped-free beams (Vaghefpour et al. 2018). In this regard, many researchers have been studying vibration and control of micro-/nanostructures. Alsaleem and Younis (2011) by using delay feedback controllers stabilize MEMS resonators especially near pull-in point. Wang (1998) investigated the feedback control of vibrations in cantilever beams with electrostatic actuators. The effects of the control gains on an electrically actuated resonator were examined by Shao et al. (2013). The control of chaotic motion of a MEMS resonator was examined by Siewe (2011), to indicate that reducing the amplitude of the parametric excitation can control the chaotic motion of a MEMS resonator. Seleim et al. (2012) considered a closed-loop control for a MEMS resonator and obtained optimal operating regions for the resonator. Vatankhah et al. (2013) brought up the problem of boundary stabilization by considering linear boundary control law to stabilize vibrating a non-classical microbeam. Quoc and Slava (2015) developed a nonlinear control algorithm to control force vibration of a microelectromechanical.

It can be seen from the literature review, although several studies have developed the dynamic modeling and vibration analysis of non-classical micro-/nanobeams in the recent years, nonlinear tracking control of the flexoelectric nanobeams has not been considered yet. The contributions of this paper are to derive the nonlinear model of the flexoelectric cantilever nanobeam as an actuator on the basis of the size-dependent piezoelectric theory implementing a higher-order curvature relation. The equation of motion for the inextensible cantilever flexoelectric nanobeams is obtained taking into account the geometric nonlinearities while neglecting shear deformation and rotary inertia. For order reduction in the beam equation of motion into ODEs, the Galerkin method is employed. The perturbation method is applied on the obtained ODEs to determine the vibration responses (Sect. 2). Nonlinear tip tracking control algorithms for flexoelectric cantilever nanobeam are developed based on sliding mode, and the simulation results are presented (Sect. 3). The results demonstrate the effectiveness of the presented algorithms. The main obtained outcomes are discussed in Sect. 4.

2 Nonlinear Modeling

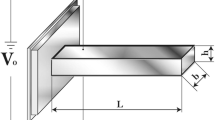
The schematic isotropic flexoelectric cantilever nanoactuator with length L, width b and thickness h considered in this work is depicted in Fig. 1. Employing the size-dependent piezoelectricity theory (Hadjesfandiari 2013), the non-dimensional equations of motion and the related boundary conditions of the cantilever flexoelectric nanoactuators can be expressed, respectively, as Vaghefpour (2019):

$$\begin{aligned}&L_Sw_{,xxxx}+G w^2_{,x}w_{,xxxx} +4Gw_{,x}w_{,xx} w_{,xxx}\nonumber \\&\quad +\,Gw^3_{,xx} +I_0w_{,\tau \tau }=0 \end{aligned}$$
(1)

and

$$\begin{aligned}&\left. \delta w\right| _{0}=0 \quad \hbox {and} \quad \left. L_Sw_{,xxx}+G w^2_{,x}w_{,xxx} +Gw_{,x}w^2_{,xx} \right| ^{1}=0\nonumber \\&\left. \delta (w_{,x})\right| _{0}=0 \quad \hbox {and} \quad \left. \left[ L_Sw_{,xx}+G w^2_{,x}w_{,xx}-FV_0(t)\right] \right| ^{1}=0 \end{aligned}$$
(2)

where

$$\begin{aligned}&L_S=(EI+A_{11})\frac{L^2}{h^2},\quad G=(\lambda +2\mu )I,\quad \nonumber \\ &\quad I_0=\frac{(\lambda +2\mu )IL^2}{h^2},\nonumber \\&\quad \hbox {and} \quad F=\frac{2bL^4f}{h^3} \end{aligned}$$
(3)

A reduced-order model is obtained by discretization of the PDE, i.e., Eq. (1), with the corresponding boundary conditions, i.e., Eq. (2). One can approximate the displacement of the flexoelectric nanoactuator as Rafiepour et al. (2013):

$$\begin{aligned} w(x,t)=\sum _{i=1}^{n}q_i(t)\phi _i(x) \end{aligned}$$
(4)

The reduced order of the equation of motion (EOM) of nanoactuator will be derived through the Galerkin method leading to:

$$\begin{aligned} {\mathbf{M }}\ddot{\mathbf{q }}(t)+{\mathbf{K }}\mathbf{q }(t) +{\mathbf{B }}\mathbf{q }^3(t)={\mathbf{E } }V_0(t) \end{aligned}$$
(5)

where \({\mathbf{q }}(t)=[q_i(t)]^\intercal\); \({\mathbf{M }}\), \({\mathbf{K }}\) and \({\mathbf{B }}\) are the time-dependent vector of generalized coordinates, the mass matrix, the linear stiffness matrix and the nonlinear stiffness matrix, respectively; and \(\intercal\) stands for the transpose. The elements of \({\mathbf{M} }\), \({\mathbf{K }}\) and \({\mathbf{B }}\) matrices and \({\mathbf{C }}\) vector are given, respectively, by:

$$\begin{aligned}&M_{ij}=I_0\int _{0}^{1}\phi _i\phi _j \mathrm{d}x,\quad K_{ij}=L_S\int _{0}^{1} \phi ^{\prime \prime }_i\phi ^{\prime \prime }_j\mathrm{d}x,\nonumber \\&B_{ij}=G\int _{0}^{1} (\phi ^{\prime \prime }_i\phi ^{\prime 2}_i\phi ^{\prime \prime }_j+\phi ^{\prime \prime 2}_i\phi ^{\prime }_i\phi ^{\prime }_j)\mathrm{d}x,\quad E_j=F\phi ^{\prime }_j(1) \end{aligned}$$
(6)

where \(\phi ^{\prime }=\frac{\mathrm {d} \phi }{\mathrm {d} x}\).

Fig. 1
figure 1

Schematic view of a flexoelectric nanoactuator

Full size image

2.1 Nonlinear Vibration Analysis

The parameterized perturbation method (PPM) is employed to develop the nonlinear vibration response of equations of motion, i.e., Eq. (5). At first, Eq. (5) is reshuffled as follows:

$$\begin{aligned} \ddot{q}(t)+\Omega q(t)+\gamma q^3(t)=\varGamma \end{aligned}$$
(7)

where \(\Omega =M^{-1}K\), \(\gamma =M^{-1}B,\) and \(\varGamma =M^{-1}HV_0\).

By introducing a new set of variables \(q=pS\), \(S=S_0+p^2S_1,\) and \(\Omega =\omega _0^2+p^2\omega _1\) (Barari et al. (2011)) and substituting the defined variables into Eq. (7), one can obtain:

$$\begin{aligned}&p({\ddot{S}}_0+p^2{\ddot{S}}_1)+(\omega _0^2+p^2\omega _1) p(S_0+p^2S_1)\nonumber \\&\quad +\,\gamma p^3(S_0+p^2S_1)^3=\varGamma \end{aligned}$$
(8)

Equating the coefficients of the same order of p yields the following ordered equations:

\(\hbox {O} (p^1):\)

$$\begin{aligned}&{\ddot{S}}_0+\omega _0^2S_0=\frac{\varGamma }{p}, \qquad S_0(0)=\dot{S_0}(0)=0 \end{aligned}$$
(9)

\(\hbox {O} (p^3):\)

$$\begin{aligned}&\qquad {\ddot{S}}_1+\omega _0^2S_1+\omega _1S_0+\gamma S_0^3=0, \qquad S_1(0)=\dot{S_1}(0)=0 \end{aligned}$$
(10)

The first-order equation, i.e., Eq. (9), delivers the first-order solution as:

$$\begin{aligned} S_0=\frac{\varGamma }{p\omega _0^2}(1-\cos \omega _0t) \end{aligned}$$
(11)

Substituting the first-order solution, i.e., Eq. (11) into Eq. (10), yields:

$$\begin{aligned}&{\ddot{S}}_1+\omega _0^2S_1+\omega _1\frac{\varGamma }{p\omega _0^2} (1-\cos \omega _0t)\nonumber \\&\quad +\,\gamma \left( \frac{\varGamma }{p\omega _0^2}(1-\cos \omega _0t)\right) ^3 =0 \end{aligned}$$
(12)

Reshuffling Eq. (12) results in:

$$\begin{aligned}&{\ddot{S}}_1+\omega _0^2S_1+\omega _1\frac{\varGamma }{p\omega _0^2}+\frac{5}{2}\gamma \left( \frac{\varGamma }{p\omega _0^2}\right) ^3\nonumber \\&\quad -\,(\omega _1\frac{\varGamma }{p\omega _0^2}+\frac{15}{4}\gamma \left( \frac{\varGamma }{p\omega _0^2}\right) ^3)\cos \omega _0t\nonumber \\&\quad +\,\frac{3}{2}\gamma \left( \frac{\varGamma }{p\omega _0^2}\right) ^3\cos \omega _02t-\frac{1}{4}\gamma \left( \frac{\varGamma }{p\omega _0^2}\right) ^3\cos \omega _03t =0 \end{aligned}$$
(13)

Following the common procedure of perturbation methods (see, for example, Alsaleem and Younis 2011) and avoiding the presence of the secular term \((\omega _1\frac{\varGamma }{p\omega _0^2}+\frac{15}{4}\gamma (\frac{\varGamma }{p\omega _0^2})^3)=0\):

$$\begin{aligned} \omega _1=-\frac{15}{4}\gamma \left( \frac{\varGamma }{p\omega _0^2}\right) ^2 \end{aligned}$$
(14)

Subsequently, one can obtain \(\omega _0^2=\Omega +\frac{15}{4}\gamma (\frac{\varGamma }{\omega _0^2})^2\).

After elimination of the secular term from Eq. (12), the corresponding solution reads as:

$$\begin{aligned} S_1&=\frac{\gamma \varGamma ^3}{p^3\omega _0^8} \left( -\frac{95}{32}\cos \omega _0t\right. \nonumber \\ &\quad \left. +\,\frac{1}{2}\cos 2\omega _0t -\frac{1}{32}\cos 3\omega _0t+\frac{10}{4}\right) \end{aligned}$$
(15)

Substituting the first- and third-order solutions, respectively, Eqs. (11) and (15) into expanded form of S, i.e., \(S=S_0+p^2S_1\), and considering \(q=pS\), the nonlinear solution of Eq. (7) can be expressed as:

$$\begin{aligned} q=&\frac{\varGamma }{\omega _0^2}\left( 1-\cos \omega _0t\right) +\frac{\gamma \varGamma ^3}{\omega _0^8} \left( -\frac{95}{32}\cos \omega _0t+\frac{1}{2}\cos 2\omega _0t\right. \nonumber \\&\left. -\frac{1}{32}\cos 3\omega _0t+\frac{10}{4}\right) \end{aligned}$$
(16)

3 Nonlinear Control Design

The control objective is to drive the deflection of the tip of the piezoelectric nanoactuator to a desired oscillation. To this end, Eq. (5) is expressed as:

$$\begin{aligned} \ddot{\mathbf{q }}(t)={\mathbf{F }}({\mathbf{q}}(t))+\varvec{\beta }{\mathbf{u}}(\tau )+{\mathbf{d}}(\tau ) \end{aligned}$$
(17)

where \({\mathbf{d}}(\tau )\) is the vector of bounded external disturbances and

$$\begin{aligned}&{\mathbf{F }}({\mathbf{q }})=\widehat{\varvec{F}}({\mathbf{q }})+\Delta {\mathbf{F }}({\mathbf{q }})\nonumber \\&\varvec{\beta }=\widehat{\varvec{\beta }}+\Delta \varvec{\beta } \quad \hbox {and}\quad {\mathbf{u }}(\tau )={\mathbf{E }}V_{0}(\tau ) \end{aligned}$$
(18)

The \(\widehat{\varvec{F}}\) and \(\widehat{\varvec{\beta }}\) are known real constant matrices, and \(\Delta ()\) are unknown matrices representing system parameter uncertainties therefore:

$$\begin{aligned}&\widehat{\varvec{F}}({\mathbf{q }})=-{\mathbf{M }}^{-1}({\mathbf{K }}{\mathbf{q }}+\varvec{\beta } {\mathbf{q }}^{3})\quad \hbox {and} \quad \widehat{\varvec{\beta }}={\mathbf{M }}^{-1}{\mathbf{E }} \end{aligned}$$
(19)

For the control design purpose, it is convenient to rewrite the ODE, i.e., Eq. (5), into a state space model.

3.1 State Space Model

For the system defined by Eq. (17), controllability condition is given by \(\varvec{\beta }\ne 0\) and the state space representation as:

$$\begin{aligned} {\mathbf{q }}(t)&= ({\mathbf{q }}^{T},\dot{{\mathbf{q }}}^{T})^{T}\quad \epsilon R^{2n} \end{aligned}$$
(20)
$$\begin{aligned} u(t)&= V_0(t) \end{aligned}$$
(21)

To design a controller, deflection of the tip of the flexoelectric nanoactuator is considered as a control output and is given by:

$$\begin{aligned} y={\mathbf{H }}{\mathbf{x}} \end{aligned}$$
(22)

where vector \({\mathbf{H}}\) is defined as:

$$\begin{aligned} {\mathbf{H }}=[\phi _1(1)\quad \phi _2(1)\ldots \phi _n(1)\quad {\mathbf{0 }}_{1\times n}] \end{aligned}$$
(23)

It is assumed that \(\widehat{\varvec{\beta }}\) and \({\mathbf{M }}\) are invertible matrices and well defined and bounded for all time. Also, regarding the system (17), \(\widehat{\varvec{F}}({\mathbf{q}})\) is a continuously differentiable function and the uncertainty terms \((\Delta {\mathbf{F }}\) and \(\Delta \varvec{\beta })\) are assumed to be bounded by:

$$\begin{aligned} |\Delta {\mathbf{F }}|&=|{\mathbf{F }}-\widehat{{\mathbf{F }}}|\le \varPi \nonumber \\ |\Delta \varvec{\beta }|&=|\varvec{\beta }-\widehat{\varvec{\beta }}|\le \varvec{\Lambda } \end{aligned}$$
(24)

where \(\varvec{\Pi }, \varvec{\Lambda }\ge 0\)

3.2 Sliding Mode Controller Design

The first step in designing a sliding mode controller is to determine a sliding surface so that the plant restricted to the sliding surface has a desired system response. In this treatise, the sliding surface is represented by:

$$\begin{aligned} S\left( {\dot{e}},e\right) ={\dot{e}}+\lambda e=0 \end{aligned}$$
(25)

where \(\uplambda\) is an positive value that must satisfy the Hurwitz condition, and e is tracking error. The tracking error and its derivative value are obtained as:

$$\begin{aligned} e={\mathbf{H }}{\mathbf{q }}-y_d,\qquad {\dot{e}}=\mathbf{H }\dot{\mathbf{q }}-{\dot{y}}_d \end{aligned}$$
(26)

In Eq. (26), \(y_d\) is the desired path (reference input) for tracking.

The next step is designing a switched feedback gains necessary to drive the state trajectory to the sliding surface. These constructions are built on the generalized Lyapunov stability theory. So, the control input for only one mode (first mode) is considered as follows:

$$\begin{aligned} u\left( t\right) =u_{\mathrm{eq}}+u_c \end{aligned}$$
(27)

where \(u_{\mathrm{eq}}\) is the equivalent control term and \(u_c\) is considered for tracking, despite the uncertainties and disturbances. \(u_{\mathrm{eq}}\) can be designed based on the Filippov’s equivalent dynamics which states that \({\dot{S}}({\dot{e}},e)=0,\) while the dynamics is on the sliding mode. For the first mode in this case:

$$\begin{aligned} {\dot{S}}\left( {\dot{e}},e\right) =\ddot{e}+\lambda {\dot{e}}=H\ddot{q}-{\ddot{y}}_d+\lambda \left( H\dot{q}-{\dot{y}}_d\right) =0 \end{aligned}$$
(28)

Therefore, considering Eqs. (17) and (18), one can obtain:

$$\begin{aligned} H(\widehat{F}\left( q\right) +\widehat{\beta }u_{\mathrm{eq}}\left( \tau \right) )-{\ddot{y}}_d+\lambda \left( H\dot{q}-{\dot{y}}_d\right) =0 \end{aligned}$$
(29)

By reshuffling Eq. (29), \(u_{\mathrm{eq}}\) can be expressed as:

$$\begin{aligned} u_{\mathrm{eq}}\left( \tau \right) ={\left[ H\widehat{\beta }\right] }^{-1}\left\{ {\ddot{y}}_d-\lambda \left( H\dot{q}-{\dot{y}}_d\right) -H\widehat{F}\left( q\right) \right\} \end{aligned}$$
(30)

As previously stated, \(u_c\) will be added to the control input in order to prove the stability and robustness of the equivalent control term, i.e., Eq. (30). To ensure the asymptotic stability of the system, the \(u_c\) must be determined in a way that the derivative of the system’s Lyapunov function is given negative. In order to achieve this goal, \(u_c\) is considered as follows:

$$\begin{aligned} u_c=-\left\{ {\left[ H\widehat{\beta }\right] }^{-1}k\right\} \hbox {Sign}(s) \end{aligned}$$
(31)

3.3 Stability Analysis

In order to proof the asymptotic stability and the reliability of a given controller, the Lyapunov function is considered as \(V=\frac{1}{2}S^2\); therefore, the derivative of Lyapunov function is:

$$\begin{aligned} {\dot{V}}=S{\dot{S}}\le -\varGamma \left| S\right| ,\quad S\ne 0 \end{aligned}$$
(32)

In Eq. (32), \(\varGamma\) is a positive arbitrary constant. By inserting Eqs. (30) and (31) in Eq. (27), the control input is obtained:

$$\begin{aligned} u\left( t\right)&=u_{\mathrm{eq}}+u_c\nonumber \\&={\left[ H\widehat{\beta }\right] }^{-1}\left\{ {\ddot{y}}_d-\lambda \left( H\dot{q}-{\dot{y}}_d\right) -H\widehat{F}\left( q\right) -k\hbox {Sign}(s)\right\} \end{aligned}$$
(33)

Substituting Eq. (33) into Eq. (17) and considering Eq. (18), one can obtain:

$$\begin{aligned} \ddot{q}&=\widehat{F}(q)+{\Delta }F(q) +\left( \widehat{\beta }+{\Delta }\beta \right) \nonumber \\ &\quad {\left[ H\widehat{\beta }\right] }^{-1} \left\{ {\ddot{y}}_d-\lambda \left( H\dot{q}-{\dot{y}}_d\right) -H\widehat{F}\left( q\right) -k\hbox {Sign}(s)\right\} \end{aligned}$$
(34)

By substituting Eq. (34) into Eq. (28), the derivative of the Lyapunov function is obtained as follows:

$$\begin{aligned} {\dot{V}}&=S\left[ H\left\{ \widehat{F}(q)+{\Delta }F(q)+(\widehat{\beta }+{\Delta }\beta ){[H\widehat{\beta }]}^{-1}\right. \right. \nonumber \\&\quad \left. \left\{ {\ddot{y}}_d-\lambda (H\dot{q}-{\dot{y}}_d) -H\widehat{F}(q)-kSign(s)\right\} \right\} \nonumber \\&\quad \left. -\,{\ddot{y}}_d+\lambda (H\dot{q}-{\dot{y}}_d)\right] \end{aligned}$$
(35)

Considering Eq. (29) and simplifying Eq. (35) result in:

$$\begin{aligned} {\dot{V}}=S\left( H{\Delta }F\left( q\right) +{\widehat{\beta }}^{-1}{\Delta }\beta \psi \right) -\eta k\left| S\right| \end{aligned}$$
(36)

where

$$\begin{aligned} \psi ={\ddot{y}}_d-\lambda \left( H\dot{q}-{\dot{y}}_d\right) -H\widehat{F}\left( q\right) \eta =1+{\widehat{\beta }}^{-1}{\Delta }\beta \end{aligned}$$
(37)

Now, if the condition \({\dot{V}}=S{\dot{S}}\le -\varGamma \left| S\right|\) is established, the asymptomatic stability of the system is guaranteed, to do this:

$$\begin{aligned} S\left( H{\Delta }F\left( q\right) +{\widehat{\beta }}^{-1}{\Delta }\beta \psi \right) -\eta k\left| S\right| \le -\varGamma \left| S\right| \end{aligned}$$
(38)

In this case, if \(S = 0\), the condition (38) is satisfied, and if S is positive, it is concluded that in worst case:

$$\begin{aligned} \left( H{\Delta }F\left( q\right) +{\widehat{\beta }}^{-1}{\Delta }\beta \psi \right) -\eta k\le -\varGamma \end{aligned}$$
(39)

Therefore, if

$$\begin{aligned} k\ge \frac{1}{\eta }\left\{ \varGamma +\left( H{\Delta }F\left( q\right) +{\widehat{\beta }}^{-1}{\Delta }\beta \psi \right) \right\} \end{aligned},$$
(40)

stability conditions are satisfied, and if S is negative, the stability conditions will be as follows:

$$\begin{aligned} k\ge \frac{1}{\eta }\left\{ \varGamma -\left( H{\Delta }F\left( q\right) +{\widehat{\beta }}^{-1}{\Delta }\beta \psi \right) \right\} \end{aligned}$$
(41)

4 Numerical Results and Discussion

As it is known, flexoelectricity effect plays a significant role just at micro-/nanoscales. Hence, for more illustration, in this paper, a cantilever flexoelectric nanobeam (CPNB) is considered for analysis which is made of \(\hbox {BaTiO}_3\). The corresponding geometrical and material data are listed in Table 1. Henceforth, all the employed parameters are same as in Table 1 unless new data are prescribed.

Table 1 The geometrical and material data of the assumed piezoelectric nanobeam (Tadi Beni 2016a)
Full size table

To verify the current results, the obtained Galerkin outcomes for the static deflection due to a constant applied voltage are compared with the available linear analytical results which is accessible in Tadi Beni (2016a) and the current bvp4c results. The comparison is depicted in Fig. 2 for \(V_0=4000 v\) by the consideration of one and three linear normal modes in Galerkin projection. A very good agreement is clear between the current three-mode Galerkin projection, the bvp4c method and the analytical results. Because the Galerkin approach is very handy in the implementation hence, hereafter, three-mode Galerkin technique is employed for the static deflection computations.

Fig. 2
figure 2

The current nonlinear static deflection achieved by one-mode Galerkin technique (dotted-dashed lines), three-mode Galerkin technique (solid lines) and the bvp4c-subroutine (dashed lines) versus the corresponding linear analytical results of Tadi Beni (2016b) (dotted lines): (\(V_0=4000 v\))

Full size image

Another verification is confirmed in calculation of linear natural frequency in comparison with Arvin (2018). The considered beam is a rotating nanocantilever beam which is made of epoxy with the mass density, Young’s modulus, the Poisson ratio and the material length scale parameter, respectively, equal to \(\rho =1220\hbox { kg/m}^3\), \(E=1.4 \hbox { GPa}\), \(\nu =0.3\) and \(l=17.6\,\upmu \hbox {m}\). The slenderness ratio, i.e., \(S=L\sqrt{\frac{A}{I}}\), and height to material scale parameter, i.e., \(\upsilon =\frac{h}{l}\), are given, respectively, as \(S=30\) and \(\upsilon =1\). In slenderness ratio, L, A and I are, respectively, the beam length, the beam cross-sectional area and the beam moment of inertia about y-axis (see Fig. 1). As the considered nanobeam is a rotating beam, the dimensionless rotation speed is considered as \(\lambda _{R}=0\) in Fig. 9 of Arvin (2018). The compared results for the first two linear natural frequencies are shown in Table 2. The results show a very good agreement. It should be noted that in Arvin (2018), the rotary inertia influences are taken into account, and hence, the neglecting of rotary inertia here seems reasonable.

Table 2 The current first two linear natural frequencies in comparison with those of Arvin (2018) (MHz)
Full size table

After confirming the current results, some case studies are addressed here.

4.1 Case Studies: Nonlinear Vibration

The effects of the length scale parameter and the flexoelectric constant on the nonlinear natural frequency of the given CFNB are examined here.

The effects of length scale parameter to beam thickness ratio, i.e., l/h, on the nonlinear natural frequency in terms of beam tip displacement and the applied voltage are presented, respectively, in Fig. 3a, b. The x-axis defines the ratio of the nonlinear natural frequency with respect to the corresponding linear natural frequency for \(l/h=0\). A hardening behavior for the first mode is obvious. For verification of the predicted treatment, it can be mention that when just the geometric nonlinearities are considered, for the cantilever beam imposing the inextensibility condition, the hardening behavior is expected (see McHugh and Dowell 2018). It can be seen that by increasing l/h parameter due to the stiffening of the beam structure, the linear and subsequently the nonlinear natural frequencies increase. On the other hand, more stiffen structure is exposed to the lower deflection at the same applied voltage.

Fig. 3
figure 3

The effect of the length scale parameter to beam thickness ratio, i.e., l/h, on the nonlinear natural frequency in terms of: a beam tip displacement and b the applied voltage (solid lines, \(l/h=0\), dashed lines, \(l/h=0.05,\) and dotted lines, \(l/h=0.1\))

Full size image

The effects of the flexoelectric constant on the first nonlinear natural frequency in terms of the applied voltage are presented in Fig. 4. It can be inferred that as it is expected, the flexoelectric constant does not change the linear natural frequency because it does not have any contributions in the linear structural stiffness. On the contrast, because the increment in its magnitude enhances the beam deflection, it makes the nonlinear structural stiffness stiffer, and hence, the nonlinear natural frequency increases.

Fig. 4
figure 4

The effect of flexoelectric constant on the first nonlinear natural frequency in terms of applied voltage (solid lines, \(f=5\,\hbox {pC/m}\), dashed lines, \(f=10\,\hbox {pC/m},\) and dotted lines, \(f=20\,\hbox {pC/m}\))

Full size image

4.2 Case Studies: Nonlinear Control

Nonlinear control simulation of the tip of the nanoflexoelectric cantilever actuator is carried out by employing sliding mode. To reduce the chattering effect, the saturation function is used in sliding mode control.

In order to examine the performance of the nonlinear controller, the designed sliding mode controller is compared with the linear fuzzy controller which is accessible in Ref. Vaghefpour et al. (2018). Figures  5 and 6 illustrate nonlinear and fuzzy linear tip tracking for the sinusoidal input, respectively. In order to verify the robustness of the sliding mode controller, a disturbance pulse signal is applied in the fifth second of the simulation. Figure 5 shows that the sliding mode controller can successfully track the reference signal (R) with a very small error, and by applying the disturbance (pulse) in 5 s of simulation, tracking is carried out with a very low oscillation range (1%) and a low settling time (about 1 s).

Fig. 5
figure 5

Nonlinear tip tracking control (dashed lines) with sinusoidal wave reference input (solid lines) and a pulse disturbance (dotted lines) at time of simulation 5

Full size image
Fig. 6
figure 6

Linear fuzzy control (dashed lines) with sinusoidal wave reference input (solid lines) and a pulse disturbance (dotted lines) at time of simulation 5

Full size image

In Fig. 6, the fuzzy controller tracking for the sinusoidal input is shown (Vaghefpour et al. (2018)). By comparing Figs. 5 and 6, it can be seen that the tracking in the nonlinear controller is more favorable than the fuzzy controller, while the fuzzy controller is more resistant than the nonlinear controller.

The tracking errors of nonlinear sliding mode and linear fuzzy controllers are illustrated in Figs. 7 and 8. It can be inferred that the both controllers are good robust controller, whereas the fuzzy controller is more robust than sliding mode controller.

Figures 7 and 8 indicate that the error in the sliding mode controller is very low and close to zero in the absence of external disturbance, while in the fuzzy controller, the trajectory of the path is smooth with an approximate error of 20%. By applying external disturbance, the error in the sliding mode controller increases to 100%; however, the external disturbance has a very small effect on the performance of the fuzzy controller.

Fig. 7
figure 7

Nonlinear tracking error with sinusoidal wave reference input and a pulse disturbance at time of simulation 5

Full size image
Fig. 8
figure 8

Linear fuzzy error with sinusoidal wave reference input and a pulse disturbance at time of simulation 5

Full size image

Figures 9 and 10 show applied voltage as the input control.

Fig. 9
figure 9

Nonlinear tracking input control with sinusoidal wave reference input and a pulse disturbance at time of simulation 5

Full size image
Fig. 10
figure 10

Linear fuzzy input control with sinusoidal wave reference input and a pulse disturbance at time of simulation 5

Full size image

As shown in Figs. 9 and 10, the input voltage for tracking the sinusoidal path in the fuzzy controller is more than sliding mode controller.

5 Summary and Conclusion

The nonlinear modeling and tip tracking control of an inextensible flexoelectric cantilever nanoactuator were investigated based on the size-dependent piezoelectric theory besides a higher-order curvature relation. The results of vibration analysis and performance of nonlinear sliding mode controller of cantilever flexoelectric nanoactuators were presented. The perturbation method was implemented to solve the nonlinear ODE for the nonlinear vibration examination. The influences of the applied voltage, the material length scale parameter with respect to the beam thickness ratio and the flexoelectric coefficient on the nonlinear natural frequency of the assumed cantilever flexoelectric nanoactuator were discussed. At the end, the results of nonlinear sliding mode controller for nanoactuator were studied. In order to compare the performance of the linear fuzzy controller and nonlinear controller, some figures were considered. Referring to the numerical results, it can be deduced that:

(1) Due to hardening effect of scale factor on the linear stiffness of the nanobeam, by increasing the scale factor to the beam thickness ratio, the existing discrepancy between the linear and the nonlinear static deflections reduces; (2) by increasing the flexoelectric coefficient and/or the applied voltage, the difference between the linear and the nonlinear static deflection increases; (3) the increment in the scale factor to the beam thickness ratio increases the linear and nonlinear natural frequency; (4) the flexoelectric does not have any contribution in the linear natural frequency, while the increment in its magnitude increases the nonlinear natural frequency; (5) the input voltage in the nonlinear controller is much less than the linear controller; (6) the fuzzy controller is more robust than sliding mode controller; (7) the comparison results show that nonlinear control performance of the proposed sliding mode is better than that of linear methods used to resolve the same problem (Vaghefpour et al. 2018) in terms of the steady-state error.