1 Introduction

Because of good thermal conductivity and unique electrical properties, carbon nanotubes (CNTs) are known as very attractive nano-scale materials with a wide variety of industrial applications. CNTs play significant roles in the design and fabrication of nano-devices such as switches and sensors (Li et al. 2008), nano-tweezers (Nakayama 2002), mass-detectors (Li and Chou 2004) and etc. Due to their tiny size, these nano-structures show distinctive mechanical properties such as ultra-low mass and high resonance frequency that make them promising devices in nanotechnology and biotechnology. Likewise, their excellent electromechanical properties can make them very good candidates to fabricate the nano-electromechanical systems (NEMS). Mahar et al. (2007) discussed the electromechanical properties of CNTs and reviewed a range of nanotube-based sensors, focusing on mechanical pressure actuators and strain actuators. Ke et al. (2005) presented the electromechanical behavior of CNT-based NEMS applying a theoretical study by employing small deformation and finite kinematics regimes. They analyzed their experiment outcomes using energy-based theoretical approaches and predicted the deflection as well as the pull-in voltage of the nano-switches. The investigation on the static and dynamic behavior of CNT-based actuators was performed by Dequesnes et al. (2004) using combined MD/continuum mechanics approach. They predicted the pull-in voltage of a CNT-based actuator suspended over a fixed electrode with the consideration of van der Waals attraction. Desquenes et al. (2002) proposed parameterized continuum models in order to investigate the pull-in characteristics of carbon nanotube switches subject to electrostatic actuation. Nonlinear dynamics and pull-in behavior of electrically actuated carbon nanotubes including geometric nonlinearity was investigated by Ouakad and Younis (2008) using reduced order method. They also determined the nonlinear resonance frequency of CNT sensors under alternating current (AC) voltage. More findings on pull-in characteristics of the CNT-based nano-switches can be found in refs. (Loh and Espinosa 2012; Koochi et al. 2014; Sedighi and Daneshmand 2014; Farrokhabadi et al. 2014).

The electromechanical and pull-in behavior of CNT structures can be examined by several approaches. Molecular mechanics modeling may be employed to model the mechanical characteristics of CNTs (Kang et al. 2006; Hwang and Kang 2005; Gupta and Batra 2008; Sears and Batra 2006; Dequesnes et al. 2002). However molecular mechanics/dynamics is very time-consuming and are not easily applicable in analyzing nano-systems with extremely large number of atoms. In this regard, most of theoretical researchers have preferred continuum beam models for simulation of the pull-in instability of CNT-based NEMS. However, conventional beam theories are not able to model all deformation modes such as rippled configuration. Rippling is the wavelike deformation/distortion on the inner arc of the bent nanotubes. Note that CNT is exceptionally flexible in bending and can undergo large elastic deformation without rupture failure. The structural characteristics and the resonant frequencies of CNTs are influenced by rippling deformation and cause the bending moment to be a non-linear function of deformation (Soltani et al. 2012). Therefore, in studying the dynamic pull-in behavior of vibrating CNTs, instantaneous curvature of nanotube including rippling effect should be taken into consideration. Arroyo and Belytschko (Arroyo and Belytschko 2003) developed a nonlinear local quasi-continuum approach to analyze the effective modulus of multiwalled CNTs undergoing rippling phenomenon. They demonstrated that the predicted effective stiffness of the structure in bending and torsional deformations were much smaller than those predicted by classical elasticity theory. With this distinct property, CNT shows local deformation i.e. formation of ripples under sever bending. Wang et al. (2005) used experimental techniques to infer the bending modulus of cantilevered CNTs. They found that the rippling phenomenon results in reduction of effective bending modulus of large diameter nanotubes. In another research, Wang and Wang (2004) numerically investigated the bending mechanical property of carbon nanotubes and developed a non-linear bending moment–curvature relation for rippled nanotubes of various sizes. This relation has been used by few researchers for modeling vibration of rippled CNTs using modified beam models (Mehdipour et al. 2012). The rippling morphology of a CNT changes the structural characteristics, hence, the bending stiffness depends on the bending deformation and the curvature of CNT. Since the rippling deformation induces nonlinearity, the linear Euler–Bernoulli beam theory might not be reliable for analysis of CNT actuators. One of the main goals of the present work is to incorporate the nonlinear effect of the rippling deformation in the theoretical beam model used for pull-in analysis of CNT actuator.

Besides the rippling, the charge distribution along the cantilever CNT is another important issue in precise modeling of the actuators via using beam models. One of the key features is the concentration of charges at the cantilever CNT end which originates from the constant electrostatic potential along conductive nanotubes. It was demonstrated that the longer nanotubes show greater charge enhancement at the end for a specific charge density (Jackson 1975). Keblinski et al. (2002) presented the comprehensive study to investigate the behavior of voltage-induced carbon nanotubes with finite-size employing density-functional analysis together with the traditional electrostatics modeling. Their findings revealed that the electrostatic force can be modeled using the classical distribution in conjunction with the charge accumulation at the nanotube end. Wang (2009) studied the impacts of external electric field on the distribution of charge density in CNT actuators. They found that the charge concentration is less important as the dielectric constant of ground plane increases or the nanotube becomes closer to the fixed electrode. Ke and Espinosa (2005) computed the charge induced on a conductive nanotube with finite length on the basis of classical electrostatic theory. They presented a formula to predict the charge distribution including end charge effects using parametric analysis. In present study, we use their proposed formulation to incorporate the CNT tip charge concentration in the governing equation of the cantilever nanotubes.

Basically, when the electronic and mechanical systems are fabricated at nano-scale size, some new phenomena originated from the nano-size quantum effects have become increasingly important and the motion of nanotube-based structure is affected by the small-scale quantum electrodynamical interactions such as vacuum fluctuations. The effect of vacuum fluctuation forces can be modeled through the Casimir attraction which is the dominant phenomenon in sub-micron separations (Farrokhabadi et al. 2014). By integrating a force-sensing micromechanical beam and an electrostatic actuator on a single chip, Zou et al. (2013) demonstrated the Casimir effect between two micromachined silicon components on the same substrate. Lombardo et al. (2008) numerically evaluate the Casimir interaction energy for configurations involving two perfectly conducting eccentric cylinders and a cylinder in front of a plane. Emig et al. (2006) found the exact Casimir force between a plate and a cylinder by assuming an intermediate geometry between parallel plates and the plate-sphere. Bordag et al. (2001) provided a review of both new experimental and theoretical developments in the Casimir effect. They demonstrated that the Casimir force strongly depends on the shape, size, geometry and topology of the boundaries. Therefore, many investigations have been conducted to compute the Casimir attraction for different geometries including parallel plates (Casimir 1948; Guo and Zhao 2004; Lin and Zhao 2005), plate-sphere (Casimir and Polder 1948), parallel cylinders (Teo 2011) and plate-cylinder (Teo 2011). A nano-scale device might adhere to its substrate due to Casimir force, if the minimum gap between the flexible beam and the substrate is not considered. Besides interfering with the stability of vibrating nanostructures, the Casimir force can also induce undesired adhesion during the fabrication stages.

The motivation behind this research is to examine the nonlinear influence of the rippling deformation, Casimir attraction and concentrated charge effects on the dynamic behavior and instability analysis of CNT actuators. While the impacts of various physico-mechanical properties on the electromechanical instability of CNT actuators have been explored in depth, the roles of rippling deformation and charge concentration on the instability characteristics have received much less attention. The precise simulating of dynamic behavior of CNTs under more realistic conditions is very crucial. Nevertheless, the impact of rippling deformation together with the concentrated charge effect on the dynamic and instability behavior of CNT actuators has not been addressed, yet. The present study intends to examine the dynamic pull-in instability of cantilever CNT actuator considering rippling and charge concentration phenomena as well as the Casimir force and mechanical damping. The influence of the rippling and the charge concentration on the dynamic pull-in value and pull-in time of CNT-based actuators are presented. The stability of the actuator is examined by plotting the phase diagrams. Accuracy of the present analysis is assessed by comparison between the obtained results and the reported results by experimental data and molecular dynamics.

2 Mathematical formulation

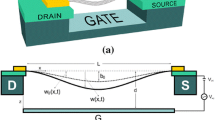
In this section, the vibrational governing equation for carbon nanotubes under suddenly applied voltage with the consideration of Casimir force by incorporating the rippling deformation and concentrated charge effects is presented. As illustrated in Fig. 1, a nanotube is suspended over graphite sheets under electrical actuation voltage (V). The electrical force together with the intermolecular attraction between the electrodes causes the CNT to deflect towards the ground plate. The CNT has mean radius R w, length L and multiwall nanotube layers of N w. The initial gap between nanotube and the ground electrode is D.

Fig. 1
figure 1

Schematic representation of cantilever CNT suspended over graphite sheets

Full size image

Figure 2 illustrates a high-resolution TEM image of rippled configuration in a bent nanotube which reveals a local buckling distortion along the inner arc of the nanotube (Farrokhabadi et al. 2014).

Fig. 2
figure 2

A TEM image of rippled configuration in a bent nanotube (Wang et al. 2005)

Full size image

The equation of transverse vibration for CNT by considering rippling deformation and concentrated charge effects is governed by:

$$ \frac{{\partial^{2} M}}{{\partial x^{2} }} + c\frac{\partial w}{\partial t} + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} = q\left( {x,t} \right) $$
(1)

where \( M\left( {x,t} \right) \) is the bending moment, \( w\left( {x,t} \right) \) is the beam deflection, c denotes the damping coefficient and \( q\left( {x,t} \right) \) is the applied distributed load per unit length of nanotube by electrical actuation and interatomic attraction. The distributed force q are given by:

$$ q\left( {x.t} \right) = F_{cas} + F_{e} $$
(2)

in which F cas represents the Casimir attraction. For the case of conducting parallel flat plates, the Casimir energy per unit area separated by a distance D is (Bordag et al. 2001):

$$ E_{pp} (D )= - \frac{{\pi^{2} \overline{h} c}}{{ 7 2 0D^{3} }} $$
(3)

where c is the light speed and \( \bar{h} \) is Planck’s constant. It should be noted that, this formula can be obtained with the consideration of the electromagnetic mode structure between the two plates in comparison with the free space by assigning a zero-point energy to each electromagnetic mode (Lamoreaux 2005). Proximity force approximation (PFA) fundamentally uses the relation described in Eq. (3) to predict the Casimir force in the case of small separation. Based on PFA approach, the interaction between any other surfaces is modeled through a summation of infinitesimal parallel plates (Bordag et al. 2001). For small separations, the correct zeroth order approximation for the Casimir energy is given by:

$$ E^{PFA} = \int\limits_{s} {E_{PP} (D )d} S = - \frac{{\pi^{2} \overline{h} C}}{ 7 2 0}\int\!\!\!\!\int {\frac{dS}{{D^{3} }}} $$
(4)

in which, S is one of the two surfaces restricting a gap. It should be emphasized that for large separation as well as non-smooth surfaces the PFA cannot be used. Therefore, another approach should be employed to model the Casimir attraction force for the case of larger separations. In order to appropriate modeling of Casimir energy in large separations, a path integral representation (Chan et al. 2008) is used. To this end, the electrodynamic Casimir energy of two disconnected metallic surfaces using Dirichlet mode definition at zero temperature is determined (Li and Kardar 1998; Buscher and Emig 2005). The Casimir energy of this mode and at zero temperature is expressed as:

$$ E^{D} = \frac{{\bar{h}c}}{ 2\pi }\mathop \int \limits_{0}^{\infty } Tr\,{\text{ln(}}MM_{\infty }^{ - 1} )dq_{0} $$
(5)

in which

$$ \begin{aligned} M_{ 1 2} \left( {u, u^{\prime } ;q_{ 0} } \right) = G_{ 0} \left( {s_{1} \left( u \right) - s_{2} \left( {u^{\prime } } \right); q_{ 0} } \right) ,\hfill \\ G_{0} \left( {x, x^{'} ;q_{ 0} } \right) = \frac{{e^{{ - q_{ 0} \left| {x - x'} \right|}} }}{{4\pi \left| {x - x'} \right|}} \hfill \\ \end{aligned} $$
(6)

where the matrix \( M_{12} \) represents the geometry of the surfaces 1 and 2, \( M_{\infty }^{ - 1} \) is the functional inverse of matrix M at infinite surface separation, \( s_{i} \left( u \right) \) is a vector referring to the ith surface parameterized by the surface vector u and G 0 denotes the free space Green function (Rahi et al. 2008). Based on the PFA (for small separations), the Casimir energy can be obtained as:

$$ E^{PFA} = - \frac{{\pi^{3} \bar{h}cL}}{ 9 6 0}\sqrt {\frac{R}{{ 2D^{5} }}} $$
(7)

where R denotes the radius of nanotubes and D is the gap distance. Therefore, the Casimir force for small separation approximation (SSA) can be obtained by differentiating the energy with respect to D as:

$$ f_{cas} = - \frac{\partial E\left( D \right)}{\partial D} = \frac{ 1}{ 7 6 8}\pi^{3} \bar{h}cL\sqrt {\frac{ 2R}{{D^{7} }}} $$
(8)

Otherwise, for the case of cylinder-plate geometry with large separation gap, i.e. \( D \gg R \), the approximate expression for the attractive Casimir energy is written as (Bulgac et al. 2006):

$$ E^{D} = - \frac{{\bar{h}cL}}{{D^{ 2} }}\frac{ 1}{{16\pi { \ln }\left( {\frac{D}{R}} \right)}} $$
(9)

thereby, the Casimir force for large separation approximation (LSA) can be expressed as:

$$ f_{cas} = \frac{{\bar{h}cL}}{{D^{ 3} }}\frac{ 1}{{ 8\pi { \ln }\left( {\frac{D}{R}} \right)}} + \frac{{\bar{h}cL}}{{D^{ 3} }}\frac{ 1}{{ 1 6\pi { \ln }^{ 2} \left( {\frac{D}{R}} \right)}} $$
(10)

Furthermore, \( F_{e} \) in Eq. (2) denotes the distributed electrostatic force. The capacitance model is used to describe the electrostatic force. The capacitance per unit length of CNT denoted by C and the electrical force can be expressed as Hayt and Buck (2001):

$$ C = \frac{{2\pi \varepsilon_{0} }}{{\cosh^{ - 1} \left( {\frac{D - w}{{R_{w} }}} \right)}} $$
(11a)
$$ F_{e} = \frac{{d\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}CV^{2} } \right)}}{d\left( D \right)} = \frac{{\pi \varepsilon_{0} V^{2} }}{{\sqrt {\left( {D - w} \right)\left( {D - w + 2R_{w} } \right)} \left( {\cosh^{ - 1} \left( {\frac{D - w}{{R_{w} }}} \right)} \right)^{2} }} $$
(11b)

in which V denotes the applied voltage and \( \varepsilon_{0} \) is the permittivity of vacuum (ε 0 = 8.854 × 10−12 C2N−1m−2). However, Ke and Espinosa (2005) demonstrated that except for the tube ends, the electrostatic charge distribution applied on the cantilevered CNTs can be expressed by Eq. (11b). They clearly showed that the impact of tip-charge concentration on the deformation of cantilever is considerable. Therefore, the expression of the electrostatic force is composed of two terms which accounts for the influence of the classical charge density distributed along the cantilevered nanotube and the impact of the concentrated charge on the tube end. Thus, the corrected electrostatic load per unit length of nanotubes can be written as follows:

$$ F_{e,c} = F_{e} \left\{ {1 + 0.85\left[ {R_{w} \left( {D + R_{w} } \right)^{2} } \right]^{{{1 \mathord{\left/{\vphantom {1 3}} \right. \kern-0pt} 3}}} \delta \left( {x - L} \right)} \right\} $$
(12)

where \( \delta \left( x \right) \) is the Dirac delta function. As mentioned earlier, while a nanotube bends, the rippled configuration happens especially for the relatively and locally large deformations. It was demonstrated that the traditional linear bending-curvature relation cannot be used anymore. Instead, as can be observed in Fig. 3, the nonlinear relation calculated from FEM simulations should be employed. Therefore, the following polynomial equation was adopted to account for the rippling deformation (Wang et al. 2005):

$$ M\left( {x,t} \right) = EI\kappa \left( {1 - a_{3} D_{w}^{2} \kappa^{2} + a_{5} D_{w}^{4} \kappa^{4} - a_{7} D_{w}^{6} \kappa^{6} + a_{9} D_{w}^{8} \kappa^{8} } \right) $$
(13)

where D w and \( \kappa \) represent mean diameter and bending curvature of CNT and a 3 = 1.755 × 103, a 5 = 2.0122 × 106, a 7 = 1.115 × 109, a 9 = 2.26610 × 1011. Using the above-mentioned relation and the following relationship between the curvature \( \kappa \) and beam deflection w as:

$$ \kappa \left( {x,t} \right) = \frac{{w^{\prime \prime } \left( {x,t} \right)}}{{\left[ {1 + w^{\prime } \left( {x,t} \right)^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }} = w^{\prime \prime } \left[ {1 - \frac{3}{2}\left( {w^{\prime } } \right)^{2} + \frac{15}{8}\left( {w^{\prime } } \right)^{4} - \ldots } \right] \approx w^{\prime \prime } \left( {x,t} \right)\left[ {1 - \frac{3}{2}\left( {w^{\prime } \left( {x,t} \right)} \right)^{2} } \right] $$
(14)

the second partial derivative of the bending moment neglecting the higher order terms can be obtained as:

$$ M^{{\prime \prime }} \left( {x,t} \right) = EI\left[ {w^{(4)} - 3a_{3} D_{w}^{2} \left( {2w^{{\prime \prime }} \left( {w^{{\prime \prime }} } \right)^{2} + \left( {w^{{\prime \prime }} } \right)^{2} w^{(4)} } \right) - \frac{3}{2}\left( {2\left( {w^{{\prime \prime }} } \right)^{3} + 6w^{{\prime }} w^{{\prime \prime }} w^{\prime\prime\prime} + \left( {w^{{\prime }} } \right)^{2} w^{(4)} } \right)} \right] $$
(15)
Fig. 3
figure 3

The relation between bending moment and curvature of CNT for two different L/Dw (Wang et al. 2005)

Full size image

Substituting Eqs. (12) and (15) into Eq. (1), the non-linear governing equation for vibrating CNTs including rippling deformation and tip-charge concentration effects can be expressed as:

$$ \begin{aligned} EIw_{,xxxx} + cw_{,t} + \rho Aw_{,tt} &= EI\left[ {3a_{3} D_{w}^{2} \left( {2w_{,xx} \left( {w_{,xxx} } \right)^{2} + \left( {w_{,xx} } \right)^{2} w_{,xxxx} } \right) + \frac{3}{2}\left( {2\left( {w_{,xx} } \right)^{3} + 6w_{,x} w_{,xx} w_{,xxx} + \left( {w_{,x} } \right)^{2} w_{,xxxx} } \right)} \right] \hfill \\ &\quad + F_{e} \left\{ {1 + 0.85\left[ {R_{w} \left( {D + R_{w} } \right)^{2} } \right]^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} \delta \left( {x - L} \right)} \right\} + f_{cas} \hfill \\ \end{aligned} $$
(16)

The governing equation is subjected to four kinematic boundary conditions:

$$ w\left( {0,t} \right) = 0,\,\,\,w_{,x} \left( {0,t} \right) = 0,\,\,\,w_{,xx} \left( {L,t} \right) = 0,\,\,\,w_{,xxx} \left( {L,t} \right) = 0, $$
(17a)

and the following initial conditions:

$$ w\left( {x,0} \right) = 0,\,\,\,w_{,t} \left( {x,0} \right) = 0, $$
(17-b)

The non-dimensional variables are introduced as:

$$ \begin{aligned} \tau = \sqrt {\frac{EI}{{\rho AL^{4} }}\,} \,t,\,\,\,W = \frac{w}{D},\,\,\,\xi = \frac{x}{L},\,\,k = \frac{D}{{R_{w} }},\,\,\,\bar{V} = \frac{{\pi \varepsilon_{0} V^{2} L^{4} }}{{EID^{2} }},\,\,\,f = \frac{{C_{6} \sigma^{2} \pi^{2} N_{w} L^{4} }}{{dEID^{4} }}, \hfill \\ \hat{c} = cL^{2} \sqrt {\frac{1}{\rho AEI}\,} ,\,\,D_{L} = \frac{D}{L},\,\,\,\gamma = \frac{{\bar{h}cL^{4} }}{{ 8\pi D^{4} EI}} \hfill \\ \end{aligned} $$
(18)

thereby, the nonlinear vibrational equation of motion in non-dimensional form can be expressed as:

$$ \begin{aligned} W^{\left( 4 \right)} + \hat{c}\dot{W} + \textit{\"{W}} = \frac{{12a_{3} \gamma D_{L}^{4} }}{{k^{2} }}\left[ {2W^{\prime\prime}\left( {W^{\prime\prime\prime}} \right)^{2} + \left( {W^{\prime\prime}} \right)^{2} W^{\left( 4 \right)} } \right] + r\chi D_{L}^{2} \left[ {2\left( {W^{\prime\prime}} \right)^{3} + 6W^{\prime}W^{\prime\prime}W^{\prime\prime\prime} + \left( {W^{\prime}} \right)^{2} W^{\left( 4 \right)} } \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \bar{F}_{e} \left( {1 + \frac{{0.85D_{L} }}{k}\left( {1 + k} \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} \delta \left( {\xi - 1} \right)} \right) + \frac{{\pi^{4} \gamma }}{ 9 6}\sqrt {\frac{ 2}{{k\left( {1 - W} \right)^{7} }}} \hfill \\ \end{aligned} $$
(19-a)

for SSA approximation and:

$$ \begin{aligned} W^{\left( 4 \right)} + \hat{c}\dot{W} + \textit{\"{W}} = \frac{{12a_{3} \gamma D_{L}^{4} }}{{k^{2} }}\left[ {2W^{\prime\prime}\left( {W^{\prime\prime\prime}} \right)^{2} + \left( {W^{\prime\prime}} \right)^{2} W^{\left( 4 \right)} } \right] + r\chi D_{L}^{2} \left[ {2\left( {W^{\prime\prime}} \right)^{3} + 6W^{\prime}W^{\prime\prime}W^{\prime\prime\prime} + \left( {W^{\prime}} \right)^{2} W^{\left( 4 \right)} } \right] \hfill \\ \,\,\,\,\,\,\, + \bar{F}_{e} \left( {1 + \frac{{0.85D_{L} }}{k}\left( {1 + k} \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} \delta \left( {\xi - 1} \right)} \right) + \frac{\gamma }{{ (1 - W )^{3} }}\frac{1}{{{ \ln }\left( {k (1 - W )} \right)}} + \frac{\gamma }{{ (1 - W )^{3} }}\frac{1}{{2\left( {\ln \left( {k (1 - W )} \right)} \right)^{2} }} \hfill \\ \end{aligned} $$
(19-b)

for LSA approximation, in which \( \,\,r = 1.5 \) and

$$ \bar{F}_{e} = \frac{{\bar{V}^{2} }}{{\sqrt {\left( {1 - W} \right)\left( {1 - W + {2 \mathord{\left/ {\vphantom {2 k}} \right. \kern-0pt} k}} \right)} \left[ {\cosh^{ - 1} \left( {1 - k\left( {W - 1} \right)} \right)} \right]^{2} }},\,\,\,\chi = \left\{ {_{{1\,\,\,\,\,\,\,\,\,\,{\text{with}}\,\,{\text{rippling}}\,{\text{effect}}}}^{{0\,\,\,\,\,\,\,\,{\text{without}}\,\,{\text{rippling}}\,\,{\text{effect}}}} } \right. $$
(20)

where prime and dot denote the derivatives with respect to ξ and τ, respectively. By applying the initial conditions to Eq. (19-a, 19-b), the dynamic displacements at all time steps can be obtained.

3 Numerical approach for the non-linear problem

Owing to the nonlinear nature of electric and Casimir forces, applying the Galerkin-based reduced order model (ROM) to transform the dynamic governing Eq. (19-a, 19-b) to the coupled ordinary differential equations results is complicated and time consuming computations (Abbasnejad et al. 2013). In order to solve this nonlinear equation, one can change the governing equation into coupled linear ones. It should be noted that the electrostatic and intermolecular forces are depend on the CNT deflection and increase by increasing the nanotube deflection. To this end, a step-by-step simulation procedure is conducted and the nonlinear term is considered as a forcing term which should be calculated using the initial conditions at each time step. Then by applying the Galerkin decomposition method on the governing equation, coupled linear ordinary differential equations is achieved. It should be emphasized that the electrostatic and Casimir forces are updated during the analysis. Choosing small enough time steps leads to accurate numerical solution. As a result, at each time step, a system of linear differential equations can be obtained and integrated over time domain by any integration scheme such as Rung-Kutta method. Therefore, the initial conditions for the next time step are obtained and the above procedure will be repeated for all time steps.

To obtain an approximate Reduced-Order-Model (ROM), the non-dimensional deflection are assumed as \( W\left( {\xi ,\tau } \right) = \sum\nolimits_{j = 1}^{N} {q_{j} \left( \tau \right)\,\phi_{j} \left( \xi \right)} \), where N is the number of considered modes, \( q_{j} \left( \tau \right) \) denotes the time dependent generalized coordinate of the system and \( \phi_{j} \left( \xi \right) \) is the jth mode shape of nano-structure which can be expressed as:

$$ \phi_{j} \left( \xi \right) = \cosh \left( {\lambda_{j} \xi } \right) - \cos \left( {\lambda_{j} \xi } \right) - \frac{{\cosh \left( {\lambda_{j} } \right) + \cos \left( {\lambda_{j} } \right)}}{{\sinh \left( {\lambda_{j} } \right) + \sin \left( {\lambda_{j} } \right)}}\left( {\sinh \left( {\lambda_{j} \xi } \right) - \sin \left( {\lambda_{j} \xi } \right)} \right) $$
(21)

in which \( \varepsilon_{0} = 0.4 \) is the jth eigenvalue of the characteristic equation. Substituting Eq. (14) into Eq. (19-a, 19-b), multiplying by each mode shape and integrating from \( \mu_{mc} = 2 \) to \( \mu_{mc} \), results in the following linear differential equations as:

$$ \sum\limits_{j = 1}^{N} {M_{ij} \textit{\"{q}}_{j} \left( \tau \right)} + \sum\limits_{j = 1}^{N} {C_{ij} \dot{q}_{j} \left( \tau \right)} + \sum\limits_{j = 1}^{N} {K_{ij} q_{j} \left( \tau \right)} = F_{i} $$
(22)

in which \( M_{ij} \), \( C_{ij} \) and \( K_{ij} \) are the elements of the effective mass, damping and stiffness matrices, respectively and \( \lambda_{C} \) describes the nonlinear terms which are given by:

$$ M_{ij} = \int_{0}^{1} {\varphi_{i} \varphi_{j} d\xi } $$
(23-a)
$$ C_{ij} = \hat{c}\int_{0}^{1} {\varphi_{i} \varphi_{j} d\xi } $$
(23-b)
$$ K_{ij} = \int_{0}^{1} {\varphi_{i} \varphi_{j}^{(iv)} d\xi } $$
(23-c)
$$ \begin{aligned} F_{i} = \int_{0}^{1} {\varphi_{i} \left( {\frac{{12a_{3} \gamma D_{L}^{4} }}{{k^{2} }}\left[ {2\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime}_{j} q_{j} } } \right)\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime\prime}_{j} \,q_{j} } } \right)^{2} + \left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime}_{j} q_{j} } } \right)^{2} \left( {\sum\limits_{j = 1}^{N} {\varphi_{j}^{(4)} q_{j} } } \right)} \right]} \right.} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { + r\chi D_{L}^{2} \left[ {2\left( {\sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{3} + 6\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime}_{j} q_{j} } } \right)\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime\prime}_{j} \,q_{j} } } \right) + \left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} \left( {\sum\limits_{j = 1}^{N} {\varphi_{j}^{(4)} q_{j} } } \right)} \right]} \right)d\xi \hfill \\ \,\,\,\,\,\,\,\, + \int_{0}^{1} {\varphi_{i} \left( {\frac{{\bar{V}^{2} }}{{\sqrt {\left( {1 - \sum\nolimits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)\left( {1 - \sum\nolimits_{j = 1}^{N} {\varphi_{j} q_{j} } + {2 \mathord{\left/ {\vphantom {2 k}} \right. \kern-0pt} k}} \right)} \left[ {\cosh^{ - 1} \left( {1 - k\left( {\sum\nolimits_{j = 1}^{N} {\varphi_{j} q_{j} } - 1} \right)} \right)} \right]^{2} }}\left( {1 + \frac{{0.85D_{L} }}{k}\left( {1 + k} \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} \delta \left( {\xi - 1} \right)} \right)} \right)d\xi } \hfill \\ \,\,\,\,\,\,\,\, + \frac{{\pi^{4} \gamma }}{ 9 6}\int_{0}^{1} {\varphi_{i} \sqrt {\frac{ 2}{{k\left( {1 - \sum\nolimits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{7} }}} d\xi } \hfill \\ \end{aligned} $$
(23-d)

for SSA approximation and:

$$ \begin{aligned} F_{i} = \int_{0}^{1} {\varphi_{i} \left( {\frac{{12a_{3} \gamma D_{L}^{4} }}{{k^{2} }}\left[ {2\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime}_{j} q_{j} } } \right)\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime\prime}_{j} \,q_{j} } } \right)^{2} + \left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime}_{j} q_{j} } } \right)^{2} \left( {\sum\limits_{j = 1}^{N} {\varphi_{j}^{(4)} q_{j} } } \right)} \right]} \right.} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { + r\chi D_{L}^{2} \left[ {2\left( {\sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{3} + 6\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime}_{j} q_{j} } } \right)\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime\prime}_{j} \,q_{j} } } \right) + \left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} \left( {\sum\limits_{j = 1}^{N} {\varphi_{j}^{(4)} q_{j} } } \right)} \right]} \right)d\xi \hfill \\ \,\,\,\,\,\,\,\, + \int_{0}^{1} {\varphi_{i} \left( {\frac{{\bar{V}^{2} }}{{\sqrt {\left( {1 - \sum\nolimits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)\left( {1 - \sum\nolimits_{j = 1}^{N} {\varphi_{j} q_{j} } + {2 \mathord{\left/ {\vphantom {2 k}} \right. \kern-0pt} k}} \right)} \left[ {\cosh^{ - 1} \left( {1 - k\left( {\sum\nolimits_{j = 1}^{N} {\varphi_{j} q_{j} } - 1} \right)} \right)} \right]^{2} }}\left( {1 + \frac{{0.85D_{L} }}{k}\left( {1 + k} \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} \delta \left( {\xi - 1} \right)} \right)} \right)d\xi } \hfill \\ \,\,\,\,\,\,\,\, + \gamma \int_{0}^{1} {\varphi_{i} \left( {\frac{1}{{ (1 - \sum\nolimits_{j = 1}^{N} {\varphi_{j} q_{j} } )^{3} }}\left[ {\frac{1}{{{ \ln }\left( {k (1 - \sum\nolimits_{j = 1}^{N} {\varphi_{j} q_{j} } )} \right)}} + \frac{1}{{2\left( {\ln \left( {k (1 - \sum\nolimits_{j = 1}^{N} {\varphi_{j} q_{j} } )} \right)} \right)^{2} }}} \right]} \right)d\xi } \hfill \\ \end{aligned} $$
(23-e)

for LSA approximation. Equation (22) is a system of linear ordinary differential equations which can be integrated over time domain by any integration scheme such as Rung-Kutta method.

4 Results and discussion

4.1 Validation of present modeling

In order to check the soundness of present modeling to predict the pull-in behavior of CNT-based NEMS, two comparisons have been carried out with the experimental data reported by Ke et al. (2005) and molecular dynamics (MD) results (Dequesnes et al. 2004). In Table 1, the pull-in voltages of cantilevered CNT actuator in the presence of tip-charge concentration computed by different approaches are compared. The parameters used for this example are: nanotube length, L = 6.8 µm; initial gap between nanotube and electrode, D = 3 µm; R = Rext = 23.5 µm; modulus of elasticity \( E = 1 \, TPa \). As can be clearly observed, the value of predicted pull-in voltage agrees well with the reported results by experiments and finite kinematics regime (Ke et al. 2005).

Table 1 Pull-in voltages computed by different approaches
Full size table

As another comparison, the variation of predicted gap between the nanotube and bottom electrode for cantilever carbon nanotube of radius R = 0.68 nm, length L = 20.7 nm and initial gap D = 3 nm is compared with the published results using molecular dynamics (Dequesnes et al. 2004) (see Fig. 4). For this analysis, the number of graphene sheets is N = 40 and the product EI extract from MD has been estimated to be 22.5 × 10−26 Pa m4 (Dequesnes et al. 2004). According to this figure, one can see that excellent agreement in comparison with molecular dynamics simulations are obtained when the rippling deformation is included by employing the non-linear bending-curvature relation described in Eq. (8).

Fig. 4
figure 4

Comparison between molecular dynamics and present analysis

Full size image

4.2 Charge effect

As mentioned earlier, charge accumulation at nanotube ends called charge concentration (enhancement) has been demonstrated by Ke and Espinosa (2005) using density-functional theory and verified by FEM simulations and experimental results (Ke et al. 2005). In order to examine the influence of tip charge concentration on the instability behavior of nanotubes, variations of tip deflection, dynamic pull-in voltage and pull-in time affected by this phenomenon are presented. Figure 5 depicts the variation of initial gap between the nanotube and substrate versus the applied voltage. It is shown that the initial gap decreased by increasing the actuation voltage up to the occurrence of pull-in instability where the free end of the nanotube suddenly diverges to the substrate. According to this figure, it is clearly observed that the effect of charge concentration is to reduce the dynamic pull-in voltage of CNT actuators. In addition, the variation of pull-in voltage as a function of parameter k is plotted in Fig. 6. As illustrated in this figure, the dynamic pull-in voltage increases by increasing this non-dimensional parameter. Furthermore, one can observe that the dynamic pull-in value shifts downward as the charge concentration of tube end is included in the simulation.

Fig. 5
figure 5

Non-dimensional gap as a function of applied voltage: charge concentration effects

Full size image
Fig. 6
figure 6

Dynamic pull-in voltage versus the geometrical parameter k: charge concentration effects

Full size image

The time taken for CNT to pull-in and touches the fixed plate starting from initial state is called the pull-in time in the MEMS literature. The effect of charge concentration on the dynamic response of actuated CNTs is displayed in Fig. 7a, b. It is shown that in the presence of charge effect, the pull-in time of nanotube is decreased and the pull-in deflection is slightly decreased due to reduction of dynamic pull-in voltage.

Fig. 7
figure 7

The influence of charge concentration on a time history and b phase diagram of CNT-based NEMS

Full size image

4.3 Rippling deformation effect

For the case of CNTs, it has been experimentally reported that the rippling phenomenon can significantly affect the bending behavior of such structures. Its influence on the dynamic instability of actuated CNTs is addressed in this section. The variation of non-dimensional gap versus the applied voltage is displayed in Fig. 8. One can observe that as the effect of rippling deformation is included in the governing equation, the nanotube collapses onto the fixed substrate at lower value of dynamic pull-in deflection. In addition, it is clearly inferred that the rippling phenomenon substantially decreases the pull-in voltage of the structure.

Fig. 8
figure 8

Non-dimensional gap as a function of applied voltage: rippling formation effects

Full size image

To achieve a more quantitative investigation, comparisons between the dynamic pull-in values for two studied cases are presented in Fig. 9. It can be seen that the dynamic pull-in voltage remarkably reduces if the rippling effect is taken into consideration. In addition, the difference between the predicted pull-in voltages is increased by increasing the geometry parameter k. To study the effect of rippling deformation on the pull-in time and pull-in deflection of CNT NEMS, the time history and phase diagram are shown in Fig. 10. One can conclude that with the consideration of rippling formation, the pull-in time which is one of the key features in NEMS switches increases while the value of pull-in deflection is decreased considerably with respect to the case in which the classical beam theory is considered. Based on the reported results, it is noticeable that the rippling influences on the dynamic instability characteristics of the studied structure are remarkable with respect to the consideration of concentrated charge effects.

Fig. 9
figure 9

Dynamic pull-in voltage versus the geometrical parameter k: rippling formation effects

Full size image
Fig. 10
figure 10

The influence of rippling formation on a time history and b phase diagram of CNT-based NEMS

Full size image

4.4 Damping effects

To investigate the impact of damping parameter on the nonlinear behavior of considered CNT, time responses and phase portraits of the system are illustrated through Fig. 11a–d for different values of actuation voltage. The damping which has a significant effect at the nano-scale devices is not considered in Fig. 11a. One can observe that in the absence of damping effect, the system exhibits periodic oscillations before the occurrence of pull-in instability. The period of harmonic motions increases by increasing the actuation voltage. When the actuation voltage approaches to the dynamic pull-in value, a little increase in the voltage converts the stable behavior of nano-switch to the unstable one where the periodic motions vanish and CNT diverges to the bottom plate. On the other hand, with consideration of damping effects, as indicated in Fig. 11b, the amplitude of vibration damps with the time and the structure converge to the stationary state. However, by increasing the applied voltage, the CNT collapses into contact with the fixed substrate. The corresponding trajectories in the phase portrait for the considered situations are shown in Fig. 11c, d. It is observed that, in the absence of damping parameter and before pull-in point, there exist limit cycle trajectories around the stable center point. When pull-in instability occurs, the unstable saddle node appears in the phase portrait which is corresponded to the time when the CNT touches the bottom electrode. In addition, in the presence of damping effect, the periodic trajectories are replaced by the spiral motions around the stable focus point; by increasing the damping parameter, the position of the focus point moves to the right until it becomes an unstable saddle node at dynamic pull-in state.

Fig. 11
figure 11figure 11

Time histories and phase portrait of actuated CNT; a, c in the absence and b, d in the presence of damping effects

Full size image

The variation of the non-dimensional gap versus the applied voltage for different values of damping parameter \( \hat{c} \) is illustrated in Fig. 12. As it can be realized from this figure, the magnitude of the damping parameter has a great effect on the instability behavior of the nanotube actuators. It is observed that with the consideration of damping effects the dynamic pull-in voltage is increased. Figure 13 indicates the relationship between the dynamic pull-in voltage and geometry parameter k which is plotted for various values of parameter \( \hat{c} \). It is clearly concluded that the influence of damping is to increase the dynamic pull-in voltage. It is inferred that as the damping parameter equals to \( \hat{c} = 0.5 \), the dynamic pull-in value increases by about 7 % with respect to the case in which the damping effects is ignored.

Fig. 12
figure 12

Non-dimensional gap as a function of applied voltage: damping effects

Full size image
Fig. 13
figure 13

Dynamic pull-in voltage versus the geometrical parameter k: damping effects

Full size image

Finally, the significant effect of this parameter on the pull-in time values at the corresponding dynamic pull-in voltages are presented in Fig. 14a and b. Numerical results reveal that the pull-in time of CNT increases as the damping ratio increases. Furthermore, the normalized pull-in deflections effectively decrease by increasing the damping parameter \( \hat{c} \).

Fig. 14
figure 14

The influence of damping parameter on a time history and b phase diagram of CNT-based NEMS

Full size image

4.5 Casimir force effect

The plot of time responses and phase portraits of the free-standing Casimir-induced nanotubes may be of interest. To this end, the influence of Casimir force on the instability characteristics of nanotubes is investigated through Figs. 15 and 16 for the case of SSA and LSA models, respectively. According to illustrated results in Figs. 15a and 16a, one can observe that the nanotube deflection and time period of vibrating nanotubes under the influence of Casimir force, is increased by increasing parameter γ up to the adhesion time. On the other hand, in the vicinity of adhesion state, any increase in the Casimir parameter changes the dynamic behavior of the system and causes the nanotube to drop to the fixed plate.

Fig. 15
figure 15

Impact of Casimir parameter on the instability characteristics of nanotubes for SSA model, a time history b phase portrait

Full size image
Fig. 16
figure 16

Impact of Casimir parameter on the instability characteristics of nanotubes for LSA model, a time history b phase portrait

Full size image

As can be observed in Figs. 15b and 16b, at lower values of Casimir parameter, the system exhibits the periodic motions around the stable center point. When the dynamic instability occurs at critical Casimir value (here \( \gamma_{cr} = 67.0171 \) for SSA and \( \gamma_{cr} = 137.0981 \) for LSA models), homoclinic orbit appears in the phase plane which separates periodic solutions from the unbounded non-periodic trajectories around an unstable saddle node. The homoclinic orbit starts from the unstable branch of saddle node and return to it via the stable one. In addition, one can conclude that the free-standing Casimir-induced nanotube collapses to the bottom plate beyond the unstable saddle node.

5 Conclusion

  1. 1.

    The significant influences of concentrated charge, rippling deformation and Casimir attraction on the instability characteristics of CNT-based NEMS were addressed in this paper. To this end, the non-linear governing equation of vibrating CNTs including Casimir attraction was derived and solved using a step-by-step numerical approach. The influence of different parameters on the pull-in behavior of actuated nanotubes was also discussed. It was concluded that:

  2. 2.

    The pull-in voltage decreases with the consideration of concentrated tip charge and rippling formation effects.

  3. 3.

    Based on the reported results, it was inferred that the rippling influences on the dynamic instability behavior of the system are remarkable with respect to the consideration of concentrated charge effects.

  4. 4.

    The effect of rippling deformation is to increase the pull-in time and decrease the pull-in deflection

  5. 5.

    If the damping effects are included in the governing equation, the stable center point becomes the stable focus point. It means that the periodic motions are replaced by convergent spiral trajectories in the phase plane.

  6. 6.

    With the consideration of damping effect, the pull-in time increases while the pull-in deflection of the system decreases.