1 Introduction

The past decade has seen tremendous growth and remarkable progress in micro-fabrication techniques. Today, smaller, cheaper, and more precise microsystems are being produced and utilized in many industrial, military, medical, automotive, space, and consumer market applications. Microdevices are usually excited using simple input signals. These signals (magnetic, piezoelectric, electrostatic, thermal, etc.) are used to drive the device to a desired static configuration (e.g., micro-switches, optical crossconnects, thermal biomorphs) or to continuously excite the device to achieve a certain dynamic behavior (e.g., microresonators, microscanners, filters). A deep understanding of the behavior of these devices in response to these simple input signals is necessary to provide designers with insight into the proper choice of the design parameters. This results in a better response and maximum performance capabilities as well as reduction in the time and cost associated with the trial-and-error design process.

A particularly important and widely used microdevice is the torsional micromirror. This device is utilized to steer, reflect, or modulate light depending on the application at hand. It consists of two main components: a mechanical component, which represents the moving parts of the device and consists of two identical microbeams fixed on one side and connected to a rigid plate (the mirror) on the other side; and an electronic component, which provides the actuation signal through two sets of electrodes mounted beneath the mirror and used to rotate the mirror in either direction by supplying a voltage to the corresponding electrode.

Torsional micromirrors are used in projection displays (Van Kessel et al. 1998), switching in fiber-optic networks (Ford et al. 1999; Lin et al. 1999), neural networks (Collins et al. 1998), phase modulating filters, optical computing (Cohn and Sampsell 1988), electrophotographic printers, and folded spectrum analyzers (Hornbeck 1983). Moreover, the fast response and large scanning angles of micromirrors make them appealing substitutes for traditional scanning technologies. Therefore, they have been successfully implemented in resonant optical microscanners (Fan and Yu 1998). To achieve large rotation angles while minimizing the voltage requirements, the micromirror is excited at a resonant frequency and then used to steer a laser beam along a surface. The laser beam is then reflected from the surface to be collected and analyzed through a photo detector. Resonant scanning mirrors are used in a variety of applications, including laser printing, confocal microscopy, and scanning video displays.

There is a significant body of research on modeling and characterization of torsional micromirrors. Many researchers treated the mirror as a 1-DOF lumped-mass torsional system attached to two springs representing the suspension beams. They developed numerical and analytical techniques to investigate the static response and hence predict the pull-in point of the mirror. Osterberg (1995) introduced a simple approach to analyze the static tilt angle of a torsional micromirror. Using the parallel-plate approximation to estimate the electrostatic torque and a linear spring model to estimate the torsional stiffness of the suspension beams, he developed the simplest analytical model of the mirror. Although the model was numerically efficient, the results were 20% away from experimental findings. Hornbeck (1989) enhanced Osterberg’s model by developing an analytical expression for the electrostatic torque based on the solution of the Laplace equation between two semi-infinite tilted plates. He numerically solved for the mirror tilt angle at a given voltage and gradually increased the voltage until pull-in was reached. This numerical approach is extremely accurate, but requires successive numerical solutions of a complex nonlinear algebraic equation. To alleviate these shortcomings, other researchers (Degani et al. 1998; Nemirovisky and Degani 2001; Degani and Nemirovisky 2002; Zhang et al. 1999; Zhang et al. 2001) developed analytical methods to calculate the pull-in parameters of a 1-DOF lumped-mass torsional micromirror.

Degani and Nemirovsky (2001) were the first to introduce a 2-DOF lumped-mass model that includes both torsion and bending to capture the static behavior of a torsional microactuator. Huang et al. (2004) adopted this model to study the static behavior of a torsional micromirror. They derived the equations governing the response of the mirror to a DC voltage and studied the effect of electrode size and position on the pull-in parameters. They found that neglecting the bending of the suspension beams can result in more than 20% error in the prediction of the tilt angles.

Most of the available dynamic models also assume a 1-DOF lumped-mass system (Wetzel and Strozewski 1993; Sattler et al. 2002; Sane et al. 2003). In one implementation, Ataman and Urey (2006) analyzed the dynamics of a resonant microscanner subjected to pure AC voltage excitations using a 1-DOF torsional lumped-mass model. Based on the solution of the Mathieu equation, they analyzed the response of the mirror and characterized the linear stability of the device. Furthermore, for large scanning angles, they numerically analyzed the nonlinear response and observed a softening-type nonlinearity. This nonlinear softening behavior was also experimentally reported by Camon and Larnaudi (2000).

Zhao et al. (2005) were the first to consider the coupling effect between torsion and bending in a dynamic model. They treated the mirror as a lumped mass attached to two springs. The springs represent the torsional and bending stiffnesses of the suspension beams. They numerically simulated the dynamic response of the mirror to step and pure AC voltage excitations. The numerical simulations also revealed a softening-type behavior.

To the authors’ knowledge, a comprehensive distributed-parameter model that captures the complete response of a torsional micromirror has yet to be developed. This model will be utilized to study the accuracy and legitimacy of the widely used SDOF and 2DOF models as well as analyze the effect of the higher dynamic modes. Furthermore, there has not been any analytical study of the nonlinear dynamics of resonant microscanners subjected to combined DC and resonant AC excitations. In this work, we treat the mirror as a distributed-parameter system. We use a Galerkin procedure to develop a reduced-order model (ROM) that accurately represents the static and significant dynamic response of the mirror. Using the ROM, we conduct a convergence analysis to determine the minimum number of assumed modes sufficient to accurately predict the mirror response. We use the method of multiple scales to analyze the nonlinear response of a microscanner subjected to combined DC and resonant AC excitations. We found that, within a range of DC voltages, a two-to-one internal resonance might be activated between the first two modes. Due to this internal resonance, even if the bending motions are very small, the energy fed to the first (torsion) mode can be channeled to the second (bending) mode. This energy transfer results in undesirable vibrations detrimental to the scanner’s performance.

2 Model

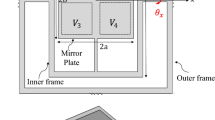
We consider the micromirror, Fig. 1, developed by Zhang et al. (1999, 2001). It consists of two identical microbeams of length l, width w, and thickness h. The beams are fixed on one side and connected to a rigid rectangular plate (the mirror) on the other side. The mirror has a length L m , width a, and thickness h. Two electrodes each of length b and width \(c=\frac{1}{2}(a_2-a_1)\) are located beneath the micromirror on both sides of the suspension beams. The perpendicular distance between the undeformed position of the mirror and the electrodes is denoted as d. The whole micro-structure is made of polysilicon. The geometric and material properties of the mirror are listed in Table 1.

Fig. 1
figure 1

A schematic of the micromirror

Full size image
Table 1 Geometric and material properties of the micromirror
Full size table

The mirror is rotated in either direction by supplying a voltage V(τ) to the corresponding electrode. The electrostatic potential between the electrode and the mirror generates an electrostatic field on the mirror, and hence produces a downward electrostatic force and an electrostatic moment around the suspension axis. Consequently, the microbeams undergo simultaneous and distributed torsion \({\hat{\theta}}(x,\tau)\) and deflection \({\hat{u}}(x,\tau)\) and the micromirror rotates an angle \({\hat{\theta}}_m (\tau)\) and deflects a distance \({\hat{u}}_m(\tau).\)

Because of the difference in rigidity between the plate and beams, we treat the micromirror as a rigid plate and write the Lagrangian of the system as

$$ \begin{aligned} {{\mathcal{L}}} &=\int\limits_0^1{\theta}_{t}^2\;d\xi+\gamma_1\int\limits_0^1 {u}_{t}^2 d \xi-\int\limits_0^1 {\theta}_\xi^2\;d\xi-\gamma_2\int\limits_0^1 {u}_{\xi \xi}^2\;d\xi \\ &\quad+ \gamma_3 {\theta}^2_{m t}+ \gamma_4 {u}^2_{m t}+\gamma_5{u}_m +\frac{\gamma_6}{\theta_m} \ln\left[\frac{1-{u}_m-\alpha {\theta}_m}{1-{u}_m-\beta {\theta}_m}\right]\\ \end{aligned} $$
(1)

where the subscripts t and ξ indicate partial derivatives with respect to these variables,

$$ \begin{array}{*{20}l} {\xi=\frac{z}{2l}}, & {t= \frac{\tau}{T}},& \\ \\ {\gamma_1=\frac{12 d^2}{\theta^2_{\rm cr}(h^2+w^2)}}, &{\gamma_2=\frac{E h^3 w d^2}{48 G J_b l^2 \theta^2_{\rm cr}}},& {\gamma_3=\frac{a L_m(h^2+a^2)}{2 l w (h^2+w^2)}}, \\ \\ {\gamma_4=\frac{6L_m a d^2}{w l(h^2+w^2) \theta^2_{\rm cr}}}, & {\gamma_5=\frac{4\rho h a L_m g d l}{G J_b\theta^2_{\rm cr}}},& {\gamma_6= \frac{2 \epsilon_0 b V^2 l}{G J_b\theta^3_{\rm cr}}},\\ \\ {\alpha=\frac{a_1}{a}},&{\beta= \frac{a_2}{a}}, &{\theta_{\rm cr}= \frac{2d}{a}},\\ \\ {{\theta}=\frac{\hat{\theta}}{\theta_{\rm cr}}},&{u=\frac{\hat{u}}{d}}&\\ \end{array} $$

are dimensionless quantities, T 2 = ρw h l 2 (h 2 + w 2)/(3 G J b ) is a time scale, and

$$ J_b=\frac{w h^3}{3}\left[1-\frac{192 h}{w\pi^5}\sum_{n=0}^\infty \frac{1}{(2n+1)^5}\hbox{tanh} \frac{(2n+1)^5}{2(w/h)}\right] $$

is the polar moment of inertia of the suspension beams including cross-sectional warping effects. In Eq. 1, the first two terms represent the kinetic energy of the suspension beams, the third and fourth terms represent the elastic energy stored in the suspension beams, the fifth and sixth terms represent the kinetic energy of the mirror plate, the seventh term represents the potential energy of the plate, and the last term represents the potential energy of the electrostatic field.

To generate the ROM, we carry out a Galerkin expansion of the rotation θ and deflection u in the Lagrangian. To this end, we write:

$$ {\theta}(\xi,t) =\sum\limits_{i=1}^{n} p_i(t)\psi_i({\xi}) , \quad {u}(\xi,t) =\sum\limits_{i=1}^{m}q_i(t)\varphi_i({\xi}) $$
(2)

where p i and q i are the generalized coordinates corresponding to the basis functions ψ i and φ i . We choose the basis sets to be the orthonormal eigenfunctions of the free torsional vibrations of a clamped-clamped beam and the bending vibrations of a clamped-clamped beam with a concentrated mass at its middle.

To obtain the equations of motion in terms of the generalized coordinates, we substitute Eq. 2 into Eq. 1, carry out the integration over the spatial domain of ξ, apply the orthogonality conditions, then use the Euler–Lagrange equation to generate the following equations:

$$ \begin{aligned} &\ddot{p}_i + \gamma_3 \sum\limits_{j=1}^{n}\ddot{p}_j \psi_i\left(\frac{1}{2}\right)\psi_j\left(\frac{1}{2}\right)+p_i \Lambda_{ii}= \frac{\gamma_6}{2\sum\nolimits_{j=1}^n p_j \psi_j\left(\frac{1} {2}\right)}\\ &\quad \times \left\{\frac{\beta}{1-\sum\nolimits_{j=1}^m q_j \varphi_j\left(\frac{1}{2}\right)- \beta\sum\nolimits_{j=1}^n p_j \psi_j\left(\frac{1}{2}\right)} -\frac{\alpha}{1-\sum\nolimits_{j=1}^m q_j \varphi_j\left(\frac{1}{2}\right)-\alpha \sum\nolimits_{j=1}^n p_j \psi_j\left(\frac{1}{2}\right)}\right.\\ \,&\quad\left. +\frac{1}{\sum\nolimits_{j=1}^n p_j \psi_j\left(\frac{1}{2}\right)} \hbox{ln}\left[\frac{1-\sum\nolimits_{j=1}^m q_j \varphi_j\left(\frac{1}{2}\right)-\beta\sum\nolimits_{j=1}^n p_j \psi_j\left(\frac{1}{2}\right)}{1-\sum\nolimits_{j=1}^m q_j \varphi_j\left(\frac{1}{2}\right)-\alpha\sum\nolimits_{j=1}^n p_j \psi_j\left(\frac{1}{2}\right)}\right]\right\}\\ \end{aligned} $$
(3)
$$ \begin{aligned} &\gamma_1\ddot{q}_i+ \gamma_4 \sum\limits_{j=1}^{\infty}\ddot{q}_j \varphi_i\left(\frac{1}{2}\right)\varphi_j\left(\frac{1}{2}\right)+\gamma_2 q_i \Upsilon_{ii} -\frac{1}{2}\gamma_5 \varphi_i\left(\frac{1}{2}\right) =\frac{\gamma_6}{2\sum\nolimits_{j=1}^n p_j \psi_j\left(\frac{1}{2}\right)}\\ &\quad\times\left\{\frac{1}{1-\sum\nolimits_{j=1}^m q_j \varphi_j\left(\frac{1}{2}\right) - \beta\sum\nolimits_{j=1}^n p_j \psi_j\left(\frac{1}{2}\right)}-\frac{1}{1-\sum\nolimits_{j=1}^m q_j \varphi_j\left(\frac{1}{2}\right)-\alpha \sum\nolimits_{j=1}^n p_j \psi_j\left(\frac{1}{2}\right)} \right\}\\ \end{aligned} $$
(4)

where

$$ \int\limits_0^1 \psi_i^{\prime}\psi_j^{\prime}\;d\xi=\Lambda_{ij}\delta_{ij}, \quad \int\limits_0^1 \varphi_i^{\prime\prime} \varphi_j^{\prime\prime}\;d\xi=\Upsilon_{ij}\delta_{ij} $$

and δ is the Kronecker delta.

3 Static analysis

In the absence of time variation, the Lagrangian, Eq. 1, reduces to the total potential energy of the system

$$ {{\mathcal{L}}}_s=U=-2\int\limits_0^{1/2} {\theta}_\xi^2\;d\xi-2\gamma_2\int\limits_0^{1/2} u_{\xi \xi}^2\;d\xi+\gamma_5{u}_m +\frac{\gamma_6}{{\theta}_m} \ln\left[\frac{1-u_m-\alpha \theta_m}{1-u_m-\beta {\theta}_m}\right] $$
(5)

We can obtain the exact solution for the static deflection and torsion of the micromirror and the suspension beams by solving the corresponding boundary-value problem analytically. The deflection problem is

$$ \begin{aligned} &\frac{d^4 {u}}{d \xi^4}=0, \quad {u}(0) =0, \quad \frac{du}{d \xi}(0)=0,\\ &u\left(\frac{1}{2} \right) = u_m, \quad \frac{du}{d\xi}\left(\frac{1}{2} \right)=0\\ \end{aligned} $$
(6)

where the slope of the beam at ξ = 1/2 is zero due to symmetry. The torsion problem is

$$ \frac{d^2{\theta}}{d\xi^2}=0,\quad {\theta}(0)=0, \quad {\theta}\left(\frac{1}{2} \right)=\theta_m $$
(7)

Solving Eqs. 6 and 7 for u(ξ) and θ(ξ), we obtain

$$ {u}(\xi)=-16 u_m d \xi^3 +24 u_m \xi^2 $$
(8)
$${\theta}(\xi)=2 {\theta}_m \xi $$
(9)

For static equilibrium, the total potential energy U is stationary. Substituting Eqs. 8 and 9 into Eq. 5, setting the partial derivatives of the potential energy equal to zero \((\partial U/\partial {u}_m=\partial U/\partial {\theta}_m=0),\) we obtain two equations that can be solved numerically for the mirror deflection u m and rotation angle θ m corresponding to a given DC voltage V. The results are then substituted into Eqs. 8 and 9 to obtain the spatial distribution of the static deflection and torsion of the suspension beams.

To study convergence of the ROM, Eqs. 3 and 4, we compare its results to the exact static solution and to available experiments. Towards that end, we set the time derivatives in Eqs. 3 and 4 equal to zero, increase the number of spatial modes (n,m) gradually, and solve Eqs. 3 and 4 for the generalized coordinates (p 1s , p 2s ,..., p ns ) and (q 1s , q 2s ,..., q ms ) until the solution converges over the voltage range. Figure 2a and b show convergence of the equilibrium solutions obtained using the ROM to the exact solution. The results of the ROM converge to the exact stable and unstable branches of solutions using nine torsional modes and three bending modes (n = 9, m = 3).

Fig. 2
figure 2

Comparison of the mirror tilt angle θ m and deflection u m obtained from the reduced-order model (ROM) to the exact solution

Full size image

To validate the converged ROM, we compare its results to the experimental results obtained by Degani et al. (1998) in Fig. 3. It demonstrates excellent agreement with the experimental results, thereby validating the ROM. It is worth noting that, when compared to the exact solution, the ROM does not provide a more efficient alternative to predicting the static response of the beam. However, the ability of the ROM to predict the dynamic response is dependent on its ability to predict the static behavior of the mirror.

Fig. 3
figure 3

Variation of the mirror tilt angle with the driving voltage V

Full size image

4 Linear dynamic response

We study the dynamics of the micromirror shown in Fig. 1 around its equilibrium position. To obtain the natural frequencies ω i and the associated eigenfunctions \({{\mathbb{A}}}_i,\) we let

$$ \begin{aligned} p_i&=p_{is}+p_{id} \quad i=1,2,\ldots,n \\ q_i&=q_{is}+q_{id} \quad i=1,2,\ldots,m\\ \end{aligned} $$
(10)

where the subscript s denotes the static part of the response, and the subscript d denotes the dynamic part. We linearize the governing equations around the static equilibrium position (p 1s , p 2s , ..., p ns , q 1s , q 2s , ..., q ms ), assume that the solution of the linearized equations has the harmonic form \({{\mathbb{A}}}_i e^{i {\omega_i}t},\) substitute this solution into the linearized equations of motion, and obtain the characteristic equation of the micromirror vibrations. We then solve the characteristic equation numerically for the eigenfrequencies ω i . To determine the number of spatial modes necessary for convergence, we gradually increase the number of modes (n,m) used in the Galerkin procedure until the addition of new modes does not change the eigenfrequencies, within a specified tolerance, over the whole voltage range. In our case, the solution converges when the numbers of torsional and bending modes are n = 8 and m = 3.

At zero voltage, there is no electrostatic field and the eigenvalue problem uncouples into two parts corresponding to torsion and bending. Solution of the uncoupled eigenvalue problems reveals that the lowest eigenvalue is associated with torsion; the next two eigenvalues are associated with bending; the fourth, fifth, and sixth are associated with torsion; the seventh is associated with bending; and so forth. The modes maintain their relative order regardless of the strength of the electrostatic field. Figures 4a–c show variations of the first five natural frequencies with the applied voltage as well as results of the convergence study for the first two frequencies.

Fig. 4
figure 4

Variation of the natural frequencies with the applied DC voltage: a first; b second; c third, fourth, and fifth natural frequencies

Full size image

As the applied voltage is increased, the first and second natural frequencies decrease sharply, reflecting the system approach to pull-in. However, the third, fourth, and fifth frequencies do not change appreciably. At the pull-in voltage, the first natural frequency ω1 passes through zero, which indicates a dynamic instability.

Next, we show evolution of the first four eigenfunctions as the voltage is increased from V = 0 to pull in, V p. Due to symmetry, we only show the eigenfunctions of the left suspension beam. Figures 5a and b show evolution of the first eigenfunction Ψ1. At zero voltage, the eigenfunction Ψ1 is purely torsional. As the voltage V is increased, coupling between torsion and bending starts, and the eigenfunction develops a bending component, which starts to grow. This coupling is due to the electrostatic field and is more pronounced for higher voltages.

Fig. 5
figure 5

Evolution of the eigenfunctions with the applied voltage: a torsional component of the first eigenfunction Ψ1; b bending component of the first eigenfunction Ψ1; c torsional component of the second eigenfunction Ψ2; d bending component of the second eigenfunction Ψ2; e torsional component of the third eigenfunction Ψ3; f bending component of the third eigenfunction Ψ3; g torsional component of the fourth eigenfunction Ψ4; h bending component of the fourth eigenfunction Ψ4

Full size image

Similarly, as shown in Fig. 5c and d, at zero voltage the eigenfunction Ψ2 is purely bending. However, as the voltage is increased, coupling between bending and torsion appears and increases gradually, resulting in the appearance and growth of a torsion component of this eigenfunction. The components of the second eigenfunction are always out-of-phase, while those of the first eigenfunction are always in-phase. Figures 5e–h show the third and fourth eigenfunctions Ψ3 and Ψ4, respectively. We note that as the voltage is increased all the way to pull-in, the eigenfunctions remain unchanged and no coupling occurs between torsion and bending.

4.1 Lumped-mass model

The natural frequencies of the higher modes are two orders of magnitude larger than the first two natural frequencies. Further, at zero voltage the eigenfunctions associated with these modes are the first torsion and bending modes of the suspension beams. Unless the micromirror is excited at high frequencies, the higher modes are not expected to either capture or transfer energy to the lower frequency modes (Nayfeh 2000). Therefore, one can safely assume that, when the mirror is excited near any of the first two modes, a two-mode assumption is enough to predict the behavior of the beam response. This is a critical finding because it implies that one can treat the micromirror as a lumped mass attached to two springs representing the suspension beams. The first spring is a torsional spring with stiffness \(k_{11}= \frac{2 G J_p}{l},\) and the second spring is a bending spring with stiffness \(k_{22}=\frac{24 EI_{b_y}} {l^3}.\) The equations of motion for the mirror can therefore be reduced to

$$ m_{11}\ddot{{\theta}}_m+\mu_1\dot{{\theta}}_m+k_{11}{\theta}_m = \frac{V^2}{2\theta_{\rm cr}}\frac{\partial C}{\partial \theta_m} $$
(11a)
$$ m_{22}\ddot{{u}}_m+\mu_2\dot{{u}}_m+k_{22}{u}_m =\frac{V^2} {2d}\frac{\partial C}{\partial u_m}+\frac{Mg}{d} $$
(11b)

where C is the capacitance between the mirror and the active electrode given by

$$ C= \frac{\epsilon_0 b}{\theta_m \theta_{\rm cr}}\ln\left[\frac{1 - u_m -\alpha \theta_m}{1 - u_m -\beta \theta_m}\right] $$

and

$$ \begin{aligned} m_{11}&=\frac{I_{{m}_{zz}}}{T^2}, \quad m_{22}=\frac{M}{T^2}, \\ \mu_1&= \frac{\sqrt{k_{11}m_{11}}}{Q_1}, \quad \mu_2 = \frac{\sqrt{k_{22}m_{22}}}{Q_2} \\ \end{aligned} $$

Here, \(I_{m_{zz}}=\frac{1}{12}M(h^2+a^2)\) is the mass moment of inertia of the mirror around the z-axis, M is the mass of the plate, and Q 1 and Q 2 are the quality factors of torsion and bending motions, respectively. In Fig. 6, we show a comparison between the first two natural frequencies obtained using the ROM and those obtained using the lumped-mass model. The figure shows good agreement over the whole operation range.

Fig. 6
figure 6

Comparison between the first two natural frequencies obtained using the lumped-mass model and the ROM

Full size image

4.2 Sensitivity of the Natural Frequencies to the Electrode Parameters

To examine sensitivity of the first two natural frequencies of the micromirror to changes in the electrode size and position, we plot ω1 and ω2 for three values of α = 0, 0.15, and 0.3 in Fig. 7 and three values of β = 0.70, 0.85, and 1 in Fig. 8. These results show the impact of changing the size of the electrostatic field, and hence its balance with the elastic energy of the suspension beams, on the linear vibrations of the micromirror. Decreasing α or increasing β increases the electrode size and hence increases the negative linear stiffness arising from the electrostatic force and moment. This, in turn, causes the first two natural frequencies to drop faster as pull-in is approached as shown in Figs. 7 and 8.

Fig. 7
figure 7

The first and second natural frequencies for α = 0, 0.15, and 0.3

Full size image
Fig. 8
figure 8

The first and second natural frequencies for β = 0.7, 0.85, and 1

Full size image

It can also be seen from Fig. 7 that the second natural frequency is more sensitive to changes in α than the first natural frequency. The bending-dominated second natural frequency responds to changes in the electrode size only. On the other hand, the torsion-dominated first natural frequency responds to changes in both of the electrode size and location with respect to the axis of rotation. Decreasing α increases the electrode size, while decreasing the distance between the centroid and the axis of rotation and hence the moment arm. Therefore, its impact on the electrostatic force is purely proportional, while its impact on the electrostatic moment is the sum of proportional and counter-proportional components.

On the other hand, changing β, which defines the position of the outer side of the electrode, has a significant impact on both of the first and second natural frequencies. This results from the fact that increasing β increases both of the size of the electrode and the moment arm and therefore significantly affects the electrostatic force and moment.

5 Nonlinear analysis

We analyze the response of the micromirror to electric excitations consisting of a DC component V dc and an AC component V accos(Ω t), where Ω is approximately equal to the natural frequency ω1 of the first mode. We start by expressing the response in the form

$$ {\theta_m}={\theta}_s+{\theta}_{\delta}, \quad {u_m}={u}_s+{u}_{\delta} $$
(12)

where the subscript s denotes the static part and the subscript δ denotes the dynamic part. Substituting Eq. 12 into Eq. 11, using the equilibrium equations describing u s and θ s , expanding the electrostatic force and moment in Taylor series around u s and θ s , and keeping only terms up to third order in θδ and u δ, we obtain

$$ \begin{aligned} m_{11} {\ddot{\theta}}_{\delta}+ \mu_1 {\dot{\theta}}_{\delta} + k_{11} \theta_{\delta} &=\Gamma_1 \alpha_{11} (2 V_{\rm dc} V_{\rm ac}\cos(\Omega t)+V_{\rm ac}^2\cos^2(\Omega t)) \\ &\quad +\Gamma_1 V^2(\alpha_{12}{\theta}_{\delta} +\alpha_{13}{u}_{\delta} +\alpha_{14}{\theta}_{\delta}{u}_{\delta} +\alpha_{15}{\theta}^2_{\delta} \\ &\quad +\alpha_{16}{u}^2_{\delta} +\alpha_{17}{\theta}_{\delta}{u}^2_{\delta} +\alpha_{18}{\theta}^2_d{u}_{\delta}+\alpha_{19}{\theta}^3_{\delta} +\alpha_{110}{u}^3_{\delta})\\ \end{aligned} $$
(13)
$$ \begin{aligned} m_{22} {\ddot{u}}_{\delta}+ \mu_2 {\dot{u}}_{\delta} + k_{22} u_{\delta}&=\Gamma_2 \alpha_{21} (2 V_{\rm dc} V_{\rm ac}\cos(\Omega t)+V_{\rm ac}^2\cos^2(\Omega t)) \\ &\quad + \Gamma_2 V^2 (\alpha_{22}{\theta}_{\delta} +\alpha_{23}{u}_{\delta} +\alpha_{24}{\theta}_{\delta}{u}_{\delta} +\alpha_{25}{\theta}^2_{\delta} \\ &\quad +\alpha_{26}{u}^2_{\delta} +\alpha_{27}{\theta}_{\delta}{u}^2_{\delta} +\alpha_{28}{\theta}^2_{\delta}{u}_{\delta} +\alpha_{29}{\theta}^3_{\delta} +\alpha_{210}{u}^3_{\delta}) \\ \end{aligned} $$
(14)

where

$$ \Gamma_1=\frac{\epsilon_0 b}{2 \theta^3_{\rm cr}}, \quad \Gamma_2=\frac{\epsilon_0 b}{2 d^2 \theta_{\rm cr}}, $$

and the α ij coefficients result from the Taylor series expansions. We use the method of multiple scales (Nayfeh 1981) to find a uniformly valid second-order approximate solution of Eqs. 13 and 14 in the form

$$ {\theta}_{\delta}=\varepsilon\theta_0(T_0, T_1,T_2)+\varepsilon^2\theta_1(T_0, T_1, T_2)+\varepsilon^3\theta_2(T_0,T_1, T_2)+\cdots $$
(15a)
$$ {u}_{\delta}=\varepsilon u_0(T_0, T_1, T_2)+\varepsilon^2u_1(T_0,T_1, T_2)+\varepsilon^3u_2(T_0,T_1, T_2)+\cdots $$
(15b)

where ɛ is a small nondimensional bookkeeping parameter and T 0 = t, T 1 = ɛt, and T 2 = ɛ2 t are time scales. We scale the forcing, damping, and frequency detuning such that the effect of the excitation is balanced by those of damping and nonlinearity; that is,

$$ V = V_{\rm dc}+ \varepsilon^3 V_{\rm ac} \cos(\Omega t), \quad \mu_i=\varepsilon^2 \mu_i, \quad \Omega=\omega_1+\varepsilon^2 \sigma $$

where σ is a detuning parameter that describes the nearness of Ω to ω1. Carrying out the perturbation analysis (Daqaq 2006), we obtain a second-order approximation of the response of the mirror as

$$ \begin{aligned} \theta_m(t)&=\theta_s+c_{11}a_1(t)\cos(\omega_1 t+\beta_1(t))+c_{12}a_2(t)\cos(\omega_2 t+\beta_2(t)) \\ &\quad +c_{13}a^2_1(t)\cos2[\omega_1t+\beta_1(t)]+c_{14}a^2_2(t)\cos 2[\omega_2t+\beta_2(t)]\\ &\quad +c_{15}a^2_1(t)+c_{16}a^2_2(t) \\ \end{aligned} $$
(16a)
$$ \begin{aligned} u_m(t)&=u_s+c_{21}a_1(t)\cos(\omega_1 t+\beta_1(t))+c_{22}a_2(t)\cos(\omega_2 t+\beta_2(t))\\ &\quad +c_{23}a^2_1(t)\cos2[\omega_1t+\beta_1(t)]+c_{24}a^2_2(t)\cos2[\omega_2t+\beta_2(t)]\\ &\quad +c_{25}a^2_1(t)+c_{26}a^2_2(t)\\ \end{aligned} $$
(16b)

where ω1 and ω2 are the linear frequencies of the mirror corresponding to a given DC voltage and c ij are functions of θ s , u s , and V dc. The amplitudes a i (t) and phases β i (t) of the response are governed by the following modulation equations:

$$ 2 \omega_1 \Lambda_{11} a_1^{\prime}=\omega_1 \Lambda_{12} a_1+ 2 \Lambda_{13}V_{\rm ac}\sin(\gamma) $$
(17a)
$$ 2 \omega_1 \Lambda_{11} a_1 (\gamma^{\prime}-\sigma a_1)=-\frac{1}{4}( 8 \Lambda_{13} V_{\rm ac}\cos(\gamma)+ \Lambda_{14} a^3_1+\Lambda_{15}a_1 a^2_2 ) $$
(17b)
$$ 2\Lambda_{21}a_2^{\prime}=\Lambda_{22}a_2 $$
(17c)
$$ 2\omega_2 \Lambda_{21} a_2\beta_2^{\prime}=-\frac{1}{4}(\Lambda_{24} a^3_1+\Lambda_{25}a_2 a^2_1) $$
(17d)

where the prime indicate the derivative with respect to time, γ = σt−β1, and the Λ ij are constants.

The behavior of the mirror is characterized by the solution of the modulation equations. A fixed-point of the modulation equations corresponds to a periodic response of the mirror. Since microscanners are designed to scan a surface periodically, we analyze the equilibrium solutions of the modulation equations and their stability. The equilibrium solutions are found by setting the time derivatives in Eq. 17 equal to zero and solving the resulting algebraic system for the roots (a 1, a 2, γ, β2). The stability of the equilibrium solutions is determined by finding the eigenvalues of the Jacobian matrix of the modulation equations evaluated at the equilibrium solution. If all of the eigenvalues associated with a given equilibrium solution have negative real parts, the equilibrium is asymptotically stable. If one or more eigenvalues have positive real parts, the solution is unstable. Setting the time derivative in Eq. 17 equal to zero, we obtain

$$ \frac{\omega^2_1 \Lambda^2_{12}}{4 \Lambda^2_{13}} a^2_1+\left[\frac{\omega_1\Lambda_{11}}{ \Lambda_{13}}\sigma a_1-\frac{\Lambda_{14}}{8 \Lambda_{13}}a^3_1\right]^2-V^2_{\rm ac}=0 $$
(18a)
$$ a_2=0 $$
(18b)

Using Eq. 18a, we study frequency–response curves of the first mode amplitude a 1 for different bias voltages V dc and V ac = 0.2 V. Figure 9a illustrates that, as the DC voltage is increased, the magnitude of the effective nonlinearity increases, and the curves bend further towards the left, indicating a softening-type behavior. The softening nonlinearity results in multiple stable solutions at excitation frequencies close but less than the natural frequency of the first mode. Operating the mirror in that region can cause abrupt jumps in the mirror response, thereby degrading the scanner performance. Figure 9b shows variation of the response amplitude a 1 with the frequency detuning σ for different values of V ac and V dc = 15 V. As the excitation level V ac is increased, the response amplitude a 1 increases, and the frequency-response curves bend more towards the left, thereby stretching further the region of multi-valued solutions.

Fig. 9
figure 9

Frequency–response curves of the microscanner for a V ac = 0.2 V; b V dc = 15 V. Dashed lines represent unstable solutions

Full size image

This softening nonlinearity of the mirror can also be seen by studying variation of the effective nonlinearity coefficient \(\left(\frac{-\Lambda_{14}}{8 {\omega_1}\Lambda_{11}}\right)\) with V dc, Fig. 10. The effective nonlinearity is negative for all values of V dc through pull-in. Its magnitude grows from very small values, and hence minimal effect on the response, for small values of V dc to large values near pull-in. In the vicinity of V dc≈13.2 V, the effective nonlinearity has a discontinuity and our approximate solution breaks down. This discontinuity occurs because of the nearness of the second natural frequency to twice the first natural frequency; that is, ω2≈2 ω1. These internal resonance channels the energy fed to the first mode, via an excitation in the neighborhood of ω1, to the second mode, thus violating the underlying assumption of our approximation that a 2 →0 as t →∞. As a result, the microscanner exhibit aperiodic (quasiperiodic in this case) response as the two modes exchange energy as shown in Fig. 11. The quasiperiodic response of the microscanner results in steady-state fluctuations of the tilt angle amplitude θ m and non-zero bending oscillations u m , thereby changing the size of the scanned area from cycle to cycle and bringing the target area in- and out-of-focus within each cycle.

Fig. 10
figure 10

The effective nonlinearity of the first mode

Full size image
Fig. 11
figure 11

Long-time histories of the micromirror response for V dc = 13.2 V, σ1 = 0, and V ac = 0.1 V

Full size image

Our analysis also reveals (Daqaq 2006) that the effect of the internal resonance extends over a wide range of bias voltages (11–14.5 V) in the neighborhood of V dc≈13.2 V. Therefore, avoiding operation in that region, in order to eliminate the possibility of internal resonance, places severe limits on the operation range of the microscanner. One solution to this problem is to design the mirror with a ratio of the second to the first natural frequencies of \(\frac{\omega_2}{\omega_1} > 2\) at V dc = 0. Since ω1 decreases faster than ω2 as V dc increases, this design will eliminate the possibility of internal resonance over the whole range of operation. A simple approach to achieve this is to shorten the suspension beams because ω2 is inversely proportional to l 3, whereas ω1 is inversely proportional to l only. However, this also increases the torsional stiffness, which increases the voltage required to achieve a desired tilt angle. For example, decreasing the length of the suspension beams by 30.7% from l = 65 to l = 45 μm while keeping all of the other mirror parameters constant, increases the ratio \(\frac{\omega_2} {\omega_1}\) to 2.24. As shown in Fig. 12, the second natural frequency ω2 stays away from twice the first natural frequency over the whole voltage range, thereby eliminating the possibility of internal resonance. However, the pull-in voltage increases by 27.3% as shown in Fig. 13. To achieve a tilt angle of θ m  = 0.3°, the voltage requirement increases from 17.1 to 21.3 V, which constitutes a major disadvantage.

Fig. 12
figure 12

Variation of the first two natural frequencies of the mirror with the applied DC voltage. Solid lines denote suspension beams of length l = 65 μm. Dashed lines denote beams of length l = 45 μm

Full size image
Fig. 13
figure 13

Variation of the stable equilibria of the mirror tilt angle θ m with the applied DC voltage. Solid lines denote suspension beams of length l = 65μm. Dashed lines denote beams of dimensions l = 45 μm

Full size image

To alleviate this shortcoming, one can revert to manipulating the electrode parameters to increase the electrostatic moment obtained for the same applied voltage. We increase α from 0.06 to 0.20 and β from 0.84 to 1. Comparing the results in Figs. 14–12 illustrates that the 37.4% decrease in the length of the suspension beams increased \(\frac{\omega_2}{\omega_1}\) to 2.24 and yet did not result in a significant change in the pull-in voltage. In fact, Fig. 15 shows that the voltage required to achieve a certain tilt angle has increased only by a maximum of 1.1% over the whole operation range.

Fig. 14
figure 14

Variation of the first two natural frequencies of the mirror with the applied DC voltage. Solid lines denote suspension beams of length l = 65 μm and electrode parameters: α = 0.06 and β = 0.84. Dashed lines denote suspension beams of length l = 45 μ m and electrode parameters: α = 0.2 and β = 1.0

Full size image
Fig. 15
figure 15

Variation of the stable equilibria of the mirror tilt angle θ m with the applied DC voltage. Solid lines denote suspension beams of length l = 65 μm and electrode parameters: α = 0.06, and β = 0.84. Dashed lines denote suspension beams of length l = 45 μm and electrode parameters: α = 0.20 and β = 1.0

Full size image

6 Conclusions

We presented a dynamic model of a torsional mirror operating as a microscanner. We conducted a convergence analysis to determine the minimum number of modes sufficient to create a finite-dimensional ROM with an accuracy comparable to that of an infinite-dimensional distributed-parameter model. We found that a two degree-of-freedom lumped mass model created using the first two modes of the mirror accurately describes the tilt angle and transverse bending of the micromirror. It has the advantages of being as accurate as distributed-parameter and higher-order models and yet being compact and computationally efficient.

We applied perturbation methods to this model to obtain a consistent second-order approximation of the microscanner response to a biased actuation signal having a frequency close to the mirror’s first natural frequency ω1. This provides a simple tool to investigate the transient and steady-state responses of the microscanner. Studying the steady-state response of the microscanner, we found that the use of higher bias voltages increases the softening nonlinearity of the device. Beyond a certain threshold of the excitation amplitude V ac, the nonlinearity causes multi-valued solutions, co-existing stable responses of the microscanner, for a frequency range in the neighborhood of and less than ω1. It is necessary to avoid triggering this threshold or at least to operate the microscanner using AC frequencies Ω > ω1 to avoid sudden jumps and hysteresis in the microscanner response.

Further, we found that an internal resonance between the first and second modes of the microscanner can occur for a significant range of the bias voltage V dc. This resonance causes severe degradation to the performance of the microscanner. Since placing limits on the actuation signal to avoid triggering the internal resonance can significantly undermine the functionality of the microscanner, we propose a simple design to eliminate the possibility of internal resonance. Microscanners should be designed so that the ratio of the second to the first natural frequencies satisfy the condition \(\frac{\omega_2}{\omega_1} {\geq}2.2\) when V = 0. To achieve this, we need to increase the ratio of the transverse stiffness k 22 to torsional stiffness k 11 of the suspension beams. This can be done by either shortening the length of the suspension beams or increasing the aspect ratio of the beam cross section using a fabrication process, such as deep reactive ion etching (DRIE). To maintain the same level of actuation voltage, we need to simultaneously increase the efficiency of the electrodes’ conversion of electrostatic energy to electrostatic moment by increasing the size and/or the moment arm of the electrodes. Finally, it should be noted that increasing the ratio \(\frac{k_{22}} {k_{11}}\) has the added advantage of minimizing the spurious transverse bending deflection u m in response to the actuation signal as well as external shock and vibration disturbances.