1 Introduction

Time series prediction is widely existed in all aspects of life [1,2,3,4], such as forecasting the number daily discharged inpatients of hospital, wind power prediction, global financial situation prediction, and so on. Typical methods include statistical regression [5], gray prediction [6] and machine learning [7]. The autoregressive moving average [8] is a commonly used statistical regression method, but it cannot solve nonlinear problems. Gray prediction [9] is suitable for time series prediction with uncertain partial information, but it is not suitable for the static dataset. Therefore, the prediction method based on machine learning [10] has been widely concerned, which requires no assumptions about the data or model.

In the field of machine learning, the commonly used methods include decision tree (DT) [11], support vector machine (SVM) [12] and artificial neural networks (ANN) [13,14,15,16,17], among which the ANN has drawn many attentions due to its nonlinear approximation ability. The most classical ANN is feed-forward neural network (FNN) [16], which can simulate any nonlinear system. However, it is difficult for FNN to capture the hidden sequence information of time series data. Therefore, the recurrent neural network (RNN) [17] is proposed to solve complex time series problems. However, its network structure and training method may lead to low training efficiency and memory loss. Therefore, Jaeger has proposed a new type of RNN, named as echo state network (ESN) [18].

Nowadays, ESN has been successfully applied in the field of time series prediction [18,19,20,21,22,23,24,25]. Unlike the traditional RNN, the ESN uses a reservoir to store and manage information. The input weights and internal weights of ESN are generated randomly and remain unchanged, only the output weights (also called readout) should be trained. In [21], the generation of reservoirs and training of readouts are reviewed. In [22], the hierarchical ESN is proposed, which is trained by stochastic gradient descent. In [23], the ESN with leaky integrator neurons is designed, which can easily adapt to time characteristics.

In reservoir initialization phase, hundreds of sparsely connected neurons are generated, and some neurons may have little influence on training performance. If all reservoir nodes are connected with network outputs, the ESN will perform very well on training data, but not good on testing data, leading to the overfitting problem. Hence, how to design a suitable reservoir size to improve the performance of ESN has always been the focus of research. In [24], the singular value decomposition-based growing ESN is proposed, which can weaken the coupling among reservoir neurons. In [25], the reservoir pruning method is designed, in which the mutual information between reservoir states is used to delete nodes. However, the pruning method may destroy the echo state characteristics of ESN [26].

To avoid overfitting problem, the regularization techniques are widely applied to sparse the readout of ESN, rather than control the size of reservoir directly [27, 28]. In [29], the reservoir nodes are dynamically added or deleted according to their importance to network performance, the l2 regularization is used to update the output weights. However, the l2 regularization is not able to generate the sparse ESN. In [30], the l1 penalty term is added into the objective function to shrink some irrelevant output weights as small values, such that the readout is sparse. In [31], the l0 regularization is used for sparse signal recovery, which is able to reduce computation complexity and improve classification ability, simultaneously. In [32], the online sparse ESN is designed, in which the l1 and l0 norms are respectively used as penalty terms to control the network size, the sparse recursive least squares and sub-gradient algorithm are combined to estimate output weights. This method has shown superior performance than other ESNs in prediction accuracy and network sparseness. Hence, the l0 and l1 regularization are the focus of this paper.

In traditional regularization approaches [27,28,29,30,31,32], the regularization coefficient is used to introduce the penalty term into the objective function,

$$F\left( {W^{{{\text{out}}}} } \right) = \left\| {T - {\mathbf{HW}}^{{{\text{out}}}} } \right\|_{2}^{2} + \mu \left\| {W^{{{\text{out}}}} } \right\|_{p}$$
(1)

where the first term and the second term are the training error and penalty term, respectively,\(\mu\) is regularization coefficient, Wout is the output weight of ESN, p = 0,1 represent the l0-norm or l1-norm, respectively. The regularization coefficient is used to balance training error and sparseness of Wout. Different \(\mu\) will lead to different optimal solutions [33], and a small change of the regularization coefficient will have a great influence on the training results. Thus, it is important to choose an appropriate regularization coefficient.

To avoid choosing regularization coefficient, in this paper, the optimization of Eq. (1) is formulated as a multi-objective optimization problem (MOP), in which the two conflicting objectives can be optimized [34]. From the view point of optimization, many Pareto-optimal solutions can be obtained by multi-objective optimization algorithms, and thus it is difficult to determine which solution can obtain the best network structure and training error. To select the appreciate solution, the preferences of decision maker should be considered [35]. The knee point is proposed in [36], in which a small change of one objective will generate a big change on the other [37,38,39]. Although the solutions in knee points does not provide the best result for some problems, they still be Pareto solutions which has the optimal performance for MOP.

In this paper, the multi-objective sparse ESN (MOS-ESN) is proposed, in which the training error and network size are treated as two optimization objectives. The main contribution is as follows. Firstly, the MOEA/D-based multi-objective optimization algorithm is designed to optimize network structure and network performance. Secondly, to improve algorithm convergence, the l1 or l0 regularization and coordinate descent algorithm-based local search strategy is designed. Thirdly, the preference information of knee point is integrated into weight vectors updating method, which guides the evolution of population toward knee region. Simulation results prove that MOS-ESN can improve the training accuracy and network sparseness without involving any regularization parameters.

The paper organization is as follows. Section 2 introduces the basic description of ESN, MOP and MOEA/D. The proposed MOS-ESN is given in Sect. 3. The simulations are discussed in Sect. 4. The paper is summarized in Sect. 5

2 Background

2.1 Original ESN

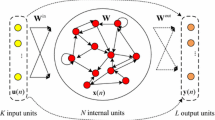
The original ESN (OESN) in Fig. 1 is constructed with an input layer, a reservoir and an output layer. The OESN has n input neurons in input layer, N nodes in reservoir and one output node. The input layer and reservoir are connected by the input weight matrix Win ∈  \(\mathbb{R}^{{N \times N}}\) the elements in reservoir are tied by the internal weight matrix W ∈  \(\mathbb{R}^{{N \times N}}\) while the input layer and reservoir are related with the output layer through the output weight matrix Wout ∈  \(\mathbb{R}^{{\left( {N + n} \right) \times 1}}\). Consider L distinct samples {u(k), t(k)}, where u(k) = [u1(k), u2(k), …, un(k)]T ∈  \(\mathbb{R}^{{\left( {N + n} \right) \times 1}}\) and t(k) are input and target, respectively, and the reservoir state x(k) is updated as below,

$${\mathbf{x}}(k) \, = {\mathbf{g}}({\mathbf{Wx}}(k - { 1}) \, + {\mathbf{W}}^{{{\text{in}}}} {\mathbf{u}}(k))$$
(2)

where g (·) = [g1(·), …, gN (·)T are the activation functions. The output y(k) is equal to (Wout)T[x(k); u(k)], where [x(k); u(k)] ∈  $$ \mathbb{R}^{{1 \times \left( {1 + n} \right)}} $$ is the concatenation of reservoir states and input matrix.

Fig. 1
figure 1

Description of OESN

Full size image

Denote T = [t(1), t(2),…, t(L)]T as target data matrix and represent H = [X(1), X(2), …, X(L)]T as internal state matrix as below

$$H = \left[ {\begin{array}{*{20}l} {X^{T} (1)} \hfill \\ {X^{T} (2)} \hfill \\ \vdots \hfill \\ {X^{T} (L)} \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {X_{11} } \hfill & {X_{12} } \hfill & \cdots \hfill & {X_{1N + n} } \hfill \\ {X_{21} } \hfill & {X_{22} } \hfill & \cdots \hfill & {X_{2N + n} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {X_{L1} } \hfill & {X_{L2} } \hfill & \cdots \hfill & {X_{LN + n} } \hfill \\ \end{array} } \right]$$
(3)

The output weight matrix Wout can be calculated by

$${\mathbf{W}}^{{{\text{out}}}} = {\mathbf{H}}^{\dag } {\mathbf{T}}$$
(4)

where H† is the Moore–Penrose pseudoinverse of H. H† can be computed by orthogonal projection methods [40], single-value decomposition, and so on. However, if the input data contain unknown random noise, the inverse calculation of H may lead to an ill-posed problem, i.e., an unstable solution is obtained.

2.2 MOPs

MOPs contain many conflicting objective functions that should be optimized at the same time. Generally speaking, the minimized MOPs can be expressed as below:

$${\text{Min}}{\mathbf{F}}\left( {\mathbf{W}} \right) \, = \, \left[ {f_{{1}} \left( {\mathbf{W}} \right),f_{{2}} \left( {\mathbf{W}} \right), \, ...,f_{{\text{m}}} \left( {\mathbf{W}} \right)} \right]^{{\text{T}}}$$
(5)

subject to W ∈ Ωwhere W is the decision variable, m is the number of objective functions, Ω is the decision space, F: Ω → Rm is consisted of m objective functions, and Rm is named as the objective space.

For two solutions W1 and W2, W1 is said to dominate W2 (denoted as W1 ≺ W2), if and only if fi(W1) ≤ fi(W2) for each objective i  ∈ {1,…,m}, and fj(W1) < fj(W2) for at least one value j ∈ {1,…,m} [40].

Furthermore, the solution W∗  ∈ Ω is defined as Pareto-optimal if there is no other feasible solution W ≺ W∗. Particularly, the set of W∗ is named as Pareto-optimal set (PS) and the union of all PS is called the Pareto-optimal front (PF) [34].

2.3 MOEA/D

MOEA/D decomposes a MOP into several single-objective subproblems by multiple weight vectors, and all the subproblems can be optimized at the same time [40]. The main steps of MOEA/D are given:

Step 1: Generate the initial population, x1, x2, …, xP, and a group of uniformly weight vectors λ = (λ1, …, λP), where P is the population size.

Step 2: Compute the Euclidean distance between any two weight vectors, find the nearest T vectors of each vector, which are denoted the neighborhood of λi and represented as B(i) = {i1, i2, …, iT}.

Step 3: Choose two index k,l from B(i) randomly. Apply genetic operators on xk and xl to generate a new individual y.

Step 4: Update neighboring solutions. When the aggregate function value of y is smaller or equal to xj, update xj = y, where j ∈ B(i).

Step 5: Determine the non-dominated solutions of population and update the external population (EP), which saves the non-dominated solutions.

The main feature of MOEA/D is its decomposition method [40], such as the weighted sum approach, Tchebycheff approach and boundary intersection approach. In the following, the form of weighted sum approach is shown

$${\text{Ming}}^{{{\text{ws}}}} \left( {{\mathbf{W}}\lambda_{i} } \right){ = }\sum\limits_{{\text{k = 1}}}^{{\text{m}}} {\lambda_{i,k} f_{k} \left( {\mathbf{W}} \right)}$$
(6)

where λi = {λi,1, λi,2, …, λi,m} represents the weight vector corresponding to each objective function, and it is noted that \(\sum\nolimits_{k = 1}^{m} {\lambda_{i,k} = 1}\).

3 MOS-ESN

To optimize the network size and training error simultaneously, the MOS-ESN is proposed. Firstly, the design of ESN is formulated as a bi-objective optimization problem, which is solved by MOEA/D. Secondly, to improve algorithm convergence, the l1 and l0 regularization-based local search strategy is designed. Furthermore, to find more solutions around the knee point, the decision maker preference-based weight vectors updating method is proposed.

3.1 Problem Formulation

The network size of ESN is closely related to training performance. To prove their relationship, a simple experiment is designed. Firstly, an ESN with 200 nodes is randomly initialized. Then, several sparse output weights are generated, and the corresponding training errors are recorded. Finally, the training error (denoted as f1) and the number of nonzero elements of output weights (denoted as f2) are drawn in Fig. 2. Obviously, the training error decreases as the network size increases, the too large network will lead to overfitting problem. However, if the network is too small, the training of ESN will be insufficient. Hence, how to achieve a balance between network size and training error becomes the key to research.

Fig. 2
figure 2

Relationship between training error and network size

Full size image

To solve this problem, the regularization methods are introduced by using the l1 or l0 norm penalty term, and then the design of ESN is realized by optimizing the following objective function

$$\min {\text{F}}_{{\left( {{\mathbf{W}}^{{{\text{out}}}} } \right)}} \left( {{\text{W}}^{{{\text{out}}}} } \right){\mkern 1mu} = {\mkern 1mu} \min \left( {\left\| {{\mathbf{T}} - {\mathbf{HW}}^{{{\text{out}}}} } \right\|_{2}^{2} + \mu \left\| {{\mathbf{W}}^{{{\text{out}}}} } \right\|_{{0/1}} } \right)$$
(7)

where \(\mu\) is regularization parameters. Actually, the selection of regularization parameters is a difficult problem, because the large \(\mu\) means a small reservoir with large training error, while the small \(\mu\) has the opposite effect [33].

To avoid choosing regularization coefficient, the problem in Eq. (9) is treated as a multi-objective optimization problem,

$$\mathop {\min }\limits_{{{\mathbf{W}}^{{{\text{out}}}} }} {\text{F}}\left( {{\mathbf{W}}^{{{\text{out}}}} } \right)\,=\,\min \left( {\left\| {{\mathbf{T}} - {\mathbf{HW}}^{{{\text{out}}}} } \right\|_{{2}}^{{2}} ,\left\| {{\mathbf{W}}^{{{\text{out}}}} } \right\|_{{0/1}} } \right)$$
(8)

where the first term is training error and the second is network size. To minimize the training error and network size simultaneously, the MOEA/D is used, in which the weighted sum approach is applied to generate a set of subproblems

$$\mathop {{\text{min}}}\limits_{{{\mathbf{W}}^{out} }} g^{ws} ({\mathbf{W}}^{out} \lambda )\,= \lambda_{1} f_{1} ({\mathbf{W}}^{out} ) + \lambda_{2} f_{2} ({\mathbf{W}}^{out} )$$
(9)

where λ1 and λ2 represent the weight of f1 and f2, respectively, and λ1 + λ2 = 1.

3.2 Local Search Method

To accelerate the convergence speed of MOEA/D, the local search strategy is proposed, in which the l1 or l0 regularization term is applied to ensure network sparsity, and the coordinate descent algorithm is introduced to update the elements of Wout.

3.2.1 The l1 regularization-based local search method

By using the l1 regularization, the problem in Eq. (8) is formulated as below:

$$\mathop {\min }\limits_{{{\mathbf{W}}^{{{\text{out}}}} }} {\text{F}}\left( {{\mathbf{W}}^{{{\text{out}}}} } \right)\,=\,\min \left( {\left\| {{\mathbf{T}}{ - }{\mathbf{HW}}^{{{\text{out}}}} } \right\|_{{2}}^{{2}} {\mathbf{ + }}\mu \left\| {{\mathbf{W}}^{{{\text{out}}}} } \right\|_{{1}} } \right)$$
(10)

where \({\Vert {\text{W}}^{\text{out}}\Vert }_{1}\text{=}\sum_{\text{i} = {1}}^{\text{N+n}}\text{|}{\text{w}}_{\text{i}}\text{|}\) represent the l1-norm of Wout. The subproblem in Eq. (9) is described as

$$E\left( {{\mathbf{W}}^{{{\text{out}}}} } \right)\,=\,\frac{{\lambda_{{1}} }}{{2}}\left\| {{\mathbf{T}}{ - }{\mathbf{HW}}^{{{\text{out}}}} } \right\|_{{2}}^{{2}} { + }\lambda_{{2}} \left\| {{\mathbf{W}}^{{{\text{out}}}} } \right\|_{{1}}$$
(11)

To facilitate computational analysis, \({{\lambda_{1} } \mathord{\left/ {\vphantom {{\lambda_{1} } 2}} \right. \kern-\nulldelimiterspace} 2}\) is applied in Eq. (11) instead of λ1. Because the two objectives in Eq. (11) are differentiable, the coordinate descent algorithm is selected to calculate the value of Wout, which has shown strong local search ability. Under the framework of coordinate descent algorithm, in each iteration, the ith variable wi (i = 1, 2, …, N + n)of Wout is updated, while the other elements remain the same. Thus, Eq. (11) becomes

$$\begin{aligned} E\left( {{\mathbf{W}}^{{out}} \left( {w_{i} } \right)} \right) &= \frac{{\lambda _{1} }}{2}\left\{ {\sum\limits_{{k = 1}}^{L} {\left[ {{\mathbf{t}}(k) - {\mathbf{X}}_{{ki}} w_{i} - \sum\limits_{{j \ne i}}^{{N + n}} {{\mathbf{X}}_{{kj}} w_{j} } } \right]} } \right\}^{2} + \lambda _{2} \sum\limits_{{i = 1}}^{{N + n}} {|w_{i} |} \hfill \\ & = \frac{{\lambda _{1} }}{2}\sum\limits_{{k = 1}}^{L} {\left( {{\mathbf{X}}_{{ki}} w_{i} } \right)^{2} } - \lambda _{1} \left\{ {\left[ {\sum\limits_{{k = 1}}^{L} {\left( {{\mathbf{t}}\left( k \right) - \sum\limits_{{j \ne i}}^{{N + n}} {{\mathbf{X}}_{{kj}} w_{j} } } \right)} {\mathbf{X}}_{{ki}} } \right] \cdot w_{i} } \right\} \hfill \\ &\quad+ \frac{{\lambda _{1} }}{2}\sum\limits_{{k = 1}}^{L} {\left[ {\left( {{\mathbf{t}}\left( k \right)) - \sum\limits_{{j \ne i}}^{{N + n}} {{\mathbf{X}}_{{kj}} w_{j} } } \right)^{2} } \right]} + \sum\limits_{{i = 1}}^{{N + n}} {\lambda _{2} |w_{i} |} \hfill \\ \end{aligned}$$
(12)

It can be found that\(\frac{{\lambda _{1} }}{2}\sum\nolimits_{{{\text{k = 1}}}}^{{\text{L}}} {\left[ {\left( {{\text{t}}\left( {\text{k}} \right) - \sum\limits_{{{\text{j}} \ne {\text{i}}}}^{{{\text{N + n}}}} {{\text{X}}_{{{\text{kj}}}} } {\text{w}}_{{\text{j}}} } \right)^{2} } \right]}\) is irrelevant to wi, thus minimizing E(Wout( wi)) in Eq. (12) is equal to minimizing Z(Wout( wi)),

$$Z\left( {{\mathbf{W}}^{{out}} \left( {w_{i} } \right)} \right) = \frac{{\lambda _{1} }}{2}\sum\limits_{{k = 1}}^{L} {\left( {{\mathbf{X}}_{{ki}} w_{i} } \right)^{2} } - \lambda _{1} \left\{ {\left[ {\sum\limits_{{k = 1}}^{L} {({\mathbf{t}}(k) - \sum\limits_{{j \ne i}}^{{N + n}} {{\mathbf{X}}_{{kj}} w_{j} } )} {\mathbf{X}}_{{ki}} } \right] \cdot w_{i} } \right\} + \sum\limits_{{{\text{i = 1}}}}^{{N + n}} {\lambda _{2} |w_{i} |}$$
(13)

The sub-gradient of l1-norm is shown as below

$$\partial \left( {\left\| {w_{i} } \right\|} \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\,w_{i} > 0} \hfill \\ { - 1,} \hfill & {{\text{if}}\,w_{i} < 0} \hfill \\ {\alpha \in \left[ { - 1,1} \right],} \hfill & {{\text{if}}\,w_{i} = 0} \hfill \\ \end{array} } \right.$$
(14)

When the derivative of Z(Wout( wi)) respect to wi is equal to zero, the minimize of Z(Wout( wi)) can be obtained. The derivative of Z(Wout( wi)) is given as

$$\frac{{\partial Z\left( {{\mathbf{W}}^{{out}} \left( {w_{i} } \right)} \right)}}{{\partial w_{i} }} = \lambda _{1} \left[ {\sum\limits_{{k = 1}}^{L} {\left( {{\mathbf{X}}_{{ki}}^{2} w_{i} } \right)} - \sum\limits_{{k = 1}}^{L} {\left( {{\mathbf{t}}\left( k \right) - \sum\limits_{{j \ne i}}^{{N + n}} {{\mathbf{X}}_{{kj}} w_{j} } } \right))} {\mathbf{X}}_{{ki}} } \right] + \lambda _{2} \frac{{\partial \left\| {w_{i} } \right\|_{1} }}{{\partial w_{i} }}$$
(15)

To simplify the calculation, two parameters D and C are introduced

$$D = \sum\limits_{k = 1}^{L} {{\mathbf{X}}_{ki}^{2} }$$
(16)
$$C = \sum\limits_{k = 1}^{L} {\left[ {{\mathbf{t}}\left( k \right) - \sum\limits_{j \ne i}^{N + n} {{\mathbf{X}}_{kj} w_{j} {\mathbf{X}}_{ki} } } \right]}$$
(17)

Thus, the derivative of Z(Wout( wi)) is given,

$$\frac{{\partial Z({\mathbf{W}}^{{out}} (w_{i} ))}}{{\partial w_{i} }} = \left\{ {\begin{array}{*{20}l} {\lambda _{1} \left( {Dw_{i} - C} \right) + \lambda _{2} ,} \hfill & {{\text{if }}w_{i} > 0} \hfill \\ {\lambda _{1} \left( {Dw_{i} - C} \right) - \lambda _{2} ,} \hfill & {{\text{if }}w_{i} < 0} \hfill \\ {\left[ { - \lambda _{1} C - \lambda _{2} , - \lambda _{1} C + \lambda _{2} } \right],} \hfill & {{\text{if }}w_{i} = 0} \hfill \\ \end{array} } \right.$$
(18)

By setting \(\frac{{\partial {\text{Z(Wout( wi))}}}}{{\partial {\text{w}}_{{\text{i}}} }} = {0}\), the update equation of wi is shown in Eq. (19), the corresponding threshold function is shown in Fig. 3a.

$$w_{i} = \left\{ {\begin{array}{*{20}l} {\frac{{C - \frac{{\lambda _{2} }}{{\lambda _{1} }}}}{D},} \hfill & {if\quad {C > \frac{{\lambda _{2} }}{{\lambda _{1} }}}} \hfill \\ {\frac{{C + \frac{{\lambda _{2} }}{{\lambda _{1} }}}}{D}} \hfill & {if\quad{C - \frac{{\lambda _{2} }}{{\lambda _{1} }}}} \hfill \\ {0,} \hfill & {if - \frac{{\lambda _{2} }}{{\lambda _{1} }} \le C \le \frac{{\lambda _{2} }}{{\lambda _{1} }}} \hfill \\ \end{array} } \right.$$
(19)
Fig. 3
figure 3

The soft thresholding function and the modified one

Full size image

In Eq. (19), wi is related to, \({{\lambda_{1} } \mathord{\left/ {\vphantom {{\lambda_{1} } {\lambda_{2} }}} \right. \kern-\nulldelimiterspace} {\lambda_{2} }}\) which is a fixed value and not related to wi-1. Therefore, an adjustment is made on Eq. (19)

$$w_{i} = \left\{ {\begin{array}{*{20}l} {\frac{{C - {\text{sgn}}\left( C \right)\frac{{\lambda _{2} }}{{\lambda _{1} }}(\varepsilon + \left| {w_{{i - 1}} } \right|)_{ + } }}{D}} \hfill & {{\text{if }}\left| C \right|\frac{{\lambda _{2} }}{{\lambda _{1} }}\left( {\varepsilon + \left| {w_{{i - 1}} } \right|} \right)_{ + } } \hfill \\ {0,} \hfill & {{\text{if }}\left| C \right| \le \frac{{\lambda _{2} }}{{\lambda _{1} }}(\varepsilon + \left| {w_{{i - 1}} } \right|)_{ + } } \hfill \\ \end{array} } \right.$$
(20)

where wi-1 represents the weight at last iteration, ε is a small positive value and located in (0,1), and (x)+ equals 1/x when x ≤ 1 and is 1 otherwise.

The advantage of above method is its modifiable threshold \(\frac{{\lambda_{{2}} }}{{\lambda_{{1}} }}\left( {\varepsilon { + }\left| {{\text{w}}_{i - 1} } \right|} \right)_{ + }\). When wi-1 is small, C has a higher probability between \(- \frac{{\lambda_{{2}} }}{{\lambda_{{1}} }}\left( {\varepsilon { + }\left| {{\text{w}}_{i - 1} } \right|} \right)_{ + }\) and \(\frac{{\lambda_{{2}} }}{{\lambda_{{1}} }}\left( {\varepsilon { + }\left| {{\text{w}}_{i - 1} } \right|} \right)_{ + }\). Therefore, wi is attracted to zero with a higher possibility (show as Fig. 3b), while the increased threshold can reduce ||Wout||1 effectively. To the contrary, if wi−1 is large, the threshold will decrease to avoid becoming to zero.

3.2.2 The smoothed l0 regularization-based local search method

Actually, the l1 regularization always generates many components that are close but not equal to zero. To generate more sparse solution, the l0 regularization is considered

$$\mathop {\min }\limits_{{{\mathbf{W}}^{{{\text{out}}}} }} {\text{F}}\left( {{\mathbf{W}}^{{{\text{out}}}} } \right)\,=\,\min \left( {\left\| {{\mathbf{T}}{ - }{\mathbf{HW}}^{{{\text{out}}}} } \right\|_{{2}}^{{2}} ,\left\| {{\mathbf{W}}^{{{\text{out}}}} } \right\|_{{0}} } \right)$$
(21)

However, the minimization of Eq. (21) is NP-hard. To solve it, the ||Wout||0 is approximated by \({\text{||Wout||0 = g}}\left( {{\text{W}}_{{{\text{out}}}} } \right){\text{ = }}\sum\nolimits_{{{\text{i = 1}}}}^{{{\text{N + n}}}} {\left( {{\text{1}} - e^{{ - {\text{Q|w}}_{{\text{i}}} {\text{|}}}} } \right)}\)where Q is an appropriate positive constant. The subdifferential of \({\text{g}}\left({\text{W}}{\text{out}}\right)\) is as below

$$\frac{{\partial g(w_{i} )}}{{\partial w_{i} }}\,=\,sgn(w_{i} ) \cdot Q \cdot e^{{{ - }Q{|}w_{i} {|}}}$$
(22)

Transform e−Q|wi| by the first-order Taylor series expansion

$${\text{e}}^{{ - Q|w_{i} |}} \approx \left\{ {\begin{array}{*{20}l} {1 - Q|w_{i} |,} \hfill & {|w_{i} | \le \frac{1}{Q}} \hfill \\ {0,} \hfill & {{\text{others}}} \hfill \\ \end{array} } \right.$$
(23)

Similar with l1 regularization, the subdifferential of objective function can be described as:

$$\frac{{\partial Z\left( {{\mathbf{W}}^{out} \left( {w_{i} } \right)} \right)}}{{\partial w_{i} }} = \left\{ {\begin{array}{*{20}l} {\lambda_{1} \left( {Dw_{i} - C} \right) - \lambda_{2} \left( {Q + Q^{2} w_{i} } \right), - \frac{1}{Q} \le w_{i} < 0} \hfill \\ {\lambda_{1} \left( {Dw_{i} - C} \right) + \lambda_{2} \left( {Q - Q^{2} w_{i} } \right),0 < w_{i} \le \frac{1}{Q}} \hfill \\ {\left[ { - \lambda_{1} C - \lambda_{2} Q, - \lambda_{1} C + \lambda_{2} Q} \right],w_{i} = 0} \hfill \\ {\lambda_{1} \left( {Dw_{i} - C} \right),w_{i} < - \frac{1}{Q}w_{i} < - \frac{1}{Q}orw_{i} > \frac{1}{Q}} \hfill \\ \end{array} } \right.$$
(24)

By setting \(\frac{{\partial {\text{Z}}\left( {{\text{Wout}}\left( {{\text{wi}}} \right)} \right)}}{{\partial {\text{w}}_{{\text{i}}} }} = {0}\), wi can be obtained by Eq. (25), and the threshold function is shown in Fig. 3(c).

$$w_{i} = \left\{ {\begin{array}{*{20}l} {\frac{{\lambda _{1} C + \lambda _{2} Q}}{{\lambda _{1} D - \lambda _{2} Q^{2} }},} \hfill & {D > \frac{{\lambda _{2} Q^{2} }}{{\lambda _{1} }}\quad{\text{and}}\quad - \frac{D}{Q} \le C < - \frac{{\lambda _{2} Q}}{{\lambda _{1} }}} \hfill \\ {\frac{{\lambda _{1} C - \lambda _{2} Q}}{{\lambda _{1} D - \lambda _{2} Q^{2} }},} \hfill & {D > \frac{{\lambda _{2} Q^{2} }}{{\lambda _{1} }}\quad{\text{and}}\quad\frac{{\lambda _{2} Q}}{{\lambda _{1} }} < C \le \frac{D}{Q}} \hfill \\ {0,} \hfill & { - \frac{{\lambda _{2} Q}}{{\lambda _{1} }} \le C \le \frac{{\lambda _{2} Q}}{{\lambda _{1} }}} \hfill \\ {\frac{C}{D},} \hfill & {{\text{others}}} \hfill \\ \end{array} } \right.$$
(25)

To improve the zero-attraction effect, the modified l0 regularization method is proposed

$$w_{{\text{i}}} = \left\{ {\begin{array}{*{20}l} {\frac{{\lambda _{1} C - {\text{sgn}}\left( C \right) \cdot \lambda _{2} Q}}{{\lambda _{1} D - \lambda _{2} Q^{2} }},} \hfill & {D > \frac{{\lambda _{{\text{2}}} Q^{{\text{2}}} }}{{\lambda _{{\text{1}}} }}\quad{\text{and}}\quad\frac{{\lambda _{{\text{2}}} Q\left( {\varepsilon {\text{ + }}\left| {{\text{w}}_{{{\text{i - 1}}}} } \right|} \right)_{{\text{ + }}} }}{{\lambda _{{\text{1}}} }} < \left| C \right| \le \frac{D}{Q}} \hfill \\ {{\text{0}},} \hfill & {\frac{{\lambda _{{\text{2}}} Q\left( {\varepsilon {\text{ + }}\left| {{\text{w}}_{{{\text{i - 1}}}} } \right|} \right)_{{\text{ + }}} }}{{\lambda _{{\text{1}}} }}} \hfill \\ {\frac{C}{D},} \hfill & {{\text{others}}} \hfill \\ \end{array} } \right.$$
(26)

which can modify the threshold based on the previous value of wi so that the small components are attracted to zeros with a higher probability (Fig. 3d).

3.3 Weight Vectors Updating Algorithm

By using MOEA/D, many non-dominated solutions can be obtained. However, only one solution is chosen to realize the nonlinear modeling problem. Generally speaking, the ESN with too large training error (λ1 is too small) or with too large network size (λ2 is too small) will not be chosen. As described in [41], the knee point is able to make a tradeoff between two objects. Thus, the knee point is selected as the final solution. In order to generate more solutions around the knee point, the weight vectors updating method is proposed, in which the information of knee point is incorporated.

3.3.1 Knee point

In this part, the distance-based method is introduced to find the knee point [41]. For a bi-objective optimization problem, a line L can be defined as ax + by + c = 0, where a, b, and c are determined by the two solutions that has minimize f1 and f2, respectively. Then, the distances d between solutions in PF and L can be calculated as

$$d = \frac{{\left| {ax + by + c} \right|}}{{\sqrt {a^{2} + b^{2} } }}$$
(27)

Considering the minimization problem in this paper, only the solutions in the convex region are of interesting. Thus, the above equation can be modified as

$$d = \left\{ {\begin{array}{*{20}l} {\frac{{\left| {ax + by + c} \right|}}{{\sqrt {a^{2} + b^{2} } }},} \hfill & {ax + by + c < 0} \hfill \\ { - \frac{{\left| {ax + by + c} \right|}}{{\sqrt {a^{2} + b^{2} } }},} \hfill & {{\text{others}}} \hfill \\ \end{array} } \right.$$
(28)

According to Eq. (28), the solution farthest from L is defined as knee point. For example, in Fig. 4, points A and B can determine the line L. By calculating the distance d between each point and L, the point E is the knee point obviously.

Fig. 4
figure 4

Example of knee point

Full size image

3.3.2 Weight Vectors Updating Method

The weight vectors are updated according to the information of knee point and decision maker preference. As shown in Fig. 5, the red point K is the projection of the knee point on the line Lw and A and B are the boundary points where the updated weight vectors should be located, i.e., the line AB is divided into two subintervals by K. Then, the same number of weight vectors \(\frac{\text{P}}{{2}}\) will be generated in each subinterval. The distance between two weight vectors is called step size, which is calculated as

figure a
$$d_{1} = \sqrt 2 ^{{\frac{1}{\alpha }}} \left( {\frac{{x - x_{1} }}{{1^{\alpha } + 2^{\alpha } + ... + \left\lceil {\frac{P}{2}} \right\rceil ^{\alpha } }}} \right)^{{\frac{1}{\alpha }}}$$
(29)
$$d_{2} = \sqrt 2 ^{{\frac{1}{\alpha }}} \left( {\frac{{x_{2} - x}}{{1^{\alpha } + 2^{\alpha } + ... + \left\lfloor {\frac{P}{2}} \right\rfloor ^{\alpha } }}} \right)^{{\frac{1}{\alpha }}}$$
(30)

where d1 is the step size in line KA, d2 is the step size in line KB, and α > 0 is the step size parameter. The value of weight vector λi in line KA is,

$$\begin{gathered} \lambda_{i,1} = x - d_{1}^{\alpha } - \left( {2d_{1} } \right)^{\alpha } - \ldots - (id_{1} )^{\alpha } \hfill \\ \lambda_{i,2} = 1 - \lambda_{i.,1} \hfill \\ \end{gathered}$$
(31)
Fig. 5
figure 5

The weight vectors updating method

Full size image

Similarly, the value of weight vector \(\lambda_{j}\) in line KB is

figure b
$$\begin{gathered} \lambda_{j,1} = x - d_{2}^{\alpha } \left( {2d_{2} } \right)^{\alpha } - ... - \left( {jd_{2} } \right)^{\alpha } \hfill \\ \lambda_{j,2} = 1 - \lambda_{j,1} \hfill \\ \end{gathered}$$
(32)

In the above weight vectors updating method, the weight vectors have a denser distribution near the knee point and are sparser at the boundary. Hence, more weight vectors will be generated near the knee point, and fewer at the boundary. Moreover, the determination of points A and B can be made by decision maker preference, which makes the algorithm converge to the region of interest.

The weight vectors updating algorithm is presented in Algorithm 1. Firstly, the two solutions which minimize f1 and f2 are selected and the line L can be calculated. Then, the distance between each solution to L is computed to find the knee point, and the weight vectors corresponding to knee point are chosen. Finally, the weight vectors are updated according to Eqs. (31) and (32).

3.4 Framework of MOS-ESN

The pseudo code of MOS-ESN is described in Algorithm 2. In Step 1, the population is randomly initialized. In Steps 2 and 3, two individuals are randomly chosen to generate the offspring, the uniform crossover operation and polynomial mutation operator are applied. In Step 4, the neighborhoods of each weight vector are updated. In Step 5, the local search is operated loca iterations to improve algorithm convergence. In Step 6, the knee point is selected from EP. In Step 7, the weight vectors are updated by the weight vectors updating method.

4 4 Simulation

In this section, the proposed MOS-ESN models are tested on two simulated benchmark problems and one practical system modeling problem, including the Rossler chaotic time series prediction [29], the nonlinear system modeling problem [42] and the effluent ammonia nitrogen (NH4-N) prediction in wastewater treatment process (WWTP) [28]. It is noted that the MOS-ESN with l0 regularization is named as MOS-ESN-l0, while the MOS-ESN with l1 regularization is termed as MOS-ESN-l1.The MOS-ESN models are compared with OESN [29], the OESN with l1 norm regularization (OESN-l1) [33], the OESN with l0 norm regularization (OESN-l0) [32], the OESN whose output weight is updated by coordinate descent and l1 or l0 norm (CD-ESN-l1 [43], CD-ESN-l0), as well as the OESN whose output weights are directly calculated by MOEA/D (OESN-MOEA/D). For each algorithm, 50 independent runs are carried out in the MATLAB 2018b environment on a personal computer with i7 core 8.0 GB memory.

The training and testing RMSE values are applied to evaluate the learning and testing performance of ESNs. Furthermore, the sparsity degree (SP) of the output weight matrix [28] is also introduced. The SP and RMSE are defined as follows:

$${\text{SP}} = \frac{{\left\| {{\mathbf{W}}^{{{\text{out}}}} } \right\|_{0} }}{N + n} \times 100\%$$
(33)
$${\text{RMSE}} = \sqrt {\sum\limits_{{k = 1}}^{L} {\frac{{\left[ {{\mathbf{y}}\left( k \right) - {\mathbf{t}}\left( k \right)} \right]^{2} }}{L}} }$$
(34)

where Wout is the output weights matrix and y(k) and t(k) stand for actual and target output, respectively. A smaller RMSE means a better training or testing accuracy. Meanwhile, the smaller SP means, the ESN has the sparser structure.

To evaluate the searching ability of a multi-objective optimization, the C-matrix [45] is introduced, which can measure the ration of the non-dominated solutions in P that are not dominated by any other solutions in P*,

$$C\left( {{\mathbf{P}},{\mathbf{P}}^{*} } \right) = \frac{{{\text{size}}\left( {{\mathbf{P}}{ - }\left\{ {{\text{x}} \in \left. {\mathbf{P}} \right|\exists {\text{y}} \in {\mathbf{P}}^{*} :{\text{y}} \prec {\text{x}}} \right\}} \right)}}{{{\text{size}}\left( {\mathbf{P}} \right)}}$$
(35)

The larger C(P, P*) value means a better non-dominated solution set P.

The parameters setting of MOS-ESN-l0 and MOS-ESN-l1 are as below: the reservoir size, the population size, and the neighborhood size are set as 1000, 200, 15 in each test instance, which is suggested in [44]. The optimal value of loca, α is selected by the grid search method, the number of local search operations local is varied from 0 to 5 by the step of 1, and the step size α is set from 0 to 3 by the step of 1. For other algorithms, their corresponding parameter settings are described in Appendix.

4.1 Rossler chaotic time series prediction

To study the performance of MOS-ESN, the Rossler chaotic time series [29], a typical chaotic dynamical time series, is introduced as below:

$$\begin{array}{*{20}l} {\frac{dx}{{dt}} = - y - z} \hfill \\ {\frac{dy}{{dt}} = x + \alpha y} \hfill \\ {\frac{dz}{{dt}} = \beta + z\left( {x - \gamma } \right)} \hfill \\ \end{array}$$
(36)

where α = 0.2, β = 0.4, γ = 5.7. There are 2000 samples in the experiment, in which 1400 are used for training and the rest 600 are applied for testing. The White Gaussian noise, which has the signal-to-noise ratio (SNR) of 20 dB, is added into the original training and testing datasets.

The testing outputs and prediction error of MOS-ESN-l0, MOS-ESN-l1, OESN are illustrated in Figs. 6 and 7, respectively, in which the red, blue, black and cyan lines are the trends of MOS-ESN-l0, MOS-ESN-l1, target and OESN, respectively. It is easily found that both MOS-ESN-l0 and MOS-ESN-l1 can predict the trends of testing output, while the OESN shows missing outputs in a partial enlargement. Furthermore, the RMSE values of MOS-ESN-l0 are concentrated in [− 0.3,0.3], which is smaller than other methods, demonstrating its stable performance.

Fig. 6
figure 6

The prediction outputs for Rossler chaotic time series prediction

Full size image
Fig. 7
figure 7

The prediction errors for Rossler chaotic time series prediction

Full size image

Simulation results of all methods are presented in Table 1, including sparsity, CUP running time for one operation, the mean RMSE and standard deviation (Std. for short) RMSE of training and testing of 50 independent runs. It is easily found that the OESN has the smallest running time, while it has the largest testing RMSE, implying its poor generalization ability. Both OESN-l1 and OESN-l0 have smaller SP, which implies the regularization method could generate the sparse output weight matrix. Besides, the proposed MOS-ESN-l0 has the smallest testing RMSE and SP among all ESN models, which proves its effectiveness in terms of network sparseness and prediction accuracy.

Table 1 Simulation results for Rossler chaotic series prediction
Full size table

4.1.1 Effect of loca

As introduced in Sect. 3.4, loca decides how many local search operators are conducted on each individual. The effects of loca on network performance are investigated through 50 independent experiments. By setting loca = 0, loca = 1 and loca = 3, the obtained non-dominated solutions of MOS-ESN-l1 and MOS-ESN-l0 are plotted in Figs. 8 and 9, respectively. The x-coordinate and y-coordinate are the objective function \({{\text{f}}_{2}\text\,=\,\Vert {\text{W}}^{\text{out}}\Vert }_{1/0}\) and \({\text{f}}_{1}\text\,=\,{\Vert {\text{T}}-{\text{H}}{\text{W}}^{\text{out}}\Vert }_{2}^{2}\), respectively. Obviously, the algorithm with loca = 3 can always generate more non-dominated solutions than the algorithms with loca = 0 or loca = 1, which implies that the local search algorithm can accelerate the algorithm convergence speed.

Fig. 8
figure 8

Effect of loca on MOS-ESN-l1

Full size image
Fig. 9
figure 9

Effect of loca on MOS-ESN-l0

Full size image

By setting loca = {1, 2, 3, 4, 5} and α = 2, the statistics results of training time, training and testing RMSE values, C-matrix and SP of MOS-ESN-l1 and MOS-ESN-l0 are reported in Tables 2 and 3, respectively. It is noted that during the calculation process of C-matrix, P* = (P1, P2, …, Pn), where Pi is the non-dominated solution set by the algorithm with loca = i (i = 1, …, 5). It is easily found that when loca is set as a small value, such as 0 or 1, the small value of C-matrix is obtained, which means the worse non-dominated solutions is obtained. When loca is set as a moderate value (loca = 3), the larger value of C-matrix, lower SP and testing RMSE values can be obtained. On the contrary, if loca is set as a too large value (loca = 5), the training and testing RMSE values are not best among all the models, because the too large value of loca may have a risk of converging to local regain. Furthermore, the too large loca will increase the computational complexity or training time.

Table 2 Simulation results of different value of loca on MOS-ESN-l1
Full size table
Table 3 Simulation results of different value of loca on MOS-ESN-l0
Full size table

4.1.2 Effect of α

For ESN design, the network with too small training error or too small network sparseness is not preferred, while the solution at the knee point maybe a good choice, which is a tradeoff between two objects. To help the algorithm converge to the knee point, the weight vectors updating algorithm is proposed, in which the weight updating step α is applied. A larger α implies that the updated weight vector is closer to the corresponding weight vector of knee point.

To show the influence of α on network performance, by setting α = {0, 1, 2}, the obtained non-dominated solution sets of MOS-ESN-l1 and MOS-ESN-l0 are compared in Figs. 10 and 11, respectively, and the x-coordinate and y-coordinate are the objective function \({{\text{f}}_{2}\text{=} \, \Vert {\text{W}}^{\text{out}}\Vert }_{1/0}\) and \({\text{f}}_{1}\text{=}{ \Vert {\text{T}}-{\text{H}}{\text{W}}^{\text{out}}\Vert }_{2}^{2}\), respectively. It is easily found that the non-dominated solutions sets with α = 1 or α = 2 are better than that with α = 0, which implies the effectiveness of weight vectors updating algorithm in terms of algorithm convergence.

Fig. 10
figure 10

Effect of α on MOS-ESN-l1

Full size image
Fig. 11
figure 11

Effect of α on MOS-ESN-l0

Full size image

With α = {0, 1, 2, 3} and loca = 3, the statistic results of 50 independent experiments of MOS-ESN-l1 and MOS-ESN-l0 are listed in Tables 4 and 5, respectively. Obviously, when α = 2, the obtained ESN has the most sparse network structure and the best testing RMSE values. However, when α = 3, the corresponding testing RMSE values become larger. Hence, the too large or too small value of α is not preferred.

Table 4 Simulation results of different value of α on MOS-ESN-l1
Full size table
Table 5 Simulation results of different value of α on MOS-ESN-l0
Full size table

4.2 Nonlinear dynamic system modeling

The proposed method is performed on the nonlinear dynamic system as below

$$\begin{aligned} y(k + 1) &= 0.72y(k) + 0.025y(k - 1)u(k - 1) \hfill \\ &\quad+ 0.01u^{2} (k - 2) + 0.2u(k - 3) \hfill \\ \end{aligned}$$
(37)

where u(k) and y(k) are input and output, respectively. y(k + 1) is predicted by y(k), y(k − 1), u(k − 1), u(k − 2), u(k − 3). In the training phase, u(k) is 1.05sin(k/45). In the testing phase, u(k) is given as

$$u(k) = \left\{ {\begin{array}{*{20}l} {\sin \frac{{\pi k}}{{25}},} \hfill & {0 < k \le 250} \hfill \\ {1.0,} \hfill & {250 < k \le 500} \hfill \\ { - 1.0,} \hfill & {500 < k \le 750} \hfill \\ {0.3} \hfill & {\sin \frac{{\pi k}}{{25}} + 0.1\frac{{\pi k}}{{32}}} \hfill \\ {0.6\sin \frac{{\pi k}}{{10}},} \hfill & {750 < k \le 1000} \hfill \\ \end{array} } \right.$$
(38)

In this experiment, 2000 samples are generated by Eq. (38). The first 1400 points are used in training stage, and the remaining 600 are used in testing phase. In addition, the 20-dB Gaussian noise is added to generate the noisy environment.

The prediction output and testing error of the resulted MOS-ESN-l1, MOS-ESN-l0 and OESN are plotted in Figs. 12 and 13, respectively. Actually, all the algorithms show similar predictive trend on nonlinear dynamic system. However, the prediction error of MOS-ESN-l0 is limited in [-0.4,0.4], which is smaller than other methods. Thus, the proposed MOS-ESN-l0 has the best prediction effect among all compared algorithms.

Fig. 12
figure 12

The prediction outputs for nonlinear dynamic system

Full size image
Fig. 13
figure 13

The prediction errors for nonlinear dynamic system

Full size image

The statistic results of 50 independent runs of compared algorithms are summarized in Table 6. Obviously, the OESN has shortest training time and smallest training error, but its testing error is largest, which indicates overfitting problem. Furthermore, the MOS-ESN-l0 obtains the smallest testing RMSE and SP values, which means the MOS-ESN-l0 has better prediction accuracy, sparser reservoir for nonlinear dynamic system modeling.

Table 6 Simulation results for nonlinear dynamic system modeling
Full size table

4.3 Effluent NH4 − N model in WWTP

Recently, the discharge of industrial and domestic wastewater has also increased sharply, and the phenomenon of water quality exceeding standard in the wastewater treatment process (WWTP) is serious. In WWTP, the excessive NH4 -N will lead to eutrophication of water body and affect human health. Thus, predicting NH4-N accurately is critical. However, the WWTP is a complex system with nonlinear, uncertainty, it is difficult to predict NH4-N. To solve this problem, the laboratory analytical techniques are used. However, these methods always require long time.

In this section, the proposed MOS-ESN models are applied to predict NH4-N in WWTP. This experiment contains 641 sets of data, which are collected from Chaoyang, Beijing in 2016. The first 400 groups are treated as training data and the rest 241 are set as testing data. The inputs of ESN include T, ORP, DO, TSS and pH, which are described in [29].

The prediction result of effluent NH4-N models of MOS-ESN-l0, MOS-ESN-l1 and OESN is demonstrated in Fig. 14, and the corresponding prediction error is shown in Fig. 15. Obviously, all the algorithms achieve the similar prediction accuracy. As compared with MOS-ESN-l0 and MOS-ESN-l1, it can be found that the l0 regularization can get sparser structure, and thus the MOS-ESN-l0-based effluent NH4-N model has smaller prediction error.

Fig. 14
figure 14

Prediction output of effluent NH4-N

Full size image
Fig. 15
figure 15

Prediction errors of effluent NH4-N model

Full size image

The comparison results of different models are shown in Table 7, including the network sparsity SP, training time, the mean and standard deviation of training and testing RMSE values of 50 independent experiments. Obviously, the OESN has small training but large testing RMSE values, which implies the overfitting problem occurs. Thus, the OESN has difficulty in predicting NH4-N in WWTP. In OESN-l1 and OESN-l0, the regularization technique is applied to make the network structure sparse, but the testing RMSE value is still large. In CD-ESN-l0 and CD-ESN-l1, the regularization technique and coordinate descent are used to updates the output weights, which can obtain better prediction performance than OESN-l1 and OESN-l0. As compared with OESN-MOEA/D, the local search and weight vectors updating algorithm are applied in MOS-ESN-l0 and MOS-ESN-l1, which helps to improve solution performance. Particularly, the MOS-ESN-l0 has the smallest testing error and the sparsest network structure, which can effectively predict NH4-N of WWTP.

Table 7 Simulation results for Effluent NH4 − N model in WWTP
Full size table

5 Conclusion

In this paper, the multi-objective sparse ESN is proposed, in which the training error and network structure are optimized simultaneously. Firstly, instead of searching the regularization parameters, the design of ESN is treated as a bi-objective optimization problem. Secondly, to improve algorithm convergence performance, the local search strategy is designed, which incorporates the l1 or l0 norm regularization and coordinate descent algorithm. Furthermore, to make the algorithm converge to the region of interest, the weight vectors updating method is designed, which applies the information of knee point. The effectiveness and usability of the proposed algorithm are evaluated by experimental results. In future work, this method will be applied in other practical engineering fields, such as garbage classification and image recognition.