Multi-agent learning algorithms for content placement in cache-enabled small cell networks: 4G and 5G use cases

Abstract

Caching popular files at the small base stations (SBSs) has proved to be an effective strategy to reduce the content delivery delay in cellular networks and to alleviate the backhaul congestion. In the optimization of the placement of contents into SBS caches (the so-called content placement problem), several key parameters play an important role, such as content popularity, the mobile users’ (MUs’) channel state information (CSI), as well as the capacity of the backhaul links. These parameters are random in general, and their instantaneous values over time give rise to a stochastic process. In this paper, we propose a mathematical formulation for the distributed optimization of content placement with the objective of minimizing the average content delivery latency. Our formulation is applicable to both conventional 4G small cell networks (SCNs) as well as 5G-compatiable mmWave integrated access and backhaul (IAB) cellular communications. In particular, the placement problem is modeled as a potential game among SBSs in which the objective of each SBS is to minimize the average delay of the MUs within its coverage range. In order to compute the Nash equilibrium (NE) of the game, we adopt the learning-theoretic approach that only relies on incomplete information (or implicit feedback) of the system’s underlying stochastic processes; i.e., the content placement is optimized in run-time by gaining experience and through the immediate noisy feedbacks of the actions actually taken in the operating environment. We propose an algorithm based on multi-agent reinforcement learning (MARL) techniques for potential games. It operates in the independent action space and can learn the optimal strategy profile of the SBSs in larger-scale scenarios, even when the actions of its peers are not observable by each SBS. Simulation experiments are conducted to investigate the convergence of the learning algorithm as well as to compare against some schemes using prior knowledge.

1 Introduction

The idea of caching contents at the edge of the wireless networks dates back to 3G and 4G cellular networks [1,2,3,4,5]. Authors in [2] have argued that with the data traffic growth over cellular networks, the current network cannot support this traffic surge, even after allocating new cellular spectrum. Thus, methods are needed to reuse the communication resources. One approach to address this problem is to use the storage capacity of small base stations (SBS) to cache contents that are requested multiple times by different users. Caching popular contents at SBSs can bring requested contents closer to mobile users (MUs) instead of repeatedly downloading the contents from remote servers via backhaul links. Thus, by locally satisfying content requests of the users, edge caching can effectively enhance network performance through alleviating the backhaul burden and reducing content access delay [6,7,8]. There are some sub-problems associated with edge caching optimization: content placement, content delivery, and content migration. The content placement problem deals with the selection of contents in order to be cached in the limited storage of the SBSs. Content delivery concerns with how to convey content to a requesting user. Content migration decides on how to update the cached content set when the cache space is full and new content has to be added. In other words, a content migration strategy specifies which content is to be removed from the cache or migrated to another SBS cache. In this paper, we focus on the content placement problem in small cell networks (SCNs).

In the optimization of the placement of contents into SBS caches, some parameters such as content popularity, the mobile users’ (MUs’) channel state information (CSI), as well as the capacity of the backhaul links play a key role. These parameters are random in general, and their instantaneous values over time give rise to a stochastic process. Many of the studies on content placement for caching in base stations rely on the availability of the instantaneous information about the channel and backhaul states (e.g., [9,10,11,12,13,14,15,16,17]), where it is unrealistically assumed that non-causal information regarding the exact trace of system states (i.e., backhaul, content popularity, and channel) is available beforehand. In addition, there exist some model-based schemes assuming the availability of prior statistical information. Albeit these schemes are more realistic, but still, they require explicit knowledge of the statistics of the system processes [18,19,20,21,22,23]. From another standpoint, many of the previous studies have proposed centralized solutions in which a centralized controller decides which SBS has to cache which content. In this approach, the computational burden of the controller increases with the size of the SCN. Our work in this paper differs from these two categories of schemes as we approach the content placement problem from a distributed model-free perspective in which no information about the environmental parameters is available a priori, and optimization can be performed only by gaining experience and through the immediate feedbacks of the actions actually taken in the operating environment.

Most existing distributed model-free schemes that minimize the downloading delay of contents (e.g., [9, 13, 24, 32,33,34,35]), assume that only one of the three factors affecting the delay, i.e., the content popularity is unknown, while the availability of information on the wireless channel qualities as well as the backhaul capacities are taken for granted. Also, the distributed computation of the optimal caching policy in these schemes has been performed using different variations of multi-armed bandit (MAB) algorithms [25]. As a result, their applicability is limited only to uncoupled or loosely coupled settings where the underlying problem is amenable to straightforward decomposition. However, in more general settings where there are tight interactions between the utility/cost functions of the caching agents, an equilibrating multi-agent learning algorithm with a game-theoretic foundation is needed to be deployed for system optimization and stabilization. Among the related work, the study in [11] has proposed a distributed equilibrium learning scheme based on a cooperative repeated game formulation; however, its objective is maximizing the cache-hit ratio, and its simplistic learning rule can result in miscoordinations between the SBSs in cases where the definition of cost function varies between the SBS agents.

In this paper, we aim to minimize the access delay of contents for the users of a SCN. We consider two separate 4G and 5G SCNs which correspond to two distinct radio access and backhaul technologies. In the conventional 4G scenario, the network operates in regular Long-Term Evolution (LTE) [26] frequency bands in the access side with capacity-limited wired backhaul links. As for the 5G setting, it is assumed that the user-SBS communications are carried over mmWave frequencies which have extremely wide available bandwidth and are able to provision multi-gigabit peak data rates. Also, we consider the integrated access and backhaul (IAB) technology [27] where the operator utilizes a portion of the radio resources for wireless backhauling, and the MBS acts as a hub of in-band wireless backhaul connections for small cells within its cell coverage. IAB has recently attracted considerable interest due to its lower cost and faster deployment. In both scenarios, we realistically consider the random content popularity, the time-varying nature of the wireless channels as well as the stochastic capacity of the backhaul links. We model the problem based on game theory and propose a multi-agent reinforcement learning (MARL) algorithm for the computation of the NE of the caching game.

More elaborately, our contributions in this paper can be summarized as follows:

• We come up with three formulations for the problem of content placement optimization in SBS caches. The first two formulations are mainly to lay the groundwork for how we relax informational assumptions in computing the optimal content placement strategies of the SBSs and what are the implications of these relaxations:

• Centralized offline formulation: Our first formulation corresponds to a binary integer-programming (BIP) problem to determine the optimal placement of content groups in SBS caches with the objective of minimizing the average delay of content delivery to the MUs. In this formulation, a central entity (e.g., macro base station or MBS) computes the placement strategies. Also, three key pieces of information, including the instantaneous MU-SBS channel gains, the instantaneous capacity of backhaul links, as well as the statistical knowledge of content popularity, are assumed to be known in advance. The BIP problem is NP-hard and needs global non-causal system knowledge. As such, this formulation has no practical worth, and its solution is only interesting as a theoretical lower-bound on the performance of the other schemes.

• Distributed model-based formulation: One significant step toward a more practical solution is to come up with a distributed computation scheme. In this second formulation, we use game theory to delegate the computation of content placement strategies to the SBSs themselves. The game-theoretic concept of Nash equilibrium [28], which describes a condition of global coordination, is used as the target of optimization. Our formulation is based on the notion of potential games [29] in which the existence of pure strategy Nash equilibrium is guaranteed, and equilibrium convergence can be achieved by executing the well-established algorithm of best-response dynamics. However, the proposed formulation is model-based in the sense that the statistical knowledge (i.e., the probabilistic model) of the random processes associated with the channel gains, backhaul capacity, and content popularity are assumed to be known at design time. The SBSs use the knowledge of these probability distributions to derive their cost functions in the caching game. Then, prior to actual network deployment, the equilibrating algorithm is executed by all SBSs to obtain an NE configuration. Actual content caching in a real-life deployment is subsequently performed based on the calculated equilibrium strategies.

• Distributed model-free formulation: Our novelty lies in this third formulation, where we relax the statistical knowledge assumption in the previous game-theoretic scheme to only work with implicit feedbacks of the SBS decisions. In particular, the problem of distributed content placement is modeled as a noisy potential game in which each SBS as a player does not know its cost function beforehand and receives only a noisy sample of cost for each content placement action it actually takes in every decision epoch. This formulation is nearest to what we encounter in practical cases. Through experiencing these noisy costs over time, the SBSs need to be equipped with a reinforcement learning scheme to shape and adapt their content placement strategies in response to the actions of other SBSs.

• We propose two multi-agent reinforcement learning algorithms which are provably convergent to the Nash equilibrium of the caching game with unknown noisy costs:

• Joint action learning (JAL): In JAL, we equip each SBS with an action selection rule along with a payoff estimation procedure. The SBS agents update their estimates of the expected costs for joint-actions using Q-learning and choose actions exploiting an appropriate $\varepsilon$-greedy-based action selection policy [30]. However, the learning is performed in the product space of the action sets of all the SBS agents, which requires that each SBS observe the actions of its peers in every round. This needs the exchange of content placement decisions between the SBSs through the backhaul links. Also, learning in the joint action space leads to an exceptionally huge memory footprint which makes the JAL algorithm impractical even in fairly small-scale setups.

• Independent action learning (IAL): In IAL, however, we no longer require that each SBS observe the other SBSs’ actions. The estimation of the cost function is done independently, and this reduced complexity makes the IAL algorithm scalable for large networks consisting of a higher number of SBSs and richer content library. The algorithm is still convergent to equilibrium but with reduced accuracy compared to JAL.

• We conduct simulation experiments to evaluate our proposed IAL algorithm in both 4G and 5G use cases in terms of its average MU delay performance. We investigate the impact of different settings, including varying intensities for the popularity of cached contents, the number of MUs and SBSs, the MUs’ transmission power, backhaul capacity, the beamwidth of the mmWave SBSs and the MUs as well as the number of content groups. The IAL algorithm is also compared against the proposed centralized offline, distributed model-based, JAL, single-agent learning as well as the DQ-based caching scheme in [11].

The remainder of the paper is organized as follows: In Sect. 2, we review the literature. In Sect. 3, the model of the system and the assumptions are presented. In Sect. 4, we present the problem formulation in terms of a potential game. Section 5 proposes two multi-agent reinforcement learning algorithms to reach an NE point. In Sect. 6, we evaluate the performance of the proposed scheme. Finally, the paper concludes in Sect. 7. Table 1 lists the acronyms used throughout the paper.

Table 1 Used main acronyms

2 Related works

The body of literature on caching contents at the edge of SCNs can generally be categorized based on two aspects: (1) centralization/decentralization of the solution and (2) informational assumption.

In a centralized algorithm, the MBS acts as a central controller to determine what to cache in each SBS. It has access to global network information, such as the distances between MUs and SBSs, the channel gain profiles, the backhaul capacity, and users’ content preferences. In a centralized setup, we may formulate the content placement as an optimization problem. However, since this problem is, in general, an instance of NP-hard integer-programming, researchers have been motivated to propose distributed methods (e.g., game-theoretic approaches) to reach near-optimal solutions [9,10,11]. Distributed algorithms avoid the computational overhead of the MBS when the number of users and SBSs increases. Additionally, to circumvent the need for global network information collection, distributed algorithms constitute a better choice. These algorithms are more scalable because they allow SBSs to determine what to cache independently of each other and by just relying on locally available information.

As for the second aspect, we consider three kinds of informational assumptions: (1) Availability of perfect (non-causal) instantaneous network information such as the channel gains and the backhaul capacity (2) Availability of only statistical knowledge of the network, i.e., just the probability distribution of the network state information is available at design time. (3) The model-free assumption under which neither instantaneous nor statistical knowledge about the network is available for decision-making. Model-free optimization is the most realistic approach to solve the content placement problem. However, the existing model-free approaches only address the unavailability of content popularity information while taking for granted the availability of the knowledge on MUs’ CSI and backhaul capacity. These model-free approaches are themselves further sub-categorized into two schemes: the popularity-prediction-based schemes [10, 12, 13] and the reinforcement-learning-based schemes [11, 14, 15]. In a popularity prediction-based scheme, the existing studies first predict the popularity of contents and then exploit the estimations to contrive caching policies. On the other hand, in a reinforcement-learning-based scheme, the caching policy is trained with observations, only based on a reward from the actions, rather than tackling every single factor that affects the performance of caching. This reward can be the offloaded traffic or QoE, which covers a wide range of factors that can affect the performance [16].

In what follows, we review the most relevant content caching schemes according to the above-mentioned categorization:

• Centralized schemes assuming the availability of perfect instantaneous information: Yang et al. [32] have investigated the random caching optimization in k-tier mmWave heterogeneous networks. They have formulated the problem of determining the cache probability to maximize the number of successful transmissions. Gu et al. [33] address both the user association and cache placement problems in a cache-enabled and relay-assisted downlink mmWave network to maximize successful backhaul offloading probability. In [34], Zheng et al. have investigated the secure content delivery for a two-tier cache-enabled mmWave heterogeneous network to achieve the maximum overall secrecy throughput. They have derived analytical expressions of connection and secrecy outage probability for the distributed beamforming and direct transmission schemes with and without artificial noise injection, respectively. Zhang et al. [35] have presented a 3GPP-inspired analytical framework for a two-tier mmWave heterogeneous network involving integrated access and backhaul architecture, and have investigated the performance of uniform caching of the most popular files with respect to the latency of file delivery, average rate, and success probability.

• Distributed schemes assuming the availability of perfect instantaneous information: Li et al. in [36] have separated the content placement into independent single knapsack problems and solve the sub-problems in a distributed way with a greedy method to minimize the average load of traffic for the requests of contents. Authors in [37] have investigated the problem in a cooperative scenario in the sense that each SBS can access files from the caches of other SBSs. They have proposed a method in which the files are placed in cooperative SBSs such that the maximum number of files can be accessed from the SBSs, thereby reducing power consumption of the backhaul. The studies [9, 31] have resorted to game theory to propose distributed methods. Guo et al. in [31] aim at minimizing the energy consumption in the cell network. They have modeled the content placement problem as an exact potential game (with guaranteed existence of pure Nash equilibrium (NE)) among the SBSs, and have proposed an iterative algorithm to solve the game. A closely related work to ours is [9], where Yang et al. have formulated the problem as a potential game and presented a distributed algorithm based on best-response dynamics (BRD) to minimize the downloading delay of contents.

• Centralized schemes assuming the availability of statistical information: Chen et al. in [18] have considered statistical information on the contact duration of small cells and mobile devices such that the contact process between SBSs and MUs follows independent Poisson processes. The other factors affecting the system performance are previously known in the form of exact values. Then, a submodular optimization technique is adopted to solve the problem. In [19], statistical information is assumed only on the popularity of content, which is modeled by Zipf distribution. The authors have exploited a fuzzy soft-set approach to find the relationship between the content popularity with the currently connected users. This relationship is then for content placement to minimize the downloading delay. Zhou et al. in [20], under the assumption of statistical knowledge for channel fading coefficients, have formulated a problem to minimize the outage probability (defined as the probability that SINR is smaller than a threshold). They have modeled the small-scale fading coefficients among the MBS and SBSs by Gaussian distribution with zero mean and unit variance and analytically obtain the optimal solution.

• Distributed schemes assuming the availability of statistical information: Liao et al. in [21] have relied on the statistical information of content popularity to estimate all possible joint user requests in different SBSs. Building on the advantages of maximum distance separable (MDS) codes, they have reformulated the original problem into a convex form to minimize the long-term average user attrition cost. The problem has then been decomposed into a number of sub-problems to be solved in a distributed way. Under similar assumptions, the same authors have extended their study in [22] by proposing a greedy approach for small-scale networks along with a multicast-aware cooperative approach for small-scale setups. Keshavarzian et al. in [23] have modeled the cache placement problem as a discrete Markov chain and assume statistical information on the state transitions. They have formulated the problem to maximize the number of served files and derive a lower bound on the optimal caching. Using the lower bound, they have replaced the problem with independent Boolean knapsack sub-problems, which are independently solved in a distributed manner.

• Centralized model-free schemes: The authors in [38] and [39] have come up with schemes assuming that the popularity of contents is unknown. They have proposed algorithms based on MAB optimization in which the popularity model of content is learned and used for content placement. Mishra et al. in [12] have shown that the prediction of content popularity is a dual sparse matrix completion problem. They have then proposed a novel Bayesian learning algorithm for popularity prediction. The authors in [40] have presented a method based on Bayesian inference, which extracts the key factors of the traffic (including content popularity and content size) and then use a Bayesian ranking model to combine the features and form a content list. Nie et al. in [13] have investigated the caching problem to minimize the average transmission delay. Among the different factors affecting the downloading delay, they have assumed that the popularity of contents is unknown and have applied a Bayesian learning algorithm for estimation.

• Distributed model-free schemes: Haw et al. in [10] have exploited an autoregressive integrated moving average (ARIMA) scheme to learn and predict the popularity of content. They have defined the system utility function in a way that it is decomposable into independent sub-problems, which can be solved by SBSs in a distributed way. Jiang et al. in [14] have modeled the content placement as a multi-agent MAB problem to minimize the downloading delay of contents without knowing the system parameters. Due to the service differentiation, they have used the weighted reduction in delays as the reward of caching for content providers. Xu et al. in [24] have also used a multi-agent MAB algorithm to directly learn the caching strategy without the knowledge of the factors affecting the downloading delay. They have extended their work in [15] to directly learn the caching strategy in a non-stationary environment. The multi-agent MAB-based algorithm has been modified by designing new perturbed terms for superior adaptation to the dynamic environment. A closely related work to ours is [11], where Lin et al. have modeled the distributed content placement problem as a fully cooperative repeated game among the SBSs with the objective of maximizing the average cache hit probability and with no knowledge about content popularities. They have proposed a distributed Q-learning algorithm to ensure the cooperation among SBSs to reach the optimal Nash equilibrium point.

Our proposed solution in Sect. 5 is also within the category of distributed model-free schemes. However, it differs from all the reviewed work in that we address the content placement problem in the absence of CSI, backhaul capacity as well as the content popularity information. Also, our proposed solution is equally applicable to both 4G and 5G use case scenarios. Table 2 summarizes the most relevant schemes from prior work.

Table 2 Comparison of related work

3 System model and assumptions

In this section, the model of the system for a SCN is introduced. Then, we elaborate on the assumptions made about the dynamics of the wireless channel, backhaul capacity, and popularity distribution of contents.

3.1 Network model

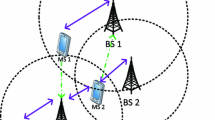
We consider a small cell network (shown in Fig. 1) in which an MBS and $N$ SBSs, deployed in the coverage area of the MBS to act as relays, serve the requests of $M$ MUs. The sets of MUs and SBSs are denoted by $\mathcal{M}=\{\mathrm{1,2},3,\dots ,M\}$ and $\mathcal{N}=\{\mathrm{1,2},3,\dots ,N\}$, respectively. The SBSs are connected to the MBS with non-ideal backhaul links having limited capacity. The coverage areas of the SBSs are in general overlapping, and thus mobile users can be served by one of many potential SBSs. Our model-free solution to content caching in Sect. 5 is applicable to both conventional as well as emerging wireless communication technologies. Hence, in the sequel, we concretize the network model by characterizing the SBS-to-UE and MBS-to-SBS connections according to both 4G and 5G use cases.

Fig. 1

A Small-Cell Network (SCN) with cache-enabled SBSs; the left-hand side depicts 5G mmWave IAB communications and the right-hand side is a conventional 4G SCN with wired backhaul

3.2 Conventional 4G scenario

3.2.1 Wireless link capacity and channel model

In the 4G scenario, the description of the link capacity is straightforward. In particular, following the standard Shannon formula, the wireless capacity between MU $m$ and SBS $n$ at time $t$ can be calculated as:

$${r}_{n,m}^{\left(4{\mathbb{G}}\right),t}=\frac{{W}^{\left(4{\mathbb{G}}\right)}}{{M}_{n}}{\mathrm{log}}_{2}\left(1+\frac{{p}_{n}^{\left(4{\mathbb{G}}\right)}{g}_{n,m}^{t}{{d}_{n,m}^{t}}^{-\alpha }}{\sum_{i\in \mathcal{N},i\ne n}{p}_{i}{g}_{i,m}^{t}{{d}_{i,m}^{t}}^{-\alpha }+{\sigma }_{\left(4{\mathbb{G}}\right)}^{2}}\right)$$

(1)

in which ${W}^{\left(4{\mathbb{G}}\right)}$ is the spectrum bandwidth and ${p}_{n}^{\left(4{\mathbb{G}}\right)}$ is the transmit power of SBS $n$. Here ${M}_{n}$ is the number of MUs associated with SBS $n$ (c.f., Sect. 3.5 on user association criteria) and the access bandwidth is equally shared among the connected MUs according to a round robin schedule. The symbol $\alpha$ is the path-loss exponent and ${\sigma }_{\left(4{\mathbb{G}}\right)}^{2}$ is the power of noise at each MU. ${d}_{n,m}^{t}$ and ${g}_{n,m}^{t}$ are respectively the distance and channel gain between SBS $n$ and MU $m$ at time $t$.

3.2.2 Backhaul capacity model

In the 4G case, traditional non-ideal wired backhaul links (with limited capacity) are assumed between the MBS and any SBS $n$. Depending on the background load conditions, the available capacity ${b}_{n}^{t}$ on each link may vary randomly with time.

3.2.3 Informational assumptions

In the content placement problem, we may distinguish between three forms of knowledge of the channel gain and backhaul capacity:

• (1) Perfect instantaneous information: In this form of knowledge, the exact value of ${g}_{n,m}^{t}$ for each pair of SBS $n$ and MU $m$ as well as the exact value of ${b}_{n}^{t}$ for each SBS $n$ at each time $t$ are known non-causally (prior action selection).

• (2) Statistical information: Only the probability distribution ${f}_{G}({g}_{n,m})$ of the channel gain as well as the distribution model ${f}_{B}({b}_{n})$ of the backhaul capacity are known beforehand, and neither the exact values of ${g}_{n,m}^{t}$ nor the values of ${b}_{n}^{t}$ are known a priori.

• (3) Implicit feedback: Actually, no information about the channel gain nor the backhaul capacity is available at the time of decision-making. SBS $n$ at time $t$ replies to the request of MU $m$ and gains feedback concerning the downloading delay MU $m$ has experienced, which is affected partly by channel gain ${g}_{n,m}^{t}$ as well as by the backhaul capacity ${b}_{n}^{t}$.

Assumption 1

(Channel and Backhaul Statistics). It is assumed that the channel gains for all pairs of SBS-MUs as well as the backhaul capacities for all SBSs are i.i.d. random processes. ■

3.3 Emerging 5G scenario

In the emerging 5G small cell networks, mmWave frequencies are being envisaged to replace the currently operational μWave networks. This is partly due to the limited range of propagation in mmWave transmissions which makes it more suitable for high density small cells. Another appealing feature is the extremely wide available bandwidth in mmWave communications so that small cell networks armed with this technology are expected to provision multi-gigabit peak data rate to meet the ever-increasing demand on mobile user traffic. Yet another evolution in 5G small cells is that the backhaul links are most preferably wireless due to several reasons such as fast deployment, cost saving and self-configuration. In particular, the IAB networks [27], where the operator utilizes a portion of the radio resources for wireless backhauling, has recently attracted considerable interest. In IAB, the MBS acts as a hub of in-band wireless backhaul connections for small cells within its cell coverage. In what follows, we express the details of the mmWave IAB communication model which is in line with the emerging 5G SCNs.

3.3.1 mmWave propagation model

While we can safely assume that no considerable blockage occurs in mmWave MBS to mm-SBS¹ backhaul links (e.g., [41, 42]), transmission over the access links can be sensitive to blockage by surrounding obstacles at the MU, e.g., human body and vehicles. Following the 3GPP Standard [43], we assume that the mm-SBS to MU channel behaves probabilistically according to a two-state blockage model. In particular, the mmWave signals are prone to blockages (e.g., due to stationary obstacles), and the channel condition between an MU and its associated mm-SBS can alternate between the two states: Line-of-Sight (LOS) and Non-Line-of-Sight (NLOS). Being in LOS state would mean that a direct propagation path exists between the MU and mm-SBS. On the other hand, NLOS happens whenever the direct path is blocked and the receiving terminal receives the signal via reflection from a blockage. Let the LOS link be of length $d$ and $\beta$ denote the blockage density, then the LOS and NLOS states will occur with probabilities ${\mathbb{P}}_{\mathcal{L}}(.)$ and ${\mathbb{P}}_{\mathcal{N}}(.)$, respectively (defined below) [44]:

$${\mathbb{P}}_{\mathcal{L}}\left(d\right)={e}^{-\beta d}, {\mathbb{P}}_{\mathcal{N}}\left(r\right)={1-e}^{-\beta d}$$

(2)

3.3.2 Beamforming model

Given the small wavelengths of mmWaves, transmitters and receivers perform directional beamforming to make up for path loss and extra noise. The actual antenna patterns can be approximated by a sectored antenna model [45] commonly used in prior work (e.g., [46, 47]). According to this model, in the main lobe, the gains are constant for all angles. In the side lobe, however, the gains are equal to another smaller constant (denoted by $z$). Let ${\theta }_{n,m}^{s}$ and ${\theta }_{n,m}^{u}$ be the angles between mm-SBS $n$ and MU $m$ with respect to their corresponding boresight directions. Furthermore, let ${\varphi }_{n,m}^{s}$ and ${\varphi }_{n,m}^{u}$ denote the operation beamwidths of mm-SBS $n$ and MU $m$ for the link in between these two. The transmission and reception gains of mm-SBS $n$ and MU $m$ (towards each other) can be given by:

$$\begin{gathered} g_{{n,m}}^{s} \left( {\theta _{{n,m}}^{s} ,\varphi _{{n,m}}^{s} } \right) = \left\{ {\begin{array}{*{20}l} {\frac{{2\pi - \left( {2\pi - \varphi _{{n,m}}^{s} } \right)z}}{{\varphi _{{n,m}}^{s} }},\,\,\,\left| {\theta _{{n,m}}^{s} } \right| \le \frac{{\varphi _{{n,m}}^{s} }}{2}} \hfill \\ {z,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,otherwise} \hfill \\ \end{array} } \right. \hfill \\ g_{{n,m}}^{u} \left( {\theta _{{n,m}}^{u} ,\varphi _{{n,m}}^{u} } \right) = \left\{ {\begin{array}{*{20}l} {\frac{{2\pi - \left( {2\pi - \varphi _{{n,m}}^{u} } \right)z}}{{\varphi _{{n,m}}^{u} }},\,\,\left| {\theta _{{n,m}}^{u} } \right| \le \frac{{\varphi _{{n,m}}^{u} }}{2}} \hfill \\ {z,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,otherwise} \hfill \\ \end{array} } \right. \hfill \\ \end{gathered}$$

(3)

where $0\le z <1$ represents the side-lobe gain ($z\ll 1$ for narrow beams). Likewise, we may compute the reception and transmission directivity gains between the beam of MBS towards mm-SBS $n$ and the beam of mm-SBS $n$ towards MBS, which we denote by ${g}_{0,n}^{B}$ and ${g}_{0,n}^{s}$, respectively.

3.3.3 Backhaul and access transmission rates

Given that the transmitting power of the MBS is much higher than that of mm-SBSs, there would be severe cross-tier interference between the backhaul and access links if the MBS and mm-SBSs transmit over the same spectrum band simultaneously. Hence, similar to [48], we assume that the backhaul and access links utilize orthogonal frequencies. Moreover, the spectrum resource dedicated to different backhaul connections are orthogonal. Denote by ${w}_{n}$ the bandwidth dedicated to the backhaul link of mm-SBS $n$. The following equation gives the MBS-to-mmSBS transmission rate over the backhaul link associated with mm-SBS $n$:

$${{r}_{0,n}^{\left(5{\mathbb{G}}\right),t}=w}_{n}{\mathrm{log}}_{2}\left(1+\frac{{p}_{0}{g}_{0,n}^{B}{{g}_{0,n}^{s}h}_{0,n}^{t}}{{\sigma }_{\left(5{\mathbb{G}}\right)}^{2}}\right)$$

(4)

where ${p}_{0}$ is the transmitting power of MBS, ${h}_{0,n}^{t}$ is the instantaneous channel gain from MBS to mm-SBS $n$, and ${\sigma }_{\left(5{\mathbb{G}}\right)}^{2}$ is the noise power for the mmWave communication.

Similarly, the transmission rate over the access link between mm-SBS $n$ and MU $m$ can be computed as:

$${r}_{n,m}^{\left(5{\mathbb{G}}\right),t}=\frac{{W}^{\left(5{\mathbb{G}}\right)}}{{M}_{n}}{\mathrm{log}}_{2}\left(1+\frac{{p}_{n}^{\left(5{\mathbb{G}}\right)}{g}_{n,m}^{s}{g}_{n,m}^{u}{h}_{n,m}^{t}{{d}_{n,m}^{t}}^{-{\alpha }_{j}}}{\sum_{i\in \mathcal{N}, i\ne n}{p}_{i}^{\left(5{\mathbb{G}}\right)}{{g}_{i,m}^{s}{g}_{i,m}^{u}h}_{i,m}^{t}{{d}_{i,m}^{t}}^{-{\alpha }_{j}}+{\sigma }_{\left(5{\mathbb{G}}\right)}^{2}}\right)$$

(5)

where ${p}_{n}^{\left(5{\mathbb{G}}\right)}$ is the transmitting power of mm-SBS $n$, ${h}_{n,m}^{t}$ is the instantaneous channel gain from mm-SBS $n$ to MU $m$, ${d}_{n,m}^{t}$ is the distance between the typical MU and its serving mm-SBS and ${\alpha }_{j}$ is the path loss exponent with $j\in \{\mathcal{L},\mathcal{N}$}.

3.3.4 Informational assumptions

The three forms of knowledge corresponding to the 5G backhaul and access transmission rates are as follow:

• (1) Perfect instantaneous information: In this form of knowledge, the exact values of ${h}_{0,n}^{t}$ and ${h}_{n,m}^{t}$ for every MBS-to-mmSBS link and every mm-SBS-to-MU link at each time $t$ is known non-causally (prior action selection).

• (2) Statistical information: Only the probability distributions of the channel gains as well as the LOS-NLOS state probabilities are known beforehand.

• (3) Implicit feedback: No information about the channel gain is available at the time of decision-making, and the mm-SBSs have to rely on implicit feedbacks from their associated MUs to update their caching strategies. Also, it is realistically assumed that the LOS-NLOS state probabilities are related to the environment, and these probabilities are typically unknown [49].

Assumption 2

(Channel Gain Statistics). It is assumed that the channel gains for all pairs of communicating entities are i.i.d. random processes.

3.4 Content and popularity model

The set of contents is denoted by $\mathcal{F}=\{1, \dots ,f,\dots , F\}$ where $F$ is the size of the content library. Each content is split into chunks of the same size. Also, we assume that the contents in $\mathcal{F}$ are divided into groups of size $H$ contents. SBSs cache contents based on these groups, and each SBS can cache just one content-group (i.e., for simplicity, it is assumed that the cache capacity for each SBS is limited to $H$ contents). Furthermore, the total number of content groups $K=F/H$ is taken to be an integer without a loss of generality, and the collection of content groups is denoted by $\mathcal{K}=\left\{1,\dots ,k,\dots ,K\right\}$.

The MUs request for contents independently based on their popularity. In decision-making for content placement, the content popularity knowledge is in one of two ways:

• (1) Statistical information: There is only a probability distribution model of the content popularity. For example, if content popularity follows the standard Zipf’s law with parameter $\gamma$, then:

  $${p}_{f} = \frac{{\frac{1}{{f^{\gamma } }}}}{{\mathop \sum \nolimits_{{\mathrm{f} \in {\mathcal{F}}}} \frac{1}{{\mathrm{f}^{\gamma } }}}},\forall f \in {\mathcal{F}}$$

  (6)

  ${p}_{f}$ describes content popularity according to the well-known Zipfian rank-frequency distribution. In other terms, ${p}_{f}$ measures the fraction of the time the f-th most popular file is requested. Hence, files which have larger popularity, are ranked with lower indices in the content library. As an additional remark, the simplest case of Zipf's law is a 1/f function. In fact, given a set of Zipfian distributed frequencies, sorted from most popular to least popular, the second most popular file will occur half as often as the first, the third most common frequency will occur 1/3 as often as the first, and the f-th most common frequency will occur 1/f as often as the first. As for the role of the exponent $\gamma$, larger values of $\gamma$ leads to a steeper distribution in the sense that the requests issued by consumers are concentrated on a smaller set of contents (i.e., more queries are focused on a set of hot contents). Hence, by only caching these hot contents in their limited memory, the SBSs can reduce their miss ratio, thereby decreasing the MUs’ total delay.

  Accordingly, the popularity of content-group $k$ can be expressed by summing the popularities of files in listed in this group:

  $${P}_{k}=\sum_{f=\left(k-1\right)H+1}^{f=kH}{\mathcal{p}}_{f}, \forall k\in \mathcal{K}$$

  (7)

  The larger the ${P}_{k}$, the more popular would be the content group $k$.

• (2) Popularity with unknown distribution: No information about the content popularity is available. Each SBS at time $t$ serves contents to its associated MUs and observes only their downloading delay (as an implicit feedback), whose expected value is affected by the content popularity.

3.5 User association criteria and effective data rate

Denote the SBS-content placement configuration at time $t$ by a $N\times K$ matrix ${I}^{t}$ in which ${I}_{n,k}^{t}$ is the element at the $n$-th row and $k$-th column taking values from $\{\mathrm{0,1}\}$. ${I}_{n,k}^{t}=1$ if SBS $n$ at time $t$ has the content-group $k$ in its cache, and 0 otherwise. Each SBS can cache just one content group, so there is only one non-zero number in each row of ${I}^{t}$. ${R}_{n,m,k}^{t}$ is the maximum data rate of MU $m$ at time $t$ when receiving a file in group $k$ from SBS $n$. If the content is in the cache of SBS $n$, it is equal to the wireless capacity between them. Otherwise, the rate is also limited by the backhaul capacity of SBS $n$. Overall, the effective data rate ${R}_{n,m,k}^{t}$ can be calculated as:

$${R}_{n,m,k}^{t}=\left\{\begin{array}{c}{r}_{n,m}^{\left(4{\mathbb{G}}\right),t}{I}_{n,k}^{t}+\mathrm{min}\left\{{r}_{n,m}^{\left(4{\mathbb{G}}\right),t},{b}_{n}^{t}\right\}\left(1-{I}_{n,k}^{t}\right), 4G\,communication\,model\\ {r}_{n,m}^{\left(5{\mathbb{G}}\right),t}{I}_{n,k}^{t}+\mathrm{min}\left\{{r}_{n,m}^{\left(5{\mathbb{G}}\right),t},{r}_{0,n}^{\left(5{\mathbb{G}}\right),t}\right\}(1-{I}_{n,k}^{t}), 5G\,communication\,model\end{array}\right.$$

(8)

Given SINR thresholds ${\delta }^{\left(4{\mathbb{G}}\right)}$ and ${\delta }^{\left(5{\mathbb{G}}\right)}$, SBSs/mm-SBSs that can offer an SINR above these thresholds to an MU can serve its request. The neighbor set of an MU consists of those SBSs that can provide an SINR above the aforementioned threshold for serving its requests. In this case, this MU is also a neighbor of those SBSs. The neighboring SBSs of MU $m$ and the neighboring MUs of SBS $n$ are denoted by $\mathcal{N}(m)$ and $\mathcal{M}(n)$, respectively. Whenever MU m has a request from content-group $k$, it associates with the SBS providing the highest rate to it. Therefore, the user association criterion is expressed by:

$${n}^{*}=\underset{n\in \mathcal{N}(m)}{\mathrm{arg max}}{R}_{n,m,k}^{t}$$

(9)

3.6 Delay model

The downloading delay for MU $m$ when requesting content from group $k$ at time $t$ is given as:

$${D}_{m,k}^{t}=L/{R}_{{n}^{*},m,k}^{t}$$

(10)

where $L$ is the size of a content. Hence, the expected value of ${D}_{m,k}^{t}$ (w.r.t. content popularity distribution) is given by:

$${D}_{m}^{t}=\underset{k}{\mathbb{E}}[{D}_{m,k}^{t}]=\sum_{k\in \mathcal{K}}{P}_{k}\times {D}_{m,k}^{t}$$

(11)

Table 3 summarizes the notations used in the system model.

Table 3 Summary of notations in the system model

4 Problem formulation

In this section, we present three formulations for the content placement problem. Each formulation corresponds to one of the informational assumptions on the stochastic processes of the wireless channel gains, backhaul capacity, and content popularity. In particular, in Sect. 4.1, we give a centralized offline scheme. Next, in Sect. 4.2, we present a distributed model-based approach, and finally, in Sect. 4.3, we present our main contribution, which is a distributed model-free scheme. The former two formulations serve for smoothing the discussion of our main scheme in the sequel. We also use their corresponding outcome for cache content placement as baselines for comparison in our numerical results.

4.1 Centralized offline formulation

In this section, we consider the problem setting in Sect. 3 and assume that the perfect non-causal information of the channel gains, as well as backhaul capacity, is available. We also assume full statistical knowledge of the content popularity. The offline approach seeks to determine the values of the matrix ${I}^{t}$ whose entries indicate which content group is to be cached at each SBS. Our aim is to minimize the sum of MUs’ expected delay. Therefore, the optimization problem can be formulated as follows:

$$\begin{gathered} \mathop {{\text{minimize}}}\limits_{{I^{t} }} \mathop \sum \limits_{{m \in {\mathcal{M}}}} D_{m}^{t} \hfill \\ {\text{subject to}} \, I_{n,k}^{t} \in \left\{ {0,1} \right\},\forall n \in {\mathcal{N}}, \forall k \in {\mathcal{K}}, \hfill \\ \mathop \sum \limits_{{k \in {\mathcal{K}}}} I_{n,k}^{t} \le 1,\forall n \in {\mathcal{N}} \hfill \\ \end{gathered}$$

(12)

This problem is a 0–1 integer programming, which is NP-hard. Also, another disadvantage here is that the global system knowledge and perfect instantaneous information are needed to provide optimal action for each SBS and minimize the expected delay for serving content requests. The optimization problem can be solved by using a binary integer programming (BIP) solver. In general, the solution of the corresponding offline optimization problem can be considered as a theoretical lower-bound on the performance of the other algorithms.

4.2 Distributed model-based formulation

In this approach, it is assumed that the perfect instantaneous information of the system is not accessible, and only its statistical model is known. In this case, the exact value of ${R}_{n,m,k}^{t}$ is not accessible, and only its expected value is computable as:

$$\bar{R}_{{n,m,k}} = \left\{ \begin{gathered} I_{{n,k}} \times \mathop {\mathbb{E}}\limits_{{g_{{n,m}} }} \left[ {r_{{n,m}}^{{\left( {4{\mathbb{G}}} \right)}} } \right] + (1 - I_{{n,k}} ) \times \mathop {\mathbb{E}}\limits_{{g_{{n,m}} ,b_{n} }} \left[ {{\text{min}}\left\{ {r_{{n,m}}^{{\left( {4{\mathbb{G}}} \right)}} ,b_{n} } \right\}} \right],\,\,\,\,\,\,\,\,4G \hfill \\ I_{{n,k}} \times \mathop {\mathbb{E}}\limits_{{h_{{n,m}} }} \left[ {r_{{n,m}}^{{\left( {5{\mathbb{G}}} \right)}} } \right] + (1 - I_{{n,k}} ) \times \mathop {\mathbb{E}}\limits_{{h_{{n,m}} ,h_{{0,n}} }} \left[ {{\text{min}}\left\{ {r_{{n,m}}^{{\left( {5{\mathbb{G}}} \right)}} ,r_{{0,n}}^{{\left( {5{\mathbb{G}}} \right)}} } \right\}} \right], 5G \hfill \\ \end{gathered} \right.$$

(13)

Hence, the relations (9), (10), and (11) are rewritten as follows:

$${n}^{*}=\underset{n\in \mathcal{N}(m)}{\mathrm{arg max}}{\overline{R} }_{n,m,k}$$

(14)

$${\overline{D} }_{m,k}=L/{\overline{R} }_{{n}^{*},m,k}$$

$${\overline{D} }_{m}=\underset{k}{\mathbb{E}}[{\overline{D} }_{m,k}]$$

Now, aside from departing from the unrealistic offline informational assumptions, here we carry our solution one step further toward practice by coming up with a distributed game-theoretic approach to determine the entries of the solution matrix ${I}_{n,k}$. For a decentralized approach, the optimization problem is modeled as a game in which each SBS is a player who aims to minimize the delay of its neighboring MUs by caching the best content group.

We develop a distributed algorithm based on a game $\mathcal{G}=\{\mathcal{N},\mathcal{A},{\left\{{\overline{C} }_{n}\right\}}_{n\in \mathcal{N}}\}$ where $\mathcal{N}$ is the set of players (SBSs) and ${\overline{C} }_{n}:{\times }_{n\in \mathcal{N}}\mathcal{A}\to {\mathbb{R}}$ is the cost of player $n$. Also, $\mathcal{A}$ is the joint (pure) strategy space. In fact, following standard game-theoretic notations, $\mathcal{A}={\times }_{n\in \mathcal{N}}{\mathcal{A}}_{n}$ and ${\varvec{a}}=({a}_{n},{{\varvec{a}}}_{-n})\in \mathcal{A}$ is a strategy (or action) profile in which ${a}_{n}$ is the strategy chosen by player $n$, and ${{\varvec{a}}}_{-n}$ is the strategy profile of all players other than $n$. In our content placement game, ${a}_{n}$ represents the choice of SBS $n$ for caching one content group from the set $\mathcal{K}$.

Let ${\overline{C} }_{n}$ denote the cost of player $n$ defined as the sum of the expected delay of its neighboring MUs, according to:

$${\overline{C} }_{n}=\sum_{m\in \mathcal{M}(n)}{\overline{D} }_{m}$$

(15)

In this game, we aim at obtaining a strategy profile ${{\varvec{a}}}^{*}\in \mathcal{A}$ for the cache content placement of SBSs, which constitutes a Nash equilibrium.

Definition 1

(Nash Equilibrium) [28]. A strategy profile ${{\varvec{a}}}^{*}\in \mathcal{A}$ is an NE if it satisfies:

$${\overline{C} }_{n}\left({{\varvec{a}}}^{*}\right)\le {\overline{C} }_{n}\left({a}_{n},{{\varvec{a}}}_{-n}^{*}\right)\forall {a}_{n}\in \mathcal{K}, \forall n\in \mathcal{N}$$

(16)

Definition 2

(Potential Game) [29]. A hypothetical game with player set $\mathcal{N},$ action set $\mathcal{A},$ and cost functions ${\left\{{\mathcal{C}}_{n}\right\}}_{n\in \mathcal{N}}$ is called a potential game if there exists a potential function $\Phi :\mathcal{A}\to {\mathbb{R}}$ such that for all ${\varvec{a}}\in \mathcal{A}$, it holds that $\forall n\in \mathcal{N}$

$${\mathcal{C}}_{n}\left({a}_{n}^{^{\prime}},{{\varvec{a}}}_{-n}\right)-{\mathcal{C}}_{n}\left({a}_{n},{{\varvec{a}}}_{-n}\right)=\Phi \left({a}_{n}^{^{\prime}},{{\varvec{a}}}_{-n}\right)-\Phi \left({a}_{n},{{\varvec{a}}}_{-n}\right)$$

(17)

Theorem 1

Game $\mathcal{G}$, with cost function (15) and potential function (18) (below), is a potential game:

$$\Phi =\sum_{m\in \mathcal{M}}{\overline{D} }_{m}$$

(18)

Proof

For game $\mathcal{G}$, relation (17) can be verified as follows:

$$\begin{aligned}&\Phi \left({a}_{n}^{\mathrm{^{\prime}}},{{\varvec{a}}}_{-n}\right)-\Phi \left({a}_{n},{{\varvec{a}}}_{-n}\right)=\sum_{m\in \mathcal{M}}{\overline{D} }_{m}\left({a}_{n}^{\mathrm{^{\prime}}},{{\varvec{a}}}_{-n}\right)-\sum_{m\in \mathcal{M}}{\overline{D} }_{m}\left({a}_{n},{{\varvec{a}}}_{-n}\right) \hfill \\ &\quad =\left[\sum_{m\in \mathcal{M}\left(n\right)}{\overline{D} }_{m}\left({a}_{n}^{\mathrm{^{\prime}}},{{\varvec{a}}}_{-n}\right)+\sum_{m\in \mathcal{M}-\mathcal{M}\left(n\right)}{\overline{D} }_{m}\left({a}_{n}^{\mathrm{^{\prime}}},{{\varvec{a}}}_{-n}\right)\right]-\left[\sum_{m\in \mathcal{M}\left(n\right)}{\overline{D} }_{m}\left({a}_{n},{{\varvec{a}}}_{-n}\right)+\sum_{m\in \mathcal{M}-\mathcal{M}\left(n\right)}{\overline{D} }_{m}\left({a}_{n},{{\varvec{a}}}_{-n}\right)\right]\\&\quad =\sum_{m\in \mathcal{M}\left(n\right)}{\overline{D} }_{m}\left({a}_{n}^{\mathrm{^{\prime}}},{{\varvec{a}}}_{-n}\right)-\sum_{m\in \mathcal{M}\left(n\right)}{\overline{D} }_{m}\left({a}_{n},{{\varvec{a}}}_{-n}\right)={\overline{C} }_{n}\left({a}_{n}^{\mathrm{^{\prime}}},{{\varvec{a}}}_{-n}\right)-{\overline{C} }_{n}\left({a}_{n},{{\varvec{a}}}_{-n}\right).\end{aligned}\blacksquare$$

(19)

Now, the main property of potential games is the existence of at least one equilibrium (in pure strategy form), and that the computation of one such equilibrium can be done by distributed sequential play based on a process called Best-Response Dynamics (BRD) [52]. BRD is an iterative process in which, at each iteration, one player is chosen to optimize its own strategy, called best-response (i.e., the acting player selects the strategy so that its cost is minimized given the most recent strategies of other players). This procedure is repeated until the strategy profile does not change anymore. The pseudo-code of BRD is demonstrated in Algorithm 1, which is guaranteed to converge to an NE of game $\mathcal{G}$. In practice, the initial strategy for all SBSs can be chosen arbitrarily. At each step, only one player can act. The player selection can be performed by a scheduler daemon and through a shared control channel among neighboring SBSs.

A main drawback with BRD is that in order to compute the best-responses, each player has to explicitly observe the other players’ recently chosen strategies. Additionally, optimizing the expected value of the cost function needs the statistical information of the channel gain, the backhaul capacity, and content popularity. In the model-based scheme discussed in this section, we have assumed that this information is available for all SBSs.

4.3 Distributed model-free formulation

In practical scenarios, it is often difficult or even impossible to attain reliable information about the stochastic processes underlying the cellular network evolution, e.g., channel gain, the backhaul capacity, and content popularity. In these conditions, we cannot adopt a model-based approach. Alternatively, in this section, we restate the problem of content placement in a distributed (game-theoretic) model-free form. This formulation is nearest to what we encounter in practical cases. The main challenge here is to compute the optimal placement action in the absence of the instantaneous and statistical knowledge of the system, and instead, by relying only on the immediate feedback (in the form of instantaneous values of cost) acquired through real-time interactions with the operating environment.

In a model-free scheme, SBSs, as learning agents, try to select the best action just based on the observed per-stage (also called sample) costs. These samples are noisy and are in fact composed of an expected value (equal to the unknown underlying cost function ${\overline{C} }_{n}$) and a noise ${e}_{n}^{t}$ arising from randomness in the parameters of the cost function (i.e., channel gain, backhaul capacity, and content popularity). Actually, randomness in these parameters causes variations in the delay experienced by MUs, and thus, the costs of SBSs are random and time-variant as well. Through experiencing these noisy costs over time, the SBSs need to shape and adapt their content placement strategies in response to the actions of other SBSs. More specifically, in a game with noisy costs, when joint-action ${\varvec{a}}\in \mathcal{A}$ is played, SBS $n$ perceives the sample cost:

$${C}_{n}(t)={\overline{C} }_{n}+{e}_{n}^{t}$$

(20)

where ${\overline{C} }_{n}$ is the expected cost to SBS $n$ (which is unknown), and ${e}_{n}^{t}$ is the noise associated with the sample cost for SBS $n$ at time $t$. It is noted that a game with noisy costs is a generalization of the bandit problem discussed by Sutton and Barto [30] to a multi-agent setting. In the next section, we shall use extensions of reinforcement learning strategies to converge to an equilibrium of the caching game.

5 Multi-agent learning for distributed model-free content placement

In this section, we propose two multi-agent learning-based algorithms for our third formulation of the caching problem (c.f., Sect. 4.3) in which no information is known about the environment. In both algorithms, we equip each SBS with an action selection rule along with a payoff estimation procedure. However, our first algorithm in Sect. 5.1 is an instance of joint action learning (JAL), while our second algorithm in Sect. 5.2 is of type independent action learning (IAL). In the sequel, we discuss these two algorithms and highlight their pros and cons.

5.1 Multi-agent joint action learning (JAL)

In this section, we consider the formulation of a caching game with unknown noisy costs (c.f., Sect. 4.3), in which the SBSs can form estimates of the true cost functions that are accurate enough to ensure that an NE (or an approximation thereof) can be found. In noisy environments, reinforcement learning is often exploited to estimate the mean value of a perturbed cost function [30], and this is the method we adopt here. In particular, if the agents update their estimates of the expected costs for joint-actions using Q-learning and select actions using an appropriate $\varepsilon$-greedy action selection policy, then with probability one (w.p.1), the cost function estimates will converge to their true mean values. In JAL, each agent keeps track of the frequency of other agents’ actions while updating the cost estimate for the joint-action played. Joint action learners learn the value of their actions in conjunction with those of the other agents. In this approach, learning happens in the product space of action sets of the different agents, and as such, the JAL algorithm requires the knowledge of other agents’ chosen actions. In other words, a joint action learner should be able to observe the actions of the other agents. In our problem setting, this requires the exchange of content placement decisions between the SBSs through the backhaul links.

Many authors have previously addressed the problem of joint action learning of Nash equilibria in games with unknown noisy rewards by applying reinforcement learning-based approaches. In [53], the authors have proposed a JAL algorithm in which each agent keeps track of the frequency of other agents’ actions, as in fictitious play ([54, 55]), while updating the reward estimate for the joint action played. However, the authors do not provide convergence conditions for their algorithms. The authors in [56] consider a continuous-time evolutionary learning procedure in a noisy game and demonstrate that under this process, the game’s strict NE is asymptotically stable. Similarly, Hofbauer and Sandholm [57] consider evolutionary better-reply learning in population games with noisy payoffs and derive a process that converges to approximate NE. The only algorithms proven to converge to a NE in all games are the regret-testing algorithms of [58] and the algorithms of [50], which will stay near an NE for a long time once it has been reached. Here, we deploy a JAL algorithm based on the work of Chapman et al. in [50], given that is specifically tailored for a potential game with unknown noisy costs and has improved convergence rate. As with any game-theoretic learning algorithm, the operation of JAL consists of two main processes: cost estimation and action selection.

5.1.1 Cost estimation

In the JAL algorithm of [50], in each step of the game, each agent chooses an action, receives a numerical sample cost, and observes the actions chosen by the other agents. This algorithm operates by each agent recursively updating an estimate of its value of a joint-action ${\varvec{a}}\in \mathcal{A}$. Specifically, after playing action ${a}_{n}(t)$, observing the others’ actions ${{\varvec{a}}}_{-n}(t)$, and receiving cost ${C}_{n}({\varvec{a}}(t))$, each agent $n$ updates estimate ${Q}_{n,{\varvec{a}}}(t)$ for ${\varvec{a}}={\varvec{a}}(t)$ using equation:

$${Q}_{n,{\varvec{a}}}\left(t+1\right)=(1-\lambda (t)){Q}_{n,{\varvec{a}}}\left(t\right)+\lambda (t){C}_{n}({\varvec{a}}(t))$$

(21)

where $\lambda (t)\in (\mathrm{0,1})$ is a learning parameter. In general, ${Q}_{n,{\varvec{a}}}\left(t\right)\to {\mathbb{E}}\left[{C}_{n}\left({\varvec{a}}\left(t\right)\right)\right|{\varvec{a}}\left(t\right)={\varvec{a}}]$ with probability one (w.p.1) if the conditions:

$$\sum\limits_{{t = 1}}^{\infty } {\lambda (t)} = \infty \,{\text{and}}\,\sum\limits_{{t = 1}}^{\infty } {\left( {\lambda \left( t \right)} \right)^{2} } < \infty$$

(22)

hold [59]. This can be obtained under the condition that all ${Q}_{n,{\varvec{a}}}$ are updated infinitely often if:

$$\lambda \left(t\right)={{({C}_{\lambda }+\#}^{t}({\varvec{a}}))}^{-{\rho }_{\lambda }}$$

(23)

where ${C}_{\lambda }\ge 0$ is an arbitrary constant, ${\rho }_{\lambda }\in (\frac{1}{2},1]$ is a learning rate parameter, and ${\#}^{t}({\varvec{a}})$ is the number of times the joint-action ${\varvec{a}}$ has been chosen up to time $t$ [50].

5.1.2 Action selection

As argued in [50], to guarantee convergence to NE, action selection needs to be performed along the lines of a generic process in strategic learning known as better-reply with inertia [60]. Under this process, at each step, with probability $\theta \left(t\right)$ an agent repeats its previous action, i.e., ${a}_{n}\left(t\right)={a}_{n}(t-1)$, while with probability $1-\theta \left(t\right)$ the agent chooses an action according to a distribution, putting positive probability only on actions that are better-replies to its full memory of length $\mathcal{l}$ than ${a}_{n}(t-1)$. In this paper, we specifically use Q-learning better-replies with inertia proposed in [50] where if an SBS agent happens to migrate from the current action, it chooses a better-reply with probability $1-\varepsilon$, or uniformly samples from its action set ${\mathcal{A}}_{n}$ with probability $\varepsilon$.

However, better-replies with inertia is a generic process, and the authors in [50] have not specified a particular instance. In fact, any algorithm that chooses from the set of better-replies according to a memory falls into this class of algorithms. Hence, it is a large class of algorithms that includes those that select actions based on either an improvement in expected cost over the current action or based on regrets computed from a finite memory, as in [60]. In this paper, the latter way is applied, and hence, each agent possesses a finite memory of length $\mathcal{l}$, called the history of the previous $\mathcal{l}$ actions taken by all agents. Let $h(t,\mathcal{l})$ be a sample joint history of length $\mathcal{l}$, i.e., $h(t,\mathcal{l})=({\varvec{a}}(t-\mathcal{l}), \dots , {\varvec{a}}(t-1))$. After observing a joint-action ${\varvec{a}}(t)$, the joint history configuration changes by eliminating the leftmost element of $h$ and adjoining ${\varvec{a}}(t)$ as the rightmost element. At each step, each agent computes regrets of all joint-actions in $h$ and then selects one of them having negative regret (with equal probability). The regret associated with each joint-action is measured as a cost difference between the average cost of that particular joint-action and the overall average cost over $h$. Table 4 summarizes the notations exploited in the joint-action learning algorithm. According to these understandings, the pseudo-code of the learning algorithm to select the optimal action for each agent is presented in Algorithm 2.

Table 4 Notations exploited in the JAL algorithm

Theorem 2

(Convergence of Algorithm 2). In the caching game ${\mathcal{G}}$ with unknown noisy cost, by considering Q-learning better-reply process with inertia and $\varepsilon \left( t \right) = t^{ - 1/mN}$, $\theta \left( t \right) = 1 - \left( {\log t} \right)^{ - 2}$ (such that if $t > 10$, then $0 < 1 - \left( {\log t} \right)^{ - 2} < 1$), $\mathop {\lim }\nolimits_{T \to \infty } {\mathbb{P}}\left( {{\varvec{a}}\left( T \right) is\,a\,Nash\,equilibrium} \right) = 1$.

Proof

(outline). Let $z\left( t \right)\mathop = \limits^{{{\text{def}}}} \left( {{\varvec{a}}\left( {t - 1} \right),{\varvec{a}}\left( t \right)} \right)$ be the joint history of play at times $t$ and $t - 1$. Also, denote by ${\varvec{B}}\mathop = \limits^{{{\text{def}}}} \left\{ {\left( {{\varvec{a}},{\varvec{a}}^{{\prime }} } \right) \in {\mathcal{A}} \times {\mathcal{A}}} \right\}$ the collection of all possible joint histories. Once an action profile ${\varvec{a}}\left( t \right)$ is played at time $t$, the joint history transitions from $z\left( t \right)$ to its successor $z\left( {t + 1} \right)$. To express the transition probabilities, consider an arbitrary move $z\left( t \right) \to z\left( {t + 1} \right)$. We partition the set of players ${\mathcal{N}}$ into two disjoint subsets: ${\Lambda }\left( {z\left( t \right) \to z\left( {t + 1} \right)} \right)$ and ${\Omega }\left( {z\left( t \right) \to z\left( {t + 1} \right)} \right)$. Partition ${\Lambda }$ entails those SBS players which have chosen their next move to be their previous action, i.e., ${\Lambda }\left( {z\left( t \right) \to z\left( {t + 1} \right)} \right)\mathop = \limits^{{{\text{def}}}} \left\{ {n \in {\mathcal{N}}{|}a_{n} \left( {t + 1} \right) = a_{n} \left( t \right)} \right\}.$. Partition ${\Omega }$ denotes the subset of SBSs that make their choice in the better-reply regret-based manner. Let the transition matrix of join plays at time $t$ with exploration factor $\varepsilon \left( t \right)$ and inertia $\theta \left( t \right)$ be ${\mathbb{P}}^{\varepsilon }$. Then, ${\mathbb{P}}^{\varepsilon \left( t \right)} \left( {z\left( t \right),z\left( {t + 1} \right)} \right)$ is given by:

$$\begin{gathered} {\mathbb{P}}^{{\varepsilon \left( t \right)}} \left( {z\left( t \right),z\left( {t + 1} \right)} \right) = \left( {\theta \left( t \right)} \right)^{n} \mathop \prod \limits_{{n \in {\mathcal{N}}}} {\mathbb{I}}\left( {a_{n} \left( {t + 1} \right) = a_{n} \left( t \right)} \right) + \left( {1 - \theta \left( t \right)} \right)^{{\left| {\Omega \left( {z\left( t \right) \to z\left( {t + 1} \right)} \right)} \right|}} \times \mathop \prod \limits_{{n \in ~\Omega \left( {z\left( t \right) \to z\left( {t + 1} \right)} \right)}} \left[ {\varepsilon \left( t \right) \times \frac{1}{{\left| {{\mathcal{A}}_{n} } \right|}}} \right. \left. { + \left( {1 - \varepsilon \left( t \right)} \right) \times {\mathbb{P}}\left( {a_{n} \left( t \right),a_{n} \left( {t + 1} \right)} \right)} \right] \end{gathered}$$

(24)

where ${\mathbb{P}}\left({a}_{n}\left(t\right),{a}_{n}(t+1)\right)$ is the probability of taking action ${a}_{n}(t+1)$ by SBS $n$ given its current regret measure. The key idea underlying the convergence analysis in [50] is to show the stochastic stability of the Markov chain $\left\{z(t)\right\}$ with transition probability matrix ${\mathbb{P}}^{\varepsilon }$. In fact, it has been proved in [50] that that the stochastically stable states of the potential game’s underlying Markov chain are the histories composed entirely by a single strict Nash equilibrium. In particular, the convergence of Algorithm 2 is established by invoking [50, Theorems 5.17 and 5.18]. According to these theorems, in any generic potential game with unknown noisy costs, the Q-learning better-reply process with inertia $\varepsilon \left(t\right)=c{t}^{-1/mN}$ and $0<\theta \left(t\right)<1$ leads to the stochastic stability of the joint play’s underlying Markov chain $\left\{z(t)\right\}$. Accordingly, the sequence of joint plays ${\varvec{a}}(t)$ would be almost surely convergent to an NE configuration. Our chosen inertia and learning rate parameters satisfy the conditions stated by [50, Theorem 5.18]. Therefore, for a sufficiently large number of iterations, we conclude the probability that Algorithm 2 directs the system to an NE ${{\varvec{a}}}^{*}$ is one, i.e., we have:

$$\begin{gathered} \mathop {\lim }\limits_{{T \to \infty }} Q_{{n,\varvec{a}^{*} }} \left( {t + T} \right) = \bar{C}_{n} \left( {{\varvec{a}}}^{*} \right) ,w.p.1. \hfill \\ \mathop {{\text{lim}}}\limits_{{T \to \infty }} \varvec{a} \left( {t + T} \right) = \varvec{a}^{*} ,w.p.1.\blacksquare \hfill \\ \end{gathered}$$

(25)

Although joint action learning has good performance, it requires that each agent observe the actions chosen by the other agents since a Q-value needs to be assigned to each joint action. Additionally, the size of the Q-table exponentially grows with the number of SBSs and content groups, thereby increasing space and time complexity as well as reducing the usefulness in large networks with a large number of content groups in the content library. Hence, in the next section, we propose an independent-action learning algorithm that has less complexity and is applicable to practical caching games.

5.2 Multi-agent independent action learning (IAL)

Under the IAL process, the SBS agents are equipped with a specialized reinforcement learning procedure that lets them update their cost estimates without observing the others’ actions. This way, each SBS shapes its strategy of play in the caching game with minimal information consisting only of their own history of actions and their own realized sample costs.

In games with unobserved opponent actions and unknown utilities, some equilibrating algorithms have been presented in the literature on game-theoretic learning [52, 61, 62]. In all these algorithms, the agents update their utility/cost estimates for their actions, independent of the other agents, using Q-learning. Also, different flavors of Boltzmann distribution have been used for action selection; for instance, in [52], an annealing schedule is used for the temperature coefficient, while [61, 62] use a constant temperature. However, none of these works is provably convergent to NE. Another IAL procedure is the work by Marden et al. in [63], which presents payoff-based dynamics that converge to NE in potential games. This algorithm alternates between two phases—exploration and exploitation. However, it needs many parameters to be set in advance to control the exploration rates, exploration phase length, and switching rates of changing strategies. These parameters depend on the problem at hand, and the algorithm may fail to converge if the parameters are incorrectly set. This means that one must have sufficient prior knowledge of the problem at hand or sets these parameters in a conservative manner, which slows the rate of convergence.

In this paper, we adopt the approach of Wang and Pavel [51], who present an algorithm that combines the strengths of Q-learning in terms of minimal information requirements while at the same time achieving faster convergence to NE. They assume that players do not have information about the other players' actions and do not have complete information about their own payoff structure. They consider a modified Q-learning (MQL) algorithm to achieve faster convergence and approach NE via a slightly modified perturbation function. In the sequel, we discuss the cost estimation as well as the action selection procedures in the MQL algorithm.

5.2.1 Cost estimation

The Q-value ${Q}_{n,k}(t)$ for each player $n$ acts as the estimation of ${\overline{C} }_{n}(k)$ (i.e., the expected cost of player $n$ for taking action ${a}_{n}\left(t\right)=k$). Now, we use the symbol ${{\varvec{Q}}}_{n}\left(t\right)$ as a $K$-dimensional vector with components ${Q}_{n,k}\left(t\right),k\in \mathcal{K}$. Each of its components is updated according to (26) as follows:

$${Q}_{n,k}\left(t+1\right)=(1-{\mu }_{n,k}(t)){Q}_{n,k}\left(t\right)+{\mu }_{n,k}(t){C}_{n}({a}_{n}(t))$$

(26)

where ${C}_{n}({a}_{n}(t))$ is the numerical sample delay cost actually experienced by the associated users of the $n$-the SBS at time slot $n$. The parameter $0<{\mu }_{n,k}(t)<1$ is the learning rate. As for the other actions ${k}^{^{\prime}}\in \mathcal{K},{k}^{^{\prime}}\ne k$, not played at time-step $t$, ${Q}_{n{,k}^{^{\prime}}}\left(t\right)$ will not change.

5.2.2 Action selection

According to the IAL algorithm of [51], at each time-step $t>0$, each agent $n\in \mathcal{N}$ updates its mixed-strategy ${{\varvec{x}}}_{n}(t)\in \Delta ({\mathcal{A}}_{n})$. More specifically, the element ${x}_{n,k}$ of the vector ${{\varvec{x}}}_{n}$ represents the probability weight that SBS agent $n$ assigns to action (i.e., content group) $k\in \mathcal{K}$. Then ${{\varvec{x}}}_{n}=({x}_{n,1},{x}_{n,2},{x}_{n,3},\dots ,{x}_{n,K})$ is a probability distribution on the action set or a mixed-strategy for agent $n\in \mathcal{N}$. Mixed-strategy ${{\varvec{x}}}_{n}(t)$ is updated according to the recursion:

$${{\varvec{x}}}_{n}\left(t+1\right)=\left(1-\beta \right){{\varvec{x}}}_{n}\left(t\right)+\beta {{\varvec{B}}}_{n}\left({{\varvec{Q}}}_{n}\left(t+1\right)\right)$$

(27)

where for any agent $n$ and time $t$, ${{\varvec{Q}}}_{n}\left(t\right)$ is the Q-value vector and ${{\varvec{B}}}_{n}$ is an estimated best-response defined as:

$${{\varvec{B}}}_{n}\left({{\varvec{Q}}}_{n}\left(t\right)\right)={\mathbf{u}}_{{k}^{*}}, {k}^{*}=\underset{k\in \mathcal{K}}{\mathrm{arg min}} \, {Q}_{n,k}\left(t\right)$$

(28)

which minimizes the Q-value. The symbol $\beta \in (\mathrm{0,1})$ is the player’s step-size, and ${\mathbf{u}}_{{k}^{*}}$ is a $K$-dimensional unit vector with a one for the ${k}^{*}$-th component and zeros elsewhere.

Now, in the algorithm we consider, at each time step $t>0$, each SBS selects an action ${a}_{n}\left(t\right)=k$ with a so-called perturbed version of its mixed strategy ${x}_{n,k}(t)$. Specifically, inspired by the perturbation scheme discussed in [64], we assume that each player $n$ chooses the $k$ th action, $k\in \mathcal{K}$ according to a modified strategy with probability:

$${\mathcal{X}}_{n,k}(t)=\left(1-{\rho }_{n}\left({{\varvec{x}}}_{n}(t),\xi \right)\right){x}_{n,k}(t)+{\rho }_{n}\left({{\varvec{x}}}_{n}(t),\xi \right)\left(1/K\right)$$

(29)

in which ${\rho }_{n}\left({{\varvec{x}}}_{n},\xi \right)$ is a perturbation function [51]. This perturbation (also called tremble) is slightly modified from the one in Chasparis et al. [64] and ensures mutation and exploration of all actions. This is very much similar to well-known ϵ-greedy exploration [30]. In particular, it chooses a random action with small probability ${\rho }_{n}$ and the best action, i.e., the one that has the minimum Q-value at the moment, with probability ($1-{\rho }_{n}$). The perturbation function ${\rho }_{n}:\Delta \left(\mathcal{K}\right)\times \left[\mathrm{0,1}\right]\to [\mathrm{0,1}]$ is chosen to be continuously differentiable. Furthermore, for some $\zeta \in (\mathrm{0,1})$ sufficiently close to one, ${\rho }_{n}$ satisfies the following properties:

$$\begin{aligned} & \rho _{n} \left( {\varvec{x}_{n} ,\xi } \right) = 0,\;\forall \varvec{x}_{n} \;{\text{such that}}\left| \varvec{x}_{n} \right|_{\infty } \zeta ,\;\forall \xi \ge 0 \hfill \\ & \mathop {\lim }\limits_{{\left| {\varvec{x}_{n} } \right|_{\infty } \to 1}} \rho _{n} \left( {\varvec{x}_{n} ,\xi } \right) = \xi \hfill \\ & \mathop {\lim }\limits_{{\left| {\varvec{x}_{n} } \right|_{\infty } \to 1}} \frac{{\partial \rho _{n} \left( {\varvec{x}_{n} ,\xi } \right)}}{{\partial \xi }} = c,\;\exists c > 0 \hfill \\ & \mathop {\lim }\limits_{{\left| {\varvec{x}_{n} } \right|_{\infty } \to 1}} \frac{{\partial \rho _{n} \left( {\varvec{x}_{n} ,\xi } \right)}}{{\partial x_{{n,k}} }} = 0,\;\forall k \in {\mathcal{K}} \hfill \\ \end{aligned}$$

(30)

In this paper, this perturbation function is defined as (31) [65]:

$$\rho _{n} \left( {\varvec{x}_{n} ,\xi } \right) = \left\{ {\begin{array}{*{20}l} {0,} & {\left| \varvec{x}_{n} \right|_{\infty } < \zeta } \\ {\frac{\xi }{{\left( {1 - \zeta } \right)^{2} }}(\left| \varvec{x}_{n} \right|_{\infty } - \zeta )^{2} ,} & {\left| \varvec{x}_{n} \right|_{\infty } \ge \zeta } \\ \end{array} } \right.$$

(31)

Table 5 summarizes the notations used in the IAL algorithm. According to these understandings, the pseudo-code of the IAL algorithm to shape the caching strategy for each SBS agent is presented in Algorithm 3.

Table 5 Notations used in the IAL algorithm

Theorem 3

(Convergence of Algorithm 3). In the caching game $\mathcal{G}$ with unknown noisy costs, by considering the modified Q-learning process with SBS learning rate ${\mu }_{n,k}\left(t\right)=1-{\mathcal{X}}_{n,k}(t)$, $\zeta =0.9999$, $\xi =0.01$, we have: $\underset{T\to \infty }{\mathrm{lim}}{{\varvec{x}}}_{n}\left(t+T\right)={{\varvec{u}}}_{{a}_{n}^{*}}(t),\forall n\in \mathcal{N}$ (i.e., Algorithm 3 is convergent to NE w.p.1.).

Proof

(outline). The convergence of Algorithm 3 is established by invoking [51, Theorem 7]. According to this theorem, three assumptions need to be satisfied: 1) For all players $n\in \mathcal{N}$ and actions $k\in \mathcal{K}$, ${\mu }_{n,k}\left(t\right)=1-{\mathcal{X}}_{n,k}(t)$, 2) For all players $n\in \mathcal{N}$ and actions $k,{k}^{^{\prime}}\in \mathcal{K}, k\ne {k}^{^{\prime}}$, ${\overline{C} }_{n}(k)\ne {\overline{C} }_{n}({k}^{^{\prime}})$, and 3) After ${\left|{{\varvec{x}}}_{n}\right|}_{\infty }<\zeta$, for all $n\in \mathcal{N}$, i.e., when every player has entered the perturbation zone, no more than one player selects an action other than the action of the Nash equilibrium at each iteration. Now, the first assumption is clearly satisfied in our case. For the second assumption, in our problem setting, if SBS $n$ caches content-group $k$, it can only satisfy the neighbor MUs requesting for contents in $k$ and the requests of the other neighbor MUs have to been responded by other SBSs or downloaded from the remote server. Similarly, if SBS $n$ caches another content-group, e.g., ${k}^{^{\prime}}$, it cannot respond to all the neighboring MUs’ requests. Therefore, different MUs are serviced with different cached content-groups, and as these MUs are not within the same distances to SBS $n$, they experience different delivery delays and hence the cost of caching content-group $k$ by SBS $n$ is different from caching content-group ${k}^{^{\prime}}$ by this SBS. For the third assumption, as mentioned in [51, Theorem 7], we can choose $\zeta$ in to be large enough and $\xi$ to be sufficiently small, so that ${(1 - \zeta (1 - \xi ))}^{2}$ is sufficiently close to 0. In this paper, it is assumed that $\zeta =0.9999$ and $\xi =0.01$, so this assumption also holds. Therefore, we conclude the probability that the process converges to a Nash equilibrium ${{\varvec{a}}}^{*}(t)$ is one, i.e., we have:

$$\underset{T\to \infty }{\mathrm{lim}}{Q}_{n,{a}_{n}^{*}(t)}(t+T)={\overline{C} }_{n}\left({a}_{n}^{*}\left(t\right)\right), w.p.1., \underset{T\to \infty }{\mathrm{lim}}{{\varvec{x}}}_{n}\left(t+T\right)={{\varvec{u}}}_{{a}_{n}^{*}}(t), w.p.1.$$

(32)

5.2.3 A note on computational complexity

In terms of computational complexity, the proposed IAL algorithm needs to update the Q-values and the mixed-strategy of SBS $n$. In each time-step, ${Q}_{n,k}(t+1)$ is calculated for the taken action $k$, argument of the minimum of ${Q}_{n,k}(t+1)$ is computed and then ${x}_{n,k}(t+1)$ is calculated over $\forall k\in \mathcal{K}$. Hence, the computational complexity is $O(K)$. This low computational complexity, as well as the low informational assumptions, are the most important advantage of the IAL algorithm in comparison to the proposed JAL algorithm. In the JAL algorithm, the Q-values ${Q}_{n,{\varvec{a}}}(t+1)$ are calculated in each time-step for the joint-action ${\varvec{a}}$, which is taken by all SBSs, so each SBS keeps track of the actions of $\forall n\in \mathcal{N}$, and for each SBS, the action space is $K$. Hence, the space complexity of the JAL algorithm is $O({K}^{N})$.

6 Performance measurement

In this section, we implement our proposed IAL and JAL algorithms for both 4G and 5G use cases in a simulation environment corresponding to the scenario depicted in Fig. 1. First, we explain the simulation setup, including the simulation parameters and experiment settings in Sect. 6.1. In Sect. 6.2, we introduce the baseline schemes used for comparison. Next, in Sect. 6.3, we report on the simulation results. In particular, we demonstrate how the average delay varies under different regimes of cached content popularity. Furthermore, we investigate the impact of the number of MUs and SBSs on the average downloading delay. We also present simulation results to compare the performance of the proposed algorithm against the schemes which utilize different prior information. Finally, in Sect. 6.4, we study the impact of the network settings on the performance of the proposed IAL algorithm.

6.1 Simulation parameters

In both 4G and 5G use cases, we consider a scenario that SBSs and MUs are uniformly distributed in a 500 m × 500 m area. The channel power gains in our 4G setup are set as independently and identically distributed exponential variables with mean 1. As for 5G channel gains, the fading is modeled as a normalized Rayleigh random variable [66, 67]. The minimum capacity of a 4G wireless link is shown by ${r}_{min}=(W/N)\mathrm{log}(1+\delta )$. Accordingly, we set the 4G backhaul capacity as a random variable uniformly distributed in $[\omega \times {r}_{min},{r}_{min}]$ in which $\omega$ is a coefficient introduced to play with the range of the backhaul capacity. The content popularity follows Zipf distribution with parameter $\gamma =0.5$. In the simulation, the random parameters (i.e., 4G/5G channel gain, 4G backhaul capacity, and user requests) are sampled from the mentioned distributions, but the (mm)SBSs as learning agents have no knowledge of these distributions nor of these sampled values. The JAL and IAL algorithms have only the implicit feedbacks in terms of the round-by-round actual downloading delay experienced by the MUs. Other important simulation parameters are given in Table 6.

Table 6 Simulation parameters

6.2 Comparison with baseline schemes

In this section, we show the performance of the proposed IAL algorithm by comparing its results against the JAL algorithm as well as other baseline approaches. In all the following experiments, the comparisons are made in terms of the moving average of the downloading delay. We have implemented six algorithms with different informational assumptions for the purpose of comparison and executed all six algorithms with identical configurations to evaluate their performance. Apart from the proposed JAL, the other baseline methods are as follows:

• Optimization with perfect non-causal information (optimal and centralized): In this case, the delay optimization is solved in an offline and centralized fashion by the MBS assuming perfect (non-causal) instantaneous values of all random parameters. In the simulation, random parameters are sampled from the distributions determined in Sect. 6.1. The minimization problem (12) is solved by optimization tools, and the result serves as a lower bound for the solution obtained by other approaches.

• Distributed optimization with perfect statistical information (equilibrium, decentralized): In this approach, known as model-based optimization, only the statistical knowledge (i.e., the probabilistic model) of the random processes is assumed to be known at design time. The SBSs use the knowledge of the distributions in Sect. 6.1 to derive their cost functions in the caching game discussed in Sect. 4.2. Prior to actual network deployment, Algorithm 1 is executed by all SBSs to obtain an NE configuration (c.f., Definition 1). Actual content caching in a real-life deployment is then performed based on the calculated equilibrium strategies.

• Distributed Q-learning (DQ-based caching) [11]: For our 5G use case, we also experiment with another state-of-the-art learning algorithm proposed by Lin et al. for distributed cache content placement. Similar to our multi-agent learning algorithms, DQ-based caching is a zero-knowledge model-free scheme applicable to both 4G and 5G use cases. However, there are two differences between the DQ-based caching and our proposed algorithms: first, in [11], a fully cooperative repeated game is assumed among the SBSs in the sense that all SBSs as learning agents have a common goal of cooperating with each other to improve a given social utility. The authors have proposed a distributed Q-learning algorithm to ensure the cooperation among SBSs to reach the optimal NE point. In our case, the definition of cost function varies between the SBS agents and there is a high chance that the simplistic update rule governing DQ-based caching result in miscoordinations between the SBSs. Our proposed JAL and IAL algorithms feature sophisticated update rules which guarantee convergence and equilibration in more complex setups than the one discussed in [11]. The second difference is that unlike our delay-centric cost function, the SBS agents in [11] work toward maximizing the system-wide average cache hit probability. However, in our implementation, we have simply changed the algorithm to optimize delay (rather than cache hit) without tampering with anything else.

• Single-agent learning: In single-agent learning, each SBS runs a standard multi-armed bandit (MAB) algorithm from the single-person decision theory [30]. Here, the multi-person game-theoretic aspect of the environment is completely ignored by the SBSs as they naively mishandle the non-stationary dynamics arisen by other SBS agents as simple stationary uncertainty. Similar to the case of our proposed JAL and IAL algorithms, the single-agent learning algorithm receives only implicit feedback in terms of the delay experienced by MUs. The pseudo-code is presented in Algorithm 4, in which the parameters ${\eta }_{1}\left(t\right), {\eta }_{2}\left(t\right)\in [\mathrm{0,1}]$ are the learning rate and the exploration factor, respectively. For the sake of experiments, we set ${\eta }_{1}\left(t\right)=0.03$ and ${\eta }_{2}\left(t\right)={(\mathrm{log} \mathop t)}^{-2}$.

6.3 Results

6.3.1 Moving average delay performance

Figure 2 plots the moving average sum of MUs’ downloading delay obtained from the proposed JAL and IAL algorithms as well as the offline centralized, model-based decentralized, single-agent learning and the DQ-based caching scheme [11]. Figure 2a depicts the results for the 4G scenario and Fig. 2b corresponds to the 5G case. The users’ sum delay in 5G is significantly lower compared to the 4G case (nearly 500 times), which is primarily due to the ultra-high data rate achievable by mmWave communications.

Fig. 2

The convergence of the sum of downloading delay with different accessibility of information. a: 4G scenario. b: 5G scenario

As seen in both figures, the centralized algorithm using the perfect instantaneous information has the least sum of downloading delay, while single-agent learning in which the SBSs mishandle the environment dynamics incurs the worst delay. In the model-based decentralized scheme, which operates in a Nash configuration, the sum of delay is higher than the centralized case. This is partly due to the sub-optimality inherent in the notion of equilibrium but, more importantly, due to the agents’ having only the statistical (as opposed to exact) information about the environment. Multi-agent IAL algorithm is a zero-knowledge equilibrium learning algorithm and can thus be considered as an approximate version of the model-based decentralized scheme. Naturally, its delay performance is higher compared to the offline and model-based variants. However, as can be seen in Fig. 2b, IAL outperforms the DQ-based caching due to its guaranteed convergence to equilibrium. This is while DQ-based caching is prone to miscoordination and out-of-equilibrium behavior. As for our multi-agent JAL algorithm, the SBS agents have the advantage of observing their peers’ actions, and since the cost estimation process is performed in the joint action space with much more accuracy compared to IAL, the JAL algorithm mimics the behavior of the model-based scheme but with injected randomness. In particular, in the experiment shown in Fig. 2, the limiting performance of the SBSs running JAL has even superseded the performance of the model-based algorithm. In fact, the NE computation in JAL is performed by a stochastic search process with lots of explorations that may luckily lead to escapes from inefficient equilibria. That being said, however, the convergence speed of JAL is significantly lower than the proposed IAL algorithm. More importantly, the JAL algorithm has an exceptionally huge memory footprint which makes it impractical even in fairly small-scale setups. In fact, due to this memory bottleneck, we were no longer able to simulate the JAL algorithm in the subsequent experiments where the network size increases.

6.3.2 The impact of content popularity

Figure 3 displays the sum of downloading delay for both 4G and 5G use cases under different values for the Zipf parameter used in content popularity distribution. In general, larger values of the Zipf parameter corresponds to a steeper distribution such that requests issued by consumers are concentrated on a smaller set of contents (i.e., more queries are focused on a set of hot contents). Therefore, by only caching these hot contents in their limited memory, the SBSs can reduce their miss ratio, thereby decreasing the MUs’ sum delay. As expected, the centralized algorithm with perfect instantaneous information has the lowest delay performance, followed by the decentralized algorithm with perfect statistical information. As shown in Fig. 3a, in the proposed multi-agent IAL and single-agent learning algorithms, we see more delay because these methods use no prior information about the environment. However, the IAL algorithm operates more closely to the model-based scheme due to its consideration of the cross-interaction between the SBSs. Also, according to the plot in Fig. 3b for the 5G use case, we observe that IAL maintains its superiority over the DQ-based caching for all values of the skewness of the content popularity.

Fig. 3

Sum of MUs’ downloading delay versus Zipf parameter a: 4G scenario. b: 5G scenario

6.3.3 The impact of the number of SBSs and MUs

Figures 4 and 5 show the sum of downloading delay versus the number of MUs and SBSs, respectively. In Fig. 4, it is observed that there is an upward trend in the users’ sum delay as the number of MUs associated with the SBSs is increasing. This is mainly because it is difficult to satisfy the minimum rate requirements for all the MUs using the limited resources. However, the sum delay does not grow linearly with the number of MUs because the impact of bandwidth portioning among the users is partly offset via the multi-user diversity. Furthermore, with a higher population of MUs, more contents are requested, which increases the chance of cache miss and backhaul congestion. Congestion of the system gradually increases the backhaul traffic load which deteriorates the achievable effective data rate (as can be noticed for the number of MUs more than 20). Also, under the single-agent and DQ-based caching, the system gets congested more quickly. Compared to these two, our IAL algorithm can allow more MUs to be accommodated without premature capacity partitioning.

Fig. 4

Sum of MUs’ downloading delay versus the number of MUs a: 4G scenario. b: 5G scenario

Fig. 5

Sum of MUs’ downloading delay versus the number of SBSs a: 4G scenario. b: 5G scenario

On the other hand, when there are more SBSs, each SBS responds to fewer requests. Also, more contents can be stored across all the SBSs, decreasing the chance of cache miss. Accordingly, in Fig. 5, the sum of delay decreases when using a higher number of SBSs. As before, the performance of our proposed multi-agent IAL algorithm lies in between single-agent learning and the schemes using prior information of the environment. In Fig. 5b for the 5G case, we notice that DQ-based caching consistently underperforms our IAL algorithm, but the gap between the two is narrower for a smaller number of SBSs. However, as the computational complexity increases due to the growth of the strategy space, the superiority of IAL over DQ-based caching would be more noticeable.

6.4 The impact of the network settings on the performance of the IAL algorithm

In this section, we investigate the impact of important network settings on the performance of the proposed IAL algorithm. In particular, in the 4G case, we study the impact of backhaul capacity, the transmission power of the SBSs, and the number of contents on the delay experienced by the MUs. In Fig. 6, we vary the parameter of backhaul capacity from $\omega =0.2$ to $\omega =1$, while other simulation settings are the same as those given in Table 6. As shown in Fig. 6, with the increase in $\omega$, the sum of downloading delay of contents is reduced. To investigate the impact of transmission power on the downloading delay, we vary ${p}_{n}$ for all SBSs from 0.1 to 100 dbm, as shown in Fig. 7. As expected, when the transmission power increases, the sum of the delays decreases. In Fig. 8, we change the number of contents from 100 to 220 files in order to study its impact on the downloading delay for MUs. With the increase in the number of files, the number of content groups also increases, but as the cache capacity at each SBS is limited, it leads to smaller cache hit ratio and hence more delay for accessing contents by MUs.

Fig. 6

Sum of MUs’ downloading delay under different ranges of backhaul capacity

Fig. 7

Sum of MUs’ downloading delay under different transmission powers

Fig. 8

Sum of MUs’ downloading delay for a different number of content-groups

As for the 5G scenario, we compare the performance of IAL and DQ-based caching for different values of the power of the backhaul links as well as the beamwidth of mm-SBSs and MUs. Figure 9 shows how the MUs’ sum delay decreases as the power levels of backhaul links increases (it is assumed that all backhaul links utilize the same power level). For this experiment, the maximum backhaul power is set to 50Watts according to [68]. In Fig. 10, we show how the MUs’ sum delay varies with the operating beamwidth of mm-SBSs and MUs (For simplicity, it is assumed that all mm-SBSs and MUs use similar beamwidth and that the MBS operates at 5°). As can be seen, increasing the beamwidth (by reducing the achievable rates) results in a gradual increase in the sum of MUs’ downloading delay. It is also noticeable that the gap between IAL and DQ-based caching narrows as the beamwidth keeps increasing. This is because a larger beamwidth leads to higher cross-link interference which will eventually play as the dominating performance factor.

Fig. 9

Impact of the power levels of backhaul links on Sum of MUs’ downloading delay

Fig. 10

Impact of the beamwidth of mm-SBSs and MUs on Sum of MUs’ downloading delay

7 Conclusion

In this paper, the problem of selecting contents to be cached was studied for small base stations deployed in the coverage area of a macro base station. Given the uncertainties posed by the randomness of the requests for contents, as well as the variations in backhaul capacity and channel qualities, the problem was formulated as a potential game among SBSs with the objective of minimizing the long-term average of downloading delay. To solve the optimization problem, we proposed a model-free reinforcement learning algorithm that computes optimal action for each SBS in adaptation to the environment dynamics. Our algorithm operates in a model-free fashion in that it does not need prior statistical knowledge of the random processes in the environment. Simulation results demonstrate that our proposed IAL algorithm converges properly and has better performance compared to the single-agent learning algorithm mishandling the environment dynamics, in addition, it has an acceptable performance in comparison with the cases using prior knowledge. The results also show that the JAL algorithm converges and has better performance compared to the other decentralized algorithms, at the expense of huge memory usage and low convergence speed. We may extend the unavailability of network information to users’ nature to consider scenarios where there are malicious users in the control of a jammer, aiming to make congestion in the network. A malicious user, who is unknown to the SBSs, tries to request for contents not cached in its associated SBS, therefore, the SBS downloads it from remote server via backhaul link. Repeating this process by malicious users cause to make congestion in backhaul links so that the system cannot respond to the ordinary users’ requests.