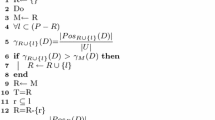New filter approaches for feature selection using differential evolution and fuzzy rough set theory

Abstract

Nowadays the incredibly advanced developments in information technologies have led to exponential growth in the datasets with respect to both the dimensionality and the sample size. This trend can be easily illustrated in popular online data repositories (e.g., UCI machine learning repository). The more growth in the datasets, the more challenging the data management becomes. This is because such datasets usually comprise a high level of noise as well as the necessary information. Therefore, the elimination of noisy features in the datasets is an important task to discover meaningful knowledge. Although a large number of feature selection approaches have been proposed in the literature to deal with noisy features, the need for the studies based on feature selection has not come to an end. In this paper, we propose differential evolution-based feature selection approaches wrapped around the principles of fuzzy rough set theory. In contrast to well-known feature selection criteria such as standard mutual information, standard rough set and probabilistic rough set, our approaches can also deal with real-valued variables without the requirement of discretization. Moreover, the feature subsets selected by our approaches can profoundly improve the classification performance compared to the recent particle swarm optimization approaches based on probabilistic rough set and the state-of-the-art filter approaches.

1 Introduction

Nowadays a real-world dataset is usually represented through many features, causing the existence of noisy features to the target. There are two kinds of noisy features, irrelevant and redundant. An irrelevant feature does not have a direct relationship with the target, but adversely affects the performance of the learning process. A redundant feature does not provide any additional information to the target. Removing such features can improve both the efficiency and the effectiveness of a learning algorithm. It can therefore be possible to get a better insight into a learning problem. However, the selection process of an optimal feature subset in the dataset is not an easy task due to the following challenges. First, an individual feature may not be significantly correlated with the target. However, if this feature is evaluated with other features, it may have a considerable relation with the target. Second, for a dataset with m number of features, there exist $2^m$ candidate feature subsets. Accordingly, the selection process of an optimal feature subset among all candidate subsets may become intensive and impractical, even for a medium number of features. Third and last, the selection process of an optimal feature subset is expected to improve not only the classification performance, but should also consider other important issues, such as interpretability, complexity, scalability and generalization of the learning model.

In the terminology of machine learning, feature selection can be applied using the principles of three fundamental schemes: supervised, unsupervised and semi-supervised [36]. Supervised feature selection requires the labeled information in the data to identify the goodness of features. The labeled information can be a real or order value, or a category depending on the specific task. Semi-supervised feature selection only requires a small amount of the labeled information. In contrast to supervised and semi-supervised schemes, unsupervised feature selection does not require any external or labeled information to carry out the selection process of an optimal feature subset and so is treated as more challenging.

In terms of evaluation, both supervised and unsupervised feature selection approaches can be divided into wrapper, embedded and filter approaches. Wrapper approaches first select a candidate feature subset using a predefined search strategy (e.g., sequential forward, sequential floating forward, random search) and then use a specific learning algorithm to evaluate the quality of the chosen feature subset. This procedure is repeated until achieving higher learning performance. However, the selected feature subset is dependent on the specific learning algorithm, i.e., may not perform well through another learning algorithm. Embedded approaches are adopted into learning algorithms through regularization methods or a penalty term in a model-based function. Compared to wrapper approaches, embedded approaches are less time-consuming, but may not perform well in terms of maximizing the performance of a learning algorithm. In contrast to wrapper and embedded approaches, filter approaches do not require a learning algorithm to carry out the selection process of features. Filter approaches are therefore computationally less intensive and more general than wrapper and embedded approaches, but may not perform well due to the independence of learning algorithms. Instead of a learning algorithm, filter approaches use data intrinsic measures such as distance, dependency and consistency to evaluate the quality of the selected subsets [11, 42]. Unfortunately, none of them have been considered as the standard for filter approaches. In our opinion, this is because none of these measures are consistently better than others on all problems, i.e., some metrics works properly in continuous data, while some metrics are suitable for discrete data. Moreover, they detect different kinds of relationships between features and output variables.

Rough set (RS) theory [31] is a mathematical tool that can be used to reduce the dimensionality using intrinsic information within the data without requiring any additional information. For the last two decades, RS theory has gained considerable interest and has been implemented to many fields [49]. For a given dataset represented through discrete-valued features, it is possible to select the most informative features among all available features using RS theory. In the terminology of feature selection, the informative features are expected to be the most predictive to the target. However, RS theory does not consider the degree of overlapping in the data. To deal with this deficiency, Yao and Zhao [45] introduced probabilistic (PRS) rough set theory. Even though PRS theory has proven to perform better than RS theory, PRS theory has still challenges to measure the dependency of features. Furthermore, both RS and PRS theories encounter problems when the values of features are real-valued. Using the principles of such theories, it is not possible to identify that two different feature values are similar and to what extend they are same. For example, two close values may only be considered as different as a result of noise, but RS theory considers them as two different values with a different order of magnitude. Data discretization may be considered as a solution to this challenge before performing RS-based and PRS-based reduction approaches; however, it is still not adequate since information loss in the data cannot be preventable. In order to alleviate such problems, fuzzy variants of RS-based criteria concerned with fuzzy rough set (FRS) theory were introduced.

In order to enhance the performance of RS-based approaches and its derived criteria, researchers have also implemented such measures in evolutionary computation (EC)-based filter approaches due to the search ability of them to find the global optima. However, there exist only few works on using EC techniques and FRS-based criteria for feature selection in the literature. Moreover, to the best of our knowledge, FRS-based standards have not been adopted in multi-objective EC framework yet. Another open issue concerning feature selection is that the works for filter feature selection concerned with differential evolution (DE) [37] are not adequate in the literature, even though DE has been widely treated as one of the most potent algorithms among a variety of EC techniques.

1.1 Goals

In this paper, we propose new filter approaches using DE algorithm and FRS theory to improve both the effectiveness and the efficiency of the classification algorithms. To achieve this objective, we designed FRS-based objective functions for single-objective and multi-objective DE algorithms. Specifically, we aim to investigate:

• the performance of FRS-based approaches versus PRS-based approaches,

• the performance of FRS-based criteria in single-objective design versus in multi-objective design.

• the performance of FRS-based approaches versus the state-of-the-art filter approaches.

1.2 Organization

The remainder of the paper is designed as follows. Section 2 presents related work: rough set theory, differential evolution, multi-objective optimization and rough set theory for feature selection. Section 3 introduces the proposed approaches: the design of FRS-based criteria and the integration of the designed FRS-based criteria in single-objective and multi-objective frameworks. Section 4 gives an outline of the experiment design. Section 5 provides empirical results with analysis. Finally, Sect. 6 draws conclusions and future work.

2 Background

2.1 Rough set (RS) theory

Proposed by Pawlak [31] in 1982, RS theory is a mathematical tool to deal with uncertainty in an efficient way in the data using a decision table. Let U be a non-empty finite set of instances (objects) in the data and A be a non-empty finite set of features such that $a:U \xrightarrow V_a$ where $V_a$ is the set of values that attribute a can take. The decision table is shown by $I=(U,A)$. Moreover, assume that P and Q be two subsets of A, and X be a subset of U. The fundamental components of RS theory are given as follows.

• 1. Indiscernibility (IND(P)) is a relation between two instances where all values are identical in relation to a subset of considered features (P), defined by Eq. (1). If $(x,y) \in IND(P)$, x and y instances are indiscernible through feature subset P. The equivalence classes of the indiscernibility relation of the instance x in subset P are denoted by $[x]_P$.

  $$\begin{aligned} IND(P)=\{ (x,y) \in U | \forall a \in P, a(x)=a(y) \} \end{aligned}$$

  (1)

• 2. Set approximation is investigated in two categories: lower approximation and upper approximation. Lower approximation of X consists of instances which can be classified with full certainty using feature subset P, defined by:

  $$\begin{aligned} {\underline{P}}X = \{ x \in U | [x]_P \subseteq X \} \end{aligned}$$

  (2)

  Upper approximation consists of instances which may be probably classified using feature subset P, defined by:

  $$\begin{aligned} {\overline{P}}X = \{ x \in U | [x]_P \cap X \ne \emptyset \} \end{aligned}$$

  (3)

• 3. Positive region comprises all instances of U that can be uniquely classified into groups of $U{\setminus}Q$ through feature subset P, defined by:

  $$\begin{aligned} POS_{P}(Q)= \bigcup _{X \in U\setminus Q} {\underline{P}}X \end{aligned}$$

  (4)

• 4. Attribute dependency measures the correlation between features, defined by Eq. (5). The dependency increases proportionally to the k value. For $k=1$, Q is completely dependent on P. In an optimal feature subset, features are expected to have the minimum dependency on each other and maximum correlation on the target.

  $$\begin{aligned} k = \gamma _P(Q) = \frac{|POS_{P}(Q)|}{|U|} \end{aligned}$$

  (5)

An example: We further provide an example to show how RS measures are calculated. We provide a dataset in Table 1. For $P= \{ a,b \}$, the partition of U created by IND(P) which is denoted as U/IND(P) is defined as follows:

$$\begin{aligned} \begin{aligned} U/IND(P)&= U/IND(\{ a \}) \otimes U/IND(\{ b \}) \\&=[\{0,3,4\}, \{1,7\}, \{ 2,5,6 \}] \otimes [\{0,2,4\}, \{ 1,3,6,7 \}, \{5\}]\\&=[\{0,4 \}, \{3 \}, \{1,7 \}, \{2 \}, \{6 \}, \{5 \}] \end{aligned} \end{aligned}$$

Let X be a subset such that $X= \{ X: e(X) = 1 \}$, and $P= \{ a,b \}$. Accordingly, $X= \{ 2,4,5,7 \}$ and $IND(P)=[\{0,4\},\{1,7\},\{2\},\{ 3 \}, \{ 5 \}, \{ 6 \}]$. The lower and upper approximations of X are defined as follows:

$$\begin{aligned} \begin{aligned}&{\underline{P}}X = \{ 2,5 \} \\&{\overline{P}}X= \{ 0, 4, 1, 7, 2, 5 \} \end{aligned} \end{aligned}$$

For $P= \{ a,b \}$, the positive region of the class labels e is determined as follows:

$$\begin{aligned} U/IND(\{e\})&= \{\{0\}, \{2,4,5,7\}, \{1,3,6\} \}\\ {\underline{P}}X&= {\left\{ \begin{array}{ll} \emptyset , X= \{ X: e(X) = 0 \} \\ \{2,5\} {, X= \{ X: e(X) = 1 \}} \\ \{3,6\} {, X= \{ X: e(X) = 2 \}} \\ \end{array}\right. } \\ POS_{a,b}(e)&= \bigcup _{X \in U/e} {\underline{P}}X = \{2,3,5,6\} \end{aligned}$$

The degree of dependency of the class labels e from the features a, b is calculated as follows:

$$\begin{aligned} \gamma _{a,b}(e) = \frac{|POS_{a,b}(e)|}{|U|}=\frac{|\{2,3,5,6\}|}{|\{0,1,2,3,4,5,6,7\}|}= \frac{4}{8} \end{aligned}$$

Table 1 An example dataset

2.2 Differential evolution (DE)

An evolutionary algorithm developed by Storn and Price [37], DE carries out searching on the solution space on the basis of directional information. DE tries to find the global optima for a given optimization problem by forming a population with candidate solutions and then evolving new candidates through mutation and recombination strategies. In the population, a candidate solution is represented by a vector such that $X_i = \{x_{i1}, x_{i2},..., x_{id},\ldots ,x_{iD} \}$, where i denotes the ith individual and D denotes the dimensionality of the optimization problem. For each $X_i$ solution, DE randomly selects three different solutions $X_{r1}$, $X_{r2}$ and $X_{r3}$ in the population and then generates a new solution $U_i$ using the direction of the selected vectors in a probabilistic manner:

$$\begin{aligned} u_{id} = {\left\{ \begin{array}{ll} x_{r_{1}d} + F \times (x_{r_{2}d}-x_{r_{3}d}) &\hbox { if }rand()<CR\hbox { or }d=I_{rand} \\ x_{id} & \hbox {otherwise} \end{array}\right. } \end{aligned}$$

(6)

where F is the constant within the range of [0,2] which controls the rate of mutating solutions; rand() is the randomly distributed number between 0 and 1; $I_{rand}$ is a randomly selected index between 1 and D which guarantee the evolution of a solution at least one position; CR is the recombination rate which controls the rate of interacting between solutions.

The general structure of DE is simple to implement and easy to understand, i.e., does not include complex components. Furthermore, it can be applied to a variety of problems such as nonlinear, non-differentiable, discrete and noisy since it does not require assumptions about the problem to be considered to optimize. On the other hand, it does not guarantee the global optima like as any other EC techniques [17, 19].

2.3 Multi-objective optimization

Nowadays we can face with many real-world problems with multiple objectives instead of a single objective. Since some objectives are tend to (partially) conflict, the design of multi-objective problems becomes more complex. The general definition of a multi-objective problem with k objectives, n inequalities and l equality constraints is posed as follows:

$$\begin{aligned} \begin{aligned}&\min _{x} \mathbf{F }(x) = [F_1(x),F_2(x),\ldots ,F_k(x)]^{\mathrm{T}} \\&\text {subject to:} \\&g_j(x) \le 0,\quad j=1,2,\ldots ,m \\&h_l(x)=0,\quad l=1,2,\ldots ,n \end{aligned} \end{aligned}$$

(7)

When we consider a multi-objective problem, there exists no such a single global solution typically. Therefore, it is often necessary to find a set of points that all compromise on a predefined definition for an optimum. The general concept for defining an optimal point concerns with Pareto-optimality. A point $x*$ is Pareto-optimal iff there is no such another point x that $F_i(x) \le F_i(x*)$ for all functions and $F_i(x) < F_i(x*)$ for at least one function. $x*$ is also referred to as a non-dominated solution. Therefore, the non-dominated solution set is called the Pareto-optimal set. For more information concerning multi-objective optimization, please see [30].

2.4 Rough set for feature selection

Earlier filter feature selection approaches on the basis of RS-based criteria generally follow traditional search strategies such as sequential forward, sequential floating forward and sequential backward. The most representative one is the Quickreduct algorithm [7] which starts with an empty set and adds a feature to this set for each iteration until reaching the maximum dependency based on the standard RS-based criterion. Prasad and Rao [32] improved the Quickreduct algorithm by a sequential reduction strategy. Another approach that uses a sequential backward elimination strategy was proposed by Gawar [13] by designing a RS-based relative dependency measure. Yong et al. [46] introduced an efficient Quickreduct algorithm by integrating neighborhood RS-based criteria. In summary, all such traditional approaches showed that RS-based criteria could be used as an alternative filter evaluation metric for feature selection. However, all of these conventional approaches tend to converge in local minima points due to their greedy search mechanisms. Accordingly, EC techniques have gained increasing attention due to their approved ability to avoid local minima while investigating the global optima.

Genetic algorithm (GA) [22], the first EC technique in the literature, was developed using the principles of evolution. Besides a variety of successful GA-based applications in many fields, GA has also been designed for RS-based filter approaches. Wroblewski [41] introduced a simple RS-based filter approach using GA. According to the empirical studies, this approach obtained better performance than traditional approaches. However, it was computationally expensive. Bjorvand [3] increased the effectiveness and efficiency of this approach by applying a software system (referred to as the Rough Enough) and a dynamic mutation rate. Jing [24] proposed a hybridized GA filter approach (HGARSTAR) which uses a RS-based local search mechanism to fine-tune parameters. HGARSTAR obtained promising results compared to existing EC-based filter approaches based on RS-based criteria; however, HGARSTAR was not tested on high-dimensional datasets. Das et al. [8] developed an incremental feature selection (IFS) approach based on GA and RS theory. From the results, it can be inferred that IFS performed better than some representative filter approaches such as ReliefF [26], Correlated Feature Subset Selection (CFS) [15] and Consistency Feature Subset Selection (CON) [10] in both discrete-valued and real-valued datasets. However, the datasets used in experiments included at most 36 features, i.e., it is not possible to make an analysis of IFS on high-dimensional datasets.

Another important EC technique, particle swarm optimization (PSO) [25] mimics the behaviors of natural species which are bird flock or fish school. PSO has also been used to develop RS-based applications. Wang et al. [39] introduced a RS-based approach (PSORSFS) using PSO. In this approach, the dependency between features and the target, and the ratio of the feature subset size to the total number of features were tried to be optimized in a weighted manner. According to the results, PSORSFS obtained great performance compared to the RS-based approaches on the basis of greedy search and GA algorithms. However, the control parameter between the dependency and the feature subset size in the fitness function is difficult to be determined. Abdul-Rahman et al. [1] introduced a two-stage wrapper-filter approach that considers a RS-based reduction approach using PSO as an earlier step to reduce the dimensionality, and a wrapper approach as a latter step to find an optimal feature subset on the reduced dimensionality. Cervante el al. [5] developed a RS-based approach (PSOPRS) using PSO and probabilistic rough set theory (PRS). The results showed that PRS theory could enhance the performance of classifiers better than the standard RS theory. However, like as previous RS-based approaches using PSO, PSOPRS is dependent on the control parameter between the dependency and the feature subset size and cannot be applied to evaluate the dependency of real-valued features without discretization. In order to alleviate the control parameter, Bing et al. [42] considered the PRS-based criterion as a multi-objective problem and introduced a multi-objective PSO filter feature selection approach. Without discretization, this multi-objective approach also cannot be applied to measure real-valued features.

Another well-known EC technique is the differential evolution (DE) algorithm [37], the details of which are presented in Sect. 2.2. Yan and Li [43] proposed a RS-based filter approach using an improved version of DE. However, it is not possible to make a consistent analysis concerning this approach since it was only tested on two datasets. Sangeetha and Kalpana [35] introduced a FRS-based filter approach (FRFSDE) using DE inspired by the fuzzy version of the Quickreduct algorithm. From the results, it can be revealed that FRFSDE can perform well compared to the fuzzy version of Quickreduct. However, the feature subset size obtained by feature selection approaches was not considered in experiments. Das et al. [9] introduced a RS theory and relational algebra-based filter approach using a multi-objective DE binary algorithm. However, the feature subset size obtained by filter approaches was not investigated and analyzed in the experimental study. Besides GA, PSO and DE, recently developed EC techniques such as artificial bee colony [6], cuckoo search [2], ant lion optimizer [28] have also been used to develop RS-based filter approaches.

In summary, it is observed that RS-based criteria can increase the performance of classification algorithms when they are incorporation with EC techniques. However, there are still some open issues that need to be considered. First, most of the RS-based approaches are based on GA and PSO. In other words, there are only a few RS-based approaches based on DE despite its potential to search the global optimal. Second, most of the RS-based criteria cannot deal with real-valued datasets due to the deficiency of them to quantify continuous variables. Third, adopting FRS-based criteria, fuzzy variants of RS-based criteria, in EC-based frameworks is not common in the literature, to the best of our knowledge. Finally and most importantly, FRS-based criteria have not been modeled as a multi-objective problem in the literature yet.

3 Proposed approaches

In this section, we first describe the concepts of fuzzy rough set theory and then give the details of FRS-based approaches using single-objective and multi-objective DE algorithms.

3.1 Fuzzy rough set (FRS) theory

In the terminology of RS theory, instances in the data belong to the lower approximation with certainty or not. In contrast to RS theory, in the terminology of FRS theory, instances may belong to the lower approximation with a membership value in the range of [0, 1]. This means FRS theory allows flexibility to deal with uncertainty. Let U be the set of instances (objects) in the data, A be the features describing instances and P and Q are two subsets of A; the decision table is defined as $I = (U,A)$. The degree of similarity between x and y instances through all features in subset P is defined by:

$$\begin{aligned} \mu _{R_P}(x,y) = T_{a \in P}\{ \mu _{R_a}(x,y) \} \end{aligned}$$

(8)

where T denotes the t-norm; and $\mu _{R_a}(x,y)$ is the degree of similarity between x and y instances for feature a, which can be measured by Eqs. (9) and (10).

$$\begin{aligned} . \mu _{R_a}(x,y) = 1 - \frac{|a(x)-a(y)|}{a_{\max }-a_{\min }} \end{aligned}$$

(9)

where $a_{\max }$ and $a_{\min }$ denote the maximum and minimum values for feature a.

$$\begin{aligned} \mu _{R_a}(x,y) = \exp \left(- \frac{(a(x)-a(y))^2}{2\sigma _a^2}\right) \end{aligned}$$

(10)

where $\sigma _a^2$ denotes the variance of feature a.

Using the degree of similarities within the feature subset P, fuzzy lower and upper approximations are defined by Eqs. (11) and (12).

$$\begin{aligned} \mu _{\underline{R_P}X}(x) = \inf _{y \in U} I(\mu _{R_P}(x,y), \mu _X(y)) \end{aligned}$$

(11)

where I denotes the fuzzy implicator.

$$\begin{aligned} \mu _{\overline{R_P}X}(x) = \sup _{y \in U} T(\mu _{R_P}(x,y), \mu _X(y)) \end{aligned}$$

(12)

The fuzzy positive region is then defined by:

$$\begin{aligned} \mu _{POS_R(P)}(x) = \sup _{X \in U/Q} \mu _{\underline{R_P}X}(x) \end{aligned}$$

(13)

Based on the fuzzy dependency of Q on P$(\gamma _{P}^{'}(Q))$ is defined by Eq. (14). For more information concerning FRS theory, please see [23].

$$\begin{aligned} \gamma _{P}^{'}(Q) = \frac{|\mu _{POS_R(P)}(x)|}{|U|} = \frac{\sum _{x \in U}\mu _{POS_R(P)}(x)}{|U|} \end{aligned}$$

(14)

3.2 Proposed FRS-based approaches

In the terminology of RS theory, the information in the data is represented by the decision table in classification tasks. Each instance in the data is considered as an object in RS theory. The target variable in the data, known as the class labels, is regarded as the decision feature D, and the features building the data are the conditional features C such that $A= C \bigcup D$. All instances (U) in the data can be divided into different classes $U_1,U_2,\ldots ,U_n$, where n is the total number of classes. The overall aim of a RS-based approach is to eliminate irrelevant, redundant and noisy features, so the remaining feature subset $P \subset A$ represents the information in the data as well as C.

(1) DEFRS approach: As described in Sect. 2.1, an equivalence relation is an essential notion to determine lower and upper approximations of the target in standard RS theory. For the lower approximation, the equivalence class should be a subset of the target. For the upper approximation, the equivalence class should have a non-empty overlap with the target. However, the lack of overlapping degrees limits the application domain of rough sets. To alleviate this deficiency, a number of generalized approximation operators have been developed. One of the generalized variants is PRS theory which is based on the notions of rough membership functions and rough inclusion. Both notions can be interpreted in terms of conditional probabilities or posteriori probabilities. However, PRS theory also limits the application domain due to the dependency of crisp binary relations. Thus, researchers have established fuzzy rough set models where a fuzzy-based similarity relation can be used instead of an equivalence relation. The main advantage of such models is that an instance can belong to more than one class with a membership degree. Based on this fuzzy measure, we propose a new DE-based single-objective approach (DEFRS), where Eq. (15) is designed as the fitness function. DEFRS aims to maximize the dependency of the feature subset to the target and also aims to minimize the feature subset size.

$$\begin{aligned} Fit_{frs} &= \beta * \frac{|\mu _{POS_R(P)}(x)|}{|U|} \\&\quad+ (1-\beta ) * \frac{1-\#subsetsize}{\#totalfeatures} \end{aligned}$$

(15)

where $\beta \in (0,1]$ controls the importance of the dependency and the importance of the feature subset size. When $\beta =1$, DEFRS directly evaluates the candidate feature subset using the FRS model. The pseudocode of DEFRS is presented in Algorithm 1. The membership values between features ($\mu _{R_a}(x,y)$) are calculated beforehand and then are considered as the inputs for the evolutionary process. By this way, it is aimed to decrease the computational complexity of the evolutionary process. If any position of a candidate solution is greater than 0.5, its corresponding feature is selected for the feature subset. After the selection process of the feature subset, the quality of the feature subset is evaluated using Eq. (15).

After the single-objective evolutionary process, the final feature subset is evaluated on the testing set with the training set through a predefined classifier to obtain the classification performance of the selected feature subset. Notice that the testing set is transparent to the user during the evolutionary process.

(2) MDEFRS approach: DEFRS uses two main objectives in a weighted manner in a single fitness function through the $\beta$ control parameter which specifies the weight degrees of the objectives. However, the $\beta$ parameter needs to be predetermined according to the problem, i.e., it is not possible to assign a general $\beta$ value for all problems. Accordingly, we design a FRS-based multi-objective DE feature selection approach (MDEFRS) to get rid of the $\beta$ parameter. In MDEFRS, the two objectives which are to maximize the dependency of the feature subset to the target and to minimize the number of features are individually evaluated without using the $\beta$ parameter.

Due to its recently proposed successful applications for feature selection in the literature [16, 18, 20], we use a simple multi-objective DE variant (MODE) [33] which can be treated as a specified version of the pure DE algorithm for multi-objective problems. Except for the selection scheme which is based on the dominance-based selection scheme inspired by Lampinen’s criterion [27], MODE follows the same procedures as in DE. The pseudocode of MDEFRS is presented in Algorithm 2. As in DEFRS, the threshold value used to select features for the feature subset is set to 0.5. After the multi-objective evolutionary process, the non-dominated solutions in the Pareto-Front are evaluated on the testing set with the training set through a predefined classifier to obtain the classification accuracies. Notice that the testing set is transparent to the user during the multi-objective evolutionary process as in the single-objective evolutionary process.

4 Experimental design

Thirty independent runs are carried out for each proposed approach to get meaningful results. All approaches are implemented using Matlab on an Intel Core i7 machine with 3.6GHz CPU and 16 GB RAM. To verify the effectiveness of the proposed FRS-based approaches, the experiments are conducted on two stages. First, we analyze the performance of the proposed FRS-based approaches by comparing them with PRS-based approaches on six well-known categorical datasets from [12], shown in Table 2. For comparisons, we directly utilize the results of PRS-based approaches reported in [42]. As in [42], we randomly divide each categorical dataset as 7/10 of the instances for training and 3/10 of the instances for testing. For the evaluation of the selected feature subsets, we choose the K-nearest neighbors (KNN) and the decision tree (DT) classification algorithms as in [42], where K is specified as 5 [20].

Table 2 Categorical datasets used in experiments

Second, we analyze the performance of the proposed single-objective FRS-based approach by comparing it with a variety of well-known filter approaches, including feature selection via concave minimization (FSV) [4], local learning-based clustering (LLC-FS) [48], mutual information (MI) [38], Pearson correlation coefficient (PCC) [40], ReliefF [34], Fisher Score [14] and OFS-Density [50] on fourteen real-valued benchmarks from popular repositories [12, 44, 47], shown in Table 3. For comparisons, we directly utilize the results of filter approaches reported in [50]. In order to make consistent and reliable analysis, we follow the same procedure used in [50] such that we apply tenfold cross-validation on each real-valued dataset to divide 9/10 of the instances for training and 1/10 of the instances for testing, and for the evaluation of the selected feature subsets, we choose the support vector machines (SVM) and the KNN classification algorithms.

Table 3 Real-valued datasets used in experiments

The parameter values of FRS-based approaches are determined as follows. The population size and the maximum number of cycles are both set to 50; F and CR are, respectively, set to 0.8 and 0.7 for single-objective DE framework, and 0.5 and 0.2 for multi-objective DE framework as suggested in [20, 29]. Notice that the maximum number of evaluations for PRS-based approaches using PSO was determined as 6000 in [42], but is determined as only 2500 for FRS-based approaches. It can therefore be undoubtedly inferred that FRS-based approaches are computationally more efficient than PRS-based approaches. In single-objective FRS-based approach, three different $\beta$ values (1, 0.9 and 0.5) are used to represent the relative importance of the dependency and the number of features in Eq. (15) (Table 4).

Table 4 Results of PSOPRS and DEFRS through 5NN and DT classifiers

5 Experimental results

To verify the effectiveness of the proposed FRS-based approaches, we make comparisons with the PRS-based and the state-of-the-art filter approaches through single-objective design and multi-objective design in this section.

5.1 Comparison between DEFRS and PSOPRS

The results of PSOPRS and DEFRS are presented in terms of the average classification accuracy and the average number of selected features through 5NN and DT classifiers in Table 4, where the best values are denoted by bold symbol, and the average number of selected features is represented by ‘NOF.’ In order to further show the difference between PSOPRS and DEFRS in terms of the classification accuracy, the Wilcoxon rank-sum test is applied with the significance level 0.05. The results of the Wilcoxon rank-sum test are presented in Table 5, where ‘+’ denotes DEFRS is significantly superior to PSOPRS, ‘−’ denotes DEFRS is worse than PSOPRS, and ‘=’ denotes DEFRS achieves similar results with PSOPRS.

Table 5 Results of Wilcoxon test between PSOPRS and DEFRS through 5NN and DT classifiers

According to Table 4, it can be indicated that DEFRS obtains higher classification accuracy than PSOPRS in most cases. Especially in the Lymph, Dermatology and Soybean datasets, the performance of DEFRS is hugely superior to that of PSOPRS. For instance, the average classification accuracy obtained by DEFRS over 5NN in the Dermatology dataset is 94.28%, whereas PSOPRS obtains only 78.17% in the same dataset. Although DEFRS sometimes selects the feature subsets with high dimensionality compared to PSOPRS, this condition may not be considered as a big deal due to the significant classification performance of the feature subsets selected by DEFRS as seen in Table 5. Only in the Spect dataset, DEFRS generally gets worse classification performance than PSOPRS. In summary, the FRS-based filter approach using DE outperforms the PRS-based filter approach using PSO in terms of selecting the most appropriate feature subsets yielding significantly better classification performance through both the 5NN and DT classifiers.

5.2 Comparison between MDEFRS and MPSOPRS

In contrast to PSOPRS and DEFRS, multi-objective approaches (MDEFRS and MPSOPRS) get a set of Pareto-optimal solutions in each independent run. Accordingly, there exist the 30 Pareto-optimal sets over 30 independent runs for each multi-objective approach. In order to analyze and compare multi-objective filter approaches, we use the following metrics [21]:

• Best front: The best front is determined by using the crowding distance metric among the 30 Pareto-optimal sets. The solution sets are first sorted according to the classification accuracies in ascending order, and then the crowding distance value of a solution is calculated by averaging the distance of its two neighbors. For the solutions with the lowest and highest accuracies which are treated as boundaries, an infinite value is assigned as a crowding distance value. It should be notified that as the classification performance may vary according to the predefined classifier even for the same solution set, different best fronts may be generated for different classifiers.

• Average front: The average front is determined by calculating the average classification accuracy of the 30 Pareto-optimal solution sets having the same number of features. Notice that if there exists only one solution for any number of features, the corresponding solution is also added to the average front.

The results of MDEFRS and MPSOPRS are presented in terms of the best (denoted as ‘-Best’) and the average (denoted as ‘-Avg’) fronts in Figs. 1 and 2 through 5NN and DT, respectively. In charts, the best front is denoted as ‘-Best,’ while the average front is denoted as ‘-Avg.’ In terms of the best front, MDEFRS generally performs better than MPSOPRS in four out of six datasets through both 5NN and DT. For the datasets where MDEFRS sometimes cannot achieve the highest classification accuracy, the space between the lines representing the best fronts is illustrated to be very close. In terms of the average front, MDEFRS outperforms MPSOPRS in all datasets except for the Chess dataset. It should be notified that the space between the lines representing the average fronts is very large. For instance, MDEFRS achieves higher average classification accuracy than MPSOPRS by 6% for the solutions including 11 features. Further, MPSOPRS can only obtain nearly 85% accuracy at most in the Dermatology dataset in terms of the average front, while there exist lots of solutions obtained by MDEFRS achieving more than 90% classification accuracy in the same dataset. It can therefore be suggested that the proposed MDEFRS approach based on MODE and fuzzy rough set theory produces more consistent and reasonable results without no doubt, i.e., the proposed MDEFRS approach is stable and robust compared to MPSOPRS.

Fig. 1

Results of MPSOPRS and MDEFRS over 5NN classifier

Fig. 2

Results of MPSOPRS and MDEFRS over DT classifier

5.3 Comparison between DEFRS and MDEFRS

The results of FRS-based approaches are presented through the 5NN and DT classifiers in Fig. 3, where the $\beta$ value in DEFRS is set to 0.9, and ‘-Avg’ and ‘-Best,’ respectively, denote the average and best fronts, the details of which are presented in Sect. 5.2. Notice that there may be illustrated in charts fewer than 30 distinct points for DEFRS over 30 independent runs since DEFRS can find the same feature subsets in different runs.

Fig. 3

Results of DEFRS and MDEFRS over 5NN and DT classifiers

According to Fig. 3, MDEFRS has shown to achieve best classification performance in all datasets except for the Chess dataset through both 5NN and DT despite the dimensionality reduction in higher rates. For instance, MDEFRS can obtain nearly 92% accuracy only using 9 features through DT, while DEFRS can generally get between 78 and 82% accuracy in spite of using more than 9 features. Not only in terms of the best fronts but also in terms of the average fronts, a remarkable difference can be observed between MDEFRS and DEFRS. For instance, DEFRS can find 81.25% accuracy through 5NN using 7 features in the Spect dataset, MDEFRS can find the same accuracy using less than 7 features, even using only one feature. For another example, DEFRS can obtain between 93 and 96% accuracy using 17–19 features through 5NN in the Dermatology dataset, MDEFRS obtains similar performance through 5NN by eliminating more than half of the features from the Dermatology dataset. In summary, adopting the principles of fuzzy rough set theory in multi-objective framework can achieve outstanding performance compared to in single-objective design.

5.4 Comparison with the state-of-the-art approaches

The results of DEFRS and the state-of-the-art approaches are, respectively, presented on fourteen real-valued benchmark datasets through 5NN and SVM in terms of the average classification accuracy and the Wilcoxon rank-sum test in Tables 6 and 7, where the best values are highlighted by bold symbol, and $\beta$ is specified as 0.9 like as Sect. 5.3. Except for DEFRS, all approaches produce a unique feature subset and so have a single classification accuracy. Notice that we could not provide information concerning the number of features obtained by each approach since this was not reported in [50]; therefore, we could not make comparisons through multi-objective framework. In Tables 6 and 7, ‘+’ (‘−’) denotes that DEFRS produces significantly better (worse) classification accuracies than the corresponding filter approach. If there exists no such a significant difference between the proposed and the corresponding approaches, this case is denoted via ‘=.’ Besides the Wilcoxon rank-sum test, we use the Kruskal–Wallis test to illustrate the difference between feature selection approaches on the classification accuracy through 5NN and SVM. The box plots obtained by the Kruskal–Wallis test for each dataset among all approaches are presented in Fig. 4.

Table 6 Results of DEFRS and state-of-the-art approaches through 5NN classifier

Table 7 Results of DEFRS and state-of-the-art approaches through SVM classifier

Fig. 4

Box plots obtained by Kruskal–Wallis test

In order to evaluate the general distribution of the classification performance obtained by all feature selection approaches on each real-valued dataset using the Kruskal–Wallis test, we observe from Fig. 4 that feature selection approaches produce a variety of feature subsets for each dataset resulting in a wide range of classification accuracies through 5NN and SVM in all datasets except for the WBCD and Hill datasets. Especially in the Srbct, Lymphoma, Prostate and Leukemia datasets, there exists a huge difference among approaches.

According to Tables 6 and 7, it can be observed that DEFRS outperforms MI, Laplacian, LLC-FS and FSV through both 5NN and SVM in all datasets except for only one case. When compared with INF, DEFRS also achieves significantly great classification performance in all datasets except for the WBCD dataset. In other words, the difference between DEFRS and these approaches (MI, Laplacian, LLC-FS and FSV) is exceptionally high. For instance, DEFRS obtains nearly 99% classification accuracy in the Leukemia dataset, while these approaches receive the classification accuracy between 47 and 64%. Similar high differences between DEFRS and these approaches can also be observed in other datasets. It can therefore be indicated that the classification performance of such approaches cannot be treated as adequate on real-valued datasets. When compared with the remaining approaches, DEFRS generally performs slightly better or significantly superior performance in ten out of fourteen datasets through both 5NN and SVM. In summary, the proposed DEFRS approach can achieve satisfactory classification performance not only in discrete-valued but also in real-valued datasets.

When evaluating approaches in terms of the computational cost, the state-of-the-art approaches generally complete the selection process in a shorter time than DEFRS. This is because most of them are based on deterministic procedures and follow greedy search mechanism to select or rank features for the feature subset rather than evaluating feature combinations. However, due to the dependency of deterministic procedures and greedy search mechanism, these approaches cannot deeply evaluate the possible solution space and so frequently encounter with local-convergence problems. This case can be also observed in terms of the classification performance in Tables 6 and 7. Furthermore, a GPU-paralleled implementation of DEFRS can be applied to improve the efficiency of DEFRS.

6 Conclusions

In this paper, we aim to propose new filter approaches for feature selection that can be used not only in discrete-valued problems but also in real-valued problems. This aim was achieved by designing filter criteria using fuzzy rough set theory and then integrating the criteria in single-objective and multi-objective DE frameworks. While DEFRS tries to optimize the dependency of the feature subset and the feature subset size using a control parameter, MDEFRS optimizes the same objectives without the requirement of a control parameter. The performance of the proposed approaches is verified by comparing them with existing approaches on discrete-valued and real-valued datasets. Notice that in order to prove the effectiveness of the proposed approaches, we directly utilize the results of existing works [42, 50] in the literature. According to the results on discrete-valued datasets, the proposed approaches achieved a much higher classification performance than the existing PSO-based approaches based on probabilistic rough set theory. Particularly, in many cases, the proposed single-objective approach achieved more than 10% better classification performance than the existing single-objective PSO-based approach. The similar remarkable difference can also be illustrated between the proposed and the existing multi-objective approaches. According to the results on real-valued datasets, the proposed single-objective approach outperforms a variety of conventional feature selection approaches. In particular, DEFRS provided more than 4% better performance than the recently introduced approach (called OFS) which has second best performance in terms of the mean classification accuracy obtained by averaging the classification accuracies in all datasets. Among the proposed approaches, which one is better? The results reveal that considering fuzzy rough set theory in multi-objective design can receive better feature subsets yielding higher classification accuracy and smaller feature subset size.

The proposed approaches based on fuzzy rough set theory sometimes tend to select a large number of features compared to existing approaches. This may increase the computational complexity in feature selection tasks. This issue will be the motivation for our future work.