A novel relative homogeneity thresholding method with optimization strategy

Abstract

Determining thresholds by measuring class variance is highly effective for image segmentation. Otsu’s method and its derivatives are common approaches that are both simple and adaptable. In spite of these methods’ excellent segmentation performance, images with particular gray distributions cause a thresholding bias that limits their usefulness. We explore the limitations of Otsu’s method and apply other evaluation criteria. In particular, we determine the relative homogeneity between the object and the background and then use it as a classification criterion along with a new binary thresholding method. Our method employs a histogram-smoothing method to improve valley-point selection, establishes a uniformity measure to identify the region with the best homogeneity, and identifies an optimization function for obtaining the best values for the adjustable parameters and threshold value. We also introduce a multilevel thresholding criterion based on a binary thresholding approach. Experiments using real and ground truth test images confirm the validity of our proposed method. Our method also offers a denoising ability when configured to use neighborhood information.

1 Introduction

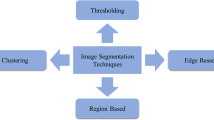
Image segmentation is a fundamental and crucial processing step in image analysis and computer vision [1]. Segmentation consists of partitioning a digital image into meaningful parts [2] or several connected regions based on a similarity criterion such as probabilistic features [3], color features [4], or shape features [5]. Medical image segmentation techniques play an essential role in clinical diagnosis, surgical planning, and treatment evaluation [6], as well as in tissue labeling according to organ intensity and shape [7]. Among image segmentation methods, thresholding is one of the most widely used techniques due to its simplicity [8]. Furthermore, Otsu’s thresholding discriminant [9] is a popular criterion because of its excellent segmentation performance on real images [10].

Otsu’s work spawned additional research as well. Xue et al. [11, 12] researched the close relationships between Otsu’s method and other popular approaches. Vala and Baxi [13] studied various algorithms related to Otsu’s method. Zou et al. [14] analyzed the relationship between Otsu’s method and the Pearson correlation coefficient and provided a novel interpretation of Otsu’s method from the perspective of maximizing image similarity. For images with a large variance between the object and background, Fan [15] proposed a modified valley-emphasis method using a weight term to adjust threshold bias. Yuan [16] applied a parameter weighted on the object variance to force the threshold value to reside at the valley points between peaks or the left bottom rim of a single peak histogram. Harb et al. [17] presented an improved algorithm to preserve high-frequency components of an image. By combining a grid-based model with the estimated background map, Moghaddam and Cheriet [18] proposed an adaptive and parameterless generalized method. By combining Otsu’s circular feature and other color and texture features, Lai and Rosin [19] developed an efficient algorithm to solve the two-class thresholding problem. Cai et al. [20] searched an iterative three-class method, achieving better performance when identifying weak objects and revealing the structures of complex objects. In addition, using the 3D Otsu and multiscale image representations, Feng et al. [21] advanced a novel thresholding algorithm for medical image segmentation. He and Schomaker [22] presented an iterative deep learning framework, using iterative learning of enhanced images and Otsu’s global thresholding techniques to obtain binary images efficiently. For multilevel image segmentation, the authors [23,24,25] also researched some methods to search for optimal thresholds efficiently and accurately.

All of these methods improved the segmentation performance of Otsu’s algorithm by adding multidimensional information, parameter-optimization strategies, weight terms, and intelligent learning. However, none of these have changed Otsu’s principle and structure. Therefore, for images with a large distribution-variance difference between objects and the background, the Otsu’s and related methods provide a biased threshold value, making it difficult to extract objects integrally. To solve the problem, Chen [26] analyzed the limitations of Otsu’s algorithm and applied homogeneity information from the foreground and background to develop a new binary method. Differing from those improved methods, Chen’s method focuses on measuring the homogeneity of objects, reducing the negative effects from unequal distribution variances. Experimental results validate its success. Based on Chen’s method, we have researched further, introducing gray probability-distribution information and presenting a new criterion function. Furthermore, considering the uniformity-distribution information of both the foreground and background, we have explored a relative homogeneity thresholding criterion between classes [27].

In this paper, we propose a new relative homogeneity criterion using region-probability features. We use a new probability-weighted item to adjust the proportion of relative homogeneity and apply a smoothing method to filter valley points. We then apply a uniformity measure to determine the threshold value region having better homogeneity. We design the characteristic function to select parameters for improving accuracy and adaptability. Thresholding results with real images show that our new method achieves better segmentation accuracy for images with very unequal distribution variances between classes, including skewed and heavy-tailed distributions. We also deduce a multilevel thresholding criterion based on the binary discriminant.

2 The criterion of focusing on objects

In Otsu’s criterion for binary thresholding, object and background pixels are viewed as having a uniform or homogeneous gray distribution. However, it is considered only partially. For some images, one class may have greater distribution uniformity or homogeneity than other classes, which means that a biased threshold estimation may result using Otsu’s method.

As a remedy, Chen [26] defined an alternative discriminant criterion, which assumes an object has a homogeneous gray distribution and focuses primarily on information from the segmented object. This method then selects an optimal gray level $t^*\in \{0, 1, 2, \ldots L-1\}$ of an image to minimize the criterion $J_{{LC}} (t)$:

$$J_{LC} (t) = \left( {\frac{{P_{1} (t)}}{{P_{2} (t)}}} \right)^{\alpha } \frac{{\sum_{(x,y) \in O} {\left[ {\lambda (g(x,y) - m)^{2} + (1 - \lambda )(\bar{g}(x,y) - m)^{2} } \right]} }}{{\sum_{(x,y) \notin O} {\left[ {\lambda (g(x,y) - m)^{2} + (1 - \lambda )(\bar{g}(x,y) - m)^{2} } \right]} }} ,$$

(1)

where $t\in \{0, 1, 2, \ldots, L-1\}$ is the gray level of image, $O$ denotes the pixel set belonging to the object, $P_{1} (t) = \frac{1}{\left| O \right|}$, $P_{2} (t) = \frac{1}{N - \left| O \right|}$, N is the total number of pixels in an image, and $m = \frac{1}{\left| O \right|}\sum_{(x,y) \in O} {g(x,y)}$. $g(x,y)$ is the gray level of pixel point (x, y), with $\bar{g}(x,y) = \frac{1}{W}\sum_{(r,l) \in W} {g(r,l)}$ as the neighboring average gray of (x, y). |W| is the size of window centered at (x, y) and usually taken as 3 × 3 or 5 × 5 pixels. Additionally, λ and α are adjustable parameters, with $\lambda (0 \le \lambda \le 1)$ being the proportion between gray and its neighborhood average and $\alpha (\alpha \ge 0)$ being used to adjust $(P_{1} (t)/P_{2} (t))^{\alpha}$.

In Eq. (1), the variance of the background to an object is counted, with the numerator term measuring the similarity within an object class. The more similar pixels in an object class, the smaller the numerator value is. The denominator measures the dissimilarity of the background class to the object class, with larger values indicating that the two classes are more scattered. This criterion emphasizes the similarity of the object classes themselves and, more importantly, the dissimilarity of the background to the object. The threshold value is selected based on the homogeneity of the object and the heterogeneity of the background, to reduce the effect of a large variance difference between the classes.

By introducing the probability distributions of a pixel and its neighborhood average gray in the calculation of Eq. (1), we obtain a more detailed description. Thus, we determine a new thresholding criterion using the gray distribution information:

$$J_{O} (t) = \left( {\frac{{P_{1} (t)}}{{P_{2} (t)}}} \right)^{\alpha } \frac{{\sum_{i \in O} {\left[{\lambda \cdot p(i) \left({i - \mu (t)} \right)^{2} + \left({1 - \lambda} \right) \cdot p(i) \left({i - \bar{\mu} (t)} \right)^{2}} \right]}}}{{\sum_{i \notin O} {\left[{\lambda \cdot p(i) \left({i - \mu (t)} \right)^{2} + \left({1 - \lambda} \right) \cdot p(i) \cdot \left({i - \bar{\mu} (t)} \right)^{2}} \right]}}}.$$

(2)

In this discriminant, O is the pixel set belonging to the object, with $P_{1} (t) = 1/\sum_{i \in O} {p(i)}$ and $P_{2} (t) = 1/\sum_{i \notin O} {p(i)}$, where $p(i)$ is the probability of gray level i. ${\mu}(t) = \sum_{i\in O}ip(i)\left/\sum_{i\in O}p(i)\right.$ denotes the mean value of the object area in the original image, and $\bar{\mu}(t)$ denotes the object area mean value. We use a size of the neighboring window as 3 × 3 pixels.

3 Relative homogeneity measure criterion between classes

In Sect. 2, we described the thresholding criterion $J_{O} (t)$ to focus on the object’s gray distribution information. However, there are two limitations in $J_{O} (t)$.

The first is that $J_{O} (t)$ only includes the consistency degree of the object (background) with respect to the other pixels. It is very likely that fewer pixels have better internal uniformity. That is, a larger number of pixels decrease the uniformity. Similarly, $J_{O} (t)$ is a monotonic function with t. The quantity $(P_{1} (t)/P_{2} (t))^{\alpha}$ provides a trade off, but it is difficult to obtain an effective adjustment. Thus, we cannot obtain an optimal thresholding value by using $J_{O} (t)$.

Figure 1 shows a sample image of red blood cells with $\lambda = 1$ and $\alpha =0.5$. Figure 1a is an original image. Figure 1b is the plot of $J_{O} (t)$, with the abscissa (x-axis) representing the gray level and the ordinate (y-axis) representing the value of $J_{O} (t)$. Figure 1b shows that $J_{O} (t)$ increases monotonically with t. Removing the 0 values, the threshold value is 49 according to criterion $J_{O} (t)$. The segmentation result is shown in Fig. 1c, which shows some object pixels segmented to the background.

Fig. 1

Red blood cells image

The second is that the image homogeneity region may be located in a region of low or high gray-level values. In this case, prior to applying criterion $J_{O} (t)$, we must determine the region with better homogeneity (i.e., the object region). This makes it inconvenient for determining thresholds.

In view of the above, combining the gray level and probability information of the object and background, we modify the discriminant $J_{O} (t)$ to construct new criterion functions. For binary segmentation, there are two position cases with better homogeneity. If the region with better homogeneity is located at a low gray level, we build the criterion as

$$J_{{OL1}} (t) = {\left({P_{F} (t)} \right)^{\alpha}} \cdot \frac{{\sum_{i =0}^{t -1} {\left[{\lambda \cdot p(i) \cdot \left({i - \mu_{1} (t)} \right)^{2} + \left({1 - \lambda} \right) \cdot p(i) \cdot \left({i - \bar{\mu}_{1} (t)} \right)^{2}} \right]}}}{{\sum_{j=t}^{L-1} {\left[{\lambda \cdot p(j) \cdot \left({j - \mu_{1} (t)} \right)^{2} + \left({1 - \lambda} \right) \cdot p(j) \cdot \left({j - \bar{\mu}_{1} (t)} \right)^{2}} \right]}}}$$

(3)

and

$$J_{{OL2}} (t) = \left({1 - \left({P_{F} (t)} \right)^{\alpha}} \right) \cdot \frac{{\sum_{i = t}^{L - 1} {\left[{\lambda \cdot p(i) \cdot \left({i - \mu_{2} (t)} \right)^{2} + \left({1 - \lambda} \right) \cdot p(i) \cdot \left({i - \bar{\mu}_{2} (t)} \right)^{2}} \right]}}}{{\sum_{j = 0}^{t} {\left[{\lambda \cdot p(j) \cdot \left({j - \mu_{2} (t)} \right)^{2} + \left({1 - \lambda} \right) \cdot p(j) \cdot \left({j - \bar{\mu}_{2} (t)} \right)^{2}} \right]}}} .$$

(4)

Here, $J_{{{{OL{1}}}}} (t)$ describes the relative information when the homogeneity foreground is in a low gray region. In addition, the homogeneity between the foreground and background should also be considered, described as $J_{{{{OL{2}}}}} (t)$. ${p(i)}$ and ${p(j)}$ are the corresponding gray probabilities, $P_{F} (t) = \sum_{i = 0}^{t - 1} {p(i)}$, $\mu_{1} (t){{= \sum_{i = 0}^{t - 1} {ip(i)}} \mathord{\left/{\vphantom {{= \sum_{i = 0}^{t - 1} {ip(i)}} {\sum_{i = 0}^{t - 1} {p(i)}}}} \right. \kern-0pt} {\sum_{i = 0}^{t - 1} {p(i)}}}$, $\mu_{2} (t) = {{\sum_{i = t}^{L - 1} {ip(i)}} \mathord{\left/{\vphantom {{\sum_{i = t}^{L - 1} {ip(i)}} {\sum_{i = t}^{L - 1} {p(i)}}}} \right. \kern-0pt} {\sum_{i = t}^{L - 1} {p(i)}}}$, and ${\bar{\mu }_{1} (t)}$ and ${\bar{\mu }_{2} (t)}$ are the mean values of the local average images in the object and background areas.

$J_{{OL{1}}} (t)$ and $J_{{OL{2}}} (t)$ differ from $J_{O} (t)$ in that we apply $\left({P_{F} (t)} \right)^{\alpha}$ to measure the relativity ratio from the homogeneous foreground to the total image and use $1-({P_{F} (t)})^{\alpha}$ to measure the other part to make the relativity measurement more consistent with the real distribution.

Similarly, when the region with better homogeneity has a high gray range, the criteria should be

$$J_{OH1} (t) = \left(1-{P_{B} (t)} \right)^{\alpha } \cdot \frac{{\sum_{i=0}^{t-1} {\left[ {\lambda \cdot p(i) \cdot \left( {i - \mu_{1} (t)} \right)^{2} + \left( {1 - \lambda } \right) \cdot p(i) \cdot \left( {i - \bar{\mu }_{1} (t)} \right)^{2} } \right]} }}{{\sum_{j=t}^{L-1} {\left[ {\lambda \cdot p(j) \cdot \left( {j - \mu_{1} (t)} \right)^{2} + \left( {1 - \lambda } \right) \cdot p(j) \cdot \left( {j - \bar{\mu }_{1} (t)} \right)^{2} } \right]} }}$$

(5)

and

$$J_{OH2} (t) = \left( {P_{B} (t)} \right)^{\alpha } \cdot \frac{{\sum_{i = t}^{L - 1} {\left[ {\lambda \cdot p(i) \cdot \left( {i - \mu_{2} (t)} \right)^{2} + \left( {1 - \lambda } \right) \cdot p(i) \cdot \left( {i - \bar{\mu }_{2} (t)} \right)^{2} } \right]} }}{{\sum_{j = 0}^{t} {\left[ {\lambda \cdot p(j) \cdot \left( {j - \mu_{2} (t)} \right)^{2} + \left( {1 - \lambda } \right) \cdot p(j) \cdot \left( {j - \bar{\mu }_{2} (t)} \right)^{2} } \right]} }} .$$

(6)

Here, $P_{B} (t)=\sum_{i = t}^{L - 1} p(i)$ is the probability sum of high gray-level region.

In image thresholding, the homogeneity of foreground or background relative to the other should be considered simultaneously. Therefore, when the low gray-level region has better homogeneity, we combine Eqs. (3) and (4) to construct the thresholding-criterion function $J_{{OBL}} (t)$. In the same way, when region with better homogeneity is in the high gray-level range, we build $J_{{OBH}} (t)$. The two methods are:

$$J_{OBL} (t) = J_{OL1} (t) + J_{OL2} (t)$$

(7)

and

$$J_{OBH} (t) = J_{OH1} (t) + J_{OH2} (t) .$$

(8)

The above criteria include the relative homogeneity information of both the foreground and the background, which is more reasonable for image-distribution descriptions than the $J_{O} (t)$ method. The relative measurements of the object and background also enable us to determine the bias caused by the class distribution difference.

4 Optimization of threshold point and criterion

4.1 Smoothing of 1d gray histogram

In some thresholding algorithms, the threshold point is selected by traversing all gray levels. In fact, the optimal threshold value is found among valley points in histogram-based methods. Therefore, instead of calculating all gray points, it is more efficient to select the optimal threshold point from among the valley points of the histogram. In real images, there are many valley points, as with the rice grains image histogram shown in Fig. 2. However, some of them are only local valley points and not globally optimal threshold points. Hence, to improve the search process, we apply a regression function to smooth the one-dimensional gray histogram (1d_histogram) curve. We choose a locally weighted scatter plot smoothing (LOESS) function to eliminate scattered or isolated points that interfere with the overall distribution. From this, we obtain a smoothed histogram that is good for finding the optimal threshold points as shown in Fig. 3. From our experiment, we set the width of the LOESS bandwidth to 10.

Fig. 2

Original 1d_histogram

Fig. 3

LOESS smoothed histogram (bandwidth = 10)

Figures 2 and 3 show the original 1d_histogram and its smoothed histogram curve. The abscissa (x-axis) is the gray level, and the vertical axis (y-axis) is the gray probability. The valley points of the 1d_histogram are marked with *.

Comparing Fig. 2 with Fig. 3, the LOESS function smoothed the curve’s burrs, producing fewer valley points and removing false valleys and stochastic noise. The reduced number of valley points speeds and simplifies in finding the optimal threshold value.

4.2 Application of uniformity measure

In Sect. 3, we proposed two thresholding functions $J_{{OBL}} (t)$ and $J_{{OBH}} (t)$ selected according to the homogeneity region. To determine the homogeneity position automatically, we offer a method based on the uniformity measurement, U. In view of its performance-evaluation ability, the uniformity measure is a popular metric [21, 23]. The uniformity measure is computed as

$$U = 1 - 2 * (K - 1) * \frac{{\sum_{j = 0}^{K - 1} {\sum_{{i \in R_{j}}} {(f_{i} - \mu_{j})^{2}}}}}{{M * N * (f_{\max} - f_{\min})^{2}}},$$

(9)

where K is the classification number, R_j is the region segmented by the threshold value t_{(K − 1)}, f_i is the gray level of pixel i, μ_j is the mean gray level in j the region, f_min and f_max are the minimum and maximum gray levels, and M  * N is the total number of image pixels. In formula (9), larger U indicates better uniformity.

The above metric usually measures the uniformity of segmented images, but it is also useful to determine the initial threshold value. For most images, the threshold value is on the side with better homogeneity.

Figures 4 and 5 show synthetic aperture radar (SAR) and lymph images illustrating this behavior. Figures 4a and 5a are original images, and Figs. 4b and 5b are the 1d-gray histogram curves of the two images. Although there are threshold deviations caused by large differences in between-class variance, the threshold position indicates the region with better homogeneity. In Figs. 4b and 5b, we use a solid line to denote the optimal uniformity threshold value and a dashed line to denote the middle of the gray-level range.

Fig. 4

SAR image

Fig. 5

Lymph image

If the optimal uniformity threshold value U is in a low gray-level range, as in Fig. 4, we choose J_OBL(t) as the criterion function. If the threshold value is in a high gray-level range, as in Fig. 5, we use $J_{OBH} (t)$. In this way, we choose the criterion function on the basis of the gray distribution automatically. We also highlight that we reduce the number of calculations by considering only the valley points of the smoothed curve.

5 Relative homogeneity criterion with optimized parameters

There are two adjustable parameters $\lambda$ and $\alpha$ in the criteria functions $J_{OBL} (t)$ and $J_{OBH} (t)$. $\lambda$ is the weighted coefficient of gray and neighboring average gray. If $\lambda = 1$, neighboring average information is not considered. When $\lambda = 0$, the neighboring values are considered to obtain better denoising performance.

The parameter $\alpha$ adjusts the relative homogeneity proportion of the object and background and ranges between 0 and 1. When $\alpha = 1$, the weight coefficients are the accumulated probabilities of the foreground and the background. Thus, $\left( {P_{F} (t)} \right)^{\alpha } = P_{F} (t)$ and $1 - \left( {P_{F} (t)} \right)^{\alpha } = P_{B} (t)$ in $J_{{OBL}} (t)$, and $\alpha = 0$ and $\left( {P_{B} (t)} \right)^{\alpha } = P_{B} (t) \,\,{\text{and}}\,\,1-\left( {P_{B} (t)} \right)^{\alpha } = P_{F} (t)$ in $J_{{OBH}} (t)$. When $\alpha = 0$, only one part of the relative homogeneity is considered, similar to using only $J_O(t)$. Thus, $\left( {P_{F} (t)} \right)^{ 0} = 1$, $1 - \left( {P_{F} (t)} \right)^{ 0} = 0$ and $\left( {P_{B} (t)} \right)^{ 0} = 1,\,\, 1-\left( {P_{B} (t)} \right)^{ 0} = 0$. Therefore, α is an important parameter in $J_{{OBL}} (t)$ or $J_{{OBH}} (t)$ and is chosen to combine the image distributions.

5.1 Parameter-optimization criterion

During thresholding segmentation, the optimal threshold value should be located at the valley point of the gray histogram. In order to emphasize the characteristics of valley points and eliminate some non-threshold special points, we also consider information from points in the neighborhood of the valley points.

Assuming the original image histogram in t is denoted as f(t), the valley-emphasis [15] function $\bar{f}(t)$ is constructed as

$$\bar{f}(t) = f(t - m) + f(t - m + 1) + \cdots f(t) + \cdots + f(t + m - 1) + f(t + m).$$

(10)

Since the optimal threshold value will be located at the valley point of the histogram, its gray and neighborhood gray probability are both minimum values, and $\bar{f}(t)$ is also a minimum. We simplify Eq. (10) as

$$\bar{f}(t) = \sum_{i = - m}^{m} {f(t + i)} ,$$

(11)

where m is a positive integer. Greater m values lengthen the filter.

In the case of some gray distribution histograms, we found that $\bar{f}(t)$ is only a condition for ideal threshold point, and the gray-level variation is smaller near the optimal threshold point. In view of this, we propose another constraint function $\mathop f\limits^{\Delta} (t)$ to represent the sum of gray absolute differences near the threshold t:

$$\mathop f\limits^{\Delta} (t) = |f(t) - f(t - m)| + |f(t) - f(t - m + 1)| + \cdots + |f(t) - f(t + m - 1)| + |f(t) - f(t + m)| .$$

(12)

We simplify this as:

$$\mathop f\limits^{\Delta } (t){ = }\sum_{i = - m}^{m} {\left| {f(t) - f(t + i)} \right|} ,$$

(13)

where m is a positive integer.

In sum, we introduce a new compound function F(t) to take the minimum valley point and gray-level deviation into account:

$$F(t) = \bar{f}(t) \cdot \mathop { \, f}\limits^{\Delta } (t) .$$

(14)

In our use of F(t), we set m = 3. At the optimal threshold point, the value of F(t) should be a minimum. We choose parameter α so that it minimizes F(t):

$$\alpha^{*} = {\text{Arg}}\mathop { \hbox{min} }\limits_{0 < t < L - 1,0 \le \alpha \le 1} \{ F[t_{(\alpha )} ]\} .$$

(15)

After determining parameter $\alpha^{*}$, we obtain the optimal threshold value t^* according to Eq. (7) or (8), i.e.,

$$t^{*} = {\text{Arg}}\mathop { \hbox{min} }\limits_{0 < t < L - 1} \{ J_{{OBL}} [t_{{(\alpha^{*} )}} ]\}$$

(16)

or

$$t^{*} = {\text{Arg}}\mathop { \hbox{min} }\limits_{0 < t < L - 1} \{ J_{{OBH}} [t_{{(\alpha^{*} )}} ]\} .$$

(17)

5.2 Implementation of relative homogeneity method

Incorporating all of the preceding, we perform the following steps in our algorithm.

• Step 1 Smooth the image 1d gray histogram by applying the LOESS function to eliminate local valley points using a bandwidth of 10.

• Step 2 Identify the valley points of the smoothed histogram.

• Step 3 Determine threshold value region having better homogeneity using the uniformity measure function.

• Step 4 According to the label, select the appropriate relative homogeneity thresholding criterion J_OBL or J_OBH.

• Step 5 Use the synthetic valley-emphasis function F(t) to select the optimal exponent parameter $\alpha^{ *}$.

• Step 6 Search all valley points to find the optimal threshold value t^* using criterion function J_OBL or J_OBH.

5.3 Multilevel thresholding

When there are multiple classifications in an image, the uniformity measure U has classification number K > 2. We can construct a multilevel thresholding criterion using our proposed binary algorithm. Using Eq. (9), we identify the class with the lowest homogeneity. We disregard denoising effects by setting $\lambda = 1$ and obtain the criterion function of the lowest homogeneity region as

$$\begin{aligned} J_{Ol} (t_{1}^{*},t_{2}^{*}, \cdots,t_{K - 1}^{*}) &= \left({1 - \mathop{\mathop{\sum}\limits_{q = 1}}\limits_{q \ne l}^{K} {\left({P_{q} (t_{q - 1})} \right)^{\alpha}}} \right) \cdot \frac{{\mathop{\mathop{\sum}\nolimits_{i = t}}\limits_{l - 1}^{t_{l}} {\left[{p(i) \cdot \left({i - \mu_{l} (t_{l - 1})} \right)^{2}} \right]}}}{{\mathop{\mathop{\sum}\nolimits_{q = 1}}\limits_{q \ne l}^{K} {\left[{\sum_{{j = t_{q - 1}}}^{{t_{q}}} {\left[{p(j) \cdot \left({j - \mu_{l} (t_{l - 1})} \right)^{2}} \right]}} \right]}}} &= \left({1 - \mathop{\mathop{\sum}\nolimits_{q = 1}}\limits_{q \ne l}^{K} {\left({P_{q} (t_{q - 1})} \right)^{\alpha}}} \right) \cdot \frac{{P_{l} (t_{l - 1}) \cdot \sigma_{l}^{2} \left({t_{l - 1}} \right)}}{{\mathop{\mathop{\sum}\nolimits_{q = 1}} \limits_{q \ne l}^{K}{\left[{P_{q} (t_{l - 1}) \cdot \sigma_{ql}^{2} \left({t_{l - 1}} \right)} \right]}}}, \end{aligned}$$

(18)

where $t_{1}^{*},t_{2}^{*}, \ldots,t_{K - 1}^{*}$ are the K − 1 thresholding values, l is the region with lowest homogeneity, q indicates the number of other regions, and ${P_{q} (t_{q - 1})}$ is the probability sum excluding the lth region. For the q regions, the criterion is:

$$\begin{aligned} J_{Oq} (t_{1}^{*},t_{2}^{*}, \ldots,t_{K -1}^{*}) &=\left(P_{q} (t_{q - 1}) \right)^{\alpha}\cdot \frac{\mathop{\mathop{\sum}\nolimits_{i = t}}\limits_{l-q}^{t_q}\left[{p(i) \cdot \left({i - \mu_{q} (t_{q -1})}\right)^{2}} \right]}{\mathop{\mathop{\sum}\nolimits_{r=1}}\limits_{r\ne q}^{K} {\left[{\mathop{\mathop{\sum}\nolimits_{j =t}}\limits_{r -1}^{t_{r}} {\left[{p(j) \cdot \left({j - \mu_{q}(t_{q - 1})}\right)^{2}} \right]}} \right]}} \\&= \left({P_{q} (t_{q - 1})}\right)^{\alpha} \cdot \frac{{P_{q} (t_{q - 1}) \cdot \sigma_{q}^{2}\left({t_{q - 1}} \right)}}{\mathop{\mathop{\sum}\nolimits_{r =1}}\limits_{r \ne q}^{K} {\left[{P_{r} (t_{r - 1}) \cdot\sigma_{rq}^{2} \left({t_{q - 1}} \right)} \right]}},\end{aligned}$$

(19)

where $\mu_{l} (t_{l - 1})$, and $\mu_{q} (t_{q - 1})$, $\sigma_{l}^{2} (t_{l - 1})$, and $\sigma_{q}^{2} (t_{q - 1})$ are the mean values and variances of lth and qth regions, respectively.

Considering the homogeneity information from all regions, we construct the thresholding criterion as

$$J_{OB} \left({t_{1}^{*},t_{2}^{*}, \ldots,t_{K - 1}^{*}} \right) = J_{Ol} \left({t_{1}^{*},t_{2}^{*}, \ldots,t_{K - 1}^{*}} \right) + \mathop{\mathop{\sum}\limits_{q = 1}}\limits_{q \ne l}^{K} {J_{Oq}} \left({t_{1}^{*},t_{2}^{*}, \ldots,t_{K - 1}^{*}} \right).$$

(20)

Then, the optimal threshold values are

$$\left({t_{1}^{*},t_{2}^{*}, \ldots,t_{K - 1}^{*}} \right) = {\text{Arg}}\mathop {\min}\limits_{{0 < t_{1}^{*},t_{2}^{*}, \ldots,t_{K - 1}^{*} < L - 1}} \left\{{J_{{OB}} \left({t_{1}^{*},t_{2}^{*}, \ldots,t_{K - 1}^{*}} \right)} \right\},$$

(21)

where $l, q, r \in [1,K]$. The parameter $\alpha$ can be selected as with the binary thresholding method.

6 Experimental results and analysis

6.1 Thresholding results

To verify the performance of our proposed method, we designed an experiment to compare results from the following eight methods, including our own method: the 1-dimensional Otsu’s method (denoted as Otsu) [7], the modified valley-emphasis method (denoted as MOtsu) [15], the parameter-weight method on the object variance (denoted as WOtsu) [16], the iterative three-class method for sub-regions (denoted as IOtsu) [20], the focusing-on-objects method (denoted as FO) [26], our relative homogeneity method without optimization (denoted as ROB, $\alpha = 0.5$) [27], our relative homogeneity criterion with $\alpha$ parameter optimization (denoted as ROBP), and our relative homogeneity method with optimized valley points and $\alpha$ (denoted as ROBVP). Here, we set parameter $\lambda < 1$.

We validated all methods through simulations in MATLAB. We used a computer with an Intel Core i7-4720HQ CPU at 2.60 GHz and 8 GB of memory running Microsoft Windows 8.

Figure 6a–j shows the 10 representative images from several fields: color, material structure, SAR, red blood cells, rice grains, numbers, lymph, cells under an optical microscope, an MRI slice, and a barcode. Their sizes are 158 × 159, 340 × 304, 256 × 256, 272 × 265, 256 × 256, 730 × 203, 130 × 130, 213 × 166, 256 × 256 and 256 × 256 pixels, respectively. Figure 7a–j shows their corresponding 1d_histograms. Among them, the color, material structure, and SAR images have large between-class variance. The number, lymph, cells, MRI slice, and barcode images have skewed or heavy-tailed histograms. The red blood cells and rice grain images have small between-class variance. Figures 8, 9, 10, 11, 12, 13, 14, 15, 16, and 17 show the segmentation results of the 10 images with (a)–(j) showing the results of Otsu, MOtsu, WOtsu, IOtsu, FO, ROB, ROBP, and ROBVP, respectively, for each source image.

Fig. 6

Original images

Fig. 7

1d_histogram

Fig. 8

Results from the color image

Fig. 9

Results from the material structure image

Fig. 10

Results from the SAR image

Fig. 11

Results from the red blood cells image

Fig. 12

Results from the rice grains image

Fig. 13

Results from the numbers image

Fig. 14

Results from the lymph image

Fig. 15

Results from the cells under an optical microscope image

The results from Figs. 8a, 9a, and 10a show that the simple Otsu’s method did not segment the object properly in the color, material structure, and SAR images. From Figs. 11, 12, 13, 14, 15, 16, and 17a, the integrity of segmented object was insufficient. The MOtsu method yielded an excellent result for the SAR image in Fig. 10b, with middling results for the red blood cells, rice grains, numbers, and MRI slice. MOtsu did not correctly extract the objects in the color, material structure, lymph, cells, and barcode images in Figs. 8, 9b, 14, 15b, and 17b. The WOtsu obtained perfect segmentation results in Figs. 11c, 14c, and 17c. Similarly, the IOtsu method had fine results in Figs. 11d and 15 and 16d, but both IOtsu and WOtsu showed limited adaptability to the overall mix of images.

Fig. 16

Results from the MRI slice image

The FO, ROB, ROBP, and ROBVP methods each had a different construction principle in the corresponding discriminant function. The FO method focused its information statistic on the object itself, segmenting the color image perfectly, but failing to do so for the other nine images with scattered objects or backgrounds. The ROB method, applying the relative homogeneity measurement, achieved preferable results in the red blood cells, lymph, and MRI slice images shown in Figs. 11f, 14f, and 16f. However, the invariant $\alpha$ value limited ROB’s adaptability to the other images. Our proposed ROBP and ROBVP methods achieved optimal results by extracting the most complete objects. This was especially true of the ROBVP method as shown in (h) of Figs. 8, 9, 10, 11, 12, 13, 14, 15, 16, and 17.

Fig. 17

Results from the barcode image

Table 1 shows the optimal threshold value t^* and optimized parameter $\alpha$ of the eight methods for the 10 images. The FO method’s threshold value tended to the lower gray level, which was smaller than that of the other methods as a result of the monotonic criterion $J_{{O}} (t)$. The ROBP and ROBVP methods had same threshold values in the material structure and number images, but ROBVP’s threshold value achieved more complete extraction results on the SAR, cells, and barcode images.

Table 1 Optimal threshold value t^* and optimized parameter $\alpha$

Moreover, the ROBVP method was faster as a result of its valley-points optimization strategy, as shown in Table 2. For the 10 images, our proposed ROBVP had the best times, taking between 45.9 and 75% of the time required by the ROBP method. It is remarkable that ROBVP’s running time was even shorter than that of the Otsu’s method on the color, rice, lymph, and MRI slice images.

Table 2 Processing time for the 10 images

6.2 Segmentation results of noisy image

The discriminant criteria in Eqs. (2)–(8) include neighborhood average information. If $\lambda < 1$, some denoising performance results. In this experiment, we compared the ROBVP method with $\lambda = 1$ and $\lambda = 0.5.$ Figures 18a, 19, and 20a are 3 representative images: color, SAR, and red blood cells with Gaussian noise of 0 mean value and 0.003 variance. Figures 18, 19, and 20b show the 1d_histograms of the 3 noisy images. Figures 18, 19, and 20i, j are the results of ROBVP with λ set to 1 and 0.5, respectively. Figures 18, 19, and 20c–h show the results from the Otsu, MOtsu, WOtsu, IOtsu, ROB, and 2d_Otsu methods for comparison. We do not include FO because of its non-ideal results.

Fig. 18

Denoising results of the color image

Fig. 19

Denoising results of the SAR image

Fig. 20

Denoising results of the red blood cells image

When $\lambda = 0.5$, the denoising performance was better than with $\lambda = 1$. For the color image, only ROBVP $(\lambda = 0.5)$ obtained the correct threshold value. For the SAR and red blood cells images, the denoising results of the ROBVP methods were superior. Table 3 shows the threshold values of the eight methods. When $\lambda = 0.5$, the threshold values from ROBVP were more accurate than ROBVP with $\lambda = 1$ as well as the 2d_Otsu method.

Table 3 Denoising threshold results of eight methods

6.3 Performance evaluation

To analyze the segmentation results quantitatively, we assessed the performance of the methods according to the misclassification error (ME). ME can reflect the percentage of background pixels wrongly assigned to foreground and, conversely, foreground pixels wrongly assigned to background. For the two-class segmentation, ME can be expressed as [28]:

$${\text{ME}} = 1 - \frac{{\left| {B_{\mathrm{O}} \cap B_{\mathrm{T}}} \right| + \left| {F_{\mathrm{O}} \cap F_{\mathrm{T}}} \right|}}{{\left| {B_{\mathrm{O}}} \right| + \left| {F_{\mathrm{O}}} \right|}},$$

(22)

where B_O and B_T denote the object of the ground truth and test images, F_O and F_T are the background of the two images, and | • | is the operator to obtain the cardinality of a set. The range of ME is from 0 to 1, 0 denotes totally correct segmentation, and 1 means totally erroneous case; their scores vary from 0 for a totally correct segmentation to 1 for a totally erroneous case.

We selected four test images from a database of nondestructive testing (NDT) images for quantitative evaluation of the thresholding methods [28]. The ground truth images for the NDT images were chosen interactively by experts [29], and we downloaded them from the Web site of Sezgin [30]. The size of the Test1 image is 232 × 131 pixels, and the sizes of Test2, Test3, and Test4 are all 256 × 256 pixels. Figures 21, 22, 23, and 24 show the results. Figures 21, 22, 23, and 24a are the original images, while Figs. 21, 22, 23, and 24b are the ground truth images. Figures 21, 22, 23, and 24c–j show the results of the Otsu, MOtsu, WOtsu, IOtsu, FO, ROB, ROBP, and ROBVP methods, respectively. Table 4 shows the segmentation threshold values and MEs of the 8 methods. The ROBVP method with λ set to 0.5 had an ME lower than the other 7 methods. The ME of the Test4 image was only 0.0054. We have marked the lowest ME values in bold in Table 4.

Fig. 21

Results of the Test1 image

Fig. 22

Results of the Test2 image

Fig. 23

Results of the Test3 image

Fig. 24

Results of the Test4 image

Table 4 The misclassification error (ME) of eight methods

For evaluating the denoising performance of the methods, we used the common peak signal-to-noise ratio (PSNR) [31] measure. PSNR gives the similarity of a thresholded image against a reference image based on the root mean square error (RMSE) [31] of each pixel. The larger the PSNR, the better the similarity. It is given by Eq. (23):

$${\text{PSNR}}(x,y) = 20\log_{10} \left({\frac{255}{{\sqrt {{\text{RMSE}}(x,y)}}}} \right)$$

(23)

The segmentation results of two test images with Gaussian noise of 0 mean value and 0.003 variance are shown in Figs. 25 and 26, and the PSNR of eight methods is displayed in Table 5. We can see that the ROBVP $(\lambda = 0.5)$ method obtained maximum PSNR values in the eight methods, which implies that our proposed method has prominent performance for noisy images segmentation. The sizes of Test5 and Test6 image are 105 × 104 and 166 × 60 pixels, respectively.

Fig. 25

Results of the noisy Test5 image

Fig. 26

Results of the noisy Test6 image

Table 5 The PSNR value of eight methods

7 Conclusion

In this paper, we have responded to the limitations of the Otsu’s method by focusing on other objects criteria and exploring image thresholding methods. We first developed the relative homogeneity measurement for images with larger distribution between-class variance. We then applied optimization strategies based on the gray distribution and region homogeneity characteristic information to propose a new thresholding segmentation method, relative homogeneity method with optimized valley points and parameter $\alpha$ (ROBVP). Furthermore, we have explored a multilevel segmentation discriminant using a single thresholding criterion.

Our work makes four main contributions. First, our method examines the relative homogeneity between the object and the background to offset the negative effects from the between-class distribution difference and to enable a more detailed and accurate image description. Second, our method uses the uniformity measure to determine the region with better homogeneity and to guide the selection of thresholding criteria. Third, our method improves the valley-points selection strategy by removing false threshold points and improving selection efficiency. Fourth, we have constructed an optimization function to find the best value for parameter $\alpha$ as part of obtaining the optimal threshold value.

Our experimental results with real images having large between-class variances or skewed or tail-heavy gray histograms show that our proposed ROBVP method obtained the most accurate threshold value and yielded a lower misclassification error than existing methods. In addition, our valley-points filter strategy shortened the time required to find a thresholding value, improving segmentation efficiency. Finally, when neighborhood image information was included, our proposed method offered superior denoising performance and higher PSNR values.