Robust subspace learning-based low-rank representation for manifold clustering

Abstract

Spectral clustering-based subspace clustering methods have attracted broad interest in recent years. This kind of methods usually uses the self-representation in the original space to extract the affinity between the data points. However, we can usually find a subspace where the affinity of the projected data points can be extracted by self-representation more effectively. Moreover, only using the self-representation in the original space cannot handle nonlinear manifold clustering well. In this paper, we present robust subspace learning-based low-rank representation learning a subspace favoring the affinity extraction for the low-rank representation. The process of learning the subspace and yielding the representation is conducted simultaneously, and thus, they can benefit from each other. After extending the linear projection to nonlinear mapping, our method can handle manifold clustering problem which can be viewed as a general case of subspace clustering. In addition, the $\ell _{2,1}$-norm used in our model can increase the robustness of our method. Extensive experimental results demonstrate the effectiveness of our method on manifold clustering.

1 Introduction

In the past two decades, subspace clustering has attracted increasing interest. Given a set of data points drawn from a union of multiple subspaces, the task of subspace clustering is to group these data points according to the underlying subspaces they are drawn from. According to the review [39], the subspace clustering methods can be roughly divided into four categories: algebraic approaches [40], iterative approaches [1], statistical approaches [38], and spectral clustering-based approaches [22]. In recent years, spectral clustering-based approaches [44, 46, 48] have aroused heated discussion since low-rank representation (LRR) [19, 20] and sparse subspace clustering (SSC) [4, 5] were proposed. This kind of approaches first builds an undirected graph representing the affinity between data points and then applies spectral clustering [25] methods such as normalized cut (NC) [30] to this graph to obtain the clustering results. The construction of the graph plays a key role in the performance of spectral clustering-based approaches. If any approach can build the graph that the weights between the data points drawn from the same subspace are larger than those between the data points in different subspaces, it is likely to achieve the right clustering results.

LRR and SSC are popular spectral clustering-based approaches. They make use of the self-representation of the data points to extract their affinities. In order that the data points can be represented by those from the same subspace, LRR and SSC add the low-rank penalty and sparse penalty on the representation matrix, respectively. In the past few years, LRR and SSC generate a lot of studies discussing their extensions [6, 8], such as subspace segmentation via quadratic programming (SSQP) [41], least squares regression (LSR) [24], correlation adaptive subspace segmentation (CASS) [23], smooth representation (SMR) [10], structure-constrained low-rank representation (SC-LRR) [35], dense block and sparse representation (DBSR) [34]. As described in [15], their models can be summarized as follows

$$\begin{aligned} \min _{\mathbf {Z},\mathbf {E}} f(\mathbf {Z})+\alpha g(\mathbf {E}) \quad \hbox{s.t.} \quad \mathbf {X}=\mathbf {XZ}+\mathbf {E}, \end{aligned}$$

(1)

where $\mathbf {X}$ denotes the dataset with each column corresponding to a data point $\mathbf {x}_{i}$, $\mathbf {Z}$ is the representation matrix whose element in the i-th row and j-th column stands for the affinity between $\mathbf {x}_{i}$ and $\mathbf {x}_{j}$, $\mathbf {E}$ denotes the noise and outliers, $f(\mathbf {Z})$ and $g(\mathbf {E})$ are the penalty on $\mathbf {Z}$ and $\mathbf {E}$, respectively, and $\alpha$ is the trade-off parameter balancing these two terms. Usually selected as Frobenius (F) norm [50], $\ell _{1,1}$-norm, and $\ell _{2,1}$-norm, $g(\mathbf {E})$ is not the main difference of these spectral clustering-based approaches. The definition of F-norm, $\ell _{1,1}$-norm, and $\ell _{2,1}$-norm can be found in Table 1. Associated with the property of $\mathbf {Z}$, $f(\mathbf {Z})$ determines the characteristics of different approaches. What these methods have in common is $\mathbf {X}=\mathbf {XZ}+\mathbf {E}$ in the constraint, meaning that they extract the affinity between the data points in the original space. Although another extension of LRR such as latent low-rank representation [21] (LLRR) exploits a different representation form, i.e., $\mathbf {X}=\mathbf {X}\mathbf {Z}+\mathbf {L}\mathbf {X}+\mathbf {E}$, it also conducts the representation in the original space.

Table 1 Notation summary

Unfortunately, in the real-world applications, the assumption that the intrinsic structure of the dataset is a union of multiple subspaces may be violated. Since the linear subspace is a special case of the manifold, the recently focused mixture of manifolds [7] is the general problem. Suppose the data points are drawn from a union of multiple manifolds, the task of manifold clustering is to group the data points with each cluster corresponding to a manifold [33]. Manifold clustering includes two branches: linear and nonlinear [42]. The linear case is the problem of subspace clustering. With respect to the nonlinear case, the data points cannot be linearly represented by the data points drawn from the same manifold, so the idea of using self-representation in the original subspace to extract the affinity between the data points will not be effective. In this situation, we can extract the features of the data points, which can also be viewed as the transformed data points in another space. Since the features of the data points may have the structure of a union of multiple subspaces, the references [3, 11, 12] handle image segmentation, saliency detection, and co-segmentation of 3D shapes by applying the extensions of LRR and SSC to the extracted features, respectively.

In fact, the above-mentioned approaches also exploit the features to handle subspace clustering problems. In their experiment, they usually preprocess the data points by projecting them into a low-dimensional space via principle component analysis (PCA). This step can reduce the dimensionality of the data points to improve the computation speed. More importantly, the extracted features can improve the performance to some extent. This result implies two aspects: The first is that even if the data points have the structure of a union of subspaces, learning features also favor the affinity extraction by self-representation. The second is that the subspace where the affinity of the transformed data points can be extracted by self-representation effectively usually exists. Hence, with respect to manifold clustering, whether the linear case or the nonlinear case, learning a subspace to favor the extraction of affinity by self-representation is worthy to be considered. Latent space sparse subspace clustering (LS3C) [29] is an approach using the strategy of learning a subspace to obtain the representation. It seeks the low-dimensional subspace by minimizing the reconstruction error, which can be understood as PCA. Therefore, the idea of learning a subspace in LS3C is more about the dimensionality reduction, not from the view of favoring affinity extraction by self-representation. In addition, its model enforcing the F-norm on the noise is not robust.

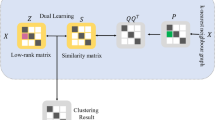
In this paper, we propose robust subspace learning-based low-rank representation (RSLLRR) for manifold clustering. RSLLRR can simultaneously learn the subspace and obtain the low-rank representation. By means of linear projection and nonlinear projection, RSLLRR can learn linear subspace and nonlinear subspace to handle the linear case and nonlinear case of manifold clustering well, respectively. It is notable that our method is distinct from the strategy in the experiment of previous work, i.e., first project the data into the low-dimensional space and then obtain the representation matrix. Their strategy separates the process of learning the subspace from obtaining the representation, leading to the result that the subspace is only determined by the dimensionality reduction methods and thus may not favor the extraction of the affinity. In our method, the learned subspace is also affected by the low-rank penalty on the representation matrix to some extent. Hence, RSLLRR can learn the subspace favoring affinity extraction by low-rank representation. In order to achieve this aim effectively, we design special term describing the property of the learned subspace instead of PCA in our model. Furthermore, since the robustness of $\ell _{2,1}$-norm is verified by previous work [17, 19, 20, 45], we add it in our model. Although $\ell _{2,1}$-norm brings the difficulty in numerical solution, we design special iteration strategy to solve this problem, enabling RSLLRR to usually perform better than our conference version using F-norm [36]. In our experiment, our algorithm always converges well and outperforms the state of the art. In summary, our contributions are as follows.

• 1. We present robust subspace learning-based low-rank representation. It can learn the subspace favoring affinity extraction by self-representation.

• 2. We successfully incorporate $\ell _{2,1}$-norm in our model; it can enhance the robustness of our method.

• 3. By designing special term describing the property of the learned subspace instead of PCA, our method performs well in manifold clustering.

The reminder of the paper is organized in the following: In Sect. 2, we present subspace learning-based low-rank representation. In Sect. 3, we extend our model as robust subspace learning-based low-rank representation. In Sect. 4, we test the performance of our method on synthetic data and five benchmark databases. In Sect. 5, we conclude this paper.

2 Subspace learning-based low-rank representation

In this section, we present the model with F-norm enforced on the noise. By means of alternating direction method (ADM) [18], we can obtain its numerical solution easily. First, we will develop our model only devoted to subspace clustering. Then, we extend the mapping to obtain the model for nonlinear manifold clustering.

2.1 The basic model

In view of the observation that the data points may exhibit more meaningful linear structure in another space instead of the original space, we present the subspace learning-based low-rank representation model (SLLRR) [36] to learn a subspace for low-rank representation in the following.

$$\begin{aligned} & \min \limits _{\mathbf {Z},\mathbf {W}} \Vert \mathbf {Z}\Vert _{*}+\alpha \Vert \mathbf {W}\mathbf {X}-\mathbf {W}\mathbf {X}\mathbf {Z}\Vert _{F}^{2}+\beta f(\mathbf {W}) \\ & \hbox{s.t.} \quad \mathbf {W}\mathbf {W}^{T}=\mathbf {I}_{d}, \end{aligned}$$

(2)

where $\mathbf {W}\in \mathbb {R}^{d\times D}$ stands for linear projection transforming D-dimensional space into d-dimensional space. The constraint $\mathbf {W}\mathbf {W}^{T}=\mathbf {I}_{d}$ is used to keep $\mathbf {W}$ as the orthogonal basis. $\mathbf {X} \in \mathbb {R}^{D\times n}$ means that the dimensionality and the number of the data points are D and n, respectively. The terms $\Vert \mathbf {Z}\Vert _{*}$ and $\Vert \mathbf {W}\mathbf {X}-\mathbf {W}\mathbf {X}\mathbf {Z}\Vert _{F}^{2}$ are used to enforce the low-rank property on the representation matrix and keep the projected data points in the learned subspace represented by itself as well as possible, respectively. Both $\alpha$ and $\beta$ are the trade-off parameters balancing these terms. $f(\mathbf {W})$ describes the property of the learned subspace. The detailed discussion about it is in the following.

Although $f(\mathbf {W})$ can be constructed by the result in graph embedding framework [43], the energy in those dimensionality reduction approaches is usually constructed for the property of discrimination since the recognition is their main application. If the data points in different subspace are projected into one subspace in spite of the desired separation in each class, it will be more difficult for us to segment these projected data points in the learned subspace by self-representation. Hence, the rule in previous dimensionality reduction work may not be suitable for the self-representation extracting the affinity between data points. Moreover, the label information required by the supervised approaches cannot be obtained in this unsupervised problem.

Our idea is to learn a subspace by keeping the local structure of the data points drawn from the same subspace. We intend to shorten the distance of the nearby data points in the same subspace to make them represented by each other better. Although the neighbors of the data points near the intersection of the subspaces will include the data points drawn from different subspaces, numerous data points with small Euclidean distance are in the same subspace. With respect to the data points close to the intersection of the subspaces, the angles between every two data points can be used to separate them. Hence, we first choose n/2c nearest neighbors of each data point by Euclidean distance, where c denotes the number of the subspaces. Then, by selecting the data points with the k smallest angles in the neighbors, we establish $\mathbf {G}$ in the following

$$\begin{aligned}{}[\mathbf {G}]_{ij}=\bigg \{ \begin{array}{ll} 1 &{} \quad \mathbf {x}_{i}\in \mathcal {N}(\mathbf {x}_{j}) \quad \text {or} \quad \mathbf {x}_{j}\in \mathcal {N}(\mathbf {x}_{i}) \\ 0 &{} \quad {\text {otherwise}}\\ \end{array}, \end{aligned}$$

(3)

where $\mathcal {N}(\mathbf {x}_{j})$ denotes the data points with the k smallest angles in the n/2c nearest neighbors. In the last, we pull these nearby data points probably in the same subspace close to each other in the learned subspace by minimizing the following energy.

$$\begin{aligned} \sum _{i,j}\Vert \mathbf {W}\mathbf {x}_{i}-\mathbf {W}\mathbf {x}_{j}\Vert _{2}^{2}[\mathbf {G}]_{ij}. \end{aligned}$$

(4)

It can be reformulated as

$$\begin{aligned} tr(\mathbf {W}\mathbf {X}\mathbf {S}\mathbf {X}^{T}\mathbf {W}^{T}), \end{aligned}$$

(5)

where $\mathbf {S}=\mathbf {H}-\mathbf {G}$ is the Laplacian matrix, $\mathbf {H}$ is the diagonal matrix with $[\mathbf {H}]_{ii}=\sum _{j=1}^{n}[\mathbf {G}]_{ij}$ . Hence, SLLRR can be formulated in the following

$$\begin{aligned} & \min \limits _{\mathbf {Z},\mathbf {W}} \Vert \mathbf {Z}\Vert _{*}+\alpha \Vert \mathbf {W}\mathbf {X}-\mathbf {W}\mathbf {X}\mathbf {Z}\Vert _{F}^{2}+\beta tr(\mathbf {W}\mathbf {X}\mathbf {S}\mathbf {X}^{T}\mathbf {W}^{T}) \\ & \hbox{s.t.} \quad \mathbf {W}\mathbf {W}^{T}=\mathbf {I}_{d}. \end{aligned}$$

(6)

2.2 Nonlinear extension

In order to make SLLRR applicable to manifold clustering, we extend our model in the following.

$$\begin{aligned} & \min \limits _{\mathbf {Z},\mathbf {W}} \Vert \mathbf {Z}\Vert _{*}+\alpha \Vert \mathbf {W}\phi (\mathbf {X})-\mathbf {W}\phi (\mathbf {X})\mathbf {Z}\Vert _{F}^{2}\\ & \quad +\beta tr(\mathbf {W}\phi (\mathbf {X})\mathbf {S}\phi (\mathbf {X})^{T}\mathbf {W}^{T}) \hbox{s.t.} \quad \mathbf {W}\mathbf {W}^{T}=\mathbf {I}_{d}. \end{aligned}$$

(7)

With regard to manifold clustering, we assume the data points can be linearly represented by the data points drawn from the same manifold after a nonlinear mapping $\phi$. Then, we also learn a subspace favoring the affinity extraction in order that we can get the effective segmentation results by the spectral clustering algorithm. Hence, we change $\mathbf {X}$ in model (6) into $\phi (\mathbf {X})$ in model (7). The new model can be understood in the perspective that we learn a nonlinear subspace for the low-rank representation.

Since the bases can be linearly represented by the mapped data points, we have $\mathbf {W}=\mathbf {U}\phi (\mathbf {X})^{T}$. Then model (7) can be reformulated in the following

$$\begin{aligned} & \min \limits _{\mathbf {Z},\mathbf {U}} \Vert \mathbf {Z}\Vert _{*}+\alpha \Vert \mathbf {U}\mathbf {K}-\mathbf {U}\mathbf {K}\mathbf {Z}\Vert _{F}^{2}+\beta tr(\mathbf {U}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}^{T}) \\ & \hbox{s.t.} \quad \mathbf {U}\mathbf {K}\mathbf {U}^{T}=\mathbf {I}_{d}, \end{aligned}$$

(8)

where $\mathbf {K}=\phi (\mathbf {X})^{T}\phi (\mathbf {X})$ is the kernel. We develop different kernels for different problems with detailed discussion provided in the experiments.

2.3 Numerical solution

Model (8) can be easily solved by ADM after introducing one auxiliary variable $\mathbf {J}$ to make the objective function separable.

$$\begin{aligned} & \min \limits _{\mathbf {Z},\mathbf {J},\mathbf {U}} \Vert \mathbf {J}\Vert _{*}+\alpha \Vert \mathbf {U}\mathbf {K}-\mathbf {U}\mathbf {K}\mathbf {Z}\Vert _{F}^{2}+\beta tr(\mathbf {U}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}^{T}) \\ & \hbox{s.t.} \quad \mathbf {U}\mathbf {K}\mathbf {U}^{T}=\mathbf {I}_{d} \quad \mathbf {Z}=\mathbf {J}. \end{aligned}$$

(9)

Then, we obtain the following augmented Lagrange function

$$\begin{aligned} \Vert {\mathbf {J}}\Vert _{*}& +\alpha \Vert{ \mathbf {UK}}-{\mathbf {UKZ}}\Vert _{F}^{2}+\beta tr({\mathbf {UKSK}}^{T}{\mathbf {U}}^{T}) \\ & +\frac{\mu }{2}(\Vert {\mathbf {Z}}-{\mathbf {J}}\Vert _{F}^{2})+\langle {\mathbf{\Lambda }}, {\mathbf {Z}}-{\mathbf {J}} \rangle . \end{aligned}$$

(10)

We iteratively update each variable by fixing the others. Fortunately, the closed-form solution exists for each optimization problem. The numerical algorithm of model (8) is provided in Algorithm 1 where the convex optimization in step 2 can be solved by singular value thresholding (SVT) operator [2]. Since the generalized eigenvalue decomposition, the singular value decomposition, and the inverse of the matrix are the main computation cost in each step, the computational complexity of this algorithm is $O(n^3)$.

3 Robust subspace learning-based low-rank representation

Compared with $\ell _{2,1}$-norm, F-norm is not robust to the outliers. In this section, we extend SLLRR by replacing the F-norm with the $\ell _{2,1}$-norm. Although this change causes some difficulty in solving the model, we design a special iteration to overcome this problem. We will start by formulating our model for manifold clustering and then provide the algorithm.

3.1 Robust extension

To enhance the robustness, we change the F-norm of model (8) into the $\ell _{2,1}$-norm. The model, named robust subspace learning-based low-rank representation (RSLLRR), can be formulated in the following

$$\begin{aligned} & \min \limits _{\mathbf {Z},\mathbf {U}} \Vert \mathbf {Z}\Vert _{*}+\alpha \Vert \mathbf {U}\mathbf {K}-\mathbf {U}\mathbf {K}\mathbf {Z}\Vert _{2,1}+\beta tr(\mathbf {U}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}^{T}) \\ & \hbox{s.t.} \quad \mathbf {U}\mathbf {K}\mathbf {U}^{T}=\mathbf {I}_{d}. \end{aligned}$$

(11)

Similar to the spectral clustering-based methods such as LRR and SSC for subspace clustering, SLLRR and RSLLRR can handle manifold clustering by Algorithm 2 after obtaining $\mathbf {Z}$ from Algorithms 1 and 3, respectively.

3.2 Numerical solution

In the following, we will show how to solve our model by ADM. First, introduce one auxiliary variable $\mathbf {J}$ to make the objective function separable

$$\begin{aligned} & \min \limits _{\mathbf {Z},\mathbf {J},\mathbf {U}} \Vert \mathbf {J}\Vert _{*}+\alpha \Vert \mathbf {U}\mathbf {K}-\mathbf {U}\mathbf {K}\mathbf {Z}\Vert _{2,1}+\beta tr(\mathbf {U}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}^{T}) \\ & \hbox{s.t.} \quad \mathbf {U}\mathbf {K}\mathbf {U}^{T}=\mathbf {I}_{d} \quad \mathbf {Z}=\mathbf {J}. \end{aligned}$$

(12)

Second, construct the augmented Lagrange function

$$\begin{aligned} \Vert \mathbf {J}\Vert _{*}& +\alpha \Vert \mathbf {U}\mathbf {K}-\mathbf {U}\mathbf {K}\mathbf {Z}\Vert _{2,1}+\beta tr(\mathbf {U}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}^{T}) \\ & +\frac{\mu }{2}\Vert \mathbf {Z}-\mathbf {J}\Vert _{F}^{2}+\langle \mathbf {\Lambda }, \mathbf {Z}-\mathbf {J} \rangle. \end{aligned}$$

(13)

Third, iteratively minimize each variable with the others fixed. Algorithm 3 outlines the ADM algorithm of RSLLRR, where $\mathbf {Z}_{k}$ denotes the value of $\mathbf {Z}$ in the k-th iteration. If we can find the optimal solution of each subproblem, the value of the augmented Lagrange function decreases after each step. The details are in the following. The value of the augmented Lagrange function in the k-th iteration is

$$\begin{aligned} L_{k,0} & = \Vert \mathbf {J}_{k}\Vert _{*}+\alpha \Vert \mathbf {U}_{k}\mathbf {K}-\mathbf {U}_{k}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1}+\beta tr(\mathbf {U}_{k}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}_{k}^{T}) \nonumber \\ & \quad +\,\frac{\mu _{k}}{2}\Vert \mathbf {Z}_{k}-\mathbf {J}_{k}\Vert _{F}^{2}+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}_{k}-\mathbf {J}_{k} \rangle . \end{aligned}$$

(14)

After step 1,

$$\begin{aligned} L_{k,0}\ge L_{k,1} & = \Vert \mathbf {J}_{k}\Vert _{*}+\alpha \Vert \mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1} \nonumber \\ & \quad +\,\beta tr(\mathbf {U}_{k+1}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}_{k+1}^{T}) +\frac{\mu _{k}}{2}\Vert \mathbf {Z}_{k}-\mathbf {J}_{k}\Vert _{F}^{2}+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}_{k}-\mathbf {J}_{k} \rangle . \end{aligned}$$

(15)

After step 2,

$$\begin{aligned} L_{k,1}\ge {} L_{k,2}&=\Vert \mathbf {J}_{k+1}\Vert _{*}+\alpha \Vert \mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1} \nonumber \\&\quad +\beta tr(\mathbf {U}_{k+1}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}_{k+1}^{T}) +\frac{\mu _{k}}{2}\Vert \mathbf {Z}_{k}-\mathbf {J}_{k+1}\Vert _{F}^{2}+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}_{k}-\mathbf {J}_{k+1} \rangle . \end{aligned}$$

(16)

After step 3,

$$\begin{aligned} L_{k,2}\ge L_{k,3} & = \Vert \mathbf {J}_{k+1}\Vert _{*}+\alpha \Vert \mathbf {U}_{k+1}\mathbf {K}_{B}-\mathbf {U}_{k+1}\mathbf {K}_{A}\mathbf {Z}_{k+1}\Vert _{2,1}\nonumber \\ & \quad +\,\beta tr(\mathbf {U}_{k+1}\mathbf {K}_{A}\mathbf {S}\mathbf {K}_{A}^{T}\mathbf {U}_{k+1}^{T}) +\frac{\mu _{k}}{2}\Vert \mathbf {Z}_{k+1}-\mathbf {J}_{k+1}\Vert _{F}^{2}+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}_{k+1}-\mathbf {J}_{k} \rangle. \end{aligned}$$

(17)

As the iteration proceeds, $\mu _{k}$ tends to be infinity. When $\mathbf {Z}=\mathbf {J}$, we obtain the optimal solution of model (11).

Next, we discuss the closed-form solution of the subproblem in Algorithm 3. The subproblem in step 2 can be reformulated as

$$\begin{aligned} \mathbf {J}_{k+1}={{\mathrm{argmin}}}\Vert \mathbf {J}\Vert _{*}+\frac{\mu _{k}}{2}\left\| \mathbf {J}-\left( \mathbf {Z}_{k}+\frac{\mathbf {\Lambda }_{k}}{\mu _{k}}\right) \right\| _{F}^{2}. \end{aligned}$$

(18)

Its optimal solution can be obtained by singular value thresholding (SVT) operator [2]. However, we do not find the optimal solution of the subproblem in step 1 and step 3. Fortunately, by means of special updating rule and the following formula:

$$\begin{aligned} \Vert \mathbf {E}\Vert _{2,1}=tr \left(\mathbf {E} \left( \begin{array}{cccc} \frac{1}{\Vert [\mathbf {E}]_{:1}\Vert _{2}} &{} 0 &{} \cdots &{} 0 \\ 0 &{} \frac{1}{\Vert [\mathbf {E}]_{:2}\Vert _{2}} &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} 0 \\ 0 &{} \cdots &{} 0 &{} \frac{1}{\Vert [\mathbf {E}]_{:n}\Vert _{2}} \\ \end{array} \right) \mathbf {E}^{T}\right), \end{aligned}$$

(19)

we can smooth these subproblems to obtain the approximate solutions. The details are in the following. With respect to the subproblem in step 1, we replace some $\mathbf {U}$ with $\mathbf {U}_{k}$ and change $\alpha$ into $\frac{\alpha }{2}$ in the $(k+1)$-th iteration. Then, it becomes

$$\begin{aligned} \mathbf {U}_{k+1}=&\mathop {{{\mathrm{argmin}}}}\limits _{\mathbf {U}\mathbf {K}\mathbf {U}^{T}=\mathbf {I}_{d}}\frac{\alpha }{2} tr(\mathbf {U}(\mathbf {K}-\mathbf {K}\mathbf {Z}_{k})\mathbf {F}_{k} (\mathbf {K}^{T}-\mathbf {Z}_{k}^{T}\mathbf {K}^{T})\mathbf {U}^{T})\\&+\beta tr(\mathbf {U}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}^{T}), \end{aligned}$$

(20)

where $\mathbf {F}_{k}=diag(\frac{1}{\Vert [\mathbf {\mathbf {U}_{k}\mathbf {K}-\mathbf {U}_{k}\mathbf {K}\mathbf {Z}_{k}}]_{:i}\Vert _{2}})$. The closed-form solution can be obtained by keeping the eigenvectors associated with the d smallest eigenvalues of the following generalized eigenvalue decomposition problem:

$$\begin{aligned} \left( \beta \mathbf {K}\mathbf {S}\mathbf {K}^{T}+\frac{\alpha }{2}(\mathbf {K}-\mathbf {K}\mathbf {Z}_{k})\mathbf {F}_{k} (\mathbf {K}-\mathbf {K}\mathbf {Z}_{k})^{T}\right) \mathbf {U}^{T}=\lambda \mathbf {K}\mathbf {U}^{T}. \end{aligned}$$

(21)

Similarly, with respect to the subproblem in step 3, we solve the following problem by replacing some $\mathbf {Z}$ with $\mathbf {Z}_{k}$ and changing $\alpha$ into $\frac{\alpha }{2}$ in the $(k+1)$-th iteration.

$$\begin{aligned} \mathbf {Z}_{k+1}= & {} {{\mathrm{argmin}}}\frac{\alpha }{2} tr\left( (\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z})\mathbf {G}_{k} (\mathbf {K}^{T}\mathbf {U}_{k+1}^{T}-\mathbf {Z}^{T}\mathbf {K}^{T}\mathbf {U}_{k+1}^{T})\right) \nonumber \\& \quad+\frac{\mu _{k}}{2}\Vert \mathbf {J}_{k+1}-\mathbf {Z}\Vert _{F}^{2}+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}-\mathbf {J}_{k+1} \rangle , \end{aligned}$$

(22)

where $\mathbf {G}_{k}=diag(\frac{1}{\Vert [\mathbf {\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}}]_{:i}\Vert _{2}})$. The i-th column of $\mathbf {Z}$ has the following closed-form solution

$$\begin{aligned} \left( \frac{\alpha \mathbf {K}^{T}\mathbf {U}_{k+1}^{T}\mathbf {U}_{k+1}\mathbf {K}}{\Vert [\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}]_{:i}\Vert _{2}}+\mu _{k}\mathbf {I}\right) ^{-1}\left( \mu _{k}[\mathbf {J}_{k+1}]_{:i}-[\mathbf {\Lambda }_{k}]_{:i} +\frac{\alpha \mathbf {K}^{T}\mathbf {U}_{k+1}^{T}\mathbf {U}_{k+1}[\mathbf {K}]_{:i}}{\Vert [\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}]_{:i}\Vert _{2}}\right) . \end{aligned}$$

(23)

Since each column of $\mathbf {Z}$ is separated, the computation of $\mathbf {Z}$ can be paralleled.

We can prove that our strategy can also make the augmented Lagrange function decreasing by the following theorems. This may be the reason that our algorithm always converges well in the extensive experiments. Similar to Algorithm 1, the computational complexity of this algorithm is also $O(n^3)$ when the computation of $\mathbf {Z}$ is paralleled.

Theorem 1

$\mathbf {\mathbf {U}_{k+1}}$ obtained by Eq. (21) satisfies inequality (15).

Theorem 2

$\mathbf {\mathbf {Z}_{k+1}}$ obtained by Eq. (23) satisfies inequality (17).

The proofs of these two theorems can be found in “Appendix”.

4 Experimental results

In this section, we evaluate the performance of our methods on synthetic data and five benchmark databases. Because our methods can be viewed as an extension of LRR, LRR and its extensions, e.g., LSR, LLRR, and SC-LRR, are selected to be compared in our experiment. In addition, since LS3C has the idea of learning a subspace for self-representation, we also compare LS3C and SSC in our experiment. In Sects. 4.2–4.6, clustering error, defined as the ratio of the number of the misclassified data points to the number of all the data points, is exploited as the evaluation metric. According to its definition, lower clustering error means better performance. In Sect. 4.7, we also report the performance of all the methods on another evaluation measure. We use the source codes provided by the original authors and tune important parameters of each compared method empirically to achieve the best result.

4.1 Synthetics data

In this section, we generate two spirals to test the performance on manifold clustering. As shown in Fig. 1a, the data points marked as triangle and circle are drawn from two nonlinear manifolds instead of linear subspaces, respectively. In this situation, the methods exploiting self-representation in the original space cannot extract the affinity well and thus will not obtain the right clustering results. As a representative, the result of LRR is provided in Fig. 1b, where the data points near the intersection are misclassified. Following the strategy often exploited in the experiment of previous work, we preprocess the data points by PCA for LRR. However, the data points drawn from the same spiral cannot be projected into one linear subspace by PCA, so LRR still achieves the wrong clustering result shown in Fig. 1c.

Fig. 1

The results of different methods on two spirals: a the original data. The data points marked as triangle and circle are drawn from two spirals, respectively. b The clustering result of LRR. c The clustering result of LRR by using PCA as a preprocessing step. d The clustering result of LS3C with the polynomial kernel. e The projected data points in the latent space of LS3C with the kernel in Eq. (24). f The clustering result of LS3C with the kernel in Eq. (24). g The transformed data points in the learned subspace of our method with the kernel constructed in Eq. (24). h The clustering result of our method with the kernel constructed in Eq. (24). i The clustering result of our method with the kernel in Eq. (24) and the criterion of PCA on the learned subspace

Since LS3C has the idea of learning a subspace for self-representation extracting the affinity, we test its performance on this synthetic data. As shown in Fig. 1d, by means of the polynomial kernel frequently used in its experiment, LS3C cannot achieve the right clustering result. Hence, we construct a kernel for LS3C in the following:

$$\begin{aligned} {[}\mathbf {K}]_{ij}=\exp \left( -\frac{1-({\hat{\mathbf{y}}}_{i}^{T}{\hat{\mathbf{y}}}_{j})^{2}}{\sigma ^{2}}\right) , \end{aligned}$$

(24)

where ${\hat{\mathbf{y}}}_{i}=\frac{\mathbf {y}_{i}}{\Vert \mathbf {y}_{i}\Vert _{2}}, i=1,\ldots ,N$, $\sigma ^{2}$ is empirically set as $\frac{\sum _{i,j}(1-({\hat{\mathbf{y}}}_{i}^{T}{\hat{\mathbf{y}}}_{j})^{2})}{N^{2}}$. $\mathbf {Y}=[\mathbf {y}_{1},\ldots ,\mathbf {y}_{i},\ldots ,\mathbf {y}_{n}]$ is constructed as follows

$$\begin{aligned} \mathbf {Y}=\mathbf {M}\odot \mathbf {Q}, \end{aligned}$$

(25)

where $\mathbf {Q}$ is similar to $\mathbf {K}$ in Eq. (24) by replacing $\mathbf {y}_{i}$ with $\mathbf {x}_{i}$, $\mathbf {M}$ is the binary matrix

$$\begin{aligned} {[}\mathbf {M}]_{ij}=\bigg \{ \begin{array}{ll} 1 & \quad \mathbf {x}_{i}\in \mathcal {D}(\mathbf {x}_{j}) \quad \hbox{or} \quad \mathbf {x}_{j}\in \mathcal {D}(\mathbf {x}_{i}) \\ 0 & \quad {\text {otherwise}} \\ \end{array}, \end{aligned}$$

(26)

where $\mathcal {D}(\mathbf {x}_{i})$ denotes the k-nearest neighbors of $\mathbf {x}_{j}$ measured by Euclidean distance.

The construction of $\mathbf {K}$ is inspired by the work [37]. Referring to its analysis, $[\mathbf {K}]_{ij}$ represents the angle between the ${\hat{\mathbf{y}}}_{i}$ and ${\hat{\mathbf{y}}}_{j}$ transformed by the Veronese map of degree 2, which can transform some disjoint but not independent subspaces into independent subspaces. Since independent subspace clustering is an easier task than disjoint subspace clustering [32], the $\mathbf {K}$ can improve the result for subspace clustering. Our idea is applying the transformed data points approximately with the structure of multiple subspaces for $\mathbf {K}$. Hence, we construct $\mathbf {Y}$ which can be viewed as the transformed data points. In order to enable $\mathbf {Y}$ to approximately have the appreciated structure, we try to let the transformed data points drawn from the same spiral have small angles between them. Both the local information collected in $\mathbf {M}$ and the angle measure represented by $\mathbf {Q}$ are integrated to achieve this aim. Although we deliberately devise the kernel for LS3C, it does not achieve the right clustering result, too. The reason may be that its penalty on the learned subspace does not favor the self-representation extracting the affinity. Figure 1e shows the transformed data points in the latent space by setting its dimensionality as 2. Since these projected data points do not have the structure of multiple subspaces, LS3C yields the wrong clustering result shown in Fig. 1f.

In the last, we try the $\mathbf {K}$ in Eq. (24) for our method on this synthetic data by setting the dimensionality of the learned subspace as 2. It can be seen from Fig. 1h that our method can achieve the right clustering result. The transformed data points in the learned subspace are shown in Fig. 1g where the data points drawn from the same spiral are projected into one line. This result indicates that our method can learn a subspace favoring the self-representation to extract affinity and thus performs well. Moreover, we apply the criterion of PCA on the learned subspace to our method and then provide the result in Fig. 1i, where our method does not perform well. This result implies the importance of the penalty on the learned subspace.

4.2 Extended Yale B

The Extended Yale [14] database includes 2432 frontal face images of 38 subjects. Each subject has 64 images under varying illumination conditions. For a Lambertian object, it has been shown that the set of all images taken under all lighting conditions forms a cone in the image space, which can be well approximated by a low-dimensional subspace [9]. Hence, the images of different subjects in the Extended Yale B are usually used as a benchmark for subspace clustering. In this experiment, we choose the kernel defined in Eq. (24) by replacing $\mathbf {y}_{i}$ with the original data points. We make two comparisons by selecting the first 20 images of the first 20 subjects and all the 38 subjects. The selected images are all resized as $48 \times 42$. The experimental results are shown in Table 2, where the second row and the third row report the clustering error on 20 and 38 subjects, respectively. It can be found that our methods outperform the state of the art. RSLLRR always achieves better results than SLLRR. LRR and its extensions achieve low clustering error than SSC and its extensions. In this experiment, the subspace number is at least 20. The reason may be that the sparse affinity matrix can easily result in over-segmentation in this case [26].

Table 2 Clustering errors of all the compared methods on Extended Yale B

4.3 CMU PIE

We choose another face database to compare these methods on the linear case of manifold clustering. Hence, we also select the kernel defined in Eq. (24) by replacing $\mathbf {y}_{i}$ with the original data points. The CMU PIE [31] database contains more than 40,000 facial images of 68 subjects under different poses, illumination conditions, and facial expressions. We conduct two experiments by selecting 40 images of the first 10 and 20 subjects to test the performance of all the compared methods. The size of the images in this experiment is $32 \times 32$. The clustering errors of all the compared methods on 10 and 20 subjects are shown in the second row and third row of Table 3, respectively. It can be found that our methods also outperform the state of the art.

Table 3 Clustering errors of all the compared methods on CMU PIE

4.4 COIL 20

In this part, we test the performance of all the compared methods on the nonlinear case of manifold clustering. Following the work [47], we choose COIL 20 [27] database to achieve this aim. The COIL 20 database consists of 1440 grayscale images of 20 objects. These images are acquired by a fixed camera capturing the rotated objects every 5${^{\circ }}$. Hence, each object has 72 images. The processed version of COIL 20 is used in our experiment. In this version, the size of the image is $128\times 128$ and the background has been discarded. We extract the spatial pyramid bag of words (SPBOW) [13] by setting the size of the dictionary at 80 and explore these descriptors as the original data points. With respect to the kernel methods, the Gaussian kernel with the Euclidean distance is exploited. Due to the effectiveness of SPBOW, the results in Table 4 are much better than those in Table 3 of the reference [47]. It can be found from Table 4 that our methods achieve better results.

Table 4 Clustering errors of all the compared methods on COIL-20

4.5 Caltech 101

Caltech 101 [16] database includes the color images of 101 objects. With respect to each object, the image number usually locates in the range [40, 800] and the image size is usually different. Different from the images used in COIL 20, several images contain both the object and the background. The images of the following ten objects: camera, dollar bill, inline-skate, pagoda, panda, pizza, starfish, wrench, and yin-yang are collected to make the comparison. We also extract SPBOW and then use the descriptors and Gaussian kernel with the Chi-square distance, but set the dictionary size at 100. With respect to the subspace clustering methods learning the affinity matrix by self-representation in the original space, this experiment is very challenging. LS3C learns a subspace to make the self-representation, but the PCA does not favor affinity extraction. Table 5 reports the clustering errors of all the compared methods. It can be found that our methods achieve a great improvement.

Table 5 Clustering errors of all the compared methods on Caltech 101

4.6 USC SIPI

USC SIPI¹ database is comprised of the $128\times 128$ grayscale texture images in 13 categories. Each kind of textures includes 112 images under the view of 0${^{\circ }}$, 30${^{\circ }}$, 60${^{\circ }}$, 90${^{\circ }}$, 120${^{\circ }}$, 180${^{\circ }}$, and 210${^{\circ }}$. We collect the first 8 images under each view of all the textures to compare the state of the art. There are 728 images in total. We extract the rotation invariant local binary pattern (LBP) on the $3\times 3$ grid as the original data points. The kernel is also selected as the Gaussian kernel with the Chi-square distance. The clustering errors of all the compared methods on USC SIPI are reported in Table 6, where our methods perform better than the state of the art. This result further confirms the effectiveness of our method.

Table 6 Clustering errors of all the compared methods on USC SIPI

4.7 More discussions

In this subsection, we make more discussions on the experiment. First, we evaluate all the compared methods by the adjusted Rand index in Table 7. Note that, the higher value indicates better performance for this measure. It can be found that our methods usually achieve better results than other methods. Second, we test the sensitivity of the parameter k in Eq. 3. Figures 2 and 3 illustrate the results on USC SIPL and Caltech 101, respectively. Although our results fluctuate with the change of k, our performance is usually better than that of the compared methods.

Table 7 The adjusted Rand index of all the compared methods

Fig. 2

a Clustering error curves of our methods versus k on USC SIPL. b The adjusted Rand index curves of our methods versus k on USC SIPL

Fig. 3

a Clustering error curves of our methods versus k on Caltech 101. b The adjusted Rand index curves of our methods versus k on Caltech 101

5 Conclusion and future works

In this paper, we extend the popular subspace clustering method LRR by proposing the method learning a subspace for self-representation extracting the affinity between the data points. After learning a nonlinear subspace, our method can handle the nonlinear manifold clustering. We construct the penalty on the learned subspace and enforce the $\ell _{2,1}$-norm on the noise successfully in our model. Extensive experimental results verify the effectiveness of our method on manifold clustering. Furthermore, the experiment indicates that the manifold clustering methods have great potential on the data analysis. They can handle the data with the nonlinear structure such as Caltech 101 by exploiting the features and special metric to construct the kernel. Because the features can be viewed as the nonlinear transformation of the dataset, developing effective features can contribute to the wide application of the manifold clustering methods. In recent years, the deep learning has achieved many fruitful results, as done in [28, 49]. We expect the combining of our methods and deep learning features for more applications.

Appendix

Proof

(Proof of Theorem 1) Because $\mathbf {\mathbf {U}_{k+1}}$ in Eq. (21) is the optimal solution of the problem Eq. (20), we can obtain

$$\begin{aligned}&\frac{\alpha }{2} tr(\mathbf {U}_{k+1}(\mathbf {K}-\mathbf {K}\mathbf {Z}_{k})\mathbf {F}_{k} (\mathbf {K}^{T}-\mathbf {Z}_{k}^{T}\mathbf {K}^{T})\mathbf {U}^{T}_{k+1})+\beta tr(\mathbf {U}_{k+1}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}^{T}_{k+1}) \nonumber \\&\quad \le \frac{\alpha }{2} tr(\mathbf {U}_{k}(\mathbf {K}-\mathbf {K}\mathbf {Z}_{k})\mathbf {F}_{k} (\mathbf {K}^{T}-\mathbf {Z}_{k}^{T}\mathbf {K}^{T})\mathbf {U}^{T}_{k})+\beta tr(\mathbf {U}_{k}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}^{T}_{k})\nonumber \\&\quad =\frac{\alpha }{2} \Vert \mathbf {U}_{k}\mathbf {K}-\mathbf {U}_{k}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1}+\beta tr(\mathbf {U}_{k}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}^{T}_{k}). \end{aligned}$$

(27)

With respect to $a>0,b>0$, we can obtain

$$\begin{aligned} \frac{b}{2}\ge a-\frac{a^{2}}{2b}. \end{aligned}$$

(28)

Hence, with respect to each $j=1,\ldots ,n$

$$\begin{aligned} \begin{array}{c} \frac{\Vert [\mathbf {U}_{k}\mathbf {K}-\mathbf {U}_{k}\mathbf {K}\mathbf {Z}_{k}]_{:j}\Vert _{2}}{2} \ge \Vert [\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}]_{:j}\Vert _{2}-\frac{\Vert [\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}]_{:j}\Vert _{2}^{2}}{2\Vert [\mathbf {U}_{k}\mathbf {K}-\mathbf {U}_{k}\mathbf {K}\mathbf {Z}_{k}]_{:j}\Vert _{2}}. \end{array} \end{aligned}$$

(29)

Computing the sum with respect to all j, we can obtain

$$\begin{aligned} \begin{array}{c} \frac{1}{2}\Vert \mathbf {U}_{k}\mathbf {K}-\mathbf {U}_{k}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1}\ge \Vert \mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1}\\ -\frac{1}{2}tr(\mathbf {U}_{k+1}(\mathbf {K}-\mathbf {K}\mathbf {Z}_{k})\mathbf {F}_{k} (\mathbf {K}^{T}-\mathbf {Z}_{k}^{T}\mathbf {K}^{T})\mathbf {U}^{T}_{k+1}). \end{array} \end{aligned}$$

(30)

By means of inequalities (30) and (27), we can obtain

$$\begin{aligned} L_{k,1}\le & {} \Vert \mathbf {J}_{k}\Vert _{*} +\beta tr\left( \mathbf {U}_{k+1}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}_{k+1}^{T}\right) +\frac{\mu _{k}}{2}\Vert \mathbf {Z}_{k}-\mathbf {J}_{k}\Vert _{F}^{2}+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}_{k}-\mathbf {J}_{k} \rangle \nonumber \\&+\alpha \left( \frac{1}{2}\Vert \mathbf {U}_{k}\mathbf {K}-\mathbf {U}_{k}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1}+\frac{1}{2}tr(\mathbf {U}_{k+1}(\mathbf {K}-\mathbf {K}\mathbf {Z}_{k})\mathbf {F}_{k} (\mathbf {K}^{T}-\mathbf {Z}_{k}^{T}\mathbf {K}^{T})\mathbf {U}^{T}_{k+1}\right) \nonumber \\\le & {} \Vert \mathbf {J}_{k}\Vert _{*}+\beta tr(\mathbf {U}_{k}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}_{k}^{T})+\frac{\mu _{k}}{2}\Vert \mathbf {Z}_{k}-\mathbf {J}_{k}\Vert _{F}^{2}+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}_{k}-\mathbf {J}_{k} \rangle \nonumber \\&+\frac{\alpha }{2} \Vert \mathbf {U}_{k}\mathbf {K}-\mathbf {U}_{k}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1}+ \frac{\alpha }{2} \Vert \mathbf {U}_{k}\mathbf {K}-\mathbf {U}_{k}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1} =L_{k,0}. \end{aligned}$$

(31)

$\square$

Proof

(Proof of Theorem 2) Because $\mathbf {\mathbf {Z}_{k+1}}$ in Eq. (23) is the optimal solution of the problem Eq. (22), we can obtain

$$\begin{aligned}&\frac{\alpha }{2} tr((\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k+1})\mathbf {G}_{k} (\mathbf {K}^{T}\mathbf {U}_{k+1}^{T}-\mathbf {Z}_{k+1}^{T}\mathbf {K}^{T}\mathbf {U}_{k+1}^{T}))\nonumber \\&\qquad +\frac{\mu _{k}}{2}\Vert \mathbf {J}_{k+1}-\mathbf {Z}_{k+1}\Vert _{F}^{2}+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}_{k+1}-\mathbf {J}_{k+1} \rangle \nonumber \\&\quad \le \frac{\alpha }{2} tr((\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k})\mathbf {G}_{k} (\mathbf {K}^{T}\mathbf {U}_{k+1}^{T}-\mathbf {Z}_{k}^{T}\mathbf {K}^{T}\mathbf {U}_{k+1}^{T}))\nonumber \\&\qquad +\frac{\mu _{k}}{2}\Vert \mathbf {J}_{k+1}-\mathbf {Z}_{k}\Vert _{F}^{2}+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}_{k}-\mathbf {J}_{k+1} \rangle \nonumber \\&\quad =\frac{\alpha }{2}\Vert \mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1} +\frac{\mu _{k}}{2}\Vert \mathbf {J}_{k+1}-\mathbf {Z}_{k}\Vert _{F}^{2}+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}_{k}-\mathbf {J}_{k+1} \rangle . \end{aligned}$$

(32)

With respect to $a>0,b>0$, we can obtain

$$\begin{aligned} \frac{b}{2}\ge a-\frac{a^{2}}{2b}. \end{aligned}$$

(33)

Hence, with respect to each $j=1,\ldots ,n$

$$\begin{aligned} \begin{array}{c} \frac{\Vert [\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}]_{:j}\Vert _{2}}{2} \ge \Vert [\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k+1}]_{:j}\Vert _{2}-\frac{\Vert [\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k+1}]_{:j}\Vert _{2}^{2}}{2\Vert [\mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}]_{:j}\Vert _{2}}. \end{array} \end{aligned}$$

(34)

Computing the sum with respect to all j, we can obtain

$$\begin{aligned} \begin{array}{c} \frac{1}{2}\Vert \mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1}\ge \Vert \mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k+1}\Vert _{2,1} \\ -\frac{1}{2}tr((\mathbf {U}_{k+1}(\mathbf {K}-\mathbf {K}\mathbf {Z}_{k+1})\mathbf {G}_{k} (\mathbf {K}^{T}-\mathbf {Z}^{T}_{k+1}\mathbf {K}^{T})\mathbf {U}_{k+1}^{T}). \end{array} \end{aligned}$$

(35)

By means of inequalities (35) and (32), we can obtain

$$\begin{aligned} L_{k,3}\le & {} \Vert \mathbf {J}_{k+1}\Vert _{*}+ \beta tr(\mathbf {U}_{k+1}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}_{k+1}^{T}) +\frac{\mu _{k}}{2}\Vert \mathbf {Z}_{k+1}-\mathbf {J}_{k+1}\Vert _{F}^{2}\nonumber \\&+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}_{k+1}-\mathbf {J}_{k} \rangle +\alpha \left(\frac{1}{2}\Vert \mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1} \right.\nonumber \\&\left.+\frac{1}{2}tr(\mathbf {U}_{k+1}(\mathbf {K}-\mathbf {K}\mathbf {Z}_{k+1})\mathbf {G}_{k} (\mathbf {K}^{T}-\mathbf {Z}^{T}_{k+1}\mathbf {K}^{T})\mathbf {U}_{k+1}^{T})\right) \le \Vert \mathbf {J}_{k+1}\Vert _{*}\nonumber \\&+\beta tr(\mathbf {U}_{k+1}\mathbf {K}\mathbf {S}\mathbf {K}^{T}\mathbf {U}_{k+1}^{T})+\frac{\mu _{k}}{2}\Vert \mathbf {Z}_{k}-\mathbf {J}_{k+1}\Vert _{F}^{2}+\langle \mathbf {\Lambda }_{k}, \mathbf {Z}_{k}-\mathbf {J}_{k} \rangle \nonumber \\&+\frac{\alpha }{2}\Vert \mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1}+\frac{\alpha }{2}\Vert \mathbf {U}_{k+1}\mathbf {K}-\mathbf {U}_{k+1}\mathbf {K}\mathbf {Z}_{k}\Vert _{2,1} = L_{k,2}. \end{aligned}$$

(36)

□