A novel support vector regression algorithm incorporated with prior knowledge and error compensation for small datasets

Abstract

To solve the modeling problem under the conditions where the measured data are insufficient but biased prior knowledge from a simulator is available, we propose a novel multi-scale $\nu$-linear programming support vector regression ($\nu$-LPSVR) called $\nu$-MPESVR. The proposed algorithm constructs a nested support vector regression model, which incorporates prior knowledge into $\nu$-LPSVR, compensates for the errors between prior knowledge data and the measured data, and simultaneously achieves small training error for both the prediction model and the error compensation model. Considering that measured data may exist in multiple feature spaces, we extend the algorithm to multi-scale $\nu$-LPSVR to achieve accurate modeling for complex problems. In addition, a strategy for parameter selection for $\nu$-MPESVR is presented in this paper. The performance of the proposed algorithm is estimated in a synthetic example and a practical application. The performances of all models are evaluated with the root mean square error (RMSE), mean absolute error (MAE), and coefficient of determination (R2). Taking the three groups of experiments in the synthetic example as an instance, we find that the $\nu$-MPESVR performs better, and it can still maintain high accuracy when the biases of prior knowledge data change (RMSE values of 0.1962, 0.1904, and 0.2261, MAE values of 0.1396, 0.1375, and 0.1623, and R2 values of 0.9919, 0.9923, and 0.9892 for the three groups of experiments, respectively). The experimental results indicate that the proposed algorithm can obtain a satisfactory model with a finite amount of measured data, and the performance is better than that of existing algorithms.

1 Introduction

Support vector regression (SVR) is based on the theory of structure risk minimization in statistical learning, which has been proven to provide excellent performance in various applications [25, 26]. In general, the sequential minimal optimization method [21] is used to solve quadratic programming problems in support vector regression (QPSVR) [25]. In order to minimize the tube parameter $\varepsilon$ automatically, Smola [23] incorporated parameter $\nu$ into the optimization objective ($\nu$-SVR) and proposed $\nu$-linear programming support vector regression ($\nu$-LPSVR) to solve the optimization problem fast and easily, and to enforce sparseness in the solution [24]. All of the above algorithms compute a nonlinear estimate in terms of kernel functions. In addition, $\nu$-LPSVR is robust to local perturbations of the training set’s target values [24], can use more general kernel functions flexibly, and offers higher calculation efficiency [14, 15].

In nonlinear mapping function estimation, $\nu$-LPSVR has proven to be able to adapt accuracy $\varepsilon$ to the noise level in the data automatically, and to provide excellent performance in various applications based on sufficient training data [24]. However, in some practical applications, such as performance prediction of small-batch aerospace components, the production of these parts is small, and the measuring methods are extremely limited and expensive [27, 30]. This leads to scarcity in measured data samples. For this reason, the accuracy and generalization performance of the model obtained with these measured data cannot meet the requirements. Moreover, a certain type and amount of prior knowledge, as with mathematical model or simulation model, is generally available. Although these models may not fully consider all the actual conditions and input characteristics, and the output results may be biased, prior models can still approximately build the main part of the real model. Consequently, obtaining an accurate model with only a few training samples and prior knowledge is the key issue in applying artificial intelligence technology to the industrial field.

In related works, a literature review of incorporating prior knowledge into SVC was presented in [10]. Prior knowledge was defined as knowledge about class-invariance and knowledge about data. Methods for incorporating prior knowledge into SVC were classified into three categories: sample methods, kernel methods, and optimization methods. In [9], the author introduced equality and inequality constraints to the SVR optimization problem by utilizing prior knowledge of particular points, derivatives, prior models, and the correlation between outputs. Considering that prior knowledge provided by simulators or prior models may be biased, Bloch [3] incorporated a vector $\nu$ of positive slack variables bounding the error on this knowledge, and the author also showed the importance of adding potential support vectors of knowledge samples to the model. In [5], Chen built a new feature according to prior distribution knowledge of data to improve the accuracy of prediction. Tahir [7] proposed a kernel function construction method based on prior knowledge and Green’s kernel. Because many complex functions comprise both steep and smooth variations [31], Zhou [32, 33] proposed a LPSVR incorporated with prior knowledge, and extended it to multiple kernel LPSVR. In addition, Zhang [28] incorporated prior knowledge into SVM with sample confidence and used weighted features to express prior knowledge. However, all the aforementioned methods are based on unbiased prior knowledge or only contain small noise error, which is inaccurate in the actual applications.

In reality, biases between prior knowledge data and measured data not only contain noise error but also the deviation caused by coupling features, other unknown properties, and the correlation between some factors is not considered in the simulator. An accurate data-driven model cannot be easily obtained by just incorporating positive slack variables to bound errors without the correction of the biased prior knowledge. In addition, the mapping function in practical applications may contain uneven distributions in high-dimensional feature spaces, and the express ability of the decision function could be improved by using the multi-scale kernel method. Compared with other multiple kernel methods, the multi-scale kernel method is more flexible and can provide a more complete scale selection.

To solve the above problem, we propose a multi-scale $\nu$-LPSVR algorithm incorporated with prior knowledge and error compensation ($\nu$-MPESVR). We first incorporate the prior knowledge data, which may be biased from the measured data into the $\nu$-LPSVR by modifying and adding the inequality constraints ($\nu$-PSVR). By setting the appropriate punishment coefficients of the slack variables in the objective function, we can adjust the tolerance of the decision function on the error in both the measured data and the prior data. Subsequently, we construct the error compensation model based on measured data and corresponding prior data. The two sets of data have the same input, but the former is the measured output and the latter is the output of the simulator. In order to improve the generalization ability of the obtained model, we incorporate the error compensation model into the $\nu$-PSVR to make it part of the $\nu$-PSVR optimization problem. In consequence, the goal is to achieve a small training error in both the error compensation model and the $\nu$-PSVR simultaneously; thus, we call it $\nu$-PESVR. Finally, multi-scale feature spaces have been utilized by incorporating multi-scale kernel functions into the $\nu$-PESVR to adapt to the multi-scale characteristic of the data. In addition, to find the global optimum or a good approximation with high probability [13], we use the chaotic particle swarm algorithm to find the optimal parameters for the model.

The rest of the paper is organized as follows. Section 2 introduces $\nu$-LPSVR briefly. The proposed $\nu$-MPESVR algorithm incorporated with compensated prior knowledge data and multi-scale kernel functions is described in Sect. 3. In Sect. 4, numerical experiments are performed on a synthetic example and a practical application. Finally, we conclude our work in Sect. 5.

In this study, all the vectors are assumed to be column vectors. Lowercase symbols like $x_{ij},y$ refer to scalars, lowercase bold symbols like $\varvec{x},\varvec{\alpha }$ refer to vectors, and uppercase bold symbols like $\varvec{K},\varvec{G}$ refer to matrices. For any two matrices $\varvec{A}$ and $\varvec{B}$, the scalar or matrix $\varvec{A}^{\mathrm{T}}\cdot \varvec{B}$ is the inner product of the matrices, where $\varvec{A}^{\mathrm{T}}$ denotes the transpose of $\varvec{A}$. For $x,y\in R^{d}$, $\varvec{X}\in R^{d\times m}$, and $\varvec{Y}\in R^{d\times n}$, the kernel function $k(\varvec{x},\varvec{y})$ is a scalar, and the kernel matrix $\varvec{K}(\varvec{X},\varvec{Y})$ is an $R^{m\times n}$ matrix that maps $R^{d\times m} \times R^{d\times n}$ into $R^{m\times n}$. The identity matrix is denoted by $\varvec{E}$, and $\varvec{0}$ is a matrix of appropriate dimensions with all components equal to 0.

2 Review of $\nu$-LPSVR

Given a dataset $\{(\varvec{x_i}, y_i), i=1,2,3,\ldots ,N\}$, where $\varvec{x_i}\in R^d$ denotes the d-dimension input vector, $y_i\in R$ denotes the real-valued output, i is the i-th training sample, and N is the number of training samples. The regression task amounts to finding a linear function in the feature space by using the kernel trick. The estimate equation can be described as follows:

$$ y_i=f(\varvec{x_i})=\varvec{\omega }\cdot \varvec{\phi }(\varvec{x_i})+b $$

(1)

where $\varvec{\omega }$ is the normal vector, b is a bias term, and $\varvec{\phi }(\varvec{x})$ is a nonlinear mapping function [18,19,20].

Because the normal vector $\varvec{\omega }$ can be considered a linear combination of the training patterns by using the dual representation, i.e., $\varvec{\omega }=\sum _{j=1}^N (\alpha _j-\alpha _j^*) \cdot \varvec{\phi }(\varvec{x_j})$, one can obtain the following kernel expansion of the regression function as

$$ y_i=f(\varvec{x_i})=\sum _{j=1}^N \big (\alpha _j-\alpha _j^*\big ) k\big (\varvec{x_j},\varvec{x_i}\big )+b $$

(2)

where $k(\varvec{x_j},\varvec{x_i})=\varvec{\phi }(\varvec{x_j}) \cdot \varvec{\phi }(\varvec{x_i})$ is the kernel function; Gaussian kernel and wavelet kernel are the two most widely used kernel functions in practical engineering [17]. Moreover, as for LPSVR, the non-Mercer kernel is available [14].

Unlike the standard SVR, which uses $\frac{1}{2}\Vert \varvec{\omega }\Vert ^2$ to make the function as flat as possible, LPSVR seeks a $\varvec{\omega }$ that can be represented as the smallest combination of training patterns by using the coefficient parameter $\varvec{\alpha }^{(*)}$, so it minimizes

$$ \min \sum _{i=1}^N (\alpha _i+\alpha _i^*) +C \sum _{i=1}^N L(y_i-f(\varvec{x_i})) $$

(3)

where the first term determines the complexity of the model, and the penalty parameter C > 0 is introduced to tune the trade-off between the error minimization and the maximization of the function flatness. $L(y_i - f(\varvec{x_i}))$ refers to the $\varepsilon$-insensitive loss function as follows, and it penalizes any deviations larger than the precision $\varepsilon$ for all the training data.

$$\begin{aligned} L(y_i-f(\varvec{x_i}))=\left\{ \begin{array}{ll} 0 &{} \quad {|y_i-f(\varvec{x_i})|\le \varepsilon } \\ |y_i-f(\varvec{x_i})|-\varepsilon &{}\quad {\text {otherwise}} \end{array} \right. \end{aligned}$$

(4)

By introducing slack variables $\varvec{\xi _i},\varvec{\xi _i}^* \ge 0$ for each sample point $(\varvec{x_i},y_i)$, and using an $\varepsilon$-insensitive loss function, the LPSVR can be formulated as

$$\begin{aligned} {\mathrm{find}} \quad&\varvec{\alpha }^{(*)},\varvec{\xi }^{(*)},b\\ {\mathrm{min}} \quad&\sum _{i=1}^N (\alpha _i+\alpha _i^*)+C \sum _{i=1}^N (\xi _i+\xi _i^*) \\ {\mathrm{s.t.}}\quad&\alpha _i^{(*)},\xi _i^{(*)}\ge 0 \\&\sum _{i=1}^N(\alpha _i-\alpha _i^*)k(\varvec{x_i},\varvec{x_j})+b-y_i\le \varepsilon +\xi _i \\&y_i-\sum _{i=1}^N(\alpha _i-\alpha _i^*)k(\varvec{x_i},\varvec{x_j})-b\le \varepsilon +\xi _i^* \end{aligned} $$

(5)

Here (*) is shorthand referring to both the variables with and without asterisks. In order to overcome problems with $|\alpha _i|$ in the objective function, $\alpha _i$ is substituted by the two positive variables $\alpha _i$ and $\alpha _i^*$ [24]. By solving the coefficient parameter $\varvec{\alpha }^{(*)}$ in Eq. (5), the decision function Eq. (2) can be expressed as

$$ y_i=f(\varvec{x_i})=\sum _{j=1}^N \big (\alpha _j-\alpha _j^*\big )k\big (\varvec{x_j},\varvec{x_i}\big )+b $$

(6)

The tube width parameter $\varepsilon$ determines the number of support vectors and errors in the model, which means that we must choose the optimal $\varepsilon$ to ensure the accuracy of the data-driven model. For this reason, Bernhard [23] achieved automatic accuracy control by making the parameter $\varepsilon$ part of the optimization problem. As a consequence, we obtain a solution with small training error and small $\varepsilon$ by rewriting Eq. (5) as

$$\begin{aligned} {\mathrm{find}} \quad&\varvec{\alpha }^{(*)},\varvec{\xi }^{(*)},\varepsilon ,b\\ {\mathrm{min}} \quad&\frac{1}{N}\sum _{i=1}^N (\alpha _i+\alpha _i^*)+\frac{C}{N} \sum _{i=1}^N (\xi _i+\xi _i^*)+C\nu \varepsilon \\ {\mathrm{s.t.}}\quad&\alpha _i^{(*)},\xi _i^{(*)},\varepsilon \ge 0 \\&\sum _{i=1}^N(\alpha _i-\alpha _i^*)k(\varvec{x_i},\varvec{x_j})+b-y_j\le \varepsilon +\xi _j \\&y_j-\sum _{i=1}^N(\alpha _i-\alpha _i^*)k(\varvec{x_i},\varvec{x_j})-b\le \varepsilon +\xi _j^* \end{aligned} $$

(7)

where $\nu \in (0,1]$ is an upper bound on the fraction of training errors and a lower bound of the fraction of support vectors. In addition, with probability 1, $\nu$ asymptotically equals both the fraction of SVs and the fraction of margin errors [4], and the decision function of the $\nu$-LPSVR is the same as Eq. (6).

3 Proposed algorithm

In this section, to improve the prediction performance of the regression model developed with insufficient measured data and biased prior knowledge data, a novel constrained optimization-based multi-scale $\nu$-LPSVR algorithm implemented with prior knowledge and error compensation is proposed.

3.1 Incorporating prior knowledge into $\nu$-LPSVR

In this work, prior knowledge is defined as the samples generated by the mathematical models or the simulation models, which are called the prior knowledge dataset.

Consider a prior knowledge dataset $S_p=\{(\varvec{x_k^p},y_k^p),k=1,2,3,\ldots ,N_p\}$ and a measured dataset $S_r=\{(\varvec{x_t^r},y_t^r),t=1,2,$$3,\ldots ,N_r\}$, where $\varvec{x_k^p},\varvec{x_t^r} \in R^d$ are the d-dimension prior knowledge input vector and measured input vector, $y_k^p,y_t^r \in R$ are the corresponding target output, and $N_p,N_r$ are the number of prior knowledge samples and measured samples, respectively. It is obvious that prior knowledge samples satisfy the mapping relationship constructed in the simulator

$$ y_k^p=T\big (\varvec{x_k^p}\big )\qquad (k=1,2,3\ldots ,N_p) $$

(8)

When prior knowledge is absolutely accurate, we would like the model to yield an exact value for these prior points rather than an approximation. The solution to this problem is to impose hard constraints on these prior points, such as

$$ y_k^p=f\big (\varvec{x_k^p}\big )=\sum _{j=1}^N \big (\alpha _j-\alpha _j^*\big )k\big (\varvec{x_j},\varvec{x_k^p}\big )+b $$

(9)

However, in practical engineering, prior knowledge is always biased, and the equality constraints will lead to an exact fit to the prior points, which may not be advised. All these constraints may result in unsolvable problems if they cannot be satisfied simultaneously [3]. To manage this situation, we change the hard constraints to soft constraints by introducing the positive slack variable $\varvec{u}^{(*)}=[u_1^{(*)},u_2^{(*)},u_3^{(*)},$$\ldots ,u_{N_p}^{(*)}]$ in constraints to bound the upper and lower deviations between the prior data $(\varvec{x^p},y^p)$ and the regression function $f(\varvec{x^p})$. Moreover, in order to include almost exact or biased prior knowledge, we use the $\varepsilon$-insensitive loss function (4) on the prior knowledge errors $\varvec{u}^{(*)}$ with threshold $\varepsilon _p$ to authorize violations of the equality constraints (9). Therefore, by applying the $\varepsilon$-insensitive loss function to the positive slack variables $\varvec{u}^{(*)}$, we can obtain the following inequality constraints

$$\begin{aligned} -\varepsilon _p -u_k^*\le y_k^p-f\big (\varvec{x_k^p}\big )\le \varepsilon _p +u_k \quad (k=1,2,3,\ldots ,N_p) \end{aligned}$$

(10)

The $l_1$-norm of the slack vectors $\varvec{u}^{(*)}$ is incorporated into the objective function of Eq. (7) with a trade-off parameter $C_p$ to minimize the error $\varvec{u}^{(*)}$, and the trade-off parameter $C_p$ allows for tuning the influence of the prior data on the regression function. In addition, like $\nu$-LPSVR , we make $\varepsilon _p$ part of the objective function with the parameter $\nu _p$ to tune $\varepsilon _p$ automatically. By consequence, approximate prior knowledge is incorporated by modifying the optimization problem (7). The modified algorithm, called $\nu$-PSVR, is expressed as

$$\begin{aligned} {\mathrm{find}}\quad&\varvec{\alpha }^{(*)},\varvec{\xi }^{(*)},\varvec{u}^{(*)},\varepsilon _r,\varepsilon _p,b\\ {\mathrm{min}}\quad&\frac{1}{N}\sum _{i=1}^{N}(\alpha _i+\alpha _i^*)+\frac{C_r}{N_r} \sum _{t=1}^{N_r} (\xi _t+\xi _t^*)\\&+\frac{C_p}{N_p}\sum _{k=1}^{N_p} (u_k+u_k^*)+C_r\nu _r\varepsilon _r+C_p\nu _p\varepsilon _p \\ {\mathrm{s.t.}}\quad&\alpha _i^{(*)},\xi _t^{(*)},u_k^{(*)},\varepsilon _r,\varepsilon _p\ge 0 \\&\sum _{i=1}^{N}(\alpha _i-\alpha _i^*)k\big (\varvec{x_i},\varvec{x_t^r}\big )+b-y_t^r\le \varepsilon _r+\xi _t \\&y_t^r-\sum _{i=1}^{N}(\alpha _i-\alpha _i^*)k\big (\varvec{x_i},\varvec{x_t^r}\big )-b\le \varepsilon _r+\xi _t^*\\&\sum _{i=1}^{N}(\alpha _i-\alpha _i^*)k\big (\varvec{x_i},\varvec{x_k^p}\big )+b-y_k^p\le \varepsilon _p+u_k \\&y_k^p-\sum _{i=1}^{N}(\alpha _i-\alpha _i^*)k\big (\varvec{x_i},\varvec{x_k^p}\big )-b\le \varepsilon _p+u_k^* \end{aligned} $$

(11)

where the two last sets of inequality constraints stand for the incorporation of prior knowledge. In this equation, $N=N_r+N_p$ is the total number of input training samples, and $\varvec{x}=\varvec{x^r}\bigcup \varvec{x^p}$. $C_r>0$ and $C_p>0$ are the trade-off parameters for the slack variables $\varvec{\xi }^{(*)}$ and $\varvec{u}^{(*)}$. $C_r$ tunes the trade-off between the error minimization and the maximization of the function flatness, and $C_p$ can tune the influence of the prior knowledge on the model. By using linear programming to solve the optimization above, we can obtain the coefficient parameter $\varvec{\alpha }^{(*)}$ and the bias term b; thus, we obtain the decision function as Eq. (6).

3.2 Compensating errors for prior knowledge

As we mentioned in Sect. 1, the biases between prior knowledge and actual mapping function are caused by noise error and the simplification of the simulator. During the construction of the simulator, some hard-to-measure, difficult-to-compute features, and complex coupling relationships between different features could not fully be considered. Alternatively, the simulator can build an approximation of the main part of the real model, implying that biases tend to be a relatively low-order mapping relationship.

Considering that the biased prior knowledge cannot be incorporated directly, we build a model developed by the $\nu$-LPSVR to compensate the biased prior knowledge data obtained from the simulator based on all measured data samples and corresponding prior data samples. As we have defined before, $S_r=\{(\varvec{x_t^r},y_t^r),t=1,2,3,\ldots ,N_r\}$ is the measured dataset, and $S_p=\{(\varvec{x_k^p},y_k^p),k=1,2,3,\ldots ,N_p\}$ is the prior dataset. Here, we add an error compensation dataset $S_e=\{(\varvec{x_t^r},z_t^{p}),t=1,2,3,\ldots ,N_r\}$ generated by the simulator, where the input of $S_e$ is consistent with the measured data input, and $z_t^{p}=T(\varvec{x_t^r}) \in R$ is the corresponding target output from the simulator. Thus, similar to $\nu$-LPSVR described above, the optimization problem of error compensation can be formulated as

$$\begin{aligned} {\mathrm{find}} \quad&\varvec{\beta }^{(*)},\varvec{\mu }^{(*)},\varepsilon _e,b_e\\ {\mathrm{min}} \quad&\frac{1}{N_r}\sum _{t=1}^{N_r} (\beta _t+\beta _t^*)+\frac{C_e}{N_r} \sum _{t=1}^{N_r} (\mu _t+\mu _t^*)+C_e\nu _e\varepsilon _e \\ {\mathrm{s.t.}}\quad&\beta _t^{(*)},\mu _t^{(*)},\varepsilon _e\ge 0 \\&\sum _{j=1}^{N_r}(\beta _j-\beta _j^*)k_e\big (\varvec{x_j^r},\varvec{x_t^r}\big )+b_e-y_t^r+z_t^p\le \varepsilon _e+\mu _t \\&y_t^r-z_t^p-\sum _{j=1}^{N_r}(\beta _j-\beta _j^*)k_e\big (\varvec{x_j^r},\varvec{x_t^r}\big )-b_e\le \varepsilon _e+\mu _t^* \end{aligned} $$

(12)

where $\varvec{\beta }^{(*)}$ are the coefficient parameters, $\varvec{\mu }^{(*)}$ are the positive slack variables, $\varepsilon _e$ is the tube width, $C_e>0$ is the penalty parameter to penalize nonzero coefficients $\varvec{\mu }^{(*)}$. Hence, the decision function of the error compensation model can be expressed as

$$\begin{aligned} \Delta =y_k^{pec}-y_k^p=f_e\big (\varvec{x_k^p}\big )=\sum _{i=1}^{N_r} (\beta _i-\beta _i^*)k_e(\varvec{x_i^r},\varvec{x_k^p})+b_e \end{aligned}$$

(13)

where $y^{pec}$ is the output of the compensated prior knowledge data samples. Thus, the compensated sample points can be written as $(\varvec{x_k^p},y_k^{pec})$.

We use the sample set $(\varvec{x_k^p},y_k^{pec})$ instead of $(\varvec{x_k^p},y_k^{p})$ in the optimization equation (11); then, we obtain the data-driven model based on the corrected prior knowledge. This method of sequential model construction we call $\nu$-$\text {PESVR}_{\text {sq}}$. However, one disadvantage of this method is that the measured data will be used twice, which may result in overfitting of the measured data.

In order to avoid this problem and ensure the generalization performance of the data-driven model, we improve the above method by incorporating an error compensation model into the optimization problem (11) of the $\nu$-PSVR. That is, the overall optimal solution is obtained by solving the optimization problem only once. According to the above analysis, the algorithm called $\nu$-PESVR can be solved by the following optimization problem

$$\begin{aligned} {\mathrm{find}} \quad&\varvec{\alpha }^{(*)},\varvec{\xi }^{(*)},\varvec{\beta }^{(*)},\varvec{\mu }^{(*)},\varvec{u}^{(*)}, \varepsilon _r,\varepsilon _e,\varepsilon _p,b,b_e \\ {\mathrm{min}}\quad&\frac{1}{N}\sum _{i=1}^{N}(\alpha _i+\alpha _i^*)+\frac{C_r}{N_r} \sum _{t=1}^{N_r} (\xi _t+\xi _t^*) \\&+\frac{1}{N_r}\sum _{t=1}^{N_r}(\beta _t+\beta _t^*)+\frac{C_e}{N_r} \sum _{t=1}^{N_r} (\mu _t+\mu _t^*) \\&+\frac{C_p}{N_p}\sum _{k=1}^{N_p} (u_k+u_k^*)+C_r\nu _r\varepsilon _r +C_e\nu _e\varepsilon _e \\&+C_p\nu _p\varepsilon _p \\ {\mathrm{s.t.}}\quad&\alpha _i^{(*)},\xi _t^{(*)},\beta _t^{(*)},\mu _t^{(*)}, u_k^{(*)},\varepsilon _r,\varepsilon _e,\varepsilon _p\ge 0 \\&\sum _{i=1}^{N}(\alpha _i-\alpha _i^*)k\big (\varvec{x_i},\varvec{x_t^r}\big )+b-y_t^r\le \varepsilon _r+\xi _t \\&y_t^r-\sum _{i=1}^{N}(\alpha _i-\alpha _i^*)k\big (\varvec{x_i},\varvec{x_t^r}\big )-b\le \varepsilon _r+\xi _t^*\\&\sum _{j=1}^{N_r}(\beta _j-\beta _j^*)k_e\big (\varvec{x_j^r},\varvec{x_t^r}\big )+b_e-y_t^r+z_t^p\le \varepsilon _e+\mu _t \\&y_t^r-z_t^p-\sum _{j=1}^{N_r}(\beta _j-\beta _j^*)k_e\big (\varvec{x_j^r},\varvec{x_t^r}\big )-b_e\le \varepsilon _e+\mu _t^*\\&\sum _{i=1}^{N}(\alpha _i-\alpha _i^*)k\big (\varvec{x_i},\varvec{x_k^p}\big )+b-y_k^p \\&-\sum _{t=1}^{N_r}(\beta _t-\beta _t^*)k_e\big (\varvec{x_t^r},\varvec{x_k^p}\big )-b_e\le \varepsilon _p+u_k \\&y_k^p+\sum _{t=1}^{N_r}(\beta _t-\beta _t^*)k_e\big (\varvec{x_t^r},\varvec{x_k^p}\big )+b_e \\&-\sum _{i=1}^{N}(\alpha _i-\alpha _i^*)k\big (\varvec{x_i},\varvec{x_k^p}\big )-b\le \varepsilon _p+u_k^* \end{aligned} $$

(14)

where we substitute the decision function of the error compensation model into the constraint formulas of prior knowledge in Eq. (11). The parameter $C_r$ penalizes those measured samples with errors greater than $\varepsilon _r$, $C_e$ controls the intensity of the error compensation, and $C_p$ tunes the influence of prior knowledge. In order to improve the generalization performance, we can structure the 3rd and 4th sets of inequality constraints with only a part of the measured samples and the corresponding prior samples. Equation (14) finds the corresponding overall optimal solution by setting the value of penalty parameters $C_r,C_e$, and $C_p$. Compared with the sequential execution method, this method is more efficient, and it has higher accuracy and better generalization performance.

The above $\nu$-PESVR algorithm can be solved easily with linear programming.

3.3 Extending $\nu$-PESVR to multi-scale space

If the unknown mapping function we need to fit is non-flat and comprises both the steep variations and the smooth variations, it would not be appropriate to estimate this mapping function using the SVR algorithm of a single kernel [31]. The small-scale kernels may lead to overfitting of training samples, and the large-scale kernels may lead to underfitting of training samples. As for multi-scale kernel SVR, the kernels with small scale can deal with the steep variations and the kernels with large scale can deal with the smooth variations. Thus, to adapt to the input space for each local area, we extend the $\nu$-PESVR algorithm to multi-scale space($\nu$-MPESVR).

The decision function of multi-scale LPSVR can be expressed as

$$\begin{aligned} f(x)=\sum _{m=1}^L \sum _{i=1}^N (\alpha _{mi}-\alpha _{mi}^*) k_m(\varvec{x_i},\varvec{x})+b \end{aligned}$$

(15)

where L is the number of the scale kernels used in the regression, the kernel function $k_m(\varvec{x_i},\varvec{x})$ denotes the m-th scale kernel. Taking the Gaussian kernel as an example, $k_m(\varvec{x_i},\varvec{x})=exp(-\frac{\parallel \varvec{x_i}-\varvec{x}\parallel ^2}{2\sigma _m^2})$, and $\alpha _{mi}^{(*)}$ are the dual variables of the corresponding kernel function. Similar to the target function of LPSVR in (3), we can obtain the optimization objective of the multi-scale $\nu$-LPSVR as

$$\begin{aligned} \min \sum _{m=1}^L C_m \sum _{i=1}^N (\alpha _{mi}+\alpha _{mi}^*)+C \sum _{i=1}^l L(f(\varvec{x_i}),y_i) \end{aligned}$$

(16)

where the parameter $C_m$ penalizes nonzero dual variables $\alpha _{mi}^{(*)}$ and C determines the trade-off between the model complexity and the training error. In order to avoid overfitting the smooth variations by the small-scale kernels, generally, a decreasing penalty sequence$(C_1> \cdots> C_m> \cdots > C_L)$ should be given for the kernel sequence with increasing scale $(\sigma _1< \cdots< \sigma _m< \cdots < \sigma _L)$.

Because the deviation mapping function between measured data and simulation data is relatively smooth, and to reduce the amount of calculation, we use a single kernel in the error compensation model. Based on the basic principles and solution of $\nu$-PESVR, the optimization problem of $\nu$-MPESVR can be formulated as

$$\begin{aligned} {\mathrm{find}} \quad&\varvec{\alpha _m}^{(*)},\varvec{\xi }^{(*)},\varvec{\beta }^{(*)},\varvec{\mu }^{(*)},\varvec{u}^{(*)}, \varepsilon _r,\varepsilon _e,\varepsilon _p,b,b_e \\&(m=1,2,\ldots ,L) \\ {\mathrm{min}}\quad&\frac{1}{N}\sum _{m=1}^LC_m\sum _{i=1}^{N}(\alpha _{mi}+\alpha _{mi}^*)+ \frac{C_r}{N_r}\sum _{t=1}^{N_r} (\xi _t+\xi _t^*) \\&+\frac{1}{N_r}\sum _{t=1}^{N_r}(\beta _t+\beta _t^*)+\frac{C_e}{N_r} \sum _{t=1}^{N_r} (\mu _t+\mu _t^*) \\&+\frac{C_p}{N_p}\sum _{k=1}^{N_p} (u_k+u_k^*)+C_r\nu _r\varepsilon _r +C_e\nu _e\varepsilon _e \\&+C_p\nu _p\varepsilon _p \\ {\mathrm{s.t.}}\quad&\alpha _{mi}^{(*)},\xi _t^{(*)},\beta _t^{(*)},\mu _t^{(*)}, u_k^{(*)},\varepsilon _r,\varepsilon _e,\varepsilon _p\ge 0 \\&\sum _{m=1}^L\sum _{i=1}^{N}(\alpha _{mi}-\alpha _{mi}^*)k_m\big (\varvec{x_i},\varvec{x_t^r}\big )+b-y_t^r\le \varepsilon _r +\xi _t \\&y_t^r-\sum _{m=1}^L\sum _{i=1}^{N}(\alpha _{mi}-\alpha _{mi}^*)k_m\big (\varvec{x_i},\varvec{x_t^r}\big )-b\le \varepsilon _r +\xi _t^*\\&\sum _{j=1}^{N_r}(\beta _j-\beta _j^*)k_e\big (\varvec{x_j^r},\varvec{x_t^r}\big )+b_e-y_t^r+z_t^p\le \varepsilon _e+\mu _t \\&y_t^r-z_t^p-\sum _{j=1}^{N_r}(\beta _j-\beta _j^*)k_e\big (\varvec{x_j^r},\varvec{x_t^r}\big )-b_e\le \varepsilon _e+\mu _t^*\\&\sum _{m=1}^L\sum _{i=1}^{N}(\alpha _{mi}-\alpha _{mi}^*)k_m\big (\varvec{x_i},\varvec{x_k^p}\big )+b-y_k^p \\&-\sum _{t=1}^{N_r}(\beta _t-\beta _t^*)k_e\big (\varvec{x_t^r},\varvec{x_k^p}\big )-b_e\le \varepsilon _p+u_k \\&y_k^p+\sum _{t=1}^{N_r}(\beta _t-\beta _t^*)k_e\big (\varvec{x_t^r},\varvec{x_k^p}\big )+b_e \\&-\sum _{m=1}^L\sum _{i=1}^{N}(\alpha _{mi}-\alpha _{mi}^*)k_m\big (\varvec{x_i},\varvec{x_k^p}\big )-b\le \varepsilon _p+u_k^* \end{aligned} $$

(17)

In order to facilitate the optimization solution of the problem, we reformulate Eq. (17) in the following matrix form for standard linear programming

$$\begin{aligned} {\mathrm{find}} \quad&\varvec{s}\\ {\mathrm{min}} \quad&\varvec{c}^{\mathrm{T}}\varvec{s}\\ {\mathrm{s.t.}} \quad&\varvec{s}\ge \varvec{l}\\&\varvec{Gs}\le \varvec{h} \end{aligned} $$

(18)

where

$$\begin{aligned} &\varvec{s}=\left[ \varvec{\alpha _1}^{(*)},\ldots ,\varvec{\alpha _L}^{(*)}, \varvec{\xi }^{(*)},\varvec{\beta }^{(*)},\varvec{\mu }^{(*)},\varvec{u}^{(*)},\varepsilon _r, \varepsilon _e,\varepsilon _p,b,b_e \right] ^{\mathrm{T}} \\&\varvec{c}=\left[ \frac{C_1}{N},\ldots ,\frac{C_L}{N},\frac{C_r}{N_r}, \frac{1}{N_r},\frac{C_e}{N_r},\frac{C_p}{N_p}, C_r\nu _r,C_e\nu _e,C_p\nu _p,0,0 \right] ^{\mathrm{T}} \\&\varvec{l}=[\varvec{0},\ldots ,\varvec{0},\varvec{0},\varvec{0},\varvec{0},\varvec{0},0,0,0,-\infty ,-\infty ]^{\mathrm{T}} \end{aligned} $$

$$\begin{aligned} &\varvec{G}=\left[ {\begin{array}{cccccccccccc} \pm \varvec{K_1^r}&{} \cdots &{} \pm \varvec{K_L^r}&{} [-\varvec{E},\varvec{0}]&{} \varvec{0}&{} \varvec{0}&{} \varvec{0}&{} -1&{} 0&{} 0&{} 1&{} 0 \\ \mp \varvec{K_1^r}&{} \cdots &{} \mp \varvec{K_L^r}&{} [\varvec{0},-\varvec{E}]&{} \varvec{0}&{} \varvec{0}&{} \varvec{0}&{} -1&{} 0&{} 0&{} -1&{} 0 \\ \varvec{0}&{} \cdots &{} \varvec{0}&{} \varvec{0}&{} \pm \varvec{K_r^e}&{} [-\varvec{E},\varvec{0}]&{} \varvec{0}&{} 0&{} -1&{} 0&{} 0&{} 1 \\ \varvec{0}&{} \cdots &{} \varvec{0}&{} \varvec{0}&{} \mp \varvec{K_r^e}&{} [\varvec{0},-\varvec{E}]&{} \varvec{0}&{} 0&{} -1&{} 0&{} 0&{} -1 \\ \pm \varvec{K_1^p}&{} \cdots &{} \pm \varvec{K_L^p}&{} \varvec{0}&{} \pm \varvec{K_p^e}&{} \varvec{0}&{} [-\varvec{E},\varvec{0}]&{} 0&{} 0&{} -1&{} 1&{} -1 \\ \mp \varvec{K_1^p}&{} \cdots &{} \mp \varvec{K_L^p}&{} \varvec{0}&{} \mp \varvec{K_p^e}&{} \varvec{0}&{} [\varvec{0},-\varvec{E}]&{} 0&{} 0&{} -1&{} -1&{} 1 \\ \end{array}} \right] ^{\mathrm{T}} \\&\varvec{h}=\left[ y_t^r,-y_t^r,y_t^r-z_t^p,z_t^p-y_t^r,y_k^p,-y_k^p \right] ^{\mathrm{T}} \end{aligned} $$

In the optimization, the matrices $\varvec{s},\varvec{c},\varvec{l}$ denote $(2L\cdot N+6N_r+2N_p+5)\times 1$ column vector, $\varvec{G}$ represents the $(4N_r+2N_p)\times (2L\cdot N+6N_r+2N_p+5)$ matrix, and $\varvec{h}$ is a $(4N_r+2N_p)\times 1$ column vector. The coefficient vector $\varvec{\alpha _m}^{(*)} = [\alpha _{m1},\alpha _{m2},\ldots ,$$\alpha _{mN}, \alpha _{m1}^*,\alpha _{m2}^*,\ldots ,\alpha _{mN}^*]^{\mathrm{T}}$ denotes a $2N \times 1$ column vector. Similar to $\varvec{\alpha }^{(*)}$, $\varvec{\xi }^{(*)},\varvec{\beta }^{(*)},\varvec{\mu }^{(*)}$ are $2N_r \times 1$ column vectors, and $\varvec{u}^{(*)}$ represents a $2N_p \times 1$ column vector. $\pm \varvec{K_m^r}=[\varvec{K_m^r},-\varvec{K_m^r}]$ and $\mp \varvec{K_m^r}=[-\varvec{K_m^r},\varvec{K_m^r}]$ are $N_r \times 2N$ matrices. Similarly, $\pm \varvec{K_r^e}$ and $\mp \varvec{K_r^e}$ are $N_r \times 2N_r$ matrices, $\pm \varvec{K_m^p}$ and $\mp \varvec{K_m^p}$ are $N_p \times 2N$ matrices, and $\pm \varvec{K_p^e}$ and $\mp \varvec{K_p^e}$ are $N_p \times 2N_r$ matrices. In addition, the kernel matrix $\varvec{K_m^r}=\varvec{K_m}(\varvec{x},\varvec{x^r})$, $\varvec{K_r^e}=\varvec{K_e}(\varvec{x^r},\varvec{x^r})$, $\varvec{K_m^p}=\varvec{K_m}(\varvec{x},\varvec{x^p})$, and $\varvec{K_p^e}=\varvec{K_e}(\varvec{x^r},\varvec{x^p})$. Moreover, in $[-\varvec{E},\varvec{0}]$ and $[\varvec{0},-\varvec{E}]$, $\varvec{E}$ is the identity matrix and $\varvec{0}$ is the zero matrix.

Using linear programming to solve the above optimization formulation, we can obtain a decision function in Eq. (15). Overall, $\nu$-MPESVR can be summarized as shown in Algorithm 1.

3.4 Parameter selection strategy for $\nu$-MPESVR

Fig. 1

Flowchart of $\nu$-MPESVR parameters optimization and model constructing procedure

The generalization performance and accuracy of the support vector machine (SVM) are greatly influenced by its model parameters, both the error penalty parameter C and the kernel parameter, such as $\sigma$. Recently, intelligent optimization methods like simulated annealing (SA) [22], genetic algorithm (GA) [1], and particle swarm optimization (PSO) [11, 12] have became very popular in solving optimization problems. In the practical engineering application, the PSO can be programmed easily and produces superior performance [11, 12, 16]. Reference [8] demonstrates that in the parameter selection of SVM, PSO converges faster and has higher accuracy than other algorithms. Additionally, in order to avoid the problem of premature convergence, Liu [13] improved PSO by combining it with an adaptive inertia weight factor and chaotic local search, which is called chaotic particle swarm optimization (CPSO). It has been proved in [13] that CPSO is much faster than other meta-heuristics and can enable the search to escape from the local optima trap. Thus, to find the global optimal parameters in $\nu$-MPESVR efficiently, in this section, we present an intelligent parameter selection strategy that uses expert knowledge for initial value screening of the CPSO to reduce the search space.

3.4.1 Expert knowledge about SVR parameters

Generally, the number L of kernel functions set to 2 or 3 may be sufficient for dealing with most practical problems, and a large L ($L \ge 4$) may be necessary for some complex problems [31]. The kernel parameter of the m-th kernel function is defined as $\sigma _m$. To avoid overfitting, we choose $C_m=1/{\sigma _m}$. As for the error penalty parameter C ($C_r$, $C_e$, and $C_p$ in $\nu$-MPESVR), it is closely related to the statistical characteristics of the training data, and Cherkassky [6] proposed the prescription for penalty parameter C as

$$ C=\max (|{\bar{y}}+3s_y|,|{\bar{y}}-3s_y|) $$

(19)

where ${\bar{y}}$ and $s_y$ are the mean and standard deviation of the output values in the training dataset. Moreover, it is well accepted that the kernel parameter should be associated with the distribution characteristics of the training data. The kernel parameter $\sigma$ is set to the following form in [29] as

$$ \sigma \sim (0.1-0.5) \cdot range(x) $$

(20)

where $range(x)=|\max (x)-\min (x)|$; thus, we get the initial value $(C_r,C_p,C_e, \sigma _e,C_1,\ldots ,C_L,\sigma _1,\ldots ,\sigma _L)_{init}$.

3.4.2 Parameter selection with CPSO

PSO is a population-based optimization technique, where each solution is a “particle” and multiple candidate solutions coexist and collaborate simultaneously to find the optimal solution in the problem search space. The state of the particle in the search space is characterized by its position and velocity, which can be updated by following equations

$$\begin{aligned} \varvec{v_i} &=w\varvec{v_i}+c_1\cdot random(0,1)\cdot (\varvec{p_i}-\varvec{x_i}) \\&\quad +\,c_2\cdot random(0,1)\cdot (\varvec{p_g}-\varvec{x_i}) \end{aligned}$$

(21)

$$\begin{aligned} \varvec{x_i} =\varvec{x_i}+\varvec{v_i} \end{aligned}$$

(22)

where the column vectors $\varvec{v_i},\varvec{x_i},\varvec{p_i},\varvec{p_g} \in R^{np}$, np is the number of particles. $\varvec{v_i}$ is the velocity of particle i, $\varvec{x_i}$ represents the position of particle i, $\varvec{p_i}$ denotes the best previous position of particle i, $\varvec{p_g}$ denotes the best position among all particles, w is the inertia factor that controls the impact of the velocity of the previous particle on its current particle. $c_1$ and $c_2$ are acceleration coefficients that control the maximum step size of the particle, and random(0, 1) is a random number between 0 and 1.

The inertia factor w in (21) controls the momentum of the current particle. A large w may cause the particle to miss the optimal region and make the algorithm unable to converge, while a small w may cause particles to become trapped in a local optimum. Thus, Liu [13] proposed the adaptive inertia weight factor (AIWF) as follows

$$\begin{aligned} w=\left\{ \begin{array}{ll} w_{\min }+\frac{(w_{\max }-w_{\min })(f-f_{\min })}{f_{\mathrm{avg}}-f_{\min }} &{}\quad {f\le f_{\mathrm{avg}}} \\ w_{\max } &{}\quad {f>f_{\mathrm{avg}}} \end{array} \right. \end{aligned}$$

(23)

where $w_{\max }$ and $w_{\min }$ are the maximum and minimum of w respectively, f is the evaluation value of the current particle, and $f_{\mathrm{avg}}$ and $f_{min}$ are the average and minimum evaluation values of all particles, respectively.

In order to enable the particles to escape from the local optima trap, Liu [13] incorporated chaotic dynamics into the above PSO with AIWF. By using the logistic equation, the process of the chaotic local search could be defined as

$$\begin{aligned}&c\varvec{x_i}^{(k)}=\frac{\varvec{x_i}^{(k)}-\varvec{x}_{\min ,\varvec{i}}}{\varvec{x}_{\max ,\varvec{i}}-\varvec{x}_{\min ,\varvec{i}}},\quad (i=1,2,\ldots ,np) \end{aligned}$$

(24)

$$\begin{aligned}&c\varvec{x_i}^{(k+1)}=4c\varvec{x_i}^{(x)}(1-c\varvec{x_i}^{(k)}) \end{aligned}$$

(25)

$$\begin{aligned}&\varvec{x_i}^{(k+1)}=\varvec{x}_{\min ,\varvec{i}}+c\varvec{x_i}^{(k+1)}(\varvec{x}_{\max ,\varvec{i}}-\varvec{x}_{\min ,\varvec{i}}) \end{aligned}$$

(26)

where $c\varvec{x_i}$ is the i-th chaotic variable, and k is the current iteration number. The iteration stops if the new solution is better than $\varvec{x}^{(0)}$ and the difference between two iterations is smaller than the set threshold, or if it reached the predefined maximum iteration.

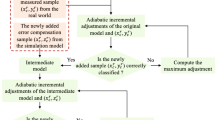
By using fivefold cross-validation as the evaluation function in CPSO, the $\nu$-MPESVR algorithm based on the above parameter selection strategy can be summarized as Fig. 1.

As Fig. 1 shows, we first obtain the training dataset $S_r$ and the test dataset $S_{\mathrm{test}}$ from the real world, and build an error compensation dataset $S_e$ and an additional prior knowledge dataset $S_p$ through the simulation model. We input $S_r$, $S_e$ and $S_p$ into the $\nu$-MPESVR model as the final training dataset. Before training the model, we need to specify the number of kernel functions $k_m$ and the type of kernel functions $k_m$ and $k_e$. Then, we initialize the model parameters C ($C_r,C_p,C_e,C_1,\dots ,C_L$) and $\sigma$ ($\sigma _1,\dots ,\sigma _L$) according to the expert knowledge in Sect. 3.4.1, and specify the parameters of CPSO (inertia factor, acceleration coefficients, search scope, and maximum iteration). Because the supply of data for training and testing is limited, we use fivefold cross-validation to find the optimal parameters of the model [2]. In each iteration of CPSO, we divide the training dataset $S_r$ into five groups ($S_e$ is also divided into five groups corresponding to $S_r$). Four of the groups are used to train a set of models that are then evaluated on the remaining group. This procedure is then repeated for all five possible choices for the held-out group, and the performance scores from the five runs are then averaged to represent the estimation of the model performance (fitness evaluation of CPSO) under these model parameters. CPSO will update the parameters and proceed to the next iteration until the stopping condition is satisfied or the maximum number of iterations is reached. Finally, we use the final optimized model parameters and all of the $S_r$, $S_e$, and $S_p$ to train the $\nu$-MPESVR, and run the model on $S_{\mathrm{test}}$ to get the final model prediction.

4 Experimental results

In this section, we validate the efficiency of our proposed algorithm by using an artificial example and a practical example. Root mean squared error (RMSE), mean absolute error (MAE), and coefficient of determinations (R(2)) are used as indicators to evaluate the accuracy and generalization performance of the obtained data-driven model. As known in statistical analysis, the best prediction performance for R2 is one and will be zero for other indices [18].

4.1 Complex function estimation

Fig. 2

Data samples $S_r$, $S_e$, $S_p$, and $S_{\mathrm{test}}$ in three groups of experiment

Fig. 3

Comparison of predicted results in the first group of experiment. a Results of measurement,$\nu$-MPESVR, MKPLPSVR, and MSSVR. b Results of measurement,$\nu$-MPESVR,$\nu$-PESVR, and $\nu$-${\text {MPESVR}}_{{\text {sq}}}$

We consider the following complex piecewise function as the base function of the real model and the simulation model.

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} -\,4x-8 &{}\quad {-\,3\le x< -1} \\ -3x^3-5x^2+5x+3 &{}\quad {-1\le x<1} \\ 2\sin (\hbox {e}^{1.2x})+0.3552 &{}\quad {1\le x<3} \end{array} \right. \end{aligned}$$

(27)

We generated the measured dataset $S_r$ with 15 samples, the error compensation dataset $S_e$ with 15 samples, the prior knowledge dataset $S_p$ with 35 samples, and the testing dataset $S_{\mathrm{test}}$ with 1000 samples from the above function randomly in the range of [− 3,3]. We should have applied the error term to $S_r$ and $S_{\mathrm{test}}$ on the basis of base function Eq. (27). However, for the convenience of the comparison and display of the predicted results, we apply the error term on $S_p$ and $S_e$ instead.

In order to validate the performance of our proposed algorithm, we designed three groups of experiments. In the first group of experiments, we modified the mapping function of the simulation model as $f_{p1}(x) = f(x)+f_{\mathrm{noise}}$, where $f_{\mathrm{noise}}$ is the Gaussian noise $N(0.1,0.2^2)$. In the second group of experiments, we added the error term with a simple mapping relationship to the mapping function of the simulation model as $f_{p2}(x)=f(x)+f_{\mathrm{noise}}+0.7x$. In the third group of experiments, we added the error term with a high-order mapping relationship to the mapping function of the simulation model as $f_{p3}(x)=f(x)+f_{\mathrm{noise}}+0.7x+0.1x^4$. Figure 2 shows the $S_r$, $S_e$, $S_p$, and $S_{\mathrm{test}}$ in the three groups of experiments.

Fig. 4

Comparison of predicted results in the second group of experiment. a Results of measurement,$\nu$-MPESVR, MKPLPSVR, and MSSVR. b Results of measurement,$\nu$-MPESVR,$\nu$-PESVR, and $\nu$-${\text {MPESVR}}_{{\text {sq}}}$

Fig. 5

Comparison of predicted results in the third group of experiment. a Results of measurement,$\nu$-MPESVR, MKPLPSVR, and MSSVR. b Results of measurement,$\nu$-MPESVR,$\nu$-PESVR, and $\nu$-${\text {MPESVR}}_{{\text {sq}}}$

For each group of experiments, we constructed five models using different algorithms, including MKPLPSVR, MSSVR, $\nu$-PESVR, $\nu$-${\text {MPESVR}}_{{\text {sq}}}$, and $\nu$-MPESVR. The MKPLPSVR was proposed in [33], MSSVR denotes standard multi-scale support vector regression [31], and $\nu$-PESVR, and $\nu$-MPESVR are proposed above. The $\nu$-${\text {MPESVR}}_{{\text {sq}}}$ algorithm is the multi-scale extension of the $\nu$-$\text {PESVR}_{\text {sq}}$ algorithm proposed in Sect. 3.2 that first constructs the error compensation model to correct the prior samples and then builds the prediction model to output the final results. Using the training data samples and setting the model parameters appropriately, we build the models separately using the above five algorithms.

For these three groups of experiments, the single-kernel algorithm exploited only a Gaussian kernel, and the multi-kernel algorithms employed three Gaussian kernels. In $\nu$-PESVR, we chose $C_r=100, C_p=100, C_e=100,$$v_r=v_p=v_e=0.5$, and the kernel parameters $\sigma =0.1118$, and $\sigma _e = 2.2361$. In $\nu$-${\text {MPESVR}}_{{\text {sq}}}$ and $\nu$-MPESVR, we chose $C_1=0.6071, C_2=0.3141, C_3=2.0707, C_r=150, C_p=100, C_e=100$, and $v_r=v_p=v_e=0.5$, and the kernel parameters $\sigma _1=0.7071,\sigma _2=0.2041, \sigma _3=0.0707, \sigma _e = 2.2361$. Moreover, the parameters in MKPLPSVR and MSSVR are the same as those in $\nu$-${\text {MPESVR}}_{{\text {sq}}}$ and $\nu$-MPESVR, except for the parameters related to error compensation.

Table 1 Result comparisons of MKPLPSVR, MSSVR, $\nu$-PESVR, $\nu$-${\text {MPESVR}}_{{\text {sq}}}$, $\nu$-MPESVR on the complex function estimation example

Figure 3 shows the comparison between the prediction of each algorithm and the actual results in the first group of experiments. It shows that all of the algorithms fit the curve accurately. However, compared with Fig. 3a, b, we can find that the multi-kernel algorithms like $\nu$-MPESVR, MKPLPSVR, and MSSVR have better performance for fitting functions with steep variations and smooth variations than the single-kernel algorithm $\nu$-PESVR and $\nu$-${\text {MPESVR}}_{{\text {sq}}}$. One possible explanation is that the $\nu$-PESVR with a small kernel parameter caused overfitting of the smooth variations, and that the $\nu$-${\text {MPESVR}}_{{\text {sq}}}$ utilizing the measured samples $S_r$ twice to compensate for the random Gaussian noise may have led to the overfitting of the training data.

Figures 4 and 5 show the estimation results in the second and third group of experiments. We can see that the algorithms with error compensation, like $\nu$-PESVR, $\nu$-${\text {MPESVR}}_{{\text {sq}}}$, and $\nu$-MPESVR, fit the practical curve more accurately than other algorithms. When the error of the prior data is large, those algorithms without error compensation cannot estimate the mapping function very well by only incorporating slack variables, and with the growing number of prior samples, the prediction curve will increasingly approximate the simulation curve, which is not what we expected.

In order to show the performance of the proposed algorithm more intuitively, Table 1 lists the predicted RMSE, MAE, R(2), the number of SVs and iterations, and the training time of all the algorithms in each group of experiments. From Table 1, we can see that for those algorithms without error compensation, RMSE and MAE become larger, and R(2) becomes smaller with an increase in the value and complexity of the error term. However, those algorithms with error compensation still maintain the approximation accuracy. Owing to the increased complexity of the algorithms with error compensation, their training time is relatively long. In addition, we found that the model generated by $\nu$-MPESVR had the best RMSE, MAE, and R(2) of all the models.

It can be seen from the results of the three groups of experiments that the data-driven model constructed by $\nu$-MPESVR obtained the most accurate predictive performance when only a few pieces of measured data were available. The multi-kernel algorithm obtained better generalization performance and accuracy when estimating a complex function with both steep and smooth variations than did the single-kernel algorithm. Incorporating the error compensation optimization formula into the solution process of the prediction model prevented the need to use the dataset $S_r$ twice, and thus improved the generalization performance and accuracy of the obtained model. As a consequence, the $\nu$-MPESVR solved the problem of deviation in prior knowledge data and scarcity in the measured data.

4.2 Coordinator gyro rotor performance prediction

The coordinator gyro rotor is the core component of the infrared missile and small spacecraft. It can search, capture, and track the target in the field of view, and then adjust the flight direction and attitude of the missile. Therefore, the quality of the coordinator gyro rotor directly determines the tactical performance of the infrared missile. In this section, in order to improve productive efficiency, we use the above method to predict the gyro drift with the assembly process parameters and adjustment parameters to guide product assembly.

Fig. 6

Schematic diagram of two-degree-of-freedom gyro

As shown in Fig. 6, a two-degree-of-freedom gyro is primarily composed of the rotor, the inner-ring and the outer-ring. We take the inertial coordinate system as $ox_iy_iz_i$, the outer-ring coordinate system as $ox_wy_wz_w$, the inner-ring coordinate system as $ox_ny_nz_n$, and the rotor coordinate system as $ox_hy_hz_h$. Then, the gyro dynamic equation considering the assembly error can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\text {d}H_h^{hz}}{\text {d}t}=0 \\ \frac{\text {d}(H_{n}^{ny}+H_{h}^{ny}+H_{h\_e}^{ny})}{\text {d}t}+(H_{n}^{nz}+H_{h}^{nz}+H_{h\_ae}^{nz})(\omega _n^{nz} \\ \quad +\omega _w^{nz})-(H_{n}^{nx}+H_{h}^{nx}+H_{h\_e}^{nx})(\omega _n^{nz}+\omega _w^{nz})=M_y \\ \frac{\text {d}(H_w^{wx}+H_h^{wx}+H_{h\_e}^{wx}+H_n^{wx}+H_{n\_e}^{wx})}{\text {d}t}=M_x \end{array} \right. \end{aligned}$$

(28)

where $H_h^{hz}$ is the projection of the rotor angular momentum on the z-axis of the rotor coordinates. $H_n^{nx},H_n^{ny},H_n^{nz}$ denote the projection of the inner-ring angular momentum on the x-, y-, and z-axis of the inner-ring coordinates, respectively. $H_w^{wx}$ is the projection of the outer-ring angular momentum on the x-axis of the outer-ring coordinates. $H_{h\_e},H_{n\_e},H_{w\_e}$ denote the angular momentums of the rotor, the inner-ring, and the outer-ring caused by assembly errors. $\omega _n^{nz},\omega _w^{nz}$ represent the projection of the angular velocity of the inner and outer-rings on the z-axis of the inner-ring coordinates, respectively. Moreover, $M_x,M_y$ are the torque of the outer-ring shaft and the inner-ring shaft, respectively.

In order to solve Eq. (28), we calculate the angular momentum of each component in the corresponding moving coordinate system. In the rotor coordinates $ox_hy_hz_h$:

$$\begin{aligned} H_h^{hz}=J_{hz}\cdot (\Omega -\dot{\theta _w} \cdot \sin {\theta _n}) \end{aligned}$$

(29)

where $J_h$ denotes the moment of inertia about the rotor. $\theta _n$ is the rotation angle of the inner-ring, and $\theta _w$ is the rotation angle of the outer-ring.

Fig. 7

Comparison of the gyro drift prediction results and the measurement result. a Results of measurement,$\nu$-MPESVR, MKPLPSVR, and MSSVR. b Results of measurement,$\nu$-MPESVR,$\nu$-PESVR, and $\nu$-${\text {MPESVR}}_{{\text {sq}}}$

In the inner-ring coordinates $ox_ny_nz_n$:

$$\begin{aligned} \left\{ \begin{array}{l} H_n^{nx}=J_{nx}\cdot \dot{\theta _w}\cdot \cos {\theta _n} \\ H_n^{ny}=J_{ny}\cdot \dot{\theta _n} \\ H_n^{nz}=-J_{nz}\cdot \dot{\theta _w} \cdot \sin {\theta _n} \end{array} \right. \end{aligned}$$

(30)

$$\begin{aligned} \left\{ \begin{array}{l}H_{hw\_e}^{nx}= m_hv_{cw}(\delta _{hy}\cos {\alpha }\cos {\theta _n}-\delta _{hx}\sin {\alpha }\sin {\theta _n}) \\H_{hw\_e}^{ny}= -m_hv_{cw}\delta _{hx}\cos {\alpha }\cos {\theta _n} \\H_{hw\_e}^{nz}= -m_hv_{cw}(\delta _{hy}\cos {\alpha }\sin {\theta _n}-\delta _{hx}\sin {\alpha }\cos {\theta _n}) \end{array} \right. \end{aligned}$$

(31)

$$\begin{aligned}\left\{ \begin{array}{l}H_{hn\_e}^{nx}= -m_h\cdot \delta _{hy}\cdot \delta _{hx}\cdot \dot{\theta _n} \\H_{hn\_e}^{ny}= m_h\cdot \delta _{hx}^2\cdot \dot{\theta _n} \\H_{hn\_e}^{nz}= m_h\cdot \delta _{hy}\cdot \delta _{hz}\cdot \dot{\theta _n} \end{array} \right. \end{aligned}$$

(32)

$$H_h^n=H_h^h $$

(33)

$$H_{h\_e}^n=H_{hw\_e}^{n}+H_{hn\_e}^{n} $$

(34)

where

$$\begin{aligned} &v_{cw}=\dot{\theta _w}\sqrt{(\delta _{hx}\sin {\theta _n}-\delta _{hz}\cos {\theta _n})^2+(\delta _n+\delta _{hy})^2} \\&\cos {\alpha }=\frac{\delta _n+\delta _{hy}}{\sqrt{(\delta _n+\delta _{hy})^2+(\delta _{hx}^2+\delta _{hz}^2)\sin {\gamma ^2}}} \\&\gamma =\arctan (\frac{\delta _{hz}}{\delta _{hx}})-\theta _n \end{aligned} $$

In the above equations, $m_h$ is the mass of the rotor, J is the moment of inertia, $\Omega$ is the rotor speed, and $\delta _{hx},\delta _{hy},\delta _{hz}$ are the offsets of the rotor barycenter position on the x-, y-, and z-axis, respectively. $H_{hw\_e}^{n},H_{hn\_e}^{n}$ are the projection of the angular momentum of the rotor in the inner-ring coordinates caused by assembly error under the effect of $\dot{\theta _w}$ and $\dot{\theta _n}$, respectively.

In the outer-ring coordinates $ox_wy_wz_w$:

$$ H_{w}^{wx}= J_{wx}\cdot \dot{\theta _w} $$

(35)

$$ H_{h}^{wx}= -J_{hz}(\Omega -\dot{\theta _w}\cdot \sin {\theta _n})\sin {\theta _n}+J_{hx}\dot{\theta _w}\cos ^2{\theta _n} $$

(36)

$$ H_{hw\_e}^{wx}= m_h\dot{\theta _w}[(\delta _n+\delta _{hy})^2-\delta _{hx}\sin {\gamma }\sin {\theta _n}\sqrt{\delta _{hx}^2+\delta _{hz}^2}] $$

(37)

$$ H_{hn\_e}^{wx}= -[m_h\dot{\theta _n}(\delta _{n}+\delta _{hy})](\delta _{hz}\sin {\theta _n}+\delta _{hx}\cos {\theta _n}) $$

(38)

$$ H_{h\_e}^{wx}= H_{hw\_e}^{wx}+H_{hn\_e}^{wx} $$

(39)

$$ H_{n}^{wx}= \dot{\theta _w}(J_{nz}\sin ^2{\theta _n}+J_{nx}\cos ^2{\theta _n}) $$

(40)

$$ H_{n\_e}^{wx}= m_n\delta _n^2\dot{\theta _w}+m_n\delta _n\delta _{nz}\dot{\theta _n}\sin {\theta _n} $$

(41)

where $m_n$ is the mass of the inner-ring, $\delta _{n},\delta _{nz}$ are the offsets of the center of mass of the inner-ring on the y- and z-axis, respectively. $H_{hw\_e}^{w},H_{hn\_e}^{w}$ are the projection of the angular momentum of the rotor in the outer-ring coordinates caused by assembly error under the effect of $\dot{\theta _w}$ and $\dot{\theta _n}$, respectively, and $H_{nw\_e}^{w},H_{nn\_e}^{w}$ are the projection of the angular momentum of the inner-ring in the outer-ring coordinates caused by assembly error under the effect of $\dot{\theta _w}$ and $\dot{\theta _n}$, respectively. According to Eqs. (28)–(41), we can get an approximate dynamic formula of gyro drift as

$$ d=D(M_x,M_y,\Omega ,\delta _{hx},\delta _{hy},\delta _n) $$

(42)

According to the model construction method proposed in Seciton3, we first obtained 30 pieces of measured data $S_r$ collected by adept operators. Second, we obtained 70 samples as the input features of the prior dataset $S_p$, and calculated the drift performance by Eq. (42) as the objective value. In addition, the error compensation dataset $S_e$ was constructed from the input in $S_r$, and the corresponding drift performance was calculated by Eq. (42). Thus, we obtained a measured dataset $S_r$, a prior dataset $S_p$, and an error compensation dataset $S_e$. Finally, we used 20 sets of testing data $S_{\mathrm{test}}$ to verify the models.

As in Sect. 4.1, we used MKPLPSVR, MSSVR, $\nu$-PESVR, $\nu$-${\text {MPESVR}}_{{\text {sq}}}$, and $\nu$-MPESVR separately to build the data-driven model, and 20 pieces of measured data, $S_{\mathrm{test}}$, were used to validate the accuracy and generalization performance of the obtained model. In this example, the single-kernel algorithm exploited only a Gaussian kernel, and the multi-kernel algorithms employed three Gaussian kernels. In $\nu$-PESVR, we chose $C_r=150, C_p=140, C_e=100$, and $v_r=v_p=v_e=0.5$, and the kernel parameters $\sigma =9.8058$, and $\sigma _e = 2.2361$. In $\nu$-${\text {MPESVR}}_{{\text {sq}}}$ and $\nu$-MPESVR, we chose $C_1=0.0126, C_2=2.1380, C_3=23.1623, C_r=150, C_p=100,$$C_e=100$, and $v_r=v_p=v_e=0.5$, and the kernel parameters $\sigma _1=79.0569, \sigma _2=1.000, \sigma _3=0.3162,$ and $\sigma _e = 2.2361$. Moreover, the parameters in MKPLPSVR and MSSVR are the same as those in $\nu$-${\text {MPESVR}}_{{\text {sq}}}$ and $\nu$-MPESVR, except for the parameters related to error compensation. Using the training data samples and the model parameters above, we built the models separately using the five algorithms. Figure 7 shows the approximating results of the gyro drift. Table 2 shows the RMSE, MAE, and R(2) of the five predicted functions.

Table 2 Result comparisons of MKPLPSVR, MSSVR, $\nu$-PESVR, $\nu$-${\text {MPESVR}}_{{\text {sq}}}$, $\nu$-MPESVR on the coordinator gyro rotor performance prediction example

As we can see in Fig. 7, the results estimated by $\nu$-MPESVR are in good agreement with the measurements from the five algorithms. As can be seen in Table 2, compared with the single-kernel algorithm, the multi-kernel algorithms have higher accuracy, especially those implementing error compensation. The model developed by $\nu$-MPESVR is more accurate than the others, and has the best RMSE, MAE, and R(2) among the five algorithms. The projected results indicate that $\nu$-MPESVR can effectively compensate for the errors between the prior knowledge data and the measured data, improve the accuracy of the obtained model, and has good generalization performance in the case of insufficient measured data.

5 Conclusion

For the purpose of building an accurate data-driven model from an insufficient amount of measured data and biased prior knowledge data, this paper proposed a nested multi-scale $\nu$-LPSVR algorithm implementing prior knowledge and error compensation. The $\nu$-MPESVR algorithm realized the incorporation of prior knowledge and the compensation of biased prior knowledge data by the addition of constraints and objective function. The proposed algorithm also used multi-scale kernel functions to incorporate multiple feature spaces into the process of modeling, which achieved accurate modeling of non-flat, complex, and changeful problems. Moreover, a strategy for hyper-parameter selection based on expert knowledge and CPSO was presented to search the optimal parameters of the $\nu$-MPESVR algorithm autonomously.

In a word, the major contributions of this study are highlighted as follows: (1) $\nu$-MPESVR considers the errors between the prior knowledge data and the measured data in the modeling process, and incorporates the compensated prior knowledge into the prediction model. Hence, the estimation accuracy of $\nu$-MPESVR is significantly better than MSSVR and MKPLPSVR, when there are biases between the prior knowledge data and the measured data; (2) unlike the method of sequentially executing error compensation and prediction ($\nu$-${\text {MPESVR}}_{{\text {sq}}}$), $\nu$-MPESVR simultaneously optimizes the prediction model and the error compensation model, so the proposed algorithm has better generalization performance; (3) the $\nu$-MPESVR model is constructed automatically where the model parameters are optimized autonomously with the use of the expert knowledge based CPSO algorithm; (4) the results of a synthetic example and a practical application demonstrate that $\nu$-MPESVR can still maintain high accuracy when the biases of prior knowledge data change, and it has higher prediction accuracy and better generalization performance. Accordingly, the proposed algorithm $\nu$-MPESVR shows great potential in solving problems when only a few measured samples can be obtained, but some approximate and biased prior knowledge is available.

In the future research, the correlation between model parameters will be considered to narrow the parameter spaces that the intelligent optimization algorithm needs to search, and integrating the prior knowledge within intelligent searching processes will be explored to enhance the stability of the algorithm.