Inference of node attributes from social network assortativity

Abstract

Social networks are known to be assortative with respect to many attributes, such as age, weight, wealth, level of education, ethnicity and gender: Similar people according to these attributes tend to be more connected. This can be explained by influences and homophily. Independently of its origin, this assortativity gives us information about each node given its neighbors. Assortativity can thus be used to improve individual predictions in a broad range of situations, when data are missing or inaccurate. This paper presents a general framework based on probabilistic graphical models to exploit social network structures for improving individual predictions of node attributes. Using this framework, we quantify the assortativity range leading to an accuracy gain in several situations, with various individual prediction profiles. We finally show how specific characteristics of the network can enhance performances further. For instance, the gender assortativity in real-world mobile phone data drastically changes according to some communication attributes. In this case, using the network topology indeed improves local predictions of node labels and moreover enables inferring missing node labels based on a subset of known vertices. In both cases, the performances of the proposed method are statistically significantly superior to the ones achieved by state-of-the-art label propagation and feature extraction schemes in most settings.

1 Introduction

Social networks currently drive an increasing attention in the research community, as they are found in diverse situations and are described by huge amounts of data notably collected through the web and mobile devices. Facebook, Twitter, Google+, mobile phone networks and other large-scale social graphs are nowadays largely studied for predicting and analyzing individual demographics [1, 23, 46]. This type of information is indeed a key input for the establishment of economic and social policies, health campaigns or market segmentation [12, 23, 37]. Nevertheless, especially (but not exclusively) in developing countries, such statistics are often scarce or even lacking, as local censuses are costly, rough, time-consuming and hence rarely up to date [25, 43]. This is the reason why recent researches address this problem by inferring demographics from large social networks [7, 12], in order to ease the access of policy makers and NGO’s toward more reliable information.

Social networks contain individual information about their users (e.g., generated tweets for Twitter), in addition to a graph topology information. These graphs present specific structures carrying many different characteristics, such as small-worldness or heterogeneous degree distribution [32]. The assortativity of social networks, defined as the nodes tendency to be linked to others which are similar in some sense [2], with respect to various demographics of their individuals such as gender, age, weight, income level, education, race, religion is well documented in the literature [22, 24, 31, 42, 48]. This property has been theorized to come from either influences or homophily or a combination of both [2]. For instance, Rosenquiest et al. [36] showed that social influence can enhance the spreading of alcohol consumption and Madan et al. [22] found that weight changes in an individual can be influenced by exposure to overweight peers with unhealthy habits or inactive lifestyles. On the other hand, the concept of homophily is easily understood as the saying goes: ‘birds of a feather flock together,’ which means that people sharing some characteristics tend to more communicate. For instance, we observe more connections between people of the same age and gender [24].

Independently of its cause, this assortativity can be used for individual prediction purposes when some labels are missing or uncertain, e.g., for demographics prediction in large networks. The task of predicting missing node labels in networks, known as node classification, makes use of the known labels and the graph structure [14], which embeds some properties such as its assortativity. Different methods of node classification, based either on feature extraction or on random walks [5], were recently developed. On the one hand, some feature extraction-based approaches aim at exploiting network assortativity [1, 16]. The general idea is, for each node, to build a feature vector summarizing information from its neighborhood. A machine learning algorithm can then be employed to predict the unknown labels based on these extracted features. In this setting, the neighborhood definition is highly important and can be carried out in different ways [15]. To define feature vectors describing each node’s neighborhood, graph embedding techniques can be considered [14]. For instance, Grover and Leskovec automated the feature extraction to preserve neighborhoods reflecting the local structures and/or the communities [15]. This approach is well suited for classification tasks as it can account for diverse node neighborhoods which can be related to the node labels. However, the feature extraction-based studies do not take the global network structure into account and could hence further benefit from its properties. Indeed, the feature extraction is constrained by the subsequent classification algorithm that is used: The fixed number of features and their ordering cannot faithfully reflect complex relationships, observed in social networks for instance, with diverse kinds of network substructures related to the users’ labels [44]. Also, this kind of approach is not intended to directly exploit uncertain label predictions with confidence levels (i.e., class probabilities) [40].

On the other hand, random walk-based approaches allow to account for the whole network structure by propagating the labels through iterative updates [50, 51]. Several variants and adaptations of this principle were proposed to solve diverse labeling tasks, such as video suggestions [3] or demographics prediction in networks [38]. Although these methods aim to model the network structure as a whole, they are based on an implicit model of the joint probability distribution of all the node labels [5]. As an alternative, inference approaches using probabilistic graphical models (PGMs) were developed as the PGM modeling explicitly fully describes the interactions between the nodes [10].

Nevertheless, none of the current approaches investigates the improvement of uncertain predictions, which can be obtained by a classical machine learning algorithm predicting the labels based on individual profiles, while modeling the network structure as a whole. Instead, the current studies focus on the propagation of known labels through a network. In addition, to the best of our knowledge, no research quantifies how the performances of label predictions in a network evolve as a function of the assortativity strength.

In this work, we propose a general framework based on probabilistic graphical models (PGMs) to exploit the social network structure to improve uncertain individual predictions and infer missing labels. The method can be applied while only knowing the labels of a limited number of pairs of connected users in order to evaluate the assortativity. Then, the inference process is based on class probability estimates for each user. These initial class probabilities may be obtained (1) by considering a subset of labeled users or (2) from a machine learning algorithm applied on the node-level individual features. A loopy belief propagation algorithm is afterward applied on a Markov random field modeling the network to improve the accuracy of the class probability estimates. The model is able to benefit from the strength of the links, quantified for example by the number of contacts. The estimation of the network assortativity allows to optimally tune the model parameters, by defining synthetic graphs. The latter simulations permit (1) to prevent overfitting a given (real) network structure, (2) to perform the parameter tuning off-line and (3) to avoid requiring the labeled users to form a connected graph. These simulations also allow to quantify the assortativity range leading to an accuracy gain over an approach ignoring the network structure. The methodology is validated on real-world mobile phone data to predict gender. As the assortativity required to significantly improve the quality of the prior class probabilities might not always be reached in practice, we show that the assortativity significantly changes according to some communication attributes, which can in turn be exploited to improve the predictions by appropriately adapting the model parameters in different parts of the network. Experiments on a real-world mobile phone network suggest the statistically significant superiority of our methodology over state-of-the-art algorithms, namely the reaction–diffusion label propagation method [38] and three machine learning classifiers relying on features extracted by the Node2vec graph embedding technique [15].

The paper is organized as follows. Section 2 introduces the framework of probabilistic graphical models (PGMs) and the notations. The readers who are already familiar with this field can safely skip this part. Then, the general methodology to improve attribute predictions in a network is detailed in Sect. 3. Its key parameters are highlighted, and their tuning based on simulated assortative networks is detailed. In Sect. 4, we introduce the real-world data sets which are studied, analyze their underlying gender homophily and assess the performances of our method compared to state-of-the-art algorithms, based on feature extraction using Node2vec [15] and on label propagation using the reaction–diffusion algorithm [38]. Section 5 then discusses the results and describes the related work more extensively. Conclusions are drawn in Sect. 6.

2 Background and notations

This section introduces undirected graphical models and how they can be used to perform inference about the variables they model. Uppercase and lowercase letters denote, respectively, random variables and observed values. The probability distribution of a random variable (or a set of random variables) $X$ is denoted by $p_{ X }$. It corresponds to the probability density (resp. mass) function for a continuous (resp. discrete) random variable $X$. For instance, the probability for a discrete random variable $X$ to be equal to $x$ is $p_{ X }( x ):=\mathbb {P}( X = x )$.

2.1 Probabilistic graphical models (PGMs)

A probabilistic graphical model is a graph ${\mathcal {G}}_M= ({\mathcal {S}}, {\mathcal {A}})$, where ${\mathcal {S}}:=\{1,\ldots ,N\}$ and ${\mathcal {A}}\subset {\mathcal {S}}\times {\mathcal {S}}$ denote, respectively, the set of nodes and edges, in which each node $i\in {\mathcal {S}}$ is associated with a random variable $X _i$ and each edge $e\in {\mathcal {A}}$ represents a direct statistical dependency between the random variables it links. Any pair of nodes which are not connected can only statistically depend on each other through some other variables on the path relating them [13]. Let $X$ denote the concatenation of all the $X _i$’s for $i=1,\ldots ,N$. A given PGM models a family of probability distributions over $X$ which, importantly, admit a particular factorization according to the graph structure. Graphical models aim to represent compactly distributions over interacting variables, allowing to decrease the complexity of inference processes. There exist mainly three kinds of PGMs: undirected graphical models (also called Markov random fields (MRFs) or Markov networks), directed acyclic graphical models (DAGs or Bayesian networks) and factor graphs [20]. MRFs are employed in this work and are defined as follows.

Definition 1

(Markov random field (MRF)) An undirected graphical model, or MRF, represents a family of probability distributions over $X$ using an undirected graph ${\mathcal {G}}_M$. The implied variables satisfy the graph separation property: For any three sets of nodes $\mathcal { H }$, $\mathcal { B }$ and $\mathcal { D } \subset {\mathcal {S}}$ in the PGM and their associated vectors of random variables $X _{\mathcal { H }}$, $X _{\mathcal { B }}$ and $X _{\mathcal { D }}$, $X _{\mathcal { H }}$ is independent from $X _{\mathcal { B }}$ conditionally to $X _{\mathcal { D }}$ ($X _{\mathcal {H}} {\perp\mkern-10mu\perp} X _{\mathcal {B}}| X _{\mathcal {D}}$) when any path in the graph from one node in $\mathcal { H }$ to one node in $\mathcal { B }$ contains a node in $\mathcal { D }$.

The Hammersley–Clifford theorem relates this definition to the factorization of the joint distribution induced by the graph:

Theorem 1

(Hammersley–Clifford) A strictly positive distribution $p_{ X }$ satisfies the graph separation property if and only if it can be factored as

$$\begin{aligned} p_{ X }( x ) = \frac{1}{Z} \prod \limits _{C\in \mathcal { C }} \psi _{ X _C}( x _C), \end{aligned}$$

(1)

where $\mathcal { C }$ is the set of maximal cliques¹in the graph ${\mathcal {G}}_M$, $Z = \sum _{ x } \prod _{C\in \mathcal { C }}\psi _{ X _C}( x _C)$ is termed as the partition function and the $\psi _{ X _C}$’s are nonnegative functions, called clique potentials.

The clique potentials define ‘compatibility’ functions between the values taken by the variables $X _C$. They do not necessarily correspond to (conditional) probabilities over the cliques. It can be noted that the potentials defined on the maximal cliques may, in some cases, also be factored as the product of potentials defined on nonmaximal cliques. In particular, when the joint probability distribution $p_{ X }$ is unknown and needs to be modeled, any factorization based on potentials defined on nonmaximal cliques can be converted to one based on maximal cliques by defining the maximal-clique potentials as being the product of a subset of the nonmaximal-clique potentials [47].

2.2 Inference on PGMs

Inference aims to compute marginal probabilities or modes of a joint distribution [47]. Assuming that discrete random variables are considered (otherwise, sums can be replaced by integrals), computing a marginal such as $p_{ X _1}( x _1)$ consists in summing over all the remaining variables: $p_{ X _1}( x _1) = \sum _{ x _2}\cdots \sum _{ x _N}$ $p_{ X }$($x$). When the joint distribution admits a factorization such as (1), it can be used to reduce the computational cost of the inference. Indeed, the sum over each variable can be performed on factors defined on subsets of nodes. The book of Koller and Friedman provides for some concrete examples [20]. This reasoning leads to the loopy belief propagation (LBP) algorithm which can be applied on any kind of PGM. If the graph is a tree, LBP converges to the correct marginals in a limited number of iterations [29]. Otherwise, the estimated marginals are optimal in the Bethe–Kikuchi sense [47].

3 Method

Given an arbitrary social network ${\mathcal {G}}$, the goal is to exploit its assortativity to infer, for each user i, an individual scalar attribute (or class) $Y_i$ taking values in a finite alphabet $\mathcal {Y}$. This class can be, for instance, the age or gender of each individual. The graph ${\mathcal {G}}$ is defined as a pair $({\mathcal {V}}, {\mathcal {E}})$, where ${\mathcal {V}}$ and ${\mathcal {E}}$ are, respectively, the sets of nodes (one for each user) and edges (connecting each pair of individuals who are in contact), with $|{\mathcal {V}}|=N$. The available individual information about user i is denoted by the random vector $X_i$. For example, in the case of Twitter, $x_i$ could consist in the tweets generated by user i and possibly in public profile details (e.g., the user’s name). It is assumed that estimates ${\widehat{p}}_{Y_i| X_i}(y_i|x_i)$ of the class membership probabilities $p_{Y_i| X_i}(y_i|x_i)$ are provided. These can be seen as ‘initial predictions’ for each user $i \in {\mathcal {V}}$, which can encode deterministic information (known labels) or which can be outputted by a machine learning algorithm applied on the individual features $x_i$ to predict the class $y_i$. If such information is missing for some users, uniform class probabilities of $\frac{1}{|\mathcal {Y}|}$ are used. In what follows, $Y$ (resp. $X$) denotes the concatenation of all the $Y_i$’s (resp. $X_i$’s).

The rest of this section is structured as follows. Our inference model is built in Sect. 3.1 based on the social network, and the employed message-passing algorithm is detailed in Sect. 3.2. Next, in Sect. 3.3, by simulating individual predictions ${\widehat{p}}_{Y_i| X_i}(y_i|x_i)$ and synthetic networks, we assess how the performance enhancement is related to the network assortativity and to the quality of the initial set of predictions, in terms of both accuracy and distribution. This procedure permits to determine the best model parameters.

3.1 Probabilistic graphical model

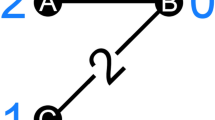
In order to improve the initial predictions ${\widehat{p}}_{Y_i| X_i}(y_i|x_i)$, the joint probability distribution $p_{}(Y, X)$ is modeled through an undirected PGM ${\mathcal {G}}_M$ (also called Markov random field, MRF). The MRF has one node (resp. one edge) for each user (resp. link) in the social network. The random variables $Y_i$ that we want to infer are assigned to the nodes of the network; each link represents a conditional dependency between two of them. As indicated in Fig. 1, the graphical model ${\mathcal {G}}_M$ contains N additional nodes associated with the $X_i$’s, each one being linked to its corresponding $Y_i$ (as in [49] for instance). The relationships between the individual data $X_i$ and the label $Y_i$ of each user i are hence captured, as well as the direct mutual influence of adjacent users. We choose an undirected graphical model to characterize the statistical dependencies between the considered random variables, since there is no causal link between the labels in the social network which could be represented with a directed PGM. Also, the joint distribution $p_{}(Y, X)$ does not admit a natural factorization through conditional probabilities [47]. Instead, our MRF represents conditional independencies. As a result, the graph separation property [20] indicates that the joint probability distribution $p_{}(Y, X)$ modeled by the PGM admits the factorization

$$\begin{aligned} p_{Y,X}(y, x) = p_{Y}(y) \cdot \prod \limits _{i} p_{X_i|Y_i}(x_i|y_i). \end{aligned}$$

(2)

The assumption underlying the graphical representation is that $X_i$ given $Y_i$ is conditionally independent from $Y_j$ and $X_j$, for all $j\ne i$. Namely, the generative probabilities of the features given the class of each node are assumed to be conditionally independent.

Fig. 1

Toy example of the Markov random field. There are two nodes per user i in the graph, $Y_i$ being her class and $X_i$ her individual data

Let us use the notations

$$\begin{aligned} \psi (y_i,x_i) := p_{X_i| Y_i}(x_i|y_i) \propto \frac{p_{Y_i| X_i}(y_i|x_i)}{p_{Y_i}(y_i)}. \end{aligned}$$

(3)

As $\psi$ is defined over the random variables associated with each node of the social network ${\mathcal {G}}$, it is called the node potential. It corresponds to the likelihood of the ith user’s individual data knowing her class. Besides, factorization (2) entails the joint distribution $p_{Y}(y)$ of the labels. The Hammersley–Clifford theorem indicates that the latter can be factored as a product of nonnegative functions defined over cliques in ${\mathcal {G}}_M$. We choose to represent pairwise interactions for $p_{Y}(y)$, i.e., we define a clique potential over each edge binding two $y_i$’s. According to our PGM, as illustrated in Fig. 1, the factorization hence develops as

$$\begin{aligned} p_{Y,X}(y, x) = \frac{1}{Z} \prod \limits _{i} \psi (y_i,x_i) \prod \limits _{(j,k)\in {\mathcal {E}}} \varPsi (y_j, y_k), \end{aligned}$$

(4)

where Z is the partition function (a normalization constant) and $\psi$ and $\varPsi$, respectively, denote the node and edge potentials. The ith node potential $\psi (y_i,x_i)$ can be estimated using the first predicted class probability ${\widehat{p}}_{Y_i| X_i}(y_i|x_i)$ and an estimated class prior ${\widehat{p}}_{Y_i}(y_i)$, which can be defined as the proportion of users initially predicted as $y_i$. Besides, in order to reflect either the label assortativity or disassortativity of each link, the edge potential $\varPsi (y_j,y_k)$ for each pair of adjacent users j and k can be defined as

$$\begin{aligned} \varPsi (y_j, y_k) = \left\{ \begin{array}{ll} s_{jk}, &{} {\text{if}}\, y_j = y_k\\ 1-s_{jk}, &{} {\text{if}}\, y_j \ne y_k \end{array} \right. \end{aligned}$$

(5)

with $s_{jk} \in [0,1]$ and $y_j$, $y_k \in \mathcal {Y}$. It is noteworthy that if $s_{jk}$ is greater than 0.5, $\varPsi (y_j, y_k)$ will encourage users j and k to share the same class. At the opposite, an $s_{jk}$ value smaller than 0.5 will favor neighboring users j and k to have different labels (anti-homophilic contacts). This parameter of label compatibility over the edges can hence be interpreted as the probability for edge (j, k) to be homophilic. Depending on the application, one may have access to some edge weights, which can be used to model these $s_{jk}$. Section 4.4 provides an example of such a refinement in the context of a real-world application. Another option is to employ a constant $s_{jk}$ value for all the edges.

3.2 Inference algorithm

Along with factorization (4) of the joint probability distribution, the defined PGM structure enables efficiently inferring the posterior probabilities $p_{Y_i|X}$, from which enhanced predictions of the users’ label are derived. Exact inference on the loopy MRF is intractable, as it would require using the junction tree algorithm [20] which, even if all the maximal cliques in ${\mathcal {G}}$ were identified, has an exponential complexity in the size of the largest one. This motivates relying on factorization (4), with pairwise potentials only, and leads to the loopy belief propagation (LBP) algorithm [20]. As further detailed hereunder, LBP provides estimates of the posterior probabilities ${\widehat{p}}_{Y_i|X}(y_i|x)$ for each node i in the graph and for all $y_i \in \mathcal {Y}$. These estimates approximate the true posterior probabilities $p_{Y_i|X}(y_i|x)$ in the Bethe–Kikuchi sense [47]. The predicted class for user i is then given by $\arg \max \nolimits _{y_i \in \mathcal {Y}} {\widehat{p}}_{Y_i|X}(y_i|x)$.

Computing the conditional probability of a random variable $Y_i$, given the observed variables, consists in marginalizing over the remaining unobserved variables. A normalization step at the end ensures that we have a valid conditional distribution. The intuition behind belief propagation algorithms is to perform these marginalizations efficiently, by avoiding to repeatedly compute the same intermediate sums. As a result, LBP is an iterative algorithm in which, at each iteration t, every node j sends a message $m_{jk}^{t}$ to each of its neighboring nodes k defined as

$$\begin{aligned} \frac{m_{jk}^{t}(y_k)}{k_1} = \sum \limits _{y_j \in \mathcal {Y}} \left( \psi (y_j,x_j) \varPsi (y_j,y_k) \prod \limits _{u \in {\mathcal {N}}(j){\setminus } k} m_{uj}^{t-1}(y_j)\right) , \end{aligned}$$

(6)

for $y_k \in \mathcal {Y}$ and where ${\mathcal {N}}(j)$ is the set of neighbors of user j. The normalization constant $k_1$ is chosen such that the messages on each edge and direction sum to 1: $\sum _{y_k\in \mathcal {Y}} m_{jk}^{t}(y_k) = 1$. The initial messages $m_{jk}^0$ are set to $1/|\mathcal {Y}|$. The summation over the values of the random variable $Y_j$ consists in marginalizing this variable. The message $m_{jk}^{t}(y_k)$ can be interpreted as all the information the sender (node j) can provide to the receiver (node k) on the probability for node k to lie in state $y_k$. After the convergence of the 2N messages after $t^*$ iterations and a normalization step, estimates of the posterior probabilities $p_{Y_i|X}(y_i|x)$, termed as beliefs and denoted by $b(y_i)$, can be computed for each node i in the graph and for all $y_i \in \mathcal {Y}$ as follows:

$$\begin{aligned} p_{Y_i| X}(y_i|x) \approx b(y_i):= k_2 \cdot \psi (y_i,x_i) \prod \limits _{u \in {\mathcal {N}}(i)} m_{ui}^{t^*}(y_i), \end{aligned}$$

(7)

where $k_2$ is a normalization constant such that $\sum _{y_i \in \mathcal {Y}} b(y_i) = 1$. The predicted class for user i is the one maximizing the estimated posterior probability:

$$\begin{aligned} y_i^{*} = \arg \max \limits _{y_i \in \mathcal {Y}} b(y_i). \end{aligned}$$

(8)

This procedure enables handling large graphs as the complexity of a single message-update iteration is ${\mathcal {O}}(|{\mathcal {E}}|\cdot |\mathcal {Y}|^2)$. In comparison, a brute-force marginalization has a complexity of $\mathcal {O}$($N \cdot |\mathcal {Y}|^N$). It can also be noted that (6) highlights the influence of the edge potential $\varPsi$: An $s_{jk}$ larger than 0.5 on a given edge encourages neighboring users to share the same class.

3.3 Parameter tuning

The $s_{jk}$ values of the edge potential (5) need to be determined. As these parameters reflect the confidence in the (dis-)assortative character of the edges, their tuning should be related to the network assortativity. The latter quantity hence has to be quantified, which is detailed in Sect. 3.3.1. Then, after defining synthetic networks with adjustable assortativity in Sect. 3.3.2, Sects. 3.3.3 and 3.3.4 study the influence of the assortativity on the model parameters and on the performances. This is done both by simulating individual predictions and by assuming that a subset of labels are known.

3.3.1 Assortativity coefficient

To quantify the assortativity of a network for a given node attribute, Newman introduced the assortativity coefficient, denoted by $r$ [31]. It assesses the correlation between the attributes of adjacent nodes, which can be categorical such as the gender or the political affiliation. For scalar, discrete or continuous, attributes such as the user’s age or the node degree, a numeric assortativity coefficient is defined. In the following, we focus on the assortativity coefficient defined for categorical attributes on an undirected graph.

The assortativity coefficient can be derived thanks to the symmetric mixing matrix $M=\left[ m_{ij}\right] _{i,j=1}^{L}$, where $m_{ij}$ is half the fraction (resp. the fraction) of edges connecting a vertex of class i to a vertex of class j when $i\ne j$ (resp. when $i=j$), and $L = |\mathcal {Y}|$ is the total number of classes of the attribute of interest. Each of the row sums of the mixing matrix, denoted by $m_i:=\sum _{j}m_{ij}$, gives the proportion of ends of edges from class i. It corresponds to the sum of degrees of the nodes from class i divided by the number of ends of edges (i.e., twice the number of edges). For a discrete attribute on an undirected graph, the assortativity coefficient expresses as

$$\begin{aligned} r= \frac{\sum _{i}m_{ii} -\sum _i m_i^2}{1 - \sum _i m_i^2} \in [-1, 1]. \end{aligned}$$

(9)

If all the edges lie between pairs of people of the same class, the network is perfectly assortative and it is straightforward to derive that $r=1$. At the opposite, in a perfectly disassortative network, r will range in $[-1,0[$, as detailed in [31]. In the intermediate case, a random mixing occurs when the classes of two connected users are independent. Hence, $m_{ii} = m_{i}^2$ which implies that $r=0$. Many studies show that social networks tend to be more assortative than other ones (e.g., technological or biological) [8], with positive assortativity coefficients ranging up to 0.6 [32] for attributes like race of partners in a bipartite graph of sexual partnerships. According to McPherson et al. [24], the latter attribute is among the most homophilic ones.

In the special case of a binary attribute, the mixing matrix becomes

$$\begin{aligned} M = \begin{pmatrix} m_{11} &{} m_{12} \\ m_{21} &{} m_{22} \end{pmatrix}, \end{aligned}$$

(10)

and the assortativity coefficient is defined as

$$\begin{aligned} r = \frac{m_{11} + m_{22} - m_1^2 - m_2^2}{1- m_1^2 - m_2^2 }. \end{aligned}$$

(11)

In this particular setting, the assortativity of a perfectly disassortative network reaches $-1$. Indeed, there can only be as many nodes from each of the two classes at the ends of the edges of such a network, since each edge is between two users from distinct classes. Hence, $m_1 = m_2=0.5$ and r is equal to $-1$.

As it is most of the time unknown, $r$ should be reliably estimated in a real setting. An efficient possibility consists in edge sampling, as described in Sect. 4.4 in the case of gender prediction in a mobile phone network. We hence assume in the following that an accurate estimate of $r$ is provided.

For a given network, the model parameters $s_{jk}$ of the edge potential $\varPsi$ can be optimized according to our confidence in the (dis-)assortativity of each link (j, k). If our sole knowledge about assortativity is $r$, a constant $s_{jk}$ value (denoted by s) can be used for all the edges. This s characterizes the confidence in the network information, which is proportional to $\left| r\right|$: as indicated by (4), large $|0.5-s|$ values dilute the initial predictions contained in the node potential $\psi$ and give a heavy weight to the network, while at the opposite an s value close to 0.5 will not change the initial predictions by much, since $\varPsi$ will remain roughly constant when its arguments (i.e., the class labels) are either equal or different. Synthetic networks, defined in the next section, with assortativity coefficients close to a given $r$, enable us to find an optimal s. To this aim, a grid search is performed: LBP is applied on the MRF with each s value from the grid, and the one achieving the highest average performances on different synthetic networks is kept as optimal. Employing a grid search is convenient as it yields robust results. Its usage is affordable thanks to the efficiency of LBP and since a single parameter needs to be optimized. Alternative optimization schemes will be considered in future works and may only be beneficial for the performances of our approach.

To get a clear picture of our approach and to identify more easily the meaning of the following sections, the different steps are summarized in Fig. 2.

Fig. 2

Summary of the proposed method. To apply the LBP algorithm to infer the node labels using the label assortativity, the edge potential (box C) and node potential (box E) have to be defined. The edge potential can be deduced from the network assortativity $r$ (box A), which can be estimated thanks to social theories or edge sampling, as detailed in Sect. 4.4.3. The estimated $r$ can then be employed to generate synthetic graphs enabling to tune the edge potential parameters (box B). On the other hand, the initial individual predictions (box D) are used to define the node potentials. The LBP algorithm (box F), using the node and edge potential, yields predicted class membership probabilities ${\widehat{p}}_{Y_i| X}(y_i|x)$ (box G). It is noteworthy that $X= \{X_i\}_{i=1}^N$ concatenates all the $X_i$’s. Therefore, the predictions ${\widehat{p}}_{Y_i| X}(y_i|x)$ (box G) rely on the whole network structure, whereas the initial predictions ${\widehat{p}}_{Y_i| X_i}(y_i|x_i)$ (box D) are only based on the individual node-level information

3.3.2 Synthetic networks

The construction of the synthetic networks relies on the same principle as the Watts–Strogatz small-world graphs [30]. It first starts with a regular circular lattice ${\mathcal {G}}_R= ({\mathcal {V}}_R, {\mathcal {E}}_R)$, each of the n nodes being linked to its k closest neighbors in a ring topology, where k is even. The attribute values $y_i$’s that need to be inferred are randomly assigned to each node i by sampling a given distribution. Some edges are then rewired in the graph until the obtained assortativity coefficient is sufficiently close to the targeted one, denoted by $r$. This last step is detailed by the following procedure, illustrated in Fig. 3:

Fig. 3

a Regular lattice, b binary label assignation and c final graph obtained after some edges rewiring, with 15 nodes, a mean degree $k = 4$ and $r\approx 0.3$. The homogeneous edges are depicted in red (color figure online)

It can be noted that if one makes additional assumptions on the graphs structure, different steps in the generation of the synthetic networks could also be considered. For instance, the LFR model allows to control the community structure (the community size distribution and the proportion of within-community edges) and the degree distribution to obtain more realistic graphs [33]. Besides, if the mixing matrix was constrained, it could be used to refine the network simulations [31]. Our simulated networks are chosen here to only control the assortativity with respect to the node label, without additional constraint on the graphs properties.

It remains to endow the synthetic network nodes with prior class probability estimates ${\widehat{p}}_{Y_i| X_i}(y_i|x_i)$. In practice, these probabilities can either be obtained from a machine learning algorithm applied on the individual features $x_i$ of each user, or from a subset of labeled users. Both of these situations can be handled in the context of the synthetic networks, as detailed in the two next sections.

3.3.3 Individual predictions

In a given application, a machine learning algorithm predicting the classes $y_i$ from the individual features $x_i$ gives access to a prior information for all the users of the real network. Sampling the distribution of these individual predictions ${\widehat{p}}_{Y_i| X_i}(y_i|x_i)$ enables assigning prior class probability estimates to the nodes of the synthetic graphs, which may afterward be employed to determine the optimal model parameters. Nevertheless, in order to analyze the behavior of our method when it is confronted to different uncertainty patterns, we here generate these prior probabilities for a binary label according to three synthetic distributions: linear, exponential and bi-uniform, as depicted in Fig. 4. The proportion of correct initial predictions, i.e., the initial accuracy, has to be controlled as it will influence the performances of the subsequent algorithms employed to refine these predictions using the network information. The initial classification rule amounts to predict $y_i^I = \arg \max _{y_i}{\widehat{p}}_{Y_i| X_i}(y_i|x_i)$. Therefore, the initial accuracy, denoted by $\beta$, corresponds to the fraction of users i for whom ${\widehat{p}}_{Y_i| X_i}(c_i|x_i)\ge 0.5$ when the label is binary, where $c_i$ is the true class of user i. The distributions of the class probabilities cover three situations with different levels of difficulty for the subsequent classification task, depending on whether the amplitude of ${\widehat{p}}_{Y_i| X_i}(y_i|x_i)$ is more or less related to the prediction correctness. With the linear and exponential distributions, the probability for a prediction to be actually correct increases with the available confidence level, whereas with the bi-uniform distribution, when ${\widehat{p}}_{Y_i| X_i}(y_i|x_i)\ge 0.5$, the proportion of correct predictions does not increase with the confidence level ${\widehat{p}}_{Y_i| X_i}(y_i|x_i)$. All the three distributions are sampled by inverse transform sampling [9].

Fig. 4

a Linear, b exponential and c bi-uniform distributions of true class prior probabilities, leading to an accuracy $\beta$ of the initial individual predictions for a binary classification problem. The true class of user i is denoted by $c_i$

The results of the parameter tuning procedure are depicted in Fig. 5 for an arbitrary binary attribute, such as the gender. The best s value and the corresponding mean accuracy gain, with respect to the accuracy $\beta$ of the initial individual predictions, are provided as a function of the assortativity and the accuracy $\beta$. For each pair of $\beta$ and $r$, the optimal s value is selected as the one maximizing the average accuracy over 30 random networks with 200 vertices containing as many nodes from each one of the two classes. The randomness covers the edge rewiring in the networks, the attribute assignations and the sampling of the prior probabilities. From the top to the bottom row of figures, the prior probabilities are simulated using the three distributions illustrated in Fig. 4.

It can be observed that the optimal s values are almost independent of $\beta$, and hence, the parameterization mainly depends on the assortativity coefficient, using any of the three distributions of initial predictions. Also, the chosen s evolves in a consistent way as a function of the assortativity $r$, increasing from smaller values for disassortative networks to higher values for assortative ones. Using these optimal s values when prior probabilities are linearly or exponentially distributed, Fig. 5b, d shows that the accuracy gain is almost always positive, except for some particular pairs of $r$ and $\beta$, especially when the assortativity is within the range $[-\,0.1, 0.1]$. This observation is consistent as our PGM is designed to exploit the assortativity, which is absent if $r = 0$, corresponding to a randomly mixed network according to the considered attribute. The results obtained using initial predictions drawn from the linear and exponential distributions are very similar. For the bi-uniform individual predictions however, much lower accuracy gains are observed. These results can be explained as, in this case, only the sign of ${\widehat{p}}_{Y_i| X_i}(c_i|x_i)-0.5$ brings information on the true class probabilities, where $c_i$ is the true class of user i. On the other hand, its amplitude also matters for the linear and exponential distributions. It would also most probably be the case in real settings: If an ML algorithm outputs a high confidence level about an individual prediction, the probability for this prediction to be indeed correct should be higher than for another prediction with a lower confidence level. From this respect, the bi-uniform distribution may not be very realistic and could correspond to a worst-case scenario. The extension to the case of nonbinary attributes is straightforward, possibly by employing the numeric assortativity coefficient, e.g., in the case of the age attribute.

Fig. 5

Parameter tuning on synthetic networks when individual predictions are considered. a, c, e Optimal s parameter of the edge potential (5), with a constant $s_{jk}$ for all the edges of the networks and b, d, f mean accuracy gain (in %) over 30 random synthetic networks, designed as detailed in Sect. 3.3.2. The s parameter is tuned by considering a grid with a 0.05 step. Each network has 200 nodes and a mean degree $k=8$, a reasonable value for common social networks [32]. The results are given as a function of the accuracy $\beta$ (in %) of the initial individual predictions and the assortativity coefficient when considering a binary attribute. The initial predictions are simulated with a linear, exponential and bi-uniform distribution from the top to the bottom row

3.3.4 Labeled data

Prior information about the users’ class can also consist in a subset of labeled users. In this case, the class of a fraction $\beta$ of all the network users is known, whereas no prior clue is provided about the class of the remaining fraction $1-\beta$ of users. The symbol $\beta$ is again used in this section, by analogy with the accuracy of the initial individual predictions of Sect. 3.3.3. Figure 6 shows the optimal s parameter computed and the accuracy of the predictions obtained on the unlabeled nodes in synthetic networks, as a function of the fraction $\beta$ of known labels and the assortativity coefficient when considering a binary attribute. Similarly to the results of Sect. 3.3.3, the evolution of the optimal s as a function of the assortativity $r$ is consistent: It roughly increases from smaller values for disassortative networks to higher values for assortative ones. However, by opposition to what is observed when individual predictions are considered as in Fig. 5, the chosen s value is not independent of the fraction $\beta$ of labeled users: When $\beta$ increases, the s parameter tends toward more extreme values, no matter the network assortativity. It can be explained as, with labeled nodes, there is no wrong initial predictions to mitigate through the inference process unlike in the initial individual prediction setting of Sect. 3.3.3. It is furthermore noteworthy to observe that, for a fixed $r$, the performances strictly increase with the training percentage $\beta$, without saturating effect.

Fig. 6

Parameter tuning on synthetic networks when a fraction of node labels are known, defining a training set. a Optimal s parameter of the edge potential (5), with a constant $s_{jk}$ for all the edges of the networks and b mean accuracy (in %) on the unlabeled nodes over 30 random synthetic networks. The s parameter is tuned by considering a grid with a 0.05 step. Each network has 200 nodes and a mean degree $k=8$. The results are given as a function of the fraction of known node labels (in %) and the assortativity coefficient when considering a binary attribute

4 Mobile phone networks

The validation task considered in this section consists in gender prediction in an undirected and weighted mobile phone network from a developed European country.

Predicting gender is of great interest to assess a demographic structure. For instance, this information is required to study gender disparities in diverse countries, allowing to refine or even undermine the available reports using social networks such as Google$+$ [23], Twitter or mobile phone networks. Among social networks, mobile phone data currently raise the interest of the research community and practitioners, as they become more and more ubiquitous, while being freely accessible at massive scale, automatically collected in real-time and powerful indicators of people behaviors [6, 27]. They also often consist in the most accessible type of population information in developing countries. A shortcoming to their use however is that they often lack even the most basic information about their carrier, such as the gender, age or socioeconomic status. Indeed, most of the mobile phone connections worldwide are prepaid, as well in developing as in developed countries. Although these connections provide fine-grained information about the mobile phone usage, they do not give any access to basic demographics.

The data set is first introduced in Sect. 4.1, detailing some of its features suggesting significant gender homophily which can be exploited for the inference process. Section 4.2 quantifies the gender assortativity as well as its dependence with some mobile communication attributes. Section 4.3 builds on the conclusions of Sect. 4.2 to refine the model parameter tuning, accounting for the communication patterns for the edge potential definition. Section 4.4 discusses the performances of the proposed methodology, by comparing them with the results of state-of-the-art classification methods based on label propagation and feature extraction.

In the following, $X_i$ denotes the individual metadata of user i and $Y_i$ is the random variable for her gender, defined on the alphabet $\mathcal {Y}= \{F,M\}$ with $F$ and $M$, respectively, for a female and male.

4.1 Data description

Two undirected and weighted mobile phone networks, denoted by ${\mathcal {G}}_S$ and ${\mathcal {G}}_L$, are used in this section: The data analysis of this work is only conducted on ${\mathcal {G}}_L$, while the performance assessment is performed on ${\mathcal {G}}_S$. This allows to avoid overfitting the particular network ${\mathcal {G}}_L$. In both ${\mathcal {G}}_L$ and ${\mathcal {G}}_S$, each node refers to one individual and an undirected edge binds any pair of users who exchanged at least one phone call or text during a fixed time period. The gender is known for the majority of the users. The communication attributes, extracted from the Call Detail Records (CDRs), of any edge e are the number of texts ($\textsc {sms}$), the number of calls ($\textsc {calls}$) and the total duration of the calls ($\textsc {call}\_\textsc {dur}$). Different functions of these edge attributes can be defined. For example, the sum of $\textsc {sms}$ and $\textsc {calls}$ is denoted by $\textsc {s}\_\textsc {and}\_\textsc {c}$ and counts the number of contacts between two given persons, which is well suited to characterize the strength of a social link [34].

Table 1 Some features of the networks

Table 1 provides general features of both networks, as well as the mean values of the three attributes of the edges between persons of both the same and different genders. As indicated, the average communication patterns differ between hetero- and homogeneous (M–M and F–F) contacts. This reflects the stronger relationships occurring within the couples. Indeed, for instance in ${\mathcal {G}}_L$, there are on average 6.4 and 9.7 contacts (calls and texts), respectively, between any homo- and heterogeneous pairs during the observation period. The same behavior is observed for the number of texts or calls distinctly. However, as shown in Fig. 7, there is no obvious dichotomy between the distributions of each attribute on the homo- and heterogeneous edges.

Fig. 7

Distribution of the edge attributes in ${\mathcal {G}}_L$, with logarithmic y-scales. ‘Homogeneous’ (homo.) and ‘heterogeneous’ (hetero.) refer to the gender of the persons linked by the edges

It can be mentioned that the mobile phone use of each individual according to her gender is not analyzed in this study, since this kind of information is typically exploited to provide the individual predictions. Finally, as the gender is binary, its assortativity coefficient is defined by (11). In ${\mathcal {G}}_S$ and ${\mathcal {G}}_L$, a moderate gender assortative mixing is observed.

4.2 Observational analysis

Since the strength of the heterogeneous communications, in terms of number of texts and calls exchanged, tends to overcome the one of the homogeneous contacts, the weights of an edge might give clues on its likelihood to be rather hetero- or homogenous. The subset of the strongest edges may hence have a completely different assortativity than the whole network. As the performances of our approach increase with the assortativity amplitude, identifying stronger (anti-)homophilic subgroups is of great interest. This section shows that the assortativity $r$ can indeed significantly change when considering subsets of the edges with specific weights. This kind of information can afterward be used to refine the edge potential, as indicated in box A of Fig. 2.

We analyze the evolution of the assortativity coefficient when subgraphs are constructed by only considering the edges with a scalar combination of their attributes above a threshold, the latter being progressively increased. For a given threshold and attribute combination, the strongest edges, according to the considered combination, constitute the strong part of the graph, while the weaker part refers to the rest. Several attribute combinations have been considered, including the attributes themselves. The most significant evolution of the assortativity $r$ is obtained using $\textsc {s}\_\textsc {and}\_\textsc {c}$ as a measure of link strength and is depicted in Fig. 8. The assortativity coefficient in the strong part (i.e., with edges such that $\textsc {s}\_\textsc {and}\_\textsc {c}$ is higher than the threshold on the x-axis) is denoted by $r_\mathrm{strong}$, while $r_\mathrm{weak}$ is the one of the weak part. The number of edges in the strong part is denoted by $n_\mathrm{strong}$. The dotted lines indicate the threshold and the corresponding $r_\mathrm{weak}$, $r_\mathrm{strong}$ and $n_\mathrm{strong}$ values such that there are 1% of the edges in the strong part of ${\mathcal {G}}_L$. Using this partition, $r_\mathrm{weak}$ is still equal to about 0.3, but $r_\mathrm{strong}$ reaches $-\,0.3$ meaning that the strong part is rather anti-homophilic, as suggested by Table 1. From a more general point of view, as the threshold on $\textsc {s}\_\textsc {and}\_\textsc {c}$ increases, $r_\mathrm{strong}$ decreases toward disassortative values. Meanwhile, $r_\mathrm{weak}$ remains quite stable since most edges have small $\textsc {s}\_\textsc {and}\_\textsc {c}$, as indicated by the evolution of $n_\mathrm{strong}$ in logarithmic scale.

Fig. 8

Gender assortativity coefficient in ${\mathcal {G}}_L$ when the edges with $\textsc {s}\_\textsc {and}\_\textsc {c}$ values larger than some increasing thresholds are kept (strong part) or discarded (weak part). The red curve (right y-axis in logarithmic scale) indicates the number of edges in the strong part, denoted by $n_\mathrm{strong}$ (color figure online)

Fig. 9

Gender assortativity coefficient in ${\mathcal {G}}_L$ when only the edges with $\textsc {sms}$ and $\textsc {calls}$ values larger than some increasing thresholds are preserved. The top (resp. right) histogram gives the number $n_\mathrm{e}$ of edges with $\textsc {calls}$ (resp. $\textsc {sms}$) larger than the corresponding value on the x-axis (resp. y-axis), using a logarithmic scale

A refinement of the previous analysis consists in combining two thresholds on two different edge attributes in order to study how $r_\mathrm{strong}$ behaves. Figure 9 depicts such an evolution using the $\textsc {sms}$ and $\textsc {calls}$ attributes. The evolution of $r_\mathrm{weak}$ as a function of the two thresholds is negligible: It stays around 0.3, as in Fig. 8. Again, this figure highlights that the strongest edges are more disassortative. However, the strong part cannot be very large and have a significantly negative $r$ in the mean time, as most of the edges have low $\textsc {sms}$ and $\textsc {calls}$ values.

4.3 Refining the parameter tuning

In Sect. 3.3, we show how to select a constant $s_{jk}$ parameter of the edge potential for all the edges of a network with a given $r$ (boxes B and C in Fig. 2). On the other hand, the analysis of Sect. 4.2 suggests that the assortativity significantly varies in distinct parts of a mobile phone network, decreasing as the strength of the links increases. This can be interpreted as a social theory (box A of Fig. 2). This information can be exploited by defining different s values in the strong and weak parts of the network, respectively, denoted by $s_\mathrm{strong}$ and $s_\mathrm{weak}$, defined from the tuning on synthetic networks (box C of Fig. 2). However, modeling $s_{jk}$ as a step function is questionable. Indeed $s_{jk}$ is the posterior probability for the edge (j, k) to be homophilic given its weights. Since this posterior probability is unlikely to abruptly change for some weight value, a smooth function should model it, with upper and lower plateaus corresponding to $s_\mathrm{weak}$ and $s_\mathrm{strong}$, respectively. Determining whether the edge (j, k) is hetero- or homophilic can moreover be seen as a binary classification problem, with the edge weights as features. Thus, inspired by logistic regression, we model $s_{jk}$ as a sigmoid function parameterized by a fixed linear combination $\textsc {s}\_\textsc {and}\_\textsc {c}$ of the edge weights,

$$\begin{aligned} s_{jk}(\textsc {s}\_\textsc {and}\_\textsc {c}) = \frac{s_\mathrm{weak} - s_\mathrm{strong}}{1+ e^{G \cdot (\textsc {s}\_\textsc {and}\_\textsc {c}- x_0)}} + s_\mathrm{strong}, \end{aligned}$$

(12)

where G and $x_0$ are two parameters to determine. Following the observations of Sect. 4.2, the strong part of the network is defined as the set of the 1% strongest edges in terms of number of contacts. The plateaus $s_\mathrm{weak}$ and $s_\mathrm{strong}$ are tuned using the synthetic networks with constant $s_{jk}$ values, according to $r_\mathrm{weak}$ and $r_\mathrm{strong}$. Let us further denote by $x_{U}$ and $x_{L}$ the x-values at which the sigmoid reaches $s_\mathrm{strong}+0.99\left( s_\mathrm{weak} - s_\mathrm{strong}\right)$ and $s_\mathrm{strong}+0.01\left( s_\mathrm{weak} - s_\mathrm{strong}\right)$. The parameters G and $x_0$ are fixed such that there are approximately 1% of the edges with a number of contacts lower (resp. higher) than $x_{U}$ (resp. $x_{L}$). Figure 10 presents the resulting smooth model of the $s_{jk}$’s for ${\mathcal {G}}_S$, which is used in Sect. 4.4 to assess our methodology. The estimated $r_\mathrm{weak}$ and $r_\mathrm{strong}$ in ${\mathcal {G}}_S$ lead us to choose $s_\mathrm{weak} = 0.55$ and $s_\mathrm{strong} = 0.4$. The percentages below the curve indicate quantiles of the $\textsc {s}\_\textsc {and}\_\textsc {c}$ distribution.

Fig. 10

Sigmoid function defining the $s_{jk}$ values of the edge potential used for ${\mathcal {G}}_S$. The threshold on the number of contacts defining the edges as strong, indicated by the vertical line, is determined to induce 1% of strong edges. The top histogram gives the distribution of the number of contacts ($\textsc {s}\_\textsc {and}\_\textsc {c}$) in ${\mathcal {G}}_S$ in logarithmic scale

4.4 Results

The overall assortative character of ${\mathcal {G}}_L$, along with the observed differences between its strong and weak parts, indicates that the genders of the neighbors of an individual may be useful to predict her own gender. Our methodology is now tested on ${\mathcal {G}}_S$ in two settings: (1) when we simulate individual prior predictions and (2) when we assume that a subset of the node labels are known and that no information is provided for the remaining ones. In these two settings, the obtained performances are compared with the results of a state-of-the-art, baseline method, termed as the reaction–diffusion algorithm [37]. When a subset of the labels are observed, i.e., in the second setting, the methods are also compared to three machine learning classifiers relying on features extracted by Node2vec, a well-known graph embedding approach. Since this latter method is not designed to employ prior class probabilities as in the first setting, it is only tested in the second one.

4.4.1 Reaction–diffusion algorithm

The reaction–diffusion (RD) algorithm iteratively updates the predicted gender probability of each user by computing a weighted sum of its initial gender probability and the current one of her direct neighbors. It is hence based on initial prediction probabilities for each user, as in our approach. The notation $p_{i}^{t} := {\widehat{p}}_{ X _i}(M)$ denotes the estimated probability for user i to be a male at iteration t. These probability estimates are updated at each iteration for each user $i \in {\mathcal {V}}$ as

$$\begin{aligned} p_{i}^{t+1} = \frac{1}{2} \cdot \left( p_{i}^{0} + \frac{1}{|{\mathcal {N}}(i)|}\cdot \left( \sum \limits _{j \in {\mathcal {N}}(i)} p_{j}^{t} \right) \right) \quad \forall i \in {\mathcal {V}}, \end{aligned}$$

(13)

until convergence, where ${\mathcal {N}}(i)$ is the set of neighbors of user i and $p_{i}^{0} := {\widehat{p}}_{Y_i| X_i}(y_i=M|x_i)$ is the initial male probability for user i.

The RD method is a variant of the previously introduced and largely studied consistency method [50], with a regularization parameter fixed to 0.5. Indeed, let us note $A \in \{0,1\}^{N\times N}$ the adjacency matrix of the graph, with $A_{i,j} = 1$ if there is an edge between nodes i and j and 0 otherwise. We also define the diagonal matrix of degrees $D \in \mathbb {R}^{N\times N}$ where $D_{i,i} = \sum _{j\in {\mathcal {V}}} A_{i,j}$. We can express (13) in a matrix form as

$$\begin{aligned} {\mathbf {p}}^{t+1} = \frac{1}{2} \cdot \left( {\mathbf {p}}^{0} + D^{-1} A {\mathbf {p}}^{t} \right) , \end{aligned}$$

(14)

where the column vector ${\mathbf {p}}^{t} :=[p_{i}^{t}]_{i=1}^{N}$. It follows that RD is the first variant of the consistency method introduced in [50]. The only difference between the original consistency method and this variant is that the random walk normalized Laplacian $W:=D^{-1} (D-A)$ used in RD is replaced by the symmetric normalized Laplacian $S = D^{-1/2} (D-A) D^{-1/2}$ in the original consistency method. We compare our approach to (14) as it was designed in a similar setting as the one of this paper.

The regularization parameter $\lambda \in [0,1]$ was set to 0.5 in the present study, as recommended in previous works [37, 38]. It has indeed been observed that the performances were robust to changes of this parameter as long as it does not take an extreme value of 0 or 1.

4.4.2 Node2vec algorithm

Node2vec is a graph embedding technique which automatically defines node features describing each node neighborhood. These neighborhoods are defined based on second-order random walks which are biased to allow favoring, to a controlled extent, the preservation of the node structural properties and/or of the community co-memberships (node homophily) [15]. The chosen bias, controlled by the return and in–out parameters p and q, determines the sampling strategy S defining the neighborhood ${\mathcal {N}}_S(i) \subset {\mathcal {V}}$ of each node $i\in {\mathcal {V}}$. A small value of p ($<1$) increases the probability for a random walker to come back to the source node, while a small value of q ($<1$) encourages the walk to move further away. Therefore, small p and q, respectively, favor breadth-first searches (BFS) and depth-first searches (DFS) through the network when defining the neighborhoods. Decreasing their values hence tends to define graph embeddings, respectively, preserving the node structures and the community co-memberships. Let us denote by d the dimension of the feature space defined by Node2vec and by $f:{\mathcal {V}}\rightarrow {\mathbb {R}}^d$ the function assigning the features to each node. This function is determined by Node2vec by maximizing the log probability of observing the neighborhood of each node i given its features:

$$\begin{aligned} \max _f \sum \limits _{i\in {\mathcal {V}}} \log (\mathbb {P}({\mathcal {N}}_S(i)|f(i))). \end{aligned}$$

(15)

The idea in defining f is to describe nodes with similar neighborhoods with close features in the embedding space. Further details are provided in the paper of Grover and Leskovec [15]. Once the node features are computed, a classification algorithm can be used to predict the labels of test nodes. In this work, we consider three machine learning algorithms for this task: logistic regression with L2 regularization (logReg), Gaussian naive Bayes (GNB) and k-nearest neighbors (kNN). Logistic regression (with L2 regularization) and Gaussian naive Bayes were successfully employed in previous works [14, 15]. On the other hand, kNN provides further baseline comparison. Although using support vector machines (SVMs) is another appealing alternative for our two-class problem, it induced unaffordable computation times during the experiments with our network. The respective hyper-parameters (HPs) of each algorithm are selected through stratified tenfold cross-validation (CV) protocols on the labeled subsets of nodes. It can be noted that we employ Node2vec as a baseline among the feature extraction-based approaches, as it has been shown to overcome several other embedding techniques for classification tasks in complex networks [14, 15]. The bias weights p and q are each learned in the grid $\{0.25,0.5,1,2,4\}$ within the CV, i.e., they are considered as HPs to tune in addition to the HPs of the classification algorithms. These p and q hyper-parameters are hence chosen among 25 possible combinations, which is as much as in the paper defining the method [15] and more than in a recent review of graph embedding techniques [14]. The best combination of these parameters is individually chosen for each of our 50 simulations associated with each considered proportion of known labels. Similar values for the remaining Node2vec hyper-parameters are employed as in previous studies [14, 15]: $d=32$, a context size of 10, walk length of 80 and number of walks of 10. The bias weights are not assigned to constant values as they control the nature of the considered node neighborhoods, which in turn determine the closeness of the nodes in the embedding space. The class labels to predict could indeed be related to a structural equivalence between the nodes or to a community membership or to a combination of both. Finally, we also considered two variants of the Node2vec feature extraction: using the edge weights or not. Following the results of the data analysis in Sect. 4.2, the number of contacts between each pair of users ($\textsc {s}\_\textsc {and}\_\textsc {c}$ attribute) is used as weight.

4.4.3 Estimating the assortativity

The best edge potential for a given assortativity $r$ can be estimated using the synthetic networks, as detailed in Sects. 3.3.3 and 3.3.4. However, the assortativity of a given real network still needs to be estimated. To this end, we propose to collect the gender of an a priori fixed number of pairs of adjacent users in the considered graph ${\mathcal {G}}$, for example by carrying out a mobile phone survey, and then to use these edges to compute an estimate of $r$ in ${\mathcal {G}}$. This procedure has been tested on ${\mathcal {G}}_L$, since it is larger than ${\mathcal {G}}_S$, which allows to consider more independent edge samplings. Figure 11 presents the results. The assortativity estimates are roughly unbiased, while the variance of the estimator decreases toward 0.029, 0.022 and 0.014 when the gender of, respectively, 1000, 2000 and 5000 pairs of adjacent users is known. Hence, knowing the gender of about 1k pairs of neighbors is sufficient to reliably estimate $r$, as it yields an error with an order of magnitude smaller than the actual assortativity value. Furthermore, an error of 0.05 on the estimation of $r$ induces at worst a small 0.05 error on the s value, as indicated in Figs. 5 and 6.

Fig. 11

Estimated assortativity $r$ as a function of the number of randomly selected pairs of adjacent users with known gender in ${\mathcal {G}}_L$. For each number in abscissa, the edge selection is performed 50 times. The vertical distance between each mean estimated $r$ (red squares) and the green lines gives the standard deviation of the estimation. The horizontal blue line indicates the true assortativity $r$ in ${\mathcal {G}}_L$, equal to 0.3 (color figure online)

It is noteworthy that using distinct edge potential parameters $s_\mathrm{strong}$ and $s_\mathrm{weak}$ in the strong and weak parts of the network requires to estimate $r$ within these two parts. As the strong part tends to be significantly smaller, the estimation of $r_\mathrm{strong}$ in a real setting should be carefully performed. Meanwhile, the users linked by the edges selected to estimate $r$ may be, for instance, used as a training set to provide initial individual gender predictions.

4.4.4 Performances

This section presents the experimental results of the proposed method and of the baseline approaches (reaction–diffusion algorithm and classifiers based on Node2vec features), both on simulated initial individual predictions and on a growing subset of network users with known labels. For all the comparisons, statistical tests are conducted using Welch’s t test with a significance level of 0.05. Whenever multiple hypotheses are tested simultaneously, Holm–Bonferroni correction is employed to bound by 0.05 the probability to consider as significant at least one nonsignificant difference [41].

Individual predictions

Figure 12 shows the accuracy and recall gains over simulated initial predictions on ${\mathcal {G}}_S$, both for our approach based on LBP and for the baseline RD. The different distributions of the initial individual predictions introduced in Sect. 3.3 are used, and the performances are given for varying initial accuracies $\beta$. As indicated by the stars at the bottom of each plot, the accuracies obtained with LBP always statistically significantly overcome the ones of RD, except when the initial accuracy is 50%, in which case LBP and RD are not significantly different. This last point was expected since the case $\beta =50\%$ corresponds to a random guessing for the first predictions. Furthermore, the well-balanced recalls obtained with LBP indicate that the weighting by the class prior in the node potential $\psi$ is effective, avoiding to favor the dominant class ($M$) to the expense of the other one. It can, however, be noted that neither the baseline RD nor LBP improve the predictions when the bi-uniform distribution of the individual predictions is used. These poor performances confirm the observations of Sect. 3.3.3 on the synthetic networks. They can be explained as, in this bi-uniform case, only the sign and not the amplitude of ${\widehat{p}}_{Y_i| X_i}(M|x_i)-0.5$ brings information on the true gender that needs to be inferred, which is very unlikely in practice.

Although optimal s values are quite independent of the initial accuracy $\beta$, the performances are not, with highest accuracy gains in the range [70, 85]%. This range covers the accuracies reached by state-of-the-art techniques aiming to predict gender using individual-level features [11, 12, 17, 37]. Likewise, for an assortativity coefficient similar to the one of ${\mathcal {G}}_S$ ($\approx 0.25$), the accuracy gains on synthetic networks are significant when $\beta \in [0.62, 0.92]$. This result is intuitive, as near-perfect initial accuracies do not let many opportunities to improve the predictions, while almost random ones induce too rough node potentials. It is interesting to observe that, depending on the distribution of the initial class probabilities employed, the profiles of the accuracy gains as a function of $\beta$ are similar for RD and LBP, suggesting that the considered distribution shape highly determines the achievable performances.

Fig. 12

Accuracy and recall gains on ${\mathcal {G}}_S$ of our LBP-based approach and of the RD method over the initial accuracies and recalls. The performances are provided as a function of the initial accuracy $\beta$ and are averaged over 50 random simulations of the initial individual predictions generated using the linear (a, d), exponential (b, e) and bi-uniform (c, f) distributions. The filled areas delimit intervals of one standard deviation around the mean gains. A star (resp. a gray square) for an initial accuracy $\beta$ drawn under one curve indicates that the accuracy of the corresponding method is higher (resp. not statistically significantly smaller) than the one of the other method for the same $\beta$ and distribution of initial predictions

Table 2 gives the average accuracy and recall gains of both RD and LBP in ${\mathcal {G}}_S$ over the initial predictions with an initial accuracy $\beta = 0.75$. LBP increases the accuracy by more than 3 and 2.5% when the linear and exponential distributions are, respectively, chosen, outperforming the RD algorithm. On the other hand, as observed above, both RD and LBP deteriorate the individual predictions when the bi-uniform distribution is used.

Table 2 Mean performances on ${\mathcal {G}}_S$ of the baseline update (RD) scheme (13) and of LBP, for 50 different assignations of the first predictions

Labeled data

The results of LBP, RD and the classifiers using Node2vec features as a function of the percentage $\beta$ of known labels are presented in Fig. 13. Table 3 further details the mean accuracy and recalls obtained by all methods when 50% of the nodes are labeled and the performances are computed on the 50% remaining ones. We observe that LBP statistically significantly outperforms all the other schemes when the fraction of known labels is higher than $\beta = 25\%$, while RD is superior for smaller percentages of labeled users. For all the explored percentages of labeled nodes, all methods lead to more than 50% accuracy on the unlabeled users. We can note, however, that LBP tends to provide highly unbalanced male and female recalls for small fractions $\beta$ of known labels. The dominant class (male) is always favored, even though the data set is hardly unbalanced. Further works will aim at overcoming this behavior. This last observation is in contrast to the results obtained for the initial individual predictions in Fig. 12, suggesting that the probabilistic framework of our approach is especially suited when prior, possibly noisy, class probabilities are available for the network users. Graphical models have indeed already proven to be particularly relevant for the sake of denoising local node information by accounting for the global network structure. Common applications include the largely studied hidden Markov models (HMM) in the field of speech recognition, error correcting codes or diverse biological networks [18].

Besides, Fig. 13 shows that the performances of the feature extraction-based methods tend to less improve when the training set size increases (especially concerning GNB and LogReg), whereas LBP and RD seem to benefit more from additional data. This suggests that learning the whole network structure allows to build richer models enabling to enhance the classification performances.

Fig. 13

Accuracy and recalls obtained on the unlabeled nodes of ${\mathcal {G}}_S$ when varying the training percentage $\beta$ (i.e., the fraction of the nodes with known labels) using our LBP-based approach (a), the RD method (b) and classifiers using features extracted by Node2vec (c–h). The performances are averaged over 50 random selections of the known labels and the filled areas delimit intervals of one standard deviation around the mean scores. A star for a training percentage drawn under one curve indicates that the accuracy of the corresponding method on the remaining unlabeled nodes is the highest among all 8 considered methods. A gray square indicates that the corresponding accuracy is not statistically significantly smaller than the best one for the same $\beta$ according to Welch’s t test with 5% significance level, with Holm–Bonferroni correction as multiple hypotheses are tested

Table 3 Mean performances on ${\mathcal {G}}_S$ of our LBP-based method, of the RD update scheme (13) and of three classifiers using features extracted by Node2vec for 50 different samplings of $\beta = 50\%$ labeled nodes

Fig. 14

Bias weights p and q of Node2vec selected with the tenfold CV within the grid $\{0.25,0.5,1,2,4\}\times \{0.25,0.5,1,2,4\}$ for 50 different samplings of $\beta = 50\%$ labeled nodes, and for the three considered classification algorithms. Some jitter (Gaussian noise with small variance) has been added to enable visualizing the overlapping data points as they are all on the same discrete grid. This figure is best viewed with colors (color figure online)

Regarding the algorithms based on Node2vec features, Fig. 13 and Table 3 show that all their performances are inferior to LBP and RD, even though this kind of feature extraction has proven to be a powerful graph embedding technique for node classification. To analyze the sorts of neighborhoods which were preserved in the extracted features, Fig. 14 shows the bias weights selected in the CV for the 50 different samplings of $\beta = 50\%$ labeled nodes. These parameters are the ones that were selected to obtain the results in Table 3. We can observe that from one run to the other (i.e., for different subsets of observed labels), the selected parameters are not always the same. Nevertheless, we can note some trends:

• In the weighted case (in Fig. 14b), lower q values tend to be favored, especially with logistic regression. This is in accordance with a previous study which has reported that low values of the in–out parameter q allow to improve subsequent classification based on the extracted features [14]. The embeddings therefore mostly preserve the community co-memberships of the nodes (highly interconnected nodes are embedded closely together) [15].

• In the unweighted case (in Fig. 14a), p and q are mostly selected close to 1 except with kNN where almost all combinations of values are chosen from one run to the other. Moderate p and q values seem coherent since, without the edge weights, a random walker is only guided by the presence of the edges and is as likely to move in any direction starting from the source node. If DFS was favored (by setting a small q) as in the weighted case, it would be likely that, without the edge weights, the genders among the neighbors sampled further away from the source node will not be related to the source user’s gender and hence that the extracted features will not be helpful for the classification task.

Surprisingly, it appears that using the edge weights for Node2vec deteriorates the reached performances in all tested cases. This confirms the observation that there is no straightforward link between the users’ communication patterns and their labels. In addition, the overall weaker performances of the Node2vec-based classifiers can at least partly be explained by the moderate gender assortativity as well as its nonuniformity across the social network.

5 Discussion

Different researches exploit mobile phone data for healthcare, epidemics containment, determination of socioeconomic status or marketing study purposes [4, 6, 28, 39, 45]. In each context, the knowledge of the users’ gender is of great importance. Most of the recent works on demographics prediction use classical machine learning algorithms on mobile phone data for predicting gender, age, income level or even personality [11, 12, 16, 26]. These algorithms rely on features defined for each user and reflecting their mobile phone usage at an individual scale, such as the recharge rate of their prepaid cards, spending speed, total call duration. Some studies further refine such standard metadata by deriving diverse behavioral indicators [27], enhancing the prediction capabilities of the models. All these studies are thus based on an ‘individual’ part of the mobile phone data. For example, Felbo et al. and Sarraute et al. predicted the gender with, respectively, 79.7% and 77.1%² accuracy, either by harnessing their temporal information using deep learning or by using linear SVM and logistic regression [11, 37]. Other works tackle the gender prediction problem in a similar way using different kinds of data sets, such as Twitter or LinkedIn data, the first name of a person or even chat texts [19, 21, 35].

In addition to the individual-level metadata, the structure of social networks carries important features that can be exploited to further refine the prediction of node-level demographics. The task of predicting missing node labels in networks, known as node classification, makes use of the known labels and the graph structure [14], which embeds some properties such as the label assortativity. A node classification method can be categorized as being based either on feature extraction or on a random walk [5]. Different methods of the both kinds were recently developed.

Some feature extraction-based approaches are defined to exploit network assortativity [1, 16]. Al Zamal et al. [1] exploited the homophily in a Twitter network to predict the users’ gender, age and political affiliation, by analyzing how the knowledge of the data from some immediate friends of a given user can improve the prediction quality. This question is studied in a usual machine learning framework: Feature vectors are defined for each user, either augmented with data from her neighbors or not. Considering the neighbors’ information in the feature vectors improves the accuracy from 3 to 5% for the age and political affiliation prediction, whereas including the immediate neighbors’ features does not improve the gender predictions. More generally, the idea of feature extraction approaches is, for each node, to build a feature vector which summarizes information from the node neighborhood. A machine learning algorithm can then be trained to predict the unknown labels based on these extracted features. In this setting, the definition of the neighborhood of each node used to extract the features is highly important and can be carried out in different ways. The exclusive preservation of the node structural properties is obtained by breadth-first sampling among the neighbors in the graph, while depth-first sampling allows to reflect the network clusters or communities [15]. Diverse graph embedding techniques can be considered to build feature vectors for each node describing its neighborhood [14]. For instance, Grover and Leskovec automated the feature extraction to preserve neighborhoods which are defined based on second-order random walks, which is a successful approach to reflect complex network interactions as it allows to trade-off the preservation of the local network structures and of the community co-memberships [15].

As the former studies do not take the global network structure into account, they could hence further benefit from its properties. Indeed, the feature extraction is constrained by the subsequent classification algorithm that is used: The number of features always has to be the same for each node, and the set of features has somehow to be ordered (since a given feature indexed i will be treated ‘equally’ for the different nodes). This cannot easily reflect complex relationships, observed in social networks for instance: A given user might have a few strong ties, each of which having a strong influence on her label, while other users from the same graph may rather have a large amount of weaker ties, influencing their classes in a different way [34]. In addition, this kind of approach is not intended to directly exploit uncertain label predictions with confidence levels (i.e., initial class probabilities), which can only, for instance, be incorporated in the definition of the features [40].

Besides, random walk-based approaches allow to account for the whole network structure by propagating the labels through iterative updates [50, 51]. Several variants and adaptations of this principle are proposed to solve diverse labeling tasks, such as video suggestions [3] or demographics prediction in networks [38]. The latter work adopts a two-step approach, first computing uncertain individual predictions using the individual part of the data and then improving them using the reaction–diffusion (RD) method exploiting the network structure [37]

Although the aforementioned random walk-based methods aim to model the network structure as a whole, they are based on an implicit model of the joint probability distribution of all the node labels [5]. As a refinement, inference approaches using probabilistic graphical models (PGMs) are proposed as this framework allows to make the models explicit and fully describes the interactions between the nodes [10]. Dong et al. [10] introduced a double dependent-variable factor graph model in order to jointly predict the users’ age and gender by benefiting from the links between these two demographic attributes in a network. Knowing 50% of the labels, the remaining unknown genders are predicted with up to 80% accuracy. However, as they do not quantify the assortativity of their network, these performances cannot be easily compared to our study. Our results may nevertheless qualitatively partly explain the success of their approach. Combining age and gender implicitly delineates in an automated manner some rather (anti-)homophilic subgraphs, as illustrated by their data analysis. As highlighted by the present work, this definition of strong and weak network parts with accentuated (anti-)homophily improves the inference performances. The latter observation is essential, as several studies mention that gender assortativity is generally rather weak [1, 24] and thus not sufficient by itself to infer the gender. For instance, the RD algorithm introduced by Sarraute et al. [37] is used to infer the age group of some users, but not their gender. Their network indeed bears a strong age homophily. When 70% of the known age labels are propagated through the network to infer the 30% remaining ones, the age group among four categories is predicted with 43.4% accuracy.

However, these recent studies focus on the propagation of known labels through a network and do not consider the improvement of uncertain predictions, which can be obtained by a classical machine learning algorithm predicting the labels based on individual information. In addition, to the best of our knowledge, no research quantifies the relation between the assortativity strength and the performances of label prediction in a network.

In this setting, we introduce a general framework based on PGMs to exploit the global social network topology for the improvement of uncertain predictions and to infer missing labels. Our study makes use of an objective measure of the assortativity to provide guarantees about the performances generalization. This quantitative measure of the network homophily is typically not provided by graphical representations [10]. It enables us to describe to which extent the sole network information improves individual demographics prediction, as a function of the assortativity. The proposed methodology easily permits to take advantage of some known labels, as well as first individual predictions obtained using individual data. Finally, the model can benefit from assortativity variations in different subgraphs. By modeling the statistical dependencies between adjacent labels, it can favor heterogeneous as well as homogeneous contacts depending on the edge weights. The experiments of Sect. 4.4.4 first show the superiority, in most settings, of our approach over the reaction–diffusion algorithm and three classifiers using Node2vec features, especially to improve uncertain predictions. Second, in the studied application, the methods exploiting the entire network structure either through label propagation (RD) or using PGM are superior to feature extraction-based approaches. Third, although it can create embeddings of nodes based on diverse types of neighborhood, the Node2vec feature extraction technique is probably not best suited when the assortativity is moderate and/or nonuniform across a network. In such cases, there is no unique relationship between a set of extracted features representing the node neighborhoods and the associated node labels.

6 Conclusion

This work presents how assortativity can be exploited to infer individual demographics in social networks. To this aim, a general approach is introduced, using a probabilistic graphical model. It can both improve noisy initial predictions performed at an individual level and propagate a subset of known labels to predict the remaining unknown ones. The achieved performances are studied on simulated networks as a function of the assortativity and the quality of the provided initial information, both in terms of accuracy and distribution in the initial individual predictions case, and in terms of the fraction of users with known labels otherwise. Indeed, the relevance of the network information compared to individual features depends on (1) the assortativity amplitude and (2) the quality of the prior information: In the initial individual predictions context, poor prior information is misleading, while excellent one does not leave much room for improvement. Also, the distribution of the initial class probabilities highly influences the achievable performances, as highlighted by the results of both our approach and the reaction–diffusion method obtained with different distributions of these first probabilities. The graph simulations allow tuning the model parameters. Our method is further validated on a real-world mobile phone network, and the model is refined to predict gender, exploiting both weak, homophilic and strong, anti-homophilic links. In this context, our approach statistically significantly overcomes, in most settings, the performances of the reaction–diffusion label propagation technique and of machine learning classifiers based on features extracted by the Node2vec graph embedding method. In particular, the approach allows individual-based gender predictions to be improved by up to 3%. On the other hand, when the gender of 60% of the users is known and no information is provided for the remaining users, the proposed approach can infer the missing labels with 70% accuracy, solely based on the network assortativity.

The analysis performed on synthetic networks illustrates that a strong assortativity can be easily exploited through our methodology. Moreover, an almost randomly mixed network may still be composed of several parts which are, if considered in isolation, assortative and disassortative. Thus even in the latter configuration, the network topology may still be useful. As a further work, the generalization of the proposed methodology to multivariate predictions would be of great interest. The model could then benefit from the relationships between the target variables and automatically make use of sub-networks presenting more pronounced homophily.