Intuitionistic fuzzy divergence measure-based multi-criteria decision-making method

Abstract

Divergence measure is a significant tool for evaluating the amount of discrimination for IFSs. Since then it has acquired concentration for their applications in different areas. In this paper, we utilize the conception of Jensen–Shannon divergence to propose new measures called Jensen-exponential divergence for measuring the discrimination between intuitionistic fuzzy sets (IFSs) and demonstrate some very elegant properties, which show its strength for applications point of view. Next, a multi-criteria decision-making (MCDM) problem for IFSs that describes information about options with respect to criteria is studied. A technique that employs the relative comparisons for IFSs (that uses all the constraints, viz. membership, non-membership and hesitancy degrees) based on the advantage and disadvantage scores of the options with respect to criterion, where criterion weights are completely unknown, is used. In addition, the score functions are applied to evaluate the strength and worst scores leading to the satisfaction degree of the options. A multi-objective optimization model for optimal weights of the criterion that maximizes the satisfaction degree of each option is constructed. Energy resources play an important role in the social and economic development of the countries. Due to the industrialization, population growth and urbanization, the demand of energy is increasing gradually and this requires the selection of most suitable energy resource for economic development of the countries. The proposed MCDM method is presented to choose the most appropriate energy alternative among set of renewable energy alternatives. In this real case study, the decision makers provide their opinions in terms of linguistic variables because it is tricky to portray exact numerical values during the evaluation of energy alternatives. Finally, a comprehensive comparison is prepared to express the effectiveness of the technique over the existing techniques for the IF MCDM problems.

1 Introduction

In the few decades, divergence measures have been extensively employed to determine the discrimination between two probability distributions, introduced by Kullback and Leibler [18], and extensively utilized in various disciplines. Afterwards, different generalizations of divergence have been introduced by various authors [41, 44] and deliberated their properties and applications in different areas. Another important information-theoretic divergence measure, introduced by Lin [22], is the Jensen–Shannon divergence (JSD) which has attracted quite some attention from researchers and fruitfully executed in various disciplines [1, 9, 33, 38].

Inspired by the notion of divergence between two probability distributions, Bhandari and Pal [4], Shang and Jiang [42], Fan and Xie [7] and Montes et al. [35] introduced different divergence measures for fuzzy sets (FSs). Bhandari and Pal [4] and Shang and Jiang [42] divergence measures for FSs are based on logarithmic information gain functions, and that of Fan and Xie [7] is derived from exponential information gain functions with the same approach being followed in Mishra et al. [10, 27,28,29]. As for FSs, divergence measures for intuitionistic fuzzy sets (IFSs) are proposed by Vlachos and Sergiadis [49], Hung and Yang [11], Zhang and Jiang [61], Xia and Xu [53], Junjun et al. [12], Mishra et al. [30, 31], Ansari et al. [2], Mishra and Rani [32] and these measures are utilized in pattern recognition, medical diagnosis, MCDM and image processing. Recently, Montes et al. [34] proposed an axiomatic definition of the notion of divergence for IFSs and recommended some new approaches for building divergence measures for IFSs.

The concept of IFSs [3] considered as an extension of FSs [60] considered by a membership, non-membership and hesitancy functions. Subsequently, various authors implemented IFSs to the multi-criteria decision-making (MCDM). Tan and Chen [46] introduced a technique for MCDM based on IF-correlated averaging operators with intuitionistic fuzzy information. Zhao and Wei [62] presented MCDM problems with intuitionistic fuzzy numbers (IFNs). Next, there are various real-world decision-making circumstances such that the weight information is either partially known or completely unknown. Li and Wan [20] proposed a fuzzy linear programming method for MCDM problems with incomplete weight. Xu and Cai [54] developed various nonlinear optimization models to evaluate the optimal weights of criterion when no weight information is available. Xu [56] proposed a linear programming model to determine optimal attribute weights where the information about attribute weights is partially known. Wei [52] initiated grey relational analysis technique to solve IF MCDM problem with partial weight information. Xu [55] discussed an interactive method for IF MADM problem where the weight information is not completely known. Li [19] proposed TOPSIS-based nonlinear programming technique for MCDM with IVIFSs. Chen and Li [5] introduced a method to determine weights using IF entropy measures. Wan and Dong [50] pioneered a possibility degree technique for IVIF MCGDM.

In this paper, we develop new Jensen-exponential divergence measures for IFSs. These measures have some elegant properties, which are revealed to enhance the applicability of these measures. The vitality of these extensions has been established by a technique for multi-criteria decision-making problem. Next, we study IF MCDM problem where the weight information on the criterion is completely or partially unknown using relative comparisons among the available options on each criterion. To evaluate the optimal weight vector, we first achieve the advantage and disadvantage scores of each option and with the help of advantage and disadvantage scores of an option with respect to the criterion are then used to find the strength and weakness scores of the option as a function of the weight vector. To find the optimal criteria weights, the satisfaction degree of each option is used to formulating a multi-objective optimization model. The optimal weights determine the overall criterion value of each option. Finally, a ranking technique is implemented to rank the options on the basis of overall criterion values.

2 Prerequisite

Throughout this paper, let $\mathbf{{{\mathbb R}}}=[0,\,\infty [,$ let FSs (X) and IFSs(X) be the sets of all fuzzy sets and intuitionistic fuzzy sets on a universal set X,  respectively, and P(X) be the set of all crisp sets on the universal set X. Further, we roughly introduce some basic knowledge about entropy, divergence measure, FSs and IFSs.

Let $\varDelta _{n} =\left\{ P=(p_{1} ,p_{2} ,\ldots ,p_{n} ):p_{i} \ge 0;\sum _{i=1}^{n}p_{i} =1 \right\} ,\, \, n>2$ be a set of discrete probability distributions. For a probability distribution $P=(p_{1} ,p_{2} ,\ldots ,p_{n} )\in \varDelta _{n},$ Shannon’s entropy [43] is defined as

$$\begin{aligned} H(P)=-\sum _{i=1}^{n}p_{i} \log p_{i} . \end{aligned}$$

(1)

Pal and Pal [39] scrutinized Shannon entropy and proposed another measure called exponential entropy as follows:

$$\begin{aligned} H_{\rm Pal} (P)=\sum _{i=1}^{n}p_{i} e^{\left( 1-p_{i} \right) } -1 . \end{aligned}$$

(2)

Note that (2) has an advantage over (1). For the uniform probability distribution $P=\left( 1/n,\, \, 1/n,\, \ldots ,\, \, 1/n\right),$ exponential entropy has an upper bound

$$\begin{aligned} \mathop {\mathrm{lim}}\limits _{n\, \rightarrow \, \infty } H\left( {1/n} ,\, {1/n} ,\, \, \ldots ,\, {1/n} \right) =e-1, \end{aligned}$$

which is not the case for Shannon’s entropy (1).

Let $P=(p_{1} ,p_{2},\ldots ,p_{n} )$ and $Q=(q_{1} ,q_{2},\ldots ,q_{n} )\in \varDelta _{n}$ be probability distribution. Then, Kullback and Leibler [18] introduced the divergence measure of P from Q as follows:

$$\begin{aligned} C_{KL} (P||Q)=\sum _{i=1}^{n}p_{i} \log \frac{p_{i} }{q_{i} } , \end{aligned}$$

(3)

Lin [22] proposed that the Jensen–Shannon divergence between P and Q is given by

$$\begin{aligned} C_{JS} \left( M||N\right) =H\left( \frac{M+N}{2} \right) -\frac{H(M)+H(N)}{2} , \end{aligned}$$

(4)

where H(.) is Shannon entropy given in (1).

Definition 2.1

(Zadeh [60]): A fuzzy set $\tilde{M}$ on a finite discourse set $X=\left\{ x_{1} ,\, \, x_{2} ,\, \, \ldots ,\, \, x_{n} \right\}$ is defined as

$$\begin{aligned} \tilde{M}=\left\{ \left( x_{i} ,\, \, \mu _{\tilde{M}} \left( x_{i} \right) \right) :\mu _{\tilde{M}} \left( x_{i} \right) \in \left[ 0,1\right] ;\, \, \forall \,\, x_{i} \in X\right\}, \end{aligned}$$

where $\mu _{\tilde{M}} (x_{i} )\left( 0\le \mu _{\tilde{M}} (x_{i} )\le 1\right)$ represents the degree of membership of $x_{i}$ to $\tilde{M}$ in X.

De Luca and Termini [25] introduced first entropy for FS $\tilde{M}$ corresponding to (1) as follows:

$$\begin{aligned} H_{D} (\tilde{M})=-\frac{1}{n} \, \, \sum _{i=1}^{n}\left[ \mu _{\tilde{M}} (x_{i} )\log \mu _{\tilde{M}} (x_{i} ) +\,(1-\mu _{\tilde{M}} (x_{i} ))\log (1-\mu _{\tilde{M}} (x_{i} ))\right] . \end{aligned}$$

(5)

Based on (2), exponential entropy for FS $\tilde{M}$ has also been introduced by Pal and Pal [39] which is given by

$$\begin{aligned} H_{P} (\tilde{M})=\frac{1}{n\left( \sqrt{e} -1\right) } \sum _{i=1}^{n}\left[ \mu _{\tilde{M}} (x_{i} )e^{\left( 1-\mu _{\tilde{M}} (x_{i} )\right) } +(1-\mu _{\tilde{M}} (x_{i} ))e^{\mu _{\tilde{M}} (x_{i} )} -1\right] .\, \end{aligned}$$

(6)

Let $\tilde{M} ,\tilde{N}\in$ FSs, then Bhandari and Pal [4] introduced divergence measure for FSs based on (3) as follows:

$$\begin{aligned} C\left( \tilde{M}||\tilde{N}\right) =\sum _{i=1}^{n}\left[ \mu _{\tilde{M}} (x_{i} )\log \frac{\mu _{\tilde{M}} (x_{i} )}{\mu _{\tilde{N}} (x_{i} )} +(1-\mu _{\tilde{M}} (x_{i} ))\log \frac{(1-\mu _{\tilde{M}} (x_{i} ))}{(1-\mu _{\tilde{N}} (x_{i} ))} \right] . \end{aligned}$$

(7)

Fan and Xie [7] initiated the divergence measure for FSs based on exponential function which is given by

$$\begin{aligned} C_{FX} \left( \tilde{M}||\tilde{N}\right) =\sum _{i=1}^{n}\left[ \left\{ 1-\left( 1-\mu _{\tilde{M}} (x_{i} )\right) e^{\left( \mu _{\tilde{M}} (x_{i} )-\mu _{\tilde{N}} (x_{i} )\right) } +(1-\mu _{\tilde{M}} (x_{i} ))e^{\left( \mu _{\tilde{N}} (x_{i} )-\mu _{\tilde{M}} (x_{i} )\right) } \right\} \right] . \end{aligned}$$

(8)

Definition 2.2

(Atanassov [3]): An IFS M on discourse set $X=\left\{ x_{1} ,\, \, x_{2} ,\, \, \ldots ,\, \, x_{n} \right\}$ is given by

$$\begin{aligned} M=\left\{ \left\langle x_{i} ,\, \mu _{M} (x_{i} ),\, \nu _{M} (x_{i} )\right\rangle \, :\, x_{i} \in X\right\} , \end{aligned}$$

(9)

where $\mu _{M} :X \rightarrow [0, 1]$ and $\nu _{M} :X \rightarrow [0, 1]$ are the degrees of membership and non- membership of $x_{i}$ to M in X,  respectively, such that $0\le \mu _{M} (x_{i} )\le 1,$$0\le \nu _{M} (x_{i} )\le 1$ and $0\le \mu _{M} (x_{i} )+\nu _{M} (x_{i} )\le 1$, $\forall \, \, x_{i} \in X.$ For an IFS M in X,  we call the intuitionistic index (hesitancy degree) of an element $x_{i} \in X$ to M the following expression: $\pi _{M} (x_{i} )=1-\mu _{M} (x_{i} )-\nu _{M} (x_{i} )$ and $0\le \pi _{M} (x_{i} )\le 1, \, \forall \,\, x_{i} \, \in X.$

Let X be a discourse set such that $X=\left\{ x_{1} ,\, \, x_{2} ,\, \, \ldots ,\, \, x_{n} \right\}$ and $M,\, N \in \, \mathrm{IFSs}(X)$ defined by

$$\begin{aligned} M=\{\langle x_{i}, \mu _{M}(x_{i}), \nu _{M}(x_{i})\rangle | x_{i}\, \in \, X\}, \end{aligned}$$

$$\begin{aligned} N=\{\langle x_{i}, \mu _{N}(x_{i}), \nu _{N}(x_{i})\rangle | x_{i}\, \in \, X\}, \end{aligned}$$

then operations on IFSs are defined as follows:

• 1. $M\subseteq N$ iff $\,\mu _{M}(x_{i})\le \mu _{N}(x_{i})$   and  $\nu _{M}(x_{i})\ge \nu _{N}(x_{i}) \, \forall \,\, x_{i} \in X;$

• 2. $M=N$ iff $M\subseteq N$ and $N\subseteq M;$

• 3. $M\cup N=\{\langle x_{i}, (\mu _{M}(x_{i})\vee \mu _{N}(x_{i})), (\mu _{M}(x_{i})\wedge \mu _{N}(x_{i}))\rangle | x_{i} \in X\};$

• 4. $M\cap N=\{\langle x_{i}, (\mu _{M}(x_{i})\wedge \mu _{N}(x_{i})), (\mu _{M}(x_{i})\vee \mu _{N}(x_{i}))\rangle | x_{i} \in X\}.$

Divergence measure is concerned to measure the discrimination information, based on Shannon’s inequality [43], Vlachos and Sergiadis [49] introduced a definition of divergence measure for IFSs.

Definition 2.3

(Vlachos and Sergiadis [49]): Let $M,N\in \mathrm{IFSs},$ then $J:\mathrm{IFS}(X)\times \mathrm{IFS}(X)\rightarrow \mathbf{{\mathbb R}}$ is called a divergence measure or cross-entropy, if it fulfils the following axioms:

• (C1). $J(M || N)\ge 0;$

• (C2). $J(M || N)=0,$ if and only if $M=N.$

2.1 Method for transforming IFSs into FSs

Li et al. [21], as briefly delineated underneath, introduced a method for transforming ‘intuitionistic fuzzy sets (IFSs)’ into ‘fuzzy sets (FSs)’ by distributing hesitation degree equally with membership and non-membership.

Definition 2.4

(Li et al. [21]): Let $M \in \mathrm{IFS}(X),$ then the fuzzy membership function $\mu _{\tilde{M}} (x_{i})$ to $\tilde{M}$ ( $\tilde{M}$ be the fuzzy set corresponding to intuitionistic fuzzy set M) is defined as

$$\begin{aligned} \mu _{\tilde{M}} (x_{i})=\mu _{M} (x_{i})+\frac{\pi _{M} (x_{i})}{2}=\frac{\mu _{M} (x_{i})+1-\nu _{M} (x_{i})}{2}. \end{aligned}$$

(10)

3 Divergence measure for IFSs

In the present section, the some existing divergence measures for IFSs are reviewed. Inspired by the concept of Jensen–Shannon divergence, we develop new Jensen-exponential divergence measures for IFSs and some refined properties of the developed measures are also studied here.

3.1 Existing divergence measure for IFSs

There are three measures to assess the difference for two IFSs viz. IF-dissimilarity, IF-distance and IF-divergence. Out of which IF-divergence is the most elegant one for applications due to the following reasons. Though a dissimilarity measure holds some enviable axioms of difference for IFSs, it is too general in nature, while a distance measure is not necessarily a measure of dissimilarity. A distance measure for IFSs is not expected to be useful for applications, i.e. image processing, because when an image is represented by an IFS, the triangular inequality may not reflect a enviable relation. Conversely, an IF-divergence measure is also a measure of dissimilarity and it holds a set of enviable axioms, which are useful for assessing differences for IFSs [34].

Here, various existing divergence measures for IFSs(X) are reviewed as follows:

Vlachos and Sergiadis [49]:

$$\begin{aligned} J_{VS} \left( M || N\right) =\sum _{i=1}^{n}\left[ \mu _{M} (x_{i} )\ln \left( \frac{\mu _{M} (x_{i} )}{\left( {1/2} \right) \left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) } \right) +\nu _{M} (x_{i} )\ln \left( \frac{\mu _{M} (x_{i} )}{\left( {1/2} \right) \left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) } \right) \right] . \end{aligned}$$

(11)

Hung and Yang [11]:

$J_{HY} (M || N)=\frac{1}{1-\rho }$

$$\begin{aligned} \sum _{i=1}^{n}\left[ \begin{array}{l} {\left( \frac{\mu _{M} (x_{i} )+\mu _{N} (x_{i} )}{2} \right) ^{\rho } -\left( \frac{\mu _{M}^{\rho } (x_{i} )+\mu _{N}^{\rho } (x_{i} )}{2} \right) } \\ {\, \, +\left( \frac{\nu _{M} (x_{i} )+\nu _{N} (x_{i} )}{2} \right) ^{\rho } -\left( \frac{\nu _{M}^{\rho } (x_{i} )+\nu _{N}^{\rho } (x_{i} )}{2} \right) } \\ {\, \, \, \, \, +\left( \frac{\pi _{M} (x_{i} )+\pi _{N} (x_{i} )}{2} \right) ^{\rho } -\left( \frac{\pi _{M}^{\rho } (x_{i} )+\pi _{N}^{\rho } (x_{i} )}{2} \right) } \end{array}\right] , \end{aligned}$$

(12)

where $\rho \ne 1\, \left( \rho >0\right) .$

Zhang and Jiang [61]:

$$\begin{aligned} J_{ZJ} (M || N)= \sum _{i=1}^{n}\left[ \begin{array}{l} {\left( \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right) } \\ {\, \ln \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{\left( {1/2} \right) \left( \left( \mu _{M} (x_{i} )-\nu _{M} (x_{i} )\right) +2+\left( \mu _{N} (x_{i} )-\nu _{N} (x_{i} )\right) \right) } } \end{array} \begin{array}{l} {+\left( \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right) } \\ {\, \, \, \ln \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{\left( {1/2} \right) \left( \left( \nu _{M} (x_{i} )-\mu _{M} (x_{i} )\right) +2+\left( \nu _{N} (x_{i} )-\mu _{N} (x_{i} )\right) \right) } } \end{array}\right] . \end{aligned}$$

(13)

Xia and Xu [53]:

$$\begin{aligned} J_{XX} (M ||| N)&= \left( \frac{1}{t} \right) \nonumber \\&\quad \sum _{i=1}^{n}\left( \begin{array}{l} {\frac{\left( 1+q\mu _{M} (x_{i} )\right) \ln \left( 1+q\mu _{M} (x_{i} )\right) +\left( 1+q\mu _{N} (x_{i} )\right) \ln \left( 1+q\mu _{N} (x_{i} )\right) }{2} } \\ { \, -\left( \frac{1+q\mu _{M} (x_{i} )+1+q\mu _{N} (x_{i} )}{2} \right) \ln \left( \frac{1+q\mu _{M} (x_{i} )+1+q\mu _{N} (x_{i} )}{2} \right) } \\ {+\frac{\left( 1+q\nu _{M} (x_{i} )\right) \ln \left( 1+q\nu _{M} (x_{i} )\right) +\left( 1+q\nu _{N} (x_{i} )\right) \ln \left( 1+q\nu _{N} (x_{i} )\right) }{2} } \\ { \, -\left( \frac{1+q\nu _{M} (x_{i} )+1+q\nu _{N} (x_{i} )}{2} \right) \ln \left( \frac{1+q\nu _{M} (x_{i} )+1+q\nu _{N} (x_{i} )}{2} \right) } \\ {+\frac{\left( 1+q\pi _{M} (x_{i} )\right) \ln \left( 1+q\pi _{M} (x_{i} )\right) +\left( 1+q\pi _{N} (x_{i} )\right) \ln \left( 1+q\pi _{N} (x_{i} )\right) }{2} } \\ {\, -\left( \frac{1+q\pi _{M} (x_{i} )+1+q\pi _{N} (x_{i} )}{2} \right) \ln \left( \frac{1+q\pi _{M} (x_{i} )+1+q\pi _{N} (x_{i} )}{2} \right) } \end{array}\right) , \end{aligned}$$

(14)

where $t=(1+q)\ln (1+q)-(2+q)(\ln (2+q)-\ln 2)$ and $q>0.$

Junjun et al. [12]:

$$\begin{aligned} J_{C} (M || N)=\sum _{i=1}^{n}\left[ \pi _{M} (x_{i} )\ln \frac{\pi _{M} (x_{i} )}{\left( {1/2} \right) \left( \pi _{M} (x_{i} )+\pi _{N} (x_{i} )\right) } +\varDelta _{M} (x_{i} )\ln \frac{\varDelta _{M} (x_{i} )}{\left( {1/2} \right) \left( \varDelta _{M} (x_{i} )+\varDelta _{N} (x_{i} )\right) } \right], \end{aligned}$$

(15)

where $\varDelta _{M} (x_{i} )=\left| \mu _{M} (x_{i} )-\nu _{M} (x_{i} )\right|$ shows the closeness of the membership and non-membership degree.

Example 3.1

Assume that IFSs(X) given by

$$\begin{aligned} M&= \left\{ \left\langle x_{1} ,\, 0.44,\, 0.385\right\rangle ,\, \left\langle x_{2} ,\, 0.43,\, 0.39\right\rangle ,\, \left\langle x_{3} ,\, 0.42,\, 0.38\right\rangle \right\} \\ N&= \left\{ \left\langle x_{1} ,\, 0.34,\, 0.48\right\rangle ,\, \left\langle x_{2} ,\, 0.37,\, 0.46\right\rangle ,\, \left\langle x_{3} ,\, 0.38,\, 0.45\right\rangle \right\} . \end{aligned}$$

The measures $J_{VS} (M || N)$ and $J_{C} (M || N)$ presume the values $J_{VS} (M || N)=-0.00712$ and $J_{JDC} (M || N)=-0.04547.$ Hence, the measures (11) and (15) do not satisfy the fundamental condition of non-negativity. The reason is that the measures (11) and (15) are based on the information-theoretic measure given by (Lin [22])

$$\begin{aligned} J_{L} (P || Q)=\sum _{i=1}^{n}p_{i} \ln \left( \frac{p_{i} }{\left( {1/2} \right) \left( p_{i} +q_{i} \right) } \right) , \end{aligned}$$

(16)

where $\, 0\le p_{i} ,\, q_{i} \le 1;\, \sum _{i=1}^{n}p_{i} = \sum _{i=1}^{n}q_{i} = 1,$$P=\left( p_{1} ,\, p_{2} ,\ldots ,p_{n} \right)$ and $Q=\left( q_{1} ,\, q_{2} ,\ldots ,q_{n} \right)$ are the finite discrete probability distribution.

Measure (16) is constantly non-negative by doctrine of Shannon inequality. However, measures (11) and (15), neither the duo $\left( \mu _{M} (x_{i} ),\, \nu _{M} (x_{i} )\right)$ nor $\left( \varDelta _{M} (x_{i} ),\, \pi _{M} (x_{i} )\right)$ spawn a probability distribution, because $0\le \mu _{M} (x_{i} )+\nu _{M} (x_{i} )\le 1$ and $0\le \varDelta _{M} (x_{i} )+\, \pi _{M} (x_{i} )\le 1,\, \forall \, \, x_{i} \in X.$ Hence, measures (11) and (15) do not hold the Shannon inequality compelling them to presume some negative values.

Example 3.2

Suppose that $M,\, N\in \mathrm{IFSs}(X),$ then

$$\begin{aligned} M&= \left\{ \left\langle x_{1} ,\, 0.0,\, 0.5\right\rangle ,\, \left\langle x_{2} ,\, 0.5,\, 0.0\right\rangle ,\, \left\langle x_{3} ,\, 0.0,\, 0.0\right\rangle \right\} \\ N&= \left\{ \left\langle x_{1} ,\, 0.5,\, 0.5\right\rangle ,\, \left\langle x_{2} ,\, 0.5,\, 0.5\right\rangle ,\, \left\langle x_{3} ,\, 0.5,\, 0.0\right\rangle \right\} . \end{aligned}$$

Here, $J_{VS} (M || N)=0,$ but M and N are not equal. Hence, postulate C2 is violated.

Example 3.3

Assume that $M,\, N\in \mathrm{IFSs}(X)$ given by

$$\begin{aligned} M&= \left\{ \left\langle x_{1} ,\, 0.0,\, 0.5\right\rangle ,\, \left\langle x_{2} ,\, 0.0,\, 0.5\right\rangle \right\} \\ N&= \left\{ \left\langle x_{1} ,\, 0.5,\, 0.0\right\rangle ,\, \left\langle x_{2} ,\, 0.5,\, 0.0\right\rangle \right\} . \end{aligned}$$

We obtain $J_{ZJ} (M || N)=0.$ Again postulate C2 is violated.

Example 3.4

Let us consider $M,\, N\in {IFSs}(X)$ given by $M=\left\{ \left\langle x_{1} ,\, 0.0,\, 0.5\right\rangle \right\}$ and $N=\left\{ \left\langle x_{1} ,\, 0.5,\, 0.0\right\rangle \right\} ,$ we get $J_{C} (M || N)=0.$ This is again a case of violation of postulate C2.

To avoid such a problem, in next subsection, we propose some new divergence measures for IFSs.

3.2 New Jensen divergence measures for IFSs

Definition 3.1

Let X be a discourse set such that $X=\left\{ x_{1} ,\, \, x_{2} ,\, \,\ldots ,\, \, x_{n} \right\}$ and $M,\, N \in \, \mathrm{IFSs}(X)$ given by

$$\begin{aligned} M&= \{\langle x_{i}, \mu _{M}(x_{i}), \nu _{M}(x_{i})\rangle | x_{i}\, \in \, X\},\\ N&= \{\langle x_{i}, \mu _{N}(x_{i}), \nu _{N}(x_{i})\rangle | x_{i}\, \in \, X\}, \end{aligned}$$

then corresponding to Verma and Sharma [48] measure, the Jensen-exponential divergence (JED) measure for IFSs M and N is defined as

$$\begin{aligned} J_{1} \left( M||N\right) =\frac{1}{n\left( \sqrt{e} -1\right) } \end{aligned}$$

$$\begin{aligned} \sum _{i=1}^{n}\left[ \left\{ \begin{array}{l} {\left\{ \frac{\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \\ {+\left\{ \frac{\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \end{array}\right\} -\frac{1}{2} \left\{ \begin{array}{l} {\left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} } \\ { +\left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} } \\ {+\left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} } \\ {\, +\left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} } \end{array}\right\} \right] , \end{aligned}$$

(17)

and based on Mishra et al. [31] entropy measure, we introduce the following JED for IFSs as follows:

$$\begin{aligned} J_{2} \left( M||N\right) =\frac{-1}{n\sqrt{e} \left( \sqrt{e} -1\right) } \sum _{i=1}^{n}\left[ \left\{ \begin{array}{l} {\left\{ \frac{\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \\ {+\left\{ \frac{\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \end{array}\right\} -\frac{1}{2}\left\{ \begin{array}{l} {\left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} } \\ {\, +\left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} } \\ {\, +\left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} } \\ {\, \, \, +\left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} } \end{array}\right\} \right] . \end{aligned}$$

(18)

Theorem 3.1

For all $L,M,\, N\in IFSs(X)$, then the exponential fuzzy cross-entropy measure $J_{\alpha } \left( M||N\right) , (\alpha =1, 2)$ in (17) and (18) holds the following postulates:

• 1. $J_{\alpha } \left( M||N\right) \ge 0$ and $0\le J_{\alpha } \left( M||N\right) \le 1,$

• 2. $J_{\alpha } \left( M||N\right) =0$ if and only if $M=N,$

• 3. $J_{\alpha } \left( M||N\right) =J_{\alpha } \left( N||M\right) ,$

• 4. $J_{\alpha } \left( M||M^{c} \right) =1,$ if and only if $M\in P(X),$

• 5. $J_{\alpha } \left( M||N\right) =J_{\alpha } \left( M^{c} ||N^{c} \right)$ and $J_{\alpha } \left( M||N^{c} \right) =J_{\alpha } \left( M^{c} ||N\right) ,$

• 6. $J_{\alpha } \left( L||M\right) \le J_{\alpha } \left( L||N\right)$ and $J_{\alpha } \left( M||N\right) \le J_{\alpha } \left( L||N\right) ,$ for $L\subseteq M\subseteq N.$

Proof

Since $f=x\exp (1-x)$ and $0\le x\le 1,$ then $f^{'} =\left( 1-x\right) \exp (1-x)\ge 0$ and $f^{''} =-\left( 2-x\right) \exp (1-x)<0;$ thus, f is convex function of x and $D_{1 } \left( M||N\right)$ is convex. Therefore, $D_{1} \left( M||N\right)$ increases as $\left\| M-N\right\| _{\gamma }$ increases, where $\left\| M-N\right\| _{\gamma } =\left| \mu _{M} -\mu _{N} \right| +\left| \nu _{M} -\nu _{N} \right| +\left| \pi _{M} -\pi _{N} \right| .$ Hence, $D_{\alpha } \left( M||N\right) \left( \alpha =1,\, 2\right) \,$ increases as $\left\| M-N\right\| _{\gamma }$ increases. Then $D_{\alpha } \left( M||N\right) \left( \alpha =1,\, 2\right) \,$ gets maximum value at $M=\left\{ \left( 1,0,0\right) \right\} ,$$N=\left\{ \left( 0,1,0\right) \right\}$ or $\left( \, M=\left\{ \left( 0,0,1\right) \right\} ,N=\left\{ \left( 0,1,0\right) \right\} \right.$ or $M=\left\{ \left( 1,0,0\right) \right\} ,$$\left. N=\left\{ \left( 0,0,1\right) \right\} \right) ,$ i. e., $M,N\in P(X)$ and reaches its minimum value $M=N.$ Hence it follows that $0\le J_{\alpha } (M||N)\le 1$ and $J_{\alpha } (M||N)=0$ if and only if $M=N.$$\square$

Let $L\subseteq M\subseteq N,$ i. e., $\mu _{L} \le \mu _{M} \le \mu _{N}$ and $\nu _{L} \ge \nu _{M} \ge \nu _{N} ,$ then $\left\| M-N\right\| _{\gamma } \le \left\| L-N\right\| _{\gamma }$ and $\left\| L-M\right\| _{\gamma } \le \left\| L-N\right\| _{\gamma }$.

Therefore, $J_{\alpha } \left( L||M\right) \le J_{\alpha } \left( L||N\right)$ and $J_{\alpha } \left( M||N\right) \le J_{\alpha } \left( L||N\right) ,$ for $L\subseteq M\subseteq N.$

Again, $\mathrm{If}\, \, \mathrm{M}\, \mathrm{=\; M}^{c} \, \mathrm{and}\, \, N=N^{c},$ in (17), then

$$\begin{aligned} J_{1} \left( M^{c} ||N^{c} \right)= & {} \frac{1}{n\left( \sqrt{e} -1\right) } \sum _{i=1}^{n}\left[ \left\{ \begin{array}{l} {\left\{ \frac{\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \\ {+\left\{ \frac{\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \end{array}\right\} -\frac{1}{2} \left\{ \begin{array}{l} {\left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} } \\ {\, +\left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} } \\ {\left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} } \\ {\, +\left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} } \end{array}\right\} \right] \\= & {} \frac{1}{n\left( \sqrt{e} -1\right) } \sum _{i=1}^{n}\left[ \left\{ \begin{array}{l} {\left\{ \frac{\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \\ {+\left\{ \frac{\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \mu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \end{array}\right\} \right. -\frac{1}{2} \left. \left\{ \begin{array}{l} {\left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} } \\ {\, +\left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} } \\ {\left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} } \\ {\, +\left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} } \end{array}\right\} \right] \\= & {} J_{1} \left( M||N\right). \end{aligned}$$

Thus, $J_{1} (M^{c} ||N^{c} )=J_{1} \left( M||N\right) .$

Similarly $J_{2} (M^{c} ||N^{c} )=J_{2} \left( M||N\right) .$

Hence $J_{\alpha } (M^{c} ||N^{c} )=J_{\alpha } \left( M||N\right) .$

Next,

$$\begin{aligned} J_{1} \left( M||N^{c} \right)= & {} \frac{1}{n\left( \sqrt{e} -1\right) }\\&\sum _{i=1}^{n}\left[ \left\{ \begin{array}{l} {\left\{ \frac{\left( \mu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \nu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \\ {+\left\{ \frac{\left( \nu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \mu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \end{array}\right\} \right. \\&-\frac{1}{2} \left. \left\{ \begin{array}{l} {\left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} } \\ {\, +\left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} } \\ {\left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} } \\ {\, +\left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} } \end{array}\right\} \right] \\&J_{1} \left( M^{c} ||N\right) =\frac{1}{n\left( \sqrt{e} -1\right) }\\&\sum _{i=1}^{n}\left[ \left\{ \begin{array}{l} {\left\{ \frac{\left( \nu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \mu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \\ {+\left\{ \frac{\left( \mu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) +2-\left( \nu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) }{4} \right\} } \\ {\, \, \exp \left\{ \frac{\left( \nu _{M} (x_{i} )+\mu _{N} (x_{i} )\right) +2-\left( \mu _{M} (x_{i} )+\nu _{N} (x_{i} )\right) }{4} \right\} } \end{array}\right\} \right. \\&-\frac{1}{2} \left. \left\{ \begin{array}{l} {\left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} } \\ {\, +\left\{ \frac{\mu _{M} (x_{i} )+1-\nu _{M} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{M} (x_{i} )+1-\mu _{M} (x_{i} )}{2} \right\} } \\ {\left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} } \\ {\, +\left\{ \frac{\nu _{N} (x_{i} )+1-\mu _{N} (x_{i} )}{2} \right\} \exp \left\{ \frac{\mu _{N} (x_{i} )+1-\nu _{N} (x_{i} )}{2} \right\} } \end{array}\right\} \right]. \end{aligned}$$

Thus, $J_{1} \left( M||N^{c} \right) =J_{1} (M^{c} ||N).$

Similarly, $J_{2} \left( M||N^{c} \right) =J_{2} (M^{c} ||N).$

Hence, $J_{\alpha } \left( M||N^{c} \right) =J_{\alpha } (M^{c} ||N).$

Proposition 3.1

If $N=M^{c} ,$ then the relation between $J_{\alpha } \left( M||N\right) ,\, \left( \alpha =1,2\right)$ and entropy $H_{\alpha } (M):$

$$\begin{aligned} H_{\alpha } (M)=1-J_{\alpha } (M||N), \end{aligned}$$

(19)

where $H_{\alpha } (.)$ is entropy for IFSs [31].

Proposition 3.2

The mapping $J_{\alpha } \left( M||N\right) ,\, \left( \alpha =1,2\right),$ is distance measures on IFSs(X).

Proposition 3.3

For all $\, M,N\in IFSs(X),$

• 1. $J_{\alpha } (M||M\cup N)=J_{\alpha } (N||M\cap N),$

• 2. $J_{\alpha } (M||M\cap N)=J_{\alpha } (N||M\cup N),$

• 3. $J_{\alpha } (M\cup N||M\cap N)=J_{\alpha } (M||N),$

• 4. $J_{\alpha } (M||M\cup N)+J_{\alpha } (M||M\cap N)=J_{\alpha } (M||N),$

• 5. $J_{\alpha } (N||M\cup N)+J_{\alpha } (N||M\cap N)=J_{\alpha } (M||N).$

4 Proposed method for MCDM

Decision-making is a procedure of selecting the best option(s) from a finite number of feasible options. It is a prominent activity that generally happens in our daily life and plays a vital task in finance, management, business, social and political sciences, engineering and computer science, biology and medicine, etc.

An MCDM problem entails obtaining the optimal solution (i.e. an option) from the available options, which are assessed on multi-criteria. Consider the set of q alternatives, $A=\left\{ a_{1} ,a_{2} ,\ldots ,a_{q} \right\} ,$ and a set of p criterion $C=\left\{ c_{1} ,c_{2} ,\ldots ,c_{p} \right\} .$ Now, we try to find the weight vector $w=\left( w_{1} ,w_{2} ,\ldots ,w_{p} \right) ^{T}$ of the criterion $c_{r} \left( r=1(1)p\right)$ such that $w_{r} >0,\, r=1(1)p,\, \sum _{r=1}^{p}w_{r} =1 ,\, w_{r} \in W,$ where W is the set of incomplete or uncertain weight information provided by the decision maker, which is illustrated via one or more of the cases [55]:

• 1. A weak ranking: $\left\{ w_{r} \ge w_{s} \right\} ,\, \, r\ne s.$

• 2. A strict ranking: $\left\{ w_{r} -w_{s} \ge \beta _{i} \right\} ,\, \, r\ne s.$

• 3. A ranking of difference: $\left\{ w_{r} -w_{s} \ge w_{t} -w_{l} \right\} ,\, \, r\ne s\ne t\ne l.$

• 4. A ranking with multiples: $\left\{ w_{r} \ge \alpha _{r} w_{s} \right\} ,\, \, r\ne s.$

• 5. An interval form:$\left\{ \beta _{r} \le w_{r} \le \beta _{r} -\varepsilon _{r} \right\} ,\, \,$ where $\beta _{r}$ and $\varepsilon _{r}$ are non-negative numbers.

A thorough analysis on how the uncertain or incomplete weight information is confined in implementation via the given cases [40]. Even if the principle idea of the communication is on incomplete weight information of criterion, it is admirable to mention that in several decision-making circumstances, the criteria weight can be fully unknown or is characterized by IFVs. Here, (1) the model of entropy weights might be employed to get the desirable weight vector [58, 59] and (2) the interval weights may be acquired via IFVs that confine the fuzzy doctrine of significance of criteria [23, 51] to describe the weight vector W. Let $\mathbf{{\mathbb Z}}=\left( z_{rs} \right) _{p\times q}$ be an IF-decision matrix, where $z_{rs} =\left( \mu _{rs} ,\nu _{rs} ,\pi _{rs} \right)$ is an IFV. In MCDM problem, the criteria are either of benefit type or of cost type. Considering their natures, a benefit attribute (the bigger the values better is it) and cost attribute (the smaller the values the better) are of rather opposite type. To deal both criterion sets concurrently, the criterion sets of the cost type are converted into the criterion sets of the benefit type by renovating $\mathbf{{\mathbb Z}}=\left( z_{rs} \right) _{p\times q}$ into the IF-decision matrix $\mathbf{{\mathbb R}}=\left( \ell _{rs} \right) _{p\times q} .$

$$\begin{aligned} \ell _{{rs}} & = \left( {\mu _{{rs}} ,\;\nu _{{rs}} ,\;\pi _{{rs}} } \right) \\ & = \left\{ {\begin{array}{*{20}l} {z_{{rs}} ,} \hfill & {{\text{benefit}}\;{\text{type}}\;{\text{criteria}}\;c_{r} } \hfill \\ {\bar{z}_{{rs}} ,} \hfill & {{\text{cost}}\;{\text{type}}\;{\text{criteria}}\;c_{r} } \hfill \\ \end{array} } \right. \\ \end{aligned}$$

(20)

where $\overline{z}_{rs}$ is the complement of $z_{rs},$ and $q=1(1)s.$ Here, the three parameters of IFVs are inferred as: (1) membership degree is referred as the more the better; (2) non-membership degree is referred as the less the better; and (3) hesitancy degree is also referred as the less the better. The advantage and disadvantage scores of an option on a criterion over the rest are evaluated as follows. To obtain advantage and disadvantage scores, we determine how much the first parameter is larger and the second and third parameters are smaller in comparison with others and vice versa. Analytically, the advantage and disadvantage scores $m_{rs}$ and $n_{rs}$ of the options $a_{s}$ on the criteria $c_{r},$ respectively, are constructed as

$$\begin{aligned} m_{rs} =\frac{1}{3} \left( \sum _{s\ne t}\max \left\{ \left( \mu _{rs} -\mu _{rt} \right) ,\, 0\right\} +\sum _{s\ne t}\max \left\{ \left( \nu _{rt} -\nu _{rs} \right) ,\, 0\right\} +\sum _{s\ne t}\max \left\{ \left( \pi _{rt} -\pi _{rs} \right) ,\, 0\right\} \right) .\end{aligned}$$

(21)

$$\begin{aligned} n_{rs} =\frac{1}{3} \left( \sum _{s\ne t}\max \left\{ \left( \mu _{rt} -\mu _{rs} \right) ,\, 0\right\} +\sum _{s\ne t}\max \left\{ \left( \nu _{rs} -\nu _{rt} \right) ,\, 0\right\} +\sum _{s\ne t}\max \left\{ \left( \pi _{rs} -\pi _{rt} \right) ,\, 0\right\} \right) . \end{aligned}$$

(22)

Next, the strength score $\vartheta _{s} (w)$ and worst score $\tau _{s} (w)$ of the option $a_{s}$ are calculated as

$$\begin{aligned} \vartheta _{s} (w)=\sum _{r=1}^{m}w_{r} \, m_{rs}, \, \, \, s=1\, (1)\, q.\end{aligned}$$

(23)

$$\begin{aligned} \tau _{s} (w)=\sum _{r=1}^{m}w_{r} \, n_{rs} ,\, \, \, \, \, s=1\, (1)\, q. \end{aligned}$$

(24)

If the $\vartheta _{s} (w)$ is large, then the option $a_{s}$ is enhanced, and if the $\tau _{s} (w)$ is small, then the option $a_{s}$ is improved. Taking into consideration solely either strength or worst scores in MCDM problems is not adequate to conclude how good or bad an option is on the given criteria. To estimate satisfaction degree of an option with respect to criteria, it is more suitable if we utilize both strength and worst scores. Hence, the satisfaction degree of option $a_{s}$ with respect to p criteria is given by

$$\begin{aligned} \eta \left( \xi _{s} (w)\right) =\frac{\vartheta _{s} (w)}{\vartheta _{s} (w)+\tau _{s} (w)} =\frac{\sum _{r=1}^{p}w_{r} m_{rs} }{\sum _{r=1}^{p}w_{r} \left( m_{rs} +n_{rs} \right) }. \end{aligned}$$

(25)

It pursues that $\eta \left( \xi _{s} (w)\right) \in [0,1]$ and greater value of $\vartheta _{s} (w)$ and lesser value of $\tau _{s} (w)$ (worst score) provide higher satisfaction degree $\eta \left( \xi _{s} (w)\right)$ of the option $a_{s}$ with respect to criteria. Hence, the option $a_{s}$ is regarded as improved in comparison with existing ones. We observe that satisfaction degree $\eta \left( \xi _{s} (w)\right)$ of the option $a_{s}$ relies on the criteria weights, which are partially or completely unknown. Next, a multi-objective optimization model for desirable weight vector $w^{*} =\left( w_{1}^{*} ,\, w_{2}^{*} ,\ldots ,w_{p}^{*} \right) ^{T}$ of the criterion is demonstrated as

$$\begin{aligned} \max \, \left\{ \eta \left( \xi _{1} (w)\right) ,\, \eta \left( \xi _{1} (w)\right) ,\, \ldots ,\eta \left( \xi _{s} (w)\right) \right\} \end{aligned}$$

subject to $w=\left( w_{1} ,w_{2} ,\ldots ,w_{r} \right) ^{T} \in W \qquad$ (M-I)

$$\begin{aligned} \sum _{r=1}^{p}w_{r} =1 ,\, \, w_{r} >0,\, r=1(1)p, \end{aligned}$$

where W is the set of incomplete weight vector given by the DMs. If weight vector W is contradictory, then W is an empty set and it desires to be amended by DM in order that the reassessed weight information is not contradictory. The model M-I is converted into the single-objective optimization model via weighted sums method with equal weights [8] as follows:

$$\begin{aligned} \max \quad \frac{\sum _{r=1}^{p}w_{r} m_{rs} }{\sum _{r=1}^{p}w_{r} \left( m_{rs} +n_{rs} \right) } \end{aligned}$$

subject to $w=\left( w_{1} ,w_{2} ,\ldots ,w_{r} \right) ^{T} \in W \qquad$ (M-II)

$$\begin{aligned} \sum _{r=1}^{p}w_{r} =1 ,\, \, w_{r} >0,\, r=1(1)p. \end{aligned}$$

The model M-II is a linear fractional programming model. The evaluation of M-II offers the desirable weight vector $w^{*} =\left( w_{1}^{*} ,\, w_{2}^{*} ,\ldots ,w_{p}^{*} \right) ^{T}.$ The overall criterion value of each option $a_{s}$ is given by

$$\begin{aligned} \xi _{s} \left( w^{*} \right) =\sum _{r=1}^{p}w_{r}^{*} z_{rs} =\left( \sum _{r=1}^{p}w_{r}^{*} \mu _{rs} ,\, \sum _{r=1}^{p}w_{r}^{*} \nu _{rs} ,\, \sum _{r=1}^{p}w_{r}^{*} \pi _{rs} \right) , \end{aligned}$$

(26)

where $s=1(1)q.$

Further, the options $a_{s}$ are ranked based on the ranking of overall criteria $\xi _{s} \left( w^{*} \right) , s=1(1)q.$ Ranking method [45] for ranking IFVs $\gamma _{s} =\left( \mu _{s} , \nu _{s} , \pi _{s} \right) , \left( s=1(1)q\right)$ is implemented.

Define

$$\begin{aligned} \mathrm{\phi }\left( \gamma _{s} \right) =0.5\left( 1+\pi _{s} \right) \, \, J_{\alpha } \left( \gamma ^{*} || \gamma _{s} \right) ,\, \, s=1(1)q,\, \, \alpha =1,2, \end{aligned}$$

(27)

where $J_{\alpha } \left( \gamma ^{*} || \gamma _{r} \right) ,\alpha =1,2$ is divergence measure for IFVs given by (17) and (18) and

$$\begin{aligned} \gamma ^{*} =\left\{ \left( \mu _{1}^{*} ,\, \nu _{1}^{*} ,\, \pi _{1}^{*} \right) ,\, \right. \left( \mu _{2}^{*} ,\, \nu _{2}^{*} ,\, \pi _{2}^{*} \right) ,\ldots ,\, \, \left. \left( \mu _{q}^{*} ,\, \nu _{q}^{*} ,\, \pi _{q}^{*} \right) \right\} , \end{aligned}$$

(28)

such that $\left( \mu _{s}^{*} ,\, \nu _{s}^{*} \right) =\left( \mathop {\max \mu _{rs} }\limits _{r} ,\mathop {\min \nu _{rs} }\limits _{r} \right) ,\, s=1(1)q.$

The smaller $\mathrm{\phi }\left( \gamma _{r} \right) ,$ the improved the overall intuitionistic fuzzy preference value $\gamma _{r}$ [45].

Fig. 1

General implementation procedure for IF-decision-making model based on divergence measure

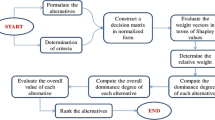
Algorithm 1

A fruitful classification of the method is discussed as follows (see Fig. 1):

• Step 1 Generate the matrix $\mathbf{{\mathbb Z}}=\left( z_{rs} \right) _{p\times q} ,$ weight vector W and transformation performed (20) if necessary.

• Step 2 Evaluate the advantage $m_{rs}$ and disadvantage $n_{rs}$ scores according to each option $a_{s} (s=1(1)q).$

• Step 3 Estimate the strength $\vartheta _{s} (w)$ and worst $\tau _{s} (w)$ scores of the option $a_{s} (s=1(1)q).$

• Step 4 Apply the satisfaction degree $\eta \left( \xi _{s} (w)\right)$ of the option $a_{s} (s=1(1)q).$

• Step 5 Utilize model M-II to obtain the desirable weight vector $w^{*} =\left( w_{1}^{*} ,\, w_{2}^{*} ,\ldots ,w_{p}^{*} \right) ^{T}.$ Compute overall criterion value $\xi _{s} \left( w^{*} \right)$ of the option $a_{s} (s=1(1)q).$

• Step 6 Corresponding to overall criterion values, implement (27) to rank the options $a_{s} (s=1(1)q).$

• Step 7 Choose the optimal option(s) based on the ranking.

• Step 8 End.

5 A real application of selection of optimal energy source

Energy resources have been considered as a propeller in the socio-economic growth of any country. In the recent years, the renewable energy sources play vital role in the development of economic activity and have been utilized in the reduction of the fossil fuels, production costs [17], environmental pollutions, maintenance of non-renewable energies sources [26, 57] etc. Nowadays, the increasing demand of energy in various countries requires the determination of an optimal energy policy under different conflicting criteria. However, selecting the most appropriate energy resource with respect to different conflicting criteria is a critical and complex problem for decision makers. To deal with this issue, many authors have developed numerous decision-making methods based on FS theory to identify the most suitable energy policy under different criteria [13, 24]. Erdogan and Kaya [6] evaluated an integrated multi-criteria decision-making method to find an optimal energy alternative among set of energy alternatives in Turkey which is based on type-2 fuzzy sets. Mousavi and Tavakkoli-Moghaddam [36] presented a hesitant fuzzy hierarchal complex proportional assessment (HF-HCOPRAS) method to choose the best energy resource under 15 conflicting criteria. Presently, Mousavi et al. [37] developed a modified elimination and choice translating reality (ELECTRE) method under hesitant fuzzy environment for solving multi-attribute group decision-making (MAGDM) problems in energy sector. Here, a new modified preference selection method on uncertain environment under intuitionistic fuzzy divergence measure is proposed to demonstrate the relative importance of desirable energy attributes in renewable energy policy atmosphere by decision maker.

One of the problems facing the city development officer is to determine the best energy resource among set of renewable energy alternatives for their city. In this case, the officer tenders five renewable energy alternatives which are (1) wind energy $(E_{1}),$ (2) solar energy $(E_{2}),$ (3) geothermal energy $(E_{3}),$ (4) biomass energy $(E_{4})$ and (5) hydro-power energy $(E_{5}).$ A team of three decision makers (DMs) is established who have to select the most optimal energy resource. The preferred alternatives are assessed under 14 criteria which are (1) feasibility $(L_{1}),$ (2) economic risks $(L_{2}),$ (3) pollutant emission $(L_{3}),$ (4) land requirement $(L_{4}),$ (5) need of waste disposal $(L_{5}),$ (6) land disruption $(L_{6}),$ (7) water pollution $(L_{7}),$ (8) Investment costs $(L_{8}),$ (9) security of energy supply $(L_{9}),$ (10) source durability $(L_{10}),$ (11) sustainability of the energy resources $(L_{11} ),$ (12) compatibility with national energy policy objective $(L_{12}),$ (13) energy efficiency $(L_{13})$ and (14) labour impact $(L_{14})$ (see Fig. 2).

Fig. 2

Decision hierarchy of selection of optimal energy source problem

Since it is not easy to provide an exact numerical value for the importance of the selected criteria, the decision makers define their judgements in linguistic variables. Now, Table 1 represents the relative importance of elected evaluation criteria and decision makers (DMs). In addition, the linguistic terms are adopted from Vahdani et al. [47] study for evaluating the candidates and weight of each criterion.

Table 1 Linguistic variables for rating the performance of criteria

Tables 2 and 3 represent the importance degree of the DMs and weights of the criteria in terms of linguistic variables.

Table 2 Importance of decision makers for rating the energy source alternatives

Table 3 Weights of the criteria in linguistic variables

Table 4 characterizes the performance ratings of the energy alternatives given by DMs, and their importance with respect to each selected criteria is given in Table 5.

Table 4 Performance rating of renewable energy policy alternatives in terms of linguistic variables

Table 5 Performance rating of renewable energy sources in linguistic variables

According to DM’s judgements, the aggregated intuitionistic fuzzy decision matrix is depicted in Table 6.

Table 6 Aggregated intuitionistic fuzzy decision matrix

5.1 Implementation and discussion

In this section, proposed technique is applied in a real case study to select the most optimal energy alternative for city development. Now, the procedural steps are as follows:

Step 1 IF-decision matrix ${\mathbb R}\, =\, \left( l_{rs} \right) _{p\times q}$ (given by Table 6) and the weight vector of the criterion is given by

$$\begin{aligned} W=\, \left\{ \left( w_{r} \right) ^{T} \left| \begin{array}{l} { 0.01 \le w_{2} \le 0.04, 0.02 \le w_{3} \le 0.04, } \\ {0.1 \le w_{1} \le 0.2, 0.01 \le w_{7} \le 0.02,}\\ { 0.01 \le w_{5} \le 0.04, 0.1 \le w_{6} \le 0.3, } \\ { 0.02 \le w_{8} \le 0.045 0.01 \le w_{9} \le 0.025, } \\ {0.02 \le w_{10} \le 0.05, 0.015 \le w_{11} \le 0.12,} \\ {w_{13} \le 0.2, w_{13} - w_{14} \le 0.1, w_{12} - w_{13} \le 0.1, } \\ { 0.1 \le w_{12} \le 0.25, w_{8} - w_{9} \ge w_{12} - w_{13} ,}\\ { 0.01 \le w_{4}\le 0.05, w_{4} - w_{5} \ge w_{7} - w_{8},}\\ { w_{r} \ge 0, r = 1 (1) p, \sum _{r =1}^{p}w_{r} =1 } \end{array}\right. \right\} . \end{aligned}$$

Step 2 By using (21) and (22), the advantage and disadvantage scores of the alternatives $E_{s} \, (s=\, 1(1)\, 5)$ with respect to criteria $L_{r} \, (r\, =1(1)\, 14)$ are obtained in Tables 7 and 8.

Table 7 Advantage scores of the alternatives

Table 8 Disadvantage scores of the alternatives

Step 3 The strength $\upsilon _{s} (w)$ and worst $\tau _{s} (w)$ scores of the alternatives $E_{s} \, (s=\, 1(1)\, 5)$ are computed by using (23) and (24), which are given as

$$\begin{aligned} \upsilon _{1} (w)&=0.1716\, w_{1} \, +\, 0.0493\, w_{2} \, +\, 0.0394\, w_{3} \, +0.0339\, w_{4} \, +\, 0.1110\, w_{5} \, \\& \quad +\, 0.0008\, w_{6} +\, 0.1085\, w_{7} +\, 0.0480\, w_{8} \, +\, 0.0246\, w_{9} \, +\, 0.0376\, w_{10} \, \\& \quad +\, 0.0683\, w_{11} \, +\, 0.0034\, w_{12} \, +\, 0.3077\, w_{13} \, +\, 0.0287\, w_{14} ,\\ \upsilon _{2} (w)&=0.1074\, w_{1} \, +\, 0.1548\, w_{2} \, +\, 0.3244\, w_{3} \, +0.1111\, w_{4} \, +\, 0.0708\, w_{5} \\& \quad +\, 0.8545\, w_{6} +\, 0.0682\, w_{7} +\, 0.0971\, w_{8} \, +\, 0.7080\, w_{9} \, +\, 0.6208\, w_{10} \\& \quad +\, 0.5684\, w_{11} \, +\, 0.2310\, w_{12} \, +\, 0.1106\, w_{13} \, +\, 0.9194\, w_{14} ,\\ \upsilon _{3} (w)&=0.0786\, w_{1} \, +\, 0.0493\, w_{2} \, +\, 0.0232\, w_{3} \, +0.3885\, w_{4} \, +\, 0.0784\, w_{5} \\& \quad +\, 0.2401\, w_{6} +\, 0.0682\, w_{7} +\, 0.1688\, w_{8} \, +\, 0.2718\, w_{9} \, +\, 0.4639\, w_{10} \\ &\quad +\, 0.2812\, w_{11} \, +\, 0.2163\, w_{12} \, +\, 0.0573\, w_{13} \, +\, 0.3037\, w_{14} ,\\ \upsilon _{4} (w)&=0.2309\, w_{1} \, +\, 0.5705\, w_{2} \, +\, 0.0566\, w_{3} \, +0.0920\, w_{4} \, +\, 0.4420\, w_{5} \\ &\quad +\, 0.0588\, w_{6} +\, 0.2735\, w_{7} +\, 0.0449\, w_{8} \, +\, 0.1050\, w_{9} \, +\, 0.0028\, w_{10} \\& \quad +\, 0.1991\, w_{11} \, +\, 0.0780\, w_{12} \, +\, 0.2602\, w_{13} \, +\, 0.0277\, w_{14} ,\\ \upsilon _{5} (w)&=0.0788\, w_{1} \, +\, 0.0399\, w_{2} \, +\, 0.0868\, w_{3} \, +0.0339\, w_{4} \, +\, 0.1292\, w_{5} \\ &\quad +\, 0.0458\, w_{6} +\, 0.1790\, w_{7} +\, 0.2503\, w_{8} \, +\, 0.0019\, w_{9} \, +\, 0.0376\, w_{10} \\ &\quad +\, 0.0000\, w_{11} \, +\, 0.0283\, w_{12} \, +\, 0.1071\, w_{13} \, +\, 0.0000\, w_{14} \\ \tau _{1} (w)&=0.2094\, w_{1} \, +\, 0.1126\, w_{2} \, +\, 0.1177\, w_{3} \, +\, 0.1533\, w_{4} \, +\, 0.0776\, w_{5} \\& \quad +\, 0.3916\, w_{6} \, +\, 0.1161\, w_{7} +\, 0.2444\, w_{8} \, +\, 0.3433\, w_{9} \, +\, 0.3142\, w_{10} \\& \quad +\, 0.2412\, w_{11} \, +\, 0.2686\, w_{12} \, +\, 0.0256\, w_{13} \, +\, 0.2868\, w_{14} ,\\ \tau _{2} (w)&=0.1452\, w_{1} \, +\, 0.0655\, w_{2} \, +\, 0.0572\, w_{3} \, +\, 0.1035\, w_{4} \, +\, 0.1644\, w_{5} \\ &\quad +\, 0.0000\, w_{6} \, +\, 0.2029\, w_{7} +\, 0.0889\, w_{8} \, +\, 0.0000\, w_{9} \, +\, 0.0101\, w_{10} \\ &\quad +\, 0.0000\, w_{11} \, +\, 0.0005\, w_{12} \, +\, 0.3429\, w_{13} \, +\, 0.0000\, w_{14} ,\\ \tau _{3} (w)&=0.1166\, w_{1} \, +\, 0.1487\, w_{2} \, +\, 0.1120\, w_{3} \, +\, 0.0379\, w_{4} \, +\, 0.1720\, w_{5} \\ &\quad +\, 0.1560\, w_{6} \, +\, 0.2038\, w_{7} +\, 0.0308\, w_{8} \, +\, 0.1101\, w_{9} \, +\, 0.0465\, w_{10} \\ &\quad +\, 0.0640\, w_{11} \, +\, 0.0178\, w_{12} \, +\, 0.2630\, w_{13} \, +\, 0.1547\, w_{14} ,\\ \tau _{4} (w)&=0.0795\, w_{1} \, +\, 0.0948\, w_{2} \, +\, 0.1564\, w_{3} \, +\, 0.2114\, w_{4} \, +\, 0.0786\, w_{5} \\ &\quad +\, 0.2015\, w_{6} \, +\, 0.0758\, w_{7} +\, 0.1654\, w_{8} \, +\, 0.2254\, w_{9} \, +\, 0.4541\, w_{10} \\ &\quad +\, 0.1523\, w_{11} \, +\, 0.0995\, w_{12} \, +\, 0.0362\, w_{13} \, +\, 0.4175\, w_{14} ,\\ \tau _{5} (w)&=0.1166\, w_{1} \, +\, 0.1393\, w_{2} \, +\, 0.1532\, w_{3} \, +\, 0.1490\, w_{4} \, +\, 0.0958\, w_{5} \\ &\quad +\, 0.3443\, w_{6} \, +\, 0.0997\, w_{7} +\, 0.0267\, w_{8} \, +\, 0.4326\, w_{9} \, +\, 0.3142\, w_{10} \\ &\quad +\, 0.7579\, w_{11} \, +\, 0.1722\, w_{12} \, +\, 0.1500\, w_{13} \, +\, 0.4699\, w_{14} . \end{aligned}$$

Step 4 By using (25), the satisfaction degrees $\eta (\xi _{s} (w))$ of the alternatives $E_{s} \, (s=\, 1(1)\, 5)$ are obtained as follows:

$$\begin{aligned}\eta (\xi _{1} (w))=\, \frac{\left( \begin{array}{l} {0.1716\, w_{1} \, +\, 0.0493\, w_{2} \, +\, 0.0394\, w_{3} \, +0.0339\, w_{4} } \\ {+\, 0.1110\, w_{5} +\, 0.0008\, w_{6} +\, 0.1085\, w_{7} +\, 0.0480\, w_{8} } \\ { +\, 0.0246\, w_{9} \, +\, 0.0376\, w_{10} +\, 0.0683\, w_{11} \, }\\ {+\, 0.0034\, w_{12} \, +\, 0.3077\, w_{13} \, +\, 0.0287\, w_{14}} \end{array}\right) }{\left( \begin{array}{l} {0.2094\, w_{1} \, +\, 0.1126\, w_{2} \, +\, 0.1177\, w_{3} \, +\, 0.1533\, w_{4} } \\ { +\, 0.0776\, w_{5}+ 0.3916\, w_{6} \, +\, 0.1161\, w_{7} +\, 0.2444\, w_{8} } \\ { +\, 0.3433\, w_{9} \, +\, 0.3142\, w_{10}+\, 0.2412\, w_{11} } \\ {+\, 0.2686\, w_{12} \, +\, 0.0256\, w_{13} \, +\, 0.2868\, w_{14}} \end{array}\right) } ,\\\eta (\xi _{2} (w))=\, \frac{\left( \begin{array}{l} {0.1074\, w_{1} \, +\, 0.1548\, w_{2} \, +\, 0.3244\, w_{3} \, +0.1111\, w_{4} } \\ { + 0.0708\, w_{5}+\, 0.8545\, w_{6} +\, 0.0682\, w_{7} +\, 0.0971\, w_{8} } \\ { +\, 0.7080\, w_{9} \, +\, 0.6208\, w_{10} +\, 0.5684\, w_{11} } \\ {+\, 0.2310\, w_{12} \, +\, 0.1106\, w_{13} \, +\, 0.9194\, w_{14}} \end{array}\right) }{\left( \begin{array}{l} {0.1452\, w_{1} \, +\, 0.0655\, w_{2} \, +\, 0.0572\, w_{3} \, +\, 0.1035\, w_{4} } \\ { +\, 0.1644\, w_{5}+\, 0.0000\, w_{6} \, +\, 0.2029\, w_{7} +\, 0.0889\, w_{8} } \\ { +\, 0.0000\, w_{9} \, +\, 0.0101\, w_{10}+\, 0.0000\, w_{11} } \\ {+\, 0.0005\, w_{12} \, +\, 0.3429\, w_{13} \, +\, 0.0000\, w_{14}} \end{array}\right) } ,\\ \eta (\xi _{3} (w))=\, \frac{\left( \begin{array}{l} {0.0786\, w_{1} \, +\, 0.0493\, w_{2} \, +\, 0.0232\, w_{3} \, +0.3885\, w_{4} } \\ { +\, 0.0784\, w_{5}+\, 0.2401\, w_{6} +\, 0.0682\, w_{7} +\, 0.1688\, w_{8} } \\ { +\, 0.2718\, w_{9} \, +\, 0.4639\, w_{10} +\, 0.2812\, w_{11} } \\ {+\, 0.2163\, w_{12} \, +\, 0.0573\, w_{13} \, +\, 0.3037\, w_{14}} \end{array}\right) }{\left( \begin{array}{l} {0.1166\, w_{1} \, +\, 0.1487\, w_{2} \, +\, 0.1120\, w_{3} \, +\, 0.0379\, w_{4} } \\ { +\, 0.1720\, w_{5}+\, 0.1560\, w_{6} \, +\, 0.2038\, w_{7} +\, 0.0308\, w_{8} } \\ { +\, 0.1101\, w_{9} \, +\, 0.0465\, w_{10}+\, 0.0640\, w_{11} } \\ {+\, 0.0178\, w_{12} \, +\, 0.2630\, w_{13} \, +\, 0.1547\, w_{14}} \end{array}\right) } ,\\ \eta (\xi _{4} (w))=\, \frac{\left( \begin{array}{l} {0.2309\, w_{1} \, +\, 0.5705\, w_{2} \, +\, 0.0566\, w_{3} \, +0.0920\, w_{4} } \\ {+\, 0.4420\, w_{5} +\, 0.0588\, w_{6} +\, 0.2735\, w_{7} +\, 0.0449\, w_{8} } \\ { +\, 0.1050\, w_{9} \, +\, 0.0028\, w_{10} +\, 0.1991\, w_{11} } \\ {+\, 0.0780\, w_{12} \, +\, 0.2602\, w_{13} \, +\, 0.0277\, w_{14}} \end{array}\right) }{\left( \begin{array}{l} {0.0795\, w_{1} \, +\, 0.0948\, w_{2} \, +\, 0.1564\, w_{3} \, +\, 0.2114\, w_{4} } \\ { +\, 0.0786\, w_{5}+\, 0.2015\, w_{6} \, +\, 0.0758\, w_{7} +\, 0.1654\, w_{8} } \\ { +\, 0.2254\, w_{9} \, +\, 0.4541\, w_{10} +\, 0.1523\, w_{11} } \\ {+\, 0.0995\, w_{12} \, +\, 0.0362\, w_{13} \, +\, 0.4175\, w_{14}} \end{array}\right) } ,\\ \eta (\xi _{5} (w))=\, \frac{\left( \begin{array}{l} {0.0788\, w_{1} \, +\, 0.0399\, w_{2} \, +\, 0.0868\, w_{3} \, +0.0339\, w_{4} } \\ { +\, 0.1292\, w_{5} +\, 0.0458\, w_{6} +\, 0.1790\, w_{7} +\, 0.2503\, w_{8} } \\ { +\, 0.0019\, w_{9} \, +\, 0.0376\, w_{10} +\, 0.0000\, w_{11} } \\ {+\, 0.0283\, w_{12} \, +\, 0.1071\, w_{13} \, +\, 0.0000\, w_{14}} \end{array}\right) }{\left( \begin{array}{l} {0.1166\, w_{1} \, +\, 0.1393\, w_{2} \, +\, 0.1532\, w_{3} \, +\, 0.1490\, w_{4} } \\ { +\, 0.0958\, w_{5} +\, 0.3443\, w_{6} \, +\, 0.0997\, w_{7} +\, 0.0267\, w_{8}} \\ { +\, 0.4326\, w_{9} \, +\, 0.3142\, w_{10}+\, 0.7579\, w_{11} } \\ {+\, 0.1722\, w_{12} \, +\, 0.1500\, w_{13} \, +\, 0.4699\, w_{14}} \end{array}\right) } . \end{aligned}$$

Step 5 To find the weight $w^{*} =\, \left( w_{1} ,\, w_{2} ,\, \ldots ,\, w_{14} \right) ^{T} ,$ model M-II is given as follows:

$$\begin{aligned}\mathrm{Maximize} \left[ \frac{\left( \begin{array}{l} {0.1716\, w_{1} \, +\, 0.0493\, w_{2} \, +\, 0.0394\, w_{3} \, +0.0339\, w_{4} } \\ {+\, 0.1110\, w_{5} +\, 0.0008\, w_{6} +\, 0.1085\, w_{7} +\, 0.0480\, w_{8} } \\ { +\, 0.0246\, w_{9} \, +\, 0.0376\, w_{10} +\, 0.0683\, w_{11} \, }\\ {+\, 0.0034\, w_{12} \, +\, 0.3077\, w_{13} \, +\, 0.0287\, w_{14}} \end{array}\right) }{\left( \begin{array}{l} {0.2094\, w_{1} \, +\, 0.1126\, w_{2} \, +\, 0.1177\, w_{3} \, +\, 0.1533\, w_{4} } \\ { +\, 0.0776\, w_{5}+ 0.3916\, w_{6} \, +\, 0.1161\, w_{7} +\, 0.2444\, w_{8} } \\ { +\, 0.3433\, w_{9} \, +\, 0.3142\, w_{10}+\, 0.2412\, w_{11} } \\ {+\, 0.2686\, w_{12} \, +\, 0.0256\, w_{13} \, +\, 0.2868\, w_{14}} \end{array}\right) } \right. \\ +\frac{\left( \begin{array}{l} {0.1074\, w_{1} \, +\, 0.1548\, w_{2} \, +\, 0.3244\, w_{3} \, +0.1111\, w_{4} } \\ { + 0.0708\, w_{5}+\, 0.8545\, w_{6} +\, 0.0682\, w_{7} +\, 0.0971\, w_{8} } \\ { +\, 0.7080\, w_{9} \, +\, 0.6208\, w_{10} +\, 0.5684\, w_{11} } \\ {+\, 0.2310\, w_{12} \, +\, 0.1106\, w_{13} \, +\, 0.9194\, w_{14}} \end{array}\right) }{\left( \begin{array}{l} {0.1452\, w_{1} \, +\, 0.0655\, w_{2} \, +\, 0.0572\, w_{3} \, +\, 0.1035\, w_{4} } \\ { +\, 0.1644\, w_{5}+\, 0.0000\, w_{6} \, +\, 0.2029\, w_{7} +\, 0.0889\, w_{8} } \\ { +\, 0.0000\, w_{9} \, +\, 0.0101\, w_{10}+\, 0.0000\, w_{11} } \\ {+\, 0.0005\, w_{12} \, +\, 0.3429\, w_{13} \, +\, 0.0000\, w_{14}} \end{array}\right) }\\ +\frac{\left( \begin{array}{l} {0.0786\, w_{1} \, +\, 0.0493\, w_{2} \, +\, 0.0232\, w_{3} \, +0.3885\, w_{4} } \\ { +\, 0.0784\, w_{5}+\, 0.2401\, w_{6} +\, 0.0682\, w_{7} +\, 0.1688\, w_{8} } \\ { +\, 0.2718\, w_{9} \, +\, 0.4639\, w_{10} +\, 0.2812\, w_{11} } \\ {+\, 0.2163\, w_{12} \, +\, 0.0573\, w_{13} \, +\, 0.3037\, w_{14}} \end{array}\right) }{\left( \begin{array}{l} {0.1166\, w_{1} \, +\, 0.1487\, w_{2} \, +\, 0.1120\, w_{3} \, +\, 0.0379\, w_{4} } \\ { +\, 0.1720\, w_{5}+\, 0.1560\, w_{6} \, +\, 0.2038\, w_{7} +\, 0.0308\, w_{8} } \\ { +\, 0.1101\, w_{9} \, +\, 0.0465\, w_{10}+\, 0.0640\, w_{11} } \\ {+\, 0.0178\, w_{12} \, +\, 0.2630\, w_{13} \, +\, 0.1547\, w_{14}} \end{array}\right) } \\ + \frac{\left( \begin{array}{l} {0.2309\, w_{1} \, +\, 0.5705\, w_{2} \, +\, 0.0566\, w_{3} \, +0.0920\, w_{4} } \\ {+\, 0.4420\, w_{5} +\, 0.0588\, w_{6} +\, 0.2735\, w_{7} +\, 0.0449\, w_{8} } \\ { +\, 0.1050\, w_{9} \, +\, 0.0028\, w_{10} +\, 0.1991\, w_{11} } \\ {+\, 0.0780\, w_{12} \, +\, 0.2602\, w_{13} \, +\, 0.0277\, w_{14}} \end{array}\right) }{\left( \begin{array}{l} {0.0795\, w_{1} \, +\, 0.0948\, w_{2} \, +\, 0.1564\, w_{3} \, +\, 0.2114\, w_{4} } \\ { +\, 0.0786\, w_{5}+\, 0.2015\, w_{6} \, +\, 0.0758\, w_{7} +\, 0.1654\, w_{8} } \\ { +\, 0.2254\, w_{9} \, +\, 0.4541\, w_{10} +\, 0.1523\, w_{11} } \\ {+\, 0.0995\, w_{12} \, +\, 0.0362\, w_{13} \, +\, 0.4175\, w_{14}} \end{array}\right) } \\ \left. +\frac{\left( \begin{array}{l} {0.0788\, w_{1} \, +\, 0.0399\, w_{2} \, +\, 0.0868\, w_{3} \, +0.0339\, w_{4} } \\ { +\, 0.1292\, w_{5} +\, 0.0458\, w_{6} +\, 0.1790\, w_{7} +\, 0.2503\, w_{8} } \\ { +\, 0.0019\, w_{9} \, +\, 0.0376\, w_{10} +\, 0.0000\, w_{11} } \\ {+\, 0.0283\, w_{12} \, +\, 0.1071\, w_{13} \, +\, 0.0000\, w_{14}} \end{array}\right) }{\left( \begin{array}{l} {0.1166\, w_{1} \, +\, 0.1393\, w_{2} \, +\, 0.1532\, w_{3} \, +\, 0.1490\, w_{4} } \\ { +\, 0.0958\, w_{5} +\, 0.3443\, w_{6} \, +\, 0.0997\, w_{7} +\, 0.0267\, w_{8}} \\ { +\, 0.4326\, w_{9} \, +\, 0.3142\, w_{10}+\, 0.7579\, w_{11} } \\ {+\, 0.1722\, w_{12} \, +\, 0.1500\, w_{13} \, +\, 0.4699\, w_{14}} \end{array}\right) }\right] \end{aligned}$$

subject to

$$\begin{aligned}W=\, \left\{ \left( w_{r} \right) ^{T} \left| \begin{array}{l} { 0.01 \le w_{2} \le 0.04, 0.02 \le w_{3} \le 0.04, } \\ {0.1 \le w_{1} \le 0.2, 0.01 \le w_{7} \le 0.02,}\\ { 0.01 \le w_{5} \le 0.04, 0.1 \le w_{6} \le 0.3, } \\ { 0.02 \le w_{8} \le 0.045 0.01 \le w_{9} \le 0.025, } \\ {0.02 \le w_{10} \le 0.05, 0.015 \le w_{11} \le 0.12,} \\ {w_{13} \le 0.2, w_{13} - w_{14} \le 0.1, w_{12} - w_{13} \le 0.1, } \\ { 0.1 \le w_{12} \le 0.25, w_{8} - w_{9} \ge w_{12} - w_{13} ,}\\ { 0.01 \le w_{4}\le 0.05, w_{4} - w_{5} \ge w_{7} - w_{8},}\\ { w_{r} \ge 0, r = 1 (1) p, \sum _{r =1}^{p}w_{r} =1 } \end{array}\right. \right\} . \end{aligned}$$

By using MATHEMATICA software, the desirable weight vector is attained as follows:

$$\begin{aligned} w^{*}&= \, (w_{1} ,\, w_{2} ,\, w_{3} ,\, w_{4} ,\, w_{5} ,\, w_{6} ,\, w_{7}, w_{8} ,\, w_{9} ,\, w_{10} ,\, w_{11} ,\, w_{12} ,\, w_{13} ,\, w_{14})^{T}\\&= ({0.1},\,{ 0.01,}\, { 0.02,}\, { 0.01,}\, { 0.01,}\, { 0.1,}\, { 0.01,}\,\mathrm{0.045,}\, { 0.01,}\, { 0.02,}\, { 0.015,}\, { 0.1,}\, { 0.065,}\, { 0.485})^{T}. \end{aligned}$$

Step 6 The overall criterion value $\xi _{s} (w^{*} )$ of the alternatives $E_{s} \, (s=\, 1(1)\, 5)$ is given as

$$\begin{aligned}\xi _{1} (w^{*} )&= (\mathrm{0.4991},\mathrm{0.4880}, \mathrm{0.0129}),\\ \xi _{2} (w^{*} )&= (\mathrm{0.7181}, \mathrm{0.2455}, \mathrm{0.0364}),\\ \xi _{3} (w^{*} )\,&= \, (\mathrm{0.5777},\, \mathrm{0.3120},\, \mathrm{0.1103}), \\ \xi _{4} (w^{*} )\,&= \, (\mathrm{0.4973},\, \mathrm{0.3897},\, \mathrm{0.1130}),\\ \xi _{5} (w^{*} )\,&= \, (\mathrm{0.4585},\, \mathrm{0.4262},\, \mathrm{0.1153}). \end{aligned}$$

Step 7 Using (17) and (27), we have $\varphi (\xi _{1} (w^{*} ))\, =\, 0.0554,$$\varphi (\xi _{2} (w^{*} ))\, =\, 0.2059,$$\varphi (\xi _{3} (w^{*} ))\, =\, 0.1275,$$\varphi (\xi _{4} (w^{*} ))\, =\, 0.0806$ and $\varphi (\xi _{5} (w^{*} ))\, =\, 0.0801,$ where

$$\begin{aligned} \gamma ^{*}&= \left\{ (0.6441,\, 0.2544), (1,\, 0), (0.7689,\, 0.128), \right. \\&\quad \left. (0.6788,\, 0.2202), (0.6441,\, 0.2544)\right\} . \end{aligned}$$

By using $\varphi (\xi _{s} (w^{*} )),$ the overall criterion values $\xi _{s} (w^{*} ) (s= 1(1)5)$ are ranked as

$$\begin{aligned} \xi _{1} (w^{*} )\,>\, \xi _{5} (w^{*} )\,>\, \xi _{4} (w^{*} )>\, \, \xi _{3} (w^{*} )\, >\, \xi _{2} (w^{*} ). \end{aligned}$$

Therefore, the ranking of energy alternatives is $E_{1} \, \succ \, E_{5} \, \succ \, E_{4} \, \succ \, E_{3} \, \succ \, E_{2} .$

Step 8 Thus, wind energy $E_{1}$ is the most suitable energy resource.

The ranking result of the energy alternatives obtained from proposed method is compared with existing methods in Table 9. The rank of the energy alternatives attained from proposed method is same as existing methods, and we observe that wind energy is the optimal energy alternative.

Table 9 Comparison of experimental result with the different existing techniques

• 1. In Kahraman et al. [14] and Kaya [15, 16], the weights of the selection criteria are determined by using fuzzy AHP method, whereas in our approach, all the three constraints of the intuitionistic fuzzy values are used to evaluate the decision maker’s opinions on the criteria weights, which is more realistic than existing methods.

• 2. In Kaya [15, 16], the decision makers are not sure about the degree of importance of one parameter over other; therefore, the decision makers cannot give a definite scale to the comparison of the parameters, and thus, they are unable to obtain some valuable information due to the lack of sufficient information. In the proposed methodology, the advantage and disadvantage scores are used to determine the relative comparison of the parameters which avoid the drawbacks of existing methods.

• 3. In Kaya [14], the distance of each alternative from PIS (1, 0, 0) and NIS (0, 0, 1) is calculated to evaluate the closeness coefficient of each alternative, and thus, the ranking of the energy alternatives is obtained on the basis of closeness coefficients. In our approach, the ranking of the alternatives is obtained on the basis of overall values which is more reasonable than Kaya [14].

6 Conclusions

In this paper, new Jensen-exponential divergence (JED) measures for IFSs have been proposed. Some elegant properties of JED measures have been discussed. The proposed measures are the outstanding complement to the existing divergence measures for IFSs. For future research, we look forward to extend the proposed measures to interval valued intuitionistic fuzzy sets (IVIFSs) and hesitant fuzzy sets (HFSs).

A technique to MCDM under the assumption that the criteria weight is completely unknown for IFSs, based on JED is introduced, and a real case study is presented on the selection of the most optimal energy alternative among the set of renewable energy alternatives. In the proposed methodology, the rating of each energy alternative with respect to criteria and the weight of the each criterion are expressed in terms of linguistic variables. Further, a satisfaction degree-based technique via strength and worst scores of options with respect to criteria for MCDM problems is discussed. The concepts of advantage, disadvantage, strength and worst scores are used.

To evaluate the optimal weights for criterion, a multi-objective optimization model via satisfaction degree of each option is constructed that are utilized to illustrate the overall criteria value and applied to choose the optimal option. To reveal the benefits of the developed technique, a realistic example of selecting the desirable financial organization is discussed and compared our results. The key advantage of the proposed technique is that the choice of optimal option is essentially based on relative comparison of performances of the options among each other rather than measuring the performance of each option via some hypothetical standards in real-world decision-making.

Based on the obtained result, wind energy is found to be the most appropriate energy alternative in this case. In comparison with some existing methods, we observe that the proposed method is more reasonable and different from the others in terms of relative importance of each alternative.

In addition, our future research will also focus on applications of IF MCDM in various vital disciplines of analysis, viz. portfolio selection, faculty recruitment, personnel examination, medical diagnosis, military system efficiency evaluation, supply chain management, marketing management.