Heuristic computational intelligence approach to solve nonlinear multiple singularity problem of sixth Painlev́e equation

Abstract

The present study investigate the numerical solution of nonlinear singular system represented with sixth Painlev́e equation by the strength of artificial intelligence using feed-forward artificial neural networks (ANNs) optimized with genetic algorithms (GAs), interior point technique (IPT), sequential quadratic programming (SQP), and their hybrids. The ANN provided a compatible method for finding nature-inspired mathematical model based on unsupervised error for sixth Painlev́e equation and adaptation of weights of these networks is carried out globally by the competency of GA aided with IPT or SQP algorithms. Moreover, a hybrid approach has been adopted for better proposed numerical results. An extensive statistical analysis has been performed through several independent runs of algorithms to validate the accuracy, convergence, and exactness of the proposed scheme.

1 Introduction

The second order ordinary differential equations (ODE) has been studies by Painlev́e, Gambier, and many researchers later on. The Painlev́e equations were discovered by Painlev́e [1] and Gambier [2]; they found six new functions which were defined by nonlinear ordinary differential equations depending on complex parameters this result led to the problem of finding new function which could be defined by nonlinear ODEs like the Painlev́e equations, while studying a problem posed by Picard [3]. Problem was about the second-order ordinary differential equations of the form,

$$ \frac{d^{2}u}{dx^{2}} = {\Psi} \left( \frac{du(x)}{dx}, u(x), x \right), $$

(1)

where Ψ is rational function in $\frac {du}{dx}$, algebraic in u and analytic in x with the Painlev́e property, i.e., the singularities other than poles of the solutions are independent of the integrating constant and so are dependent only on the equation. The differential equations, possessing Painlev́e property, are called Painlev́e type equations. Painlev́e showed that within a Mobius transformation, there are fifty canonical equations [4] of the form (1). Among the 50 equations, the 6 were well known. Remaining 44 are integrable in terms of known elementary functions and they are reducible to one of these 6 equation. These six equations are commonly known as Painlev́e equations and denoted by PI-PVI. Although the Painlev́e equations were discovered from mathematical considerations, they occur in many physical situations; plasma physics, statistical mechanics, nonlinear waves, quantum gravity, general relativity, quantum field theory, nonlinear optics, and fiber optics. Painlev́e equations have attracted much interest as reduction of the soliton equations which are solvable by inverse scattering transformation [5,6,7].

The general solution of Painlev́e equations are called Painlev́e transcendent. However, for certain values of parameters, PI-PVI having rational solutions and solutions are expressible in terms of special functions [8,9,10]. The PII-PVI expression admitted Backlund transformations which relate one solution to another solution of the same equation but with different values of parameters [11, 12]. Painlev́e equations can be written as Hamiltonian systems [13, 14]. Painlev́e equations appear on the compatibility conditions of linear system of equation, Lax-pairs, possessing irregular singular points. By using Lax-pairs, one can find the general solution of a given Painlev́e equations as the Fredholm integral equation.

At the end of the nineteenth century, it was proposed that new transcendental functions could be found as solutions of ordinary differential equations (ODEs). For those, a classification process was undertaken, which it was foreseen would proceed order by order of ODEs having what is today known as the Painlev́e property. An ODE is said to have the Painlev́e property if its general solution is free of movable branched singularities (movable means, the location of the singularity depends on initial conditions). This is the base of discovery of the well-known six Painlev́e equations [4, 15,16,17], which did indeed define new transcendental functions. However, this classification process then stalled somewhat, with only partial classifications being undertaken at third order [18,19,20,21,22], and no new transcendent being found. At fourth order, even the classification of dominant terms for the polynomial case was left incomplete [23]. Interest in the six Painlev́e equations was reignited by the work of Ablowitz et al. [24, 25], they found that similarity reductions of completely integrable partial differential equations (PDEs) gave rise to ODEs with the Painlev́e property. In many cases, one or other of the Painlev́e equations themselves.

Airault [26] made the next step of using higher order integrable PDEs to derive higher order ODEs with the Painlev́e property. She derived a whole hierarchy of ODEs, a second Painlev́e hierarchy, i.e., having as first member the second Painlev́e equation, by similarity reduction of the Korteweg de Vries and modified Korteweg de Vries hierarchies. This open the possibility of deriving higher order Painlev́e equations as sequences of ODEs of increasing order, as opposed to the classification of ODEs order-by-order originally proposed. However, it was not until the work of Kudryashov [27], who derived both a first and second Painlev́e hierarchy, that further work in this direction was undertaken. Later on, many researchers have been interested in deriving Painlev́e hierarchies and in investigating their properties and underlying structures [28,29,30,31,32,33,34,35]. At the same time, the present day continuation of the original order-by order classification process [36,37,38,39,40] is informed by knowledge of the connection with higher order completely integrable PDEs.

There are many types of Painlev́e equations but commonly known are only following six Painlev́e equations. A brief introductory material about the one to six Painlev́e equations is described here. These equations are used extensively by the research community in different applications in physical science and engineering technologies.

$$\left\{\begin{array}{ll} u^{\prime\prime} = 6u^{2} + x, & \qquad\text{Painle\'{v}e~equation-I~or~(PI)}\\ u^{\prime\prime} = 2u^{3} + xu + \alpha, & \qquad\text{Painle\'{v}e~equation-II~or~(PII)} \\ u^{\prime\prime} = \frac{u^{\prime2}}{u} - \frac{u^{\prime}}{x} + \frac{\alpha u^{2} + \beta}{x} + \gamma u^{3} + \frac{\delta}{u}, & \qquad\text{Painle\'{v}e~equation-III(PIII)} \\ u^{\prime\prime} = \frac{u^{\prime2}}{2u} + \frac{3}{2} u^{3} + 4xu^{2} + 2(x^{2} - \alpha) u + \frac{\beta}{u}, & \qquad\text{Painle\'{v}e~equation-IV(PIV)} \\ u^{\prime\prime} = \left( \frac{1}{2u} + \frac{1}{u-x}\right) u^{\prime2} - \frac{u^{\prime}}{x} + \frac{(u-1)^{2}}{x^{2}} \left( \alpha u + \frac{\beta}{u}\right)\\ \quad + \frac{\gamma u}{x} + \frac{\delta u(u+1)}{u-1}, & \qquad\text{Painle\'{v}e~equation-V(PV)} \\ u^{\prime\prime} = \frac{1}{2} \left( \frac{1}{u} + \frac{1}{u-1} + \frac{1}{u-x}\right) u^{\prime2} - \left( \frac{1}{x} + \frac{1}{x-1} + \frac{1}{u-x}\right)u^{\prime}\\ \quad + \frac{u(u-1)(u-x)}{x^{2}(x-1)^{2}} \left( \alpha + \frac{\beta x}{u^{2}} + \frac{\gamma(x-1)}{(u-1)^{2}} + \frac{\delta x(x-1)}{(u-x)^{2}}\right) , & \qquad\text{Painle\'{v}e~equation-VI(PVI)} \end{array}\right. $$

The PI-equation based on quadratic nonlinear factor in one of its term, PII-equation has special importance due to its cubic nonlinearity along with variations of one constant parameter α, PIII-equation is well recognized due to its singularity at origin with variation in four constants parameters α, β, γ, and δ. Comparatively, very few numerical and analytical solvers are available to handle such type of problem. The Painlev́e -IV equation is famous for its strong nonlinearity. Moreover, this problem has two constants parameters α, β, as well and the PV-equation is very complicated differential equation, that has three terms possess singularities and also four constants parameters namely α, β, γ, and δ. The last Painlev́e equation which focus of our study is known as PVI-equation have special attention among all six Painlev́e and this is the most complicated Painlev́e equation having multiple singularities. This equation have multiple singularities at x = 1,0, and u = 1,0, u = x. It depends upon the four constants parameters known as α, β, γ, and δ. It has quadratic nonlinearity in many terms as well [41,42,43,44,45].

General properties of Painlev́e equations

• (a) PII-PVI have Backlund transformations which relate solutions of a given Painlev́e equation to solutions of the same Painlev́e equation, though with different values of the parameters with associated Affine Weyl groups that act on the parameter space.

• (b) PII-PVI have rational, algebraic, and special function solutions expressed in terms of the classical special functions

• (c) These rational, algebraic and special function solutions of PII-PVI, called classical solutions, can usually be written in determinant form, frequently know as wronskians. Often, these can be written as Hankel determinants or Toeplitz determinants

• (d) PI-PVI can be written as a (non-autonomous) Hamiltonian system and the Hamiltonians satisfy a second-order, second-degree differential equations (PI-PVI)

• (e) PI-PVI possess Lax pairs (isomonodromy problems)

2 Design methodology for sixth Painlev́e equation

The brief description of designed methodology will be presented for the solution of the nonlinear sixth Painleve differential equation. In this section, the procedure has been developed two feed-forward unsupervised neural networks models of the equation.

2.1 Heuristic mathematical modeling

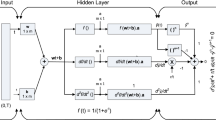
Generalized design methodology for sixth Painlev́e differential equation can be expressed as a MATLAB function. Mathematical model for the sixth Painlev́e equation is constructed with the strength of feed-forward ANN, in the form of following continuous mapping for the solution $\hat {u}(x)$, and its first- and second-order derivatives are ${d\hat {u}}/{dx}$ and ${d^{2}\hat {u}}/{dx^{2}}$ respectively,

$$\begin{array}{@{}rcl@{}} \hat{u}(x) &=& \sum\limits_{i=1}^{k} {A_{i} f(B_{i} x + C_{i})}, \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} \frac{d\hat{u}}{dx} &=& \sum\limits_{i=1}^{k} {A_{i}}\frac{d}{dx} [f(B_{i} x + C_{i})], \end{array} $$

(3)

$$\begin{array}{@{}rcl@{}} \frac{d^{2}\hat{u}}{dx^{2}} &=& \sum\limits_{i=1}^{k} {A_{i}}\frac{d^{2}}{d x^{2}} [f(B_{i} x + C_{i})]. \end{array} $$

(4)

Equations (2–4) are based on defined log-sigmoid function $f(t) = \frac {1}{1 + e^{-t}}$ and its respective derivatives are working as activation functions, therefore, system of equations can be written as,

$$\begin{array}{@{}rcl@{}} \hat{u}(x) \!&=&\! \sum\limits_{i=1}^{k}\! {A_i} \frac{1}{1 \,+\, e^{-(B_{i} x + C_{i})}}, \end{array} $$

(5)

$$\begin{array}{@{}rcl@{}} \frac{d\hat{u}}{dx} \!&=&\! \sum\limits_{i=1}^{k} \!{A_{i} B_{i}}\frac{e^{-(B_{i} x + C_{i})}}{(1 \,+\, e^{-(B_{i} x + C_{i})})^{2}}, \end{array} $$

(6)

$$\begin{array}{@{}rcl@{}} \frac{d^{2}\hat{u}}{dx^{2}} \!&=&\! \sum\limits_{i=1}^{k}\! {A_{i}{B}_{i}^{2}}\! \left[\frac{2 e^{-2(B_{i} x + C_{i})}}{(1 \,+\, e^{-(B_{i} x + C_{i})})^{3}} \,-\, \frac{e^{-(B_{i} x + C_{i})}}{(1 \,+\, e^{-(B_{i} x + C_{i})})^{2}}\right]\!.\\ \end{array} $$

(7)

The suitable combination of these above equations can be used to model the differential equations like (5–7), for reader interest see more references like [46, 47] and [48].

2.2 Fitness function

A fitness function or objective function E is developed in an unsupervised manner and it is defined by sum of two mean square error E₁ and E₂. Therefore, E can be written as

$$ E = E_{1} + E_{2}, $$

(8)

where E₁ is error function associated with given differential equation and it is given as

$$\begin{array}{@{}rcl@{}} E_{1} \!&=&\! \frac{1}{N\,+\,1} \sum\limits_{m=0}^{N} \left[\frac{d^{2}{\hat{u}_{m}}}{d^{2}x} \,-\, \frac{1}{2} \left( \frac{1}{\hat{u}_{m}} \,+\, \frac{1}{\hat{u}_{m}-1} \,+\, \frac{1}{\hat{u}_{m}-x_{m}}\right) \right.\\ &&\! \times \!\left( \frac{d\hat{u}_{m}}{dx}\right)^{2} \,+\, \left( \frac{1}{x_{m}} \,+\, \frac{1}{x_{m}-1} \,+\, \frac{1}{\hat{u}_{m}-x_{m}}\right)\\ &&\! \times \frac{d\hat{u}_{m}}{dx} \,-\, \frac{\hat{u}_{m}(\hat{u}_{m}-1)(\hat{u}_{m}-x_{m})}{{x^{2}_{m}}(x_{m}-1)^{2}}\\ &&\!\left. \times\! \left( \alpha \,+\, \frac{\beta x_{m}}{\hat{u}^{2}_{m}} \,+\, \frac{\gamma(x_{m}\,-\,1)}{(\hat{u}_{m}\,-\,1)^{2}} \,+\, \frac{\delta x_{m}(x_{m}\,-\,1)}{(\hat{u}_{m}\,-\,x_{m})^{2}}\right)\right]^{2}. \end{array} $$

(9)

Similarly, E₂ is the error function associated with boundary conditions for given equation is given as:

$$ E_{2}=\frac{1}{2} [(\hat{u}_{0}-l)^{2} + ({\hat{u}}_{0}^{\prime} - m)^{2}] . $$

(10)

3 Numerical and analytical learning techniques

Differential equations are solved under the conditions of existing techniques. A lot of analytical and numerical solvers have been developed by researchers to solve higher order nonlinear boundary value problems. Painlev́e equations have been examined by number of researchers by means of several techniques including both analytical, as well as, numerical solvers. For example, variation iteration method (VIM), homotopy perturbation method (HPM) [49], Adomian decomposition method (ADM), Legendre-Tau methods, Sinc-collocation method, wavelet method, and so on. In all of these methods, the solution is generally given in the form of an infinite series usually convergent to an accurate approximate solution. The results showed that all of these methods have their own limitations and advantages over others. As per our literature survey about the stochastic solver to Painlev́e equation, no body yet applied to solve sixth Painlev́e equation; however, the first Painlev́e equation is solved using neural networks optimized with evolutionary and swarm intelligence technique. Further, some latest work has been done through these techniques [50, 51].

3.1 Hybrid approach

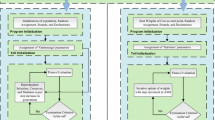
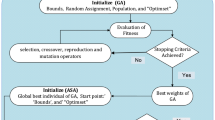
Hybrid approach is one of the best algorithms in the class of constrained optimization techniques. Alongside GA, AST, IPT, and SQP, their hybrid combination GA-AST, GA-IPT, and GA-SQP are also used to train the design parameters of neural network models for solving problems of sixth painlev́e type. Flow diagram of the generic hybrid approach based on GA-AST is shown in Fig. 1.

Fig. 1

Flow chart of proposed algorithms

3.2 Parameter setting

MATLAB function GA and FMINCON have used in graphical user interface (GUI) of optimization tool box for learning of unknown parameter of ANN model. The parameters setting used for GA and AST have listed in Tables 1 and 2, respectively.

Table 1 Parameters setting for GA

Table 2 Parameters setting for AST

3.3 Procedural steps of proposed method

The main points of proceeding our solvers algorithm are discussed below

• 1. InitializationInitial values of parameters are set in this step with random assignment and declarations. These setting are also tabulated in Table 1 for important parameter of GA.

• 2. Fitness evaluationCalculate the fitness of each individual or chromosome of population using the (9) and (10), for first and second type of modeling, respectively.

• 3. Termination criteriaTerminate the algorithm when either of following criteria matches:

  • Predefined fitness values |E|≤ 10⁻¹⁵ is achieved.

  • Predefine number of generations are executed.

  • Any of termination setting given in Table 1 for GA is fulfilled.

  If termination criterion meets, then go to step 5.

• 4. ReproductionCreate next generation on the basis of Crossover: call for scattered function, Mutation: call for adaptive feasible function, Selection: call for stochastic uniform function and elitism account is step 4, etc. Repeat the procedure from step 2 to step 4 with newly produced population and continues.

• 5. ImprovementsActive set technique has used for further refinement of results by taking final adaptive weights of GA as initial weights (start point) of AST algorithm. AST has applied as per setting of parameters given in Table 2. Store also the refined final weights of the algorithm.

• 6. Neurons analysisRepeat steps 1 to 5 for by taking size of initial weights, i.e., 30 and 45 for N = 10, 15 neurons, respectively. These results are used for detail analysis of algorithm later. The architectural diagram of proposed model is presented in Fig. 2.

Fig. 2

Architectural diagram of physical model of sixth Painlev́e equation

4 Numerical results of Painlev́e equation-VI

Consider Painlev́e equation-VI

$$\begin{array}{@{}rcl@{}} u^{\prime\prime} &=& \frac{1}{2} \left( \frac{1}{u} \,+\, \frac{1}{u-1} \,+\, \frac{1}{u-x}\right) u^{\prime2} -\! \left( \frac{1}{x} \,+\, \frac{1}{x-1} + \frac{1}{u-x}\right)u^{\prime}\\ && + \frac{u(u-1)(u-x)}{x^{2}(x-1)^{2}} \left[\alpha \,+\, \frac{\beta x}{u^{2}} + \frac{\gamma(x-1)}{(u-1)^{2}} + \frac{\delta x(x-1)}{(u-x)^{2}}\right].\\ \end{array} $$

(11)

with boundary conditions defined as

$$u(0) = l, \quad u^{\prime}(1) = m $$

Now, our main objective is to find the solution of the proposed problem using scheme based on two neural networks models. The fitness functions constructed for proposed problem (11) is given as

$$ E=E_{1}+E_{2}, $$

(12)

where E₁ is error function associated with (11) and it is defined by

$$\begin{array}{@{}rcl@{}} E_{1} \!&=&\! \frac{1}{10} \sum\limits_{m=1}^{10} \left[\frac{d^{2}\hat{u}_{m}}{d^{2}x} \,-\, \frac{1}{2} \left( \frac{1}{\hat{u}_{m}} \,+\, \frac{1}{\hat{u}_{m}\,-\,1} \,+\, \frac{1}{\hat{u}_{m}\,-\,x_{m}}\right)\right.\\ &&\! \times \!\left( \frac{d\hat{u}_{m}}{dx}\right)^{2} \,+\, \left( \frac{1}{x_{m}} \,+\, \frac{1}{x_{m}\,-\,1} \,+\, \frac{1}{\hat{u}_{m}\,-\,x_{m}}\right)\\ && \!\times \frac{d\hat{u}_{m}}{dx} \,-\, \frac{\hat{u}_{m}(\hat{u}_{m}\,-\,1)(\hat{u}_{m}\,-\,x_{m})}{{x}_{m}^{2}(x_{m}\,-\,1)^{2}}\\ && \left.\! \times\! \left( \alpha \,+\, \frac{\beta x_{m}}{{\hat{u}}_{m}^{2}} \,+\, \frac{\gamma(x_{m}\,-\,1)}{(\hat{u}_{m}\,-\,1)^{2}} \,+\, \frac{\delta x_{m}(x_{m}\,-\,1)}{(\hat{u}_{m}\,-\,x_{m})^{2}}\right)\right]^{2}. \end{array} $$

(13)

Similarly, E₂ is the error function associated with proposed boundary conditions for given problem is as

$$ E_{2} = \frac{1}{2} [(\hat{u}_{0} - l)^{2} + ({\hat{u}}_{0}^{\prime} - m)^{2}]. $$

(14)

Case 1

For N = 30 (number of neurons)Let us define the series solution of (11) in the form of our proposed weights as,

$$\hat{u}(x) = \sum\limits_{i=1}^{10} A_{i} \left( \frac{1}{1+e^{-(B_{i}x + C_{i})}}\right) $$

The proposed solution of (11) can be written in the form of neurons, which are obtained by optimal technique (AST, SQP, IPT, GA, GA-AST, GA-SQP, GA-IPT). Therefore, proposed solution of equation is written as

$$\begin{array}{@{}rcl@{}} \hat{u}(x) \!&=&\! \frac{A_{1}}{1\,+\,e^{-(B_{1}x+C_{1})}} \,+\, \frac{A_{2}}{1\,+\,e^{-(B_{2}x+C_{2})}} \,+\, \frac{A_{3}}{1\,+\,e^{-(B_{3}x+C_{3})}}\\ &&\! +\frac{A_{4}}{1\,+\,e^{-(B_{4}x+C_{4})}} \,+\, \frac{A_{5}}{1\,+\,e^{-(B_{5}x+C_{5})}} \,+\, \frac{A_{6}}{1\,+\,e^{-(B_{6}x+C_{6})}}\\ &&\! + \frac{A_{7}}{1\,+\,e^{-(B_{7}x+C_{7})}} \,+\, \frac{A_{8}}{1\,+\,e^{-(B_{8}x+C_{8})}} \,+\, \frac{A_{9}}{1\,+\,e^{-(B_{9}x+C_{9})}}\\ &&\! + \frac{A_{10}}{1\,+\,e^{-(B_{10}x+C_{10})}} \end{array} $$

(15)

$$\begin{array}{@{}rcl@{}} \hat{u}_{SQP} &=& \frac{3.852664207}{1+e^{-(-4.557692131x-4.650552422)}}\\ && + \frac{-1.319761307}{1+e^{-(-2.187930899x+1.300007309)}}\\ && + \frac{-0.792153668}{1+e^{-(4.263719327x-0.609608606)}}\\ && + \frac{4.462553295}{1+e^{-(-3.269979902x-4.20889754)}}\\ && + \frac{2.205781656}{1+e^{-(-3.607747507x-4.012823819)}}\\ && + \frac{0.13768719}{1+e^{-(-0.108773444x-1.244950893)}}\\ && + \frac{3.521925914}{1+e^{-(1.589236886x-2.309019827)}}\\ && + \frac{-3.494923022}{1+e^{-(-3.852467942x-5.137719643)}}\\ && + \frac{1.211888186}{1+e^{-(-1.168642848x+4.192646853)}}\\ && + \frac{-2.632461101}{1+e^{-(-4.256236816x-1.883428072)}} \end{array} $$

(16)

$$\begin{array}{@{}rcl@{}} \hat{u}_{IPT} &=& \frac{-0.494413203}{1+e^{-(-0.563576778x-0.071732859)}}\\ && + \frac{0.296910551}{1+e^{-(0.253029768x+0.138304721)}}\\ && + \frac{1.017894435}{1+e^{-(1.042155805x-0.073318396)}}\\ && + \frac{0.22529088}{1+e^{-(0.224535628x+0.025924206)}}\\ && + \frac{0.142823162}{1+e^{-(0.17406687x+0.178422266)}}\\ && + \frac{-0.042499223}{1+e^{-(-0.082284884x-0.255089136)}}\\ && + \frac{0.738827939}{1+e^{-(0.739655909x+0.149972895)}}\\ && + \frac{-0.019671964}{1+e^{-(0.052666701x-0.028173882)}} \end{array} $$

$$\begin{array}{@{}rcl@{}} && + \frac{-0.9770742}{1+e^{-(-1.086652624x-0.07626653)}}\\ && + \frac{-0.981215871}{1+e^{-(-0.924084278x+0.042974028)}} \end{array} $$

(17)

$$\begin{array}{@{}rcl@{}} \hat{u}_{GA} &=& \frac{0.484693387}{1+e^{-(2.282534095x+1.430452867)}}\\ && + \frac{-0.85062687}{1+e^{-(-2.260429318x+0.67352394)}}\\ && + \frac{-0.832460344}{1+e^{-(-0.121752802x-0.828405606)}}\\ && +\frac{-0.565902282}{1+e^{-(0.162374497x+1.410502354)}}\\ && + \frac{0.570241973}{1+e^{-(-0.202643046x-0.573694337)}}\\ && + \frac{-0.192332919}{1+e^{-(-0.467847963x+0.333378428)}}\\ && + \frac{-0.80671863}{1+e^{-(0.147407103x+1.540733481)}}\\ && + \frac{0.894866112}{1+e^{-(1.725851575x+0.363518104)}}\\ && + \frac{0.832144068}{1+e^{-(0.364845716x-0.222055111)}}\\ && + \frac{0.701006282}{1+e^{-(-0.307744349x+1.319595699)}} \end{array} $$

(18)

$$\begin{array}{@{}rcl@{}} \hat{u}_{GA-AST} &=& \frac{1.592316553}{1+e^{-(-3.200480077x-3.347382524)}}\\ && + \frac{-1.320208838}{1+e^{-(-0.355295927x+1.032001828)}}\\ && + \frac{0.319825968}{1+e^{-(2.955042366x-0.83990283)}}\\ && + \frac{1.952266267}{1+e^{-(-2.007219521x-2.827048245)}}\\ && + \frac{1.705335008}{1+e^{-(-1.818440181x-2.884065761)}}\\ && + \frac{1.408759062}{1+e^{-(2.959565675x-0.246105986)}}\\ && + \frac{1.216380832}{1+e^{-(-1.140500523x-1.894501887)}}\\ && + \frac{-2.277300978}{1+e^{-(-2.051183478x-2.492644937)}}\\ && + \frac{0.058806128}{1+e^{-(-1.275458961x+2.264150473)}}\\ && + \frac{-0.570777737}{1+e^{-(-1.524116854x-2.789580802)}} \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}} \hat{u}_{GA-SQP} &=& \frac{3.852668073}{1+e^{-(-4.557699082x-4.650538173)}}\\ && + \frac{-1.319791365}{1+e^{-(-2.187967501x+1.299977048)}} \end{array} $$

$$\begin{array}{@{}rcl@{}} && + \frac{-0.792077223}{1+e^{-(4.263700406x-0.609537199)}}\\ && + \frac{4.462556044}{1+e^{-(-3.269989174x-4.208886822)}}\\ && + \frac{2.2057858448}{1+e^{-(-3.607753592x-4.012815346)}}\\ && + \frac{0.137684982}{1+e^{-(-0.108773898x-1.244951139)}}\\ && + \frac{3.521911929}{1+e^{-(1.589188478x-2.309027891)}}\\ && + \frac{-3.49492136}{1+e^{-(-3.852464502x-5.137725322)}}\\ && + \frac{1.211878857}{1+e^{-(-1.16864842x+4.192644345)}}\\ && + \frac{-2.632431741}{1+e^{-(-4.256187358x-1.883462931)}} \end{array} $$

(20)

$$\begin{array}{@{}rcl@{}} \hat{u}_{GA-IPT} &=& \frac{-0.494413203}{1+e^{-(-0.563576778x-0.071732859)}}\\ && + \frac{0.296910551}{1+e^{-(0.253029768x+0.138304721)}}\\ && + \frac{1.017894435}{1+e^{-(1.042155805x-0.073318396)}}\\ && + \frac{0.22529088}{1+e^{-(0.224535628x+0.025924206)}}\\ && + \frac{0.142823162}{1+e^{-(0.17406687x+0.178422266)}}\\ && + \frac{-0.042499223}{1+e^{-(-0.082284884x-0.255089136)}}\\ && + \frac{0.738827939}{1+e^{-(0.739655909x+0.149972895)}}\\ && + \frac{-0.019671964}{1+e^{-(0.052666701x+0.028173882)}}\\ && + \frac{-0.9770742}{1+e^{-(-1.086652624x-0.07626653)}}\\ && + \frac{-0.981215871}{1+e^{-(-0.924084278x+0.042974028)}} \end{array} $$

(21)

The values of the number of weights of our six proposed techniques like SQP, IPT, GA, and their hybrid approach GA-AST, GA-SQP, and GA-IPT are presented in Tables 3 and 4. Furthermore, we concluded on the basis of 100 times runs through these solvers results that there are minimum five digits in each value of the weights are good for approximated solution of proposed problem. The comparison of the proposed results with reference solution are presented in Table 5, which showed that, there are up to one to three digits places accuracy with the reference solution of our techniques SQP, IPT, GA, GA-AST, GA-SQP, and GA-IPT and their graphical representation is shown in Fig. 3. Moreover, we calculated the absolute error (AEs) of proposed results with reference solution as shown in Fig. 4. Table 6 showed that hybrid technique GA-AST is more accurate than the others techniques but SQP technique is also good in accuracy than IPT, GA, GA-SQP, and GA-IPT. The absolute errors of GA-AST, SQP, IPT, GA, GA-SQP, and GA-IPT lie in the range of [1.65E − 09,9.18E − 04], [1.04E − 08,8.88E − 02], [6.48E − 02,1.18E − 01], [4.99E − 08,1.08E − 01], [4.28E − 08,9.45E − 02], and [4.33E − 08,1.05E − 01] respectively.

Table 3 Weights by taking N = 30 along their corresponding solvers SQP, IPT, and GA

Table 4 Weights by taking N = 30 along their corresponding solvers GA-AST, GA-SQP, and GA-IPT

Table 5 Comparison of Ref Sol. with results of proposed techniques

Table 6 The presentation of absolute errors(AEs) of proposed solvers

Fig. 3

Comparison of reference solution and proposed solutions case 1

Fig. 4

Graphical representation of independent runs case 1

Case 2

For N = 45 (number of neurons)The proposed solution of (11) by taking N = 45 is written as:

$$\begin{array}{@{}rcl@{}} \hat{u}(x) &=& \frac{A_{1}}{1+e^{-(B_{1}x+C_{1})}} + \frac{A_{2}}{1+e^{-(B_{2}x+C_{2})}}\\ && + \frac{A_{3}}{1+e^{-(B_{3}x+C_{3})}} + \frac{A_{4}}{1+e^{-(B_{4}x+C_{4})}}\\ && + \frac{A_{5}}{1+e^{-(B_{5}x+C_{5})}} + \frac{A_{6}}{1+e^{-(B_{6}x+C_{6})}}\\ && + \frac{A_{7}}{1+e^{-(B_{7}x+C_{7})}} + \frac{A_{8}}{1+e^{-(B_{8}x+C_{8})}}\\ && + \frac{A_{9}}{1+e^{-(B_{9}x+C_{9})}} + \frac{A_{10}}{1+e^{-(B_{10}x+C_{10})}}\\ && + \frac{A_{11}}{1+e^{-(B_{11}x+C_{11})}} + \frac{A_{12}}{1+e^{-(B_{12}x+C_{12})}}\\ && + \frac{A_{13}}{1+e^{-(B_{13}x+C_{13})}} + \frac{A_{14}}{1+e^{-(B_{14}x+C_{14})}}\\ && + \frac{A_{15}}{1+e^{-(B_{15}x+C_{15})}} \end{array} $$

(22)

$$\begin{array}{@{}rcl@{}} \hat{u}_{SQP} &=& \frac{-2.981186883}{1+e^{-(-0.190071148x-0.42872715)}}\\ && + \frac{0.768616578}{1+e^{-(-1.853284783x+2.538759738)}}\\ && + \frac{-1.215459689}{1+e^{-(-1.104744276x-0.089031497)}}\\ && + \frac{1.424318279}{1+e^{-(-0.451934839x-0.833612481)}}\\ && + \frac{-1.035748313}{1+e^{-(0.562284442x-0.995318799)}}\\ && + \frac{-1.411659669}{1+e^{-(-0.324662445x-0.599500242)}}\\ && + \frac{2.789462715}{1+e^{-(0.910323891x-0.8778286)}}\\ && + \frac{0.515239938}{1+e^{-(-0.135572375x+1.64395686)}}\\ && + \frac{-1.038899223}{1+e^{-(-1.052128095x-0.414849175)}}\\ && + \frac{-1.222779538}{1+e^{-(0.828456626x-1.453050204)}} \end{array} $$

$$\begin{array}{@{}rcl@{}} && + \frac{0.879583272}{1+e^{-(-0.709296653x-0.322501933)}}\\ && + \frac{0.29290285}{1+e^{-(-0.53697887x-1.583655045)}}\\ && + \frac{-3.626280806}{1+e^{-(-0.308258981x-0.449521512)}}\\ && + \frac{-1.3971885}{1+e^{-(-0.277507868x-0.570155554)}}\\ && + \frac{3.676629109}{1+e^{-(-0.03750609x+0.495244765)}} \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}} \hat{u}_{IPT} &=& \frac{0.105796212}{1+e^{-(0.080383331x-0.020161484)}}\\ && + \frac{-0.145795475}{1+e^{-(-0.107082733x+0.064312681)}}\\ && + \frac{0.205000139}{1+e^{-(0.230299485x-0.233354609)}}\\ && + \frac{-0.466410003}{1+e^{-(-0.428127661x+0.046290178)}}\\ && + \frac{-0.393013417}{1+e^{-(-0.323632235x+0.074518818)}} \end{array} $$

$$\begin{array}{@{}rcl@{}} && + \frac{0.187759073}{1+e^{-(0.150674136x-0.089083839)}}\\ && + \frac{0.391188015}{1+e^{-(0.373659129x-0.046799459)}}\\ && + \frac{0.920319338}{1+e^{-(0.868965041x-0.098826133)}}\\ && + \frac{-0.511364835}{1+e^{-(-0.470590439x+0.009932894)}}\\ && + \frac{0.014103156}{1+e^{-(-0.081362585x+0.131736388)}}\\ && + \frac{-0.229638271}{1+e^{-(-0.188128634x+0.047032649)}}\\ && + \frac{-1.125716815}{1+e^{-(-1.084292981x+0.0087882)}}\\ && + \frac{1.075167372}{1+e^{-(0.98252266x-0.163357974)}}\\ && + \frac{-0.083327541}{1+e^{-(-0.139448038x-0.050729697)}}\\ && + \frac{0.274628645}{1+e^{-(0.241834313x-0.023923033)}} \end{array} $$

(24)

$$\begin{array}{@{}rcl@{}} \hat{u}_{GA} &=& \frac{-1.363656406}{1+e^{-(0.085099021x-0.74394221)}}\\ && + \frac{2.851296596}{1+e^{-(0.678304643x+0.185175216)}}\\ && + \frac{0.18928619}{1+e^{-(-0.752937035x-1.198717482)}}\\ && + \frac{-1.468523246}{1+e^{-(-0.899679259x-0.351393344)}}\\ && + \frac{-0.427997736}{1+e^{-(-1.863585975x+3.271144744)}}\\ && + \frac{1.308881139}{1+e^{-(0.262833207x+0.121821713)}}\\ && + \frac{1.520387638}{1+e^{-(-0.576342064x-1.806363518)}}\\ && + \frac{0.459316583}{1+e^{-(-0.928668084x-0.562269335)}}\\ && + \frac{2.047062888}{1+e^{-(0.619184027x+1.66014717)}}\\ && + \frac{-1.109575745}{1+e^{-(0.819231638x+1.912083154)}}\\ && + \frac{-1.823556932}{1+e^{-(-0.296418298x+2.025872201)}}\\ && + \frac{-0.609796375}{1+e^{-(0.07971307x-1.157468048)}}\\ && + \frac{0.189710124}{1+e^{-(-0.755677982x-0.343193098)}}\\ && + \frac{-0.97524152}{1+e^{-(-1.203725087x-0.61630144)}}\\ && + \frac{0.059209499}{1+e^{-(-0.610467037x+1.494353009)}} \end{array} $$

(25)

$$\begin{array}{@{}rcl@{}} \hat{u}_{GA-AST} &=& \frac{-0.262149427}{1+e^{-(-0.502904887x+0.411557222)}}\\ && + \frac{-0.093910624}{1+e^{-(-0.74609434x-3.024753985)}}\\ && + \frac{-0.46955918}{1+e^{-(0.051263983x-1.08694692)}}\\ && + \frac{1.011389247}{1+e^{-(1.008870957x-1.857829674)}}\\ && + \frac{-0.631127888}{1+e^{-(-0.113952018x-4.171619951)}}\\ && + \frac{-1.482027465}{1+e^{-(-0.480267545x+2.558155694)}}\\ && + \frac{0.830997251}{1+e^{-(-2.360117472x-1.096744456)}}\\ && + \frac{-0.457799099}{1+e^{-(-0.554426409x-2.002721757)}} \end{array} $$

$$\begin{array}{@{}rcl@{}} && + \frac{2.745655273}{1+e^{-(2.73178381x+2.301075457)}}\\ && + \frac{1.201934267}{1+e^{-(0.193172473x-3.088996794)}}\\ && + \frac{-1.57557471}{1+e^{-(-0.748204934x+0.665750072)}}\\ && + \frac{0.43355072}{1+e^{-(1.795329929x-2.188184223)}}\\ && + \frac{-0.995547425}{1+e^{-(-0.795671929x-0.664101683)}}\\ && + \frac{1.075274473}{1+e^{-(-1.003233661x-1.089874647)}}\\ && + \frac{-1.525039869}{1+e^{-(-2.03388967x-2.575473059)}} \end{array} $$

(26)

$$\begin{array}{@{}rcl@{}} \hat{u}_{GA-SQP} &=& \frac{-2.981184974}{1+e^{-(-0.190067542x-0.428731301)}}\\ && + \frac{0.768592809}{1+e^{-(-1.853259645x+2.538768879)}}\\ && + \frac{-1.215453209}{1+e^{-(-1.104729159x-0.089016331)}}\\ && + \frac{1.424322616}{1+e^{-(-0.451946811x-0.833612338)}}\\ && + \frac{-1.035742911}{1+e^{-(0.562272943x-0.995318751)}}\\ && + \frac{-1.411657607}{1+e^{-(-0.324656112x-0.59950122)}}\\ && + \frac{2.789471327}{1+e^{-(0.910357066x-0.877847887)}}\\ && + \frac{0.515246149}{1+e^{-(-0.135570607x+1.643957452)}} \end{array} $$

$$\begin{array}{@{}rcl@{}} && + \frac{-1.038890188}{1+e^{-(-1.052110455x-0.414841108)}}\\ && + \frac{-1.222769852}{1+e^{-(0.828434642x-1.45305147)}}\\ && + \frac{0.879589313}{1+e^{-(-0.709305143x-0.322505566)}}\\ && + \frac{0.292906802}{1+e^{-(-0.53698189x-1.583654578)}}\\ && + \frac{-3.626278978}{1+e^{-(-0.308247123x-0.44952392)}}\\ && + \frac{-1.397186564}{1+e^{-(-0.277503099x-0.570156893)}}\\ && + \frac{3.676633577}{1+e^{-(-0.037499309x+0.495251782)}} \end{array} $$

(27)

$$\begin{array}{@{}rcl@{}} \hat{u}_{GA-IPT} &=& \frac{0.105796212}{1+e^{-(0.080383331x-0.020161484)}}\\ && + \frac{-0.145795475}{1+e^{-(-0.107082733x+0.064312681)}}\\ && + \frac{0.205000139}{1+e^{-(0.230299485x-0.233354609)}}\\ && + \frac{-0.466410003}{1+e^{-(-0.428127661x+0.046290178)}}\\ && + \frac{-0.393013417}{1+e^{-(-0.323632235x+0.074518818)}}\\ && + \frac{0.187759073}{1+e^{-(0.150674136x-0.089083839)}}\\ && + \frac{0.391188015}{1+e^{-(0.373659129x-0.046799459)}}\\ && + \frac{0.920319338}{1+e^{-(0.868965041x-0.098826133)}}\\ && + \frac{-0.511364835}{1+e^{-(-0.470590439x+0.009932894)}}\\ && + \frac{0.014103156}{1+e^{-(-0.081362585x+0.131736388)}}\\ && + \frac{-0.229638271}{1+e^{-(-0.188128634x+0.047032649)}}\\ && + \frac{-1.125716815}{1+e^{-(-1.084292981x+0.0087882)}}\\ && + \frac{1.075167372}{1+e^{-(0.98252266x-0.163357974)}}\\ && + \frac{-0.083327541}{1+e^{-(-0.139448038x-0.050729697)}}\\ && + \frac{0.274628645}{1+e^{-(0.241834313x-0.023923033)}} \end{array} $$

(28)

The values of the number of weights of six proposed techniques for case 2 like SQP, IPT, GA, GA-AST, GA-SQP, and GA-IPT are plotted in Tables 7 and 8, respectively. We obtained accuracy in weights up to five digit places is good approximation for proposed series solutions. We also tabled the values of proposed techniques to construct a comparison table of the values with the reference solution and presented in Table 9, which showed that there are accuracy up to three decimal places with the reference solution of other proposed techniques SQP, IPT, GA, GA-AST, GA-SQP, and GA-IPT. Moreover, their plot is presented in Fig. 5. For a better picture of the whole analysis, the absolute errors is presented in Fig. 6. Table 10 showed that hybrid technique GA-AST is more accurate as compared to other techniques. GA-SQP technique is also good in accuracy than other optimizers SQP, IPT, GA, and GA-IPT. The absolute errors (AEs) of GA-AST, GA-SQP, SQP, IPT, GA, and GA-IPT lie in the range of [2.45E − 08,7.39E − 03], [5.27E − 09,2.55E − 02], [8.46E − 08,2.50E − 02], [3.86E − 08,4.99E − 02], [2.85E − 08,6.98E − 02], and [2.45E − 08,4.92E − 02] respectively.

Table 7 Weights by taking N = 45 along their corresponding solvers SQP, IPT, and GA

Table 8 Weights by taking N = 45 along their corresponding solvers GA-AST, GA-SQP, and GA-IPT

Table 9 Comparison of Ref Sol. with proposed techniques

Table 10 The estimated absolute errors(AE) of proposed solvers in case 2

Fig. 5

Comparison of reference solution and proposed solutions

Fig. 6

Graphical representation of independent runs case 2

4.1 Statistical analysis

The probability plots with 95% confidence interval (CI) is used to determine whether a solver result follow the Normal distribution or not. It was also used to compare the accuracy of all proposed solvers. The p values for the Anderson-Darling (AD) test in each case was higher than the chosen significance level (0.05), so we concluded that all solver results follow the normal distributions. Moreover, the p values of SQP and Hybrid-SQP at level 30 were higher than the others which showed the best result. Similarly, IPT and Hybrid-IPT at level 45 have best results than others. The results have been shown in Figs. 7 and 8 for cases 1 and 2, respectively.

Fig. 7

Fitting at normal distribution to all solvers for case 1

Fig. 8

Fitting at normal distribution to all solvers for case 2

5 Conclusion

The sixth Painlev́e equation is highly nonlinear with multiple singularities, so very hard to find the solution of such type problems. However, in this study, we obtained the approximated solution of this problem through artificial neural network (ANN) with log-sigmoid as transfer function inside the hidden layer of structure by using optimizers like active set techniques, interior point techniques, sequential quadratic programming, and their hybridization GA-AST, GA-SQP, GA-IPT. Proposed techniques provide the better numerical solution of sixth Painlev́e equation. It is not so easy to find analytical solutions of nonlinear, stiff, and multi-singular differential equation in literature.

The best least absolute errors (AEs) are obtained through ANNs which provided the best fitted solution with reference solution. We presented the numerical results of sixth painlev́e equation for N = 10 in Table 5 by using solvers SQP, IPT, GA, GA-AST, GA-SQP, and GA-IPT. The least absolute errors are calculated by the difference of numerical results of proposed solutions with respect to the reference solution and are presented in Table 6 and the absolute errors of solvers SQP, IPT, GA, GA-AST, GA-SQP, and GA-IPT lie in the range of [1.04E − 08,8.88E − 02], [6.48E − 02,1.18E − 01], [4.99E − 08,1.08E − 01], [1.65E − 09,9.18E − 04], [4.28E − 08,9.45E − 02], and [4.33E − 08,1.05E − 01] respectively. Similarly for case 2, the absolute errors of solvers SQP, IPT, GA, GA-AST, GA-SQP, and GA-IPT lie in the range of [8.45E − 08,2.50E − 02], [3.86E − 08,4.99E − 02], [2.85E − 08,6.98E − 02], [2.45E − 08,7.39E − 03], [5.27E − 09,2.55E − 02], and [2.45E − 08,4.92E − 02] respectively.

Thus from absolute errors (AEs), it has clear that hybrid technique (GA-SQP) was more effective than others technique like sequential quadratic programming and hybrid techniques (GA-AST, GA-IPT) in case 1. However, IPT takes less time to converge the desired solution as compared to AST and SQP technique. In the case of by taking lesser number of neurons, the performance of our methods were efficient and fast to converge the solution; however, with the increase of neurons in number, we should need strong CPU configuration; we spend more time to find the solution due to stiffness of problem in nature. Moreover, for future work, one can construct the more reliable optimal techniques based on neural network to investigate it and compare with other numerical results.