Trapezoidal interval type-2 fuzzy aggregation operators and their application to multiple attribute group decision making

Abstract

A type-2 fuzzy set, which is characterized by a fuzzy membership function, involves more uncertainties than the type-1 fuzzy set. As the most widely used type-2 fuzzy set, interval type-2 fuzzy set is a very useful tool to model the uncertainty in the process of decision making. As a special case of interval type-2 fuzzy set, trapezoidal interval type-2 fuzzy set can express linguistic assessments by transforming them into numerical variables objectively. The aim of this paper is to investigate the multiple attribute group decision-making problems in which the attribute values and the weights take the form of trapezoidal interval type-2 fuzzy sets. First, we introduce the concept of trapezoidal interval type-2 fuzzy sets and some arithmetic operations between them. Then, we develop several trapezoidal interval type-2 fuzzy aggregation operators for aggregating trapezoidal interval type-2 fuzzy sets and examine several useful properties of the developed operators. Furthermore, based on the proposed operators, we develop two approaches to multiple attribute group decision making with linguistic information. Finally, a practical example is given to illustrate the feasibility and effectiveness of the developed approach.

1 Introduction

The purpose of multiple attribute group decision making (MAGDM) is to choose the most desirable candidate(s) from a set of alternatives according to the decision information about attribute weights and attribute values provided by a group of decision makers [1, 2]. Considering that the information about attribute values is usually uncertain or fuzzy due to the increasing complexity of the socio-economic environment and the vagueness of inherent subjective nature of human thinking [2]; fuzzy set theory [3] has been utilized to model the uncertainty and vagueness in the process of decision making. In recent years, a lot of methods [4–17] have been developed for dealing with fuzzy multiple attributes group decision-making problems based on type-1 fuzzy sets [3]. It is worth noting that the above fuzzy multiple attribute group decision-making methods are based on type-1 fuzzy sets. If we apply interval type-2 fuzzy sets instead of type-1 fuzzy sets to handle fuzzy group decision-making problems, then there is room for more flexibility due to the fact that interval type-2 fuzzy sets provide more flexibility to present uncertainties than type-1 fuzzy sets [1, 18, 19].

The concept of a type-2 fuzzy set, initially introduced by Zadeh [3], can be regarded as an extension of the concept of a type-1 fuzzy set. Different from a type-1 fuzzy set in which the membership degree is a crisp number in [0, 1] [20], the membership degree of a type-2 fuzzy set is a type-1 fuzzy set in [0, 1]. Type-2 fuzzy sets can therefore provide us with more degrees of freedom to represent the uncertainty and the vagueness of the real world than type-1 fuzzy sets. Interval type-2 fuzzy sets [21] are the most widely used of the higher order fuzzy sets owing to the high computational complexity of using general type-2 fuzzy sets. Interval type-2 fuzzy sets are more capable than ordinary fuzzy sets of handling imprecision and imperfect information in real-world applications. Interval type-2 fuzzy sets have been applied productively in many practical fields [20, 22–28], especially in the decision-making field, and numerous useful methods have been developed to address MAGDM problems with trapezoidal interval type-2 fuzzy sets [19, 29–48]. For example, Wu and Mendel [49, 50] presented a method using the linguistic weighted average and interval type-2 fuzzy sets for handling fuzzy multiple criteria hierarchical group decision-making problems. Chen and Lee [18, 51] presented a method for fuzzy multiple attributes group decision-making based on ranking values and the arithmetic operations of interval type-2 fuzzy sets. Chen and Lee [1, 51] presented a fuzzy multiple attributes group decision-making method based on the interval type-2 TOPSIS method. Chen et al. [19] presented a new method to deal with fuzzy multiple attributes group decision-making problems based on ranking interval type-2 fuzzy sets. Chen and Lee [52] presented a new method for handling fuzzy multiple criteria hierarchical GDM problems based on arithmetic operations and fuzzy preference relations of trapezoidal interval type-2 fuzzy sets. Wang et al. [2, 53] investigated the MAGDM problems under trapezoidal interval type-2 fuzzy set environment, and developed an approach to handling the situations where the attribute values are characterized by trapezoidal interval type-2 fuzzy sets, and the information about attribute weights is partially known.

Uncertain and imprecise assessment information is usually present in practical MAGDM problems because decision makers are not always certain of their given decision or preference information and often use a certain degree of uncertainty to express their subjective judgments [54]. In such cases, decision makers commonly use linguistic variables to evaluate the importance weights of criteria and the ratings of alternatives with respect to various criteria [21]. In particular, the concept of linguistic variables is useful in the case of complex or ill-defined situations. The linguistic values generally can be represented with ordinary fuzzy numbers. Nevertheless, interval type-2 fuzzy sets have a better ability to address linguistic uncertainties by modeling the vagueness and unreliability of information [30]. To address linguistic or numerical uncertainties associated with a subjective environment, the ratings of alternatives with respect to each criterion and the weights of criteria used in MAGDM can be appropriately expressed as trapezoidal interval type-2 fuzzy sets using a linguistic rating system. Most of the trapezoidal interval type-2 fuzzy sets corresponding to linguistic terms are non-negative. Thus, the trapezoidal interval type-2 fuzzy data required in the MAGDM problem can be established by employing the linguistic scales with the corresponding trapezoidal interval type-2 fuzzy sets. In the interval type-2 fuzzy context, several useful linguistic rating systems have been presented to transform the linguistic values into appropriate IT2TrF numbers, i.e., three-point scales [52], four-point scales [52], five-point scales [46, 52], seven-point scales [2, 18, 19, 55], and nine-point scales [33, 37, 38]. Using these linguistic rating systems, decision makers or analysts can conveniently convert the linguistic responses into trapezoidal interval type-2 fuzzy sets. Consequently, the current paper primarily focuses on the development of a new interval type-2 fuzzy MAGDM method within the trapezoidal interval type-2 fuzzy environment.

In a MAGDM problem under interval type-2 fuzzy environment, how to combine the individual interval type-2 fuzzy information into the collective one is an important topic. In order to do this, some aggregation operators should be developed. However, it is worthwhile to mention that the existing interval type-2 fuzzy MAGDM methods do not develop some aggregation operators for aggregating interval type-2 fuzzy information. To overcome this limitation, in Sect. 3 of this paper, we develop some trapezoidal interval type-2 fuzzy aggregation operators for aggregating trapezoidal interval type-2 fuzzy sets, including the trapezoidal interval type-2 fuzzy weighted averaging (TIT2FWA) operator, generalized trapezoidal interval type-2 fuzzy weighted averaging (GTIT2FWA) operator, trapezoidal interval type-2 fuzzy ordered weighted averaging (TIT2FOWA) operator, generalized trapezoidal interval type-2 fuzzy ordered weighted averaging (GTIT2FOWA) operator, trapezoidal interval type-2 fuzzy hybrid averaging (TIT2FHA) operator, and generalized trapezoidal interval type-2 fuzzy hybrid averaging (GTIT2FHA) operator. Then, we investigate some fundamental properties of the developed operators, such as commutativity, idempotency, boundedness, and monotonicity. Next, in Sect. 4, we present an approach based on the developed operators to MAGDM problems under interval type-2 fuzzy environment. Moreover, Sect. 5 provides a numerical example to illustrate the application of the proposed approach. Finally, we conclude the paper in Sect. 6.

2 Preliminaries

In this section, we will briefly introduce the basic concepts and operations of trapezoidal interval type-2 fuzzy sets. More details about type-2 fuzzy sets can be found in "Appendix 1".

Let $\tilde{A}$ be an interval type-2 fuzzy set. If the upper membership function and lower membership function of $\tilde{A}$ are two trapezoidal type-1 fuzzy sets, then $\tilde{A}$ is referred to as a trapezoidal interval type-2 fuzzy set.

Let Ω be the set of all trapezoidal interval type-2 fuzzy sets.

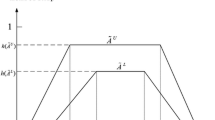
We use the reference points in the universe of discourse and the heights of the upper and the lower membership functions of trapezoidal interval type-2 fuzzy sets to characterize trapezoidal interval type-2 fuzzy sets. For example, Fig. 1 shows a trapezoidal interval type-2 fuzzy set $\tilde{A} = \left( {\tilde{A}^{U} ,\tilde{A}^{L} } \right) = \left( {\left( {a_{1}^{U} ,a_{2}^{U} ,a_{3}^{U} ,a_{4}^{U} ;H_{1} \left( {\tilde{A}^{U} } \right),H_{2} \left( {\tilde{A}^{U} } \right)} \right),\left( {a_{1}^{L} ,a_{2}^{L} ,a_{3}^{L} ,a_{4}^{L} ;H_{1} \left( {\tilde{A}^{L} } \right),H_{2} \left( {\tilde{A}^{L} } \right)} \right)} \right)$, where $H_{i} \left( {\tilde{A}^{U} } \right)$ denotes the membership value of the element a ^U _i+1 in the upper trapezoidal membership function $\tilde{A}^{U}$, 1 ≤ i ≤ 2, $H_{i} \left( {\tilde{A}^{L} } \right)$ denotes the membership value of the element a ^L _i+1 in the lower trapezoidal membership function $\tilde{A}^{L}$, 1 ≤ i ≤ 2, $H_{1} \left( {\tilde{A}^{U} } \right) \in \left[ {0,1} \right]$, $H_{2} \left( {\tilde{A}^{U} } \right) \in \left[ {0,1} \right]$, $H_{1} \left( {\tilde{A}^{L} } \right) \in \left[ {0,1} \right]$, and $H_{2} \left( {\tilde{A}^{L} } \right) \in \left[ {0,1} \right]$ [1, 18, 19].

Fig. 1

A trapezoidal interval type-2 fuzzy set

Let $\tilde{A} = \left( {\tilde{A}^{U} ,\tilde{A}^{L} } \right)$ be a trapezoidal interval type-2 fuzzy set. If $\tilde{A}^{U} = \tilde{A}^{L}$, then the trapezoidal interval type-2 fuzzy number $\tilde{A}$ becomes a trapezoidal type-1 fuzzy set. Let $\tilde{A}$ be a trapezoidal type-1 fuzzy set, where $\tilde{A} = \left( {a_{1} ,a_{2} ,a_{3} ,a_{4} ;H_{1} \left( {\tilde{A}} \right),H_{2} \left( {\tilde{A}} \right)} \right)$. Then, the trapezoidal type-1 fuzzy set $\tilde{A}$ also can be extended into the trapezoidal interval type-2 fuzzy set representation, i.e., $\tilde{A} = \left( {\left( {a_{1} ,a_{2} ,a_{3} ,a_{4} ;H_{1} \left( {\tilde{A}} \right),H_{2} \left( {\tilde{A}} \right)} \right),\left( {a_{1} ,a_{2} ,a_{3} ,a_{4} ;H_{1} \left( {\tilde{A}} \right),H_{2} \left( {\tilde{A}} \right)} \right)} \right)$ [1, 18, 19].

In the real decision making, it is difficult for the decision makers to directly adopt the form of trapezoidal interval type-2 fuzzy sets to give the attribute values and weights. We usually adopt the form of linguistic terms. Because the upper membership functions and lower membership functions of trapezoidal interval type-2 fuzzy sets are piecewise linear and trapezoidal, we can utilize trapezoidal interval type-2 fuzzy sets to capture the vagueness of some linguistic terms. Table 1 shows the linguistic terms “very low,” (VL) “low,” (L) “medium low,” (ML) “medium,” (M) “medium high,” (MH) “high,” (H) “very high,” (VH) and their corresponding trapezoidal interval type-2 fuzzy sets, respectively [55]. The membership function curves of the trapezoidal interval type-2 fuzzy sets in Table 1 are shown in Fig. 2 [55].

Table 1 Linguistic terms and their corresponding trapezoidal interval type-2 fuzzy sets

Fig. 2

Membership functions of the linguistic terms

Some operational laws and comparison laws about trapezoidal interval type-2 fuzzy sets can be founded in "Appendix 2".

3 Trapezoidal interval type-2 fuzzy aggregation operators

In this section, we will develop several trapezoidal interval type-2 fuzzy aggregation operators for aggregating trapezoidal interval type-2 fuzzy sets.

Definition 3.1

Let $\tilde{A}_{i} = \left( {\tilde{A}_{i}^{U} ,\tilde{A}_{i}^{L} } \right) = \left( {\left( {a_{i1}^{U} ,a_{i2}^{U} ,a_{i3}^{U} ,a_{i4}^{U} ;H_{1} \left( {\tilde{A}_{i}^{U} } \right),H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right),\left( {a_{i1}^{L} ,a_{i2}^{L} ,a_{i3}^{L} ,a_{i4}^{L} ;H_{1} \left( {\tilde{A}_{i}^{L} } \right),H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n) be a collection of trapezoidal interval type-2 fuzzy sets, and let $\tilde{w} = \left( {\tilde{w}_{1} ,\tilde{w}_{2} , \ldots ,\tilde{w}_{n} } \right)^{\text{T}}$ be the weight vector of $\tilde{A}_{i}$ (i = 1, 2, …, n) with $\tilde{w}_{i} = \left( {\tilde{w}_{i}^{U} ,\tilde{w}_{i}^{L} } \right) = \left( {\left( {w_{i1}^{U} ,w_{i2}^{U} ,w_{i3}^{U} ,w_{i4}^{U} ;H_{1} \left( {\tilde{w}_{i}^{U} } \right),H_{2} \left( {\tilde{w}_{i}^{U} } \right)} \right),\left( {w_{i1}^{L} ,w_{i2}^{L} ,w_{i3}^{L} ,w_{i4}^{L} ;H_{1} \left( {\tilde{w}_{i}^{L} } \right),H_{2} \left( {\tilde{w}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n). Then, a generalized trapezoidal interval type-2 fuzzy weighted averaging (GTIT2FWA) operator is a mapping Ωⁿ → Ω, where

$${\text{GTIT2FWA}}_{{\tilde{w},\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) = \left( {\mathop \oplus \limits_{i = 1}^{n} \left( {\tilde{w}_{i} \otimes \tilde{A}_{i}^{\lambda } } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}}$$

(1)

with λ > 0.

Especially, if $\tilde{w} = \left( {\frac{1}{n},\frac{1}{n}, \ldots ,\frac{1}{n}} \right)^{\text{T}}$, then the GTIT2FWA operator reduces to the generalized trapezoidal interval type-2 fuzzy averaging (GTIT2FA) operator:

$${\text{GTIT2FA}}_{\lambda } \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) = \left( {\mathop \oplus \limits_{i = 1}^{n} \left( {\frac{1}{n}\tilde{A}_{i}^{\lambda } } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} .$$

(2)

By the operational laws given in "Appendix 2", Eq. (2) can be transformed into the following form:

$$\begin{aligned} & {\text{GTIT2FWA}}_{{\tilde{w},\lambda }}\left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} }\right) \\ & \quad = \left( \begin{aligned} \left(\begin{array}{ll} \left( {\sum\limits_{i = 1}^{n} {\left( {w_{i1}^{U}\times \left( {a_{i1}^{U} } \right)^{\lambda } } \right)} }\right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right.\kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n}{\left( {w_{i2}^{U} \times \left( {a_{i2}^{U} } \right)^{\lambda } }\right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }}\right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i =1}^{n} {\left( {w_{i3}^{U} \times \left( {a_{i3}^{U} }\right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/{\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad\left( {\sum\limits_{i = 1}^{n} {\left( {w_{i4}^{U} \times \left({a_{i4}^{U} } \right)^{\lambda } } \right)} } \right)^{{{1\mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda}}} ; \hfill \\ \mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{{\hbox{min} \left\{ {H_{1} \left( {\tilde{w}_{i}^{U} } \right),\quad H_{1} \left( {\tilde{A}_{i}^{U} } \right)} \right\}} \right\},\quad\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {\hbox{min}\left\{ {H_{2} \left( {\tilde{w}_{i}^{U} } \right),\quad H_{2}\left( {\tilde{A}_{i}^{U} } \right)} \right\}} \right\} \hfill \\\end{array}\right), \hfill \\ \left( \begin{array}{ll} \left({\sum\limits_{i = 1}^{n} {\left( {w_{i1}^{L} \times \left({a_{i1}^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n} {\left( {w_{i2}^{L} \times \left( {a_{i2}^{L} } \right)^{\lambda } } \right)} }\right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right.\kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n}{\left( {w_{i3}^{L} \times \left( {a_{i3}^{L} } \right)^{\lambda } }\right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }}\right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i =1}^{n} {\left( {w_{i4}^{L} \times \left( {a_{i4}^{L} }\right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/{\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ; \hfill \\\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {\hbox{min}\left\{ {H_{1} \left( {\tilde{w}_{i}^{L} } \right),H_{1} \left({\tilde{A}_{i}^{L} } \right)} \right\}} \right\},\quad \mathop{\hbox{min} }\limits_{1 \le i \le n} \left\{ {\hbox{min} \left\{{H_{2} \left( {\tilde{w}_{i}^{L} } \right),\quad H_{2} \left({\tilde{A}_{i}^{L} } \right)} \right\}} \right\} \hfill \\ \end{array}\right) \hfill \\ \end{aligned} \right) \\ \end{aligned}$$

(3)

Theorem 3.1

Let $\tilde{A}_{i} = \left( {\tilde{A}_{i}^{U} ,\tilde{A}_{i}^{L} } \right) = \left( {\left( {a_{i1}^{U} ,a_{i2}^{U} ,a_{i3}^{U} ,a_{i4}^{U} ;H_{1} \left( {\tilde{A}_{i}^{U} } \right),H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right),\left( {a_{i1}^{L} ,a_{i2}^{L} ,a_{i3}^{L} ,a_{i4}^{L} ;H_{1} \left( {\tilde{A}_{i}^{L} } \right),H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n) be a collection of trapezoidal interval type-2 fuzzy sets, and let $\tilde{w}_{i}$ (i = 1, 2, …, n) be real numbers. Then, the following properties hold.

Theorem 3.2

Let $\tilde{A}_{i} = \left( {\tilde{A}_{i}^{U} ,\tilde{A}_{i}^{L} } \right) = \left( {\left( {a_{i1}^{U} ,a_{i2}^{U} ,a_{i3}^{U} ,a_{i4}^{U} ;H_{1} \left( {\tilde{A}_{i}^{U} } \right),H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right),\left( {a_{i1}^{L} ,a_{i2}^{L} ,a_{i3}^{L} ,a_{i4}^{L} ;H_{1} \left( {\tilde{A}_{i}^{L} } \right),H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n) be a collection of trapezoidal interval type-2 fuzzy sets, and let $\tilde{w}_{i}$ (i = 1, 2, …, n) be real numbers, and let λ > 0. Then, the following properties hold.

• 1. Idempotency: if $\tilde{A}_{i} = \tilde{A} = \left( {\left( {a_{1}^{U} ,a_{2}^{U} ,a_{3}^{U} ,a_{4}^{U} ;H_{1} \left( {\tilde{A}^{U} } \right),H_{2} \left( {\tilde{A}^{U} } \right)} \right),\left( {a_{1}^{L} ,a_{2}^{L} ,a_{3}^{L} ,a_{4}^{L} ;H_{1} \left( {\tilde{A}^{L} } \right),H_{2} \left( {\tilde{A}^{L} } \right)} \right)} \right)$ for all i, then

  $${\text{GTIT2FWA}}_{{\tilde{w},\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) = \tilde{A}.$$

  (4)

• 2. Boundedness:

  $$\tilde{A}_{\hbox{min} } \le {\text{GTIT2FWA}}_{{\tilde{w},\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) \le \tilde{A}_{\hbox{max} } ,$$

  (5)

  where

  $$\tilde{A}_{\hbox{min} } = \left( \begin{array}{ll} \left( {\mathop{\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i1}^{U} }\right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{{a_{i2}^{U} } \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n}\left\{ {a_{i3}^{U} } \right\},\mathop {\hbox{min} }\limits_{1 \le i\le n} \left\{ {a_{i4}^{U} } \right\};\mathop {\hbox{min}}\limits_{1 \le i \le n} \left\{ {H_{1} \left( {\tilde{A}_{i}^{U} }\right)} \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n}\left\{ {H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right\}}\right), \hfill \\ \left( {\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i1}^{L} } \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i2}^{L} } \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i3}^{L} } \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i4}^{L} } \right\};\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {H_{1} \left( {\tilde{A}_{i}^{L} } \right)} \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right\}} \right) \hfill \\ \end{array}\right)$$

  and

  $$\tilde{A}_{\hbox{max} } = \left( \begin{array}{ll} \left( {\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i1}^{U} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i2}^{U} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i3}^{U} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i4}^{U} } \right\};\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {H_{1} \left( {\tilde{A}_{i}^{U} } \right)} \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right\}} \right), \hfill \\ \left( {\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i1}^{L} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i2}^{L} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i3}^{L} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i4}^{L} } \right\};\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {H_{1} \left( {\tilde{A}_{i}^{L} } \right)} \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right\}} \right) \hfill \\ \end{array}\right).$$

• 3. Monotonicity: let $\tilde{A}_{i} = \left( {\tilde{A}_{i}^{U} ,\tilde{A}_{i}^{L} } \right) = \left( {\left( {a_{i1}^{U} ,a_{i2}^{U} ,a_{i3}^{U} ,a_{i4}^{U} ;H_{1} \left( {\tilde{A}_{i}^{U} } \right),H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right),\left( {a_{i1}^{L} ,a_{i2}^{L} ,a_{i3}^{L} ,a_{i4}^{L} ;H_{1} \left( {\tilde{A}_{i}^{L} } \right),H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n) and $\tilde{B}_{i} = \left( {\tilde{B}_{i}^{U} ,\tilde{B}_{i}^{L} } \right) = \left( {\left( {b_{i1}^{U} ,b_{i2}^{U} ,b_{i3}^{U} ,b_{i4}^{U} ;H_{1} \left( {\tilde{B}_{i}^{U} } \right),H_{2} \left( {\tilde{B}_{i}^{U} } \right)} \right),\left( {b_{i1}^{L} ,b_{i2}^{L} ,b_{i3}^{L} ,b_{i4}^{L} ;H_{1} \left( {\tilde{B}_{i}^{L} } \right),H_{2} \left( {\tilde{B}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n) be two collections of trapezoidal interval type-2 fuzzy sets. If a ^U _ij  ≤ b ^U _ij , a ^L _ij  ≤ b ^L _ij , $H_{1} \left( {\tilde{A}_{i}^{U} } \right) \le H_{1} \left( {\tilde{B}_{i}^{U} } \right)$, $H_{2} \left( {\tilde{A}_{i}^{U} } \right) \le H_{2} \left( {\tilde{B}_{i}^{U} } \right)$, $H_{1} \left( {\tilde{A}_{i}^{L} } \right) \le H_{1} \left( {\tilde{B}_{i}^{L} } \right)$, and $H_{2} \left( {\tilde{A}_{i}^{L} } \right) \le H_{2} \left( {\tilde{B}_{i}^{L} } \right)$, for all i = 1, 2, …, n and j = 1, 2, 3, 4, then

  $${\text{GTIT2FWA}}_{{\tilde{w},\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) \le {\text{GTIT2FWA}}_{{\tilde{w},\lambda }} \left( {\tilde{B}_{1} ,\tilde{B}_{2} , \ldots ,\tilde{B}_{n} } \right).$$

  (6)

Theorem 3.3

For the given arguments $\tilde{A}_{i} \in\Omega$ (i = 1, 2, …, n) and the weight vector $\tilde{w} = \left( {\tilde{w}_{1} ,\tilde{w}_{2} , \ldots ,\tilde{w}_{n} } \right)^{\text{T}}$, the GTIT2FWA operator is monotonically increasing with respect to the parameter λ.

Proof

See "Appendix 2".

Definition 3.2

Let $\tilde{A}_{i} = \left( {\tilde{A}_{i}^{U} ,\tilde{A}_{i}^{L} } \right) = \left( {\left( {a_{i1}^{U} ,a_{i2}^{U} ,a_{i3}^{U} ,a_{i4}^{U} ;H_{1} \left( {\tilde{A}_{i}^{U} } \right),H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right),\left( {a_{i1}^{L} ,a_{i2}^{L} ,a_{i3}^{L} ,a_{i4}^{L} ;H_{1} \left( {\tilde{A}_{i}^{L} } \right),H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n) be a collection of trapezoidal interval type-2 fuzzy sets, $\tilde{A}_{\sigma \left( i \right)}$ be the ith largest of them, $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{n} } \right)^{\text{T}}$ be the aggregation-associated vector such that $\tilde{\omega }_{i} = \left( {\tilde{\omega }_{i}^{U} ,\tilde{\omega }_{i}^{L} } \right) = \left( {\left( {\omega_{i1}^{U} ,\omega_{i2}^{U} ,\omega_{i3}^{U} ,\omega_{i4}^{U} ;H_{1} \left( {\tilde{\omega }_{i}^{U} } \right),H_{2} \left( {\tilde{\omega }_{i}^{U} } \right)} \right),\left( {\omega_{i1}^{L} ,\omega_{i2}^{L} ,\omega_{i3}^{L} ,\omega_{i4}^{L} ;H_{1} \left( {\tilde{\omega }_{i}^{L} } \right),H_{2} \left( {\tilde{\omega }_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n), then, a generalized trapezoidal interval type-2 fuzzy ordered weighted averaging (GTIT2FOWA) operator is a mapping Ωⁿ → Ω, where

$${\text{GTIT2FOWA}}_{{\tilde{\omega },\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) = \left( {\mathop \oplus \limits_{i = 1}^{n} \left( {\tilde{\omega }_{i} \otimes \tilde{A}_{\sigma \left( i \right)}^{\lambda } } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}}$$

(7)

with λ > 0.

By the operational laws given in "Appendix 2", Eq. (7) can be transformed into the following forms, respectively:

$$\begin{aligned} & {\text{GTIT2FOWA}}_{{\tilde{\omega },\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) \\ & \quad = \left( \begin{array}{ll} \left( \begin{array}{ll} \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i1}^{U} \times \left( {a_{\sigma \left( i \right)1}^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i2}^{U} \times \left( {a_{\sigma \left( i \right)2}^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i3}^{U} \times \left( {a_{\sigma \left( i \right)3}^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i4}^{U} \times \left( {a_{\sigma \left( i \right)4}^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ; \hfill \\ \mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {\hbox{min} \left\{ {H_{1} \left( {\tilde{\omega }_{i}^{U} } \right),\quad H_{1} \left( {\tilde{A}_{\sigma \left( i \right)}^{U} } \right)} \right\}} \right\},\quad \mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {\hbox{min} \left\{ {H_{2} \left( {\tilde{\omega }_{i}^{U} } \right),\quad H_{2} \left( {\tilde{A}_{\sigma \left( i \right)}^{U} } \right)} \right\}} \right\} \hfill \\ \end{array}\right), \hfill \\ \left( \begin{array}{ll} \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i1}^{L} \times \left( {a_{\sigma \left( i \right)1}^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i2}^{L} \times \left( {a_{\sigma \left( i \right)2}^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i3}^{L} \times \left( {a_{\sigma \left( i \right)3}^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i4}^{L} \times \left( {a_{\sigma \left( i \right)4}^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ; \hfill \\ \mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {\hbox{min} \left\{ {H_{1} \left( {\tilde{\omega }_{i}^{L} } \right),\quad H_{1} \left( {\tilde{A}_{\sigma \left( i \right)}^{L} } \right)} \right\}} \right\},\quad \mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {\hbox{min} \left\{ {H_{2} \left( {\tilde{\omega }_{i}^{L} } \right),\quad H_{2} \left( {\tilde{A}_{\sigma \left( i \right)}^{L} } \right)} \right\}} \right\} \hfill \\ \end{array}\right) \hfill \\ \end{array}\right) \\ \end{aligned}$$

(8)

In Definition 3.2, if $\tilde{\omega } = \left( {\frac{1}{n},\frac{1}{n}, \ldots ,\frac{1}{n}} \right)^{\text{T}}$, then the GTIT2FOWA operator reduces to the generalized trapezoidal interval type-2 fuzzy averaging (GTIT2FA) operator. If λ = 1, then the GTIT2FOWA operator reduces to the TIT2FOWA operator:

$${\text{TIT2FOWA}}_{{\tilde{\omega }}} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) = \mathop \oplus \limits_{i = 1}^{n} \left( {\tilde{\omega }_{i} \otimes \tilde{A}_{\sigma \left( i \right)} } \right).$$

(9)

The TIT2FWA and GTIT2FWA operators weight only the trapezoidal interval type-2 fuzzy sets. However, by Definition 3.2, the GTIT2FOWA operator weights the ordered positions of the trapezoidal interval type-2 fuzzy sets instead of weighting the trapezoidal interval type-2 fuzzy sets themselves. The prominent characteristic of the GTIT2FOWA operator is that the input arguments are rearranged in descending order, in particular, a trapezoidal interval type-2 fuzzy set $\tilde{A}_{i}$ is not associated with a particular weight $\tilde{\omega }_{i}$ but rather a weight $\tilde{\omega }_{i}$ is associated with a particular ordered position i of the trapezoidal interval type-2 fuzzy sets.

Theorem 3.4

Let $\tilde{A}_{i} = \left( {\tilde{A}_{i}^{U} ,\tilde{A}_{i}^{L} } \right) = \left( {\left( {a_{i1}^{U} ,a_{i2}^{U} ,a_{i3}^{U} ,a_{i4}^{U} ;H_{1} \left( {\tilde{A}_{i}^{U} } \right),H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right),\left( {a_{i1}^{L} ,a_{i2}^{L} ,a_{i3}^{L} ,a_{i4}^{L} ;H_{1} \left( {\tilde{A}_{i}^{L} } \right),H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n) be a collection of trapezoidal interval type-2 fuzzy sets, and let $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{n} } \right)^{\text{T}}$ be real numbers, and let λ > 0. Then, the following properties hold.

• 1. Commutativity: if $\left( {\tilde{A}_{1}^{{\prime }} ,\tilde{A}_{2}^{{\prime }} , \ldots ,\tilde{A}_{n}^{{\prime }} } \right)$ is any permutation of $\left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right)$, then

  $${\text{GTIT2FOWA}}_{{\tilde{\omega },\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) = {\text{GTIT2FOWA}}_{{\tilde{\omega },\lambda }} \left( {\tilde{A}_{1}^{{\prime }} ,\tilde{A}_{2}^{{\prime }} , \ldots ,\tilde{A}_{n}^{{\prime }} } \right).$$

  (10)

• 2. Idempotency: if $\tilde{A}_{i} = \tilde{A} = \left( {\left( {a_{1}^{U} ,a_{2}^{U} ,a_{3}^{U} ,a_{4}^{U} ;H_{1} \left( {\tilde{A}^{U} } \right),H_{2} \left( {\tilde{A}^{U} } \right)} \right),\left( {a_{1}^{L} ,a_{2}^{L} ,a_{3}^{L} ,a_{4}^{L} ;H_{1} \left( {\tilde{A}^{L} } \right),H_{2} \left( {\tilde{A}^{L} } \right)} \right)} \right)$ for all i, then

  $${\text{GTIT2FOWA}}_{{\tilde{\omega },\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) = \tilde{A}.$$

  (11)

• 3. Boundedness:

  $$\tilde{A}_{\hbox{min} } \le {\text{GTIT2FOWA}}_{{\tilde{\omega },\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) \le \tilde{A}_{\hbox{max} } ,$$

  (12)

where

$$\tilde{A}_{\hbox{min} } = \left( \begin{array}{ll} \left( {\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i1}^{U} } \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i2}^{U} } \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i3}^{U} } \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i4}^{U} } \right\};\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {H_{1} \left( {\tilde{A}_{i}^{U} } \right)} \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right\}} \right), \hfill \\ \left( {\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i1}^{L} } \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i2}^{L} } \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i3}^{L} } \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {a_{i4}^{L} } \right\};\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {H_{1} \left( {\tilde{A}_{i}^{L} } \right)} \right\},\mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right\}} \right) \hfill \\ \end{array}\right)$$

and

$$\tilde{A}_{\hbox{max} } = \left( \begin{array}{ll} \left( {\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i1}^{U} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i2}^{U} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i3}^{U} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i4}^{U} } \right\};\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {H_{1} \left( {\tilde{A}_{i}^{U} } \right)} \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right\}} \right), \hfill \\ \left( {\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i1}^{L} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i2}^{L} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i3}^{L} } \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {a_{i4}^{L} } \right\};\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {H_{1} \left( {\tilde{A}_{i}^{L} } \right)} \right\},\mathop {\hbox{max} }\limits_{1 \le i \le n} \left\{ {H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right\}} \right) \hfill \\ \end{array} \right).$$

• 4. Monotonicity: let $\tilde{A}_{i} = \left( {\tilde{A}_{i}^{U} ,\tilde{A}_{i}^{L} } \right) = \left( {\left( {a_{i1}^{U} ,a_{i2}^{U} ,a_{i3}^{U} ,a_{i4}^{U} ;H_{1} \left( {\tilde{A}_{i}^{U} } \right),H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right),\left( {a_{i1}^{L} ,a_{i2}^{L} ,a_{i3}^{L} ,a_{i4}^{L} ;H_{1} \left( {\tilde{A}_{i}^{L} } \right),H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n) and $\tilde{B}_{i} = \left( {\tilde{B}_{i}^{U} ,\tilde{B}_{i}^{L} } \right) = \left( {\left( {b_{i1}^{U} ,b_{i2}^{U} ,b_{i3}^{U} ,b_{i4}^{U} ;H_{1} \left( {\tilde{B}_{i}^{U} } \right),H_{2} \left( {\tilde{B}_{i}^{U} } \right)} \right),\left( {b_{i1}^{L} ,b_{i2}^{L} ,b_{i3}^{L} ,b_{i4}^{L} ;H_{1} \left( {\tilde{B}_{i}^{L} } \right),H_{2} \left( {\tilde{B}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n) be two collections of trapezoidal interval type-2 fuzzy sets. If a ^U _ij  ≤ b ^U _ij , a ^L _ij  ≤ b ^L _ij , $H_{1} \left( {\tilde{A}_{i}^{U} } \right) \le H_{1} \left( {\tilde{B}_{i}^{U} } \right)$, $H_{2} \left( {\tilde{A}_{i}^{U} } \right) \le H_{2} \left( {\tilde{B}_{i}^{U} } \right)$, $H_{1} \left( {\tilde{A}_{i}^{L} } \right) \le H_{1} \left( {\tilde{B}_{i}^{L} } \right)$, and $H_{2} \left( {\tilde{A}_{i}^{L} } \right) \le H_{2} \left( {\tilde{B}_{i}^{L} } \right)$, for all i = 1, 2, …, n and j = 1, 2, 3, 4, then

  $${\text{GTIT2FOWA}}_{{\tilde{\omega },\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) \le {\text{GTIT2FOWA}}_{{\tilde{\omega },\lambda }} \left( {\tilde{B}_{1} ,\tilde{B}_{2} , \ldots ,\tilde{B}_{n} } \right).$$

  (13)

Similar to Theorem 3.3, we have the following result.

Theorem 3.5

For the given arguments $\tilde{A}_{i} \in\Omega$ (i = 1, 2, …, n) and the aggregation-associated vector $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{n} } \right)^{\text{T}}$, the GTIT2FOWA operator is monotonically increasing with respect to the parameter λ.

By Definitions 3.1 and 3.2, it is worth noting that all the operators mentioned above have some inherent limitations. Concretely, the GTIT2FWA only weight the trapezoidal interval type-2 fuzzy set itself, but ignore the importance of the ordered position of the arguments, whereas the GTIT2FOWA operators only weight the ordered position of each given argument, but ignore the importance of the argument. To overcome this drawback, we next present two hybrid aggregation operators for aggregating trapezoidal interval type-2 fuzzy sets, which weight not only all the given arguments but also their ordered positions.

Definition 3.3

For a collection of trapezoidal interval type-2 fuzzy sets $\tilde{A}_{i} = \left( {\tilde{A}_{i}^{U} ,\tilde{A}_{i}^{L} } \right) = \left( {\left( {a_{i1}^{U} ,a_{i2}^{U} ,a_{i3}^{U} ,a_{i4}^{U} ;H_{1} \left( {\tilde{A}_{i}^{U} } \right),H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right),\left( {a_{i1}^{L} ,a_{i2}^{L} ,a_{i3}^{L} ,a_{i4}^{L} ;H_{1} \left( {\tilde{A}_{i}^{L} } \right),H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n), $\tilde{w} = \left( {\tilde{w}_{1} ,\tilde{w}_{2} , \ldots ,\tilde{w}_{n} } \right)^{\text{T}}$ is the weight vector of them with $\tilde{w}_{i} = \left( {\tilde{w}_{i}^{U} ,\tilde{w}_{i}^{L} } \right) = \left( {\left( {w_{i1}^{U} ,w_{i2}^{U} ,w_{i3}^{U} ,w_{i4}^{U} ;H_{1} \left( {\tilde{w}_{i}^{U} } \right),H_{2} \left( {\tilde{w}_{i}^{U} } \right)} \right),\left( {w_{i1}^{L} ,w_{i2}^{L} ,w_{i3}^{L} ,w_{i4}^{L} ;H_{1} \left( {\tilde{w}_{i}^{L} } \right),H_{2} \left( {\tilde{w}_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n), n is the balancing coefficient which plays a role of balance, then we define the following aggregation operators, which are all based on the mapping Ωⁿ → Ω with an aggregation-associated vector $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{n} } \right)^{\text{T}}$ such that $\tilde{\omega }_{i} = \left( {\tilde{\omega }_{i}^{U} ,\tilde{\omega }_{i}^{L} } \right) = \left( {\left( {\omega_{i1}^{U} ,\omega_{i2}^{U} ,\omega_{i3}^{U} ,\omega_{i4}^{U} ;H_{1} \left( {\tilde{\omega }_{i}^{U} } \right),H_{2} \left( {\tilde{\omega }_{i}^{U} } \right)} \right),\left( {\omega_{i1}^{L} ,\omega_{i2}^{L} ,\omega_{i3}^{L} ,\omega_{i4}^{L} ;H_{1} \left( {\tilde{\omega }_{i}^{L} } \right),H_{2} \left( {\tilde{\omega }_{i}^{L} } \right)} \right)} \right)$ (i = 1, 2, …, n). Then, a generalized trapezoidal interval type-2 fuzzy hybrid averaging (GTIT2FHA) operator is a mapping Ωⁿ → Ω, such that

$${\text{GTIT2FHA}}_{{\tilde{w},\tilde{\omega },\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) = \left( {\mathop \oplus \limits_{i = 1}^{n} \left( {\tilde{\omega }_{i} \otimes \tilde{B}_{\sigma \left( i \right)}^{\lambda } } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,$$

(14)

where λ > 0 and $\tilde{B}_{\sigma \left( i \right)}$ is the ith largest of $\tilde{B}_{k} = n\left( {\tilde{w}_{k} \otimes \tilde{A}_{k} } \right)$ (k = 1, 2, …, n).

Especially, if λ = 1, then GTIT2FHA operator reduces the trapezoidal interval type-2 fuzzy hybrid averaging (TIT2FHA) operator:

$${\text{TIT2FHA}}_{{\tilde{w},\tilde{\omega }}} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) = \mathop \oplus \limits_{i = 1}^{n} \left( {\tilde{\omega }_{i} \otimes \tilde{B}_{\sigma \left( i \right)} } \right) ,$$

(15)

where $\tilde{B}_{\sigma \left( i \right)}$ is the ith largest of $\tilde{B}_{k} = n\left( {\tilde{w}_{k} \otimes \tilde{A}_{k} } \right)$ (k = 1, 2, …, n).

Especially, if $\tilde{w} = \left( {\frac{1}{n},\frac{1}{n}, \ldots ,\frac{1}{n}} \right)^{\text{T}}$, then the TIT2FHA operator reduces to the TIT2FOWA operator and the GTIT2FHA operator reduces to the GTIT2FOWA operator; if $\tilde{\omega } = \left( {\frac{1}{n},\frac{1}{n}, \ldots ,\frac{1}{n}} \right)^{\text{T}}$, then the TIT2FHA operator reduces to the TIT2FWA operator and the GTIT2FHA operator reduces to the GTIT2FWA operator; if λ = 1, then the GTIT2FHA operator reduces to the TIT2FHA operator.

By the operational laws given in "Appendix 2", Eq. (14) can be transformed into the following forms, respectively:

$$\begin{aligned} & {\text{GTIT2FHA}}_{{\tilde{w},\tilde{\omega },\lambda }} \left( {\tilde{A}_{1} ,\tilde{A}_{2} , \ldots ,\tilde{A}_{n} } \right) \\ & \quad = \left( \begin{array}{ll} \left( \begin{array}{ll} \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i1}^{U} \times \left( {n \times w_{\sigma \left( i \right)1}^{U} \times a_{\sigma \left( i \right)1}^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i2}^{U} \times \left( {n \times w_{\sigma \left( i \right)2}^{U} \times a_{\sigma \left( i \right)2}^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} , \hfill \\ \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i3}^{U} \times \left( {n \times w_{\sigma \left( i \right)3}^{U} \times a_{\sigma \left( i \right)3}^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i4}^{U} \times \left( {n \times w_{\sigma \left( i \right)4}^{U} \times a_{\sigma \left( i \right)4}^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ; \hfill \\ \mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {\hbox{min} \left\{ {H_{1} \left( {\tilde{\omega }_{i}^{U} } \right),\quad \hbox{min} \left\{ {H_{1} \left( {\tilde{w}_{\sigma \left( i \right)}^{U} } \right),\quad H_{1} \left( {\tilde{A}_{\sigma \left( i \right)}^{U} } \right)} \right\}} \right\}} \right\},\quad \mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {\hbox{min} \left\{ {H_{2} \left( {\tilde{\omega }_{i}^{U} } \right),\quad \hbox{min} \left\{ {H_{2} \left( {\tilde{w}_{\sigma \left( i \right)}^{U} } \right),\quad H_{2} \left( {\tilde{A}_{\sigma \left( i \right)}^{U} } \right)} \right\}} \right\}} \right\} \hfill \\ \end{array} \right), \hfill \\ \left( \begin{array}{ll} \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i1}^{L} \times \left( {n \times w_{\sigma \left( i \right)1}^{L} \times a_{\sigma \left( i \right)1}^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i2}^{L} \times \left( {n \times w_{\sigma \left( i \right)2}^{L} \times a_{\sigma \left( i \right)2}^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} , \hfill \\ \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i3}^{L} \times \left( {n \times w_{\sigma \left( i \right)3}^{L} \times a_{\sigma \left( i \right)3}^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{i = 1}^{n} {\left( {\omega_{i4}^{L} \times \left( {n \times w_{\sigma \left( i \right)4}^{L} \times a_{\sigma \left( i \right)4}^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ; \hfill \\ \mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {\hbox{min} \left\{ {H_{1} \left( {\tilde{\omega }_{i}^{L} } \right),\quad \hbox{min} \left\{ {H_{1} \left( {\tilde{w}_{\sigma \left( i \right)}^{L} } \right),\quad H_{1} \left( {\tilde{A}_{\sigma \left( i \right)}^{L} } \right)} \right\}} \right\}} \right\},\quad \mathop {\hbox{min} }\limits_{1 \le i \le n} \left\{ {\hbox{min} \left\{ {H_{2} \left( {\tilde{\omega }_{i}^{L} } \right),\quad \hbox{min} \left\{ {H_{2} \left( {\tilde{w}_{\sigma \left( i \right)}^{L} } \right),\quad H_{2} \left( {\tilde{A}_{\sigma \left( i \right)}^{L} } \right)} \right\}} \right\}} \right\} \hfill \\ \end{array} \right) \hfill \\ \end{array} \right) \\ \end{aligned}$$

(16)

Similar to Theorems 3.3 and 3.5, we have the following result.

Theorem 3.6

For the given arguments $\tilde{A}_{i} \in\Omega$ (i = 1, 2, …, n), the weight vector $\tilde{w} = \left( {\tilde{w}_{1} ,\tilde{w}_{2} , \ldots ,\tilde{w}_{n} } \right)^{\text{T}}$, and the aggregation-associated vector $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{n} } \right)^{\text{T}}$, the GTIT2FHA operator is monotonically increasing with respect to the parameter λ.

4 An approach to multiple attribute group decision making with linguistic information

In this section, we shall utilize the proposed trapezoidal interval type-2 fuzzy aggregation operators to develop an approach to multiple attribute group decision making with linguistic information.

A multiple attribute group decision-making problem with linguistic information can be summarized as follows: let X = {x ₁, x ₂, …, x _m } be a set of m alternatives, C = {c ₁, c ₂, …, c _n } be a collection of n attributes, and D = {d ₁, d ₂, …, d _l } be a set of l decision makers whose weight vector is $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{l} } \right)^{\text{T}}$, where $\tilde{\omega }_{k}$ (k = 1, 2, …, l) are the linguistic terms. Assume that each decision maker d _k (k = 1, 2, …, l) uses the linguistic terms to represent the weights of n attributes and provides the weight vector $\tilde{w}^{\left( k \right)} = \left( {\tilde{w}_{1}^{\left( k \right)} ,\tilde{w}_{2}^{\left( k \right)} , \ldots ,\tilde{w}_{n}^{\left( k \right)} } \right)^{\text{T}}$, where $\tilde{w}_{j}^{\left( k \right)}$ (j = 1, 2, …, n) is the weight of the attribute c _j and $\tilde{w}_{j}^{\left( k \right)}$ is a linguistic term. Suppose that each decision maker d _k (k = 1, 2, …, l) provides his/her own linguistic decision matrix $\tilde{A}^{\left( k \right)} = \left( {\tilde{A}_{ij}^{\left( k \right)} } \right)_{m \times n}$ (k = 1, 2, …, l), where $\tilde{A}_{ij}^{\left( k \right)}$ is a preference value, which takes the form of linguistic term, given by the decision maker d _k  ∊ D, for the alternative x _i  ∊ X with respect to the attribute c _j  ∊ C.

In general, attributes can be classified into two types: benefit attributes and cost attributes. In other words, the attribute set C can be divided into two subsets: C ₁ and C ₂, which are the subset of benefit attributes and cost attributes, respectively. Furthermore, we have C ₁ ∪ C ₂ = C and C ₁ ∩ C ₂ = ∅, where ∅ is an empty set. The linguistic decision matrices $\tilde{A}^{\left( k \right)}$ need to be normalized unless all the attributes c _j (j = 1, 2, …, n) are of the same type. In this paper, we transform the linguistic decision matrices $\tilde{A}^{\left( k \right)} = \left( {\tilde{A}_{ij}^{\left( k \right)} } \right)_{m \times n}$ into the normalized linguistic decision matrices $\tilde{R}^{\left( k \right)} = \left( {\tilde{R}_{ij}^{\left( k \right)} } \right)_{m \times n}$ by the following method given in [2]:

$$\tilde{R}_{ij}^{\left( k \right)} = \left\{ {\begin{array}{*{20}l} {\tilde{A}_{ij}^{\left( k \right)} ,} \hfill & {j \in C_{1} ,} \hfill \\ {\left( {\tilde{A}_{ij}^{\left( k \right)} } \right)^{c} ,} \hfill & {j \in C_{2} ,} \hfill \\ \end{array} } \right.$$

(17)

where $\left( {\tilde{A}_{ij}^{\left( k \right)} } \right)^{c}$ is the complement of $\tilde{A}_{ij}^{\left( k \right)}$.

Table 2 shows complementary relations about the linguistic terms shown in Table 1.

Table 2 The complementary relations

In the following, we utilize the proposed operators to develop an approach to multiple attribute group decision making with linguistic information, which involves the following steps:

Algorithm 4.1

Step 1. Transform the linguistic decision matrices $\tilde{A}^{\left( k \right)} = \left( {\tilde{A}_{ij}^{\left( k \right)} } \right)_{m \times n}$ (k = 1, 2, …, l) into the normalized linguistic decision matrices $\tilde{R}^{\left( k \right)} = \left( {\tilde{R}_{ij}^{\left( k \right)} } \right)_{m \times n}$ (k = 1, 2, …, l) using Eq. (17).

Step 2. Convert the normalized linguistic decision matrices $\tilde{R}^{\left( k \right)} = \left( {\tilde{R}_{ij}^{\left( k \right)} } \right)_{m \times n}$ into the trapezoidal interval type-2 fuzzy decision matrices

$$\tilde{R}^{\left( k \right)} = \left( {\tilde{R}_{ij}^{\left( k \right)} } \right)_{m \times n} = \left( {\left( {\tilde{R}_{ij}^{\left( k \right)} } \right)^{U} ,\,\left( {\tilde{R}_{ij}^{\left( k \right)} } \right)^{L} } \right)_{m \times n} = \left( \begin{array}{ll} \left( {\left( {r_{ij1}^{\left( k \right)} } \right)^{U} ,\quad \left( {r_{ij2}^{\left( k \right)} } \right)^{U} ,\quad \left( {r_{ij3}^{\left( k \right)} } \right)^{U} ,\quad \left( {r_{ij4}^{\left( k \right)} } \right)^{U} ;\quad H_{1} \left( {\left( {\tilde{R}_{ij}^{\left( k \right)} } \right)^{U} } \right),\quad H_{2} \left( {\left( {\tilde{R}_{ij}^{\left( k \right)} } \right)^{U} } \right)} \right), \hfill \\ \left( {\left( {r_{ij1}^{\left( k \right)} } \right)^{L} ,\quad \left( {r_{ij2}^{\left( k \right)} } \right)^{L} ,\quad \left( {r_{ij3}^{\left( k \right)} } \right)^{L} ,\quad \left( {r_{ij4}^{\left( k \right)} } \right)^{L} ;\quad H_{1} \left( {\left( {\tilde{R}_{ij}^{\left( k \right)} } \right)^{L} } \right),\quad H_{2} \left( {\left( {\tilde{R}_{ij}^{\left( k \right)} } \right)^{L} } \right)} \right) \hfill \\ \end{array} \right)_{m \times n} .$$

Convert the weight vector $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{l} } \right)^{\text{T}}$ of decision makers to the trapezoidal interval type-2 fuzzy weight vector $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{l} } \right)^{\text{T}}$, where $\tilde{\omega }_{k} = \left( {\tilde{\omega }_{k}^{U} ,\tilde{\omega }_{k}^{L} } \right) = \left( {\left( {\omega_{k1}^{U} ,\omega_{k2}^{U} ,\omega_{k3}^{U} ,\omega_{k4}^{U} ;H_{1} \left( {\tilde{\omega }_{k}^{U} } \right),H_{2} \left( {\tilde{\omega }_{k}^{U} } \right)} \right),\left( {\omega_{k1}^{L} ,\omega_{k2}^{L} ,\omega_{k3}^{L} ,\omega_{k4}^{L} ;H_{1} \left( {\tilde{\omega }_{k}^{L} } \right),H_{2} \left( {\tilde{\omega }_{k}^{L} } \right)} \right)} \right)$ (k = 1, 2, …, l) is the trapezoidal interval type-2 fuzzy sets.

Convert the weight vector $\tilde{w}^{\left( k \right)} = \left( {\tilde{w}_{1}^{\left( k \right)} ,\tilde{w}_{2}^{\left( k \right)} , \ldots ,\tilde{w}_{n}^{\left( k \right)} } \right)^{\text{T}}$ (k = 1, 2, …, l) of attributes to the trapezoidal interval type-2 fuzzy weight vector $\tilde{w}^{\left( k \right)} = \left( {\tilde{w}_{1}^{\left( k \right)} ,\tilde{w}_{2}^{\left( k \right)} , \ldots ,\tilde{w}_{n}^{\left( k \right)} } \right)^{\text{T}}$ (k = 1, 2, …, l), where

$$\tilde{w}_{j}^{\left( k \right)} = \left( {\left( {\tilde{w}_{j}^{\left( k \right)} } \right)^{U} ,\left( {\tilde{w}_{j}^{\left( k \right)} } \right)^{L} } \right) = \left( \begin{array}{ll} \left( {\left( {w_{j1}^{\left( k \right)} } \right)^{U} ,\quad \left( {w_{j2}^{\left( k \right)} } \right)^{U} ,\quad \left( {w_{j3}^{\left( k \right)} } \right)^{U} ,\quad \left( {w_{j4}^{\left( k \right)} } \right)^{U} ;\quad H_{1} \left( {\left( {\tilde{w}_{j}^{\left( k \right)} } \right)^{U} } \right),\quad H_{2} \left( {\left( {\tilde{w}_{j}^{\left( k \right)} } \right)^{U} } \right)} \right), \hfill \\ \left( {\left( {w_{j1}^{\left( k \right)} } \right)^{L} ,\quad \left( {w_{j2}^{\left( k \right)} } \right)^{L} ,\quad \left( {w_{j3}^{\left( k \right)} } \right)^{L} ,\quad \left( {w_{j4}^{\left( k \right)} } \right)^{L} ;\quad H_{1} \left( {\left( {\tilde{w}_{j}^{\left( k \right)} } \right)^{L} } \right),\quad H_{2} \left( {\left( {\tilde{w}_{j}^{\left( k \right)} } \right)^{L} } \right)} \right) \hfill \\ \end{array}\right)$$

(k = 1, 2, …, l; j = 1, 2, …, n) is the trapezoidal interval type-2 fuzzy set.

Step 3. Utilize the GTIT2FHA operator (Eq. (16)):

$$\begin{aligned} \tilde{R}_{i}^{\left( k \right)} & = {\text{GTIT2FHA}}_{{\tilde{w}^{\left( k \right)} ,\tilde{\varpi},\lambda }} \left( {\tilde{R}_{i1}^{\left( k \right)} ,\tilde{R}_{i2}^{\left( k \right)} , \ldots ,\tilde{R}_{in}^{\left(k \right)} } \right) \\ & = \left( \begin{array}{ll} \left( \begin{array}{ll} \left( {\sum\limits_{j = 1}^{n} {\left( {\varpi_{j1}^{U} \times \left( {n \times \left( {w_{\sigma \left( j \right)1}^{\left( k \right)} } \right)^{U} \times \left( {r_{i\sigma \left( j \right)1}^{\left( k \right)} } \right)^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{j = 1}^{n} {\left( {\varpi_{j2}^{U} \times \left( {n \times \left( {w_{\sigma \left( j \right)2}^{\left( k \right)} } \right)^{U} \times \left( {r_{i\sigma \left( j \right)2}^{\left( k \right)} } \right)^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} , \hfill \\ \left( {\sum\limits_{j = 1}^{n} {\left( {\varpi_{j3}^{U} \times \left( {n \times \left( {w_{\sigma \left( j \right)3}^{\left( k \right)} } \right)^{U} \times \left( {r_{i\sigma \left( j \right)3}^{\left( k \right)} } \right)^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{j = 1}^{n} {\left( {\varpi_{j4}^{U} \times \left( {n \times \left( {w_{\sigma \left( j \right)4}^{\left( k \right)} } \right)^{U} \times \left( {r_{i\sigma \left( j \right)4}^{\left( k \right)} } \right)^{U} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ; \hfill \\ \mathop {\hbox{min} }\limits_{1 \le j \le n} \left\{ {\hbox{min} \left\{ {H_{1} \left( {\tilde{\varpi }_{j}^{U} } \right),\quad \hbox{min} \left\{ {H_{1} \left( {\left( {\tilde{w}_{\sigma \left( j \right)}^{\left( k \right)} } \right)^{U} } \right),\quad H_{1} \left( {\left( {\tilde{R}_{i\sigma \left( j \right)}^{\left( k \right)} } \right)^{U} } \right)} \right\}} \right\}} \right\},\quad \mathop {\hbox{min} }\limits_{1 \le j \le n} \left\{ {\hbox{min} \left\{ {H_{2} \left( {\tilde{\varpi }_{j}^{U} } \right),\quad \hbox{min} \left\{ {H_{2} \left( {\left( {\tilde{w}_{\sigma \left( j \right)}^{\left( k \right)} } \right)^{U} } \right),\quad H_{2} \left( {\left( {\tilde{R}_{i\sigma \left( j \right)}^{\left( k \right)} } \right)^{U} } \right)} \right\}} \right\}} \right\} \hfill \\ \end{array} \right), \hfill \\ \left( \begin{array}{ll} \left( {\sum\limits_{j = 1}^{n} {\left( {\varpi_{j1}^{L} \times \left( {n \times \left( {w_{\sigma \left( j \right)1}^{\left( k \right)} } \right)^{L} \times \left( {r_{i\sigma \left( j \right)1}^{\left( k \right)} } \right)^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{j = 1}^{n} {\left( {\varpi_{j2}^{L} \times \left( {n \times \left( {w_{\sigma \left( j \right)2}^{\left( k \right)} } \right)^{L} \times \left( {r_{i\sigma \left( j \right)2}^{\left( k \right)} } \right)^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} , \hfill \\ \left( {\sum\limits_{j = 1}^{n} {\left( {\varpi_{j3}^{L} \times \left( {n \times \left( {w_{\sigma \left( j \right)3}^{\left( k \right)} } \right)^{L} \times \left( {r_{i\sigma \left( j \right)3}^{\left( k \right)} } \right)^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\quad \left( {\sum\limits_{j = 1}^{n} {\left( {\varpi_{j4}^{L} \times \left( {n \times \left( {w_{\sigma \left( j \right)4}^{\left( k \right)} } \right)^{L} \times \left( {r_{i\sigma \left( j \right)4}^{\left( k \right)} } \right)^{L} } \right)^{\lambda } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ; \hfill \\ \mathop {\hbox{min} }\limits_{1 \le j \le n} \left\{ {\hbox{min} \left\{ {H_{1} \left( {\tilde{\varpi }_{j}^{L} } \right),\quad \hbox{min} \left\{ {H_{1} \left( {\left( {\tilde{w}_{\sigma \left( j \right)}^{\left( k \right)} } \right)^{L} } \right),\quad H_{1} \left( {\left( {\tilde{R}_{i\sigma \left( j \right)}^{\left( k \right)} } \right)^{L} } \right)} \right\}} \right\}} \right\},\quad \mathop {\hbox{min} }\limits_{1 \le j \le n} \left\{ {\hbox{min} \left\{ {H_{2} \left( {\tilde{\varpi }_{j}^{L} } \right),\quad \hbox{min} \left\{ {H_{2} \left( {\left( {\tilde{w}_{\sigma \left( j \right)}^{\left( k \right)} } \right)^{L} } \right),\quad H_{2} \left( {\left( {\tilde{R}_{i\sigma \left( j \right)}^{\left( k \right)} } \right)^{L} } \right)} \right\}} \right\}} \right\} \hfill \\ \end{array} \right) \hfill \\ \end{array} \right) \\ i & = 1, 2, \ldots , m,\quad k = 1, 2, \ldots , l. \\ \end{aligned}$$

(18)

to aggregate the attribute values $\left( {\tilde{R}_{i1}^{\left( k \right)} ,\tilde{R}_{i2}^{\left( k \right)} , \ldots ,\tilde{R}_{in}^{\left( k \right)} } \right)$ in the ith line of $\tilde{R}^{\left( k \right)}$, and then get the comprehensive attribute value

$$\tilde{R}_{i}^{\left( k \right)} = \left( {\left( {\tilde{R}_{i}^{\left( k \right)} } \right)^{U} ,\,\left( {\tilde{R}_{i}^{\left( k \right)} } \right)^{L} } \right) = \left( \begin{aligned} \left( {\left( {r_{i1}^{\left( k \right)} } \right)^{U} ,\quad \left( {r_{i2}^{\left( k \right)} } \right)^{U} ,\quad \left( {r_{i3}^{\left( k \right)} } \right)^{U} ,\quad \left( {r_{i4}^{\left( k \right)} } \right)^{U} ;\quad H_{1} \left( {\left( {\tilde{R}_{i}^{\left( k \right)} } \right)^{U} } \right),\quad H_{2} \left( {\left( {\tilde{R}_{i}^{\left( k \right)} } \right)^{U} } \right)} \right), \hfill \\ \left( {\left( {r_{i1}^{\left( k \right)} } \right)^{L} ,\quad \left( {r_{i2}^{\left( k \right)} } \right)^{L} ,\quad \left( {r_{i3}^{\left( k \right)} } \right)^{L} ,\quad \left( {r_{i4}^{\left( k \right)} } \right)^{L} ;\quad H_{1} \left( {\left( {\tilde{R}_{i}^{\left( k \right)} } \right)^{L} } \right),\quad H_{2} \left( {\left( {\tilde{R}_{i}^{\left( k \right)} } \right)^{L} } \right)} \right) \hfill \\ \end{aligned} \right)$$

of the alternative x _i (corresponding to d _k  ∊ D), where λ ∊ (0, + ∞), $\tilde{w}^{\left( k \right)} = \left( {\tilde{w}_{1}^{\left( k \right)} ,\tilde{w}_{2}^{\left( k \right)} , \ldots ,\tilde{w}_{n}^{\left( k \right)} } \right)^{\text{T}}$ is the weight vector of attributes provided by d _k  ∊ D, and $\tilde{\varpi } = \left( {\tilde{\varpi }_{1} ,\tilde{\varpi }_{2} , \ldots ,\tilde{\varpi }_{n} } \right)^{\text{T}}$ is the associated weighting vector of the GTIT2FHA operator with

$$\tilde{\varpi }_{j} = \left( {\tilde{\varpi }_{j}^{U} ,\tilde{\varpi }_{j}^{L} } \right) = \left( {\left( {\varpi_{j1}^{U} ,\varpi_{j2}^{U} ,\varpi_{j3}^{U} ,\varpi_{j4}^{U} ;H_{1} \left( {\tilde{\varpi }_{j}^{U} } \right),\quad H_{2} \left( {\tilde{\varpi }_{j}^{U} } \right)} \right),\,\left( {\varpi_{j1}^{L} ,\varpi_{j2}^{L} ,\varpi_{j3}^{L} ,\varpi_{j4}^{L} ;\,H_{1} \left( {\tilde{\varpi }_{j}^{L} } \right),\quad H_{2} \left( {\tilde{\varpi }_{j}^{L} } \right)} \right)} \right)\quad (j = 1, 2, \ldots , n).$$

Step 4. Utilize the GTIT2FWA operator (Eq. (3)):

$$\begin{aligned} \tilde{R}_{i} & ={\text{GTIT2FWA}}_{{\tilde{\omega },\lambda }} \left( {\tilde{R}_{i}^{\left( 1 \right)} ,\tilde{R}_{i}^{\left( 2 \right)} , \ldots ,\tilde{R}_{i}^{\left( l \right)} } \right) \\ & = \left( {\begin{array}{l} {\left( {\begin{array}{l} {\left( {\sum\limits_{k = 1}^{l} {\left( {\omega_{k1}^{U} \times \left( {\left( {r_{i1}^{\left( k \right)} } \right)^{U} } \right)^{\lambda } } \right)} } \right)^{{^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \lambda }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\lambda $}}}} }} ,\quad \left( {\sum\limits_{k = 1}^{l} {\left( {\omega_{k2}^{U} \times \left( {\left( {r_{i2}^{\left( k \right)} } \right)^{U} } \right)^{\lambda } } \right)} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \lambda }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\lambda $}}}} ,\quad \left( {\sum\limits_{k = 1}^{l} {\left( {\omega_{k3}^{U} \times \left( {\left( {r_{i3}^{\left( k \right)} } \right)^{U} } \right)^{\lambda } } \right)} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \lambda }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\lambda $}}}} ,\quad \left( {\sum\limits_{k = 1}^{l} {\left( {\omega_{k4}^{U} \times \left( {\left( {r_{i4}^{\left( k \right)} } \right)^{U} } \right)^{\lambda } } \right)} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \lambda }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\lambda $}}}} ;} \\ {\mathop {\hbox{min} }\limits_{1 \le k \le k} \left\{ {\hbox{min} \left\{ {H_{1} \left( {\tilde{\omega }_{k}^{U} } \right),\quad H_{1} \left( {\left( {\tilde{R}_{i}^{\left( k \right)} } \right)^{U} } \right)} \right\}} \right\},\quad \mathop {\hbox{min} }\limits_{1 \le k \le k} \left\{ {\hbox{min} \left\{ {H_{2} \left( {\tilde{\omega }_{k}^{U} } \right),\quad H_{2} \left( {\left( {\tilde{R}_{i}^{\left( k \right)} } \right)^{U} } \right)} \right\}} \right\}} \\ \end{array} } \right),} \\ {\left( {\begin{array}{l} {\left( {\sum\limits_{k = 1}^{l} {\left( {\omega_{k1}^{L} \times \left( {\left( {r_{i1}^{\left( k \right)} } \right)^{L} } \right)^{\lambda } } \right)} } \right)^{{^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \lambda }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\lambda $}}}} }} ,\quad \left( {\sum\limits_{k = 1}^{l} {\left( {\omega_{k2}^{L} \times \left( {\left( {r_{i2}^{\left( k \right)} } \right)^{L} } \right)^{\lambda } } \right)} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \lambda }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\lambda $}}}} ,\quad \left( {\sum\limits_{k = 1}^{l} {\left( {\omega_{k3}^{L} \times \left( {\left({r_{i3}^{\left( k \right)} } \right)^{L} } \right)^{\lambda } } \right)} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \lambda }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\lambda $}}}} ,\quad \left( {\sum\limits_{k = 1}^{l} {\left( {\omega_{k4}^{L} \times \left( {\left( {r_{i4}^{\left( k \right)} } \right)^{L} } \right)^{\lambda } } \right)} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \lambda }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\lambda $}}}} ;} \\ {\mathop {\hbox{min} }\limits_{1 \le k \le k} \left\{ {\hbox{min} \left\{ {H_{1} \left( {\tilde{\omega }_{k}^{L} } \right),\quad H_{1} \left( {\left( {\tilde{R}_{i}^{\left( k \right)} } \right)^{L} } \right)} \right\}} \right\},\quad \mathop {\hbox{min} }\limits_{1 \le k \le k} \left\{ {\hbox{min} \left\{ {H_{2} \left( {\tilde{\omega }_{k}^{L} } \right),\quad H_{2} \left( {\left( {\tilde{R}_{i}^{\left( k \right)}} \right)^{L} } \right)} \right\}} \right\}} \\ \end{array} } \right)} \\ \end{array} } \right) \\ \end{aligned}$$

(19)

to aggregate $\tilde{R}_{i}^{\left( k \right)}$ (k = 1, 2, …, l) corresponding to the alternative x _i , and then get the collective value

$$\tilde{R}_{i} = \left( {\tilde{R}_{i}^{U} ,\tilde{R}_{i}^{L} } \right) = \left( \begin{aligned} \left( {r_{i1}^{U} ,\quad r_{i2}^{U} ,\quad r_{i3}^{U} ,\quad r_{i4}^{U} ;\quad H_{1} \left( {\tilde{R}_{i}^{U} } \right),\quad H_{2} \left( {\tilde{R}_{i}^{U} } \right)} \right), \hfill \\ \left( {r_{i1}^{L} ,\quad r_{i2}^{L} ,\quad r_{i3}^{L} ,\quad r_{i4}^{L} ;\quad H_{1} \left( {\tilde{R}_{i}^{L} } \right),\quad H_{2} \left( {\tilde{R}_{i}^{L} } \right)} \right) \hfill \\ \end{aligned} \right)$$

of the alternative x _i , where λ ∊ (0, + ∞), and $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{l} } \right)^{\text{T}}$ is the weight vector of decision makers with $\tilde{\omega }_{k} = \left( {\tilde{\omega }_{k}^{U} ,\tilde{\omega }_{k}^{L} } \right) = \left( {\left( {\omega_{k1}^{U} ,\quad \omega_{k2}^{U} ,\quad \omega_{k3}^{U} ,\quad \omega_{k4}^{U} ;\quad H_{1} \left( {\tilde{\omega }_{k}^{U} } \right),\quad H_{2} \left( {\tilde{\omega }_{k}^{U} } \right)} \right),\quad \left( {\omega_{k1}^{L} ,\quad \omega_{k2}^{L} ,\quad \omega_{k3}^{L} ,\quad \omega_{k4}^{L} ;\quad H_{1} \left( {\tilde{\omega }_{k}^{L} } \right),\quad H_{2} \left( {\tilde{\omega }_{k}^{L} } \right)} \right)} \right)$ (k = 1, 2, …, l).

Step 5. Calculate the ranking value ${\text{RV}}\left( {\tilde{R}_{i} } \right)$ (i = 1, 2, …, m) of the collective value $\tilde{R}_{i}$ (i = 1, 2, …, m) using the following formula given by Chen et al. [57] :

$$\begin{aligned} {\text{RV}}\left( {\tilde{R}_{i} } \right) & = \left[ {\frac{{\left[ {r_{i1}^{U} + r_{i4}^{U} } \right]}}{2} + \frac{{\left( {H_{1} \left( {\tilde{R}_{i}^{U} } \right) + H_{2} \left( {\tilde{R}_{i}^{U} } \right) + H_{1} \left( {\tilde{R}_{i}^{L} } \right) + H_{2} \left( {\tilde{R}_{i}^{L} } \right)} \right)}}{4}} \right] \\ {\kern 1pt} & \quad \times \frac{{\left[ {r_{i1}^{U} + r_{i2}^{U} + r_{i3}^{U} + r_{i4}^{U} + r_{i1}^{L} + r_{i2}^{L} + r_{i3}^{L} + r_{i4}^{L} } \right]}}{8} \\ \end{aligned}$$

(20)

and then rank all of the collective value $\tilde{R}_{i}$ (i = 1, 2, …, m) using the comparison laws defined by Chen et al. [57].

Step 6. Rank all the alternatives x _i (i = 1, 2, …, m) and then select the best alternative(s) according to $\tilde{R}_{i}$ (i = 1, 2, …, m). The larger $\tilde{R}_{i}$ is the better the alternatives x _i (i = 1, 2, …, m) will be.

Step 7. End.

5 Illustrative example

In this section, we use an example from [2, 54] to illustrate the proposed methods.

Example 5.1

Assume that the problem discussed here is concerned with a manufacturing company, searching the best global supplier for one of its most critical parts used in assembling process (adapted from [2, 54]). There are three potential global suppliers x _i (i = 1, 2, 3) to be evaluated with four attributes: (1) c ₁: quality of the product, (2) c ₂: risk factor, (3) c ₃: service performance of supplier, and (4) c ₄: supplier’s profile. Assume that the three decision makers d ₁, d ₂, and d ₃ use the linguistic terms shown in Table 1 to represent the weights of the four attributes, respectively, as shown in Table 3. Assume that the weight vector of decision makers is $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} ,\tilde{\omega }_{3} } \right)^{\text{T}} = \left( {H,{\text{ML}},{\text{VH}}} \right)^{\text{T}}$. Assume that the three decision makers d ₁, d ₂, and d ₃ use the linguistic terms shown in Table 1 to represent the characteristics of the potential global suppliers x _i (i = 1, 2, 3) with respect to different attributes c _j (j = 1, 2, 3, 4), respectively, as shown in Tables 4, 5 and 6.

Table 3 Weights of the attributes evaluated by the decision makers

Table 4 The linguistic decision matrix $\tilde{A}^{\left( 1 \right)}$ provided by the decision maker d ₁

Table 5 The linguistic decision matrix $\tilde{A}^{\left( 2 \right)}$ provided by the decision maker d ₂

Table 6 The linguistic decision matrix $\tilde{A}^{\left( 3 \right)}$ provided by the decision maker d ₃

Step 1. Among four attributes, c ₂ is the cost attribute, and c _j (j = 1, 3, 4) are the benefit attributes. Therefore, based on Tables 1 and 2, the weight vectors of the four attributes can be transformed into the normalized weight vectors, as shown in Table 7. Linguistic decision matrices $\tilde{A}^{\left( k \right)} = \left( {\tilde{A}_{ij}^{\left( k \right)} } \right)_{3 \times 4}$ (k = 1, 2, 3) can be transformed into the normalized linguistic decision matrices $\tilde{R}^{\left( k \right)} = \left( {\tilde{R}_{ij}^{\left( k \right)} } \right)_{3 \times 4}$ (k = 1, 2, 3), as shown in Tables 8, 9 and 10.

Table 7 The normalized weights of the attributes evaluated by the decision makers

Table 8 The normalized linguistic decision matrix $\tilde{R}^{\left( 1 \right)}$ provided by the decision maker d ₁

Table 9 The normalized linguistic decision matrix $\tilde{R}^{\left( 2 \right)}$ provided by the decision maker d ₂

Table 10 The normalized linguistic decision matrix $\tilde{R}^{\left( 3 \right)}$ provided by the decision maker d ₃

Step 2. Convert the weight vector $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} ,\tilde{\omega }_{3} } \right)^{\text{T}} = \left( {H,{\text{ML}},{\text{VH}}} \right)^{\text{T}}$ of decision makers to the trapezoidal interval type-2 fuzzy weight vector

$$\tilde{\omega } = \left( {\text{H,ML,VH}} \right)^{\text{T}} = \left( \begin{array}{l} \left( {\left( { 0. 6 5 , { 0} . 7 5 , { 0} . 8 5 , { 0} . 9 5 ; { 1, 1}} \right) ,\quad \left( { 0. 7 , { 0} . 8 , { 0} . 8 , { 0} . 9 ; { 0} . 8 , 0. 8} \right)} \right) ,\hfill \\ \left( {\left( { 0. 2 , { 0} . 3 , { 0} . 4 , { 0} . 5 ; { 1, 1}} \right) ,\quad \left( { 0. 2 5 , { 0} . 3 5 , { 0} . 3 5 , { 0} . 4 5 ; { 0} . 8 , { 0} . 8} \right)} \right) ,\hfill \\ \left( {\left( { 0. 8 , { 0} . 9 , { 1, 1; 1, 1}} \right) ,\quad \left( { 0. 8 5 , { 0} . 9 5 , { 1, 1; 1, 1}} \right)} \right) \hfill \\ \end{array} \right)^{\text{T}}$$

Convert the weight vectors $\tilde{w}^{\left( k \right)} = \left( {\tilde{w}_{1}^{\left( k \right)} ,\tilde{w}_{2}^{\left( k \right)} ,\tilde{w}_{3}^{\left( k \right)} ,\tilde{w}_{4}^{\left( k \right)} } \right)^{\text{T}}$ (k = 1, 2, 3) of the attributes to the trapezoidal interval type-2 fuzzy weight vectors $\tilde{w}^{\left( k \right)} = \left( {\tilde{w}_{1}^{\left( k \right)} ,\tilde{w}_{2}^{\left( k \right)} ,\tilde{w}_{3}^{\left( k \right)} ,\tilde{w}_{4}^{\left( k \right)} } \right)^{\text{T}}$ (k = 1, 2, 3), as shown in Table 11. Convert the normalized linguistic decision matrices $\tilde{R}^{\left( k \right)}$ (k = 1, 2, 3) into the trapezoidal interval type-2 fuzzy decision matrices $\tilde{R}^{\left( k \right)}$ (k = 1, 2, 3), as shown in Tables 12, 13 and 14.

Table 11 The trapezoidal interval type-2 fuzzy weight vectors of the attributes

Table 12 The trapezoidal interval type-2 fuzzy decision matrix $\tilde{R}^{\left( 1 \right)}$

Table 13 The trapezoidal interval type-2 fuzzy decision matrix $\tilde{R}^{\left( 2 \right)}$

Table 14 The trapezoidal interval type-2 fuzzy decision matrix $\tilde{R}^{\left( 3 \right)}$

Step 3. Let λ = 2. Utilize the GTIT2FHA operator (Eq. (18)) (whose associated weighting vector is

$$\tilde{\varpi } = \left( {H , {\text{VH,}}M ,{\text{MH}}}\right)^{\text{T}} = \left( \begin{array}{l} \left({\left( { 0. 6 5, { 0} . 7 5 , { 0} . 8 5 , { 0} . 9 5 ; { 1, 1}}\right) ,\quad \left( { 0. 7 , { 0} . 8 , { 0} . 8 , { 0} . 9 ; { 0}. 8 , 0. 8} \right)} \right), \hfill \\ \left( {\left( { 0. 8 , { 0}. 9 , { 1, 1; 1, 1}} \right) ,\quad \left( { 0. 8 5 , { 0} . 9 5 , {1, 1; 1, 1}} \right)} \right) ,\hfill \\ \left( {\left( { 0. 3 5 , {0} . 4 5 , { 0} . 5 5 , { 0} . 6 5 ; { 1, 1}} \right) ,\quad \left({ 0. 4 , { 0} . 5 , { 0} . 5 , { 0} . 6 ; { 0} . 8 , { 0} . 8}\right)} \right) ,\hfill \\ \left( {\left( { 0. 5 , { 0} . 6 , { 0}. 7 , { 0} . 8 ; { 1, 1}} \right) ,\quad \left( { 0. 5 5 , { 0} . 65 , { 0} . 6 5 , { 0} . 7 5 ; { 0} . 8 , { 0} . 8} \right)} \right)\hfill \\ \end{array}\right)^{\text{T}}\left.\right)$$

to aggregate the attribute values $\left( {\tilde{R}_{i1}^{\left( k \right)} ,\tilde{R}_{i2}^{\left( k \right)} ,\tilde{R}_{i3}^{\left( k \right)} ,\tilde{R}_{i4}^{\left( k \right)} } \right)$ in the ith line of $\tilde{R}^{\left( k \right)}$, and then get the comprehensive attribute value $\tilde{R}_{i}^{\left( k \right)}$ of the alternative x _i . We obtain the aggregation results shown in Table 15.

Table 15 The comprehensive attribute value $\tilde{R}_{i}^{\left( k \right)}$

Step 4. Let λ = 2. Utilize the GTIT2FWA operator (Eq. (19)) to aggregate $\tilde{R}_{i}^{\left( k \right)}$ (k = 1, 2, 3) corresponding to the alternative x _i , and then get the collective value $\tilde{R}_{i}$ of the alternative x _i :

$$\begin{aligned} \tilde{R}_{1} & = \left( {\left( {2.4660, \,3.9113, \, 5.8483, \, 7.5904; \, 1, \, 1} \right),\quad\quad \left( {3.1319, \, 4.8135, \, 5.0791, \, 6.6842; \, 0.8, \, 0.8} \right)} \right), \\ \tilde{R}_{2} & = \left( {\left( {3.1969, \, 4.8791, \, 7.0742, \, 8.5633; \, 1, \, 1} \right),\quad\quad \left( {3.9789, \, 5.9066, \, 6.3985, \, 7.7938; \, 0.8, \, 0.8} \right)} \right), \\ \tilde{R}_{3} & = \left( {\left( {2.4075, \, 3.8758, \, 5.8442, \, 7.6145; \, 1, \, 1} \right),\quad\quad \left( {3.0847, \, 4.7902, \, 5.0696, \, 6.6908; \, 0.8, \, 0.8} \right)} \right). \\ \end{aligned}$$

Step 5. Utilize Eq. (20) to calculate the ranking value $RV\left( {\tilde{R}_{i} } \right)$ (i = 1, 2, 3) of the collective value $\tilde{R}_{i}$ (i = 1, 2, 3):

$${\text{RV}}\left( {\tilde{R}_{1} } \right) = 29.2886,\quad {\text{RV}}\left( {\tilde{R}_{2} } \right) = 40.5039,\quad {\text{RV}}\left( {\tilde{R}_{3} } \right) = 29.0950,$$

and then rank all of the collective value $\tilde{R}_{i}$ (i = 1, 2, 3) as follows:

$$\tilde{R}_{2} > \tilde{R}_{1} > \tilde{R}_{3} .$$

Step 6. Rank all the alternatives x _i (i = 1, 2, 3) as follows:

x ₂ ≻ x ₁ ≻ x ₃.

Thus, the most desirable global supplier is x ₂.

When we change the parameter λ, we can obtain different results (see Table 16). The decision makers can choose values of λ according to their preferences.

Table 16 The ranking values $RV\left( {\tilde{R}_{i} } \right)$ and the rankings of alternatives

6 Conclusions

In this paper, we have developed several trapezoidal interval type-2 fuzzy aggregation operators, such as the TIT2FWA, GTIT2FWA, TIT2FOWA, GTIT2FOWA, TIT2FHA, and GTIT2FHA operators. We have studied some basic properties of the developed operators, including commutativity, idempotency, boundedness, and monotonicity. Furthermore, we have utilized the proposed operators to develop an approach to multiple attribute group decision making with linguistic information. Finally, a numerical example is provided to illustrate the developed approach.

In the current study, some basic properties of the TIT2FHA and GTIT2FHA operators do not be investigated in detail. In addition, the develop operators are a weighted-average aggregation tool, and they are unsuitable to deal with the arguments taking the forms of multiplicative preference information. In the future, we will pay attention to addressing these problems. We will examine some desirable properties of the TIT2FHA and GTIT2FHA operators, and develop some new geometric aggregation operators, including the trapezoidal interval type-2 fuzzy weighted geometric (TIT2FWG) operator, the generalized trapezoidal interval type-2 fuzzy weighted geometric (GTIT2FWG) operator, the trapezoidal interval type-2 fuzzy ordered weighted geometric (TIT2FOWG) operator, the generalized trapezoidal interval type-2 fuzzy ordered weighted geometric (GTIT2FOWG) operator, the trapezoidal interval type-2 fuzzy hybrid geometric (TIT2FHG) operator, and the generalized trapezoidal interval type-2 fuzzy hybrid geometric (GTIT2FHG) operator, and apply them to group decision making based on multiplicative preference information.

Appendices

Appendix 1: type-2 fuzzy sets

A type-2 fuzzy set $\tilde{A}$ in the universe of discourse X can be represented by a type-2 membership function $\mu_{{\tilde{A}}}$, shown as follows [20, 21, 56]:

$$\tilde{A} = \left\{ {\left( {\left( {x,u} \right),\mu_{{\tilde{A}}} \left( {x,u} \right)} \right)\left| {\forall x \in X,\quad \forall u \in J_{x} \subseteq \left[ {0,1} \right]} \right.} \right\},$$

where $0 \le \mu_{{\tilde{A}}} \left( {x,u} \right) \le 1$. The type-2 fuzzy set $\tilde{A}$ also can be represented as follows:

$$\tilde{A} = \int_{x \in X} {\int_{{u \in J_{x} }} {{{\mu_{{\tilde{A}}} \left( {x,u} \right)} \mathord{\left/ {\vphantom {{\mu_{{\tilde{A}}} \left( {x,u} \right)} {\left( {x,u} \right)}}} \right. \kern-0pt} {\left( {x,u} \right)}}} } = \int_{x \in X} {{{\left[ {\int_{{u \in J_{x} }} {{{\mu_{{\tilde{A}}} \left( {x,u} \right)} \mathord{\left/ {\vphantom {{\mu_{{\tilde{A}}} \left( {x,u} \right)} u}} \right. \kern-0pt} u}} } \right]} \mathord{\left/ {\vphantom {{\left[ {\int_{{u \in J_{x} }} {{{\mu_{{\tilde{A}}} \left( {x,u} \right)} \mathord{\left/ {\vphantom {{\mu_{{\tilde{A}}} \left( {x,u} \right)} u}} \right. \kern-0pt} u}} } \right]} x}} \right. \kern-0pt} x}} ,$$

where x is the primary variable, J _x  ⊆ [0, 1] is the primary membership of x, u is the secondary variable, and $\int_{{u \in J_{x} }} {{{\mu_{{\tilde{A}}} \left( {x,u} \right)} \mathord{\left/ {\vphantom {{\mu_{{\tilde{A}}} \left( {x,u} \right)} u}} \right. \kern-0pt} u}}$ is the secondary membership function (MF) at x. ∫ denotes union among all admissible x and u. For discrete universe of discourse, ∫ is replaced by Σ.

Let $\tilde{A}$ be a type-2 fuzzy set in the universe of discourse X represented by the type-2 membership function $\mu_{{\tilde{A}}} \left( {x,u} \right)$. If all $\mu_{{\tilde{A}}} \left( {x,u} \right) = 1$, then $\tilde{A}$ is called an interval type-2 fuzzy set. An interval type-2 fuzzy set $\tilde{A}$ can be regarded as a special case of a type-2 fuzzy set, shown as follows [21]:

$$\tilde{A} = \int_{x \in X} {\int_{{u \in J_{x} }} {{1 \mathord{\left/ {\vphantom {1 {\left( {x,u} \right)}}} \right. \kern-0pt} {\left( {x,u} \right)}}} } = \int_{x \in X} {{{\left[ {\int_{{u \in J_{x} }} {{1 \mathord{\left/ {\vphantom {1 u}} \right. \kern-0pt} u}} } \right]} \mathord{\left/ {\vphantom {{\left[ {\int_{{u \in J_{x} }} {{1 \mathord{\left/ {\vphantom {1 u}} \right. \kern-0pt} u}} } \right]} x}} \right. \kern-0pt} x}} ,$$

where x is the primary variable, J _x  ⊆ [0, 1] is the primary membership of x, u is the secondary variable, and $\int_{{u \in J_{x} }} {{1 \mathord{\left/ {\vphantom {1 u}} \right. \kern-0pt} u}}$ is the secondary membership function (MF) at x.

Uncertainty about an interval type-2 fuzzy set $\tilde{A}$ is conveyed by the union of all of the primary memberships, which is called the footprint of uncertainty (FOU) of $\tilde{A}$, i.e.,

$${\text{FOU}}\left( {\tilde{A}} \right) = \bigcup\nolimits_{x \in X} {J_{x} }$$

The upper membership function and lower membership function of $\tilde{A}$ are two type-1 membership functions that bound the FOU. The upper membership function is associated with the upper bound of ${\text{FOU}}\left( {\tilde{A}} \right)$ and is denoted by $\tilde{A}^{U}$, and the lower membership function is associated with the lower bound of ${\text{FOU}}\left( {\tilde{A}} \right)$ and is denoted by $\tilde{A}^{L}$.

Let $\tilde{A}$ be a trapezoidal type-1 fuzzy set, $\tilde{A} = \left( {a_{1} ,a_{2} ,a_{3} ,a_{4} ;H_{1} \left( {\tilde{A}} \right),H_{2} \left( {\tilde{A}} \right)} \right)$, as shown in Fig. 3, where $H_{1} \left( {\tilde{A}} \right)$ denotes the membership value of the element a ₂, $H_{2} \left( {\tilde{A}} \right)$ denotes the membership value of the element a ₃, $0 \le H_{1} \left( {\tilde{A}} \right) \le 1$ and $0 \le H_{2} \left( {\tilde{A}} \right) \le 1$. If a ₂ = a ₃, then the trapezoidal type-1 fuzzy set $\tilde{A}$ becomes a triangular type-1 fuzzy set.

Fig. 3

A trapezoidal type-1 fuzzy set

Appendix 2: some operational laws and comparison law

The operation between the trapezoidal interval type-2 fuzzy sets $\tilde{A}_{1} = \left( {\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} } \right) = \left( {\left( {a_{11}^{U} ,a_{12}^{U} ,a_{13}^{U} ,a_{14}^{U} ;H_{1} \left( {\tilde{A}_{1}^{U} } \right),H_{2} \left( {\tilde{A}_{1}^{U} } \right)} \right),\quad \left( {a_{11}^{L} ,a_{12}^{L} ,a_{13}^{L} ,a_{14}^{L} ;H_{1} \left( {\tilde{A}_{1}^{L} } \right),H_{2} \left( {\tilde{A}_{1}^{L} } \right)} \right)} \right)$ and $\tilde{A}_{2} = \left( {\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} } \right) = \left( {\left( {a_{21}^{U} ,a_{22}^{U} ,a_{23}^{U} ,a_{24}^{U} ;H_{1} \left( {\tilde{A}_{2}^{U} } \right),H_{2} \left( {\tilde{A}_{2}^{U} } \right)} \right),\quad \left( {a_{21}^{L} ,a_{22}^{L} ,a_{23}^{L} ,a_{24}^{L} ;H_{1} \left( {\tilde{A}_{2}^{L} } \right),H_{2} \left( {\tilde{A}_{2}^{L} } \right)} \right)} \right)$ is defined as follows [1, 18, 19]:

1.

$$\begin{aligned} \tilde{A}_{1} \oplus \tilde{A}_{2} & = \left( {\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} } \right) \oplus \left( {\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} } \right) \\ & = \left( \begin{array}{l} \left( {a_{11}^{U} + a_{21}^{U} ,a_{12}^{U} + a_{22}^{U} ,a_{13}^{U} + a_{23}^{U} ,a_{14}^{U} + a_{24}^{U} ;\, \hbox{min} \left\{ {H_{1} \left( {\tilde{A}_{1}^{U} } \right),H_{1} \left( {\tilde{A}_{2}^{U} } \right)} \right\},\,\hbox{min} \left\{ {H_{2} \left( {\tilde{A}_{1}^{U} } \right),H_{2} \left( {\tilde{A}_{2}^{U} } \right)} \right\}} \right), \hfill \\ \left( {a_{11}^{L} + a_{21}^{L} ,a_{12}^{L} + a_{22}^{L} ,a_{13}^{L} + a_{23}^{L} ,a_{14}^{L} + a_{24}^{L} ;\,\hbox{min} \left\{ {H_{1} \left( {\tilde{A}_{1}^{L} } \right),H_{1} \left( {\tilde{A}_{2}^{L} } \right)} \right\},\,\hbox{min} \left\{ {H_{2} \left( {\tilde{A}_{1}^{L} } \right),H_{2} \left( {\tilde{A}_{2}^{L} } \right)} \right\}} \right) \hfill \\ \end{array}\right) \\ \end{aligned}$$

2.

$$\begin{aligned} \tilde{A}_{1} \otimes \tilde{A}_{2} & = \left( {\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} } \right) \otimes \left( {\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} } \right) \\ {\kern 1pt} & = \left( \begin{array}{l} \left( {a_{11}^{U} \times a_{21}^{U} ,a_{12}^{U} \times a_{22}^{U} ,a_{13}^{U} \times a_{23}^{U} ,a_{14}^{U} \times a_{24}^{U} ;\, \hbox{min} \left\{ {H_{1} \left( {\tilde{A}_{1}^{U} } \right),H_{1} \left( {\tilde{A}_{2}^{U} } \right)} \right\},\, \hbox{min} \left\{ {H_{2} \left( {\tilde{A}_{1}^{U} } \right),H_{2} \left( {\tilde{A}_{2}^{U} } \right)} \right\}} \right), \hfill \\ \left( {a_{11}^{L} \times a_{21}^{L} ,a_{12}^{L} \times a_{22}^{L} ,a_{13}^{L} \times a_{23}^{L} ,a_{14}^{L} \times a_{24}^{L} ;\, \hbox{min} \left\{ {H_{1} \left( {\tilde{A}_{1}^{L} } \right),H_{1} \left( {\tilde{A}_{2}^{L} } \right)} \right\},\, \hbox{min} \left\{ {H_{2} \left( {\tilde{A}_{1}^{L} } \right),H_{2} \left( {\tilde{A}_{2}^{L} } \right)} \right\}} \right) \hfill \\ \end{array}\right) \\ \end{aligned}$$

3.

$$k\tilde{A}_{1} = \left( {k\tilde{A}_{1}^{U} ,k\tilde{A}_{1}^{L} } \right) = \left( \begin{aligned} \left( {k \times a_{11}^{U} ,k \times a_{12}^{U} ,k \times a_{13}^{U} ,k \times a_{14}^{U} ;\,H_{1} \left( {\tilde{A}_{1}^{U} } \right),H_{2} \left( {\tilde{A}_{2}^{U} } \right)} \right), \hfill \\ \left( {k \times a_{11}^{L} ,k \times a_{12}^{L} ,k \times a_{13}^{L} ,k \times a_{14}^{L} ;\,H_{1} \left( {\tilde{A}_{1}^{L} } \right),H_{2} \left( {\tilde{A}_{2}^{L} } \right)} \right) \hfill \\ \end{aligned} \right),\quad {\text{where}}\quad k > 0$$

4.

$$\tilde{A}_{1}^{k} = \left( {\left( {\tilde{A}_{1}^{U} } \right)^{k} ,\left( {\tilde{A}_{1}^{L} } \right)^{k} } \right) = \left( \begin{aligned} \left( {\left( {a_{11}^{U} } \right)^{k} ,\left( {a_{12}^{U} } \right)^{k} ,\left( {a_{13}^{U} } \right)^{k} ,\left( {a_{14}^{U} } \right)^{k} ;\,H_{1} \left( {\tilde{A}_{1}^{U} } \right),H_{2} \left( {\tilde{A}_{1}^{U} } \right)} \right), \hfill \\ \left( {\left( {a_{11}^{L} } \right)^{k} ,\left( {a_{12}^{L} } \right)^{k} ,\left( {a_{13}^{L} } \right)^{k} ,\left( {a_{14}^{L} } \right)^{k} ;\,H_{1} \left( {\tilde{A}_{1}^{L} } \right),H_{2} \left( {\tilde{A}_{1}^{L} } \right)} \right) \hfill \\ \end{aligned} \right),\quad {\text{where}}\quad k > 0$$

Let $\tilde{A} = \left( {\tilde{A}^{U} ,\tilde{A}^{L} } \right) = \left( {\left( {a_{1}^{U} ,a_{2}^{U} ,a_{3}^{U} ,a_{4}^{U} ;H_{1} \left( {\tilde{A}^{U} } \right),H_{2} \left( {\tilde{A}^{U} } \right)} \right),\left( {a_{1}^{L} ,a_{2}^{L} ,a_{3}^{L} ,a_{4}^{L} ;H_{1} \left( {\tilde{A}^{L} } \right),H_{2} \left( {\tilde{A}^{L} } \right)} \right)} \right)$ be a trapezoidal interval type-2 fuzzy set. Chen et al. [57] defined the ranking value $RV\left( {\tilde{A}} \right)$ of $\tilde{A}$ as follows:

$$\begin{aligned} {\text{RV}}\left( {\tilde{A}} \right) & = \left[ {\frac{{\left[ {\left( {a_{1}^{U} + K} \right) + \left( {a_{4}^{U} + K} \right)} \right]}}{2} + \frac{{\left( {H_{1} \left( {\tilde{A}^{U} } \right) + H_{2} \left( {\tilde{A}^{U} } \right) + H_{1} \left( {\tilde{A}^{L} } \right) + H_{2} \left( {\tilde{A}^{L} } \right)} \right)}}{4}} \right] \\ & \quad \times \frac{{\left[ {\left( {a_{1}^{U} + K} \right) + \left( {a_{2}^{U} + K} \right) + \left( {a_{3}^{U} + K} \right) + \left( {a_{4}^{U} + K} \right) + \left( {a_{1}^{L} + K} \right) + \left( {a_{2}^{L} + K} \right) + \left( {a_{3}^{L} + K} \right) + \left( {a_{4}^{L} + K} \right)} \right]}}{8} \\ \end{aligned}$$

where $K = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\quad a_{1}^{U} \ge 0,} \hfill \\ {\left| {a_{1}^{U} } \right|,} \hfill & {{\text{if}}\quad a_{1}^{U} < 0.} \hfill \\ \end{array} } \right.$

To rank any two trapezoidal interval type-2 fuzzy sets, Chen et al. [57] defined the following comparison laws: Let $\tilde{A}$ and $\tilde{B}$ be two trapezoidal interval type-2 fuzzy sets. If ${\text{RV}}\left( {\tilde{A}} \right) < {\text{RV}}\left( {\tilde{B}} \right)$, then we define $\tilde{A} < \tilde{B}$. If ${\text{RV}}\left( {\tilde{A}} \right) = {\text{RV}}\left( {\tilde{B}} \right)$, then we define $\tilde{A} = \tilde{B}$.