1 Introduction

As indoor location-based service (indoor LBS) [1] has been more and more important in our daily life, indoor location estimation is becoming the key problem. At present, the most popular techniques implementing indoor location is Wi-Fi-based location fingerprinting [2–4]. It has the major advantage of exploiting existing wireless network infrastructures and consequently avoiding extra deployment costs.

Location fingerprinting requires to operate a spatial signal strength map from different access points (APs) strategically located in a given area. It becomes a classical classification problem where different supervised machine learning techniques have been used to train classifiers, using the signal strength from different APs as their input data and providing the location estimation as their output estimation. K-NN (nearest neighbor) [5], decision tree [6], Bayesian [7], neural networks [8], extreme learning machine (ELM) [9] are most frequently used by location fingerprinting. Among all the algorithms above, ELM is more and more widely used for its competitive fast learning speed during both offline and online phrases.

Nevertheless, due to Wi-Fi signal is dynamically changing over time [10], the location accuracy decreases as time goes on. The dynamism of Wi-Fi signals is diverse.

On the one hand, the dynamism means the signal strength value, which is caused by the volatility of Wi-Fi signal and the change of environment. It will lead occasional received signal strength indication (RSSI) value missing, as shown in Table 1. For this situation, the general approach is to supplement it with a default value according to the data’s distribution. Chen [11] sets all the missing values to −95, the minimum strength of the signal received in the environment. Roos [12] replaces the missing values with some constant smaller than any of the measured values.

Table 1 Wi-Fi location fingerprints
Full size table

On the other hand, the dynamism also denotes the number of APs. Due to the basic function of Wi-Fi APs is to provide Internet, it is very common that some APs are removed or some new APs are added in the environment, shown in Fig. 1. This situation will be difficult to solve when the missing APs offer the fingerprint information, or the new coming APs will be used as the feature. It will bring the change of feature dimension, which is a challenge for traditional machine learning algorithms. By using these traditional methods, such as support vector machine (SVM) [4, 13] and ELM, we can do nothing but collect new data and retrain a model, it requires a lot of extra computation and labor costs. At the same time, there are no direct machine learning algorithms, which can handle the training data of varying feature dimension.

Fig. 1
figure 1

The increase or decrease in the APs number. a AP6 is removed from the environment, which will lead decreasing of the feature dimension, b a new AP7 is added in the area, which can offer positive influence on location accuracy

Full size image

Focusing on this problem, we regard it as a feature transfer learning problem and propose a Feature Adaptive Online Sequential Extreme Learning Machine (FA-OSELM) algorithm. It can transfer the original model to a new one with a few of incremental data, rather than completely retrain a new model. The experiments show that the transferred model can get high accuracy.

The rest of the paper is organized as follows. We firstly review ELM and OS-ELM briefly in Sect. 2. Then in Sect. 3, we introduce FA-OSELM in detail. After that, we do some experiments and evaluate the performance in Sect. 4. At last, in Sect. 5, we make a short conclusion.

2 Brief of ELM and OS-ELM

In this section, we review ELM [9, 14, 15] and OS-ELM [16] algorithms by introducing their motivation, modeling and algorithm steps.

ELM is developed by Huang et al. And it belongs to artificial neural network (ANN) family, especially an single-layer feedforward networks (SLFN), where learning is made without iterative tuning. According to ELM learning theory [17], if SLFNs \(f({\mathbf{x}}) = h({\mathbf{x}})\beta\) with tunable piecewise continuous hidden-layer feature mapping h(x) can approximate any target continuous functions, tuning is not required in the hidden layer then. All the hidden-node parameters, which are supposed to be tuned by conventional learning algorithms, can be randomly generated according to any continuous sampling distribution [18, 19].

Comparing with other traditional learning methods, ELM has not only better performance in classification precision and regression fitting degree, but also less time consumption in offline learning and online prediction [20].

Now, more and more work has been done to develop ELM. Andrés [21] and Wang [22] propose some new method to improve the generalization capability of ELM. Miche [23] improves the optimally pruned extreme learning machine (OP-ELM) with LARS and Tikhonov regularization to a double-regularized ELM. Therefore, it can maintain numerical stability and efficient pruning of the neurons. Dealing with some problems, especially relatively large datasets, ELM suffers from instability and over-fitting. Zhai et al. [24] propose an approach of fusion of extreme learning machine (F-ELM) with fuzzy integral based on probabilistic SLFNs.

And in order to alleviate some extent the problems of instability and over-fitting problems of ELM when dealing with large datasets, Zhai et al. [25] propose a dynamic ensemble extreme learning machine based on sample entropy. The experimental results show that the proposed approach is robust and efficient. Furthermore, ELM has been widely utilized in various kinds of applications such as indoor localization [26, 27], activity recognition [28, 29], transportation mode recognition [30, 31], context-aware computing [32] and so on.

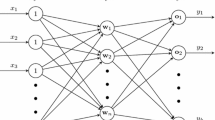
Given N arbitrary distinct samples \(\left( {{\mathbf{x}}_{i} ,{\mathbf{t}}_{i} } \right) \in R^{n} \times R^{m} , \;i = 1,2, \ldots ,N\). Here, \({\mathbf{x}}_{i}\) is a n × 1 input vector \({\mathbf{x}}_{i} = \left[ {x_{i1} ,x_{i2} , \ldots ,x_{in} } \right]^{T}\) and \({\mathbf{t}}_{i}\) is a m × 1 target vector \({\mathbf{t}}_{i} = \left[ {t_{i1} ,t_{i2} , \ldots ,t_{im} } \right]^{T}\). The network with L hidden nodes is shown in Fig. 2. The output function of this network can be represented as follows:

$$f_{L} \left( {{\mathbf{x}}_{j} } \right) = \mathop \sum \limits_{i = 1}^{L} \beta_{i} G\left( {{\mathbf{a}}_{i} ,b_{i} ,{\mathbf{x}}_{j} } \right),\quad j = 1, \ldots ,N$$
(1)

where \({\mathbf{a}}_{i}\) and b i are the learning parameters of hidden nodes, and β i is the weight connecting the ith hidden node to the output node. \(G\left( {{\mathbf{a}}_{i} ,b_{i} ,{\mathbf{x}}} \right)\) is the output of the ith hidden node with respect to the input x. For additive hidden node with the activation function g(x): R → R (e.g., sigmoid and threshold), \(G\left( {{\mathbf{a}}_{i} ,b_{i} ,{\mathbf{x}}} \right)\) is given by

Fig. 2
figure 2

SLFN with L hidden nodes

Full size image
$$G\left( {{\mathbf{a}}_{i} ,b_{i} ,{\mathbf{x}}} \right) = g\left( {{\mathbf{a}}_{i} \cdot {\mathbf{x}} + b_{i} } \right),\quad b_{i} \in R$$
(2)

If an SLFN with L hidden nodes can approximate these N samples with zero error, it then implies that there exist \(\beta_{i} , {\mathbf{a}}_{i}\) and b i such that

$$f_{L} \left( {{\mathbf{x}}_{j} } \right) = \mathop \sum \limits_{i = 1}^{L} \beta_{i} G\left( {{\mathbf{a}}_{i} ,b_{i} ,{\mathbf{x}}_{j} } \right) = {\mathbf{t}}_{j} ,\quad j = 1, \ldots ,N.$$
(3)

Equation (3) can be summarized as

$$H\beta = T$$
(4)

where

$$H\left( {{\mathbf{a}}_{1} , \ldots ,{\mathbf{a}}_{L} ,b_{1} , \ldots ,b_{L} ,{\mathbf{x}}_{1} , \ldots ,{\mathbf{x}}_{L} } \right) = \left[ {\begin{array}{*{20}c} {G\left( {{\mathbf{a}}_{1} ,b_{1} ,{\mathbf{x}}_{1} } \right)} & \cdots & {G\left( {{\mathbf{a}}_{L} ,b_{L} ,{\mathbf{x}}_{1} } \right)} \\ \vdots & \ddots & \vdots \\ {G\left( {{\mathbf{a}}_{1} ,b_{1} ,{\mathbf{x}}_{N} } \right)} & \cdots & {G\left( {{\mathbf{a}}_{L} ,b_{L} ,{\mathbf{x}}_{N} } \right)} \\ \end{array} } \right]$$
(5)
$$\beta = \left[ {\begin{array}{*{20}c} {\beta_{1}^{T} } \\ \vdots \\ {\beta_{L}^{T} } \\ \end{array} } \right]_{L \times m} \quad {\text{and}}\quad T = \left[ {\begin{array}{*{20}c} {{\mathbf{t}}_{1}^{T} } \\ \vdots \\ {{\mathbf{t}}_{N}^{T} } \\ \end{array} } \right]_{N \times m}$$
(6)

According to [10], the hidden-node parameters a i and b i (input weights and biases or centers and impact factors) of SLFNs do not need to be tuned during training and may simply be assigned with random values. The smallest norm least-squares solution of the above linear system is

$$\hat{\beta } = H^{\dag } T$$
(7)

where H † is the Moore–Penrose generalized inverse of matrix H [33, 34]. Different methods can be used to calculate the Moore–Penrose generalized inverse of a matrix: orthogonal projection method, orthogonalization method, iterative method and singular value decomposition (SVD) [34]. The orthogonal projection method [34] can be used in two cases: when \(H^{T} H\) is nonsingular and H † = (H T H)−1 H T or when HH T is nonsingular and H † = H T(HH T)−1.

2.1 OS-ELM

The batch ELM described previously assumes that all the training data (N samples) are available for training. However, in real applications, the training data may arrive chunk by chunk or one by one (a special case of chunk), and hence, the batch ELM algorithm has to be modified for this case so as to make it online sequential.

First, given a chunk of initial training set \(\aleph_{0} = \left\{ {\left( {{\mathbf{x}}_{i} ,{\mathbf{t}}_{i} } \right)} \right\}_{i = 1}^{{N_{0} }}\) and N 0 ≥ L, if one considers using the batch ELM algorithm, one need to consider only the problem of minimizing \(\| H_{0} \beta - T_{0} \|\). According to [16], the solution to minimizing \(\| H_{0} \beta - T_{0} \|\) is given by \(\beta^{(0)} = K_{0}^{ - 1} H_{0}^{T} T_{0}\) where \(K_{0} = H_{0}^{T} H_{0}\).

Now support that we are given another chunk of data \(\aleph_{1} = \left\{ {\left( {{\mathbf{x}}_{i} ,{\mathbf{t}}_{i} } \right)} \right\}_{{i = N_{0} + 1}}^{{N_{0} + N_{1} }}\), where N 1 denotes the number of observations in the chunk, the problem then becomes minimizing

$$\left\| {\left[ {\begin{array}{*{20}c} {H_{0} } \\ {H_{1} } \\ \end{array} } \right]\beta - \left[ {\begin{array}{*{20}c} {T_{0} } \\ {T_{1} } \\ \end{array} } \right]} \right\|$$
(8)

where

$$H_{1} = \left[ {\begin{array}{*{20}c} {G({\mathbf{a}}_{1} ,b_{1} ,{\mathbf{x}}_{{N_{0} + 1}} )} & \cdots & {G({\mathbf{a}}_{L} ,b_{L} ,{\mathbf{x}}_{{N_{0} + 1}} )} \\ \vdots & \ddots & \vdots \\ {G({\mathbf{a}}_{1} ,b_{1} ,{\mathbf{x}}_{{N_{0} + N_{1} }} )} & \cdots & {G({\mathbf{a}}_{L} ,b_{L} ,{\mathbf{x}}_{{N_{0} + N_{1} }} )} \\ \end{array} } \right]_{{N_{1} \times L}} ,\quad T_{1} = \left[ {\begin{array}{*{20}c} {{\mathbf{t}}_{{N_{0} + 1}}^{T} } \\ \vdots \\ {{\mathbf{t}}_{{N_{0} + N_{1} }}^{T} } \\ \end{array} } \right]_{{N_{1} \times m}}$$
(9)

Considering both chunks of training data sets ℵ0 and ℵ1, the output weight β is formulated as

$$\beta^{(1)} = K_{1}^{ - 1} \left[ {\begin{array}{*{20}c} {H_{0} } \\ {H_{1} } \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {T_{0} } \\ {T_{1} } \\ \end{array} } \right]$$
(10)

where

$$K_{1} = \left[ {\begin{array}{*{20}c} {H_{0} } \\ {H_{1} } \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {H_{0} } \\ {H_{1} } \\ \end{array} } \right]$$
(11)

and

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {H_{0} } \\ {H_{1} } \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {T_{0} } \\ {T_{1} } \\ \end{array} } \right] & = H_{0}^{T} T_{0} + H_{1}^{T} T_{1} = K_{0} K_{0}^{ - 1} H_{0}^{T} T_{0} + H_{1}^{T} T_{1} = K_{0} \beta^{\left( 0 \right)} + H_{1}^{T} T_{1} \\ & = \left( {K_{1} - H_{1}^{T} H_{1} } \right)\beta^{\left( 0 \right)} + H_{1}^{T} T_{1} = K_{1} \beta^{(0)} - H_{1}^{T} H_{1} \beta^{\left( 0 \right)} + H_{1}^{T} T_{1} \\ \end{aligned}$$
(12)

So the model of OS-ELM will be updated by the incremental data. The contribution of incremental data \(x^{*}\) is reflected by the correction \(\Delta \beta\), of existing parameter of training model \(\beta^{{\prime }}\), which forms the new parameter of training model \(\beta^{ *}\) as Eq. (13).

$$\beta^{*} = \beta^{{\prime }} +\Delta \beta \left( {x^{*} } \right)$$
(13)

Obviously, the result of \(\beta^{*}\) is based on previous result \(\beta^{{\prime }}\), but the calculation burden is not heavy for it do not need all the data to retrain the model.

Combining (10) and (12), β (1) is given by

$$\begin{aligned} \beta^{\left( 1 \right)} & = K_{1}^{ - 1} \left[ {\begin{array}{*{20}c} {H_{0} } \\ {H_{1} } \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {T_{0} } \\ {T_{1} } \\ \end{array} } \right] = K_{1}^{ - 1} \left( {K_{1} \beta^{\left( 0 \right)} - H_{1}^{T} H_{1} \beta^{\left( 0 \right)} + H_{1}^{T} T_{1} } \right) \\ & = \beta^{\left( 0 \right)} + K_{1}^{ - 1} H_{1}^{T} \left( {T_{1} - H_{1} \beta^{\left( 0 \right)} } \right) \\ \end{aligned}$$
(14)

where

$$K_{1} = \left[ {\begin{array}{*{20}c} {H_{0} } \\ {H_{1} } \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {H_{0} } \\ {H_{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {H_{0}^{T} } & {H_{1}^{T} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {H_{0} } \\ {H_{1} } \\ \end{array} } \right] = K_{0} + H_{1}^{T} H_{1}$$
(15)

Obviously, Eq. (14) corresponds to Eq. (13), the new β (1) is drives from β (0), we only need the new coming incremental data to update the β (0) to β (1). So we greatly reduce the computation cost because only a few data are used for updating.

With the incremental number increasing, when the (k + 1)th chunk of data set \(\aleph_{k + 1} = \left\{ {\left( {{\mathbf{x}}_{i} ,{\mathbf{t}}_{i} } \right)} \right\}_{{i = \left( {\sum\nolimits_{j = 0}^{k} {N_{j} } } \right) + 1}}^{{\sum\nolimits_{j = 0}^{k + 1} {N_{j} } }}\) is received, where k ≥ 0 and N k+1 denotes the number of observations in the (k + 1)th chunk, the Eq. (14) for updating β (k+1) will be written as

$$\beta^{(k + 1)} = \beta^{(k)} + K_{k + 1}^{ - 1} H_{k + 1}^{T} \left( {T_{k + 1} - H_{k + 1} \beta^{(k)} } \right)$$
(16)

\(K_{k + 1}^{ - 1} H_{k + 1}^{T} \left( {T_{k + 1} - H_{k + 1} \beta^{(k)} } \right)\) can be seen as the correction of the original model β (k) with the new samples \(\aleph_{k + 1} = \left\{ {\left( {{\mathbf{x}}_{i} ,{\mathbf{t}}_{i} } \right)} \right\}_{{i = \left( {\sum\nolimits_{j = 0}^{k} {N_{j} } } \right) + 1}}^{{\sum\nolimits_{j = 0}^{k + 1} {N_{j} } }}\).

3 FA-OSELM

In Sect. 2, we have reviewed the ELM and OS-ELM algorithms. Fortunately, they have already been applied indoor localization research area. Xiao et al. [35] achieved a perfect performance in Wi-Fi indoor location using ELM. But due to the basic function of Wi-Fi is to provide Internet, it is very common that some APs are removed or some new APs are added. This change will affect the variation of feature dimension, and thus, the old model will not work anymore.

Considering the problem, we propose a FA-OSELM. When the number of features is changed, we can update the model using a small amount of incremental data with new features.

Firstly, given N 0 arbitrary distinct samples \(\left( {{\mathbf{x}}_{i} ,{\mathbf{t}}_{i} } \right) \in R^{n} \times R^{m} , i = 1,2, \ldots ,N_{0}\). Here, \({\mathbf{x}}_{i}\) is a n × 1 input vector \({\mathbf{x}}_{i} = \left[ {x_{i1} ,x_{i2} , \ldots ,x_{in} } \right]^{T}\) and \({\mathbf{t}}_{i}\) is a m × 1 target vector \({\mathbf{t}}_{i} = \left[ {t_{i1} ,t_{i2} , \cdots ,t_{im} } \right]^{T}\).

When the number of APs used as the features changes, we can collect a new batch data to update the model. Given another N 1 arbitrary distinct samples \(\left( {{\mathbf{x}}_{i}^{{\prime }} ,{\mathbf{t}}_{i} } \right) \in R^{{n^{{\prime }} }} \times R^{m} , i = 1,2, \ldots ,N_{1}\). Here, \({\mathbf{x}}_{i}^{'}\) is a n′ × 1 input vector \({\mathbf{x}}_{i}^{{\prime }} = \left[ {x_{i1}^{\prime } ,x_{i2}^{\prime } , \ldots ,x_{{in^{\prime } }}^{\prime } } \right]^{T}\), but \({\mathbf{t}}_{i}\) is still a m × 1 target vector \({\mathbf{t}}_{i} = \left[ {t_{i1} ,t_{i2} , \ldots ,t_{im} } \right]^{T}\).

If n′ < n, it means some APs in the location area are missing; if n′ > n, it means that we set some new APs to the location area. In these two situations, the problem is still to minimize

$$\left\| {\left[ {\begin{array}{*{20}c} {H_{0} } \\ {H_{1} } \\ \end{array} } \right]\beta - \left[ {\begin{array}{*{20}c} {T_{0} } \\ {T_{1} } \\ \end{array} } \right]} \right\|$$
(17)

But the \(H_{0} ,H_{1} ,T_{0}\) and \(T_{1}\) refer the follows:

$$H_{0} = \left[ {\begin{array}{*{20}c} {G({\mathbf{a}}_{1} ,b_{1} ,{\mathbf{x}}_{1} )} & \cdots & {G({\mathbf{a}}_{L} ,b_{L} ,{\mathbf{x}}_{1} )} \\ \vdots & \ddots & \vdots \\ {G({\mathbf{a}}_{1} ,b_{1} ,{\mathbf{x}}_{{N_{0} }} )} & \cdots & {G({\mathbf{a}}_{L} ,b_{L} ,{\mathbf{x}}_{{N_{0} }} )} \\ \end{array} } \right]_{{N_{0} \times L}} ,\quad T_{0} = \left[ {\begin{array}{*{20}c} {{\mathbf{t}}_{1}^{T} } \\ \vdots \\ {{\mathbf{t}}_{{N_{0} }}^{T} } \\ \end{array} } \right]_{{N_{0} \times m}}$$
(18)
$$H_{1} = \left[ {\begin{array}{*{20}c} {G({\mathbf{a}}_{1}^{ '} ,b_{1} ,{\mathbf{x}}_{{N_{0} + 1}}^{ '} )} & \cdots & {G({\mathbf{a}}_{L}^{ '} ,b_{L} ,{\mathbf{x}}_{{N_{0} + 1}}^{ '} )} \\ \vdots & \ddots & \vdots \\ {G({\mathbf{a}}_{1}^{ '} ,b_{1} ,{\mathbf{x}}_{{N_{0} + N_{1} }}^{ '} )} & \cdots & {G({\mathbf{a}}_{L}^{ '} ,b_{L} ,{\mathbf{x}}_{{N_{0} + N_{1} }}^{ '} )} \\ \end{array} } \right]_{{N_{1} \times L}} ,\quad T_{1} = \left[ {\begin{array}{*{20}c} {{\mathbf{t}}_{{N_{0} + 1}}^{T} } \\ \vdots \\ {{\mathbf{t}}_{{N_{0} + N_{1} }}^{T} } \\ \end{array} } \right]_{{N_{1} \times m}}$$
(19)

where

$$\left\{ {{\mathbf{a}}_{i} = \left\{ {a_{1} ,a_{2} , \ldots ,a_{n} } \right\}} \right\}_{i = 1}^{L} ,\quad \left\{ {{\mathbf{x}}_{i} = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}} \right\}_{i = 1}^{{N_{0} }}$$
(20)
$$\left\{ {{\mathbf{a}}_{i}^{{\prime }} = \left\{ {a_{1}^{{\prime }} ,a_{2}^{{\prime }} , \ldots ,a_{{n^{{\prime }} }}^{{\prime }} } \right\}} \right\}_{i = 1}^{L} , \quad \left\{ {{\mathbf{x}}_{i}^{{\prime }} = \left\{ {x_{1}^{{\prime }} ,x_{2}^{{\prime }} , \ldots ,x_{{n^{{\prime }} }}^{{\prime }} } \right\}} \right\}_{i = 1}^{{N_{1} }}$$
(21)

\({\mathbf{a}}_{i}\) is the weight vector connecting the input layer to the ith hidden node, and b i is the bias of the ith hidden node. \({\mathbf{a}}_{i} \cdot {\mathbf{x}}_{i}\) denotes the inner product of vectors \({\mathbf{a}}_{i}\) and \({\mathbf{x}}_{i}\) in \(R^{n}\). \({\mathbf{a}}_{i}\) and \(b_{i}\) can be random generated. Once determined, they cannot be changed any more. According to Eqs. (18) and (19), we can see that \({\mathbf{a}}_{i}\) has the same dimension with \({\mathbf{x}}_{i}\), \({\mathbf{a}}_{i}^{{\prime }}\) has the same dimension with \({\mathbf{x}}_{i}^{{\prime }}\). Actually, \({\mathbf{a}}_{i}\) and \({\mathbf{x}}_{i}\) have one by one corresponding relationship for each column, so as to \({\mathbf{a}}_{i}^{{\prime }}\) and \({\mathbf{x}}_{i}^{{\prime }}.\)

As shown in Fig. 3, when the feature dimension is changed, the bone structure of network has no change. But as the feature dimension is different from previous, we have to adjust \({\mathbf{a}}_{i}\) to fit new feature dimension. As the same time, the hidden node has no change, so the b i will not change.

Fig. 3
figure 3

FA-OSELM network

Full size image

Therefore, we propose a input-weight transfer matrix P, and a input-weight supplement vector Q i to generate \(a_{i}^{{\prime }}\) by Eq. (22).

$$\left\{ {{\mathbf{a}}_{i}^{{\prime }} = {\mathbf{a}}_{i} \cdot P + {\mathbf{Q}}_{i} } \right\}_{i = 1}^{L}$$
(22)

where

$$P = \left[ {\begin{array}{*{20}c} {P_{11} } & \cdots & {P_{{1n^{'} }} } \\ \vdots & \ddots & \vdots \\ {P_{n1} } & \cdots & {P_{{nn^{'} }} } \\ \end{array} } \right]_{{n \times n^{'} }}$$
(23)
$${\mathbf{Q}}_{i} = \left[ {\begin{array}{*{20}c} {Q_{1} } & \cdots & {Q_{{n^{{\prime }} }} } \\ \end{array} } \right]_{{1 \times n^{{\prime }} }}$$
(24)

matrix P has the following rules:

  • Each line has only one ‘1,’ and the rest are all ‘0’;

  • Each column has one ‘1’ at most, and the rest are all ‘0’;

  • If \(P_{ij} = 1\), it means that after the change of feature dimension, the ith dimension of the original feature vector has become the jth dimension of the new feature vector.

\({\mathbf{Q}}_{\varvec{i}}\) is used to supplement when the feature dimension increases, we need to add the corresponding InputWeight for the new adding features. \({\mathbf{Q}}_{\varvec{i}}\) has the following rules:

  • When feature dimension decreased, the \({\mathbf{Q}}_{i}\) is an all-zero vector, that is to say, we do not need to add corresponding InputWeight for the new adding features;

  • When feature dimension increased, if the ith item of \({\mathbf{a}}_{i}^{{\prime }}\) is new feature, the ith item of \({\mathbf{Q}}_{i}\) should be generated randomly according to the distributing of \({\mathbf{a}}_{i}\).

We take the Wi-Fi APs as an example:

  • if features: \(\left\{ {{\text{Ap}}_{1,} {\text{Ap}}_{2,} {\text{Ap}}_{3,} {\text{Ap}}_{4,} {\text{Ap}}_{5} } \right\} \to \left\{ {{\text{Ap}}_{1,} {\text{Ap}}_{2,} {\text{Ap}}_{3,} {\text{Ap}}_{5} } \right\}\):

  • we can generate: \(P = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ \end{array} } \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ 1 \\ 0 \\ \end{array} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ 1 \\ \end{array} } \\ \end{array} } \right]\), \(Q_{i} = \left\{ {0,0,0,0} \right\}\);

  • if features: \(\left\{ {{\text{Ap}}_{1,} {\text{Ap}}_{2,} {\text{Ap}}_{3,} {\text{Ap}}_{4,} {\text{Ap}}_{5} } \right\} \to \left\{ {{\text{Ap}}_{1,} {\text{Ap}}_{2,} {\text{Ap}}_{3,} {\text{Ap}}_{6} ,{\text{Ap}}_{4,} {\text{Ap}}_{5} } \right\}\):

  • we can generate: \(P = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & {\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\), \(Q_{i} = \left\{ {0,0,0,Q_{4} ,0,0} \right\},\) where \(Q_{4}\) can be generated randomly.

As mentioned above, FA-OSELM can be summarized in the following steps:

  1. 1.

    Determine the model parameters by the original dataset of N 0 samples, such as the number of hidden nodes L and the activation function g(x).

  2. 2.

    Randomly assign the value of weight vector \({\mathbf{a}}_{i}\) and bias scalar b i , i = 1, 2, …, L.

  3. 3.

    Calculate the original hidden-layer output matrix \(H_{0}\).

  4. 4.

    Calculate the initial model parameter β (0) = H †0 T 0.

  5. 5.

    When coming N 1 samples data \(X_{1} ,T_{1}\) with different feature, generate the input-weight transfer matrix P and input-weight supplement vector \({\mathbf{Q}}_{i}\), i = 1, 2, …, L according to rules mentioned above.

  6. 6.

    Calculate the new weight vector \({\mathbf{a}}_{i}^{{\prime }} = {\mathbf{a}}_{i} \cdot P + {\mathbf{Q}}_{i}\), i = 1, 2, …, L.

  7. 7.

    Divide the newly incremental data into k parts, set j = 1, then go to iterative process.

  8. 8.

    Using the new weight vector \({\mathbf{a}}_{i}^{{\prime }}\) to calculate the jth iteration of model parameter \(H_{j}\) by Eq. (19).

  9. 9.

    Calculate the β j by the Eq. (16).

  10. 10.

    If j < k, set j = j + 1 and go to (8); else go to (11).

  11. 11.

    After k times iteration, we can get the final parameter β* = β j .

From Step (5) to Step (10), when a new batch of data comes, we will adjust the weight vector basing on the change of features. So we name our algorithm FA-OSELM. The workflow of the algorithm can be concisely given in Fig. 4.

Fig. 4
figure 4

The workflow of algorithm

Full size image

4 Experiments and performance evaluation

As the Wi-Fi access points always move, which will leads the change of feature dimension, we use FA-OSELM to enable the existing model to overcome it with a small amount of incremental data, saving human labeling work and time-consuming.

All the experiments are running on the computer with following configuration:

Operation System :

Windows XP Professional SP3

CPU :

Intel Pentium(R) 4 CPU

Main Frequency :

3.2 GHz

RAM :

2G

4.1 Data preparing

For the classification studies, four benchmark problems have been considered: two Wi-Fi indoor location data sets: (1) office area dataset and (2) lounge area dataset; two UCI [36] datasets: (3) image segment and (4) satellite image. We use the Wi-Fi datasets to show FA-OSELM has good performance on lifelong indoor localization. Meanwhile, the experiments on UCI datasets show that FA-OSELM is also effective in other applications.

Office area is a 12 × 6 m2 working space in eighth floor of our institute, shown in Fig. 5. Red points are the locations where data are mostly collected with distance about 2 m. We collect the data at different time of a day and last for a month. Finally, we collected 5,635 data. We choose the most stable 7 APs as the feature, so each fingerprint is a seven dimension vector.

Fig. 5
figure 5

Wi-Fi indoor location (office area)

Full size image

Lounge area is an 8.7 × 55 m2 space in first floor of our institute, shown in Fig. 6. Also the red points show the locations where data are mostly collected with distance 2–3 m. A total of 2,484 data are collected for a week, and 18APs are selected as the feature.

Fig. 6
figure 6

Wi-Fi indoor location (lounge area)

Full size image

The image segmentation problem consists of a database of images drawn randomly from seven outdoor images and consists of 2,310 regions of 3 × 3 pixels. The goal is to recognize each region into one of the seven paths, and grass using 19 attributes extracted from each square region.

The satellite image problem consists of a database generated from landsat multispectral scanner. One frame of landsat multispectral scanner imagery consists of four digital images of the same scene in four different spectral bands. The database is a (tiny) subarea of a scene, consisting of 82 × 100 pixels. Each data in the database corresponds to a region of 3 × 3 pixels. The aim is to classify of the central pixel in a region into the six categories, namely red soil, cotton crop, gray soil, damp gray soil, soil with vegetation stubble, and very damp gray soil using 36 spectral values for each region.

Specifications of two UCI datasets are shown in Table 2. Before being used, they were normalized with z-score method.

Table 2 Specifications of two UCI data sets
Full size table

4.2 Experimental performance

4.2.1 Model selection

According to Huang [20], the accuracy will be improved with regularization factor C, which can optimize the architecture of learning model. Thus, for FA-OSELM, only two user-specified parameters, regularization factor and number of hidden nodes (C, L), should be determined.

We divide the training data of each dataset into two equal subsets and use cross-validation method to determine user-specified parameters (C, L), where C is chosen from the range {2−20, 2−18,…, 218, 220} and L is chosen from the range{10, 20,…, 990, 1,000}. The performance of each data sets’ parameters is illustrated in Figs. 7, 8, 9 and 10.

Fig. 7
figure 7

Performances with different user-specified parameters (C, L) for image segment dataset

Full size image
Fig. 8
figure 8

Performances with different user-specified parameters (C, L) for satellite image dataset

Full size image
Fig. 9
figure 9

Location accuracy (<5 m) with different user-specified parameters (C, L) for Wi-Fi location dataset (office area)

Full size image
Fig. 10
figure 10

Location accuracy (<15 m) with different user-specified parameters (C, L) for Wi-Fi location dataset (lounge area)

Full size image

From all above mentioned in Figs. 7, 8, 9 and 10, for different datasets, we need to select the optimal parameter settings of L and C to achieve good performance. For example in Fig. 7, we can obtain the optimal performance with the optimal parameter pair (L = 350, C = 2−6) in Table 3. Generally speaking, the performance can be reached the higher accuracy increasingly as long as the number of hidden nodes L is getting larger, but due to the over-fitting problem, the accuracy will decrease in some cases in Figs. 8 and 9. Meanwhile, regularization factor C also can help to achieve high accuracy when taking the specific value. To tradeoff between high accuracy and computation complexity, we obtain the optimal parameter settings for all the datasets in Table 3. Additionally, we use the RBF activation function in all experiments.

Table 3 User-specified parameters
Full size table

4.2.2 FA-OSELM’s performance when dealing with feature dimension reducing

In the study of Wi-Fi indoor localization, when one AP we used as the feature is missing, it will lead one feature missing. For this case, the old ELM model cannot be used any more and there are two common handing methods: (1) According to the distribution of the missing feature, we can fulfill the lost item with a default value, such as mean value or a random value; (2) train another new model with some new offline training data. Besides, we can use FA-OSELM to update the old model to a new one with a few of incremental data.

We apply all the methods on four datasets. We divide each dataset into three parts: training data, incremental data and testing data. Incremental data and testing data have the same feature dimension, but one less than the training data. This missing one feature dimension is random selected from the original (Figs. 11, 12).

Fig. 11
figure 11

Location accuracy of feature missing experiment (lounge area dataset)

Full size image
Fig. 12
figure 12

Location accuracy of feature missing experiment (office area dataset)

Full size image

The results of two UCI datasets are shown in Table 4. We can see that FA-OSELM has a better performance than retraining a new model. The reason is that when one feature is lost, the original model still contains the majority information of the new feature. However, the incremental data are too little to retain a good new model, but it is effective to transfer the original model and overcome the change of the features. FA-OSELM also performs better than the methods of supplementing with a mean value or random values because the supplemented values only enable the old model, but offer meaningless information.

Table 4 Testing accuracy in feature missing experiments
Full size table

4.2.3 FA-OSELM’s performance when dealing with feature dimension increasing

On the contrary, when a new AP is equipped in the location area, it can offer some new feature information, but the old ELM model cannot involve it, as the feature dimension will be changed. If we want to utilize it, we can do nothing but collect a bench of data and train a new model, which needs extra labor cost. Otherwise, we have to just ignore it and still use the old model. Fortunately, FA-OSELM allows us to transfer the old model to a new one, and it can take full use of the new feature dimension with a little labor cost. As the former experiments, we also divide each datasets into three parts: training data, incremental data and testing data. But in order to test the performance when feature dimension increases, we set the feature dimension of incremental data equals to testing data, but one more than the training data.

The results of UCI datasets are shown in Table 5. We can obtain the same conclusion that FA-OSELM still works well in feature increasing situation. We can explain the low accuracy of retraining a new model as the underfitting caused by less scale of incremental data. But for FA-OSELM, the little scale of incremental data can further bring in the incremental information to the old model and improve the testing accuracy. Comparing with using the old model directly, FA-OSELM offers limited accuracy increasing for the two UCI datasets. The reason is that it is variable that how much influence each feature can affect the accuracy.

Table 5 Testing accuracy in feature increasing experiments
Full size table

As shown in Figs. 13 and 14, FA-OSELM’s performances are much better than the other two for the Wi-Fi location problems. The reason is that, for Wi-Fi location problem, FA-OSELM can not only maintain the old model’s information, but also take full of the new added feature.

Fig. 13
figure 13

Location accuracy of feature increasing experiment (lounge area dataset)

Full size image
Fig. 14
figure 14

Location accuracy of feature increasing experiment (office area dataset)

Full size image

4.2.4 FA-OSELM’s performance as more and more incremental data comes

While adapt to the new feature dimension, FA-OSELM performs better than any other methods mentioned above with a small amount of incremental data. For the Wi-Fi-based indoor localization problem, if we can get more incremental data, we will have more information about the new location environment. We want to value whether FA-OSELM is stable and can get better performance with more incremental data.

Thus, we extend the Wi-Fi location dataset of office area to be 6,835 with another 1,200 data. We maintain the original training data and select 600 of the new data to be the testing data, and the rest are used as incremental data. They are ordered chronologically and divided into ten equal parts. We design the experiments as the previous two to measure the capability in two situations: when a feature is missing and a new feature is added. The results are shown in Figs. 15 and 16.

Fig. 15
figure 15

Accuracy increasing as incremental data comes chunk by chunk in feature missing case (office area dataset)

Full size image
Fig. 16
figure 16

Accuracy increasing as incremental data comes chunk by chunk in feature increasing case (office area dataset)

Full size image

As shown in Figs. 15 and 16, as more incremental data chunks come, the accuracy will keep stable after a period of increasing. Because more incremental data offer more positive information to help FA-OSELM to transfer the old model so as to fit the new feature. When the accuracy keeps stable, it means the new model has already overcome the accuracy gap caused by the change of the feature.

5 Conclusion

In this paper, we proposed a FA-OSELM method for lifelong indoor localization. Why we raise this problem is that: Indoor location estimate based on Wi-Fi is difficult for the sake of the APs’ high dynamics. The high dynamics means not only the APs’ signal strength, but also the increase or decrease in APs’ number. If the lack of signal strength is accidental, we can supplement with a default value. But if the APs used as the features are missing (maybe someone removed them), or we set new APs in somewhere, the location accuracy is not high enough. We can do nothing but to recollect a batch of new data and retrain a new model. Not only data collection will consume a lot of time and money, but also it is a waste of previous data. So we propose the FA-OSELM method which can use a small amount of data to transfer the original model to a new one. The new model not only retains the original features’ characteristic, but also fit for the features’ change. All the experiments show that FA-OSELM has better performance than the other methods in all the designed experiments.