1 Introduction

The nonlinear problem often arising in exact modeling of phenomena in mechanics and physics and study of them is of interest to many researchers. The traditional methods to solve this nonlinear problem cannot be applied if no small parameter exists in equation. To overcome the shortcoming, several analytical methods such as energy balance method [1], homotopy perturbation method [2], harmonic balance method [3], Hamiltonian approach [4], homotopy analysis method [5], max–min approach [6], optimal homotopy perturbation method [7], homotopy perturbation transform method [8], Laplace decomposition method [9], Adomian decomposition method [10], and coupling of homotopy-variational method [11] were proposed by researchers and used for analysis of nonlinear equation [12–23]. First-order approximation of these methods by simple calculation yields good accuracy, but interest to reduce the relative error induced the researchers to implement higher order of approximations, for example, Ma et al. [24] applied higher-order homotopy perturbation method to periodic solutions of nonlinear Jerk equation, Belendez et al. [25] by second-order harmonic balance method obtained accurate frequency–amplitude relation for nonlinear oscillator in which the restoring force is inversely proportional to the dependent variable, and Pirbodaghi et al. [26] obtained an accurate analytical solution for Duffing equations with cubic and quintic nonlinearities using the homotopy analysis method.

Energy balance method was first proposed by professor He [1]; in this method, a variational principle for the nonlinear oscillation is established, and then, a Hamiltonian is constructed, from which the angular frequency can be readily obtained by collocation method. First-order energy balance method yields accurate solution in comparison with first-order approximation of other techniques. Durmaz et al. [27] obtain higher-order approximation of energy balance method based on collocation approach for nonlinear Duffing oscillator. Sfahani et al. [28] improved the accuracy of energy balance method using a new trial function. Durmaz and Kaya [29] used Galerkin method as weighting function and obtain higher-order approximations.

In the present study, the accuracy of He’s energy balance method for analysis of conservative nonlinear oscillator is improved based on combining features of collocation method and Galerkin–Petrov method [30]. Results shows that this approach very effectively reduce relative error of first-order energy balance method.

2 The basic idea of He’s energy balance method

Consider a general form on nonlinear oscillator with initial conditions in the form

$$ \textit{\"{u}} + f(u) = 0,\,u(0) = A,\dot{u}(0) = 0. $$
(1)

Its variational can be written as

$$ J(u) = \int\limits_{0}^{{{\raise0.7ex\hbox{$T$} \!\mathord{\left/ {\vphantom {T 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}}} {\left[ { - \frac{1}{2}\dot{u}^{2} + F(u)} \right]} dt. $$
(2)

where \( T = \frac{2\pi }{\omega } \) is period of nonlinear oscillation and \( F(u) = \int {f(u)du} \).

The Hamiltonian, therefore, can be written in the form

$$ H\left( t \right) = - \frac{1}{2}\dot{u} + F\left( u \right) = F\left( A \right), $$
(3)

Equation (3) yields the following residual

$$ R\left( t \right) = - \frac{1}{2}\dot{u} + F\left( u \right) - F\left( A \right) = 0. $$
(4)

We assume the first-order approximate solution as follows

$$ u\left( t \right) = A\cos \omega t, $$
(5)

Substituting Eq. (5) into Eq. (4) yields the following residual

$$ R(t) = \frac{1}{2}A^{2} \omega^{2} \sin^{2} \omega t + F(A\cos \omega t) - F(A) = 0. $$
(6)

And finally collocation at \( \omega t = \frac{\pi }{4} \) gives

$$ \omega = \frac{2}{A}\sqrt {F\left( A \right) - F\left( {\frac{\sqrt 2 }{2}A} \right)} . $$
(7)

3 Improved energy balance method

In order to improve the accuracy of energy balance method, we consider the solution of Eq. (1) as follows

$$ u\left( t \right) = b\cos \omega t + b_{1} \cos 3\omega t, $$
(8)

Equation (8) must satisfy initial conditions; therefore, we have

$$ A = b + b_{1} , $$
(9)

It should be noted that method does not have any limitation for trial solution, and other functions could be considered as trial solution in Eq. (8). Other possible trial functions could be found in [31].

Now, by using Eq. (9), we can rewrite Eq. (8) as follows

$$ u\left( t \right) = b\cos \omega t + \left( {A - B} \right)(A - b)\cos 3\omega t. $$
(10)

By inserting Eq. (10) into Eq. (4), residual are obtained. Obtained residual contain two unknown parameters, one of them is ω and other is b. In order to determine unknown parameters, we need two equations; the first equation obtained based on collocation method as follows

$$ \mathop {Lim}\limits_{{\omega t \to \frac{\pi }{4}}} R\left( t \right) = 0, $$
(11)

Also, the second equation obtained based on Galerkin–Petrov method [30] as follows

$$ \int\limits_{0}^{{{\raise0.7ex\hbox{$T$} \!\mathord{\left/ {\vphantom {T 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}}} {R\left( t \right)\cos \omega tdt = 0} . $$
(12)

Finally, by simultaneously solution of Eqs. (11) and (12), unknown parameters are determined for different value of A.

4 Application

4.1 Example 1

Consider Duffing oscillator with cubic nonlinear term in the following form

$$ \textit{\"{u}} + u + \varepsilon u^{3} = 0,\,u\left( 0 \right) = A,\dot{u}\left( 0 \right) = 0. $$
(13)

The variational of Eq. (13) is given as follows

$$ J(u) = \int\limits_{0}^{t} {\left( { - \frac{{\dot{u}^{2} }}{2} + \frac{{u^{2} }}{2} + \varepsilon \frac{{u^{4} }}{4}} \right)dt} $$
(14)

Its Hamiltonian, therefore, can be written in the form

$$ H = \frac{{\dot{u}^{2} }}{2} + \frac{{u^{2} }}{2} + \varepsilon \frac{{u^{4} }}{4} = \frac{{A^{2} }}{2} + \varepsilon \frac{{A^{4} }}{4} $$
(15)

In order to determine residual, we substitute Eq. (10) into Eq. (15), and then, we have

$$ \begin{aligned} R(t) = & \frac{1}{2}\left( { - b\sin \left( {\omega t} \right)\omega - 3\left( {A - b} \right)\sin \left( {3\omega t} \right)\omega } \right)^{2} + \frac{1}{2}\left( {b\cos \left( {\omega t} \right) + \left( {A - B} \right)\cos \left( {3\omega t} \right)} \right)^{2} \\ \quad + \frac{1}{4}\varepsilon \left( {b\cos \left( {\omega t} \right) + \left( {A - b} \right)\cos \left( {3\omega t} \right)} \right)^{4} - \frac{1}{2}A^{2} - \frac{1}{4}\varepsilon A^{4} , \\ \end{aligned} $$
(16)

Based on collocation method, we have

$$ \mathop {Lim}\limits_{{\omega t \to \frac{\pi }{4}}} R\left( t \right) = b^{2} \omega^{2} - 3b\omega^{2} A + \frac{9}{4}\omega^{2} A^{2} + b^{2} - bA - \frac{1}{4}A^{2} + \varepsilon b^{4} - 2\varepsilon b^{3} A + \frac{3}{2}\varepsilon b^{2} A^{2} - \frac{1}{2}\varepsilon bA^{3} - \frac{3}{16}\varepsilon A^{4} = 0, $$
(17)

Also, based on Galerkin–Petrov method [30], we have

$$ \begin{aligned} \int\limits_{0}^{\frac{T}{4}} {R\left( t \right)\cos \omega tdt = } & - \frac{1}{180180\omega }\left( {43758A^{2} + 27549\varepsilon A^{4} + 679536b\omega^{2} A - 82368b^{2} - 71680\varepsilon b^{4} } \right. \\ \quad \left. { + 68640bA - 393822\omega^{2} A^{2} - 315744b^{2} \omega^{2} - 140544\varepsilon b^{2} A^{2} + 52096\varepsilon bA^{3} + 153600\varepsilon b^{3} A} \right) = 0. \\ \end{aligned} $$
(18)

By solving Eqs. (17) and (18) simultaneously, one can obtain amplitude–frequency relation. Simple energy balance method based on collocation method yields the following amplitude–frequency relation [27] for this example

$$ \omega = \sqrt {1 + \frac{3}{4}\varepsilon A^{2} } . $$
(19)

Comparisons between approximate frequencies obtained by different techniques are given in Table 1.

Table 1 Comparisons between frequencies obtained by different techniques for example 1
Full size table

Consider a case with ε = 10 and A = 5; for this case by using Eq. (19), simple EBM solution was obtained in the following form

$$ u\left( t \right) = 5\cos \left( {13.7295t} \right), $$
(20)

Also, improved EBM solution was obtained as follows

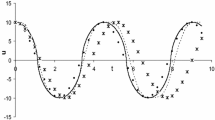
$$ u\left( t \right) = 4.8285\cos \left( {13.3692t} \right) + 0.1715\cos \left( {40.1076t} \right). $$
(21)

The comparison between analytic solutions obtained in Eqs. (20) and (21) in conjunction with fourth-order Runge–Kutta numerical solution was presented in Fig. 1. Comparison between phase-plane diagram obtained with analytical and numerical solution was presented in Fig. 2. The difference between analytical and numerical solution is plotted in Fig. 3. As seen in Table 1 and Figs. 1, 2 and 3, the results obtained by improved energy balance method yield very good accuracy and are in better agreement with numerical solution.

Fig. 1
figure 1

A comparison between the simple EBM and improved EBM in conjunction with the fourth-order Runge–Kutta method for example 1

Full size image
Fig. 2
figure 2

Phase-plane diagram obtained by analytical and numerical solution for example 1

Full size image
Fig. 3
figure 3

Difference between analytical and numerical solution for example 1

Full size image

4.2 Example 2

The Duffing equation with a double-well potential (with a negative linear stiffness) is an important model. One physical realization of such a Duffing oscillator model is a mass particle moving in a symmetric double-well potential. This form of the equation also appears in the transverse vibrations of a beam when the transverse and longitudinal deflections are coupled [32, 33]. Double-well Duffing oscillator is in the following form

$$ \textit{\"{u}} - u + u^{3} = 0,\,u\left( 0 \right) = A,\dot{u}\left( 0 \right) = 0. $$
(22)

When A > 2, oscillation occurs between symmetric limits [− A, A]. For the case 1 < A < 2, the oscillation occurs around stable equilibrium points u = +1 and is asymmetric about it. In the present study, we consider first case with A > 2.

The variational of Eq. (22) is given as follows

$$ J\left( u \right) = \int\limits_{0}^{t} {\left( { - \frac{{\dot{u}^{2} }}{2} - \frac{{u^{2} }}{2} + \frac{{u^{4} }}{4}} \right)dt} , $$
(23)

Its Hamiltonian, therefore, can be written in the form

$$ H = \frac{{\dot{u}^{2} }}{2} - \frac{{u^{2} }}{2} + \frac{{u^{4} }}{4} = - \frac{{A^{2} }}{2} + \frac{{A^{4} }}{4}, $$
(24)

In order to determine residual, we substituting Eq. (10) into Eq. (24); then, we have

$$ \begin{aligned} R\left( t \right) = & \frac{1}{2}\left( { - b\sin \left( {\omega t} \right)\omega - 3\left( {A - b} \right)\sin \left( {3\omega t} \right)\omega } \right)^{2} - \frac{1}{2}\left( {b\cos \left( {\omega t} \right) + \left( {A - b} \right)\cos \left( {3\omega t} \right)} \right)^{2} \\ \quad \quad + \frac{1}{4}\left( {b\cos \left( {\omega t} \right) + \left( {A - b} \right)\cos \left( {3\omega t} \right)} \right)^{4} + \frac{1}{2}A^{2} - \frac{1}{4}A^{4} , \\ \end{aligned} $$
(25)

Based on collocation method, we have

$$ \mathop {Lim}\limits_{{\omega t \to \frac{\pi }{4}}} R\left( t \right) = b^{2} \omega^{2} - 3b\omega^{2} A + \frac{9}{4}\omega^{2} A^{2} - b^{2} + bA + \frac{1}{4}A^{2} + b^{4} - 2b^{3} A + \frac{3}{2}b^{2} A^{2} - \frac{1}{2}bA^{3} - \frac{3}{16}A^{4} = 0, $$
(26)

Also, based on Galerkin–Petrov method [30], we have

$$ \begin{aligned} \int\limits_{0}^{\frac{T}{4}} {R\left( t \right)\cos \omega tdt = } & - \frac{1}{180180\omega }\left( { - 43758A^{2} + 27549A^{4} + 679536b\omega^{2} A + 82368b^{2} - 71680b^{4} } \right. \\ \quad \left. { - 68640bA - 393822\omega^{2} A^{2} - 315744b^{2} \omega^{2} - 140544b^{2} A^{2} + 52096bA^{3} + 153600b^{3} A} \right) = 0. \\ \end{aligned} $$
(27)

By solving Eqs. (26) and (27) simultaneously, one can obtain amplitude–frequency relation. Simple energy balance method based on collocation method yields the following amplitude–frequency relation [33] for this example

$$ \omega = \sqrt { - 1 + \frac{3}{4}\varepsilon A^{2} } . $$
(28)

Comparisons between approximate periods obtained by simple and improved energy balance method and exact period are given in Table 2. Frequency and period of oscillation have the following relation with together

$$ T = \frac{2\pi }{\omega }. $$
(29)

When A = 1.7, by using Eq. (28), simple EBM solution obtained in the following form

$$ u\left( t \right) = 1.7\cos \left( {1.08053t} \right), $$
(30)

And improved EBM solution obtained as follows

$$ u\left( t \right) = 1.6059\cos \left( {0.99809t} \right) + 0.0941\cos \left( {2.99427t} \right). $$
(31)
Table 2 Comparison between simple and improved EBM in conjunction with exact period
Full size table

Also, when A = 10, by using Eq. (28), simple EBM solution obtained in the following form

$$ u\left( t \right) = 10\cos \left( {8.60239t} \right), $$
(32)

For this case, improve EBM solution obtained as follows

$$ u\left( t \right) = 9.65168\cos \left( {8.36893t} \right) + 0.34832\cos \left( {25.10679t} \right). $$
(33)

The comparison between analytic solutions obtained in Eqs. (30), (31), (32), and (33) in conjunction with fourth-order Runge–Kutta numerical solution was presented in Figs. 4 and 5. The results show that the improved energy balance method very effectively reduce error and yields better accuracy.

Fig. 4
figure 4

A comparison between the simple EBM and improved EBM in conjunction with the fourth-order Runge–Kutta method for example 2 (A = 1.7)

Full size image
Fig. 5
figure 5

A comparison between the simple EBM and improved EBM in conjunction with the fourth-order Runge–Kutta method for example 2 (A = 10)

Full size image

4.3 Example 3

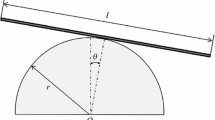
Mathematical model of the nonlinear oscillation of pendulum attached to a rotating support [34–36] is in the following form

$$ \ddot{\theta } + \sin \left( \theta \right)\left( {1 - \varLambda \cos \left( \theta \right)} \right) = 0,\,\theta \left( 0 \right) = A,\dot{\theta }\left( 0 \right) = 0. $$
(34)

where Λ is a function of rotating support angular velocity, the acceleration of gravity, and length of pendulum. Without loss of generality, we set Λ = 1. In order to solve Eq. (34) by improved energy balance method, we rewrite this equation based on Taylor expansion in the following form

$$ \ddot{\theta } + \frac{{\theta^{3} }}{2} - \frac{{\theta^{5} }}{8} + \frac{{\theta^{7} }}{80} = 0,\,\theta \left( 0 \right) = A,\dot{\theta }\left( 0 \right) = 0. $$
(35)

The variational of Eq. (35) is given as follows

$$ J\left( u \right) = \int\limits_{0}^{t} {\left( { - \frac{1}{2}\dot{\theta }^{2} + \frac{{\theta^{4} }}{8} - \frac{{\theta^{6} }}{48} + \frac{{\theta^{8} }}{640}} \right)dt} , $$
(36)

Its Hamiltonian, therefore, can be written in the form

$$ H = \frac{1}{2}\dot{\theta }^{2} + \frac{{\theta^{4} }}{8} - \frac{{\theta^{6} }}{48} + \frac{{\theta^{8} }}{640} = \frac{{A^{4} }}{8} - \frac{{A^{6} }}{48} + \frac{{A^{8} }}{640}, $$
(37)

In order to determine residual, we substituting Eq. (10) into Eq. (37); then, we have

$$ \begin{aligned} R\left( t \right) = & \frac{1}{2}\left( { - b\sin \left( {\omega t} \right)\omega - 3\left( {A - b} \right)\sin \left( {3\omega t} \right)\omega } \right)^{2} + \frac{1}{8}\left( {b\cos \left( {\omega t} \right) + \left( {A - b} \right)\cos \left( {3\omega t} \right)} \right)^{4} \\ -\frac{1}{48}\left( {b\cos \left( {\omega t} \right) + \left( {A - b} \right)\cos \left( {3\omega t} \right)} \right)^{6} + \frac{1}{640}\left( {b\cos \left( {\omega t} \right) + \left( {A - b} \right)\cos \left( {3\omega t} \right)} \right)^{8} \\ \quad - \frac{1}{8}A^{4} + \frac{1}{48}A^{6} - \frac{1}{640}A^{8} , \\ \end{aligned} $$
(38)

Based on collocation method, we have

$$\mathop {Lim}\limits_{{\omega t \to \frac{\pi }{4}}} R\left( t \right) = \frac{9}{4}\omega^{2} A^{2} - \frac{3}{2048}A^{8} - \frac{7}{160}b^{3} A^{5} - \frac{7}{40}b^{5} A^{3} - \frac{1}{10}b^{7} A + \frac{7}{64}b^{4} A^{4} + \frac{7}{40}b^{6} A^{2} - \frac{1}{640}bA^{7} + \frac{7}{640}b^{2} A^{6} + b^{2} \omega^{2} + \frac{3}{4}b^{2} A^{2} \quad - b^{3} A - \frac{1}{4}bA^{3} + \frac{1}{32}bA^{5} - \frac{5}{32}b^{2} A^{4} + \frac{5}{12}b^{3} A^{3} + \frac{1}{2}b^{5} A - \frac{5}{8}b^{4} A^{2} \quad - \frac{3}{32}A^{4} + \frac{7}{384}A^{6} + \frac{1}{2}b^{4} + \frac{1}{40}b^{8} - 3b\omega^{2} A - \frac{1}{6}b^{6} = 0,$$
(39)

Also based on Galerkin–Petrov method [30], we have

$$ \begin{gathered} \int\limits_{0}^{\frac{T}{4}} {R\left( t \right)\cos \omega tdt = } - \frac{1}{1070845776000\omega }\left( { - 2340562910400\omega^{2} A^{2} + 1197025389A^{8} } \right. \hfill \\ \quad + 50757697536b^{3} A^{5} + 12994058646b^{5} A^{3} + 50381979648b^{7} A - 101033246720b^{4} A^{4} \hfill \\ \quad - 106092822528b^{6} A^{2} + 2845175808bA^{7} - 16206962688b^{2} A^{6} - 1876529740800b^{2} \omega^{2} \hfill \\ \quad - 417640550400b^{2} A^{2} + 456437760000b^{3} A + 154808473600bA^{3} - 32421094400bA^{5} \hfill \\ \quad + 136065792000b^{2} A^{4} - 288370688000b^{3} A^{3} - 237404160000b^{5} A + 355446784000b^{4} A^{2} \hfill \\ \quad + 81864608400A^{4} - 15065943000A^{6} - 213004288000b^{4} - 10796138496b^{8} \hfill \\ \quad \left. { + 4038618355200b\omega^{2} A + 69638553600b^{6} } \right) = 0. \hfill \\ \end{gathered} $$
(40)

By solving Eqs. (39) and (40) simultaneously, one can obtain amplitude–frequency relation. Simple energy balance method based on collocation method yields the following amplitude–frequency relation [36] for this example

$$ \omega = \frac{2}{A}\sqrt {\cos \left( {\frac{\sqrt 2 }{2}A} \right) - \frac{1}{4}\cos \left( {\sqrt 2 A} \right) - \cos \left( A \right) + \frac{1}{4}\cos \left( {2A} \right)} . $$
(41)

When A = 1, by using Eq. (41), simple EBM solution obtained in the following form

$$ y = \cos \left( {0.55468t} \right), $$
(42)

And improve EBM solution obtained as follows

$$ y = 0.96382\cos \left( {0.54117t} \right) + 0.03618\cos \left( {1.62351t} \right), $$
(43)

Comparison between simple EBM, improved EBM, and numerical solution has been done in Table 3; as can been seen, improved EBM solution yields better accuracy, and results are in good agreement with numerical solution.

Table 3 A comparison between results of simple EBM, improved EBM and numerical solution for θ(t). (A = 1)
Full size table

When A = 1.5, by using Eq. (41), simple EBM solution obtained in the following form

$$ y = 1.5\cos \left( {0.73132t} \right), $$
(44)

And improved EBM solution obtained as follows

$$ y = 1.44376\cos \left( {0.72016t} \right) + 0.05624\cos \left( {2.16048t} \right), $$
(45)

The comparison between analytic solutions obtained in Eqs. (44) and (45) in conjunction with the fourth-order Runge–Kutta numerical solution was presented in Fig. 6.

Fig. 6
figure 6

A comparison between the simple EBM and improved EBM in conjunction with the fourth-order Runge–Kutta method for example 3 (A = 1.5)

Full size image

5 Conclusion

In this study, accuracy of He’s energy balance method is improved for the analysis of conservative nonlinear oscillator. To illustrate the accuracy of proposed method, three examples are considered. Obtained results are in very good agreement with those obtained via numerical solution, and error of simple energy balance method is very effectively reduced. We conclude this method is very effective and convenient for analysis of conservative nonlinear oscillators.