1 Introduction

In many researches carried out recently, it has been proved that the nature has the best optimization techniques in it, for maintaining the global systems. Sharing the information between chromosomes in giving birth to offspring and finding the shortest path of the food sources of ants, movements of bird flocks, foraging behavior of honey bees, etc., bring the idea of optimization techniques (like GA, ACO, PSO, ABC and other hybrid methods) that have opened a wide door and scope for researches. In the last two decades, the use of these evolutionary techniques extremely got the attention of the researchers in hydrological field. The main problem is that the development of the model and application of the methodology are totally problem dependent. None of these methods are unique for all types of problem formulation. Also, the application in real-world problem is full of complexities. Here, we analyzed these methods in solving reservoir release optimization problem and build up the problem formulation as a purpose of practical application. We have prepared a curve that can tell us how much water release would be an optimum release for a definite period of time with a known inflow condition and storage volume.

Reservoir operation is a complex task as it deals with the natural uncertainties and directly handles the human needs. Irrigation, flood protection, storage of the water, domestic water supply and hydropower generations are the common functions of reservoir systems. The consumable water is limited in our world and careful uses of water resources are very much essential. So, only a proper optimization technique can assure these aspects. Artificial methods (inspired by natural techniques) are the powerful and popular tools as till now the researchers are using these in solving different kind of complex problems like global positioning system [1], improving quality service of computer networks [2], designing spread footing [3], water quality prediction [4]. Wardlaw and Sharif [5] used GA to solve the well-known “four reservoir problem” where they concluded that the real-coded GA can produce the best results more efficiently. Kennedy and Eberhart [6] added a new level of accuracy and simplicity in optimization technique inspiring from the natural bird flocking, and they named it as particle swarm optimization (PSO). Kumar and Reddy [7] successfully applied PSO to reservoir optimization problem. In PSO, the algorithm is free from the complexity of using the basic operators of GA, that is, crossover and mutations. Even though PSO is very fast in searching optimal solution, it has some drawbacks and application difficulties too. Premature convergences, failing in finding better solutions for complex functions and asking for fine tuning of the parameters are the common problems of PSO algorithm [8].

In this study, we use the most recently developed artificial bee colony (ABC) optimization algorithm [9] to solve the reservoir optimization problem. ABC optimization algorithm is another population-based swarm intelligence and inspired by natural foraging behavior of honey bees. The optimization results obtained from ABC algorithm were compared with the results of GA and PSO techniques. The detailed explanation of ABC optimization is given in Sect. 3 of this paper. In searching for an optimal reservoir release rules, whole inflow pattern was categorized into three states on the basis of available historical data. For each monthly inflow states, we developed release curves with respect to different storage conditions.

2 GA and PSO algorithms in reservoir release optimization

2.1 Genetic algorithm

Application of GA is not new in reservoir optimization field. Both binary- and real-coded GA were already successfully applied in many reservoir release problems, and the efficiency of these models is comparatively very good with previously used methods like dynamic programming [10] and linear programming [11]. As GA is already well developed in this research field, we took the opportunity to skip the basic description of the problem formulation, and besides, we referred some previous excellent works for basic understanding and future developments [5, 10, 12, 13].

In this study, we have adopted the modified mating technique in GA algorithm given by Haupt and Haupt [14]. For binary GA, a single mating point was selected by using the following equation:

$$ matingpo\text{int} = round((nbits \times n\text{var} ^{-1}) \times [r]) $$
(1)

In Eq. (1), nbits represents total number of bits, nvar number of variables and [r] a row matrix of randomly generated numbers between 0 and 1. After selecting the mating point, the parent chromosomes were allowed to interchange their genes (bits) in respect of this mating point to produce new offsprings. In cases of real-coded GA, the mating point was selected by using Eq. (2).

$$ matingpo\text{int} = round(n\text{var} \times [r]) $$
(2)

After selecting the mating point, new chromosomes were created by interchanging the information between the two chromosomes that are selected as parents. Binary mutation was done easily by changing 0 to 1 and vice versa by maintaining a mutation rate. The following mathematical equations were used in the main algorithm to perform mutation process for real-coded GA.

$$ n_{\text{mut}} = (popsize - 1) \times n\text{var} \times rate_{\text{mut}} $$
(3)
$$ row_{\text{mut}} = {\text{sort}}({\text{roundup}}([r] \times (popsize - 1)) + 1) $$
(4)
$$ column_{\text{mut}} = {\text{roundup}}([r] \times n\text{var} ) $$
(5)

In Eqs. (3), (4) and (5), n mut represents total mutation number, popsize population size, nvar variable number, row mut selected row number for the variable to be mutated, Column mut selected column number for the variable to be mutated, and [r] a row matrix (dimension −1, discard/2) consisting of random numbers between 0 and 1.

The application procedure followed in this study to implement GA in finding the optimal release by maintaining storage bounds and continuity constraints is given as:

  1. 1.

    Set the objective function

  2. 2.

    Generate an initial population with random values within the allowable water release ranges

  3. 3.

    Compute the fitness value of the objective function using population members

  4. 4.

    Search the minimum fitness values and the responsible strings causing the lower fitness

  5. 5.

    Replace the weaker string (string posing greater fitness values in minimizing the water deficit) by the string stored in step 4

  6. 6.

    Create new population members by using the basic operators of GA, that is, selection, crossover and mutation

  7. 7.

    Update the old population with newest member of step 6

  8. 8.

    Back to the step 3, until the iteration condition is fulfilled.

2.2 Particle swarm optimization

PSO is also a population-based search technique where a population of particles starts their journey in a space with respect to the current best position. The basic algorithm comes up from the idea of the natural technique of bird flocking and firstly proposed by Kennedy and Eberhart [6]. Kumar and Reddy [7] used an improved PSO and proved its nobility in reservoir optimization field. In this technique, a population starts to move toward a global optimum solution by following the current best position. So, initially it searches for a local solution and after that it updates the particles (in PSO literature, it is called adding velocity) and compares the fitness with the previous one. Thus, the particles tend toward the global optimum solution. The PSO algorithm is controlled by the following two equations:

$$ v_{ij}^{t + 1} = \chi [wv_{ij}^{t} + \phi_{1} r_{1}^{t} (p_{ij}^{t} - x_{ij}^{t} ) + \phi_{2} r_{2}^{t} (p_{gj}^{t} - x_{ij}^{t} )] $$
(6)
$$ x_{ij}^{t + 1} = v_{ij}^{t + 1} + x_{ij}^{t} $$
(7)

Here, Eq. (6) expressed the velocity updates and Eq. (7) represents the position updates of the particles. If we have a problem consisting of D variables, then j = 1, 2, 3,…, D; and if the size of the swarm was considered as N, then i = 1, 2,…, N. During the tth iteration, if a particle is holding a position \( x_{ij}^{t} \) with a local best position of \( p_{ij}^{t} \)and yet the global best position of \( p_{gj}^{t} \), then for the next iteration (t + 1), the velocity will update as \( v_{ij}^{t\; + \;1} \) by using Eq. (1), where χ represents constriction coefficient, ϕ 1 and ϕ 2 acceleration coefficient, w inertial weight, and r 1 and r 1 random numbers in [0, 1].

To control the velocity, a maximum value was considered to be followed by the algorithm (as given in Equation 5.3). The value of the maximum velocity was taken as the fraction of the differences between upper and lower limits of the decision variables.

$$ v_{\hbox{max} } = (R_{\hbox{max} } - R_{\hbox{min} } ) \times r $$
(8)
$$ v_{\text{initial}} = v_{\hbox{max} } \times [r]_{{(popsize,n\text{var} )}} $$
(9)

The initial velocity was generated by using Eq. (9). Here, R represents the release options and r represents a fraction number between 0 and 1. Instead of adopting the standard way for using the value of the weight (w) in velocity updating process (Eq. 6), here an improved technique was followed. Different values were assigned to the inertial weight for updating the velocity for each step of iteration. The following expressions will help describe the procedures:

$$ weightstep = \frac{{w_{\hbox{max} } - w_{\hbox{min} } }}{\text{total iteration number}} $$
(10)
$$ w_{i} = w_{\hbox{max} } - (weightstep \times i) $$
(11)

Equation (10) represents the weight steps for each iteration where w max and w min are the considered limits of the weight. This weight step was used in any ith iteration to calculate the actual inertial weight for that particular iteration as given in Eq. (11).

The steps followed in this study in view of applying PSO algorithm in searching optimum release are given below:

  1. 1.

    Building up the objective function

  2. 2.

    Set the PSO parameters

  3. 3.

    Generate an initial population with random values within the allowable water release ranges

  4. 4.

    Compute the fitness values of the objective function (mentioned in step 1.) using population members

  5. 5.

    Generate random initial velocity with the same dimension as population in step 3

  6. 6.

    Store the local best and global best among the population

  7. 7.

    Update the particles to create new population by using Eqs. (6) and (7)

  8. 8.

    Crop to upper and lower range to maintain the allowable water release bounds

  9. 9.

    Compute the fitness values and compare with the previous solutions

  10. 10.

    Back to the step 6, until the iteration condition is fulfilled.

3 Artificial Bee Colony Optimization

3.1 Foraging behavior of honey bee

Based on the reaction–diffusion equations, Tereshko [15] developed a model of honey bee colony. He observed two dominating components of bee’s colony: recruitment and abandonment of the located food sources. The main components of his model consist of the following:

Food sources: A forager bee chooses a food source on the basis of some quality like distance of it from the hive, amount of food, and difficulties involved in getting the food.

Employed foragers: Employed foragers are those bees that are currently busy in exploiting a specific food source and should carry the information about that source. After returning to the hive, they share this information with other bees.

Unemployed foragers: A forager was known as an unemployed bee if it either never involved in collecting nectar before or abandoned a food source. Unemployed foragers normally wait in the hive to involve in the process and it happened in two ways. They could be selected either as “Scout Bees” to explore outside in search of previously undiscovered food sources or as “Onlooker Bees” to wait for the information of employed bee and to follow him to the food source.

To share the information of the food source that was carried by the employed bees, a physical movement technique is adopted known as “Waggle Dance.” The intensity and the pattern of the dance pass the information to the onlooker bees. The activities of the employed, onlooker and scout bees are nicely described by Karaboga and Akay [16]. All honey bees are identical in nature and shape, so it is easy to replace one with another among positions of these three categories. Let us examine Fig 1 for better understanding the foraging behavior of honey bees. In Fig. 1, an employed bee follows the path E from food source to hive. After storing the nectar, he has three options to choose on the basis of the current situation of the source: E1, to continue exploiting; E2, waggle dancing to pass the information; and E3, to become an unemployed bee after abandoning the food source. On the other hand, onlooker bees were waiting in the hive and observing the waggle dance (position O) to get recruited. After getting a signal from an employed bee, he followed the path O1 and reached the food source. Sometimes, it might be needed to explore new food sources and then the scout foragers’ follow path S. With the combination of these three interchanging behaviors and sharing the knowledge of local optima, bees show their intelligence in finding global optima.

Fig. 1
figure 1

Foraging behavior of honey bees

Full size image

3.2 ABC algorithm in reservoir release optimization

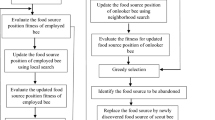
The application of ABC algorithm is very new in reservoir release optimization. Karaboga and Basturk [17] compared ABC with other evolutionary methods in solving classical benchmark functions. Hossain and El-Shafie [18] used ABC in optimization release policy for a reservoir system. In different optimization problems and application platform, many studies suggested adopting ABC methodology in both standards improved the form [19, 20]. In this algorithm, the position of a food sources was considered as the solution (here release options) for the optimization problem and the fitness values of the corresponding solutions represent the food source quality. So for the monthly time period, a set of 12 numbers of release options together represents a food source. As the number of employed and onlooker bees is same, we can consider a set of N food sources and thus create the initial population with N numbers of strings. The bees carry the information about the food source quality (fitness values) and share the information about them to others. The algorithm is actually run with the performance of these three types of bees; here, the word “types” means the bees characteristics according to their working manners. And also they are identical and interchangeable with each other. The individual working principles are given as follows.

Function of employed bees: An employed bee goes to the source and save the information about the food sources. They can modify the position of a food source in their memory keeping in mind the present quality of food sources. A candidate solution that was randomly chosen and modified can be expressed as:

$$ v_{ij} = x_{ij} + \phi_{ij} (x_{ij} - x_{ik} ) $$
(12)

Here, x ij represents the current candidate solution of any randomly chosen source, and x ik represents other randomly chosen solution but must be taken from different neighbor source. ϕ ij is taken as a random number between [−1 to 1].

Function of onlooker bees: The onlooker bees followed the direction and information given by employed bees. Each food sources have a probability of being selected by the onlooker, and this probability is assigned on the basis of the corresponding source quality. If the fitness value of ith food source is f(x i ), then with a total n = 1,2,…, N population, the probability for the ith food source for being selected can be determined by

$$ p_{i} = \frac{{f(x_{i} )}}{{\sum\nolimits_{n = 1}^{N} {f(x_{n} )} }} $$
(13)

After selecting the food sources, onlookers again update the candidate solution using Eq. (12). It is important to note that the onlookers deal with the food sources that are already filtered by the employed bees.

Function of scout bees: The position of the abandoned food sources needs to be taken by new sources and scout bees can provide such new sources. The new source was also created in a random fashion within the variable bounds.

The steps followed in this study to apply ABC algorithm in search of optimal release of a reservoir are described as

  1. 1.

    Building up the objective function

  2. 2.

    Create a population of decision variables that represent the food sources

  3. 3.

    Calculate the fitness of each source and save the minimum fitness and corresponding solutions

    Begin Iteration

          Introduce Employed Bees

  4. 4.

    Select a random candidate of any source and a different random neighbor source

  5. 5.

    Modify the source using Eq. (12)

  6. 6.

    Compute the fitness of new solutions and compare with the previous best result

  7. 7.

    Store the better sources and point out the abandoned food sources

  8. 8.

    Perform the processes 4–7 for all sources

          Introduce Onlooker Bees

  9. 9.

    Calculate the probability using Eq. (13) for each food source provided by employed bees

  10. 10.

    Select the sources according to their probability of selection

  11. 11.

    Improve the candidate solution using Eq. (12)

  12. 12.

    Compute the fitness of new solutions and compare with the previous best result

  13. 13.

    Store the better sources and point out the abandoned food sources

  14. 14.

    Perform the processes of 10 to 13 for all sources

          Introduce Scout Bees

  15. 15.

    Find the positions of the abandoned food source

  16. 16.

    Replace the abandoned source with randomly created source

  17. 17.

    Provide the population that is free from abandoned sources for the next iteration

    End Iteration

4 Case studies and model implementations

4.1 Klang gate dam (KGD)

The Klang gate dam was opened in 1958 and is located in Taman Melawati, Malaysia. The main functions of the dam are the water supply for the people of Klang area and to protect them from the flood. The monthly inflow for the dam was categorized into three states (high, medium and low) from the analysis of 264 sequential monthly historical inflow data and given in Table 1. Other constraints and reservoir bounds (in MG) are given below:

Table 1 Monthly inflow and water demand (in MG) for KGD
Full size table

  • Storage constraint: The reservoir storage in a month should not be less than the dead storage and should not be more than the capacity of the reservoir, 1,648.67 ≤ S t  ≤ 6,194

  • Release constraint: The release of water from the reservoir to meet the water demand of the area has a lower and upper bound, 868 ≤ R t  ≤ 1,379.50

For KGD, the authority assumed the loss that relates the inflow amount for a particular month. This study followed the following guideline provided by Puncak Niaga (M) Sdn. Bhd, Malaysia, to compute the water losses. The losses were computed and are given in Table 2.

Table 2 Range of inflow and value of loss (in MG)
Full size table

4.2 Model formulation

A reservoir optimization model may deal with maximizing benefits, minimization of operational cost, meeting various (municipal and/or industrial) water demands or any combination of these objectives. Here, the minimization of water deficit was used as the main objective. The formulation of the objective function and the constraint handling methods are given below:

Objective function: The main objective considered in this study is to minimize the squared deviation of monthly release to water demand and can be expressed as Eq. (14).

$$ \hbox{min} \;f(x) = \sum\nolimits_{t = 1}^{12} {\left( {D_{t} - x_{t} } \right)^{2} } $$
(14)

Here, D t and x t are the downstream water demands and release in any time period t, respectively.

Constraint handling: As the releases are considered as the decision variables, the population with random values for each technique was build by using the upper limit and lower limit of the release as Eq. (15), where N is the population size and the D is the total number of decision variables.

$$ [population]_{N,D} = release_{\hbox{min} } + [rand]_{N,D} *(release_{\hbox{max} } - release_{\hbox{min} } ) $$
(15)

It is very important to maintain the continuity equation for any hydrological modeling, and in this study, the continuity equation is readily satisfied as the final storage for any month is determined by using Eq. (16).

$$ S_{(t + 1)} = S_{t} + I_{t} - R_{t} - {\text{Losses}}_{t} $$
(16)

However, some of the final storages calculated here may violate the storage bounds, and using the penalty function approach, we recovered the problem. In penalty function approach, a penalty term is introduced with the main objective function, and for this minimization problem, the variables that caused to violate the storage constraints are eliminated through the optimization process. The penalty terms used in this study are given below:

$$ penalty1 = \left\{ {\begin{array}{*{20}c} 0 \hfill & {{\text{if }}S_{t} \; > \;S_{\hbox{min} } } \hfill \\ {C_{1} (S_{\hbox{min} } - S_{t} ) \, ^{2} } \hfill & {{\text{if }}S_{t} \; < \;S_{\hbox{min} } } \hfill \\ \end{array} } \right.\quad {\text{and}}\quad penalty2 = \left\{ {\begin{array}{*{20}c} 0 \hfill & {{\text{if }}S_{t} \; < \;S_{\hbox{max} } } \hfill \\ {C_{2} (S_{t} - S_{\hbox{max} } ) \, ^{2} } \hfill & {{\text{if }}S_{t} \; > \;S_{\hbox{max} } } \hfill \\ \end{array} } \right. $$

In the above-mentioned penalty terms, the penalty coefficient C generally got a big numerical value to maintain the elimination of constraint-violating solutions. The entire working pattern is shown in Fig. 2.

Fig. 2
figure 2

Working pattern in search of optimal reservoir release

Full size image

4.3 Performance checking

In order to check the performance of all optimization tools used here, a simulation is done based on historical monthly inflow data. The general indices like reliability, vulnerability, resilience and shortage index calculated with the release were provided by ABC, PSO and GA optimization models. The periodical reliability was calculated as a percentage of how many times the proposed water release is able to meet the demand over the total time period. The reliability of firm water (R FY ) can be calculated by using Eq. (17).

$$ R_{FY} = 1 - \frac{S}{FY} $$
(17)

In the above equation, S represents the average annual water deficit, and FY is the firm yield and can be taken as the annual target demand. In this study, we have calculated the average annual water deficit for a sequence of T = 22 years of historical data using Eq. (18).

$$ S = \frac{1}{T}\sum_{i = 1}^{T} {\frac{{\sqrt {\left( {Deficit_{i} } \right)^{2} } }}{Demand}} $$
(18)

Shortage index (SI) also can be used as a measure of performance checking. The SI carries the information about the periodical reliability as well as the magnitude of deficit. Here, we used Eq. (19) to calculate the shortage index.

$$ SI = \frac{100}{T}\sum {\left( {\frac{{{\text{annual}}\;{\text{deficit}}}}{{{\text{annual}}\;{\text{demand}}}}} \right)}^{2} $$
(19)

Vulnerability is the measure of worst-case scenario that can be experienced by a reservoir system. During the simulation, the maximum deficit occurred in any period, was taken as the vulnerability of the model and represented as percentage of demand. In this study, we considered another way to define vulnerability. Here, we calculated the average annual inflow of available historical data, and for the lowest annual inflow, we observed the model performances. Resilience is the probability for a shortage period to meet the demand for the next period release. In order to compute the resiliency, Loucks and Beek [21] took the ratio of the number of satisfied releases that follows an unsatisfied value to the total number of unsatisfactory occurred. According to this formula, simply the ratio of maximum number of consecutive satisfied period occurred by a model output to the total number of water shortage period was calculated. So, mathematically, it can be expressed as Eq. (20).

$$ \text{Re} {\text{silience}} = \frac{{{\text{no}} .\;{\text{of}}\;{\text{period}}\;{\text{a}}\;{\text{satisfactory}}\;{\text{value}}\;{\text{follows}}\;{\text{an}}\;{\text{shortage}}}}{{{\text{no}} .\;{\text{of}}\;{\text{total}}\;{\text{shortage}}\;{\text{period}}}} $$
(20)

There is another simple way to define resiliency. The maximum number of consecutive failure can be taken to measure the ability of a model to get back in track after a single failure. But in this way, the lower number of consecutive failure is better in comparing the resiliency of different release policy modeling.

5 Results and discussions

The best release options for all months with different initial storages were determined by using four optimization techniques. The primary objective was to produce a curve that can show the optimum releases for a defined inflow category. So here, we have twelve different release policies for each inflow category. Figure 3a, b, c is such calibrated curves for the month of January considering high (Fig. 3a), medium (Fig. 3b) and low (Fig. 3c) inflow states. The aim of these optimization models was to provide a release policy that can minimize the water deficit as far as possible, maintaining the release bounds for every month and safe storage volume. So here, the storage condition was also provided with the release options to get the clear picture of the reservoir system.

Fig. 3
figure 3

Release options for the month of January

Full size image

To find the closest curve to a demand for a specific inflow category, the root mean square error (RMSE) approach is used (given as Eq. 21). In Eq. (11), i is denoted as the indexes of 10 known values of the release curve (i = 1, 2,…, 10). The RMSE for every month is given in Table 3 for medium inflow (medium inflow is chosen because no violation of storage constraint has occurred). ABC optimization showed the lowest error in this case study.

Table 3 RMSE (in MG) of all techniques for medium-inflow category
Full size table
$$ {\text{RMSE}} = \sqrt {mean((x_{i} - Demand)^{2} )} $$
(21)

The fitness through the all iteration processes is shown in Fig. 4. From the figure, we can see that both the swarm intelligence techniques, ABC and PSO, performed better than the genetic algorithms for the same problem configuration and formulation. Totally, 22 years (from 1887 to 2008) of historical actual inflow data were used for checking the model efficiency and verification purpose. The selection of the release curve among high, medium and low category was done by observing the actual inflow amount of a month. After the selection of the correct curve, the amount of release can be determined for a specific initial storage condition of the reservoir. The demand and the releases from the simulation are shown in Fig. 5a, b, c, d. For graphical convenience, here we only presented the optimum release of the time period starting form January 1995 to December 2008.

Fig. 4
figure 4

Fitness values for different optimization techniques

Full size image
Fig. 5
figure 5

Release and demand analysis using historical inflow, obtained from a ABC optimization b PSO c Real-coded GA and d Binary GA

Full size image

In Fig. 5, for all cases, we can see some scarcity of water, which occurred mainly for low inflow during that time period. For example, on February 1996, the inflow was only 221.3 MG, and so, the logical optimum release must be below the demand of that month to keep the storage of reservoir in allowable range. The releases given by the binary-coded GA are rarely meeting the actual demands where ABC and PSO seem to lead among these four methods in meeting the demand most of the time period. Here, from Fig. 5a–d, we can see that the swarm intelligences showed better performance than evolutionary GA algorithms. In addition, Fig. 6 shows the performance of swarm intelligences over real-coded GA. In this figure, the release curve for the month of June is presented considering the medium inflow.

Fig. 6
figure 6

Comparing GA and ABC algorithms

Full size image

Figure 6 shows that the ABC release options are reached and follow the demand line more quickly and closely than GA releases. Also, during the dead storage, ABC release curve shows the minimum deficit. To analyze the periodical reliability, a useful technique was applied. After using actual historical inflow of 22 years, each model gives monthly release policy, which linked 1 month to another. So for analyzing 22 years, there is a chain of optimum release options consisting of 264 values of release for 264 consecutive months (from January 1987 to December 2008). For example, from the very beginning, we used the actual inflow and reservoir storage for the month of January 1987, and each model provides the optimum release option for that particular month. With this optimum release, we calculate the final storage and used this storage value as initial storage for the next consecutive month (i.e., February 1987). Now, we can count for every year how many times the releases are meeting the demands and how many months they are not for all methods. The results for these observations are given in Table 4. Among the total of 264 months, 162 times the optimum release options of ABC optimization technique are able to meet the demand which is 61.36 % of total number of release results. PSO results meet the demands 157 times (59.47 %), real-coded GA 147 times and binary GA only 62 times. Excess release from demand also causes wastage of water and is not preferable for any hydrological optimization models. In this case, ABC optimization and PSO model provide excess release for 32 times (12.12 %), which is less than other two models. Table 5 shows the reliability, vulnerability and other performance checking measures.

Table 4 Periodical reliabilities: categorized in terms of meeting demand
Full size table
Table 5 Performance checking measures
Full size table

The average annual inflow for 22 years is shown in Fig. 7. According to this figure, lowest average inflow occurred in the year of 1992. So in this period of time, water deficit is very usual and logical. Also, the maximum consecutive period of failure (resilience) and the maximum deficit (vulnerability) occurred in this time period. We observed the performances of the release curves generated by ABC, PSO and GA methods individually in this particular year. The deficit occurred due to the release options given by these optimization methods, which are tabulated in Table 6. In this critical period of lowest inflow, ABC optimization and PSO algorithm were able to provide the release options with the minimum water deficit.

Fig. 7
figure 7

Average annual historical inflows for KGD

Full size image
Table 6 Water deficits for the year of 1992
Full size table

After observing all the experimental results, a conclusion can be made that the swarm intelligence performs better in providing optimum releases for a reservoir system. The application of ABC optimization technique is very new in reservoir release policy and provides comparatively better results than the well-established methods in this field like PSO and GA. Some indices seem very near to each other among the ABC and PSO, but the overall performance of ABC is better than PSO in this study.

6 Conclusion

The verification of all the models was done using actual historical inflow of 22 years. The release policy was developed for different inflow states with a view of using in practical reservoir system management. The decision maker easily can have the optimum release for a month with the help of release curves generated in this study. ABC and PSO algorithms are very fast, and the results are very close to each other in finding optimal solutions. The simplicity of the ABC optimization technique is the main attraction over PSO algorithm in finding release policy of a reservoir. Less parameter handling, simple analysis of the problem and, also very important, the practical applications in a reservoir system suggest considering the ABC algorithm in this research field.