A recurrent neural network-based identification of complex nonlinear dynamical systems: a novel structure, stability analysis and a comparative study

Abstract

For the purpose of identifying nonlinear dynamic systems, a compound recurrent feed-forward neural network based on the combination of feed-forward neural network (FFNN) and locally recurrent neural network is proposed. FFNNs are known to approximate any function, but since they lack memory in their structures, they are unable to reliably forecast the outputs of complex dynamical systems, which are characterized by severe non-linearities. On the other hand, recurrent neural networks (RNNs) lack simplicity (in their structure) but are able to capture the temporal relationship existing between the input–output data. In this study, an attempt is made to merge the FFNN and RNN to provide a straightforward and efficient model for capturing the complex dynamics of any nonlinear systems. Back-propagation (BP) algorithm is used to derive the weight update equations and the Lyapunov-stability principles are applied to test the stability of the proposed framework. The proposed model performance is evaluated and compared with state-of-the-art neural models by applying it for the identification of the unknown dynamics of three complex nonlinear systems. The results of the simulation demonstrate that, in comparison to other neural models, the suggested structure has provided greater prediction accuracy, better performance in the scenario of disturbance signals, and better response in the case of parameter variation.

1 Introduction

The use of neural networks for dynamic system identification and control has attracted a lot of attention in recent years. If there is insufficient knowledge about the system being modeled, identification is required. In contrast to mathematical modeling, which bases the behavior of the system on the physical principles, one simply needs observed input–output data and the order of the system for identification. Neural networks can be used to readily obtain an empirical model, rather than a mathematical model, to characterize the system once input–output data have been seen and the system’s order has been established (Coban 2013). The limits of conventional techniques to nonlinear, resilient, and adaptive control of uncertain complex systems have been increasingly addressed by the application of intelligent and cognitive control mechanisms. Although uncertain complex systems are undoubtedly difficult to regulate, such intelligent controllers have achieved significant theoretical advancements. For example, while NN and fuzzy systems are essentially intelligent architectures inspired by the way the human mind and brain work, they are also architectures with a shown capacity for universal approximation, and they have frequently been utilized to create controllers with theoretically verifiable stability (Baghbani et al. 2018). According to Mohammed et al. (2018) and Mostafa et al. (2019), the neural network (NN) is a well-known supervised machine learning technology that can classify difficult and nonlinear situations. It is a computational approach that is used to provide answers to some classification or prediction issues based on a collection of parameters that are expressed in mathematical operations (Pathiravasam et al. 2020; Kumar Chandar 2021). There are many different types of NN, such as feed forward neural networks, multi-layer perceptron, recurrent neural networks (RNN), such as the Elman and Jordan recurrent neural networks, as well as modular neural networks, radial basis function neural networks, convolutional neural networks, and self-organizing neural networks. The RNN model is utilized in numerous applications, such as forecasting financial data or power consumption, evaluating water quality, modeling nonlinear systems, adaptive control, and forecasting medical data (Yu et al. 2019; Nawi et al. 2019; Bai et al. 2019; Chen et al. 2020).

Dynamic systems serve as the fundamental structure for modeling and control of a vast variety of complex systems with research significance (Kumpati and Kannan 1990). Dynamic systems, such as heat transfer, distillation column, robotic manipulator, and Mackey glass series prediction to mention a few, have unknown non-linearity that arise at random and are challenging to model and control using linear model structures, such as ARMAX and OE models (Schoukens and Ljung 2019). There are many articles in the literature that examine the social component of supply chain resilience and sustainability (Abbasi and Choukolaei 2023; Abbasi and Erdebilli 2023; Abbasi et al. 2021, 2022, 2023a, b, c). Contrarily, the social dimension is complex and has a variety of uncertain components that cannot be adequately characterized by the traditional Boolean logic of totally true or false. Simulation of nonlinear models is one of the commonly used approaches for studying the complex nature of dynamic systems. With the increasing necessity to generate accurate models, complex models of dynamic systems with various possible configurations are being developed (Quaranta et al. 2020). To overcome this computational complexity, it is now necessary to design an accurate model that is fast and efficient in approximating the full-order dynamic system over an entire range of parameters. The advancement of technology in the field of ANN has created a subject of interest among researchers. ANN is widely been used to solve a variety of applications including image recognition, medical diagnosis, control and identification, forecasting, and speech recognition (Noël and Kerschen 2017; Quaranta et al. 2020; Basheer and Hajmeer 2000; Kroll and Schulte 2014). ANN is distinguished from other state-of-art approaches for its flexibility and self-learning ability based on experience (Basheer and Hajmeer 2000). ANN is categorized as static and dynamic models. The static type of ANN known as Feed Forward Neural Networks (FFNN) only traverses receiving signals in the forward direction. The output layer’s influence does not alter the input layer’s characteristics. FFNN is further classified into Multi-Layer Perceptron (MLP) and Radial Basis Function Network (RBFN). Elman Neural Network (ENN), the Hopfield neural network (HNN), Jordan Neural Network (JNN), Diagonal Recurrent Neural Network (DRNN), LSTM, and GRU networks form the dynamic models of ANN. RNN structures traverse the receiving signals in both forward and feedback direction (Ge et al. 2009). MLP is a single or several hidden layer network with weight connections between the input and output without dynamic mapping (Savran 2007). An alternate approach to MLP is RBFN, which has only one hidden layer. The output of the hidden layer is calculated by computing the radial distance between the inputs and the weights. ENN (Elman 1990), JNN (Jordan 1986), and DRNN (Kumar et al. 2017) are the extensions of MLP with the addition of a context layer that acts as memory neurons. They possess dynamic mapping by nature (Laddach et al. 2022). ENN and JNN belong to the Fully Recurrent Neural Networks (FRNN) and DRNN belongs to the group of Partial RNN (PRNN). Hopfield structures are fully recurrent structures that depend on the initial conditions due to the absence of external input (Hopfield 1982). Higher order LSTM and GRU are widely used in most of the current applications. They are known for capturing long-time dependencies and do not suffer from optimization issues as RNN (Hochreiter and Schmidhuber 1997). MLP offers better processing capabilities as compared to other structures in literature but lacks proper identification of dynamic systems due to the absence of dynamic mapping.

1.1 Related work

In Perrusquía and Yu (2021), the author has proposed a temporal convolutional network for the identification of dynamic systems. TCN is verified against MLP and LSTM. TCN and LSTM were found to give better results for large data sets and non-white noise. In Psichogios and Ungar (1992), the authors have proposed a hybrid Jordan–Elman network for a single-input single-output system. Online training and control of the CSTR plant are carried out. Extended Kalman Filter (EKF) is used as an optimization algorithm. In this paper (Şen et al. 2020), a modified Elman–Jordan structure with GA as an optimization algorithm is used. Optimization algorithms, such as EKF, and GA though perform better than BP, yet suffer long training times due to their confined search space. With the addition of white noise into the system, the optimization fails to predict accurate models. A novel Dynamic Neural Network (DNN) is proposed in this paper (Kumar et al. 2017). Though DNNs can be used with online control methods, they suffer from mapping capability due to their fixed structures. In Mohajerin and Waslander (2019), Hybrid NN based on global clustering and local learning is proposed. The clustering algorithm is used for updating model weights. Though this structure performs well, a good number of input densities is required for cluster pairing and faster convergence. In Hernández et al. (2020), the authors have proposed a modified dynamic Hopfield network. The dynamic network was found to perform multi-step prediction using the past information of the system. Following the single ANN architecture, hybrid architecture resulting from the combination of the above structures is also implemented in the literature. In Alkhasawneh (2019), the authors have proposed a cascaded FFNN with ENN called HECFNN for disease prediction The results were verified on six different data sets and hybrid models are found to outperform single models efficiently. In Wang and Lin (1998), the author has used FNN, RBFNN, Runge–Kutta neural networks, and ANFIS mechanisms for the identification of nonlinear systems. Runge–Kutta ANN has shown better performance than feed-forward structures and ANFIS. In this work (Huang et al. 2021), the authors have proposed a novel hybrid deep learning model for 1 h-ahead solar forecasting. A hybrid WPD–CNN–LSTM–MLP model is designed and the proposed method is found to give better forecasting results compared to standard MLP and RNN models. The authors in Alkhasawneh and Tay (2018) have proposed a cascaded FFNN with ENN to predict six categories of diseases. The results demonstrate the higher accuracy of the proposed method over other standard ENN models. In Kalinli and Sagiroglu (2006), Elman with Nonlinear ARX is designed for system identification. The results once again show better performance with hybrid models over single models. Compound FNN (CFNN) is combined with ENN for time-series prediction of linear and nonlinear systems. The ability of the proposed model is tested on six data sets and found to perform with greater accuracy. Identification of twin rotor multi-input multi-output system is done on modified MLP and Elman structure in Toha et al. (2008). Many-to-one RNN for recommendation system is proposed by the authors in Dadoun and Troncy (2008). In this Hong et al. (2020), a total of six algorithms like Decision tree algorithm (DT), MLP, random forest algorithm (RF), gradient boosting algorithm (GB), RNN–LSTM, and CNN–LSTM were tested to predict the dam inflow. MLP has shown the best results over others. Further, a hybrid model based on ensemble methods was combined with MLP for the prediction of inflow. The author has extended the conclusion that simple machine learning algorithms along with ensemble methods produce accurate results. In Wang et al. (2023), a time-delay recursive neural network is used to develop the suggested controller. The proposed control method can be easily generalized to the actual systems, which exhibit hysteresis behavior, in contrast to those current DAC approaches established under the generic Lipschitz condition. A Hopfield neural network (HNN) estimator is then suggested as a means of online parametrization of the proposed controller. In the meantime, a modular model based on the HNN estimator is created to represent the piezo-actuated stage in this study. It consists of a linear sub-model, a hysteresis sub-model, and lumped uncertainty. In Legaard et al. (2023), the authors provided a survey of the various approaches for building neural network models of dynamical systems. In addition to providing a general overview, we evaluate the pertinent literature and list the most significant challenges this modeling paradigm faces as a result of numerical simulations. We offer a discussion on promising research areas based on the examined literature and highlighted difficulties. In de Carvalho Junior et al. (2023), the major component of the model reference control method for the rotary inverted pendulum is a recurrent para-consistent neural network. The rotating inverted pendulum is a perfect tool for applying and testing the recurrent para-consistent neural network due to its non-linearity, two-degree-of-freedom motion, and under-actuated system. Three of these neural models are used by the developed para-consistent neural model reference controller: two of them are used to represent the arm and pendulum angles, and the third one is used to operate the system while following a reference trajectory. In Yang et al. (2023), the authors developed a stock price prediction model through neural network to enhance the stock price prediction effect based on the enhanced Particle Swarm Optimization (PSO) algorithm. To improve the global search ability of the algorithm in the early stage of evolution and the local search ability in the later stage of evolution, the adaptive adjustment of inertial weight is proposed, and the algorithm is improved by combining with neural network. This approach is based on the idea of avoiding particles falling into the same local solution as much as possible and always keeping the particles with a certain diversity. This research also builds a neural network-based stock price prediction system on the basis of the enhanced algorithm. In Villegas et al. (2023), for the purpose of predicting COVID-19 patient death, the authors used deep learning algorithms. Two datasets containing clinical data were used. Two Spanish hospitals had received 2307 and 3870 COVID-19-infected patients, respectively. First, they created a time-line of events, compiling all the clinical data for each patient and evaluating several data representation techniques. The sequences were then utilized to train an RNN model with an attention mechanism to investigate interpretability. They carried out a thorough cross-validation and hyper-parameter search, and then, they ensemble the resulting RNNs to increase sensitivity. In Zhao et al. (2023), the authors created a reduced-order machine learning model for distributed model predictive control of nonlinear processes utilizing feature selection techniques. A subset of input characteristics that significantly affects the prediction of system output is initially chosen using filter, wrapper, and embedded feature selection approaches. The creation of reduced-order RNN models utilizing only the chosen input features after integrating the feature selection techniques to capture the system dynamics. To stabilize the nonlinear system at steady state, the reduced-order RNN models are then included into sequential and iterative distributed model predictive controls. In Hu et al. (2023), the main goal of the proposed study is to construct a Lyapunov-based economic model predictive control technique that makes use of RNNs with an online update to maximize the economic advantages of switched non-linear systems according to a predetermined switching schedule. To increase model prediction accuracy, we first create an initial offline-learning RNN using operational data from the past. We then update RNNs with data from the present. For RNNs updated online using independent and identically distributed (i.i.d.) and non-i.i.d. data samples, the generalized error bounds are calculated, accordingly. Then, for switched non-linear systems accounting for the RNN generalized error constraint, probabilistic closed-loop stability and economic optimality are concurrently attained by introducing online updating RNNs into Lyapunov-based economic model predictive control. In Han et al. (2023a), an iterative learning model predictive control (FNN-ILMPC) for complicated nonlinear systems is based on a fuzzy neural network. A data-driven model is first created using a dynamic linearization technique that solely uses input and output data. An FNN is utilized to analyze the disturbance in the established model, since it has an unidentified disturbance term that could affect the control performance. This captures the uncertainty of the system. The development of an FNN-ILMPC approach to reduce the impact of disruptions is then done on the basis of the data-driven model discussed above. The developed controller is then shown to be capable of ensuring the stability of the closed-loop system while gradually reducing both modeling error and tracking error. Finally, the experimental findings support the superiority and efficacy of the created controller. In Han et al. (2023b), for the uncertain nonlinear systems, the data-driven robust optimum control approach is suggested. The proposed technique has three advantages: To capture the relationship between the approximation errors and the control variables, a data-driven assessment technique is first developed. After that, nonlinear systems’ control performance indices can be determined inside uncertain disturbances. Second, a co-evolution technique is used to construct a multi-objective resilient optimization algorithm. The control performance can then be enhanced by obtaining reliable optimal control laws. Third, a theoretical discussion of data-driven robust optimum control’s robust boundedness is presented. Analytical assurance of the control systems’ stability is then possible. Last but not least, two multiple-input multiple-output second-order nonlinear systems are used to demonstrate the efficacy of data-driven robust optimum control. In Luo et al. (2021), a numerous large data-related application, including the terminal interaction pattern analysis system under research, typically uses a weighted directed networks is analyzed. It consists of extensive dynamic interactions between a great number of nodes. A dynamically weighted directed network that results is high dimensional and unfinished when the number of involved nodes rises sharply, since it is difficult to see all of their interactions at each time slot. In spite of its shortcomings, it provides extensive knowledge about the diverse behavioral patterns of the involved nodes. A unique alternating direction multipliers-based non-negative latent factorization of tensors model is proposed in this research. In Luo et al. (2023), the authors put forth a unique method for nonlinear canonical polyadic decomposition on a high-dimensional, incomplete tensor called the neural latent factorization of tensors model. Three interesting ideas are used to implement it: using the density-oriented modeling principle to create rank-one tensor series with high computational efficiency and low storage costs; treating each rank-one tensor as a hidden neuron to create an effective neural network structure; and creating an adaptive backward propagation learning strategy for effective model training. In Luo et al. (2020), to prevent accuracy loss due to premature convergence without adding to the computational load, the authors carefully examined the evolution of a particle swarm optimization (PSO) algorithm and then proposed to incorporate more dynamic information into it. This creatively led to the development of a novel position-transitional PSO algorithm.

Based on the above literature, we find the following shortcomings :

• 1. Feedforward models (MLP and RBFN) cannot be used as a standalone structure, since they lack the memory to record previous observations. They have to be supplied with a large number of inputs and are easily affected by external noise (Kumpati and Kannan 1990). To make MLP dynamic, they must be supplied with the system’s order in advance or combined with any of the suggested ANN models above.

• 2. Although fully recurrent structures, such as Elman, Jordan, and DRNN, are successful in the identification of many applications, they always require modification of the original structure for better prediction accuracy. Most of the original structure causes slow convergence and is therefore unsuitable for online identification and time-series applications. The majority of the modified structure necessitates the use of a complex optimization algorithm to update their parameters, resulting in high computational complexity.

• 3. LSTM and GRU are very efficient at identifying complex sequential data than feedforward and standard RNN models. The major limitations of these structures are that they are more complicated and require large datasets to learn efficiently. They do not work well with highly noisy data.

• 4. Even with massive models and methodologies cited in the literature, the best benchmark neural architecture for the identification of dynamic systems is not available.

This has motivated us to attempt to improve the architecture of ANN by designing a novel hybrid neural network for the identification of dynamic systems. A hybrid neural network called CRFNN is proposed in this work. The main motivation and outcome of this work are as follows:

• 1. An effective structure for dynamic system identification is proposed. The hybrid structure takes advantage of both the feed-forward and feedback structure (fast processing and the presence of memory neurons). With the addition of dynamic LRNN, it also overcomes the shortcomings of static MLP.

• 2. The proposed model is independent of the order of the plant and takes minimum inputs for prediction (present value of external input and one-time delayed value of the plant).

• 3. Gradient descent-based BP algorithm is used to develop a weight update equation and the convergence is proved using Lyapunov stability principles.

• 4. The performance of the proposed structure is evaluated by comparing it with two identification approaches on the benchmark problems. The hybrid structure is found to give better accuracy and prediction of dynamic models as compared to LRNN and FFNN single models.

• 5. The proposed structure is also analyzed for robustness and parameter variation for various plant complexity. The structure is found to have less mean square error and better accuracy than single models. The performance of the structure is found perform equally well as other suggested methods in the literature.

• 6. The proposed structure can be identified both online and offline, and hence can be extended for adaptive control of nonlinear dynamic systems.

The rest of the paper is organized as follows: The introduction section discusses the shortcomings of single models and the need for hybrid models. The novel works carried out by different researchers are also elaborated. Section 2 briefs the problem statement. Section 3 discusses the identification structure, learning algorithm, and design of the proposed structure. The convergence of the update weight equations is also proved using Lyapunov stability analysis in this section. Section 4 discusses the simulation results obtained. Two examples of complex plant equations and one example of a benchmark problem are selected and the performance of the hybrid structure is discussed. In Sect. 5 conclusion based on the simulation results is discussed.

2 Problem statement

Let the nonlinear plant has r(k) inputs and $y_\textrm{p}(k)$ outputs. The discrete difference equation of the nonlinear plant is given by

$$\begin{aligned} y_d(k)= & {} {} f[y_\textrm{p}(k),y_\textrm{p}(k-1),y_\textrm{p}(k-2),\ldots ,y_\textrm{p}(k-n),\nonumber \\{} & {} r(k),r(k-1), r(k-2),\ldots ,r(k-m)], \end{aligned}$$

(1)

where f is the unknown differentiable nonlinear function. m and n are the orders of the plant and $n\le m$. Here, the output depends on both present as well as past output and the external input of the plant. If CRFNN is considered an identifier, the difference equation of the identifier will be as below

$$\begin{aligned} y_\textrm{crfnn}(k)={}{\hat{f}}[y_\textrm{p}(k-1),r(k)]. \end{aligned}$$

(2)

The output of CRFNN depends on the present external input and one delayed output of the plant. The main objective of this work is to make ${\hat{f}}\simeq f$, so that the identified model becomes the exact representation of the plant. To achieve this, a series–parallel type of identification is selected and the weights are updated continuously using the BP algorithm. With training progress, the weights converge to desired values and the model starts following the desired plant trajectory with error decreasing to a very minimal value or zero. That is

$$\begin{aligned} \lim _{k \rightarrow \infty } |y_\textrm{p}(k)-y_\textrm{crfnn}(k)|\le \in , \end{aligned}$$

(3)

where $\in \rightarrow 0$.

3 Structural comparison of FFNN, LRNN, and CRFNN

See Figs. 1, 2, and 3.

Fig. 1

FFNN structure

Fig. 2

LRNN structure

Fig. 3

Proposed CRFNN structure

3.1 Feed forward neural networks

The structure of MLP is as shown in Fig. 1. It consists of input nodes, output nodes, and weights connecting input and output nodes. The input layer has four weight connections between input and hidden layer. This structure takes present and one delayed value of external input denoted as r(k) and $r(k-1)$, respectively, and present value and one delayed value of plant output denoted as $y_\textrm{p}(k)$ and $y_\textrm{p}(k-1)$, respectively. The input vector $X(k)=[r(k),y(k),y(k-1),r(k-1)]$. The weight vector associated between input and the hidden layer $w_{if}(k)=[w_{if_1},w_{if_2},\ldots ,w_{if_n}]$. The hidden layer receives three weight connections from input layer and sends one weight connection to the output layer. The hidden layer vector $F(k)=[F_1(k),F_2(k),\ldots ,F_n(k)]$. The weight vector associated between hidden and the output layer $w_{of}(k)=[w_{of_1},w_{of_2},\ldots ,w_{of_m}]$. The output layer computes the final output of the network by receiving signals from hidden layer. The output of FFNN is denoted as $y_\textrm{ffnn}$. One hidden layer is sufficient for most of the time-series prediction problem. The output of the feedforward MLP is given by

$$\begin{aligned} y_\textrm{ffnn}(k)=f_1\left( \sum _{i=1}^{m}F_i(k)w_{if_i}(k)+b_{ff_i}(k)w_{of_i}(k)\right) , \end{aligned}$$

(4)

where $b_{ff_i}(k)$ denotes the output bias vector and $w_{of}(k)$ denotes the associated output bias weight vector. $f_1$ denotes the linear activation function acting at output node. The output of the induced field is given by

$$\begin{aligned} F_i(k)=g_1\left( \sum _{i=1}^{n}X(k-i)w_{if_i}(k)+b_{fx_i}(k)w_{b_i}(k)\right) , \end{aligned}$$

(5)

where $b_{fx_i}(k)$ denotes the input bias vector and $w_{if_i}(k)$ denotes the associated input bias weight vector. $g_1$ denotes the non-linear activation function acting at hidden nodes.

3.2 Local recurrent neural networks

The structure of LRNN is as shown in Fig. 2. The LRNN is the subset of partial recurrent neural networks. The structure is an extension of FFNN with dynamic memory to retain long-interval data. It consists of input layer, output layer, and local weights that act as memory neurons. The local weights sends the output of the hidden neuron as an input to same hidden neuron. The input layer has three weight connections between input and hidden layer. This structure takes present value of external input r(k), present value and one delayed value of plant output denoted as $y_\textrm{p}(k)$ and $y_\textrm{p}(k-1)$, respectively. The input vector $X(k)=[r(k),y(k),y(k-1)]$. The weight connections of input layer are given by $w_{ir}(k)=[w_{ir_1}(k),w_{ir_2}(k),\ldots ,w_{ir_n}(k)]$. The hidden layer receives three weight connections from input layer and from self hidden local neurons and sends one weight connection to the output layer. The hidden layer vector is denoted by $R(k)=[R_1(k),R_2(k),\ldots ,R_m(k)]$. The weight connection between of the output layer $w_{or}(k)=[w_{or_1}(k),w_{or_2}(k),\ldots ,w_{or_m}(k)]$. The local weight vector also containing the adjustable weight elements is denoted by $w_{lr}(k)=[w_{lr_1}(k),w_{lr_2}(k),\ldots , w_{lr_n}(k)]$. The output layer computes the final output of the network by receiving signals from hidden layer. The output of RNN is denoted as $y_\textrm{rnn}(k)$. One hidden layer is considered in this work. The output of the LRNN is given by

$$\begin{aligned} y_\textrm{rnn}(k)=f_2\left( \sum _{i=1}^{m}R_i(k)w_{ir_i}(k)+b_{or_i}(k)w_{or_i}(k)\right) , \end{aligned}$$

(6)

where $b_{or_i}(k)$ denotes the output bias vector and $w_{or}(k)$ denotes the associated output bias weight vector. $f_2$ denotes the linear activation function acting at output node. The output of the induced field is given by

$$\begin{aligned} R_i(k)= & {} g_2\Bigg (\sum _{j=1}^{n}X(k-j)w_{ir_j}(k)+L(k)w_{lr}(k)\nonumber \\{} & {} +b_{rr_j}(k)w_{r_j}(k)\Bigg ), \end{aligned}$$

(7)

where $b_{rr_j}(k)$ denotes the input bias vector and $w_{r_j}(k)$ denotes the associated input bias weight vector. L(k) denotes the input signal vector from local hidden neurons and $w_{lr}(k)$ denotes the associated local weight vector. $g_2$ denotes the non-linear activation function acting at hidden nodes. When the local weights of LRNN are made zero, the LRNN structure resembles a simple FFNN.

3.3 Hybrid CRFNN structure

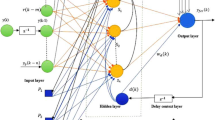
To combine the merits and demerits of both the static and dynamic network, a hybrid FFNN–LRNN model is proposed in this work and it is addressed as CRFNN. Figure 3 shows the structure of CRFNN. The structure has input layer, two hidden layers, and one output layer. The input layer sends two weight connections to the hidden layer. The hidden layer receives three weight connections from input layer and local self hidden layer and computes the output of FFNN and the LRNN. The hidden layer sends two weight connection to the output layer. The output layer computes the final network output.

• 1. Input layer: The input layer comprises two inputs, namely the present input r(k) and the delayed output of the plant $y_\textrm{p}(k-1)$. The input vector X(k) is $X(k)=[r(k-1),y_\textrm{p}(k-1)]$. These inputs are passed to both the feed-forward and recurrent paths of the structure. The input signals are passed to FNN portion of the hidden layer (indicated by green lines in the figure) through the feed forward weight connections $w_{if}(k)$ and are passed to RNN portion of the hidden layer (indicated by orange lines in the figure) through the recurrent weight links denoted as $w_{ir(k)}$.

• 2. Hidden layer: The hidden layer output is computed into two paths. In the FNN path, the output of induced field is due to the received input signals, and in the RNN path, the output of the induced field is due to the received input signals from input layer and the local self hidden neurons. Both the hidden layer outputs are acted upon by non-linear activation function and further sent to output layer.

• 3. Output layer: The output layer computes the final hybrid network output that has the characteristics of both static and recurrent networks.

The induced field of hidden layer is computed as below

$$\begin{aligned} F_j(k)= & {} f_{1}\left( \sum _{j=1}^{n}X(k-j)w_{if_j}(k)+b_{fx_j}(k)w_{b_j}(k)\right) \nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned} R_j(k)= & {} g_{1}\Bigg (\sum _{j=1}^{m}X(k-j)w_{if_j}(k)+L(k)w_{lr}(k)\nonumber \\{} & {} +b_{fx_j}(k)w_{b_j}(k)\Bigg ), \end{aligned}$$

(9)

where $f_1$ and $g_1$ indicates the non-linear tangent hyperbolic activation function at the hidden node. The output of hybrid CRFNN is given by

$$\begin{aligned} y_\textrm{crfnn}(k)= & {} f\Bigg (\sum _{i=1}^{m}F_j(k)w_{of}(k) \nonumber \\{} & {} +b_{oh}(k)w_{bh}(k)+R_j(k)w_{or}(k)\Bigg ), \end{aligned}$$

(10)

where $w_{of}(k)$ and $w_{or}(k)$ is the weight connection of FFNN and RNN to the output layer. $w_{bh}(k)$ is the output layer weight vector and $b_{oh}$ denotes the associated output bias vector. f is the linear activation function used in the output layer.

3.4 Learning and identification scheme for CRFNN

The system being dynamic, output is dependent on both present and past values of inputs and outputs. The identification scheme can be of parallel type or serial-parallel type. Here, series–parallel identification scheme is used to maintain the overall stability of the structure. The identification scheme used is shown in Fig. 4. Next step will be used to update the weights continuously. A gradient-based back propagation algorithm is used. The update equations are designed to follow the stability principles of Lyapunov theorem. Hence, they also give fast convergence. Now, first step will be to set up a cost function. Mean Square Error (MSE) is taken as the cost function. The MSE is defined as

$$\begin{aligned} E(k)=\frac{1}{2}[y_\textrm{p}(k)-y_\textrm{crfnn}(k)]^2, \end{aligned}$$

(11)

where $e(k)=y_\textrm{p}(k)-y_\textrm{crfnn}(k)$ is identification error. The MSE is computed until the identification error reaches zero.

Fig. 4

Series–parallel identification configuration based on the proposed model

3.5 Update equation between output layer and hidden layer

The error is back-propagated from the output layer $y_\textrm{crfnn}(k)$ to the hidden layer of FFNN $F_j(k)$ and RNN $R_j(k)$ by updating the weights of the output layer associated with FFNN $w_{of}(k)$ and RNN $w_{or}(k)$ as below

$$\begin{aligned} \frac{\partial E(k)}{\partial w_{of}(k)}= & {} \frac{\partial E(k)}{\partial y_\textrm{crfnn}(k)}\times \frac{\partial y_\textrm{crfnn}(k)}{\partial w_{of}(k)} \end{aligned}$$

(12)

$$\begin{aligned} \frac{\partial E(k)}{\partial w_{or}(k)}= & {} \frac{\partial E(k)}{\partial y_\textrm{crfnn}(k)}\times \frac{\partial y_\textrm{crfnn}(k)}{\partial w_{or}(k)}. \end{aligned}$$

(13)

This equation thus becomes

$$\begin{aligned} \frac{\partial E(k)}{\partial w_{of}(k)}= & {} -e(k)\times F_j(k) \end{aligned}$$

(14)

$$\begin{aligned} \frac{\partial E(k)}{\partial w_{or}(k)}= & {} -e(k)\times R_j(k), \end{aligned}$$

(15)

where $F_j(k)$ and $R_j(k)$ indicate the induced fields of CRFNN.

3.6 Update equation between the hidden layer and input layer

The error when back propagated further from to hidden to input layer updates the weights such as $w_{lr}(k)$, $w_{if}(k)$, and $w_{ir}(k)$. The weight update equation of hidden layer local weights $w_{lr}(k)$ are calculated as below

$$\begin{aligned} \frac{\partial E(k)}{\partial w_{lr}(k)}=\frac{\partial E(k)}{\partial y_\textrm{crfnn}(k)}\times \frac{\partial y_\textrm{crfnn}(k)}{\partial R_j(k)}\times \frac{\partial R_j(k)}{\partial w_{lr}(k)}. \end{aligned}$$

(16)

Further, the weights $w_{if}(k)$ and $w_{ir}(k)$ are updated as follows:

$$\begin{aligned} \frac{\partial E(k)}{\partial w_{ir}(k)}= & {} \frac{\partial E(k)}{\partial y_\textrm{crfnn}(k)}\times \frac{\partial y_\textrm{crfnn}(k)}{\partial R_j(k)}\times \frac{\partial R_j(k)}{\partial w_{ir}(k)}\end{aligned}$$

(17)

$$\begin{aligned} \frac{\partial E(k)}{\partial w_{if}(k)}= & {} \frac{\partial E(k)}{\partial y_\textrm{crfnn}(k)}\times \frac{\partial y_\textrm{crfnn}(k)}{\partial F_j(k)}\times \frac{\partial F_j(k)}{\partial w_{if}(k)}. \end{aligned}$$

(18)

The weights are calculated using the update equations from Eqs. (12)–(15) and the stochastic gradient formula is used to derive the new weights. For example, to calculate new local weight $w_{lr}(k)(new)$, the formula is as below

$$\begin{aligned} w_{lr}(k)(new)=w_{lr}(old)-\eta e(k)\frac{\partial E(k)}{\partial w_{lr}(k)}. \end{aligned}$$

(19)

Here, $\eta$ denotes the learning rate and the range considered is between 0 and 1. Similarly, other tunable weights are updated using the above formula.

3.7 Stability analysis

These proposed update weight equations guarantee stability in the sense of Lyapunov. According to the Lyapunov stability theorem, when the Lyapunov-based error reaches a minimum and is positive, the system remains stable irrespective of any condition. Mathematically, it is given by

$$\begin{aligned} E(x)>0 \text { for }x>0\,\textrm{and}\, E(x)=0 \text { for }x=0, \end{aligned}$$

(20)

Here, E(x) is the Lyapunov function. The rate of change of Lyapunov error is given by

$$\begin{aligned} {\dot{E}}= & {} \left( \frac{\partial E(k)}{\partial w_{of}(k)}+\frac{\partial E(k)}{\partial w_{or}(k)}+\frac{\partial E(k)}{\partial w_{lr}(k)}+ \frac{\partial E(k)}{\partial w_{ir}(k)}\nonumber \right. \\{} & {} \left. + \frac{\partial E(k)}{\partial w_{if}(k)}\right) . \end{aligned}$$

(21)

When above equation is substituted with value ${(x-y)}^2$ for $\frac{\textrm{d}w_{of}(k)}{\textrm{d}t}, \frac{\textrm{d}w_{or}(k)}{\textrm{d}t} \frac{\textrm{d}w_{lr}(k)}{\textrm{d}t}, \frac{\textrm{d}w_{if}(k)}{\textrm{d}t}$, and $\frac{\textrm{d}w_{ir}(k)}{\textrm{d}t}$, it becomes

$$\begin{aligned} {\dot{E}}= & {} (x-y)^2\left( \frac{\partial E(k)}{\partial w_{of}(k)}+\frac{\partial E(k)}{\partial w_{or}(k)}+\frac{\partial E(k)}{\partial w_{lr}(k)}\right. \nonumber \\{} & {} \left. + \frac{\partial E(k)}{\partial w_{if}(k)}+\frac{\partial E(k)}{\partial w_{ir}(k)}\right) . \end{aligned}$$

(22)

For various ranges of x and y, the Lyapunov-based error $\dot{E(k)}\le 0$ . This ensures that the update equations satisfy BIBO stability, and hence, the structure under test also remains BIBO stable. In ‘Algorithm 1’: the learning procedure is described as a pseudo code:

Algorithm 1

Learning procedure

4 Simulation results and discussion

In this section, the performance of the Compound Recurrent Feed-forward Neural network is evaluated. Two examples of real-time plant equation that is highly nonlinear and one nonlinear benchmark problem are considered. The proposed structure is supplied with external input and past output of the plant as inputs. The proposed structure is compared against neural models, such as Elman neural network (Elman) Gao et al. (1996), Jordan neural network (Jordan) Jordan (1986), Local recurrent neural network (LRNN) Kumar et al. (2017), and Feed-forward neural network (FFNN). Average Mean Square Error (AMSE), Average Mean Absolute Error (AMAE), and Relative Mean Square (RMSE) are selected as evaluation index to measure the efficiency of the proposed structure. Various degrees of complexity of nonlinear plant equation is supplied and all the neural models considered have a single hidden layer. A fixed learning rate of 0.0001 is considered for identification.

4.1 Example 1: A nonlinear plant with order 3

To check the efficiency of the proposed structure, a real-time nonlinear plant equation is considered in Kumpati and Kannan (1990).

$$\begin{aligned} y_{\textrm{p}}(k)=\frac{y_\textrm{p}(k-1)}{1+y_\textrm{p}^2(k-2)}+r^3(k-2), \end{aligned}$$

(23)

where $y_\textrm{p}(k)$ is the plant equation. The plant’s output depends on both the present and past input–output values. The plant equation is of order 3 and follows the following identification structure:

$$\begin{aligned} y_{\textrm{p}}(k)=f[y_\textrm{p}(k-1),y_\textrm{p}(k-2),r(k-2)]. \end{aligned}$$

(24)

Here, f is the nonlinear function that maps the inputs and outputs. The proposed structure is applied with an external input $r(k)=\sin (\frac{2\pi k}{100})$ as well as time-delayed plant outputs. When CRFNN, FFNN, LRNN, Elman, and Jordan are chosen as identifiers, the difference equations of the identifiers are as below

$$\begin{aligned} y_\textrm{crfnn}(k)= & {} \hat{f_1}[y_\textrm{p}(k-1),r(k-1)] \end{aligned}$$

(25)

$$\begin{aligned} y_\textrm{lrnn}(k)= & {} \hat{f_2}[y_\textrm{p}(k-1),y_\textrm{p}(k-2),r(k-1)] \end{aligned}$$

(26)

$$\begin{aligned} y_\textrm{ffnn}(k)= & {} \hat{f_3}[y_\textrm{p}(k-1),y_\textrm{p}(k-2),r(k),r(k-1)] \end{aligned}$$

(27)

$$\begin{aligned} y_\textrm{Elman}(k)= & {} \hat{f_4}[y_\textrm{p}(k-1),y_\textrm{p}(k-2),r(k-1)] \end{aligned}$$

(28)

$$\begin{aligned} y_\textrm{Jordan}(k)= & {} \hat{f_5}[y_\textrm{p}(k-1),y_\textrm{p}(k-2),r(k-1)], \end{aligned}$$

(29)

where the symbols $y_\textrm{crfnn}(k), y_\textrm{lrnn}(k), y_\textrm{ffnn}(k), y_\textrm{Elman}(k)$, and $y_\textrm{Jordan}(k)$ denote the output of CRFNN, LRNN, FFNN, Elman, and Jordan, respectively. The inputs mentioned above are applied to the models and the output is generated. Where $\hat{f_1},\hat{f_2},\hat{f_3},\hat{f_4},\hat{f_5}$ are the nonlinear functions of the respective identifier. When $\hat{f_1},\hat{f_2},\hat{f_3},\hat{f_4},\hat{f_5}\simeq f$, the network is said to follow the plant model, and the identified model is found to be accurate. About 900 samples are provided to the network for training and 400 samples are used for validation. The training is conducted in offline mode for about 900 time-epochs.

4.2 Parameter variation in testing phase [Example 1]

During the testing phase, a varied input pattern is supplied to the network to check the effect of parameter variation on the structure. The new input signal r(k) is given as below

$$\begin{aligned} r(k)={\left\{ \begin{array}{ll} \frac{\sin (\pi k)}{40},&{} \text { for }\,0<k\le 250 \\ \frac{0.09\sin (\pi k)}{45}\\ -\frac{cos(2 \pi k)}{40}, &{} \text { for }\,250<k\le 450 \\ \frac{0.3\sin (2\pi k)}{15}\\ +\frac{0.1\sin (2 \pi k)}{320}\\ +\frac{0.6\sin (2 \pi k}{40}, &{} \text { for }\,450<k\le 00. \end{array}\right. } \end{aligned}$$

(30)

Fig. 5

Response from CRFNN, LRNN, and FFNN models [Example 1]

Figure 5 shows the response obtained from CRFNN and other selected neural structures. This concludes that the proposed identifier performs superior to other selected neural models. The error is also found to decrease to a very minimum value with very less computational time. The performance of the identifiers is evaluated against major performance parameters, such as Average Mean Square Error (AMSE), Average Mean Absolute Error (AMAE), and Root Mean Square Error (RMSE). Figure 6 shows the MSE curve obtained from CRFNN and other selected neural structures. Figure 7 shows the MAE curve obtained from CRFNN and other selected neural structures. From the figures, it can be seen that the proposed CRFNN model is capable of extracting the dynamics of the system.

Fig. 6

MSE curves obtained from CRFNN, LRNN, and FFNN models [Example 1]

Fig. 7

MAE curves obtained from CRFNN, LRNN, and FFNN models [Example 1]

4.3 Random sine wave noise injection test [Example 1]

Now, a random sine wave was added to the network as external noise between the time interval $250<k<450$. A sine wave with a value of $\sin (\frac{2\pi k}{15})$ was added. The network initially fluctuated during this interval and deviated from the plant response. However, the network still managed to track back the plant response in a very short time. The proposed network is found efficient in learning the input–output patterns and predicting the similar unknown patterns supplied to them. The response of the proposed CRFNN under the effect of random noise is shown in Fig. 8. Table 1 gives the comparison of proposed CRFNN with Elman, Jordan, FFNN, and LRNN. From the table, the proposed structure is found to have better performance indices.

Fig. 8

Effect of random sine noise [Example 1]

4.4 Example 2: A nonlinear plant with order 4

The proposed method is further tested for identification ability by applying another nonlinear plant equation of order 3. The plant equation is given below as in Kumpati and Kannan (1990)

$$\begin{aligned} y_\textrm{p}(k)= & {} {} 0.72y_\textrm{p}(k-1)+0.025y_\textrm{p}(k-2)r(k-1)\nonumber \\{} & {} +0.001r^2(k-2)+0.2r(k-3). \end{aligned}$$

(31)

The plant equation takes the series–parallel identification form as below

$$\begin{aligned} y_{\textrm{p}}(k)= & {} g[y_\textrm{p}(k-1),y_\textrm{p}(k-2),\nonumber \\{} & {} (k-1),r(k-2),r(k-3)], \end{aligned}$$

(32)

where g is the nonlinear function. To predict $y_\textrm{p}(k)$, both time-delayed values of external input and that of the plant are used. When CRFNN, LRNN, FFNN, Elman, and Jordan are selected as neural identifiers to map the nonlinear function g, they are defined to take the following identification model forms:

$$\begin{aligned} y_\textrm{cfrnn}(k)= & {} \hat{g_1}[y_\textrm{p}(k-2),r(k)] \end{aligned}$$

(33)

$$\begin{aligned} y_\textrm{lrnn}(k)= & {} \hat{g_2}[y_\textrm{p}(k-2),r(k-1),r(k)] \end{aligned}$$

(34)

$$\begin{aligned} y_\textrm{ffnn}(k)= & {} \hat{g_3}[y_\textrm{p}(k-2),y_\textrm{p}(k-1),r(k-2),r(k-3)] \nonumber \\ \end{aligned}$$

(35)

$$\begin{aligned} y_\textrm{Elman}(k)= & {} \hat{g_4}[y_\textrm{p}(k-2),r(k-1),r(k)] \end{aligned}$$

(36)

$$\begin{aligned} y_\textrm{Jordan}(k)= & {} \hat{g_5}[y_\textrm{p}(k-2),r(k-1),r(k)], \end{aligned}$$

(37)

where $\hat{g_1},\hat{g_2},\hat{g_3}, \hat{g_4}, \hat{g_5}$ are the nonlinear functions to be identified. The models are tested by supplying about 900 samples in batch mode of identification. From the results, it can be seen that the proposed method shows the best efficiency compared to other selected neural models.

4.5 Parameter variation in testing phase [Example 2]

During validation, a multi-varied input r(k) is supplied to the network as below

$$\begin{aligned} r(k)={\left\{ \begin{array}{ll} \frac{\sin (\pi k)}{40},&{} \text {for }\,0<k\le 250\\ \frac{0.09\sin (\pi k)}{45}\\ -\frac{cos(2 \pi k)}{40}, &{} \text {for }\,250<k\le 450\\ \frac{0.3\sin (2\pi k)}{15}\\ +\frac{0.1\sin (2 \pi k)}{320}\\ +\frac{0.6\sin (2 \pi k}{40}, &{} \text {for }\,450<k\le 900. \end{array}\right. } \end{aligned}$$

(38)

Fig. 9

Response from CRFNN, LRNN, and FFNN models [Example 2]

Fig. 10

MSE curves obtained from CRFNN, LRNN, and FFNN models [Example 2]

Fig. 11

MAE curves obtained from CRFNN, LRNN, and FFNN models [Example 2]

Table 1 Performance comparison of CRFNN with other selected identifiers [Example 1]

Figure 9 shows the response obtained from all the selected neural structures. The error is found to decrease with time to a very minimum value. The performances of FFNN are also found to good as the proposed structure for this example, yet they have a large computation time and require neurons compared to the proposed structure. Figure 10 shows the MSE curve obtained from selected neural structures. Figure 11 shows the MAE curve obtained from selected neural structures. From the figures, it can be concluded that the proposed CRFNN model identifies better dynamics of the system.

4.6 Random sine wave noise injection test [Example 2]

A random sine wave as noise is supplied to the network between $250<k<450$ time interval. When a sine wave of value, $\sin (\frac{2\pi k}{15})$, was added to the network, the structure was initially found to fluctuate and deviate from the plant’s desired trajectory. However, the structure still recovered and was found to track the desired plant trajectory. This was due to learning ability caused by the dynamic self-recurrent links in their structures. Figure 12 shows the effect of random noise on the network. Table 2 gives the comparison of proposed CRFNN with other selected identifiers. The proposed model is found to give better performance indices over Elman, Jordan, LRNN, and FFNN.

Fig. 12

Effect of random sine noise [Example 2]

Table 2 Performance comparison of CRFNN with other selected identifiers [Example 2]

4.7 Example 3: Mackey–Glass time-series identification

Further, the proposed method is tested on the benchmark nonlinear time–series prediction problem. The well-known Mackey–Glass identification problem equation is considered in this section. The time-series prediction is given below as from Kumar et al. (2017)

$$\begin{aligned} \frac{\textrm{d}y_\textrm{p}(t)}{\textrm{d}t}=-\beta \times y_\textrm{p}(t)+\frac{\alpha \times y_\textrm{p}(t-\tau )}{1+y_\textrm{p}^{10}(t-\tau )}. \end{aligned}$$

(39)

The series is applied with parameter values such as $\alpha =0.2$ and $\beta =0.1$. Symbol t denotes the time-series sequence of the prediction. When $\tau \ge 17$, the time-series prediction is found to have a chaotic behavior. Hence, the value of the sampling rate is selected as, $\tau =17$. The differential equation is given by

$$\begin{aligned} y_\textrm{p}(k)=-\beta \times y_\textrm{p}(k)+\frac{\alpha \times y_\textrm{p}(k-\tau )}{1+y_\textrm{p}^{10}(k-\tau )}. \end{aligned}$$

(40)

Out of the 900 samples considered, 500 values were taken for training, and the remaining 400 values were taken for validation. The proposed identifier takes the series–parallel model form as $y_\textrm{crfnn}(k)=[y_\textrm{p}(k),y_\textrm{p}(k-17)]$. The problem is applied to all the selected neural structures. Figure 13 shows the response obtained for the time-series prediction problem. The response proves that the proposed structure can perform superior to other selected network structures. Figure 14 shows the MSE curve obtained. Figure 15 shows the MAE curves obtained from CRFNN, LRNN, and FFNN models.

Fig. 13

Response from CRFNN, LRNN, and FFNN models [Example 3]

Fig. 14

MSE curves obtained from CRFNN, LRNN, and FFNN models [Example 3]

Fig. 15

MAE curves obtained from CRFNN, LRNN, and FFNN models [Example 3]

4.8 Random sine wave noise injection test [Example 3]

The problem was also introduced to a sudden disturbance of sine wave with a value, $\sin (\frac{2\pi k}{15})$ between the time-interval $250<k<450$ to test its learning ability. Figure 16 shows the effect of random noise on the network. The network is found to work superior and more efficiently compared to other selected neural structures. The same can be concluded from the results of Table 3. The number of neurons required to follow the desired trajectory is only 4 for the proposed structure. The other selected neural structures require 6 neurons to achieve the same. The overall performance parameters are also achieved minimum for the proposed Compound Recurrent Feed forward Neural Network structure.

Fig. 16

Effect of random sine noise [Example 3]

Table 3 Performance comparison of CRFNN with other selected identifiers [Example 3]

4.9 Discussion

In this work, we have proposed a novel recurrent neural structure CRFNN for the identification of complex nonlinear dynamic systems. The performance is evaluated on three nonlinear real-time plant equations of varying degrees and complexities and is compared with Feed-forward structure (FFNN), Locally recurrent neural structure (LRNN), and the fully connected recurrent neural structures (Elman and Jordan). The results show that the proposed structure is able to effectively identify the changing dynamics of the plant. The AMSE and AMAE values obtained are far less than other selected neural structures considered in this work. The structure also required only a lesser number of inputs as compared to other structures in this work to efficiently train the tunable parameter and reach the optimum value. This is also an indication that the proposed structure is independent of the order of the plant. From the results of a random noise injection test, it is evident that the proposed structure is able to recover quickly and adjust itself to the changing dynamics of the system. These characteristics make the structure an efficient one for nonlinear identification.

5 Conclusion

In this paper, a Compound Recurrent Feed-forward Neural Network (CRFNN) is proposed for the identification of the complex nonlinear dynamical systems. The proposed structure is the hybridization of the LRNN and a single-layer FFNN model that are combined to develop the proposed model. With the help of three benchmark non-linear problems, the structure’s performance is evaluated and compared with other well-known neural models. The proposed structure is found to perform super,ior since it provided the least of the values of the error-based indicators, such as MSE, MAE, and RMSE, require lesser number of the number of input parameters, require lesser number of trainable weights. Additionally, the structure is discovered to be resistant to perturbations and parameter changes applied to the system.

5.1 Limitations and recommendations for future research

To make the proposed model simpler, the number of neurons is currently fixed equal to 4; however, this option has a significant impact on the model’s overall accuracy. We may need more neurons in some systems (to be identified) to accurately define the dynamics. The development of a strategy to optimize the number of neurons in the model (depending on the system to be identified) is thus one topic of future research. To enhance the overall performance of the learning algorithm, another option may be to create new optimization techniques inspired by nature or integrate the already available optimization techniques with the BP method. The starting settings of the model’s parameter can also have an impact on how well the model performs as predicted. One can anticipate the model to tune rapidly and give the desired accuracy (in a short amount of training time) if the values of these parameters are initialized correctly. The creation of an adaptive learning rate scheme is another area of research that will be the focus of our efforts in the future. This is because the rate at which a model evolves depends on its learning rate value, and evolving a model iteratively could help iterate. the model more quickly