1 Introduction

Wiener process is a stochastic process with stationary and independent normal random increments, which plays an important role in mathematics, finance, and physics. As a type of differential equation driven by Wiener process, stochastic differential equation pioneered by Kiyosi Ito laid a substantial foundation for stochastic finance theory. Based on this, Black and Scholes (1973) and Merton (1973) presented Black–Scholes formula to price the stock option. Following that, many researchers such as Garman and Kohlhagen (1983) and Rogers and Shi (1995) investigated various options pricing problems. Particularly, swaption is an option which gives its owner the right but not the obligation to enter into an underlying interest rate swap, where the owner of a payer (receiver) swaption has the right to pay fixed (floating) interest rate cash flow and receive floating (fixed) interest rate cash flow. Quantitative analysts valued swaptions by construction complex lattice-based term structure and short rate models that describe the movement of interest rate over time (Frank 1998).

All above option pricing methods assumed the assets’ price following some stochastic differential equations under the framework of probability theory, which was found by Kolmogorov in 1933. Since then, probability theory has become an important tool for dealing with indeterminacy when we can obtain enough data to estimate the probability distribution. Unfortunately, for some technological or economical reasons we can only obtain inadequate or even no sample data and have to use belief degrees given by some domain experts, which have a much larger range than the real frequency (Kahneman and Tversky 1979) and cannot be regarded as probability (Liu 2012). Addressing this, Liu (2007) found the uncertainty theory and refined it (Liu 2010) based on normality, duality, subadditivity, and product axioms, which has brought many branches such as uncertain finance (Liu 2013, 2009; Chen 2011; Yang and Zhu 2021; Zhang and Wang 2021; Zhang et al. 2021) and uncertain statistics (Liu 2010; Lio and Liu 2013; Yao and Liu 2018; Liu and Yang 2020; Liu and Jia 2020; Lio 2021) up to now. Noting the fact that the evolution of some undetermined phenomena behaves like uncertainty rather than randomness (Liu 2007), Liu pioneered uncertain process (Liu 2008) which is essentially a sequence of uncertain variables indexed by time. Later, as a Lipschitz continuous uncertain process with stationary and independent uncertain normal increments, Liu process (Liu 2009) was initiated by Liu. Based on this, Liu proposed the uncertain differential equation (Liu 2008) driven by Liu process to deal with uncertain dynamic systems. Following that, the existence and uniqueness theorem (Chen and Liu 2010) and stability theorem (Yao et al. 2013) of the solution of uncertain differential equation were proved. Analytic solutions for some special types of uncertain differential equations were provided by many scholars such as Chen and Liu (2010) and Liu (2012). Moreover, Yao and Chen (2013) proposed Yao–Chen formula connecting an uncertain differential equation with a family of ordinary differential equations.

In order to solve the paradox of stochastic finance theory (Liu 2013), Liu (2009) modeled stock price via uncertain differential equation and derived its European option’s price for the first time, laying a foundation for uncertain finance theory. Later, the price formulae of American option and Asian option were given by Chen (2011) and Sun and Chen (2015), respectively. Besides, Peng and Yao (2011) employed another uncertain stock model and gave the pricing formulae of its European and American option. In addition, Chen and Gao (2013) proposed three types of uncertain interest rate models and valued the zero-coupon bond. Furthermore, some other interest rate derivatives attracted many scholars’ attention. For example, Xiao et al. (2016) discussed the interest rate swap’s pricing formula in uncertain financial market, and Zhang et al. (2016) provided the price of interest rate ceiling and interest rate floor.

As another interest rate derivative, swaption is also an important risk management tool in financial market. The issue of how to determine swaption price under the framework of uncertainty theory has not been touched in previous studies. This paper joins the research stream by providing pricing formulae for payer swaption and receiver swaption with an assumption that the interest rate follows the uncertain differential equation. The remainder of this paper is organized as follows. In Sect. 2, some needed fundamental definitions in uncertainty theory will be recalled. After that, price problems for payer swaption and receiver swaption are going to be investigated in Sects. 3 and 4, respectively. Then, Sect. 5 will provide some examples to illustrate our methods. At last, some conclusions will be given in Sect. 6.

2 Preliminaries

In this section, some basic definitions in uncertainty theory are reviewed.

Definition 1

(Liu (2008)) Consider an uncertainty space \((\Gamma , \text{ L }, \text{ M})\) and a totally ordered set T. An uncertain process \(X_{t}(\gamma )\) is a measurable function from \(T \times (\Gamma ,\text{ L },\text{ M})\) to the set of real numbers such that for any Borel set B of real numbers, \(\{X_{t} \in B\}\) is an event at each time t. An uncertain process \(X_{t}\) has independent increments if the following uncertain variables

$$\begin{aligned} X_{t_{1}}, X_{t_{2}}-X_{t_{1}}, \ldots , X_{t_{k}}-X_{t_{k-1}} \end{aligned}$$

are independent for any time \(t_{1}, \ldots , t_{k}\) with \(t_{1}<\cdots < t_{k}\). And \(X_{t}\) has stationary increments if uncertain variables

$$\begin{aligned} X_{s+t}-X_{s} \end{aligned}$$

are identically distributed for all \(s>0\).

An important and useful stationary independent increment uncertain process, Liu process (Liu 2008), was investigated by Liu.

Definition 2

(Liu (2008)) Liu process \(C_{t}\) is an uncertain process which satisfies the following three conditions,

  1. 1.

    Almost all sample paths are Lipschitz continuous and \(C_{0}=0\),

  2. 2.

    \(C_{t}\) has stationary and independent increments,

  3. 3.

    the increment \(C_{s+t}-C_{s}\) is a normal uncertain variable with expected value 0 and variance \(t^{2}\).

As a new type of differential equation driven by Liu process \(C_{t}\), the uncertain differential equation (Liu 2008) is defined as follows.

Definition 3

(Liu (2008)) Denote a Liu process as \(C_{t}\) and measurable functions as f and g. Then, an uncertain differential equation is given as

$$\begin{aligned} dX_{t} = f(t, X_{t})dt+g(t,X_{t})dC_{t} \end{aligned}$$
(1)

with an initial value \(X_{0}\). An uncertain process \(X_{t}\) which satisfies the above equation identically in t is a solution.

Following that, Yao and Chen (2013) introduced the \(\alpha \)-path for uncertain differential equation connecting an uncertain differential equation with a spectrum of ordinary differential equations.

Definition 4

(Yao and Chen (2013)) For a number \(\alpha \in (0,1)\), the \(\alpha \)-path of the uncertain differential equation (1) is the solution of the corresponding ordinary differential equation

$$\begin{aligned} dX_{t}^{\alpha } = f(t, X_{t}^{\alpha })dt+|g(t,X_{t}^{\alpha })|\frac{\sqrt{3}}{\pi } \ln \frac{\alpha }{1-\alpha } dt. \end{aligned}$$
(2)

3 Payer swaption

The buyer of a payer swaption has the right to pay fixed interest rate cash flow and receive floating interest rate cash flow at the expiration time T. In this section, we propose the pricing formula, derive the calculation formula, and present a numerical method for the payer swaption in uncertain financial market.

Denote the fixed interest rate as r, the floating interest rate as \(r_{t}\) which is modeled by the uncertain differential equation (1), i.e.,

$$\begin{aligned} \mathrm{d}r_{t} = f(t, r_{t})\mathrm{d}t+g(t,r_{t})\mathrm{d}C_{t} \end{aligned}$$

with an initial value \(r_{0}\), the expiration date as T, the notional principal amount as \(S_{0}\), and the price of the payer swaption as \(f_{p}\). Then, it costs the buyer \(f_{p}\) to buy it at time 0 and gives the buyer a payoff

$$\begin{aligned} S_{0} \left( \exp \left( \int _{0}^{T} r_{t} \mathrm{d}t\right) -\exp (rT) \right) ^{+} \end{aligned}$$

at time T since the swaption is rationally exercised if and only if

$$\begin{aligned} S_{0} \exp \left( \int _{0}^{T} r_{t} \mathrm{d}t\right) > S_{0} \exp (rT). \end{aligned}$$

Thus, the net return of the buyer at time 0 is

$$\begin{aligned} \begin{aligned}&-f_{p}+\exp \left( -\int _{0}^{T} r_{t} dt\right) S_{0} \\&\left( \exp \left( \int _{0}^{T} r_{t} dt\right) -\exp (rT) \right) ^{+} \\ =&-f_{p}+ S_{0} \left( 1 -\exp \left( -\int _{0}^{T} r_{t}dt +rT\right) \right) ^{+}. \end{aligned} \end{aligned}$$

Correspondingly, the seller’s net return at time 0 is

$$\begin{aligned} f_{p}-S_{0} \left( 1 -\exp \left( -\int _{0}^{T} r_{t}dt +rT\right) \right) ^{+}. \end{aligned}$$

It follows from the fair price principle that the fair price \(f_{p}\) should make the buyer and the seller have an identical expected return, which means

$$\begin{aligned} \begin{aligned}&-f_{p}+E \left[ S_{0} \left( 1 -\exp \left( -\int _{0}^{T} r_{t}dt +rT\right) \right) ^{+} \right] \\&\quad = f_{p}- E \left[ S_{0} \left( 1 -\exp \left( -\int _{0}^{T} r_{t}dt +rT\right) \right) ^{+} \right] . \end{aligned} \end{aligned}$$

Thus, we propose the pricing formula for payer swaption as follows.

Definition 5

Consider a payer swaption with an expiration date T, a notional principal amount \(S_{0}\), a fixed interest rate r, and a floating interest rate \(r_{t}\) satisfying the uncertain differential equation (1), i.e.,

$$\begin{aligned} \mathrm{d}r_{t} = f(t, r_{t})\mathrm{d}t+g(t,r_{t})\mathrm{d}C_{t} \end{aligned}$$

with an initial value \(r_{0}\), where \(C_{t}\) is a Liu process, and f and g are measurable functions. Then, its price is defined by

$$\begin{aligned} f_{p}=E \left[ S_{0} \left( 1 -\exp \left( -\int _{0}^{T} r_{t}dt +rT\right) \right) ^{+} \right] . \end{aligned}$$
(3)

Theorem 1

Consider a payer swaption with an expiration date T, a notional principal amount \(S_{0}\), a fixed interest rate r, and a floating interest rate \(r_{t}\) satisfying the uncertain differential equation (1), i.e.,

$$\begin{aligned} \mathrm{d}r_{t} = f(t, r_{t})\mathrm{d}t+g(t,r_{t})\mathrm{d}C_{t} \end{aligned}$$

with an initial value \(r_{0}\) and an \(\alpha \)-path \(r_{t}^{\alpha }\). Then, its price (3) can be calculated as

$$\begin{aligned} f_{p}=\int _{0}^{1} S_{0} \left( 1 -\exp \left( -\int _{0}^{T} r_{t}^{\alpha }\mathrm{d}t +rT\right) \right) ^{+} \mathrm{d}\alpha , \end{aligned}$$

where \(r_{t}^{\alpha }\) is the solution of the corresponding ordinary differential equation

$$\begin{aligned} dr_{t}^{\alpha } = f(t, r_{t}^{\alpha })dt+|g(t,r_{t}^{\alpha })|\frac{\sqrt{3}}{\pi } \ln \frac{\alpha }{1-\alpha } dt. \end{aligned}$$

Proof

It follows from Yao (2013) that the inverse uncertainty distribution of the uncertain variable

$$\begin{aligned} \int _{0}^{T} r_{t} \mathrm{d}t \end{aligned}$$

is

$$\begin{aligned} \Psi ^{-1}(\alpha )= \int _{0}^{T} r_{t}^{\alpha }dt. \end{aligned}$$

Since the function

$$\begin{aligned} S_{0}\left( 1-\exp \left( -x+rT\right) \right) ^{+} \end{aligned}$$

is increasing with respect to x, it is obtained from the operational law of the inverse uncertainty distribution (Liu 2007) that the inverse uncertainty distribution of

$$\begin{aligned} S_{0} \left( 1 -\exp \left( -\int _{0}^{T} r_{t}dt +rT\right) \right) ^{+} \end{aligned}$$

is

$$\begin{aligned} \Upsilon ^{-1}(\alpha )=S_{0} \left( 1 -\exp \left( -\int _{0}^{T} r_{t}^{\alpha }dt +rT\right) \right) ^{+}. \end{aligned}$$

From the expected value formula of the uncertain variable (Liu 2007), we have

$$\begin{aligned} \begin{aligned} f_{p}&= E \left[ S_{0} \left( 1 -\exp \left( -\int _{0}^{T} r_{t}dt +rT\right) \right) ^{+} \right] \\&= \int _{0}^{1} S_{0} \left( 1 -\exp \left( -\int _{0}^{T} r_{t}^{\alpha }dt +rT\right) \right) ^{+} \mathrm{d}\alpha . \end{aligned} \end{aligned}$$

The proof follows immediately. \(\square \)

When the price of payer swaption shown in Eq. (3) cannot be calculated explicitly, we present a numerical method as follows.

Step 0:

Fix \(\alpha =0\), the fixed interest rate r, the initial interest rate value of \(r_{t}=r_{0}\), the notional principal \(S_{0}\), and the maturity data T.

Step 1:

Set \(\alpha \leftarrow \alpha +1/N\) for a given large enough N.

Step 2:

Use the numerical method to solve the corresponding ordinary differential equation

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \mathrm{d}r_{t}^{\alpha }= f\left( t,r_{t}^{\alpha } \right) \mathrm{d}t+|g\left( t, r_{t}^{\alpha } \right) | \frac{\sqrt{3}}{\pi } \ln \frac{\alpha }{1-\alpha } \mathrm{d}t \\ \displaystyle r_{0}^{\alpha }=r_{0}, \\ \end{array} \right. \end{aligned}$$

and get the partition \(t_{i}\) and \(r_{t_{i}}^{\alpha }\) with \(0=t_{0}<t_{1}<\cdots <t_{n}=T\).

Step 3:

Repeat Steps 1 and 2 for \(N-1\) times.

Step 4:

Calculate

$$\begin{aligned} \begin{aligned} f_{p}=&S_{0}\sum _{j=1}^{N-1}\frac{1}{N-1} \\&\left( 1-\exp \left( rT-\sum _{i=0}^{n-1}r_{t_{i}}^{\frac{j}{N}}(t_{i+1}-t_{i}) \right) \right) ^{+}. \end{aligned} \end{aligned}$$

4 Receiver swaption

The buyer of a receiver swaption has the right to pay floating interest rate cash flow and receive fixed interest rate cash flow. In this section, we propose the pricing formula, derive the calculation formula, and present a numerical method for the receiver swaption in uncertain financial market.

Denote the fixed interest rate as r, the floating interest rate as \(r_{t}\) which is modeled by the uncertain differential equation (1), i.e.,

$$\begin{aligned} \mathrm{d}r_{t} = f(t, r_{t})\mathrm{d}t+g(t,r_{t})\mathrm{d}C_{t} \end{aligned}$$

with an initial value \(r_{0}\), the expiration date as T, the notional principal amount as \(S_{0}\), and the price of the receiver swaption as \(f_{r}\). Then, it costs the buyer \(f_{r}\) to buy it at time 0 and gives the buyer a payoff

$$\begin{aligned} S_{0}\left( \exp (rT)-\exp \left( \int _{0}^{T}r_{t} \mathrm{d}t\right) \right) ^{+} \end{aligned}$$

at time T since the receiver swaption is rationally exercised if and only if

$$\begin{aligned} S_{0}\exp (rT)>S_{0}\exp \left( \int _{0}^{T}r_{t} \right) . \end{aligned}$$

Thus, the net return of the buyer at time 0 is

$$\begin{aligned} \begin{aligned}&-f_{r}+\exp \left( -\int _{0}^{T} r_{t} dt\right) S_{0} \left( \exp (rT) \right. \nonumber \\ {}&\quad \left. -\exp \left( \int _{0}^{T} r_{t} dt\right) \right) ^{+} \\ =&-f_{r}+ S_{0} \left( \exp \left( -\int _{0}^{T} r_{t}dt +rT\right) -1 \right) ^{+}. \end{aligned} \end{aligned}$$

Correspondingly, the seller’s net return at time 0 is:

$$\begin{aligned} f_{r}-S_{0} \left( \exp \left( -\int _{0}^{T} r_{t}dt +rT\right) -1 \right) ^{+}. \end{aligned}$$

It follows from the fair price principle that the fair price \(f_{r}\) should make the buyer and the seller have an identical expected return, which means

$$\begin{aligned} \begin{aligned}&-f_{r}+E \left[ S_{0} \left( \exp \left( -\int _{0}^{T} r_{t}dt +rT\right) -1 \right) ^{+} \right] \\&\quad = f_{r}-E\left[ S_{0} \left( \exp \left( -\int _{0}^{T} r_{t}dt +rT\right) -1 \right) ^{+} \right] . \end{aligned} \end{aligned}$$

Thus, we propose the pricing formula for receiver swaption as follows.

Definition 6

Consider a receiver swaption with an expiration date T, a notional principal amount \(S_{0}\), a fixed interest rate r, and a floating interest rate \(r_{t}\) satisfying the uncertain differential equation (1), i.e.,

$$\begin{aligned} \mathrm{d}r_{t} = f(t, r_{t})\mathrm{d}t+g(t,r_{t})\mathrm{d}C_{t} \end{aligned}$$

with an initial value \(r_{0}\), where \(C_{t}\) is a Liu process, and f and g are measurable functions. Then, its price is defined by

$$\begin{aligned} f_{r}=E \left[ S_{0} \left( \exp \left( -\int _{0}^{T} r_{t}dt +rT\right) -1 \right) ^{+} \right] . \end{aligned}$$
(4)

Theorem 2

Consider a receiver swaption with an expiration date T, a notional principal amount \(S_{0}\), a fixed interest rate r, and a floating interest rate \(r_{t}\) satisfying the uncertain differential equation (1), i.e.,

$$\begin{aligned} \mathrm{d}r_{t} = f(t, r_{t})\mathrm{d}t+g(t,r_{t})\mathrm{d}C_{t} \end{aligned}$$

with an initial value \(r_{0}\) and an \(\alpha \)-path \(r_{t}^{\alpha }\). Then, its price (4) can be calculated as

$$\begin{aligned} f_{r}=\int _{0}^{1} S_{0} \left( \exp \left( -\int _{0}^{T} r_{t}^{\alpha }\mathrm{d}t +rT\right) -1 \right) ^{+} \mathrm{d}\alpha , \end{aligned}$$

where \(r_{t}^{\alpha }\) is the solution of the corresponding ordinary differential equation

$$\begin{aligned} dr_{t}^{\alpha } = f(t, r_{t}^{\alpha })dt+|g(t,r_{t}^{\alpha })|\frac{\sqrt{3}}{\pi } \ln \frac{\alpha }{1-\alpha } dt. \end{aligned}$$

Proof

It follows from Yao (2013) that the inverse uncertainty distribution of the uncertain variable

$$\begin{aligned} \int _{0}^{T} r_{t} \mathrm{d}t \end{aligned}$$

is

$$\begin{aligned} \Psi ^{-1}(\alpha )= \int _{0}^{T} r_{t}^{\alpha }dt. \end{aligned}$$

Since the function

$$\begin{aligned} S_{0}\left( \exp \left( -x+rT\right) -1 \right) ^{+} \end{aligned}$$

is decreasing with respect to x, it is obtained from the operational law of the inverse uncertainty distribution (Liu 2007) that the inverse uncertainty distribution of

$$\begin{aligned} S_{0} \left( \exp \left( -\int _{0}^{T} r_{t}dt +rT\right) -1 \right) ^{+} \end{aligned}$$

is

$$\begin{aligned} \Gamma ^{-1}(\alpha )=S_{0} \left( \exp \left( -\int _{0}^{T} r_{t}^{1-\alpha }dt +rT\right) -1 \right) ^{+}. \end{aligned}$$

From the expected value formula of the uncertain variable (Liu 2007), we have

$$\begin{aligned} \begin{aligned} f_{r}&= E \left[ S_{0} \left( \exp \left( -\int _{0}^{T} r_{t}dt +rT\right) -1 \right) ^{+} \right] \\&=\int _{0}^{1} S_{0} \left( \exp \left( -\int _{0}^{T} r_{t}^{\alpha }dt +rT\right) -1 \right) ^{+} \mathrm{d}\alpha . \end{aligned} \end{aligned}$$

The proof follows immediately.

When the price of receiver swaption shown in Eq. (4) cannot be calculated explicitly, we present a numerical method as follows.

Step 0:

Fix \(\alpha =0\), the fixed interest rate r, the initial interest rate value \(r_{0}\), the notional principal \(S_{0}\), and the maturity data T.

Step 1:

Set \(\alpha \leftarrow \alpha +1/N\) for a given large enough N.

Step 2:

Use the numerical method to solve the corresponding ordinary differential equation

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \mathrm{d}r_{t}^{\alpha }= f\left( t, r_{t}^{\alpha } \right) \mathrm{d}t+ |g\left( t,r_{t}^{\alpha } \right) | \frac{\sqrt{3}}{\pi } \ln \frac{\alpha }{1-\alpha } \mathrm{d}t \\ \displaystyle r_{0}^{\alpha }=r_{0}, \\ \end{array} \right. \end{aligned}$$

and get the partition \(t_{i}\) and \(r_{t_{i}}^{\alpha }\) with \(0=t_{0}<t_{1}<\cdots <t_{n}=T\).

Step 3:

Repeat Steps 1 and 2 for \(N-1\) times.

Step 4:

Calculate

$$\begin{aligned} f_{r}= \sum _{j=1}^{N-1}\frac{1}{N-1}\left( \exp \left( rT-\sum _{i=0}^{n-1}r_{t_{i}}^{\frac{j}{N}}(t_{i+1}-t_{i}) \right) -1 \right) ^{+}. \end{aligned}$$

\(\square \)

5 Examples

In this section, we document some numerical examples to illustrate our methods. Recall the uncertain interest rate model given by Chen and Gao (2013), i.e.,

$$\begin{aligned} \mathrm{d}r_{t}=a(b-r_{t})\mathrm{d}t+\sigma \sqrt{r_{t}} \mathrm{d}C_{t}, \end{aligned}$$
(5)

where a, b, and \(\sigma \) are given constants, and \(C_{t}\) is the Liu process.

Example 1

Consider a payer swaption with a notional principal \(S_{0}=1\), a fixed interest rate \(r=0.03\), and a floating interest rate \(r_{t}\) satisfying the uncertain interest rate model (5) with \(a=0.001\), \(b=0.03\), \(\sigma =0.005\), and \(r_{0}=0.03\). According to Theorem 1, the price of this payer swaption with a set of expiration time T can be calculated as

$$\begin{aligned} f_{p}=\int _{0}^{1} S_{0} \left( 1 -\exp \left( -\int _{0}^{T} r_{t}^{\alpha }\mathrm{d}t +rT\right) \right) ^{+} \mathrm{d}\alpha , \end{aligned}$$

where \(r_{t}^{\alpha }\) is the solution of the corresponding ordinary differential equation

$$\begin{aligned} dr_{t}^{\alpha } = a(b-r_{t}^{\alpha }) dt+\sigma \sqrt{r_{t}^{\alpha }} \frac{\sqrt{3}}{\pi } \ln \frac{\alpha }{1-\alpha } dt. \end{aligned}$$

Results are shown in Fig. 1. As we can see, the payer swaption’s price is increasing with respect to the expiration time T under this parameter settings.

Fig. 1
figure 1

The price \(f_{p}\) for payer swaption with respect to the expiration time T in Example 1

Full size image

Consider a payer swaption with the expiration time \(T=2\), a notional principal \(S_{0}=1\), and a floating interest rate \(r_{t}\) satisfying uncertain interest rate model (5) with \(a=0.001\), \(b=0.03\), \(\sigma =0.005\), and \(r_{0}=0.03\). According to Theorem 1, the price of this payer swaption with a set of fixed interest rates r is shown in Fig. 2. As we can see, the payer swaption’s price is decreasing with respect to the fixed interest rate r under this parameter settings.

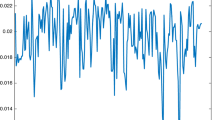
Consider a payer swaption with the expiration time \(T=2\), a notional principal \(S_{0}=1\), a fixed interest rate \(r=0.02\), and a floating interest rate \(r_{t}\) satisfying the uncertain interest rate model (5) with \(a=0.001\), \(b=0.03\), \(\sigma =0.005\), and a set of initial values \(r_{0}\). According to Theorem 1, the price of this payer swaption with a set of initial values \(r_{0}\) is shown in Fig. 3. As we can see, the payer swaption’s price is increasing with respect to the initial value \(r_{0}\) under this parameter settings.

Fig. 2
figure 2

The price \(f_{p}\) for payer swaption with respect to the fixed interest rate r in Example 1

Full size image
Fig. 3
figure 3

The price \(f_{p}\) for payer swaption with respect to the initial value \(r_{0}\) in Example 1

Full size image

Example 2

Consider a receiver swaption with a notional principal \(S_{0}=1\), a fixed interest rate \(r=0.03\), and a floating interest rate \(r_{t}\) satisfying the uncertain interest rate model (5) with \(a=0.001\), \(b=0.03\), \(\sigma =0.005\), and \(r_{0}=0.03\). According to Theorem 2, the price of this receiver swaption with a set of expiration time T can be calculated as

$$\begin{aligned} f_{r}=\int _{0}^{1} S_{0} \left( \exp \left( -\int _{0}^{T} r_{t}^{\alpha }\mathrm{d}t +rT\right) -1 \right) ^{+} \mathrm{d}\alpha , \end{aligned}$$

where \(r_{t}^{\alpha }\) is the solution of the corresponding ordinary differential equation

$$\begin{aligned} dr_{t}^{\alpha } = a(b-r_{t}^{\alpha })dt+\sigma \sqrt{r_{t}^{\alpha }} \frac{\sqrt{3}}{\pi } \ln \frac{\alpha }{1-\alpha } dt. \end{aligned}$$

Results are shown in Fig. 4. As we can see, the receiver swaption’s price is decreasing with respect to the expiration time T under this parameter settings.

Consider a receiver swaption with the expiration time \(T=2\), a notional principal \(S_{0}=1\), and a floating interest rate \(r_{t}\) satisfying uncertain interest rate model (5) with \(a=0.001\), \(b=0.03\), \(\sigma =0.005\), and \(r_{0}=0.03\). According to Theorem 2, the price of this receiver swaption with a set of fixed interest rates r is shown in Fig. 5. As we can see, the receiver swaption’s price is increasing with respect to the fixed interest rate r under this parameter settings.

Consider a receiver swaption with the expiration time \(T=2\), a notional principal \(S_{0}=1\), a fixed interest rate \(r=0.03\), and a floating interest rate \(r_{t}\) satisfying the uncertain interest rate model (5) with \(a=0.001\), \(b=0.03\), \(\sigma =0.005\), and a set of initial values \(r_{0}\). According to Theorem 2, the price of this receiver swaption with a set of initial values \(r_{0}\) is shown in Fig. 6. As we can see, the receiver swaption’s price is decreasing with respect to the initial value \(r_{0}\) under this parameter settings.

Fig. 4
figure 4

The price \(f_{r}\) for receiver swaption with respect to the expiration time T in Example 2

Full size image
Fig. 5
figure 5

The price \(f_{r}\) for receiver swaption with respect to the fixed interest rate r in Example 2

Full size image
Fig. 6
figure 6

The price \(f_{r}\) for receiver swaption with respect to the initial value \(r_{0}\) in Example 2

Full size image

6 Conclusion

Noting the paradox of stochastic finance theory, this paper investigated swaption pricing problems under the framework of uncertainty theory. We proposed pricing formulae for swaptions, derived calculation formulae, and corresponding numerical methods with the assumption that the interest rate follows uncertain differential equations. Finally, some examples were given to illustrate our methods.