Optimal type-2 fuzzy synchronization of two different fractional-order chaotic systems with variable orders with an application to secure communication

Abstract

In this paper, the synchronization problem of two different fractional-order chaotic systems has been investigated. Variable fractional orders are considered in this problem. An optimal synchronization strategy is defined for the fractional case. The optimality conditions are obtained using the fuzzy modeling of fractional-order systems. These models are with the type-1 and type-2 Takagi–Sugeno structures. Also, using chaotic masking, the synchronization method is applied for secure communication. Finally, using the simulation examples, the performance of the proposed method is shown.

1 Introduction

Chaotic behavior is shown in many cases in daily life. Then, study on these systems and applications of these systems is an important problem (Pecora and Carroll 1990). Fractional-order dynamical modeling of chaotic systems is one of the new topics on these systems (Odibat and Momani 2006; Momani and Odibat 2007). In this paper, we study the fractional-order chaotic systems. Chaos synchronization for different fractional-order systems is one of the challenging problems in this area (Behinfaraz et al. 2019; Behinfaraz and Badamchizadeh 2015). According to the different dynamics of systems, the control signal, in the synchronization of chaotic systems, would not become zero. Therefore, in these systems synchronizing with the minimum control signal is an important point.

To the best of our knowledge, for optimal synchronization of different fractional-order systems, there is not any significant study. Then, in this paper, we focus on the optimal synchronization problem of different fractional-order systems.

Simplifying the complex structure with simple models is an effective method in the system analysis. According to the complex structure of variable-order chaotic systems, fuzzy models of these systems are introduced. This type of modeling simplifies the nonlinearity of chaotic systems which is an important problem in the proposed optimal control method. Different types of fuzzy modeling can be used in this case (Antão et al. 2018). One of the well-known fuzzy models is Takagi–Sugeno (T–S) model. Two types of T–S fuzzy modeling is used in this paper. First, we model the chaotic systems with type-1 T–S structure. Then, we use a type-2 T–S structure. According to the structure of these models, it seems the type-2 fuzzy model leads to better results than the type-1 fuzzy model.

Secure communication of data is one of the important tasks in the age of communications. One of the most important applications of chaos synchronization is in the secure communication (Behinfaraz et al. 2020). In this paper, secure communication using the synchronization of the fractional-order chaotic systems is discussed.

One of the innovative points of this work is that we introduced a method to achieve optimal synchronization between two different chaotic systems with variable orders and secure communication in this condition is done. It is shown that in fractional cases by decreasing the fractional order, less control effort needs to synchronize two systems. For the secure transmission of the information, we need two chaotic systems that are synchronized with each other. The main contributions of this paper can be listed as follows:

• A new type of stability conditions on fractional-order systems is introduced

• A TS type-1 and type-2 fuzzy modeling are represented for a fractional-order chaotic system with variable orders

• An optimal synchronization between two different fractional-order chaotic systems is introduced

• Secure signal transmission with the minimum required energy is introduced.

This paper is organized as follows: In Sect. 2, the literature review of the paper is written. In the next section, basic definitions and relations around the proposed method are introduced. In Sect. 4, the proposed method of this paper is formulated. The simulation results of the proposed method are shown in Sect. 5. Finally, in Sect. 6 main conclusions of the paper are presented.

2 Literature review

Chaos synchronization problem for the first time was introduced by Pecora and Carroll for two chaotic systems with different initial conditions (Pecora and Carroll 1990). After that, many other methods have been used for the synchronization of chaotic systems in different conditions. Some popular method for synchronization of chaotic systems is the Lyapunov method, linear and nonlinear feedback control (Odibat and Momani 2006; Behinfaraz et al. 2019). Fractional-order modeling of different dynamics has attracted great attention in recent years because modeling of systems with fractional-order equations has a wide range of applications in many fields such as engineering physics and mathematics (Momani and Odibat 2007). For chaotic systems, it is proved that some fractional-order differential systems behave chaotically, such as the fractional-order Chua’s system, the fractional-order Rössler system, the fractional-order modified Duffing system, fractional-order Lorenz system, Chen system and Lü system (Behinfaraz and Badamchizadeh 2015). Chaos synchronization problems in fractional-order systems are widely investigated (Behinfaraz and Badamchizadeh 2015; Jiang et al. 2020; Wang et al. 2020; Behinfaraz et al. 2019, 2020).

The nonlinear structure of the chaotic system with fractional order makes an analysis of these systems so challenging. Then, appropriate modeling can help to reduce the complexity of the system. It was shown that Takagi–Sugeno (TS) fuzzy modeling is one of the best tools in modeling nonlinear structures (Soltani et al. 2019). TS fuzzy modeling is a model with some if–then rules. These rules can change a nonlinear system to a locally linear one. Then, an analysis of the system can be simplified (Gil et al. 2019). So in this paper, the dynamic of each system is modeled by TS fuzzy model. It was shown that in many cases type-2 fuzzy systems have a better performance compared to the type-1, especially when the variation and uncertainty were on the system (Tao 2004; Castillo et al. 2011).

Optimal control is the control and synchronization of integer-order chaotic systems, previously (Motallebzadeh et al. 2012; El-Gohary 2006). Fractional-order optimal control for the first time appeared in optimal control of fractional Brownian motion (Duncan et al. 2000; Hu and Øksendal 2003). The fractional optimal control problem is an optimal control problem for fractional differential equations. In this field of study, or more specifically, fractional optimal control there are a few works (Manabe 2003). Also, there are some works about optimal synchronization of integer-order chaotic systems (Motallebzadeh et al. 2012; El-Gohary 2006).

Secure communications using chaos synchronization are one of the most important applications of chaotic systems. Different methods have been introduced for this task (Arman et al. 2009; Behinfaraz et al. 2020, 2020). These methods are separated into the analog and digital modulation methods (Guerra and Yu 2008; Samimi et al. 2020). Chaotic masking is one of the well-known methods for the secure communication (Hashemi et al. 2020).

3 Preliminaries

3.1 Fractional-order derivative

The first step on the use of fractional-order modeling is the definition of fractional-order operator. One of the well-known definitions of fractional-order operator is Caputo definition (Tavazoei and Haeri 2007). This definition for a function as f(t) is shown as follows:

$$\begin{aligned} \frac{\mathrm{d}^\alpha }{\mathrm{d}t^\alpha } f(t)= \frac{1}{\varGamma (n-\alpha )} \int _{0}^{t} \frac{f^{(n)}(\tau )}{(t-\tau )^{n-\alpha +1}}\mathrm{d}\tau \end{aligned}$$

(1)

where $\alpha$ is fractional order, n is the first integer number bigger than $\alpha$ and $\varGamma (.)$ is the Gamma function. Also RL definition of fractional-order operator is described by:

$$\begin{aligned} \frac{\mathrm{d}^\alpha }{\mathrm{d}t^\alpha } f(t)= \frac{1}{\varGamma (n-\alpha )} \frac{\mathrm{d}^n}{\mathrm{d}t^n} \int _{0}^{t} \frac{f(\tau )}{(t-\tau )^{n-\alpha +1}}\mathrm{d}\tau \end{aligned}$$

(2)

where n is an integer such that $n-1<\alpha < n$ and $\varGamma (.)$ is the Gamma function.

The Laplace transform of the Riemann–Liouville fractional derivative is

$$\begin{aligned} {\mathcal {L}}\left( \frac{\mathrm{d}^\alpha }{\mathrm{d}t^\alpha } f(t)\right) = s^\alpha {\mathcal {L}}(f(t)) - \sum _{k=0}^{n-1} \left[ \frac{\mathrm{d}^{\alpha -1-k}f(t)}{\mathrm{d}t^{\alpha -1-k}}\right] _{t=0} \end{aligned}$$

(3)

where ${\mathcal {L}}$ is Laplace transformer and s is a complex variable. Zero initial condition changes this definition to:

$$\begin{aligned} {\mathcal {L}}\left( \frac{\mathrm{d}^\alpha }{\mathrm{d}t^\alpha } f(t)\right) = s^\alpha {\mathcal {L}}(f(t)) \end{aligned}$$

(4)

3.2 Fractional-order chaotic systems

3.2.1 Fractional-order Lorenz system

Fractional version of chaotic Lorenz system is described by Behinfaraz and Badamchizadeh (2015):

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\alpha _1} x = \sigma (y -x) \\ D^{\alpha _2} y = \rho x -xz -y \\ D^{\alpha _3} z = xy -\beta z \end{array}\right. } \end{aligned}$$

(5)

where x, y, z are the states of system. Also $\sigma$ , $\rho$ and $\beta$ are the parameters of system. It was shown with parameter as $\sigma =10$, $\rho =28$ and $\beta =8/3$; system (5) is chaotic in the integer case. With this parameter, chaotic behavior of system is happened for $\alpha _i>0.99$ for $i=1,2,3$ (Behinfaraz and Badamchizadeh 2015). The state trajectories of the system for $\alpha _1=\alpha _2=\alpha _3 =0.993$ are illustrated in Fig. 1.

Fig. 1

Chaotic behavior of fractional-order Lorenz system

3.2.2 Fractional-order Chen system

Dynamic of this system is similar to Lorenz system with some differences. Fractional version of this system is described as follows (Tavazoei and Haeri 2007):

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\alpha _1} x = a(y -x) \\ D^{\alpha _2} y = (c-a) x -xz +c y\\ D^{\alpha _3} z = xy -b z \end{array}\right. } \end{aligned}$$

(6)

where x, y, z are the states of system. Also a , b and c are the parameters of system. Chen system exhibits chaotic behavior at the parameters $(a, b, c)=(35, 3,28)$ (Tavazoei and Haeri 2007).

Reference Tavazoei and Haeri (2007) pointed out that fractional-order Chen system (6) exhibits chaotic behavior for fractional-order $0.85 \le \alpha$. The chaotic attractor with $\alpha _1=\alpha _2=\alpha _3=0.993$ is shown in Fig. 2.

Fig. 2

Chaotic behavior of fractional-order Chen system

3.3 TS fuzzy modeling

TS fuzzy molding uses some if–then for local relation of a nonlinear function. These local relations are linear, and this is the main advantage of TS fuzzy modeling.

3.3.1 Type-1 fuzzy modeling

For a system as Eqs. (5) or (6), we can represent a TS fuzzy model as follows:

Rule n: if $v_1(t)$ is $fs_{1}^i$ and $v_2(t)$ is $fs_{2}^i$ and ... and $v_p(t)$ is $fs_{p}^l$, then

$$\begin{aligned} D^\alpha X(t)=L_i X(t) \end{aligned}$$

(7)

where X is the vector of system states, $v_1(t),\ldots ,v_p(t)$ are the state variables of the fuzzy system; $fs_{i}^j$ is the fuzzy sets and $L_i$ is a constant matrix. Now the fuzzy system needs a fuzzifier and defuzzification method. We use a singleton fuzzifier and weighted average defuzzifier; then, the final TS fuzzy modeling can be represented as follows:

$$\begin{aligned} D^\alpha X(t)=\sum _{i=1}^{n} g_i(v(t)) (L_i X(t)) \end{aligned}$$

(8)

where $v(t) = (v_1(t),\ldots ,v_p(t))$ are proper state variables and n is the number of the fuzzy rules. Also

$$\begin{aligned} g_i(v(t))=\frac{w_i(v(t))}{\sum _{i=1}^{r}(w_i (v(t)))} , w_i(v(t))=\prod _{k=1}^{n} {\mu }_k^i(v_k(t)) \end{aligned}$$

(9)

where for the ith rule, ${\mu }_k^i(.)$ is the membership function of fuzzy set with $k=1,\ldots ,p$.

3.3.2 Type-2 fuzzy modeling

For a type 2 fuzzy modeling, type of rules are similar to type 1 and for a system as Eqs. (5) or (6) we have the following fuzzy rules:

For a system as Eqs. (5) or (6), we can represent a TS fuzzy model as follows:

Rule n: if $v_1(t)$ is $\tilde{fs}_{1}^i$ and $v_2(t)$ is $\tilde{fs}_{2}^i$ and ... and $v_p(t)$ is $\tilde{fs}_{p}^l$, then

$$\begin{aligned} D^\alpha X(t)=L_i X(t) \end{aligned}$$

(10)

where X is the vector of system states; $v_1(t),\ldots ,v_p(t)$ are the state variables of fuzzy system; $mf_{i}^j$ is the type-2 fuzzy sets and $L_i$ is constant matrix. Also firing strength of the i-th rule is as

$$\begin{aligned} \tilde{w(v(t))}_i=[w(v(t))_i^{lo}, w(v(t))_i^{up}] \end{aligned}$$

(11)

where

$$\begin{aligned} w_i(v(t))_i^{lo}=\prod _{k=1}^{n} \underline{\mu }_k^i(v(t)) \end{aligned}$$

(12)

and

$$\begin{aligned} w_i(v(t))_i^{up}=\prod _{k=1}^{n} \bar{\mu }_k^i(v(t)) \end{aligned}$$

(13)

where $\underline{\mu }$ and $\bar{\mu }$ are the lower and upper bound of membership functions, respectively. Then, by model reduction and defuzzification final modeling of type-2 system can be shown as Eq. (8).

3.4 Optimal fuzzy control of fractional-order systems

Euler–Lagrange equations for fractional-order optimal control:

The fractional-order optimal control problem can be formulated as follows. We want to find the optimal control U(t) for a fractional-order differential equation that minimizes the cost function. We defined cost function as below:

$$\begin{aligned} J=\int _{0}^{T}G(X,U,\tau )\mathrm{d}\tau \end{aligned}$$

(14)

where x are state variables and t represent the time, and subject to some constraints, these cost functions will be minimized.

$$\begin{aligned} D^\alpha X(t)=\sum _{i=1}^{n} g_i(v(t)) (L_i X(t)) \end{aligned}$$

(15)

and initial conditions

$$\begin{aligned} X(0)=X_0 \end{aligned}$$

Note that with $\alpha = 1$, fractional-order optimal control problem converts to a standard optimal control problem with integer order. In our systems, we consider $0<\alpha <1$ . These are not the limitations of the approach and derivative can be of any order.

Because we want to find the optimal control, we must follow the Euler–Lagrange approach and define a modified performance index as Manabe (2003):

$$\begin{aligned} \bar{J}=\int _{0}^{T}\left[ G(X,U,\tau )+\lambda \left( \sum _{i=1}^{n} g_i(v(t)) (L_i X(t))-D^{\alpha }X\right) \right] \mathrm{d}\tau \end{aligned}$$

(16)

where $\lambda$ is the Lagrange multipliers and in following these multipliers lead to co-state equations which must solve to achieve an optimal solution. Bases of our method construct by using calculation of variations, and it is proved that minimization of J requires to solving the following equations (Motallebzadeh et al. 2012):

$$\begin{aligned}&D^\alpha X(t)=\sum _{i=1}^{n} g_i(v(t)) (L_i X(t)) \end{aligned}$$

(17)

$$\begin{aligned}&D^{\alpha }\lambda =\frac{\partial G}{\partial X}+\lambda \frac{\partial \sum _{i=1}^{n} g_i(v(t)) (L_i X(t))}{\partial X} \end{aligned}$$

(18)

$$\begin{aligned}&\frac{\partial G}{\partial U}+\lambda \frac{\partial \sum _{i=1}^{n} g_i(v(t)) (L_i X(t))}{\partial U}=0; \end{aligned}$$

(19)

and $X(0)=X_0$ and $\lambda (T)=0$.

Equations (17–19) represent Euler–Lagrange equations for fractional-order optimal control problem where Eq. (17) is the state equations and Eq. (18) is co-state equations. Like classical optimal control theories, in fractional-order optimal control, Eq. (17) has a forward solution with initial conditions and Eq. (18) has a backward solution with final conditions.

4 General method

4.1 Stability theorem of fractional-order system

Consider the following fractional-order equation

$$\begin{aligned} D^\alpha x(t)= f(x(t)) \end{aligned}$$

(20)

where $x = [x_1, x_2,\ldots , x_n]^T \in R^n$ are the states of system and $f(x) = [f_1(x), f_2(x),\ldots , f_n(x)]^T$ describe the system’s equations. Also we suppose $0 < \alpha \le 1$. For this condition, we have the following Lemma.

Lemma 1

If there exists a positive definite matrix P that satisfies

$$\begin{aligned} J = x(t)^T P \frac{\mathrm{d}^\alpha x(t)}{\mathrm{d}t^\alpha } \le 0 \end{aligned}$$

Then, system (20) is asymptotically stable (Jian-Bing et al. 2015).

Proof

A Lyapunov candidate function as

$$\begin{aligned} V(t)=x(t)^TPx(t) \end{aligned}$$

(21)

leads to

$$\begin{aligned} \dot{V}(t)=2x(t)^TP\frac{\mathrm{d}x(t)}{\mathrm{d}t} \end{aligned}$$

(22)

With Caputo definition of fractional operator, we can get

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=\lim _{\delta t\rightarrow 0} \frac{\delta x}{\delta t} =\lim _{\delta t\rightarrow 0} \frac{\frac{1}{\varGamma (\alpha )} \int _{t-\delta t}^{t}(t-\tau )^{\alpha -1}(D^\alpha x(\tau ))\mathrm{d}\tau }{\delta t} \end{aligned}$$

(23)

Substituting Eq. (23) in Eq. (22) and using inequality of Lemma 1 lead to the following inequality.

$$\begin{aligned} \lim _{\delta t\rightarrow 0} { \int _{t-\delta t}^{t}(t-\tau )^{\alpha -1} P (D^\alpha x(\tau ))\mathrm{d}\tau } \le 0 \end{aligned}$$

(24)

Then,

$$\begin{aligned} \dot{V}=2\lim _{\delta t\rightarrow 0} \frac{{ \int _{t-\delta t}^{t} (t-\tau )^{\alpha -1} P (D^\alpha x(\tau ))\mathrm{d}\tau }}{\delta t} \le 0 \end{aligned}$$

(25)

The above inequality is verified the Lyapunov stability theorem for system (20). $\square$

Integer version of system (20) is described as

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=f(x) \end{aligned}$$

(26)

Lemma 2

For a positive definite matrix P,if a Lyapunov function as $V=x(t)^TPx(t)$ leads to

$$\begin{aligned} \dot{V}=2x(t)^TP \frac{\mathrm{d}x(t)}{\mathrm{d}t} (t)\le 0, \end{aligned}$$

then the system (26) is asymptotically stable. In other words, if there exists a positive definite matrix P that satisfies $x(t)^T P \frac{\mathrm{d} x(t)}{\mathrm{d}t} \le 0$, then system (26) is asymptotically stable.

Corollary 1

According to stability proof for Lemma 1 , we can achieve stability of fractional-order system with $0<\alpha <1$ from stability of integer-order system.

Corollary 1 proves that a integer-order system is stable when fractional version of system with $0<\alpha <1$ is stable.

4.2 Synchronization method

Now using the TS fuzzy modeling (8), we define chaotic master and slave systems as follows

$$\begin{aligned} D^\alpha X_m(t)=\sum _{i=1}^{n} g_i(v(t)) (L_i X_m(t)) \end{aligned}$$

(27)

and

$$\begin{aligned} D^\alpha X_s(t)=\sum _{i=1}^{n} g_i(v(t)) (L'_i X_s(t))+U(X_s,X_m) \end{aligned}$$

(28)

where $X_m,X_s \in R^n$ are state vectors for n-dimensional master and slave systems; also $g_i$ and L and $L'$ are calculated in the TS fuzzy modeling. $\alpha$ is fractional-order vector for the master and slave systems, which are $R^n$, $\alpha =[\alpha _1, \alpha _2,\ldots ,\alpha _n]^T$, $\alpha _i \in (0,1]$. Note that in our method the fractional orders are with a condition $0 < \alpha _i \le 1$. U is the control signal input which is determined later. With defining synchronization of two systems with conditions that states of master and slave systems are equal, then the synchronization errors are defined as:

$$\begin{aligned} e = X_s-X_m \end{aligned}$$

(29)

Our objective is to find an effective and minimum controller function U to ensure synchronization of the master system (27) and slave system (28) achieved. According to (29), we can write

$$\begin{aligned} D^\alpha e = D^\alpha X_s-D^\alpha X_m \end{aligned}$$

(30)

By replacing Eqs. (27), (28) in Eq. (30), we have

$$\begin{aligned} D^\alpha e&= \sum _{i=1}^{n} g_i(v(t)) (L'_i e(t)) +U(X_s,X_m)\nonumber \\&\quad + \left( \sum _{i=1}^{n} g_i(v(t)) ((L'_i-L_i) X_m(t))\right) \end{aligned}$$

(31)

Now we define new controller for using in Euler–Lagrange equations as:

$$\begin{aligned} U'= U(X_s,X_m)+ \left( \sum _{i=1}^{n} g_i(v(t)) ((L'_i-L_i) X_m(t))\right) \end{aligned}$$

(32)

We can get the error dynamic systems as:

$$\begin{aligned} D^\alpha e = \sum _{i=1}^{n} g_i(v(t)) (L'_i e(t))+U'(X_s,X_m) \end{aligned}$$

(33)

4.3 Secure communication

In this part, we use fractional-order chaotic systems for the chaotic masking. Chaotic masking is one of the well-known algorithms in information transmitting. The diagram of this method is shown in Fig. 3. A chaotic system generates the carrier and this carrier combined with information signal, and summation of two signals is transmitted through a communication channel. In the receiver, chaotic synchronization is completed and after subtraction detected signal is obtained.

Fig. 3

Block diagram of secure communication process

Main steps of the proposed method for secure communication using synchronization are listed as follows:

• 1 Messages are selected as sent massages.

• 2 Selected massages are modulated to the chaotic system as master system.

• 3 Appropriate control laws are defined.

• 4 Massage signals are recovered from slave side.

5 Application and simulation

In this part, we consider the synchronization between the fractional-order Lorenz system and fractional-order Chen system with the mentioned parameters in Sect. 2. By using the system equations (5) and (6), the master and slave systems are given as follows:

$$\begin{aligned} { Master} : {\left\{ \begin{array}{ll} D^{0.99} x_m = 10(y_m -x_m) \\ D^{0.99} y_m = 28 x_m -x_m z_m -y_m \\ D^{0.99} z_m = x_m y_m -8z_m/3 \end{array}\right. } \end{aligned}$$

(34)

where $x_m$, $y_m$, $z_m$ are the states of system. Then, type-1 TS fuzzy modeling of master system is defined as:

Rule 1::

If $x_m$ is $fs_1(x_m)$, then $D^\alpha X=L_1X$

Rule 2::

If $x_m$ is $fs_2(x_m)$, then $D^\alpha X=L_2X$

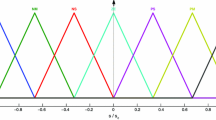
where $X(t)=(x_m(t),y_m(t),z_m(t))^T$ , $fs_1=20$, $fs_2=-20$ and

$$\begin{aligned}&L_1=\begin{bmatrix} -10 &{} 10 &{} 0 \\ 28 &{} -1 &{} -20 \\ 0 &{}20 &{}-8/3 \end{bmatrix}\\&L_2=\begin{bmatrix} -10 &{} 10 &{} 0 \\ 28 &{} -1 &{} 20 \\ 0 &{}-20 &{}-8/3 \end{bmatrix} \end{aligned}$$

where the membership functions are as $\mu _1(x)=\frac{1}{2}(1-x_m)/k)$ and $\mu _2(x)=\frac{1}{2}(1+x_m/k)$ with $k=20$.

Also for type-2 fuzzy modeling, we have the following rules.

Rule 1::

If $x_m$ is $\tilde{fs}_1(x_m)$, then $D^\alpha X=L_1X$

Rule 2::

If $x_m$ is $\tilde{fs}_2(x_m)$, then $D^\alpha X=L_2X$

where $X(t)=(x_m(t),y_m(t),z_m(t))^T$ and

$$\begin{aligned}&L_1=\begin{bmatrix} -10 &{} 10 &{} 0 \\ 28 &{} -1 &{} -20 \\ 0 &{}20 &{}-8/3 \end{bmatrix}\\&L_2=\begin{bmatrix} -10 &{} 10 &{} 0 \\ 28 &{} -1 &{} 20 \\ 0 &{}-20 &{}-8/3 \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\mu }_1(x_m)=\frac{20-xm}{40}\\ \bar{\mu }_1(x_m)=\frac{20-xm}{20}\\ \underline{\mu }_2(x_m)=\frac{20+xm}{40}\\ \bar{\mu }_2(x_m)=\frac{20+xm}{20}\\ \end{array}\right. } \end{aligned}$$

(35)

For slave system, we have

$$\begin{aligned} { Slave} : {\left\{ \begin{array}{ll} D^{0.99} x_s = -35 (x_s-y_s)+u_1 \\ D^{0.99} y_s = 7 x_s -x_s z_s +28 y_s +u_2 \\ D^{0.99} z_s = x_s y_s -3 z_s+u_3 \end{array}\right. } \end{aligned}$$

(36)

where $x_s$, $y_s$, $z_s$ are the states of system. Again, TS fuzzy modeling of master system is defined as:

Rule 1::

If $x_s$ is $fs_1(x_s)$, then $D^\alpha X=L'_1X$

Rule 2::

If $x_s$ is $fs_2(x_s)$, then $D^\alpha X=L'_2X$

where $X(t)=(x_s(t),y_s(t),z_s(t))^T$ , $fs_1=20$, $fs_2=-20$ and

$$\begin{aligned}&L'_1=\begin{bmatrix} -35 &{} 35 &{} 0 \\ 7 &{} 28 &{} -20 \\ 0 &{}20 &{}-3 \end{bmatrix}\\&L'_2=\begin{bmatrix} -35 &{} 35 &{} 0 \\ 7 &{} 28 &{} 20 \\ 0 &{}-20 &{}-3 \end{bmatrix} \end{aligned}$$

where the membership functions are as $mf_1(x_s)=\frac{1}{2}(1-x_s)/k)$ and $mf_2(x_s)=\frac{1}{2}(1+x_s/k)$ with $k=20$.

Also for type-2 fuzzy modeling, we have the following rules.

Rule 1::

If $x_m$ is $\tilde{fs}_1(x_m)$, then $D^\alpha X=L_1X$

Rule 2::

If $x_m$ is $\tilde{fs}_2(x_m)$, then $D^\alpha X=L_2X$

where $X(t)=(x_m(t),y_m(t),z_m(t))^T$ and

$$\begin{aligned}&L'_1=\begin{bmatrix} -35 &{} 35 &{} 0 \\ 7 &{} 28 &{} -20 \\ 0 &{}20 &{}-3 \end{bmatrix} \\&L'_2=\begin{bmatrix} -35 &{} 35 &{} 0 \\ 7 &{} 28 &{} 20 \\ 0 &{}-20 &{}-3 \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\mu }_1(x_m)=\frac{20-xm}{40}\\ \bar{\mu }_1(x_m)=\frac{20-xm}{20}\\ \underline{\mu }_2(x_m)=\frac{20+xm}{40}\\ \bar{\mu }_2(x_m)=\frac{20+xm}{20}\\ \end{array}\right. } \end{aligned}$$

(37)

Now for a cost function, it is as follows:

$$\begin{aligned} J=\int _{0}^{t_f} (e_1(t)^2+e_2(t)^2+e_3(t)^2+u_1'(t)^2+u_2'(t)^2+u_3'(t)^2)\mathrm{d}t \end{aligned}$$

(38)

and using Eqs. (32) and (33) Euler–Lagrange equations Eqs. (17–19) can be rewritten as follows:

$$\begin{aligned}&D^\alpha E(t) =\sum _{i=1}^{n} g_i(v(t)) (L'_i E(t)) \end{aligned}$$

(39)

$$\begin{aligned}&D^{\alpha }\lambda =2 E +\lambda \sum _{i=1}^{n} g_i(v(t)) (L'_i) \end{aligned}$$

(40)

$$\begin{aligned}&U'+\lambda =0 \end{aligned}$$

(41)

where $\lambda$ is a vector of the Lagrange multipliers, E is the vector of synchronization error and $U'$ is the vector of control signals. Also $E(0)=e_0$ and $\lambda (T)=0$. Equation (39) has a forward solution and with the initial condition, and Eq. (40) has a backward solution with the final condition and note that all of the above equations must be solved simultaneously.

The main steps of the proposed method can be listed as follows:

• 1 The fuzzy model of fractional-order chaotic systems are defined.

• 2 Fractional-order operator is defined as Eq. (1)

• 3 Signal massages are modulated on the drive system.

• 4 Synchronization problem is defined using two systems.

• 5 Appropriate feedback controllers are suggested.

• 6 Solve the Euler–Lagrange equations as Eqs. (17–19) to get the optimal feedback gains.

• 7 implement the obtained gains on the controller and simulate the problem.

5.1 Synchronization with constant orders

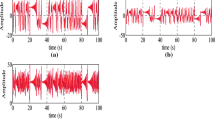
Initial conditions for master and slave systems are selected as $(x_m,y_m,z_m)=(2,3,5)$ and $(x_s,y_s,z_s)=(-9,-5,14)$, respectively. Also, the simulation time is 20 s. Discretization step for simulation is considered as 0.1 ms. In the numerical simulations, the initial conditions for the master and slave systems are $(x_m(0),y_m(0),z_m(0))^T =(2,3,5)^T$ and $(x_s(0),y_s(0),z_s(0))^T = (3,5,8)^T$ , respectively. Three information signals are selected as $m_1(t)=10 sin(10t) cos(20t)$, $m_2(t)=5sin(5t)-5cos(40t)$ and $m_3(t)=(5+10 sin(40t)) cos(20t)$. Synchronization errors are illustrated in Fig. 4. For comparison and showing optimality of the result of the proposed method, here we synchronize two systems with active control method (Behinfaraz and Badamchizadeh 2015; Tavazoei and Haeri 2007), and the result of two methods is illustrated in Fig. 5.

Fig. 4

Secure communication three information signals, a first signal, b second signal, c third signal

Fig. 5

Synchronization errors, a $e_1$, b $e_2$, c $e_3$

For synchronizing two systems with the feedback control method, we can define control signals as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1 =k_{11}e_1+k_{12}e_2+k_{k13}e_3 \\ u_2=k_{21}e_1+k_{22}e_2+k_{23}e_3 \\ u_3 =k_{13}e_1+k_{23}e_2+k_{33}e_3 \end{array}\right. } \end{aligned}$$

(42)

where $e = [e_1,e_2,e_3]^T$ and $e_1 = x_s - x_m$, $e_2 = y_s -y_m$, $e_3 = z_s - z_m$ are synchronization errors. Now we choose the element of K matrix such that synchronization errors by using the stability theorem of fractional-order systems, converging to zero. With this control input error, equations convert to:

$$\begin{aligned} \left\{ \begin{aligned} D^{0.99} e_1(t)&=\sum _{i=1}^{n} (g_i(x_s)-g_i(x_{m}))e_1\\&\quad +10e_2-10e_1 +k_{11}e_1+k_{12}e_2+k_{k13}e_3 \\ D^{0.99} e_2(t)&= \sum _{i=1}^{n} (g_i(x_s)-g_i(x_{m}))e_2\\&\quad +7e_1+28e_2+k_{21}e_1+k_{22}e_2+k_{23}e_3 \\ D^{0.99} e_3(t)&= \sum _{i=1}^{n} (g_i(x_s)-g_i(x_{m}))e_3\\&\quad + -3e_3+k_{13}e_1+k_{23}e_2+k_{33}e_3 \end{aligned}\right. \end{aligned}$$

(43)

Table 1 Power of control signals with different fractional orders

Table 2 Power of control signals with different fractional orders with method of Ref. Behinfaraz and Badamchizadeh (2015)

Fig. 6

Synchronization errors with variable orders, a $e_1$, b $e_2$, c $e_3$

Now with solving Euler–Lagrange equations Eqs. (17–19), we have

$$\begin{aligned} K_{type1}=\begin{bmatrix} -4 &{} -2 &{} 0 \\ -6 &{} -35 &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} K_{type2}=\begin{bmatrix} 0 &{} -10 &{} 0 \\ -7 &{} -29 &{} 0 \\ 0 &{} 0 &{} 0 \end{bmatrix} \end{aligned}$$

We can rewrite Eq. (43) for type-2 modeling as:

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{0.99} e_1(t) = -10e_1 \\ D^{0.99} e_2(t) = - e_2 \\ D^{0.99} e_3(t) = -3e_3 \end{array}\right. } \end{aligned}$$

(44)

Letting $E_i(s) = {\mathcal {L}}(e_i(t))$ where $(i = 1,2,3)$, and by using Laplace transform of fractional-order differential equations we have $\frac{\mathrm{d}^\alpha }{\mathrm{d}t^\alpha } (e_i(t)) = s^\alpha Ei(s)-s^{\alpha -1}e_i(0)$ .

Using this method for Eq. (44) leads to

$$\begin{aligned} {\left\{ \begin{array}{ll} s^{0.99} E_1(s)-s^{-0.01}e_1(0) = -10E_1(s) \\ s^{0.99} E_2(s)-s^{-0.01}e_2(0) = -E2(s) \\ s^{0.99} E_3(s)-s^{-0.01}e_3(0) = -3E_3(s) \end{array}\right. } \end{aligned}$$

(45)

By using final value theorem of Laplace transform and solving above equation, it is proved that

$$\begin{aligned} {\left\{ \begin{array}{ll} \lim _{t\rightarrow \infty }e_1(t) = \lim _{s\rightarrow 0}sE_1(s)=0 \\ \lim _{t\rightarrow \infty }e_2(t) = \lim _{s\rightarrow 0}sE_2(s)=0 \\ \lim _{t\rightarrow \infty }e_3(t) = \lim _{s\rightarrow 0}sE_3(s)=0 \end{array}\right. } \end{aligned}$$

(46)

Since $E_1(s),E_2(s),E_3(s)$ are bounded, owing to the attractiveness of the attractors of systems (5) and (6), there exists $\zeta > 0$, such that $|x_i(t)| \le \zeta < \infty$ and $|y_i(t)| \le \zeta < \infty$ where $(i=1,2,3)$. Therefore, $\lim _{t\rightarrow \infty }e_1(t) =\lim _{t\rightarrow \infty }e_2(t)=\lim _{t\rightarrow \infty }e_3(t)= 0$. Consequently, the synchronization between the master and slave systems (5) and (6) is achieved.

Through simulations, the secure communication with the synchronized state variables in the slave fractional-order Chen system, with the states in the master fractional-order Lorenz system, is shown in Fig. 4. The numerical results show that the synchronization of the commensurate fractional-order Lorenz system and the commensurate fractional-order Chen system is achieved, which verifies the validity of the proposed controller. Changing the power of the fractional order of control signals in two methods is mentioned in Tables 1 and 2.

5.2 Synchronization with variable orders

In this case, orders of two fractional-order chaotic systems are considered as a variable orders. The selected order for the master system is as $\alpha _1(t)=0.99 u(t)+0.003u(t-5)+.003u(t-10)$ ,$\alpha _2(t)=0.99 u(t)+0.003u(t-5)+0.003u(t-10)$ and $\alpha _3(t)=0.99 u(t)+0.003u(t-5)+0.003u(t-10)$. The designed approach is as the same as last part, but in this section we use a type-2 fuzzy modeling of systems using Eqs. (35), (37). The results of simulation in this conditions are shown in Fig. 6. Also method of Ref. Behinfaraz and Badamchizadeh (2015) is simulated in this condition. Results are shown in Fig. 7. Power of control signals is shown in Tables 3 and 4. As seen in this figure, the method of ref. Behinfaraz and Badamchizadeh (2015) cannot synchronize two systems with variable orders. Also type-2 fuzzy modeling has a better performance.

Fig. 7

Synchronization errors with variable orders with method of Ref. Behinfaraz and Badamchizadeh (2015)

Table 3 Mean square of synchronization error

Table 4 Power of control signals with variable orders

6 Conclusion

In this paper, we investigated the problem of the synchronization between different fractional-order chaotic systems using optimal fuzzy modeling control. By using fractional calculus and the stability theorems of the fractional-order linear systems, we propose a method to attain synchronization of two different systems with optimal control inputs and also minimum synchronization times. The used model to give a better response was done by TS fuzzy structure. After getting synchronization, secure communication of information signals using the chaotic masking method was done. The controller is designed by writing Euler–Lagrange equations for fractional-order error dynamics and by solving these equations. To verify the effectiveness of the designed controller, we illustrated two examples with two well-known fractional-order chaotic systems. Two conditions were considered. First, for systems with constant orders, we developed an optimal type-1 fuzzy modeling. By comparing with the active control method, the effectiveness and optimization of designed input signals and synchronization times were shown. In the second example, the orders of systems were considered variable. It was shown that in this condition compared method cannot synchronize two systems, but the proposed method done it well. Also, the results were shown that type-2 fuzzy modeling leads to better performance in the variable case.