1 Introduction

Consider the following unconstrained optimization problem:

$$\begin{aligned} \min _{x\in \mathfrak {R}^n} f(x), \end{aligned}$$
(1.1)

where \(f:\mathfrak {R}^n\rightarrow \mathfrak {R}\), \(f\in C^2\) is continuously differentiable. Conjugate gradient (CG) methods (Dai 2001; Grippo and Lucidi 1997; Khoda et al. 1992; Nocedal and Wright 2006; Shi 2002) are particularly powerful for solving large-scale problems due to their simplicity and lower storage (Birgin and Martínez 2001; Cohen 1972; Shanno 1978; Yuan 1993); thus, they are especially popular for solving unconstrained optimization problems. CG methods generate an iterative sequence \(\{x_k\}\) by:

$$\begin{aligned} x_{k+1}=x_k+\alpha _kd_k,\,\,k=0,\,1,\,2,\ldots , \end{aligned}$$
(1.2)

where \(x_k\) is the k-th iteration point, the step size \(\alpha _k> 0\) can be computed by certain line search techniques, and the search direction \(d_k\) is defined by the following formula:

$$\begin{aligned} d_{k}=\left\{ \begin{array}{ll} -g_{k},&{} \quad \text{ if } \,\, k=0,\\ -g_{k}+\beta _kd_{k-1}, &{}\quad \text{ if } \,\, k\ge 1,\\ \end{array} \right. \end{aligned}$$

where \(\beta _k\) is a scalar and can be defined by the following six formulas (or other formulas):

$$\begin{aligned} \beta ^{PRP}_k= & {} \frac{g^T_{k}(g_{k}-g_{k-1})}{\Vert g_{k-1}\Vert ^2}, \,\,\beta ^{FR}_k=\frac{\Vert g_k\Vert ^2}{\Vert g_{k-1}\Vert ^2},\\ \beta ^{HS}_k= & {} \frac{g^T_k(g_k-g_{k-1})}{d^{T}_{k-1}(g_k-g_{k-1})},\\ \beta ^{CD}_k= & {} \frac{\Vert g_k\Vert ^2}{-d^T_{k-1}g_{k-1}}, \,\,\beta ^{LS}_k=\frac{g^T_{k}(g_{k}-g_{k-1})}{-d^T_{k-1}g_{k-1}},\\ \beta ^{DY}_k= & {} \frac{\Vert g_k\Vert ^2}{(g_{k}-g_{k-1})^Td_{k-1}}, \end{aligned}$$

where \(g_{k-1}\) is the gradient \(\nabla f(x_{k-1})\) of f(x) at the point \(x_{k-1}\) and \(\Vert \cdot \Vert \) is the Euclidean norm. The corresponding methods are called the Polak–Ribière–Polyak (PRP) (Polak and Ribière 1969; Polyak 1969), Fletcher–Reeves (FR) (Fletcher and Reeves 1964), Hestenses–Stiefel (HS) (Hestenes and Stiefel 1952), conjugate descent (CD) (Fletcher 1997), Liu-Storrey (LS) (Liu and Storey 2000), and Dai-Yuan (DY) (Dai and Yuan 1999) CG methods, respectively. The convergence of the CD method, DY method, and FR method are relatively easy to establish, but their numerical results are not ideal in real computations. Powell (1986) presented an explanation of the numerical disadvantages of the FR method, such as subsequent steps being very short if a small step is originated away from the solution point. However, if a poor direction occurs in practical computation, the PRP, HS, or LS method will perform a restart, so these three methods perform much better than the above three methods. They are generally regarded as the most efficient conjugate gradient methods.

In this paper, we specifically study the modified PRP method. There has been extensive study regarding the global convergence of the PRP method. Polak and Ribière (1969) proved that the PRP method with an exact line search is globally convergent for strongly convex functions but that it fails to satisfy the property of global convergence for the general functions under the Wolfe line search technique, and this is a still an open problem. Yuan (1993) further established global convergence with the modified Wolfe line search under the condition that the search direction is descending. All convergence discussion of the PRP algorithm hinted that the key issue for the study of the PRP method is the sufficient descent condition. However, there are several limitations of the PRP method such that it may not provide a descent direction of the objective function under the exact line search, which creates serious consequences for the global convergence of the algorithm for general functions. For example, Powell (1984) provided a counterexample to show that the PRP method might circle infinitely without approaching the solution even if \(\alpha _k\) is chosen as the least positive minimizer of the line search. Through Powell’s analysis Powell (1986), the PRP method did not satisfy global convergence, probably due to \(\beta _k\) being negative, so inspired by his study, Gilbert and Nocedal (1992) found a convergent consequence in the PRP method when \(\beta ^{PRP+}_k=\max \{0,\beta ^{PRP}\}\) for general nonconvex functions with a suitable line search. Hence, other researchers (Cheng 2007; Yuan et al. 2020, 2020) modified \(\beta _k\) such that the algorithm satisfies global convergence for general functions. Inspired by Li et al. (2015), Yuan and Wei (2010), in this paper we, present a modified PRP method as follows:

$$\begin{aligned} d_{k}=\left\{ \begin{array}{ll} -g_{k},&{} \text{ if }\,\,\,\,k=0,\\ -g_{k}+\beta ^{*PRP}_kd_{k-1}, &{} \text{ if }\,\,\,\, k\ge 1,\\ \end{array} \right. \end{aligned}$$
(1.3)

and

$$\begin{aligned} \beta ^{*PRP}_k=\frac{g^T_{k}\tilde{y}_{k-1}}{\Vert g_{k-1}\Vert ^2}, \end{aligned}$$
(1.4)

where \(\tilde{y}_{k-1}=y_{k-1}+\frac{\rho _{k-1}s_{k-1}}{\Vert s_{k-1}\Vert ^2}\), \(\rho _{k-1}=2[f(x_{k-1})-f(x_k)]+[g(x_k)+g(x_{k-1})]s_{k-1}\) and \(s_{k-1}=x_k-x_{k-1}\). In addition to modifying \(\beta _k\), some researchers choose to modify the line search to obtain the global convergence of the PRP method for general functions. Grippo and Lucidi (1997) presented a new descent line search technique as follows. There exist constants \(\mu >0\), \(\delta >0\) and \(0<t<1\), \(\alpha _k=\max \{t^j\left( \frac{\mu |g^T_kd_k|}{\Vert d_k\Vert ^2}\right) ;\,j=0,1,\ldots \}\) such that

$$\begin{aligned} f(x_{k+1})\le f(x_k)+\delta \alpha ^2_k\Vert d_k\Vert ^2, \end{aligned}$$
(1.5)

and

$$\begin{aligned} -t_2\Vert g_{k+1}\Vert ^2\le g^T_{k+1}d_{k+1}\le -t_1\Vert g_{k+1}\Vert ^2, \end{aligned}$$
(1.6)

where \(0<t_1<1<t_2\) are constants. Dai (2002) proposed another descent line search as follows:

$$\begin{aligned} f(x_{k+1})\le f(x_k)+\delta \alpha g^T_kd_k, \end{aligned}$$
(1.7)

and

$$\begin{aligned} g^T_{k+1}d_{k+1}\le -\sigma _2\Vert d_{k+1}\Vert ^2, \end{aligned}$$
(1.8)

where \(t\in (0,1)\), \(\delta >0\), \(\sigma _2\in (0,1)\) and \(\alpha _k=t^m\), \(m>0\). When the above two line searches are used, the PRP method satisfies the property of convergence for general functions. (1.5), (1.6) or (1.7), (1.8) will require more time to compute gradient evaluations compared with the Aromijo line search, so Zhou and Li (2014) introduced a non-descent backtracking-type line search in a different way from that in Grippo and Lucidi (1997), Dai (2002). For given constants \(\tau >0\), \(\mu >0\), \(\delta \in (0,1)\), \(t\in (0,1)\), and \(\sigma _k=\min \{\tau , \frac{\mu \Vert g_k\Vert ^2}{\Vert d_k\Vert ^2}\}\), let \(\alpha _k=\max \{\sigma _kt^j;\,j=0,1,\ldots \}\) satisfy

$$\begin{aligned} f(x_{k+1})\le f(x_k)-\delta \Vert \alpha _kg_k\Vert ^2+\eta _k\min \{1,\Vert g_k\Vert ^2\}, \end{aligned}$$
(1.9)

where \({\eta _k}\) is a positive sequence satisfying

$$\begin{aligned} \sum ^{\infty }_{k=0}\eta _k\le \eta <\infty , \end{aligned}$$
(1.10)

where \(\eta \) is a positive constant. It is easy to see that the line search technique (1.9) is well defined and does not compute other gradient evaluations except \(g_k\) regardless of whether \(d_k\) is a descent direction or not. Based on the above discussion, the modified PRP method that we present has the following attributes.

  • The modified PRP method possesses the information about function values.

  • Strongly global convergence and R-linear convergence are established.

  • The numerical results demonstrate that the modified PRP method is competitive with the normal PRP method for the given problems.

  • The modified PRP method is applied to the engineering Muskingum model and image restoration problems.

The present paper is organized as follows. In Sect. 2, we show that the modified PRP method has strong convergence and a locally R-linear convergence rate for general functions under the non-descent backtracking line search. In Sect. 3, we perform some numerical experiments to compare the performance of the classical PRP method and modified PRP method with some of the line search techniques mentioned above.

2 Convergence properties

Based on the above line search technique and the modified PRP formula, we present a modified PRP algorithm, which is listed as follows.

Algorithm (Modified PRP Algorithm)

Step 1:

Choose an initial point \(x_0\in \mathfrak {R}^n\), \(\tau >0\), \(\mu >0\), \(\varepsilon \in (0,1)\), and \(\delta \in (0,1 )\), \(t\in (0,1)\). Set \(d_0=-g_0=-\nabla f(x_0)\) and a positive sequence \(\eta _k\) satisfying (1.10), k:=0.

Step 2:

Stop if \(\Vert g_k\Vert \le \varepsilon \).

Step 3:

Compute the step size \(\alpha _k\) using the non-descent line search rule (1.9).

Step 4:

Let \(x_{k+1}=x_k+\alpha _kd_k\).

Step 5:

If \(\Vert g_{k+1}\Vert \le \varepsilon \), then the modified PRP algorithm stops.

Step 6:

Calculate the search direction

$$\begin{aligned} d_{k+1}=-g_{k+1}+\beta ^{*PRP}_{k}d_k. \end{aligned}$$
(2.1)
Step 7:

Set k:=k+1 and go to step 3.

In the following paper, there are some indispensable assumptions for the global convergence of the algorithm on objective functions.

Assumption B (i) The level set \(T_0=\{x\mid f(x)\le f(x_0)+\eta \}\) is bounded.

(ii) In some neighbourhood N of \(T_0\), f is differentiable, and its gradient function g is Lipschitz continuous, namely,

$$\begin{aligned} \Vert g(x)-g(y)\Vert \le L\Vert x-y\Vert , \end{aligned}$$
(2.2)

where \(L>0\) is a constant and any \(x,y\in N\).

Remark

(i) Assumption B implies that there exists a constant \(A>0\) satisfying

$$\begin{aligned} \Vert g(x)\Vert \le A,\quad \forall x\in N. \end{aligned}$$
(2.3)

Moreover, from (1.9) and (1.10) such that

$$\begin{aligned} f(x_k+\alpha _kd_k)&\le f(x_k)-\delta \Vert \alpha _kg_k\Vert ^2+\eta _k\min \{1,\Vert g_k\Vert ^2\}\\&\le f(x_k)+\eta _k\\&\le f(x_0)+\sum ^{\infty }_{j=0}\eta _j\\&<f(x_0)+\eta , \end{aligned}$$

where \(x_k\in T_0\) for all \(k\ge 0\). The following useful lemmas are presented to conveniently show the strongly global convergence of the modified PRP method with the line search (1.9).

Lemma 2.1

Let \(\{\xi _k\}\) and \(\{\beta _k\}\) be positive sequences satisfying \(\xi _k\le (1+\beta _k)\xi _k+\beta _k\) and \(\sum ^{\infty }_{k=0}\beta _k<\infty \). \(\{\xi _k\}\) is able to converge.

Proof

Omitted. The proof of the above lemma is the same as the proof of Lemma 3.3 Dennis and Moré (1974). \(\square \)

Lemma 2.2

Based on Assumption B, the sequence \(\{f(x_k)\}\) that satisfies the line search technique (1.9) in the algorithm converges.

Proof

We can find a constant \(\kappa \) such that \(f(x)>\kappa \) for all \(x\in T_0\) from Assumption B (i), so we have \(f(x_{k+1})-\kappa \le f(x_k)-\kappa +\eta _k\) under the line search technique (1.9), which shows that the sequence \(\{f(x_k)-\kappa \}\) converges through Lemma 2.1. Then, \(\{f(x_k)\}\) converges.\(\square \)

Lemma 2.3

\(d_k\) is defined by (1.3); then, we have

$$\begin{aligned} \Vert d_k\Vert \le \lambda \Vert g_k\Vert . \end{aligned}$$
(2.4)

Proof

First, by (1.9), such that

$$\begin{aligned} \alpha _k\Vert d_k\Vert ^2\le \sigma _k\Vert d_k\Vert ^2\le \frac{\mu \Vert g_k\Vert ^2}{\Vert d_k\Vert ^2}\Vert d_k\Vert ^2=\mu \Vert g_k\Vert ^2. \end{aligned}$$
(2.5)

On the other hand, from (2.2), using the mean-value theorem we have

$$\begin{aligned} \rho _{k-1}= & {} (g_{k-1}+g_k-2g(x_{k-1}+as_{k-1}))^Ts_{k-1}\nonumber \\\le & {} (\Vert g_{k-1}-g(x_{k-1}+as_{k-1})\Vert \nonumber \\&+\Vert g_k-g(x_{k-1}+as_{k-1})\Vert )\Vert s_{k-1}\Vert \nonumber \\\le & {} (La\Vert s_{k-1}\Vert +L(1-a)\Vert s_{k-1}\Vert )\Vert s_{k-1}\Vert \nonumber \\= & {} L\Vert s_{k-1}\Vert ^2, \end{aligned}$$
(2.6)

where \(a\in (0,1)\). Combining (1.3), (1.4), (2.2), (2.6), (2.5), then,

$$\begin{aligned} \Vert d_k\Vert&\le \Vert g_k\Vert +\Vert \beta ^{*PRP}_{k}d_{k-1}\Vert \\&\le \Vert g_k\Vert +\Vert \beta ^{*PRP}_{k}\Vert \Vert d_{k-1}\Vert \\&\le \Vert g_k\Vert +\frac{\Vert g^T_ky_{k-1}\Vert \Vert d_{k-1}\Vert }{\Vert g_{k-1}\Vert ^2} +\frac{\Vert g^T_k\rho _{k-1}s_{k-1}\Vert \Vert d_{k-1}\Vert }{\Vert g_{k-1}\Vert ^2\Vert s_{k-1}\Vert ^2}\\&\le \Vert g_k\Vert +\frac{L\alpha _{k-1}\Vert g_k\Vert \Vert d_{k-1}\Vert ^2}{\Vert g_{k-1} \Vert ^2}+\frac{L\alpha _{k-1}\Vert g_k\Vert \Vert d_{k-1}\Vert ^2}{\Vert g_{k-1}\Vert ^2}\\&\le \Vert g_k\Vert +L\mu \Vert g_k\Vert +L\mu \Vert g_k\Vert =(1+2L)\mu \Vert g_k\Vert , \end{aligned}$$

where \(\lambda =(1+2L)\mu \). Hence, the proof is complete.

It is obvious that \(\lim \limits _{k\rightarrow \infty }\alpha _k\Vert g_k\Vert =0\) holds from the line search technique (1.9) and Lemma 2.2; when combined with (2.4), we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert s_k\Vert =\lim _{k\rightarrow \infty }\alpha _k\Vert d_k \Vert \le \lim _{k\rightarrow \infty }\lambda \alpha _k\Vert g_k\Vert =0. \end{aligned}$$
(2.7)

\(\square \)

Lemma 2.4

Let Assumption B hold and the sequence \(\{x_k\}\) be generated by the algorithm; then, there exists a constant \(A_1>0\) satisfying

$$\begin{aligned} \alpha _k\ge A_1\min \left\{ 1,\frac{-g^T_kd_k}{L\Vert d_k\Vert ^2+\delta \Vert g_k\Vert ^2} \right\} . \end{aligned}$$
(2.8)

Proof

Case i If \(\alpha _k=\sigma _k=\min \{\tau ,\frac{\mu \Vert g_k\Vert ^2}{\Vert d_k\Vert ^2}\}\), from (2.4), we obtain

$$\begin{aligned} \alpha _k\ge \min \left\{ \tau ,\frac{\mu }{\lambda ^2} \right\} =A_1. \end{aligned}$$

Hence, together with \(\min \{1,\frac{-g^T_kd_k}{L\Vert d_k\Vert ^2+\delta \Vert g_k\Vert ^2}\}\le 1\), we obtain (2.8).

Case ii If \(\alpha _{k}\ne \sigma _{k}\), let \(\alpha ^{*}_{k}\doteq \frac{\alpha _{k}}{t}\) not satisfy (1.9), namely,

$$\begin{aligned}&f(x_k+\alpha ^{*}_kd_k)>f(x_k)-\delta \Vert \alpha ^{*}_kg_k\Vert ^2+\eta _k \min \{1,\Vert g_k\Vert ^2\}\nonumber \\&\quad >f(x_k)-\delta \Vert \alpha ^{*}_kg_k\Vert ^2. \end{aligned}$$
(2.9)

By the mean value theorem and (2.2), we have

$$\begin{aligned} f(x_k+\alpha ^{*}_kd_k)-f(x_k)&=g(x_k+\nu _k\alpha ^{*}_kd_k)^T\alpha ^{*}_kd_k\\&=\alpha ^{*}_kg^T_kd_k\\&\quad +(g(x_k+\nu _k\alpha ^{*}_kd_k)-g_k)^T\alpha ^{*}_kd_k\\&\le \alpha ^{*}_kg^T_kd_k+L\Vert \alpha ^{*}_kd_k\Vert ^2, \end{aligned}$$

where \(\nu _k\in (0,1)\), combining with (2.9), shows that (2.8) holds with \(A_1=t\).

The above lemma gives an estimation to the step size \(\alpha _k\). Now, we can prove the global convergence property of the modified PRP method under the line search (1.9).\(\square \)

Theorem 2.1

Supposing that Assumption B holds, consider the modified PRP method where \(d_k\) is satisfied (1.3). Then,

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert g_k\Vert =0. \end{aligned}$$
(2.10)

Proof

We will obtain this result by contradiction. We suppose that (2.10) does not hold; then, there exists a constant \(n_1>0\) and an infinite index G such that

$$\begin{aligned} \Vert g_k\Vert \ge n_1, \quad \forall k\in G. \end{aligned}$$
(2.11)

By (2.2), (2.4) and \(\alpha _k\le \sigma _k\le \tau \) such that

$$\begin{aligned} \Vert g_k\Vert&\le \Vert g_k-g_{k-1}\Vert +\Vert g_{k-1}\Vert \le L\alpha _{k-1}\Vert d_{k-1}\Vert +\Vert g_{k-1}\Vert \nonumber \\&\le A_2\Vert g_{k-1}\Vert , \end{aligned}$$
(2.12)

where \(A_2=1+L\tau \lambda \). from (1.3), (1.4), (2.4), (2.6), (2.7) and (2.12), we obtain

$$\begin{aligned} \Vert g_k+d_k\Vert&=|\beta ^{*PRP}_k|\Vert d_{k-1}\Vert \le \frac{L\Vert g_k\Vert \Vert s_{k-1} \Vert \Vert d_{k-1}\Vert }{\Vert g_{k-1}\Vert ^2}\\&\quad +\frac{\Vert g_k\Vert \Vert \rho _{k-1}s_{k-1}\Vert \Vert d_{k-1}\Vert }{\Vert g_{k-1}\Vert ^2\Vert s_{k-1}\Vert ^2}\\&\le 2LA_2\lambda \Vert s_{k-1}\Vert \rightarrow 0. \end{aligned}$$

From (2.11), we know that there exists a constant \(n_2>0\) such that

$$\begin{aligned} \Vert d_k\Vert \ge n_2. \end{aligned}$$
(2.13)

Combining with (2.7) we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\alpha _k=0,\,\,\,\,\forall k\in G. \end{aligned}$$
(2.14)

By (1.3), (2.4), and (2.8), for all \(k\in G\), we have

$$\begin{aligned} \alpha _k\ge & {} A_1\frac{\Vert g_k\Vert ^2-\beta ^{*PRP}g^T_k d_{k-1}}{L\Vert d_k\Vert ^2 +\delta \Vert g_k\Vert ^2}\nonumber \\= & {} A_1\frac{\Vert g_k\Vert ^2}{L\Vert d_k\Vert ^2+\delta \Vert g_k\Vert ^2}-A_1\frac{\beta ^{*PRP} g^T_kd_{k-1}}{L\Vert d_k\Vert ^2+\delta \Vert g_k\Vert ^2}\nonumber \\\ge & {} \frac{A_1}{L\lambda ^2+\delta }- A_1\frac{\beta ^{*PRP}g^T_kd_{k-1}}{L\Vert d_k\Vert ^2+\delta \Vert g_k\Vert ^2}. \end{aligned}$$
(2.15)

For the last inequality, from (2.2), (2.3), (2.4), (2.6), (2.11), and (2.13), such that

$$\begin{aligned}&A_1\frac{|\beta ^{*PRP}g^T_kd_{k-1}|}{L\Vert d_k\Vert ^2+\delta \Vert g_k\Vert ^2} \le \frac{A_1}{Ln^2_2+\delta n^2_1}\\&\quad \left( \frac{L\Vert g_k\Vert ^2\Vert s_{k-1} \Vert \Vert d_{k-1}\Vert }{\Vert g_{k-1}\Vert ^2}+\frac{\Vert g^T_k\rho _{k-1}s_{k-1}\Vert \Vert g_k \Vert \Vert d_{k-1}\Vert }{\Vert g_{k-1}\Vert ^2\Vert s_{k-1}\Vert ^2} \right) \\&\le \frac{2LAA_1A_2\lambda }{Ln^2_2+\delta n^2_1}\Vert s_{k-1}\Vert \rightarrow 0. \end{aligned}$$

This with (2.15) implies that (2.14) does not hold, thus contradicting (2.14). The proof is completed.\(\square \)

Theorem 2.2

Supposing that Assumption B holds, consider the modified PRP method and (1.9); then, for large k, we have a positive constant \(n_3\) such that

$$\begin{aligned} \alpha _i\ge n_3 \end{aligned}$$
(2.16)

holds for at least half of the indices \(i\in \{0,1,2 \ldots ,k\}\).

Proof

Without loss of generality, by (2.8), we have

$$\begin{aligned} \alpha _k\ge A_1\frac{-g^T_kd_{k}}{L\Vert d_k\Vert ^2+\delta \Vert g_k\Vert ^2}, \end{aligned}$$

using (1.3), (1.4), (1.10), and (2.4), (2.6); then,

$$\begin{aligned} \alpha _k&\ge A_1\frac{\Vert g_k\Vert ^2-g^T_k\beta ^{*PRP}_kd_{k-1}}{L\Vert d_k\Vert ^2 +\delta \Vert g_k\Vert ^2}\\&\ge A_1\frac{\Vert g_k\Vert ^2}{L\Vert d_k\Vert ^2+\delta \Vert g_k\Vert ^2}(1-2L\lambda ^2\alpha _{k-1}). \end{aligned}$$

If \(\alpha _{k-1}<\frac{1}{2L\lambda ^2}\), we obtain

$$\begin{aligned} \alpha _k\ge \frac{A_1}{L\lambda ^2+\delta }(1-2L\lambda ^2\alpha _{k-1})=n_4-n_5\alpha _{k-1}, \end{aligned}$$

where

$$\begin{aligned} n_4=\frac{A_1}{L\lambda ^2+\delta }, \quad n_5=\frac{2LA_1\lambda ^2}{L\lambda ^2+\delta }. \end{aligned}$$

Then, we obtain \(n_4\le \alpha _k+n_5\alpha _{k-1}\le 2\max \{1,n_5\}\max \{\alpha _k, \alpha _{k-1}\}\), so

$$\begin{aligned} \max \{\alpha _k,\alpha _{k-1}\}\ge \frac{n_4}{2\max \{1, n_5\}}, \end{aligned}$$

Otherwise, from \(\alpha _{k-1}\ge \frac{1}{2L\lambda ^2}\), we can obtain

$$\begin{aligned} \max \{\alpha _k,\alpha _{k-1}\}\ge \alpha _{k-1}\ge \frac{1}{2L\lambda ^2}. \end{aligned}$$

Thus, when \(n_3=\min \{\frac{n_4}{2\max \{1,n_5\}}, \frac{1}{2L\lambda ^2}\}\), the theorem holds.\(\square \)

Table 1 Test problems
Full size table

Theorem 2.1 shows that every limit point of the sequence \(\{x_k\}\) is a stationary point of f. Moreover, if the Hessian matrix at one limit point \(x^*\) is positive definite, which means that \(x^*\) is a strict local optimal solution of the problem (1.1), then the whole sequence \(\{x_k\}\) converges to \(x^*\). Hence, in the local convergence analysis, we assume that the whole sequence \(\{x_k\}\) converges.

Lemma 2.5

Assume that f is twice continuously differentiable and uniformly convex on \(R^n\) and that Assumption B holds; then, \(f(x_k)\) has a unique minimal point \(x^*\), and there exist constants \(0<m<M\) satisfying

$$\begin{aligned} m\Vert x-x^*\Vert ^2\le \Vert g(x)\Vert ^2\le M\Vert x-x^*\Vert ^2 \end{aligned}$$
(2.17)

and

$$\begin{aligned} m\Vert x-x^*\Vert ^2\le f(x)-f(x^*)\le M\Vert x-x^*\Vert ^2. \end{aligned}$$
(2.18)

Proof

Omitted. For the proof, see (Ortega and Rheinboldt 1970; Rockafellar 1970).\(\square \)

Theorem 2.3

Let f be twice continuously differentiable. Consider the modified PRP method, where \(d_k\) satisfies (1.3), and suppose that \(\{x_k\}\) converging to \(x^*\) satisfies \(g(x^*)=0\) and that \(\nabla ^2f(x^*)\) is positive definite. Then, there exists a constant \(A_3>0\) and \(r\in (0,1)\) such that

$$\begin{aligned} \Vert x_k-x^*\Vert \le A_3r^k. \end{aligned}$$
(2.19)

Proof

Since \(\nabla ^2f(x^*)\) is positive definite, f is uniformly convex in some neighbourhood \(N_1\) of \(x^*\) if \(\{x_k\}\subset N_1\) and \(\{x_k\}\) satisfies (2.17) and (2.18). Denote the index as follows:

$$\begin{aligned} I_1=\{i|i\le k, \quad \alpha _i\ge n_3\}. \end{aligned}$$
(2.20)

Case i If \(k\in I_1\), using (1.9) and (2.16),

$$\begin{aligned} f(x_{k+1})\le & {} f(x_k)-\delta \Vert \alpha _kg_k\Vert ^2+\eta _k\Vert g_k\Vert ^2\\\le & {} f(x_k)-\delta n^2_3\Vert g_k\Vert ^2+\eta _k\Vert g_k\Vert ^2, \end{aligned}$$

and \(\eta _k\rightarrow 0\) since (1.10) holds, so we have \(f(x_{k+1})\le f(x_{k})-\frac{\delta n^2_3}{2}\Vert g_k\Vert ^2\), following from (2.17) and (2.18), such that

$$\begin{aligned} f(x_{k+1})-f(x^*)\le r_0(f(x_k)-f(x^*)), \end{aligned}$$

where \(0<r_0=1-\frac{\delta n^2_{3}m}{2M}<1\).

Fig. 1
figure 1

Performance profiles of these methods (CPU)

Full size image
Fig. 2
figure 2

Performance profiles of these methods (NI)

Full size image
Fig. 3
figure 3

Performance profiles of these methods (NFG)

Full size image
Table 2 Results of the algorithms
Full size table
Fig. 4
figure 4

Performance of Data in 19

Full size image

Case ii If \(k\in I/I_1\), using the line search (1.9), we obtain \(f(x_{k+1})\le f(x_k)+\eta _k\Vert g_k\Vert ^2\) from (2.17) and (2.18), such that

$$\begin{aligned} f(x_{k+1})-f(x^*)\le \left( 1+\frac{M}{m}\eta _k \right) (f(x_{k})-f(x^*)), \end{aligned}$$

we can know that there exists a constant \(A_4>0\) satisfying the following inequality from (1.10):

$$\begin{aligned} \prod ^{\infty }_{k=0}\left( 1+\frac{M}{m}\eta _k\right) \le A_4, \end{aligned}$$

for all large k, combining Case i and Case ii, we obtain

$$\begin{aligned} f(x_{k+1})-f(x^*)&\le \left( \prod _{i\in I/I_1}\left( 1+\frac{M}{m}\eta _i\right) \right) \left( r^{\sum _{k\in I_1}}_{0}\right) \\&\quad \times (f(x_0)-f(x^*))\\&\le A_4r^{k/2}_0(f(x_0)-f(x^*)), \end{aligned}$$

by (2.18), such that

$$\begin{aligned} \Vert x_{k+1}-x^*\Vert \le \left( \frac{A_4(f(x_0)-f(x^*))}{mr^{\frac{1}{2}}_0}\right) ^{\frac{1}{2}}(r^{\frac{1}{4}}_0)^{k+1}. \end{aligned}$$

Then, (2.19) holds, where \(A_3=(\frac{ A_4(f(x_0)-f(x^*))}{mr^{\frac{1}{2}}_0})^{\frac{1}{2}}\) and \(r=r^{\frac{1}{4}}_0\). The proof is complete.\(\square \)

3 Numerical experiments

In this section, we report some different numerical results for the PRP algorithm and modified PRP algorithm. Normal unconstrained optimization problems and engineering problems are included. All codes are written in MATLAB and run on a 2.30 GHz CPU with 8.00 GB of memory on the Windows 10 operating system.

Fig. 5
figure 5

Restoration of the Lena image, Baboon image, and Barbara image by the modified PRP method and the normal PRP method. From left to right: a noisy image with 30% salt-and-pepper noise and restorations obtained by minimizing z with the normal PRP method and modified PRP method

Full size image
Fig. 6
figure 6

Restoration of the Lena image, Baboon image, and Barbara image by the modified PRP method and the normal PRP method. From left to right: a noisy image with 55% salt-and-pepper noise and restorations obtained by minimizing z with the normal PRP method and modified PRP method

Full size image
Fig. 7
figure 7

Restoration of the Lena image, Baboon image, and Barbara image by the modified PRP method and normal PRP method. From left to right: a noisy image with 70% salt-and-pepper noise, restorations obtained by minimizing z with the normal PRP method and the modified PRP method

Full size image

3.1 Normal unconstrained optimization problems

The test problems are listed in Table 1. We will report on various numerical experiments with the modified PRP algorithm and the normal PRP algorithm with the same non-descent line search technique to demonstrate the effectiveness for the given problems. We introduce the stop rules, dimension and some parameters in the numerical experiments as follows:

Stop rules (the Himmeblau stop rule Yuan and Sun 1999): If \(|f(x_k)|>e_1\), let \(stop1=\frac{|f(x_k)-f(x_{k+1})|}{|f(x_k)|}\) or \(stop1=|f(x_k)-f(x_{k+1})|\). If the conditions \(\Vert g(x)\Vert <\epsilon \) or \(stop1<e_2\) are satisfied, where \(e_1=e_2=10^{-5}\) and \(\epsilon =10^{-6}\), the algorithm will stop if the number of iterations is greater than 1000.

Dimension: 3000, 6000, and 9000 variables.

Parameters: \(\tau \)=1, \(\mu \)=5, \(\delta \)=0.2, and \(t=0.8\).

The columns of Table 1 have the following meanings:

Nr.: The number of tested problems.

Test problem: The name of the problem.

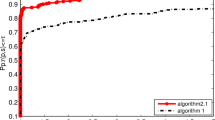
Dolan and Moré (2002) presented a new tool to show their performance in order to analyse the efficiency of these two methods, and Figs. 1, 2 and 3 show the profiles relative to the CPU time, NI, and NFG, respectively.

From Figs. 1, 2 and 3, we can see that modified PRP algorithm is more competitive than the normal method since its performance curves corresponding to the number of iterations, the total of the function and gradient evaluations, and the CPU time are best in the three figures. The modified PRP algorithm can successfully solve most of the test problems. Altogether, it is clear that the modified method is efficient based on the experimental results. The modified PRP algorithm is slightly more robust than the normal PRP algorithm in terms of the CPU time, as shown in Fig. 1. In further work, from the number of iterations in Fig. 2 and , it is not difficult to see that the modified PRP algorithm performs best between the two methods. However, from the total of the function and gradient values of the methods in Fig. 3, The modified PRP algorithm is not very good di?erent from the performances of Figs. 1 and 2. But that does not change the fact that we think the modified method is better than the normal method. Overall, we think that the modified method provides one of the most efficient approaches for solving unconstrained optimization problems.

3.2 The Muskingum model in engineering problems

As is known, some optimization algorithms are considered a significant challenge in engineering problems. Many authors endeavour to design effective algorithms for solving these engineering problems. Parameter estimation is one of the important means for the study of a well-known hydrologic engineering application problem called the nonlinear Muskingum model. This subsection discusses the nonlinear Muskingum model, a common example of such an application.

Muskingum Model Ouyang et al. (2015): is defined by:

$$\begin{aligned}&\min \,\, f(x_1,x_2,x_3) \\&= \sum _{i=1}^{n-1}\bigg ((1-\frac{\Delta t}{6})x_1\big (x_2I_{i+1}+(1-x_2)Q_{i+1}\big )^{x_3}\\&-(1-\frac{\Delta t}{6})x_1\big (x_2I_{i}+(1-x_2)Q_{i}\big )^{x_3}-\frac{\Delta t}{2}(I_{i}-Q_{i})\\&+\frac{\Delta t}{2}(1-\frac{\Delta t}{3})(I_{i+1}-Q_{i+1})\bigg )^2, \end{aligned}$$

where n denotes the total time, \(x_1\) denotes the storage time constant, \(x_2\) denotes the weighting factor, \(x_3\) denotes an additional parameter, \(\Delta t\) is the time step at time \(t_i\) (\(i=1,2, \ldots ,n\)), \(I_{i}\) is the observed inflow discharge and \(Q_{i}\) is the observed outflow discharge. In the experiment, observed data of the flood run-off process between Chenggouwan and Linqing of Nanyunhe in the Haihe Basin, Tianjin, China, is used. In the experiment, \(\Delta t=12(h)\) and the initial point \(x=[0,1,1]^T\) are chosen. The detailed data for \(I_{i}\) and \(Q_{i}\) in 1961 can be found in Ouyang et al. (2014). The tested results of the final points are listed in Table 2.

Table 3 The CPU time of algorithm 1 and the normal PRP algorithm in seconds
Full size table

From Fig. 4 and Table 2, we make the following conclusions: (i) Similar to the BFGS method and the HIWO method, the modified algorithm provides a good approximation for these data, and the given algorithm is effective for the nonlinear Muskingum model. (ii) The final points are competitive with the final points of similar algorithms. (iii) The Muskingum model may have more optimum approximation points since the final points (\(x_1,x_2,\) and \(x_3\)) of the modified PRP algorithm are different from those of the BFGS method and the HIWO method.

3.3 Image restoration problems

This subsection deals with image restoration problems to recover an original image from an image corrupted by impulse noise. These problems are proven to be difficult, and they have many applications in many fields. The code will be stopped if the condition \(\frac{\mid \Vert f_{k+1}\Vert -\Vert f_k\Vert \mid }{\Vert f_k\Vert }< 10^{-3}\) or \(\frac{ \Vert x_{k+1}-x_k\Vert }{\Vert x_k\Vert }< 10^{-3}\) holds. The experiments choose Lena \((256 \times 256)\), Baboon\((512 \times 512)\) and Barbara \((512\times 512)\) as the test images. The detailed performance results are given in Figs. 5, 6 and 7. It is easy to see that both of these algorithms are successful for restoring these three images. The CPU time spent is listed in Table 3 to compare these two algorithms. The proposed algorithm is competitive with other approaches in terms of CPU time.

The results from Table 3, Figs. 5, 6 and 7, indicate that the modified PRP method with a non-descent line search is effective for image restoration. This method requires approximately one minute to restore the image from a noisy image with 55% salt-and-pepper noise, but the cost is higher to restore the image from a noisy image with 70% salt-and-pepper noise, so as the salt-and-pepper noise increases, the cost to restore the image increases.

4 Conclusion

In this paper, we present a non-descent line search and prove the global convergence and R-linear convergence of the modified PRP method with this technique for nonconvex functions. The numerical results show that the modified PRP method is competitive with the normal PRP method for nonconvex optimization. For further research, we can study the proposed algorithm with other line searches such as the Yuan-Wei-Lu line search technique Yuan et al. (2017), which guarantees the convergence property; additionally, the non-descent line search likely can be applied in nonlinear equations and nonsmooth convex minimization. Moreover, more numerical experiments for large practical problems should be performed in the future.