An improved hybrid grey wolf optimization algorithm

Abstract

The existing grey wolf optimization algorithm has some disadvantages, such as slow convergence speed, low precision and so on. So this paper proposes a grey wolf optimization algorithm combined with particle swarm optimization (PSO_GWO). In this new algorithm, the Tent chaotic sequence is used to initiate the individuals’ position, which can increase the diversity of the wolf pack. And the nonlinear control parameter is used to balance the global search and local search ability of the algorithm and improve the convergence speed of the algorithm. At the same time, the idea of PSO is introduced, which utilize the best value of the individual and the best value of the wolf pack to update the position information of each grey wolf. This method preserves the best position information of the individual and avoids the algorithm falling into a local optimum. To verify the performance of this algorithm, the proposed method is tested on 18 benchmark functions and compared with some other improved algorithms. The simulation results show that the proposed algorithm can better search global optimal solution and better robustness than other algorithm.

1 Introduction

One of the salient features of the development of modern science and technology is that life sciences and engineering sciences cross, interpenetrate, and influence each other. The vigorous development of swarm intelligence algorithm reflects this characteristic and trend of scientific development. In recent years, swarm intelligence algorithm has gradually become the focus of scholars. Due to its simplicity, flexibility, non-derivation mechanism and avoidance of local optimality, swarm intelligence algorithm is applied to not only computers but also agriculture (Zou et al. 2016), metallurgy (Reihanian et al. 2011), military (Zheng et al. 2017), civil, and hydraulic engineering (Quiniou et al. 2014), etc.

Recently, many nature inspired optimization algorithm are proposed. Artificial fish swarm algorithm (AFSA) (Xian et al. 2017) imitates the foraging, gathering, and rear-tailing behaviour of fish group by constructing artificial fish to achieve optimal results; ant colony optimization (ACO) (Chen et al. 2017) is inspired by the behaviour of ants in finding the path during the search for food; butterfly optimization algorithm (BOA) (O’Neil et al. 2010) is a natural heuristic algorithm that mimics butterfly foraging behaviour; cuckoo search (CS) (Rakhshani and Rahati 2017) effectively solves the optimization problem by simulating some of the cuckoo species’ brood parasitism. At the same time, CS also use the relevant Levy flight search mechanism; firefly algorithm (FA) (Nekouie and Yaghoobi 2016) is mainly to use the characteristics of firefly luminescence for random optimization; krill herd algorithm (KH) (Gandomi and Alavi 2012) simulates the response behaviour of krill for the biochemical processes and environments evolve; fruit fly optimization algorithm (FOA) (Pan 2012) is a method for seeking global optimization based on fruit fly foraging behaviour; flower pollination algorithm (FPA) (Yang 2013) is a stochastic global optimization algorithm developed to mimic the biological characteristics of self-pollination and cross-pollination of flowering plants in nature; chicken optimization algorithm (COA) (Meng et al. 2014) simulates the chicken hierarchy and chicken behaviour.

The above metaheuristic algorithms show that many swarm intelligence technologies have been proposed. Some of them simulate animal predatory behaviour. However, they ignored the grey wolf, which is a predator in the top of the food chain. Researchers have not established a mathematical model of grey wolf social hierarchy and predatory behaviour. Therefore, Mirjalili et al. (2014) proposed a novel metaheuristic algorithm, which imitated leadership hierarchy and hunting process of grey wolves. Based on nature of grey wolves, they proposed a grey wolf optimization algorithm (GWO). GWO is a heuristic algorithm based on population. It mainly simulates the leadership hierarchy of wolves and grey wolf predation behaviour. Through a series of standard test functions, GWO algorithm can converge to a better quality near-optimal solution, possesses better convergence characteristics than other prevailing population-based techniques, such as genetic algorithm (GA), particle swarm optimization (PSO), firefly algorithm (FA), artificial fish swarm algorithm (AFSA) and differential evolution algorithms (DE). At the same time, the GWO algorithm is simple to operate in the optimization process, easy to implement, and has few adjustment parameters. Therefore, the GWO algorithm is widely concerned and is applied to solve many practical problems, such as multilevel thresholding problem (Khairuzzaman and Chaudhury 2017), chemistry experiment (Bian et al. 2018), multi-objective optimal reactive power dispatch (Nuaekaew et al. 2017), etc.

Like other swarm intelligent optimization algorithms, the grey wolf optimization algorithm also has some disadvantages. For example, the original GWO algorithm is easy to fall into stagnation when attacking prey, and the speed of convergence gradually slows down in the late search period. Therefore, Saremi et al. (2015) and Mirjalili et al. (2016) proposed the combination of dynamic evolutionary population and grey wolf algorithm to improve the local search ability of the algorithm. But it neglects the algorithm’s global search ability. Mittal et al. (2016) presented a modified GWO(mGWO) to balance exploration and exploitation ability. Long et al. (2016) proposed a hybrid grey wolf optimization (HGWO), which utilizes chaotic sequence to strengthen the diversity of global searching. Zhu et al. (2015) and Yao and Wang (2016) introduced differential evolution algorithm to improve the searching ability of wolf algorithm. In order to increase the diversity of the population, Long and Wu (2017), Zuo et al. (2017) and Guo et al. (2017) proposed the good point set theory to update the grey wolves individuals’ position, so that the initial population is evenly distributed. Kohli and Arora (2017) presented the chaos theory into the GWO algorithm and aimed at accelerating its global convergence speed. Tawhid and Ali (2017) combined grey wolf optimization and genetic algorithm to improve the convergence performance of the algorithm. Jitkongchuen (2016) proposed a hybrid differential evolution algorithm with grey wolf optimizer, which solves function optimization problem. But, the above algorithms do not consider the influence of the individual wolves’ experience on the whole population when studying the grey wolf predation process. So Singh and Singh (2017) presented a newly hybrid nature inspired algorithm called HPSOGWO. This algorithm improves the ability of exploitation in particle swarm optimization with the ability of exploration in grey wolf optimizer to produce both variants’ strength.

On this basis, this paper presents a grey wolf optimization algorithm combined with particle swarm optimization (PSO_GWO). This algorithm contains three main improvement concepts. Firstly, it initializes the population by using Tent mapping; secondly, it adopts nonlinear control parameter strategy to coordinate the exploration and exploitation ability; thirdly, inspired by the particle swarm optimization (PSO) algorithm, a new position update equation of individuals by incorporating the information of individual historical best solution into the position update equation is designed to speed up convergence.

The rest of this paper is organized as follows. Section 2 presents a brief description of GWO. Section 3 illustrates the proposed approach. Section 4 comprises benchmark test functions and experimental results. Section 5 concludes the work and outlines some ideas for future works.

2 Grey wolf optimization algorithm

2.1 Grey wolf social rank and hunting behaviour

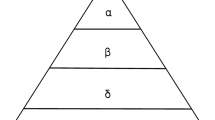
Grey wolf is a predator in the top of the food chain. Most of the wolves live in groups, which has 5–12 wolves per population on average. And each wolf has its own role in the population, so they have a very strict social hierarchy, as shown in Fig. 1.

Fig. 1

The leadership hierarchy of wolves

The first layer is the highest leader of the grey wolves, called $\alpha$, which is mainly responsible for making decisions about hunting, habitat and so on; the second layer is the grey wolf in the subordinate leader of the grey wolf, called $\beta$, which is mainly responsible for assisting leadership management group or other wolf pack activities; the third layer is $\delta$, which is mainly responsible for watching the boundaries of the territory, warning the wolf pack in case of any danger and caring for the weak and wounded grey wolves. The fourth layer is the lowest level grey wolf in the population, called $\upomega$, which has to submit to all the other dominant grey wolves. It may seem that the $\upomega$ wolves are not an important character in the wolf pack, but indispensable for balancing the internal relations of the population.

The leadership hierarchy of wolves plays a crucial role in hunting of prey. Firstly, the grey wolves search and track the prey; secondly, the $\alpha$ grey wolf leads the other wolves to encircle the prey in all directions; thirdly, $\alpha$ grey wolf commands the $\beta$ and $\delta$ wolves to attack the prey. If the prey escapes, the other wolves which are supplied from the rear will continue to attack the prey; finally, grey wolves catch the prey.

2.2 Grey wolf optimization algorithm description

Grey wolf optimization algorithm simulates the leadership hierarchy of wolves and predatory behaviour, and then utilizes the grey wolf abilities, which are search, encirclement, hunting and other activities in the predation process, to achieve the purpose of optimization. Assuming that the number of wolves is N and the search area is d, the position of the ith wolf can be expressed as: $X_{i}=(X_{{i1}},X_{{i2}}, X_{{i3}}, {\ldots }, X_{{id}})$. In order to mathematical model the social hierarchy of wolves, the fittest solution is considered as the alpha ($\alpha )$ wolf. Consequently, the second- and third-best solutions are named beta ($\beta$) and delta ($\delta$) wolves, respectively. The rest of the candidate solutions are assumed to be omega ($\upomega$) wolves. In the algorithm, the location of the prey corresponds to the position of the alpha wolf.

The encircling behaviour of grey wolves can be mathematically modelled as follows:

$$\begin{aligned} D= & {} \left| {C\times X_\mathrm{p} (t)-X(t)} \right| \end{aligned}$$

(1)

$$\begin{aligned} X(t+1)= & {} X_\mathrm{p} (t)-A\times D \end{aligned}$$

(2)

where the set t indicates the current iteration, and the set $X_{p}(t)$ represents the position vector of the prey, the set X(t) is the position vector of a grey wolf, the set C is a control coefficient, which is determined by the following formula:

$$\begin{aligned} C=2r_1 \end{aligned}$$

(3)

where the set $r_{1}$ is the random variable in the range of [0, 1]. The set A is convergence factor, which is calculated as follows:

$$\begin{aligned} A= & {} 2ar_2 -a \end{aligned}$$

(4)

$$\begin{aligned} a= & {} 2\left( 1-\frac{t}{T\max }\right) \end{aligned}$$

(5)

where the set $r_{2}$ is the random variable in the range of [0, 1]. The set a is the control coefficient, which linearly decreases from 2 to 0 over the course of iterations, that is (Sahoo and Chandra 2016), $a_{\max }=2, a_{\min }=0$.

When the grey wolves catch prey, firstly, the leader wolf $\alpha$ leads the other wolves to surround the prey. Then, the $\alpha$ wolf leads $\beta$ and $\delta$ wolves to capture the prey. In the grey wolves, $\alpha ,\beta$ and $\delta$ wolves are the closest to the prey, so the location of the prey can be calculated by their positions. The specific mathematical model is as follows:

$$\begin{aligned} D_\alpha= & {} \left| {C_1 \times X_\alpha (t)-X(t)} \right| \end{aligned}$$

(6)

$$\begin{aligned} D_\beta= & {} \left| {C_2 \times X_\beta (t)-X(t)} \right| \end{aligned}$$

(7)

$$\begin{aligned} D_\delta= & {} \left| {C_3 \times X_\delta (t)-X(t)} \right| \end{aligned}$$

(8)

$$\begin{aligned} X_1= & {} X_\alpha -A_1 \times D_\alpha \end{aligned}$$

(9)

$$\begin{aligned} X_2= & {} X_\beta -A_2 \times D_\beta \end{aligned}$$

(10)

$$\begin{aligned} X_3= & {} X_\delta -A_3 \times D_\delta \end{aligned}$$

(11)

$$\begin{aligned} X(t+1)= & {} \frac{X_1 +X_2 +X_3 }{3} \end{aligned}$$

(12)

The distance between X(t) and $\alpha ,\beta , \upomega$ wolves is calculated by formula (6)–(11), and then, the position of the wolves move to the prey is calculated by formula (12). The flowchart of GWO is given in Fig. 2.

Fig. 2

GWO algorithm optimization process

3 Improved hybrid grey wolf algorithm

3.1 Chaos initialization

GWO algorithm usually solves function optimization problem by using randomly generated data as the initial population information, which will not retain the diversity of the population and lead to the poor optimization result of the algorithm. Therefore, this paper proposes Tent chaotic map to initialize the population.

Chaotic motion has the characteristics of randomness, regularity, and ergodicity. When solving function optimization problems, these features can lead algorithm to escape local optima, so as to maintain the diversity of the population and improve the global search ability. Chaotic maps include Tent maps, Logistic maps and so on. However, different chaotic mappings have different search characteristics. So far logistic map is mostly used in the literature. But it has a higher value rate in [0, 0.1] and [0.9, 1] that leads to inhomogeneous distribution of values. Shan et al. (2005) proves that the Tent map can perform better than the Logistic mapping in traversal homogeneity and generate a more uniform initial value between [0, 1], so as to improve the optimization speed of the algorithm.

Therefore, this paper proposes Tent chaos initialization, that is, we use Tent chaos to initialize the grey wolves. The mathematical model of Tent chaos map is as follows:

$$\begin{aligned} x(t+1)=\left\{ {\begin{array}{ll} \frac{x(t)}{u} &{}\quad 0\le x(t)<u \\ \frac{1-x(t)}{1-u} &{}\quad u\le x(t)\le 1 \\ \end{array}} \right. \end{aligned}$$

(13)

When $u= 1/2$, the Tent map has the most typical form. At this time, the resulting sequence has a uniform distribution and has an approximately uniform distribution density for different parameters.

Thus, the formula for the Tent chaotic map cited in this article is:

$$\begin{aligned} x_{t+1} =\left\{ {\begin{array}{ll} 2x_t &{}\quad 0\le x_t \le \frac{1}{2}\\ 2(1-x_t ) &{}\quad \frac{1}{2}<x_t \le 1 \\ \end{array}} \right. \end{aligned}$$

(14)

The steps for generating a sequence of Tent chaos maps are as follows:

• Step 1 Take the random initial value $x_{\textit{0}}$ to avoid falling into the small cycles points{0.2, 0.4, 0.6, 0.8}. Mark the array $y(1)=x_{\textit{0}},i=1, j=1$;

• Step 2 According to formula (14) to produce a set of x sequences. After each iteration, $i=i+1$;

• Step 3 If the number of iterations reaches the maximum, jump Step 4; Else If there is $x_{i}=\{0, 0.25, 0.5, 0.75\}$ or $x_{i}=x_{i-k}, k=\{0, 1, 2, 3, 4\}$, replace the initial value of the iteration by the formula $x(i)=y(j+1)=y(j)+c, j=j+1$; Else go to Step 2;

• Step 4 Terminate the operation, save x sequence data.

3.2 Nonlinear control parameter strategy

The GWO algorithm is mainly composed of two steps: the prey positioning and the grey wolf individual’s predatory behaviour. According to formula (1), the parameter A plays a very crucial role in balancing the global exploration and local exploitation capability of the GWO algorithm. When ${\vert }A{\vert }>1$, the group will expand the search range to find a better candidate solution, which is the global exploration ability of the GWO algorithm. When ${\vert }A{\vert }<1$, the group will narrow the search range and perform detailed search in the local area, which is the local exploitation capability of the GWO algorithm. At the same time, we can see from formula (2) that in the process of iteration, the value of A changes continuously with the change of control parameter a. From formula (4), it can be seen that the control parameter a decreases linearly with the increase in the number of iterations. However, the optimization process of GWO algorithm is very complicated. The linear change of parameter a cannot reflect the actual optimization search process of the algorithm. Wei et al. (2016) and Yi-Tung and Erwie (2008) proposed that the control parameter a varies nonlinearly with the number of iterations. And through the standard test function optimization results show that the use of nonlinear change strategy is better than the linear strategy optimization. But they still cannot meet the needs of the algorithm.

Therefore, this paper presents a new nonlinear control parameters, as shown in the following formula:

$$\begin{aligned} a_1 (t)=a_\mathrm{ini} -\left( a_\mathrm{ini} -a_\mathrm{fin} \right) \times \left( \frac{t}{T\max }\right) ^{2} \end{aligned}$$

(15)

where the set $a_\mathrm{ini}$ and $a_\mathrm{fin}$, respectively, represent the initial value and final value of the control parameter a. The set t is current iteration and the set Tmax is the maximum number of iterations.

In order to verify the validity of the control parameter a proposed in this paper, we compare it with the linear control parameters and the nonlinear control parameters which are proposed in Yang (2013) and Mirjalili et al. (2014), and the formula is as follows:

$$\begin{aligned} a_2 (t)= & {} a_\mathrm{ini} -a_\mathrm{ini} \times \left( \frac{t}{T\max }\right) \end{aligned}$$

(16)

$$\begin{aligned} a_3 (t)= & {} a_\mathrm{ini} -\left( a_\mathrm{ini} -a_\mathrm{fin} \right) \times \tan \left( \frac{1}{\varepsilon }\times \frac{t}{T\max }\times \pi \right) \end{aligned}$$

(17)

$$\begin{aligned} a_4 (t)= & {} a_\mathrm{ini} -a_\mathrm{ini} \times \left( \frac{1}{e-1}\times \left( e^{\frac{t}{T\max }}-1\right) \right) \end{aligned}$$

(18)

where the set $\varepsilon$ is a nonlinear adjustment coefficient.

Four kinds of control parameters are simulated as shown in Fig. 3. It can be seen from Fig. 3 that the nonlinear control parameter as proposed in this paper slowly declines at the early stage and falls fast in the later period. So the nonlinearity of the proposed algorithm is better.

Fig. 3

The change curve of the control parameter a

Meanwhile, the formula for the convergence factor A is as follows:

$$\begin{aligned} A=2a_1 r_2 -a_1 \end{aligned}$$

(19)

Fig. 4

Convergence factor dynamic curve

The dynamic curve of the four kinds of convergence factor A is shown in Fig. 4. It can be seen that the decline speed of convergence factor A is slow in the early stage, which can increase the global search ability and avoid the algorithm falling into the local optimum. The decline speed of convergence factor A is quick in the later stage, which can improve local search and speed up algorithm optimization. Therefore, this improvement can further weigh the exploration and exploitation capabilities.

3.3 PSO thought

In the process of location updating, GWO algorithm takes into account only the location information of individual wolves and the optimal solution, second-best solution, and third-best solution location information of the wolf pack, which realizes the exchange of information between individuals and wolf pack. But it ignores the exchange of information between the wolf and its own experience. Therefore, the idea of PSO algorithm is introduced to improve the location updating process.

In the PSO algorithm, the current position of the particle is updated by using the best position information of the particle itself and the best position information of the group. This paper combining with PSO algorithm will introduce the optimal location of individual experience into the position updating formula, which enables it to keep its own optimal position information. The new location update formula is as follows:

$$\begin{aligned} X_i (t+1)= & {} c_1 r_1 (w_1 X_1 (t)+w_2 X_2 (t)+w_3 X_3 (t))\nonumber \\&+\,c_2 r_2 (X_\mathrm{ibest} -X_i (t)) \end{aligned}$$

(20)

where the set $c_{1}$ is a social learning factor, the set $c_{2}$ is a cognitive learning factor. They, respectively, represent the influence of the individual optimal value and the group optimal value. The value of $c_{1}$ is large which can improve the global search capability; the value of $c_{2}$ is large which can improve the local search capability. But if the $c_{1}$ is too large, it will result in too many particles remain in the vicinity of the local. If the $c_{2}$ is too large, it will cause the particles to reach the local optimum in advance and converge to this value. According to Clerc (2002), this paper selects $c_{1}=c_{2}=2.05$. The set $r_{1}$ and $r_{2}$ are the random variable in the range of [0, 1]. The set $X_{\mathrm{ibest}}$ indicates that the grey wolf has experienced the best position. The set $w_{1},w_{2}, w_{3}$ are inertia weight coefficients. By adjusting weight ratio of the $\alpha ,\beta ,\delta$ wolves, the global and local search ability of the algorithm can be balanced dynamically. The specific formula is as follows:

$$\begin{aligned} w_1= & {} \frac{\left| {X_1 } \right| }{\left| {X_1 +X_2 +X_3 } \right| } \end{aligned}$$

(21)

$$\begin{aligned} w_2= & {} \frac{\left| {X_2 } \right| }{\left| {X_1 +X_2 +X_3 } \right| } \end{aligned}$$

(22)

$$\begin{aligned} w_3= & {} \frac{\left| {X_3 } \right| }{\left| {X_1 +X_2 +X_3 } \right| } \end{aligned}$$

(23)

In Eq. (20), the first part is expressed as the mean value of the best prey position which utilizes $\alpha ,\beta$ and $\delta$ wolf to search, which expands the search interval to increase the global search ability of the algorithm; the second part is expressed as the effect of the personal historical best position on algorithm search, which preserves the optimal position experienced by the individual.

3.4 PSO_GWO algorithm flow

The specific implementation steps of the improved wolf algorithm are as follows:

• Step 1 Set the size of the population to N, dimension d, and initialize the A, C, a values;

• Step 2 Generate population individuals by using Tent mapping {$X_{i}, i=1,2,3,\ldots ,N\}$, then calculate the individual fitness value {$f_{i}, i=1,2,3,\ldots ,N\}$;

• Step 3 Sort the order of fitness values by size, and take the first three fitness values corresponding to the individual as $\alpha , \beta ,\delta$. The corresponding position information is: $X_{\alpha },X_{\beta },X_{\delta }$;

• Step 4 Use formula (15) to calculate the nonlinear control parameters a, and then update the value of A and C according to formula (2) and (19);

• Step 5 Use formula (20) to update the location of individuals, then recalculate the fitness values and update values of $\alpha , \beta ,\delta$;

• Step 6 Judge whether t reaches Tmax value, if reached, the fitness value of $\alpha$ is output, that is, the best solution. Else go to Step 3.

4 Experimental data and simulation analysis

4.1 Benchmark functions

In order to verify the effectiveness of the improved hybrid wolf algorithm, this paper selects 18 benchmark functions (Liu and Yin 2016; Lu et al. 2017) to do simulation, compares with the grey wolf optimization algorithm (GWO) (Mirjalili et al. 2014), the improved grey wolf optimization algorithm (IGWO) (Yao and Wang 2016) and the grey the wolf algorithm based on the third strategy (GWO_3) (Zuo et al. 2017). The specific benchmark functions are shown in Table 1, and Figs. 5, 6 and 7 illustrate the 2D versions of the benchmark functions used.

Table 1 Benchmarking function

Fig. 5

2-D versions of unimodal benchmark functions

Fig. 6

2-D versions of multimodal benchmark functions

Fig. 7

2-D version of fixed-dimension multimodal benchmark functions

4.2 Experimental parameters

The performances of the proposed algorithm have been evaluated by using 18 commonly used benchmark functions. For all the experimentation, population size is $N=30$; dimensions are $d=30$, 50, 100. The maximum number of iterations is $T\max = 500$. In the IGWO algorithm, $\varepsilon =5,b_{1}=0.5, b_{2}=0.5$. In the PSO_GWO algorithm, $c_{1}=c_{2}=2.05; a_{\mathrm{ini}}=2, a_{\mathrm{fin}}=0; r_{1}=r_{2}=r_{3}=r_{4}=\hbox {rand } [0, 1]$.

4.3 Simulation analysis

In order to verify the optimal performance of PSO_GWO, we use 18 benchmark functions to test the performance of four algorithms. These benchmark functions are described in Table 1 and classified in Figs. 5, 6 and 7.

First of all, we use 30 wolves as the grey wolf population and separately conduct simulation experiments on 30, 50 and 100 dimension. We separately simulate 30 times on unimodal and multimodal functions and record the average value and standard deviation. The specific results are shown in Table 2.

Table 2 GWO, GWO_3, IGWO, PSO_GWO algorithm optimization results on unimodal and multimodal functions

Table 3 Comparison between the methods: average and standard deviation with the fixed-dimension multimodal benchmark functions

Table 4 Time-consuming results of benchmark functions

We use the mean and standard deviation as reliability criteria. It can be seen from Table 2 that when the dimension is same, the PSO_GWO can obtain better average in benchmark function F1–F9. Especially in the test function F8, the PSO_GWO algorithm can converge to zero. In addition, the standard deviation of the PSO_GWO algorithm is small in 9 benchmark functions experiments, which indicates that the robustness of this algorithm is better. This is because the PSO_GWO algorithm introduces nonlinear control parameters to balance the global exploration and local exploitation capability. However, the control parameters of other algorithms have poor nonlinearity, resulting in not balancing the local and global search ability well and easily fall into local optimum during the search period. Meanwhile, regardless of dimension $d=30$, 50 or 100, PSO_GWO algorithm can get better optimal solution than the other three algorithms. But the optimization ability of PSO_GWO algorithm decreases slightly with the increase in dimension.

In addition, we also propose the next set of the benchmark functions analysed in this paper, which are the fixed-dimension multimodal benchmark functions. Then we separately simulate 30 times and record the average value and standard deviation. The results are shown in the following table.

Table 3 shows a comparison among GWO, GWO_3, IGWO, PSO_GWO four algorithms based on the average and standard deviation. It can be known from the above table data that the algorithm presented in this paper is not enough different with the simulation results of the other three algorithms.

Simultaneously, this paper calculates the algorithm’s time statistics from both CPU and TIC/TOC. The CPU reflects the time it takes to complete the process when the CPU is working at full speed, while the TIC/TOC is used to calculate the time the program is running. The calculation results are shown in Table 4.

The accuracy of the PSO_GWO algorithm can be verified by starting and ending time of algorithm (TIC and TOC), and CPU time. These experimental data are shown in Table 4. As it can be seen from Table 4, the PSO_GWO algorithm has lower computational complexity than IGWO algorithm. But comparing with the GWO algorithm, the PSO_GWO algorithm has a large computational complexity and has a long running time. This is because the PSO_GWO algorithm is based on the basic GWO algorithm to introduce PSO algorithm ideas, thereby increasing the computational complexity of the algorithm. Therefore, the PSO_GWO algorithm improves convergence accuracy at the expense of computational complexity. Figure 5 shows the eight test function optimization curve of the GWO, GWO_3, IGWO, PSO_GWO algorithm.

As can be seen from Figs. 8, 9 and 10, the search speeds of the four algorithms are roughly the same during the initial search, but as the number of iterations increases, the PSO_GWO algorithm proposed in this paper continues to search until the search for the optimal solution. However, the other three algorithms reach the stagnation state in advance, resulting in poor search results. Therefore, the proposed algorithm has better convergence performance on benchmark function. This is because the other three algorithms did not consider the impact of the individual experience of the grey wolf during the search process. However, the algorithm proposed in this paper uses its own experience to delay the algorithm into a local optimum during the predation process.

To sum up, all simulation results indicate the improved hybrid grey wolf optimization algorithm is very helpful in improving the efficiency of the GWO in the terms of result quality.

Fig. 8

Convergence curve of GWO, GWO_3, IGWO, and PSO_GWO on unimodal functions

Fig. 9

Convergence curve of GWO, GWO_3, IGWO, and PSO_GWO on multimodal functions

Fig. 10

Convergence curve of PSO, GWO, IGWO and PSO_GWO variants on fixed-dimension multimodal functions

5 Conclusion

In this paper, we proposed an improved grey wolf algorithm. As described in Sect. 3, it first used Tent chaotic map to initialize grey wolf population, then used nonlinear control parameters to balance the local and global search capabilities of the algorithm and introduced PSO algorithm thought into the position update formula. And in Sect. 4, a series of experiments on the 18 benchmark test functions are executed to verify the effectiveness of the improved hybrid wolf algorithm. The experimental results show that the proposed algorithm is superior to other algorithms in the search capability. And it is evident that the proposed algorithm can improve the performance of GWO algorithm in terms of result quality and better robustness. In this work, we justify the problems that were used for testing benchmark test functions. Although the PSO_GWO algorithm improves result quality, the computational complexity is increased. So in the future, we will conduct research on the issue of reducing the computational complexity. At the same time, we will also apply the improved algorithm to solve wireless sensor networks coverage problem.