Fuzzy model predictive control of normalized air-to-fuel ratio in internal combustion engines

Abstract

In this paper, a fuzzy model predictive controller is developed to reduce the emission pollutants in spark ignition internal combustion engines. The path to this control goal is regulating the amount of normalized air-to-fuel ratio in the engine. In order to generate the simulation data, mean value engine model is simulated. To approximate the nonlinear and fast time-varying dynamics of the engine, a modified fuzzy relational model is trained offline in batch mode. For training, gradient descent back propagation algorithm along with evolutionary asexual reproduction optimization algorithm is used. Nonlinear structure of the fuzzy model of the engine imposes nonlinear optimization to produce control signals. Hence, gradient descent algorithm is used to generate online control signals. The effectiveness and robustness of the controller are evaluated through simulations.

1 Introduction

Exhaust pipe emission pollutants of internal combustion engines (ICEs), such as nitrogen oxides $\mathrm{NO}_x$, carbon monoxide CO and unburned hydro-carbons (HC), are one of the main causes of air pollution in urban areas. These pollutants have carcinogenic and destructive effect on humans (Kiencke and Nielsen 2005). Based on different emission standards such as OBD II, EURO 6 and LEV III, automotive industry is strictly required to regulate the amount of exhaust pipe pollutants in ICEs. Meanwhile, the overall performance of the engine in terms of producing enough torque and traction force should be maintained at a satisfactory level (Kiencke and Nielsen 2005). Hence, regulation of emission pollutants is an important control goal in automotive industry which led to huge number of research works in the last three decades (Carnevale et al. 1995; Hendricks and Luther 2001; Jansri and Sooraksa 2012; Kaidantzis et al. 1993; Kiencke 1988; Kopačka et al. 2011; Lauber et al. 2007; Li and Yurkovich 1999; Meyer et al. 2013; Morelos and Anzurez Marin 2012; Shamdani et al. 2007; Sardarmehni et al. 2013a, b; Wang and Yu 2005, 2008; Wang et al. 2006; Yildiz et al. 2008; Zhai and Yu 2009; Zhai et al. 2010).

In spark ignition (SI) engines, as one of the most common transport vehicles, the amount of exhaust pipe emission pollutants can be effectively reduced, to almost zero, by use of three-way catalytic converters (TWCCs) (Kiencke and Nielsen 2005). TWCC is a device that is integrated at the end of exhaust pipe. It is composed of a coated metal or ceramic carrier substrate with a large surface which is again covered with a thin layer of platinum and rhodium. In summary, platinum and rhodium accelerate simultaneous oxidation and reduction processes which lead to conversion of $\mathrm{NO}_x$, $\mathrm{CO}$ and unburned HC to $\mathrm{CO}_2$, $\mathrm{N}_2$, and $\mathrm{H}_2 \mathrm{O}$ (Kiencke and Nielsen 2005). The performance of TWCC is strongly dependent on the amount of air-to-fuel ratio (AFR), defined as mass ratio of air to fuel in the combustion chamber (Carnevale et al. 1995; Hendricks and Luther 2001; Kaidantzis et al. 1993; Kiencke 1988; Kiencke and Nielsen 2005; Lauber et al. 2007; Li and Yurkovich 1999; Meyer et al. 2013; Morelos and Anzurez Marin 2012; Shamdani et al. 2007; Sardarmehni et al. 2013a, b; Wang and Yu 2005, 2008; Wang et al. 2006; Yildiz et al. 2008; Zhai and Yu 2009; Zhai et al. 2010). If the amount of air is enough to burn the fuel completely, the mixture is called stoichiometric mixture and its AFR is called stoichiometric AFR. Usually the normalized AFR, typically denoted by $\lambda$ in the literature, is used which is the ratio of instantaneous AFR to stoichiometric AFR. TWCC can eliminate the exhaust emission pollutants only if $\lambda$ is controlled within $\pm \,1\%$ of the stoichiometric value equal to 1. This region for $\lambda$ is referred to as lambda window (Kiencke and Nielsen 2005). As a results, regulating the amount of $\lambda$ in the lambda window is the backbone of emission control systems in SI engines.

Due to low cost of proportional integral (PI) controllers, they are widely used in the automotive industry to regulate $\lambda$. However, PI controllers demonstrate poor performance in the presence of noise/disturbance, the engines time-varying and fast dynamics, structured/unstructured uncertainties in the engine model and they usually have a time-consuming calibration process. As a result, interests in designing novel controllers for improving the robustness and quality of $\lambda$ control have been increased in both industrial and academic investigations (Carnevale et al. 1995; Hendricks and Luther 2001; Jansri and Sooraksa 2012; Kaidantzis et al. 1993; Kiencke 1988; Kiencke and Nielsen 2005; Lauber et al. 2007; Li and Yurkovich 1999; Meyer et al. 2013; Morelos and Anzurez Marin 2012; Shamdani et al. 2007; Sardarmehni et al. 2013a, b; Wang and Yu 2005, 2008; Wang et al. 2006; Yildiz et al. 2008; Zhai and Yu 2009; Zhai et al. 2010).

Modeling and control of ICEs have been studied since late 1980s by evolution of control oriented engine models. The idea of modeling the fast and time-varying dynamics of ICEs by mathematically compact but precise physic-based models were almost fulfilled by presentation of mean value engine models (MVEMs). MVEM describes the dynamical behavior of ICEs in the state space and models dynamics of every state variable through fitting it to the mean value of the corresponding state in the previous time steps. Although MVEM neglects unnecessary complexities in combustion process, accuracy in modeling the required state variables is guaranteed. As studied in Hendricks et al. (1996), simulated dynamics of a real engine in the state space by MVEM are as accurate as a typical dynamo-meter measurement in the steady-state mode and yields $\pm \,2\%$ mean absolute error (MAE) in the transient mode. At first, MVEM for any arbitrary SI engine was not compatible to be applied to another SI engine because of the difficulties in modeling of engines volumetric efficiency. Hendricks et al. (1996) have improved the MVEM by introducing a simple model of the volumetric efficiency, and therefore, the improved model is compatible for application in a wide range of SI engines. Further studies in mean value modeling approach led to mean value modeling of SI engines with exhaust gas recirculation (EGR). EGR technology is importing a portion of exhaust gas to the combustion chamber. Through EGR, the amount of $\mathrm{NO}_x$ is considerably reduced and the exhaust emission temperature is decreased which protects the TWCC from thermal damages. At first, EGR control strategies were based on static relationships depending on stationary engine mapping which led to no satisfactorily AFR control (Azzoni et al. 1997; Fons et al. 1999). However, by developments in MVEM of SI engines with EGR as dynamic engine models a considerable change in the quality of AFR control in EGR engines has been achieved (Azzoni et al. 1997). The first models of MVEM including EGR were isothermal models. The extension of isothermal models led to dynamic adiabatic models which show sufficient accuracy for control purpose (Azzoni et al. 1997).

Many classical and modern control strategies have been studied and applied to control AFR in ICEs (Carnevale et al. 1995; Hendricks and Luther 2001; Kaidantzis et al. 1993; Kiencke 1988; Kiencke and Nielsen 2005; Lauber et al. 2007; Li and Yurkovich 1999; Meyer et al. 2013; Morelos and Anzurez Marin 2012; Shamdani et al. 2007; Sardarmehni et al. 2013a, b; Wang and Yu 2005, 2008; Wang et al. 2006; Yildiz et al. 2008; Zhai and Yu 2009; Zhai et al. 2010). In accordance with the purpose of the present study, a brief literature survey on model predictive control (MPC) for regulating AFR is going to be presented. The main idea in MPC of AFR is dedicated to using a simple mathematical model to identify (predict) the engine dynamics and using this model in the prediction horizon of the MPC in order to generate a sequence of controls which minimizes a performance index throughout a short and finite horizon. As a result, a time-dependent control sequence is generated and at each time step only the first component of this sequence is applied as the control. The rest of the components of the control sequence are used as initial values for the calculation of control in the next time step. Artificial neural networks and fuzzy systems are two research interests in modern MPCs. Due to the ability of neural networks in uniform approximation of continuous functions in a compact set, neural networks have been widely used in identification stage of MPC of AFR in ICEs. In this regard, applications of offline and online multilayer perceptron (Wang et al. 2006; Wang and Yu 2005; Zhai and Yu 2009), radial-based function neural network (Sardarmehni et al. 2013a; Wang and Yu 2008), and dynamic recurrent neural networks (Zhai et al. 2010), have been reported. Meanwhile, the potential of fuzzy systems in handling the unknown dynamics and uncertainties in modeling and control of dynamical systems has led to their widespread applications, especially in MPC of $\lambda$ in ICEs (Ghaffari et al. 2008; Kopačka et al. 2011; Wong et al. 2013).

A fuzzy relational model (FRM) has a structure in which the fuzzy inputs and the fuzzy output are in vector form. A (multi-dimensional) fuzzy relational matrix (FRX) is composed with the fuzzy input vectors to calculate the fuzzy output vector. This constitutes a fuzzy relational equation in matrix form. The fuzzy input vectors are constructed through the vectorizing fuzzifiers, and the final (crisp) output is extracted from the fuzzy output vector through a discrete defuzzifier. It is interesting that the elements of the FRX in an FRM can be interpreted as the truth values of the fuzzy if–then rules. Indeed, all possible rules are present in the fuzzy rule-base of an FRM. In this way, every FRM can be considered as a linguistic fuzzy model with a fuzzy relational equation in its core. The fuzzy relational modeling structure can be used for modeling nonlinear functions with adequate accuracy.

In this paper, a modified fuzzy relational mode (MFRM) proposed in Aghili-Ashtiani and Menhaj (2014) is used. The MFRM is based on the fuzzy relational inner composition (FRIC) introduced in Aghili-Ashtiani and Menhaj (2012). The MFRM is itself the base for g-normal fuzzy relational modeling which is proposed in Aghili-Ashtiani and Menhaj (2015). The MFRM supports multiple inputs in a transparent manner which means that the knowledge stored in the FRX can be directly understood and used by an expert, and vice versa, the knowledge of an expert can be directly translated and inserted in the FRX. For example, an expert’s experience can be used to determine the FRX as an starting point and then the FRX can be fine-tuned through an iterative algorithm which uses the provided data. In this study, the structure of the MFRM is adapted for modeling the dynamics of MVEM to predict the amount of AFR in the prediction horizon of MPC. The application of MFRM in MPC was first introduced in Amiraskari and Menhaj (2013). However, improper design of the fuzzy system led to application of model-free optimization methods with heuristic solution for the MPC system.

Training the MFRM of the engine is preformed via offline data gathered from the MVEM model subjected to bounded random inputs. These random inputs are selected such that they can generate both transient and steady-state data which engine might encounter. The training is initiated with gradient descent back propagation (GDBP) with a fixed learning rate. The main drawback of GDBP is possibility of getting stuck in local minima. This issue occurred in the training process of MFRM. Hence, an evolutionary optimization method called asexual reproduction optimization (ARO) (Mansouri et al. 2011) is used to precede the training process with the final output of GDBP as the initial guess for starting the training process. The combination of these two algorithms results in a faster convergence of the training process compared with using solely ARO from the beginning of the training. Once trained, the MFRM is used to predict the amount of lambda in the prediction horizon and control signals are derived through online minimization of a selected cost function. For minimization of the cost function, gradient descent (GD) algorithm is used. According to simulation results, the proposed fuzzy MPC system has a good performance in terms of regulating lambda. Besides, the proposed fuzzy MPC system has a robust performance in the presence of moderate disturbances.

The rest of this paper is organized as follows. Section 2 and 3 describe the MVEM and the MFRM of the engine. In Sect. 4, the training process of the MFRM is discussed and the MPC structure is discussed in Sect. 5. Simulation results and discussions are presented in Sect. 6, and Sect. 7 concludes the paper.

Table 1 MVEM Notations

Fig. 1

Schematic of MVEM with EGR

2 MVEM of SI engine including EGR

The schematic of an MVEM with EGR is shown in Fig. 1, and the notations used for presenting the MVEM are depicted in Table 1. As one can see from Fig. 1, an MVEM with EGR is composed of 5 sub-systems which are exhaust gas recirculation, intake manifold air mass flow, crank shaft and loading, fuel vapor and fuel film, and lambda sensor model. In general, the inputs of the engine are injected fuel mass flow rate, $\dot{m}_{fi}$, throttle plate angle, $\alpha$, and ignition advance. In this study, it is assumed that ignition advance is a constant and throttle plate angle is regarded as a noise signal. Hence, injected fuel mass flow rate is the only control signal. The state variables are selected from the output of the three basic sub-systems of the MVEM which are intake manifold air mass flow, crankshaft/loading and fuel vapor/film sub-system. Therefore, the state variables are fuel mass flow deposited in the intake manifold, $\dot{m}_{\mathrm{ff}}$, manifold pressure, $P_i$, and crankshaft speed, n (Hendricks and Sorenson 1990; Hendricks et al. 1996). Since the purpose of the closed-loop system is to control AFR, the measured AFR by sensor, $\lambda _{\mathrm{sensor}}$, is considered as the fourth state of the MVEM (Sardarmehni et al. 2013b). At last, the output of the system is selected as the measured AFR by sensor, $\lambda _{\mathrm{sensor}}$.

The first two sub-systems in Fig. 1 address the dynamics of the intake manifold air mass flow and EGR. Considering the intake manifold as the control volume, the first state equation is obtained from applying conservation of mass (Azzoni et al. 1997; Fons et al. 1999; Hendricks and Sorenson 1990; Hendricks et al. 1996).

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}m_\mathrm{i} = \dot{m}_{\mathrm{at}} + \dot{m}_{\mathrm{EGR}} - \dot{m}_{\mathrm{ap}} \end{aligned}$$

(1)

In Eq. (1), $m_\mathrm{i}$ is air mass in intake manifold ($\mathrm{kg}$) and $\dot{m}_{\mathrm{at}}$ is air mass flow rate passing the throttle plate ($\mathrm{kg}/\mathrm{s}$). $\dot{m}_{\mathrm{EGR}}$ is EGR mass flow rate ($\mathrm{kg/s}$) and $\dot{m}_{\mathrm{ap}}$ is air mass flow rate entering the combustion chamber ($\mathrm{kg/s}$). Using energy conservation in adiabatic processes, one has

$$\begin{aligned} \dot{m}_{\mathrm{at}}{h_\mathrm{a}} + \dot{m}_{\mathrm{EGR}}{h_{\mathrm{EGR}}} - \dot{m}_{\mathrm{ap}}{h_\mathrm{i}}= & {} \frac{\mathrm{d}}{\mathrm{d}t}\left( {m_\mathrm{i}} \right) \nonumber \\= & {} {\dot{m}_\mathrm{i}}{c_\mathrm{v}}{T_\mathrm{i}} + {m_\mathrm{i}}{c_\mathrm{v}}{\dot{ T}_\mathrm{i}} \end{aligned}$$

(2)

In Eq. (2), $h_a$, $h_{\mathrm{EGR}}$, $h_\mathrm{i}$ are enthalpy of ambient air ($\mathrm{kj/kg}$), enthalpy of EGR air ($\mathrm{kj/kg}$), and enthalpy of manifold air ($\mathrm{kj/kg}$), respectively. $c_\mathrm{v}$ is constant volume specific heat ($\mathrm{kj}$$/ \mathrm{k g}\,^ {\circ } K$) and $T_\mathrm{i}$ is intake manifold temperature ($^{\circ }\mathrm{K}$). Enthalpy can be expressed as

$$\begin{aligned} {h_x} = {T_x}\frac{{R {\mathscr {K}}}}{{{\mathscr {K}} - 1}} \end{aligned}$$

(3)

where R shows the gas global constant ($\mathrm{kj/kg}^{\circ }\mathrm{K}$) and ${\mathscr {K}}$ is ratio of the specific heats. The sub-script x in Eq. (3) can be either of ambient air, EGR air or air in the manifold. Therefore, Eq. (2) can be written as a differential equation by taking time derivatives of Eq. (3) and substituting in Eq. (2) as follows¹.

$$\begin{aligned} \begin{aligned} {\dot{T}_\mathrm{i}}&= \frac{{{{\dot{m}}_{\mathrm{at}}}{T_a}R{\mathscr {K}}}}{{\left( {{\mathscr {K}} - 1} \right) {m_\mathrm{i}}{c_\mathrm{v}}}} +\frac{{{{\dot{m}}_{\mathrm{EGR}}}{T_{\mathrm{EGR}}}R{\mathscr {K}}}}{{\left( {{\mathscr {K}} - 1} \right) {m_\mathrm{i}}{c_\mathrm{v}}}} \\&\quad - \frac{{{{\dot{m}}_{\mathrm{ap}}}{T_\mathrm{i}}R{\mathscr {K}}}}{{\left( {{\mathscr {K}} - 1} \right) {m_\mathrm{i}}{c_\mathrm{v}}}} - \frac{{{{\dot{m}}_\mathrm{i}}{T_\mathrm{i}}}}{{{m_\mathrm{i}}}} \end{aligned} \end{aligned}$$

(4)

In Eq. (4), $T_\mathrm{i}$ is intake manifold temperature ($^{\circ } K$), $T_a$ is ambient air temperature ($^{\circ } K$) and $T_{\mathrm{EGR}}$ is EGR temperature ($^{\circ } K$). Thermodynamically ${\mathscr {K}}$ and $c_v$ can be expressed by

$$\begin{aligned} {\mathscr {K}}= & {} \frac{{{c_p}}}{{{c_v}}} \end{aligned}$$

(5)

$$\begin{aligned} {c_v}= & {} \frac{R}{{{\mathscr {K}} - 1}} \end{aligned}$$

(6)

In Eq. (5), $c_p$ is constant pressure specific heat ($\mathrm{kj/kg}^{\circ }\mathrm{K}$). Substituting Eqs. (5) and (6) in Eq. (4) and assuming air as an ideal gas yields to

$$\begin{aligned} \begin{aligned} {\dot{T}_\mathrm{i}}&= \frac{{{{\dot{m}}_{at}}{T_a}R{\mathscr {K}}{T_\mathrm{i}}}}{{{P_\mathrm{i}}{V_\mathrm{i}}}} + \frac{{{{\dot{m}}_{\mathrm{EGR}}}{T_{\mathrm{EGR}}}R{\mathscr {K}}{T_\mathrm{i}}}}{{{P_\mathrm{i}}{V_\mathrm{i}}}} - \frac{{{{\dot{m}}_{\mathrm{ap}}}{T^2}_iR{\mathscr {K}}}}{{{P_\mathrm{i}}{V_\mathrm{i}}}}\\&\quad - \frac{{{{\dot{m}}_\mathrm{i}}{T}_\mathrm{i}}^2}{{{P_\mathrm{i}}{V_\mathrm{i}}}} \end{aligned} \end{aligned}$$

(7)

where $P_\mathrm{i}$ is manifold air pressure (bar) and $V_\mathrm{i}$ is intake manifold and port passage volume ($m^3$). Applying the mass conservation from Eq. (1) and assuming air as an ideal gas, one has

$$\begin{aligned} \begin{aligned} {\dot{P}_\mathrm{i}}&= \frac{R}{{{V_\mathrm{i}}}}\left( {{{\dot{m}}_\mathrm{i}}{T_\mathrm{i}} + {m_\mathrm{i}}{{\dot{T}}_\mathrm{i}}} \right) \\&= \frac{{{\mathscr {K}}R}}{{{V_\mathrm{i}}}}\left( { - {{\dot{m}}_{\mathrm{ap}}}{T_\mathrm{i}} + {{\dot{m}}_{at}}{T_a} + {{\dot{m}}_{\mathrm{EGR}}}{T_{\mathrm{EGR}}}} \right) \end{aligned} \end{aligned}$$

(8)

The dynamics of intake manifold in SI engine including EGR can be expressed by mean value approach as Eq. (7) and Eq. (8). The key assumption here is that perfect mixing of fresh air and EGR flow is happening in the intake manifold. In order to use adiabatic MVEM, it is necessary to specify the EGR mass flow and temperature. A device for EGR control is the Delphi Linear Exhaust Recirculation Valve (LERV). Study of EGR valve flow characteristics revealed that $\dot{m}_{\mathrm{EGR}}$ can be approximated as Fons et al. (1999), Azzoni et al. (1997)

$$\begin{aligned} {\dot{m}_{\mathrm{EGR}}}\left( {{D_\mathrm{c}},\Delta P} \right) = \frac{1}{2}a\left( {\Delta P} \right) \left[ {\tanh \left[ {\frac{{{D_\mathrm{c}} - {D_{\mathrm{cm}}}}}{{{\tau _{\mathrm{dc}}}}}} \right] + 1} \right] \end{aligned}$$

(9)

In Eq. (9), $D_\mathrm{c}$ is mark/space ratio (MSR) of the PWM² drive signal and $D_{\mathrm{cm}}$ is common PWM MSR center value for all pressure ratios. $\tau _{\mathrm{dc}}$ is the effective relaxation MSR of the PWM control signal. Meanwhile,

$$\begin{aligned} a\left( {\Delta P} \right) = {\dot{m}_{\mathrm{EGR}}}\left( {\max } \right) \left[ {1 - \exp \left( {\frac{{ - \Delta P}}{{{\tau _{\Delta P}}}}} \right) } \right] \end{aligned}$$

(10)

where $\tau _{\Delta P}$ is the effective relaxation pressure for the valve. In (9) and (10), $\Delta P$ is the pressure drop across the EGR valve and it is a function of crank shaft speed and normalized air charge per cycle and can be expressed as

$$\begin{aligned} \Delta P = {P_\mathrm{e}} - {P_\mathrm{i}} = - {S_\mathrm{e}}\left( n \right) {m_{\mathrm{ap}'}} + {y_\mathrm{e}}\left( n \right) \end{aligned}$$

(11)

In Eq. (11), $P_\mathrm{e}$ is exhaust manifold pressure ($\mathrm{bar}$) and $S_\mathrm{e}$ is slope of pressure difference curve with normalized air charge. $y_\mathrm{e}$ is intercept of pressure difference curve, with normalized air charge. n is crank shaft speed ($\mathrm{kRPM}$). $S_\mathrm{e}$ and $y_\mathrm{e}$ are constants (Hendricks et al. 1996) and

$$\begin{aligned} {m_{\mathrm{ap}'}} = \frac{{120R{T_\mathrm{i}}}}{{{V_\mathrm{d}}n}}{\dot{m}_{\mathrm{ap}}} \end{aligned}$$

(12)

where $V_\mathrm{d}$ is engine displacement volume ($\mathrm{l}$). In Eq. (12), $\dot{m}_{\mathrm{ap}}$ is a function of crank shaft speed, n, and manifold pressure, $P_\mathrm{i}$, and can be defined as Hendricks and Sorenson (1990), Hendricks et al. (1996)

$$\begin{aligned} {\dot{m}_{\mathrm{ap}}}\left( {n,{P_\mathrm{i}}} \right) = \frac{{{V_\mathrm{d}}}}{{120}}\left( {{e_\mathrm{v}}{P_\mathrm{i}}} \right) n \end{aligned}$$

(13)

In Eq. (13), $e_\mathrm{v}$ is volumetric efficiency. $\dot{m}_{\mathrm{at}}$ is a function of the throttle plate angle, $\alpha$, and the manifold pressure, $P_\mathrm{i}$, which can be defined as Hendricks and Sorenson (1990), Hendricks et al. (1996)

$$\begin{aligned} {\dot{m}_{at}}\left( {\alpha ,{P_\mathrm{i}}} \right) = {m_{\mathrm{at}1}}\frac{{{P_\mathrm{a}}}}{{\sqrt{{T_\mathrm{a}}} }}{\beta _1}\left( \alpha \right) {\beta _2}\left( {{P_\mathrm{r}}} \right) + {m_{\mathrm{at}0}} \end{aligned}$$

(14)

The intermediate terms of $\beta _1$ and $\beta _2$ are considered as

$$\begin{aligned} {\beta _1}\left( \alpha \right)= & {} 1 - {\alpha _1}\cos \left( \alpha \right) + {\alpha _2}{\cos ^2}\left( \alpha \right) \end{aligned}$$

(15)

$$\begin{aligned} {P_\mathrm{r}}= & {} \frac{{{P_\mathrm{i}}}}{{{P_\mathrm{a}}}}\end{aligned}$$

(16)

$$\begin{aligned} {\beta _2}\left( {{P_\mathrm{r}}} \right)= & {} {\left\{ \begin{array}{ll} \frac{1}{P_n} \sqrt{{P_\mathrm{r}}^{P_1} - {P_\mathrm{r}}^{P_2}} &{} \text {if}\,P_\mathrm{r} \ge P_\mathrm{c}\\ 1 &{}\text {if} \,{P_\mathrm{r}} < {P_\mathrm{c}} \end{array}\right. } \end{aligned}$$

(17)

In Eqs. (14)–(17), $m_{\mathrm{at}1}$, $m_{\mathrm{at}0}$, $\alpha _1$, $\alpha _2$, $P_n$, $P_1$, $P_2$ and $P_\mathrm{c}$ are constants (Hendricks and Sorenson 1990; Hendricks et al. 1996).

The second state space equation is obtained through the energy conservation for the crankshaft rotation (Hendricks and Sorenson 1990; Hendricks et al. 1996).

$$\begin{aligned} \begin{aligned} \dot{n} =&\frac{{ - 1}}{{In}}\left( {{P_\mathrm{f}}\left( {{P_\mathrm{i}},n} \right) + {P_\mathrm{p}}\left( {{P_\mathrm{i}},n} \right) + {P_\mathrm{b}}\left( n \right) } \right) \\&+ \frac{1}{{In}}{H_\mathrm{u}}{\eta _\mathrm{i}}\left( {n,{P_\mathrm{i}},\lambda } \right) {\dot{m}_\mathrm{f}}\left( {t - {\tau _d}} \right) \end{aligned} \end{aligned}$$

(18)

In Eq. (18), I is total engines moment of inertia ($\mathrm{kg} \,\mathrm{m}^2 *(\pi /30)^2 * 1000$). $P_f$ is engine mechanical friction loss power ($\mathrm{kW}$), $P_\mathrm{p}$ is engine pumping loss power ($\mathrm{kW}$), and $P_\mathrm{b}$ is engine load power ($\mathrm{kW}$). $H_\mathrm{u}$ is fuel heating value ($\mathrm{kj/kg}$) and $\eta _\mathrm{i}$ is indicated efficiency. At last, $\tau _\mathrm{d}$ is time delay for the injected fuel to make power ($\mathrm{s}$).

The third state equation is achieved from the dynamics of the fuel film. Considering $X_\mathrm{f}$ as the ratio of fuel deposits as liquid in the intake manifold after reaching the cold air in the manifold, and $1-X_\mathrm{f}$ as the ratio of the fuel remains as fuel vapor, the condensed fuel film gradually vaporizes to be mixed with the fuel vapor and makes entering the combustion chamber as Hendricks and Sorenson (1990), Hendricks et al. (1996)

$$\begin{aligned} {\ddot{m}_{\mathrm{ff}}} = \frac{1}{{{\tau _\mathrm{f}}}}\left( {{{\dot{m}}_{\mathrm{ff}}} + {X_f}{{\dot{m}}_{\mathrm{fi}}}} \right) \end{aligned}$$

(19)

In Eq. (19), $\dot{m}_{\mathrm{ff}}$ is fuel film mass flow rate ($\mathrm{kg/s}$) and $\dot{m}_{fi}$ denotes injected fuel mass flow rate ($\mathrm{kg/s}$). Meanwhile, one has

$$\begin{aligned} {\dot{m}_{\mathrm{fv}}}= & {} \left( {1 - {X_\mathrm{f}}} \right) {\dot{m}_{\mathrm{fi}}} \end{aligned}$$

(20)

$$\begin{aligned} {\dot{m}_\mathrm{f}}= & {} {\dot{m}_{\mathrm{fv}}} + {\dot{m}_{\mathrm{ff}}} \end{aligned}$$

(21)

where $\dot{m}_{\mathrm{fv}}$ is fuel vapor mass flow rate ($\mathrm{kg/s}$) and $\tau _\mathrm{f}$ is fuel film evaporation time constant ($\mathrm{s}$).

The fourth state equation determines the dynamics of a first-order lambda sensor which is summarized as Sardarmehni et al. (2013a)

$$\begin{aligned} {\dot{\lambda }_{\mathrm{sensor}}} = \frac{1}{{{\tau _\mathrm{e}}}}\left( { - {\lambda _{\mathrm{sensor}}} + {\lambda _m}(t - \delta )} \right) \end{aligned}$$

(22)

where $\lambda _{\mathrm{sensor}}$ is the measured lambda by lambda sensor and $\lambda _\mathrm{m}$ is the computed lambda from MVEM model. $\tau _\mathrm{e}$ defines the time delay in the measurements made by the sensor. In (22), $\delta$ is the total delay of the lambda sensor.

$$\begin{aligned} \delta = \left( {\frac{{{\theta _{\mathrm{EVO}}}}}{{720}}} \right) \left( {\frac{{120}}{{{n_{\mathrm{cyl}}}n}}} \right) + {t_d} \end{aligned}$$

(23)

At last, the computed lambda from the MVEM, $\lambda _m$, is defined as

$$\begin{aligned} {\lambda _{\mathrm{m}}} = \frac{{{\dot{m}}_{\mathrm{ap}}}}{{AF{R_{\mathrm{st}}}{{\dot{m}}_f}}} \end{aligned}$$

(24)

3 Structure of the MFRM

Every MFRM as introduced in Aghili-Ashtiani and Menhaj (2014) and depicted in Fig. 2 is comprised of three blocks: (1) fuzzy discretization (fuzzification) (called $\phi$-block); (2) fuzzy relational inner composition by a fuzzy relational matrix (called R-block); (3) output extraction (defuzzification) (called $\psi$-block).

Fig. 2

Structure of a typical MFRM (Aghili-Ashtiani and Menhaj 2014)

Regarding Fig. 2, consider the input vector of the MFRM as ${\mathbf {x}} \in {\mathbb {R}}^p$. Each respective element of ${\mathbf {x}}$ is a scalar which is referred to as $x_\mathrm{i}$, $i = 1, \ldots , p$. The working mechanism of MFRM is as follows. As it is shown in Fig. 2, each $x_\mathrm{i}$ is first fuzzified and makes a corresponding fuzzy vector ${\mathbf {a}}_\mathrm{i} \in {\mathbb {R}}^{q_\mathrm{i}}$, where $q_\mathrm{i}$ is the number of the membership functions across which $x_\mathrm{i}$ is evaluated. The p fuzzy vectors are composed with $(p+1)$-dimensional FRX ${\mathbf {R}}$ through a fuzzy relational inner composition (FRIC) to make the fuzzy output vector ${\mathbf {b}}$ according to Aghili-Ashtiani and Menhaj (2012) as

$$\begin{aligned} \mathbf{{b}} = \mathbf{{R}} \circ {\mathbf{{a}}_\mathbf{{1}}} \circ {\mathbf{{a}}_\mathbf{{2}}} \circ \ldots \circ {\mathbf{{a}}_\mathbf{{p}}}, \end{aligned}$$

(25)

in which ${\mathbf {R}}$ is a ${ q_{p+1} \times q_{p} \times \cdots \times q_1 }$ FRX. The sign “$\circ$” stands for the FRIC for which we have used the algebraic product as the t-norm and the algebraic sum as the t-conorm. The output of the MFRM is obtained from ${\mathbf {b}}$ via output extraction methods; one of the most important of them is the weighted average defuzzification represented as

$$\begin{aligned} y = \frac{\sum \nolimits _{i = 1}^{q_{p+1}} {{\mathbf {c}}\left( i \right) {\mathbf {b}}\left( i \right) } }{\sum \nolimits _{i = 1}^{q_{p+1}} {{\mathbf {b}}\left( i \right) } } , \end{aligned}$$

(26)

where ${\mathbf {c}}$ is the vector of the centers for the output variable and acts as a weight matrix and ${\mathbf {c}}(i)$ denotes its i-th element. This completes the overall view of the structure of an MFRM. The heart of the MFRM is the FRIC which will be discussed more in the training section.

Remark 1

Choosing the membership functions in the $\phi$-block must be handled with caution. The MFRM is going to act as the engine model for model predictive control of $\lambda$, where nonlinear minimization of a cost function is required for generating the control actions. In this paper, a derivative-based optimization algorithm is used for this minimization and so it is necessary for the overall relation of the MFRM to be differentiable. To this end, we have used Gaussian membership functions in the $\phi$-block.

If we determine the membership functions in the $\phi$-block, the type of t-norm and t-conorm in the R-block, and the type of output extraction in the $\psi$-block, then the identification of an MFRM is performed by tuning the elements of its FRX. In other words, training the MFRM is equivalent to tuning its FRX. A derivative-based tuning algorithm has been presented in Aghili-Ashtiani and Menhaj (2014) which can be performed iteratively and so it can be used online if the sampling time is not too small.

Remark 2

When we want to employ the structure of MFRM in the predictive control scheme, we should notice the computational cost of the overall scheme, i.e., the tuning procedure for model identification and the nonlinear minimization for control action. As a result, a low computational burden is desired in the identification phase to speed up the overall performance of the control system. In this regard, the idea of training MFRM via offline data in batch mode seems to alleviate the problem of heavy computations. The FRX that is trained by offline training method is a constant matrix and does not need further modifications during the simulations.

4 Training

In order to ensure the offline training process, one needs to select a rich set of training patterns which covers the domain of interest in which the engine is functioning. In the training process, one can consider two regions of interest for the engine as transient and steady state. To achieve the suitable training patterns, with the same procedure reported in Zhai and Yu (2009), random bounded square signals with random pulse widths are imposed to the engine model for the throttle plate angle and injected fuel mass flow. While longer pulse widths represent the steady-state working conditions of the engine, the shorter pulse widths are meant to simulate the transient performance of the engine. For generating the training patterns, throttle plate angle is confined to $\alpha \in [20, 40]$ (deg) and injected fuel mass flow rate is bounded to $\dot{m}_{fi} \in [0.001, 0.008]$ ($\mathrm{kg/s}$), respectively. The resulted lambdas of the MVEM are stored. Since the throttle plate angle is regarded as an input noise, it is not considered in the input vector of the MFRM. Considering $\lambda _{\mathrm{sensor}}(t)$ as the output of the MVEM at the current time instant, t, the input vector of MFRM is composed of the fuel mass flow, and $\lambda$ as

$$\begin{aligned} \mathbf{{x}} = {\left[ {{{\dot{m}}_{fi}}\left( t \right) ,{{\dot{m}}_{fi}}\left( {t - 1} \right) ,\lambda \left( {t - 1} \right) ,\lambda \left( {t - 2} \right) } \right] ^T} \end{aligned}$$

(27)

In Eq. (27), $\lambda _{\mathrm{sensor}}(.)$ is shown as $\lambda (.)$ for notational brevity. In order to start the training process, 1000 training patterns with data collection sample time of 0.01 (sec) were selected from widespread simulation data subjected to bounded random inputs. All training patterns are normalized into the interval [0, 1]. For normalization, one can use (Zhai and Yu 2009)

$$\begin{aligned} {x_{i,normal}} = \frac{{{x_\mathrm{i}} - {x_{i,\min }}}}{{{x_{i,\max }} - {x_{i,\min }}}} \end{aligned}$$

(28)

where $x_{i,\min }$ and $x_{i, \max }$ show the minimum and maximum of a signal $x_\mathrm{i}$ used as training patterns, respectively.

In the MFRM, three Gaussian functions were selected as the membership functions. These membership functions are illustrated in Fig. 3.

Fig. 3

Illustration of the membership functions

Considering the input vector of MFRM as ${\mathbf {x}}\in {\mathbb {R}}^4$, the fuzzified vectors as ${\mathbf {x}}_i \in {\mathbb {R}}^3$ with $i = 1, 2,3,4$, modified fuzzy relational matrix (MFRX) becomes as ${\mathbf {R}} \in {\mathbb {R}}^{3 \times 3 \times 3 \times 3 \times 3}$. Each element in the ${\mathbf {R}}$ can be addressed by

$$\begin{aligned} \mathbf{{R}}\left( {i,j,k,l,m,n} \right) \mathrm{{ }}\quad where \quad \mathrm{{ }}i,j,k,l,m,n = 1,\ldots ,q \nonumber \\ \end{aligned}$$

(29)

In Eq. (29), $q=3$ is the number of membership functions. The computations begin with fuzzification of the input vector in which each element of the input vector changes to its respective fuzzy vector. Considering $x_i$ as the $i{\mathrm{th}}$ element of the input vector ${\mathbf {x}}$, one has

$$\begin{aligned} \mathbf{{x}}_\mathbf{{i}} = \left[ {{s_1}\left( {{x_i}} \right) ,{s_2}\left( {{x_i}} \right) ,{s_3}\left( {{x_i}} \right) } \right] , i = 1,\ldots ,p \end{aligned}$$

(30)

In Eq. (30), $s_1(.)$, $s_2(.)$ and $s_3(.)$ are the mathematical models for the membership functions and $p=4$ is the number of elements in the input vector. As mentioned before, $x_i$ is the $i{\mathrm{th}}$ element of the input vector ${\mathbf {x}}$ and $\mathbf {x}_i$ the fuzzified vector associated with scalar $x_i$. For notational simplicity, we refer to $j{\mathrm{th}}$ element of $\mathbf {x}_i$ as ${\mathbf {x}}_{{\mathbf {i}}} (j)$. The FRC can be preformed through some algebraic calculations as

$$\begin{aligned} \mathbf{{M}} = \sum \limits _{m = 1}^{q = 3} {\mathbf{{R}}\left( {:,:,:,:,m} \right) } \times \mathbf{{x}}_\mathbf{{1}}\left( m \right) \end{aligned}$$

(31)

In Eq. (31), M has one dimension less than R which means $\mathbf{{M}} \in {\mathbb {R}}^{3 \times 3 \times 3 \times 3}$. Accordingly one can get $\mathbf {M_1}$ as

$$\begin{aligned} {\mathbf{{M}}_\mathbf{{1}}} = \sum \limits _{l = 1}^{q = 3} {\mathbf{{M}}\left( {:,:,:,l} \right) } \times \mathbf{{x}}_\mathbf{{2}}\left( l \right) \end{aligned}$$

(32)

which leads to $\mathbf{{M}}_1 \in {\mathbb {R}}^{3 \times 3 \times 3}$. Continuing of FRC leads to

$$\begin{aligned} {\mathbf{{M}}_\mathbf{{2}}} = \sum \limits _{k = 1}^{q = 3} {{\mathbf{{M}}_\mathbf{{1}}}\left( {:,:,k} \right) } \times \mathbf{{x}}_\mathbf{{3}}\left( k \right) \end{aligned}$$

(33)

which leads to $\mathbf{{M}}_\mathbf{{2}} \in {\mathbb {R}}^{3 \times 3}$. With the same procedure, one has

$$\begin{aligned} \mathbf{{b}} = \sum \limits _{j = 1}^{q = 3} {{\mathbf{{M}}_\mathbf{{2}}}\left( {:,j} \right) } \times \mathbf{{x}}_\mathbf{{4}}\left( j \right) \end{aligned}$$

(34)

Finally, the output of the MFRM can be defined as

$$\begin{aligned} y = \frac{{\mathbf{{C}} \times \mathbf{{b}}}}{{\sum \nolimits _{i = 1}^{q = 3} {\mathbf{{b}}\left( i \right) } }} \end{aligned}$$

(35)

For offline training of the MFRM, GDBP algorithm is firstly used. Although no good results could be obtained by GDBP, this algorithm is described here for the sake of completeness and re-appearance of some of formulations in the control unit (optimization). Consider the training error as

$$\begin{aligned} e(t) = y(t) - {y_d}(t) \end{aligned}$$

(36)

In Eq. (36), y(t) is the output of the MFRM and $y_d(t)$ is the output of MVEM which is the desired output for MFRM training. The accumulated error can be defined as

$$\begin{aligned} E\left( z \right) = \frac{1}{2}\sum \limits _{t = 1}^{1000} {{e^2}(t)} \end{aligned}$$

(37)

where z is the iteration number and 1000 defines the total number of training patterns. Training begins with updating matrix ${\mathbf {C}}$ and ${\mathbf {R}}$. Assuming $\mathbf{{C}} = {[{\mathbf{{C}}_i}]_{i = 1,\ldots ,q}}$, based on GDBP algorithm one has

$$\begin{aligned} {\mathbf{{C}}_i}\left( {z + 1} \right) = {\mathbf{{C}}_i}\left( z \right) - \alpha _{GDBP} \frac{{\partial E\left( z \right) }}{{\partial {\mathbf{{C}}_i}\left( z \right) }} \end{aligned}$$

(38)

In Eq. (38), $\alpha _{GDBP}$ is a small positive number called learning rate. Using chain rule, Eq. (38) can be written as

$$\begin{aligned} \frac{{\partial E}}{{\partial {\mathbf{{C}}_i}}} = \frac{{\partial E}}{{\partial e}}\frac{{\partial e}}{{\partial y}}\frac{{\partial y}}{{\partial {\mathbf{{C}}_i}}} \end{aligned}$$

(39)

The first and second terms on the right-hand side of (39) can be easily defined. For the third term, one has

$$\begin{aligned} \frac{{\partial y}}{{\partial {\mathbf{{C}}_i}}} = \frac{{{\mathbf{{b}}_i}}}{{\sum \nolimits _{i = 1}^{q = 3} {{\mathbf{{b}}_i}} }} \end{aligned}$$

(40)

According to GDBP, each element of FRX, ${\mathbf {R}}$, can be update as

$$\begin{aligned} {\mathbf{{R}}_{ijklm}}\left( {z + 1} \right) = {\mathbf{{R}}_{ijklm}}\left( z \right) - \alpha _{GDBP} \frac{{\partial E\left( z \right) }}{{\partial {\mathbf{{R}}_{ijklm}}\left( z \right) }} \end{aligned}$$

(41)

where

$$\begin{aligned} \frac{{\partial E}}{{\partial {\mathbf{{R}}_{ijklm}}}} = \frac{{\partial E}}{{\partial e}}\frac{{\partial e}}{{\partial y}}\frac{{\partial y}}{{\partial {\mathbf{{b}}_i}}}\frac{{\partial {\mathbf{{b}}_i}}}{{\partial {\mathbf{{M}}_{\mathbf{{2}},ij}}}}\frac{{\partial {\mathbf{{M}}_{\mathbf{{2}},ij}}}}{{\partial {\mathbf{{M}}_{\mathbf{{1}},ijk}}}}\frac{{\partial {\mathbf{{M}}_{\mathbf{{1}},ijk}}}}{{\partial {\mathbf{{M}}_{ijkl}}}}\frac{{\partial {\mathbf{{M}}_{ijkl}}}}{{\partial {\mathbf{{R}}_{ijklm}}}} \end{aligned}$$

(42)

For defining the partial derivatives in Eq. (42), one has

$$\begin{aligned} \frac{{\partial y}}{{\partial {\mathbf{{b}}_i}}}= & {} \frac{{{C_i}\left( {\sum \nolimits _n^{q = 3} {{\mathbf{{b}}_n}} } \right) - \mathbf{{C}} \times \mathbf{{b}}}}{{{{\left( {\sum \nolimits _n^{q = 3} {{\mathbf{{b}}_n}} } \right) }^2}}} \end{aligned}$$

(43)

$$\begin{aligned} \frac{{\partial {\mathbf{{b}}_i}}}{{\partial {\mathbf{{M}}_{\mathbf{{2}},ij}}}}= & {} \mathbf{{x}}_\mathbf{{4}}\left( j \right) \end{aligned}$$

(44)

$$\begin{aligned} \frac{{\partial {\mathbf{{M}}_{\mathbf{{2}},ij}}}}{{\partial {\mathbf{{M}}_{\mathbf{{1}},ijk}}}}= & {} \mathbf{{x}}_\mathbf{{3}}\left( k \right) \end{aligned}$$

(45)

$$\begin{aligned} \frac{{\partial {\mathbf{{M}}_{\mathbf{{1}},ijk}}}}{{\partial {\mathbf{{M}}_{ijkl}}}}= & {} \mathbf{{x}}_\mathbf{{2}}\left( l \right) \end{aligned}$$

(46)

$$\begin{aligned} \frac{{\partial {\mathbf{{M}}_{ijkl}}}}{{\partial {\mathbf{{R}}_{ijklm}}}}= & {} \mathbf{{x}}_\mathbf{{1}}\left( m \right) \end{aligned}$$

(47)

In summary, one updates ${\mathbf {C}}$ and ${\mathbf {R}}$ from Eqs. (38) and (41), respectively. This iterative process continues until no meaningful differences can be found in updated ${\mathbf {C}}$ and ${\mathbf {R}}$. The training algorithm is summarized in Algorithm 1.

4.1 MFRM validation data

The offline training process with GDBP was preformed with two constant learning rate until no meaningful changes were detected in the accumulated error. The learning rate was selected as $\alpha _{GDBP} = 0.001$ when the accumulate error was greater than 0.5 and $\alpha _{GDBP} = 0.0001$ for accumulate error less than 0.5. After 20000 iterations of the GDBP, the accumulated error reached $E= 0.37$ and did not change considerably. The history of the accumulated error versus the GDBP iteration index is shown in Fig. 4.

Fig. 4

Accumulated error in offline training with GDBP in batch mode

Afterward, the MFRM of MVEM was tested with new random bounded signals for throttle plate angle and injected fuel mass flow rate. The validation results are shown in Fig. 5. As it is shown in Fig. 5, there is a significant difference between the MFRMs response and that of the MVEM which shows poor training by the GDBP. To improve the offline training, asexual reproduction optimization (ARO), reported in Farasat et al. (2010), Mansouri et al. (2011) is used.

Fig. 5

Validation data of the MFRM trained by GDBP

ARO algorithm is inspired from the budding method of asexual reproduction mechanism. ARO is an individual-based algorithm. Individuals are defined by a set of chromosomes as binary strings made by some binary elements called genes. Each chromosome has a length of $L = l_1 + l_2 + 1$ genes where the first gene is simply showing the sign of that chromosome. The next $L_1$ number of genes represents the integer part of the individual, and the last $L_2$ genes represent the decimal part of the individual (Mansouri et al. 2011).

The basic idea in ARO is competing for survival. To start the algorithm, an individual is randomly initiated in an arbitrary search domain. We call this individual as parent. Afterward, the parent reproduces an offspring called bud by a particular operator called reproduction mechanism which is going to be discussed in the sequel. The parent and its offspring compete to survive according to a fitness function. If the bud wins the competition, its parent will be discarded. Therefore, the parent is replaced with its bud which forms the new parent. If the parent wins, the bud will be discarded and a new bud will be reproduced. This exhaustive search continues until the stopping criteria are satisfied (Mansouri et al. 2011).

The reproduction mechanism in ARO has two steps which can be summarized as follows. First, a copy of parent named larva is produced. Then, a sub-string with g bits where $g \in [1, LI]$ (LI is the length of individual) in larva is randomly chosen. Afterward bits of the sub-string mutate such that in any selected gene, 1 is replaced by 0 and vice versa (Mansouri et al. 2011). The next step in the reproduction mechanism is forming a bud from a larva. At this point, one notes that larva and parent are different only in the selected and mutated g genes which were chosen randomly in generating larva. For producing a bud, for each gene in the mutated g-length of larva, one first generates a random number uniformly distributed in [0, 1]. If this number is less than 0.5, the gene will be selected from the parent. Otherwise, the gene will be selected from larva. This procedure continues until bud is completely formed. The reproduction mechanism is illustrated in Fig. 6.

When bud is formed, its fitness is compared to that of its respective parent based on a selected fitness function. Based on this comparison, the most merited individual, i.e., bud or parent, will be kept as a new parent and the other one would be discarded as explained earlier (Mansouri et al. 2011).

Fig. 6

Reproduction mechanism generating bud individual (Mansouri et al. 2011)

The offline training of MFRM with ARO in batch mode is summarized in Algorithm 2. For training MFRM with ARO, the final values of ${\mathbf {C}}$ and ${\mathbf {R}}$ from offline training with GDBP are chosen as the initial values of individuals. An individual containing $\left( {3 + {3^5}} \right) \times \left( {{l_1} + {l_2} + 1} \right)$ genes was selected. It is worthy of attention that $3 + {3^5}$ is the number of unknowns as the number of the elements of ${\mathbf {C}}$ and ${\mathbf {R}}$. The history of the accumulated error versus the ARO iteration index is shown in Fig. 7. When training was concluded, the MFRM that was trained by ARO was validated by the same inputs used for validation of the trained MFRM by GDBP. As shown in Fig 8, the resulted MFRM can identify the dynamics of the engine with a very good precision. The mean absolute error in validation is only 0.0087 which proves the effectiveness of the training process.

Fig. 7

Accumulated error in offline training with ARO in batch mode

Fig. 8

Validation data of the MFRM trained by ARO

Fig. 9

Schematics of MPC with MFRM

5 MPC

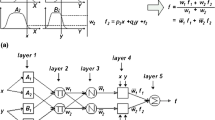
A schematic of MPC system is shown in Fig. 9. The purpose of MPC is generating a time-dependent sequence of control signals which minimizes a performance index throughout $N_u$ future time steps. $N_u$ defines the length of the prediction horizon in MPC and in Fig. 9 it equals $N_u = 5$. MPC uses the trained MFRM of the engine to predict and construct the input vector of the MFRM in the prediction horizon, i.e., $\mathbf {P_i}$ in Fig. 9 where ${\mathbf {i}} = 1, \ldots , 5$. The working mechanism of MPC can be described as follows. Consider ${\dot{m}_{fi}}\left( {{t_0}} \right)$ as the injected fuel mass flow rate at time $t_0$ which is known and $\lambda (t_0- \Delta t)$ as the amount of $\lambda (.)$ which was measured at time $t_0- \Delta t$. During the time interval $t_0$ through $t_0+\Delta t$, all the components of the input vector of MFRM as $\mathbf {P}_0$ in Fig. 9 are known. Now, imagine one needs to form $\mathbf {P_1}$. As shown in Fig. 9, $\mathbf {P_1}$ has four elements which two of them, as the second and forth elements, can be found directly through $\mathbf {P_0}$ which was fully known. The problem is finding the first and third elements of $\mathbf {P_1}$. For this purpose, MPC uses the MFRM for predicting the amount of $\lambda (t_0)$ as the third element of $\mathbf {P_1}$ and $U_1$ is calculated based on an optimization which will be discussed in the sequel. Hence, with a similar procedure, the goal of MPC is constructing all $\mathbf{{P}_i}$s as

$$\begin{aligned} \begin{aligned} {\mathbf{{P}}_i} =&[{\dot{m}_{fi}}\left( {{t_0} + i\Delta t} \right) ,{\dot{m}_{fi}}\left( {{t_0} + \left( {i - 1} \right) \Delta t} \right) ,\\&\lambda \left( {{t_0} + i\Delta t} \right) ,\lambda \left( {{t_0} + \left( {i - 1} \right) \Delta t} \right) ]^T\mathrm{{, }}\ i = 0,\ldots ,{N_u} \end{aligned} \end{aligned}$$

(48)

For this purpose, MPC predicts the amount of $\lambda (t_0+(i+1)\Delta t)$ by using MFRM of the engine. The input vector of MFRM is simply $\mathbf {P_i}$ as in Eq. (48), and the output is $\lambda (t_0+(i+1)\Delta t)$. Therefore, in the interval, $t_0+ (i \Delta t)$ to $t_0+(i+1) \Delta t$, MPC requires the predicted values for both ${\dot{m}_{fi}}(.)$ and $\lambda (.)$ at time samples $t_0+i\Delta t$ ($i=0,\ldots ,N_u$). As mentioned before, the values of $\lambda (t_0+i\Delta t)$ for each $\mathbf {P_i}$ are predicted through the trained MFRM of the engine using $P_{i-1}$ for $i=1,. . .,N_u$. Moreover, the values of ${\dot{m}_{fi}}\left( {{t_0} + i\Delta t} \right)$ are obtained through minimization of the following cost function.

$$\begin{aligned} \begin{aligned} J =&\frac{1}{2}\sum \limits _{i = k}^{k + N_u} {{{\underbrace{\left( {{{\hat{\lambda }}} \left( i \right) - {\lambda _d}\left( i \right) } \right) }_{e\left( i \right) }}^2}} \\&+ \xi \sum \limits _{i = k}^{k + N_u} {{{\left( {{{\dot{m}}_{fi}}\left( i \right) - {{\dot{m}}_{fi}}\left( {i - 1} \right) } \right) }^2}} \end{aligned} \end{aligned}$$

(49)

where ${\hat{\lambda }}$ is the predicted $\lambda$ at time $t_0+(i+1)\Delta t$. $\lambda _d$ is the desired value of $\lambda$ which is the stoichiometric value and it equals 1. $\xi$ shows the control penalizing weight which is a positive number less than one and prevents excessive control expenditure in online control. As one can see from Fig. 9, at each time step MPC generates a sequence of control actions for $N_u$ future time steps. However, only the first element of this sequence is sent to the system at time instant t, i.e., $U_1$. The rest of $U_i$s are stored and used as an initial value for the computations in the next time step.

5.1 Optimization

According to gradient descent algorithm, the vector of control signals in the control horizon, ${\mathbf {U}}=[U_1,U_2,..,U_{N_u}]$ is updated as

$$\begin{aligned} \mathbf{{U}}(z + 1) = \mathbf{{U}}(z) - \eta \frac{{\partial J(z)}}{{\partial \mathbf{{U}}(z)}} \end{aligned}$$

(50)

In Eq. (50), $\eta$ is the learning rate and z shows the iteration number. J(.) is defined in Eq. (49). Assuming $N_u=1$, $\mathbf {U}$ becomes a scalar $U_1$ and the partial derivative in the last term of Eq. (50) is computed as follows.

$$\begin{aligned} \frac{{\partial J}}{{\partial {U_1}}} = \frac{{\partial J}}{{\partial e}}\frac{{\partial e}}{{\partial \hat{\lambda }}}\frac{{\partial {{\hat{\lambda }}}}}{{\partial {U_1}}} + 2\zeta \left( {u\left( i \right) - u\left( {i - 1} \right) } \right) \end{aligned}$$

(51)

In Eq. (51), e(.) is defined in Eq. (49) as $e(i) = {{\hat{\lambda }}} \left( i \right) - {\lambda _d}$. For calculating $\frac{{\partial {{\hat{\lambda }}}}}{{\partial {u_1}}}$, one can use chain rule as

$$\begin{aligned} \frac{{\partial {{\hat{\lambda }}}}}{{\partial {U_1}}} = \frac{{\left( {\sum \nolimits _{i = 1}^{q = 3} {{\mathbf{{C}}_i}\frac{{\partial {\mathbf{{b}}_i}}}{{\partial {U_1}}}} } \right) \left( {\sum \nolimits _{i = 1}^{q = 3} {{\mathbf{{b}}_i}} } \right) - \left( {\sum \nolimits _{i = 1}^{q = 3} {\frac{{\partial {\mathbf{{b}}_i}}}{{\partial {U_1}}}} } \right) \left( {\sum \nolimits _{i = 1}^{q = 3} {{\mathbf{{C}}_i}{\mathbf{{b}}_i}} } \right) }}{{{{\left( {\sum \nolimits _{i = 1}^{q = 3} {{\mathbf{{b}}_i}} } \right) }^2}}}\nonumber \\ \end{aligned}$$

(52)

Through some algebraic manipulations, one can get $\frac{{\partial {\mathbf{{b}}_i}}}{{\partial {U_1}}}$ as

$$\begin{aligned} \frac{{\partial {\mathbf{{b}}_i}}}{{\partial {U_1}}} = \sum \limits _{j = 1}^{q = 3} {\mathbf{{x}}_\mathbf{{4}}\left( j \right) } \sum \limits _{k = 1}^{q = 3} {\mathbf{{x}}_\mathbf{{3}}\left( k \right) } \sum \limits _{l = 1}^{q = 3} {\mathbf{{x}}_\mathbf{{2}}\left( l \right) \sum \limits _{m = 1}^{q = 3} {{\mathbf{{R}}_{ijklm}}{} \mathbf{{A}}\left( m \right) } } \nonumber \\ \end{aligned}$$

(53)

In Eq. (53), $\mathbf {x_i}$s are the vectors generated from fuzzification unit and $\mathbf {A}$ is defined as

$$\begin{aligned} \mathbf{{A}} = \left[ {\frac{{\partial \mathbf{{x}}_\mathbf{{1}}\left( 1 \right) }}{{\partial {U_1}}},\frac{{\partial \mathbf{{x}}_\mathbf{{1}}\left( 2 \right) }}{{\partial {U_1}}},\frac{{\partial \mathbf{{x}}_\mathbf{{1}}\left( 3 \right) }}{{\partial {U_1}}}} \right] \end{aligned}$$

(54)

Also, one has

$$\begin{aligned} \frac{{\partial \mathbf{{x}}_\mathbf{{1}}\left( i \right) }}{{\partial {U_1}}} = \frac{{ - 2\left( {{U_1} - {{\varvec{\tau }}_i}} \right) }}{{2{\varvec{\sigma }}_i^2}}\exp \left( { - \frac{{\left( {{U_1} - {{\varvec{\tau }}_i}} \right) }}{{2{\varvec{\sigma }}_i^2}}} \right) \end{aligned}$$

(55)

In Eq. (55), $\varvec{\tau }$ and $\varvec{\sigma }$ are the vectors that contains the mean and the standard deviation of the Gaussian membership functions, therefore

$$\begin{aligned} {\varvec{\tau }}= & {} {\left[ {{{\varvec{\tau }}_i}} \right] _{i = 1,\ldots ,q}}\nonumber \\ {\varvec{\sigma }}= & {} {\left[ {{{\varvec{\sigma }}_i}} \right] _{i = 1,\ldots ,q}} \end{aligned}$$

(56)

6 Numerical simulation

Before starting the simulations, it is better to modify the desired lambda, $\lambda _d$, to help the control system in the start of the process. For this purpose, one can define the modified desired lambda as

$$\begin{aligned} \lambda _d(t) = 1 - exp(-{\mathscr {C}} t) \end{aligned}$$

(57)

In Eq. (57), ${\mathscr {C}}$ is a constant. As ${\mathscr {C}}$ increases, the behavior of the modified desired lambda resembles the behavior of the step function with step size of 1 which jumps to 1 at $t=0$. To speed up the calculations for online control and also avoid the accumulation of identification errors in long prediction horizon, the prediction horizon is shortened to $N_u=1$. Since the overall control goal is to regulate lambda within $\pm \,1 \%$ of its stoichiometric value, the iterations of the gradient descent algorithm in Eq. (50) are continued until a threshold value, 0.01 for absolute tracking error is fulfilled. Also, the learning rate of the gradient descent optimization is chosen to be 0.001 in Eq. (50). At last, $u_1$ in Eq. (50) should satisfy its upper and lower bounds which are considered one and zero, respectively. It is worthy of attention that MFRM is working with the normalized data. Hence, the output of the MPC unit is a normalized fuel mass flow rate which should be de-normalized with the exact min–max values used for normalization in training.

For a better comparison of the performance of the proposed fuzzy MPC with that of the recent applications, the same profile of throttle plate angle in Sardarmehni et al. (2013a), Zhai and Yu (2009) subjected to $\pm \, 10\%$ uncertainty is used in the simulations. Figures 10 and 11 show the profile of the throttle plate angle with $\pm \,10\%$ uncertainty and the simulation results of the proposed fuzzy MPC within the lambda window, respectively. In Fig. 11, the mean absolute tracking error for desired lambda tracking is 0.0418. By neglecting the first 2 s of the simulation, the mean absolute tracking error becomes 0.00207 which shows the good performance of the MPC system.

Fig. 10

Throttle plate angle profile with $10 \%$ uncertainty (Zhai and Yu 2009)

Fig. 11

Simulation results of the MPC with $10\%$ input uncertainty

To evaluate the robustness of the MPC system to larger uncertainties, the uncertainty on the throttle plate angle is increased to $25\%$ as shown in Fig. 12. The performance of the fuzzy MPC system with $25 \%$ uncertainty is shown in Fig. 13. In spite of the large uncertainty imposed to the system, the fuzzy MPC system demonstrates a good performance. The mean absolute tracking error of this simulation is 0.0447 which confirms the robustness of the controller in rejecting moderate disturbances. By neglecting the first 2 s of the simulation, the mean absolute tracking error becomes 0.00481.

Fig. 12

Throttle plate angle profile with $25\%$ uncertainty (Zhai and Yu 2009; Sardarmehni et al. 2013a)

Fig. 13

Simulation results of the MPC with $25\%$ input uncertainty

7 Conclusion

A fuzzy model predictive control strategy based on modified relational fuzzy theory was developed for nonlinear control of normalized air-to-fuel ratio in spark ignition internal combustion engines. To produce the simulation data, mean value engine model for a spark ignition internal combustion engine equipped with exhaust gas recirculation was simulated. Initially, the fuzzy model was trained with offline engine data subjected to random inputs of throttle plate angle and injected fuel mass flow rate by gradient descent back propagation algorithm. However, the gradient descent back propagation algorithm did not demonstrate good results in validation of the fuzzy model after training. Hence, a model-free optimization algorithm based on asexual reproduction method was used to train the fuzzy model of the engine. The resulted fuzzy model was validated with a negligible error. In the control unit, a model predictive control system was developed based on nonlinear minimization of the cost function by online gradient descent algorithm. The robustness of the model predictive control system was evaluated through simulations.