Comparison of metamodeling techniques in evolutionary algorithms

Abstract

Although researchers have successfully incorporated metamodels in evolutionary algorithms to solve computational-expensive optimization problems, they have scarcely performed comparisons among different metamodeling techniques. This paper presents an in-depth comparison study over four of the most popular metamodeling techniques: polynomial response surface, Kriging, radial basis function neural network (RBF), and support vector regression. We adopted six well-known scalable test functions and performed experiments to evaluate their suitability to be coupled with an evolutionary algorithm and the appropriateness to surrogate problems by regions (instead of surrogating the entire problem). Notwithstanding that most researchers have undertaken accuracy as the main measure to discern among metamodels, this paper shows that the precision, measured with the ranking preservation indicator, gives a more valuable information for selecting purposes. Additionally, nonetheless each model has its own peculiarities; our results concur that RBF fulfills most of our interests. Furthermore, the readers can also benefit from this study if their problem at hand has certain characteristics such as a low budget of computational time or a low-dimension problem since they can assess specific results of our experimentation.

1 Introduction

Evolutionary algorithms (EAs) gather a set of algorithms, inspired by neo-Darwinism, that have been successfully applied to an important variety of difficult optimization problems.

In many science and engineering problems, researchers have used computer simulations to avoid expensive physical experiments with the aim of improving the quality and performance of engineered products and devices, but using a fraction of the needed effort. Analogously, researchers have proposed a number of EAs that make use of metamodels¹ to solve computational-expensive optimization problems (Nain and Deb 2002; Gaspar-Cunha and Vieira 2005; Voutchkov and Keane 2006; Isaacs et al. 2007).

Although distinct metamodeling techniques can produce different solutions, little emphasis has been placed on exploring their behavior when coupled to EAs. Even when we understand the scarcity of comparative works, since such an exploration would require gaining deep knowledge on each approach, it is important to note that some approaches are bound to specific domains. Therefore, it is necessary to carry out comparative studies among metamodeling techniques before selecting one.

In this regard, Carpenter and Barthelemy (1993) adopted several test problems with up to 15 decision variables to compare the accuracy of polynomial regression (PRS) and artificial neural networks (ANN) to be used as metamodeling approaches. In their study, although PRS required a lower construction time, both approaches showed a similar performance according to their achieved number of function evaluations and their required parameters. Therefore, they stated that the selection would depend on the user preferences.

Shyy et al. (2001) compared the accuracy of a PRS, a back propagation ANN, and a radial basis function neural network (RBF) approaches, concluding that PRS and RBF performed similarly in several problems with up to 11 variables.

Rasheed et al. (2002) adopted several test problems with up to 16 decision variables to compare the behavior of PRS, RBF, and Quickprop ANN when they were coupled to a genetic algorithm (GA). Such a comparison showed that PRS had the fastest time for building and executing the metamodel. Additionally, it did not require any parameter to be fine-tuned. For these reasons, the authors agreed in favor of PRS.

Willmes et al. (2003) compared the behavior of ANN and Kriging (KRG) methods when they are coupled to an evolution strategy (ES) with covariance matrix adaptation (CMA) (Hansen and Ostermeier 2001) in three scalable test problems with up to 50 decision variables. However, there is no clear conclusion about which metamodel performed best.

Simpson et al. (1998) compared the performance of KRG and PRS with respect to the design of an aerospike nozzle with three decision variables. According to their results, both approaches were comparable with respect to their accuracy.

Jin et al. (2001) compared the accuracy, robustness, efficiency, transparency, and simplicity of PRS, multivariate adaptive splines, RBF, and KRG, using several test problems with up to 16 decision variables. The conclusion of their comparison was that PRS behaved the best in low-dimension problems, while the RBF approach was the best when dealing with high-dimension problems. It is worth noting that although this paper compares several metamodeling approaches, they were not incorporated into an EA.

Although the above proposals selected the best metamodeling technique from a comparison methodology, some of them were evaluated based only on a small group of metamodeling techniques, adopting a reduced set of test problems, or taking into account only a single criterion (most works selected accuracy as their main criterion).

Furthermore, they usually omit measuring two important factors: the performance with the increase in the dimensionality and the suitability of the metamodel to be combined with population-based metaheuristics. Moreover, most of the existing algorithms used a single metamodel to approximate the whole search space of the problem, even though results from certain researchers (Isaacs et al. 2007; Georgopoulou and Giannakoglou 2009; Pilat and Neruda 2013) suggest that using metamodels to approximate specific regions of the search space produces an improvement in the accuracy of the approximation.

In Díaz-Manríquez et al. (2011), we fine-tuned the parameters of four metamodeling techniques using accuracy as performance measure. Then, we evaluated the metamodels’ accuracy, robustness, efficiency, scalability, and suitability when they were combined with an EA. From the results, we found that accuracy and suitability were in conflict, in the sense that not always the most accurate metamodel produced the best results when it was coupled to a EA. On the other hand, we found that our ranking preservation indicator, which measures the percentage of solutions in the metamodel that preserves the hierarchy according to the original objective function, could be a better measure to evaluate the performance of a metamodel.

This paper compares the results achieved by the metamodels fine-tuned with the accuracy indicator (presented in  Díaz-Manríquez et al. 2011) with respect to the results produced by ranking preservation fine-tuned approaches. Such a new parametrization will endorse the selection of the metamodeling technique. Then, we will explore its capabilities to surrogate the entire problem (also known as the global surrogate model, or GM for short) with respect to surrogating the problems by regions (also known as the local surrogate model or LM for short). It is worth noting that unlike the results presented in Díaz-Manríquez et al. (2013), the baseline approach used to analyze the use of GM and LM was fine-tuned trough the ranking preservation indicator.

The remainder of this paper is organized as follows: Section 2 gives a brief overview of the metamodeling techniques commonly used in the literature. Section 3 presents our experimental setting. We divided our experimentation into four parts: Section 4 introduces our first experiment where besides fine-tuning the parameters of the adopted metamodeling approaches with respect to the accuracy performance measure, it compares their obtained accuracy, robustness, and scalability. Our second experiment, which is shown in Sect. 5, measures the suitability of each technique to be incorporated into an EA. Section 6 introduces our third experiment. It presents the use of ranking preservation indicator to fine-tuning the parameters of the adopted metamodeling approaches. We compare the results obtained in this section with respect to that obtained with the accuracy fine-tuned methods. Our fourth experiment, presented in Sect. 7, measures the efficiency of the compared approaches. Then, Sect. 8 presents three different approaches for using LM, analyzes their parameters, and compares their results with respect to the use of GM. Finally, Sect. 9 summarizes our main conclusions and outlines future work.

2 Background

A metamodel is an approximation of a simulation used to construct simpler and lower computational cost models; if the original simulation is represented as $f(\mathbf {x})$, and the metamodel is represented as $f'(\mathbf {x})$, then, $f'(\mathbf {x})=f(\mathbf {x})+e(\mathbf {x})$, where $e(\mathbf {x})$ is the approximated error. The internal behavior of $f(\mathbf {x})$ does not need to be known (or understood); only the input/output behavior is important. A model is constructed based on the response of the simulator to a limited number of intelligently chosen data points. Metamodels generate simpler representations that capture relations between the relevant information of the input and output variables and not in the underlying process.

Among the techniques to create metamodels, we have rational functions (Press et al. 2007), radial basis functions (Hardy 1971), Kriging models (Sacks et al. 1989), support vector machines (Vapnik 1998), polynomial regression (Myers and Anderson-Cook 2009), and splines (Schumaker 2007). Below, we review the most common approaches for constructing approximate models:

2.1 Polynomial approximation models

The response surface methodology (RSM) (Myers and Anderson-Cook 2009) employs statistical techniques for regression and analysis of variance to obtain a minimum variance of the responses.

The simplicity of polynomials makes them a good approach to approximate most polynomial response surfaces (PRS).

A polynomial in the coded inputs $\mathbf {x}_1,\mathbf {x}_2,\ldots ,\mathbf {x}_n$ (n data in the training set) is a function which is a linear aggregate (or combination) of powers and products of the input.

The polynomial model is usually written in matrix notation, $\hat{y}^{(p)}=\beta ^T \mathbf {x}^{p}$, where $\beta$ is the vector of coefficients to be estimated, and $\mathbf {x}^{p}$ is the vector corresponding to the form of the $x_{1}^{(p)}$ and $x_{2}^{(p)}$ terms in the polynomial model.

To estimate the unknown coefficients of the polynomial model, both the least-squares method (LSM) and the gradient method, can be used. However, both approaches require the number of samples to be equal to the number of coefficients.

PRS can also be built using stepwise regression (Draper and Smith 1981). The basic procedure for stepwise regression involves (1) identifying an initial model, (2) iteratively “stepping”, that is, repeatedly altering the model at the previous step by adding or removing a predictor variable in accordance with the “stepping criterion”, and (3) terminating the search when a specified maximum number of steps has been reached.

In practice, we can often proceed by supposing that, a polynomial of first or second degree might represent adequately the real function over limited regions of the design space. Although higher-order polynomials can be used, instabilities may arise (Barton 1992), or it can be highly difficult to take enough sample data to estimate the coefficients of the polynomial equation (particularly in high dimensions). This work considers second degree PRS models.

2.2 Kriging-DACE

Kriging (KRG) (Matheron 1963) is a spatial prediction method that belongs to the group of geo-statistical methods. It is based on minimizing the mean squared error, and it describes the spatial and temporal correlation among the values of an attribute.

The design and analysis of computer experiments (DACE) is a parametric regression model developed by Sacks et al. (1989), which is an extension of the KRG approach to be able to manage three or more dimensions.

The DACE model can be expressed as a combination of a known function $a(\mathbf {x})$ (e.g., polynomial function, trigonometric series) and a Gaussian random process $b(\mathbf {x})$ that is assumed to have mean zero and covariance:

$$\begin{aligned} \text{ E }(b(\mathbf {x}^{(i)}),b(\mathbf {x}^{(j)}))= & {} \text{ Cov }(b(\mathbf {x}^{(i)}),b(\mathbf {x}^{(j)}))\nonumber \\= & {} \sigma ^ { 2 } \mathcal {R}(\theta ,\mathbf {x}^{(i)},\mathbf {x}^{(j)}), \end{aligned}$$

(1)

where $\sigma ^{2}$ is the process variance of the response and $\mathcal {R}(\mathbf {\theta },\mathbf {x}^{(i)},\mathbf {x}^{(j)})$ is the correlation function with parameters $\mathbf {\theta }$. Among the different types of correlation models, we have Gaussian, cubic, exponential, linear, spherical, and splines.

In the downside of KRG, we have that besides its model construction can be very time-consuming, the estimation of the parameters requires to solve an n-dimensional optimization problem (where n is the number of variables in the design space), which can also be computationally expensive.

2.3 Radial basis function neural network

The radial basis function method (RBF) was proposed by Hardy (1971). An RBF is a real-value function whose value depends only on the distance from the input to the center of the neuron, so that $\phi (\mathbf {x})=\phi (||\mathbf {x}||)$ or alternatively on the distance from some other point c, called a center. Any function $\phi$ that satisfies the property $\phi (\mathbf {x})=\phi (||\mathbf {x}||)$ is a radial function. The norm is usually the Euclidean distance, although other distance functions can be used.

Typical choices for the RBF include linear, cubic, multi-quadratic, or Gaussian functions.

An RBF commonly has three layers: an input layer with the identity function, a hidden layer with non-linear RBF activation functions, and a linear output layer. The output, $\varphi :\mathbb {R}^{n}\rightarrow \mathbb {R}$, of the network is thus $\varphi (\mathbf {x})=\sum \nolimits _{i=1}^{N}w_{i}\phi (||\mathbf {x}-\mathbf {c}_{i}||)$.

In order to adapt the RBF network for a particular task, three parameters need to be fine tuned: the weights $w_i$, the center vector $\mathbf {c}_i$, and the RBF width parameters $\beta _i$. In this work, the center vector was tuned according to the centers of a clustering technique (there are as many clusters as RBFs). The width parameter was tuned averaging the distance from its own center to its two closest RBFs. Finally, in this paper we adopted the Gaussian function to serve as RBF.

Table 1 Important features of the adopted test problems

2.4 Support vector regression

Support vector machines (SVMs) draw inspiration from statistical learning theory (Vapnik 1998). An SVM is a set of related supervised learning methods which analyzes data and recognizes patterns. An SVM constructs a hyperplane or a set of hyperplanes in a high-dimensional space that can be used for classification, regression, or other tasks.

An SVM maps its inputs to a larger space; however, the cross products may be computed easily in terms of the variables in the original space making the computational load reasonable. The cross products in larger spaces are defined in terms of a kernel function K(x, y), which can be selected to suit the problem.

Through the introduction of an alternative loss function, an SVM can also be applied to regression problems.² The loss function must be modified to include a distance measure. In this work, we adopted the Gaussian RBF as kernel function. Moreover, C, $\gamma$ and $\epsilon$ were fine-tuned using a methodology explained later.

3 Experimental settings

Evaluating the performance of a metamodeling technique is not an easy task. Most approaches only consider the accuracy in performing the selection (Carpenter and Barthelemy 1993; Shyy et al. 2001; Simpson et al. 1998; Giunta and Watson 1998). However, other approaches suggest the use of multiple criteria (e.g., the robustness, the efficiency, or the simplicity) for assessing the quality of a metamodel (Jin et al. 2001). The success of a technique not only depends exclusively on the accuracy, but also on several factors, such as the parameters of the metamodeling technique, the dimensionality of the problem, the data sampling technique, etc.

To evaluate the performance of the compared approaches, six scalable unconstrained global optimization test functions were taken from the specialized literature (De Jong 1975; Rastrigin 1974; Bäck 1996; Schwefel 1981). The test functions were selected according to both, the shape of the search space, and the number of local minima, i.e., they contain characteristics that are representative of what can be considered “difficult” in global optimization. A summary of such features is given in Table 1. Since all the adopted problems can be scaled in the number of decision variables, we evaluate them using the following problem sizes: $v=\{2,4,6,8,10,15,20,25,50\}$. If an instance has more than 15 variables ($v>15$), we list it as a high-dimension instance. Contrariwise, if it has less than 15 variables, we named it as low-dimension ($v\le 15$).

We gathered our research from four main experiments. The first experiment besides fine-tuning the parameters of the adopted metamodeling approaches, compares their accuracy, robustness, and scalability. Our second experiment measures the efficiency of the compared metamodeling approaches, while our third experiment measures their suitability to be incorporated into an EA. Finally, our fourth experiment is intended to clarify the advantages and disadvantages of local metamodels with respect to global metamodels.

4 Experiment 1: fine-tuning, accuracy, robustness, and scalability

We performed a full factorial design of the most widely used parameters to avoid affecting the techniques with a poor parameter tuning. Therefore, we discretized the parameters used by each technique as follows:

• PRS Degree of the polynomial $=$ 2, technique for constructing the regression $=$ {traditional, stepwise}.

• KRG Correlation function $=$ {Gaussian, cubic, exponential, linear, spherical, splines}.

• RBF Neurons in the hidden layer $=$ {3–100} with a step size of 1, Radial basis function=Gaussian, center vector were set through the k-means algorithm, the widths of each RBF were calculated according to the average distance between the two closest centers.

• SVM $C=${$2E^{-5}-2E^{15}$}, $\gamma =${$0.1-2$}, $\epsilon =${$2E^{-10}-2E^{5}\}$ with a step size of 0.1, and a Gaussian RBF kernel function.

We executed the different variants 31 times on all problem sizes of each test problem according to the performed full factorial design and processed the results with respect to the achieved accuracy. The accuracy was measured according to the coefficient of determination ($R^2$) performance measure (Jin et al. 2001).

$$\begin{aligned} R^2=1-\frac{\sum _{i=1}^{\mathrm{NV}}\left( y_{i}-\hat{y}_{i}\right) ^{2}}{\sum _{i=1}^{\mathrm{NV}}\left( y_{i}-\bar{y}_{i}\right) ^{2}}=1-\frac{\mathrm{MSE}}{\mathrm {Variance}}, \end{aligned}$$

(2)

where NV is the size of the validation dataset, $\hat{y}_{i}$ is the predicted value for the input i, and $y_i$ is the real value; $\bar{y}$ is the mean of the real values. The mean square error (MSE) measures the difference between the estimator and the real value. In this metric, larger values of $R^2$ are preferred since this represents a more accurate metamodel.

Then, we selected two different set of parameters: (1) the parameters that produced the best average accuracy considering all problems and instances, and (2) the parameters that behaved best for each problem and on each instance size. We called them best overall settings (BOS) and best local settings (BLS), respectively. Since BLS involves a different setting for each approach on each test function, we did not show the obtained results because of their length. However, BOS parameters are shown below:

• PRS Degree of the polynomial $=$ 2, technique for construct the regression $=$ {stepwise}.

• KRG Correlation function $=$ {Exponential}.

• RBF Number of neurons in the hidden layer $=$ {6}.

• SVR $C=${$2E^{10.5}$}, $\gamma =${0.2}, $\epsilon =${$2E^{-2.5}$}.

Then, we measured the accuracy, robustness, and scalability of the compared approaches according to the following methodology:

• 1. We create a training dataset using Latin hypercubes³ (McKay et al. 1979) with 100 points (a size of 100 was selected since most EAs typically handle this population size).

• 2. We train each technique (PRS, KRG, RBF, and SVR) with the training dataset created in the previous step.

• 3. We use Latin hypercubes to create a validation dataset with the double of query points of the training dataset (200).

• 4. We predict the validation dataset with each metamodel.

• 5. We compute the performance measure for the following adopted criteria:

  • Accuracy For accuracy, we refer to the capability of the technique to have a prediction close to the real objective function. The previously defined $R^2$ performance measure was used to achieve such a goal.

  • Robustness This refers to the capability of a technique to achieve good accuracy on adopted test problems. We measured the robustness of a technique by averaging its obtained accuracy in the adopted test cases.

  • Scalability The scalability refers to achieving good accuracy even when the number of variables increases.

4.1 Analysis of results

We used boxplot graphics to present our results since they simultaneously show different descriptive measures that facilitate the comprehension of many competing approaches. In these graphics, the median (second quartile) of the plotted data is shown with a straight line inside the box. The average accuracy of the technique is shown with a diamond. The beginning and end of the box indicate the first and third quartiles, respectively. Therefore, we prefer smaller boxes because they represent a more robust behavior.

Fig. 1

Boxplots graphics obtained from the application of $R^2$ metric to the results produced by PRS, KRG, RBF, and SVR. a, b Unimodal and multimodal, while c gathers the results for all the adopted test functions

Since multimodal problems usually induce erratic behavior in probabilistic-based techniques, we divided our test functions according their modality. Figure 1 displays the obtained results according the application of the $R^2$-metric to the solutions produced by each metamodeling technique using the two adopted set of parameters BLS and BOS.

Figure 1a, b shows the average results considering unimodal and multimodal test functions, respectively. Finally, the average results gathering all the adopted test functions are shown in Fig. 1c. These results indicate that BOS and BLS induced a similar behavior in the adopted metamodeling approaches regardless of whether they are unimodal or multimodal. Therefore, we will use BOS settings in our remaining experiments.

Also, when we analyzed the size and position of the box of each boxplot, we found that RBF behaved slightly better than KRG, and both outperform SVR. In these graphics, we also found that PRS produced the worst results according to $R^2$ and our robustness performance measures.

To corroborate our previous results, we separately averaged the results obtained by the studied algorithms on each test function, and plotted them in Fig. 2. This experiment confirms the lack of accuracy of PRS even in low-dimension problems. PRS was capable of creating a surrogate model for step and ackley functions for up to eight variables (shown in Fig. 2a, d, respectively), but it had the poorest accuracy among the tested approaches.

Although PRS improved its own performance in sphere, rosenbrock, and rastrigin when using two, four, eight, and ten variables (see Fig. 2b, c, e, respectively), it has the poorest results among the compared metamodels. PRS behaved reasonably well only for schwefel, which is shown in Fig. 2f (where it could approximate the problem in all the sizes tested, and showed good performance even for the 50 variables instance).

The SVR approach had an inconsistent behavior in step and ackley when using two, four, six, eight, and ten variables (shown in Fig. 2a, d). However, it performed considerably better than PRS, and it improved its behavior for the rest of the test functions. Although KRG had a similar behavior to SVR for the sphere (see Fig. 2b), rastrigin (see Fig. 2e), and schwefel functions (see Fig. 2f), it outperformed SVR in low-dimension instances when optimizing the rosenbrock test function (shown in Fig. 2c). KRG had an impressive performance in low-dimension instances on all the tested problems since it outperformed the other techniques. However, its performance decreased after 15 variables in all test functions as we can see in Fig. 2.

Contrary to the KRG behavior, RBF had an average performance with the initial sizes of all problems, as is easily seen in Fig. 2, but it was capable of maintaining its performance according to the $R^2$-metric in high-dimension problems.

Fig. 2

Average values of the application of the $R^2$ metric to the produced results by PRS, KRG, RBF, and SVR approaches on each problem. The x-axis shows the number of variables, while the y-axis shows the $R^2$ metric value obtained by each metamodeling technique. This figure intends to clarify the accuracy robustness and scalability of the adopted approaches

Figure 3 shows the performance of the compared techniques on the adopted functions. KRG was the technique that showed the best performance when working with low-dimension instances ($v<15$), while RBF had the best performance with high-dimension instances. The results obtained by SVR show that the behavior of this technique was just behind KRG. Finally, PRS was the technique with the worst overall performance.

Fig. 3

Average values of the application of the $R^2$ metric to the produced results by PRS, KRG, RBF, and SVR approaches on all problems. The x-axis shows the number of variables, while the y-axis shows the $R^2$ metric value obtained by each metamodeling technique. This figure intends to clarify the accuracy robustness and scalability of the adopted approaches

From the above results, we were able to identify an instance size (with approximately ten variables) where the performances of KRG and RBF are intersected. This intersection can be used as a reference point to choose the approach to be incorporated into an EA according to the dimensionality of the problem at hand (KRG in low-dimension problems, and RBF in high-dimension problems).

According to the discussed results, RBF is the most efficient approach among the reviewed ones. However, when we search for the most accurate approach, we can say that KRG is the best approach to be used in low-dimension problems (followed by SVR). On the other hand, RBF is the best approach in high-dimension problems (followed by SVR). However, if we want to select a single approach for both low- and high-dimension problems, we suggest using RBF, since our results indicate that this approach was the less affected with the increase in the dimensionality. Therefore, we concur that this approach is also the most scalable and robust approach.

5 Experiment 2: suitability

The suitability refers to the ability of an EA to optimize the fitness landscape produced by a specific surrogate model.

We propose two approaches to measure this criterion. For the first approach, we used a differential evolution (DE) algorithm (Storn and Price 1997) to optimize the created metamodel at hand. Then, we computed the distance from the best solution (obtained by the DE algorithm) to the optimum of the original test function. The DE used is a DE/rand/1/bin, with a population size of 100, a $\mathrm{CR} = 0.8$, a $F = 0.5$, and the algorithm was executed for 100 iterations.

Since the optimum solution on each test function is known, we can say that a metamodel approach A induces better behavior than another approach B into an EA; this is if the best solution found when optimizing metamodel A is closer to the optimum than an obtained solution when it is optimized with approach B.

The second approach was motivated by the manner with which EAs select solutions. They usually compare two solutions to select the one with the best fitness value. Therefore, it would be interesting to complete the following steps: (1) build a metamodel, (2) produce a number of distributed points with it, and (3) compare each pair of the generated points using both the surrogate function and the original function. We can say that a metamodel approach is more suitable to be used with an EA if it best preserves the comparative relation with respect to the original function. In order to quantify this assumption, we propose measuring the ranking preservation (RP) indicator.

RP refers to the ability of a metamodel to maintain the same rank of the query points with respect to the original function. A metamodel $f'(x)$ has a perfect ranking preservation under the original function f(x) if

$$\begin{aligned} \forall x,y \in \mathcal {F}&:(f(x)<f(y)\Rightarrow f'(x)<f'(y))\nonumber \\&\vee (f(x)>f(y)\rightarrow f'(x)>f'(y))\\&\vee (f(x)=f(y)\Rightarrow f'(x)=f'(y)),\nonumber \end{aligned}$$

(3)

where $\mathcal {F}$ is the feasible region of the problem. Therefore, the performance measure can be defined as follows:

$$\begin{aligned} \mathrm{RP}=\left( \sum _{i=1}^{\mathrm{ND}}\sum _{j=i+1}^{\mathrm{ND}}h(i,j)\right) \Bigg / {\mathrm{ND}\atopwithdelims ()2}, \end{aligned}$$

(4)

where h(i, j):

$$\begin{aligned} h(i,j) = \left\{ \begin{array}{ll} &{}\quad \text{ if }( (f(i)<f(j)\wedge f'(i)<f'(j))\\ 1 &{}\quad \vee (f(i)>f(j)\wedge f'(i)>f'(j))\\ &{}\quad \vee (f(i)=f(j)\wedge f'(i)=f'(j)))\\ 0 &{}\quad \text{ otherwise }, \end{array} \right. \end{aligned}$$

(5)

where N refers to the number of solutions to validate the model. The adopted methodology to measure the RP consisted of training each metamodel with 100 solutions and then measuring the RP using 1000 solutions. The procedure was applied to the six test problems previously introduced with their full range of instance sizes ($v=\{2,4,6,8,10,15,20,25,50\}$).

For this performance measure, larger RP values are preferred. Since this value is normalized between zero and one, we will prefer the solutions closer to one.

5.1 Analysis of results

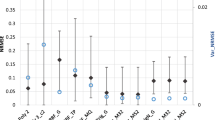
Figure 4 shows the results obtained by our first proposal to measure the suitability. It indicates that although KRG and SVR approaches were competitive, RBF was the approach that induced the best performance for the adopted EA. However, since in general, SVR, KRG, and RBF showed a similar performance in most of the problems, this experiment suggests that an EA (in this case a DE) can produce acceptable results even with a metamodel that is not very accurate.

Fig. 4

Distance from the best solution found by a tuple (metamodel, DE) to the optimum of the problem at hand. The x-axis shows the number of variables, while the y-axis shows the distance of the best solution found by each model with respect to the optimum

Figure 5 displays a boxplot graphic of the general behavior of the approaches with respect to RP on all test problems. From this figure, we can see that the RBF produced the best behavior according to RP since its boxplot is closest to one and also presents the smallest deviation. Therefore, we conclude that RBF was the approach that induced the best RP. Figure 6 shows the behavior of RP with respect to the number of variables of the adopted problems while Fig. 7 illustrates the results of the RP performance measure in all the adopted problems by instance size. From both figures, we observed that RBF was very consistent in all problem sizes. Moreover, in most of the problems, the performance of PRS up to 20 variables was better than the performance of SVR. Finally, KRG presented the worst performance with respect to the increase in the dimensionality.

It is worth noting that the higher the RP value, the lower the probability to add a false optimum to the problem. This feature is a very important characteristic when optimizing a metamodel.

With this analysis of results, we can state that even if a metamodel had a poor performance according to $R^2$ metric but a good performance according to our RP metric, one could expect good behavior in the metaheuristic (in this case we used a DE). However, if the metamodel had good performance on $R^2$ metric but a bad RP performance, then we do not have elements to predict its behavior in the optimization process. RBF was the metamodeling approach that behaved best according to this experiment.

Fig. 5

Boxplots summarizing the ranking preservation of a metamodel with respect to the original test function of the problem at hand. Higher values of this y-axis are preferred

6 Experiment 3: suitability with RP-based fine-tuning

Although the results obtained in our second experiment (shown in Sect. 5) indicate that our adopted accuracy measure does not reflect properly the behavior of the adopted metamodels when we they are incorporated within an EA, we found that the RP performance measure does. Therefore, we decided to perform the fine-tuning process all over again, but using RP as performance measure.

The fine-tuning process was undertaken on the same parameters of our first experiment (shown in Sect. 4). After analyzing the results, we selected two different set of parameters: (1) the parameters that produced the best average accuracy considering all problems and instances (the best overall settings, or BOS-RP for short), and (2) the parameters that behaved best for each problem and on each instance size (best local settings or BLS-RP for short), respectively. However, since the results of BOS-RP and BLS-RP are similar, we decided to adopt BOS-RP for simplicity. Below, we present these parameters:

• PRS Degree of the polynomial $=$ 2, technique for construct the regression $=$ {stepwise}.

• KRG Correlation function $=$ {Exponential}.

• RBF Number of neurons in the hidden layer $=$ {15}.

• SVR $C=${$2E^{12}$}, $\gamma =${0.6}, $\epsilon =${$2E^{-5.0}$}.

The new parameter-tuning produced a different set parameters for RBF and SVR. Therefore, we will focus exclusively on these two approaches in the remaining of this experiment.

Fig. 6

Behavior of each metamodeling technique on each size of the adopted functions according to the ranking preservation. The x-axis shows the number of variables, while the y-axis shows the ranking preservation achieved for each metamodeling technique

Fig. 7

Average behavior on all the adopted problems by each metamodeling technique according to the ranking preservation. The x-axis shows the number of variables, while the y-axis shows the ranking preservation achieved for each metamodeling technique

Then, we optimized the created metamodel at hand in a DE algorithm and computed the distance from the best solution to the optimum of the original test function to identify the metamodel that produces the best behavior in our implemented EA (similar to the first approach of our second experiment).

6.1 Analysis of results

Similarly to our experiment 1 (shown in Sect. 4), we divided our test functions according their modality. Figure 8 displays the obtained results according the application of the RP-metric to the solutions produced by each metamodeling technique using the two adopted set of parameters BLS and BOS.

Figure 8a, b shows the average results considering unimodal and multimodal test functions, respectively. Finally, the average results gathering all the adopted test functions are shown in Fig. 8c. Besides, these results indicate that BOS-RP and BLS-RP induced a similar behavior in the adopted metamodeling approaches regardless of whether they are unimodal or multimodal; when we compare these results (see Fig. 8c) with respect to those obtained in the second approach of our second experiment (shown in Fig. 7), we can clearly realize that the new results outperform the previous ones. From these results we can observe that RBF improved significantly as it consistency topped the best result of our adopted performance measure. Additionally, we can observe that 75 % of the solutions that SVR produced on this new experiment outperformed the median of the results of our previous one.

Figure 9 gathers the results produced by the execution of the DE on each metamodel. Since we are interested in evaluating the results produced by SVR and RBF (the approaches with different parameters), each graphic only show both results, as well as their counterparts of our previous experiment. In order to differentiate the results, we added ‘RP’ postfix to the labels of the new results.

Figure 9e shows the comparison of results of when the approaches solved Rastrigin test function. From this figure, we realized that SVR worsen its performance when it solved instances up to 25 variables. However, it produced similar results with 50 variables. On the other hand, the new parametrization of RBF slightly outperformed the results obtained with the previous one.

Fig. 8

Boxplots graphics obtained from the application of RP metric to the results produced by PRS, KRG, RBF, and SVR. a, b Unimodal and multimodal, while c gathers the results for all the adopted test functions

Figure 9d presents the results obtained in Ackley test function. It is easy to identify on this figure that RBF improved its performance with the new tuning, since it outperform our former experiment on all problem sizes. Moreover, SVR also presented a noticeable improvement since in our former study it presented an undesirable behavior with low-dimensional problems. Additionally, this approach improved the distance measure on every problem size.

The results shown in Figure 9b, c, f indicate that the new tuning of RBF and SVR induced a slight improvement than the former tuning in Rosenbrock, Schwefel, and sphere test functions, respectively.

Finally, the results obtained in the step test problem, presented in Fig. 9a, show that RBF and SVR induce a slight improvement for instances with 25 variables and fewer, but only RBF enhanced its results for the 50 variable instance.

The new parameters’ tuning eases the comparison of results when we consider all the adopted test functions, since RBF induced the best results of all the compared metamodeling approaches across all the instance sizes. Also, although SVR improved its over all performance, it could not outfperform the results produced by KRG in all problems. Similar to our previous experiment, PRS produced the worst results in this new experiment.

Fig. 9

Distance from the best solution found by a tuple (metamodel, DE) to the optimum of the problem at hand. The metamodel was fine-tuned with the $R^2$ or with RP performance measure. The x-axis shows the instance size, represented by its number of variables, while the y-axis shows the distance of the best solution found by each model with respect to the optimum

7 Experiment 4: efficiency

Our fourth experiment measures the efficiency of the adopted approaches. In order to calculate efficiency, we measured the time employed to construct a metamodel with 100 points and the required time that it takes to predict 100 other responses. All the experiments were executed in a computer Intel Core i3 with 2.6 GHz and 4 GB de RAM. The results of this experiment are shown in Fig. 10. These results indicate that the time consumed by KRG is relatively large, mainly produced by the embedded optimization method used to find the best values of its parameter ($\theta$). On the other hand, SVR and RBF required almost constant time in this experiment. Finally, the expended computational time for PRS and KRG was very similar. In conclusion, if the metamodel needs to be constructed several times in the optimization process, we recommend using a metamodeling technique that requires a small amount of time, i.e., RBF or SVR. However, if the metamodel only needs to be constructed a single time, any metamodeling technique can be used.

Fig. 10

Average execution time required by each metamodel when training and predicting the adopted problems. The x-axis shows the number of variables, while y-axis shows the average training $+$ prediction time

8 Experiment 5: global and local metamodels (GM vs. LMs)

When a metamodel is implemented into an EA, a fixed-size repository of real-function-evaluated solutions is usually managed (solutions from this repository are used to create the metamodel). However, under the premise that it is difficult to have a representative set of solutions to approximate the whole search space of a function, we explored the idea to approximate it by regions. This decision was strengthened in practice since in our previous experiments we often found that there were regions with either no solution or only a few solutions. Such a scarcity of solutions in certain regions of the search space induced a bias to dense regions (when using GM).

Below, three different approaches for creating LMs are proposed; the first two are based on clustering techniques while the third is based on a data structure. These approaches are briefly explained below:

• The k nearest neighbors approach (k-nn) is a method to classify objects based on the closest training examples in the design space (Silverman and Jones 1989). We will use k-nn to select the k real-evaluated solutions nearest to a query point. The selected solutions will serve to create an LM. The computational complexity to find the solutions to create the LM of this approach depends linearly on the size of the repository ($N_{\mathrm{rep}}$). For a problem of a specific dimensionality ($d_{p}$) and using the Euclidean distance, the computational complexity to find the solutions belonging to the LM is of order $O(N_{\mathrm{rep}}d_{p})$.

• The use of k-means (Forgy 1965) to create metamodels consists of splitting the decision space into k subspaces. The LM is created with the solutions that are located in the same subspace as the solution to be evaluated. The computational complexity of the k-means is given with respect to the number of iterations (I) required in the k-means algorithm, the size of the repository ($N_{\mathrm{rep}}$), the dimensionality of the problem ($d_{\mathrm{prob}}$), and the required number of clusters (k). Therefore, the complexity to obtain the clustered solutions required to create the LM is of $O(N_{\mathrm{rep}}kId_{\mathrm{prob}})$.

• Binary space partitioning (BSP) is a technique for subdividing a space into a convex set by hyperplanes. The subdivision can be represented by means of a tree data structure known as a BSP Tree. A BSP Tree is thus a point access method that stores all the solutions of the repository. The construction of the tree is similar as the proposals of Chow and Yuen (2011) and Yuen and Chow (2009), although in both works the BSP Tree was used for other purposes. The tree will store the positions and fitness of the real-evaluated solutions (in the variable space). The pseudo-code for the insertion in the BSP Tree is shown in Algorithm 1. The root $\mathcal {S}$ of the BSP Tree represents the whole search space and each node in a BSP Tree represents a hyperplane that divides the space into two halves. Therefore, the terminal nodes are the stored solutions, and each non-terminal node or root node represents a subspace ($Sp_i$) of the search space.

  

  It is possible to create an LM in each subspace of the BSP Tree. Therefore, to select the solutions to create the metamodel, the BSP Tree is traversed until the solution to be evaluated is found. All solutions belonging to the solution’s subspace are going to feed the training set of the metamodel. If the number of solutions is fewer than expected, then the solutions belonging to the parent node are taken. This procedure is repeated until a minimum number of required solutions (k) is reached. The computational complexity to find the solutions in a BSP Tree with a certain number of solutions ($N_{\mathrm{BSP}}$) and a problem of D dimensions is of $O(\log (N_{\mathrm{BSP}})D)$. In this approach, it is necessary to take into account the complexity to store the solutions in the BSP Tree, which is $O(\log (N_{\mathrm{BSP}})D)$. However, the store procedure is carried out exclusively when the training dataset is updated.

8.1 Influence of the parameters in the local surrogate models

To evaluate the performance of the different approaches, we selected the same test functions used in our previous experiments. Below, we describe in detail the employed methodology to compare the metamodels:

• 1. Create a training dataset with a Latin hypercube of size 100.

• 2. Train the LMs and the GM with the previously created training dataset.

• 3. Create the validation dataset with Latin hypercubes of size 200.

• 4. Predict the validation dataset using LM and GM.

• 5. Compute the mean squared error (MSE).

The metamodels were created using an RBF since it resulted in the most suitable approach in our previous experiments. The parameters used in the RBF were the $\mathrm{BOS}-\mathrm{RP}$ found in the experiment 6. Moreover, in this case we classified the size of our problems in low-, medium-, and high-dimension sizes, having 2, 15, and 30 variables, respectively.

Table 2 Adjustment of the required k closest training examples to a query point in low-, medium-, and high-dimension instances according to normalized root-mean-square deviation

Table 3 Adjustment of the required number of clusters (k) required by k-means in low-, medium-, and high-dimension instances according to normalized root-mean-square deviation

Table 4 Adjustment of the k number of minimal solutions to create the LM using a BSP Tree in low-, medium-, and high-dimension instances according to normalized root-mean-square deviation

The results from this experiment are shown in Tables 2, 3, and 4. These tables contain the normalized MSE obtained by each tested approach on each of the six tested functions. We normalized the MSE according to the highest and lowest errors in the entire table⁴ to have errors between zero and one since this would facilitate the comparison of results. We prefer values with error predictions closer to zero.

In order to have a deeper understanding about the behavior of the adopted metamodeling techniques, we studied the behavior induced by different parameter settings.

8.2 k-nn tuning

We studied the required k closest training examples to a query point. We selected 10, 25, and 50 values to be given as input to this approach since by having 100 individuals as the population, the selection of these values are intended to represent small, medium, and big clusters with respect to the whole population. The obtained results are shown in Table 2. The first three columns of this table display the behavior for two variables (low-dimension sizes). These results indicate that the metamodeling technique behaves better when a high number of solutions is used (50 out of 100) in low-dimension instances. Therefore, we suggest using as much information as possible when we are working with low-dimension instances. However, when the size of the instance increases, the metamodel requires narrowing its width, concentrating on local information, as Table 2 clearly indicates. Accordingly, we suggest the use of $k=50$ in low-dimension instances, and $k=10$ in medium- and high-dimension instances.

Table 5 Comparison of the normalized root-mean-square deviation obtained by k-nn, k-means, BSP Tree, and the GM in low-dimension instances

8.3 k-means tuning

We studied the required number of clusters (k) of the k-means algorithm. We selected 2, 4, and 10 to be given as input to this approach. The idea behind the selection of these values is that by having two clusters ($k=2)$, in the best case each cluster will have about $50\,\%$ of the population, i.e., 50 solutions each. Similarly, when having four and ten clusters we intended to group about 25 and $10\,\%$ of the population in each cluster. Results shown in Table 3 corroborate our previous findings that the metamodel prefers having as much information as possible (i.e., $k=2$) in low-dimension sizes, while for medium- and high-dimension instances it is better to concentrate on specific regions (i.e., $k=10$).

8.4 BSP Tree tuning

In the BSP Tree approach, the parameter k refers to the number of minimal solutions to create the LM; however, this number does not restrict the whole set of points to train the metamodel. For example, if the subspace of the solution to evaluate contains more than k solutions, the LM will also contain more than k solutions. The adopted values were $k=\{10,25,50\}$. The main idea behind the selection of these parameters was to be fair with respect to the previous two approaches. The results shown in Table 4 indicate that for low-dimension instances, the metamodel prefers to use as much information as possible ($k=50$), while for medium- and high-dimension instances, it performs better by focusing on a specific region ($k=10$).

8.5 Comparison of results

According to our results, the selected metamodeling approach (RBF) prefers to have as much information as possible when solving low-dimension instances. However, for medium- and high-dimension instances, RBF prefers to have solutions focused around the region of interest.

Table 5 shows that the GM had the best performance in low-dimension instances, confirming our previous results with this, while Tables 6 and 7 assure that the compared LMs approaches outperformed the GM in medium- and high-dimension instances. These results provide evidence that LMs are a viable strategy for improving the prediction of metamodels. Finally, in medium- and high-dimension instances the best averaged results were obtained by the BSP Tree approach followed by the k-nn approach.

Table 6 Coparison of the normalized root-mean-square deviation obtained by k-nn, k-means, BSP Tree, and the GM in medium dimensional problems

Table 7 Comparison of the normalized root-mean-square deviation obtained by k-nn, k-means, BSP Tree, and the GM in high-dimension problems

9 Conclusions and future work

In order to avoid a biased comparison for bad parameter tuning, we decided to search for the parameter configuration of each meta-modeling technique that performs best (in average) in all the adopted test functions. We called this the “best overall settings” (BOS). Also, we wanted to discover the parameters that induced the best performance on each meta-modeling technique for each test function. We called this the “best local settings” (BLS). A comparison of the results shows us that the advantage of having BLS is minimal. Therefore, we suggest tuning the metamodeling parameters according to our BOS.

We also found that RBF and SVR are the most efficient approaches among the reviewed ones. However, when we search for the most accurate approach, we select KRG as the best approach to be used in low-dimension problems (followed by SVR). On the other hand, RBF is the most accurate approach in high-dimension problems (followed by SVR). However, if we consider all instance sizes, we would select RBF as the most robust and scalable approach.

Moreover, since we wanted to evaluate how convenient metamodeling techniques are when incorporated into EAs, we propose measuring their suitability. We proposed two approaches to evaluate such a criterion; our first approach measured the distance from best solution obtained by the metamodeling technique-EA to the optimal solution (in the objective function space), while our second approach measures the percentage of solutions in the metamodel that preserves the hierarchy according to the original objective function. Our results indicate that RBF was the best approach in both studies.

After realizing that our RP performance measure was better aligned with the manner with which EAs select solutions, we decided to perform a parameters’ tuning based on such a performance measure. The new tuning phase produced a different parameter selection on two out of four metamodels. The new parameter sets induced the better performance on their approaches. This new experiment endorses our previous findings that RBF is the metamodeling technique that induced the best performance of our EA. This experiment also found that although the accuracy of the metamodel does not reflect properly the behavior of the adopted metamodels when we they are incorporated within an EA, the RP performance measure does. Therefore, we suggest the use of this performance measure for future comparisons among metamodeling techniques.

In addition, we also evaluated three different approaches to select solutions to create LMs. The first two approaches are based on clustering algorithms. The last approach uses a data structure, called BSP Tree, to split the entire search space according to the repository of solutions. The compared algorithms were tuned with respect to a single parameter. Results showed that the RBF method prefers to have as much information as possible in low-dimension problems. However, the method prefers to have more clustered information when the problem size increases.

A comparison of results indicates that for medium- and high-dimension instances the best approach to be selected is either BSP or the k-nn (the average performance of BSP was better than k-nn, but the latter performed better in more instances).

Part of our future work will include the incorporation of more metamodeling techniques into the comparative study. Additionally, some meta-modeling techniques train a metamodel that minimizes the MSE in a validation dataset. The maximization of RP may produce good results. Therefore, we would like to use the RP indicator to train metamodels. Finally, we would like to evaluate the LM with other meta-modeling techniques, because there may be interesting results.