The hull-kernel topology on prime ideals in posets

Abstract

In this paper, we continue our study of prime ideals in posets that was started in Joshi and Mundlik (Cent Eur J Math 11(5):940–955, 2013) and, Erné and Joshi (Discrete Math 338:954–971, 2015). We study the hull-kernel topology on the set of all prime ideals $\mathcal {P}(Q)$, minimal prime ideals $\mathrm{Min}(Q)$ and maximal ideals $\mathrm{Max}(Q)$ of a poset Q. Then topological properties like compactness, connectedness and separation axioms of $\mathcal {P}(Q)$ are studied. Further, we focus on the space of minimal prime ideals $\mathrm{Min}(Q)$ of a poset Q. Under the additional assumption that every maximal ideal is prime, the collection of all maximal ideals $\mathrm{Max}(Q)$ of a poset Q forms a subspace of $\mathcal {P}(Q)$. Finally, we prove a characterization of a space of maximal ideals of a poset to be a normal space.

1 Introduction

The co-equivalence of the category of bounded distributive lattices and certain category of topological spaces was developed in the classical paper of Stone (1937). It was observed that the set of prime ideals of a Boolean algebra can be made into a topological space in a natural way, the open sets of which correspond to ideals of the algebra. More precisely, to an ideal I, we associate the open set which consist of all prime ideals which do not contain I.

Venkatanarasimhan (1972) studied Stone’s topology on the set of prime dual ideals $\mathcal {F}(L)$ of a pseudocomplemented and bicomplemented lattice L. In fact, he has proved that $\mathcal {F}(L)$ is compact, $T_0$, and it is $\pi _0$ if $\{1\}$ is the only dense element of L. These results are generalized in Sect. 3 of this paper.

The topology of minimal prime ideals $\mathrm{Min}(L)$ of a distributive lattice L with 0 is studied in Speed (1974) and it is proved that $\mathrm{Min}(L)$ is compact if and only if L is quasicomplemented. This result is exetended for 0-distributive semilattices by Pawar and Thakare (1978, 1982); see also Pawar (1978).

In this paper, we introduce the concept of quasicomplemented and weakly quasicomplemented poset and prove that if the space of minimal prime ideals is compact then the corresponding poset is weakly quasicomplemented.

Grätzer (1998) gave a topological representation for the class of distributive join-semilattices extending the known topological representation of Stone (1937) for distributive lattices.

During last few years, the theory of prime ideals of posets has been developed; see David and Erné (1992), Erné (2006), Erné and Joshi (2015), Halaš et al. (2010), Halaš and Rachůnek (1995) and, Joshi and Mundlik (2013). In fact, Venkatanarasimhan (1970) seems to be first who introduced the topology on the set of all prime semi-ideals of a poset and characterized $T_1$-spaces. He proved that for a bounded poset Q, the space of prime semi-ideals is $T_1$ if and only if Q is the two-element chain.

This motivated us to study the topology on the set of prime ideals, minimal prime ideals and maximal ideals of a poset. It can be observed that the space of prime ideals $\mathcal {P}(Q)$ is a subspace of the space of prime semi-ideals $\mathcal {P}_s(Q)$. If a poset Q is different from the two-element chain then the space of prime semi-ideals is not $T_1$ and hence not $T_2$. But we prove that the space $\mathcal {P}(Q)$ of prime ideals of Q is completely regular and totally disconnected space if Q is a complemented poset. Also, we give necessary and sufficient condition for a space of prime ideals to be $T_1$ which generalizes the results of Balasubramani (2008).

The last section extends the results of Pawar and Thakare (1977), Balasubramani (2008) for pm-(semi)lattices, that is, bounded distributive (semi)lattices in which every prime ideal is contained in a unique maximal ideal. In the last section, we extend the following Theorem 1.1 of Balasubramani (2008) to posets.

Theorem 1.1

A bounded pseudocomplemented meet-semilattice is a pm-semilattice if and only if the space of maximal ideals is normal.

We begin with necessary concepts and terminology in a poset Q.

Let $A \subseteq Q$. The set $A^u = \{ x \in Q\; |\; x \ge a$ for every $a \in A\}$ is called the upper cone of A. Dually, we have the concept of lower cone $A^{ \ell }$ of A. $A^{u \ell }$ shall mean $\{A^u\}^{ \ell }$ and $A^{ \ell u}$ shall mean $\{A^{ \ell }\}^u$. The upper cone $\{a\}^u$ is simply denoted by $a^u$ and $\{a,b\}^u$ is denoted by $(a,b)^u$. Similar notations are used for lower cones. We note that $A \subseteq A^{u \ell }$ and $A \subseteq A^{ \ell u}$. If $A \subseteq B$ then $A^{ \ell } \supseteq B^{ \ell }$ and $A^u \supseteq B^u$. Moreover, $A^{\ell u \ell } = A^{ \ell }$, $A^{ u \ell u} = A^u$, $\{a^u\}^{ \ell }=a^{ \ell }$ and $\{a^\ell \}^u=a^u$.

A poset Q is called distributive (see Larmerová and Rachůnek 1988) if for all $a,b,c\in Q, \{(a,b)^u,c\}^{\ell }=\{(a,c)^\ell , (b,c)^\ell \}^{u\ell }$. More details about distributive posets as well as distributive pairs can be found in Waphare and Joshi (2007). A poset Q with the least element 0 is said to be 0-distributive (see Joshi and Waphare 2005) if for all $a,b,c\in Q, (a,b)^\ell =(a,c)^\ell =\{0\}$ imply $\{a, (b,c)^u \}^{\ell }=\{0\}$.

Dually, we have the concept of a 1-distributive poset.

A bounded poset Q is said to be 0-1-distributive if it is both 0-distributive and 1-distributive.

If Q is a lattice, then Q is distributive (0-distributive) as a poset if and only if it is distributive (0-distributive) as a lattice.

Let Q be a poset with 0 and 1. An element $y\in Q$ is said to be a complement of $x\in Q$ if $(x,y)^{u\ell }=(x,y)^{\ell u}=Q$. A poset Q is said to be complemented if each element of Q has a complement in Q. A distributive complemented poset is called Boolean. More details about Boolean posets can be found in Waphare and Joshi (2005).

Let Q be a poset with 0. An element $x^* \in Q$ is said to be the pseudocomplement of $x \in Q$, if $(x,x^*)^\ell =\{0\}$ and for $y \in Q$, $(x,y)^\ell =\{0\}$ implies $y \le x^*$. A poset Q with 0 is called pseudocomplemented if each element of Q has the pseudocomplement (see Venkatanarasimhan 1971 and Halaš 1993).

Given a poset Q and a non-empty subset $I\subseteq Q$, we call I a semi-ideal of Q if $x \le y, ~~~y\in I$ imply $x \in I.$ A non-empty subset I of Q is said to be an ideal if $a,b\in I$ yields $(a,b)^{u\ell }\subseteq I$ (see Halaš 1993). An ideal I is said to be a principal ideal generated by $a\in Q$ if $I=(a]=\{x\in Q\;|\;x\le a\}$. An ideal I is called a u -ideal if, for all $x,y \in I$, $(x,y)^u \cap I\ne \emptyset$. Note that every principal ideal is a u-ideal but not conversely. Dually, we have the concepts of a filter and an $\ell$ -filter.

The following result is easy to prove, hence we omit its proof.

Lemma 1.2

Let Q be a poset and I, J be u-ideals of Q. Then $I\vee J=\{x\in Q\;|\;x\in (a,b)^{u\ell }\;\text { for some }a\in I,b\in J\}$.

It is known that every ideal in a join-semilattice is a u-ideal. Therefore the following corollary is an easy consequence of the above lemma.

Corollary 1.3

Let I and J be ideals of a join-semilattice Q. Then

$$\begin{aligned} I\vee J=\{x\in Q\;|\; x\le i\vee j, \text { for some } i\in I, j\in J\}. \end{aligned}$$

The set of all ideals of a poset Q is denoted by Id(Q) and it forms an algebraic lattice with respect to set inclusion. A poset Q is called ideal-distributive if $(Id(Q),\subseteq )$ is a distributive lattice.

For a non-empty subset $A\subseteq Q$, the annihilator of A is denoted by $A^\perp =\{y\in Q\;|\;(x,y)^\ell =\{0\}\text { for all }x\in A\}$. In particular, if $A=\{x\}$ then the annihilator of x is $x^\perp =\{y\in Q\;|\;(x,y)^\ell =\{0\}\}$ (see Joshi and Waphare 2005).

A proper semi-ideal (ideal) I of Q is called prime if for $x,y\in Q, (x,y)^\ell \subseteq I$ implies $x\in I\text { or } y\in I.$ Dually, we have the concept of a prime filter. The set of all prime ideals of a poset Q is denoted by ${\mathcal {P}}(Q)$. Minimal elements of the poset of all prime ideals (prime u-ideals) of Q will be called minimal prime ideals (minimal prime u -ideals) of Q. A proper ideal (u-ideal) I is said to be a maximal ideal (u -ideal) if there is no proper ideal (u-ideal) J such that $I\subsetneqq J\subsetneqq Q$. Dually, we have the concept of a maximal filter (maximal $\ell$ -filter). The set of all minimal prime ideals of a poset Q with 0 is denoted by $\mathrm{Min}(Q)$.

Fig. 1

A maximal u-ideal is not a maximal ideal

Remark 1.4

Note that a maximal u-ideal, that is, maximal among all u-ideals, is not a maximal ideal, that is, maximal among all ideals.

Consider the ideal $I=\{0\}\cup \{i_n\;|\;n\in \mathbb {N}\}$ in the poset visualized in Fig. 1. Clearly, I is a maximal u-ideal but not a maximal ideal whereas the ideal $J=I\cup \{j\}$ is a maximal ideal but not a u-ideal, as $(j,i_1)^u\cap J=\emptyset$.

Remark 1.5

Note that in a pseudocomplemented poset, maximal filters need not be prime, contrary to the lattice case. However, every maximal $\ell$-filter of a pseudocomplemented poset is prime, see Joshi and Mundlik (2013, Theorem 2.2). Consider the pseudocomplemented poset (in fact a Boolean poset) depicted in Fig. 2. The filter $F=\{1,a',b',c',d'\}$ is maximal but F is not prime as $(a,b)^u\subseteq F$ for $a,b\notin F$.

Fig. 2

A Boolean poset in which a maximal filter is not prime

Denote by $\mathcal {P}_s(Q)$ the set of all prime semi-ideals of a poset Q. It is clear that $\mathcal {P}(Q)\subseteq \mathcal {P}_s(Q)$. However, for a poset depicted in Fig. 3, we have $\mathcal {P}(Q)=\emptyset$ (as there is no prime ideal) but $\mathcal {P}_s(Q)\ne \emptyset$ as $I=\{0,a,b\}$ is a prime semi-ideal but not a prime ideal.

Fig. 3

A poset in which $\mathcal {P}(Q)=\emptyset$ but $\mathcal {P}_s(Q)\ne \emptyset$

Remark 1.6

We denote by $\mathbb {P}_\mathrm{MFP}$, the class of posets having the least element 0 in which every maximal filter is prime and by $\mathbb {P}_\mathrm{MIP}$, the class of posets having the greatest element 1 in which every maximal ideal is prime. We denote by $\mathbb {P}^\ell _\mathrm{MFP}$, the subclass of $\mathbb {P}_\mathrm{MFP}$ (see Remark 1.4) consisting of all posets having the least element 0 and with the property that every maximal $\ell$-filter (i.e., maximal among all $\ell$-filters) is a maximal filter (i.e., maximal among all filters). Hence every maximal $\ell$-filter F of a poset Q in $\mathbb {P}_\mathrm{MFP}^\ell$ is also prime. Dually, we have the class $\mathbb {P}^u_\mathrm{MIP}$.

In what follows we present the relationship between the above mentioned concepts.

Theorem 1.7

For a poset Q with 0, consider the following statements:

• (1) Q is a pseudocomplemented meet-semilattice.

• (2) Every maximal filter of Q is prime.

• (3) Every maximal $\ell$-filter of Q is prime.

• (4) Q is 0-distributive.

• (5) $A^\perp$ is an ideal for any non-empty subset A of Q.

• (6) Id(Q) is 0-distributive.

• (7) Id(Q) is pseudocomplemented, where $I^{\perp }$ is the pseudocomplement of $I\in Id(Q)$.

Then the implications $(1) \Rightarrow (2),(1) \Rightarrow (3),(2) \Rightarrow (4), (3) \Rightarrow (4)$ and $(4) \Leftrightarrow (5) \Leftrightarrow (6) \Leftrightarrow (7)$ hold. Moreover, if Q happens to be a lattice then (2) to (7) are equivalent.

Proof

$(1) \Rightarrow (2)\text { and }(3)$: It follows from Joshi and Mundlik (2013, Theorem 2.2) and the fact that every filter of a meet-semilattice is an $\ell$-filter.

$(2) \Rightarrow (4)$: Let $a,b,c\in Q$ be such that $(a,b)^\ell =\{0\}=(a,c)^\ell$. Suppose on the contrary that $\{a,(b,c)^u\}^\ell \ne \{0\}$, that is, there exists $x\in \{a,(b,c)^u\}^\ell$ such that $x\ne 0$. By Zorn’s Lemma there is a maximal filter F containing x. By the hypothesis F is a prime filter. As $x\in (b,c)^{u\ell }$, we have $(b,c)^u\subseteq x^u\subseteq F$. Primeness of F implies that $b\in F$ or $c\in F$. Since $a \in F$, we have $Q=(a,b)^{\ell u}\subseteq F$ or $Q=(a,c)^{\ell u}\subseteq F$, a contradiction. Hence Q is 0-distributive.

$(3) \Rightarrow (4)$: Using similar techniques as in the implication $(2) \Rightarrow (4)$, except that by Zorn’s Lemma, there exists a maximal $\ell$-filter F containing x.

$(4) \Leftrightarrow (5) \Leftrightarrow (6) \Leftrightarrow (7)$: It follows from Joshi and Waphare (2005, Theorems 2.13, 2.16).

It is easy to observe that in lattices every filter is an $\ell$-filter. Hence, the last part follows from Pawar and Thakare (1977, Theorem 5). $\square$

Remark 1.8

From the above theorem, it is clear that the class $\mathbb {P}^\ell _\mathrm{MFP}$ is richer than the class of 0-distributive posets but weaker than the class of pseudocomplemented meet-semilattices. Note that there is a 0-distributive poset in which there exists a maximal $\ell$-filter such that it is not prime; see Mokbel and Kharat (2013, Remark 2.15). On the other hand, it is not difficult to verify that for a finite poset these two concepts coincide.

The following theorem is due to Halaš and Rachůnek (1995).

Theorem 1.9

Let Q be a poset. Let I be a prime ideal of Q. Then $Q{\setminus } I$ is a filter. $Q{\setminus } I$ is a prime filter if and only if I is a u-ideal. Moreover, $Q{\setminus } I$ is then an $\ell$-filter.

The following lemma shows the existence of a prime ideal in the class $\mathbb {P}^\ell _\mathrm{MFP}$.

Lemma 1.10

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$. Then there is a prime ideal P in Q.

Proof

Let Q be a poset in $\mathbb {P}^\ell _\mathrm{MFP}$ and let $x\in Q$ be any non-zero element. Then $(0]\cap [x)=\emptyset$. By Zorn’s lemma, there exists a maximal $\ell$-filter $F\supseteq [x)$ such that $(0]\cap F=\emptyset$. Due to the assumption every maximal $\ell$-filter is maximal among all filters, we have that F is a maximal filter. Further, $Q\in \mathbb {P}^\ell _\mathrm{MFP}$, so F is a prime filter. This further yields $Q{\setminus } F$ is an ideal. Moreover, $Q{\setminus } F$ is a prime ideal and consequently $\mathcal {P}(Q)\ne \emptyset .$ $\square$

2 Properties of the topological space $\mathcal {P}(Q)$

The following result about $\mathcal {P}_s(Q)$ can be found in Venkatanarasimhan (1970).

Lemma 2.1

(Venkatanarasimhan 1970) Let Q be a poset with the smallest element 0 and $I,J,I_{\alpha }$ be semi-ideals of $Q, \alpha \in \Lambda .$ Then

• (1) $F(Q)=\emptyset ,\ F((0])={\mathcal P}_s(Q),$ where F(I) is the set of all prime semi-ideals which contains the semi-ideal I;

• (2) $F(I)\cup F(J)=F(I\cap J);$

• (3) $\bigcap \{ F(I_{\alpha })\;|\;\alpha \in \Lambda \} = F( \cup \left\{ I_{\alpha }\;|\;\alpha \in \Lambda \right\} )$.

According to Lemma 1.10, there is a guarantee of the existence of a prime ideal in $Q\in \mathbb {P}^\ell _\mathrm{MFP}$, that is, $\mathcal {P}(Q)\ne \emptyset$. Thus if we restrict ourselves to $\mathcal {P}(Q)$ then for any ideal I of a poset Q, we denote by $V(I)= \{ P\in {\mathcal P}(Q)\;|\;\,P\supseteq I \}$ the subset of $\mathcal {P}(Q)$ of prime ideals which contain an ideal I.

The following lemma is similar to Lemma 2.1 but for the sake of completeness we provide its proof.

Lemma 2.2

Let Q be a poset with 0 and $I,J,I_{\alpha }\in Id(Q), \alpha \in \Lambda .$ Then

• (1) $V(Q)=\emptyset ,\ V((0])={\mathcal P}(Q)$;

• (2) $V(I)\cup V(J)=V(I\cap J);$

• (3) $\bigcap \{ V(I_{\alpha })\;|\;\alpha \in \Lambda \} = V( \vee \left\{ I_{\alpha }\;|\;\alpha \in \Lambda \right\} ).$

Proof

(1) There is no prime ideal containing Q, hence $V(Q)=\emptyset$. Also every prime ideal contains 0, which gives $V((0])=\mathcal {P}(Q)$.

(2) Let $P\in V(I)\cup V(J)$, that is, $P\in V(I)$ or $P\in V(J)$, and without loss of generality, assume that $P\in V(I)$. This implies that $I\cap J\subseteq I\subseteq P$. Thus $V(I)\cup V(J)\subseteq V(I\cap J)$.

To prove the converse, let $P\in V(I\cap J).$ Assume on the contrary that $P\notin V(I)\cup V(J)$. Then choose $x\in I{\setminus } P$ and $y\in J{\setminus } P$. This implies that $(x,y)^\ell \subseteq I\cap J\subseteq P$. By primeness of P, we have $x\in P$ or $y\in P$, a contradiction. Hence $P\in V(I)\cup V(J).$

(3) Assuming $P\in \bigcap \{ V(I_{\alpha })\;|\;\alpha \in \Lambda \} ,$ we have $P\supseteq I_{\alpha }$ for each $\alpha \in \Lambda$, which gives $P\supseteq \vee \{ I_{\alpha }\;|\;\alpha \in \Lambda \}$ and $P\in V( \vee \big \{ I_{\alpha }\;|\;\alpha \in \Lambda \}).$ Hence $\bigcap \{ V(I_{\alpha })\;|\;\alpha \in \Lambda \} \subseteq V( \vee \left\{ I_{\alpha }\;|\;\alpha \in \Lambda \right\} ).$

Conversely, let $P\in V( \vee \left\{ I_{\alpha }\;|\;\alpha \in \Lambda \right\} )$. Then $\vee \{ I_{\alpha }\;|\;\alpha \in \Lambda \} \subseteq P$ which yields $I_\alpha \subseteq P$ for every $\alpha \in \Lambda$. Consequently, $P\in V(I_\alpha )$ for every $\alpha \in \Lambda$ and thus $P\in \bigcap \{V(I_\alpha )\;|\;\alpha \in \Lambda \}$. $\square$

Due to Lemmas 2.1 and 2.2, the sets F(I) for a semi-ideal I (V(I) for an ideal I) of Q can be considered as closed sets in a topological space on ${\mathcal P}_s(Q)$ $(\mathcal {P}(Q))$.

Definition 2.3

For a poset Q with the least element 0, the topological space $\mathcal {P}_s(Q)$ having $\{F(I)\;|\;I \text { is a semi-ideal of } Q\}$ as the collection of closed sets is called the prime semi-ideal space of Q.

Remark 2.4

Since every prime ideal is a prime semi-ideal, we can consider the prime ideal space $\mathcal {P}(Q)$ as a subspace of $\mathcal {P}_s(Q)$, where the collection of all closed sets is $\{\mathcal {P}(Q)\cap F(I)\;|\; I \text { is a semi-ideal of } Q\}$. We now prove that the collection of all closed sets of the subspace $\mathcal {P}(Q)$ is $\{V(I)\;|\;I \text { is an ideal of } Q\}.$ For this, let V(I) be a closed set in $\mathcal {P}(Q)$ for some ideal I. Since every ideal is a semi-ideal, it follows that $V(I)=\mathcal {P}(Q) \cap F(I)$. Then $V(I)\in \{\mathcal {P}(Q)\cap F(J)\;|\; J \text { is a semi-ideal of } Q\}$. Let $U_1\in \{\mathcal {P}(Q)\cap F(I)\;|\; I \text { is a semi-ideal of } Q\}$. Then $U_1=\mathcal {P}(Q)\cap F(I)$ for some semi-ideal I. Consider $J=\cap \{P|P\in \mathcal {P}(Q)\cap F(I)\}$. Clearly, J is an ideal of Q such that $I\subseteq J$. Now we prove that $U_1=V(J)$. If $R\in U_1$ then $R\supseteq J$, hence $R\in V(J)$. Conversely, let $T\in V(J)$. Then $T\supseteq J\supseteq I$ and hence $T\in \mathcal {P}(Q)\cap F(I)$. This proves that $\mathcal {P}(Q)$ is a subspace with $\{V(I)\;|\; I \text { is an ideal of } Q\}$ as the collection of all closed sets. However, if a poset $Q\in \mathbb {P}^\ell _\mathrm{MFP}$ then $\mathcal {P}(Q)$ is a non-empty subspace of $\mathcal {P}_s(Q)$. If $\mathcal {P}(Q)=\emptyset$ then the results are trivial.

Lemma 2.5

Let Q be a poset with 0. The collection $\{{\mathcal P}_s(Q){\setminus } F((x])\;|\;x\in Q\}$ forms a basis for the open sets of $\mathcal {P}_s(Q).$

Proof

Let U be any open set in $\mathcal {P}_s(Q)$ and $P\in U$. By Lemma 2.1, $U=\mathcal {P}_s(Q){\setminus } F(I)$ for some semi-ideal I of Q. Therefore $I\nsubseteq P$. Let $x\in I{\setminus } P$. Then $P\in \mathcal {P}_s(Q){\setminus } F((x])\subseteq \mathcal {P}_s(Q){\setminus } F(I)$. Thus the collection $\{{\mathcal P}_s(Q){\setminus } F((x])\;|\;x\in Q\}$ forms a basis for the open sets of $\mathcal {P}_s(Q).$ $\square$

Corollary 2.6

For a poset Q in $\mathbb {P}^\ell _{MFP}$, the collection $\{{\mathcal P}(Q){\setminus } V((x])\;|\;x\in Q\}$ forms a basis for the open sets of $\mathcal {P}(Q).$

For any subset $X\subseteq {\mathcal P}(Q)$, denote by $\overline{X}$ the closure of X in $\mathcal {P}(Q),$ the smallest closed set containing X.

The following lemma for $\mathcal {P}_s(Q)$ can be found in Venkatanarasimhan (1970), in fact it generalizes Theorem 3 of Venkatanarasimhan (1972) and for the sake of completeness, we provide its proof.

Lemma 2.7

Let Q be a poset with 0 and X be any non-empty subset of $\mathcal {P}(Q)$. Then $\overline{X}=V(\cap _{P\in X} P)$.

Proof

Clearly, $V(\cap _{P\in X} P)$ is a closed set of $\mathcal {P}(Q)$ and $X\subseteq V(\cap _{P\in X} P)$. We show that any closed set Y containing X also contains $V(\cap _{P\in X} P)$. Indeed, by Remark 2.4, $Y=V(I)$ for some ideal I of Q. As $X\subseteq V(I)$, we have $I\subseteq P$ for every $P\in X$. Therefore $I\subseteq \cap _{P\in X} P$ and thus $V(\cap _{P\in X} P)\subseteq V(I)=Y$. Hence $\overline{X}=V(\cap _{P\in X} P)$. $\square$

Definition 2.8

A topological space X is said to be a $T_0$ -space if for any two distinct points of X, there is a neighborhood containing just one of them.

Theorem 2.9

(Venkatanarasimhan 1970) The space $\mathcal {P}_s(Q)$ is always a $T_{0}$-space.

Corollary 2.10

The subspace P(Q) of $\mathcal {P}_s(Q)$ is always a $T_{0}$-space.

A topological space X is said to be a $T_1$ -space, if $\{x\}$ is a closed set for any $x\in X$.

We recall Theorem 24 from Venkatanarasimhan (1970).

Theorem 2.11

(Venkatanarasimhan 1970) Let Q be a bounded poset. Then $\mathcal {P}_s(Q)$ is a $T_1$-space if and only if Q is the two-element chain.

Fig. 4

A poset for which $\mathcal {P}(Q)$ is not a $T_1$-space

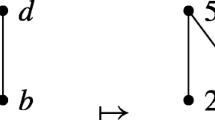
In a bounded poset Q with more than one prime ideal the space $\mathcal {P}(Q)$ need not be a $T_1$-space. For instance, consider the poset depicted in Fig. 4. Here $\mathcal {P}(Q)=\{(a],(b],(c],(d]\}$. Observe that $\overline{\{(a]\}}=V((a])=\{(a],(c],(d]\}\ne \{(a]\}$. Hence $\{(a]\}$ is not closed and thus $\mathcal {P}(Q)$ is not $T_1$.

Now, for the poset depicted in Fig. 5 we have $\mathcal {P}(Q)=\{(a],(b]\}$. Clearly, $\overline{\{(a]\}}=V((a])=\{(a]\}$ and $\overline{\{(b]\}}=V((b])=\{(b]\}$. Thus $\mathcal {P}(Q)$ is a $T_1$-space. However, by Theorem 2.11, $\mathcal {P}_s(Q)$ is not a $T_1$-space.

Fig. 5

A Boolean poset in which $\mathcal {P}(Q)$ is $T_1$ but $\mathcal {P}_s(Q)$ is not $T_1$

The following lemma characterizes $\mathcal {P}(Q)$ as a $T_1$-space.

Lemma 2.12

For a poset Q in $\mathbb {P}^\ell _{MFP}$, the following conditions are equivalent:

• (1) $\mathcal {P}(Q)$ is a $T_{1}$-space;

• (2) $\{ P\} =V(P)$ for all $P\in {\mathcal P}(Q);$

• (3) $({\mathcal P}(Q),\subseteq )$ is an antichain.

Proof

$(1)\Rightarrow (2)$: It follows from Lemma 2.7.

$(2)\Rightarrow (3)$: Suppose there exist $P,R\in \mathcal {P}(Q)$ such that $P\subsetneqq R.$ Then $R\in V(P)=\{P\}$, a contradiction.

$(3)\Rightarrow (1)$: If $({\mathcal P}(Q),\subseteq )$ is an antichain, then $\{ P\} =V(P)$ for each $P\in {\mathcal P}(Q).$ Thus $\mathcal {P}(Q)$ is a $T_{1}$-space. $\square$

Corollary 2.13

For a pseudocomplemented meet-semilattice Q, the following conditions are equivalent:

• (1) $\mathcal {P}(Q)$ is a $T_{1}$-space;

• (2) $\{ P\} =V(P)$ for all $P\in {\mathcal P}(Q);$

• (3) $({\mathcal P}(Q),\subseteq )$ is an antichain.

Definition 2.14

Let X be a topological space. A closed subset V of X is said to be reducible if $V=V_1\cup V_2$, where $V_1$ and $V_2$ are closed sets in X, and $V_1, V_2$ are proper subsets of V. Otherwise, V is called irreducible.

The following lemma relates the irreducibility of sets in $\mathcal {P}_s(Q)$ with the primeness of semi-ideals in Q.

Lemma 2.15

Let Q be a poset with the least element 0 and V be a non-empty closed subset of $\mathcal {P}_s(Q)$. Then V is irreducible if and only if $I=\cap _{P\in V}P$ is a prime semi-ideal of Q.

Proof

Let V be irreducible in $\mathcal {P}_s(Q)$. We claim that $I=\cap _{P\in V}P$ is a prime semi-ideal of Q. As $V\ne \emptyset$, I is a proper semi-ideal of Q. Now, suppose that there exist $x,y\in Q$ with $(x,y)^\ell \subseteq I$ and $x,y\notin I$. This implies that $x\notin P_i$ and $y\notin P_j$ for some $P_i,P_j\in V$. Consider the closed sets $V_1=V\cap V((x])=\{P\in V\;|\;x\in P\}$ and $V_2=V\cap V((y])$. As $P_i\notin V_1$ and $P_j\notin V_2$, we have $V_1$ and $V_2$ are proper subsets of V. Suppose there exists $P\in V$ but $P\notin V_1\cup V_2$. Then $x\notin P$ and $y\notin P$. By primeness of P, we have $(x,y)^\ell \not \subseteq P$. Then there exists $z\in (x,y)^\ell \subseteq I$ such that $z\notin P$, a contradiction. Hence $V=V_1\cup V_2$, where $V_1$ and $V_2$ are non-empty proper subsets of V. This contradicts the irreducibility of V and thus I is a prime semi-ideal of Q.

Conversely, assume that $I=\cap _{P\in V}P$ is a prime semi-ideal. Suppose on the contrary that $V=V_1\cup V_2$, where $V_1$ and $V_2$ are proper closed sets. Let $J=\cap _{P\in V_1}P$ and $K=\cap _{P\in V_2}P$. Since $V_1\subsetneqq V$, there exists a prime semi-ideal $P\in V$ such that $P\notin V_1.$ As $V_1$ is closed, there is a neighborhood of P, say $\mathcal {P}_s(Q){\setminus } V((a])$, disjoint from $V_1$. Therefore $(\mathcal {P}_s(Q){\setminus } V((a]))\cap V_1=\emptyset$ which yields $V_1\subseteq V((a])$, that is, $a\in P_i$ for all $P_i\in V_1$. Thus we get $a\in J$. Observe that $a\notin P\supseteq I$, and hence $J\supsetneqq I$. Similarly, $K\supsetneqq I$. Therefore there exist $x\in J$, $y\in K$ such that $x,y\notin I$. Since $V=V_1\cup V_2$, we have $I=J\cap K$. Hence $(x,y)^\ell \subseteq J\cap K=I$, a contradiction to primeness of I. Thus V is an irreducible set. $\square$

If we restrict ourselves to the subspace $\mathcal {P}(Q)$ of prime ideals then by Lemma 1.10, we have the following corollary for a poset $Q\in \mathbb {P}^\ell _\mathrm{MFP}$.

Corollary 2.16

Let $Q\in \mathbb {P}^\ell _{MFP}$ and V be a non-empty closed subset of $\mathcal {P}(Q)$. Then V is irreducible if and only if $I=\cap _{P\in V}P$ is a prime ideal of Q.

Proof

It follows by similar arguments as in Lemma 2.15. $\square$

3 Space of minimal prime ideals

Henriksen and Jerison (1965) investigated the space of minimal prime ideals of a commutative ring while Kist (1963) discussed the space of minimal prime ideals in the context of commutative semigroups with 0. Speed (1974) studied the space of minimal prime ideals for distributive lattices and characterized the compactness in terms of quasicomplementedness of a lattice. This was further generalized by Pawar (1978) for semilattices. We extend these concepts to the space of minimal prime ideals of posets.

Recall that if a poset Q is in $\mathbb {P}^\ell _\mathrm{MFP}$, then $\mathcal {P}(Q)\ne \emptyset .$ As $0\in Q$, there exists a minimal prime ideal in Q. Thus if poset Q is in $\mathbb {P}^\ell _\mathrm{MFP}$, then the set Min(Q) of all minimal prime ideals of Q is non-empty.

We recall the following lemma from Joshi and Mundlik (2013, Lemma 4.1).

Lemma 3.1

Let Q be a poset with 0 and F be an $\ell$-filter of Q. Then $Q{\setminus } F$ is a prime semi-ideal. Further, every prime semi-ideal contains a minimal prime semi-ideal.

Now, we prove the following theorem.

Theorem 3.2

Let I be an ideal of a poset Q. If $Q{\setminus } I$ is a maximal $\ell$-filter then I is a minimal prime ideal, and the converse is true if Q is in $\mathbb {P}^\ell _{MFP}$.

Proof

Let I be an ideal of Q such that $Q{\setminus } I$ is a maximal $\ell$-filter. From the fact that $Q{\setminus } I$ is an $\ell$-filter, it is clear that I is a prime ideal of Q. Let J be a prime ideal such that $J\subsetneqq I$. Therefore $Q{\setminus } I\subsetneqq Q{\setminus } J$. We claim that $Q{\setminus } J$ is an $\ell$-filter. Let $x,y\in Q{\setminus } J$. Since J is prime, $(x,y)^{\ell }\nsubseteq J$. Let $t\in (x,y)^{\ell u}$. We show that $t\in Q{\setminus } J$. Assume on the contrary that $t\in J$. Then $(x,y)^{\ell }\subseteq t^{\ell }\subseteq J$, a contradiction to the fact that $(x,y)^{\ell }\nsubseteq J$. Hence $Q{\setminus } J$ is a filter.

By primeness of J, we get $Q{\setminus } J$ is an $\ell$-filter. Thus $Q{\setminus } I\subsetneqq Q{\setminus } J$, a contradiction to the maximality of $Q{\setminus } I$. Hence I is a minimal prime ideal.

Conversely, suppose that I is a minimal prime ideal of a poset $Q\in \mathbb {P}^\ell _\mathrm{MFP}$. Since I is a prime ideal, it is easy to observe that $Q{\setminus } I$ is an $\ell$-filter. Let J be a maximal $\ell$-filter such that $Q{\setminus } I \subseteq J$, that is, $Q{\setminus } J \subseteq I$. We claim that $Q{\setminus } J$ is a prime ideal. Since $Q\in \mathbb {P}^\ell _\mathrm{MFP}$, J is a prime filter. We show that $Q{\setminus } J$ is an ideal. Let $x,y\in Q{\setminus } J$. Suppose there is $t\in (x,y)^{u\ell }$, such that $t\notin Q{\setminus } J$. Since $t\in (x,y)^{u\ell }$ and $t\in J$, we have $(x,y)^{u}\subseteq J$. Since J is a prime filter, either $x\in J$ or $y\in J$, a contradiction to $x,y\in Q{\setminus } J$. Thus $Q{\setminus } J$ is an ideal.

Primeness of $Q{\setminus } J$ follows from the fact that J is an $\ell$-filter. Since I is a minimal prime ideal, we have $I=Q{\setminus } J$, that is, $J=Q{\setminus } I$. Thus $Q{\setminus } I$ is a maximal $\ell$-filter. $\square$

Remark 3.3

From Lemma 3.1 and Theorem 3.2, it is easy to prove that if a poset Q is in $\mathbb {P}^\ell _\mathrm{MFP}$ then every minimal prime semi-ideal is a minimal prime ideal. Thus if $\mathrm{Min}_s(Q)$ denotes the set of all minimal prime semi-ideals of a poset Q in $\mathbb {P}^\ell _\mathrm{MFP}$ then $\mathrm{Min}(Q)=\mathrm{Min}_s(Q)$.

In this section, we study the subspace topology of $\mathcal {P}(Q)$ on the set $\mathrm{Min}(Q)$ of minimal prime ideals of a poset Q.

Let X be a subset of $\mathrm{Min}(Q)$. We denote by $k(X)=\bigcap _{P\in X}P$ and we call it the kernel of X. For an ideal I of Q, we denote by h(I) the set $\{P\in \mathrm{Min}(Q)\;|\; I\subseteq P\}$ and call it the hull of I. Further, for $x\in Q$, $m(x)=\{P\in \mathrm{Min}(Q)\;|\; x\notin P\}=\mathrm{Min}(Q)\cap (\mathcal {P}(Q){\setminus } V((x]))$.

The following lemma is an easy consequence of the above definitions.

Lemma 3.4

For a poset Q in $\mathbb {P}^\ell _{MFP}$, the collection $\{m(x)\;|x\in Q\}$ forms a basis of open sets of Min(Q).

The following lemma, very essential and frequently used in the sequel, can be found in Joshi and Mundlik (2013, Lemma 2.1).

Lemma 3.5

Let F be an $\ell$-filter of a poset Q with 0. Suppose that every maximal $\ell$-filter is maximal among all filters. Then F is a maximal $\ell$-filter if and only if the following condition $(*)$ holds:

$(*)$ for any $x\notin F$, there exists $y\in F$ such that $(x,y)^{\ell }=\{0\}$.

The following result follows from the dual statement of Lemma 3.5. For the sake of completeness, we provide its proof.

Lemma 3.6

Let Q be a poset with 1 and M be a u-ideal of Q. Suppose that every maximal u-ideal is maximal among all ideals. Then M is a maximal u-ideal if and only if the following condition $(*)$ holds:

$(*)$ for any $x\notin M$, there exists $y\in M$ such that $(x,y)^{u}=\{1\}$.

Proof

Let M be a maximal u-ideal of Q and let $x\notin M$. By the assumption, maximal u-ideals are maximal among all ideals, hence we have $M\vee (x]=Q$. As M is a u-ideal, by Lemma 1.2 there exists $y\in M$ with $(x,y)^u=\{1\}$.

Conversely, suppose the condition $(*)$ holds. Let $M_1$ be any ideal such that $M\subsetneqq M_1\subseteq Q$ and choose $x\in M_1{\setminus } M$. Then by the condition $(*),$ there exists $y\in M\subsetneqq M_1$ such that $(x,y)^u=\{1\}$. This implies $M_1=Q$ and thus M is a maximal ideal. $\square$

For join-semilattices, we have the following corollary.

Corollary 3.7

Let Q be a join-semilattice with 1 and M be an ideal of Q. Then M is a maximal ideal if and only if for any $x\notin M$ there is $y\in M$ such that $x\vee y=1.$

Theorem 3.8

Let P be a prime ideal of a poset Q in $\mathbb {P}^\ell _{MFP}$. Then the following statements are equivalent:

• (1) P is a minimal prime ideal;

• (2) P contains precisely one of (x] or $x^{\perp }$ for any $x\in Q$:

• (3) $x^{\perp }{\setminus } P\ne \emptyset$ for any $x\in P$;

• (4) $O(P)=P$, where $O(P)=\{x\in Q\;|\;(x,y)^\ell =\{0\}\text { for some }y\notin P\}$.

Proof

$(1)\Rightarrow (2)$: Suppose P is a minimal prime ideal of Q. Assume on the contrary that $x^{\perp }\subseteq P$ for $x\in P$. Since P is a minimal prime ideal, by Theorem 3.2, $Q{\setminus } P$ is a maximal $\ell$-filter. Now, $x\notin Q{\setminus } P$ and by Lemma 3.5, there exists $y\in Q{\setminus } P$ such that $(x,y)^{\ell }=\{0\}$. This implies that $y\in x^{\perp }\subseteq P$, a contradiction to the fact that $y\in Q{\setminus } P$. Hence $x^{\perp }\nsubseteq P$. On the other hand, if $x\notin P$ then we show that $x^{\perp }\subseteq P$. If $t\in x^{\perp }$ then $(x,t)^{\ell }=\{0\}\subseteq P$. Since P is prime and $x\notin P$, we get $t\in P$. Thus $x^{\perp }\subseteq P$.

$(2)\Rightarrow (3)$: Let x be any element of P. By (2), $x^{\perp }\nsubseteq P$. Therefore $x^{\perp }{\setminus } P\ne \emptyset$.

$(3)\Rightarrow (4)$: Obviously, $O(P)\subseteq P$. Let $x\in P$. By (3), $x^{\perp }{\setminus } P\ne \emptyset$. Hence there exists $t\in x^{\perp }{\setminus } P$. This implies that $(x,t)^{\ell }=\{0\}$. Hence by definition of O(P), we have $x\in O(P)$.

$(4)\Rightarrow (1)$: Suppose $O(P)=P$. In view of Theorem 3.2, to show that P is a minimal prime ideal, it is enough to verify that $Q{\setminus } P$ is a maximal $\ell$-filter. Let $x\notin Q{\setminus } P$. Then $x\in P=O(P)$. Therefore $(x,y)^{\ell }=\{0\}$ for some $y\in Q{\setminus } P$. By Lemma 3.5, $Q{\setminus } P$ is a maximal $\ell$-filter. $\square$

We prove the following theorem characterizing minimal prime ideals of a poset Q.

Theorem 3.9

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$ and P be a prime ideal of Q. Then P is a minimal prime ideal of Q if and only if for any $x\in P$ there exists $y\notin P$ such that $(x,y)^\ell =\{0\}$.

Proof

Let $x\in P$. As P is a minimal prime ideal, $x\in O(P)$ by Theorem 3.8. Then there exists $y\notin P$ such that $(x,y)^\ell =\{0\}$.

Conversely, suppose $x\in P$. Then by the assumption, there exists $y\notin P$ such that $(x,y)^\ell =\{0\}$. Therefore $y\in x^\perp {\setminus } P,$ that is, $x^\perp {\setminus } P\ne \emptyset$. Hence by Theorem 3.8, P is a minimal prime ideal of Q. $\square$

Lemma 3.10

If $Q \in \mathbb {P}^\ell _{MFP}$, then the intersection of all prime ideals of Q is zero.

Proof

Suppose $\displaystyle \bigcap \nolimits _{P\in \mathcal {P}(Q)} P\ne \{0\}.$ Then there exists $t\in \displaystyle \bigcap \nolimits _{P\in \mathcal {P}(Q)}P$ such that $t\ne 0$. By Zorn’s Lemma, there is a maximal $\ell$-filter F containing t. Applying Theorem 3.2, $Q{\setminus } F$ is a minimal prime ideal not containing t, a contradiction. $\square$

Lemma 3.11

If X and Y are any subsets of Min(Q) then $k(X\cup Y)=k(X)\cap k(Y).$

Proof

Obviously, $k(X\cup Y)\subseteq k(X),k(Y)$, thus $k(X\cup Y)\subseteq k(X)\cap k(Y)$. Suppose $k(X\cup Y)\subsetneqq k(X)\cap k(Y)$. Then there exists $x\in k(X)\cap k(Y)$ such that $x\notin k(X\cup Y)$. This implies $x\notin \bigcap _{P\in X\cup Y}P.$ Therefore $x\notin P$ for some $P\in X\cup Y$. Without loss of generality assume that $P\in X$. Then $x\notin \bigcap _{P\in X}P=k(X),$ a contradiction to the fact that $x\in k(X)\cap k(Y)$. $\square$

Note that $\mathrm{Min}(Q){\setminus } m(x)=h(x)$. Thus by Lemma 3.4, h(x) is a closed set.

Lemma 3.12

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$ and X be any open set of Min(Q). Then there is an ideal $I=\cap _{P\notin X}P$ in Q such that $X=Min(Q){\setminus } h(I)$.

Proof

Let X be an open set in $\mathrm{Min}(Q)$. Then $\mathrm{Min}(Q){\setminus } X$ is a closed set in $\mathrm{Min}(Q)$. Thus by Lemma 2.7, $\mathrm{Min}(Q){\setminus } X=\overline{(\mathrm{Min}(Q){\setminus } X)}=h(\cap _{P\notin X}P)$ and $\mathrm{Min}(Q){\setminus } h(\cap _{P\notin X}P)=X$. Considering $I=\cap _{P\notin X}P$, we have $X=\mathrm{Min}(Q){\setminus } h(\cap _{P\notin X}P)=\mathrm{Min}(Q){\setminus } h(I)$. $\square$

Remark 3.13

For any ideal I of a poset Q in $\mathbb {P}^\ell _\mathrm{MFP}$, the set h(I) is closed in $\mathrm{Min}(Q)$.

We prove the following lemma on annihilators.

Lemma 3.14

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$. Then the annihilator of an ideal I of Q is the intersection of all minimal prime ideals not containing I.

Proof

Let $I^{\perp }$ be the annihilator of I in Q. Then $I\cap I^\perp =\{0\}\subseteq P$, where P is any minimal prime ideal not containing I. As P is a minimal prime ideal not containing I, we have $I^\perp \subseteq P$. Hence $I^\perp \subseteq \bigcap \{ P\in \mathrm{Min}(Q)\;|\;I\nsubseteq P\}$. If $I^\perp \subsetneqq \bigcap \{ P\in \mathrm{Min}(Q)\;|\;I\nsubseteq P\}$ then there exists $x\in \bigcap \{ P\in \mathrm{Min}(Q)\;|\;I\nsubseteq P\}$ such that $x\notin I^\perp$. Therefore $(x,y)^{\ell }\ne \{0\}$ for some $y\in I$. Let $(0\ne )$ $a \in (x,y)^{\ell }$. Therefore [a) is a proper $\ell$-filter of Q. By Zorn’s Lemma, there exists a maximal $\ell$-filter, $M\supseteq [a)$. Now, $x,y\in [a)\subseteq M$. As M is a maximal $\ell$-filter, by Theorem 3.2, $Q{\setminus } M$ is a minimal prime ideal. Observe that $y\in I$ and $y\notin Q{\setminus } M$. Hence $I\nsubseteq Q{\setminus } M$. Therefore $Q{\setminus } M\in \{ P\in \mathrm{Min}(Q)\;|\;I\nsubseteq P\}$. But $x\in \bigcap \{ P\in \mathrm{Min}(Q)\;|\;I\nsubseteq P\}\subseteq Q{\setminus } M$, a contradiction to the fact that $x\in M$. $\square$

Using the above lemma, we have the following result.

Lemma 3.15

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$. Then for an ideal I of Q, $I^\perp =\bigcap \{P\in Min(Q)\;|\;I\nsubseteq P\}=k(Min(Q){\setminus } h(I)).$

Corollary 3.16

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$. Then $x^\perp =k(m(x))$ for any $x\in Q$.

A subset A of a topological space X is said to be clopen if it is both closed and open.

Corollary 3.17

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$ and $x\in Q$. Then the set m(x) is clopen in Min(Q).

Proof

It is clear that h(x) and $h(x^\perp )$ are closed in $\mathrm{Min}(Q)$. By Theorem 3.8, it is easy to prove that $h(x^\perp )=\mathrm{Min}(Q){\setminus } h(x)=m(x)$. Thus m(x) is both open and closed. $\square$

Definition 3.18

A topological space X is said to be a Hausdorff space ($T_2$ -space) if for each pair x, y of distinct points of X there exist neighborhoods $U_1$ and $U_2$ of x and y respectively, that are disjoint.

The following lemma extends the result of Pawar (1978).

Lemma 3.19

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$. Then Min(Q) is a Hausdorff space.

Proof

It follows from Corollary 3.17. $\square$

Corollary 3.20

Let Q be a pseudocomplemented meet-semilattice. Then Min(Q) is Hausdorff.

Lemma 3.21

If Q is a complemented poset then $\mathcal {P}(Q)$ is an antichain.

Proof

Let P be a prime ideal of Q. Let R be an ideal such that $P\subsetneqq R\subseteq Q$. Then choose $a\in R{\setminus } P$. By complementedness of Q there exists $a'$ such that $a'\in P\subsetneqq R$. Thus $Q=(a,a')^{u\ell }\subseteq R$ implies that $R=Q$. Thus P is a maximal ideal. $\square$

Remark 3.22

It is clear from Theorem 2.11, that if Q is a complemented poset distinct from a two-element chain then $\mathcal {P}_s(Q)$ is not a $T_1$-space and hence it is not Hausdorff. However, as a consequence of Lemmas 3.19 and 3.21, we prove the following corollary in which the subspace $\mathcal {P}(Q)$ is Hausdorff.

Corollary 3.23

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$ which is complemented. Then $\mathcal {P}(Q)$ is a Hausdorff space.

Proof

It follows from Lemma 3.21 that $\mathcal {P}(Q)=\mathrm{Min}(Q)$. By Lemma 3.19, $\mathcal {P}(Q)$ is Hausdorff. $\square$

In view of Theorem 1.7, we have the following corollary.

Corollary 3.24

(Balasubramani 2008) If Q is a pseudocomplemented meet-semilattice then $\mathcal {P}(Q)$ is Hausdorff.

Definition 3.25

A topological space X is said to be totally disconnected if given distinct points $x,y \in X$, there exists a clopen subset U of X such that $x\in U$ and $y \not \in U$.

Lemma 3.26

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$. Then Min(Q) is totally disconnected.

Proof

Consider any distinct minimal prime ideals $P_1,P_2$ of Q, and let e.g. $x\in P_1{\setminus } P_2$. By Corollary 3.17, m(x) is the clopen set of $\mathrm{Min}(Q)$ with $P_1\notin m(x)$ and $P_2\in m(x)$. $\square$

In view of Lemmas 3.21 and 3.26, we have following result as a corollary.

Corollary 3.27

Let Q be a complemented poset in $\mathbb {P}^\ell _{MFP}$. Then $\mathcal {P}(Q)$ is totally disconnected.

Definition 3.28

A topological space X is said to be completely regular, if it is a $T_1$-space and if for each point $x_0$ and each closed set A of X not containing $x_0$, there is a continuous function $f:X\rightarrow [0,1]$ such that $f(x_0)=\{1\}$ and $f(A)=\{0\}$.

Theorem 3.29

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$. Then Min(Q) is completely regular.

Proof

It follows from the fact that m(x) is clopen and $\mathrm{Min}(Q)$ is Hausdorff. $\square$

Corollary 3.30

If Q is a complemented poset in $\mathbb {P}^\ell _{ \mathrm MFP}$ then $\mathcal {P}(Q)$ is completely regular.

The concept of a quasicomplemented lattice was introduced and studied by Grillet and Varlet (1967). We extend it to posets as follows.

Definition 3.31

A poset Q with 0 is called quasicomplemented if for any $x\in Q$ there exists y such that $(x,y)^\ell =\{0\}$ and $\Big ((x]\vee (y]\Big )^\perp =\{0\}$.

In the following lemma, we need not require $Q\in \mathbb {P}^\ell _\mathrm{MFP}$.

Lemma 3.32

Let Q be a poset in $\mathbb {P}_{MFP}$ and $I,J\in Id(Q)$. Then $(I\vee J)^\perp =I^\perp \cap J^\perp .$

Proof

As $Q\in \mathbb {P}_\mathrm{MFP}$, applying Theorem 1.7, we have Q is a 0-distributive poset and hence Id(Q) is a pseudocomplemented lattice. We know that in a pseudocomplemented lattice $(I\vee J)^\perp =I^\perp \cap J^\perp$ for any $I,J\in Id(Q)$. $\square$

We characterized quasicomplemented posets as follows.

Lemma 3.33

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$. Then Q is quasicomplemented if and only if for any $x\in Q$ there exists $y\in Q$ such that $x^\perp =y^{\perp \perp }$.

Proof

Suppose Q is quasicomplemented. Then for any $x\in Q$ there exists $y\in Q$ such that $(x,y)^\ell =\{0\}$ and $((x]\vee (y])^\perp =\{0\}$. We claim that $x^\perp =y^{\perp \perp }$. Let $t\in x^\perp$. This gives $(t]\cap y^\perp \subseteq x^\perp \cap y^\perp =((x]\vee (y])^\perp =\{0\}$ by Lemma 3.32. Thus $(t]\cap y^\perp =\{0\}$, that is, $t\in y^{\perp \perp }$, and therefore $x^\perp \subseteq y^{\perp \perp }$. Now, we show that $y^{\perp \perp }\subseteq x^\perp$. As $(x,y)^\ell =\{0\}$ implies that $y\in x^\perp$, that is, $y^{\perp \perp }\subseteq x^\perp$. Hence $x^\perp =y^{\perp \perp }$.

Conversely, let for any $x\in Q$ there is $y\in Q$ such that $x^\perp =y^{\perp \perp }$. Then $x^\perp \cap y^\perp =y^{\perp \perp }\cap y^\perp =\{0\}$. This implies that $((x]\vee (y])^\perp =\{0\}$ by Lemma 3.32. Finally, $y\in y^{\perp \perp }=x^\perp$ yields $(x,y)^\ell =\{0\}$. $\square$

A poset Q is said to be a weakly quasicomplemented if for any $x\in Q$ there exist $y_1,y_2,\ldots ,y_n$ distinct from x such that $x^{\perp \perp }=\displaystyle \bigcap \nolimits _{i=1}^ny_i^\perp$.

It is clear that every quasicomplemented poset is also weakly quasicomplemented.

Lemma 3.34

If a poset Q is a 0-distributive join-semilattice then weak quasicomplementedness coincides with quasicomplementedness.

Proof

Let Q be a weakly quasicomplemented 0-distributive join-semilattice and $x\in Q$. By definition, there exist $y_1,y_2,\ldots ,y_n$ such that $x^{\perp \perp }=\cap _{i=1}^ny_i^\perp$. By Lemma 3.32, we have $x^{\perp \perp }=\cap _{i=1}^ny_i^\perp =(y_1\vee y_2\vee \ldots \vee y_n)^\perp$. Put $y=y_1\vee y_2\vee \ldots \vee y_n$. Then $x^{\perp \perp }=y^\perp$ and thus Q is quasicomplemented. $\square$

A topological space X is said to be compact if for every family of open sets $\{A_\alpha \}_{\alpha \in \Lambda }$ with $X\subseteq \bigcup _{\alpha \in \Lambda }A_\alpha$ there are $A_{\alpha _1},A_{\alpha _2},\ldots ,A_{\alpha _n}$ such that $X\subseteq \bigcup _{i=1}^n A_{\alpha _i}$.

The following result gives the necessary condition for compactness of $\mathrm{Min}(Q)$ which extends the result of Pawar (1978).

Theorem 3.35

Let Q be a poset in $\mathbb {P}^\ell _{MFP}$. If Min(Q) is compact then Q is weakly quasicomplemented.

Proof

Suppose $\mathrm{Min}(Q)$ is compact. Let $x \in Q$. If $x\notin P$ for all $P\in \mathrm{Min}(Q)$ then we claim that $x^\perp =\{0\}$. Let $t\in x^\perp$ and suppose $t\ne 0$. By Zorn’s Lemma, there exists a maximal $\ell$-filter F containing t. By Theorem 3.2, $Q{\setminus } F$ is a minimal prime ideal not containing t. Since $x\notin Q{\setminus } F$, and moreover since $Q{\setminus } F\in \mathrm{Min}(Q)$, we have $x^\perp \subseteq Q{\setminus } F$. But then $t\in x^\perp \subseteq Q{\setminus } F$, a contradiction. Therefore $x^\perp =\{0\}$ and thus $x^{\perp \perp }=0^\perp$.

Now, suppose that $x\in P$ for some $P\in \mathrm{Min}(Q)$. We prove that $\mathrm{Min}(Q)= m(x)\cup \{m(y)\;|\;y\in x^\perp {\setminus } P',~ P'\in h(x)\}$. Let $P_1\in \mathrm{Min}(Q)$. If $x\notin P_1$ then $P_1\in m(x)$ and we are done. Let $x\in P_1$ for $P_1\in \mathrm{Min}(Q)$. Then by Theorem 3.9, there exists $y\notin P_1$ such that $(x,y)^\ell =\{0\}$. Thus $P_1\in h(x)$ and $P_1\in m(y)$ for $y\in x^\perp {\setminus } P_1$. Therefore $\mathrm{Min}(Q)\subseteq m(x)\cup \{m(y)\;|\;y\in x^\perp {\setminus } P',~ P'\in h(x)\}$. The converse inclusion is obvious. Since $\mathrm{Min}(Q)$ is compact, there exist $y_1\in x^\perp {\setminus } P_1,y_2\in x^\perp {\setminus } P_2,\ldots ,y_n\in x^\perp {\setminus } P_n$ with $P_1,P_2,\ldots ,P_n\in h(x)$. Thus $\mathrm{Min}(Q)=m(x)\cup (\bigcup _{i=1}^n m(y_i))$. We show that $m(x)\cap (\bigcup _{i=1}^n m(y_i))=\emptyset$. Suppose there exists a minimal prime ideal $T\in m(x)\cap (\bigcup _{i=1}^n m(y_i))$. Then $x\notin T$ and $y_i\notin T$ for some $i\in \{1,2,\ldots ,n\}$. Since $y_i\in x^\perp$, we have $(x,y_i)^\ell =\{0\}\subseteq T$, a contradiction. Thus $m(x)\cap (\bigcup _{i=1}^n m(y_i))=\emptyset$. Now, $\{0\}=k(\mathrm{Min}(Q))=k(m(x)\cup (\bigcup _{i=1}^n m(y_i)))=k(m(x))\cap k(\cup _{i=1}^nm(y_i))=k(m(x))\cap (\bigcap _{i=1}^nk(m(y_i)))$, by Lemma 3.11. Thus by Corollary 3.16, we obtain $x^\perp \cap (\bigcap _{i=1}^ny_i^\perp )=\{0\}$. This implies $\bigcap _{i=1}^ny_i^\perp \subseteq x^{\perp \perp }$. Let $t\in x^{\perp \perp }$. Then $(t,y)^\ell =\{0\}$ for every $y\in x^\perp$. In particular, $(t,y_i)^\ell =\{0\}$, for every $i=1,2,\ldots ,n$. This yields $t\in y_i^\perp$, for every $i=1,2,\ldots ,n$ and $t\in \bigcap _{i=1}^{n}y_i^\perp$. Thus $x^{\perp \perp }= \bigcap _{i=1}^ny_i^\perp$. $\square$

Corollary 3.36

(Pawar 1978) For a 0-distributive meet-semilattice Q, the space Min(Q) is compact if and only if Q is weakly quasicomplemented.

4 Space of maximal ideals

In this section, we study the space of maximal ideals of a poset Q. Let $\mathrm{Max}(Q)$ be the set of all maximal ideals of a poset Q. Note that if a poset Q possesses 1 then by Zorn’s Lemma there exists a maximal ideal in Q. Therefore $\mathrm{Max}(Q)\ne \emptyset$.

Consider the ideal $M=\{0,a,b,c,d\}$ of the poset depicted in Fig. 2. It is easy to prove that M is not prime. Consequently, maximal ideals of a poset need not be prime. Therefore to study $\mathrm{Max}(Q)$ as a subspace of $\mathcal {P}(Q)$, first of all we need to fulfill the inclusion $\mathrm{Max}(Q)\subseteq \mathcal {P}(Q)$.

Remark 4.1

Recall that $\mathbb {P}^u_\mathrm{MIP}$ is the subclass of $\mathbb {P}_\mathrm{MIP}$ consisting of all posets having the greatest element 1 and with the property that every maximal u-ideal (maximal among all u-ideals) is a maximal ideal (maximal among all ideals). Note that if a poset Q is in $\mathbb {P}^u_\mathrm{MIP}$ then $\mathrm{Max}(Q)\subseteq \mathcal {P}(Q)$. Thus the assumption $Q\in \mathbb {P}^u_\mathrm{MIP}$ yields that $\mathrm{Max}(Q)$ forms a subspace of $\mathcal {P}(Q)$.

In view of Remark 1.4, it is clear that the class $\mathbb {P}^u_\mathrm{MIP}$ is richer than the class of 1-distributive posets (the dual of 0-distributive posets).

Any open set of $\mathrm{Max}(Q)$ is of the form $(\mathcal {P}(Q){\setminus } V(I))\cap \mathrm{Max}(Q)$. For every ideal I of Q we consider $U(I)=\{M\in \mathrm{Max}(Q)\;|\;I\subseteq M\}$ and we thus obtain $\mathrm{Max}(Q){\setminus } U(I)= (\mathcal {P}(Q){\setminus } V(I))\cap \mathrm{Max}(Q)$.

Lemma 4.2

Let Q be a poset in $\mathbb {P}^u_{MIP}$. Then the family $\{Max(Q){\setminus } U((x])\;|\;x\in Q\}$ forms a basis of Max(Q).

An element x of a poset Q with the greatest element 1 is said to be dually dense if $x^\top =\{1\},$ where $x^\top =\{y\in Q\;|\; (y,x)^u=\{1\}\}$. The set of all dually dense elements of a poset Q will be denoted by $D_1$.

Lemma 4.3

Let Q be a bounded poset. Suppose every maximal u-ideal is maximal among all ideals. Then the intersection of all maximal u-ideals of Q equals to $D_1$, the set of all dually dense elements of Q.

Proof

Let $x\in D_1$, that is, $x^\top =\{1\}$. Suppose on the contrary that $x\notin \displaystyle \bigcap M$, where the intersection is taken over all maximal u-ideals of Q. Then there exists a maximal u-ideal M such that $x\notin M$. By Lemma 3.6, there exists $y\in M$ such that $(x,y)^u=\{1\}.$ This gives $y\in x^\top =\{1\}$, a contradiction to the fact that $y\in M$.

Conversely, let $x\in \bigcap M$ and suppose that $x\notin D_1$. Then $x^\top \ne \{1\}$, that is, there exists $y\in x^\top$ such that $y\ne 1$. By Zorn’s Lemma, there is a maximal u-ideal M with $(y]\subseteq M$. As $x,y\in M,$ we have $Q=(x,y)^{u\ell }\subseteq M$, a contradiction to the maximality of M. $\square$

Corollary 4.4

Let Q be a bounded poset and suppose every maximal u-ideal is maximal among all ideals. Then $D_1$ is an ideal of Q.

Lemma 4.5

Let Q be a poset in $\mathbb {P}^u_{MIP}$. Then the closure of the set $Max_u(Q)$ of all maximal u-ideals of Q in $\mathcal {P}(Q)$ is $V(D_1)$.

Proof

Applying Lemma 2.7, we obtain $\overline{\mathrm{Max}_u(Q)}=V(\displaystyle \cap _{M\in \mathrm{Max}_u(Q)}M)=V(D_1)$. $\square$

The following concept is studied in Balasubramani (2004).

Definition 4.6

A topological space is said to be a $\pi _0$ -space, if every non-empty open set contains a non-empty closed set.

Obviously, every $T_1$-space is a $\pi _0$-space. We provide an example of a poset Q for which $\mathcal {P}(Q)$ is not $\pi _0$. Consider the poset depicted in Fig. 6. Here $\mathcal {P}(Q)=\{(a],(b],(c],(d]\}$. The collection of open sets is $\{\emptyset ,\mathcal {P}(Q){\setminus } V((a]),\mathcal {P}(Q){\setminus } V((b]),\mathcal {P}(Q){\setminus } V((c]),\mathcal {P}(Q){\setminus } V((d]),\mathcal {P}(Q){\setminus } V(\{0,a,b\}), \mathcal {P}(Q) \}$. Now, $\mathcal {P}(Q){\setminus } V((a])=\{(b]\}$ is a non-empty open set which does not contain any closed set. Thus $\mathcal {P}(Q)$ is not $\pi _0$. Hence it is not a $T_1$-space, as every $T_1$-space is a $\pi _0$-space.

Fig. 6

Example of a poset for which $\mathcal {P}(Q)$ need not be $\pi _0$

The following lemma essentially extends the result of Venkatanarasimhan (1972, Theorem 7) [see also Balasubramani (2008, Theorem 2.4)].

Lemma 4.7

Let Q be a poset in $\mathbb {P}^u_{MIP}$ with the least element 0. If the intersection of all maximal u-ideals is zero then $\mathcal {P}(Q)$ is $\pi _0$.

Proof

Suppose that the intersection of all maximal u-ideals is zero. By Lemma 4.3, $D_1=\{0\}$. Let $\mathcal {P}(Q){\setminus } V(I)$ be any non-empty open set of $\mathcal {P}(Q)$. Clearly, $I\supsetneqq D_1=\{0\}$. Then there exists $x\in I$ such that $x\notin D_1$. By Lemma 4.3, $x\notin \displaystyle \bigcap \nolimits _{M\in \mathrm{Max}_u(Q)}M$, where $\mathrm{Max}_u(Q)$ is the set of all maximal u-ideals of Q. Hence there is a maximal u-ideal M such that $x\notin M$ and thus $I\nsubseteq M$. Since $Q\in \mathbb {P}^u_\mathrm{MIP}$, it follows that M is a prime ideal. Further, $V(M)=\{M\}$ yields $\{M\}$ is a closed set. Therefore we get a non-empty closed set $\{M\}$ such that $\{M\}\subseteq \mathcal {P}(Q){\setminus } V(I)$ and consequently, $\mathcal {P}(Q)$ is $\pi _0$. $\square$

Fig. 7

A poset for which $\mathcal {P}(Q)$ is $\pi _0$ but the intersection of all maximal ideals need not be zero

The converse of Lemma 4.7 need not be true. Consider the poset depicted in Fig. 7. Here $\mathcal {P}(Q)=\{(e],(f]\}$. By Lemma 2.12, $\mathcal {P}(Q)$ is a $T_1$-space and hence it is $\pi _0$, but the intersection of all maximal ideals of Q is non-zero.

Definition 4.8

Let A and B be any two subsets of a topological space X. A is said to be weakly separable from B if $A\cap \overline{B}=\emptyset$.

We extend Theorem 2.6 of Balasubramani (2008) to posets as follows.

Theorem 4.9

Let Q be a poset in $\mathbb {P}^u_{MIP}.$ Then the subspace Max(Q) of $\mathcal {P}(Q)$ is the least subspace among all subspaces X of $\mathcal {P}(Q)$ such that X is not weakly separable from any point outside it.

Proof

First, we prove that $\mathrm{Max}(Q)$ has the stated property. For this, let $A\in \mathcal {P}(Q)$ be any element outside of $\mathrm{Max}(Q)$, that is, $A\notin \mathrm{Max}(Q)$. By Lemma 2.7, $\overline{\{A\}}=V(A)$. As $A\notin \mathrm{Max}(Q)$, there exists a maximal ideal $M\supseteq A$. By the hypothesis, M is a prime ideal. Thus $M\in V(A)$ and hence $M\in \overline{\{A\}}$. This implies $\mathrm{Max}(Q)\cap \overline{\{A\}}\ne \emptyset$ and therefore $\mathrm{Max}(Q)$ is not weakly separable from any element outside it.

Let Y be any subspace of $\mathcal {P}(Q)$ such that Y is not weakly separable from any point outside it. We claim that $\mathrm{Max}(Q)\subseteq Y$. Assume the opposite, that is, $\mathrm{Max}(Q)\nsubseteq Y$. Then there exists $M\in \mathrm{Max}(Q)$ such that $M\notin Y$. But $\overline{\{M\}}=\{M\}$. Thus $Y\cap \overline{\{M\}}=\emptyset ,$ a contradiction to the fact that Y is not weakly separable from any point outside it. $\square$

Recall that the set Id(Q) of all ideals of a poset Q forms an algebraic lattice with respect to the set inclusion and every principal ideal is a compact element of Id(Q).

In what follows, we study the compactness of the space of prime ideals and the space of maximal ideals. The following lemma extends Theorem 12 of Venkatanarasimhan (1972) (see also Theorem 2.7 of Balasubramani 2008) to posets.

Lemma 4.10

Let Q be a poset with 1 such that $Q\in \mathbb {P}^u_{MIP}$ and X be any subspace of $\mathcal {P}(Q)$ containing Max(Q). Then X is compact.

Proof

Let $X\subseteq \bigcup \{\mathcal {P}(Q){\setminus } V((x_\alpha ])\;|\;\alpha \in \Lambda \}$. Then we have$X\subseteq \mathcal {P}(Q){\setminus } \bigcap \{V((x_\alpha ])\}_{\alpha \in \Lambda }=\mathcal {P}(Q){\setminus } V(\vee (x_\alpha ])_{\alpha \in \Lambda }$. Hence $\mathrm{Max}(Q)\subseteq X\subseteq \mathcal {P}(Q){\setminus } V(\vee (x_\alpha ])_{\alpha \in \Lambda }$. If $\bigvee _{\alpha \in \Lambda } (x_\alpha ]\ne Q$ then there exists a maximal ideal $M\in \mathrm{Max}(Q)$ such that $\vee (x_\alpha ]\subseteq M$. Thus $M\in V(\vee (x_\alpha ])$, a contradiction to the fact that $\mathrm{Max}(Q)\subseteq X\subseteq \mathcal {P}(Q){\setminus } V(\vee (x_\alpha ])_{\alpha \in \Lambda }$. Thus $\bigvee _{\alpha \in \Lambda }(x_\alpha ]=Q=(1]$ which implies $\mathrm{Max}(Q)\subseteq X\subseteq \mathcal {P}(Q){\setminus } V(Q)$. Since Id(Q) is algebraic and every principal ideal is a compact element of Id(Q), there exist $x_1,x_2,\ldots ,x_n\in \{x_\alpha \;|\;\alpha \in \Lambda \}$ such that $(x_1]\vee \ldots \vee (x_n]=(1]=Q$. Thus $X\subseteq \mathcal {P}(Q){\setminus } V((x_1]\vee \ldots \vee (x_n])=\mathcal {P}(Q){\setminus } \bigcap _{i=1}^n\{V((x_i])\}=\bigcup _{i=1}^n\mathcal {P}(Q){\setminus } V((x_i])$ and, consequently, X is compact. $\square$

Corollary 4.11

Let Q be a poset in $\mathbb {P}^u_{MIP}$. Then Max(Q) as well as $\mathcal {P}(Q)$ both are compact.

Corollary 4.12

(Balasubramani 2008) If Q is a bounded pseudocomplemented semilattice then $\mathcal {P}(Q)$ is compact. In particular, Max(Q) is compact.

We extend Theorem 2.17 of Balasubramani (2008) to posets as follows.

Theorem 4.13

Let Q be a poset in $\mathbb {P}^u_{MIP}$. Then the subspace Max(Q) of $\mathcal {P}(Q)$ is Hausdorff if and only if there exist $a, b\in Q$ such that $a\notin M_1$, $b\notin M_2$ and $(a,b)^\ell \subseteq \bigcap _{M\in Max(Q)}M$ for any distinct $M_1,M_2 \in Max(Q)$. In particular, if Q is complemented then $\mathcal {P}(Q)$ is Hausdorff.

Proof

Suppose that $\mathrm{Max}(Q)$ is Hausdorff. Let $M_1, M_2$ be any two distinct elements of $\mathrm{Max}(Q)$. As $\mathrm{Max}(Q)$ is Hausdorff, there exist disjoint open neighborhoods $\mathrm{Max}(Q){\setminus } U(I)$ and $\mathrm{Max}(Q){\setminus } U(J)$ containing $M_1$ and $M_2$, respectively. This gives $I\nsubseteq M_1$ and $J\nsubseteq M_2$. Then there exist $a\in I$ and $b\in J$ such that $a\notin M_1$ and $b\notin M_2$. But $(\mathrm{Max}(Q){\setminus } U(I))\bigcap (\mathrm{Max}(Q){\setminus } U(J))=\emptyset$ yields $\mathrm{Max}(Q){\setminus } U(I\cap J)=\emptyset$. Therefore $U(I\cap J)=\mathrm{Max}(Q)$. This gives $(a,b)^\ell \subseteq I\cap J\subseteq M$ for all $M\in \mathrm{Max}(Q)$ and hence $(a,b)^\ell \subseteq \bigcap _{M\in \mathrm{Max}(Q)}M$.

Conversely, let $M_1$ and $M_2$ be any two distinct maximal ideals. By the hypothesis, there exist $a\notin M_1$ and $b\notin M_2$ such that $(a,b)^\ell \subseteq \bigcap _{M\in \mathrm{Max}(Q)}M$. Clearly, $\mathrm{Max}(Q){\setminus } U((a])$ and $\mathrm{Max}(Q){\setminus } U((b])$ are the neighborhoods of $M_1$ and $M_2$ respectively in $\mathrm{Max}(Q)$. As $(a,b)^\ell \subseteq \bigcap _{M\in \mathrm{Max}(Q)}M$, we have $(\mathrm{Max}(Q){\setminus } U((a]))\bigcap (\mathrm{Max}(Q){\setminus } U((b]))=\mathrm{Max}(Q){\setminus } U((a]\cap (b])=\emptyset$. This shows that $\mathrm{Max}(Q)$ is Hausdorff.

Since Q is complemented by Lemma 3.21, we have $\mathcal {P}(Q)$ is an anti-chain. Therefore every prime ideal is a minimal prime ideal. Let $P_1$ and $P_2$ be any two prime ideals of Q. Then $P_1\nsubseteq P_2$ and $P_2\nsubseteq P_1$. Therefore there exists $a\in P_1$ such that $a\notin P_2$. Let $a'$ be a complement of a. Then $a'\notin P_1$, as otherwise, $Q=(a,a')^{u\ell }\subseteq P_1$, a contradiction. Thus there exist $a'\notin P_1$ and $a\notin P_2$ such that $(a,a')^\ell \subseteq \bigcap _{P\in \mathcal {P}(Q)}P$ and $\mathcal {P}(Q)$ is Hausdorff. $\square$

Pawar and Thakare (1977) introduced the concept of a pm -lattice, that is, a bounded distributive lattice in which every prime ideal is contained in a unique maximal ideal. In the following theorem, Pawar (1978) gave a characterization of pm-lattices.

Theorem 4.14

(Pawar 1978) Let L be a bounded distributive lattice. Then L is a pm-lattice if and only if for any two distinct maximal ideals $M_1$ and $M_2$, there exist $a\notin M_1$ and $b\notin M_2$ with $a\wedge b=0$.

We adopt this equivalent condition to define the concept of pm-poset.

Definition 4.15

A bounded poset Q is said to be a pm -poset, if for any two distinct maximal ideals $M_1$ and $M_2$, there exist $a\notin M_1$ and $b\notin M_2$ such that $(a,b)^\ell =\{0\}$.

Note that in the definition of a pm-poset, we do not assume its distributivity.

Lemma 4.16

Let Q be a poset in $\mathbb {P}_{MIP}$. If Q is a pm-poset then every prime ideal is contained in a unique maximal ideal.

Proof

Let Q be a pm-poset. Suppose on the contrary that there exists a prime ideal P which is contained in two distinct maximal ideals $M_1$ and $M_2$. By the definition of a pm-poset, there exist $a\notin M_1$ and $b\notin M_2$ such that $(a,b)^\ell =\{0\}$. As $(a,b)^\ell =\{0\}\subseteq P$, we have $a\in P$ or $b\in P$. In either the case, we get a contradiction. Therefore every prime ideal is contained in a unique maximal ideal. $\square$

A topological space X is said to be normal if for each pair A, B of disjoint closed sets, there exist disjoint open sets containing A and B, respectively. Note that any compact Hausdorff space is normal.

Lemma 4.17

Let Q be a poset in $\mathbb {P}^u_{MIP}$. If Q is a pm-poset then Max(Q) is Hausdorff. Moreover, it is normal.

Proof

Let $M_1$ and $M_2$ be distinct elements of $\mathrm{Max}(Q)$. Since Q is a pm-poset, there exist $a\notin M_1$ and $b\notin M_2$ such that $(a,b)^\ell =\{0\}\subseteq \bigcap _{M\in \mathrm{Max}(Q)}M$. By Theorem 4.13, $\mathrm{Max}(Q)$ is Hausdorff. By Corollary 4.11, $\mathrm{Max}(Q)$ is a compact space. Thus $\mathrm{Max}(Q)$ is a normal space. $\square$

The converse of the above lemma is true if the intersection of all maximal ideals of Q is zero.

Theorem 4.18

Let Q be a poset in $\mathbb {P}^u_{MIP}$ with the least element 0 and such that the intersection of all maximal ideals of Q is zero. Then Max(Q) is Hausdorff if and only if Q is a pm-poset.

Proof

It follows from Lemma 4.13. If $\mathrm{Max}(Q)$ is Hausdorff, there exist $a\notin M_1$ and $b\notin M_2$ such that $(a,b)^\ell \subseteq \bigcap _{M\in \mathrm{Max}(Q)}M=\{0\}$ for any distinct maximal ideals $M_1$ and $M_2$. Thus Q is a pm-poset.

The converse follows from Lemma 4.17. $\square$

We conclude this paper by extending Theorem 1.1 to posets.

Theorem 4.19

Let Q be a poset in $\mathbb {P}^u_{MIP}$ with the least element 0 and such that the intersection of all maximal ideals of Q is zero. Then the following statements are equivalent:

• (1) Q is a pm-poset;

• (2) For any pair of distinct points $M_1$ and $M_2$ of Max(Q) there exist disjoint neighborhoods of $M_1$ and $M_2$ in $\mathcal {P}(Q)$;

• (3) Max(Q) is normal.

Moreover, if Q is a complemented poset, then the following statements are equivalent with the above three statements:

• (4) $\mathcal {P}(Q)$ is a normal space;

• (5) Min(Q) is a normal space.

Proof

$(1)\Rightarrow (2)$: Let Q be a pm-poset. Then for any two distinct elements $M_1$ and $M_2$ of $\mathrm{Max}(Q)$ there exist $a\notin M_1$ and $b\notin M_2$ with $(a,b)^\ell =\{0\}$. Thus $\mathcal {P}(Q){\setminus } V((a])$ and $\mathcal {P}(Q){\setminus } V((b])$ are the neighborhoods of $M_1$ and $M_2$ in $\mathcal {P}(Q)$, respectively. Since $(a,b)^\ell =\{0\}$, we have $(\mathcal {P}(Q){\setminus } V((a]))\bigcap (\mathcal {P}(Q){\setminus } V((b]))=\emptyset$.

$(2)\Rightarrow (3)$: First we show that $\mathrm{Max}(Q)$ is Hausdorff. Let $M_1$ and $M_2$ be distinct elements of $\mathrm{Max}(Q)$. By the assumption, there are disjoint neighborhoods $\mathcal {P}(Q){\setminus } V(I)$ and $\mathcal {P}(Q){\setminus } V(J)$ of $M_1$ and $M_2$, respectively. Therefore $I\nsubseteq M_1$ and $J\nsubseteq M_2$ and there exist $a\in I$ and $b\in J$ such that $a\notin M_1$ and $b\notin M_2$. As $(\mathcal {P}(Q){\setminus } V(I))\bigcap (\mathcal {P}(Q){\setminus } V(J))=\emptyset$, we have $I\cap J\subseteq P$ for all $P\in \mathcal {P}(Q)$, that is, $(a,b)^\ell \subseteq \bigcap _{P\in \mathcal {P}(Q)}P\subseteq \bigcap _{M\in \mathrm{Max}(Q)}M=\{0\}$. By Lemma 4.13, $\mathrm{Max}(Q)$ is a Hausdorff space. Since Q is a bounded poset, by Corollary 4.11, $\mathrm{Max}(Q)$ is a compact space. Hence $\mathrm{Max}(Q)$ is both compact and Hausdorff, that is, also normal.

$(3)\Rightarrow (1)$: It follows from Theorem 4.18.

$(3)\Leftrightarrow (4)\Leftrightarrow (5)$: It follows from Lemma 3.21.$\square$

Note that in a bounded distributive lattice $L,\cap \big \{P|P\in \mathcal {P}(L)\big \} =\{0\}$. Hence from the proof of Theorem 4.19, we have the following corollary.

Corollary 4.20

(Pawar and Thakare 1977) Let Q be a bounded distributive lattice. Then the following conditions are equivalent:

• (1) Q is a pm-lattice;

• (2) For any two maximal ideals $M_1$ and $M_2$ there exist $a\notin M_1$ and $b\notin M_2$ with $a\wedge b=0$;

• (3) For any pair of distinct points $M_1$ and $M_2$ of Max(Q) there exist disjoint neighborhoods of $M_1$ and $M_2$ in $\mathcal {P}(Q)$;

• (4) Max(Q) is a normal space.

Moreover, if Q is a complemented lattice, then the following statements are equivalent to the above four statements:

• (5) $\mathcal {P}(Q)$ is a normal space;

• (6) $\mathrm{Min}(Q)$ is a normal space.