A two-agent single-machine scheduling problem with late work criteria

Abstract

This paper addresses a two-agent scheduling problem where the objective is to minimize the total late work of the first agent, with the restriction that the maximum lateness of the second agent cannot exceed a given value. Two pseudo-polynomial dynamic programming algorithms are presented to find the optimal solutions for small-scale problem instances. For medium- to large-scale problem instances, a branch-and-bound algorithm incorporating the implementation of a lower bounding procedure, some dominance rules and a Tabu Search-based solution initialization, is developed to yield the optimal solution. Computational experiments are designed to examine the efficiency of the proposed algorithms and the impacts of all the relative parameters.

1 Introduction

1.1 Problem definition

The two-agent single-machine scheduling problem with late work criteria can be formally stated as follows. Assume that there are two competing agents, called agents A and B, respectively, where each agent has a set of non-preemptive jobs to be processed on a common machine. The machine can handle only one job at a time. Let $J^A=\left\{ {J_1^A ,J_2^A ,\ldots ,J_{n_A }^A } \right\}$ and $J^B=\left\{ {J_1^B ,J_2^B ,\ldots ,J_{n_B }^B } \right\}$ denote the job sets of agents Aand B, respectively, and let$X\in \{A,B\}$. The jobs of agent X are called X-jobs. All jobs in the X set are available at time zero, and associated with each job $J_j^X$, there is a nonnegative processing time $p_j^X$ and a due date $d_j^X$. Let S be a feasible schedule of the $n=n_A +n_B$ jobs, i.e., a feasible assignment of starting times for the jobs of both agents. The completion time of job $J_j^X$ is denoted as $C_j^X (S)$, the lateness of job $J_j^X$is given by $L_j^X (S)=C_j^X (S)-d_j^X$, and the late work $V_j^X (S)$ is defined as the amount of processing performed on job $J_j^X$after its due date $d_j^X$, i.e.,

$$\begin{aligned} V_j^X (S)=\left\{ {{\begin{array}{ll} 0,&{}\quad {C_j^X (S)\le d_j^X } \\ {C_j^X (S)-d_j^X ,} &{}\quad {d_j^X <C_j^X (S)<d_j^X +p_j^X } \\ {p_j^X ,}&{}\quad {d_j^X +p_j^X \le C_j^X (S)}. \end{array} }} \right. \end{aligned}$$

For convenience, let $C_j^X$, $L_j^X$ and $V_j^X$ denote $C_j^X (S)$, $L_j^X (S)$ and $V_j^X (S)$, respectively, whenever there is no confusion. If $V_j^X =0$, then job $J_j^X$ is said to be early; if $0<V_j^X <p_j^X$, then job $J_j^X$ is said to be partially early; alternatively, if $V_j^X =p_j^X$, then job $J_j^X$ is said to be late. Clearly, in the non-preemptive case, $V_j^X =\min \{ {\max \{ {C_j^X -d_j^X ,0} \},p_j^X } \}$. It is desired to minimize the total late work of agentA while keeping the maximum lateness of agent B not to exceed the fixed value of U. Adopting the three-field notation scheme $\alpha \vert \beta \vert \gamma ^A:\gamma ^B$, introduced by Agnetis et al. (2004) for two-agent scheduling problems, the problem is denoted by $1| |\sum {V_j^{A} } :L_{\max }^B$, where $L_{\max }^B =\max \{ {L_{j}^{B} \vert J_{j}^{B} \in J^{B} } \}$.

The problem described above may be found in various manufacturing applications. For example, a factory may process orders from two types of customers. The customer orders are interpreted as jobs to be executed. Each job from customer A is associated with a due date, while each job from customer B has a deadline. Jobs from customer A are penalized according to those parts of their jobs which are not executed on time, i.e., the total late work. Obviously, customer A is concerned with minimizing these late parts, and the manufacturer is also concerned with minimizing any order delays which cause financial loss. On the other hand, to provide a satisfactory quality of service, it is necessary to maintain the completion time of each job from customer B, less than or equal to its deadline, which is equivalent to keeping the maximum lateness of customer B less than or equal to some fixed value (if the fixed value is given as U, the due date of each B-job $J_j^B$, say $d_j^B$, can be defined as $d_j^B =\overline{d} _j^B -U$, where $\overline{d} _j^B$ is the deadline of job $J_j^B )$. This situation can be modeled as the problem under consideration.

1.2 Relevant previous work

Literature released that most researchers focused on studying all jobs belong to the same agent (Blazewicz et al. 1999, 2004; Guo et al. 2014; Li and Lu 2015; Potts and Van Wassenhove 1991a, b; Pei et al. 2015; Ren et al. 209; Sterna 2007, 2011; Zhao et al. 2014). However, recent developments in the field of distributed decision making have led to growing interest in multi-agent scheduling, whereby different agents share a common processing resource, and each agent wants to minimize a cost function depending only on its own jobs. These issues arise in different application contexts, including real-time systems, integrated service networks, industrial districts, telecommunications systems, and so on. Baker and Smith (2003) and Agnetis et al. (2004) were among the pioneers that introduced the two-agent concept to the scheduling field. The objective functions considered in their research include the maximum of regular functions (makespan or lateness), the total weighted completion time, and the number of tardy jobs. Baker and Smith (2003) focused on minimizing a convex combination of the objectives of the two agents on one machine, while Agnetis et al. (2004) studied the constrained optimization problem (i.e., one of the two objectives has to be minimized while the value of another objective has to be kept less than, or equal to, a fixed value) and the Pareto optimization problem (i.e., find the set of all nondominated pairs and a corresponding schedule of the two agents for each pair) in various machine settings. They obtained different scenarios for different combinations of objective functions for the two agents, and addressed the complexity of the various problems for each scenario. Since then, scheduling with multiple agents has attracted considerable attention in the literature, and most of the literature has been focused on dealing with the constrained optimization problem, such as Agnetis et al. (2009), Cheng et al. (2011), Gerstl and Mosheiov (2012), Lee et al. (2011, 2009), Leung et al. (2010), Li and Yuan (2012), Liu et al. (2011), Mor and Mosheiov (2010, 2011), Ng et al. (2006), Wan et al. (2010), Tuong et al. (2012), Yin et al. (2012a, b), Zhao and Lu (2013).

This paper focuses on the constrained optimization problem by including the late work criteria that estimates the quality of a schedule based on the duration of the late parts of jobs, not taking into account the amount of delay for the fully late jobs. Such a concept of an objective function has not been widely investigated, although it has found many practical applications. For example, in information processing, a job is a message carrying an amount of information proportional to its length, and all information received after a given due date is useless and is, therefore, referred to as information loss; in the process of collecting data in control systems, where the amount of exposed information after a due date influences the accuracy of a steering algorithm; in agriculture to optimize the land cultivation process, the amount of fertilizers not yet spread or plant protection substances, should be minimized, and so on. The late work criterion is first proposed in the context of parallel machines (Blazewicz 1984) and then applied to the one-machine scheduling problem (Potts and Van Wassenhove 1991a, b). Blazewicz (1984) considered parallel processors in a computing environment. He showed that the problem of scheduling jobs with release dates on identical parallel machines to minimize the total weighted late work is NP-hard in the strong sense, while the preemptive case can be solved in polynomial time by transformation to a min-cost flow problem. Potts and Van Wassenhove (1991a) considered the single-machine non-preemptive scheduling problem of minimizing the total late work. They showed that this problem is NP-hard and presented a pseudo-polynomial dynamic programming algorithm which established that it is NP-hard in the ordinary sense. They also showed that the special cases where all processing times are equal, and all due dates equal are polynomially solvable, respectively. Potts and Van Wassenhove (1991b) further proposed a branch-bound algorithm for the total late work problem, and derived two families of fully polynomial time approximation schemes. Lin and Hsu (2005) addressed the total late work problem on a single machine with release dates. They developed a branch-bound algorithm for solving it, and designed two $O(n\log n)$ algorithms for its special cases where all due dates are equal and preemptions are allowed, respectively. Ren et al. (209) considered the unbounded parallel-batching scheduling with the objective of minimizing total late work, and showing that this problem can be solved by a generic dynamic programming algorithm. Sterna (2007) deliberated on the two-machine non-preemptive flow shop scheduling problem with a total late work criterion and a common due date. Recently, this performance measure has been analyzed in the shop environment (Blazewicz et al. 1999, 2004). For papers that consider the scheduling problem of minimizing other late work criteria, the reader may refer to the survey paper of Sterna (2011).

In this paper, we combine the above two areas of machine scheduling, and address the scheduling problem to minimize the total late work of one agent subject to a given upper bound on the maximum lateness of the other agent on a single machine. To achieve these objectives, we

• (1) analyze the complexity of the problem and demonstrate that it is NP-hard based on a known NP-hard problem;

• (2) develop two pseudo-polynomial dynamic programming algorithms establishing that the problem is NP-hard in the ordinary sense;

• (3) present a branch-and-bound algorithm incorporating the implementation of a lower bounding procedure, some dominance rules and a Tabu Search-based solution initialization to derive the optimal solutions.

The rest of the paper is organized as follows: in Sect. 2, two pseudo-polynomial dynamic programming algorithms are derived for solving small-scale problems. In Sect. 3, a branch-and-bound algorithm is proposed for solving medium- to large-scale problems. In Sect. 4, computational experiments are designed to examine the effectiveness of the proposed algorithms. Section 5 concludes the paper and suggests some future research topics.

2 Two pseudo-polynomial time dynamic programming algorithms for the problem $1| |\sum {V_j^A } :L_{\max }^B$

Potts and Van Wassenhove (1991a) showed that the problem of minimizing the total late work, which could be denoted by $1| |\sum {V_j^A }$ is NP-hard based on a reduction from the Knapsack problem. Actually, our problem $1| |\sum {V_j^A } :L_{\max }^B$ can be viewed as an extension of problem $1| |\sum {V_j^A }$ in the following way: If the value U is appropriately large, our problem $1| |\sum {V_j^A } :L_{\max }^B$ is equivalent to the problem $1| |\sum {V_j^A }$. Thus, our problem is NP-hard, too. In the sequel we develop a pseudo-polynomial dynamic programming algorithm for problem $1||\sum {V_j^A } :L_{\max }^B$, establishing that it is NP-hard in the ordinary sense.

Let us first state a simple but useful property, which will be used in the algorithm design.

For each B-job $J_j^B$, let us define a deadline $D_j^B$, such that $C_j^B -d_j^B \le U$ for $C_j^B \le D_j^B$ and $C_j^B -d_j^B >U$ for $C_j^B >D_j^B$, i.e., $D_j^B -d_j^B =U$, implying that job $J_j^B$ is feasible if $C_j^B \le D_j^B$ and infeasible otherwise.

Proposition 2.1

For the problem $1| |\sum {V_j^A } :L_{\max }^B$, an optimal schedule exists which satisfies the following properties:

• (1) all the jobs are processed consecutively without idle time and the first job starts at time 0;

• (2) all the tardy A-jobs are processed after all the early, and partially early, A-jobs and all the B-jobs;

• (3) the early and partially early A-jobs are scheduled according to the earliest due date first (EDD) rule (i.e., in the non-decreasing order of $d_j^A$);

• (4) the B-jobs are scheduled according to the non-decreasing order of $D_j^B$.

Proof

The proof of (1) is straightforward and omitted. We prove (2)–(4).

• (2) Suppose that there exists a tardyA-job, $J_j^A$ which is scheduled before an early A-job, or a partially early A-job, or a B-job, in an optimal schedule. We can move job $J_j^A$ to the end of this schedule, which will decrease the completion times of the jobs scheduled after job $J_j^A$ in the original schedule and not affect the contribution of job $J_j^A$ to the objective of agent A, implying that the resulting schedule is still feasible and is not worse than the original one. When continuously doing this moving argument, the resulting schedule will satisfy the statement.

• (3) Consider an optimal schedule S where the A-jobs are not ordered according to the EDD rule. Let $J_i^A$ and $J_j^A$ be the first pair of jobs such that $d_i^A >d_j^A$. Assume that in schedule S, job $J_i^A$ starts at time t, then a set of B-jobs are consecutively scheduled (with a total load of, say, P), and then job $J_j^A$. We move job $J_i^A$ to be scheduled immediately after job $J_j^A$, leaving the remaining jobs in their original positions, to derive a new schedule $S'$ from schedule S. Then $C_i^A (S)=t+p_i^A , \quad C_j^A (S)=t+p_i^A +P+p_j^A =C_i^A (S')$ and $C_j^A (S')=t+P+p_j^A$. It is clear that all the B-jobs in $S'$ start their processing earlier (not later) than their starting times in S, implying that schedule $S'$ is feasible. In what follows, we prove that $S'$ is not an inferior schedule when compared to S, which suffices to show $V_i^A (S)+V_j^A (S)\ge V_j^A (S')+V_i^A (S').$ There are two cases to consider. Case 1 Job $J_j^A$ is early in $S'$. Then $V_j^A (S')=0$. Since $J_j^A$ is not late in S and $d_i^A >d_j^A$, we have

  $$\begin{aligned} V_i^A (S){+}V_j^A (S)\ge & {} V_j^A (S)=\max \{ {t{+}P{+}p_i^A {+}p_j^A {-}d_j^A ,0} \}\\\ge & {} \max \{ {t+P+p_j^A +p_i^A -d_i^A ,0} \}\\\ge & {} V_i^A (S')=V_i^A (S')+V_j^A (S'). \end{aligned}$$

  Case 2 Job $J_j^A$ is partially early in $S'$. Then $J_j^A$ is also partially early in S, and $V_j^A (S')=t+P+p_j^A -d_j^A$. Thus, we have

  $$\begin{aligned} V_i^A (S)+V_j^A (S)\ge & {} V_j^A (S)=t+P+p_i^A +p_j^A -d_j^A\\= & {} p_i^A +V_j^A (S')\\\ge & {} V_i^A (S')+V_j^A (S'). \end{aligned}$$

  In both cases, we have $V_i^A (S)+V_j^A (S)\ge V_j^A (S')+V_i^A (S')$, as required. Note also that if job $J_i^A$ is late in $S'$, then it is moved to the last position and the resulting schedule will be better than $S'$. Thus, repeating this interchange argument for all A-jobs not sequenced according to the required rule will yield the result.

• (4) Analogous to the proof of (3), consider an optimal schedule S where the B-jobs are not ordered according to the non-decreasing order of $D_j^B$. Let $J_i^B$ and $J_j^B$ be the first pair of jobs such as that of $D_i^B >D_j^B$. Assume that in schedule S, job $J_i^B$ starts its processing at time t, then a set of A-jobs are consecutively scheduled, and then job $J_j^B$. We move job $J_i^B$ to be scheduled immediately after job $J_j^B$, leaving the remaining jobs in their original positions, to derive a new schedule $S'$ from scheduleS. Then we have:

  • (i) Schedule $S'$ is feasible. Since S is feasible, we have $C_j^B (S)\le D_j^B$. It follows from $C_i^B (S')=C_j^B (S)$ and $D_i^B >D_j^B$ that $J_i^B$ is feasible in $S'$. Job $J_j^B$ is scheduled earlier in $S'$, and thus remains feasible.

  • (ii) The total late work of A-jobs in $S'$ is not larger than that in S, since all the A-jobs in $S'$ start their processing earlier (not later) than their starting times in S.

Thus, repeating this interchange argument for all B-jobs not sequenced according to the required rule will yield the result. This completes the proof.

Hereafter, it is assumed in this paper that the A-jobs are re-indexed according to the earliest due date first (EDD) rule of $d_j^A$ and the B-jobs are re-indexed according to the non-decreasing order of deadline $D_j^B$.

Now a dynamic programming algorithm, DP1, is presented for the problem of using the trial state representation that strongly relies on Proposition 2.1. In the dynamic programming formulation, the completion time of the last early A-job, or partially early A-job, or B-job, is the state variable, while the total late work of A-jobs is a function value. Specifically, in the dynamic programming algorithm DP1, (i, j, t) denotes a state representing the situation where the jobs $\{ {J_1^A ,J_2^A ,\ldots ,J_i^A } \}$ and $\{ {J_1^B ,J_2^B ,\ldots ,J_j^B } \}$ have been scheduled, t denotes the completion time of the last early A-job, or partially early A-job, or B-job, and no B-job completes after its induced deadline; F(i, j, t) represents the minimum total late work of A-jobs for the partial schedules corresponding to the state (i, j, t); and S(i, j, t) denotes any schedule in state (i, j, t) with solution value F(i, j, t). By definition, we set $F(i,j,t)=+\infty$ if no such schedule exists. Since all early and partially early A-jobs and B-jobs among $\{ {J_1^A ,J_2^A ,\ldots ,J_i^A ,J_1^B ,J_2^B ,\ldots ,J_j^B } \}$ are completed by this time

$$\begin{aligned} a_{ij}= & {} \min \left\{ \sum \limits _{k=1}^i p_k^A +\sum \limits _{k=1}^j p_k^B ,\max \right. \\&\quad \times \left. \left\{ {\max _{k=1,\ldots ,i} \{ {p_k^A +d_k^A -1} \},D_j^B } \right\} \right\} , \end{aligned}$$

and so F(i, j, t) is defined for $i=1,2,\ldots ,n_A$, $j=1,2,\ldots ,n_B$ and $t=0,1,\ldots ,a_{ij}$. The schedule S(i, j, t) must have been constructed by taking one of the following three decisions in a previous state.

• (1) Job $J_i^A$ is early, or partially early, scheduled after job $J_j^B$. In this case, there must be $t-d_i^A \le p_i^A$ and S(i, j, t) must have been obtained from schedule $S(i-1,j,t-p_i^A )$ and $F(i,j,t)=F(i-1,j,t-p_i^A )+\max \{ {t-d_i^A ,0} \}$.

• (2) Job $J_i^A$ is late. In this case, S(i, j, t) must have been obtained from schedule $S(i-1,j,t)$ and $F(i,j,t)=F(i-1,j,t)+p_i^A$.

• (3) Job $J_j^B$ is scheduled after the last early, or partially early, A-job. In this case, there must be $t\le D_j^B$ and S(i, j, t) must have been obtained from schedule $S(i,j-1,t-p_j^B )$ and $F(i,j,t)=F(i,j-1,t-p_j^B )$.

Based on the results of the above analysis, a dynamic programming recursion can be written as follows.

Theorem 2.2

Algorithm DP1 solves the problem $1| |\sum {V_j^A } :L_{\max }^B$ in $O( n_A n_B \mathrm{min} \{ P^A+P^B,\max \{ {\max _{k=1,\ldots ,n_A } \{ {p_k^A +d_k^A -1} \},D_{n_B }^B } \} \})$ time, where $P^A=\sum \nolimits _{J_j^A \in J^A} {p_j^A }$ and $P^B=\sum \nolimits _{J_j^B \in J^B} {p_j^B }$.

Proof

Optimality is guaranteed by Proposition 2.1 and the principles underlying dynamic programming. Consider the computational complexity of the dynamic programming solution algorithm. Step 1 implements two sorting procedures that require $O(n_A \log n_A)$ time and $O(n_B \log n_B)$ time, respectively. In Step 2, there are at most $O( n_A n_B \min \{ \sum \nolimits _{k=1}^{n_A } p_k^A +\sum \nolimits _{k=1}^{n_B } p_k^B ,\max \{ \max _{k=1,\ldots ,n_A } \{ p_k^A + d_k^A -1 \}, D_{n_B }^B \} \})$ states (i, j, t), while computing each F(i, j, t) requires constant time. Therefore, the overall computational complexity of the algorithm is indeed $O( n_A n_B \min \{ {P^A+P^B,\max \{ {\max _{k=1,\ldots ,n_A } \{ {p_k^A +d_k^A -1} \},D_{n_B }^B } \}} \})$.

As an alternative, we present another pseudo-polynomial time dynamic programming algorithm DP2 for the problem $1| |\sum {V_j^A } :L_{\max }^B$, in which the total late work of A-jobs is the state variables while the completion time of the last early A-job or partially early A-job or B-job is a function value.

Let $C(i,j,V^A)$ denote the minimum completion time of the last early job A-job or partially early A-job or B-job subject to that jobs $\{ {J_1^A ,J_2^A ,\ldots ,J_i^A } \}$ and $\{ {J_1^B ,J_2^B ,\ldots ,J_j^B } \}$ are scheduled, and the total late work of A-jobs is $V^A$. A formal statement of this dynamic programming algorithm is as follows.

Theorem 2.3

Algorithm DP2 solves the problem $1| |\sum {V_j^A } :L_{\max }^B$ in $O( {n_A n_B P^A})$ time.

Proof

The proof is similar to that of Theorem 2.2.

The above dynamic programming algorithm can find an optimal solution for the problem. Although these exact algorithms may be very difficult to solve with the increase of the number of jobs, they are valid algorithms for optimally solving the problem if computation capacity of the running environment is available and the problem scale is small. Despite this, there is still the need to find optimal or near-optimal solutions for the medium- to large-scale problem. In the following sections, we will propose a branch-and-bound algorithm combining a lower bounding procedure, some dominance rules and a Tabu Search-based solution initialization to solve the problem considered here.

3 The branch-and-bound algorithm

The branch-and-bound method has been successfully used to solve many combinatorial problems (see Ke amd Ma 2014; Lee et al. 2011; Lin and Hsu 2005; Li et al. 2014; Roy et al. 2014; Wu et al. 2014; Yin et al. 2013a, b; Yuan et al. 2014). Inspired by these observations, we apply this method to solve our problem. To develop an efficient branch-and-bound algorithm, a Tabu Search-based solution initialization is introduced to acquire a near-optimal solution, a lower bound computation is designed to improve the performance, and a number of policies are taken into consideration to reduce the search space. Then the procedure of branch-and-bound algorithm with depth-first plus backtracking search strategy are provided.

3.1 Tabu Search-based solution initialization

To start the branch and bound algorithm from a near-optimal solution, we adopt a Tabu Search algorithm which has been widely applied in many combinatorial optimization problems (refer to Glover 1977, 1989). A Tabu Search algorithm begins with an initial solution. Then, in each iteration, a move is performed to the best neighboring solution although its quality maybe not better than the current one. To avoid cycling, a short-term memory (called tabu list) is used for recording a fixed number of recent moves. The main function of the tabu list is to prevent returning to a local minimum that has been visited before (Liao and Huang 2011).

Based on the above statements and Proposition 2.1, the details about the Tabu Search steps are summarized as follows;

• Step 1 initialize an empty Tabu list and the iteration number.

• Step 2 construct the initial solution, where the B-jobs, re-indexed according to the non-decreasing order of $D_j^B$, are scheduled first, followed by the A-jobs re-indexed according to the EDD rule, and set the current solution as the best solution S$^{*}$.

• Step 3 explore the associated neighborhood of the current sequence and determine whether there is a solution $S_{1}$ with the minimum objective function value in associated neighborhood and it is not in the Tabu list.

• Step 4 update the Tabu list. If $S_1 <S^{*}$, then set $S^{*}$ = $S_{1}$.

• Step 5 update the iteration number. If there is not a solution in the/an associated neighborhood, and it is not in the Tabu list, or the maximum number of iterations is reached, then output the final solution. Otherwise, go to Step 3.

3.2 Lower bound computation

The efficiency of the branch-and-bound algorithm largely depends on the lower bound of the partial sequence. In most cases, computing a lower bound consists of relaxing some constraints in different ways, and in solving a new, easier problem. In this subsection, two lower bounds are proposed for the problem $1| |\sum {V_j^A } :L_{\max }^B$ by considering the preemption version of the problem, denoted as $1\left| {\mathrm{prmp}} \right| \sum {V_j^A } :L_{\max }^B$ and by relaxing due dates of A-jobs in such a way that the resulting problem is polynomially solvable, respectively.

Let us first consider the lower bound reached by relaxing the non-preemptive constraint. Define the latest starting time $\mathrm{LS}_j^B$ of job $J_j^B$ as the maximum value of the starting time of $J_j^B$ that can attain a feasible schedule, such that $C_j^B \le D_j^B$ for all $J_j^B \in J^B$. Start from the last B-job $J_{n_B }^B$ and set $\mathrm{LS}_{n_B } =D_{n_B }^B -p_{n_B }^B$. Continue backwards, letting $\mathrm{LS}_j =\min \{ {\mathrm{LS}_{j+1} ,D_j^B } \}-p_j^B$ for all $j=n_B -1,\ldots ,k$. Clearly if job $J_j^B$ starts after time $\mathrm{LS}_j$, at least one B-job attains $C_j^B -d_j^B >U$.

For each B-job $J_j^B$, let it start its processing at $\mathrm{LS}_j^B$. Define B-block i as the i set of contiguously processed jobs of agent B. Let the starting time and completion time of each block i be s(i) and f(i), respectively. For each B-block i, the B-jobs belonging to the set $\{J_j^B \in J^B\vert s(i)\le \mathrm{LS}_j^B <f(i)\}$ are said to be associated with B-block i.

Proposition 3.1

There exists an optimal schedule to the problem $1\left| {\mathrm{prmp}} \right| \sum {V_j^A } :L_{\max }^B$, in which B-jobs are non-preemptively scheduled in the B-blocks.

Proof

The proof is similar to that of Lemma 6.2 in Agnetis et al. (2004). For completeness, it is briefly repeated as below. In an optimal schedule to the problem $1\left| {\mathrm{prmp}} \right| \sum {V_j^A } :L_{\max }^B$, all the B-jobs associated with B-block i complete before f(i). Thus, if we move all the pieces of each such job to exactly fit the interval [s(i), f(i)], we obtain a new schedule in which the completion times of A-jobs are equal to, or less than that in the original schedule, because we only moved pieces of A-jobs backward.

Proposition 3.1 allows us to fix the position of the B-jobs in an optimal schedule to the problem $1\left| {\mathrm{prmp}} \right| \sum {V_j^A } :L_{\max }^B$. The position of the A-jobs can then be found by solving an auxiliary instance of the well-known single-agent problem $1\vert \vert \sum {V_j}$ solved by Potts and Van Wassenhove (1991a). Given an instance of $1\left| {\mathrm{prmp}} \right| \sum {V_j^A } :L_{\max }^B$, such an auxiliary instance which consists of the A-jobs only with modified due dates is constructed as follows.

For each job $J_j^A$, if $d_j^A$ falls outside any B-block, we subtract from $d_j^A$ the total length of all B-blocks preceding $d_j^A$, i.e., we define the modified due date $\mathrm{D}_j^A$ as $\mathrm{D}_j^A =d_j^A -\sum \nolimits _{f(i)\le d_j^A } {(f(i)-s(i)} )$. If $d_j^A$falls within the B-blockk, we let $\mathrm{D}_j^A =s(k)-\sum \nolimits _{f(i)<d_j^A } {(f(i)-s(i)} )$.

Renumber the A-jobs in non-decreasing order of $\mathrm{D}_j^A$, we have the following result.

Theorem 3.2

(Potts and Van Wassenhove 1991a) $T_{\max } =\max \{ {\max _{j=1,2,\ldots ,n_A } \{ {\sum \nolimits _{i=1}^j {p_i^A -\mathrm{D}_j^A } } \},0} \}$ is the optimal solution value for the problem $1\left| {\mathrm{prmp}} \right| \sum {V_j^A }$ with modified due dates.

Based on the above analysis, our first lower bound algorithm for the problem $1| |\sum {V_j^A } :L_{\max }^B$ can be formally described as follows.

In what follows, another lower bound is developed by considering a special case where the due dates of A-jobs are equal, i.e., $d_j^A =\max _{J_j^A \in J^A} \{d_j^A \}$ for $j=1,\ldots ,n_A$. For this special case, it is easy to see that the total late work for the problem $1\vert \vert \sum {V_j^A }$ with modified due dates is equal to $LB_2 =\max \{ {\sum \nolimits _{J_j^A \in J^A} {p_j^A -\mathrm{D}_{\max }^A ,0} } \}$, where $\mathrm{D}_{\max }^A =\max _{J_j^A \in J^A} \{\mathrm{D}_j^A \}$, which is also the optimal solution value for the problem $1\left| {\mathrm{prmp}} \right| \sum {V_j^A } :L_{\max }^B$ and hence a lower bound for the original problem.

3.3 Dominance rules

Proposition 2.1 plays an important role because the sequencing element of the problem can be eliminated. To further speed up the search process, we will establish some dominance rules in this subsection.

Assume that schedule S has two adjacent jobs $J_i^X$ and $J_j^Y$ with $J_i^X$ immediately preceding $J_j^Y$, where $X,Y\in \{A,B\}$. Now, we create from S a new schedule $S'$ by swapping jobs $J_i^X$ and $J_j^Y$, and leaving the other jobs unchanged in schedule S. In addition, it is assumed that the starting time to process $J_i^X$ in S is t. The following two propositions develop conditions for one schedule to dominate another.

Proposition 3.3

If $J_i^X \in J^A,J_j^Y \in J^B$ and $t+p_i^A +p_j^B -d_j^B \le U$, then S dominates $S'$.

Proposition 3.4

If $J_i^X ,J_j^Y \in J^B$,$t+p_i^B -d_i^B \le U<t+p_j^B +p_i^B -d_i^B$ and $t+p_i^B +p_j^B \quad -d_j^B \le U$, then S dominates $S'$.

Next, a result is presented to determine the feasibility of a partial schedule. Let $(\pi ,\pi ')$ be a schedule of jobs where $\pi$ is the scheduled part with k jobs and $\pi '$ is the unscheduled part. Moreover, let $C_{[k]}$ be the completion time of the last job in $\pi$.

Proposition 3.5

If there is a B-job $J_j^B$ in $\pi '$ such that $C_{[k]} +p_j^B -d_j^B >U$, then $(\pi ,\pi ')$ is not a feasible schedule.

3.4 Main procedure of branch-and-bound

Based on the Tabu algorithm, the lower bound procedure and the dominance rules, a procedure of branch-and-bound with depth-first plus backtracking search strategy is developed. The proposed branch-and-bound algorithm uses a basic scheme. During the computation, we keep the list of unexplored nodes arranged in increasing order of the corresponding lower bound ($\mathrm{LB}=\max \left\{ {\mathrm{LB}_1 ,\mathrm{LB}_2 } \right\} )$ computed using Algorithms $\mathrm{LB}_1$ and $\mathrm{LB}_2$ (ties are broken according to the nonincreasing order of the number of scheduled jobs). Each node represents a partial schedule which is also a partial list. The algorithm always tries to develop the head of the list. The branching from a node consists in creating new nodes by adding an unscheduled job to the end of the partial list. Before any new node is created, the properties (Propositions 2.1, 3.3–3.5) are applied in the order of Propositions 2.1, 3.5 and 3.3 and then Proposition 3.4. For each node of the search tree, which cannot be eliminated by dominance properties, a lower bound ($\mathrm{LB}=\max \{ {\mathrm{LB}_1 ,\mathrm{LB}_2 } \})$ and an upper bound (obtained using the Tabu Search algorithm) are calculated, respectively. At each bounding procedure, if the resulting value of an upper bound is lower than the global upper bound, we immediately update the global upper bound with the resulting value. Meanwhile, once the lower bound is larger than the upper bound, this node will be also discarded without further searching. Finally, all nodes have been either fathomed or identified, and then we have completed the branch-and-bound algorithm.

4 Computational experiments

To examine the performances of the proposed branch-and-bound (B&B) algorithm, small-scale and medium- to large-scale problem instances are considered in the following computational experiments. All the algorithms are implemented in MATLAB and run on a PC with 4G RAM, Intel Core i5 CPU 2.5 GHz.

For the small-scale problems in the first part, cases with job number $n=14$ and 16 are generated. The job processing times are randomly generated from a uniform distribution over the integers 1–100. Meanwhile, following the design of Hall and Posner (2001), the due dates of the jobs are randomly generated from another uniform distribution over the integers between $Td^l$ and $Td^u$, where T is the sum of the normal processing times of the n jobs, i.e., $T=\sum \nolimits _{i=1}^n {p_i }$, and the six combinations of $(d^l,d^u)$ including (0.0, 0.2), (0.0, 0.6), (0.0, 1.0), (0.4, 0.6), (0.4, 1.0), and (0.8, 1.0), are used to evaluate the impacts of all the proposed algorithms when the due date changes. For each of the six settings of $(d^l,d^u)$, the values of $(n_A ,n_B )$ are taken as (6, 8), (7, 7). and (8, 6) at $n=14$, and (7, 9), (8, 8), and (9, 7) at n=16, respectively, to evaluate the impacts of all the proposed algorithms when the value of $(n_A ,n_B )$ changes. A total of 36 cases are examined and 50 independent runs take place for each case, and thus a total of 1800 instances are tested in this part. To evaluate the performance of the branch-and-bound algorithm, we report the average and the maximum numbers of nodes as well as the average and the maximum execution times (in s). We also record the mean and maximum error percentages of the heuristic algorithms. The error percentage of the solution produced by the heuristic algorithm is defined by

$$\begin{aligned} {(H-H^*)}/ {H^*}, \end{aligned}$$

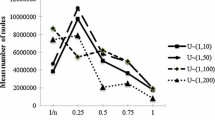
where H is the total late work obtained from the heuristic method or Tabu algorithm and $H^*$ is the total late work of the optimal schedule obtained from the branch-and-bound method. The computational time of the heuristic algorithms is not recorded since they finish in a small amount of time. For time-saving reason, the branch-and-bound algorithm end when the number of nodes exceeded 10$^{9}$, and we record those instances with the number of nodes less than 10$^{9}$ as feasible solution (FS). All the results are reported in Table 1 and Figs. 1, 2, 3, 4 and 5. Moreover, Table 1 is further summarized in Table 2 and Figs. 6, 7, 8 and 9.

Table 1 The performances of the branch-and-bound and Tabu algorithms

Table 2 The impacts of parameters for the branch-and-bound and Tabu algorithms

As shown in Figs. 1 and 2, when fixed $d^l=0.0$, it can be seen that the branch-and-bound algorithm takes more nodes as the value of $d^u$ increases. On the other hand, when fixed $d^u=1.0$, it can be observed in Figs. 3 and 4 that the branch-and-bound algorithm takes more nodes as the value of $d^l$ becomes larger. Both observations demonstrate that the branch-and-bound algorithm needs a bit more time to solve an instance as the values of $(d^l,d^u)$ are growing larger. The situation also indicates in Table 1 that the number of FS decreases as the values of $(d^l,d^u)$ are growing larger. For the impact of branch-and-bound algorithm over different values of $(n_A ,n_B )$, it can be seen from Figs. 1, 2, 3 and 4 that the branch-and-bound algorithm can easily solve an instance within a reasonable time, or nodes, as the number of $n_A$ increases or $n_B$ decreases. A similar trend also indicates in Table 1 that when fixed $n=16$, FS declines as the number of $n_A$ increases or $n_B$ decreases. In addition, the nodes grow sharply as n increases due to the fact that the problem is an NP-hard one. However, the ratio of instances solved out is up to 1700/1800 or 94 % under the help of proposed dominances, a lower bound, and an initial solution in the branch-and-bound method. A similar performance can be observed in Table 2 that the mean of nodes increases as $d^u$ increases or $n_A$ decreases. The most difficult case occurs at the range of $(d^l,d^u)$= (0.8, 1.0).

Fig. 1

The performance of B&B when fix $n=14$ and $d^l=0.0$

Fig. 2

The performance of B&B when fix $n=16$ and $d^l=0.0$

Fig. 3

The performance of B&B when fix $n=14$ and $d^u=1.0$

Fig. 4

The performance of B&B when fix $n=16$ and $d^u=1.0$

Fig. 5

The performance of three proposed Tabu algorithms for the small number jobs

Fig. 6

The performance of three proposed Tabu algorithms for the small number jobs ($n=14$)

Fig. 7

The performance of three proposed Tabu’s algorithms for the small number jobs ($n=16$)

Fig. 8

The performance of three proposed Tabu algorithms for the small number jobs ($n=14$)

Fig. 9

The performance of three proposed Tabu algorithms for the small number jobs ($n=16$)

To guarantee that the initial solution is feasible, it is generated by arranging the jobs of the second agent in the non-decreasing order of $D_j^B$, followed by arranging the jobs of the first agent in the EDD order. The second is generated by arranging the jobs of the second agent in the non-decreasing order of $D_j^B$, followed by arranging the jobs of the first agent in the SPT order. The third is generated by arranging the jobs of the second agent in the non-decreasing order of $D_j^B$, followed by arranging the jobs of the first agent in a non-decreasing order of the sum of processing time and due date. We recode Tabu_1, Tabu_2, and Tabu_3, for three Tabu Search algorithms and $H_{1}$, $H_{2}$, and $H_{3}$, for their corresponding initials, respectively. Tabu Search algorithm proposed terminates after 2000 iterations according to the pretest.

It can be seen in Table 1 that on average, the performance for the three initials is not good since the mean error percentages are 312.96, 555.33, and 344.47, for $H_{1}$, $H_{2}$, and $H_{3}$, respectively. When using the three Tabu search algorithms for solution initialization, it can be observed that the mean error percentages are 2.30 and 1.36 for Tabu_1, 3.67 and 1.33 for Tabu_2, and 1.70 and 2.31 for Tabu_3 at $n=14$ and 16, respectively. When further evaluating the impact of the due dates, it can be seen in Table 2 and Figs. 6 and 7 that the mean error percentage increases as $d^l(d^u)$, increases when fixed $d^u(d^l)$, no matter whether it is Tabu_1, or Tabu_2, or Tabu_3. As for the impact of the number of jobs from each agent, as shown in Table 2 and Figs. 8 and 9, all three Tabu algorithms perform well when the number of jobs from agent B increases. It can be seen in Table 1 and Fig. 5 that the mean error percentages stayed at the interval (0.00, 16.38) for Tabu_1 (0.00, 17.11) for Tabu_2, and (0.00, 9.61), respectively. It can also be seen that the maximum error percentages are found up to 600 for Tabu_1, 700 for Tabu_2, and 333.33 for Tabu_3. In such a case, the instance has a larger value of due date, which is sometime a bit smaller value of an optimal solution. Overall, on average, Tabu_1 of 1.84 performs slightly better than Tabu_3 of 2.00 and Tabu_2 of 2.54. However, as shown in Fig. 5, there is no absolute dominance relationship among the three proposed algorithms. Furthermore, each algorithm takes a solution within less than a second. To obtain a good solution, we further combine three proposed algorithms into Tabu$^{*}$ where Tabu$^{*}=\min${Tabu_1, Tabu_2, Tabu_3}. It can be seen that the mean error percentage of Tabu$^{*}$ could be further declined to 0.48. In addition, the performance of the Tabu $^{*}$ will not be affected by changing the values of $(n_A ,n_B )$ or $(d^l,d^u)$.

For the medium- to large-scale problems in the second part, cases with job number $n=30$, 60, and 90 are generated. The six combinations of $(d^l,d^u)$ consist of (0.0, 0.2), (0.0, 0.6), (0.0, 1.0), (0.4, 0.6), (0.4, 1.0), and (0.8, 1.0). For the nine settings of the numbers jobs $(n_A ,n_B )$ from agent A and agent B, the values of $(n_A ,n_B )$ are taken as (14, 16), (15, 15), and (16, 14) at $n=30$, (29, 31), (30, 30), and (31, 29) at $n=60$, and (44, 46), (45, 45), and (46, 44) at $n=90$, respectively. A total of 45 cases are examined and 50 independent runs are taken for each case. In total, 2250 instances are solved in this part. Other relative parameters are set as those at the previous part. For the performance of each Tabu Search algorithm, its relative percentage deviation is recorded as

$$\begin{aligned} \mathrm{RPD} = \frac{(\mathrm{Tabu}_- i-\mathrm{Tabu}^*)}{\mathrm{Tabu}^*}\times 100\% , \end{aligned}$$

where $\mathrm{Tabu}_- i$ is the sum of the late work job of the first agent obtained from each Tabu Search algorithm$_{, }$and $\mathrm{Tabu}^*=\min \{\mathrm{Tabu}_- i,i=1,2,3\}$ is the Tabu Search algorithm that yielded the smallest objective function value among the three Tabu algorithms. The Tabu algorithms are terminated after $100\times n$ iterations based on the pretest. In addition, Tabu Search are ended when it produces a zero solution. The results are summarized in Table 3 and Fig. 10.

Table 3 The performance of the Tabu algorithms for the big number jobs

As shown in Table 3, it can be observed that the performances among the three initials that, on average, $H_{1}$ with the mean RPD of 2056.84 performs slightly better than $H_{3}$ of 2096.40 and better than $H_{2}$ of 2874.36. Table 3 and Fig. 10 indicated that the mean RPDs stayed at the interval (0.02, 147.29) for Tabu_1, (0.02, 108.35) for Tabu_2, and (0.01, 41.47) for Tabu_3, respectively. It can also be seen that the maximum RPDs were found up to 4500 for Tabu_1, 2100 for Tabu_2, and 1000 for Tabu_3. On average, Tabu_3 with the RPD of 8.47 performs better than Tabu_1 of 16.83, and Tabu_2 of 16.62. On the other hand, Table 3 indicates that Tabu_3 performs better than Tabu_1, and Tabu_2, in terms of the numbers yielded of the smallest objective function value among the three Tabu algorithms. It can be seen that there is no trend of the RPD in Table 4 as $d^u$ or $n_A$ changes.

Based on the above observations, all three Tabu algorithms are affected on the performance for the small-scale problems as the value of $d^u$ or $n_A$ changes, but the trend disappears for the medium- to large-scale problems. In addition, there is no absolute dominance relationship among the performances of all three Tabu Search algorithms. Thus, it is recommended to combine them into one.

Fig. 10

The performance of three proposed Tabu algorithms for the big number jobs

Table 4 The impacts of parameters for the Tabu algorithms for the big number jobs

5 Conclusions

This paper addresses the problem of scheduling a given set of independent jobs on a single machine. The objective is to minimize the total late work of agent A with the restriction that the maximum lateness is allowed of an upper bound for agent B. Two pseudo-polynomial dynamic programming algorithms and a branch-and-bound algorithm are presented for the proposed problem. Simple (conditional) dominance rules are also derived to help eliminate unpromising nodes in the branch-and-bound search tree. Computational results showed that the branch-and-bound algorithm performs well on solving an instance of up to 16 jobs with a reasonable CPU time. The computational experiments also showed that the Tabu search based solution initialization procedure performed well in terms of both accuracy and stability. One way in which the performance of the algorithm might be improved is to use tighter, but computationally slower, lower, and upper bounds. However, more efficient bounding procedures that can generate tighter bounds than ours, but require little extra computational effort will be necessary for solving larger sized problems. Also, additional research to develop stronger (unconditional) dominance rules to further cut down the size of the search tree may permit more larger sized problems to be solved, or to investigate the same measure used for both agents.