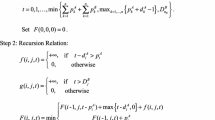Single-machine scheduling with multi-agents to minimize total weighted late work

Abstract

We consider the competitive multi-agent scheduling problem on a single machine, where each agent’s cost function is to minimize its total weighted late work. The aim is to find the Pareto-optimal frontier, i.e., the set of all Pareto-optimal points. When the number of agents is arbitrary, the decision problem is shown to be unary $\mathcal {NP}$-complete even if all jobs have the unit weights. When the number of agents is two, the decision problems are shown to be binary $\mathcal {NP}$-complete for the case in which all jobs have the common due date and the case in which all jobs have the unit processing times. When the number of agents is a fixed constant, a pseudo-polynomial dynamic programming algorithm and a $(1+\epsilon )$-approximate Pareto-optimal frontier are designed to solve it.

1 Introduction

1.1 Problem description

The problem of single-machine scheduling with multi-agents to minimize total weighted late work can be stated as follows. Assume that there are m agents, called agent $A_x$ for $x \in \{1, 2, \ldots , m\}$, where each agent competes to schedule its own set of independent and non-preemptive jobs on a single machine. Agent $A_x$ has to schedule the job set ${\mathcal J}^{(x)}=\{J_1^{(x)}, J_2^{(x)}, \ldots , J_{n_x}^{(x)}\}$. Let n be the total number of all jobs, i.e., $n=n_1+n_2+\cdots +n_m$, and $\mathcal {J}$ be the set of all jobs, i.e., $\mathcal {J}=\mathcal {J}^{(1)} \cup \mathcal {J}^{(2)} \cup \cdots \cup \mathcal {J}^{(m)}$. Note that ${\mathcal J}^{(x)}\cap {\mathcal J}^{(x')}=\emptyset$ when $x \not =x'$. All jobs are simultaneously available at time zero, and we call the jobs of agent $A_x$ the x-jobs. Each job $J_j^{(x)}$ is characterized by a processing time $p_j^{(x)}$, a weight $w_j^{(x)}$, and a due date $d_j^{(x)}$. We assume that all parameters $p_j^{(x)}$, $w_j^{(x)}$, and $d_j^{(x)}$ are known integers. Given a feasible schedule $\sigma$ of the n jobs, the completion time of job $J_j^{(x)}$ is denoted by $C_j^{(x)}(\sigma )$, and the late work of job $J_j^{(x)}$ is defined as $Y_j^{(x)}(\sigma )=\min \{T_j^{(x)}(\sigma ), p_j^{(x)}\}$, where $T_j^{(x)}(\sigma )=\max \{0, C_j^{(x)}(\sigma )-d_j^{(x)}\}$ is the tardiness of job $J_j^{(x)}$. Note that the late work $Y_j^{(x)}(\sigma )$ is the amount of processing performed on job $J_j^{(x)}$ after its due date $d_j^{(x)}$ in $\sigma$. If there is no confusion, we simply use $C_j^{(x)}$, $T_j^{(x)}$ and $Y_j^{(x)}$ to denote $C_j^{(x)}(\sigma )$, $T_j^{(x)}(\sigma )$ and $Y_j^{(x)}(\sigma )$, respectively. As in Potts and Van Wassenhove (1991), job $J_j^{(x)}$ is said to be early if $Y_j^{(x)}=0$; job $J_j^{(x_j)}$ is said to be partially early if $0< Y_j^{(x)}< p_j^{(x)}$; job $J_j^{(x)}$ is said to be late if $Y_j^{(x)}=p_j^{(x)}$. A job which is either early or partially early is also called non-late. Each agent $A_x$ desires to minimize its total weighted late work $\sum w_j^{(x)}Y_j^{(x)}(\sigma )$, which relies on its own jobs’ completion times only.

In the general competitive multi-agent scheduling problem, each agent $A_x$ desires to minimize its own scheduling criterion $F_x$. Let CO denote that the m agents are competitive on the machine. Following the three-field classification scheme in Agnetis et al. (2014), we use the following approaches to describe the different types of multi-agent scheduling problems.

• Decision problem $\mathbf{P} _1$: $1 | CO, F_x \le K_x, x=1, 2, \ldots , m |-$. The problem is to determine whether there exists a feasible schedule $\sigma$ with $F_x(\sigma ) \le K_x$ for $x \in \{1, 2, \ldots , m\}$.

• Restricted optimization problem $\mathbf{P} _2$: $1|CO, F_x \le K_x, x=2, 3, \ldots , m| F_1$. The problem is to determine a feasible schedule $\sigma$ such that $F_1(\sigma )$ is minimized subject to the restriction that $F_x(\sigma ) \le K_x$ for $x \in \{2, 3, \ldots , m\}$.

• Linear combination optimization problem $\mathbf{P} _3$: $1|CO| \sum _{j=1}^m \lambda _x F_x$. The problem is to determine a feasible schedule $\sigma$ to minimize a linear combination of the m criteria, $\sum _{j=1}^m \lambda _x F_x$, where $\lambda _x$ is a positive real number for $x \in \{1, 2, \ldots , m\}$.

• Pareto optimization problem $\mathbf{P} _4$: $1 | CO | \mathcal {P}(F_1, F_2, \ldots ,F_m)$. The problem is to determine all the Pareto-optimal points and, for each Pareto-optimal point, provide a corresponding Pareto-optimal schedule. A feasible schedule $\sigma$ is called Pareto-optimal (or efficient) if there exists no other schedule $\sigma '$ such that $F_x(\sigma ') \le F_x(\sigma )$ for all $x=1, 2, \ldots , m$ and at least one of the m inequalities is strict. In this case, $(F_1(\sigma ), F_2(\sigma ), \ldots , F_m(\sigma ))$ is called a Pareto-optimal point. The set (referred to as $\mathcal {POF}$) of all Pareto-optimal points is called the Pareto-optimal frontier.

Remark 1.1

It is observed that (i) solving problem $\mathbf{P} _4$ also solves problems $\mathbf{P} _1-\mathbf{P} _3$ as a by-product; (ii) problem $\mathbf{P} _4$ is at least as difficult as problem $\mathbf{P} _1$; (iii) problem $\mathbf{P} _2$ is at least as difficult as problem $\mathbf{P} _1$.

In this paper, we seek to investigate the Pareto optimization of the multi-agent scheduling problem in which each agent desires to minimize its total weighted late work. Using the above notation, the problem can be denoted by $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)}, \ldots , \sum w_j^{(m)}Y_j^{(m)})$.

One real-life application of the above-described scheduling model arises in the production and delivery of goods that are perishable or time sensitive in the manufacturing industry. Assume that these goods (jobs) belong to m different customers (agents), and each of them is associated with a given due date. Since the jobs have a short life span, all parts of a job that are finished after the given due date are useless and it is modeled with the late work. In addition, the disposal of a job that cannot be finished before its given due date has to be dealt with a discounted price or results in a remanufacturing cost, which is always proportionate to its late work. From the perspective of each customer, it is interested in minimizing its own total weighted late work. While from the perspective of the decision maker, in order to reduce the global financial loss or increase the customers’ satisfaction, it needs to determine a feasible schedule to satisfy all customers’ requirements or make a trade-off between the goals of different customers. Therefore, the above-described situation can be modeled as a Pareto optimization problem in which each agent desires to minimize its total weighted late work.

1.2 Literature review

The above-described scheduling model falls into the category of late work scheduling and the category of multi-agent scheduling.

The late work scheduling has received much attention in the past three decades. Applications of late work scheduling models have been found in different industry situations, and these include information collection in control systems (Blazewicz 1984), optimization of land cultivation in agriculture domain (Blazewicz et al. 2004), bugs detecting in software development (Sterna 2011), sensitive cargos transportation in the shipping industry (Liu et al. 2018), and so on. The late work scheduling problem was initiated by Blazewicz (1984). By exploiting the method of linear programming, he showed that the preemptive parallel-machine problem $P|r_j, pmtn|\sum w_j Y_j$ is polynomially solvable. Potts and Van Wassenhove (1991) showed that the problem $1||\sum Y_j$ is $\mathcal {NP}$-hard and proposed a pseudo-polynomial dynamic programming (DP) algorithm. They also presented an $O(n \log n)$-time algorithm for the problem $1|pmtn|\sum Y_j$. Potts and Van Wassenhove (1992) further designed a branch-and-bound algorithm and two fully polynomial time approximation schemes (FPTASs) for the problem $1||\sum Y_j$. Kovalyov et al. (1994) devised an FPTAS for the weighted problem $1||\sum w_j Y_j$. Hariri et al. (1995) showed that the problem $1|pmtn|\sum w_jY_j$ can be solved in $O(n \log n)$ time, and they further showed that the problems $1|d_j=d|\sum w_jY_j$ and $1|p_j=p|\sum w_jY_j$ can be solved in O(n) and $O(n^3)$ time, respectively. Blazewicz et al. (2004) showed that the problem $O2|d_j=d|\sum w_j Y_j$ is binary $\mathcal {NP}$-hard and presented a pseudo-polynomial algorithm for it. They also presented polynomial algorithms for the problems $O2|d_j=d|\sum Y_j$ and $O|r_j, pmtn|\sum w_j Y_j$, respectively. Blazewicz et al. (2005) showed that the problem $F2|d_j=d|\sum w_j Y_j$ is binary $\mathcal {NP}$-hard and presented a pseudo-polynomial algorithm for it. Blazewicz et al. (2007) designed a pseudo-polynomial algorithm to solve the problem $J2|d_j=d, n_j \le 2|\sum w_j Y_j$. Yin et al. (2016) presented two pseudo-polynomial algorithms and an FPTAS for the problem $1|\mathrm{MA}|\sum Y_j$, where MA denotes that the machine has to undergo a fixed maintenance activity. Chen et al. (2016) investigated a common due date scheduling problem on parallel–identical machines with the late work criterion. They showed that the problem $P2|d_j=d|\sum Y_j$ is binary $\mathcal {NP}$-hard and the problem $P|d_j=d|\sum Y_j$ is unary $\mathcal {NP}$-hard. Moreover, a constant competitive ratio algorithm is given for the online version of maximizing the total early work, where the early work of a job is defined as the amount of processing executed before the due date. Sterna and Czerniachowska (2017) showed that there exists no polynomial approximation algorithm with finite performance guarantee for the problem $P2|d_j=d|\sum Y_j$ and designed a polynomial time approximation scheme for the problem of maximizing the total early work. Chen et al. (2017) showed that the problem $F3|d_j=d|\sum w_j Y_j$ is unary $\mathcal {NP}$-hard and proposed a particle swarm optimization algorithm for the general flow-shop problem with learning effect. Piroozfard et al. (2018) proposed a multi-objective evolutionary algorithm for the problem of minimizing the total carbon footprint and total late work criterion in a flexible job shop environment. Gerstl et al. (2019) addressed a scheduling problem with the objective of minimizing the total late work on a proportionate flow shop. They presented pseudo-polynomial algorithms for the case in which the late work refers to the last operation of the job and the case in which the late work refers to all the operations on all machines. Chen et al. (2019b) studied the single-machine scheduling problem with deadlines to minimize the total weighted late work, i.e., $1|\bar{d}_j|\sum w_jY_j$. They showed that the problem is unary $\mathcal {NP}$-hard even if all jobs have the unit weights, the problem is binary $\mathcal {NP}$-hard and admits a pseudo-polynomial algorithm and an FPTAS if all jobs have a common due date. The reader may refer to the surveys of Leung (2004), Sterna (2011), and Shioura et al. (2018) for more relevant and detailed discussion of this aspect.

The multi-agent scheduling, in which different agents are competing for the usage of common processing resource and each agent wants to optimize a cost function that depends on its own jobs’s completion times, has found numerous applications in various industrial situations such as data packets transmission in telecommunication network (Arbib et al. 2004), preventive maintenance scheduling in manufacturing and service industries (Leung et al. 2010), aircraft landings in air traffic management (Agnetis et al. 2014), optimizing product consolidation operations of a cross-docking distribution center (Kovalyov et al. 2015), and so on. This line of research has been surveyed by Perez-Gonzalez and Framinan (2014) and Agnetis et al. (2014), so we only review the results that are related to our study. The multi-agent scheduling was originally proposed by Baker and Smith (2003) and Agnetis et al. (2004), in which the considered criteria include maximum cost function $f_{\max }$ (e.g., makespan $C_{\max }$ and maximum lateness $L_{\max }$), total (weighted) completion time $\sum (w_j) C_j$, and number of tardy jobs $\sum U_j$. Baker and Smith (2003) studied the linear combination optimization problem on a single machine, while Agnetis et al. (2004) addressed the restricted optimization and the Pareto optimization problems in single-machine, flow-shop, and open-shop environments. Ng et al. (2006) showed that the problem $1|CO, \sum U_j^{(2)} \le K_2|\sum C_j^{(1)}$ is $\mathcal {NP}$-hard under high-multiplicity encoding and provided a pseudo-polynomial algorithm for it. Leung et al. presented a pseudo-polynomial algorithm for the problem $1|CO, \sum C_j^{(2)} \le K_2|\sum T_j^{(1)}$. Recently, Chen et al. (2019a) showed that the problem $1|CO, \sum U_j^{(2)} \le K_2|\sum C_j^{(1)}$ is binary $\mathcal {NP}$-hard even if the jobs of agent $A_1$ have the equal processing times.

Next, we review some works on scheduling problems with more than two agents. Cheng et al. (2006) showed that the problem $1|CO, \sum w_j^{(x)} U_j^{(x)} \le K_x, x=1, 2, \ldots , m|-$ is unary $\mathcal {NP}$-complete when the number m of agents is arbitrary, and proposed an FPTAS for it when m is a fixed constant. Agnetis et al. (2007) provided polynomial algorithms for problems $1|CO, f_{\max }^{(x)} \le K_x, x=2, 3, \ldots , m|f_{\max }^{(1)}$ and $1|CO, f_{\max }^{(x)} \le K_x, x=2, 3, \ldots , m|\sum C_j^{(1)}$. Lee et al. (2009) considered the problem $1|CO, \sum C_j^{(x)} \le K_x, x=2, 3, \ldots , m|\sum C_j^{(1)}$ and reduced it to a multi-objective shortest-path problem, which implies that the problem $1|CO, \sum C_j^{(2)} \le K_2|\sum C_j^{(1)}$ admits an FPTAS. Yin et al. (2017) designed pseudo-polynomial time algorithms for the problems $1|CO, \mathrm{DIF}, \mathrm{MA}, \gamma ^{(x)} \le K_x, x=2, 3, \ldots , m|\sum (\alpha d_j^{(1)} +w_j^{(1)} U_j^{(1)})$, where $\gamma ^{(x)} \in \{f_{\max }^{(x)}, \sum C_j^{(x)},\sum w_j^{(x)} U_j^{(x)}\}$ and DIF means that the jobs are assigned different due dates with no restrictions. Yuan (2017) solved the open problem $1|CO|\sum _{x=1}^{m_1} \lambda _x (\sum _{J_j^{(x)} \in {\mathcal J}^{(x)}} U_j^{(x)}) +\sum _{x=m_1+1}^m \lambda _x C_{\max }^{(x)}$ in the literature by presenting a polynomial algorithm when m is a fixed constant. Li et al. (2018) showed that the problem $1 |CO, \sum _{J_j^{(x)} \in \mathcal {U}_x} w_j^{(x)} \ge K_x, x=1, 2, \ldots , m|-$ is unary $\mathcal NP$-complete when m is arbitrary, and presented a pseudo-polynomial algorithm and an FPTAS for the general proportionate flow-shop problem when m is a fixed constant, where $\mathcal {U}_x$ denotes the set of just-in-time x-jobs. More results on multi-agent scheduling can be found in Agnetis et al. (2014), Yuan (2016), and Yuan et al. (2020).

To the best of our knowledge, the only researches that study late work criterion in the framework of multi-agent scheduling are Wang et al. (2017), Zhang and Wang (2017), Liu et al. (2018), and Zhang and Yuan (2019). Specifically, Wang et al. (2017) proposed two pseudo-polynomial algorithms and a branch-and-bound algorithm to solve the problem $1|CO, L_{\max }^{(2)} \le K_2|\sum Y_j^{(1)}$. Zhang and Wang (2017) presented a polynomial algorithm for the problem $1|CO, p_j^{(1)}=p^{(1)}, f_{\max }^{(2)} \le K_2|\sum w_j^{(1)}Y_j^{(1)}$ and a pseudo-polynomial algorithm for the problem $1|CO, f_{\max }^{(2)} \le K_2|\sum w_j^{(1)}Y_j^{(1)}$. Liu et al. (2018) extended the problem of Wang et al. (2017) by introducing a sum-of-processing-times-based learning effect. Zhang and Yuan (2019) showed that the problem $1|CO, d_j^{(1)}=d, C_{\max }^{(2)} \le K_2|\sum Y_j^{(1)}$ is binary $\mathcal {NP}$-hard.

1.3 Our contribution

Seeking to explore the theoretically challenging and practically relevant problem, the contribution of this paper is fivefold.

• We propose an interesting and practical multi-agent scheduling model in which each agent wants to minimize its total weighted late work.

• We show that the un-weighted problem $1 | CO, \sum Y_j^{(x)} \le K_x, x=1, 2, \ldots , m |-$ is unary $\mathcal {NP}$-complete when m is arbitrary.

• We show that the two-agent problems $1 | CO, d_j^{(x)}=d, \sum Y_j^{(x)} \le K_x, x=1, 2 | -$ and $1 | CO, p_j^{(x)}=1, \sum w_j^{(x)}Y_j^{(x)} \le K_x, x=1, 2 | -$ are both binary $\mathcal {NP}$-complete.

• When m is a fixed constant, we develop an exact pseudo-polynomial DP algorithm for the problem $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)}, \ldots , \sum w_j^{(m)}Y_j^{(m)})$. This generalizes the algorithms of Kovalyov et al. (1994) and Hariri et al. (1995) for the single-agent problem $1 || \sum w_jY_j$.

• Let $\epsilon > 0$ and m be a fixed constant. We design a $(1+\epsilon )$-approximate Pareto-optimal frontier for the problem $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)}, \ldots , \sum w_j^{(m)}Y_j^{(m)})$.

The remaining part of this paper is organized as follows. In Sect. 2, we prove the binary $\mathcal {NP}$-completeness of the decision problems for two special cases in the two-agent setting and the strong $\mathcal {NP}$-completeness of the decision problem in the multi-agent setting. In Sect. 3, we develop an exact DP algorithm for the problem under study. In Sect. 4, we design a $(1+\epsilon )$-approximate Pareto-optimal frontier for it when the number of agents is a fixed constant. In Sect. 5, we conclude the paper and suggest some directions for future research.

2 Complexity analysis

When there is a single agent, Potts and Van Wassenhove (1991) showed that the problem $1||\sum Y_j$ is $\mathcal {NP}$-hard even if there are only two distinct due dates, while Hariri et al. (1995) presented O(n)-time and $O(n^3)$-time algorithms for the problems $1|d_j=d|\sum w_j Y_j$ and $1|p_j=p|\sum w_j Y_j$, respectively. In the following, we show that the problems $1 | CO, d_j^{(x)}=d, \sum Y_j^{(x)} \le K_x, x=1, 2 |$, and $1 | CO, p_j^{(x)}=1, \sum w_j^{(x)}Y_j^{(x)} \le K_x, x=1, 2 |$, are both binary $\mathcal {NP}$-complete, and the problem $1 | CO, \sum Y_j^{(x)} \le K_x, x=1, 2, \ldots , m |$, is unary $\mathcal {NP}$-complete when m is arbitrary.

Theorem 2.1

Problem $1 | CO, d_j^{(x)}=d, \sum Y_j^{(x)} \le K_x, x=1, 2 | -$ is binary $\mathcal {NP}$-complete.

Proof

The proof uses the reduction from the binary $\mathcal {NP}$-complete SUBSET SUM problem (Garey and Johnson 1979), which can be defined as follows:

SUBSET SUM Given r positive integers $b_1,b_2, \ldots , b_{r}$ and an integer bound B, does there exist a subset $\mathcal {S}_1 \subset \mathcal {S}:=\{1, 2, \ldots , r\}$ such that $\sum _{j \in \mathcal {S}_1} b_j = B$?

Given an arbitrary instance $\mathcal {I}$ of the SUBSET SUM problem, we construct an instance $\mathcal {I}'$ of the problem $1 | CO, d_j^{(x)}=d, \sum Y_j^{(x)} \le K_x, x=1, 2 | -$ as follows:

• $m=2$ agents and $n=2r$ jobs, where ${\mathcal J}^{(x)}=\{J_1^{(x)}, J_2^{(x)}, \ldots , J_{r}^{(x)}\}$ for $x=1, 2$.

• The processing times are defined by $p_{j}^{(x)}=b_j$ for $x=1, 2$ and $j=1, 2, \ldots , r$.

• The common due date is defined by $d_{j}^{(x)}=d=2B$ for $x=1, 2$ and $j=1, 2, \ldots , r$.

• The threshold values are defined by $K_1=K_2=\sum _{j=1}^r b_j-B$.

We first show that if instance $\mathcal {I}$ has a solution, then there exists a feasible schedule $\sigma$ for instance $\mathcal {I}'$ with $\sum _{j=1}^{r} Y_j^{(x)}(\sigma ) \le K_x$, $x=1, 2$. Let $\mathcal {S}_1$ be a solution of $\mathcal {I}$ such that $\sum _{j \in \mathcal {S}_1} b_j=B$. Define $\mathcal {O}=\{J_j^{(x)}: j \in \mathcal {S}_1, x=1, 2\}$. We construct a feasible schedule $\sigma$ for $\mathcal {I}'$ as follows: The jobs in $\mathcal {O}$ are sequenced in an arbitrary order, followed by the jobs in $\mathcal {J} {\setminus } \mathcal {O}$ also sequenced arbitrarily. It can be easily checked that $\sum _{j=1}^{r}Y_j^{(1)}(\sigma )=\sum _{j=1}^{r}Y_j^{(2)}(\sigma )=\sum _{j=1}^r b_j-B$.

Conversely, we show that if instance $\mathcal {I}'$ has a feasible schedule $\sigma$ with $\sum _{j=1}^{r}Y_j^{(x)}(\sigma ) \le K_x$ for $x=1, 2$, then there exists a solution to instance $\mathcal {I}$. Let $\sigma$ be a feasible schedule of $\mathcal {I}'$ with $\sum _{j=1}^{r}Y_j^{(x)}(\sigma ) \le K_x$ for $x=1, 2$. Then, we have

$$\begin{aligned} \sum _{j=1}^r Y_j^{(1)}(\sigma )+\sum _{j=1}^r Y_j^{(2)}(\sigma ) \le K_1+K_2. \end{aligned}$$

(1)

However, the total amount of processing performed after d is at least $(\sum _{j=1}^{r} p_j^{(1)}+\sum _{j=1}^{r} p_j^{(2)})-d=2(\sum _{j=1}^r b_j-B)=K_1+K_2$. Thus, we have

$$\begin{aligned} \sum _{j=1}^r Y_j^{(1)}(\sigma )+\sum _{j=1}^r Y_j^{(2)}(\sigma ) \ge K_1+K_2. \end{aligned}$$

(2)

From (1) and (2), we deduce that

$$\begin{aligned} \sum _{j=1}^r Y_j^{(1)}(\sigma )=\sum _{j=1}^r Y_j^{(2)}(\sigma )=\sum _{j=1}^r b_j-B. \end{aligned}$$

(3)

Define $\mathcal {O}_1=\{j: C_j^{(1)}(\sigma ) \le d\}$ and $\mathcal {O}_2=\{j: C_j^{(2)}(\sigma ) \le d\}$. Recalling that the jobs are non-preemptive and $p_j^{(x)}=b_j$ for $x=1, 2,$ and $j=1, 2, \ldots , r$, from (3), we can conclude that either $\sum _{j \in \mathcal {O}_1} b_j =B$ or $\sum _{j \in \mathcal {O}_2} b_j =B$. Therefore, the instance $\mathcal {I}$ has a solution. $\square$

When all jobs have the unit processing times and the due dates are integers, Blazewicz et al. (2004) showed that in all machine setting, the problem with the total (weighted) number of tardy jobs criterion is equivalent to the one with the total (weighted) late work criterion in the single-agent case. Obviously, this equivalent relation also holds in the multi-agent case. Oron et al. (2015) showed that the problem $1 | CO, p_j^{(x)}=1, \sum w_j^{(x)}U_j^{(x)} \le K_x, x=1, 2| -$is binary $\mathcal {NP}$-complete, and the problem $1 | CO, p_j^{(x)}=1| \mathcal {P}(\sum w_j^{(1)}U_j^{(1)}, \sum U_j^{(2)})$ can be solved in $O(\max \{n_1 \log n_1, n n_2\})$ time. Hence, the following results hold.

Theorem 2.2

Problem $1 | CO, p_j^{(x)}=1, \sum w_j^{(x)}Y_j^{(x)} \le K_x, x=1, 2 | -$ is binary $\mathcal {NP}$-complete.

Theorem 2.3

Problem $1 | CO, p_j^{(x)}{=}1| \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum Y_j^{(2)})$ can be solved in $O(\max \{n_1 \log n_1, n n_2\})$ time.

When m is a fixed constant, Cheng et al. (2006) provided an $O(n \prod _{x=1}^m K_x)$-time algorithm for the problem $1|CO, \sum w_j^{(x)} U_j^{(x)} \le K_x, x=1, 2, \ldots , m|-$. Clearly, their algorithm can be easily adapted for the problem $1 | CO| \mathcal {P}(\sum w_j^{(1)}U_j^{(1)}, \sum w_j^{(2)}U_j^{(2)}, \ldots , \sum w_j^{(m)}U_j^{(m)})$. Hence, the following result holds.

Theorem 2.4

Problem $1 | CO, p_j^{(x)}=1| \mathcal {P}(\sum w_j^{(1)}V_j^{(1)}, \sum w_j^{(2)}V_j^{(2)}, \ldots , \sum w_j^{(m)}V_j^{(m)})$ is binary $\mathcal {NP}$-hard and can be solved in $O(n \prod _{x=1}^m \sum _{j=1}^{n_x} w_j^{(x)})$ time when m is a fixed constant.

Theorem 2.5

Problem $1 | CO, \sum Y_j^{(x)} \le K_x, x=1, 2, \ldots , m |-$ is unary $\mathcal {NP}$-complete when m is arbitrary.

Proof

The proof uses the reduction from the unary $\mathcal {NP}$-complete 3-PARTITION problem (Garey and Johnson 1979), which can be defined as follows:

3-PARTITION Given 3r positive integers $b_1,b_2, \ldots , b_{3r}$ and an integer bound B such that $\sum _{j=1}^{3r} b_j= r B$, and $B/4<b_j < B/2$ for $j=1, 2, \ldots , 3r$, can the index set $\mathcal {S}=\{1, 2, \ldots , 3r\}$ be partitioned into r disjoint subsets $\mathcal {S}_1, \mathcal {S}_2, \ldots , \mathcal {S}_r$ (i.e., $\mathcal {S}_1 \cup \mathcal {S}_2 \cup \cdots \cup \mathcal {S}_r=\mathcal {S}$ and $\mathcal {S}_i \cap \mathcal {S}_k = \emptyset$ for $i \ne k$), such that $\sum _{j \in \mathcal {S}_i} b_j =B$ and $|\mathcal {S}_i|=3$ for $i=1, 2, \ldots , r$?

Given an arbitrary instance $\mathcal {I}$ of the 3-PARTITION problem, we first re-index the 3r numbers in $\mathcal {I}$ such that $b_1 \le b_2\le \cdots \le b_{3r}$. An instance $\mathcal {I}'$ of the problem $1 | CO, \sum Y_j^{(x)} \le K_x, x=1, 2, \ldots , m|-$ is constructed as follows:

• $m=r+1$ agents and $n=3r^2+1$ jobs, where ${\mathcal J}^{(x)}=\{J_1^{(x)}, J_2^{(x)}, \ldots , J_{3r}^{(x)}\}$ for $x=1, 2, \ldots , r$, and ${\mathcal J}^{(r+1)}=\{J_1^{(r+1)}\}$.

• The processing times are defined by $p_{j}^{(x)}=\Delta _1+b_j$ for $x=1, 2, \ldots , r$, $j=1, 2, \ldots , 3r$, and $p_1^{(r+1)}=1$, where $\Delta _1=3r^2B$.

• The due dates are defined by $d_{j}^{(x)}=(r-1)(j \Delta _1+\lambda _j)$ for $x=1, 2, \ldots , r$, $j=1, 2, \ldots , 3r$, and $d_1^{(r+1)}=3r(r-1)\Delta _1+r(r-1)B+1$, where $\lambda _j=b_1+b_2+\cdots +b_j$.

• The threshold values are defined by $K_x=3 \Delta _1+B$ for $x=1, 2, \ldots , r$ and $K_{r+1}=0$.

To simplify the argument, write $P_j=\Delta _1+b_j$ and $D_j=(r-1)(j \Delta _1+\lambda _j)$, which denote the common processing time and due date of job $J_j^{(x)}$ for $x=1, 2, \ldots , m$ and $j=1, 2, \ldots , 3r$. Moreover, for each subset $\mathcal {Q} \subseteq \mathcal {J}=\bigcup _{x=1}^{r+1} {\mathcal J}^{(x)}$, let $P(\mathcal {Q})=\sum _{J_j^{(x)} \in \mathcal {Q}} p_j^{(x)}$ be the total processing time of all jobs in $\mathcal {Q}$. Then, we have

$$\begin{aligned} P(\mathcal {J})= & {} \sum _{x=1}^{r} \sum _{j=1}^{3r} p_j^{(x)}+p_1^{(r+1)}\nonumber \\= & {} \sum _{x=1}^{r} \sum _{j=1}^{3r} (\Delta _1+b_j)+1\nonumber \\= & {} r^2(3 \Delta _1+B)+1. \end{aligned}$$

(4)

We first show that if $\mathcal {I}$ has a solution, then there exists a feasible schedule $\sigma$ for $\mathcal {I}'$ with $\sum _{j=1}^{n_x} Y_j^{(x)}(\sigma ) \le K_x$ for $x=1, 2, \ldots , r+1$. Let $\mathcal {S}_1, \mathcal {S}_2, \ldots , \mathcal {S}_r$ be a solution of $\mathcal {I}$ such that $|\mathcal {S}_i|=3$ and $\sum _{j \in \mathcal {S}_i} b_j=B$ for $i=1, 2, \ldots , r$. Define $\mathcal {T}=\{J_j^{(x)}: j \in \mathcal {S}_x, x=1, 2, \ldots , r\}$. We construct a feasible schedule $\sigma$ for $\mathcal {I}'$ as follows: The jobs in $\mathcal {J} \setminus \mathcal {T}$ are sequenced in non-decreasing order of their due dates (EDD), followed by the jobs in $\mathcal {T}$ sequenced arbitrarily. For each $j=1, 2, \ldots , 3r$, define $\mathcal {O}_j=\{J_i^{(x)}: J_i^{(x)} \in \mathcal {J} \setminus \mathcal {T} ~ \mathrm {and} ~ d_i^{(x)} \le D_j\}$. Since the processing time of each job in $\mathcal {O}_j \setminus \mathcal {O}_{j-1}$ is $P_j$ and $|\mathcal {O}_j|= (r-1) j$, we have

$$\begin{aligned} P(\mathcal {O}_j)= & {} \sum _{J_i^{(x)} \in \mathcal {O}_j} p_i^{(x)}\nonumber \\= & {} (r-1)\sum _{i=1}^j P_i=(r-1)\sum _{i=1}^j(\Delta _1+b_i)\nonumber \\= & {} (r-1)(j \Delta _1+\lambda _j)=D_j. \end{aligned}$$

(5)

This implies that all jobs in $\mathcal {O}_j {\setminus } \mathcal {O}_{j-1}$ are scheduled from time $D_{j-1}$ to $D_j$ for $j=1, 2, \ldots , 3r$, where $\mathcal {O}_0=\emptyset$.

Recall that $\lambda _{3r}=b_1+b_2+\cdots +b_{3r}=rB$. Then, we have

$$\begin{aligned} C_1^{(r+1)}(\sigma )= & {} P(\mathcal {J} {\setminus } \mathcal {T}) =P(\mathcal {O}_{3r})+p_1^{(r+1)}\nonumber \\= & {} (r-1)(3r \Delta _1+\lambda _{3r})+1 =d_1^{(r+1)}. \end{aligned}$$

(6)

This implies that job $J_1^{r+1}$ is also early.

Combining the above discussion, we know that all the jobs in $\mathcal {J} {\setminus } \mathcal {T}$ are early and all the jobs in $\mathcal {T}$ are late in $\sigma$. Therefore, the total late work of agent $A_x$ ($x=1, 2, \ldots , r$) is

$$\begin{aligned}&\sum _{j=1}^{3r} Y_j^{(x)}(\sigma )=\sum _{j \in \mathcal {S}_x} Y_j^{(x)}(\sigma )\\&=\sum _{j \in \mathcal {S}_x} P_j =\sum _{j \in \mathcal {S}_x} (\Delta _1+b_j)=3 \Delta _1+B=K_x, \end{aligned}$$

and the total late work of agent $A_{r+1}$ is $0=K_{r+1}$.

Conversely, we show that if $\mathcal {I}'$ has a feasible schedule $\sigma$ with $\sum _{j=1}^{n_x}Y_j^{(x)}(\sigma ) \le K_x$ for $x=1, 2, \ldots , r+1$, then there exists a solution to $\mathcal {I}$. Let $\sigma$ be a feasible schedule for $\mathcal {I}'$ with $\sum _{j=1}^{n_x}Y_j^{(x)}(\sigma ) \le K_x$ for $x=1, 2, \ldots , r+1$. Then, we have

$$\begin{aligned} \sum _{J_j^{(x)} \in \mathcal {J}} Y_j^{(x)}(\sigma ) =\sum _{x=1}^{r+1} \sum _{j=1}^{n_x}Y_j^{(x)}(\sigma ) \le \sum _{x=1}^{r+1} K_x =r(3 \Delta _1+B). \end{aligned}$$

(7)

However, the total amount of processing performed after $d_1^{(r+1)}$ is at least $P(\mathcal {J})-d_1^{(r+1)}=r(3 \Delta _1+B)$. Thus, we have

$$\begin{aligned} \sum _{J_j^{(x)} \in \mathcal {J}} Y_j^{(x)}(\sigma ) \ge P(\mathcal {J})-d_1^{(r+1)} =r(3 \Delta _1+B)=\sum _{x=1}^{r+1} K_x. \end{aligned}$$

(8)

Recall that $\sum _{j=1}^{n_x}Y_j^{(x)}(\sigma ) \le K_x$ for $x=1, 2, \ldots , r+1$. From (7) and (8), we deduce that

$$\begin{aligned} \sum _{j=1}^{3r} Y_j^{(x)}(\sigma )=K_x=3 \Delta _1+B ~\mathrm {for}~ x=1, 2, \ldots , r, \end{aligned}$$

(9)

and

$$\begin{aligned} Y_1^{(r+1)}(\sigma )=0. \end{aligned}$$

(10)

Let $\mathcal {T}$ be the set of all late jobs in $\sigma$. From the above discussion, the following three results immediately hold.

Observation 1

Job $J_1^{(r+1)}$ is early in $\sigma$ and it is scheduled from $D_{3r}$ to $d_1^{(r+1)}$.

Observation 2

All jobs scheduled before time $D_{3r}$ in $\sigma$ are early and no partially early jobs exist. In particular, $P(\mathcal {T})=\sum _{J_j^{(x)} \in \mathcal {J}} Y_j^{(x)}(\sigma )=r(3 \Delta _1+B)$.

Observation 3

The total processing time of the late jobs of agent $A_x$, $x=1, 2, \ldots , r$, is $3 \Delta _1+B$, i.e., $P(\mathcal {T} \cap \mathcal {J}^{(x)})=\sum _{J_j^{(x)} \in \mathcal {T} \cap \mathcal {J}^{(x)}} P_j=3 \Delta _1+B$.

W.l.o.g., we can assume that the jobs in $\mathcal {J} {\setminus } \mathcal {T}$ are scheduled in EDD order. Also, from the construction of the instance $\mathcal {I}'$ and Observation 3, we can deduce that $|\mathcal {T} \cap \mathcal {J}^{(x)}|=3$ for $x=1, 2, \ldots , r$.

Recall that $b_1 \le b_2\le \cdots \le b_{3r}$. We can define an unique index sequence $(\theta _1, \theta _2, \ldots , \theta _h)$ that satisfies the following conditions:

$$\begin{aligned} \mathrm{(i)}&0=\theta _0< \theta _1<\theta _2 \cdots < \theta _h=3r; \nonumber \end{aligned}$$

(11)

$$\begin{aligned} \\ \mathrm{(ii)}&b_{\theta _i+1} =b_{\theta _{i}+2} = \cdots = b_{\theta _{i+1}}, i=0, 1, \ldots , h-1; \nonumber \end{aligned}$$

(12)

$$\begin{aligned} \\ \mathrm{(iii)}&b_1=b_{\theta _1}< b_{\theta _2}< \cdots < b_{\theta _h}=b_{3r}. \end{aligned}$$

(13)

Note that $h=1$ if and only if $b_1=b_2=\cdots =b_{3r}$. For each $g=1, 2, \ldots , 3r$, set $\mathcal {F}_g=\{J_j^{(x)}: x=1, 2, \ldots , r, j=1, 2, \ldots , g\}$ and $\mathcal {T}_g= \mathcal {T} \cap \mathcal {F}_g$. We next show the following observation.

Observation 4

$|\mathcal {T}_{\theta _l}|=\theta _l$ for $l=1, 2, \ldots , h$.

Proof of Observation 4

Notice that $|\mathcal {T}_{\theta _h}|=|\mathcal {T}_{3r}|=|\mathcal {T}|=3r=\theta _h$ always holds. Then, the result holds if $h=1$. Suppose in the following that $h\ge 2$, implying $b_{3r}> b_1$. We only need to show that $|\mathcal {T}_{\theta _l}| = \theta _l$ for $l=1, 2,\ldots , h-1$. Recall that $p_j^{(x)}=P_j=\Delta _1+b_j < \Delta _1+B$ for $x=1, 2, \ldots , r$, $j=1, 2, \ldots , 3r$.

Suppose to the contrary that $|\mathcal {T}_{\theta _l}| < \theta _l$ for some l with $l=1, 2,\ldots , h-1$. Since $P(\mathcal {F}_{\theta _l})=\sum _{J_j^{(x)} \in \mathcal {F}_{\theta _l}} p_j^{(x)} =\sum _{x=1}^{r} \sum _{j=1}^{\theta _l} P_j {=}r(\theta _l \Delta _1+\lambda _{\theta _l})$ and $P(\mathcal {T}_{\theta _l}) {=}\sum _{J_j^{(x)} \in \mathcal {T}_{\theta _l}} p_j^{(x)}< (\theta _l-1)(\Delta _1+B) < \theta _l \Delta _1+\lambda _{\theta _l}$, we have

$$\begin{aligned} P(\mathcal {F}_{\theta _l} {\setminus } \mathcal {T}_{\theta _l}) =P(\mathcal {F}_{\theta _l})-P(\mathcal {T}_{\theta _l}) >(r-1)(\theta _l \Delta _1+\lambda _{\theta _l})=D_{\theta _l}, \end{aligned}$$

which contradicts the definition of $\mathcal {T}_{\theta _l}$. As a consequence, $|\mathcal {T}_{\theta _l}| \ge \theta _l$ for $l=1, 2,\ldots , h-1$.

Suppose to the contrary that $|\mathcal {T}_{\theta _l}| > \theta _l$ for some l with $l=1, 2,\ldots , h-1$. Since $\mathcal {T}=(\mathcal {T}_{\theta _1}{\setminus } \mathcal {T}_{\theta _0}) \cup (\mathcal {T}_{\theta _2}{\setminus } \mathcal {T}_{\theta _1}) \cup \cdots \cup (\mathcal {T}_{\theta _h}{\setminus } \mathcal {T}_{\theta _{h-1}})$ and $|\mathcal {T}|=3r$, we have

$$\begin{aligned} P(\mathcal {T})= & {} \sum _{g=1}^{h} \sum _{J_j^{(x)} \in T_{\theta _g}{\setminus } T_{\theta _{g-1}}} P_j \\= & {} \sum _{g=1}^{h} (|\mathcal {T}_{\theta _g}|-|\mathcal {T}_{\theta _{g-1}}|)b_{\theta _g}+3r \Delta _1 \\= & {} \sum _{g=1}^{h} \left( (|\mathcal {T}_{\theta _g}|- \theta _g)-(|\mathcal {T}_{\theta _{g-1}}|-\theta _{g-1})\right) b_{\theta _g}\\&\quad +\sum _{g=1}^{h}(\theta _g-\theta _{g-1})b_{\theta _g}+3r \Delta _1 \\= & {} \sum _{g=1}^{h-1} \left( (|\mathcal {T}_{\theta _g}|- \theta _g)(b_{\theta _g}-b_{\theta _{g+1}})\right) +\sum _{j=1}^{3r} b_j+3r \Delta _1 \\< & {} r(3 \Delta _1+B), \end{aligned}$$

which contradicts Observation 2. This completes the proof of Observation 4. $\square$

From (11)–(13) and Observation 4, we know that there are exactly $\rho _g=|\mathcal {T}_{\theta _g}|-|\mathcal {T}_{\theta _{g-1}}| =\theta _g-\theta _{g-1}$ late jobs in $\mathcal {T}_{\theta _g}{\setminus } \mathcal {T}_{\theta _{g-1}}$ with the same processing time $P_{\theta _g}=\Delta _1+b_{\theta _g}$ for $g=1, 2, \ldots , h$.

For each $g=1, 2, \ldots , h$, do the following: Label the $\rho _g$ late jobs in $\mathcal {T}_{\theta _g}{\setminus } \mathcal {T}_{\theta _{g-1}}$ arbitrarily, say $J_{g,1}, J_{g,2}, \ldots , J_{g, \rho _g}$. Denote by z(g, k) the agent index such that $J_{g,k} \in \mathcal {J}^{(z(g,k))}$ for $k=1, 2, \ldots , \rho _g$. It can be observed that jobs $J_{g,k}$ and $J_{\theta _{g-1}+k}^{(z(g,k))}$ both belong to the same agent $A_{z(g,k)}$ for $k=1, 2, \ldots , \rho _g$. (Note that $J_{g,k}$ and $J_{\theta _{g-1}+k}^{(z(g,k))}$ may be the same job.) Write $\mathcal {X}_{(g)}=\{J_{\theta _{g-1}+k}^{(z(g,k))}: k=1, 2, \ldots , \rho _g\}$. Then, all the jobs in $\mathcal {X}_{(g)}$ have the same processing time $P_{\theta _{g}}=\Delta _1+b_{\theta _g}$. Set $\mathcal {X}=\mathcal {X}_{(1)} \cup \mathcal {X}_{(2)} \cdots \cup \mathcal {X}_{(h)}$.

Moreover, let $\Psi : \mathcal {T} \rightarrow \mathcal {X}$ be defined as $\Psi (J_{g,k})=J_{\theta _{g-1}+k}^{(z(g,k))}$ for $g=1, 2, \ldots , h$, $k=1, 2, \ldots , \rho _g$; and $\Phi : \mathcal {X} \rightarrow \mathcal {S}$ be defined as $\Phi (J_{\theta _{g-1}+k}^{(z(g,k))})=\theta _{g-1}+k$ for $g=1, 2, \ldots , h$, $k=1, 2, \ldots , \rho _g$. Clearly, both functions $\Psi$ and $\Phi$ are one to one.

Define $\mathcal {S}_x=\{j: J_j^{(x)} \in \mathcal {X}\}$ for all $x=1, 2, \ldots , r$. From the above discussion and Observation 3, we deduce that $\mathcal {S}_1, \mathcal {S}_2, \ldots , \mathcal {S}_r$ form a partition of $\mathcal {S}$ such that $\sum _{j \in \mathcal {S}_x} b_j =B$ and $|\mathcal {S}_x|=3$ for $x=1, 2, \ldots , r$. Therefore, the 3-PARTITION instance $\mathcal {I}$ has a solution. $\square$

Corollary 2.6

Problem $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)}, {\ldots }, \sum w_j^{(m)}Y_j^{(m)})$ with m being arbitrary is unary $\mathcal {NP}$-hard even if all jobs have the unit weights.

3 An exact algorithm

In this section, for problem $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)}, \ldots , \sum w_j^{(m)}Y_j^{(m)})$, we first provide two key structural properties of the Pareto-optimal solutions and then we design an exact DP algorithm for solving it.

Lemma 3.1

For any Pareto-optimal point, there exists a corresponding Pareto-optimal schedule in which all jobs are processed contiguously from time zero until the last job is completed.

Proof

The result holds since the criteria of all agents are regular and all jobs are simultaneously available at time zero. $\square$

Based on the result of Lemma 3.1, an optimal schedule can be characterized by a sequence of early and partially early jobs of all agents which we call a non-late sequence (referred to as $\mathcal {NLS}$); the late jobs can then be appended to this sequence in an arbitrary order.

In the remainder part of this paper, we assume that the jobs in $\mathcal {J}$ are indexed from $J_1$ to $J_n$ in the EDD order, such that $d_1 \le d_2 \le \cdots \le d_n$, and $w_i \ge w_k$ if $i <k$, $x_i=x_k$ and $d_i=d_k$, where $x_j$ is the agent index such that $J_j \in \mathcal {J}^{(x_j)}$ for $j=1, 2, \ldots , n$. Note that, according to the above indexing rule, the x-jobs of agent $A_x$ ($x=1, 2, \ldots , m$) with the same due date are indexed in the non-increasing order of their weights, while the jobs of different agents with the same due date can be indexed arbitrarily.

Under a given $\mathcal {NLS}$, job $J_j$ is said to be I-deferred (from its EDD position) if it is sequenced after a job $J_k$ with a due date larger than $d_j$, i.e., $d_j<d_k$; and it is said to be II-deferred (from its EDD position) if it is sequenced after a job $J_k$ with $j<k$, $x_j \ne x_k$ and $d_j=d_k$. For convenience, we allow a deferred job in a $\mathcal {NLS}$ to be early. The following result is very critical to establish the ordering of the jobs in an optimal $\mathcal {NLS}$.

Lemma 3.2

For any Pareto-optimal point, there exists a corresponding Pareto-optimal $\mathcal {NLS}$$\sigma$ which has the following two properties:

• (i) jobs of the same agent with the same due date are sequenced in the non-increasing order of their weights in $\sigma$, and

• (ii) for each job $J_j$ in $\sigma$, at most one job $J_k$ having an index smaller than j, i.e., $k<j$, appears after $J_j$ in $\sigma$.

Proof

Consider a Pareto-optimal $\mathcal {NLS}$$\sigma$ which violates property (i). Then, there exist two jobs $J_i$ and $J_k$ in $\sigma$ such that $J_i$ is sequenced before $J_k$, where $x_i=x_k$, $d_i=d_k$ and $w_i<w_k$. Write $x_i=x_k \equiv x$. Clearly, job $J_i$ is early in $\sigma$, i.e., $Y_i(\sigma )=0$; since if it were partially early, job $J_k$ would be late. First, assume that $Y_k(\sigma ) \ge p_i$. We can obtain another $\mathcal {NLS}$$\sigma '$ from $\sigma$ by removing job $J_i$ from $\sigma$ so that it is deemed to be late. Then, we have $Y_i(\sigma ')=p_i$ and $Y_k(\sigma ')=Y_k(\sigma )-p_i$. Moreover, all other jobs’ completion times will not increase in $\sigma '$. Thus, we obtain that $\sum w_j^{(x)}Y_j^{(x)}(\sigma ')-\sum w_j^{(x)}Y_j^{(x)}(\sigma ) \le w_iY_i(\sigma ')+w_kY_k(\sigma ')-w_iY_i(\sigma )-w_kY_k(\sigma ) =p_i(w_i-w_k)<0$, and $\sum w_j^{(y)}Y_j^{(y)}(\sigma ') \le \sum w_j^{(y)}Y_j^{(y)}(\sigma )$ for all $y \in \{1, 2, \ldots , x-1, x+1, \ldots , m\}$. However, this contradicts the fact that $\sigma$ is a Pareto-optimal $\mathcal {NLS}$. Therefore, we must have $0 \le Y_k(\sigma ) < p_i$. Now we can obtain another $\mathcal {NLS}$$\sigma ''$ from $\sigma$ by removing job $J_i$ from its original position in $\sigma$ and inserting it immediately after job $J_k$. Clearly, $Y_k(\sigma '')=0$ and $Y_i(\sigma '')=Y_k(\sigma )$. Moreover, only job $J_i$ has a later completion time in $\sigma ''$ than in $\sigma$. Thus, we obtain that $\sum w_j^{(x)}Y_j^{(x)}(\sigma '')-\sum w_j^{(x)}Y_j^{(x)}(\sigma ) \le w_iY_i(\sigma '')+w_kY_k(\sigma '')-w_iY_i(\sigma )-w_kY_k(\sigma ) =Y_k(\sigma )(w_i-w_k) \le 0$, and $\sum w_j^{(y)}Y_j^{(y)}(\sigma '') \le \sum w_j^{(y)}Y_j^{(y)}(\sigma )$ for all $y \in \{1, 2, \ldots , x-1, x+1, \ldots , m\}$. This shows that $\sigma '$ is also a Pareto-optimal $\mathcal {NLS}$. By repeating this argument, we can eventually obtain a Pareto-optimal $\mathcal {NLS}$ in which jobs of the same agent with the same due date are sequenced in the non-increasing order of their weights. This proves property (i).

Assume in the following that $\sigma$ is a Pareto-optimal $\mathcal {NLS}$ which satisfies property (i), i.e., jobs of the same agent with the same due date are sequenced in the non-increasing order of their weights, but violates property (ii). Select the last job $J_j$ of $\sigma$ that is sequenced before some jobs $J_k$ and $J_l$, where $k<j$ and $l<j$. W.l.o.g., we can assume that job $J_k$ is sequenced before job $J_l$ in $\sigma$, i.e., $J_j \prec J_k\prec J_l$ in $\sigma$. From the indexing rule, we have $d_k \le d_j$ and $d_l\le d_j$. Notice that either $d_h < d_j$ or $d_h = d_j$ and $x_h \not =x_j$ for $h=k, l$. Because $J_l$ is early or partial early in $\sigma$, we have $C_k(\sigma )< d_l$. This implies that $C_k(\sigma ) < d_j$. We can obtain another $\mathcal {NLS}$$\sigma '$ from $\sigma$ by removing $J_j$ from its original position in $\sigma$ and inserting it immediately after $J_k$. Clearly, job $J_j$ is still early in $\sigma '$ since $C_j(\sigma ')=C_k(\sigma )< d_j$. Moreover, all jobs’ completion times will not increase in $\sigma '$ except $J_j$. Therefore, $\sigma '$ is also a Pareto-optimal $\mathcal {NLS}$. It is observed that property (i) still holds for $\sigma '$ since $J_j$ is the last job that does not satisfy property (ii). By repeating this argument, we can eventually obtain a Pareto-optimal $\mathcal {NLS}$ with the required property (ii). The lemma follows. $\square$

A schedule of $\{J_1, J_2, \ldots , J_n\}$ is called standard if it satisfies the properties stated in Lemmas 3.1 and 3.2. We will only consider standard schedules in the remaining part of this paper.

We next proceed with the design of our DP algorithm (referred to as $\mathcal {H}_1$). Our algorithm generalizes the algorithms of Kovalyov et al. (1994) and Hariri et al. (1995) for solving the single-agent problem $1 || \sum w_jY_j$.

By exploiting the structural properties stated in Lemmas 3.1 and 3.2 for standard schedules, algorithm $\mathcal {H}_1$ is proposed, using the state representation, to solve the problem by finding the set of all (partial) efficient schedules. Recall that the jobs are indexed in the EDD order $J_1, J_2, \ldots , J_n$ by the above indexing rule. In our algorithm, jobs are considered in the indexed EDD order. In a schedule $\sigma$, each job $J_k$ may be scheduled either late or non-late. In the case that $J_k$ is non-late in $\sigma$, it either appears in its EDD position or is deferred. If job $J_k$ is deferred (I-deferred or II-deferred) to be sequenced after a job $J_j$ in $\sigma$, where $j>k$, Lemma 3.2 guarantees that all non-late jobs among $J_{k+1}, J_{k+2}, \ldots , J_j$ are sequenced in EDD order.

Definition 3.3

In a schedule $\sigma$ of $\{J_1, J_2, \ldots , J_n\}$, job $J_k$ is called strictly deferred with respect to job$J_j$ if $1\le k\le j\le n$, $J_k$ is a deferred job, and $C_{j'}(\sigma )< C_k(\sigma )$ for some job $J_{j'}$ with $j+1\le j'\le n$.

From Definition 3.3, if $J_j$ is a deferred job, then $J_j$ is also strictly deferred with respect to itself. From 3.1 and 3.2, we have the following lemma.

Lemma 3.4

In every standard schedule of $\{J_1, J_2, \ldots , J_n\}$, for each job $J_j$, there is at most one strictly deferred job with respect to job $J_j$. Moreover, if some job other than $J_j$ is strictly deferred with respect to job $J_j$, then $J_j$ is either an early job or a late job, or equivalently, $J_j$ is not a partially early job.

For each $j\in \{1,2, \ldots , n\}$, we use $\Pi _j$ to denote the set of all schedules $\sigma$ of the jobs in $\{J_1, J_2, \ldots , J_j\}$ such that $\sigma$ is a partial schedule of some standard schedule $\sigma '$ of $\{J_1, J_2, \ldots , J_n\}$, i.e., $\sigma$ is obtained from $\sigma '$ by deleting the jobs $J_{j+1}, J_{j+2}, \ldots , J_n$. Each schedule $\sigma \in \Pi _j$ determines a unique state$\mathbf{S} (\sigma )=(j, t, U_1, \ldots , U_m, k)$ such that: (i) $k\in \{0,1, \ldots , j\}$ and $J_k$ is strictly deferred with respect to job $J_j$ if $k \ne 0$; (ii) the completion time of the non-late jobs among $\{J_1, J_2, \ldots , J_j\}{\setminus } \{J_k\}$ is t; and (iii) the total weighted late work for the x-jobs of $\{J_1, J_2, \ldots , J_j\}{\setminus }\{J_k\}$ is $U_x$ for $x= 1, 2, \ldots , m$. Note that if $k=0$, there is no strictly deferred job with respect to job $J_j$; and if $k \in \{1, 2, \ldots , j\}$, then job $J_k$ is deferred and should be sequenced immediately after some job $J_h$ with $h \in \{j+1, \ldots , n\}$. We will use $\mathcal {L}_j=\{\mathbf {S}(\sigma ):\sigma \in \Pi _j\}$ to denote the set of all states determined by the schedules in $\Pi _j$. Moreover, we initially set $\mathcal {L}_0=\{(0, 0, 0, \ldots , 0, 0)\}$. Note that the weighted late work of any job $J_j$, $j=1, 2, \ldots , n$, when it is completed at a specified time point u, is given by

$$\begin{aligned} \Phi _j(u)=\left\{ \begin{array}{ll} 0, &{}\quad \hbox {if}~~u \le d_j; \\ w_j(u-d_j), &{}\quad \hbox {if}~~d_j< u<d_j+p_j; \\ w_j p_j, &{}\quad \hbox {if}~~u \ge d_j+p_j. \end{array} \right. \end{aligned}$$

(14)

Principle of algorithm${\pmb {\mathcal {H}}_1}$ For each index $j\in \{1,2, \ldots , n\}$, the state set ${\mathcal L}_j$ can be generated from ${\mathcal L}_{j-1}$. In fact, given a state $(j, t^*, U^*_1, \ldots , U^*_m, k^*) \in \mathcal {L}_{j}$, there must be a schedule $\sigma _j\in \Pi _j$ such that

$$\begin{aligned} \mathbf{S} (\sigma _j)= (j, t^*, U^*_1, \ldots , U^*_m, k^*). \end{aligned}$$

(15)

Let $\sigma _{j-1}$ be the schedule of $\{J_1, J_2, \ldots , J_{j-1}\}$ which is obtained from $\sigma _j$ by deleting job $J_j$. Clearly, we have $\sigma _{j-1}\in \Pi _{j-1}$. Let

$$\begin{aligned} \mathbf{S} (\sigma _{j-1})= (j-1, t, U_1, \ldots , U_m, k) \in \mathcal {L}_{j-1}. \end{aligned}$$

(16)

Four different scenarios related to job $J_j$ are analyzed as follows:

Case 1 Job $J_j$ is late in $\sigma _j$. Then, $t^*=t$ and $k^*=k$. Moreover, the contribution of job $J_j$ to the objective value of agent $A_{x_j}$ in $\sigma _j$ is $\Phi _j(\infty )=w_j p_j$. Thus, $U^*_{x_j}=U_{x_j}+\Phi _j(\infty )$ and $U^*_x=U_x$ for $x\in \{1,2, \ldots , m\}{\setminus }\{x_j\}$. It follows that the state $(j, t^*, U^*_1, \ldots , U^*_m, k^*) \in \mathcal {L}_{j}$ is given by $(j, t, U_1, \ldots , U_{x_j-1}, U_{x_j}+\Phi _j(\infty ), U_{x_j+1}, \ldots , U_m, k)$.

Case 2 Job $J_j$ is deferred in $\sigma _j$. Then, job $J_j$ is strictly deferred with respect to itself in $\sigma _j$. This means that $k^*=j$. Thus, the definitions of $\mathbf{S} (\sigma _{j-1})$ and $\mathbf{S} (\sigma _{j})$ imply that the state $(j, t^*, U^*_1, \ldots , U^*_m, k^*) \in \mathcal {L}_{j}$ is given by $(j, t, U_1, \ldots , U_m, j)$. Note that this case occurs only if $k=0$ and $t<d_j$.

Case 3 Job $J_j$ is non-late and not deferred in $\sigma _j$, and moreover, job $J_k$ (if $k\ne 0$) is strictly deferred with respect to job $J_j$ in $\sigma _j$. Then, $k^*=k$, $t^*=t+p_j$ is the completion time of job $J_j$ in $\sigma _j$, and the contribution of job $J_j$ to the objective value of agent $A_{x_j}$ is $\Phi _j(t+p_j)=w_j \max \{t+p_j-d_j, 0\}$ in $\sigma _j$. Thus, the state $(j, t^*, U^*_1, \ldots , U^*_m, k^*) \in \mathcal {L}_{j}$ is given by $(j, t+p_j, U_1, \ldots , U_{x_j-1}, U_{x_j}+\Phi _j(t+p_j), U_{x_j+1}, \ldots , U_m, k)$. Note that this case occurs only if either $k=0$ and $t<d_j$, or $k>0$ and $t+p_j<d_k$.

Case 4$1\le k<j$ and job $J_{k}$ is sequenced immediately after job $J_j$ in $\sigma _j$. Then, $k^*=0$, job $J_j$ is early in $\sigma _j$, the completion time of job $J_k$ is $t+p_j+p_k$ in $\sigma _j$, and the contribution of job $J_k$ to the objective value of agent $A_{x_k}$ is $\Phi _k(t+p_j+p_k)=w_k \max \{t+p_j+p_k-d_k, 0\}$ in $\sigma _j$. It follows that the state $(j, t^*, U^*_1, \ldots , U^*_m, k^*) \in \mathcal {L}_{j}$ is given by $(j, t+p_j+p_k, U_1, \ldots , U_{x_k-1}, U_{x_k}+\Phi _k(t+p_j+p_k), U_{x_k+1}, \ldots , U_m, 0)$, where $k^*=0$ holds since there are no deferred jobs with respect to $J_j$ in $\sigma _j$. Note that this case occurs only if $k>0$ and $t+p_j<d_k$.

To further reduce the state space of algorithm $\mathcal {H}_1$, the following elimination property is provided.

Lemma 3.5

For any two states $(j, t, U_1, U_2, \ldots , U_m, k)$ and $(j, t', U'_1, U'_2, \ldots , U'_m, k)$ in $\mathcal {L}_j$ with $t \le t'$ and $U_x \le U'_x$ for $x=1, 2, \ldots , m$, the second state can be eliminated from ${\mathcal L}_j$.

Proof

The property holds since any extension of the latter state to a complete schedule $\sigma '$, the corresponding extension of the former state yields a schedule $\sigma$ with $\sum w_j^{(x)} Y_j^{(x)} (\sigma ) \le \sum w_j^{(x)} Y_j^{(x)} (\sigma ')$ for $x=1, 2, \ldots , m$, while the reverse is not true. $\square$

Our DP algorithm $\mathcal {H}_1$ consists of n iterations in which it constructs some sets of states. The algorithm is initialized by setting $\mathcal {L}_0=\{(0, 0, 0, \ldots , 0, 0)\}$ and ${\mathcal L}_j=\emptyset$ for $j=1, 2, \ldots , n$. In the j-iteration, the state space $\mathcal {L}_j$ will be dynamically generated from $\mathcal {L}_{j-1}$, $j=1, 2, \ldots , n$. Now the algorithm $\mathcal {H}_1$ is given as follows.

Algorithm

$\mathcal {H}_1$: For problem $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)}, \ldots , \sum w_j^{(m)}Y_j^{(m)})$.

• Step 1. [Initialization] Set $\mathcal {L}_0=\{(0, 0, 0, \ldots , 0, 0)\}$, ${\mathcal L}_j=\emptyset$ for $j=1, 2, \ldots , n$ and $j:=0$.

• Step 2. [Generation] If $j < n$, set $j:=j+1$. Do the following:

  • Step 2.1. For each $(j-1, t, U_1, \ldots , U_m, k) \in \mathcal {L}_{j-1}$, do the following:

    • (1) Set $\mathcal {L}_j \leftarrow \mathcal {L}_j \cup \{(j, t, U_1, \ldots , U_{x_j-1}, U_{x_j}+\Phi _j(\infty ), U_{x_j+1}, \ldots , U_m, k)\}$ unconditionally;

    • (2) If $k=0$ and $t<d_j$, set $\mathcal {L}_j \leftarrow \mathcal {L}_j \cup \{(j, t, U_1, \ldots , U_m, j)\}$;

    • (3) If [$k=0$ and $t<d_j$] or [$k>0$ and $t+p_j<d_k$], set $\mathcal {L}_j \leftarrow \mathcal {L}_j \cup \{ (j, t+p_j, U_1, \ldots , U_{x_j-1}, U_{x_j}+\Phi _j(t+p_j),U_{x_j+1}, \ldots , U_m, k)\}$;

    • (4) If $k>0$ and $t+p_j<d_k$, set $\mathcal {L}_j \leftarrow \mathcal {L}_j \cup \{(j, t+p_j+p_k, U_1, \ldots , U_{x_k-1}, U_{x_k}+\Phi _k(t+p_j+p_k), U_{x_k+1}, \ldots , U_m, 0)\}$.

  • Step 2.2. [Elimination] For any two states $(j, t, U_1, U_2, \ldots , U_m, k)$ and $(j, t', U'_1, U'_2, \ldots , U'_m, k)$ in $\mathcal {L}_j$ with $t \le t'$ and $U_x \le U'_x$ for $x=1, 2, \ldots , m$, eliminate the latter one.

• Step 3. [Refinement] For any two states $(n, t, U_1, U_2, \ldots , U_m, 0)$ and $(n, t', U'_1, U'_2, \ldots , U'_m, 0)$ in $\mathcal {L}_n$ with $U_x \le U'_x$ for $x=1, 2, \ldots , m$, eliminate the latter one.

• Step 4. [Result] Set $\mathcal {R}=\{(U_1, U_2, \ldots , U_m): (n, t, U_1, U_2, \ldots , U_m, 0) \in \mathcal {L}_n\}$. For each efficient point $(U_1, U_2, \ldots , U_m) \in \mathcal {R}$, obtain the corresponding Pareto-optimal schedule by backtracking.

In algorithm $\mathcal {H}_1$, each job $J_j$ is considered in succession in the EDD order, and all possible decisions are discussed in Step 2.1. Lemma 3.4 demonstrates that there is at most one strictly deferred job with respect to $J_j$ in the j-iteration. The case that $J_j$ is late (Case 1) is dealt with in Step 2.1-1. The case that $J_j$ is deferred (Case 2) is handled in Step 2.1-2. The case that $J_j$ is non-late and not deferred and the strictly deferred job $J_k$ with $1\le k<j$ (if it exists) is not sequenced immediately after $J_j$ (Case 3) is considered in Step 2.1-3. The case that the deferred (but not strictly deferred) job $J_k$ with $1 \le k \le j-1$ is sequenced immediately after $J_j$ (Case 4) is examined in Step 2.1-4. The [Elimination] procedure in Step 2.2 and the [Refinement] procedure is guaranteed by Lemma 3.5.

Remark 3.6

In the n-iteration of algorithm $\mathcal {H}_1$, for each state $(n-1, t, U_1, \ldots , U_m, k) \in \mathcal {L}_{n-1}$, we only need to consider two cases. Specifically, if $k=0$, we can set $\mathcal {L}_{n}\leftarrow \mathcal {L}_n \cup \{(n, t+p_n, U_1, \ldots , U_{x_n-1}, U_{x_n}+\varPhi _n(t+p_n), U_{x_n+1}, \ldots , U_m, 0)\}$; else if $k>0$ and $k+p_n < d_k$, we can set $\mathcal {L}_{n} \leftarrow \mathcal {L}_n \cup \{(n, t+p_n+p_k, U_1, \ldots , U_{x_k-1}, U_{x_k}+\varPhi _k(t+p_n+p_k), U_{x_k+1}, \ldots , U_m, 0)\}$.

Let $\mathrm {UB}_x$ be an upper bound on the objective value of agent $A_x$ for $x=1, 2, \ldots , m$. Because sequencing all the x-jobs late is a feasible schedule, we can set $\mathrm {UB}_x=\sum _{J_j \in \mathcal {J}^{(x)}} w_jp_j$ for $x=1, 2, \ldots , m$.

Theorem 3.7

Problem $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)}, \ldots , \sum w_j^{(m)}Y_j^{(m)})$ can be solved by algorithm $\mathcal {H}_1$ in $O(n^2\prod _{x=1}^{m} \mathrm {UB}_x)$ time. When m is a fixed constant, it is pseudo-polynomial.

Proof

The optimality of algorithm $\mathcal {H}_1$ follows from the fact that it implicitly enumerates all the schedules that meet the optimal properties in Lemmas 3.1–3.5. We next discuss the time complexity of $\mathcal {H}_1$. In Step 1, it takes O(n) time for initialization. In Step 2, for each state $(j, t, U_1, U_2, \ldots , U_m, k) \in \mathcal {L}_j$, $0 \le U_x \le \mathrm {UB}_x$ for $x=1, 2, \ldots , m$, and $k \le j$. Due to the elimination rule, at most $O(n\prod _{x=1}^{m} \mathrm {UB}_x)$ distinct states in $\mathcal {L}_j$ are retained. Moreover, out of each state in $\mathcal {L}_{j-1}$, at most three new states are generated in $\mathcal {L}_j$. Therefore, the construction of list $\mathcal {L}_j$ in Step 2 requires at most $O(n\prod _{x=1}^{m} \mathrm {UB}_x)$ time, which is also the time needed for the elimination procedure. Because the refinement procedure requires $O(\prod _{x=1}^{m}\mathrm {UB}_x)$ time and Step 2 is repeated n times, the overall running time of algorithm $\mathcal {H}_1$ is given by $O(n^2\prod _{x=1}^{m}\mathrm {UB}_x)$. $\square$

To facilitate the understanding, we give in “Appendix” a numerical example to illustrate the execution of algorithm $\mathcal {H}_1$ for problem $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)}, \ldots , \sum w_j^{(m)}Y_j^{(m)})$.

4 $(1+\epsilon )$-approximate Pareto-optimal frontier

Since the problem $1 | CO, \sum Y_j^{(x)} \le K_x, x=1, 2, \ldots , m |-$ is already unary $\mathcal {NP}$-complete when m is arbitrary, and its two special cases $1 | CO, d_j^{(x)}=d, \sum Y_j^{(x)} \le K_x, x=1, 2, \ldots , m |-$ and$1 | CO, p_j^{(x)}=1, \sum w_j^{(x)}Y_j^{(x)} \le K_x, x=1, 2 | -$ are both binary $\mathcal {NP}$-complete, we consider the approximate Pareto-optimal frontier, which was first introduced by Papadimitriou and Yannakakis (2000).

A $(1+\epsilon )$-approximate Pareto-optimal frontier is a set (referred to as $\mathcal {POF}_{\epsilon }$) of m-vectors such that for each $\eta =(\eta _1, \eta _2, \ldots , \eta _m) \in \mathcal {POF}$, there exists an $\eta '=(\eta '_1, \eta '_2, \ldots , \eta '_m) \in \mathcal {POF}_{\epsilon }$ with $\eta '_x \le (1+\epsilon ) \eta$ for $x=1, 2, \ldots , m$, and there exists a feasible solution $s'$ with $F_x(s')=\eta '_x$ for $x=1, 2, \ldots , m$.

Let $m \ge 2$ be a fixed constant and $\epsilon >0$. Next we convert algorithm $\mathcal {H}_1$ into a $(1+\epsilon )$-approximate Pareto-optimal frontier. The main idea is based on the improvement of algorithm $\mathcal {H}_1$ by eliminating some special states from the search space in each iteration and reducing the size of $\mathcal {L}_j$ to a polynomial-size state set $\widetilde{\mathcal {L}_j}$ at the end of the jth iteration.

Algorithm

$\mathcal {H}_2$: A $(1+\epsilon )$-approximation for $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \ldots , \sum w_j^{(m)}Y_j^{(m)})$.

• Step 0. [Partition] For $x=1, 2, \ldots , m$, partition the interval $[0, \mathrm {UB}_x]$ into $\xi _x+1$ subintervals $I_0^{(x)}, I_1^{(x)},\ldots , I_{\xi _x}^{(x)}$ such that $I_0^{(x)}=[0, 1)$, $I_r^{(x)}=[(1+\epsilon )^{\frac{r-1}{n}}, (1+\epsilon )^{\frac{r}{n}})$ for $1 \le r \le \xi _x-1$, and $I_{\xi _x}^{(x)}=[(1+\epsilon )^{\frac{\xi _x-1}{n}}, \mathrm {UB}_x]$, where $\xi _x=n \lceil \log _{1+\epsilon } \mathrm {UB}_x \rceil =O(\frac{n}{\epsilon } \log \mathrm {UB}_x)$.

• Step 1. [Initialization] Set $\widetilde{\mathcal {L}_0}=\{(0, 0, 0, \ldots , 0, 0)\}$, $\widetilde{{\mathcal L}_j}=\emptyset$ for $j=1, 2, \ldots , n$ and $j:=0$.

• Step 2. [Generation] If $j < n$, set $j:=j+1$.

  • Step 2.1. Perform the same operations as Step 2.1 of algorithm $\mathcal {H}_1$.

  • Step 2.2. [Elimination] For any two states $(j, t, U_1, U_2, \ldots , U_m, k)$ and $(j, t', U'_1, U'_2, \ldots , U'_m, k)$ in $\widetilde{\mathcal {L}_j}$ in which $(U_1, U_2, \ldots , U_m)$ and $(U'_1, U'_2, \ldots , U'_m)$ fall within the same m-dimensional boxes $I_{r_1}^{(1)} \times I_{r_2}^{(2)} \times \cdots \times I_{r_{m}}^{(m)}$ with $t \le t'$, eliminate the latter one.

• Step 3. [Refinement] For any two states $(n, t, U_1, U_2, \ldots , U_m, 0)$ and $(n, t', U'_1, U'_2, \ldots , U'_m, 0)$ in $\widetilde{\mathcal {L}_n}$ with $U_x \le U'_x$ for $x=1, 2, \ldots , m$, eliminate the latter one.

• Step 4. [Result] Set $\widetilde{\mathcal {R}}=\{(U_1, U_2, \ldots , U_m): (n, t, U_1, U_2, \ldots , U_m, 0) \in \widetilde{\mathcal {L}_n}\}$. For each point $(U_1, U_2, \ldots , U_m) \in \widetilde{\mathcal {R}}$, obtain the corresponding approximate schedule by backtracking.

Lemma 4.1

For any eliminated state $(j, t, U_1, U_2, \ldots , U_m, k) \in \mathcal {L}_j$, algorithm $\mathcal {H}_2$ finds a state $(j, \widetilde{t}, \widetilde{U_1}, \widetilde{U_2}, \ldots , \widetilde{U_m}, k) \in \widetilde{\mathcal {L}_j}$ such that $\widetilde{t} \le t$ and $\widetilde{U_x} \le (1+\epsilon )^{\frac{j}{n}}U_x$ for $x=1, 2, \ldots , m$.

Proof

Correctness of the result is proved by induction over $j=1,2, \ldots , n$. Note that the three states $(0, 0, 0, \ldots , 0, \varPhi _1(\infty ), 0, \ldots , 0, 0)$, $(0, 0, 0, \ldots , 0, 1)$, $(0, p_1, 0, \ldots , 0, \varPhi _1(p_1), 0, \ldots , 0, 0)$, which correspond to the cases where job $J_1$ is late, deferred, and scheduled early or partially early, respectively, are generated in $\mathcal {L}_1$ and $\widetilde{\mathcal {L}_1}$ in the first iteration, and no one is eliminated in $\mathcal {H}_2$. Then, we have $\widetilde{{\mathcal L}_1}={\mathcal L}_1$. Thus, the result is correct for $j=1$.

Inductively, we assume that $j \ge 2$ and the result is correct for $i=1,2, \ldots , j-1$. Then, for each $i\in \{1,2, \ldots , j-1\}$ and each eliminated state $(i, t, U_1, U_2, \ldots , U_m, k) \in \mathcal {L}_i$, there exists a state $(i, \widetilde{t}, \widetilde{U_1}, \widetilde{U_2}, \ldots , \widetilde{U_m}, k) \in \widetilde{\mathcal {L}_i}$ such that $\widetilde{t} \le t$ and $\widetilde{U_x} \le (1+\epsilon )^{\frac{i}{n}}U_x$ for $x=1, 2, \ldots , m$. We have to show that the result is correct for $i=j$ in the sequel.

Let $(j, t, U_1, U_2, \ldots , U_m, k) \in \mathcal {L}_j$ be an eliminated state. W.l.o.g., we can assume that job $J_j$ is a 1-job, i.e., $x_j=1$. When implementing $\mathcal {H}_1$, the state $(j, t, U_1, U_2, \ldots , U_m, k)$ is introduced from some state $(j-1, t', U'_1, U'_2, \ldots , U'_m, k') \in \mathcal {L}_{j-1}$. From the induction hypothesis, we know that there exists a state $(j-1, \widetilde{t'}, \widetilde{U'_1}, \widetilde{U'_2}, \ldots , \widetilde{U'_m}, k') \in \widetilde{\mathcal {L}_{j-1}}$ such that

$$\begin{aligned} \widetilde{t'} \le t', \end{aligned}$$

(17)

and

$$\begin{aligned} \widetilde{U'_x} \le (1+\epsilon )^{\frac{j-1}{n}}U'_x ~\mathrm {for}~ x=1, 2, \ldots , m. \end{aligned}$$

(18)

Depending on different state transitions, the following four cases have to be distinguished.

Case 1$(j, t, U_1, U_2, \ldots , U_m, k)=(j, t', U'_1+\varPhi _j(\infty ), U'_2, \ldots , U'_m, k')$. This implies that job $J_j$ is late. Recall that $(j-1, \widetilde{t'}, \widetilde{U'_1}, \widetilde{U'_2}, \ldots , \widetilde{U'_m}, k') \in \widetilde{\mathcal {L}_{j-1}}$. Then, the state $(j, \widetilde{t'}, \widetilde{U'_1}+\varPhi _j(\infty ), \widetilde{U'_2}, \ldots , \widetilde{U'_m}, k')$ is generated in the j-iteration of $\mathcal {H}_2$ just before the elimination procedure. It follows directly from the elimination procedure in $\mathcal {H}_2$ that there exists a state $(j, \widetilde{t}, \widetilde{U_1}, \widetilde{U_2}, \ldots , \widetilde{U_m}, k') \in \widetilde{\mathcal {L}_j}$ such that

$$\begin{aligned} \widetilde{t} \le \widetilde{t'} \le t' = t, \end{aligned}$$

(19)

$$\begin{aligned}&\widetilde{U_1} \le (1+\epsilon )^{\frac{1}{n}}(\widetilde{U'_1}+\varPhi _j(\infty ))\nonumber \\&\le (1+\epsilon )^{\frac{1}{n}}((1+\epsilon )^{\frac{j-1}{n}}U'_1+\varPhi _j(\infty ))\nonumber \\&\le (1+\epsilon )^{\frac{j}{n}}U_1, \end{aligned}$$

(20)

and

$$\begin{aligned}&\widetilde{U_x} \le (1+\epsilon )^{\frac{1}{n}}\widetilde{U'_x}\nonumber \\&\le (1+\epsilon )^{\frac{1}{n}}((1+\epsilon )^{\frac{j-1}{n}}U'_x)\nonumber \\&=(1+\epsilon )^{\frac{j}{n}}U_x ~\mathrm {for}~ x=2, 3, \ldots , m, \end{aligned}$$

(21)

where the above inequalities follow from inequalities (17)–(18). Since $k=k'$, the result holds for the j-iteration in this case.

Case 2$(j, t, U_1, U_2, \ldots , U_m, k)=(j, t', U'_1, U'_2, \ldots , U'_m, j)$. This implies that job $J_j$ is deferred, $k'=0$ and $t'<d_j$. Recall that $(j-1, \widetilde{t'}, \widetilde{U'_1}, \widetilde{U'_2}, \ldots , \widetilde{U'_m}, k') \in \widetilde{\mathcal {L}_{j-1}}$ and $\widetilde{t'} \le t'$. Then the state $(j, \widetilde{t'}, \widetilde{U'_1}, \widetilde{U'_2}, \ldots , \widetilde{U'_m}, j)$ is generated in the j-iteration of $\mathcal {H}_2$ just before the elimination procedure. It follows directly from the elimination procedure in $\mathcal {H}_2$ that there exists a state $(j, \widetilde{t}, \widetilde{U_1}, \widetilde{U_2}, \ldots , \widetilde{U_m}, j) \in \widetilde{\mathcal {L}_j}$ such that

$$\begin{aligned} \widetilde{t} \le \widetilde{t'} \le t' = t, \end{aligned}$$

(22)

and

$$\begin{aligned}&\widetilde{U_x} \le (1+\epsilon )^{\frac{1}{n}}\widetilde{U'_x}\nonumber \\&\quad \le (1+\epsilon )^{\frac{1}{n}}((1+\epsilon )^{\frac{j-1}{n}}U'_x)\nonumber \\&\quad =(1+\epsilon )^{\frac{j}{n}}U_x ~\mathrm {for}~ x=1, 2, \ldots , m, \end{aligned}$$

(23)

where the above inequalities follow from inequalities (17)–(18). Since $k=j$, the result holds for the j-iteration in this case.

Case 3$(j, t, U_1, U_2, \ldots , U_m, k)=(j, t'+p_j, U'_1+\varPhi _j(t'+p_j), U'_2, \ldots , U'_m, k')$. This implies that job $J_j$ is non-late and not deferred and the strictly deferred job $J_{k'}$ ($k'<j$), if it exists, is not sequenced immediately after job $J_j$. Recall that $(j-1, \widetilde{t'}, \widetilde{U'_1}, \widetilde{U'_2}, \ldots , \widetilde{U'_m}, k') \in \widetilde{\mathcal {L}_{j-1}}$ and $\widetilde{t'} \le t'$. Then, the state $(j, \widetilde{t'}+p_j, \widetilde{U'_1}+\varPhi _j(\widetilde{t'}+p_j), \widetilde{U'_2}, \ldots , \widetilde{U'_m}, k')$ is generated in the j-iteration of $\mathcal {H}_2$ just before the elimination procedure. It follows directly from the elimination procedure in $\mathcal {H}_2$ that there exists a state $(j, \widetilde{t}, \widetilde{U_1}, \widetilde{U_2}, \ldots , \widetilde{U_m}, k') \in \widetilde{\mathcal {L}_j}$ such that

$$\begin{aligned} \widetilde{t} \le \widetilde{t'}+p_j \le t'+p_j = t, \end{aligned}$$

(24)

$$\begin{aligned}&\widetilde{U_1} \le (1+\epsilon )^{\frac{1}{n}}(\widetilde{U'_1}+\varPhi _j(\widetilde{t'}+p_j))\nonumber \\&\quad \le (1+\epsilon )^{\frac{1}{n}}((1+\epsilon )^{\frac{j-1}{n}}U'_1+\varPhi _j(t'+p_j))\nonumber \\&\quad \le (1+\epsilon )^{\frac{j}{n}}U_1, \end{aligned}$$

(25)

and

$$\begin{aligned}&\widetilde{U_x} \le (1+\epsilon )^{\frac{1}{n}}\widetilde{U'_x}\nonumber \\&\quad \le (1+\epsilon )^{\frac{1}{n}}((1+\epsilon )^{\frac{j-1}{n}}U'_x)\nonumber \\&\quad =(1+\epsilon )^{\frac{j}{n}}U_x ~\mathrm {for~} x=2, 3, \ldots , m, \end{aligned}$$

(26)

where the above inequalities follow from inequalities (17)–(18) and $\varPhi _j(\cdot )$ is a non-decreasing function. Since $k=k'$, the result holds for the j-iteration in this case.

Case 4$(j, t, U_1, U_2, \ldots , U_m, k)=(j, t'+p_j+p_{k'}, U'_1, \ldots , U'_{x_{k'-1}}, U'_{x_{k'}}+\varPhi _{k'}(t'+p_j+p_{k'}), U'_{x_{k'+1}}, \ldots , U'_m, 0)$. This implies that the deferred (but not strictly deferred) job $J_{k'}$ is sequenced immediately after job $J_j$ and $t'+p_j<d_{k'}\le d_j$, where $0<k'<j$. Recall that $(j-1, \widetilde{t'}, \widetilde{U'_1}, \widetilde{U'_2}, \ldots , \widetilde{U'_m}, k') \in \widetilde{\mathcal {L}_{j-1}}$ and $\widetilde{t'}+p_j \le t'+p_j<d_{k'}$. Then, the state $(j, \widetilde{t'}+p_j+p_{k'}, \widetilde{U'_1}, \ldots , \widetilde{U'_{x_{k'-1}}}, \widetilde{U'_{x_{k'}}}+\varPhi _{k'}(\widetilde{t'}+p_j+p_{k'}), \widetilde{U'_{x_{k'+1}}}, \ldots , \widetilde{U'_m}, 0)$ is generated in the j-iteration of $\mathcal {H}_2$ just before the elimination procedure. It follows directly from the elimination procedure in $\mathcal {H}_2$ that there exists a state $(j, \widetilde{t}, \widetilde{U_1}, \widetilde{U_2}, \ldots , \widetilde{U_m}, 0) \in \widetilde{\mathcal {L}_j}$ such that

$$\begin{aligned} \widetilde{t} \le \widetilde{t'}+p_j+p_{k'} \le t'+p_j+p_{k'}= t, \end{aligned}$$

(27)

$$\begin{aligned}&\widetilde{U_x} \le (1+\epsilon )^{\frac{1}{n}}\widetilde{U'_x}\nonumber \\&\quad \le (1+\epsilon )^{\frac{1}{n}}((1+\epsilon )^{\frac{j-1}{n}}U'_x)\nonumber \\&\quad =(1+\epsilon )^{\frac{j}{n}}U_x ~\mathrm {for}~ x=1, \ldots , x_{k'}-1, x_{k'}+1, \ldots , m,\nonumber \\ \end{aligned}$$

(28)

and

$$\begin{aligned}&\widetilde{U_{x_{k'}}} \le (1+\epsilon )^{\frac{1}{n}}(\widetilde{U'_{x_{k'}}}+\varPhi _{k'}(\widetilde{t'}+p_j+p_{k'}))\nonumber \\&\quad \le (1+\epsilon )^{\frac{1}{n}}((1+\epsilon )^{\frac{j-1}{n}}U'_{x_{k'}}+\varPhi _{k'}(t'+p_j+p_{k'}))\nonumber \\&\quad \le (1+\epsilon )^{\frac{j}{n}}U_{x_{k'}}, \end{aligned}$$

(29)

where the above inequalities follow from inequalities (17)–(18) and $\varPhi _j(\cdot )$ is a non-decreasing function. Since $k=0$, the result holds for the j-iteration in this case.

Combining the above four cases, the lemma holds. $\square$

Theorem 4.2

Let $m \ge 2$ be a fixed constant and let $\epsilon >0$. Algorithm $\mathcal {H}_2$ finds a $(1+\epsilon )$-approximate Pareto-optimal frontier for problem $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)}, \ldots , \sum w_j^{(m)}Y_j^{(m)})$ in $O(\frac{n^{m+2}}{\epsilon ^{m}} \Pi _{x=1}^{m} \log \mathrm {UB}_x)$ time.

Proof

Let $(\eta _1, \eta _2, \ldots , \eta _m)$ be an arbitrary Pareto-optimal point on the Pareto-optimal frontier. By Theorem 3.7, algorithm $\mathcal {H}_1$ will find a Pareto-optimal schedule which corresponds to a feasible state $(n, t, U_1, U_2, \ldots , U_m, 0) \in \mathcal {L}_n$ with $U_x=\eta _x$ for $x=1, 2, \ldots , m$. From Lemma 4.1, if it has been eliminated during the execution of algorithm $\mathcal {H}_2$, then there exists a non-eliminated state $(n, \widetilde{t}, \widetilde{U_1}, \widetilde{U_2}, \ldots , \widetilde{U_m}, 0) \in \widetilde{\mathcal {L}_n}$ such that $\widetilde{U_x} \le (1+\epsilon )^{\frac{n}{n}}U_x=(1+\epsilon )U_x$ for $x=1, 2, \ldots , m$. From the execution of $\mathcal {H}_2$, we know that there exists a state $(\eta '_1, \eta '_2, \ldots , \eta '_m) \in \widetilde{R}$ such that $\eta '_x \le \widetilde{U_x} \le (1+\epsilon )\eta _x$ for $x=1, 2, \ldots , m$. Hence, it follows that algorithm $\mathcal {H}_2$ finds a $(1+\epsilon )$-approximate Pareto-optimal frontier for problem $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)}, \ldots , \sum w_j^{(m)}Y_j^{(m)})$.

We next discuss the time complexity of $\mathcal {H}_2$. In Step 0, it takes $O(\sum _{x=1}^{m}n \lceil \log _{1+\epsilon } \mathrm {UB}_x \rceil ) =O(\frac{n}{\epsilon }\sum _{x=1}^{m} \log \mathrm {UB}_x)$ time to partition the intervals and Step 1 needs O(n) time for initialization. Since $[0, \mathrm {UB}_x]$ is partitioned into $O(\frac{n}{\epsilon }\log \mathrm {UB}_x)$ subintervals, due to the elimination procedure, there are at most $O(\frac{n^{m+1}}{\epsilon ^{m}} \Pi _{x=1}^{m} \log \mathrm {UB}_x)$ distinct states in $\widetilde{\mathcal {L}_j}$. Moreover, out of each state in $\widetilde{\mathcal {L}_{j-1}}$, at most three new states are generated in $\widetilde{\mathcal {L}_j}$. Therefore, the construction of list $\widetilde{\mathcal {L}_j}$ in Step 2 requires at most $O(\frac{n^{m+1}}{\epsilon ^{m}} \Pi _{x=1}^{m} \log \mathrm {UB}_x)$ time, which is also the time needed for the elimination procedure. Because the refinement procedure in Step 3 requires $O(\frac{n^{m}}{\epsilon ^{m}} \Pi _{x=1}^{m} \log \mathrm {UB}_x)$ time and Step 2 is repeated n times, the overall running time of algorithm $\mathcal {H}_2$ is given by $O(\frac{n^{m+2}}{\epsilon ^{m}} \Pi _{x=1}^{m} \log \mathrm {UB}_x)$. $\square$

5 Conclusions

In this paper, we investigate a scheduling problem with m competitive agents on a single machine in which each agent seeks to minimize its own total weighted late work. The goal is to find the Pareto-optimal frontier and identify a Pareto-optimal schedule for each Pareto-optimal point on the Pareto-optimal frontier. We show that (i) when m is arbitrary, the problem is unary $\mathcal {NP}$-hard, and (ii) when m is two, the problems are binary $\mathcal {NP}$-hard for the two cases where all jobs have the common due date and all jobs have the unit processing times. We develop a pseudo-polynomial algorithm and a $(1+\epsilon )$-approximate Pareto-optimal frontier when m is a fixed constant.

For future research, we suggest several interesting directions as follows:

• Generalizing our work to different machine settings such as the flow-shop, open-shop, or parallel machines.

• Designing the effective meta-heuristic algorithm for the unary $\mathcal {NP}$-hard problem $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)}, \ldots , \sum w_j^{(m)}Y_j^{(m)})$ when m is arbitrary.

• Analyzing the multi-agent problem for the case where job preemption is allowed.

• Studying the more general case of non-disjoint sets of jobs among different agents.

Appendix

Example

Consider a two-agent scheduling problem $1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)})$, in which $\mathcal {J}^1=\{J_1^{(1)}, J_2^{(1)}\}$, $\mathcal {J}^2=\{J_1^{(2)}, J_2^{(2)}, J_3^{(2)}\}$, and the corresponding job parameters are given in Table 1.

Table 1 Job data of the problem set

Before executing algorithm $\mathcal {H}_1$, the jobs are first indexed in the EDD order, see Table 2.

Table 2 The indexed job data of the problem set

Table 3 Generation of $\mathcal {L}_1$ from $\mathcal {L}_0$

Table 4 Generation of $\mathcal {L}_2$ from $\mathcal {L}_1$

Table 5 Generation of $\mathcal {L}_3$ from $\mathcal {L}_2$

Table 6 Generation of $\mathcal {L}_4$ from $\mathcal {L}_3$

In the sequel, we apply algorithm $\mathcal {H}_1$ to solve this numerical example.

Step 1 [Initialization] Set $\mathcal {L}_0=\{(0, 0, 0, 0, 0)\}$, ${\mathcal L}_j=\emptyset$ for $j=1, 2, \ldots , 5$ and $j:=0$.

Step 2 [Generation] For $j=1$, $\mathcal {L}_1=\{(1, 0, 2, 0, 0)$, $(1, 0, 0, 0, 1), (1, 2, 0, 0, 0)\}$, see Table 3 for the generation process.

For $j=2$, $\mathcal {L}_2=\{(2, 0, 2, 6, 0), (2, 0, 2, 0, 2), (2, 3, 2, 0, 0)$, $(2, 0, 0, 6, 1), (2, 2, 0, 6, 0), (2, 2, 0, 0, 2), (2, 5, 0, 2, 0)\}$, see Table 4 for the generation process.

For $j=3$, $\mathcal {L}_3=\{(3, 0, 14, 6, 0), (3, 0, 2, 6, 3),$$(3, 4, 2, 6, 0), (3, 0, 14, 0, 2),$ (3, 3, 14, 0, 0), (3, 3, 2, 0, 3),  $(3, 7, 2, 0, 0),$ (3, 0, 12, 6, 1), (3, 2, 12, 6, 0),  $(3, 2, 0, 6, 3), (3, 6, 0, 6, 0),$ (3, 2, 12, 0, 2),  $(3, 5, 12, 2, 0), (3, 5, 0, 2, 3), (3, 9, 6, 2, 0)\}$, see Table 5 for the generation process.

Table 7 Generation of $\mathcal {L}_5$ from $\mathcal {L}_4$

For $j=4$, $\mathcal {L}_4=\{(4, 0, 14, 14, 0), (4, 0, 14, 6, 4),$ (4, 2, 14, 6, 0), (4, 0, 2, 14, 3), (4, 2, 2, 6, 3),  $(4, 6, 2, 6, 0), (4, 4, 2, 14, 0), (4, 4, 2, 6, 4),$$(4, 0, 14, 8, 2), (4, 2, 14, 0, 2), (4, 3, 14, 0, 4),$ (4, 5, 14, 0, 0), (4, 5, 2, 0, 3), (4, 9, 8, 0, 0),  (4, 0, 12, 14, 1), (4, 2, 12, 6, 1),  $(4, 2, 12, 14, 0), (4, 2, 12, 6, 4), (4, 4, 12, 6, 0)$, $(4, 2, 0, 14, 3), (4, 4, 0, 6, 3), (4, 6, 0, 14, 0),$ (4, 6, 0, 6, 4), (4, 8, 0, 10, 0), $(4, 2, 12, 8, 2), (4, 5, 12, 2, 4), (4, 7, 12, 2, 0)\}$, see Table 6 for the generation process, where the underlined states are eliminated in Step 2.2.

For $j=5$, $\mathcal {L}_5=\{(5, 0, 14, 23, 0), (5, 3, 14, 14, 0),$ (5, 2, 14, 15, 0),  (5, 5, 14, 6, 0), (5, 9, 8, 6, 0),  $(5, 4, 2, 23, 0), (5, 7, 2, 14, 0),$ (5, 6, 2, 15, 0), (5, 9, 2, 12, 0),  $(5, 8, 14, 3, 0), (5, 7, 2, 14, 0),$ (5, 2, 12, 23, 0), (5, 5, 12, 14, 0),  (5, 4, 12, 15, 0),  (5, 7, 12, 6, 0), (5, 6, 0, 23, 0),  $(5, 8, 0, 19, 0)\}$, see Table 7 for the generation process (note that we do not need to consider the case where job $J_5$ is deferred as it is the last job), where the underlined states are eliminated in Step 2.2.

Step 3 [Refinement] $\mathcal {L}_5=\{(5, 8, 0, 19, 0), (5, 9, 2, 12, 0),$$(5, 9, 8, 6, 0), (5, 8, 14, 3, 0)\}$.

Step 4 [Result] The Pareto-optimal frontier is $\mathcal {R}=\{(0, 19), (2, 9),$$(8, 6), (14, 3)\}$.

• The Pareto-optimal schedule corresponding to (0, 19) is $J_1^{(1)} \prec J_2^{(1)} \prec J_2^{(2)} \prec \underline{J_1^{(2)}} \prec \underline{J_3^{(2)}}$;

• The Pareto-optimal schedule corresponding to (2, 12) is $J_2^{(1)} \prec J_2^{(2)} \prec J_3^{(2)} \prec \underline{J_1^{(1)}} \prec \underline{J_1^{(2)}}$;

• The Pareto-optimal schedule corresponding to (8, 6) is $J_2^{(2)} \prec J_3^{(2)} \prec J_2^{(1)} \prec \underline{J_1^{(1)}} \prec \underline{J_1^{(2)}}$;

• The Pareto-optimal schedule corresponding to (14, 3) is $J_1^{(2)} \prec J_2^{(2)} \prec J_3^{(2)} \prec \underline{J_1^{(1)}} \prec \underline{J_2^{(1)}}$;

where the underlined jobs are late in the corresponding Pareto-schedule.