1 Introduction

Resource-constrained project scheduling problem (RCPSP) is an important, but NP-hard problem in project planning research Blazewicz et al. (1983). Though, in the past, a number of methods using linear programming, heuristics and meta-heuristics have been proposed to solve the RCPSP, these methods do not often produce good results and take substantial amount of time to converge. In recent times, researchers have intensified their interest towards optimal solution for RCPSP using evolved heuristics and meta-heuristics (Chen and Huang 2007; Valls et al. 2005) making this an active research area.

RCPSP contains a set of activities with deterministic execution time, precedence relation among activities, accumulative resources availability constraints and its consumption by the activities. The objectives in RCPSP is to find a feasible schedule with some quality characteristics such as optimal makespan and computation time, response time and throughput, such that all the constraints are satisfied.

In literature, many exact scheduling algorithms to solve the RCPSP problem that uses linear programming approach (Pritsker et al. 1969; Kaplan 1996; Klein 2006; Mingozzi et al. 1998; Kone et al. 2011) are available. Out of these, the algorithms proposed by Brucker et al. (1998) and Mingozzi et al. (1998) seem to be the most effective and comprehensive. The drawback of their algorithms is that it solves the problem of small instances only (60 activities) in a satisfactory manner. Their method succumbs to higher convergence time for large instances as the solution search space increases drastically, leaving the space for heuristic and meta-heuristic to solve the RCPSP problem in an efficient and satisfactory manner (Bean 1994). Researchers have proposed many scheduling algorithms based on the variants of heuristics and meta-heuristics that include branch and bound (BB) (Dorndorf et al. 2000; Brucker et al. 1998; Demeulemeester and Herroelen 1995; Heilmann 2003), Tabu search (TS) (Nonobe and Ibaraki 2002), genetic algorithm (GA) (Hartmann 1998, 2002; Alcaraz et al. 2003; Valls et al. 2005), simulated annealing (SA) (Bouleimen and Lecocq 2003), adaptive search (AS) (Schirmer 2000), Ant colony optimization (ACO) (Merkle et al. 2002; Herbots et al. 2004), artificial bee colony (ABC) (Shi et al. 2010; Akbari et al. 2011; Ziaratia et al. 2011; Qiong and Yoonho 2013), particle swarm optimization (PSO) (Chen et al. 2010; Kolisch and Hartmann 2006; Zhang et al. 2005, 2006; Jarboui et al. 2008; Lu et al. 2008; Qiong and Yoonho 2013) etc., to produce efficient and satisfactory results for RCPSP.

Particle swarm optimization, an emerging meta-heuristic, has been applied to solve a number of optimization problems because of its distinguishing characteristics (Bai 2010; Jones 2005; Singh et al. 2014) such as (1) simple and easy enumeration, (2) being free from derivation, (3) robustness to control parameters, (4) having limited number of parameters, (5) sensitivity towards the objective function and parameters, (6) less dependency on initial particles, (7) relatively quick convergence and (8) good quality solution. Apart from the mentioned benefits, PSO has been found to be extremely efficient for solving the RCPSP applications (Zhang et al. 2005).

Initially, Zhang et al. (2006) proposed PSO to solve the RCPSP problem with good individual conjunction of priority-based and permutation-based representation and observed that the permutation-based representation scheme performed better. In their proposal, a general framework of PSO was used and a direction to successive use of PSO for RCPSP was mentioned as future research work. Later, Jarboui et al. (2008) proposed a combinatorial PSO (CPSO) with multiple execution modes to solve the RCPSP problem. In their work, modes to each activity were assigned and local search optimization was used to better prioritize the sequence of associated activities. Results indicate that CPSO performs better than SA and was close to the PSO proposed by Zhang et al. (2006). Lu et al. (2008) analyzed the resource-constrained critical path and proposed a PSO-based approach in the generation of resource-constrained schedule for the shortest makespan. Chen et al. (2010) proposed an algorithm for solving RCPSP using delay local search (Zhang et al. 2005) and bidirectional scheduling in PSO. Conclusively, the above proposed methods are practically good to solve the RCPSP problem. Recently, Qiong and Yoonho (2013) proposed an improved PSO to solve the RCPSP using rank priority-based representation, double justification operator and move operator along with the greedy search. Results indicate better performance of the model over other contemporary PSO approaches. The operators used in the above discussed model (e.g. double justification and move operator) are time consuming as these are applied in addition to the normal PSO procedures for the refinement of their results. Further, it uses an obsolete inertia weight selection procedure which requires extra preprocessing time.

Though the above discussed models use PSO and its variants, these often lack efficiency in terms of convergence and computational time. Nevertheless, it gives a direction for further exploration of PSO with introduction of newer and faster operators/parameters and integration of external knowledge to solve the RCPSP problem with improved quality of the solutions and faster convergence.

This paper proposes a PSO variant, an adaptive PSO (A-PSO) to solve the RCPSP problem. The proposed A-PSO is easy and simple (similar to standard PSO), but at the same time effective and faster in producing good results. It is observed that many a times particles become invalid due to the updation of velocity and position in PSO. An operator named valid particle generator (VPG) is proposed and embedded into PSO. By applying VPG, the invalid particles are converted into valid particles in an effective way. Further, an adaptive inertia weight tuner is proposed, which tunes the inertia weight by considering three particles’ parameters: fitness value, previous inertia weight and iteration counter. These three parameters are highly responsible for the effective convergence of the PSO. Fitness of the solution is evaluated in terms of makespan by the assignment of the RCPSP activity to the best processing unit (core) at the moment. To test the effectiveness of the model, a number of experiments were designed on standard instance sets of J30, J60 and J120 from well-known project scheduling Problem Library (PSPLIB) (http://www.om-db.wi.tum.de/psplib/data.html). The result shows that the model works efficiently over 25, 17 and 23 existing state-of-the-art heuristics/meta-heuristics for the instance sets of J30, J60 and J120, respectively.

The outline of this paper is as follows. After an introduction in Sect. 1, the RCPSP problem is described in Sect. 2. Section 3 briefs the standard PSO, whereas the proposed model is fully described in Sect. 4. Experimental studies for the performance of the proposed model along with the comparative experimental results are given in Sect. 5. Finally, the work is concluded in Sect. 6.

2 The RCPSP problem

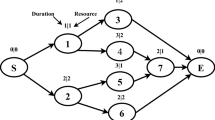
A classical RCPSP problem with specified availabilities of multiple renewable resources (Kolisch and Hartmann 2006, 1999) is as follows. A project includes a set of activities \(V=0,1,2\ldots N,N+1\), each with \(K\) renewable resource types. The duration of an activity \(i\) in \(V\) is denoted by \(d_i ,\) and \(R_k \) is the availability (depicted in time period) of each resource type \(k\in K\) in each time period. An activity \(i\) requires \(r_{ik}\) units of \(k\) type of resources during each time period in its total duration. The activities \(0 \)and \(N+1 \)i.e. the beginning and the end of the project are dummy activities, where \(d_0 =d_{N+1} =0\) and \(r_{0k} =r_{N+1k} =0\). The parameters \(d_i \),\(R_k \) and \(r_{ik} \) are assumed to have non-negative integer values. Activities are interconnected with two types of constraints: one is the precedence constraint of an activity which prevents the start of the execution of that activity while its parent activities \(\mathrm{parent}_i \) are yet to finish, and the other is that sum of all the required resources of a resource type \(k\) at any time period that cannot exceed \(R_k \). The objective of the classical RCPSP problem is to find a feasible schedule with the given precedence constraint among the activities, so that the makespan is minimized (Schirmer 2000). Figure 1a shows an example of the classical RCPSP problem with six (\(N=6\)) activities to be scheduled on \(K=1\) renewable resource of \(R_k =6\) units. One of the feasible schedules for 1(a) is shown in Fig. 1b. \(t \)on X-axis and \(R\) on Y-axis of Fig. 1b represent the time and resource instance, respectively. The example has six maximum available instances of resource type \(R_1 \).

Let us assume that the completion time of an activity \(i\) is denoted as \(C_{i }\) and the completion times for the schedule S, consisting of various activities, is denoted as \(C_{1}\); \(C_{2}\); ...; \(C_{N}\). The mathematical formulation for the classical RCPSP is as follows (Alba and Chicano 2007; Christofides et al. 1987):

$$\begin{aligned} \mathrm{Minimize} \quad C_{N+1}, \end{aligned}$$
(1)
$$\begin{aligned}&\text{ Subject } \text{ to } \quad C_i \le C_j -d_j \;\; \mathrm{for }\, i=1,2,\ldots N+1;\nonumber \\&\quad \mathrm{and}\, j\in \mathrm{parent}_i, \end{aligned}$$
(2)
$$\begin{aligned} \mathop \sum \limits _{i\in A(t)} r_{i,k} \le R_k, \qquad \qquad k\in K;t\ge 0 \end{aligned}$$
(3)
$$\begin{aligned} \mathrm{and} \qquad C_i \ge 0, \qquad i=1,2,\ldots ..N+1. \end{aligned}$$
(4)
Fig. 1
figure 1

a A project example. b A feasible schedule corresponding to the problem 1(a)

Full size image

Equation 1 shows the objective function which is makespan minimization of the schedule. Equation 2 represents the precedence relationship between activities and Eq. 3 depicts the resource limitation constraint. Finally, the constraint of the decision variables is described in Eq. 4.

3 Overview of PSO

Kennedy et al. (2001) proposed PSO as an optimization technique that mimics the behaviour of social creatures (particles) in food searching (Badawi and Shatnawi 2013; Tasgetiren et al. 2004). In this technique, all the particles search for the food in multidimensional search space based on their two important characteristics: position (referred to as the suggested solution) and velocity (rate of change of particle position). If any particle finds a better path to the food location, it attracts other particles to follow its path. The optimal path is evaluated based on its fitness. All particles move slowly towards the obtained solution updating their personal best and the global best solution. At the end, all particles reach the same position following the most probable optimal path. The standard canonical PSO is shown below as mentioned in (Mendes et al. 2004; Sevkli et al. 2004).

Canonical PSO

figure a

Canonical PSO starts with a set of particles with their corresponding random position and velocity vector and is referred to as initial population. To know the relevance of the particle towards the solution, a fitness function is used. Personal best and global best solutions are updated. Initially, each particle’s personal best is considered as its initial solution and the solution with optimum fitness value of all the particles is considered as global best. With each iteration, the position and the velocity vector of each particle is updated using some rules by evaluating the fitness of each particle. The particle with the best fitness value is compared with the global best solution; if it is better, the global best is updated. This procedure is repeated until the predefined termination condition is satisfied.

4 The proposed A-PSO for RCPSP

This section presents the detailed description of the proposed A-PSO to solve the RCPSP problem.

4.1 The proposed model

The model is initiated by random initial population of the particles. The random particles are in the form of random position and velocity values which are evaluated using the fitness function. Now, the termination conditions are verified; if the termination criteria are met, then exit; otherwise, the inertia weight is adaptively tuned to update velocities and positions of each particle. Smallest position value (SPV) rule (sec. 4.3) is applied to convert a continuous value vector into a discrete vector. Some of the produced discrete sequence vectors, corresponding to the particles, may be an invalid sequence. A VPG operator is applied to convert them into a valid sequence. Now, the fitness of each particle is evaluated and based on the fitness value pbest and gbest solutions are initialized. The same procedure is repeated until a termination criterion is met. The flowchart of the proposed model is given in Fig. 2.

The pseudo-code of the proposed A-PSO model for RCPSP is as follows.

figure b
Fig. 2
figure 2

The flowchart of the proposed model

Full size image

The proposed A-PSO begins with the predefined number of random particles where \(X_i^d (k)\) and \(V_i^d (k)\) are the position and velocity of the \(i\)th particle at the \(k\)th iteration in the \(d\)th dimension. To convert a continuous value vector of PSO particles into a discrete value vector, the SPV rule is applied to the \(X_i ( k)\) and a sequence vector \(S_i ( k) \text{ is } \text{ produced }\). The sequence vector may have an invalid sequence; to verify and convert it into a valid sequence, a valid particle generator, i.e. \(VPG(S_i ( k),X_i ( k),V_i ( k)),\) is applied which changes an invalid sequence \(S_i ( k)\) to a valid sequence \(S_i' ( k)\). This sequence is evaluated using a fitness function \(F( {S_i' ( k)})\). On the basis of the fitness values, the \(pbest_i ( 0)\) and gbest are initialized. This procedure is iterated until the termination condition is met. In each next iteration, the values corresponding to \(\omega ,V_i^d ( k)\) and \(X_i^d ( k)\) are updated using Eqs. 10, 11 and 12, respectively. Using the same procedure the values of \(pbest_i ( k)\) and gbest are updated. Finally, gbest is obtained.

4.2 Particle initialization

Initially, a predefined number of random particles are generated by assigning an initial position and velocity for each particle. For this, the following equations have been used.

Position vector \(\overrightarrow{X_i^d } \) depicts the position vector for the \(i\)th particle corresponding to the \(d\)th dimension at the \(0\)th iteration (initially) and is generated by Eq. 5.

$$\begin{aligned} X_i^d ( o)=X_\mathrm{min} +( {X_\mathrm{max} -X_\mathrm{min} })*r, \end{aligned}$$
(5)

where \(X_\mathrm{min} \) and \(X_\mathrm{max} \) have values 0.0 and 4.0, respectively, to make the procedure random and \(r \)takes uniform random values between 0 and 1.

The velocity vector \(\overrightarrow{V_i^d } \) is for the \(i\)th particle corresponding to the \(d\)th dimension at the \(0\)th iteration (initially) and is generated by Eq. 6.

$$\begin{aligned} V_i^d (0)=V_\mathrm{min} +( {V_\mathrm{max} -V_\mathrm{min} })*r, \end{aligned}$$
(6)

where \(V_\mathrm{min}\) and \(V_\mathrm{max} \) have values \(-4.0\) and \(4.0,\) respectively, to make the procedure random and \(r\) takes uniform random value between 0 and 1.

The input range of values for the experiment corresponding to the random position and velocity of the particles have been taken from Badawi and Shatnawi (2013). By taking the modulus of the maximum value after each updation, the scope of the particle’s position and velocities are controlled.

The encoding of the \(i\)th particle with seven dimensions (D) (i.e. activities) is shown in Table 1.

Table 1 Particle encoding representation
Full size table

where an activity of the problem represents a value in the corresponding dimension. In Table 1, values corresponding to the first row represent activities of the problem and the values in the second and third rows, i.e. \(X_i^d (0)\) and \(V_i^d (0)\) represent the random position and velocity of the \(i\)th particle at the \(0\)th iteration of the \(d\)th dimension, respectively.

4.3 Smallest position value (SPV)

Smallest position value (SPV) is a heuristic proposed by Tasgetiren et al. (2004) to convert a continuous value vector of PSO into a discrete value vector so that it can be applied to all sequencing problems. This concept is similar to the random key concept proposed by Bean (1994) for genetic algorithm. With this heuristic, a continuous position value vector of wandering particles is easily converted into discrete activity vector. Conclusively, this heuristic produces the discrete value sequence vector \(\overrightarrow{S} \) by sorting the particle’s continuous value position vector \({X}''\) in ascending order. The detailed description is given in Badawi and Shatnawi (2013), Tasgetiren et al. (2004), whereas the pseudo-code for SPV is given as follows.

figure c

A demonstration of the SPV rule is given in Table 2.

Table 2 Particle encoding representation
Full size table

In Table 2, the values corresponding to \(S_i^d (0)\) represent the ascending order of the activities of the \(i\)th particle at \(0\)th iteration in \(d\)th dimension corresponding to their position values \(X_i^d (0)\).

4.4 The proposed valid particle generator

PSO is one of the best population-based optimization techniques that operates in multidimensional search space (Tasgetiren et al. 2004). The initial population in PSO is the collection of randomly generated particles (Tasgetiren et al. 2004) covering multidimensional search space. Particles are the set of activities along with their associated position and velocity values updated with each iteration. It works smoothly if all the activities of the optimization problem are independent. When the activities of the optimization problem are constrained or dependent in some manner (e.g. activities in RCPSP), a possibility exists that updated particle may become invalid (violating precedence constraint). Normally, a huge amount of computation (in updating the position and velocity vector) and number of iteration are involved in dealing with an invalid particle. Further, in an optimization problem of the order of 1,000 or higher activities, there is a possibility of huge computational energy wastage to the tune of many hours or days in reaching to a valid particle. Since RCPSP is a precedence-constrained optimization problem, it suffers the same. To overcome this problem of PSO, a valid particle generator is proposed. This checks only those suspected activities of the particle that results in the creation of an invalid particle and converts it into a valid particle by swapping the suspected activities. In other words, VPG changes the direction of the particle if it is going in the wrong direction. The pseudo-code for VPG is as follows.

figure d

The sequence vector \(S_i ( k)\) along with its \(X_i ( k)\) and \(V_i ( k)\) passes through the VPG operator to verify its correctness and making it a valid particle. The VPG operator begins with the calculation of in-degree of each activity (using \({\varvec{indegree}}({\varvec{\alpha }}))\) in the particle and stores in \(\phi _i^d ( k)\). The activities with the zero in-degree are contained in \(\lambda ,\) which represents the activities ready to be scheduled without violating the dependency constraint (i.e. their parents have already been scheduled). Further, the out-degree of each activity (using \({\varvec{outdegree}}({\varvec{\alpha }}))\) which belongs to \(\lambda \) is calculated and stored in \(\tau \). Now, each activity in the sequence vector \(S_i^d ( k)\) is checked for its belonging to \(\lambda .\) If it belongs, it does nothing. Otherwise, if the out-degree of all the activities in \(\tau \) is different, an activity is selected with the maximum out-degree (a maximum out-degree activity is preferred to increase the degree of parallelism) and swap it with the activity. In case the out-degrees of the activities in \(\tau \) are the same, a random activity is selected from \(\lambda \) and swapped with the activity. Random activity is selected using the \({\varvec{random}}()\) function and swapping is done using the \({\varvec{swap}}(y_1 ,y_2)\) function. All activities are verified in a similar manner and finally a valid sequence of activities along with the corresponding position and velocity, i.e. \(S_i' ( k),X_i' ( k),V_i' ( k),\) is returned.

4.5 Fitness function

Once a particle passes through the valid particle generator, it is confirmed to be a valid particle. This confirmation allows us to use a simple fitness function to evaluate the makespan of the schedule. Hence, the fitness function evaluates particles with input such as sequence vector (discrete sequence corresponding to continuous position values), number of cores, available resource instances and required resource instances of the respective activity represented as \(S'(k),P,R_A \text{ and } R_R ,\) respectively. Fitness function, shown in Eq. 7, is the makespan on \(P\) homogeneous cores such that the resource constraint (Eq. 8) is satisfied.

$$\begin{aligned} F( {S( k)})=&\mathrm{max}_{i=1,2,\ldots ,D} \left\{ {\mathrm{max}_{j=1,2,\ldots .,P} \left\{ {\mathrm{FT}( {S_i ( k),j})} \right\} } \right\} \nonumber \\&\text{ Such } \text{ that }\,R_R \le R_A \end{aligned}$$
(7)
$$\begin{aligned}&\left\{ {r_1 \le r_{1a} } \right\} ,\left\{ {r_2 \le r_{2a} } \right\} ,\ldots ..\nonumber \\&\left\{ {r_m \le r_{ma} } \right\} ,\,\mathrm{where}\,( {r_1 ,r_2 \ldots ..r_m })\in R_R \,\mathrm{and}\nonumber \\&\quad \,( {r_{1a} ,r_{2a} \ldots ..r_{ma} })\in R_A, \end{aligned}$$
(8)

where \(\text{ FT }(\alpha , j)\) represents the finish time of activity \(\alpha \) on the best suitable core \(j\in P\) at the time and the resource constraint for each activity, i.e. \(R_R \le R_A \) is represented in Eq. 8.

4.6 Tuning of inertia weight \((\omega )\)

Before discussing the proposed adaptive tuning of \(\omega \), it is necessary to understand the impact of \(\omega \) on the particle movement and its role in fast convergence of the PSO algorithm. Initially, all randomly generated particles are widely spread over the search space of the potential solution. It is less likely that particles, in the initial iteration itself, visit optimal search space. After a number of iterations, a possibility arises that at least some particles have visited the optimal search space orbit. At this point, attention is required for the tuning of \(\omega \) as it plays a vital role in the convergence. For large \(\omega \) values between 0.9 and 1, the algorithm works as a global search algorithm. With the decrease in \(\omega \) value, it slightly moves towards the optimal/local search space. To handle \(\omega \), the following two rules may be considered.

  1. 1.

    During initial iterations of the algorithm, the value of \(\omega \) should be kept large (between 0.9 and 1), so that particles can navigate the search space globally in multidimensional space.

  2. 2.

    As particles approach the optimal multidimensional search space orbit, the value of \(\omega \) should be tuned in a way that it provides effective and optimal local search.

To achieve effective convergence in the A-PSO, \(\omega \) is adaptively tuned. Three important factors are taken into account to tune the value of \(\omega \) used in the A-PSO: first, a normalized fitness value of the swarm, as it provides a good direction to the particles towards the optimal solution; second, the iteration counter and finally the previous value of \(\omega \) (\(\omega ^{K-1})\) to keep track of the movement of the particles from their previous position. Normalized fitness value is calculated using Eq. 9.

$$\begin{aligned}&\mathrm{Normalized\, Fitness \,Value \,(NFV)}\nonumber \\&\quad =\frac{\mathrm{Fitness}_\mathrm{Current} -\mathrm{Fitness}_{\min } }{\mathrm{Fitness}_{\max } -\mathrm{Fitness}_{\min } }, \end{aligned}$$
(9)

where \(\mathrm{Fitness}_\mathrm{Current} \) represents the global best and \(\mathrm{Fitness}_\mathrm{max} \) represents the maximum personal best of the particle at the current iteration. \(\mathrm{Fitness}_\mathrm{min} \) is taken as optimal makespan or critical path lower bound value (as per availability).

\(\omega \) is calculated using Eq. 10:

$$\begin{aligned} \omega ^k=\omega _\mathrm{max} -\left( {\frac{\omega _\mathrm{max} -\left( {\frac{\mathrm{NFV}+\omega ^{K-1}}{2}}\right) }{K_\mathrm{max} }}\right) \times K. \end{aligned}$$
(10)

Generally, when the value of \(\omega \) is high it works as global search, and when it slowly becomes low it turns in to local search. Further, it is observed that if the global best solution of the current iteration is better than the previous one, it indicates that the particles are moving in a good direction, i.e. the value of \(\omega \) should be low for the next iteration. On the other side, if the global best solution of the current iteration is poorer than the previous one, it indicates that the particles are not moving in a good direction, i.e. a global search is further required and the value of \(\omega \) should be high relatively to the previous iteration value. Hence, the proposed tuner (Eq. 10) works by considering the above-mentioned facts with a good combination of \(\omega ^{K-1}, \quad \mathrm{NFV}\) and iteration counter. The effectiveness of the tuner is proved in Sect. 5.

4.7 Rules for velocity and position update

Two important rules for updating velocity and position of the particles are as follows:

Velocity vector updating rule The velocity at the \(k\)th iteration is updated using Eq. 11.

$$\begin{aligned} \overrightarrow{V_k }&=\omega *\overrightarrow{V_{k-1} } +c_1 r_1 ( {\overrightarrow{pbest_{k-1} } -\overrightarrow{X_{k-1} } })\nonumber \\&\quad +c_2 r_2 ( {\overrightarrow{gbest} -\overrightarrow{X_{k-1} } }), \end{aligned}$$
(11)

Where c\(_{1}\) and c\(_{2}\) are self-recognition and social constants, respectively, and r\(_{1}\), r\(_{2}\) are uniform random numbers between 0 and 1.

Position vector updating rule The position of the particle is updated at the \(k\)th iteration using Eq. 12.

$$\begin{aligned} \overrightarrow{X_k } =\overrightarrow{X_{k-1} } +\overrightarrow{V_k }. \end{aligned}$$
(12)

4.8 Critical path (CP) length

CP length is the longest path from the source to the sink node (Badawi and Shatnawi 2013; Tasgetiren et al. 2004) as represented by Eq. 13. The motive of CP length is to provide a bound to the optimal solution (Badawi and Shatnawi 2013):

$$\begin{aligned} \mathrm{CP\, length}= \sum W_j. \end{aligned}$$
(13)

where \(W_{j}\) is the processing time of task \(j\) belonging to the critical path, \(j\in N\) and \(N\) is the number of tasks in the directed acyclic graph (DAG). To parallelize this DAG, minimum \(M\) number of cores is required, which is obtained using Eq. 14.

$$\begin{aligned} M=\frac{\sum W_i }{\text{ CP } \text{ length }}\,\,1\le i\le N. \end{aligned}$$
(14)

According to Eqs. 13 and 14, CP length is equal to the optimal schedule if there is minimum M number of cores available and the communication cost is negligible.

4.9 Termination condition

Three termination conditions have been used in the proposed PSO model: first, the specified number of iterations passed; second, the length of \(gbest\) equal to CP length; third, when all the particles reach the same position (i.e. pbest of all the particles become same).

5 Experimental analysis

The proposed A-PSO model is applied to the standard data sets of J30, J60 and J120 generated by a standard problem generator as given in Kolisch and Sprecher (Kolisch and Sprecher 1997). J30 and J60 have a set of 480 instances each with 30 and 60 activities, respectively, and J120 has a set of 600 instances each with 120 activities. These sets of instances are publicly available at the well-known PSBLIB (http://www.om-db.wi.tum.de/psplib/data.html) with known optimum or best-known solutions as obtained by various researchers over the years. The optimum solutions are known only for J30 instances and the upper bounds (current best value of the solution) and lower bounds are provided for J60 and J120 set of instances. In this experimental work, two lower bounds are considered best lower bound \(({\mathrm{LB}_f })\) and critical path lower bound \(({\mathrm{LB}_o })\) with resource relaxation in RCPSP, same as in Qiong and Yoonho (2013). For fair comparison of the proposed model with other state-of-the-art models, 1,000 and 5,000 schedules are generated. The solution quality of the model is measured by three performance parameters, i.e. average deviation \((\mathrm{{Avg\_dev}})\) (Eq. 15), optimal rate \((\mathrm{Optimal})\) (Eq. 16) and average computational time (Hartmann 1998; Alcaraz et al. 2003; Hartmann 2002; Valls et al. 2005; Bouleimen and Lecocq 2003; Schirmer 2000; Chen et al. 2010; Merkle et al. 2002; Herbots et al. 2004; Shi et al. 2010; Akbari et al. 2011; Ziaratia et al. 2011; Qiong and Yoonho 2013; Zhang et al. 2005; Kolisch and Hartmann 2006; Mendes et al. 2004; Sevkli et al. 2004; Zhang et al. 2006). \(\mathrm{Avg\_dev}\) shows the deviation between the solution given by the proposed model and the best solution, \(\mathrm{Optimal}\) accounts for the percentage of solutions reaching the optimal value, and the average computation time represents the average time taken by an instance while computing in its execution unit.

$$\begin{aligned} \mathrm{Avg\_dev}=\frac{\Sigma ^{\text{ instances }}\Big ( {\frac{{\text{ Obtained-Best }}}{\text {Best}}\times 100\% }\Big )}{\text{ instances }}, \end{aligned}$$
(15)
$$\begin{aligned} \mathrm{Optimal}=\frac{{\text{ Optimal } \text{ instances }}}{\text{ instances }}\times 100\%. \end{aligned}$$
(16)

5.1 Parameter setting

The model starts by random initialization of the particles in which the position vector of all the particles are initialized with random continuous values between 0 and 4 as given in Badawi and Shatnawi (2013) and Tasgetiren et al. (2004). The velocity vectors of all the particles are initialized by random continuous values between \(-4\) and 4 as in Badawi and Shatnawi (2013) and Tasgetiren et al. (2004). The self-learning factor \(C_{1}\) and social learning factor \(C_{2}\) are set to 2 (suggested value 2.05 in “standard” PSO) (Bratton and Kennedy 2007). The inertia weight \(\omega \) is adaptively tuned using Eq. 10 with its initial (maximum) value as 0.9 (good enough for global search in general). The iteration-wise tuning behaviour of values of \(\omega ,\) generated by the proposed tuner with respect to NFV, are shown in Fig. 3. It is observed that the tuned value of \(\omega \) slightly increases when the value of NFV moves away from the optimal value of the solution, which means it needs more global search. The tuned value of \(\omega \) goes down when the number of iterations is increased, and when the value of NFV slightly moves towards the optimal value, it means that the particles move globally to local search. Further, to test the effectiveness of the adaptive tuner (in Eq. 10), a comparison with F-race approach (Birattari et al. 2010; Montes de Oca et al. 2011) is done. Totally, 16 treatments are done and for each treatment 48 instances out of 480 from J30 and J60, and 60 instances out of 600 from J120 are randomly selected. For each experiment, 1,000 schedules with 100 maximum numbers of iterations are run. The results corresponding to each treatment in the form of \(\text{ Avg }\_\text{ Dev }._\mathrm{opt}\) (average deviation from optimal makespan for J30) and \(\text{ Avg }\_\text{ Dev }._{\mathrm{LB}_0}\)(average deviation from the lower bound of the critical path for J60 and J120) are shown in Table 3.

Fig. 3
figure 3

Relation among NFV, \(\omega \) and the iterations

Full size image
Table 3 Average deviation on training instances by F-race (Birattari et al. 2010) and the proposed adaptive tuner
Full size table

Figure 4 shows the comparative study of the average of average deviation resulting from the F-race approach and the proposed adaptive tuner of inertia weight (\(\omega )\) corresponding to 16 treatments done in Table 3. From the results, it is easy to analyze that the proposed adaptive tuner performs effectively over the F-race approach. Hence, the adaptive tuner is used for further experimentation to perform effective global to local search.

Fig. 4
figure 4

The comparison of average of average deviation for training instances corresponding to Table 3

Full size image

In all the experiments, A-PSO is evaluated for 480 instances of J30 and J60, and 600 instances of J120, and the average deviation is calculated. The maximum number of iterations used is 100.

5.2 Experimental results

A comparative study of the proposed model with other heuristics, discussed in literature (Hartmann 1998; Alcaraz et al. 2003; Hartmann 2002; Valls et al. 2005; Bouleimen and Lecocq 2003; Schirmer 2000; Chen et al. 2010; Merkle et al. 2002; Herbots et al. 2004; Shi et al. 2010; Akbari et al. 2011; Ziaratia et al. 2011), is done on 1,000 and 5,000 randomly generated schedules. The compared heuristics/meta-heuristics are branch and bound (BB), Tabu search (TS), genetic algorithm (GA), simulated annealing (SA), adaptive search (AS), ant colony optimization (ACO), artificial bee colony (ABC), particle swarm optimization (PSO), etc.

Table 4 shows the percentage of average deviation and optimally solved instances with respect to optimal makespan for J30 instances. The model is evaluated for 1,000 and 5,000 number of schedules. The average deviation of the model is calculated as 0.28 and 0.06 % for 1,000 and 5,000 schedules, respectively, and the proposed model solved 88.92 and 97.48 % instances optimally for both the set of schedules, respectively. As obvious from Table 4, the model performs better over 25 other heuristics and meta-heuristics.

Table 4 Results of algorithms corresponding to the J30 case study (%)
Full size table

Tables 5 and 6 show the comparative results for the instances of J60 and J120 sets, respectively. For these instances, the proposed model is compared on percentage average deviation from the best lower bound and critical path lower bound of makespan, because optimal solutions for J60 and J120 sets of instances are not available. Again, the model is evaluated for two sets of numbers of schedules, i.e. 1,000 and 5,000. The average deviations of the model with respect to the best lower bound and critical path lower bound are obtained as 11.94 and 11.12 % and the A-PSO solves 73.02 and 75.58 % optimal instances of the J60 set of instances for both the set of schedules, respectively. The average deviations on the J120 set of instances with respect to the best lower bound and critical path lower bound are obtained as 34.935 and 32.49 % by solving 30.75 and 32.96 % optimal instances for both the set of schedules, respectively. So, with the same number of schedules, it gives better results over 21 other heuristics/meta-heuristics on J60 set of instances and over 27 other heuristics/meta-heuristics on J120 set of instances, respectively.

Table 5 Results of algorithms corresponding to the J60 case study (%)
Full size table
Table 6 Results of algorithms corresponding to the J120 case study (%)
Full size table

Table 7 shows the average computational time and used CPU core’s frequency by A-PSO to evaluate the experimental results for the respective instance sets. The average CPU time taken by A-PSO is very low, which is possible with the significant contribution of VPG and adaptive tuning of inertia weight.

Furthermore, Table 8 presents the comparative study with other heuristics for average computational time. The average commutation time, average deviation and the used clock cycles of cores are shown in the third, fourth and fifth columns of Table 8, respectively. The performance of the reported heuristics/meta-heuristics was obtained from survey and original papers (Kolisch and Hartmann 2006; Chen et al. 2010; Birattari et al. 2010). The performance of A-PSO, shown in Table 8, is limited to 5,000 evaluated schedules. From Table 8, it is easy to see that A-PSO has significant lower average computation time for J30, J60 and J120 over other heuristics along with economic and acceptable average deviation.

Analysing the computational results, it is observed that the proposed A-PSO algorithm gives much better results for the same number of RCPSP schedules in comparison to other algorithms/heuristics. The reasons for this are: the VPG operator which continuously changes invalid particles into valid particles effectively (saving huge amount of computation) and inertia weight tuner which controls particle’s movement effectively from global to local (or vice versa) search in large multidimensional search space. In other words, the direction of the particles changes smoothly from the infeasible region towards the feasible region. Hence, in each iteration of the procedure, all the particles survive with effective fitness. Both VPG and adaptive tuning of inertia weight contribute substantively to the PSO to get a better and time-efficient solution.

Table 7 A-PSO average computation time for various schedules of J3, J60 and J120
Full size table
Table 8 Comparative study of average computation time for J3, J60 and J120
Full size table

6 Conclusion

This work proposes a variant of the PSO algorithm called adaptive PSO or A-PSO. A-PSO has been applied and tested for the RCPSP problem. A new operator, called a valid particle generator (VPG), has been proposed and inertia weight \(\omega \) is adaptively tuned. The proposed VPG operator and \(\omega \) play a significant role in the quick convergence of the PSO, saving a huge amount of computation. The proposed A-PSO offers low average deviation and its computation time for the experimentation is also low in comparison to other similar models. The VPG operator may prove to be important for many other variants of PSO to solve similar types of optimization problems.

The model has been simulated to study its performance on different sizes of RCPSP problem instances, e.g. J30, J60 and J120. A comparative study is done in terms of standard deviation and computation time. The results show that the model offers competitive results, as the average deviations are 0.06, 11.12 and 32.49 % for J30, J60 and J120, respectively, and it takes 0.091, 0.32 and 1.9 % s average computation time for the schedule of J30, J60 and J120, respectively. Furthermore, the model performs better over 25, 21 and 27 other existing heuristics/meta-heuristics for a set of instances corresponding to J30, J60 and J120, respectively. The advantage of the model is faster convergence in comparison to other models for the same purpose. The proposed model can be used for solving other combinatorial optimization problems efficiently.