Solving fully fuzzy linear system with arbitrary triangular fuzzy numbers $( {m,\alpha ,\beta })$

Abstract

In this paper, we discuss some new numerical methods to solve a fully fuzzy linear system (FFLS) with triangular fuzzy numbers of the form $( {m,\alpha ,\beta })$. Almost every existing method that intends to solve a FFLS confines the coefficient matrix and the solutions to be non-negative fuzzy numbers. The main intent of the proposed methods is to remove these restrictions and widen the scope of fuzzy linear systems in scientific applications. The methods are illustrated with the help of numerical examples and are conceptually easy to understand and apply in real life situations.

1 Introduction

System of simultaneous linear equations plays a major role in various areas such as operational research, physics, statistics, engineering and social sciences. When the estimation of the system coefficients is imprecise and only some vague knowledge about the actual values of the parameters is available, it may be convenient to represent some or all of them with fuzzy numbers (Zadeh 1965). Fuzzy number arithmetic is widely applied and useful in computation of linear system whose parameters are represented by fuzzy numbers, which are called fuzzy linear systems (FLS). A general model for solving a $n\; \times \;n$ fuzzy linear system whose coefficient matrix is crisp and the right-hand side column is an arbitrary fuzzy vector was first proposed by Friedman et al. (1998). A review of some methods for solving these systems can be found in (Abbasbandy et al. 2005, 2006; Abbasbandy and Jafarian 2006; Allahviranloo 2004a, b, 2005; Allahviranloo and Ghanbari 2010; Buckley and Qu 1991; Dehghan and Hashemi 2006; Friedman et al. 2000; Mosleh and Otadi 2010; Sun and Guo 2009; Yin and Wang 2009).

In addition, another important kind of fuzzy linear systems including fuzzy numbers in which all parameters are fuzzy numbers and is named as FFLS. For a $n \times n$ fully fuzzy linear systems, Dehghan and Hashemi (2006a) and Dehghan et al. (2007) proposed the Adomian decomposition method, and other iterative methods to find the positive fuzzy vector solution of fully fuzzy linear system. Dehghan et al. (2006) proposed some computational methods such as Cramer’s rule, Gauss elimination method, LU decomposition method and linear programming approach for finding the approximated solution of FFLS. Muzzioli and Reynaerts (2006) introduced an algorithm to find vector solution by transforming the system $A_{1} x + b_{1} = A_{2} x + b_{2}$ into the FFLS $Ax = b$ where $A = A_{1} - A_{2}$ and $b = b_{1} - b_{2} .$

Mosleh et al. (2007) proposed a method to find the solution of fully fuzzy linear system of the form $Ax + b = Cx + d$ with $A,C$ square matrices of fuzzy coefficients and $b,d$ fuzzy number vectors and the unknown vector $x$ is vector consisting of $n$ fuzzy numbers. Nasseri et al. (2008) used decomposition methods of the coefficient matrix for solving fully fuzzy linear system of equations. Allahviranloo et al. (2008) proposed a method for solving FFLS $Ax = b,$ when coefficient matrix is positive. Gao (2009) proposed a unified iterative scheme for solving non-square FFLS. Nasseri et al. (2009) proposed Greville’s method to find the positive solution of FFLS. Mosleh et al. (2009) discussed symmetric times triangular (ST) decomposition to find the positive solution of FFLS. Nasseri and Zahmatkesh (2010) proposed a new method for computing the non-negative solution of FFLS. Liu (2010) developed a block homotopy perturbation method (HPM) for finding the approximation of the solution of FFLS. Nasseri and Sohrabi (2010) used a certain decomposition of the coefficient matrix of the FFLS to construct a new algorithm for solving FFLS. Kumar et al. (2010) proposed a new method to find the approximate solution of FFLS with trapezoidal fuzzy numbers as parameters. All the methods that have been reported in the literature presume the non-negativity constraint on the coefficients and the solutions that has greatly reduced the applicability and employability of FFLS in scientific applications with almost negligible use.

In this paper, we firstly discuss a new computational method for finding the non-negative solutions of a FFLS $\tilde{A} \otimes \tilde{x} = \tilde{b},$ where $\tilde{A}$ is a fuzzy matrix with no restriction on its elements and $\tilde{x}$ and $\tilde{b}$ are fuzzy vectors with appropriate sizes. Later, we present a method to find all the solutions of a FFLS $\tilde{A} \otimes \tilde{x} = \tilde{b}$ with non-negative restriction on the coefficient matrix $({\tilde{A} \ge 0}).$ Lastly, a new method is proposed which jointly removes the sign constraints on the coefficients and the solution vector. All the methods are illustrated by solving numerical examples which cannot be solved by any of the existing methods. Further the methods are conceptually and computationally very simple. This simplicity is necessary and is required so as to revive the inclusion of fuzzy linear systems in scientific applications, which till date has limited applications due to the restricted nature of operations on fuzzy numbers and narrow mathematical usability.

The rest of this paper is organized as follows: In Sect. 2, shortcomings of the existing methods to solve FFLS are described. In Sect. 3 some basic definitions are reviewed. In Sect. 4 new methods are proposed for solving FFLS and also to illustrate the proposed methods, numerical examples are solved. In Sect. 5 the implications of the proposed methods are discussed and the paper is concluded in Sect. 6.

2 Shortcomings of existing methods

In this section, the shortcomings in the existing methods (Abbasbandy et al. 2005, 2006; Abbasbandy and Jafarian 2006; Allahviranloo 2004a, b, 2005; Allahviranloo and Ghanbari 2010; Allahviranloo et al. 2008; Buckley and Qu 1991; Dehghan and Hashemi 2006a, b; Dehghan et al. 2006; Dehghan and Hashemi 2007; Gao 2009; Engineering Mathematics 1 2010; Liu 2010; Mosleh and Otadi 2010; Mosleh et al. 2009; Nasseri et al. 2008, 2009; Nasseri and Sohrabi 2010; Nasseri and Zahmatkesh 2010; Sun and Guo 2009; Yin and Wang 2009) are pointed out:

• 1. All the existing methods presume the non-negativity of the coefficient matrix, i.e., $\tilde{A} \ge 0.$ This restriction creates difficulty in using the existing methods to solve FFLS occurring in real life situations for which the coefficient matrix may not be entirely non-negative.

• 2. In all the existing methods, it is assumed that the system of equations is consistent and then the methods are developed, i.e., consistency of the FFLS cannot be checked using the existing methods. Also, in the existing methods there is no provision for determining if the solution is unique or infinite and the nature of infinite solution.

• 3. Further all the existing methods aim at finding the “non-negative” solutions of a FFLS. This apriori restriction creates difficulty in using the methods as the solutions may not be entirely non-negative.

This abundance of methods with several restrictions on the parameters will eventually serve no purpose if the concept of fuzzy linear systems is not suitably applied in scientific problems. There is thus an overwhelming need to develop computational methods which assume no restrictions on the parameters and widen the boundaries of applied fuzzy mathematics. To overcome the above described shortcomings, in Sect. 4 three new computational methods are proposed for solving a FFLS which tend to remove the sign restrictions imposed.

3 Preliminaries

In this section, some necessary backgrounds and notions of fuzzy set theory are reviewed (Dubois and Prade 1980; Kaufmann and Gupta 1985).

Definition 3.1

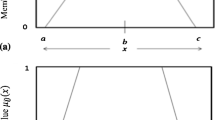
Let $X$ denote a universal set. Then the fuzzy subset $\tilde{A}$ of $X$ is defined by its membership function $\mu_{{\tilde{A}}} :X \to [ {0,1} ]$ which assigns a real number $\mu_{{\tilde{A}}} (x)$ in the interval $[ {0,1}]$ to each element $x \in X,$ where the value of $\mu_{{\tilde{A}}} ( x )$ at $x$ shows the grade of membership of $x$ in $\tilde{A}.$

Definition 3.2

A fuzzy set $\tilde{A},$ defined on the universal set of real number $R,$ is said to be a fuzzy number if its membership function has the following characteristics:

• (i) $\tilde{A}$ is convex, i.e., $\mu_{{\tilde{A}}} ( {\lambda x_{1} + ( {1 - \lambda } )x_{2} }) \ge$ minimum $( {\mu_{{\tilde{A}}}( {x_{1} }),\mu_{{\tilde{A}}}( {x_{2} })} ) \,\forall x_{1,} x_{2} \in R,\ \forall \lambda \in [ {0,1} ].$

• (ii) $\tilde{A}$ is normal, i.e., $\exists \,x_{0} \in R$ such that $\mu_{{\tilde{A}}} ( {x_{0} }) = 1.$

• (iii) $\mu_{{\tilde{A}}}$ is piecewise continuous.

Support of a fuzzy number is defined by the set ${\text{Supp}} ({\tilde{A}}) = \{ {x|x \in X, \mu_{\tilde{A}} (x) > 0} \}$.

Definition 3.3

A fuzzy number $\tilde{A} = ( {m,\alpha ,\beta })$ is said to be a triangular fuzzy number if its membership function is given by:

$$ \mu_{{\tilde{A}}} (x) = \left\{ \begin{array}{ll} 1 - \frac{m - x}{\alpha}, & m - \alpha \le x \le m,\ \alpha > 0, \\ 1 - \frac{x - m}{\beta}, & m \le x \le m + \beta ,\ \beta > 0 \\ 0 &{\text{otherwise}} \end{array} \right. $$

where, $m,\alpha ,\beta \in R$.

Support of a triangular fuzzy number is the open interval $(m - \alpha ,m + \beta ).$

Definition 3.4

A triangular fuzzy number $\tilde{A} = ( {m,\alpha ,\beta } )$ is said to be non-negative (negative) triangular fuzzy number, i.e., $\tilde{A} \ge 0 ( {\tilde{A} > 0} )$ if and only if $m - \alpha \ge 0 ( {m - \alpha > 0}).$

A triangular fuzzy number $\tilde{A} = ( {m,\alpha ,\beta })$ is said to be non-positive triangular fuzzy number, i.e., $\tilde{A} \le 0( {\tilde{A} < 0})$ if and only if $m + \beta \le 0 ( {( {m + \beta < 0})}).$ A zero triangular fuzzy number is denoted by (0, 0, 0).

Definition 3.5

Two fuzzy numbers $\tilde{M} = ( {m,\alpha ,\beta })$ and $\tilde{N} = (n,\gamma ,\delta )$ are said to be equal if and only if $m = n, \alpha = \gamma \,{\rm and} \,\beta = \delta .$

Definition 3.6

A matrix $\tilde{A} = ( {\tilde{a}_{ij} })$ is called a fuzzy matrix, if each element of $\tilde{A}$ is a fuzzy number. $\tilde{A}$ will be positive (negative) and denoted by $\tilde{A} > 0$ $( {\tilde{A} < 0} )$ if each element of $\tilde{A}$ be positive (negative). $\tilde{A}$ will be non-positive (non-negative) and denoted by $\tilde{A} \le 0$ $( {\tilde{A} \ge 0} )$ if each element of $\tilde{A}$ be non-positive (non-negative). We may represent $n \times m$ fuzzy matrix $\tilde{A} = ( {\tilde{a}_{ij} } )_{n \times m} ,$ where $\tilde{a}_{ij} = ( {a_{ij} ,b_{ij} ,c_{ij} } ) .$

Definition 3.7

Let $\tilde{A} = (\tilde{a}_{ij} )$ and $\tilde{B} = (\tilde{b}_{ij} )$ be two $m \times n$ and $n \times p$ fuzzy matrices. We define $\tilde{A} \otimes \tilde{B} = \tilde{C} = ( {\tilde{c}_{ij} } )$ which is the $m \times p$ matrix where $\tilde{c}_{ij} = \sum\nolimits_{k = 1, \ldots ,n}^{ \oplus } {\tilde{a}_{ik} \otimes \tilde{b}_{kj} } .$

Definition 3.8

Let $\tilde{A}_{1} = ( {m,\alpha ,\beta } )$ and $\tilde{A}_{2} = (n,\gamma ,\delta )$ be two triangular fuzzy numbers, then

• (i) $( {m,\alpha ,\beta } ) \oplus ( { n,\gamma ,\delta } ) = ( {m + n,\alpha + \gamma ,\beta + \delta } )$

• (ii) $- ( {m,\alpha ,\beta }) = ( { - m,\beta ,\alpha })$

• (iii) $(m,\alpha ,\beta ) \ominus (n,\gamma ,\delta ) = (m - n,\alpha + \delta ,\beta + \gamma ) .$

3.1 Extended multiplication operation

In the literature (Dubois and Prade 1980; Kaufmann and Gupta 1985), the product of two fuzzy numbers $\tilde{A}_{1} = ( {m,\alpha ,\beta })$ and $\tilde{A}_{2} = (n,\gamma ,\delta )$ is defined as:

$$\tilde{A}_{1} \otimes \tilde{A}_{2} = ( {m,\alpha ,\beta }) \otimes ( {n,\gamma ,\delta }) = \\ (mn,mn - { \hbox{min} }( {( {m - \alpha } )( {n - \gamma }),( {m + \beta })( {n - \gamma })( {n + \delta }),( {m + \beta })( {n + \delta }),( {m - \alpha })( {n + \delta })}), \\ \hbox{max} ( {( {m - \alpha })( {n - \gamma }),( {m + \beta } )( {n - \gamma }),( {m + \beta })( {n + \delta }),( {m - \alpha })( {n + \delta })}) - mn)$$

If either $\tilde{A}_{1}$or $\tilde{A}_{2}$ is an unknown fuzzy number then it is cumbersome to use this expression to find the product $\tilde{A}_{1} \otimes \tilde{A}_{2} .$ To overcome this difficulty, the expression can be simplified on the basis of the sign of the operand:

$$ \tilde{A}_{1} \otimes \tilde{A}_{2} = \left\{ {\begin{array}{ll} {(mn,f_{1} ,f_{2} )\quad {\text{if }} (m,\alpha ,\beta ) \ge 0} \\ \begin{gathered}( {mn,f_{3} ,f_{4} })\quad {\text{if }} ({m,\alpha ,\beta } ) \le 0 \hfill \\ (mn,f_{5} ,f_{6} ) \quad {\text{otherwise }} \hfill \\ \end{gathered} \\ \end{array} }\right.. $$

$$ \begin{gathered} f_{1} = mn - \hbox{min} ( {( {m - \alpha } )( {n - \gamma } ),( {m + \beta } )( {n - \gamma } )} ), \hfill \\ f_{2} = \hbox{max} ( {( {m - \alpha } )( {n + \delta } ),( {m + \beta } )( {n + \delta } )} ) - mn \hfill \\ f_{3} = mn - \hbox{min} ( {( {m - \alpha } )( {n + \delta } ),( {m + \beta } )( {n + \delta } )} ) \hfill \\ f_{4} = {\text{max}}( {( {m - \alpha } )( {n - \gamma } ),( {m + \beta } )( {n - \gamma } )} ) - mn \hfill \\ f_{5} = mn - \hbox{min} ( {( {m - \alpha } )( {n + \delta } ),( {m + \beta } )( {n - \gamma } )} ) \hfill \\ f_{6} = \hbox{max} ( {( {m - \alpha } )( {n - \gamma } ),( {m + \beta } )( {n + \delta } )} ) - mn \hfill \\ {\text{min}}( {x,y} ) = \left ({\frac{x + y}{2}}\right ) - \left| {\frac{x - y}{2}} \right|,\quad \hbox{max} ( {x,y} ) = \left({\frac{x + y}{2}} \right) + \left| {\frac{x - y}{2}} \right| \hfill \\ \end{gathered} $$

4 Proposed methods

In this section, three new computational methods are proposed to solve a FFLS $\tilde{A} \otimes \tilde{x} = \tilde{b}$ comprising triangular fuzzy numbers. The methods are conceptually simple and rely on analytical decomposition of a fuzzy linear system into its equivalent crisp linear form. Consider the $n \times n$ FFLS as:

$$ \begin{array}{c} ( {\tilde{a}_{11} \otimes \tilde{x}_{1} } ) \oplus ( {\tilde{a}_{12} \otimes \tilde{x}_{2} } ) \oplus \cdots \oplus ( {\tilde{a}_{1n} \otimes \tilde{x}_{n} } ) = \tilde{b}_{1} \\ ( {\tilde{a}_{21} \otimes \tilde{x}_{1} } ) \oplus ( {\tilde{a}_{22} \otimes \tilde{x}_{2} } ) \oplus \cdots \oplus ( {\tilde{a}_{2n} \otimes \tilde{x}_{n} } ) = \tilde{b}_{2}\\ \vdots \\( {\tilde{a}_{n1} \otimes \tilde{x}_{1} } ) \oplus ( {\tilde{a}_{n2} \otimes \tilde{x}_{2} } ) \oplus \cdots \oplus ( {\tilde{a}_{nn} \otimes \tilde{x}_{n} } ) = \tilde{b}_{n}\\ \end{array} $$

The matrix form of the above equation is $\tilde{A} \otimes \tilde{x} = \tilde{b}$ where the coefficient matrix $\tilde{A} = ( {\tilde{a}_{ij} }), 1 \le i,j \le n$ is a $n \times n$ fuzzy matrix. Let $\tilde{a}_{ij} = ( {a_{ij} ,m_{ij} ,n_{ij} } ),\quad \tilde{x} = ( {x_{i} ,y_{i} ,z_{i} } ) \ge 0,\quad \tilde{b} = ( {b_{i} ,g_{i} ,h_{i} })$ be triangular fuzzy numbers. We may represent a $n \times n$ fuzzy matrix $\tilde{A} = ( {\tilde{a}_{ij} })_{n \times n}$ where $( {\tilde{a}_{ij} }) = ( {a_{ij} ,m_{ij} ,n_{ij} })$ with the notation $\tilde{A} = ( {A,M,N} ),$ where $A =( {a_{ij} } ),$ $M = ( {m_{ij} })$ and $N = ( {n_{ij} })$ are three $n \times n$ crisp matrices.

Before formally stating the method we introduce the following category of fuzzy numbers to simplify the concept of including arbitrary triangular fuzzy coefficients with no non-negative restriction.

4.1 “Near zero” triangular fuzzy numbers

A fuzzy number $\tilde{M} = ( {m,\alpha ,\beta } )$ is called near-zero fuzzy number, denoted by $\tilde{M} \equiv 0$ if its membership function $\mu_{{\tilde{M}}} ( x )$ satisfies $\mu_{{\tilde{M}}} ( {0^{ + } }) = \mu_{{\tilde{M}}} ( {0^{ - } }) = \mu_{{\tilde{M}}}( 0) \ne 0.$ Alternatively it specifies that $0 \,{\text{falls in}}\,{\text{Supp}}( {\tilde{M}}) , {\text{i}} . {\text{e}} . , { }m - \alpha < 0 < m + \beta .$ An Example of a “near-zero” triangular fuzzy number is (2, 4, 5) which is neither non-negative, nor non-positive.

4.2 Decomposition method to find non-negative solutions of a FFLS with arbitrary coefficient matrix

In this section, we propose a simplified polynomial-time computational method to solve the $n \times n$ FFLS $\tilde{A} \otimes \tilde{x} = \tilde{b}$ under the apriori non-negative constraint on the solution vector. Here, we rewrite the FFLS as:

$$ ( {A,M,N} ) \otimes ( {x,y,z}) = ( {B,G,H}) $$

Further, we decompose the coefficient matrix into its non-negative, non-positive and near zero fuzzy components, i.e.,

$$ \tilde{A} = \tilde{A}_{p} \oplus \tilde{A}_{n} \oplus \tilde{A}_{o} $$

where

$$ \tilde{A}_{p} = \left\{ {\begin{array}{*{20}l} ({\tilde{a}_{ij} })& {\text{if}}\;\tilde{a}_{ij} \ge 0,\;{\text{i}}.{\text{e}}.,\; a_{ij} - m_{ij} \ge 0 \\ {0}&{\text{otherwise}}\end{array} } \right. $$

$$ \tilde{A}_{n} = \left\{ {\begin{array}{*{20}l} ({\tilde{a}_{ij} }) &{\text{if}}\;\tilde{a}_{ij} \ge 0,\;{\text{i}}.{\text{e}}.,\; a_{ij} - n_{ij} \ge 0 \\ {0}&{\text{otherwise}}\end{array}} \right. $$

$$ \tilde{A}_{0} = \left\{ {\begin{array}{*{20}l} (\tilde{a}_{{ij}} ) & {\text{if}}\;\tilde{a}_{{ij}} \equiv 0, {{\text{i}}{\text{.e}}{\text{. }}, a_{{ij}} - m_{{ij}} < 0 < a_{{ij}} + n_{{ij}} } \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right.$$

Thus we can write $\tilde{A} \otimes \tilde{x} = \tilde{b}$ as:

$$ ( {\tilde{A}_{p} \oplus \tilde{A}_{n} \oplus \tilde{A}_{o} }) \otimes ( { x,y,z}) = ( {B,G,H}) $$

(1)

This system is equivalent to the system

$$( {A_{p} ,M_{p} ,N_{p} }) \otimes ( {x,y,z}) \oplus ( {A_{n} ,M_{n} ,N_{n} }) \otimes ( {x,y,z}) \oplus ( {A_{o} ,M_{o} ,N_{o} }) \otimes ( {x,y,z}) = ( {B,G,H}) $$

Note that the weakly distributive extended multiplication operation on two fuzzy numbers holds exactly here (Proposition 4.2). Using the arithmetic operations on triangular fuzzy numbers

$$ \tilde{A}_{p} \otimes \tilde{x} =( {A_{p} ,M_{p} ,N_{p} }) \otimes ( {x,y,z} ) = ( {A_{p} x, M_{p} x + ( {A_{p} - M_{p} } )y, ( {A_{p} + N_{p} })z + N_{p} x}) $$

Similarly,

$$ \tilde{A}_{n} \otimes \tilde{x} = ( {A_{n} x, M_{n} x -( {A_{n} - M_{n} } )z,N_{n} x -( {A_{n} + N_{n} })y}) $$

$$ \tilde{A}_{o} \otimes \tilde{x} = ( {A_{o} x, M_{o} x - {A_{o} - M_{o} })z,N_{0} x + ( {A_{o} + N_{o} })z}) $$

Note that crisp relation $A = A_{p} + A_{n} + A_{o}$ is universally true. Similar relations hold for matrices M and N also. Substituting the above obtained values in the FFLS (1), we obtain the following set of crisp equations:

$$ \left\{ {\begin{array}{ll} {Ax = B} \\ {Mx +( {A_{p} - M_{p} })y + ( {M_{n} - A_{n} + M_{o} - A_{o} })z = G} \\ {Nx -( {A_{n} + N_{n} })y + ( {A_{p} + N_{p} + A_{o} + N_{o} })z = H} \\ \end{array} } \right. $$

(2)

To solve the systems of equations obtained in (2) employ any method for solving crisp system of linear equations. A direct matrix inversion yields the following results:

$$ \left\{ {\begin{array}{ll} {x = A^{ - 1} B} \\ {y = \alpha_{1}^{ - 1} (\gamma_{1} - \beta_{1} (\alpha_{2} \alpha_{1}^{ - 1} \beta_{1} - \beta_{2} )^{ - 1} (\alpha_{2} \alpha_{1}^{ - 1} \gamma_{1} - \gamma_{2} ))} \\ {z = (\alpha_{2} \alpha_{1}^{ - 1} \beta_{1} - \beta_{2} )^{ - 1} (\alpha_{2} \alpha_{1}^{ - 1} \gamma_{1} - \gamma_{2} )} \\ \end{array} } \right. $$

(3)

where $\alpha_{1} = A_{p} - M_{p} , \alpha_{2} = - A_{n} - N_{n} ,\beta_{1} = M_{n} - A_{n} + M_{o} - A_{o} ,\beta_{2} = A_{p} + N_{p} + A_{o} + N_{o} , \gamma_{1} = G - MA^{ - 1} B$ and $\gamma_{2} = H - NA^{ - 1} B.$

Note that the linear system (2) can be solved by a variety of available classical methods to solve a crisp linear system. The solution of the FFLS can be written as $\tilde{x} = ( {x,y,z})$ where $x,y,z$ are three $n \times 1$ crisp vectors obtained directly using a matrix inversion rule (3) or by solving the linear system using any classical method.

4.2.1 Feasibility condition

The solution obtained above is considered (strong) feasible if and only if the obtained solution is non-negative and the non-negativity of the spreads is fulfilled, i.e., $x - y \ge 0,\quad y \ge 0\quad {\text{and}}\quad z \ge 0.$ If these constraints are violated then the FFLS would be said to have a (weak) infeasible fuzzy solution.

Remark 4.1

The $n \times n$ FFLS $\tilde{A} \otimes \tilde{x} = \tilde{b}$ will have a (strong) feasible fuzzy non-negative solution $\tilde{x} =( {x_{i} ,y_{i} ,z_{i} })\,\,\forall i = 1,2, \ldots ,n$ if $( {x_{i} ,y_{i} ,z_{i} } ) \ge 0,\,{\text{i}} . {\text{e}} . ,\;x_{i} - y_{i} \ge 0, y_{i} \ge 0, z_{i} \ge 0 \,\forall i = 1,2 \ldots ,n;$ otherwise the solution will be (weak) Infeasible.

Remark 4.2

The proposed method for solving a $n \times n$ FFLS $\tilde{A} \otimes \tilde{x} = \tilde{b}$ with arbitrary coefficient matrix has a polynomial time computational complexity $O( {n^{3} })$, as it relies on the computation of inversion and multiplication of finite number of crisp matrices.

Remark 4.3

Under the constraint of non negativity of the coefficient matrix $\tilde{A}_{n} ,\tilde{A}_{o} = \tilde{0}_{n \times n}$ and the solution to FFLS reduces to the solution of the following equivalent crisp system. This crisp linear system has been solved by variety of methods by different researchers, for e.g., (Dehghan and Hashemi 2006a, b; Dehghan et al. 2006; Dehghan and Hashemi 2007; Nasseri et al. 2008, 2009; Nasseri and Sohrabi 2010; Nasseri and Zahmatkesh 2010).

$$ \left\{ {\begin{array}{ll} {Ax = B} \\ {Mx + ( {A_{p} - M_{p} })y = G} \\ {Nx + ( {A_{p} + N_{p} })z = H} \\ \end{array} } \right. $$

Remark 4.4

The $n \times n$ FFLS may be consistent or inconsistent depending upon the consistency of the crisp linear system obtained in (2). Further the FFLS may generate trivial, unique or infinitely many feasible solutions depending upon the solutions obtained by solving the crisp linear system (2).

Proposition 4.1

The necessary condition for the $n \times n$ FFLS $\tilde{A} \otimes \tilde{x} = \tilde{b}$ to have a feasible fuzzy non-negative solution $\tilde{x} =( {x_{i} ,y_{i} ,z_{i} })\ \forall i = 1,2, \ldots ,n$ obtained directly using matrix inversion (3) if the matrices $A,\alpha_{1} ,\alpha_{2}$ and $\alpha_{2} \alpha_{1}^{ - 1} \beta_{1} - \beta_{2}$ are non singular.

Proof

Straightforward.

Proposition 4.2

The transformation of FFLS (1) into crisp linear system (2) is conditioned upon the exactness of the weakly distributive law of fuzzy multiplication over addition:

$$ ( {\tilde{A}_{p} \oplus \tilde{A}_{n} \oplus \tilde{A}_{o} }) \otimes \tilde{x} = ( {\tilde{A}_{p} \otimes \tilde{x}}) \oplus ( {\tilde{A}_{n} \otimes \tilde{x}}) \oplus ( {\tilde{A}_{o} \otimes \tilde{x}} ) $$

Proof

Clearly,

$$ \tilde{A} \otimes \tilde{x} =( {\tilde{A}_{p} \oplus \tilde{A}_{n} \oplus \tilde{A}_{o} } ) \otimes \tilde{x} $$

From definition 3.7

$$ ( {\tilde{A} \otimes \tilde{x}})_{i} = \mathop \sum \limits_{j = 1,..,n}^{ \oplus } \tilde{a}_{ij} \otimes \tilde{x}_{j}\quad\forall i = 1,2, \ldots ,n $$

By segregating coefficients into three groups we easily get:

$$ \sum\limits_{j = 1, \ldots ,n}^{ \oplus } {\tilde{a}_{ij} \otimes \tilde{x}_{j} } = \sum\limits_{\begin{subarray}{l} j = 1, \ldots ,n \\ \tilde{a}_{ij} \ge 0 \end{subarray} }^{ \oplus } {\tilde{a}_{ij} \otimes \tilde{x}_{j} } \oplus \sum\limits_{\begin{subarray}{l} j = 1, \ldots ,n \\ \tilde{a}_{ij} \le 0 \end{subarray} }^{ \oplus } {\tilde{a}_{ij} \otimes \tilde{x}_{j} } \oplus \sum\limits_{\begin{subarray}{l} j = 1, \ldots ,n \\ \tilde{a}_{ij} \equiv 0 \end{subarray} }^{ \oplus } {\tilde{a}_{ij} \otimes \tilde{x}_{j} } $$

Clearly:

$$ ( {\tilde{A}_{p} \otimes \tilde{x}})_{i} = \sum\limits_{\begin{subarray}{l} j = 1, \ldots n \\ \tilde{a}_{ij} \ge 0 \end{subarray} }^{ \oplus } {\tilde{a}_{ij} \otimes \tilde{x}_{j} ;( {\tilde{A}_{n} \otimes \tilde{x}})_{i} } = \sum\limits_{\begin{subarray}{l} j = 1, \ldots n \\ \tilde{a}_{ij} \le 0 \end{subarray} }^{ \oplus } {\tilde{a}_{ij} \otimes \tilde{x}_{j} ;( {\tilde{A}_{n} \otimes \tilde{x}})_{i} } = \sum\limits_{\begin{subarray}{l} j = 1, \ldots n \\ \tilde{a}_{ij} \equiv 0 \end{subarray} }^{ \oplus } {\tilde{a}_{ij} \otimes \tilde{x}_{j} } $$

which completes the proof

$$ \tilde{A} \otimes \tilde{x} = ( {\tilde{A}_{p} \oplus \tilde{A}_{n} \oplus \tilde{A}_{o} } ) \otimes \tilde{x} = ( {\tilde{A}_{p} \otimes \tilde{x}}) \oplus ( {\tilde{A}_{n} \otimes \tilde{x}}) \oplus ( {\tilde{A}_{o} \otimes \tilde{x}}) $$

Proposition 4.3

The $n \times n$ FFLS $\tilde{A} \otimes \tilde{x} = \tilde{b}$ is called a homogeneous FFLS if $\tilde{b}$ is a null column vector, i.e., with all elements as zero triangular fuzzy numbers. This FFLS will always have a trivial solution. The possibility of infinitely many solutions does not exist.

Proof

The homogeneous FFLS $\tilde{A} \otimes \tilde{x} = \tilde{0}$ will always have only a trivial solution $\tilde{x} = \tilde{0} = ( {0,0,0})_{n \times 1} .$ The case of infinite solutions is ruled out because for any fuzzy number $\tilde{A}, \tilde{A} \ominus \tilde{A} \ne 0.$

Proposition 4.4

The $n \times n$ FFLS $\tilde{A} \otimes \tilde{x} = \tilde{b}$ with a “near zero” coefficient matrix $\tilde{A}$ , i.e., all the elements as “near zero” triangular fuzzy numbers will always hold the possibility of the existence of infinite feasible solutions.

Proof

As $\tilde{A}_{n} ,\tilde{A}_{p} = \tilde{0}_{n \times n} ,$ the FFLS in (2) reduces to the following crisp linear system. Clearly this FFLS will either yield infinite solutions or no solution.

$$ \left\{ {\begin{array}{ll} {A_{o} x = B} \\ {M_{o} x + (M_{o} - A_{o} )z = G} \\ {N_{o} x + (N_{o} + A_{o} )z = H} \\ \end{array} } \right. $$

The given system will yield no solution if the following crisp linear system is inconsistent

$$ \left\{ {\begin{array}{ll} {( {M_{o} - A_{o} } )z = G - M_{o} A_{o}^{ - 1} B} \\ {( {N_{o} + A_{o} } )z = H - N_{o} A_{o}^{ - 1} B} \\ \end{array} } \right. $$

However, if the above crisp linear system is consistent then the FFLS will yield infinite solutions of the form $\tilde{x} = \left\{ {( {x,y,z})\left| {x - y \ge 0,\,y \ge 0,\,z \ge 0} \right.} \right\}.$ Where x, z are obtained from solving the above crisp system. This is illustrated by example 4.3.

Example 4.1

A ball swings from point A to point B with a constant approximate velocity of $( {3,2,3} )\,{\text{ms}}^{ - 1}$ for a time of $\tilde{t}_{1} =( {x_{1} ,y_{1} ,z_{1} })\,{\text{s}}$ and then retracts with an approximate velocity of $( { - 2,1,1} )\,{\text{ms}}^{ - 1}$ for a time of $\tilde{t}_{2} = ( {x_{2} ,y_{2} ,z_{2} })\,{\text{s}}$ with a net displacement of (5, 16, 17) mts. In another instance the ball is pulled backwards with a constant velocity of $( { - 4,1,2} )\,{\text{ms}}^{ - 1}$ for a time of $\tilde{t}_{1}$ and pushed forward with a velocity of $( {4,2,1} )\,{\text{ms}}^{ - 1}$ covering $( { - 4,12,22} )\,{\text{mts}}$ from the original point. Considering all other parameters constant find $\tilde{t}_{1}$ and $\tilde{t}_{2} .$

Solution The problem can be simply modeled as a FFLS:

$$( {3,2,3} ) \otimes ( {x_{1} ,y_{1} ,z_{1} } ) \oplus ( { - 2,1,1} ) \otimes ( {x_{2} ,y_{2} ,z_{2} }) = ( {5,16,17} ) $$

$$ ( { - 4,1,2} ) \otimes( {x_{1} ,y_{1} ,z_{1} }) \oplus ( {4,2,1} ) \otimes ( {x_{2} ,y_{2} ,z_{2} }) =( { - 4,12,22} ) $$

Note that we have apriori knowledge that $\tilde{t}_{1}$ and $\tilde{t}_{2}$ have to be non-negative fuzzy numbers. Also as all the fuzzy coefficients are not entirely non-negative, hence this FFLS can not be solved by any of the existing methods. Using the proposed method we obtain the following matrices

$$ \tilde{A}_{p} = \left[ {\begin{array}{*{20}c} {( {3,2,3} )} & 0 \\ 0 & {( {4,2,1} )} \\ \end{array} } \right], \quad \tilde{A}_{o} = \tilde{0}, \quad \tilde{A}_{n} = \left[ {\begin{array}{*{20}c} 0 & {( { - 2,1,1} )} \\ {( { - 4,1,2} )} & 0 \\ \end{array} } \right], \quad \tilde{B} = \left[ {\begin{array}{*{20}c} {( {5,16,17} )} \\ {( { - 4,12,22} )} \\ \end{array} } \right] $$

Further we obtain the equivalent crisp linear system using (2) as follows:

$$ \begin{aligned} &3x_{1} - 2x_{2} = 5 \hfill \\& - 4x_{1} + 4x_{2} = - 4 \hfill \\ &2x_{1} + x_{2} + y_{1} + 3z_{2} = 16 \hfill \\& x_{1} + 2x_{2} + 2y_{2} + 5z_{1} = 12 \hfill \\ &3x_{1} + x_{2} - y_{2} + 6z_{1} = 17 \hfill \\ &2x_{1} + x_{2} + 2y_{1} + 5z_{2} = 22 \hfill \\ \end{aligned} $$

On solving this crisp linear system we obtain the following solution $x_{1} = 3, \;x_{2} = 2,\;y_{1} = 2, \;y_{2} = 0\;{\text{and}} \;z_{1} = 1,\; z_{2} = 2.$ Hence the solution of the FFLS is $\tilde{t}_{1} = ( {3,2,1})\,{\text{and}}\,\tilde{t}_{2} = ( {2,0,2} ).$ Both the fuzzy numbers are non-negative. Hence the FFLS is consistent and has a unique (strong) feasible solution.

Example 4.2

Solve the following FFLS for non-negative solutions:

$$ ( {4,6,1}) \otimes ( {x_{1} ,y_{1} ,z_{1} }) \oplus ( {4,2,4} ) \otimes ( {x_{2} ,y_{2} ,z_{2} }) = ( {24,26,31}) $$

$$ ( {3,2,1}) \otimes ( {x_{1} ,y_{1} ,z_{1} }) \oplus ( {2,3,1} ) \otimes ( {x_{2} ,y_{2} ,z_{2} }) = ( {14,18,13}) $$

Solution Clearly

$$ \tilde{A}_{p} = \left[ {\begin{array}{*{20}c} 0 & {( {4,2,4} )} \\ {( {3,2,1} )} & 0 \\ \end{array} } \right],\quad \tilde{A}_{o} = \left[ {\begin{array}{*{20}c} {( {4,6,1} )} & 0 \\ 0 & {( {2,3,1} )} \\ \end{array} } \right], \quad \tilde{A}_{n} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ \end{array} } \right],\quad \tilde{B} = \left[ {\begin{array}{*{20}c} {( {24,26,31} )} \\ {( {14,18,13} )} \\ \end{array} } \right] $$

Substituting $\tilde{A}_{n} = 0$ in Eq. (2) we obtain the following reduced set of a crisp linear system

$$ \left\{ {\begin{array}{l} {Ax = B} \\ {Mx + ( {A_{p} - M_{p} } )y + ( {M_{o} - A_{o} } )z = G} \\ {Nx + (A + N)z = H} \\ \end{array} } \right. $$

which can be easily solved by matrix inversion as follows:

$$ \left\{ {\begin{array}{l} {x = A^{ - 1} B} \\ {y = ( {A_{p} - M_{p} } )^{ - 1} ( {G - MA^{ - 1} B - ( {M_{o} - A_{o} } )( {A + N^{ - 1} } )( {H - NA^{ - 1} B} )} )} \\ {z = ( {A + N^{ - 1} } )( {H - NA^{ - 1} B} )} \\ \end{array} } \right. $$

On solving this system we obtain the following feasible solution: $x_{1} = 2, \;x_{2} = 4,\;y_{1} = 1,\; y_{2} = 2 \;{\text{and}}\; z_{1} = 1,\; z_{2} = 1.$Putting the obtained values in $\tilde{x}_{1} = ( {x_{1} ,y_{1} ,z_{1} } ) \,{\text{and}}\, \tilde{x}_{2} = ( {x_{1} ,y_{1} ,z_{1} } )$ we get, $\tilde{x}_{1} = ( {2,1,1} ) \,{\text{and }}\,\tilde{x}_{2} = ( {4,2,1} ).$ Both the fuzzy numbers are non-negative and the solution is thus unique and feasible.

Example 4.3

Solve the FFLS for non-negative solutions:

$$ ( { - 1,2,3} ) \otimes ( {x_{1} ,y_{1} ,z_{1} } ) \oplus ( {2,3,2} ) \otimes ( {x_{2} ,y_{2} ,z_{2} } ) = ( {3,18,17} ) $$

$$ ( { - 4,1,10} ) \otimes ( {x_{1} ,y_{1} ,z_{1} } ) \oplus ( { - 1,1,2} ) \otimes ( {x_{2} ,y_{2} ,z_{2} } ) = ( { - 6,20,33} ) $$

Solution Using the proposed method we obtain the following matrices

$$ \tilde{A}_{o} = \left[ {\begin{array}{*{20}c} {( { - 1,2,3} )} & {( {2,3,2} )} \\ {( { - 4,1,10} )} & {( { - 1,1,2} )} \\ \end{array} } \right], \quad \tilde{A}_{p} = \tilde{0}, \quad \tilde{A}_{n} = \tilde{0}, \quad \tilde{B} = \left[ {\begin{array}{*{20}c} {( {3,18,17} )} \\ {( { - 6,20,33} )} \\ \end{array} } \right] $$

Further we obtain the equivalent crisp linear system using (2) as follows:

$$ \begin{aligned} &- x_{1} + 2x_{2} = 3 \hfill \\& - 4x_{1} - x_{2} = - 6 \hfill \\ &2x_{1} + 3x_{2} + 3z_{1} + z_{2} = 18 \hfill \\& x_{1} + x_{2} + 5z_{1} + 2z_{2} = 20 \hfill \\ &3x_{1} + 2x_{2} + 2z_{1} + 4z_{2} = 17 \hfill \\ &10x_{1} + 2x_{2} + 6z_{1} + z_{2} = 33 \hfill \\ \end{aligned} $$

On solving this crisp linear system we obtain the following solution $x_{1} = 1, \;x_{2} = 2,\;{\text{and}} \;z_{1} = 3,\; z_{2} = 1.$ Note that the system is consistent because $( {M_{o} - A_{o} } )^{ - 1} ( {G - M_{o} A_{o}^{ - 1} B} ) = ( {N_{o} + A_{o} } )^{ - 1} ( {H - N_{o} A_{o}^{ - 1} B} ).$ Further this FFLS has infinite feasible solutions which may be represented as follows:

$$ \tilde{x} = \left\{ {\tilde{x}_{1} = ( {1,\alpha ,3} );\;\tilde{x}_{2} = ( {2,\beta ,1} )\left| {\alpha \in \, \left[ {0,1} \right],\; \beta \in \left[ {0,2} \right]} \right.} \right\} $$

4.3 Linear programming method to solve a FFLS with arbitrary solution vector and non-negative coefficients

In this section, we introduce a new technique to solve a FFLS with a non-negative coefficient matrix and no restrictions on the solution vector, i.e., the proposed method does not assume any apriori constraint of non negativity on the unknown quantity and generates the solution irrespective of its sign. The steps of the proposed method are as follows:

Step 1

Substituting $\tilde{A} = ( {\tilde{a}_{ij} } )_{n \times n} ,\,\tilde{x} = ( {\tilde{x}_{j} } )_{n \times 1} \,{\text{and}}\,\tilde{B} = ( {B_{i} } )_{n \times 1}$ the $n \times n$ FFLS may be written as:

$$ \mathop \sum \limits_{j = 1, \ldots ,n}^{ \oplus } \tilde{a}_{ij} \otimes \tilde{x}_{j} = \tilde{B}_{i} \quad \forall i = 1,2, \ldots ,n $$

Step 2

If $\tilde{a}_{ij} ,\tilde{x}_{j}$ and $\tilde{B}_{i}$ are represented by triangular fuzzy numbers $( {a_{ij} ,b_{ij} ,c_{ij} }) \ge 0,$ $( {x_{j} ,y_{j} ,z_{j} } )$ and $( {B_{i} ,g_{i} ,h_{i} } )$ then the FFLS obtained in Step 1, may be written as:

$$ \mathop \sum \limits_{j = 1, \ldots ,n}^{ \oplus } ( {a_{ij} ,b_{ij} ,c_{ij} } ) \otimes ( {x_{j} ,y_{j} ,z_{j} } ) = ( {B_{i} ,g_{i} ,h_{i} } )\quad \forall i = 1,2, \ldots ,n $$

Step 3

By Assuming $( {a_{ij} ,b_{ij} ,c_{ij} } ) \otimes ( {x_{j} ,y_{j} ,z_{j} } ) = ( {f_{ij} ,p_{ij} ,q_{ij} } ),$ the FFLS obtained in step 2 may be written as:

$$ \mathop \sum \limits_{j = 1, \ldots ,n}^{ \oplus } ( {f_{ij} ,p_{ij} ,q_{ij} } ) = ( {B_{i} ,g_{i} ,h_{i} } )\quad \forall i = 1,2 \ldots ,n $$

using Sect. 3.1.

$$ \begin{aligned} &(f_{ij} ,p_{ij} ,q_{ij} ) = ( {a_{ij} ,b_{ij} ,c_{ij} } ) \otimes ( {x_{j} ,y_{j} ,z_{j} } ) \hfill \\ &f_{ij} = a_{ij} x_{j} \hfill \\& p_{ij} = f_{ij} - {\text{m}}in( {( {a_{ij} - b_{ij} } )( {x_{j} - y_{j} } ),( {a_{ij} + c_{ij} } )( {x_{j} - y_{j} } )} ) \hfill \\ &p_{ij} = f_{ij} - \frac{{2a_{ij} - b_{ij} + c_{ij} }}{2}( {x_{j} - y_{j} } ) + \left| {\frac{{b_{ij} + c_{ij} }}{2}} \right|\left| {x_{j} - y_{j} } \right| \hfill \\ &q_{ij} = {\text{m}}ax( {( {a_{ij} - b_{ij} } )( {x_{j} + z_{j} } ),( {a_{ij} + c_{ij} } )( {x_{j} + z_{j} } )} ) - p_{ij} \hfill \\ &q_{ij} = - p_{ij} + \frac{{2a_{ij} - b_{ij} + c_{ij} }}{2}( {x_{j} + z_{j} } ) + \left| {\frac{{b_{ij} + c_{ij} }}{2}} \right|\left| {x_{j} + z_{j} } \right| \hfill \\ &\quad\forall i = 1,2, \ldots ,n, \quad \forall j = 1,2, \ldots ,n \hfill \\ \end{aligned} $$

For notational convenience we substitute $x_{j} - y_{j} = L_{j}$ and $x_{j} + z_{j} = R_{j} \forall j = 1,2, \cdots ,n$ where $x_{j} ,y_{j} ,z_{j} ,w_{j} ,L_{j} ,R_{j} \in R.$

Step 4

Substitute $f_{ij} ,p_{ij} ,q_{ij}$ in the FFLS obtained in step 3 to obtain the following semi-linear system of equations:

For $i = 1,2 \ldots ,n.$

$$ \mathop \sum \limits_{j = 1}^{n} f_{ij} = B_{i} \Rightarrow \mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} = B_{i} $$

(4)

Similarly,

$$ \mathop \sum \limits_{ j = 1}^{n} p_{ij} = g_{i} \Rightarrow \mathop \sum \limits_{j = 1}^{n} \frac{{2a_{ij} - b_{ij} + c_{ij} }}{2}L_{j} - \left( {\frac{{b_{ij} + c_{ij} }}{2}} \right)\left| {L_{j} } \right| = B_{i} - g_{i} $$

(5)

$$ \mathop \sum \limits_{j = i}^{n} q_{ij} = k_{i} \Rightarrow \mathop \sum \limits_{j = 1}^{n} \frac{{2a_{ij} - b_{ij} + c_{ij} }}{2}R_{j} + \left( {\frac{{b_{ij} + c_{ij} }}{2}} \right)\left| {R_{j} } \right| = B_{i} + h_{i} $$

(6)

Step 5

Substitute $L_{j} = L_{j}^{'} - L_{j}^{''}$ and $\left| {L_{j} } \right| = L_{j}^{'} + L_{j}^{''} ,$ where $L_{j}^{'} = \left\{ {\begin{array}{*{20}l} {L_{j} } & {{\text{if}}\;L_{j} > 0} \\ 0 & {\text{otherwise}} \\ \end{array} } \right.$ and $L_{j}^{''} = \left\{ {\begin{array}{*{20}l} { - L_{j}} & {\text{if}}\; L_{j} < 0 \\ {0}&{\text{otherwise}} \\ \end{array} } \right..$ Similarly, $R_{j} = R_{j}^{'} - R_{j}^{''} {\text{and}} \,\,\left| {R_{j} } \right| = R_{j}^{'} + R_{j}^{''} .$ Therefore the equations, obtained in Step 4, may be written as for $i = 1,2, \ldots ,n$

$$ \mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} = B_{i} $$

(7)

$$ \mathop \sum \limits_{j = 1}^{n} \frac{{2a_{ij} - b_{ij} + c_{ij} }}{2}( {L_{j}^{'} - L_{j}^{''} } ) - \left( {\frac{{b_{ij} + c_{ij} }}{2}}\right )( {L_{j}^{'} + L_{j}^{''} } ) = B_{i} - g_{i} $$

(8)

$$ \mathop \sum \limits_{j = 1}^{n} \frac{{2a_{ij} - b_{ij} + c_{ij} }}{2}( {R_{j}^{'} - R_{j}^{''} } ) + \left({\frac{{b_{ij} + c_{ij} }}{2}} \right)( {R_{j}^{'} + R_{j}^{''} } ) = B_{i} + h_{i} $$

(9)

$$ L_{j}^{'} ,L_{j}^{''} ,R_{j}^{'} ,R_{j}^{''} \ge 0\quad \forall j = 1,2, \ldots ,n $$

Step 6

To solve the original FFLS we construct the following linear programming problem (LPP)

Minimize $\bar{Z} = \mathop \sum \limits_{i = 1}^{n} Z_{i} + \mathop \sum \limits_{i = 1}^{n} Z_{i}^{'} + \mathop \sum \limits_{i = 1}^{n} Z_{i}^{\prime \prime }$

subject to

$$ \mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} + Z_{i} = B_{i} \quad\forall i = 1,2, \ldots ,n $$

$$ \mathop \sum \limits_{j = 1}^{n} ( {( {a_{ij} - b_{ij} } )L_{j}^{'} - ( {a_{ij} + c_{ij} } )L_{j}^{''} } ) + Z_{i}^{'} = B_{i} - g_{i} \quad\forall i = 1,2, \ldots ,n $$

$$ \mathop \sum \limits_{j = 1}^{n} ( {( {a_{ij} + c_{ij} } )R_{j}^{'} - ( {a_{ij} - b_{ij} } )R_{j}^{''} } ) + Z_{i}^{'''} = B_{i} + h_{i} \quad\forall i = 1,2, \ldots ,n $$

$$ x_{j} - L_{j}^{'} + L_{j}^{''} \ge 0\quad\forall j = 1,2, \ldots ,n $$

$$ R_{j}^{'} - R_{j}^{''} - x_{j} \ge 0\quad\forall j = 1,2, \ldots ,n $$

$$ L_{j}^{'} ,L_{j}^{''} ,R_{j}^{'} ,R_{j}^{''} ,Z_{j} ,Z_{j}^{'} , Z_{j}^{''} \ge 0\quad\forall j = 1,2, \ldots ,n $$

For obtaining the equivalent matrix representation of the above LPP, we define the following matrices

Define $U$ as a unit column vector with all the entries equal to 1 and order $n \times 1.$ We may obtain the equivalent expressions for other matrices as follows:

$$ \begin{gathered} Z = ( {Z_{i} } )_{n \times 1} ,\;Z^{\prime } = ( {Z_{i}^{\prime } } )_{n \times 1} ,\;Z^{\prime \prime } = ( {Z^{\prime \prime }_{i} } )_{n \times 1} ,\;L^{\prime } ( {L^{\prime } } )_{n \times 1} ,\;L^{\prime \prime } ( {L^{\prime \prime } } )_{n \times 1} ,R^{\prime } = ( {R^{\prime } } )_{n \times 1} \hfill \\ R^{''} = ( {R_{i}^{''} } )_{n \times 1} ,A = ( {a_{ij} } )_{n \times n} , M = ( {b_{ij} } )_{n \times n} ,N = ( {c_{ij} } )_{n \times n} ,B = ( {B_{i} } )_{n \times 1} ,G = ( {g_{i} } )_{n \times 1} , \hfill \\ H = (h_{i} )_{n \times 1} \hfill \\ \end{gathered} $$

Thus the LPP can be rewritten as follows:

Minimize $\bar{Z} = U^{T} Z + U^{T} Z^{'} + U^{T} Z^{\prime \prime }$

subject to

$$ \begin{aligned} &Ax + Z = B \hfill \\ &( {A - M} )L^{'} + ( {A + N} )L^{''} + Z^{'} = B - G \hfill \\ &( {A + N} )R^{'} - ( {A - M} )R^{''} + Z^{''} = B + H \hfill \\ &x - L^{'} + L^{''} \ge 0 \hfill \\ &R^{'} - R^{''} - x \ge 0 \hfill \\& L^{'} ,L^{''} ,R^{'} ,R^{''} ,Z,Z^{'} ,Z^{''} \ge 0 \hfill \\ \end{aligned} $$

Step 7

Solve the LPP obtained in step 6 and substitute the values of $x,L^{'} ,L^{''} ,R^{'} ,R^{''}$obtained in step 6 in $\tilde{x}_{j} = ( {x_{j} ,x_{j} - L_{j}^{'} + L_{j}^{''} ,R_{j}^{'} - R_{j}^{''} - x_{j} } ) \,\forall j = 1,2, \ldots ,n$ to find the solution of the above FFLS.

Remark 4.5

The FFLS will be consistent, i.e., it will generate a solution if and only if the LPP is consistent. Further, the necessary condition for the above LPP to generate a feasible (strong) solution (if it is consistent) is that the value of the objective function must be zero $\bar{Z} = 0$ otherwise the solution will be termed as an (weak) infeasible solution. Thus, the sufficient conditions for the FFLS to have a feasible (strong) fuzzy solution are $L^{\prime } \cdot L^{\prime \prime T} = R^{\prime } \cdot R^{\prime \prime T} = \bar{Z} = 0.$

Remark 4.6

The nature of the solutions of the FFLS depends upon the nature of the solutions of the LPP which may be unique, trivial or infinitely many, i.e., the FFLS may yield no solution, unique solution or infinitely many solutions depending upon the nature of the LPP that is constructed.

Remark 4.7

Under the constraint of the non negativity of the solution vector $L^{''} = R^{''} = 0,$ substituting these into the LPP obtained in step 6 we obtain a simple crisp linear system (similar to as discussed in Remark 4.3) which has been solved by variety of classical methods by several researchers.

Example 4.4

Solve the following FFLS

$$ \left[ {\begin{array}{*{20}c} {( {5,1,1} )} & {( {6,1,2} )} \\ {( {3,1,4} )} & {( {5,2,1} )} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{x}_{1} } \\ {\tilde{x}_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {( {8,22,12} )} \\ {( {9,31,7} )} \\ \end{array} } \right] $$

where, $\tilde{x}_{1} , \tilde{x}_{2}$ are arbitrary triangular fuzzy numbers

Solution

The solution of the chosen FFLS may be obtained by using the steps of the above method and converting the FFLS into the LPP as follows:

Minimize $Z = ( {Z_{1} + Z_{2 } + Z_{1}^{'} + Z_{2}^{'} + Z_{1}^{''} + Z_{2}^{''} } )$

subject to

$$ \begin{aligned} &5x_{1} + 6x_{2} + Z_{1} = 8 \hfill \\ &3x_{1} + 5x_{2} + Z_{2} = 9 \hfill \\ &4L_{1}^{'} - 6L_{1}^{''} + 5L_{2}^{'} - 8L_{2}^{''} + Z_{1}^{'} = - 14 \hfill \\ &2L_{1}^{'} - 7L_{1}^{''} + 3L_{2}^{'} - 6L_{2}^{''} + Z_{2}^{'} = - 22 \hfill \\ &6R_{1}^{'} - 4R_{1}^{''} + 8R_{2}^{'} - 5R_{2}^{''} + Z_{1}^{''} = 20 \hfill \\& 7R_{1}^{'} - 2R_{1}^{''} + 6R_{2}^{'} - 3R_{2}^{''} + Z_{2}^{''} = 16 \hfill \\& x_{1} - L_{1}^{'} + L_{1}^{''} \ge 0 \hfill \\ &x_{2} - L_{2}^{'} + L_{2}^{''} \ge 0 \hfill \\ &R_{1}^{'} - R_{1}^{''} - x_{1} \ge 0 \hfill \\ &R_{2}^{'} - R_{2}^{''} - x_{2} \ge 0 \hfill \\ &Z_{1} ,Z_{2 } ,Z_{1}^{'} , Z_{2}^{'} ,Z_{1}^{''} ,Z_{2}^{''} ,L_{1}^{'} ,L_{2}^{'} ,L_{1}^{''} ,L_{2}^{''} ,R_{1}^{'} ,R_{2}^{'} ,R_{1}^{''} ,R_{2}^{''} \ge 0 \hfill \\ \end{aligned} $$

On solving the above LPP, the following solution is obtained:

$$ \begin{gathered} x_{1} = - 2, x_{2} = 3,L_{1}^{'} = 0,L_{1}^{''} = 4,L_{2}^{'} = 2,L_{2}^{''} = 0, R_{1}^{'} = 0,R_{1}^{''} = 1,R_{2}^{'} = 3,R_{2}^{''} = 0, \hfill \\ Z_{1} = Z_{2 } = Z_{1}^{'} = Z_{2}^{'} = Z_{1}^{''} = Z_{2}^{''} = 0 \hfill \\ \end{gathered} $$

Clearly the FFLS meets the necessary and sufficient conditions for the possibility of a feasible fuzzy solution. Substituting the values obtained in the following equation yields the solution of the FFLS. $\tilde{x}_{j} = ( {x_{j} ,x_{j} - L_{j}^{'} + L_{j}^{''} ,R_{j}^{'} - R_{j}^{''} - x_{j} } ) \,\forall j = 1,2,$ we obtain the following solution:

$$ \tilde{x}_{1} = ( { - 2,2,1} ) \quad{\text{and}}\quad \tilde{x}_{2} = ( {3,1,0} ) $$

Note that $\tilde{x}_{1} \le 0\, {\text{and}}\,\tilde{x}_{2} \ge 0$. This clearly justifies that the existing methods can not be used to solve this FFLS because all the methods presume the non negativity of the solution vector.

4.4 Fuzzy Cramer’s rule for solving an arbitrary FFLS with no joint restrictions on the sign of coefficients and the sign of variables

In this section, we propose a polynomial time algorithm to solve a FFLS where the coefficient matrix and the solution vector are unconstrained on the dimension of sign; however, we exclude the possibility of “near zero” fuzzy numbers in the solution vector, i.e., the only constraint that is now imposed on an arbitrary FFLS is that the solution vector cannot include elements which have zero in their support. The reason for this restriction lies in the structure of arithmetic operations on fuzzy numbers that is explained in Proposition 4.6.

The FFLS is written as:

$$ ( {A,M,N} ) \otimes ( {x,y,z} ) = ( {B,G,H} ) $$

Now we decompose the coefficient matrix into its non-negative, non-positive and near zero fuzzy components and the solution vector into its non-negative and non-positive components, i.e.,

$\tilde{A} = \tilde{A}_{p} \oplus \tilde{A}_{n} \oplus \tilde{A}_{o}$ and $\tilde{x} = \tilde{x}_{p} \oplus \tilde{x}_{n}$ where

$$ \tilde{x}_{p} = \left\{ \begin{array}{ll} ( {\tilde{x}_{i} } ) &\quad{\text{if}}\,\tilde{x}_{i} \ge 0,\, {\text{i}} . {\text{e}} . , x_{i} - y_{i} \ge 0 \\ 0&\quad {\text{otherwise}} \end{array} \right. $$

$$ \tilde{x}_{n} = \left\{\begin{array}{ll} ( {\tilde{x}_{i} } ) &\quad{\text{if}}\, \tilde{x}_{i} \le 0, \,{\text{i}} . {\text{e}} . ,x_{i} + z_{i} \le 0 \\ 0 &\quad {\text{otherwise}}\end{array} \right. $$

Thus we can write $\tilde{A} \otimes \tilde{x} = \tilde{b}$ as:

$$ \tilde{A}_{p} \otimes \tilde{x}_{p} \oplus \tilde{A}_{n} \otimes \tilde{x}_{p} \oplus \tilde{A}_{o} \otimes \tilde{x}_{p} \oplus \tilde{A}_{p} \otimes \tilde{x}_{n} \oplus \tilde{A}_{n} \otimes \tilde{x}_{n} \oplus \tilde{A}_{o} \otimes \tilde{x}_{n} = \tilde{b} $$

(10)

which is equivalent to:

$$ \begin{gathered} ( {A_{p} ,M_{p} ,N_{p} } ) \otimes ( {x_{p} ,y_{p} ,z_{p} } ) \oplus ( {A_{n} ,M_{n} ,N_{n} } ) \otimes ( {x_{p} ,y_{p} ,z_{p} } ) \oplus ( {A_{o} ,M_{o} ,N_{o} } ) \otimes ( {x_{p} ,y_{p} ,z_{p} } ) \hfill \\ \oplus ( {A_{p} ,M_{p} ,N_{p} } ) \otimes ( {x_{n} ,y_{n} ,z_{n} } ) \oplus ( {A_{n} ,M_{n} ,N_{n} } ) \otimes ( {x_{n} ,y_{n} ,z_{n} } ) \oplus ( {A_{o} ,M_{o} ,N_{o} } ) \hfill \\ \otimes ( {x_{n} ,y_{n} ,z_{n} } ) = ( {B,G,H} ) \hfill \\ \end{gathered} $$

Note that the weakly distributive extended multiplication operation on two fuzzy numbers holds exactly here (Proposition 4.2). Using the arithmetic operations on triangular fuzzy numbers

$$ \begin{gathered} \tilde{A}_{p} \otimes \tilde{x}_{p} = ( {A_{p} x_{p} , M_{p} x_{p} + ( {A_{p} - M_{p} } )y_{p} , ( {A_{p} + N_{p} } )z_{p} + N_{p} x_{p} } ) \hfill \\ \tilde{A}_{n} \otimes \tilde{x}_{p} = ( {A_{n} x_{p} , M_{n} x_{p} - ( {A_{n} - M_{n} } )z_{p} ,N_{n} x_{p} - ( {A_{n} + N_{n} } )y_{p} } ) \hfill \\ \tilde{A}_{o} \otimes \tilde{x}_{p} = ( {A_{o} x_{p} , M_{o} x_{p} - ( {A_{o} - M_{o} } )z_{p} ,N_{0} x_{p} + ( {A_{o} + N_{o} } )z_{p} } ) \hfill \\ \tilde{A}_{p} \otimes \tilde{x}_{n} = ( {A_{p} x_{n} , - N_{p} x_{n} + ( {A_{p} + N_{p} } )y_{n} , ( {A_{p} - M_{p} } )z_{n} - M_{p} x_{n} } ) \hfill \\ \tilde{A}_{n} \otimes \tilde{x}_{n} = ( {A_{n} x_{n} , - N_{n} x_{n} - ( {A_{n} + N_{n} } )z_{n} , - M_{n} x_{n} - ( {A_{n} - M_{n} } )y_{n} } ) \hfill \\ \tilde{A}_{o} \otimes \tilde{x}_{n} = ( {A_{o} x_{n} , - N_{o} x_{n} + ( {A_{o} + N_{o} } )y_{n} , - M_{0} x_{n} - ( {A_{o} - M_{o} } )y_{n} } ) \hfill \\ \end{gathered} $$

Note that crisp relation $A = A_{p} + A_{n} + A_{o}$ is universally true. Similar relations hold for matrices $M$ and $N$ also. Further $x = x_{p} + x_{n} , y = y_{p} + y_{n}$ and $z = z_{p} + z_{n} .$

For convenience we create two step functions: $u( a ) = \left\{ {\begin{array}{*{20}l} {1}& {\text{if}}\; a \ge 0 \\ {0} &{\text{otherwise}} \\ \end{array} } \right.;\,v( a ) = \left\{ {\begin{array}{*{20}l} {1}& {\text{if}}\; a < 0 \\ {0}& {\text{otherwise}} \\ \end{array} } \right.$

We define two diagonal matrices: $U = ( {u( {x_{i} } )} )_{n \times n} ,\,{\text{i}} . {\text{e}} . ,U = ( {u_{ij} } ) = \left\{ {\begin{array}{*{20}l} {u( {x_{i} }} ) &\forall i = j \\ {0}& \forall i \ne j \\ \end{array} } \right..$ Similarly, $V = ( {v( {x_{i} } )} )_{n \times n}$ such that $x_{p} = Ux,y_{p} = Uy, z_{p} = Uz, x_{n} = Vx,y_{n} = Vy,$ and $z_{n} = Vz.$

This on substituting in (10) yields following set of crisp equations:

$$ \left\{ {\begin{array}{ll} {Ax = B} \\ {Q_{11} y + Q_{12} z = G - A_{1} x} \\ {Q_{21} y + Q_{22} z = H - A_{2} x} \\ \end{array} } \right. $$

(11)

where

$$ \begin{aligned} &A_{1} = MU - NV, A_{2} = - MV + NU \hfill \\ &Q_{11} = ( {A_{p} - M_{p} } )U + ( {A_{p} + N_{p} + A_{o} + N_{o} } )V \hfill \\ &Q_{12} = ( {M_{n} - A_{n} + M_{o} - A_{o} } )U - ( {A_{n} + N_{n} } )V \hfill \\& Q_{21} = - ( {A_{n} + N_{n} } )U - ( {A_{n} - M_{n} + A_{o} - M_{o} } )V \hfill \\ &Q_{22} = ( {A_{p} + N_{p} + A_{o} + N_{o} } )U + ( {A_{p} - M_{p} } )V \hfill \\ \end{aligned} $$

To solve the systems of equations obtained in (2) we employ cramer’s rule to solve the block linear system.

$$ x_{i} = \frac{{\det ( {A^{i} } )}}{\det ( A )},\quad i = 1,2, \cdot \cdot n $$

where $A^{i}$ is the matrix obtained by replacing the $i{\rm th}$ column of A by B.

$$ y_{i} = \frac{{\det (\bar{Q}^{i} )}}{\det (Q)},\quad i = 1,2, \ldots n, $$

where $\det ( Q ) = \det ( {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } \\ {Q_{21} } & {Q_{22} } \\ \end{array} } ) = \det ( {Q_{11} - Q_{12} Q_{22}^{ - 1} Q_{21} } )\det ( {Q_{22} } ).$ (Note that evaluating the determinant of the $2n \times 2n$ block matrix significantly reduces the number of computational operations by evaluating the determinant of two $n \times n$ matrices with two matrix multiplication and one inverse operation. However, the computational complexities in both cases remain same). and $\bar{Q}^{i}$ is the matrix obtained by replacing the $i{\text{th}}^{{}}$ column of $Q_{11}$ with $G - A_{1} x$ and $Q_{21}$ with $H - A_{2} x.$

Similarly

$$ z_{i} = \frac{{\det (\overline{\overline{Q}}^{i} )}}{\det (Q)},\quad i = 1,2, \ldots n, $$

and $\overline{\overline{Q}}^{i}$ is the matrix obtained by replacing the $i{\text{th}}$ column of $Q_{12}$ with $G - A_{1} x$ and $Q_{22}$ with $H - A_{2} x.$

Note that the $3n \times 3n$ linear system (11) can be solved by a variety of available classical methods to solve a crisp linear system. The solution of the FFLS can be written as $\tilde{x} = ( {x,y,z} )$ where x, y, z are three $n \times 1$ crisp vectors obtained directly using the fuzzy cramer’s rule or by solving the linear system using any classical method.

Remark 4.8

The $n \times n$ FFLS $\tilde{A} \otimes \tilde{x} = \tilde{b}$ will have a (strong) feasible fuzzy solution $\tilde{x} = ( {x_{i} ,y_{i} ,z_{i} } ) \,\forall i = 1,2, \ldots ,n$ if $y_{i} \ge 0,z_{i} \ge 0\, {\text{and}}\, 0 \notin {\text{Supp}}( {\tilde{x}} )\quad \forall i = 1,2 \ldots ,n;$ otherwise the solution will be (weak) Infeasible.

Remark 4.9

Under the constraint of non negativity of the solution vector $V = 0_{n \times n}$ and the method of solving the FFLS reduces to the method described in Sect. 4.2.

Remark 4.10

Under the constraint of negligibility of spreads (or small spreads) with respect to mean of a fuzzy number, the product of spreads in the extended multiplication operation is neglected, for example, See (Dehghan and Hashemi 2006a, 2006b; Dehghan et al. 2006; Dehghan and Hashemi 2007; Nasseri et al. 2008, 2009; Nasseri and Sohrabi 2010; Nasseri and Zahmatkesh 2010). However this further aggravates the encumbrance of restrictions applied in solving an FFLS and thus is removed in the methods described in this paper. Under this constraint of negligibility of spreads $Q_{ij}$ takes the following form: $Q_{11} = A_{p} U + ( {A_{p} + A_{o} } )V,\,Q_{12} = ( { - A_{n} - A_{o} } )U - A_{n} V,\,Q_{21} = - A_{n} U - ( {A_{n} + A_{o} } )V$ and $Q_{22} = ( {A_{p} + A_{o} } )U + A_{p} V .$

Proposition 4.5

The necessary condition for the $n \times n$ FFLS $\tilde{A} \otimes \tilde{x} = \tilde{b}$ to have a unique and feasible fuzzy solution $\tilde{x} = ( {x_{i} ,y_{i} ,z_{i} } ) \,\forall i = 1,2, \ldots ,n$ obtained directly using cramer’s rule (4.4) is that the determinant of matrices $A,A^{i} ,Q,\bar{Q}^{i}$ and $\overline{\overline{{Q^{i} }}}$ should not be zero.

Proof

Straightforward.

Proposition 4.6

Allowing the possibility of “near-zero” fuzzy numbers in the solution vector, combinatorially explodes the solution space with computationally complexity growing from polynomial time $O( {n^{3} } )$ (P-class) to exponential time $O( {2^{n} n^{3} } )$ (i.e., an unconstrained FFLS is an NP problem).

Proof

The modified fuzzy cramer’s rule has a straightforward computational complexity of $O( {n^{3} } )$ with finite number of matrix multiplications, inverse and determinant operations. However, this polynomial-time complexity is a consequence of the constraint on the solutions that propels the exclusion “near-zero” fuzzy numbers in the solution vector. The reason lies in the structure of arithmetic operations on fuzzy numbers primarily in the multiplication between two “near-zero” fuzzy numbers, i.e., if the solution vector is unconstrained then the multiplication operation $\tilde{A}_{o} \otimes \tilde{x}_{o}$ results in indeterminacy giving rise to a non-polynomial time complexity of the algorithm for solving the FFLS: $\tilde{A}_{o} \otimes \tilde{x}_{0} = ( {A_{o} x_{0} , A_{o} x_{0} - \hbox{min} ( {( {A_{0} - M_{o} } )( {x_{0} + z_{o} } ),( {A_{0} + N_{o} } )( {x_{0} - y_{o} } )} ), A_{o} x_{0} + \hbox{max} ( {( {A_{0} - M_{o} } )( {x_{0} - y_{o} } ),( {A_{0} + N_{o} } )( {x_{0} + z_{o} } )} )} ) .$ The splitting of this system into linear tuples without min–max constraints is infeasible considering the entropy associated in the operation. Note that the operation is totally uncertain as we have no apriori information of $( {x_{0} + z_{o} } )\,\,or\,( {x_{0} - y_{o} } )$ which is paradoxically the objective of the problem. Consequently this can be solved only be decomposing the system into $2^{n}$ FFLS’s (of order $n \times n$) with each FFLS constrained with an additional assumption (Ex. $( {A_{0} - M_{o} } )( {x_{0} + z_{o} } ) < ( {A_{0} + N_{o} } )( {x_{0} - y_{o} } ))$ leading to an overall exponential complexity of $O( {2^{n} n^{3} } ).$ The verifier algorithm is evidently polynomial time resulting to the conclusion that solving an unconstrained FFLS is an NP-problem. Commenting on the NP-completeness and NP-hardness is left as a potential topic of future research.

Example 4.5

Solve the following FFLS

$$ \begin{gathered} ( {2,1,1} ) \otimes ( {x_{1} ,y_{1} ,z_{1} } ) \oplus ( { - 1,1,0} ) \otimes ( {x_{2} ,y_{2} ,z_{2} } ) = ( {6,4,11} ) \hfill \\ ( { - 5,1,4} ) \otimes ( {x_{1} ,y_{1} ,z_{1} } ) \oplus ( {9,3,6} ) \otimes ( {x_{2} ,y_{2} ,z_{2} } ) = ( { - 28,50,21} ) \hfill \\ \end{gathered} $$

where, $\tilde{x}_{1} , \tilde{x}_{2}$ are arbitrary triangular fuzzy numbers

Solution

As the coefficients and the solution vector both are arbitrary, hence the given FFLS cannot be solved by any of the existing methods. Using the proposed method following solution is obtained:

$$ x_{1} = \frac{{\det \left( {\begin{array}{ll} 6 & { - 1} \\ { - 28} & 9 \\ \end{array} }\right )}}{{\det\left ( {\begin{array}{ll} 2 & { - 1} \\ { - 5} & 9 \\ \end{array} } \right)}} = 2; x_{2} = \frac{{\det \left( {\begin{array}{ll} 2 & 6 \\ { - 5} & { - 28} \\ \end{array} } \right)}}{{\det \left( {\begin{array}{ll} 2 & { - 1} \\ { - 5} & 9 \\ \end{array} }\right )}} = - 2 $$

Hence following matrices are constructed:

$$ \begin{gathered} U = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ \end{array} } \right], V = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 1 \\ \end{array} } \right], A_{1} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 1 & 6 \\ \end{array} } \right], A_{2} = \left[ {\begin{array}{*{20}c} 1 & { - 1} \\ 4 & { - 3} \\ \end{array} } \right], Q_{11} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {15} \\ \end{array} } \right],Q_{12} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ 6 & 0 \\ \end{array} } \right] \hfill \\ Q_{21} = \left[ {\begin{array}{*{20}c} 0 & 2 \\ 1 & 0 \\ \end{array} } \right],Q_{22} = \left[ {\begin{array}{*{20}c} 3 & 0 \\ 0 & 6 \\ \end{array} } \right] \hfill \\ \end{gathered} $$

$$ \det ( Q ) = \det \left( {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } \\ {Q_{21} } & {Q_{22} } \\ \end{array} } \right) = \det ( {Q_{11} - Q_{12} Q_{22}^{ - 1} Q_{21} } )\det ( {Q_{22} } ) = 165 $$

$$ \det ( {\bar{Q}^{1} } ) = 165,\,\det ( {\bar{Q}^{2} } ) = 330, \det ( {\overline{\overline{Q}}^{1} } ) = 165,\det ( {\overline{\overline{Q}}^{2} } ) = 165 $$

This gives: $y_{1} = 1,y_{2} = 2,z_{1} = 1,z_{2} = 1$ i.e.

$$ \tilde{x}_{1} = ( {2,1,1} )\quad {\text{and}}\quad \tilde{x}_{2} = ( { - 2,2,1} ) $$

Note that the FFLS has a unique and a feasible (strong) solution and $\tilde{x}_{1} \ge 0; \tilde{x}_{2} \le 0$.

Example 4.6

Solve the following FFLS taken from (Dehghan et al. 2006)

$$ \begin{gathered} ( {5,1,1} ) \otimes ( {x_{1} ,y_{1} ,z_{1} } ) \oplus ( {6,1,2} ) \otimes ( {x_{2} ,y_{2} ,z_{2} } ) = ( {50,10,17} ) \hfill \\ ( {7,1,0} ) \otimes ( {x_{1} ,y_{1} ,z_{1} } ) \oplus ( {4,0,1} ) \otimes ( {x_{2} ,y_{2} ,z_{2} } ) = ( {48,5,7} ) \hfill \\ \end{gathered} $$

Solution The method described in (Dehghan et al. 2006) constrains the coefficient and solutions to be positive fuzzy numbers. However, as the methods described in the paper do not assume positivity constraint on the parameters, hence any of the above methods (4.2, 4.3, 4.4) can be applied to solve such a kind of problem. Further (Dehghan et al. 2006) unexplainably constrains the spreads of the fuzzy solution to be negligible as compared to the mean. Under this assumption the method 4.4 gives following matrices: $A = \left[ {\begin{array}{*{20}c} 5 & 6 \\ 7 & 4 \\ \end{array} } \right],U = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right], V = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ \end{array} } \right], A_{1} = \left[ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 0 \\ \end{array} } \right], A_{2} = \left[ {\begin{array}{*{20}c} 1 & 2 \\ 0 & 1 \\ \end{array} } \right], Q_{11} = \left[ {\begin{array}{*{20}c} 5 & 6 \\ 7 & 4 \\ \end{array} } \right],Q_{22} = \left[ {\begin{array}{*{20}c} 5 & 6 \\ 7 & 4 \\ \end{array} } \right]$ and $Q_{12} = 0,Q_{21} = 0.$ On solving the crisp system (Eq. 11) following solution is generated $x_{1} = 4,x_{2} = 5, y_{1} = 1/11,y_{2} = 1/11,z_{1} = 0,z_{2} = 1/2$ which is exactly same as that of (Dehghan et al. 2006), i.e., $\tilde{x}_{1} = ( {4,1/11,0} )\, {\text{and}} \,\tilde{x}_{2} = ( {5,1/11,1/2} ).$ This establishes the equivalence of new techniques with earlier proposed paradigms.

5 Discussion and results

The paper studies the domain of FFLS that is unconstrained on the dimension of sign. Three new computational approaches toward solving a FFLS in polynomial time (i.e. P-class FFLS) are discussed which have profound implications. The category of “near-zero” fuzzy numbers which have not been taken care of in the earlier research is conceptualized and their impact in terms of computational complexity of the algorithms for solving a FFLS is described. The manuscript progresses in three stages. First, the signed decomposition method (4.2) removes the sign restriction on the coefficient matrix, as a result of which all kinds of FFLS which have non-negative, non-positive or near-zero fuzzy coefficients can be solved easily in polynomial time complexity. The linear optimization problem (4.3) removes all apriori sign restrictions on the solution vector which is a tough criterion. Finally the fuzzy cramer’s rule (4.4) removes joint restrictions on the coefficients as well as the solution vector; however, confining the solutions to exclude near zero fuzzy numbers, the reasons of which are explained earlier. The implications can be summarized as follows:

• 1. The polynomial time algorithms significantly advance the theory of FFLS by removing sign constraints on the parameters in gradual steps (firstly on the coefficient matrix, then on the solution vector and then jointly on all parameters).

• 2. As a result the implementation scope of FFLS is widely increased as the number of restrictions has been greatly reduced.

• 3. Using the proposed methods it is easy to check whether the FFLS is consistent or inconsistent and generates feasible or infeasible solutions. Further interestingly we see that a FFLS can have unique, trivial and infinitely many solutions- a concept that has not been studied so far.

Six new numerical examples have also been solved to demonstrate the usability of the proposed algorithms. Example 4.1 establishes real-life usage of a FFLS and also demonstrates the need of methods for solving an arbitrary coefficient FFLS and that apriori knowledge of sign of solution vector can greatly reduce the computational effort. Examples 4.3 demonstrates the case where solving a FFLS results in infinitely feasible solutions. Also the examples 4.1–4.5 cannot be solved by any of the existing methods (Abbasbandy et al. 2005, 2006; Abbasbandy and Jafarian 2006; Allahviranloo 2004a, b, 2005; Allahviranloo and Ghanbari 2010; Allahviranloo et al. 2008; Buckley and Qu 1991; Dehghan and Hashemi 2006; Dehghan and Hashemi 2006a, b; Dehghan et al. 2006, 2007; Gao 2009; Kumar et al. 2010; Liu 2010; Mosleh and Otadi 2010; Mosleh et al. 2009; Nasseri et al. 2008, 2009; Nasseri and Sohrabi 2010; Nasseri and Zahmatkesh 2010; Sun and Guo 2009; Yin and Wang 2009) due to varied number of imposed restrictions used in the existing methods. Example 4.6 illustrates clearly the backward compatibility of the newly devised algorithms.

6 Conclusion

In this paper, three new computational methods for solving a FFLS are presented. The proposed methods are easy to understand and apply in real life situations. The methods are illustrated with the help of numerical examples. Further the methods tend to remove several constraints that are usually considered and hence widen the scope of fuzzy linear systems. The formulation of such simple conceptual and numerical methods will erect several possible paths of employability of fuzzy linear systems in engineering and scientific problems. Future work to solve a FFLS with less computational effort involving no joint restrictions on the coefficients and the solution and to demonstrate the practical usability of fuzzy linear systems in science unavoidably persists.