1 Introduction

Understanding spatio-temporal dynamics of species or diseases is a key issue in many research areas such as ecology or epidemiology. Indeed, the so-called Species Distribution Models (SDMs), which link information on the presence/absence or abundance of a species to environmental variables to predict where (and how much of) a species is likely to be present in unsampled locations or time periods, are important tools in many applied fields.

In the particular case of ecology, SDMs have been implemented in different theoretical and practical cases, including the identification of critical habitats (Zhang 2007; Zhang et al. 2008; Paradinas et al. 2015; Rufener et al. 2017; Sadykova et al. 2017), the study of the risk associated with invasive species (Fitzpatrick et al. 2007; Luo and Opaluch 2011), the potential effects of climate change (Iverson et al. 2004; Araújo et al. 2005; Brown et al. 2016), the design of protected areas, the protection of threatened species (Parviainen et al. 2008; Roos et al. 2015), the distribution of bioclimatic indices (Barber et al. 2017), the reintroduction of vulnerable species (Danks and Klein 2002; Martinez-Meyer et al. 2006; Hendricks et al. 2016), the delineation of hot spots of biodiversity and species richness (Jiménez-Valverde and Lobo 2007; Gotelli et al. 2009; Goetz et al. 2014), the potential distribution of infectious diseases (Peterson et al. 2002; Fatima et al. 2016; Juan et al. 2017; Martínez-Bello et al. 2017; Martínez-Minaya et al. 2018), among many others.

SDMs have also been used in many other contexts, for instance evolutionary biology, where they have been applied to topics such as speciation or hybrid zones (Kozak et al. 2008); in humans epidemiology, to predict the spread of diseases in humans (Gosoniu et al. 2006), in veterinary epidemiology (González-Warleta et al. 2013; Barber et al. 2016), in plants epidemiology (Meentemeyer et al. 2011; Václavík and Meentemeyer 2009; Neri et al. 2014; White et al. 2017), etc.

Several review papers on SDMs already exist (see for example, Guisan and Thuiller 2005; Elith and Leathwick 2009), but most of them are focused on the modeling of species data, maintaining a more general overview of the statistical critical issues. Our intention in this review is to describe in more detail some of the statistical issues that arise when dealing with SDMs.

In addition, the quantity and the quality of available datasets has substantially increased over the past ten years, resulting in a higher complexity of the statistical issues that have to be addressed when a SDM is performed. Moreover, a detailed spatial and temporal description of the modeled phenomenon is becoming mandatory in many research fields. As a consequence of this increasing complexity, the performance of the SDM inferential and predictive processes are becoming more challenging, forcing researchers to develop new sophisticated statistical techniques. Accordingly, new modeling approaches continue to be developed because using only geographic information systems (GIS) tools is not totally satisfactory because of the type of spatial data usually available. Indeed, over time model complexity has generally increased over time from the use of simple environmental matching (two good examples are BIOCLIM, Busby 1991, and DOMAIN, Carpenter et al. 1993) to the use of models incorporating more complex non-linear relationships between species presence and the environment, such as generalized additive models (Guisan et al. 2002), neural networks (Park et al. 2003), or multivariate adaptive regression splines (Leathwick et al. 2005).

But more importantly, although most of the methods described in previous reviews (see for example, Guisan and Thuiller 2005; Elith and Leathwick 2009) have increased in their complexity, they are based on the assumption that the observations are conditionally-independent, while species distribution data often depict residual spatial autocorrelation (Kneib et al. 2008; Beale et al. 2010). In this review, we will focus on the fact that the spatial autocorrelation should be taken into account in species distribution models, even if the data were collected in a standardized sampling, since the observations are often close and subject to similar environmental features (Muñoz et al. 2013). Other complications also arise in the modeling of the species due to imperfect survey data such as observer error, gaps in the sampling, missing data, the spatial mobility of the species (Latimer et al. 2006) and the fact that data have been collected over long periods of time. As a consequence, ignoring these issues in this type of analysis could lead to misleading results.

As a consequence, the use of spatial and spatio-temporal models has grown enormously, allowing the incorporation of all these issues into the modeling process (Banerjee et al. 2014). Although there are other types of spatial data that could describe the behavior of a species (see for instance, Gelfand et al. 2010, for a detailed description of the three types of spatial data), we will focus in this review on geostatistical or point-referenced data that derive from those situations where the concern is to analyze spatially continuous phenomena. Bearing in mind that we want to include the effect of possible covariates in the modeling or to apply it to situations in which the stochastic variation in the data is known to be non-Gaussian, we will deal with the model-based geostatistics approach (Diggle and Ribeiro 2007).

This combination of non-Gaussian data, a linear predictor and unobserved latent variables usually makes estimation and prediction computationally difficult. Bayesian inference proves to be a good option to deal with spatial hierarchical models because it allows both the observed data and model parameters to be random variables (Banerjee et al. 2014), resulting in a more realistic and accurate estimation of uncertainty. Another advantage of the Bayesian approach is the ease with which prior information can be incorporated. Note that prior information can usually be very helpful in discriminating spatial autocorrelation effects from ordinary non-spatial linear effects (Gaudard et al. 1999). But, as is usual in Bayesian complex models, inference needs numerical approaches. Among them, in this review we will emphasize on the use of the integrated nested Laplace approximation (INLA) methodology (Rue et al. 2009) and software (http://www.r-inla.org) as an alternative to Markov chain Monte Carlo (MCMC) methods, the main reason being the speed of calculation.

To summarize, our intention in this review is to describe in more detail the main statistical issues that arise when dealing with these models. In particular, in Sect. 2 we focus on the statistical aspects of the available data, while Sect. 3 discusses the basic structure of these models and how to perform inference. In particular, we provide a critical review of the Bayesian approach along with a detailed description of INLA. Our review also includes a discussion on some of the particularities appearing when dealing with them, including temporal correlation, preferential sampling, spatial misalignment, non-stationarity, imperfect detection and excess of zeros in Sect. 4. Finally Sect. 5 concludes. To be noted is that we have tried to be simple in the notation so that the paper is readable by a large community of scientists.

2 Sources of information in SDMs

SDMs require basically two types of data input: data describing the observed species’ distribution, and data describing the landscape and the environmental characteristics in which the species can be found. In this Section we first present biological data, i.e. the observed species distribution, and then the environmental data and the usual covariates that characterize the species distribution.

2.1 Biological data

The first type of data, which usually represent the response variable, can be either presence-only (i.e. records of localities where the species has been observed), presence/absence (i.e. records of presence and absence of the sampling localities), abundance data (i.e. the quantity of the species at the sampling locations), or proportional data (i.e. the proportion of the species at the sampling locations). Consequently, biological data can be measured at nominal (e.g. presence/absence type), ordinal (e.g. ranked abundance), ratio (e.g. frequency of detection) or continuous (e.g. abundance, richness) levels, which impacts on the selection of the appropriate types of modeling algorithms to use, and subsequently the measurement level of model of this kind (e.g. probability or suitability of occurrence, type, expected mean).

Presence-only data lack absence observations, so that this type of dataset is unsuitable for many of the commonly used species distribution algorithms, unless \(pseudo-absences\) are assigned to unsampled portions of the study area. Inclusion of \(pseudo-absences\) records can seriously bias analyses. Indeed, methods used to generate pseudo-absences and their effects on model performance are an open research field in the species distribution context (Barbet-Massin et al. 2012; Iturbide et al. 2015).

With respect to abundance, this could be expressed as a continuous variable (biomass of the species) or as count data (number of individuals). Abundance data reflect the quantitative spatial distribution of the species within the area of interest, while presence/absence information can be used to measure the relative occurrence of species, thereby giving a different approximation. Although abundance data provide greater information for conservation and management purposes, they are less common, because occurrence data are easier and less expensive to be collected. Indeed, abundance estimations are sensitive to detectability, and sampling methods seldom detect all individuals present in an area. Consequently, many research studies rely on approximations of species abundance from species occurrence, although whether abundance can be inferred from such information has been questioned, because detection is not perfect and occurrence probability may not be linearly related to density (Nielsen et al. 2005; Joseph et al. 2006).

Proportional data are also widely used in many ecological processes. The traditional approach in ecology is based on Gaussian linear models with previous transformation in the proportions. However, model parameters cannot be easily interpreted in terms of the original response, and measures of proportions typically display asymmetry: hence, inferences based on the normality assumption can be misleading (Ferrari and Cribari-Neto 2004). Beta regression has recently appeared as a good alternative to deal with data of this type, allowing bounded estimates and intervals with model parameters that are directly interpretable in terms of the mean of the response (Paradinas et al. 2016, 2017b).

Also to be noted is that different species do not behave independently. There are several species whose abundance (or presence) is constrained by competition: a large increase in one is unavoidably linked to declines in others. In these cases, the response variable should be considered by using a joint distribution. The models used for data of this type are known as joint species distribution models (Clark et al. 2014; Pollock et al. 2014; Hui 2017; Taylor-Rodríguez et al. 2017).

All these types of biological data describing the observed species distribution can be obtained in a variety of ways, such as museum collection, designed field surveys, related activities (i.e. fisheries) or on-line resources.

2.2 Environmental data

With respect to the explanatory variables that could help to describe the species behavior, a wide range of environmental variables have been usually incorporated in SDMs. These variables are commonly related to climate (e.g. temperature, precipitation), topography (e.g., elevation, aspect, bathymetry, slope of the seabed), land cover type or seabed type in marine ecosystems. Variables tend to describe primarily the abiotic environment, although there is potential to include biotic interactions within the modeling.

These variables can be collected in situ, but they are usually derived from remoted sensing data. CRU (New et al. 2002), WorldClim (Hijmans et al. 2005), and MARSPEC (Sbrocco and Barber 2013) are all examples of spatially explicit datasets of climatic remote sensing conditions. These datasets encompass climatic information based on interpolations from global weather stations. However, interpolations are only as good as the underlying data, and uneven geographical coverage leads to high model uncertainty, especially in developing countries where few weather stations are in place (Daly 2006; He et al. 2015). When uncertainty in spatial climate variables is not accounted for, coefficient estimates tend to be biased, and this leads to poor performances of the SDMs, as recently shown with simulations by Stoklosa et al. (2015). This problem, also known as misalignment, is treated in this review in Sect. 4.3.

3 Inference

In what follows, after presenting the traditional methods that have been used to perform inference in SDMs, we first discuss the hierarchical modeling as one of the most flexible and encompassing approaches to deal with them. The second subsection presents the Bayesian framework as a good option for dealing with hierarchical models. The final subsection deals with the INLA approach to approximating the marginal posterior distributions of the parameters involved in the SDMs.

3.1 Gaussian fields and hierarchical modeling

A number of alternative modeling algorithms have been applied to classify species distribution as a function of a set of environmental variables. A first group of methods developed to deal with presence-only datasets includes maximum entropy algorithm, environmental distance, similarity, and envelope methods such as MAXENT (Phillips et al. 2006), Gower metric, Mahalanobis distance, and ecological niche factor analysis, all of which describe some measure of habitat suitability.

A second group involves machine-learning algorithms that are iterative in nature, such as artificial neural networks. These ensemble methods (e.g. Boosting Regression Trees, Classification Trees and Random Forests) generally involve developing multiple models on different subsets of the data, the results of which are averaged (Franklin 2010).

A third group of methods relates to traditional regression and includes generalized linear models (GLM) and their non-parametric extension, generalized additive models (GAM), both of which can handle several measurement levels of the response variable by using a different link function (e.g. logistic for presence/absence or log for counts). GAM and a related method, multivariate adaptive regression splines (MARS), are more flexible than GLM as they are fitted using smoothing and piecewise linear splines, respectively, and are particularly useful for identifying the shape of species responses (Leathwick et al. 2005). MARS is computationally faster than GAM and the results are more easily converted to map predictions in a GIS; however, the currently used algorithms require normally distributed error terms. This makes MARS unsuitable for use with presence/absence data unless the basis functions are extracted and used to parameterize a GLM (Leathwick et al. 2005). Rodríguez de Rivera and López-Quílez (2017) present a comparison of these three groups of methodologies stating that GAM models gave the best results.

However, most of the above mentioned methods are based on the assumption that the observations are conditionally-independent. But this is not always the case beacause data of species distribution usually present residual spatial autocorrelation (Kneib et al. 2008). GAMs and MARS can model spatial and temporal autocorrelation using smoothing splines. A very powerful and flexible alternative is to incorporate this spatial relationship by considering the species distribution data as point-referenced or geostatistical data. Data of this type appear in those situations where the interest is to analyze spatially continuous phenomena. The most basic format for data of this kind is a pair composed by the spatial location coordinates defined throughout a continuous study region and the measurement value observed in the location. Geostatistical data require methods that make it possible to relate the species data with potential related covariates by quantifying the spatial dependence. However, one of the main interests in geostatistics concerns predicting the underlying process on those non-observed locations (Cressie and Wikle 2011; Banerjee et al. 2014).

Geostatistical or point-referenced data can be seen as realizations of a spatial process (random field) \(\{y(\varvec{s}), \varvec{s} \in {\mathcal {D}}\}\) characterized by a spatial index \(\varvec{s}\) which varies continuously in the fixed domain \({\mathcal {D}}\). This process is called a Gaussian field (GF) if for any \(n\ge 1\) and for each set of locations \((\varvec{s}_1, \ldots , \varvec{s}_n)\), the vector \((y(\varvec{s}_1), \ldots , y(\varvec{s}_n))\) follows a multivariate Normal distribution with mean \(\varvec{\mu }=(\mu (\varvec{s}_1), \ldots , \mu (\varvec{s}_n))\) and with covariance matrix \(\varvec{\varSigma }\) defined by a covariance function \({\mathcal {C}}(\cdot , \cdot )\), such that \(\varSigma _{ij}=Cov(y(\varvec{s}_i), y(\varvec{s}_j))={\mathcal {C}}(y(\varvec{s}_i), y(\varvec{s}_j))\). If the mean is constant in space, i.e. \(\mu (\varvec{s}_i)=\mu\) for each i, and the generic spatial covariance matrix element depends only on the difference vector \((\varvec{s}_i-\varvec{s}_j) \in {\mathbb {R}}^2\), the spatial process is second-order stationary. In addition, if the covariance function only depends on the Euclidean distance \(||\varvec{s}_i - \varvec{s}_j||\), the process is said to be isotropic.

In a hierarchical framework, the first step in defining a model for a random field is to identify a probability distribution for the observations available at n spatial locations and represented by the vector \(\varvec{y}=(y(\varvec{s}_1), \ldots , y(\varvec{s}_n))=(y_1, \ldots , y_n)\) (the notation is simplified and the index i is used for denoting the generic spatial points \(\varvec{s}_i\)). At the first level of the hierarchy, we usually select a distribution from the exponential family, characterized by a set of parameters. These parameters are linked with a linear predictor which also includes a latent GF denoted by \(\xi (\varvec{s})\) whose covariance function \(\varvec{\varSigma }\) depends on two parameters: \(\sigma ^2\) which represents the variance (partial sill in kriging terminology) and the range \(\phi\) of the spatial effect.

Computational costs required to estimate these parameters are high when we deal with the spatial covariance function because the generated matrices are dense. This problem is known as the “big n problem” (Banerjee et al. 2014; Jona Lasinio et al. 2013) and despite computational power today, it is still a computational bottleneck in many situations. A computationally effective alternative is given by the stochastic partial differential equation (SPDE) approach proposed by Lindgren et al. (2011) (see Sect. 3.3).

In addition to the spatial pattern, the temporal variation could be equally important because the phenomenon can vary not only in space but also in time (see Hefley and Hooten 2016, for a comprehensive overview of modeling species distribution with a spatio-temporal perspective). Then, extending the spatial case to the spatio-temporal case including a time dimension, the process indexed by space and time can be defined as \(\{y(\varvec{s}, t), (\varvec{s}, t) \in {\mathcal {D}} \subset {\mathbb {R} }\times {\mathbb {R}}\}\), and is observed at n spatial locations and at T time points.

The general structure for modeling the spatial distribution of species is given by the following formulation and notation. If \(\varvec{y}=(y_1, \ldots ,y_n)\) represents the observed values of the corresponding response variable Y with mean \(\varvec{\mu }=(\mu _1, \ldots , \mu _n)\), each \(\mu _i\) can be easily linked to a structured additive predictor \(\eta _i\) through a link function \(g(\cdot )\), so that \(g(\varvec{\mu })=\varvec{\eta }\). The structured additive predictor \(\varvec{\eta }\) accounts for the effect of various covariates in an additive way:

$$\begin{aligned} \eta _i = \beta _0 + \sum _{m=1}^M \beta _m x_{mi} + \sum _{l=1}^L f_l(z_{li}), \end{aligned}$$
(3.1)

where \(\beta _0\) corresponds to the intercept; the coefficients \(\varvec{\beta }=\{\beta _1, \ldots , \beta _M\}\) quantify the (linear) effect of some covariates \(\varvec{x}=(\varvec{x}_1, \ldots , \varvec{x}_M)\) on the response; and \(\varvec{f}=\{f_{1}(\cdot ), \ldots , f_{L}(\cdot )\}\) are unknown functions of the covariates \(\varvec{z}=(\varvec{z}_1, \ldots , \varvec{z}_L)\), and can assume different forms such as smooth nonlinear effects of covariates, time trends and seasonal effects, random intercept and slopes as well as temporal or spatial random effects. Note that this general structure can also be seen as a Generalized Additive Mixed Model (GAMM). Also to be noted is that here it is assumed that covariates are observed at the same locations of the response variable. The situation where covariates are observed in locations different from those of the response variable (misalignment) will be discussed in Sect. 4.3.

In many statistical applications, in particular, in SDMs, the model involves multiple parameters that can be regarded as related or connected in some way by the structure of the problem, implying that a joint probability model for these parameters should reflect their dependence (Gelman et al. 2014). It is common to model such a problem hierarchically, with observable outcomes modeled conditionally on certain parameters, which in turn are given a probabilistic specification in terms of further parameters, adding various levels of the modeling and thus defining a hierarchical model (HM). Note that Hierarchical models provide a generalization of all the models presented here; and moreover that they are able to deal with all the types of the data that we can be found when dealing with SDMs. Table 1 describes all the models mentioned in this subsection along with a diagram emphasizing their nested nature.

Although other approaches can be used such as maximum likelihood (MLE; Le Cam 1990), restricted maximum likelihood (RMLE; Bartlett 1937), quasi-maximum likelihood (QMLE; Cox and Reid 2004), the method of moments (Bowman and Shenton 2006), the generalized method of moments (GMM; Hansen 1982), M-estimators (Shapiro 2000), the maximum spacing estimation (MSE; Anatolyev and Kosenok 2005), etc., here we will focus on the Bayesian approach to making inference for hierarchical models with a linear predictor of the form (3.1).

Table 1 Matching of models presented and data types
Full size table

3.2 Bayesian approach

The use of the Bayesian framework as a way to make inference has increased in the past 50 years and it has been applied in different areas, such as social sciences (Jackman 2009), medicine and public health (Berry and Stangl 1999), finance (Rachev et al. 2008), ecology (McCarthy 2007), bioinformatics (Mallick et al. 2009), health economics (Baio 2012), physical sciences (Andreon and Weaver 2015) and econometrics (Gómez-Rubio et al. 2014). Bayesian reasoning is based on the assumption that parameters are random variables, and prior knowledge has to be incorporated via the corresponding prior distributions of the said parameters. Bayes’ theorem is the tool that combines prior information with the likelihood yielding the posterior distributions. To be noted is that the Bayesian approach is perfectly suited for complex spatial models such as SDMs because it allows model parameters to be random variables, resulting in a more realistic and accurate estimation of uncertainty.

SDMs are a very good example of a hierarchical structure that can be expressed as a hierarchical Bayesian model (Wikle and Hooten 2010; Hefley and Hooten 2016). They can be structured in three levels: the first one refers to the data and is conditioned on the process and parameters in whatever aspects of the process are appropriate. The second level contains the latent components, which can be spatial and/or dynamic and the stochastic form can be univariate or multivariate. Finally, the third stage defines the priors for the parameters on which the latent processes depend. The parameters in this level are also known as hyperparameters.

The approach most commonly used to perform Bayesian inference for spatial species distribution models is based on MCMC methods (Gelfand et al. 2006); they are flexible computational tools which can be easily adapted to any kind of inferential problem. The software most frequently used to implement MCMC algorithms are WinBUGS (Lunn et al. 2000; Brooks et al. 2011), OpenBUGS (Lunn et al. 2009) and JAGS (Plummer 2016), which can also be run within other programs like R (through the R2OpenBUGS, R2WinBUGS, BRugs and rjags packages), Stata and SAS. Alternatively other R packages are BayesX (Brezger et al. 2003), CARBayes (Lee 2013), stocc (for binary data only), spatcounts (for count data only), CARramps (for Gaussian data only), and spdep (for Gaussian data only). Several hierarchical models including ecological processes (habitat suitability, spatial dependence and anthropogenic disturbance) and observation processes (species detectability) can also be performed using the hSDM package of R developed by Vieilledent et al. (2014). Functions in this R package use an adaptive Metropolis algorithm (Robert and Casella 2011) in a Gibbs sampler (Gelfand and Smith 1990) to obtain the posterior distribution of model parameters. The Gibbs sampler is written in C code and compiled to optimize computation efficiency. Thus, the hSDM package can be used for very large data-sets while drastically reducing the computation time. However, with hSDM it is not possible at present to model spatio-temporal or proportion response variables.

Despite their generalized use, to be noted is that MCMC methods still have many challenges to deal with (like the so-called “big n problem” mentioned above; see Banerjee et al. 2014; Jona Lasinio et al. 2013). Indeed, they can be extremely slow and even computationally unfeasible especially when the models are extremely complex (with many random effects or hierarchical levels) or when big datasets are considered in the space-time setting.

As a result, other options have appeared to make inference in SDMs. Taking advantage of the hierarchical structure of SDMs, Golding and Purse (2016) propose the use of an empirical Bayesian approach. In particular, they maximize the marginal posterior density of the model, which, in their words, enables the incorporation of prior knowledge over hyperparameters whilst being much less computationally intensive than fully Bayesian inference.

Here, we will focus on the integrated nested Laplace approximation (INLA) methodology (Rue et al. 2009), as a computational effective alternative to MCMC. Our choice is due to two considerations: the speed of calculation, and the ease with which model comparison can be performed.

3.3 INLA and SPDE framework

The INLA methodology is now a well-established tool for Bayesian inference in several research fields, including ecology, epidemiology, econometrics and environmental science (Rue et al. 2017). It can be used through R with the R-INLA package. For more details on INLA for spatial and spatio-temporal models we refer the reader to Blangiardo et al. (2013) and Blangiardo and Cameletti (2015), where practical examples and code guidelines are also provided.

The reason why INLA can be used is that SDMs can be seen as latent Gaussian models (Rue and Held 2005), for which the class of models INLA is designed. After identifying the distribution for the observed data, we can link its corresponding mean to the linear predictor as in Eq. (3.1). If conditional independence is assumed, the distribution of the n observations is given by the likelihood

$$\begin{aligned} p(\varvec{y} \mid \varvec{\theta }, \varvec{\psi })=\prod _{i=1}^n p(y_i \mid \theta _i,\varvec{\psi }), \end{aligned}$$
(3.2)

where \(\varvec{\theta }\) represents the set of latent (nonobservable) components of interest \(\varvec{\theta }=\{\beta _0, \varvec{\beta }, \varvec{f} \}\), also known as the latent field, and \(\varvec{\psi }=(\psi _1, \ldots , \psi _K)\) denotes the vector of K hyperparameters. As we can observe in Eq. (3.2), each data point \(y_i\) is connected to one element \(\theta _i\) in the latent field. This assumption can be relaxed, and each observation can be connected with a linear combination of elements in \(\varvec{\theta }\) (Martins et al. 2013). In addition, the multiple likelihood case can also be taken into account.

In the context of latent Gaussian models, assumed is a multivariate Normal prior distribution on \(\varvec{\theta }\) with mean \(\varvec{0}\) and precision matrix \(\varvec{Q(\psi )}\), i.e, \(\varvec{\theta } \sim \text {N}(\varvec{0}, \varvec{Q}^{-1} (\varvec{\psi }))\) with density function given by

$$\begin{aligned} p(\varvec{\theta } \mid \varvec{\psi })= (2\pi )^{-n/2} |\varvec{Q(\varvec{\psi })}|^{1/2}\exp \left( -\frac{1}{2} \varvec{\theta }'\varvec{Q(\varvec{\psi })} \varvec{\theta }\right) , \end{aligned}$$
(3.3)

being \(| \cdot |\) the matrix determinant and \('\) the transpose operation. When the precision matrix \(\varvec{Q(\psi )}\) is sparse a GF becomes a Gaussian Markov random field (GMRF, Rue and Held 2005). Interestingly, when making inference with GMRFs, linear algebra operations are performed using numerical methods for sparse matrices, and this yields computational benefits.

In spite of the wide acceptance of INLA, its precision and its computational efficiency in many latent Gaussian models (see for instance, Martino et al. 2011; Schrödle et al. 2011; Ruiz-Cárdenas et al. 2012, for a description of how to use INLA in spatio-temporal disease mapping, in state-space models and in survival models, respectively), INLA cannot be directly applied when dealing with models that incorporate geostatistical data (that is, continuously indexed Gaussian Fields). The underlying reason is that a parametric covariance function needs to be specified and fitted based on the data, which determines the covariance matrix \(\varvec{\varSigma }\) and enables prediction in unsampled locations. But from the computational perspective, the cost of factorizing the dense covariance matrix \(\varvec{\varSigma }\) is cubic in its dimension. Despite current computational power, in many situations it is still challenging to factorize it for computing the inverse and the determinant.

Lindgren et al. (2011) proposed an alternative approach by using an approximate stochastic weak solution to a Stochastic Partial Differential Equation (SPDE) as a GMRF approximation to a continuous Gaussian Field (GF) with Matérn covariance structure. Specifically, they used the fact that a Gaussian Field \(\xi (\varvec{s})\) with Matérn covariance is a solution to the linear fractional SPDE

$$\begin{aligned} (\kappa ^2-\varDelta )^{\alpha /2}(\tau \xi (\varvec{s})) & = {} {\mathcal{W}}(\varvec{s}), \qquad \varvec{s} \in {\mathbb {R}}^d,\, \alpha = \nu + \delta /2,\, \kappa>0,\, \nu >0, \qquad \end{aligned}$$
(3.4)

where \(\varDelta\) is the Laplacian, \(\alpha\) controls the smoothness, \(\kappa\) is the scale parameter, \(\tau\) controls the variance, and \({\mathcal {W}}(\varvec{s})\) is a Gaussian spatial white noise process. The exact and stationary solution to this SPDE is the stationary GF \(\xi (\varvec{s})\) with Matérn covariance function given by:

$$\begin{aligned} \text {Cov}(\xi (\varvec{s}_i), \xi (\varvec{s}_j)) = {\mathcal {C}}(\xi _i, \xi _j) = \frac{\sigma ^2}{2^{\nu -1}\varGamma (\nu )} (\kappa ||\varvec{s}_i - \varvec{s}_j||)^\nu K_\nu (\kappa ||\varvec{s}_i - \varvec{s}_j||), \qquad \end{aligned}$$
(3.5)

being \(||\varvec{s}_i - \varvec{s}_j||\) the Euclidean distance between two locations \(\varvec{s}_i, \varvec{s}_j \in {\mathbb {R}}^d\), and \(\sigma ^2\) the marginal variance. Moreover, \(K_\nu\) is the modified Bessel function of the second kind and order \(\nu > 0\), which measures the degree of smoothness of the process. This parameter is usually kept fixed due to its poor identifiability. Conversely, \(\kappa >0\) is a scaling parameter related to the distance at which the spatial correlation becomes almost null, i.e., the range (for more information on the Matérn covariance model see Handcock and Stein 1993; Stein 1999). Typically, as pointed out in Lindgren et al. (2011), the empirically derived definition for the range is \(r=\frac{\sqrt{8 \nu }}{\kappa }\), with r corresponding to the distance at which the spatial correlation is close to 0.1, for each \(\nu \ge \frac{1}{2}\).

The link between Eqs. (3.4) and (3.5) is given by the expressions \(\nu =\alpha - \frac{\delta }{2}\), and \(\sigma ^2=\frac{\varGamma (\nu )}{\varGamma (\alpha )(4\pi )^{\delta /2}\kappa ^{2\nu }\tau ^2}\). In the particular case where the dimension is 2, i.e., \(\delta =2\), it follows that \(\nu =\alpha - 1\) and \(\sigma ^2=\frac{\varGamma (\nu )}{\varGamma (\alpha )(4\pi )\kappa ^{2\nu }\tau ^2}\).

Finally, in R-INLA, the Gaussian field \(\xi (\varvec{s})\) is found numerically as a weak solution to the SPDE in (3.4), and by default the smoothness parameter \(\alpha\) is fixed to 2, corresponding with \(\nu =1\). With this assumption, the range is given by \(\phi \approx r = \sqrt{8}/\kappa\), while the variance is given by \(\sigma ^2 = 1/(4\pi \kappa ^2\tau ^2)\).

Bayesian geostatistical analysis using R-INLA has already been applied in various contexts. Along with introducing the geostatsinla package for performing geostatistics with INLA in an easy way, Brown (2015) applies it in the context of mapping the Loa loa filiarasis disease (a dataset previously cited in Diggle and Ribeiro 2007). Moreover, Karagiannis-Voules et al. (2013) have used Bayesian geostatistical negative binomial models to analyze reported incidence data of cutaneous and visceral leishmaniasis in Brazil covering a 10-year period, while González-Warleta et al. (2013) have used Bayesian geostatistical binomial models to predict the probability of infection of paramphistomosis in Galicia (NW Spain). In the context of fisheries, Bayesian geostatistical analysis using R-INLA has also been used to predict the presence/absence, the abundance, or the proportion of fish species (Muñoz et al. 2013; Pennino et al. 2013, 2014, 2016, 2017; Paradinas et al. 2015, 2016; Cosandey-Godin et al. 2015; Quiroz et al. 2015; Roos et al. 2015; Rufener et al. 2017).

4 Extending statistical modeling of species distribution

There are a number of additional potential sources of bias and error that should be carefully considered when analyzing and modeling species distribution data. Errors may arise through the incorrect identification of species, or inaccurate spatial referencing of samples. Biases can also be introduced because collectors tend to sample in easily accessible locations. Here we discuss some of these issues.

4.1 Temporal autocorrelation

As mentioned above, in addition to the spatial pattern, the temporal variation could be equally important because the phenomenon may vary not only in space but also in time. This happens in problems such as the evolution of epidemics (Stein et al. 1994; Hefley et al. 2017b), the spatio-temporal evolution of temperature (Hengl et al. 2012) or the understanding of the spatial dynamism of species over time (Wikle 2003; Hooten et al. 2007; Hooten and Wikle 2008; Paradinas et al. 2015, 2017a; Williams et al. 2017).

As pointed out by Cressie and Wikle (2011), temporal correlation depends on the same principle as spatial correlation: temporally close observations tend to be more related than temporally distant ones. Consequently, model fitting and predictions improve when a temporal term is added. However, temporal and spatial scales are different and the spatio-temporal analysis is more complicated than the simple addition of an extra dimension to the continuous spatial domain.

In the context of species distribution modeling, most studies (surveys, plant coverage surveys, air pollution surveys, etc.) have been repeated periodically for long periods of time (Gitzen 2012; Aizpurua et al. 2015). Although the main interest is the spatial evolution of the system under study, it must be considered that it varies not only in space but also in time. Here we focus on this most common situation of discrete and regular time observations. For situations in which data are collected in irregular time-lags—that is, when the issue is handling continuous-time data—a good option is to consider 1D SPDE models with a second order B-Spline basis representation (Lindgren and Rue 2015a, b).

The spatio-temporal behavior of the data can vary depending on the nature of the process under study and the available sampling resolution. In particular, the basic model in (3.1) can be rewritten by splitting the f term into two terms, one indicating different possible spatio-temporal structures, and the other indicating any other latent model or non-linear effect. If \(y_{it}\) represents the response variable analyzed at location \(\varvec{s}_i\) (\(i =1, \ldots , n\)) at time t (\(t=1, \ldots , T\)), then the mean of the response variable \(\mu _{it}\) is linked to the linear predictor with a link function \(g(\cdot )\), as

$$\begin{aligned} \eta _{it} = g(\mu _{it}) = \beta _0 + \sum _{m=1}^M \beta _m x_{mit} +\sum _{k=1}^{K} f_{k}(z_{kit}) + u_{it}, \end{aligned}$$
(4.1)

where \(\beta _0\) corresponds to the intercept; the coefficients \(\varvec{\beta }=\{\beta _1, \ldots , \beta _M\}\) quantify the linear effect of some covariates on the response; \(u_{it}\) represents the spatio-temporal structure of the model; \(z_{kit}\) is the value of the k-th explanatory variable at a given location \(\varvec{s}_i\) and time t; and f represents any latent model applied to the covariates.

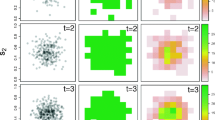
Among other structures, and following Paradinas et al. (2017a), we comment here on four basic structures for \(u_{it}\), each one allowing for different degrees of flexibility in the temporal domain of the spatio-temporal model. Paradinas et al. (2017a) provide a figure that schematically illustrates all these structures:

  • Opportunistic spatial distribution this flexible structure consists in expressing \(u_{it}\) as different spatial realizations \(\varvec{w}_t=\{w_{1t},\ldots ,w_{it}, \ldots , w_{nt} \}\) of the same spatial field for each time unit t, while sharing a common covariance function (same \(\kappa\) and \(\tau\)) to avoid overfitting:

    $$\begin{aligned} u_{it}= & {} \ w_{it}, \nonumber \\ \varvec{w}_t\sim & {} \ \text {N}(\mathbf{0} ,\varvec{Q}^{-1}(\kappa , \tau )). \end{aligned}$$
    (4.2)

    This structure is a good approximation for processes where the spatial distribution varies considerably among different time units and unrelatedly among neighboring times. This structure has been used in Cosandey-Godin et al. (2015) and in Paradinas et al. (2015).


  • Persistent spatial distribution with random intensity changes over time when the pattern of spatial variation persists over time, but with possibly varying scales of intensity, a time structure is introduced into the model using a zero mean Gaussian random noise effect \(v_t\). In this case, \(u_{it}\) is decomposed in a common spatial realization \(w_{it}\) along with an independent random noise effect \(v_t\) that absorbs the different mean intensities at each time t:

    $$\begin{aligned} u_{it}= & {} \ w_{it} + v_{t},\nonumber \\ \varvec{w}_t\sim & {} \ \text {N}(\mathbf{0} ,\varvec{Q}^{-1}(\kappa , \tau )), \nonumber \\ v_t\sim & {} \ \text {N}(0, \tau _{v}^{-1}). \end{aligned}$$
    (4.3)

    For processes where the spatial component persists in time, this structure may be the most suitable. It has been used by Pennino et al. (2014) and in Paradinas et al. (2015).


  • Persistent spatial distribution with temporal intensity trend the process could show a temporal progression in its mean. To model that, a temporal trend effect h(t) can be added to the linear predictor. In this case, \(u_{it}\) is decomposed into a common spatial realization \(w_{i}\) and an independent temporal structured trend h(t) to absorb the temporal progression of the process:

    $$\begin{aligned} u_{it}= & {} \ w_{i} + h(t),\nonumber \\ \varvec{w}\sim & {} \ \text {N}({\mathbf{0}} ,\varvec{Q}^{-1}(\kappa , \tau )). \end{aligned}$$
    (4.4)

    This structure is highly recommended in situations where a temporal tendency is present. It was proposed by Paradinas et al. (2016) to identify intra-annual trends in fishery discards.


  • Progressive spatio-temporal distribution this structure incorporates both spatial and temporal correlation of the data to accommodate those cases where the spatial realizations change in a related manner over time. Here, \(u_{it}\) is decomposed into a common spatial realization \(w_{it}\) and an autoregressive temporal term \(r_{it}\) expressing the correlation among temporal neighbors of order K:

    $$\begin{aligned} u_{it}= & {} \ w_{it} + r_{it},\nonumber \\ \varvec{w}_t\sim & {} \ \text {N}(\mathbf{0} , \varvec{Q}^{-1}(\kappa , \tau )), \nonumber \\ r_{it}\sim & {} \ {\text {N} \left( \sum _{k=1}^K \rho _k r_{i(t-k)}, \tau _r^{-1} \right) }. \end{aligned}$$
    (4.5)

    This structure is preferred when the spatial realization varies between different times but not as much as in (4.3). Indeed, the structure has been used by Cameletti et al. (2011, 2013) and also by Cosandey-Godin et al. (2015).

Note that this list is only an overview of the different spatio-temporal structures which allow us to discern the nature of the general spatial behavior of the process over time. Unfortunately, the temporal resolution of spatio-temporal datasets is typically too low to fit most of the highly structured models.

4.2 Preferential sampling

In studies on species distributions, collecting data on the species of interest is not a trivial problem. With the exception of a few studies, species distribution models rely on opportunistic data collection due to the high cost and time-consuming nature of collecting data in the field, especially on a large spatial scale. As an example, studies on bird monitoring data are often collected by volunteers who concentrate the sampling process on areas where they expect to find species of interest. These types of opportunistically collected data tend to suffer from a specific complication: the sampling process that determines the data locations and the species observations are not independent (Diggle et al. 2010). Statistical models used for species distribution usually assume, if only implicitly, that sampling is non-preferential and that the selection of the sampling locations does not depend on the values of the spatial variable. However, opportunistic data are a clear example of preferential sampling, that occurs because sampling locations are deliberately chosen in areas where the values of the species of interest are thought likely to be particularly high or low (Diggle et al. 2010).

Hence, applying standard geostatistical methods to preferentially sampled data potentially yields biased results if the choice of monitoring locations is not accounted for in the modeling process. A possible approach to correct this issue is to interpret the data as a marked point pattern (Fortin and Dale 2005; Diggle 2013) where the sampling locations form a point pattern and the observations taken in those locations are the marks. By assuming that the intensity of the point process depends on the amount of species of interest, the marks and the pattern become not independent.

A preferential sampling model can be considered as a two-part model that share information. Firstly, it is supposed that the observed locations \((\varvec{s}_1, \ldots , \varvec{s}_n)\) come from a non-homogeneous Poisson process with intensity \(\varLambda _i = \text {exp}\left\{ \alpha _1 + w_i \right\}\), i.e., a log-Gaussian Cox process (LGCP; Fortin and Dale 2005; Diggle 2013) is assumed, being \(\alpha _1\) the intercept of the LGCP and \(w_i\) the spatial effect of the model and \(i=1, \ldots , n\) the index corresponding to the \(\varvec{s}_i\) location. Secondly, the species characteristic (usually the abundance) \(y_i\) is assumed to follow an exponential family distribution (such as a Normal or a Gamma distribution when dealing with abundances, although other options such as exponential, lognormal, etc., could clearly be possible), whose mean is related with the spatial term using a link function \(g(\cdot )\), \(g(\mu _i)=\alpha _2 + \beta w_i\), being \(\alpha _2\) the intercept of the model and \(w_i\) the spatial term shared with the LGCP, but scaled by \(\beta\) to allow for the differences in scale between the abundances and the LGCP. More formally, the model can be expressed as follows:

$$\begin{aligned} y_i\sim & {} \ \text {F}(\mu _{i},\gamma ^2) \nonumber \\ \text {g}(\mu _i)= & {} \ \alpha _2 + \beta w_i\nonumber \\ \varvec{w}\sim & {} \ \text {N}(\mathbf{0},\varvec{Q^{-1}}(\kappa ,\tau )) \end{aligned}$$
(4.6)

where \(\varvec{w}=\{w_1, \ldots , w_n\}\), the precision matrix \(\varvec{Q}(\kappa ,\tau )\) is computed internally by the SPDE approach and represents the GMRF approximation to the continuous GF (see Illian et al. 2012; Krainski et al. 2017; Pennino et al. 2018, for details about how to implement these models within INLA), and \(F(\mu , \gamma )\) represents a distribution coming from the Exponential family with mean \(\mu\) and variance \(\gamma ^2\).

4.3 Spatial misalignment

A crucial issue in studying the effect of environmental physical factors on species distribution concerns spatial misalignment (Clark and Gelfand 2006; Gelfand et al. 2010; Foster et al. 2012; Miller 2012).

This occurs when the response biological variable (e.g. presence/absence of the species) is observed in locations which are different from the spatial points where covariate data are available. Additionally, it can happen that covariates have a different spatial scale if they are defined at the area or cell grid level (as in the case of remote sensing data).

The naïve solution for spatial misalignment is a two-stage approach: the first step consists in the prediction of the covariate in the spatial locations where the response variable is observed (through a geostatistical model by means of kriging or inverse-distance weighting) or in the downscaling of the gridded covariate to the point-level resolution (usually considered is the value of the cell where the spatial point is located). Then, at the second stage, these predicted values are plugged into the linear predictor (3.1) as known constants. The problem with this approach is that it does not take account of the uncertainty related to the covariate spatial estimation of the first stage, with the consequence of erroneous inference of the statistical model and a potential biased estimate of the environmental variable effect on the response variable (Foster et al. 2012).

A solution to incorporate the spatial prediction uncertainty in SDMs consists in implementing one of the so-called errors-in-variables models (Carroll et al. 2016) which can be estimated in a frequentist (by means of the EM-algorithm) or Bayesian framework (with MCMC or INLA). If we assume for example that the predicted covariate is a noisy version of the true one, a classic measurement error model can be adopted (Stoklosa et al. 2015). Otherwise, a Berkson-error model can be considered if the predicted covariate is a smoothed (i.e. less variable) version of the true variable (Foster et al. 2012). As reported in Stoklosa et al. (2015) “Which of these two types of error models to consider will depend on what the analyst believes to be the true underlying explanatory variable, and how the data were collected/measured. The analyst must take into account: how and whether the species responds to a particular climate observation (Berkson); or that it might respond to an average, such that relatively minor deviations from this are immaterial (classical)”.

Another alternative to the two-stage approach is the joint modeling strategy implemented in Barber et al. (2016) to evaluate the presence of the Fasciola hepatica in Galicia (Spain) using the annual mean temperature as covariate. In this case a spatial geostatistical model is specified for the covariate and is estimated jointly with the species distribution models in a Bayesian context. The joint model is specified as follows

$$\begin{aligned} y_i&\sim \text {Bernoulli}(\pi _{i}) \nonumber \\ \text {logit}(\pi _i)&= \beta _0+{\beta _1 \phi }_i + w_i \nonumber \\ \varvec{w}&\sim \text {N}(\varvec{0},\varvec{Q^{-1}}(\kappa ,\tau ))\nonumber \\ x_i&\overset{iid}{\sim } \text {N}(\phi _i,\sigma ^2_x) \nonumber \\ \varvec{\phi }&\sim \text {N}(\varvec{0},\varvec{Q^{-1}}(\gamma ,\delta )) \end{aligned}$$
(4.7)

where \(\pi _i\) is the probability of occurrence at site \({\varvec{s}}_i\), \(x_i\) is the covariate of interest whose spatial distribution is specified through its mean (a realization of the Matérn Gaussian process \(\varvec{\phi }\) depending on the parameters \(\gamma\) and \(\delta\)), and through its variance \(\sigma ^2_x\), which is introduced to express any possible measurement error. The model also includes another spatial process for the response represented by \(\varvec{w}\). This kind of model pertains to the latent Gaussian model family and can be estimated using the SPDE-INLA approach (see Blangiardo and Cameletti, 2015, Chap. 8 and Muff et al. 2015). The advantage is that this joint model allows to properly propagate all the uncertainty related to the covariate prediction; on the other it can be extremely computationally expensive especially when there is more than one explanatory variable.

Finally, another alternative is the one proposed by Gómez-Rubio and Rue (2017) that, using a more general approach, deals with missing values in the covariates, based on fitting conditional latent Gaussian models where covariates are imputed using a Metropolis-Hastings algorithm.

4.4 Non-stationarity

The Matérn spatial covariance function \({\mathcal {C}}(\cdot ,\cdot )\) specified by Eq. (3.5) enjoys the second-order stationarity and isotropy property, i.e. it depends only on the distance between the spatial locations and not on the direction or the coordinates. In some situations, this stationarity assumption, which is very convenient to simplify the inferential procedures, may not be suitable. For example, for some applications it is not realistic to assume that the spatial dependence structure is the same throughout the domain considered, especially when geographical elements or physical barriers (river, lakes, islands, etc.) exist. In such situations characterized by spatial heterogeneity and barriers, it may be more reasonable to adopt a non-stationary Gaussian field (see Gelfand et al. 2010, Chapter 9 and Risser 2016 for a review).

In ecological applications, heterogeneity in space (i.e. non-stationarity) occurs when a latent global process is also affected by some underlying local processes (Miller 2012). A local modeling technique to include this heterogeneity in SDMs is given by the geographically weighted regression (GWR) characterized by covariate coefficients which vary spatially and are specific for each spatial location; a spatial kernel function is used to define spatial neighborhoods (see e.g. Brunsdon et al. 1998; Windle et al. 2010; Holloway and Miller 2015; Liu et al. 2017). Some authors do not completely agree with the use of these models due to the large degree of multicollinearity that their coefficients tend to exhibit, as well as strong positive spatial autocorrelation. As an alternative, spatial filtering provides a methodology for dealing better with multicollinearity, while accounting for spatial autocorrelation (see e.g. Griffith 2008). The Bayesian counterpart of GWR models, which are usually estimated by weighted least squares, is given by spatially-varying coefficients models (Gelfand et al. 2003; Finley 2011).

In the SPDE framework non-stationarity is achieved by allowing the Matérn covariance function parameters to vary smoothly over space according to a log-linear function: thus, we will have \(\sigma ^2(\varvec{s})\) for the marginal variance in (3.5) and \(r(\varvec{s})\) for the spatial range (Ingebrigtsen et al. 2014; Lindgren and Rue 2015b). Bakka et al. (2016) extend this approach to solve specifically the barrier problem for SDMs. In particular, they force the spatial correlation to go around the barriers (and not through them) by means of a partition of the considered spatial field—in a normal and in a barrier area—and in the specification of two corresponding non-stationary processes with different range parameters (in particular for the barrier region the range parameter is almost zero). The application considered in Bakka et al. (2016) regards fish larvae data in the Finnish archipelago.

4.5 Imperfect detection

Studies on species abundance and distribution are often imperfect due to observer error (Nichols et al. 2000), species rarity (Dettmers et al. 1999) or because detection varies with confounding variables such as environmental conditions (Gu and Swihart 2004; Pennino et al. 2017). When detection is imperfect, additional steps are usually needed to improve inference. Indeed, failure to do so could result in biased estimation and erroneous conclusions.

In recent years, new models called site-occupancy (Hoeting et al. 2000; MacKenzie et al. 2002) for presence-absence data and N-mixture models (Royle 2004) for abundance data have been developed to solve this problem. These models combine two processes: an ecological process to describe habitat suitability and an observation process to take imperfect detection into account. To estimate detectability, these models use information from repeated observations at several sites. Detectability may vary with site characteristics such as habitat variables, or survey characteristics such as weather conditions, since suitability relates only to site characteristics. Various studies showing the advantages of site occupancy and N-mixture models over classical models that do not consider the problem of detectability can be found in the literature: Royle (2004), Dorazio et al. (2006) for birds, MacKenzie et al. (2002) for amphibians or Pennino et al. (2017) for cetaceans. In addition to the detectability problem, a variety of methods have been developed to correct for the effects of spatial autocorrelation (Latimer et al. 2006; Johnson et al. 2013; Hefley et al. 2017a).

A Bayesian version for site-occupancy spatial models and N-mixture spatial models could also be implemented to take simultaneously account of both imperfect detection and spatial autocorrelation. To describe Bayesian site-occupancy spatial models, let \(z_i\) be a random variable describing habitat suitability at site \(\varvec{s}_i\). It can take the value 1 or 0 depending on the habitat suitability, i.e. \(z_i\) = 1 or \(z_i\) = 0, thus a Bernoulli distribution is assumed with parameter \(\pi _i\). Several visits at time \(t=1, \ldots , T\) can happen at site i. Let \(y_{it}\) be a random variable representing the presence of the species at site i and time t. The species is observed at site i \((\sum _{t}y_{it} \ge 1)\) only if the habitat is suitable \((z_i=1)\). The species is unobserved at site i \((\sum _{t} y_{it}=0)\) if the habitat is not suitable \((z_i=0)\), or if the habitat is suitable \((z_i=1)\) but the probability \(\alpha _{it}\) of detecting the species at site \(\varvec{s}_i\) and time t is lower than 1. Then, \(y_{it}\) follows a Bernoulli distribution of parameter \(z_i \alpha _{it}\), and the model is expressed as follows


Ecological process

$$\begin{aligned} {z}_{i} & \sim {} \text {Bernoulli}({\pi }_{i}), \nonumber \\ \text {logit}({\pi }_{i})& = {} \beta _0 + \sum _{m=1}^{M_1} \beta _m x^{(1)}_{mi} +{w}_{i}, \end{aligned}$$
(4.8)

Detection process

$$\begin{aligned} {y}_{it} & \sim {} \text {Bernoulli}({z}_{i} \, {\alpha }_{it}), \nonumber \\ \text {logit}({\alpha }_{it})&= {} \gamma _0 + \sum _{m=1}^{M_2} \gamma _m x^{(2)}_{mit}, \end{aligned}$$
(4.9)

where \(\{\beta _0, \ldots , \beta _{M_1}\}\) and \(\{\gamma _0, \ldots , \gamma _{M_2}\}\) are the parameters that quantify the linear effects of some covariates \((\varvec{x}^{(1)}_{1}, \ldots , \varvec{x}^{(1)}_{M_1})\) and \((\varvec{x}^{(2)}_{1}, \ldots , \varvec{x}^{(2)}_{M_2})\) in the ecological and observation process respectively. These covariates are usually variables refereed to site characteristics such as habitat variables or survey characteristics such as weather conditions. \(\varvec{w} = (w_1, \ldots , w_n)\) represents the spatial effect in the ecological process. Normally, this spatial effect is a Gaussian process that can be incorporated as geostatistical terms (in the way already introduced in Sect. 3), but other options are possible (such as CAR Normal distributions, as in Pennino et al. (2017)). The R-package hSDM, which make inference using MCMC, can be used easily to fit some of these models. In addition, the inlabru package also handle the problem of detectability (Yuan et al. 2016).

With respect to N-mixture models, which are used for count data with imperfect detection, they implement a Poisson distribution for the ecological process, while using a Binomial distribution for the observability process (Royle and Nichols 2003; Dodd and Dorazio 2004; Royle 2004). The structure of the model is similar to the site-occupancy model, in particular:


Ecological process

$$\begin{aligned} {N}_{i} & \sim {} \text {Poisson}({\lambda }_{i}), \nonumber \\ \text {log}({\lambda }_{i}) & = {} \beta _0 + \sum _{m=1}^{M_1} \beta _m x^{(1)}_{mi} +{w}_{i}, \end{aligned}$$
(4.10)

Detection process

$$\begin{aligned} {y}_{it} & \sim {} \text {Bernoulli}({N}_{i} \, {\alpha }_{it}), \nonumber \\ \text {logit}({\alpha }_{it})& = {} \gamma _0 + \sum _{m=1}^{M_2} \gamma _m x^{(2)}_{mit}. \end{aligned}$$
(4.11)

The R-package hSDM allow us to fit some of these models. In addition, the INLA group is developing some methods to fit N-mixture models (Meehan et al. 2017).

4.6 Excess of zeros

The study of datasets with zero excess has an important role in the literature, particularly, in species distribution modeling (Agarwal et al. 2002; Ver Hoef and Jansen 2007; Neelon et al. 2013), becoming highly relevant in recent years especially. Bayesian softwares like INLA already contain different functions to handle situations with zero excess. Generally, these situations are a source of overdispersion caused by a disagreement between the data and the distribution assumed: there are more zeros in the dataset than the proposed distribution could reasonably explain.

Zero-inflated models are a widely known tool for dealing with this problem. These models assume that the data follow a finite mixture of a degenerate distribution with all its mass at zero with a discrete distribution with support in \({\mathbb {Z}}^{+} \cup \{0\}\) (Yau et al. 2003). If \(1-\pi _i\) represents the probability of species presence, \(\pi _i\) the probability of the species absence, i.e., \(p(y_i|\pi _i)=\pi _i\) and \(p(y_i>0)=1-\pi _i\), and h a probability mass function (pmf) of some parametric discrete distribution with support on \({\mathbb {Z}}^{+} \cup \{0\}\), the distribution of \(y_i\) has the following mixture density:

$$\begin{aligned} p(y_i|\pi _i, \mu _i, \varvec{\psi }_1)= \pi _i \delta _0 + (1-\pi _i) h(y_i|\mu _i, \varvec{\psi }_1), \end{aligned}$$
(4.12)

being \(\delta _0\) the Dirac delta function, \(\mu _{i}\) and \(\varvec{\psi }_1\) hyperparameters depending on h, and h is a pmf coming from a Poisson, binomial or negative-binomial (note that this latter distribution is one of those considered to account for overdispersion). The model is completed when linking \(\pi _i\) and \(\mu _i\) with the linear predictors by means of:

$$\begin{aligned} \text {logit}(\pi _i)&= {} \eta _i^{(1)}=\alpha ^{(1)} + \sum _{m=1}^{M^{(1)}} \beta ^{(1)}_m x_{mi}^{(1)}+ \sum _{l=1}^{L^{(1)}} f_{l}^{(1)} (z_{li}^{(1)}), \nonumber \\ g(\mu _i)&= {} \eta _i^{(2)} = \alpha ^{(2)} + \sum _{m=1}^{M^{(2)}} \beta ^{(2)}_m x_{mi}^{(2)}+ \sum _{l=1}^{L^{(2)}} f_{l}^{(2)} (z_{li}^{(2)}), \end{aligned}$$
(4.13)

where logit denotes the link function between the linear predictor \(\eta ^{(1)}_i\) and the probability of absence \(\pi _i\), and \(g(\cdot )\) is an appropriate link for the mean of h.

An alternative to these models is given by hurdle models (Mullahy 1986; Cameron and Trivedi 1998), where data are assumed to follow a finite mixture of a degenerate distribution with all its mass at zero and a zero truncated discrete distribution. That is, unlike the zero inflated models, in hurdle models, all observed zeros come from the zero-degenerate distribution. Following the same notation of Eq. (4.12), a hurdle model can be expressed as follows:

$$\begin{aligned} p(y_i|\pi _i, \mu _i, \varvec{\psi }_1) = \pi _i \delta _0 + (1-\pi _i) h(y_i|\mu _i, \varvec{\psi }_1)I_{[y_i>0]}. \end{aligned}$$
(4.14)

As in (4.13), the hurdle model is completed when linking \(\pi _i\) and \(\mu _i\) with their corresponding linear predictors.

However, the response variable is not always a discrete variable. Semi-continuous processes like rain, plant coverage, chemical concentrations, etc., are measured in the \([0, \infty )\) interval having high proportions of zero values, and there are neither an appropriate probability distribution nor a transformation available to fit them adequately. To model processes of this type, an extension of hurdle models for continuous data is required (Aitchison 1955; Quiroz et al. 2015). Again, data are modeled as two independent sub-processes: one determines whether the response is zero, and the other determines the intensity when the response is non-zero using a continuous well known distribution like the log-Normal or the Gamma (Stefánsson 1996; Brynjarsdóttir and Stefánsson 2004; Paradinas et al. 2017b). In this case, hurdle models are defined as a finite mixture of a degenerate distribution with point mass at zero and a distribution with support on \({\mathbb {R}}^{+}\). If h is a pdf of some parametric continuous distribution with support on \({\mathbb {R}}^{+}\) (e.g. Gamma, log-Normal or log-logistic), the hurdle model for \(y_i\) (now assumed to be a continuous distribution) has the same mixture density as in (4.14). Although there exist an extensive list of zero-inflated or hurdle models dealing with correlated discrete data in many fields (Agarwal et al. 2002; Ver Hoef and Jansen 2007), this approach has not been widely used with continuous responses.

It is worth noting that all the models commented upon in this section are a mixture of two processes, and in almost all cases, they are modeled independently (Neelon et al. 2013; Balderama et al. 2016). However, generally both sub-processes are related: low intensities are linked to low probabilities of presence and vice versa. Shared component modeling (SCM) is a good tool to deal with it by combining information both from the two subprocesses (Paradinas et al. 2017b).

5 Discussion

This paper has reviewed some of the statistical challenges that can arise when the distribution of the species is modeled using geostatistical or point-referenced data. In particular, after describing in detail data and methods commonly used to model species distribution, we have focused on complex issues and we have discussed how they can be solved using Bayesian hierarchical spatio-temporal models. Specifically, in this review we have focused on the Bayesian approach and the INLA methodology (Rue et al. 2009) because they have several benefits with respect to the classic geostatistical methods. INLA makes it possible to perform complex models with a minimum computational effort while obtaining accurate estimates. Its importance in the context of SDMs can be even more appreciated with the appearance of the recent project inlabru which has been created to develop and implement innovative methods to model spatial distribution and change from ecological survey data (https://sites.google.com/inlabru3.org/inlabru). In addition, classic geostatistical methods typically overestimate their predictive accuracy by using plug-in estimations of parameters in their predictive equations. (Diggle and Ribeiro 2007). On the contrary, inference about uncertainty, based on the observations and models, is a byproduct of the model predictions when the Bayesian framework is employed.

However, some limitations can arise when the INLA approach is used. For example, INLA can not handle missing values in spatially structured covariates. This issue can be framed in the misalignment problem discussed in Sect. 4.3; this means that it could be overcome by applying a two-stage or joint modeling approach that allows prediction of the covariate values in the locations where they were not measured. As mentioned above, an alternative is the one proposed by Gómez-Rubio and Rue (2017) that, using a more general approach, deals with missing values in the covariates, based on fitting conditional latent Gaussian models where covariates are imputed using a Metropolis-Hastings algorithm.

We would like to remark that, due to space limitations, we have not fully reviewed the several complications that can derive from the sampling process. Indeed, we have only focused on the preferential sampling problem (Diggle et al. 2010), which, as previously mentioned, refers to the possibility that the sample design is stochastically dependent on the studied process. Nevertheless, other types of sampling procedures could produce different issues that should be taken into account in the statistical analysis. For example, one of the most popular methods used in ecology to estimate an animal population’s size is the capture-recapture method that involves capturing, marking and releasing an initial sample of individuals (Otis et al. 1978; McInerny and Purves 2011). Subsequently, a second sample of animal individuals is obtained independently and it is noted how many of them in that sample were marked. To model data of this type, a feasible solution could be the implementation of Bayesian hierarchical N-mixture models described in Sect. 4.5, which are currently being developed in INLA (Meehan et al. 2017).

Finally, an important point to consider is that INLA is not the only computational approach to making inference for Bayesian spatio-temporal models. In recent years, other approaches that also make it possible to achieve accurate species distribution models results, such as stan (Stan Development Team 2017; Monnahan et al. 2017), have been widely used.