Testing the type of non-separability and some classes of space-time covariance function models

Abstract

In statistical space-time modeling, the use of non-separable covariance functions is often more realistic than separable models. In the literature, various tests for separability may justify this choice. However, in case of rejection of the separability hypothesis, none of these tests include testing for the type of non-separability of space-time covariance functions. This is an important and further significant step for choosing a class of models. In this paper a method for testing positive and negative non-separability is given; moreover, an approach for testing some well known classes of space-time covariance function models has been proposed. The performance of the tests has been shown using real and simulated data.

1 Introduction

Separable covariance function models allow for computationally efficient estimation and inference, hence they have been used even in situations in which they were not physically justifiable (Genton 2007; Gneiting et al. 2007; Posa 1993; Stein 1986). Indeed, although this subclass of space-time processes has several advantages, including rapid fitting and simple extensions of many techniques developed and successfully used in time series and classical Geostatistics, separable models are not always realistic, as can be confirmed by many statistical tests for separability. On the other hand, non-separable covariance function models (Cressie and Huang 1999; De Iaco et al. 2002; Gneiting 2002; Hristopulos and Tsantili 2016; Kolovos et al. 2004; Ma 2003, 2008; Mateu et al. 2007; Porcu et al. 2006, 2007, 2008; Rodrigues and Diggle 2010; Stein 2005, among others) are more realistic since they are more flexible to handle empirical covariance functions in applications.

Some of the tests for separability are based on parametric models (Shitan and Brockwell 1995; Guo and Billard 1998; Brown et al. 2000; Genton and Koul 2008); Mitchell et al. (2005, 2006) used a likelihood ratio test for separability in the setting of multivariate repeated measures and suggested its application to space-time data sets that are rich in the time dimension. Matsuda and Yajima (2004), Scaccia and Martin (2005) and Fuentes (2006) presented a test for separability of covariances based on the spectral representation of the process. The proposed method consists essentially in studying if the coherence function of the process is constant across frequencies and can just be applied to integrable covariance functions. Li et al. (2007), Li et al. (2008a, b) and Shao and Li (2009) proposed some nonparametric tests for assessing various properties of space-time covariance functions, including separability. These are based on the asymptotic joint normality of sample space-time covariance estimators or on an asymptotic distribution of the given test statistic, whose critical values are tabulated in Lobato (2001).

However, statistical test for separability can only help to decide on the use of a separable versus a non-separable model; thus, in case of rejection of the hypothesis of separability, a further step to overcome concerns the selection of a non-separable class of covariance function models to be fitted to the space-time empirical covariance surface. For this reason, first of all it is advisable to apply a statistical test for evaluating the type of non-separability (i.e., uniformly positive, uniformly negative or pointwise non-separability). Note that a detailed analysis on the type of non-separability has only recently been considered in Rodrigues and Diggle (2010) and De Iaco and Posa (2013). After analyzing the type of non-separability and other geometric characteristics of the experimental covariance surfaces, one should select, preferably through hypothesis testing, the class of covariance function models, which is consistent with the empirical features of the covariance surface.

In this paper two original and important aspects are discussed: (a) a statistical test for the type of non-separability; (b) a statistical test for some classes of space-time covariance function models. The testing procedure described in the paper is based on a test statistic which is asymptotically normal, in the former case, and on a test statistic which is asymptotically Chi-square for the latter, thanks to the multivariate delta theorem of Mardia et al. (1979) and the results in Li et al. (2007). The novelty is related to the types of tests proposed, the way of formulating the null hypothesis and of generating the test statistics (with the corresponding contrasts used for these tests) and the practical aspects associated with their application. In particular, the tests on the classes of covariance function models are based on some mathematical characteristics of the selected classes which have been used to define the fundamental elements of the hypothesis testing (null hypothesis, contrasts and test statistic).

This paper is organized as follows. In Sect. 2, a review on testing some properties of covariance functions has been given. In Sect. 3, after introducing the notion of type of non-separability (Rodrigues and Diggle 2010; De Iaco and Posa 2013), a test statistic for assessing different forms of non-separability has been proposed. In space-time geostatistical analysis, this is a further and relevant aspect for choosing a space-time correlation model for a given data set. In Sect. 4 a technique for testing some classes of covariance functions, as well as applications to the classes of Rodrigues and Diggle models (Rodrigues and Diggle 2010), product-sum models (De Iaco et al. 2001), Gneiting models (Gneiting 2002), integrated product models (De Iaco et al. 2002; Ma 2003) and Cressie-Huang models (Cressie and Huang 1999) have also been provided. Moreover, a brief discussion on the procedure for choosing a class of space-time covariance function models has been given. Some empirical results, obtained by using the R package covatest (De Iaco et al. 2017), are presented in Sect. 5.

2 Review on testing covariance functions properties

Before introducing the new results, it is worth recalling the theoretical framework given by Li et al. (2007), where the authors provided a technique for testing some covariance functions properties, included the separability assumption. For this aim, let $\{Z({\mathbf{s}},t): {\mathbf{s}} \in {\mathbb {R}}^d, t\in {\mathbb {R}}\}$ be a real-valued space-time random field which is assumed to be strictly stationary (in the sense that the multivariate distributions are translation invariant) with $Var[Z({\mathbf{s}},t)]<\infty$ (finite variance), where ${\mathbf{s}}$ is the spatial location and t the temporal coordinate. Strict stationarity of a random function is a much stronger condition than second order stationarity, however, as any form of the stationarity hypothesis, there is no way to test whether this assumption is true. It is a model decision, not some intrinsic property of the actual distribution of the characteristics (Journel 1989; Christakos 2011). An immediate consequence of the strict stationarity of the random field Z together with the existence of its variance is that the expectation $E(Z({\mathbf{s}} ,t))$ is a constant function, which can be taken to be zero. This assumption reduces notational complexity with no loss of generality (Adler 1981, p. 24), indeed by assuming that the mean function can be adequately modelled, one can reasonably focus on the covariance structure of the residual random field Z (Li et al. 2008b).

A second consequence of the same assumptions is that the covariance function

$$\begin{aligned} C({\mathbf{h}},u)=E[Z({\mathbf{s}}+{\mathbf{h}},t+u) \cdot Z({\mathbf{s}},t)] \end{aligned}$$

(1)

depends only on the spatial and temporal lags ${\mathbf{h}}$ and u, respectively. In other terms, a strictly stationary random field with finite variance is also second order stationary (Adler 1981, p. 23–24; Brockwell and Davis 2006, p. 13). Note that a covariance function C, as in (1), is fully symmetric if $C({\mathbf {h}} ,u) = C({\mathbf {h}} ,-u)$ or if $C({\mathbf {h}} ,u) = C(-{\mathbf {h}} ,u)$. Among the class of fully symmetric covariance functions, a covariance function C or, equivalently, a space-time correlation function $\rho$ are separable (Sherman 2011), if and only if

$$\begin{aligned} {C({\mathbf {h}} ,u)} = {{C({\mathbf {0}},u) C({\mathbf {h}} ,0)}\over C({\mathbf {0}},0)}, \qquad \quad \rho ({\mathbf{h}},u)=\rho ({\mathbf{h}}, 0) \rho ({\mathbf{0}}, u). \end{aligned}$$

(2)

In Li et al. (2007), the authors provided a technique for testing some covariance properties, included the symmetry and separability. In particular, they proposed a test statistic based on the asymptotic joint normality of sample space-time covariance estimators, as specified hereafter. Different sample space-time covariance estimators can be considered depending on whether the observations are regularly or irregularly spaced and whether one part or the whole domain of interest is fixed or increasing (Li et al. 2008a). In the following, the observations are supposed to be taken at the same spatial locations over time, which is very common for environmental applications (Haslett and Raftery 1989; Gneiting 2002; de Luna and Genton 2005; Stein 2005), thus the proposed tests are based on this particular setting.

Given a strictly stationary space-time random field Z with finite variance, let $\Lambda$ be a set of space-time lags with cardinality equal to m and let ${\mathbf {G}} =\{C({\mathbf {h}},u): ({\mathbf {h}},u) \in \Lambda \}$ be a vector of covariances at the specified lags in Λ.

Let $\widehat{C}_n({\mathbf {h}},u)$, with $({\mathbf {h}},u)\in \Lambda$, denote the covariance estimators based on random variables in the sequence of the index sets $D_n= S \times T_n$, with a fixed space $S\subset {\mathbb {R}}^d$ (closed under addition and subtraction) and regularly spaced times $T_n = \{1, \ldots , n\}$, and let $\widehat{{\mathbf {G}}}_n = \left\{ \widehat{C}_n({\mathbf {h}}, u) : ({\mathbf {h}}, u) \in \Lambda \right\}$ denote the estimator of ${\mathbf {G}}$ computed over $D_n$. If it is assumed that

• the asymptotic variance ${\mathbf {\Sigma }}$ of the covariance estimator exists, i.e.

  $$\begin{aligned} \sum _{t \in \mathbb {Z}}|cov[Z({\mathbf {0}},0)Z({\mathbf {h}}_1,u_1), Z({\mathbf {s}},t)Z({\mathbf {s}}+{\mathbf {h}}_2,t+u_2)|<\infty , \end{aligned}$$

  (3)

  $\forall {\mathbf {h}}_1, {\mathbf {h}}_2\in S, {\mathbf {s}}\in S({\mathbf {h}}_2), \forall u_1,u_2,$ with $S({\mathbf {h}}_2)=\{{\mathbf {s}}: {\mathbf {s}} \in S, {\mathbf {s}}+{\mathbf {h}}_2 \in S \}$, so that ${\mathbf {\Sigma }}= \lim _ {n\rightarrow \infty } |T_n|cov(\widehat{{\mathbf {G}}}_n,\widehat{{\mathbf {G}}}_n)$ exists. Note that a matrix ${\mathbf M} _n=[m_{ij}^n]$ is convergent to a matrix ${\mathbf M} =[m_{ij}]$ if and only if $m_{ij}^n\rightarrow m_{ij}$, for all i, j, as $n\rightarrow \infty$;

• given the mixing coefficient (Ibragimov and Linnik 1971, p. 306)

  $$\begin{aligned} \alpha (u)=\sup _{A,B} \{|P(A\cup B)-P(A)P(B)|,\,A\in {{\mathfrak {I}}_{-\infty }^{0},}\,B\in \mathfrak {I}_u^{\infty }\}, \end{aligned}$$

  where ${{\mathfrak {I}}_{-\infty }^{0}}$ is the $\sigma -$algebra generated by the past time process until $t = 0$ and $\mathfrak {I}_u^{\infty }$ is the $\sigma -$algebra generated by the future time process from $t = u$, the mixing coefficient $\alpha (u)$ satisfies the following strong mixing condition

  $$\begin{aligned} \alpha (u) = O(u^{-\epsilon }) \quad \hbox {for some} \quad \epsilon > 0, \end{aligned}$$

  (4)

• the moments of $\widehat{C}_n({\mathbf {h}},u)$ are such that

  $$\begin{aligned} \sup _n E\{|\sqrt{|T_n|} [\widehat{C}_n({\mathbf {h}},u)-C({\mathbf {h}},u)]|^{2+\delta }\}\le C_{\delta } \end{aligned}$$

  (5)

  for some $\delta >0, C_{\delta } <\infty$,

then

$$\begin{aligned} \sqrt{|T_n|}[\widehat{{\mathbf {G}}}_n-{{\mathbf {G}}}]{\mathop {\rightarrow }\limits ^{d}} N_m({\mathbf {0}},{\mathbf {\Sigma }}), \end{aligned}$$

(6)

as $n\rightarrow \infty$, where m is the cardinality of $\Lambda$ and ${\mathbf {G}}$. If ${\mathbf {f}} = (f_1, \ldots , f_r)^{\top }$ is a vector of real-valued functions that are differentiable at ${\mathbf {G}}$ (Harville 2001, p. 295), using the asymptotic joint normality of $\widehat{{\mathbf {G}}}_n$ and the multivariate delta theorem (Mardia et al. 1979), the following asymptotic distribution is derived

$$\begin{aligned} \sqrt{|T_n|}[{\mathbf {f}}(\widehat{{\mathbf {G}}}_n)-{\mathbf {f}}({{\mathbf {G}}})]{\mathop {\rightarrow }\limits ^{d}} N_r({\mathbf {0}},\mathbf {B}^{\top } {\mathbf {\Sigma }}\mathbf {B}), \end{aligned}$$

(7)

where r is the cardinality of ${\mathbf {f}}$ and the generic element of the matrix $\mathbf {B}$ is ${B}_{ij} =\displaystyle {\partial f_j\over \partial G_i}, i=1,\ldots ,m, j=1,\ldots ,r$, with $f_j$ and $G_i$ the j-th component of ${\mathbf {f}}$ and the i-th component of ${\mathbf {G}}$, respectively. Note that there are no assumptions on the marginal or the joint distribution of observations other than mild moment and mixing conditions on the random field (Li et al. 2008a).

As specified in Li et al. (2007), the covariance estimator at the vector lag $({\mathbf {h}} ,u)$, for the above mentioned zero-mean random field, is

$$\begin{aligned} \widehat{C}_n({\mathbf {h}} ,u)= {1\over |S({\mathbf {h}} )||T_n|}\sum _{{\mathbf{s}} \in S({\mathbf {h}} )}{\sum _{t=1}^{n-u} [Z({\mathbf{s}} +{\mathbf {h}} , t + u) Z({\mathbf{s}} ,t)],} \end{aligned}$$

(8)

where $|S({\mathbf {h}} )|$ is the cardinality of $S({\mathbf {h}} )=\left\{ {\mathbf{s}} :{\mathbf{s}} +{\mathbf {h}} '\in S, {\mathbf{s}} \in S,\hbox { with } ||{\mathbf {h}} -{\mathbf {h}} '||< \delta _s \right\} ,$ and $\delta _s$ the spatial tolerance. It is worth to underline that, in the literature, although some of the available covariance estimators differ in the denominator, they can be used all equally in case of long time series or large number of spatial locations. Moreover, note that the estimator in (8) is the analog of the simple empirical variance estimator which is characterized by wide confidence intervals even for random sampling from a Gaussian distribution, unless the sample size is quite large. Regarding the number of pairs of data locations in space-time, the observations are taken in $D_n = S \times T_n$, where S is supposed to be a fixed space in the sense that finitely many observations are located within this space, and $T_n = \{1, \ldots , n\}$; in particular the structure of the space-time observations is the one described in Sherman (1996) and in Li et al. (2007). On the basis of this structure of data locations (where the set of time points is exactly the same for each spatial location and the time points are integers), the above covariance estimator uses a non-constant increment tolerance for time (as contrasted with the spatial tolerance). This assumption is consistent with sample space-time data available in many applications, as for example in environmental monitoring. A comparison of infill and increasing-domain asymptotics and the consequences for maximum likelihood estimators of covariance parameters can be found in Zhang and Zimmerman (2005).

Note that the above results in (6) and (7) regard the asymptotic distribution of $\widehat{{\mathbf {G}}}_n$, which are important in the literature for several reasons, such as assessing the covariance structure of a random field, or testing some properties of space-time covariance functions (Li et al. 2007).

The general form of hypotheses applied to check full symmetry and separability of a space-time covariance function is formulated as follows:

$$\begin{aligned} H_0: {\mathbf {A}}{\mathbf {f}}({\mathbf {G}}) = {\mathbf {0}}, \end{aligned}$$

(9)

where ${\mathbf {A}}$ is a contrast matrix of row rank q. Note that, in case of symmetry, ${\mathbf {f}}({\mathbf {G}}) ={\mathbf {G}},$ thus the null hypothesis is usually written as $H_0: {\mathbf {A}}{\mathbf {G}} = {\mathbf {0}}$.

Consequently, the proposed test statistics for checking symmetry and separability are respectively

$$\begin{aligned} TS_1= & {} \left| T_n\right| \left[ {\mathbf {A}} \widehat{{\mathbf {G}}}_n\right] ^{\top } ({\mathbf {A}} {\mathbf {\Sigma }} {\mathbf {A}}^{\top })^{-1}\left[ {\mathbf {A}} \widehat{{\mathbf {G}}}_n\right] \end{aligned}$$

(10)

$$\begin{aligned} TS_2= & {} \left| T_n\right| \left[ {\mathbf {A}} {\mathbf {f}}(\widehat{{\mathbf {G}}}_n)\right] ^{\top }({\mathbf {A}} \mathbf {B}^{\top } {\mathbf {\Sigma }} \mathbf {B} {\mathbf {A}}^{\top })^{-1}\left[ {\mathbf {A}} {\mathbf {f}}(\widehat{{\mathbf {G}}}_n) \right] \end{aligned}$$

(11)

and, under $H_0$, they converge in distribution to a Chi-square with q degrees of freedom.

For the sake of simplicity it is assumed in the following that the expectation of Z is known and equal to zero; however if this assumption is removed, it is enough to denote with $\widehat{C}_n^*({\mathbf {h}},u)$ and $\widehat{{\mathbf {G}}}_n^*$ the mean-corrected estimators of $C({\mathbf {h}},u)$ and ${\mathbf {G}}$, since ${\mathbf {G}}_n^*$ and ${\mathbf {G}}_n$ have the same asymptotic properties (see Lemma A.6 in Li et al. 2008a and Sherman (2011, p. 135)). Note that, even the data used in the case studies are consistent with this assumption since we have worked with $PM_{10}$ residuals and zero-mean simulated data.

If the model is non-separable then the type of non-separability should be determined.

3 Testing for positive and negative non-separability

As pointed out in the introduction, the first step in choosing a class of space-time covariance function models is to assess whether a separable or a non-separable model might be used for describing the correlation structure of a given space-time data set. If the second option is chosen, it is important to investigate the type of non-separability. At last, a test for the selected class of models can be applied. The first two steps of the above described procedure will be treated in this Section, while the last step will be discussed in the next Section.

3.1 Non-separability indexes

Rodrigues and Diggle (2010) proposed simple definitions of pointwise positive and negative non-separability, without pointing out that a covariance function model usually depends on a vector of parameters ${\varvec{\Theta }}$. Hence, a generalization of the above pointwise definition of non-separability is given below.

Definition 1

Given a covariance function model $C({\mathbf{h}},u;{\varvec{\Theta }})$ and the corresponding space-time correlation function $\rho ({\mathbf{h}},u;{\varvec{\Theta }})$, where ${\varvec{\Theta }}$ is a vector of parameters, let

$$\begin{aligned} r({\mathbf{h}},u;{\varvec{\Theta }})={\rho ({\mathbf{h}},u;{\varvec{\Theta }})\over {\rho ({\mathbf{h}},0;{\varvec{\Theta }})\rho ({\mathbf{0}},u;{\varvec{\Theta }})}}, \end{aligned}$$

(12)

where $\rho ({\mathbf{h}},u;{\varvec{\Theta }})>0, \rho ({\mathbf{h}},0;{\varvec{\Theta }})>0$ and $\rho ({\mathbf{0}},u;{\varvec{\Theta }})>0$. Thus, if $r({\mathbf{h}},u;{\varvec{\Theta }})> 1,$ for some $({\mathbf{h}}, u;{\varvec{\Theta }})$, the covariance function model is pointwise positive non-separable at $({\mathbf{h}}, u;{\varvec{\Theta }});$ alternatively, it is pointwise negative non-separable at $({\mathbf{h}}, u;{\varvec{\Theta }}),$ if $r({\mathbf{h}},u;{\varvec{\Theta }})< 1,$ for some $({\mathbf{h}}, u;{\varvec{\Theta }}).$ Moreover, the covariance function model C is uniformly positive (negative) non-separable, if $r({\mathbf{h}},u;{\varvec{\Theta }})> 1$ ($r({\mathbf{h}},u; {\varvec{\Theta }})< 1$), for any spatio-temporal lag $({\mathbf{h}}, u)$ and any value of the parameters specified in ${\varvec{\Theta }}$.

An alternative non-separability index can also be defined in terms of the difference $d^{\prime }({\mathbf{h}},u;{\varvec{\Theta }})$ between ${\rho ({\mathbf{h}},u;{\varvec{\Theta }})}$ and the product ${\rho ({\mathbf{h}},0;{\varvec{\Theta }})\rho ({\mathbf{0}},u;{\varvec{\Theta }})}$, that is

$$\begin{aligned} d^{\prime }({\mathbf{h}},u;{\varvec{\Theta }})= {\rho ({\mathbf{h}},u;{\varvec{\Theta }})-{\rho ({\mathbf{h}},0;{\varvec{\Theta }})\rho ({\mathbf{0}},u;{\varvec{\Theta }})}}, \end{aligned}$$

(13)

or in terms of the following difference

$$\begin{aligned} d({\mathbf {h}} , u; {\varvec{\Theta }}) = C({\mathbf {h}} , u; {\varvec{\Theta }})C({\mathbf {0}}, 0; {\varvec{\Theta }}) - C({\mathbf {h}} , 0; {\varvec{\Theta }})C({\mathbf {0}}, u; {\varvec{\Theta }}). \end{aligned}$$

(14)

The sign of (13) and (14) will give information about the type of non-separability. Moreover, note that the difference in (13) is zero if and only if the difference in (14) is zero, but the two differences are not equal.

Then, a covariance function which is uniformly positive (negative) non-separable, is also pointwise positively (negatively) non-separable, but the converse is not true. Thus, the index of non-separability depends on the specific lag and on the model parameters. Concerning these aspects, a detailed analysis and some examples were provided in De Iaco and Posa (2013).

Some classes of models for covariance functions can be classified according to the type of non-separability, as summarized below:

• uniformly non-separable models: the Gneiting class of models (Gneiting 2002), as well as the class of space-time covariance functions generated by positive power mixtures (Ma 2002), are uniformly positive non-separable, otherwise the product-sum class (De Iaco et al. 2001) is uniformly negative non-separable;

• models with different non-separability indexes: wide classes of non-separable stationary covariance functions, which can be uniformly positive or negative non-separable, or pointwise positive or negative non-separable, for some choices of $({\mathbf{h}},u;{\varvec{\Theta }})$, belong to this family. In particular, the classes generated by a linear combination of product-sum models, integrated product-sum models, one of the examples given by Cressie and Huang (1999), the convolution-based models proposed by Rodrigues and Diggle (2010), the more general positive power mixture model proposed by Ma (2002), and the metric model (Dimitrakopoulos and Luo 1994) could be either uniformly positive and negative non-separable, or pointwise non-separable.

Although in the literature the above mentioned classes of models are known to be non-separable, the class of separable models can be often obtained as a special case. For example, the Rodrigues and Diggle model, the product-sum model, the Gneiting covariance function model as well as the metric model are separable for specific choices of the functions involved and their parameters.

In the following, the dependence of the covariance function model C from the vector of parameters ${\varvec{\Theta }}$ will be omitted in order to simplify the notation.

3.2 Statistical test for the type of non-separability

The tests proposed in the literature are commonly applied to check symmetry and separability and, in general, the corresponding test statistics are used to decide whether or not the null hypothesis is rejected (in favor of the alternative). Moreover, if separability is rejected, then the type of non-separability (i.e. uniformly positive, uniformly negative or pointwise positive or negative) has to be analyzed. Taking into account the results in Mardia et al. (1979) and Li et al. (2007), a statistical test for assessing the type of non-separability of a covariance function is provided below.

Let Z be a strictly stationary space-time random field with finite variance.

Let $\Lambda = \left\{ ({\mathbf {0}},0), ({\mathbf {h}}_i,u_i), ({\mathbf {h}}_i, 0), ({\mathbf {0}},u_i), i=1,\ldots , l\right\}$ be a set of space-time lags and $|\Lambda |=m=3l+1$ its cardinality, with $l\in \mathbb {N}, l\ge 1$.

Given the vector ${\mathbf {G}}$ of the covariances of Z at the lags $({\mathbf {h}},u)\in \Lambda$, the corresponding vector ${\widehat{\mathbf G}}_{n}$ of the covariance estimators ($\widehat{C}_{n}({\mathbf {h}},u)$, with $({\mathbf {h}},u)\in \Lambda$), evaluated over the set $D_{n} = S \times T_n$, and the vector of functions

$$\begin{aligned} {\mathbf {f}}({\mathbf {G}})=\left[ {C({\mathbf {h}}_1,u_1)\over C({\mathbf {h}}_1,0)} \quad {C({\mathbf {0}},u_1)\over C({\mathbf {0}},0)} \ldots {C({\mathbf {h}}_i,u_i)\over C({\mathbf {h}}_i,0)} \quad {C({\mathbf {0}},u_i)\over C({\mathbf {0}},0)}\ldots {C({\mathbf {h}}_l,u_l)\over C({\mathbf {h}}_l,0)} \quad {C({\mathbf {0}},u_l)\over C({\mathbf {0}},0)}\right] ^{\top }, \end{aligned}$$

(15)

with 2l elements, let ${\mathbf {A}}$ be the general form of the contrast matrix with l rows and 2l columns

$$\begin{aligned} {\mathbf {A}}= \left[ \begin{array}{ccccccc} 1 &{}\quad -1 &{}\quad 0&{}\quad 0 &{}\quad \ldots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad -1 &{}\quad \ldots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \ldots &{}\quad 1 &{}\quad -1\\ \end{array} \right] . \end{aligned}$$

(16)

Under the assumptions (3), (4) and (5) on the strictly stationary random field, the test statistic for the type of non-separability is based on the following function

$$\begin{aligned} \sqrt{|T_n|}[\mathbf {1}_l^{\top }{\mathbf {A}}{\mathbf {f}}(\widehat{{\mathbf {G}}}_n)-\mathbf {1}_l^{\top }{\mathbf {A}}{\mathbf {f}}({{\mathbf {G}}})]{\mathop {\rightarrow }\limits ^{d}} N({0},\mathbf {1}_l^{\top }{\mathbf {A}}\mathbf {B}^{\top } {\mathbf {\Sigma }}\mathbf {B}{\mathbf {A}}^{\top }\mathbf {1}_l), \end{aligned}$$

(17)

and the hypotheses on the type of non-separability are defined as follows:

$$\begin{aligned} H^{\tiny (-)}_0: \mathbf {1}_l^{\top }{\mathbf {A}}{\mathbf {f}}({\mathbf {G}})\le 0, \qquad \hbox {against} \qquad H^{\tiny (+)}_1: \mathbf {1}_l^{\top }{\mathbf {A}}{\mathbf {f}}({\mathbf {G}})>0, \end{aligned}$$

(18)

or alternatively

$$\begin{aligned} H^{{\tiny (+)}}_0: \mathbf {1}_l^{\top }{\mathbf {A}}{\mathbf {f}}({\mathbf {G}})\ge 0, \qquad \hbox {against} \qquad H^{{\tiny (-)}}_1: \mathbf {1}_l^{\top }{\mathbf {A}}{\mathbf {f}}({\mathbf {G}})<0. \end{aligned}$$

(19)

This statistical test is based on the asymptotic distribution in (17) which is a consequence of results in (6) and (7). In particular, the key point is based on the asymptotic normality of the statistic $\sqrt{|T_n|} \bigl[{\widehat{C}_{n}({\mathbf {h}},u)- C({\mathbf {h}},u)}\bigr]$, which is proved by applying a blocking technique (Li et al. 2007).

If the test statistic in (17) is standardized, it converges in distribution, under the null hypothesis, to a standard normal distribution. In the following, this statistic will be denoted as $TS_3$.

At the significance level $\alpha$, if $H^{{\tiny (-)}}_0$ is set against $H^{{\tiny (+)}}_1$, as in (18), the test is conducted on the right tail $]z_\alpha , +\infty [$ of the standard normal distribution, or alternatively if $H^{{\tiny (+)}}_0$ is set against $H^{{\tiny (-)}}_1$, as in (19), the test is conducted on the left tail $]-\infty , -z_\alpha [$ of the standard normal distribution.

Failing to reject $H^{{\tiny (-)}}_0$ formulated against $H^{{\tiny (+)}}_1$, given in (18), means that there is no statistical evidence that the space-time covariance function is positive non-separable for the specified lags; on the other hand, failing to reject $H^{{\tiny (+)}}_0$ formulated against $H^{{\tiny (-)}}_1$, given in (19), means that there is no statistical evidence that the space-time covariance function is negative non-separable for the specified lags.

Remarks

• The type of pointwise non-separability can be tested for $l=1$.

• The test statistic is always computed for lags characterized by the same type of non-separability, in such a way that compensations among terms of the test statistic with different signs are avoided.

• A simple way to fix the direction of the one-tailed test on the type of non-separability and the set of lags to be tested is to analyze as a first step the box-plots of the sample non-separability ratios (i.e. from definition (12), the ratio computed between the empirical space-time correlation and the product of the corresponding sample spatial and temporal marginals), classified by spatial and temporal lags. Indeed, it is advisable to use a right tailed test for a given space-time lag, if the box-plots of the sample non-separability ratios support the assumption of negative non-separability (sample ratios less than one in average); analogously, for the left tailed test. However, in order to test the type of non-separability, it is reasonable to choose space-time lags with sample non-separability ratios much less/greater than one. The basic steps of the testing procedure are given in “Appendix 1”.

4 Testing some classes of space-time models

In this Section, a non-parametric test procedure for the choice of some peculiar classes of space-time covariance function models, well-known in the literature, has been provided. In particular, the classes of models proposed by Rodrigues and Diggle (2010), De Iaco et al. (2001), Gneiting (2002), Cressie and Huang (1999), De Iaco et al. (2002), have been considered and a generalization for a given construction of space-time covariance function models has been also furnished. The original and interesting aspects of the following tests are based on the analysis of some mathematical features of the selected classes of models, which have been used to specialize the null hypotheses in the various cases. The idea is to appropriately define the set of lags $\Lambda$, consequently the covariances involved in the vector ${\mathbf {G}}$, the vector of functions ${\mathbf {f}}$ and the corresponding contrast matrix ${\mathbf {A}}$, such that the null hypothesis ${\mathbf {A}}{\mathbf {f}}({\mathbf {G}})={\mathbf {0}}$ is true under the selected class of models. In the following, some properties for some classes of models are detected by fixing a spatial lag and then looking at the behavior of the covariance model (or function of it) for different temporal lags, or vice versa by fixing a temporal lag and then looking at the behavior of the same function for different spatial lags.

4.1 Testing the Rodrigues and Diggle model

The class of models proposed by Rodrigues and Diggle (2010) is given below

$$\begin{aligned} C({\mathbf {h}}, u)={\sigma ^2\over 2}\left[ \rho _{s,1}({\mathbf {h}})\rho _{t,1}(u)+ \rho _{s,2}({\mathbf {h}})\rho _{t,2}(u)\right], \end{aligned}$$

(20)

where $\rho _{s,1}({\mathbf {h}}), \rho _{s,2}({\mathbf {h}}), \rho _{t,1}(u), \rho _{t,2}(u)$ are non-negative and integrable spatial and temporal correlation functions.

As stated in the following proposition, this class of covariance function models satisfies some specific properties.

Proposition 4.1

Let $C$ be a finite covariance function of a strictly stationary space-time random field. If the class of covariance function models in (20) is considered, then for any set of spatial lags ${\mathbf {h}}_i$ and temporal lags $u_i$, $i=1,2$, the differences $d({\mathbf {h}}_i,u_j)$, $i,j=1,2$, defined in (14), are such that

$$\begin{aligned} {d({\mathbf {h}}_1,u_1) }= {d({\mathbf {h}}_1,u_2) {d({\mathbf {h}}_2, u_1) }\over {d({\mathbf {h}}_2, u_2) }}. \end{aligned}$$

(21)

The proof is given in “Appendix 2”.

The properties of this class of covariance function models can be used to formulate the statistical hypotheses on the same class, as described below.

Given a strictly stationary space-time random field Z with finite variance, suppose that

• $C({\mathbf {h}},u)$ is the non-separable covariance function of Z;

• $\Lambda = \{({\mathbf {0}},0),({\mathbf {h}}_i,u_j), ({\mathbf {h}}_i,0), ({\mathbf {0}}, u_j); \quad i=1,\ldots ,l_s, j=1,\ldots , l_t, l_s\ge 2,l_t>2\},$ is a set of space-time lags and $|\Lambda |=m=(l_s+1)(l_t+1)+1$ its cardinality;

• ${\mathbf {G}}$ is the vector of the non-separable covariances at the lags $({\mathbf {h}},u) \in \Lambda$, and $\widehat{{\mathbf {G}}}_n$ be the vector of the corresponding covariance estimators ($\widehat{C}_n({\mathbf {h}},u)$, with $({\mathbf {h}},u)\in \Lambda$) defined over the domain $D_{n} = S \times T_n$;

• ${\mathbf {f}}^{{\tiny RD}}$ is the vector of functions, whose generic couple of consecutive elements (used for the contrast) for a pair of spatial lags ${\mathbf {h}}_{i_1}, {\mathbf {h}}_{i_2}$ and a pair of temporal lags $u_{j_1},u_{j_2}$, $i_1,i_2\in \{1,\ldots ,l_s\}$, $j_1,j_2\in \{1,\ldots ,l_t\}$, ${i_1}\ne {i_2}$, ${j_1}\ne {j_2}$, is the following

  $$\begin{aligned} {{C({\mathbf {h}}_{i_1}, u_{j_1})C({\mathbf {0}}, 0) - C({\mathbf {h}}_{i_1}, 0)C({\mathbf {0}}, u_{j_1})} \over {C({\mathbf {h}}_{i_2}, u_{j_1})C({\mathbf {0}}, 0) - C({\mathbf {h}}_{i_2}, 0)C({\mathbf {0}}, u_{j_1})}} \qquad {{C({\mathbf {h}}_{i_1}, u_{j_2})C({\mathbf {0}}, 0) - C({\mathbf {h}}_{i_1}, 0)C({\mathbf {0}}, u_{j_2})} \over {C({\mathbf {h}}_{i_2}, u_{j_2})C({\mathbf {0}}, 0) - C({\mathbf {h}}_{i_2}, 0)C({\mathbf {0}}, u_{j_2})}}. \biggr . \end{aligned}$$

  (22)

Then, given the general form of the contrast matrix ${\mathbf {A}}$, as in (16), with at most $\displaystyle \left( {\begin{array}{c}l_s\\ 2\end{array}}\right) \displaystyle \left( {\begin{array}{c}l_t\\ 2\end{array}}\right)$ rows and $2\displaystyle \left( {\begin{array}{c}l_s\\ 2\end{array}}\right) \displaystyle \left( {\begin{array}{c}l_t\\ 2\end{array}}\right)$ columns, the null hypothesis for the class of models in (20) is written as $H_0: {\mathbf {A}}{\mathbf {f}}^{{\tiny RD}}({\mathbf {G}}) = {\mathbf {0}}$, against   the   alternative   hypothesis   $H_1: {\mathbf {A}}{\mathbf {f}}^{{\tiny RD}}({\mathbf {G}}) \ne {\mathbf {0}}$.

Under the asymptotic probability distributions in (6) and (7), the test statistic (11), which can be used in this case to assess the above hypotheses, converges in distribution to a Chi-square with degrees of freedom equal to the row rank of the contrast matrix ${\mathbf {A}}$. In particular, the test statistic (11) can be used to decide whether to reject the null hypothesis (in favor of the alternative hypothesis) or non-reject the null hypothesis in case of a lack of evidence against it.

For example, given the following set of space-time lags:

$$\begin{aligned} \begin{aligned} \Lambda = \{({\mathbf {0}},0),({\mathbf {h}}_1,u_1), ({\mathbf {h}}_2, u_1), ({\mathbf {h}}_1,u_2), ({\mathbf {h}}_2, u_2), ({\mathbf {h}}_1,u_3),({\mathbf {h}}_2, u_3), ({\mathbf {h}}_1,0), ({\mathbf {h}}_2,0), ({\mathbf {0}},u_1), ({\mathbf {0}},u_2), ({\mathbf {0}},u_3)\}, \end{aligned} \end{aligned}$$

(23)

and the corresponding ${\mathbf {G}}$, let us define

$$\begin{aligned}&{\mathbf {f}}^{{\tiny RD}}({\mathbf {G}})\nonumber \\&\quad =\left[ {{C({\mathbf {h}}_1, u_1)C({\mathbf {0}}, 0) - C({\mathbf {h}}_1, 0)C({\mathbf {0}}, u_1)}\over {C({\mathbf {h}}_2, u_1)C({\mathbf {0}}, 0) - C({\mathbf {h}}_2, 0)C({\mathbf {0}}, u_1)}} \qquad { {C({\mathbf {h}}_1, u_2)C({\mathbf {0}}, 0) - C({\mathbf {h}}_1, 0)C({\mathbf {0}}, u_2)}\over {C({\mathbf {h}}_2, u_2)C({\mathbf {0}}, 0) - C({\mathbf {h}}_2, 0)C({\mathbf {0}}, u_2)}}\right. \nonumber \\&\qquad\quad {{C({\mathbf {h}}_1, u_1)C({\mathbf {0}}, 0) - C({\mathbf {h}}_1, 0)C({\mathbf {0}}, u_1)}\over {C({\mathbf {h}}_2, u_1)C({\mathbf {0}}, 0) - C({\mathbf {h}}_2, 0)C({\mathbf {0}}, u_1)}} \qquad { {C({\mathbf {h}}_1, u_3)C({\mathbf {0}}, 0) - C({\mathbf {h}}_1, 0)C({\mathbf {0}}, u_3)}\over {C({\mathbf {h}}_2, u_3)C({\mathbf {0}}, 0) - C({\mathbf {h}}_2, 0)C({\mathbf {0}}, u_3)}}\nonumber \\&\left. \qquad\quad {{C({\mathbf {h}}_1, u_2)C({\mathbf {0}}, 0) - C({\mathbf {h}}_1, 0)C({\mathbf {0}}, u_2)}\over {C({\mathbf {h}}_2, u_2)C({\mathbf {0}}, 0) - C({\mathbf {h}}_2, 0)C({\mathbf {0}}, u_2)}} \qquad { {C({\mathbf {h}}_1, u_3)C({\mathbf {0}}, 0) - C({\mathbf {h}}_1, 0)C({\mathbf {0}}, u_3)}\over {C({\mathbf {h}}_2, u_3)C({\mathbf {0}}, 0) - C({\mathbf {h}}_2, 0)C({\mathbf {0}}, u_3)}} \right] ^{\top }. \end{aligned}$$

(24)

Note that the vector ${\mathbf {f}}^{{\tiny RD}}$ includes all the couples associated to the possible pairs of spatial lags and temporal lags specified in the set $\Lambda$.

$$\begin{aligned} {\mathbf {A}}= \left[ \begin{array}{cccccc} 1 &{} -1 &{} 0 &{} 0 &{}0&{}0 \\ 0 &{} 0 &{} 1 &{} -1 &{}0&{}0\\ 0 &{} 0 &{} 0 &{} 0 &{}1&{}-1\\ \end{array} \right] . \end{aligned}$$

(25)

Then ${\mathbf {A}}{\mathbf {f}}^{{\tiny RD}}({\mathbf {G}})={\mathbf {0}}$ is the null hypothesis for the Rodrigues and Diggle model defined in (20), since for $i,j=1,2$

$$\begin{aligned} C({\mathbf {h}}_i, u_j)C({\mathbf {0}}, 0) - C({\mathbf {h}}_i, 0)C({\mathbf {0}}, u_j)={\sigma ^4\over 4}[\rho _{s,1}({\mathbf{h}}_i)-\rho _{s,2}({\mathbf{h}}_i) ][\rho _{t,1}(u_j)-\rho _{t,2}(u_j)]. \end{aligned}$$

(26)

The test statistic (11), which converges in distribution to a Chi-square with $q=3$ degrees of freedom, can be used to decide whether to reject the null hypothesis (in favor of the alternative $H_1: \,{\mathbf {A}}{\mathbf {f}}^{{\tiny RD}}({\mathbf {G}})\ne {\mathbf {0}}$) or non-reject the null hypothesis in case of no significant empirical evidence against it.

4.2 Testing the product-sum model

The product-sum model is defined as

$$\begin{aligned} C({\mathbf{h}},u)=k_1C_s({\mathbf{h}})C_t(u)+k_2C_s({\mathbf{h}}) +k_3C_t(u), \quad k_1>0,k_2\ge 0, k_3\ge 0, \end{aligned}$$

(27)

where $C_s$ is a spatial covariance function in ${\mathbb {R}}^d$ and $C_t$ is a temporal covariance function in ${\mathbb {R}}$; analogously it can be expressed in terms of the generalized product-sum variogram model as

$$\begin{aligned} \gamma ({\mathbf {h}},u)=\gamma ({\mathbf {h}},0) +\gamma ({\mathbf {0}},u)-k \gamma ({\mathbf {h}},0) \gamma ({\mathbf {0}},u), \end{aligned}$$

(28)

where $\gamma ({\mathbf {h}},0)$ and $\gamma ({{\mathbf {0}}},u)$ are valid spatial and temporal bounded variogram functions, and k is the only model parameter. See De Iaco et al. (2001) for details on the admissibility condition. This model has been widely used in the literature (Cichota et al. 2006; Gething et al. 2007; Jost et al. 2005; Lee et al. 2012; Liang and Kumar 2013; Pebesma 2012; Zeng et al. 2014); moreover, model (27) is strictly positive definite if and only if the spatial and temporal covariance functions are strictly positive definite (De Iaco et al. 2011; De Iaco and Posa 2017). As shown in the following proposition, this class of models satisfies some specific properties.

Proposition 4.2

Let $C$ be a finite continuous covariance function model of a strictly stationary space-time random field. For any set of spatial lags ${\mathbf {h}}_i$, $i=1,2,3$, and temporal lag u, the increments $C({\mathbf {h}}_i,u)-C({\mathbf {h}}_j, u)$ and $C({\mathbf {h}}_i,0)- C({\mathbf {h}}_j,0)$, $i,j=1,2,3,$ are such

$$\begin{aligned} {C({\mathbf {h}}_3,u)-C({\mathbf {h}}_2,u) \over {C({\mathbf {h}}_3,0) - C({\mathbf {h}}_2,0)}}={C({\mathbf {h}}_2,u)-C({\mathbf {h}}_1,u) \over {C({\mathbf {h}}_2,0) - C({\mathbf {h}}_1,0)}},\end{aligned}$$

(29)

$with \;\,C({\mathbf {h}}_i,0)\ne C({\mathbf {h}}_j,0)$, and ${\mathbf {h}}_i\ne {\mathbf {h}}_j$, if and only if the class of covariance function models in (27), is considered.

A similar condition is satisfied for any spatial lag ${\mathbf {h}}$ and any set of temporal lags $u_1$, $u_2$, and $u_3$:

$$\begin{aligned} {C({\mathbf {h}},u_3)-C({\mathbf {h}},u_2) \over {C({\mathbf {0}}, u_3) - C({\mathbf {0}},u_2)}}- {C({\mathbf {h}},u_2)-C({\mathbf {h}},u_1) \over {C({\mathbf {0}},u_2) - C({\mathbf {0}},u_1)}}=0, \end{aligned}$$

(30)

with $C({\mathbf {0}},u_i)\ne C({\mathbf {0}},u_j)$, and $u_i\ne u_j$.

The proof is given in “Appendix 3”.

In the following, the statistical test on this class of covariance function models will be based on the specific properties of the same class.

Given a strictly stationary space-time random field Z with finite variance, suppose that

• $\Lambda = \{({\mathbf {h}}_i,u_j), ({\mathbf {h}}_i,0), ({\mathbf {0}}, u_j);\quad i=1,\ldots ,l_s,\quad j=1,\ldots , l_t\},$ is the set of space-time lags, where at least $l_s$ or $l_t$ must be greater than 2, and $m=(l_s+1)(l_t+1)$ its cardinality;

• ${\mathbf {G}}$ is the vector of a specific covariance function $C({\mathbf {h}},u)$, evaluated at a finite number of lags $({\mathbf {h}},u) \in \Lambda$, with $C({\mathbf {h}}_i,0)\ne C({\mathbf {h}}_j,0)$, if ${\mathbf {h}}_i\ne {\mathbf {h}}_j$, and $C({\mathbf {0}},u_i)\ne C({\mathbf {0}},u_j)$, if $u_i\ne u_j$;

• $\widehat{{\mathbf {G}}}_n$ is the vector of the corresponding covariance estimators ($\widehat{C}_n({\mathbf {h}},u)$, with $({\mathbf {h}},u)\in \Lambda$) computed over $D_{n} = S \times T_n$;

• ${\mathbf {f}}^{{\tiny PS}}$ is the vector of functions whose generic couple of consecutive elements (used for the contrasts) is defined for a) a triplet of spatial lags ${\mathbf {h}}_{i_1}, {\mathbf {h}}_{i_2}, {\mathbf {h}}_{i_3}$ and a temporal lag $u_{j_1}$, $i_1,i_2,i_3\in \{1,\ldots ,l_s\}$, $j_1\in \{1,\ldots ,l_t\},$ ${i_1}\ne {i_2}\ne {i_3}$, as follows

  $$\begin{aligned} {C({\mathbf {h}}_{i_2},u_{j_1})-C({\mathbf {h}}_{i_1},u_{j_1})\over C({\mathbf {h}}_{i_2},0)-C({\mathbf {h}}_{i_1},0)} \quad {C({\mathbf {h}}_{i_3},u_{j_1})-C({\mathbf {h}}_{i_2},u_{j_1})\over C({\mathbf {h}}_{i_3},0)-C({\mathbf {h}}_{i_2},0)} \end{aligned}$$

  (31)

  or similarly for b) a triplet of temporal lags ${u}_{j_1}, {u}_{j_2}, {u}_{j_3}$ and a spatial lag ${\mathbf {h}}_{i_1},$ $i_1\in \{1,\ldots ,l_s\}$, $j_1,j_2,j_3\in \{1,\ldots ,l_t\}$, ${j_1}\ne {j_2}\ne {j_3}$ as follows

  $$\begin{aligned} {C({\mathbf {h}}_{i_1},u_{j_2})-C({\mathbf {h}}_{i_1},u_{j_1})\over C({\mathbf {0}},u_{j_2})-C({\mathbf {0}},u_{j_1})}\quad {C({\mathbf {h}}_{i_1},u_{j_3})-C({\mathbf {h}}_{i_1},u_{j_2})\over C({\mathbf {0}},u_{j_3})-C({\mathbf {0}},u_{j_2})}. \end{aligned}$$

  (32)

Then, the null hypothesis for the class of models defined in (28) is written as $H_0: {\mathbf {A}}{\mathbf {f}}^{{\tiny PS}}({\mathbf {G}}) = {\mathbf {0}}$, where the general form of the contrast matrix ${\mathbf {A}}$, with at most $\displaystyle \left( {\begin{array}{c}l_s\\ 3\end{array}}\right) l_t+ l_s\displaystyle \left( {\begin{array}{c}l_t\\ 3\end{array}}\right)$ rows and $2\displaystyle \left( {\begin{array}{c}l_s\\ 3\end{array}}\right) l_t+ l_s\displaystyle \left( {\begin{array}{c}l_t\\ 3\end{array}}\right)$ columns, is given in (16).

Thus, under the asymptotic probability distributions in (6) and (7), the test statistic (11), which can be used in this case to assess the above null hypothesis, converges in distribution to a Chi-square with degrees of freedom equal to the row rank of the contrast matrix ${\mathbf {A}}$, equal at most to $\displaystyle \left( {\begin{array}{c}l_s\\ 3\end{array}}\right) l_t+ l_s\displaystyle \left( {\begin{array}{c}l_t\\ 3\end{array}}\right).$

For example, given the following set of space-time lags:

$$\begin{aligned} \begin{aligned} \Lambda = \{({\mathbf {h}}_1,u_1), ({\mathbf {h}}_2, u_1), ({\mathbf {h}}_3,u_1), ({\mathbf {h}}_1,0), ({\mathbf {h}}_2,0), ({\mathbf {h}}_3,0), \\ ({\mathbf {h}}_4,u_1), ({\mathbf {h}}_4, u_2), ({\mathbf {h}}_4,u_3), ({\mathbf {0}},u_1), ({\mathbf {0}},u_2), ({\mathbf {0}},u_3)\}, \end{aligned} \end{aligned}$$

(33)

and the corresponding ${\mathbf {G}}$, let us consider the elements ${\mathbf {f}}^{{\tiny PS}}({\mathbf {G}}) \, {\rm and}\; {\mathbf {A}},$  respectively

$$\begin{aligned}&{\mathbf {f}}^{{\tiny PS}}({\mathbf {G}})=\left[ {C({\mathbf {h}}_2,u_1)-C({\mathbf {h}}_1,u_1)\over C({\mathbf {h}}_2,0)-C({\mathbf {h}}_1,0)} \quad {C({\mathbf {h}}_3,u_1)-C({\mathbf {h}}_2,u_1)\over C({\mathbf {h}}_3,0)-C({\mathbf {h}}_2,0)}\right. \\\nonumber &\;\,\qquad\;\qquad \left. {C({\mathbf {h}}_4,u_2)-C({\mathbf {h}}_4,u_1)\over C({\mathbf {0}},u_2)-C({\mathbf {0}},u_1)}\quad {C({\mathbf {h}}_4,u_3)-C({\mathbf {h}}_4,u_2)\over C({\mathbf {0}},u_3)-C({\mathbf {0}},u_2)} \right] ^{\top }, \end{aligned}$$

(34)

$$\begin{aligned}&{\mathbf {A}}= \left[ \begin{array}{cccc} 1 &{} -1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} -1\\ \end{array} \right] . \end{aligned}$$

(35)

Then, the null hypothesis ($H_0: {\mathbf {A}} {\mathbf {f}}^{{\tiny PS}}({\mathbf {G}}) = {\mathbf {0}}$) regarding the class of models defined in (28), can be tested by applying the test statistic (11), which converges in distribution to a Chi-square with $q=2$ degrees of freedom.

4.3 Testing some general classes of covariance function models

Some classes of space-time covariance function models share some properties, which can be useful in the testing procedure. Before going into details, it is worth introducing the following general result.

Proposition 4.3

Given a class of covariance function models, suppose that there exist two functions $\phi ({\mathbf {h}}, u)= \Phi [C({\mathbf {h}}, 0),C({\mathbf {0}}, u),C({\mathbf {h}}, u)]$ and $\psi ({\mathbf {h}}, u)=\Psi [C({\mathbf {h}}, 0),C({\mathbf {0}}, u),C({\mathbf {h}}, u)]$ such that

$$\begin{aligned} \phi ({\mathbf {h}}, u)= & {} a(u)||{\mathbf{h}}||^{2\gamma }+b(u), \qquad \forall u, \end{aligned}$$

(36)

$$\begin{aligned} \psi ({\mathbf {h}}, u)= & {} c(||{\mathbf{h}}||) u^{2\alpha }+d(||{\mathbf{h}}||), \qquad \forall {\mathbf {h}}, \end{aligned}$$

(37)

where $\alpha ,\gamma \in ]0,1]$ and $a(\cdot ),b(\cdot ), c(\cdot )$, $d(\cdot )$ are differentiable functions. Then, for any set of spatial lags ${\mathbf {h}}_{i}$, $i=1,2,3$, such that $||{\mathbf {h}}_{1}||^{2\gamma }- ||{\mathbf {h}}_{2}||^{2\gamma } = ||{\mathbf {h}}_{2}||^{2\gamma }-||{\mathbf {h}}_{3}||^{2\gamma }$, and temporal lag u, the increments

$$\begin{aligned} \phi {({\mathbf {h}}_{2},u)}-{\phi ({\mathbf {h}}_{1},u)}\quad \; {\phi ({\mathbf {h}}_{3},u)}-{\phi ({\mathbf {h}}_{2},u)} \end{aligned}$$

(38)

are equal. Similarly, for any set of temporal lags ${u}_{i}$, $i=1,2,3,$ such that $u_{1}^{2\alpha }-u_{2}^{2\alpha }=u_{2}^{2\alpha }-u_{3}^{2\alpha }$, and spatial lag ${\mathbf {h}},$ the increments

$$\begin{aligned} {\psi ({\mathbf {h}},u_{2})}-{\psi ({\mathbf {h}},u_{1})}\quad \; {\psi ({\mathbf {h}},u_{3})}-{\psi ({\mathbf {h}},u_{2})} \end{aligned}$$

(39)

are equal.

The proof follows from the assumptions (36) and (37), thus the difference between the elements of any couple of the type given in (38) is zero; similarly, the difference between the elements of any couple of the type given in (39) is zero.

This general result can be utilized for testing some special classes of space-time covariance function models, such as the integrated product, Gneiting and Cressie-Huang models, as described below.

Let Z be a strictly stationary space-time random field with finite variance. Assume that for a given class of covariance function models, chosen to describe the space-time dependency of the random field Z, there exist two functions $\phi ({\mathbf {h}}, u)= \Phi [C({\mathbf {h}}, 0),C({\mathbf {0}}, u),C({\mathbf {h}}, u)]$ and $\psi ({\mathbf {h}}, u)=\Psi [C({\mathbf {h}}, 0),C({\mathbf {0}}, u),C({\mathbf {h}}, u)]$ such that

$$\begin{aligned} \phi ({\mathbf {h}}, u)= & {} a(u)||{\mathbf{h}}||^{2\gamma }+b(u), \qquad \forall u, \end{aligned}$$

(40)

$$\begin{aligned} \psi ({\mathbf {h}}, u)= & {} c(||{\mathbf{h}}||) u^{2\alpha }+d(||{\mathbf{h}}||), \qquad \forall {\mathbf {h}}, \end{aligned}$$

(41)

where $\alpha ,\gamma \in ]0,1]$ and $a(\cdot ),b(\cdot ), c(\cdot )$, $d(\cdot )$ are differentiable functions. Suppose that

• ${\Lambda} = \{({\mathbf {h}}_i,u_j), ({\mathbf {h}}_i,0), ({\mathbf {0}}, u_j); i=1,\ldots ,l_s,\; j=1,\ldots , l_t\},$ be a set of space-time lags, where at least $l_s$ or $l_t$ must be greater than 2 and there are at least $n_s=1$ triplets of spatial lags ${\mathbf {h}}_{i_1}, {\mathbf {h}}_{i_2}, {\mathbf {h}}_{i_3}$, such that $||{\mathbf {h}}_{i_1}||^{2\gamma }- ||{\mathbf {h}}_{i_2}||^{2\gamma } = ||{\mathbf {h}}_{i_2}||^{2\gamma }-||{\mathbf {h}}_{i_3}||^{2\gamma }$, ${i_1}\ne {i_2}\ne {i_3}$ or $n_t=1$ triplets of temporal lags ${u}_{j_1}, {u}_{j_2}, {u}_{j_3}$, such that $u_{j_1}^{2\alpha }-u_{j_2}^{2\alpha }=u_{j_2}^{2\alpha }-u_{j_3}^{2\alpha }$, ${j_1}\ne {j_2}\ne {j_3}$;

• $m=(l_s+1)(l_t+1)$ denote the cardinality of $\Lambda$;

• ${\mathbf {G}} =\{C({\mathbf {h}},u): ({\mathbf {h}},u) \in \Lambda \}$ and $\widehat{{\mathbf {G}}}_n = \left\{ \widehat{C}_n({\mathbf {h}}, u) : ({\mathbf {h}}, u) \in \Lambda \right\}$, where $\widehat{C}_n({\mathbf {h}},u)$, for a specific lag $({\mathbf {h}},u)$, denotes the covariance estimator based on random variables in the sequence of the index sets $D_n= S \times T_n$;

• ${\mathbf {f}}^{{\tiny GC}}$ be the vector of functions whose generic couple of consecutive elements (used for the contrast) is defined a) for a triplet of spatial lags ${\mathbf {h}}_{i_1}, {\mathbf {h}}_{i_2}, {\mathbf {h}}_{i_3}$, such that $||{\mathbf {h}}_{i_1}||^{2\gamma }- ||{\mathbf {h}}_{i_2}||^{2\gamma } = ||{\mathbf {h}}_{i_2}||^{2\gamma }-||{\mathbf {h}}_{i_3}||^{2\gamma }$, and a temporal lag $u_{j_1}$, ${i_1}\ne {i_2}\ne {i_3},$ as follows

  $$\begin{aligned} \phi {({\mathbf {h}}_{i_2},u_{j_1})}-{\phi ({\mathbf {h}}_{i_1},u_{j_1})}\quad \; {\phi ({\mathbf {h}}_{i_3},u_{j_1})}-{\phi ({\mathbf {h}}_{i_2},u_{j_1})}, \end{aligned}$$

  (42)

  and b) for a triplet of temporal lags ${u}_{j_1}, {u}_{j_2}, {u}_{j_3}$, such that $u_{j_1}^{2\alpha }-u_{j_2}^{2\alpha }=u_{j_2}^{2\alpha }-u_{j_3}^{2\alpha }$, and a spatial lag ${\mathbf {h}}_{i_1},$ ${j_1}\ne {j_2}\ne {j_3},$ as follows

  $$\begin{aligned} {\psi ({\mathbf {h}}_{i_1},u_{j_2})}-{\psi ({\mathbf {h}}_{i_1},u_{j_1})}\quad \; {\psi ({\mathbf {h}}_{i_1},u_{j_3})}-{\psi ({\mathbf {h}}_{i_1},u_{j_2})}. \end{aligned}$$

  (43)

Then, the null hypothesis for the above general class of covariance function models can be written as $H_0: {\mathbf {A}}{\mathbf {f}}^{{\tiny GC}}({\mathbf {G}}) = {\mathbf {0}}$, where the contrast matrix ${\mathbf {A}}$ is of the general form given in (16), with at most $({n_s}l_t+ l_s{n_t})$ rows and $2({n_s}l_t+ l_s{n_t})$ columns. Thus, the testing procedure can be conducted on the basis of the statistic (11) which converges in distribution, under the null hypothesis and the usual assumption on the asymptotic probability distributions in (6) and (7), to a Chi-square with degrees of freedom equal to the row rank of the contrast matrix ${\mathbf {A}}$ (at most ${n_s}l_t+ l_s{n_t}$).

Proposition 4.3 can be easily applied to some well-known classes of space-time covariance function models, with variance $\sigma ^2>0$, smoothness parameters $\alpha ,\gamma \in ]0,1]$ and range parameters $a,b>0$, such as:

• the integrated product covariance functions (De Iaco et al. 2002)

  $$\begin{aligned} C({\mathbf{h}},u)={\sigma ^2c \over (a{||{\mathbf{h}}||^{2\gamma }}+b{u}^{2\alpha }+ c)}, \qquad c >0, \end{aligned}$$

  (44)

  by assuming: $\quad \Phi (C({\mathbf {h}},u))= [{C({\mathbf {h}},u)}]^{-1},\qquad \Psi (C({\mathbf {h}},u))= [{C({\mathbf {h}},u)}]^{-1};$

• Gneiting covariance functions (Gneiting 2002)

  $$\begin{aligned} C({\mathbf{h}}, u) =\sigma ^2 \left( {1\over (b|{u}|^{2\alpha } +1)^{\tau } } \right) \cdot exp \left( - {a||{\mathbf{h}}|| ^{2\gamma }\over ( b|{u}|^{2\alpha } +1)^{\gamma \beta } } \right) , \quad \beta \in [0,1], \tau \ge \beta d/2, \end{aligned}$$

  (45)

  by assuming

  $$\begin{aligned} \Phi (C({\mathbf {h}},u))={\ln C({\mathbf {h}},u)},\qquad \Psi (C({\mathbf {0}},u),C({\mathbf {h}},u))=\left\{ {\ln {C({\mathbf {0}},u)\over C({\mathbf {h}},u)}} \right\} ^{-1\over \gamma \beta }; \end{aligned}$$

  (46)

• Cressie-Huang covariance functions (Cressie and Huang 1999)

  $$\begin{aligned} C({\mathbf{h}}, u) =\sigma ^2 \left( {1\over (a|u| +1)^{d\over 2}} \right) \cdot exp \left( - {b^2||{\mathbf{h}}||^2 \over ( a|u| +1) } \right) , \end{aligned}$$

  (47)

  by assuming (with $\alpha =0.5$, $\gamma =1$)

  $$\begin{aligned} \quad \Phi (C({\mathbf {h}},u))= {\ln {C({\mathbf {h}},u)}}, \quad \Psi (C({\mathbf {0}},u),C({\mathbf {h}},u))= \left\{ {\ln {C({\mathbf {0}},u)\over C({\mathbf {h}},u)}}\right\} ^{-1}, \end{aligned}$$

  (48)

  or alternatively the following class of Cressie-Huang models

  $$\begin{aligned} C({\mathbf{h}}, u) ={{\sigma ^2 (a|u| +1)}\over {[(a|u| +1)^{2} +b^2||{\mathbf {h}}||^2]^{(d+1)\over 2}}}, \end{aligned}$$

  (49)

  by assuming (with $\alpha =0.5$, $\gamma =1$): $\quad \Phi (C({\mathbf {0}},u),C({\mathbf {h}},u))= \left\{ { {C({\mathbf {0}},u)\over C({\mathbf {h}},u)}}\right\} ^{2\over d+1},$

  $$\begin{aligned} \Psi (C({\mathbf {0}},u),C({\mathbf {h}},u),C({\mathbf {h}}',u))= \left\{ {{\Phi (C({\mathbf {0}},u),C({\mathbf {h}},u))}-{\Phi (C({\mathbf {0}},u),C({\mathbf {h}}',u))}}\right\} ^{-2}. \end{aligned}$$

  (50)

In particular, if the integrated product model (44) is considered, then for any set of spatial lags ${\mathbf {h}}_1$, ${\mathbf {h}}_2$, and ${\mathbf {h}}_3$, such that $||{\mathbf {h}}_1||^{2\gamma }- ||{\mathbf {h}}_2|| ^{2\gamma }= ||{\mathbf {h}}_2||^{2\gamma }-||{\mathbf {h}}_3||^{2\gamma }$, or alternatively for any set of temporal lags $u_1$, $u_2$, and ${u}_3$, such that $u_1^{2\alpha }-u_2^{2\alpha }=u_2^{2\alpha }-u_3^{2\alpha }$, the following properties are satisfied:

$$\begin{aligned} \begin{aligned} {1\over {C({\mathbf{h}}_2, u)}}-{1\over {C({\mathbf{h}}_1, u)}}={1\over {C({\mathbf{h}}_3, u)}}-{1\over {C({\mathbf{h}}_2, u)}}, \qquad \forall \, u,\\ {1\over {C({\mathbf{h}}, u_2)}}-{1\over {C({\mathbf{h}} , u_1)}}={1\over {C({\mathbf{h}} , u_3)}}-{1\over {C({\mathbf{h}} , u_2)}}, \qquad \forall \, {\mathbf{h}}. \end{aligned} \end{aligned}$$

(51)

Thus, given the contrast matrix as in (35) and the vector of functions, denoted for the integrated product class as ${\mathbf {f}}^{{\tiny IP}}$, i.e.,

$$\begin{aligned} \begin{aligned} {\mathbf {f}}^{{\tiny IP}}({\mathbf {G}})=\left[ {1\over C({\mathbf {h}}_2,u)} -{1\over C({\mathbf {h}}_1,u)}\quad \; {1\over C({\mathbf {h}}_3,u)}-{1\over C({\mathbf {h}}_2,u)} \quad \;\right. \\ \left. {1\over C({\mathbf {h}},u_2)}-{1\over C({\mathbf {h}},u_1)}\quad \; {1\over C({\mathbf {h}},u_3)}-{1\over C({\mathbf {h}},u_2)}\right] ^{\top } \end{aligned} \end{aligned}$$

(52)

the null hypothesis $H_0: {\mathbf {A}} {\mathbf {f}}^{{\tiny IP}}({\mathbf {G}}) = {\mathbf {0}},$ can be tested by using the statistic (11), which converges in distribution to a Chi-square with $q=2$ degrees of freedom. Proposition 4.3 can also be applied to the following generalization of the subclass of the integrated product model (44)

$$\begin{aligned} C({\mathbf{h}},u)={k c^{n+1} \over (a{||{\mathbf{h}}||}^{2\gamma }+b{u}^{2\alpha }+ c)^{n+1}}, \end{aligned}$$

(53)

with $\Phi (C({\mathbf {h}},u))= \{C({\mathbf {h}},u)\}^{-1\over {n+1}},\qquad \Psi (C({\mathbf {h}},u))=\{C({\mathbf {h}},u)\}^{-1\over {n+1}},$ ($n\in \mathbb {N}$).

For example, if the Gneiting model (45) is considered and the spatial and temporal marginals present a linear behavior near the origin ($\alpha =0.5$, $\gamma =0.5$), then the following properties are valid (a) for any set of spatial lags ${\mathbf {h}}_1$, ${\mathbf {h}}_2$, and ${\mathbf {h}}_3$, such that $||{\mathbf {h}}_1||- ||{\mathbf {h}}_2||= ||{\mathbf {h}}_2||-||{\mathbf {h}}_3||$, and $\forall u$,

$$\begin{aligned} \ln {C({\mathbf {h}}_1, u)}-\ln {C({\mathbf {h}}_2, u)} = \ln {C({\mathbf {h}}_2, u)}-\ln {C({\mathbf {h}}_3, u)}, \end{aligned}$$

(54)

or alternatively, (b) for any set of temporal lags $u_1$, $u_2$, and ${u}_3,$ such that $u_1-u_2=u_2-u_3$ and $\forall {\mathbf {h}}$,

$$\begin{aligned} \left\{ {\ln {C({\mathbf {0}}, u_2)\over C({\mathbf {h}},u_2)}}\right\} ^{-2\over \beta }-\left\{ {\ln {C({\mathbf {0}}, u_1)\over C({\mathbf {h}},u_1)}}\right\} ^{-2\over \beta }=\left\{ {\ln {C({\mathbf {0}}, u_3)\over C({\mathbf {h}},u_3)}}\right\} ^{-2\over \beta }-\left\{ {\ln {C({\mathbf {0}}, u_2)\over C({\mathbf {h}},u_2)}}\right\} ^{-2\over \beta }. \end{aligned}$$

(55)

Then, given the contrast matrix as in (35) and the vector of functions, denoted as ${\mathbf {f}}^{{\tiny Gn}}$, i.e.,

$$\begin{aligned} \begin{aligned} {\mathbf {f}}^{{\tiny Gn}}({\mathbf {G}})=\left[ \ln {C({\mathbf {h}}_1, u)}-\ln {C({\mathbf {h}}_2, u)}\qquad \ln {C({\mathbf {h}}_2, u)}-\ln {C({\mathbf {h}}_3, u)}\right. \\ \left. \left\{ {\ln {C({\mathbf {0}}, u_2)\over C({\mathbf {h}},u_2)}}\right\} ^{-2\over \beta } -\left\{ {\ln {C({\mathbf {0}}, u_1)\over C({\mathbf {h}},u_1)}}\right\} ^{-2\over \beta } \qquad \left\{ {\ln {C({\mathbf {0}}, u_3)\over C({\mathbf {h}},u_3)}}\right\} ^{-2\over \beta }-\left\{ {\ln {C({\mathbf {0}}, u_2)\over C({\mathbf {h}},u_2)}}\right\} ^{-2\over \beta }\right] ^{\top }, \end{aligned} \end{aligned}$$

(56)

the null hypothesis $H_0: {\mathbf {A}}{\mathbf {f}}^{{\tiny Gn}}({\mathbf {G}})={\mathbf {0}}$ can be used for testing the Gneiting model defined in (45).

Note that, since ${\mathbf {f}}^{{\tiny Gn}}({\mathbf {G}})$ depends on the parameter $\beta$, the test can be computed by considering different admissible values of this parameter, whose domain is $[0,\, 1]$. For example, the test for the selected class of models can be computed starting from 0.1, with consecutive increments of 0.2, up to 0.9, as shown in De Iaco et al. (2016). Evidently, if the hypothesis of separability is rejected, the value $\beta =0$ is not be considered as an admissible value since this case corresponds to a separable model, which is inconsistent with rejection of separability.

Remarks

• The statistical tests proposed in the paper keep stimulating the interest in this subject and enrich the usefulness of the tests proposed in the literature.

• Regarding the estimation of the covariance matrix, the subsampling estimation method has been used for the case studies, with a block length consistent with a number of blocks close to the number of contrasts (rank of the contrast matrix). However, there is a closely related literature on the block size selection in the context of spectrum estimation and resampling dependent data (Hall et al. 1995; Politis et al. 1999; Lahiri 2003).

• Different methods can be used for the estimation of the covariance matrix. In particular, by extending the random normalization idea presented in Lobato (2001) and in Shao and Li (2009), alternative tests, with an asymptotic null distributions which are free of tuning parameters, can be used instead of the ones based on the asymptotic Chi-square distribution.

• The estimation method of the model parameters does not affect the performance of the proposed test, since the specific covariance function model is fitted (i.e., its parameters are estimated) after testing the class of models (to which the specific model belongs).

The basic steps of the testing procedure for a class of models is given in “Appendix 4”.

4.4 Hints for choosing a space-time model

In this Section a simple procedure which can help practitioners in selecting a class of space-time covariance function models is proposed. The procedure can be described through the following steps:

• 1. use the test (11) to check the null hypothesis for a space-time covariance function to be separable or not; if the hypothesis of separability is rejected, then a non-separable class of models is needed;

• 2. use the technique described in Sect. 3 to check the type of non-separability (i.e. uniformly positive, uniformly negative or pointwise non-separable);

• 3. according to the type of non-separability, select a class of models as described in Sect. 4;

• 4. consider further useful features, such as behavior at the origin, asymptotic behavior of the marginals and anisotropy aspects.

It is clear that the above testing procedure regards a class of covariance function models, not a specific model. The class of models to be tested is selected on the basis of the main characteristics of the empirical covariance surface, such as full symmetry, separability, behavior at the origin, anisotropy aspects, as well as type of non-separability and asymptotic behavior (De Iaco et al. 2016).

Regarding the test on the type of non-separability, it is worth to underline that the conditions fixed in the null hypothesis are necessary and sufficient only for pointwise negative or positive non-separability ($l=1$), otherwise if $l >1$ they are only necessary. Moreover, l is set to be greater than 1, only in the case the analyst decides to put together (for the test) more than one lag characterized by the same type of non-separability (homogeneus lags). In other words, the tests (18) and (19) can be used to decide to reject or non-reject the hypothesis on positive or negative non-separability for the specific sets of lags selected for the test. After testing the type of non-separability on sets of homogeneus lags, the final conclusions on uniform non-separability might be just supported by the graphical inspection of the box-plots of the sample non-separability ratios.

Moreover, note that all the tests are based on spatio-temporal covariance functions, estimated for different spatio-temporal lags. From a practical point of view, it is common to select and combine various spatial lags or couples of spatial points as well as different temporal lags according to the specific characteristics of the phenomenon under study or simply by taking into account the geometry of the sample points and the lags where the correlation is strong. This aspects have been clarified in the next Section.

5 Case studies

In this Section the procedure for testing the type of non-separability, as well as a class of space-time covariance functions, has been applied to the well known data set AirBase, provided by the European Environmental Agency and available with the package spacetime of the R environment (Pebesma 2012; Bivand et al. 2013). Moreover, simulated data sets have been used to assess the size and the power of the tests.

The results, concerning each case study, have been obtained by using the R package covatest (De Iaco et al 2017). It is worth pointing out that the choice regarding the specific spatial points to be selected can be justified on the basis of different reasons: for example, they can be chosen by taking into account the pairs of points with the smallest or, alternatively, with the largest ratio between the east-west component and the north-south component of the spatial lag, as well as the pairs of points with the shortest distance $\Vert {\mathbf{h}}\Vert$. In general, the analyst can start with few pairs of spatial locations spread out over the domain. In some empirical cases, the selection of the pairs of spatial locations might be based on intrinsic characteristics of the phenomenon under study. For example, for wind speed data, the pairs of spatial locations might be selected along the prevalent wind direction over the study area, as suggested in the paper of Li et al. (2007), where the authors highlighted that the test results might depend on the spatio-temporal lags chosen. Regarding the temporal lags, it is common to use a) lags for which the sample non-separability ratios are much greater/less than one (these lags can be detected by inspecting the box-plots of the sample non-separability ratios grouped by temporal lags), for the test on the type of non-separability, or b) lags which are characterized by strong correlation (often short lags $u_1, u_2, u_3$), for the test on the type of model.

5.1 $PM_{10}$ daily residuals

In this case study, the air quality data base AirBase has been used and in particular, the $PM_{10}$ daily data, measured from the 1st of January 2004 to the 31st of December 2009, at 26 rural background stations (Fig. 1) located in Germany have been selected. These data represent a subset of the whole database, since only the temporal span and the stations with a very small percentage of missing data (around 3%) have been retained. As highlighted in Gräler et al. (2015), the $PM_{10}$ daily data are characterized by a periodic component, then by using the program “REMOVE” given in De Cesare et al. (2002), this component has been estimated by moving averages (Brockwell and Davis 2006) and removed simultaneously before applying the tests. In case of missing values, this program uses linear interpolation to replace a prescribed number (set equal to 5) of consecutive missing values.

Fig. 1

Pairs of spatial points considered for the test of separability and the type of non-separability (continuous line) and for the test on the type of class of models (dashed line)

In the literature, non-separable symmetric covariance function models have been already fitted to the empirical space-time covariance surface computed for these data (Gräler et al. 2012, 2015; Pebesma 2004). Indeed, daily mean $PM_{10}$ concentrations measured at rural stations across Germany did not show any strong asymmetric pattern due to prevailing environmental effects; on the other hand these data violated the assumption of separability. This is confirmed by applying the tests of symmetry and separability on 15 pairs of monitoring stations among 325 pairs and on the first 3 temporal lags (where the correlation is strong): the null hypothesis of symmetry is not rejected ($TS_1=18.839,\, q=45;p\hbox { value}=0.999$) and the null hypothesis of separability is rejected ($TS_2=273.579,\, q=45;p\hbox { value}=1.63e^{-34}$). Consequently, the type of non-separability and the class of covariance function models to be used have been checked. In particular, the testing procedures have been applied by considering 15 pairs of survey stations, spread out over the domain, at various distances, and different temporal lags, where the correlation is strong and the sample non-separability ratios are much less than one.

Fig. 2

Box-plots of sample non-separability ratios, computed using the sample space-time covariance function of residuals and classified for spatial a and temporal, b lags

Before testing the type of non-separability, it is worth exploring the box-plots of the sample ratios between the empirical space-time covariance and the product of the sample spatial and temporal marginals, classified by spatial and temporal lags. Looking at Fig. 2, a uniform negative non-separability can be detected. Hence, as discussed in Sect. 3, a right tailed test, over a range of spatial couples and temporal lags, has been applied. Thus, this type of non-separability has been tested by considering 15 pairs of monitoring stations at different distances (Fig. 1) and temporal lags from 1 to 6 (where the sample non-separability ratios are equal or less than one). From the test results ($\hat{r}=-0.200$, $TS_{3}= -0.064$, p value = 0.526), the null hypothesis regarding the presence of negative non-separability is not rejected, at 5% significant level, for the selected spatial couples and temporal lags. Moreover, it is worth pointing out that the p value of the test statistic increases when the temporal lags are larger. In particular, for the same 15 pairs of monitoring stations and temporal lags from 3 to 8 (where the negative non-separability is stronger, i.e., the sample non-separability ratios are much less than one $\hat{r}=-1.801$), the non-rejection decision is strengthened ($TS_{3}= -0.427$, p value = 0.665).

Hence, a uniformly negative non-separable covariance function model can be suitably selected in order to describe the space-time correlation exhibited by the data. Moreover, by looking at the spatial and temporal profiles of the sample space-time covariance versus, respectively, $||{\mathbf{h}}||$ and |u|, it is easy to observe a different variability along space with respect to time (Fig. 3).

Fig. 3

Sample space-time covariogram

All these features are consistent with the class of product-sum models in (27), which can be tested by using the procedure proposed in Sect. 4. For this aim, the elements ${\mathbf {A}}, {\mathbf {G}}$ and ${\mathbf {f}}^{{\tiny PS}}$, of the general null hypothesis ${\mathbf {A}}{\mathbf {f}}^{{\tiny PS}}({\mathbf {G}})= {\mathbf {0}}$ have been suitably fixed. As in the previous case, this last test has been applied to 15 couples of survey stations and temporal lags from 1 to 6. The testing procedure indicates the non-rejection of the null hypothesis regarding the class of product-sum models (27), since $TS^{{\tiny PS}}=5.463$, $q=32$, with p value = 1.000.

In addition, the test is applied on a class of models which is not consistent with respect to the type of non-separability empirically detected; in particular, the test has been applied to the Gneiting model in (45), by using the same couples of stations and temporal lags considered to test the product-sum class. In this case, the test statistic ($TS^{{\tiny Gn}}=103.548$, $q=32$) and the p value ($1.79e^{-9}$) reasonably support the rejection of the null hypothesis at 5% of significance.

Note that after the selection of a class of models, traditional structural analysis should be performed, including fitting process of the covariance function model and cross-validation. As a further step, space-time mapping of predicted values should be also considered to provide a visual representation.

5.2 Simulated data

In this case study, the null hypotheses formulated on different types of non-separability and classes of covariance function models have been tested on zero-mean simulated space-time realizations. In particular, two classes of covariance function models, i.e., the product-sum model (27) and the Gneiting model (45), have been used to generate simulated space-time data regularly distributed over a range of grid sizes (spatial grids of dimensions $12\times 12$ and $16\times 16$), with temporal lengths $|T_n|=600$, $|T_n|=800$, $|T_n|=1000$. The product-sum model has exponential marginals with spatial and temporal effective ranges equal, respectively, to 4 and 20 and parameters $(k_1,k_2,k_3)=(0.5, 0.3, 0.2)$, while the Gneiting model has marginals with linear behaviour near the origin (with smoothness parameters $\gamma$ and $\alpha$ equal to 0.5) and $(a,b,\beta ,\tau ,\sigma ^2)=(0.75,0.75,1,1,1)$ (which correspond to spatial and temporal marginals that decay approximately at 4 and 20, respectively). Note that the idea of considering the test on these two classes of covariance function models to produce alternative simulations is interesting since they present two opposite types of non-separability, i.e, the former is uniformly negative non-separable and the latter is uniformly positive non-separable. 900 replicates have been obtained through a Gaussian-related program, that is the sequential simulation algorithm, based on the above-mentioned classes of covariance function models.

The conclusions have been supported by the analysis of the empirical size and power of the tests over a range of grid sizes, temporal lengths and classes of models. Regarding the test on the type of non-separability,

• data sets simulated through the Gneiting model (which is uniformly positive non-separable) have been used to determine 1) the empirical size   through the  frequency   of   rejecting the   uniform   positive   non-separability,   denoted   with $Fr\{R_{H_0^{{\tiny (+)}}}|H^{{\tiny (+)}}_0\}$, and 2) the empirical power through the frequency of rejecting the uniform negative non-separability, denoted with $Fr\{R_{H_0^{{\tiny (-)}}}|H^{{\tiny (+)}}_1\}$;

• similarly, data sets simulated through the product-sum model (which is uniformly negative non-separable) have been considered to compute 1) the empirical size through the frequency of rejecting the uniform negative non-separability, denoted with $Fr\{R_{H_0^{{\tiny (-)}}}|H^{{\tiny (-)}}_0\}$, and 2) the empirical power through the frequency of rejecting the uniform positive non-separability, denoted with $Fr\{R_{H_0^{{\tiny (+)}}}|H^{{\tiny (-)}}_1\}$.

For both types of data sets, an indirect way of approximating the power of the test, which consists on evaluating how large is the p value for the decision of non-rejection (when the null hypothesis is true), has been also proposed. In particular, the frequencies of non-rejecting the null hypotheses with large p values (greater than 0.9), denoted with $Fr\{\bar{R}_{H_0^{{\tiny (+)}}}|H^{{\tiny (+)}}_0;p\,\hbox {values}>0.9\}$ and $Fr\{\bar{R}_{H_0^{{\tiny (-)}}}|H^{{\tiny (-)}}_0;p\hbox { values}>0.9\}$, have been computed. Moreover, for the size and power of the tests on the type of class of models,

• Gneiting model-based data have been used to compute the empirical size $Fr\{R_{H_0^{{\tiny Gn}}}|H^{{\tiny Gn}}_0\}$, which is equivalent to the frequency of rejecting the same Gneiting model; on the other hand the empirical power has been evaluated through the frequency of rejecting the null hypotheses formulated on two different classes, such as the product-sum model or the integrated product model; these two frequencies are denoted, respectively, with $Fr\{R_{H_0^{{\tiny PS}}}|H^{{\tiny Gn}}_1\}$ and $Fr\{R_{H_0^{{\tiny IP}}}|H^{{\tiny Gn}}_1\}$. Note that the power of the test on the Gneiting class has been analyzed with respect to two classes, whereof one of them is negative non-separable (the product-sum model) and the other one is positive non-separable (the integrated product model);

• similarly, product-sum model-based data have been considered to determine the empirical size through the frequency of rejecting the product-sum model, denoted with $Fr\{R_{H_0^{{\tiny PS}}}|H^{{\tiny PS}}_0\}$; as in the previous case, the empirical powers, denoted with $Fr\{R_{H_0^{{\tiny Gn}}}|H^{{\tiny PS}}_1\}$ and $Fr\{R_{H_0^{{\tiny IP}}}|H^{{\tiny PS}}_1\}$ have been computed under the null hypotheses formulated on two types of classes, i.e. the Gneiting class and the integrated product class.

In addition, in order to approximate indirectly the power of the test, the frequencies of non-rejecting the null hypotheses (when it is true) with large p values (greater than 0.9) have been computed; they are denoted with $Fr\{\bar{R}_{H_0^{{\tiny Gn}}}|H^{{\tiny Gn}}_0;p\hbox { values}>0.9\}$ and $Fr\{\bar{R}_{H_0^{{\tiny PS}}}|H^{{\tiny PS}}_0;p\hbox { values}>0.9\}$.

Thus, the testing procedure has been applied to the zero-mean simulated data sets, obtained for different alternatives in terms of grid size, temporal length and class of models; spatial couples and temporal lags at distances 1, 2, 3 have been considered for the tests. The first step concerns the test on the type of non-separability, which has been implemented by considering the above mentioned alternatives; the empirical size with respect to the nominal level 0.05 and power are given in Table 1. Looking at the results, it is clear that the size of the test ($p_1$ and $p'_1$) is close to the nominal level and the power ($p_3$ and $p'_3$) approaches 1 as the grid size and temporal length increase; similarly for the approximated powers ($p_2$ and $p'_2$), measured in terms of frequencies of non-rejecting the null hypotheses (when it is true) with large p values (greater than 0.90); this confirms the reliability of the test. It makes sense that there is strong confidence in the conclusion of rejecting the null hypothesis of negative/positive non-separability when the alternative hypothesis is valid, as well as in the conclusion of failing to reject the null hypothesis when the null hypothesis is valid.

Table 1 Values of the empirical size and power for the tests on type of non-separability for data simulated through a uniform negative non-separable model ($p_1=Fr\{R_{H_0^{{\tiny (-)}}}|H^{{\tiny (-)}}_0\}$, $p_2=Fr\{\bar{R}_{H_0^{{\tiny (-)}}}|H^{{\tiny (-)}}_0;p\hbox { values}>0.9\}$ and $p_3=Fr\{R_{H_0^{{\tiny (+)}}}|H^{{\tiny (-)}}_1\}$) and through a uniform positive non-separable model ($p'_1=Fr\{R_{H_0^{{\tiny (+)}}}|H^{{\tiny (+)}}_0\}$, $p'_2=Fr\{\bar{R}_{H_0^{{\tiny (+)}}}|H^{{\tiny (+)}}_0;p\hbox { values}>0.9\}$ and $p'_3=Fr\{R_{H_0^{{\tiny (-)}}}|H^{{\tiny (+)}}_1\}$)

Next, the selected classes of covariance function models have been tested. In Table 2 the results obtained for the test on the classes of covariance function models show that the size ($p_1$ and $p'_1$) is sufficiently stable around the nominal level for each option, while the empirical power ($p_3$, $p_4$ and the corresponding $p'_3$, $p'_4$) fully supports the rejection decision of the null hypothesis when it is false as well as the approximated powers ($p_2$ and $p'_2$) are consistent with respect to the nominal frequency of the non-rejection decision of the null hypothesis (when it is valid) with p value greater than 0.9. Note also that the powers (including the approximated powers) of all alternatives are not appreciably different when the temporal length is equal to 1000. Moreover, there is evidence that the tests have greater power when the underlining data are generated by a covariance model characterized by a different type of non-separability with respect to the class of model under the null hypothesis (i.e., $p_3$ is greater than $p_4$).

Table 2 Values of the empirical size and power for the tests on type of class of covariance function models for data simulated through the Gneiting model ($p_1=Fr\{R_{H_0^{{\tiny Gn}}}|H^{{\tiny Gn}}_0\}$, $p_2=Fr\{\bar{R}_{H_0^{{\tiny Gn}}}|H^{{\tiny Gn}}_0;p\hbox { values}>0.9\}$, $p_3=Fr\{R_{H_0^{{\tiny PS}}}|H^{{\tiny Gn}}_1\}$ and $p_4=Fr\{R_{H_0^{{\tiny IP}}}|H^{{\tiny Gn}}_1\}$) and through the product-sum model ($p'_1=Fr\{R_{H_0^{{\tiny PS}}}|H^{{\tiny PS}}_0\}$, $p'_2=Fr\{\bar{R}_{H_0^{{\tiny PS}}}|H^{{\tiny PS}}_0;p\hbox { values}>0.9\}$, $p'_3=Fr\{R_{H_0^{{\tiny Gn}}}|H^{{\tiny PS}}_1\}$ and $p'_4=Fr\{R_{H_0^{{\tiny IP}}}|H^{{\tiny PS}}_1\}$)

Fig. 4

Empirical distribution function of $TS_3$ and values of the Kolmogorov–Smirnov test statistic with p values: a product-sum model-based simulations, b Gneiting model-based simulations (Kolmogorov-Smirnov statistic $KS_1$, including tails, and $KS_2$, excluding tails)

Both Table 1 and 2 show that (a) the grid size does not significantly affect the size of the test, which is around the nominal level even if the series length is equal to 600; (b) the power increases as temporal length increases.

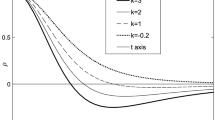
As specified in the previous Sections, the test statistics recalled in this testing procedure converge in distribution to a Chi-square (as in the case of $TS_1$ and $TS_2$) or to a normal (as in the case of $TS_3$), then all the above results are based on these statements. In the following, a discussion of how rapidly the sequence of distributions converges, has been given as the temporal length increases from 400 up to 1000, with increments of 200 time points for each step. Thus, the Kolmogorov–Smirnov tests have been applied for comparing the observed cumulative distribution functions of $TS_2$ (used to test the class of models) and $TS_3$ (used to test the type of non-separability) with their specified theoretical distributions. Moreover, since the convergence in distribution is pointwise, i.e. not uniform, the Kolmogorov–Smirnov tests have been computed by considering the empirical distributions of the test statistics, evaluated for the simulated realizations, with and without the tails at $5\%$. Fig. 4, which illustrates the empirical distribution function of the test statistic $TS_3$, shows a rapid convergence to a normal distribution, even when the temporal length is greater than 400; moreover, the p values for the Kolmogorov–Smirnov tests support the non-rejection of the null hypothesis for all options. Fig. 5 illustrates the empirical distribution function of the test statistic $TS_2$, used to test the selected class of models. In this case, the p values, which support the non-rejection of the null hypothesis for all options, are greater than 0.8 (in particular, $KS_2$ is in the interval 0.846–0.868) when the temporal length is greater than 800 and approach 1 (in particular, $KS_2$ is in the interval 0.903–0.984) when the temporal length is equal to 1000.

Fig. 5

Empirical distribution function of $TS_2$ and values of the Kolmogorov–Smirnov test statistic with p values: a product-sum model-based simulations, b Gneiting model-based simulations (Kolmogorov–Smirnov statistics $KS_1$, including tails, and $KS_2$, excluding tails)

6 Conclusions

In this paper the definitions of uniformly positive/negative non-separability and pointwise positive/negative non-separability were reviewed and a statistical test for checking different forms of non-separability was introduced. Moreover, a technique for testing some classes of space-time covariance function models (such as the Rodrigues and Diggle class of models, the product-sum model, the Gneiting models, the integrated product models and the Cressie-Huang models) was also given. The empirical results analyzed through some case studies can stimulate the use of these tests since they can help the practitioners to better select a space-time covariance function model. Further developments might also regard other testing procedures for a different geometry of spatio-temporal points, i.e. an irregular data frame, where data locations $({\mathbf {s}}_1, 1), ({\mathbf {s}}_2, 2), ({\mathbf {s}}_3,3), \ldots , ({\mathbf {s}}_n, n)$ are such that no two of ${\mathbf {s}}_1, {\mathbf {s}}_2, {\mathbf {s}}_3, \ldots , {\mathbf {s}}_n$ are the same (typical of environmental monitoring network based on mobile sensors).

Appendices

Appendix 1: Test for the type of non-separability

If the non-separability assumption is reasonable, the type of non-separability have to be investigated through the following steps:

• 1. Estimation of the space-time covariance surface ($\widehat{C}({\mathbf{h}},u)$ for a set of space-time lags $({\mathbf{h}},u)$) and of the corresponding empirical space-time correlation function ($\widehat{\rho }({\mathbf{h}},u)$).

• 2. Computation of the non-separability index ratio $\widehat{r}({\mathbf{h}},u)$ (i.e. from definition (12), the ratio computed between the empirical space-time correlation and the product of the corresponding sample spatial and temporal marginals).

• 3. Graphical representation of the sample non-separability ratio through box-plots, classified for spatial lags and temporal lags. The inspection of box-plots could help to decide for a right tailed test (18) or a left tailed test (19).

• 4. Fix the null hypothesis, i.e. the type of the test: a right tailed test for testing the negative non-separability, a left tailed test for testing the positive non-separability.

• 5. Selection of spatial and temporal lags ($\Lambda$) with sample non-separability ratios much greater/less than one. The test statistic is always computed for lags characterized by the same type of non-separability, in such a way that compensations among terms of the test statistic with different signs are avoided.

• 6. Computation of the test statistic, which requires the estimation of ${\mathbf {\Sigma }}, \widehat{{\mathbf {G}}}, {\mathbf {f}}(\widehat{{\mathbf {G}}})$ and the construction of the contrast matrix A (Li et al. 2007), and of the corresponding p value.

• 7. If the p value associated with the test statistic is less than 0.05 the null hypothesis is rejected.

As explained in Li et al. (2007), De Iaco et al. (2016), the analyst can compute the tests on a set of spatial and temporal lags chosen on the basis of different reasons. In general, the analyst can start with few pairs of spatial locations (spatial lags), which are spread out over the domain and are representative of the spatio-temporal correlation of the data set. In some empirical cases, the selection of the pairs of spatial locations might be based on intrinsic characteristics of the phenomenon under study (some examples for wind data are in the above mentioned papers). Moreover, the lags or pairs of locations can be chosen by taking into account the pairs of points with the smallest or, alternatively, with the largest ratio between the east-west component and the north-south component of the spatial lag, as well as the pairs of points with the shortest distance $\Vert {\mathbf{h}}\Vert$. Regarding the temporal lags, it is common to use short temporal lags characterized by strong correlation. In addition to the above mentioned insights, the analyst can select, for the test on the type on non-separability, spatial and temporal lags for which the sample non-separability ratios are much greater/less than one. For this aim, an useful support is given by the inspection of box-plots of the sample non-separability ratios, classified by spatial and temporal lags.

Appendix 2: Proof of Proposition 4.1

Given $d({\mathbf{h}}_1,u_2)=C({\mathbf {h}}_1, u_2)C({\mathbf {0}}, 0) - C({\mathbf {h}}_1, 0)C({\mathbf {0}}, u_2)$, it is easy to show that

$$\begin{aligned} d({\mathbf{h}}_i,u_j)={\sigma ^4\over 4}[\rho _{s,1}({\mathbf{h}}_i)-\rho _{s,2}({\mathbf{h}}_i) ][\rho _{t,1}(u_j)-\rho _{t,2}(u_j)], \qquad i,j=1,2. \end{aligned}$$

(57)

Then for any set of spatial lags ${\mathbf {h}}_1$ and ${\mathbf {h}}_2$ and temporal lags $u_1$ and $u_2$ the following properties are satisfied:

$$\begin{aligned}&{d({\mathbf {h}}_1,u_1) \over {d({\mathbf {h}}_2, u_1) }}- {d({\mathbf {h}}_1,u_2) \over {d({\mathbf {h}}_2, u_2) }} =0, \qquad \forall \, u_1, u_2, \end{aligned}$$

(58)

$$\begin{aligned}&{d({\mathbf {h}}_1,u_1) \over {d({\mathbf {h}}_1, u_2) }}- {d({\mathbf {h}}_2,u_1) \over {d({\mathbf {h}}_2, u_2) }}=0, \qquad \forall \, {\mathbf {h}}_1,{\mathbf {h}}_2. \end{aligned}$$

(59)

Appendix 3: Proof of Proposition 4.2

Part 1 (if)

For the proof, consider that because of (28) the following properties are satisfied for any set of spatial lags ${\mathbf {h}}_1$, ${\mathbf {h}}_2$, and ${\mathbf {h}}_3$

$$\begin{aligned}&\gamma ({\mathbf {h}}_1,u)-\gamma ({\mathbf {h}}_2, u)=[\gamma ({\mathbf {h}}_1,0) - \gamma ({\mathbf {h}}_2,0)][1-k\gamma ({\mathbf {0}},u)], \qquad \forall \, u, \end{aligned}$$

(60)

$$\begin{aligned}&\gamma ({\mathbf {h}}_3,u)-\gamma ({\mathbf {h}}_2,u)=[\gamma ({\mathbf {h}}_3,0) - \gamma ({\mathbf {h}}_2,0)][1-k\gamma ({\mathbf {0}},u)], \qquad \forall \, u, \end{aligned}$$

(61)

or equivalently

$$\begin{aligned} {\gamma ({\mathbf {h}}_3,u)-\gamma ({\mathbf {h}}_2,u) \over {\gamma ({\mathbf {h}}_3,0) - \gamma ({\mathbf {h}}_2,0)}}- {\gamma ({\mathbf {h}}_1,u)-\gamma ({\mathbf {h}}_2,u) \over {\gamma ({\mathbf {h}}_1,0) - \gamma ({\mathbf {h}}_2,0)}}=0, \qquad \forall \, u. \end{aligned}$$

(62)

Recalling the relationship between $\gamma$ and C, the expression (62) can be rewritten as:

$$\begin{aligned} {C({\mathbf {h}}_3,u)-C({\mathbf {h}}_2,u) \over {C({\mathbf {h}}_3,0) - C({\mathbf {h}}_2,0)}}- {C({\mathbf {h}}_2,u)-C({\mathbf {h}}_1,u) \over {C({\mathbf {h}}_2,0) - C({\mathbf {h}}_1,0)}}=0, \qquad \forall \, u. \end{aligned}$$

(63)

Analogously, for the proof of the property in (30).

Part 2 (only if)

Let C be a space-time covariance function. The ratio of increments in (29), where the spatial marginal $C({\mathbf {h}} ,0)$ is interpreted as an independent variable, is constant with respect to this last variable and depends solely on u. This implies that the space-time covariance C is a linear function of the spatial marginal. Analogously, the incremental ratio in (30), where the temporal marginal $C(\mathbf 0 ,u)$ is interpreted as an independent variable, is constant with respect to this last variable and depends solely on ${\mathbf {h}}$. This implies that the space-time covariance function C is a linear function of the temporal marginal. In conclusion, the space-time covariance function C is a linear function of both marginals, thus the most general form that ensures this feature is given by the construction (27).

Appendix 4: Test for some classes of covariance function models

The appropriateness of a class of space-time covariance function models can be investigated through the following steps:

• 1. Estimation of the space-time covariance surface ($\widehat{C}({\mathbf{h}},u)$ for a set of space-time lags $({\mathbf{h}},u)$) and of the corresponding empirical space-time correlation function ($\widehat{\rho }({\mathbf{h}},u)$).

• 2. Fix the class of models to be tested on the basis of empirical evidences (such as type of non-separability, behavior at the origin and to infinity) and the corresponding null hypothesis.

• 3. Selection of spatial and temporal lags ($\Lambda$). Note that the integrated product, Gneiting and Cressie class of models have to be tested at least on one triplet of spatial lags ${\mathbf {h}}_{i_1}, {\mathbf {h}}_{i_2}, {\mathbf {h}}_{i_3}$, such that $||{\mathbf {h}}_{i_1}||^{2\gamma }- ||{\mathbf {h}}_{i_2}||^{2\gamma } = ||{\mathbf {h}}_{i_2}||^{2\gamma }-||{\mathbf {h}}_{i_3}||^{2\gamma }$, ${i_1}\ne {i_2}\ne {i_3}$ or at least on one triplets of temporal lags ${u}_{j_1}, {u}_{j_2}, {u}_{j_3}$, such that $u_{j_1}^{2\alpha }-u_{j_2}^{2\alpha }=u_{j_2}^{2\alpha }-u_{j_3}^{2\alpha }$, ${j_1}\ne {j_2}\ne {j_3}$.

• 4. Computation of the test statistic which requires the estimation of ${\mathbf {\Sigma }}, \widehat{{\mathbf {G}}}, {\mathbf {f}}(\widehat{{\mathbf {G}}})$ and the construction of the contrast matrix A (Li et al. 2007).

• 5. If the p value associated with the test statistic is less than 0.05 the null hypothesis is rejected.