PAR(p)-vine copula based model for stochastic streamflow scenario generation

Abstract

Synthetic streamflow data is vital for the energy sector, as it feeds stochastic optimisation models that determine operational policies. Considered scenarios should differ from each other, but be the same from a statistical point of view, i.e., the scenarios must preserve features of the original time series such as the mean, variance, and temporal dependence structures. Traditionally, linear models are applied for this task. Recently, the advent of copulas has led to the emergence of an alternative that overcomes the drawbacks of linear models. In this context, we propose a methodology based on vine copulas for the stochastic simulation of periodic streamflow scenarios. Copula-based models that focus on single-site inflow simulation only consider lag-one time dependence. Therefore, we suggest an approach that incorporates lags that are greater than one. Furthermore, the proposed model deals with the strong periodicity that is commonly present in monthly streamflow time series. The resulting model is a non-linear periodic autoregressive model. Our results indicate that this model successfully simulates scenarios, preserving features that are observed in historical data.

1 Introduction

A unique characteristic of the Brazilian Electricity Sector is that most energy is generated by hydroelectric power plants. This means that planning is a tremendous challenge, owing to the uncertainty associated with hydrological and rainfall regimes.

The operation is centralised, and is usually determined by computational platforms based on stochastic programming. Streamflow scenarios are one of the primary inputs of these platforms. Hence, models capable of simulating realistic scenarios are crucial for the successful operation of the system.

Linear time series models belonging to the Box and Jenkins family are commonly employed for the stochastic simulation of streamflows (see Salas et al. 1980; Jimenez et al. 1989; Pereira and Souza 2014; Souto et al. 2014; Ursu and Pereau 2016).

In general, such models adopt simplifying assumptions, modelling only linear effects. Sharma and O’Neill (2002) described the disadvantages of these models, such as limitations in representing non-standard probability distribution functions or restrictions in modelling non-linear dependencies between current and previous flow values. Streamflow data routinely is not normally distributed. Therefore, the Gaussian assumption that is implicit in these models may not be appropriate. Moreover, for the simulation of scenarios via Monte Carlo methods, the Gaussian assumption produces sampled values in the range ($-\infty ,\infty$), which does not ensure that all generated scenarios will be positive. Transformations of the original data may overcome these drawbacks, but according to Hao and Singh (2011) this may introduce some bias into the simulated scenarios.

Recently, with the advent of copulas, an alternative type of model has emerged. Owing to their flexibility, copulas have been applied to describe various phenomena in hydrology (see Grimaldi and Serinaldi 2006; Song and Singh 2010; Song-Bai and Kang 2011; Zhang et al. 2013; Xu et al. 2017). In terms of the simulation of streamflow scenarios, Lee and Salas (2011) were the first to apply bivariate copulas to model the temporal dependence of yearly streamflow time series. They studied the properties of such a series, and performed a case study for the Nile River.

Hao and Singh (2012) proposed a method using copulas and the entropy principle to construct a model for monthly streamflow simulation. The marginal distributions were obtained using entropy methods, whereas the bivariate joint distributions of two adjacent months were estimated via bivariate copulas. The authors also proposed an alternative version, by inserting an aggregated variable so that trivariate copulas were required.

Zachariah and Reddy (2013) developed an entropy-copula-based model for the simulation of monthly inflows of the Hirakud Dam, India. They employed a bivariate Gumbel-Hougaard copula to model the time dependence between two consecutive months. Similarly, Kong et al. (2015) proposed a maximum entropy Gumbel-Hougaard copula method for the simulation of monthly scenarios of the Xiangxi River, China.

Li et al. (2013) estimated a conditional joint distribution between two adjacent months, conditioned on covariates such as climatic variables or aggregated flow variables. The temporal dependence was captured via bivariate conditional copulas. The results were satisfactory, although the authors highlighted the limitations of the model in reproducing time lags greater than one.

Jeong and Lee (2015) employed the approach proposed by Lee and Salas (2011) associated with a periodic Markov Chain to simulate seasonal intermittent streamflows. They applied bivariate copulas to estimate the joint distribution between two subsequent months.

The copula-based models outlined above have focused on modelling lag-one time dependence. For this reason, the main goal of the present paper is to propose a methodology based on high dimensional copulas for the stochastic simulation of periodic streamflow time series. Our approach allows the model to consider lags that are greater than one. Moreover, our approach accommodates the periodicity that is commonly present in hydrologic data. The resulting model can be understood as a (non-)linear periodic autoregressive model of order p, where the orders, as well as the copulas, alternate according to the period.

The proposed model was tested using the streamflow time series of the Manso River. A Monte Carlo study demonstrates that the model can successfully capture the time dependence structure. In addition, an analysis of scenarios indicates that the model is capable of simulating streamflow data such that historical features observed in the original time series are preserved.

This paper is organised as follows. Section 2 briefly introduces the concept of copulas and vine copulas. Section 3 describes the proposed methodology, and Sect. 4 presents the case study. Finally, in Sect. 5 we present our conclusions.

2 Copulas

Consider a joint density function $f(y_1,\ldots ,y_d)$ of d random variables $\mathbf {Y}=(Y_1,\ldots ,Y_d)$. A simple and intuitive way to understand copulas is to think of a multivariate distribution F as a composition of a copula C and marginals distributions $F_1,\ldots ,F_d$. In fact, this statement traces back to Sklar’s theorem (see Sklar 1959), who formally stated that if F is a d-dimensional distribution function with margins $F_1,\ldots ,F_d$, then there exists a copula $C\,{:}\,[0,1]^d \rightarrow [0,1]$ such that for all $\mathbf {y}=(y_1,\ldots ,y_d) \in \mathfrak {R}^d$,

$$F(y_1,\ldots ,y_d)=C(F_1(y_1),\ldots ,F_d(y_d)).$$

(1)

In terms of a multivariate density function, $f(x_1,\ldots ,x_d)$ is written as

$$f(y_1,\ldots ,y_d)=c_{1,2,\ldots ,d}(F_1(y_1),\ldots ,F_d(y_d))\prod _{i=1}^{d}f_i(y_i),$$

(2)

where $c_{1,2,\ldots ,d}(\cdot )$ is a d-variate copula density.

If the marginal distributions are continuous, then the copula C is unique. This theorem is of practical relevance, because it says that it is possible to build multivariate distributions by modelling the marginal components separately from the dependence structure (represented by the copula C).

Copulas can represent any type of association. They are not restricted to the usual linear dependence represented by correlations, as they are sufficiently flexible to model any kind relationship between variables. For a broad discussion regarding the dependence structures and some fallacies relating to correlations, see McNeil et al. (2010).

2.1 Vine copulas

Until a few years ago, major advances regarding copulas mainly occurred in the bi-dimensional case. Hence, the number of bivariate copulas, as well as their flexibility regarding dependence structures, is considerably high. On the other hand, in higher than three dimensions, the number of d-dimensional copulas is limited. Moreover, these copulas usually possess restrictions, making their use less attractive.

A pair-copula construction (PCC) provides an alternative to constructing d-dimensional copulas. This was first considered by Joe (1996), and subsequently addressed by Bedford and Cooke (2001, 2002) and Aas et al. (2009). A PPC can be viewed as a decomposition of a multivariate density function f into a set of conditional and unconditional bivariate copulas and marginal densities. This enables the construction of d-dimensional copulas that incorporate all the flexibility of bivariate copulas (see Aas et al. 2009).

In general, any multivariate density function can be decomposed as

$$f(y_1,\ldots ,y_d) = f(y_d|y_1,\ldots ,y_{d-1}) \cdot f(y_{d-1}|y_1,\ldots ,y_{d-2})\cdot \cdot \cdot f(y_1).$$

(3)

According to Aas et al. (2009), the conditional densities in Eq. (3) can be written in terms of copula densities using the general expression

$$f(y/\pmb {v}) = c_{y,v_j|\pmb {v}_{-j}}(F(y|\pmb {v}_{-j}),F(v_j|\pmb {v}_{-j}))\cdot f(y|\pmb {v}_{-j}),$$

(4)

where $c_{y,v_j|\pmb {v}_{-j}}(\cdot ,\cdot )$ is a bivariate copula density, $\pmb {v}$ is a d-dimensional vector, $v_j$ is one component of $\pmb {v}$, and $\pmb {v}_{-j}$ is a vector equal to $\pmb {v}$ excluding the jth component.

For example, in the three dimensional case (see Aas et al. 2009), one possible pair-copula construction of the joint density function $f(y_1,y_2,y_3)$ is

$$\begin{aligned} f(y_1,y_2,y_3) &= {} f_{1|2,3}(y_1|y_2,y_3)f_{2|3}(y_2|y_3)f_{3}(y_3) \nonumber \\ &= {} c_{1,2}(F_1(y_1),F_2(y_2)) c_{2,3}(F_2(y_2),F_3(y_3)) c_{1,3|2}(F_{1|2}(y_1|y_2)F_{3|2}(y_3|y_2))\prod_{i=1}^3f_i(y_i). \nonumber \\ &\quad \end{aligned}$$

(5)

Joe (1996) demonstrated that the conditional distribution functions, i.e., the arguments of the conditional copula, can be obtained recursively by applying

$$F(y|\pmb {v})=\frac{\partial C_{y,v_j| {\pmb {v}_{-j}}}(F(y|\pmb {v}_{-j}),F(v_j|\pmb {v}_{-j}))}{\partial F(v_j|\pmb {v}_{-j}) }.$$

(6)

When $\pmb {v}$ is a scalar and v and y are uniform, e.g., $y=u_1$ and $v=u_2$ with $u_1,u_2 \sim U[0,1]$, Eq. (6) assumes the form

$$\begin{aligned} w &=h(u_1;u_2,\theta _{12})=F_{1|2}(u_1|u_2)=C_{1|2}(u_1|u_2)\\ &=\frac{\partial C_{u_1,u_2}(u_1,u_2,\theta _{12})}{\partial u_2}.\end{aligned}$$

(7)

Equation (7) is known as the h-function. The second argument is the conditioning variable, and $\theta _{12}$ denotes the set of copula parameters. More details can be found in Aas et al. (2009). Furthermore, it is possible to define the inverse h-function; that is,

$$u_1=h^{-1}(w;u_2,\theta _{12})=F^{-1}_{1|2}(w|u_2)=C^{-1}_{1|2}(w|u_2),$$

(8)

where w is uniformly distributed.

Aas et al. (2009) derived conditional copulas for some commonly employed bivariate copulas. Joe (2014) presented a comprehensive list of h-functions and inverse h-functions.

The inverse h-function plays a pivotal role in the simulation process, in that the algorithms for sampling from a PPC are based on the inverse transformation procedure. For further details, see Mai and Scherer (2012).

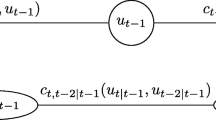
For the purpose of organising the PCCs, Bedford and Cooke (2001, 2002) proposed a graphic model named the regular vine (R-vine model). Broadly speaking, this consists of a nested set of trees $V=(T_1,\ldots ,T_{d-1})$, where the edges in $T_j$ are nodes in the tree $T_{j+1}$. Moreover, two edges in $T_j$ are only joined by an edge in $T_{j+1}$ if these edges share a common node, as described by Kurowicka and Cooke (2006). Figure 1 illustrates an example of an R-vine with three variables. This particular tree structure, where each node in $T_1$ has a degree of at most two, is known as a D-vine.

Fig. 1

Example of a three-dimensional D-vine

Copulas have been applied to model multivariate distributions. In particular, in cases where the number of variables is high, the use of vine copulas is fairly common. In addition, copulas are useful for modelling the temporal dependence of a time series. For example, see Chen and Fan (2006), Mendes and Aíube (2011), Mendes and Accioly (2014), Brechmann and Czado (2015), Smith (2015) and Joe (2014), and references therein.

Joe (2014) presented some copula formulations of a univariate stationary time series. According to his work, these formulations extend the Gaussian models, thereby allowing the modelling of non-linear effects. In particular, a Markov order p time series represented via a copula can be understood as a non-linear version of the Gaussian autoregressive model AR(p). The general form of a Markov order one series is $y_t = g(\varepsilon _t;y_{t-1})$, where $\{\varepsilon _t\}$ is a sequence of independent and identically distributed random variables and $\{y_t\}$ is a sequence of observed random variables. Here, $\varepsilon _i$ is independent of $y_j$ for $j < i$. For $p \ge 2$, the general form assumes that $y_t = g(\varepsilon _t;y_{t-p},\ldots ,y_{t-1})$. This means that $y_t$ is only dependent on the past by way of the most recent p observations.

Under certain conditions, $u_t = F_y(y_t)$, with $u_t \sim U[0,1]$. If $p=1$, then we have a copula between $u_{t-1}$ and $u_t$. If $p=2$, then we have $C_{t-2,t-1,t}(u_{t-2},u_{t-1},u_{t})$, where the marginal copula $C_{t-2,t-1}$ must be identical to $C_{t-1,t}$ in order to ensure stationarity. For $p \ge 2$, we have $C_{t-p,\ldots ,t}(u_{t-p},\ldots ,u_t)$, where marginal copulas that correspond to the same time lag must be the same (see Joe 2014). According to Joe (2014), one possibility for obtaining a copula that respects these constraints is to use a D-vine.

Next, we present an example of how a Markov p time series can be written in terms of pair-copulas. For this, consider a univariate time series $\mathbf {Y}=\{Y_1,\ldots ,Y_T\}$, where the joint density distribution of $\mathbf {Y}$ is $f(y_T,\ldots ,y_1)$. This can be factorized as

$$f(y_T,\ldots ,y_1)= f(y_1) \cdot \prod _{t=2}^{T}f(y_t|y_{t-1},\ldots ,y_1).$$

(9)

Assuming a Markov process of order two, the joint density becomes

$$f(y_T,\ldots ,y_1)=f(y_1) \cdot \prod _{t=2}^{T}f(y_t|y_{t-1},y_{t-2}).$$

(10)

We also know that

$$f(y_t|y_{t-1},y_{t-2})= c_{t,t-2|t-1}(u_{t|t-1},u_{t-2|t-1}) \cdot c_{t,t-1}(u_t,u_{t-1}) \cdot f(y_t),$$

(11)

where $u_{t|t-1}=F_{t|t-1}(y_t|y_{t-1})$ and $u_{t-2|t-1}=F_{t-2|t-1}(y_{t-2}|y_{t-1})$. By inserting Eq. (11) into Eq. (10), we obtain that

$$f(y_T,\ldots ,y_1)=f(y_1) \cdot \prod _{t=2}^{T}c_{t,t-2|t-1}(u_{t|t-1},u_{t-2|t-1}) \cdot c_{t,t-1}(u_t,u_{t-1}) \cdot f(y_t).$$

(12)

For example, if the marginal distributions are Gaussian and all pair-copulas are bivariate Gaussian copulas, then Eq. (12) represents a stationary Gaussian AR(2) (see Smith et al. 2012).

3 Proposed model

In this section, we introduce the proposed periodic methodology based on a vine copula model. First, let us assume that $y_t$, with $t=1,\ldots ,T$, is a streamflow time series with period s (the number of intervals within a year). Here, N is the number of years, i.e., $T/s = N$. Hence, we can rewrite the time index as $t=t(r,m)=(r-1)s + m$, where $r=1,\ldots ,N$ and $m=1,\ldots ,s$. In a monthly-based time series, r represents the number of years, while m denotes the number of months.

Moreover, let $u_{t(r,m)} = F^m(y_{t(r,m)})$ and $u_{t(r,m)-i} = F^{m-i}(y_{t(r,m)-i})$. In this manner, the multivariate distribution of a specific period m and its $d-1$ previous months is

$$\begin{aligned} & F^m(y_{t(r,m)-d+1},\ldots ,y_{t(r,m)-1},y_{t(r,m)}) \\ &\quad =C^m_{t,\ldots ,t-d+1} (u_{t(r,m)-d+1},\ldots ,u_{t(r,m)-1},u_{t(r,m)}). \end{aligned}$$

(13)

The idea behind our approach is to estimate a d-dimensional vine copula for each period m, where both the order and the copulas vary according to the period. Our methodology has a straightforward relationship with the periodic autoregressive models (PAR(p), see Salas et al. 1980). The PAR(p) model represents an extension of the autoregressive model, where both the autoregressive parameters and the orders change over the periods. Thus, our model can be viewed as a (non-)linear version of PAR(p). Mathematically, the PAR(p) model of order $\mathbf {p}=[p_1,\ldots ,p_{s}]$ can be defined as

$$\left( \frac{y_t-\mu _m}{\sigma _m}\right) =\sum _{k=1}^{p_m}\phi _{k,m}\left( \frac{y_{t-k}-\mu _{m-k}}{\sigma _{m-k}}\right) + a_t,$$

(14)

where m represents the month ($m=1,\dots ,s$), $\mu _m$ is the monthly mean, $\sigma _m$ is the monthly standard deviation, $\phi _{k,m}$, is the kth autoregressive parameter of the period $m, p_m$ is the autoregressive order of the period m, and $a_t$ represents a series of independent noises with zero average and variance $\sigma ^{2(m)}_a$.

3.1 Streamflow simulation based on the periodic vine copula model

Consider a d-dimensional distribution function F of some random vector $\mathbf {Y}=(Y_1,\ldots ,Y_d)$, with inverse conditional distribution functions $F^{-1}_{i|1,\ldots ,i-1}(\cdot |y_1,\ldots ,y_{i-1})$ for $i=2,\ldots ,d$. The sampling of new observations $y_1,\ldots ,y_d$ from F can be performed by applying the inverse transformation procedure. The general approach is based on a sequence of inverse conditional distributions, and is summarised as follows. We initially sample $w_i \sim U(0,1)$ for $i=1,\ldots ,d$, and we subsequently iterate $y_1:=w_1, y_2:=F^{-1}_{2|1}(w_2|y_1), y_3:=F^{-1}_{3|1,2}(w_2|y_1,y_2)$, etc., until $y_d:=F^{-1}_{d|1,\ldots ,d-1}(w_d|y_1,\ldots ,y_{d-1})$. The resulting $(y_1,\ldots ,y_d)$ is a sample from F. For further details, see Joe (2014).

This approach can also be employed to simulate new observations from a copula, because any conditional distribution function can be expressed in terms of its copulas. This proceeds as $u_1:=w_1, u_2:=C^{-1}_{2|1}(w_2|u_1), u_3:=C^{-1}_{3|1,2}(w_2|u_1,u_2),\ldots ,u_d:=C^{-1}_{d|1,\ldots ,d-1}(w_d|u_1,\ldots ,u_{d-1})$. The resulting $(u_1,\ldots ,u_d)$ is a sample of dependent uniform random variables.

In a streamflow simulation, the only variable in which we are interested is the simulation of $u_t$ conditioned on the previous $d-1$ observations. Assuming that t belongs to a period m, we have that

$$u_t:=C^{-1}_{t|t-1,t-2,\ldots ,t-d+1}(w_t|u_{t-1},u_{t-2},\ldots ,u_{t-d+1}).$$

(15)

The simulated variable $u_t \sim U(0,1)$ must be transformed back to the original scale using the corresponding inverse cumulative distribution function. The inverse of the conditional copula distribution (Eq. 15) can be written in terms of h-functions and inverse h-functions, obtained via Eqs. 6, 7 and 8. For more details, see Aas et al. (2009) and Mai and Scherer (2012).

4 Case study

We tested our approach on a monthly mean inflow $(\mathrm{m}^3/\mathrm{s})$ time series, measured at the Manso hydroelectric power plant. The data was provided by the Operator of the National Electricity System (ONS). The time period covered runs from January 1931 to December 2012, totalling 82 complete years. By $y_t$, we denote a realization of the monthly mean inflow random variable $Y_t\,(t=1,\ldots ,984)$.

Figure 2 depicts the original streamflow time series (left hand side). On the right hand side, we observe the same time series organised according to the months. It is possible to observe that during drought periods (winter in Brazil, which occurs in the middle of the year), the average and variance are considerably smaller than for the wet periods (summer, at the beginning and end of the year). This reveals the strong periodicity that is present in these types of time series.

Fig. 2

Manso River. a Streamflow of the Manso River. b Periodicity of the Manso River

In the copula framework, the first step is to transform the original data into copula data, i.e., to transform the original time series $y_1,\ldots ,y_{984}$ to $u_1,\ldots ,u_{984} \sim U[0,1]$. For this task, following an inspection of the data, we decided to apply the gamma distribution as the marginal model. The use of the gamma distribution to represent hydrologic data is also common, mainly because its flexibility and positive support (see, for example, Lee and Salas 2011; Li et al. 2013; Jeong and Lee 2015). Thus, for each month a gamma distribution was fitted. The probability density function is given by:

$$f(x|\alpha ,\beta ) = \frac{1}{\beta ^\alpha \varGamma (\alpha )}x^{\alpha -1}e^{-x/\beta },$$

(16)

where $x \ge 0, \alpha$ is the shape parameter, and $\beta$ is the scale parameter. Both $\alpha$ and $\beta$ are greater than zero.

Finally, the copula data is obtained through the probability integral transform

$$\hat{u}_{t(r,m)} = F^m(y_{t(r,m)}|\hat{\alpha }^m,\hat{\beta }^m), \quad r=1,\ldots ,82,\quad m=1,\ldots , 12,$$

(17)

where $F^m$ is the estimated gamma cumulative distribution function of the period m.

Following the transformation, it is vital to check whether the copula data follows a standard uniform distribution. This can be achieved by applying the Anderson–Darling test. The results indicate that the gamma distribution is a reasonable choice for the monthly marginal distributions.

Having obtained the copula data, the next step is to estimate the monthly vine copulas. One question that emerges is that of how to choose the appropriate dimension. In our case, we allowed the periodic vine copula to assume a dimension between two and four. This means that we are constructing non-linear autoregressive models of order equal to one, two, or three.

To determine these dimensions, we suggest performing an iterative procedure together with a bivariate asymptotic independence test (see Genest and Favre 2007). In doing so, for each month we start with a two-dimensional copula. In sequence, we estimate a three-dimensional copula, and check if the conditional copula of $u_{t-2}$ and $u_{t}$ given $u_{t-1}$ is an independence copula by using the independence test. If it is an independence copula, then we choose the dimension as two. Otherwise, we increase the dimension to four. Again, we test if the conditional copula of $u_{t-3}$ and $u_{t}$ given $u_{t-1},u_{t-2}$ is an independence copula or not. If we have evidence that $C_{{t-3},{t}|{t-1},{t-2}}$ is not a product copula, then we choose the dimension as four. On the other hand, if we cannot reject the hypothesis that $C_{{t-3},{t}|{t-1},{t-2}}$ is an independence copula, then we decrease the order to three.

The idea behind this methodology is that we only need to check the last tree of the vine. This is equivalent to testing whether or not the conditional copula $C_{{t-d+1},{t}|{t-1},\ldots ,{t-d+2}}$ is an independence copula. In other words, we are analysing the association between $u_{t-d+1}$ and $u_t$, excluding all intermediate effects. Thus, if the variable $u_{t-d+1}$ has no association with $u_t$, then we consider that the dimensional d does not introduce any additional information to explain the temporal dependence.

Regarding bivariate copulas, we allowed our model to choose between the independence (I), Gaussian (N), Student-t (S-t), Gumbel (G), Clayton (C), and Frank (F) copulas.

The selection of the bivariate copulas was carried out via the Bayesian information criterion (BIC). Table 1 presents the selected bivariate copulas. The Clayton copula, which only has a lower tail dependence coefficient, occurs the most often. Thus, it is possible to affirm that there is a dependence between lowflows, while the occurrence of highflows is more random. In terms of simulation, this means that small streamflow values are very likely to be followed by small values. In addition, the high frequency of Archimedean copulas indicates the presence of asymmetric dependence structures.

Table 1 Copula families

Table 2 depicts the selected dimensions of the monthly copulas. Bivariate copulas are predominant. In fact, the highest dimensions occurred between May and August, which coincides with the winter/drought periods in Brazil.

Table 2 Selected dimensions

In order to better understand the potential of the estimated model, we performed an in-sample analysis. For this, we calculated the one step ahead forecast. Unlike linear models, the forecasts here cannot be obtained analytically, and for this reason they must be evaluated via simulation.

For each one step ahead forecast, we simulated 5000 observations, given the past values of the streamflow time series. The collection of these observations represents the forecast conditional distribution, which means that the conditional expectation can be obtained by calculating the average of these simulations. Figure 3 depicts the original time series (black line) and the fitted values (one step ahead forecast—red line).

Fig. 3

Real and fitted values for Manso River streamflow

In addition, we also estimated the monthly residuals, using the aforementioned forecasts. Figure 4 shows the autocorrelation function of the residuals based on Kendall’s $\tau$ coefficient. The autocorrelations are close to zero. The critical values of the independence test (Genest and Favre 2007) are represented by the dotted lines. In practical terms, if the autocorrelation lies between these two lines, then we cannot reject the hypothesis that it is equal to zero. Thus, we conclude that the proposed model is capable of modelling the time dependence. Moreover, the proposed approach appears to be reasonable for the identification of the orders.

Fig. 4

Auto-dependence function of residuals. a January. b February. c March. d April. e May. f June. g July. h August. i September. j October. k November. l December

We now present the simulated scenarios obtained from the estimated periodic vine copula model. We simulated 200 scenarios, each containing 60 months. To initialize the procedure, we used the most recent year of the historical time series. The simulation procedure has taken forty-seven seconds on an Intel^®Core(TM) i5-2430M with a CPU of 2.40 GHz and 4 GB of RAM. Our approach was implemented in R based on the VineCopula R-Package (Schepsmeier et al. 2015).

Figure 5 shows all the 200 generated scenarios (grey lines), as well as their monthly averages (blue line) and the historical average (red line). It can be observed that, the proposed model was able to represent the strong periodicity that exists in the data set. Furthermore, we clearly see that the average of the scenarios practically coincides with the historical average.

Fig. 5

Simulated streamflow scenarios

We performed some statistical tests to analyse these scenarios in more depth. The variables of interest are the monthly mean, the monthly variance, and the form of the distribution in each month. For each one of the 60 months, we verified whether this was statistically equal to the corresponding month in the historical record. This analysis was repeated for all of the 60 simulated periods.

We employed the t-test, the Levene test, and the Kolmogorov–Smirnov test. The Kolmogorov–Smirnov test is a non-parametric test that assesses whether two samples come from the same distribution.

Figure 6 summarizes the results of these three tests. The bars represent the p-values of the tests carried out for each of the 60 periods. The black line indicates the significance level of 5%. P-values greater than this level indicate that the null hypothesis cannot be rejected. In practical terms, these results indicate that the simulated scenarios replicated the historical features of the observed streamflow time series. The approval rates were 99% for all three of the employed tests.

Fig. 6

Statistical tests over the simulated scenarios. a t test. b Levene test. c K–S test

Finally, we demonstrate that the simulated scenarios replicate the historical time dependence. For this analysis, a new set composed of 200 scenarios consisting of 100 years was simulated. For each scenario, we calculated the monthly Kendall’s $\tau$ coefficient up to lag five. Figure 7 presents a comparison between the historical values (red triangle) and the average of the simulated values (blue dot). The simulated values are reasonably close to the historical values for the majority of periods and lags. This allows us to conclude that the proposed methodology accurately models and replicates the time dependence.

Fig. 7

Analysis of the simulated autocorrelation based on Kendall’s $\tau$ coefficient for lags 1–5

5 Conclusion

Copula-based models for a single-site stochastic simulation only consider a lag-one time dependence. For this reason, the aim of this paper was to propose a new methodology based on vine copulas, in order to correctly deal with lags that are greater than one. Our model can be understood as a non-linear periodic autoregressive model, where the dimensions and the copulas vary according to the periods.

The copula approach overcomes some drawbacks of the ARMA models. It does not simulate unrealistic scenarios (scenarios with negative values), can correctly model non-linear effects, and is flexible to the point of modelling non-standard marginal distributions. Unlike the outlined copula models for hydrologic simulation, our approach can also model high-order periodic streamflow time series.

An in-sample analysis indicated that the model was able to accurately model the temporal structure of the Manso River. Furthermore, an investigation of the generated scenarios demonstrated that the proposed model is capable of simulating scenarios that preserve features that are observed in the historical time series.