1 Introduction

Drought is a natural hazard characterized by lower than expected precipitation. When drought extends over a season or longer time periods, it leads to water shortages, and the available water is insufficient to meet the demands of human activities and environment (WMO 2006). As compared to other natural hazards, such as floods and hurricanes, the spatial extent of droughts is usually much larger (Obasi 1994). Drought events are mainly characterized by its magnitude or intensity, duration and spatial coverage. Intensity refers to the degree of deficit in precipitation (for meteorological drought assessment) or stream flow (for hydrological drought assessment) and is measured by the departure from normal condition. Droughts also differ significantly in terms of its spatial characteristics from one region to another.

Drought is a multivariate phenomenon, often characterized by its severity, duration, intensity and spatial extent. In order to understand spatial and temporal nature of droughts in regional scale, several studies have been carried out in the past. Regional drought risk can be evaluated through multivariate relationship such as development of drought severity–area–frequency (S–A–F) or intensity–area–frequency (I–A–F) curves. These curves were derived based on mathematical relationships between drought severity or intensity and areal extent for various return periods. Most commonly used probability distributions to derive these relationships are the Extreme value distributions. For a given percentage areal extent of drought, the associated drought magnitude of particular event is extracted from the historical records and then frequency analysis is performed. In some cases, when only a few years’ data are available, the exceedance series for drought property may be determined by ranking the data and then empirical relationship can be established. Kim and Valdés (2002) investigated the temporal and spatial characteristics of droughts using palmer drought severity index (PDSI) for the Conchos River basin Mexico using intensity-area-frequency curves. In their study the point estimates of PDSI were interpolated using kriging method. Hisdal and Tallaksen (2003) derived S–A–F curves in Denmark analyzing monthly precipitation and streamflow time series using empirical orthogonal functions (EOF) method. The entire Denmark was divided into 260 grid-cells of 14 × 17 km, and the monthly mean and the EOF-weight coefficients were interpolated by kriging. Using Monte Carlo simulation, long time series of precipitation and streamflow were generated at each grid cell. The area under drought and the deficit based on stream flow and precipitation were then used to produce drought S–A–F curves. Loukas and Vasiliades (2004) studied spatio-temporal variability of meteorological droughts in Thessaly region of Greece during 1960–1993. The observed monthly precipitation data from 50 meteorological stations were spatially interpolated over the study region using multiple linear regression. The drought characteristics were examined using standardized precipitation index (SPI) values at spatial resolution of 8 × 8 km and at multiple time scales, and then drought S–A–F curves were developed. Mishra and Desai (2005) analyzed SPI-based drought S–A–F relationship for the time period 1965–2001 in Kansabati River basin in India. In their study, inverse distance weighting approach was used as a spatial interpolation of SPI data. Andreadis et al. (2005) employed gridded precipitation and temperature data at 0.5° spatial resolutions as input to the variable infiltration capacity model—a physically based macroscale hydrologic model to obtain soil moisture and runoff. Then they identified hydrological droughts during 1920–2003 over continental US. A clustering algorithm was used to identify individual drought events and their spatial extent at each monthly time step. Severity–area–duration curves at different drought durations (3, 12, 24 and 48 months) were constructed to relate area of each drought to its severity. Their analysis showed that the droughts of the 1930s and 1950s were covering larger geographical area, whereas the early 2000s drought in western US was found to be the most severe drought in terms of magnitude during the study period. Pai et al. (2010) evaluated district-wise drought climatology over India during southwest monsoon period using SPI and percent of normal indices during 1901–2003. The study concluded that as drought climatology based on SPI was not biased by aridity, hence SPI is better drought index for district-wise drought monitoring. Santos et al. (2010) analyzed meteorological droughts in Portugal from September 1910 to October 2004 using SPI at multiple time scales such as 1, 6 and 12 months. In their study, the southern part of the country was found to be severely affected by drought as compared to northern region. Tallaksen et al. (2011) analyzed drought over Europe for the period 1963–2000, based on observed streamflow and runoff simulated by WATCH (Water and Global change) multi-model ensemble comprising nine large scale models. Drought S–A–F curves were then derived based on simulated runoff from one of the ensemble model. Kumar et al. (2012) studied the drought pattern across space and time in India using gridded daily precipitation data at 1° spatial resolution from June to September (1951–2007). They noted increasing trend of all India drought during the month of July.

In a large country like India where precipitation varies both in space and time, drought is one of the most frequently occurring natural calamities in several parts of the country. The probability of drought varies from once in 2 years in western Rajasthan to once in 15 years in Assam (NDMA 2010). Although Rajasthan is the largest State in India occupying about 10.4 % of the India’s geographical extent but contributes only 1 % of the country’s total water resources (Drought report 2004). The state has maximum probability of drought occurrences in the country (Mall et al. 2006). The period of monsoon is about 2–3 months (July to September) and the annual precipitation varies from 150 to 900 mm in different parts of the state with an average annual precipitation of about 576 mm and the temperature varies from 5 to 45 °C in different seasons (RACP 2012). In India although few studies were carried out for drought analysis based on precipitation data at coarser resolution covering a larger area (Chowdhury et al. 1989; Sinha Ray and Shewale 2001; Guhathakurta 2003; Pai et al. 2010; Ganguli and Janga Reddy 2012; Kumar et al. 2012), but not many studies analyzed spatio-temporal pattern and multivariate risks of droughts in the western Rajasthan region, which is highly vulnerable to frequent droughts. Analyzing drought characteristics including spatial extent and intensity are critical to understand nature of droughts.

The copula approach is a flexible method that allows marginal distribution of any form to model multivariate dependence between drought variables. Copulas are joint distribution functions of standard uniform random variates (Sklar 1959). One of the earlier applications of copulas in drought hydrology was by Shiau (2006). Shiau (2006) investigated bivariate joint distribution of drought properties severity and duration in Southern Taiwan using SPI and theory of copulas. Song and Singh (2010) modeled joint probability distribution of drought duration, severity and inter-arrival time of droughts using trivariate Plackett copula for a case study in China. The parameters of bivariate and trivariate Plackett copulas are estimated using pseudo log-likelihood and genetic algorithm methods. Janga Reddy and Ganguli (2012) applied four different classes of bivariate copulas—Archimedean, extreme value, Plackett, and elliptical families for modelling joint distribution of drought characteristics, and noted that extreme value class Gumbel–Hougaard copula family performed better as compared to other classes of copulas. This copula was also used for deriving severity–duration–frequency curves for western Rajasthan region in India. Mir Abbasi et al. (2012) employed bivariate copulas to model meteorological drought properties—severity and duration of northwestern Iran. According to error analysis and tail dependence coefficient, the Galambos copula was found as best fitted model, which was then used to analyze bivariate probabilistic properties of droughts using secondary as well as conditional return periods. Lee et al. (2012) studied influence of tail shape of four different copula families—Gumbel-Hougaard, Frank, Clayton and Gaussian for bivariate drought frequency analysis in Canada and Iran. Their study showed that Clayton copula is not an appropriate choice for modeling droughts as dependence between two variables in the upper tail of Calyton copula was very weak and similar to the independence case, whereas Frank and Gumbel-Hougaard copula showed better performance for modeling bivariate drought properties. Sadri and Burn (2012) investigated frequency analysis of droughts using copula and performed regionalization by applying 36-nonregulated streamflow data in Canadian Prairies. K-means clustering approach was employed to form initial cluster and then fuzzy c-means algorithm was employed for deciding final groups. Then bivariate copula-based regionalization was compared with traditional multivariate approach defined using bivariate-Gamma distributions. From the analysis it was noted that copula-based model provides shorter return periods as compared to return periods computed using bivariate Gamma distribution, assuming same value of severity and duration respectively.

The present study analyzes meteorological droughts in one of the most drought prone region in India—western Rajasthan. Gridded precipitation (0.5° latitude × 0.5° longitude) data for 35-years (1971–2005) is used to build SPI time series at a time scale of 6-months (SPI-6) for modeling metrological droughts in the region. The main objectives of the present paper are: (1) Modeling drought characteristics at finer resolution in western Rajasthan of India and identify the spatio-temporal trends of droughts using the non-parametric Mann–Kendall test and Sen’s slope estimators; (2) Evaluate the performance of Gumbel-Hougaard, Frank and Plackett copulas for modeling dependence structure of drought properties, and apply copula-based methodology to derive I–A–F curves for the region.

The paper is organized as follows: In Sect. 2, the theoretical concepts of copula modeling, goodness-of-fit test and the tail dependence tests to select suitable copula family are described. The case study and data details are described in Sect. 3.1. The spatial characteristics of droughts, identification of drought spatial extent, analysis of trends and dependence pattern of drought variables are presented in Sect. 3.2. Then marginal distribution fitting of drought variables are presented. The next sub-section deals with application of copulas in modeling joint dependence of drought variables. The subsequent sub-section presents copula-based joint and conditional distributions to derive drought I–A–F curves at various return periods for the selected copula family. Finally summary and conclusions are presented in Sect. 4.

2 Methodology

2.1 Characterization of droughts

In this study drought is modeled using SPI. Calculation of SPI (McKee et al. 1993) for any location and time scale (such as 3, 6, 9 and 12 months) involves fitting aggregated long term precipitation of specific time scale to a probability distribution function (generally Gamma or Pearson Type III distribution), which is then transformed into a standardized normal distribution so that the mean SPI for the location and desired period is zero. This study adopted SPI-6, which uses 6-month aggregated precipitation data. The aggregated precipitation data is fitted to Gamma distribution function. As two-parameter gamma function is undefined for zero values but precipitation distribution may contain zeros, hence a mixed distribution function (which can account zeros and real values of precipitation) is employed and the corresponding cumulative distribution function (CDF) is defined as

$$ F_{X} \left( x \right) = q + \left( {1 - q} \right)G_{X} \left( x \right) $$
(1)

where \( G_{X} \left( x \right) \) is the CDF of Gamma distribution estimated for nonzero precipitation and q is the zero precipitation probability obtained from historical time series. As precipitation is not normally distributed, an equiprobability transformation is carried out from the CDF of mixed distribution to the CDF of the standard normal distribution with zero mean and unit variance. This transformed probability gives the SPI. i.e., \( Z = \psi^{ - 1} \left( {F_{X} \left( x \right)} \right) \), where \( \psi \left( \cdot \right) \) is the CDF of standard normal distribution, and \( \psi^{ - 1} \left( \cdot \right) \) is the inverse of standard normal CDF.

Drought condition in each grid is identified when the SPI value falls below a threshold limit, which is taken as 20 percentile value (≈threshold value of approximately −0.8) of SPI in the grid (Svoboda et al. 2002). In specific, the drought properties are defined as:

  • Percentage area under drought (PAUD): the area is considered to be under drought (in percentage) when spatial coverage of drought exceeds certain percentage thresholds limits of its spatial extent at each monthly time step. Accordingly drought areal extent (\( A_{t} \)) at a time step t is computed using the expression

$$ A_{t} = \frac{{\sum\nolimits_{i = 1}^{{N_{grid} }} {1\left\{ {Z_{i,t} \le Z_{thr} } \right\} \cdot A_{i} } }}{{\sum\nolimits_{i = 1}^{{N_{grid} }} {A_{i} } }},\quad \forall t = 1,2, \ldots ,n $$
(2)

where \( 1\left\{ \Uptheta \right\} \) is a logical indicator function of set \( \Uptheta \), taking the value of either 0 (if \( \Uptheta \) is false) or 1 (if \( \Uptheta \) is true), \( Z_{i,t} \) is the SPI value at month t, \( Z_{thr} \) is the threshold limit of SPI for identifying drought in the grid, \( A_{i} \) denotes influence area of grid i and \( N_{grid} \) is the total number of grids in the region.

  • Intensity (I t ): It is defined as the average of SPI values at various grid points under drought during time step ‘t’ and is computed using the expression

$$ I_{t} = - \frac{1}{{N_{dr\_grids} }}\sum\limits_{i = 1}^{{N_{grid} }} {\left[ {1\left\{ {Z_{i,t} \le Z_{thr} } \right\} \cdot Z_{i,t} } \right]} ,\quad \forall t = 1,2, \ldots ,n $$
(3)

where \( N_{dr\_grids} \) is the total number of grids under droughts, which can be estimated by \( N_{dr\_grids} = \sum\nolimits_{i = 1}^{{N_{grid} }} {1\left\{ {Z_{i,t} \le Z_{thr} } \right\}} \).

2.2 Copula-based joint distributions for modeling drought variables

2.2.1 Copula definition and properties

A two-dimensional copula C is a real function defined on \( \left[ {0,1} \right] \times \left[ {0,1} \right] \) with range \( \left[ {0,1} \right] \). Every element (u, v) in the domain satisfies the following conditions: \( C\left( {u,0} \right) = C\left( {0,v} \right) = 0 \); and \( C\left( {u,1} \right) = u \) and \( C\left( {1,v} \right) = v \). For every rectangle in the domain \( \left[ {u_{1} ,u_{2} } \right] \times \left[ {v_{1} ,v_{2} } \right] \), such that \( u_{1} \le u_{2} \) and \( v_{1} \le v_{2} \), the 2-D copula satisfies the condition C(u 2, v 2) − C(u 2, v 1) − C(u 1,v 2) + C(u1, v 1) ≥ 0. Since copulas are joint distribution functions of standard uniform distributions, a copula function computed at \( F_{X} \left( x \right) \) and \( F_{Y} \left( y \right) \) gives joint distribution function at (x,y) in accordance to Sklar’s (1959) theorem:

$$ C\left( {u,v} \right) = C\left[ {F_{X} \left( x \right),F_{Y} \left( y \right)} \right] = F_{X,Y} \left( {x,y} \right) $$
(4)

The parametric form of copula function allows grouping them into various families. More details about copula functions, associated properties and different copula families can be found in Nelsen (2006). The important copula classes are Archimedean, Elliptical and Plackett copulas. In this study, Archimedean class of Gumbel-Hougaard, Frank family and Plackett copulas are employed to model joint dependence of drought variables. The expressions for the CDF and associated parameters range of copula families are presented in Table 1.

Table 1 Expression of CDF, associated parameter and parameter space of the copula families
Full size table

2.2.2 Estimation of copula parameters

The estimation of copula parameters are performed using maximum pseudo-likelihood (MPL) method. In this procedure, first marginals are estimated using empirical distributions and then copula parameters are estimated using maximization of pseudo log-likelihood function. From d-dimensional random vector \( X \in X_{i,1} ,X_{i,2} , \ldots ,X_{i,d} \) empirical distributions (CDF) of the observations are estimated using their associated ranks, i.e.,

$$ U_{i,d} = \frac{1}{n + 1}\sum\limits_{j = 1}^{n} {1\left\{ {X_{j,d} \le X_{i,d} } \right\}} \quad \forall i = 1,2, \ldots ,n,\;j \ne i,\;d = 1,2 \ldots ,n $$
(5)

For bivariate case, \( U = \left\{ {U_{i,1} ,U_{i,2} } \right\},\quad \forall i = 1,2, \ldots ,n,U_{i,1} \) and \( U_{i,2} \) are the vectors of pseudo-samples of two random variables. Then on substituting the empirical CDFs into bivariate copula density yields log-likelihood function of the form (Genest and Favre 2007)

$$ L_{U} \left( \theta \right) = \sum\limits_{i = 1}^{n} {\ln \left[ {c_{\theta } \left\{ {U_{i,1} ,U_{i,2} } \right\}} \right]} = \sum\limits_{i = 1}^{n} {\ln \left\{ {c_{\theta } \left( {\frac{{R_{i,1} }}{n + 1},\frac{{R_{i,2} }}{n + 1}} \right)} \right\}} \quad \forall i \in \left\{ {1, \ldots ,n} \right\} $$
(6)

where \( c_{\theta } \left( \cdot \right) \) denotes bivariate copula density, \( R_{i,1} \) and \( R_{i,2} \) denotes ranks of the observed data. The parameter \( \theta \) can be obtained by maximizing this rank-based pseudo log-likelihood function numerically,

$$ \hat{\theta } = \arg \,\hbox{max} \,\left\{ {L_{U} \left( \theta \right)} \right\} $$
(7)

In order to avoid trapping at local optimal solution while using a gradient based search technique, a real-coded genetic algorithm (R-GA) is employed to get the optimal parameters of the copula function.

2.2.3 Goodness-of-fit (GOF) test for copulas

The goodness of fit test based on empirical copula process is employed to check the adequacy of copula families in modeling the data. The test is based on empirical process \( \sqrt n \left\{ {C_{n} \left( {u,v} \right) - C_{\theta } \left( {u,v} \right)} \right\},\;u,v \in \left[ {0,1} \right] \), which consists of comparing the distance between rank-based empirical copula \( C_{n} \left( \cdot \right) \) with estimated parametric family of copula \( C_{\theta } \left( \cdot \right) \). The empirical copula \( C_{n} \) of data \( \left( {x_{1} ,y_{1} } \right) \),…, \( \left( {x_{n} ,y_{n} } \right) \) is defined as (Genest et al. 2009)

$$ C_{n} \left( {u,v} \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {1\left\{ {\hat{U}_{i,1} \le u,\hat{U}_{i,2} \le v} \right\}} \quad \left\{ {u,v} \right\} \in \left[ {0,\;1} \right]^{2} $$
(8)

The test statistic is given by Cramér-von Mises (CVM) distance, which is given by (Genest et al. 2009)

$$ S_{n}^{e} = \int\limits_{{\left[ {0,1} \right]^{2} }} {n\left\{ {C_{n} \left( {u,v} \right) - C_{\theta } \left( {u,v} \right)} \right\}^{2} dC_{n} \left( {u,v} \right) = \sum\limits_{i = 1}^{n} {\left\{ {C_{n} \left( {U_{i,1} ,U_{i,2} } \right) - C_{\theta } \left( {U_{i,1} ,U_{i,2} } \right)} \right\}^{2} } } $$
(9)

An approximate p value for the corresponding test statistic is obtained via large sample simulations using parametric bootstrap method (Genest et al. 2009), which consist of following steps:

  • For some large integer N, \( k \in \left\{ {1, \ldots ,N} \right\} \) generate random samples \( X_{i,d}^{k*} = \left\{ {X_{i,1}^{k*} ,X_{i,2}^{k*} } \right\},\;\forall i = \left\{ {1,2, \ldots ,n} \right\},d \in \left\{ {1,2} \right\} \) from distribution \( C_{\theta } \) and compute their associated rank vectors \( R_{i,d}^{k*} = \left\{ {R_{i,1}^{k*} ,R_{i,2}^{k*} } \right\} \).

  • Compute \( U_{i,d}^{k*} = {{R_{i,d}^{k*} } \mathord{\left/ {\vphantom {{R_{i,d}^{k*} } {\left( {n + 1} \right)}}} \right. \kern-0pt} {\left( {n + 1} \right)}} \) for \( i \in \left\{ {1, \ldots ,n} \right\},d \in \left\{ {1,2} \right\} \) and simulate

  • $$ C_{n}^{k*} \left( {u,v} \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {I\left( {\hat{U}_{i,1}^{k*} \le u,\hat{U}_{i,2}^{k*} \le v} \right)} \quad u,v \in \left[ {0,\;1} \right]^{2} $$
    (10)

  • Estimate \( \theta_{n}^{k*} \) from simulated ranked data and compute corresponding CVM distance

$$ S_{n}^{k*} = \sum\limits_{i = 1}^{n} {\left\{ {C_{n}^{k*} \left( {U_{i,1}^{k*} ,U_{i,2}^{k*} } \right) - C_{{\theta_{n}^{k*} }} \left( {U_{i,1}^{k*} ,U_{i,2}^{k*} } \right)} \right\}^{2} } $$
(11)

If \( S_{1:n}^{k*} \le \ldots \, \le S_{n:n}^{k*} \) denote the ordered value of test statistics computed in Eq. 11, then critical value of test statistic at α significance level based on S n is given as \( S_{{\left\lfloor {\left( {1 - \alpha } \right)n} \right\rfloor :n}}^{k*} \). Here \( \left\lfloor x \right\rfloor \) denotes the integer part of x The p value corresponding to test statistic \( S_{n} \) is given by using \( p_{val} = \frac{1}{N}\sum\limits_{k = 1}^{N} {1\left\{ {S_{n}^{k*} \ge S_{n}^{e} } \right\}} \).

2.2.4 Tail dependence test

The tail dependence coefficient (TDC) captures the concordance between extreme values in the lower left quadrant tail and upper right quadrant tails of the distribution. For modeling extremes, upper tail dependence is of much interest. If u be a threshold value then upper tail dependence between two variables X and Y, denoted as \( \lambda_{U} \) is given by

$$ \lambda_{U} = \mathop {\lim }\limits_{{u \to 1^{ - } }} \left\{ {F_{X} \left( x \right) > u|F_{Y} \left( y \right) > u} \right\} $$
(12)

Using copula the above equations can also be expressed as (Nelsen et al. 2008)

$$ \lambda_{U} = \mathop {\lim }\limits_{{u \to 1^{ - } }} \frac{{1 - 2u + C\left( {u,u} \right)}}{1 - u} = 2 - \mathop {\lim }\limits_{{u \to 1^{ - } }} \frac{{1 - C\left( {u,u} \right)}}{1 - u} = 2 - \delta^{\prime}_{C} \left( {1^{ - } } \right) $$
(13)

where the function \( \delta_{C} \left( \cdot \right) \) is the diagonal section of copula C and given by \( \delta_{C} \left( u \right) = C\left( {u,u} \right) \) for every \( u \in \left[ {0,1} \right] \). The estimate \( \lambda_{U} \) measures the concordance between extremely low values and extremely high values of random variables respectively. If \( \lambda_{U} \in \left( {0,1} \right] \), then \( F_{X} \left( x \right) \) and \( F_{Y} \left( y \right) \) are said to show upper tail dependence or extremal dependence. As discussed by Frahm et al. (2005) the model error could be large in a parametric TDC estimate. The limitations of parametric TDC can be overcome by estimating non-parametric TDC. In this study, Capéraá–Fougéres–Genest (CFG estimator \( \lambda_{U}^{CFG} \); Capéraá et al. 1997; Frahm et al. 2005) estimator is employed to study non-parametric TDC. If \( \left\{ {\left( {u_{1} ,v_{1} } \right), \ldots ,\left( {u_{n} ,v_{n} } \right)} \right\} \) be random sample obtained from Copula \( C\left( \cdot \right) \), then bivariate upper tail dependence coefficient using \( \lambda_{U}^{CFG} \) is given by (Frahm et al. 2005)

$$ \hat{\lambda }_{U}^{CFG} = 2 - 2\exp \left[ {\frac{1}{n}\sum\limits_{i = 1}^{n} {\log \left\{ {{{\sqrt {\log \left( {\frac{1}{{u_{i} }}} \right)\log \left( {\frac{1}{{v_{i} }}} \right)} } \mathord{\left/ {\vphantom {{\sqrt {\log \left( {\frac{1}{{u_{i} }}} \right)\log \left( {\frac{1}{{v_{i} }}} \right)} } {\log \left( {\frac{1}{{\hbox{max} \left( {u_{i} ,v_{i} } \right)^{2} }}} \right)}}} \right. \kern-0pt} {\log \left( {\frac{1}{{\hbox{max} \left( {u_{i} ,v_{i} } \right)^{2} }}} \right)}}} \right\}} } \right] $$
(14)

2.3 Copula-based conditional return period of droughts

The conditional return period \( T_{I|A} \left( {i|a} \right) \) of drought intensity given PAUD A = a can be expressed as

$$ T_{I|A} \left( {i|a} \right) = \frac{\zeta }{{1 - F_{I|A} \left( {i|a} \right)}} = \frac{\zeta }{{1 - C_{I|A = a} }} $$
(15)

where \( \zeta = \frac{N}{n} \), N = total length of SPI time series (in years), n = total number of drought events during N years and \( C_{I|A = a} \) denotes conditional CDF of drought intensity given PAUD. The conditional distribution from copula-based joint distribution can be derived using relationship \( C_{I|A = a} = \frac{{\partial C\left( {F_{I} \left( i \right),F_{A} \left( a \right)} \right)}}{{\partial F_{A} \left( a \right)}} \).

3 Case study application

3.1 Study area and data

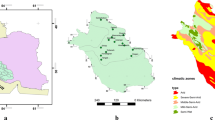
The state of Rajasthan in India has variable topographic features. The dry and parched region occupies major portion of the state. The state is surrounded by the Aravalli Hills stretching from Mount Abu in southwest Kota and Bundi in northeast, covering more than 850 km2 area. The location map of the study region western Rajasthan is shown in Fig. 1. The location lies between the latitude 69.5°–76.5°E and the longitude 24.50°–30.50°N. On an average the altitude of the state varies from 100 to 350 m, but in some places altitude is over 750 m high. The Thar Desert lies in north-west part of the state. The average temperature during winter varies between 8 and 28 °C, and in the summer, it rises up to about 25–46 °C.

Fig. 1
figure 1

Location of the study area—western Rajasthan, India

Full size image

Gridded (0.5° latitude × 0.5° longitude) daily precipitation data obtained from Indian Meteorological Department (IMD), Pune for 35 years (1971–2005) is used to study drought risk at western Rajasthan. The study area comprises 98 grid points with total area 2,00,063 Km2. The details of the development of high-resolution daily gridded precipitation data for Indian region were given in Rajeevan and Bhate (2008). Daily precipitation data are aggregated to monthly time scales, which in turn are used to develop SPI, calculated at monthly time scales, in order to identify droughts in each grid.

3.2 Trend analysis of droughts

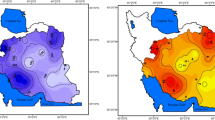
The SPI values calculated at each grid cell are used to analyse the spatio-temporal patterns of drought. The SPI values at various grid cells vary from minimum of −3.92 to maximum of 3.60 during the study period. To analyse the trends, modified Mann–Kendall trend test (Hamed and Rao 1998) with correction for auto-correlation is employed (since SPI time series are generally auto-correlated). Brief details of Mann–Kendall test are given in Appendix. The Mann–Kendall test statistic is computed for each month of monsoon season (June, July, August and September) after correcting for ties. Figures 2 and 3 show Mann–Kendall test statistics for the months of June (Fig. 2a), July (Fig. 2b), August (Fig. 3a) and September (Fig. 3b). The figures show that central part of the region experienced decreasing trend of SPI, resulting in drought conditions as compared to rest of the region. Significance of trend is checked at 5 % significance level. Positive trend in SPI time series is observed during the month of June in northern region, indicating wet conditions in the region. During the month of August 12 % of the grid cells in the region showed downward trend, which is statistically significant at 5 % level, whereas none of the upward trends in SPI time series over the grid cells is significant. Since, monsoon is very important for agricultural operations, the trends during monsoon season are also evaluated using seasonal Mann–Kendall trend test (Hirsch et al. 1982). Figure 4 presents seasonal Mann–Kendall trend statistics for monsoon period. As observed from the figure, most of the central region and few grids in north-eastern region (i.e., the block numbers 30, 31, 32, 41, 42, 43, 44, 55, 56, 61, 67 and 68) experienced increase in droughts as indicated by the Mann–Kendall test statistic.

Fig. 2
figure 2

Trend maps of SPI-6 during 1971–2005 for western Rajasthan during a June, b July. M–K test statistics denote modified Mann–Kendall test statistics \( Z_{MK}^{*} \)

Full size image
Fig. 3
figure 3

Trend maps of SPI-6 during 1971–2005 for western Rajasthan during a August, b September

Full size image
Fig. 4
figure 4

Seasonal (June–September) trend map of SPI-6 for western Rajasthan (1971–2005)

Full size image

At each monthly time step, the drought affected grids in the region are identified based on SPI value of 20 percentile threshold limit. The magnitude of trends for number of grids under drought during monsoon months are quantified using two methods: (1) Least square linear regression (2) Sen’s slope estimator. Linear regression fit relating number of grid cells under drought with years during each month in the monsoon season are depicted in Fig. 5. The graphs show presence of increasing linear trend in the number of grids under droughts for the months of August and September. The slope of least square regression estimate can be sensitive to extreme values. To address this problem, Sen’s slope estimator (Sen 1968; Hirsch et al. 1982) based on non-parametric method is employed to estimate the magnitude of temporal trends in the data. The significance of trends is evaluated using Mann–Kendall test statistics at 5 and 10 % significance level. Table 2 lists corresponding test statistics and the magnitude of the trend obtained using Sen’s slope estimator. The results of Mann–Kendall test show upward trend in number of grids under drought but not statistically significant except in the month of June. The increase in trend during total monsoon period is found to be 0.13/season, which is statistically significant (at significance level α = 0.10) as evaluated by Mann–Kendall trend test.

Fig. 5
figure 5

Linear regression fit relating number of grids under drought with years during monsoon months—a June, b July, c August and d September. \( b_{linear} \) denotes slope estimated using linear regression fit

Full size image
Table 2 Mann–Kendall test statistics (\( Z_{MK}^{*} \)) and magnitude of trends (b np ) using Sen’s slope for number of grids under drought during each month of monsoon (/month) and for total monsoon season (/seasons)
Full size table

3.3 Selection of drought areal threshold

The areal threshold of drought from gridded drought data is identified using histogram analysis of percentage area under drought and number of months under drought at different areal extents. Figure 6 presents number of months under drought for different areal threshold limits (j = 1, 2,…, \( \left\lfloor K \right\rfloor \); where K is the maximum percentage of area under drought in month t) (Fig. 6a), histograms of percentage area under drought (Fig. 6b) and number of months under drought (Fig. 6c). From Fig. 6, it is noticed that as areal threshold increases, the months under drought are decreasing in number. Figure 6b and c indicate positively skewed distribution of data. The number of bins in the histograms is taken as \( \sqrt {N_{obs} } \), where \( N_{obs} \) is the number of observations. From Fig. 6b it can be observed that from second bin onwards, the histogram tends to be uniform in shape. Hence, areal threshold for the present analysis is selected as 7 %. As observed from Fig. 6c, the number of months, which have at least 7 % of areal extent under drought, is 240 months out of total 415 months considered (i.e., SPI-6 time series computed for the time periods of 1971–2005). A minimum of 7 % area under drought is about 14,004 km2. Based on this criteria total 30 drought events are identified during the study period. Figure 7 presents intensity and PAUD in different months at areal threshold of 7 % during the study period (1971–2005).

Fig. 6
figure 6

Identification of drought areal threshold. a Number of months under drought at different percentage areal threshold, b histogram of percentage area under drought (PAUD), c histogram of number of months under drought

Full size image
Fig. 7
figure 7

Drought Intensity and PAUD for different months during study period (1971–2005)

Full size image

3.4 Analyzing dependence of drought variables

The qualitative assessment of dependence between drought variables is analyzed using graphical tools such as ranked scatter plots, Chi plots and Kendall plots as shown in Fig. 8. Details about Chi-plot and Kendall plots for assessing dependence were available in Genest and Favre (2007). From the ranked scatter plot (Fig. 8a), it can be observed that the drought variables are positively associated with each other as most of points concentrated in the upper-right quadrant of the ranked scatter plot. The control limits in case of Chi-plots (Fig. 8b) are set to enclose 0.95 confidence limit \( \left( {{{1.78} \mathord{\left/ {\vphantom {{1.78} {\sqrt n }}} \right. \kern-0pt} {\sqrt n }}} \right) \). Most of the observation pairs \( \left( {\lambda_{i} ,\chi_{i} } \right) \)are found to be clustered outside the upper end of the control limits, which indicates that significant positive dependence exists between drought variables. The Kendall plot (Fig. 8c) shows that at the origin, the observation pairs \( \left( {W_{i:n} ,H_{i} } \right) \) touch the diagonal line. This is an indication that there is no lower tail dependence. Further, \( \left( {W_{i:n} ,H_{i} } \right) \) pairs are closer to the diagonal line in the lower part and far from it in the middle and upper parts of the plot. The points in the upper portion of the Kendall-plot diverge from the diagonal line, indicating the presence of upper tail dependence.

Fig. 8
figure 8

Graphical depiction of dependence between drought variables—intensity and PAUD using a ranked scatter plot, b Chi plot and c Kendall plots. \( U_{{I_{i} }} \) and \( U_{{A_{i} }} \) denotes empirically transformed marginal distribution for intensity and PAUD

Full size image

For quantitative assessment, the sample estimates of Pearson’s linear correlation r and two non-parametric dependence measures viz., Spearman’s ρ, Kendall’s τ are computed. The Pearson’s r between drought variables is 0.49 and Kendall’s τ and Spearman’s ρ are 0.34 and 0.47 respectively. The statistical significance of dependence is assessed by two-tailed t test and p values of correlation coefficient, which are less than 0.0001 for all the three cases, indicating that the correlations are significant at 5 % significance level.

3.5 Marginal distributions for drought variables

In order to fit marginal distribution for drought variables, several parametric class of distributions are investigated, such as generalized extreme value (GEV), Lognormal, Gamma and Exponential distribution functions. The validity of each probability model is tested using K–S GOF test. The results of estimated parameters along with their performance measures are presented in Table 3. For each of the cases, K–S test is checked at 5 % significance level. The critical value of K–S test statistics (\( d_{critical}^{\alpha = 0.05} \)) is obtained from 1,000 bootstrapped samples generated from the distributions. It is found that intensity and PAUD can be best modelled by GEV and lognormal distributions respectively. The suitability of these distributions in modeling drought variables is also evident from higher p value of the estimate. Figure 9 gives graphical illustration of the PDF, CDF and probability–probability (P–P) plots of marginal distribution of drought variables. All three figures show good agreement between theoretical and empirical distributions.

Table 3 Estimated parameters and performance measures for the fitted marginal distributions for drought variables
Full size table
Fig. 9
figure 9

PDF, CDF and P–P plots of marginal distributions of a intensity and b PAUD. Histograms in the plot represent density histograms of observed data

Full size image

3.6 Joint dependence modeling of drought variables using copula

Bivariate joint distribution of drought variables intensity and PAUD is modeled using Gumbel-Hougaard, Frank and Plackett copulas. The copula parameters are estimated using MPL method, in which maximization of log-likelihood function is performed using GA. The GA parameters used include: population size of 50, generations of 100, scattered cross-over function with crossover rate of 0.8, Gaussian mutation function with mutation rate of 0.01. Table 4 presents estimated copula parameters, log-likelihood values (LL) and GOF statistics of copula families estimated at 5 % significance level. Associated Cramer-von-Mises distance statistics S n and p values of the estimate are also listed in the Table 4. The probability-values (p values) are computed using parametric bootstrap procedure with N = 500 and 1,000 replications. It can be seen that Gumbel-Hougaard copula resulted in higher LL values. It is also observed that the Gumbel-Hougaard copula resulted in larger p value as compared to other two-copulas. The GOF test statistics show that Frank and Plackett copulas failed at 5 % significance level. For further graphical assessment, a Monte Carlo simulation is performed for generating a series of random pairs from each of the copula families and compared it with actual observations. Figure 10 gives comparison of observed drought variables with thousand paired samples generated from copula families. It is noticed that Kendall’s τ value of the simulated samples from Gumbel-Hougaard copula family is close to that of the observed drought variables (\( \tau \approx \)0.34).

Table 4 Estimated copula parameter and associated goodness-of-fit tests for copula families
Full size table
Fig. 10
figure 10

Scatter plots of observed versus thousand simulated samples from copula families a Gumbel-Hougaard, b Frank and c Plackett characterizing drought intensity and PAUD values. Observed and simulated drought variables are denoted by black and gray dots respectively

Full size image

To evaluate the performance of the copulas in modeling extremes (tails) of the data, non-parametric CFG estimator \( \left( {\lambda_{U}^{CFG} } \right) \) based tail dependence test is performed for the copula models. For evaluating \( \lambda_{U}^{CFG} \) estimate of copula families selected, a number of (n = 1,000 and 5,000) random samples are generated from each copula family and the computation of \( \hat{\lambda }_{U}^{CFG} \) is repeated for hundred different runs. Then corresponding mean \( \hat{\mu }\left( {\hat{\lambda }_{U}^{CFG} } \right) \) and standard deviation \( \hat{\sigma }\left( {\hat{\lambda }_{U}^{CFG} } \right) \) of hundred runs are computed. Then, empirical CFG estimate is calculated from observed data by empirically transforming the drought variables, which is found to be \( \hat{\lambda }_{empirical}^{CFG} \) = 0.407. The corresponding results are presented in Table 5, which shows satisfactory performance of Gumbel-Hougaard copula for modeling upper tail dependence of drought properties. The parametric upper tail dependence coefficient of Gumbel-Hougaard copula is computed as \( \lambda_{U}^{param} = 2 - 2^{{{1 \mathord{\left/ {\vphantom {1 \theta }} \right. \kern-0pt} \theta }}} \) = 0.413, which is found to be very close to the non-parametric CFG estimate \( \mu \left( {\lambda_{U}^{CFG} } \right) \) = 0.414 (for n = 5,000 simulated random pair) and also close to the empirical estimate \( \hat{\lambda }_{empirical}^{CFG} \) = 0.407. The results indicate satisfactory performance of Gumbel-Hougaard copula in modeling upper tail dependence of drought variables.

Table 5 Coefficient of upper tail dependence for copula families
Full size table

3.7 Drought intensity–area–frequency (I–A–F) relationship

Drought I–A–F curve gives the relationship between spatial intensity of drought and its areal extent corresponding to a return period. In other words, I–A–F curves give information about the frequency of area that would be affected by drought of a given intensity (Hisdal and Tallaksen 2003). The drought I–A–F \( T_{I|A} \left( {i|a} \right) \)relationships are derived from copula-based joint and conditional distribution of drought variables. For a specified value of return period \( T_{I|A} \left( {i|a} \right) \), the drought intensity corresponding to an areal extent can be obtained by numerically solving Eq. 15, in which the value of δ = 1.15. For Gumbel-Hougaard copula the expression for \( C_{I|A = a} \) is given by

$$ C_{I|A = a} = u_{{}}^{ - 1} \exp \left\{ { - \left( {\left( { - \log \left( u \right)} \right)^{\theta } + \left( { - \log \left( v \right)} \right)^{\theta } } \right)^{{\frac{1}{\theta }}} } \right\}\left[ {1 + \left( {\frac{ - \log \left( v \right)}{ - \log \left( u \right)}} \right)^{\theta } } \right]^{{ - 1 + \frac{1}{\theta }}} $$
(16)

where \( u = F_{A} \left( a \right) \) and \( v = F_{I} \left( i \right) \). The results obtained for various combinations of PAUD and intensity values are used to plot historical drought I–A–F curves for different return periods as shown in Fig. 11. From Fig. 11, it can be observed that intensity of drought increases with increase in PAUD.

Fig. 11
figure 11

Drought intensity–area–frequency curves at different return periods

Full size image

Using the derived I–A–F relationships, it is possible to estimate drought intensity quantiles for specified percentage areal extent and return periods. For example, the drought event with 50-year return period and 8.8 % PAUD has intensity value of 1.55, whereas drought event with 25-year return period and 90 % PAUD has intensity value of 2.13. The derived I–A–F curves can be useful to understand spatial characteristics of drought events (i.e., spatial coverage and intensity values) and the associated risks. This information can be helpful in drought preparedness planning and management.

4 Conclusions

As drought is one of the creeping natural disasters that can take place virtually in all climatic regions, the analysis of drought spread and its magnitude is having high importance in planning and management of droughts in various regions. In this study, gridded precipitation data are used to model droughts at finer resolution and to quantify the occurrence, trends and spatio-temporal characterization of droughts. Drought is modelled spatially by computing SPI-6 at various grids from gridded precipitation data. The drought condition in each grid is identified when SPI-6 falls 20 percentile values or below threshold limit. Trends in spatial distribution of droughts are analyzed for individual monsoon months and for the whole monsoon season. The trend analysis indicates a significant decrease in SPI magnitude (indicating increase in dry or drought conditions) in the central part of the region as compared to other parts. Also, the non-parametric Mann–Kendall seasonal trend analysis indicates increase in number of grids under drought.

Based on histogram analysis for PAUD a minimum of 7 % PAUD is chosen to identify an effective drought event in the region. Then a copula-based methodology is applied to analyze spatio-temporal patterns of droughts in terms of I–A–F curves for different return periods. The marginal distribution of drought variables, intensity and PAUD are separately modeled by GEV and lognormal distributions respectively. For modeling joint distribution of drought variables, three copula families—Gumbel-Hougaard, Frank and Plackett copulas are employed. Based on analytical goodness-of-fit test and tail dependence test, the results show that Gumbel-Hougaard copula best represents the joint distribution of drought variables. Then copula-based joint and conditional distributions are used for investigating the relationships between drought intensity and areal extent in terms of I–A–F curves, which could be useful in planning and management of droughts in the region.