On the spatial pattern of the distribution of the tsunami run-up heights

Abstract

This study suggests the map representing the best-fit distribution of the tsunami run-up height time series. To obtain the map, the tsunami numerical simulations corresponding to the 11 different causative undersea earthquake were firstly performed. Then, the best-fit distribution representing the tsunami run-up height values for each modeling in-land grid point was determined using the probability plot correlation coefficient test. Then, the probability that the tsunami run-up height exceeding a 30 cm was estimated using the fitted distribution for each of the modeling grid point. Finally, the map of the best-fit distribution was produced based on the maximum exceedance probability out of the total 11 simulations. The log-normal distribution represents the distribution of the tsunami run-up heights for the wide area of the back of the quay while the normal distribution does the same along the coast line. The Gumbel and exponential distribution did not show a specific spatial pattern but were sparsely located. In addition, the map representing the probability that the tsunami run-up height exceeds a given criterion depth (30 cm) was created. We expect these two maps help the disaster managers and policy makers in making more precise decisions while placing and designing coastal structures by providing important information regarding the risk of the tsunami attack from statistical and temporal perspective.

1 Introduction

In the recent past, catastrophic tsunamis triggered by undersea earthquakes in subduction zones around the Pacific Ocean have frequently caused the loss of a large number of human lives as well as property damage. According to the report of the National Oceanic and Atmospheric Administration (2012), Sumatra tsunami event that occurred on December 26, 2004 caused ~220,000 human deaths and 10 billion US dollars in property damage. The East Japan tsunami event on March 11, 2011, caused ~16,000 human deaths and 210 billion US dollars in property damage. This extensive human casualty and financial loss has been drawing considerable attentions from the public and research community focusing on the prevention of tsunami disasters.

Unfortunately, observational data regarding tsunami is highly limited because the occurrence of tsunami is as much scarce as its impact is catastrophic. For this reason, the analysis of tsunami has been limited too because otherwise it requires numerical simulation which needs extensive amount of input data regarding topography bathymetry and the spatial pattern of the causative undersea earthquakes. This limitation triggered the efforts of estimating tsunami run-up heights based on the statistical methods. Van Dorn (1965) is the first effort in this regard, which found that the log-normal distribution was the best-fit for the observational data. Kajiura (1983), Go (1987, 1997), and Pelinovsky and Ryabov (1999) confirmed the finding of Van Dorn (1965) through various occurrences of tsunamis. On the other hand, Choi et al. (1994) and Pelinovsky et al. (1997a, b) showed that the tsunami run-up heights can better be represented using other distributions such as uniform and Poisson distribution. Choi et al. (2002) showed that the log-normal distribution fits well the tsunami run-up heights obtained from the numerical simulation. They also indicated that the irregular topography and coastline are major factors highly influence the distribution. While these former studies mainly investigate the spatially distributed tsunami heights observed at several locations, few studies have so far dealt with the distribution of the tsunami height which varies with time at a given spatial location. The hazard caused by tsunami is not only the function of the maximum run-up heights, but also the function of the residence time of the tsunami wave height exceeding a given criterion value, so the analysis on this subject can provide crucial information regarding the risk of the tsunami from the temporal viewpoint.

In this context, this study investigates the spatial pattern of the best-fit distribution of the tsunami run-up height time series. This purpose was achieved by analyzing the result of the 11 plausible tsunami occurrences in the study area obtained by numerical simulation. After the numerical simulation, the best-fit distribution representing the tsunami run-up height time series was determined using the probability plot correlation coefficient (PPCC) test for each modeling grid and for each of the 11 plausible tsunami occurrences. Then, the probability that the tsunami run-up height exceeding the criterion height (30 cm) was estimated using the fitted distribution for each of the modeling grid and for each of the 11 plausible tsunami occurrences. Finally, the distribution corresponding to the greatest exceedance probability was chosen for each of the grid points. The obtained exceedance probability value was used to produce the risk map of the study area.

The result of this study is particularly meaningful in that (1) the spatial pattern of the temporal structure of the tsunami run-up height was comprehensively analyzed, which can provide useful information in the design of the coastal structures; and that (2) the map of the run-up height exceedance probability is provided, which can be used to analyze the risk of tsunami attack from a quantitative and temporal perspective.

2 Methodology

2.1 Study area

In this study, the Samcheok Port located in the Gangwon province in Korea was selected as the target area. The port is the largest trade port in the Gangwon province in Korea. The port is located at a latitude of 37° 26′ 11″ N and a longitude of 129° 11′ 20″ E. The quay wall is 776 m, the breakwater is 1,030 m, the groyne is 361 m, the inclined wharf is 1,388 m, the revetment is 746 m, and the cargo-handling capacity is 8,694,000 tons/year. The current conditions and location of the Samcheok Port are noted in Table 1 and Fig. 1, respectively.

Table 1 The current conditions of the Samcheok Port

Fig. 1

The location of the Samcheok Port (Google Earth 2012)

The detailed topography and bathymetry of the Samcheok Port for the numerical simulation are presented in Fig. 2. The north breakwater and groyne are located in front of the Samcheok Port and the Osip river is located to the south of the Samcheok Port as shown in Fig. 2. In addition, hilly areas are located to the north of the port.

Fig. 2

The detailed topography and bathymetry of the Samcheok Port

The Samcheok Port was attacked by both the 1983 Central East Sea Tsunami and the 1993 Hokkaido Tsunami. Even though human casualties have not occurred in the Port, substantial property damage has occurred. If an earthquake happens on the Western Coast of Japan, most of the ports located on the Eastern Coast of Korea, including the Samcheok Port, will be attacked by the tsunamis. Therefore, all of the ports should prepare for tsunami attacks.

2.2 Numerical simulation of tsunamis

Numerical simulation of tsunamis is the essential part of the most of the tsunami studies including the present study especially when the observational data is scarce. Here, we briefly explain the previous studies which investigated the propagation of the tsunami waves and the associated inundation processes using the numerical simulations. Imamura et al. (1988) developed a numerical model that solves the shallow-water equations with a leap-frog scheme in order to simulate the propagation of transoceanic tsunamis. This numerical model was improved by Cho and Yoon (1998) in order to obtain the proper dispersive effects for tsunamis propagating obliquely to the principal axes of the computational grids. However, the numerical models of Imamura et al. (1988) and Cho and Yoon (1998) are limited to cases where there is a constant water depth if a uniform finite difference grid is employed. Therefore, both of the numerical models are limited so that the spatial grid size and time step size should be changed continuously in order to apply them to real topography. Yoon (2002) also improved the numerical model of Cho and Yoon (1998) by using a uniform grid. However, the numerical model of Yoon (2002) used a cubic interpolation function in order to calculate the value of the variables at a hidden grid point and this can cause the errors, because of the many interpolation processes. In the recent past, Cho et al. (2007) developed a simple and practical numerical model using a dispersion-correction scheme. The model was based on the leap-frog scheme that was similar to the models of Imamura et al. (1988) and Cho and Yoon (1998). However, the newly proposed model of Cho et al. (2007) is free of spatial grid and time step sizes and the accuracy is better than that of Yoon’s (2002) model due to the absence of the interpolation process. The accuracy of the scheme proposed by Cho et al. (2007) was also verified (Sohn et al. 2009). For this reason, the model of Cho et al. (2007) was used in the present study to simulate the tsunami propagation and inundation.

The tsunamis considered in this study consist of 2 historical tsunamis and 9 virtual tsunamis. The 1983 Central East Sea and 1993 Hokkaido Tsunamis were selected as the historical tsunamis (Korea Meteorological Administration 2012). Both of the historical tsunamis attacked the Eastern Coast of Korea. The 9 virtual tsunamis are selected based on the 9 locations that have a high probability of earthquake occurrence according to the Korean Peninsula Energy Development Organization (1999). The location and fault parameters information for the 2 historical tsunamis and the 9 virtual tsunamis are presented in Fig. 3 and Table 2.

Fig. 3

The location information for 2 historical and 9 virtual tsunamis

Table 2 The fault parameters for 2 historical and 9 virtual tsunamis

In Table 2, θ is the strike angle, H is the depth of the fault plane, δ is the dip angle, $\lambda$ is the slip angle, L is the length of the fault, W is the width of the fault, D is the dislocation of the fault, and M is the magnitude of the earthquake. The length of the fault, the width of the fault, and the dislocation of the fault were obtained using Eqs. (1)–(3) as proposed by the Korea Meteorological Administration and the magnitude of the virtual earthquakes was fixed at 8.0.

$$ \log L = 0.5M - 1.9 $$

(1)

$$ W = 0.5L $$

(2)

$$ \log D = 0.5M - 1.2 $$

(3)

The depth of the fault plane, the dip angle, and the slip angle were obtained by using the Mansinha and Smylie (1971). The initial free surface displacement of the 2 historical tsunamis and the 9 virtual tsunamis were reproduced using the location and fault parameters in Table 2.

The nonlinearity terms can be ignored in the numerical simulation for tsunami propagation, because the free surface displacement for tsunamis is relatively less than the water depth. On the other hand, the frequency dispersion effects play important roles in tsunami propagation and should be taken into consideration in its governing equations, because the wave length of tsunamis compared to the tide is relatively short and the tsunamis are propagated over a long distance. Therefore, the governing equations that address the dispersion effect, namely the linear Boussinesq equations, should be used in the numerical simulation of tsunami propagation (Cho et al. 2007). The linear Boussinesq equations are written below in Eqs. (4)–(6).

$$ \frac{\partial \zeta }{\partial t} + \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} = 0 $$

(4)

$$ \frac{\partial P}{\partial t} + gh\frac{\partial \zeta }{\partial x} = \frac{{h^{2} }}{2}\frac{\partial }{\partial x}\left[ {\frac{\partial }{\partial x}\left( {\frac{\partial P}{\partial t}} \right) + \frac{\partial }{\partial y}\left( {\frac{\partial Q}{\partial t}} \right)} \right] - \frac{{h^{3} }}{6}\frac{\partial }{\partial x}\left[ {\frac{{\partial^{2} }}{\partial t\partial x}\left( \frac{P}{h} \right) + \frac{{\partial^{2} }}{\partial t\partial y}\left( \frac{Q}{h} \right)} \right] $$

(5)

$$ \frac{\partial Q}{\partial t} + gh\frac{\partial \zeta }{\partial y} = \frac{{h^{2} }}{2}\frac{\partial }{\partial y}\left[ {\frac{\partial }{\partial x}\left( {\frac{\partial P}{\partial t}} \right) + \frac{\partial }{\partial y}\left( {\frac{\partial Q}{\partial t}} \right)} \right] - \frac{{h^{3} }}{6}\frac{\partial }{\partial y}\left[ {\frac{{\partial^{2} }}{\partial t\partial x}\left( \frac{P}{h} \right) + \frac{{\partial^{2} }}{\partial t\partial y}\left( \frac{Q}{h} \right)} \right] $$

(6)

where $\zeta$ is the free surface displacement, h is the still-water depth, P and Q are the depth-averaged volume fluxes in the x-axis and y-axis directions, respectively, and g is the gravity acceleration.

The linear Boussinesq equations are no longer valid as the governing equations in the coastal region, because the wave length of tsunamis becomes shorter and the amplitude becomes larger as the tsunami is propagated in the coastal region. In addition, the bottom friction effects become more important in the coastal region. Therefore, the nonlinear convective inertia force and the bottom friction terms become increasingly important, while the frequency dispersion terms become less relevant. As a result, the nonlinear shallow-water equations that include the bottom friction term should be used as the governing equations in order to simulate the tsunami inundation. The nonlinear shallow-water equations are represented in the following Eqs. (7)–(9).

$$ \frac{\partial \zeta }{\partial t} + \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} = 0 $$

(7)

$$ \frac{\partial P}{\partial t} + \frac{\partial }{\partial x}\left( {\frac{{P^{2} }}{H}} \right) + \frac{\partial }{\partial y}\left( \frac{PQ}{H} \right) + gH\frac{\partial \zeta }{\partial x} + \tau_{x} H = 0 $$

(8)

$$ \frac{\partial Q}{\partial t} + \frac{\partial }{\partial x}\left( \frac{PQ}{H} \right) + \frac{\partial }{\partial y}\left( {\frac{{Q^{2} }}{H}} \right) + gH\frac{\partial \zeta }{\partial y} + \tau_{y} H = 0 $$

(9)

where H is the total water depth, and $\tau_{x}$ and $\tau_{y}$ are the bottom friction terms represented by the Manning equation. The Manning equations can be written in the following form, where n is the Manning coefficient.

$$ \tau_{x} = \frac{{gn^{2} }}{{H^{10/3} }}P\left( {P^{2} + Q^{2} } \right)^{1/2} $$

(10)

$$ \tau_{y} = \frac{{gn^{2} }}{{H^{10/3} }}Q\left( {P^{2} + Q^{2} } \right)^{1/2} $$

(11)

The linear and nonlinear terms of Eqs. (7)–(9) were differenced using the leap-frog scheme and upwind scheme, respectively.

The descriptions of the numerical scheme are substituted for the references in this study, because the above-mentioned contents were verified and published in numerous previous journal articles (Liu et al. 1994; Cho 1995; Cho et al. 2007 and Sohn et al. 2009).

A small grid size should be used in order to obtain high resolution results for tsunami simulations. However, it was almost impossible to construct such small grid meshes for our tsunami simulations, because a large numerical domain including the East Sea was used in order to simulate the tsunami propagation. Therefore, the large numerical domain was divided into several detailed regions having a different grid size and each region was connected using the dynamic linking technique. The dynamic linking method was used in order to connect the two regions with different grid sizes and the grid size was decreased by one-third according to the dynamic linking method.

The computational domain was divided into 6 regions from region A to F. Each region used a different boundary condition. Region A used the free transmission condition, while other regions used the dynamic linking technique as a boundary condition for an open sea. From region A to D, a fully reflected condition was used, while regions E and F used the moving boundary condition as a boundary condition in order to track the movement of the coastline. Figure 4 shows the composition of the computational domain and bathymetry of each region. The smallest region in Fig. 4b, which is region F, is described in detail in Fig. 2. The computational information and boundary conditions used in this study are presented in Tables 3 and 4, respectively.

Fig. 4

The composition of the computational domain and bathymetry of each region

Table 3 The computational information for each region

Table 4 The boundary conditions for each region

By employing simulation conditions, 2 historical and 9 virtual tsunami events were numerically simulated in order to obtain the flooding data. As a result, the tsunami run-up heights corresponding to all 11 events were obtained at all of the in-land grid points. The temporal resolution of the simulation model was 0.05 min, and the total duration of the simulation was 200 min which starts from the occurrence of the undersea causative earthquake. This time duration is sufficiently long enough to include the time at which end of the last tsunami wave arrives for all in-land grid points.

2.3 Determination of the flooding probability

2.3.1 The goodness-of-fit test

The goodness-of-fit test was conducted in order to determine the proper probability distribution type for the obtained tsunami run-up heights. The time series of the run-up heights considered in the distribution fitting was obtained by trimming out the zero height values existing before the arrival of the first tsunami wave and after the end of the last tsunami wave. The normal, Gumbel, lognormal, and exponential distributions were assumed to be the probability distribution types for the tsunami run-up heights for this study. The choice of these four distributions are based on the suggestion of Choi et al. (2002).

There are many different types of goodness-of-fit test including χ² test, Cramer–von Mises test, Kolmogrov–Smirnov test, Anderson–Darling test, and PPCC. The detailed comparison between these tests can be found in Shin et al. (2012). This study chose the PPCC test to find the proper distribution type for the tsunami run-up heights. The PPCC test has been widely used since it was first developed by Filliben (1975) to examine the normality of the given data. Vogel (1986) applied the test to the Gumbel distribution and Vogel and Kroll (1989) applied the test to the two-parameter Weibull and uniform distribution. Vogel and McMartin (1991) generated the PPCC test statistics for gamma distribution with a 5 % significance level and Chowdhury et al. (1991) generated the PPCC test statistics for the generalized extreme value (GEV) distribution. Heo et al. (2008) developed the regression equations to obtain the PPCC test statistics as a function of sample size and significance level for several probability distribution types. Compared to the other testing methods, the PPCC test has greater power to reject null hypothesis and can easily be applied to more various types of probability distribution.

The PPCC test determines the best-fit probability distribution among the assumed probability distributions by using the correlation coefficient, $\gamma_{c}$, between the quantile of the ranked samples $X_{i}$ and the fitted quantile $M_{i}$. The fitted quantiles are calculated using the plotting positions $P_{i}$, for each ranked sample $X_{i}$ based on the inverse function of the cumulative probability distribution. The plotting position has to be carefully determined because it greatly affects the estimated correlation coefficient. The studies to find the proper plotting position for each probability distribution type were conducted by Blom (1958), Cunnane (1978), and Gringorten (1963). The corresponding formulas are listed in Table 5.

Table 5 The plotting position formulas for each probability distribution type

In Table 5, i is a rank, n is a sample size, and $P_{i}$ is the plotting position. In this study, the plotting position formulas developed by Blom (1958) and Gringorten (1963) were used in order to estimate the plotting positions for each probability distribution type.

Once the plotting positions for each probability distribution type were estimated, the fitted quantiles were calculated based on the inverse function of the cumulative probability distribution function. These functions are listed in Table 6.

Table 6 The inverse functions of the cumulative probability distribution

In Table 6, x is a random variable, $z_{x}$ and $z_{y}$ are the normalized random variables for the normal and lognormal distributions, respectively, F is a quantile, and $\eta$, $\xi$, and $\alpha$ are the shape, location, and scale parameter, respectively. These parameters were estimated using the method of moments. The normalized random variables $z_{x}$ and $z_{y}$ were calculated using Eqs. (12) and (13), respectively.

$$ z_{x} = \frac{{x - \mu_{x} }}{{\sigma_{x} }} $$

(12)

$$ z_{y} = \frac{{y - \mu_{y} }}{{\sigma_{y} }} $$

(13)

where $y = \ln \left( x \right)$, $\mu_{x}$ and $\mu_{y}$ are the mean of $x$ and $y$, and $\sigma_{x}$ and $\sigma_{y}$ are the standard deviations of $x$ and $y$, respectively.

Finally, the fitted quantiles were calculated using Eq. (14), which is written as:

$$ M_{i} = \Upphi^{ - 1} \left( {P_{i} } \right) $$

(14)

where $\Upphi^{ - 1}$ is the inverse function of a cumulative probability distribution listed in Table 6.

After the calculation of the fitted quantiles, the correlation coefficient $\gamma_{c}$ was obtained by using Eq. (15) (Filliben 1975).

$$ \gamma_{c} = \frac{{\sum\limits_{i = 1}^{n} {\left( {X_{i} - \overline{X} } \right)\left( {M_{i} - \overline{M} } \right)} }}{{\sqrt {\sum\limits_{i = 1}^{n} {\left( {X_{i} - \overline{X} } \right)^{2} \sum\limits_{i = 1}^{n} {\left( {M_{i} - \overline{M} } \right)^{2} } } } }} $$

(15)

where $\overline{X}$ and $\overline{M}$ are the mean values of $X_{i}$ and $M_{i}$, respectively, and n is the number of samples. The normalized random variables $z_{x}$ and $z_{y}$ were used instead of the ranked sample $X_{i}$ for the normal and lognormal distributions. If the samples agree well with the assumed probability distribution, then the scatters of the ranked samples versus the expected values in the assumed probability distribution in the quantile–quantile plot (Q–Q plot) will be concentrated around the 1:1 line and the corresponding correlation $\gamma_{c}$will be close to 1.

The PPCC test statistics should be compared with the correlation coefficients $\gamma_{c}$ in order to determine whether or not the samples follow the assumed probability distribution. However, such approach was not adopted in this study because the test has to be performed for all simulation in-land grid points (which varied between 314 and 4513 grid points depending on the tsunami simulation case), and estimating the test statistics for such many grid points was practically impossible. Regarding this, Heo et al. (2008) derived the regression equations to obtain the PPCC test statistics for the normal, Gumbel, gamma, GEV, and Weibull probability distributions, but the ones corresponding to the lognormal and exponential probability distributions, which are the candidate distribution of this study, have not been developed yet. For this reason, the probability distribution type with the maximum correlation coefficient was chosen among the four assumed probability distributions at each modeling grid points instead of comparing the correlation coefficients with the PPCC test statistics.

2.3.2 Risk mapping through the concept of “maximum possible flooding probability”

After the probability distribution type was determined for all in-land grid points and for all 11 plausible tsunami occurrences, the probability that flooding would exceed the criterion height was calculated using the cumulative distribution functions corresponding to the determined probability distribution. The cumulative distribution functions used in this study are presented in Table 7.

Table 7 The cumulative distribution functions

In Table 7, $F\left( x \right)$ and $F\left( y \right)$ are the cumulative probabilities for the random variables x and y, respectively. The criterion height was determined to be 30 cm in this study with an assumption that people will be affected by a tsunami flooding height exceeding 30 cm.

For the determination of the distribution and mapping of the flooding risk, the flooding probability results of the 11 tsunami events should be compiled into one result. To achieve this purpose, the concept of the “maximum possible flooding probability” was employed in this study. According to this concept, the probability distribution corresponding to the maximum probability of the flooding is chosen among the result of all 11 tsunami simulations for each in-land modeling grid point. The reason why the maximum value is chosen is because the damages done by tsunami are catastrophic, so the choice of conservative risk value and designing the structures based on it guarantees the minimal loss caused by the tsunami.

Here, it also has to be noted that the distribution corresponding to the maximum possible flooding probability for each grid point is determined based on the assumption that each causative undersea earthquake has exactly same probability of occurrence, which may distort the reality. In the mean time, it also has to be noted that obtaining the information regarding this issue precise enough to be used in quantitative analysis is difficult because (1) not many historical data regarding the causative undersea earthquakes has been gathered in the study area and that (2) the major undersea earthquakes occurred in the eastern side of Japan were spatially well distributed and did not show any spatial patterns according to USGS (2012).

3 Results and discussion

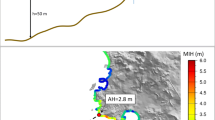
Figure 5 presents the maximum flooding height obtained by numerical simulation in Samcheok Port for 3 virtual tsunami events (case 3, case 5, and case 8 in Table 2) and 1 historical tsunami event (1993 Hokkaido Tsunami). It can be noted that the area near coastline generally has a higher flooding height than the other flooding areas. In general, the case 5 simulation caused the highest run-up for most area with maximum flooding height being ~1.8 m.

Fig. 5

The maximum flooding height in the Samcheok Port

Figure 6 shows the empirical exceedance probability overlapped on the plot of the exceedance probability of the best-fit probability distribution for the case 5 simulation for the point 1 through point 4 shown in Fig. 2. Overall, good matches were observed for all different four types of the assumed distributions for most grid points and for all 11 simulation cases. This result is particularly meaningful in that the distribution of the tsunami run-up heights, which varies substantially with the various properties of the underlying topography and geology, can be well modeled with the distributions which have at most two parameters.

Fig. 6

The empirical exceedance probability overlapped on the plot of the exceedance probability of the best-fit probability distribution

Figure 7 presents the map of the maximum correlation coefficient for the aforementioned four tsunami events (case 3, case 5, case 8, and 1993 Hokkaido Tsunami). It can be noted that, for the first 3 virtual cases, correlation coefficients are higher than 0.95 for most in-land grid points. The fact that the value of the maximum correlation coefficient was close to 1.0 indicates that the tsunami run-up heights agrees well with at least one of the four assumed probability distribution types. On the other hand, relatively low values of correlation coefficients were obtained for the 1993 Hokkaido tsunami case. This is because the run-up duration is relatively shorter than the other simulation cases. As the run-up duration of tsunami gets shorter, the number of the tsunami height values to fit the distribution becomes smaller, which yields relatively lower correlation coefficient.

Fig. 7

The map of the maximum correlation coefficient

The most valuable result of the present study may be Fig. 8, which shows the map of the best-fit probability distribution type for the study area because it illustrates the overall spatial pattern of the probability distribution type of the tsunami run-up height. It is notable that the lognormal distribution was widely represented in the back of the quay and the normal distribution was located along the coastline. The Gumbel and exponential distributions were sparse at several of the points. The number of points corresponding to each probability distribution type is presented in Table 8. According to Table 8, the lognormal distribution was chosen as the best-fit probability distribution at most of the points if the flooding area extended inland like the virtual tsunami in case 5. On the contrary, the normal distribution was determined to be the best-fit probability distribution at most of the points if the flooding areas were restricted to near the coastline like the 1993 Hokkaido Tsunami.

Fig. 8

The map of the best-fit probability distribution type

Table 8 The number of points corresponding to each probability distribution type

Most of the grid points with the log-normal distribution were characterized by the relatively long duration of the tsunami wave residence and high maximum run-up height. Both of these characteristics contribute to the increase of the skewness of the distribution. On the other hand, the grid points with normal distribution were characterized by relatively short tsunami residence and low maximum run-up height.

Figure 9 shows the probabilities of the flooding exceeding the criterion height (30 cm) calculated for each tsunami event. As shown in Fig. 9, relatively high probabilities exist along the coastline meaning that such locations are submerged by tsunami with the depth greater than 30 cm for the greater portion of the entire duration of the tsunami event compared to the other locations. In particular, high probabilities are present around the docking facility and the north breakwater.

Fig. 9

The probabilities of flooding exceeding the criterion height for each tsunami event

Figure 10 shows the maximum possible tsunami run-up height. The map was obtained by overlapping the maps of the maximum tsunami run-up height for all 11 simulation cases and selecting the maximum run-up height for each of the modeling grid point. The run-up height of the case 5 simulation greatly affected the determination of the maximum possible run-up heights for most of the area while the remaining tsunamis affected the area where the tsunami wave of the case 5 simulation did not reach.

Fig. 10

The maximum possible tsunami run-up height

Figure 11 shows the maximum possible flooding probability. The map was obtained by overlapping the maps of the probability exceeding the 30 cm of the criterion height and choosing the maximum probability values for each modeling grid point. It can be noted that the areas around the docking facility and the north breakwater has relatively higher risk in terms of tsunami residence time with the height being greater than 30 cm.

Fig. 11

The maximum possible flooding probability

4 Conclusion

In this study, the spatial pattern of the distribution representing the tsunami run-up height time series was analyzed. It turned out that the log-normal distribution represents the tsunami run-up heights for the area that is more susceptible to tsunami attack. This is particularly because such area has longer tsunami residence time and relatively high run-up height, both of which contribute to the increase of the skewness of the distribution. On the other hand, the normal distribution represented the tsunami height time series of the most portion of the remaining area, which has relatively lower risk against tsunami attack. This is because the residence time of the tsunami of such area is relatively short and the temporal structure of the tsunami wave is less variable. The Gumbel and exponential distribution did not show a specific spatial pattern but were sparsely located over the modeling region. In addition, the map representing the probability that the tsunami run-up height exceeds the given criterion height was produced. We expect this map help the disaster managers and policy makers in making more precise decisions while placing and designing coastal structures by providing important information regarding the risk of the tsunami attack from statistical and temporal perspective.