Introduction

Several formulas have been used to estimate the strength loss (i.e., loss in load-bearing capacity) caused by internal defects in living trees, and most are based on the difference in the second moment of area, I (m4), between a hollow and solid trunk section (Kane et al. 2001). I represents the load-bearing capacity of a shape where the contribution of a material element to a total bending moment is proportional to the square of its distance (y) from the neutral axis (Ennos 2012); it can be determined by summing the many, infinitesimally small moments distributed over a cross section of area (A):

$$I=\int {{y^2}{\text{d}}A} .$$
(1)

Practically, this means that wood situated near the trunk periphery contributes greater to overall rigidity. Coder (1989) used the formula to estimate the percent loss in I, ILOSS (%), of a hollow pipe relative to a solid rod:

$${I_{{\text{LOSS}}}}={\raise0.7ex\hbox{${{d^4}}$} \!\mathord{\left/ {\vphantom {{{d^4}} {{D^4}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${{D^4}}$}},$$
(2)

where d and D are the diameters of hollow and solid circles, respectively. Wagener (1963) modified this formula as the cube of the same ratio:

$${I_{{\text{LOSS}}}}={\raise0.7ex\hbox{${{d^3}}$} \!\mathord{\left/ {\vphantom {{{d^3}} {{D^3}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${{D^3}}$}}.$$
(3)

It is unclear why Wagener (1963) chose this specific exponent. Most observe that it produces a larger and more conservative estimate over the range of possible d/D (Ciftci et al. 2014; Kane et al. 2001), but he implied that it offered a coarse approximation of strength loss, presumably as a compromise between the geometric properties governing bending stress (I ∝ D4) and compression stress (A ∝ D2) (Wagener 1963). Later, Smiley and Fraedrich (1992) modified this formula to approximate trees with open cavities as a sector of a circular annulus:

$${I_{{\text{LOSS}}}}={\raise0.7ex\hbox{${{d^3}}$} \!\mathord{\left/ {\vphantom {{{d^3}} {{D^3}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${{D^3}}$}}+{\raise0.7ex\hbox{${R({D^3} - {d^3})}$} \!\mathord{\left/ {\vphantom {{R({D^3} - {d^3})} {{D^3}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${{D^3}}$}},$$
(4)

where R is the ratio of cavity opening to stem circumference. For trees without a cavity opening, estimates given by Eq. 4 are identical to Eq. 3. Among the three formulas, only the latter was validated with empirical data (Smiley and Fraedrich 1992).

However, several limitations of these formulas diminish their applicability to many common situations. The formulas are appropriate for circular cylinders composed of isotropic, homogeneous material, and Wagener’s (1963) and Coder’s (1989) implicitly assume concentric areas of decay in which the decayed and solid areas share the same centroid. A circle is often an inexact approximation of the shape of a tree, especially near the base of those with pronounced buttress roots, and circles frequently do not accurately describe the shape of decayed areas. In addition, decay is often formed asymmetrically, so that its centroid is offset from that of the trunk, and these formulas ignore the potentially significant contributions of offset decayed areas (Kane and Ryan 2004).

To address these limitations, Ciftci et al. (2014) used the section modulus, Z (m3), to evaluate the loss in load-bearing capacity, taken as moment capacity, due to decay:

$$Z=I/y,$$
(5)

where y is the maximum perpendicular distance (m) between the neutral axis and outermost trunk fibers. The ratio is needed to calculate bending stress, σ (N·m−2), for beams, or beam-like plant organs (Niklas 1992):

$$\sigma =My/I,$$
(6)

where M (N m) is a bending moment causing rotation about the neutral axis. Equation 6 shows that, for any loading situation, the maximum stress experienced by a cross section of any shape can be minimized by maximizing Z (Niklas 1992). Ciftci et al. (2014) estimated the percent loss in Z, ZLOSS (%), between a solid and hollow trunk section, and considered cases with both concentric and non-concentric decayed areas. The authors also considered the effects of material anisotropy on ZLOSS, which was negligible (Ciftci et al. 2014).

Many of the limitations associated with the existing strength-loss formulas arise from the unavailability of analytical solutions to the moments of irregular shapes (Ciftci et al. 2014; Kane et al. 2001), but numerical approaches can be used to compute these values for any shape (Koizumi and Hirai 2006). Numerical analysis could address many of the limitations associated with existing approaches to estimating strength loss, including irregular geometry and non-concentric decayed areas, but this would require an accurate description of the size, position, and shape of decay in a trunk cross section.

Among consulting arborists, sonic tomography (SoT) is increasingly recognized as a useful way to evaluate the internal condition of trees (Smiley et al. 2011), offering reasonably accurate, non-invasive, and convenient assessments of the internal condition of the tree (Johnstone et al. 2010). Sonic tomography measures variation in acoustic transmission speeds, which is proportional to the ratio of wood stiffness to density (Arciniegas et al. 2014). The advantages and limitations of SoT have been documented by several studies (Brazee et al. 2011; Li et al. 2012; Ostrovsky et al. 2017; Wang et al. 2009). Although SoT generally depicts the internal condition of trees accurately, some authors reported that measurements often underestimate the size of decayed areas (Liang et al. 2007; Wang et al. 2009), overestimate the size of cracks (Wang et al. 2007), and suffer inaccuracies on irregularly shaped trunks (Gilbert et al. 2016). Notwithstanding these minor shortcomings, sonic tomography is a natural choice to provide the raw data necessary for a numerical approach to estimating the loss in load-bearing capacity of trees with internal defects. In this study, the existing analytical methods for estimating ZLOSS were compared to a numerical estimate derived from sonic tomograms. The method was validated by applying it to sonic tomograms and the corresponding cross-sectional photographs from a previous study (Marra et al. 2018), in which trees were destructively harvested to assess the accuracy of interpretations derived from sonic tomograms.

The specific objectives of this study were to: (1) compare the estimates of internal damage in three hardwood species provided by SoT with internal damage measured on destructively sampled trees; (2) compare analytical and numerical estimates of strength loss derived from SoT and destructively sampled trees; and (3) test whether geometric features of damaged parts (i.e., size, position, and shape) affect the accuracy of different approaches to estimating strength loss.

Materials and methods

Site and tree material

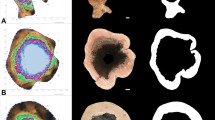
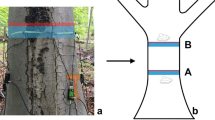
All tomograms and corresponding cross-sectional photographs used for this study were obtained from a previous study in which the accuracy of tomographic predictions was assessed by destructive sampling (Marra et al. 2018). In 2014, individuals of three species [American beech (AB, Fagus grandifolia); sugar maple (SM, Acer saccharum); yellow birch (YB, Betula alleghaniensis)] were chosen based on the appearance of signs and symptoms suggestive of internal decay. Trees were assessed using the PiCUS® Sonic Tomograph 3 (Argus Electronic GmbH, Rostock, Germany) at one-to-four levels on the lower trunk, with the lowest cross section typically positioned 50 cm above the soil line. Tomograms display the relative sound transmission speeds on a colorimetric scale: the greatest sonic transmission speeds, associated with non-decayed wood, are depicted using varying shades of brown; decreasing speeds associated with lower density-specific stiffness, and more advanced stages of decay, are depicted, in order, as green, violet, and blue (Fig. 1b). After felling trees, cross sections corresponding with each tomogram were excised from the trunk and photographed (Fig. 1c). For this study, only cross sections with internal defects detected by SoT were used for analysis. See Marra et al. (2018) for more details.

Fig. 1
figure 1

For each trunk cross section, three images were used for analysis, including a geometry file showing the blue trunk boundary line (a), a sonic tomogram showing the visualized decay pattern (b), and a photograph of the destructively harvested cross section (c). The reference photograph was used to produce a binary image (D), in which black (0) and white (1), respectively, represent damaged and solid parts. This set of images depicts the internal trunk condition of one American beech (Fagus grandifolia) 50 cm above ground (AB07–050)

Full size image

Image analysis

Three separate image files were used for analysis: a geometry image showing only the blue trunk boundary line (Fig. 1a), a sonic tomogram showing the visualized decay pattern (Fig. 1b), and a reference photograph of the tree’s destructively measured internal condition (Fig. 1c). The geometry and tomogram images were oriented identically without annotation and exported as JPEG files from the PiCUS® software. The size of the exported images was 770 × 770 pixels.

A tomogram is displayed by the PiCUS® software in a Cartesian coordinate plane. To extract boundary coordinates for the solid and damaged parts, an object was created to relate the intrinsic coordinates of the tomogram images to the spatial coordinates of a Cartesian coordinate system. Similarly, the recorded distances between measurement points on each trunk were used to relate the intrinsic coordinates of the reference photographs to a Cartesian coordinate system. These objects used the calculated physical extent of each pixel to convert a pixel index (row, column) to a coordinate pair (x, y).

The geometry and tomogram images were segmented using specific ranges in the hue, saturation, brightness (HSV), and LAB color space, respectively (Table 1). Each sonic tomogram was segmented to select either violet and blue (VB) or green, violet, and blue (GVB). This distinction between color combinations was made, because the PiCUS® software excludes green areas when calculating the percent solid and damaged area in tomograms, but all parts of the cross section need to be classified as either solid or damaged for ZLOSS calculations.

Table 1 Histogram thresholds used to select specific ranges in the HSV and LAB color space, respectively, associated with solid and damaged parts in sonic tomograms
Full size table

Reference images of each tree’s destructively measured internal condition were manually binarized into black (0) and white (1) images using Adobe Photoshop CS6 Extended (Adobe Systems, Inc., San Jose, CA, USA) in which black and white, respectively, represented damaged and solid parts (Fig. 1d). The trunk boundary, excluding bark, was used to define an enclosed region of interest, and the extent of damaged parts was determined visually by the presence of discoloration, cavities, cracks, and decayed wood. Wood discolored by the host defensive response and heartwood formation was classified as solid parts. Visual identification of damaged parts in cross sections is consistent with most existing studies (Brazee et al. 2011; Gilbert and Smiley 2004; Liang and Fu 2012; Ostrovsky et al. 2017).

After selecting specific colors, the boundaries of visible features in the segmented images were traced to determine the intrinsic coordinates for the perimeter of the solid and damaged parts (Fig. 2a, b). These sets were converted from intrinsic to Cartesian coordinates using the associated reference object. Each set consisted of n clockwise-ordered coordinate pairs (xi, yi), {i | \(\in\) 1…n}, that collectively described a simple, closed curve enclosing a solid or damaged part.

Fig. 2
figure 2

Using specific ranges in the HSV and LAB color space, respectively, sonic tomograms were segmented to acquire the boundary of solid (a: dashed black line) and damaged (b: solid white lines) parts. For a given orientation, the perimeters of shapes comprising each hollow section were used to determine several features, including the neutral axis (c: dashed horizontal line), centroid (c: solid dot), and the outermost trunk fibers oriented perpendicular to the neutral axis (c: solid horizontal lines). The ZLOSS estimates are displayed as color intensity values on a circular annulus surrounding an outline of each hollow section (d). The red, green, blue continuous color scale represents directional ZLOSS between the minimum and maximum values for a given cross section

Full size image

Numerical estimates

Consistent with the existing methods (Smiley et al. 2011), damaged wood parts were considered hollow, or missing, for the purposes of these calculations. Four parameters were computed for the individual shape(s) comprising each section, including the area, A (m2):

$$A=\int {{\text{d}}A} ;$$
(7)

the first moment of area with respect to the y-axis, Ax (m3):

$${A_x}=\int {x~{\text{d}}A} ;$$
(8)

the first moment of area with respect to the x-axis, Ay (m3):

$${A_y}=\int {y{\text{d}}A} ;$$
(9)

and the second moment of area with respect to the x-axis, Ixx (m4), as in Eq. 1:

$${I_{xx}}=\int {{y^2}{\text{d}}A} .$$
(10)

Green’s theorem was used to reduce the formulas to a curve integral over the clockwise-ordered boundary coordinates enclosing each shape. See Steger (1996) for the complete derivation of the corresponding numerical formulas. Specifically, A was computed as follows:

$$A=1/2~\mathop \sum \limits_{{i=1}}^{n} ({x_i}{y_{i+1}} - {x_{i+1}}{y_i}),$$
(11)

where (xi, yi), {i | \(\in\) 1…n}, are the coordinate pairs for a given shape; Ax was computed as follows:

$${A_x}=1/6\mathop \sum \limits_{{i=1}}^{n} ({x_i}+{x_{i+1}})({x_i}{y_{i+1}} - {x_{i+1}}{y_i});$$
(12)

Ay was computed as follows:

$${A_y}=1/6\mathop \sum \limits_{{i=1}}^{n} ({y_i}+{y_{i+1}})({x_i}{y_{i+1}} - {x_{i+1}}{y_i});$$
(13)

and Ixx was computed as follows:

$${I_{xx}}=1/12~\mathop \sum \limits_{{i=1}}^{n} (y_{i}^{2}+{y_i}{y_{i+1}}+y_{{i+1}}^{2})({x_i}{y_{i+1}} - {x_{i+1}}{y_i}).$$
(14)

For small strains, the location of the neutral axis coincides with the shape’s centroidal axis, \(\overline {y}\) (m), which is given by the following:

$$\overline {y} ={A_y}/A.$$
(15)

The corresponding x-coordinate of each shape’s centroid was similarly determined as follows:

$$\overline {x} ={A_x}/A.$$
(16)

For composite sections consisting of n smaller solid and hollow shapes, the centroid was determined as follows:

$$\overline {y} ={{\mathop \sum \limits_{{j=1}}^{n} {A_{{y_j}}}} \mathord{\left/ {\vphantom {{\mathop \sum \limits_{{j=1}}^{n} {A_{{y_j}}}} {\mathop \sum \limits_{{j=1}}^{n} {A_j}}}} \right. \kern-0pt} {\mathop \sum \limits_{{j=1}}^{n} {A_j}}},$$
(17)

where Ayj and Aj were multiplied by − 1 if the jth shape represented a void. Similarly, the parallel axis theorem was used to determine Ixx for composite sections as follows:

$${I_{xx}}=\mathop \sum \limits_{{j=1}}^{n} ({I_{x{x_j}}}+{A_j}c_{j}^{2}),$$
(18)

where cj is the perpendicular distance between the neutral axis of the composite section and the centroid of the jth smaller shape. Similarly, Ixxj and Aj were multiplied by − 1 if the jth shape represented a void. Ultimately, Z was computed as follows:

$$Z={I_{xx}}/y,$$
(19)

where y is the maximum perpendicular distance between the section’s neutral axis and outermost trunk fibers. The reduction to Z for a hollow section, relative to a solid section with identical trunk geometry, was determined as a percent difference:

$${Z_{{\text{LOSS}}}}=({Z_{{\text{SOLID}}}} - {Z_{{\text{HOLLOW}}}})/{Z_{{\text{SOLID}}}}.$$
(20)

After calculation, the estimates obtained for a given orientation were stored, and the analysis was repeated after incrementally rotating each set of coordinate pairs about the respective section’s centroidal coordinates by an arbitrarily small angle. Each coordinate pair was rotated counter-clockwise about the z-axis using the following rotation matrix:

$${R_z}\left( \alpha \right)=\left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{ - \sin \alpha } \\ {\sin \alpha }&{\cos \alpha } \end{array}} \right],$$
(21)

where α (rad) is the incremental rotation angle. The complete rotation for each coordinate pair was achieved by the following matrix operation:

$${\varvec{A}}^{\prime}={R_x}(\alpha )({\varvec{A}} - {\varvec{B}})+{\varvec{B}},$$
(22)

where A is a vector in ℝ2 with elements [xiyi] and B is a similar vector composed of a given section’s centroidal coordinates. After each incremental rotation, identical calculations were performed to compute ZLOSS until the cumulative total rotation for a section equaled 2π rad. The preceding image processing and numerical analysis steps were written as a MATLAB (MathWorks, Natick, MA, USA) function named zloss (Burcham 2017).

In addition, several attributes of the solid and damaged parts displayed in tomograms and binary images were calculated. The percent of total damaged cross-sectional area, AD (%), was computed as follows:

$${A_{\text{D}}}={\raise0.7ex\hbox{${\mathop \sum \nolimits_{{i=1}}^{n} {a_{{{\text{D}}_i}}}}$} \!\mathord{\left/ {\vphantom {{\mathop \sum \nolimits_{{i=1}}^{n} {a_{{{\text{D}}_i}}}} {{A_{\text{S}}}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${{A_{\text{S}}}}$}},$$
(23)

where aD is the area (m2) of ith damaged part and AS is the area (m2) enclosed by the trunk boundary, excluding the bark. The offset length, LO (m), between the centroid of the trunk and the centroid of the largest damaged part was determined using the distance formula:

$${L_{\text{O}}}=\sqrt {{{({x_2} - {x_1})}^2}+{{({y_2} - {y_1})}^2}} ,$$
(24)

where (x1, y1) and (x2, y2), respectively, are the centroidal coordinates of the trunk and largest damaged part determined numerically using Eqs. 15 and 16. The roundness, R (dimensionless), of the trunk, RT, and largest damaged part, RD, was determined using the following:

$$R={\raise0.7ex\hbox{${4A}$} \!\mathord{\left/ {\vphantom {{4A} {\pi {L^2}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${\pi {L^2}}$}},$$
(25)

where A is the area (m2), determined numerically using Eq. 11, and L (m) is the major axis of the shape, determined as the maximum distance between any two points on the boundary. The latter two attributes only considered the largest damaged part, because the existing analytical methods only explicitly consider one damaged area (Ciftci et al. 2014; Coder 1989; Smiley and Fraedrich 1992; Wagener 1963).

Analytical estimates

To compute analytical estimates of ZLOSS, two basic approaches described by Ciftci et al. (2014) were used to approximate irregular shapes as circles. Again, only the circular approximation of the largest damaged part in a tomogram was used in the associated ZLOSS calculations. For the first method (“Ciftci I”), the irregularly shaped trunk and largest damaged part were approximated using a minimum circumscribed circle, “Ciftci I(a);” maximum inscribed circle, “Ciftci I(b);” and the average of these two circles, “Ciftci I(c).” The radius and centroidal coordinates of the minimum circumscribed and maximum inscribed circles were determined using the MATLAB functions minboundcircle and incircle, respectively, from the matGeom library (Legland 2015). For the second method (“Ciftci II”), the radius of the circular equivalent of an irregular shape was calculated as follows:

$$r=~\sqrt {{\raise0.7ex\hbox{$A$} \!\mathord{\left/ {\vphantom {A \pi }}\right.\kern-0pt}\!\lower0.7ex\hbox{$\pi $}}} ,$$
(26)

where A (m2) is the area of an irregular shape determined numerically using Eq. 11. To position the circular equivalent shape on the centroid of its irregular counterpart, the centroidal coordinates of the trunk and largest damaged part were determined numerically using Eqs. 15 and 16. The analytical estimates of ZLOSS were determined using these radii and centroidal coordinates; see Ciftci et al. (2014) for more information about the associated calculations. Since ILOSS = ZLOSS for a hollow circle, Eq. 2 was used, as employed by Coder (1989), to compute analytical estimates of ZLOSS. Likewise, Eq. 3 proposed by Wagener (1963) was used to compute analytical estimates, not strictly ZLOSS, for comparison with the other available methods. For Eqs. 2 (“Coder”) and 3 (“Wagener”), the radius of the circular equivalent of an irregular shape, determined using Eq. 26, was used to calculate ZLOSS.

Statistical analysis

Three coefficients were computed to examine the accuracy of tomograms at depicting internal conditions, in terms of the size, position, and shape of damaged parts. Pearson’s product-moment correlation (r) and Spearman’s rank-order correlation (ρ) were computed to measure the strength of a general linear relationship of the form y = ax + b between features estimated from tomograms and destructive measurements, including AD, LO, RT, RD, and their rank-order counterparts. Lin’s concordance coefficient (pc) was computed to measure the strength of a linear relationship of the form y = x (i.e., 1:1 similarity) between the same data sets. Cook’s D, measured during regression, was used to identify potential outliers in each comparison, with cases exerting influence greater than 4/n inspected more closely (Marasinghe and Kennedy 2008).

In addition, two linear models were fit to the error associated with various approaches to estimating ZLOSS from sonic tomograms relative to the same computed numerically from binary images. Since ZLOSS computed numerically from binary images was based on destructive measurements and accommodated the most geometric detail, it was assumed that it provided the best available approximation of the actual ZLOSS for a measured section and offered a useful standard to distinguish among other methods based on SoT. First, analysis of variance (ANOVA) was used to test the effect of the mathematical methods and colors used to select damaged wood parts on the absolute difference (%) between maximum ZLOSS determined using sonic tomograms and binary images. The fixed effects included mathematical methods used to estimate ZLOSS: Ciftci I(a), Ciftci I(b), Ciftci I(c), Ciftci II, Coder, zloss, and Wagener; colors used to select damaged wood parts in sonic tomograms: violet and blue (VB) and green, violet, and blue (GVB); and their interaction: methods × colors. For significant fixed effects, mean separation was performed using Tukey’s honestly significant difference.

Second, analysis of covariance was used to test the effect of the mathematical methods on the absolute difference (%) between maximum ZLOSS determined using tomograms and binary images, after accounting for geometric features of cross sections. In total, eight covariates were tested for inclusion in the model: AD, AD (error), LO, LO (error), RT, RT (error), RD, and RD (error). The covariates were computed from binary images of each section as described in Eqs. 23‒26, and the error associated with each covariate was determined as the absolute difference between the estimate from tomograms and binary images. Since AD represented the percent of total damaged area, the fixed effect for colors was removed from this model. The form of the model was determined by iteratively testing the significance of a simple linear relationship between each covariate and the absolute difference (%) between maximum ZLOSS determined using tomograms and binary images. The validity of statistical assumptions for linear regression was checked by testing the normality of observations and homoscedasticity, respectively, with the Kolmogorov–Smirnov statistic and the Spearman rank correlation between absolute studentized residuals and observations of the dependent variable (Kutner et al. 2004). For each of the selected covariates, the homogeneity of slopes among levels of the fixed effect was tested and, if rejected, an unequal slope model was fit for the associated covariate. For significant fixed effects, mean separation was performed using Tukey’s honestly significant difference at multiple values of each covariate. Statistical analyses were performed using SAS 9.4 (SAS Institute, Inc., Cary, NC, USA); the ANOVA and ANCOVA models were fit using proc glm, and pc was computed using the CCC macro v9 (Crawford et al. 2007).

Results

AD, the percent of total damaged cross-sectional area measured in sonic tomograms, was mostly less than binary images, but the difference was smaller when using GVB to select damaged parts in tomograms. On average, AD measured in tomograms was 25% and 14%, respectively, less than binary images when using VB or GVB to select damaged parts. Significant correlations between AD measured in tomograms and binary images indicated that the size of damaged parts in tomograms was proportional to their actual size in binary images, but the difference in pc showed that AD computed using GVB was closer to the actual AD in binary images (Table 2). For one yellow birch (Betula alleghaniensis) section 160 cm above ground (YB04–160), AD measured using GVB was overpredicted by 23%, and this value was a distinct outlier (D = 2.12) because of the disproportionately large green area in the associated tomogram. Excluding this outlier, regression indicated significant linear relationships between AD measured from tomograms and binary images using GV (p < 0.001) and GVB (p < 0.001) (Table 3). For these functions, coefficients of determination indicated that AD measured from tomograms using GV (r2 = 0.54) and GVB (r2 = 0.59) accounted for considerable variation in AD measured from binary images, suggesting that the repeated underestimation of AD in the examined cross sections was reasonably predictable (Fig. 3).

Table 2 For a set of 51 trunk cross sections, Pearson’s product-moment correlation (r), Spearman’s rank-order correlation (ρ), and Lin’s concordance correlation (pc) between geometric attributes derived from sonic tomograms and binary images of the destructively measured internal condition of trees
Full size table
Table 3 Parameter estimates, confidence intervals, and coefficients of determination for linear regression models fit to geometric attributes derived from sonic tomograms and binary images of the destructively measured internal condition of trees
Full size table
Fig. 3
figure 3

Scatter plot of the percent of total damaged cross-sectional area, AD (%), measured in sonic tomograms against AD measured in a reference binary image of the destructively measured internal condition of trees. For the estimates derived from tomograms, damaged parts were selected using either green, violet, and blue (GVB, circle) or violet and blue (VB, plus). Most values are located above the solid black 1:1 comparison line, indicating a repeated underestimation of AD in tomograms relative to binary images. In contrast, AD measured using GVB for one yellow birch (Betula alleghaniensis) trunk 160 cm above ground (labeled YB04–160) was overpredicted by 23%, a distinct outlier. Least-squares regression equations are y = 0.22 + 1.27x (blue, long dash line) and y = 0.16 + 0.92x (blue, short dash line) for AD computed using VB and GVB, respectively. See Table 3 for model parameter estimates and fit statistics

Full size image

In contrast, LO measured in sonic tomograms was mostly greater than in binary images, but the measurements differed less when using GVB to select damaged parts in tomograms. On average, LO measured in tomograms was 4.4 cm and 3.2 cm, respectively, greater than binary images when using GV or GVB to select damaged parts. Significant correlations between LO measured in tomograms and binary images indicated that the position of damaged parts in tomograms was proportional to their actual position in binary images, but the difference in pc showed that LO computed using GVB was closer to the actual LO in binary images (Table 2). For one yellow birch cross section 100 cm above ground (YB05–100), LO measured using VB was overpredicted by 26.3 cm. This value was a distinct outlier (D = 2.11), because the largest damaged part was depicted near the trunk periphery in the tomogram—a considerable distance from the largest damaged part at the center of the cross section in the corresponding binary image. Excluding this outlier, regression indicated significant linear relationships between LO measured from tomograms and binary images using GV (p < 0.001) and GVB (p < 0.001) (Table 3). For these functions, coefficients of determination indicated that LO measured from tomograms using GV (r2 = 0.62) and GVB (r2 = 0.56) accounted for considerable variation in LO measured from binary images, suggesting that the repeated overestimation of LO in the examined cross sections was reasonably predictable (Fig. 4). For these regression functions, the intercept was not significantly different from zero when using GV (p = 0.736) or GVB (p = 0.927) to select damaged parts in tomograms, indicating that the overestimation of LO in tomograms increased in proportion to the actual LO in binary images (Fig. 4).

Fig. 4
figure 4

Scatter plot of the offset length, LO (m), measured in sonic tomograms against LO measured in a reference binary image of the destructively measured internal condition of trees. For the estimates derived from tomograms, damaged parts were selected using either green, violet, and blue (GVB, circle) or violet and blue (VB, plus). Most values are located below the solid black 1:1 comparison line, indicating a repeated overestimation of LO in tomograms relative to binary images. Uniquely, LO measured using two colors for one yellow birch (Betula alleghaniensis) trunk 100 cm above ground (labeled YB05–100) was overpredicted by 26.3 cm, a distinct outlier. Least-squares regression equations are y = 6.59 × 10−4 + 0.60x (blue, long dash line) and y = 2.18 × 10−3 + 0.52x (blue, short dash line) for LO computed using VB and GVB, respectively. See Table 3 for model parameter estimates and fit statistics

Full size image

On average, RT for sonic tomograms (mean 0.850) and binary images (mean 0.841) was greater than RD measured in binary images (mean 0.570) and tomograms using GV (mean 0.512) or GVB (mean 0.570), indicating that a circle better approximated the shape of trunks than damaged parts for this set of trees. Among all geometric features examined in this study, r, ρ, and pc were the greatest for RT measured in tomograms and binary images, indicating that RT depicted in tomograms was very similar to the actual RT in binary images (Table 2). Regression indicated a significant linear relationship between RT measured from tomograms and binary images (p < 0.001) with a high coefficient of determination (r2 = 0.66) (Table 3; Fig. 5).

Fig. 5
figure 5

Scatter plot of the roundness, R (dimensionless), of the largest damaged part, RD, and trunk, RT, measured in sonic tomograms against the same measured in a binary image of the destructively measured internal condition of trees. For the estimates derived from tomograms, RD was determined using either green, violet, and blue (GVB, circle) or violet and blue (VB, plus); RT was computed using the blue trunk geometry line (triangle). Least-squares regression equations are y = 0.47 + 0.22x (blue, long dash line) and y = 0.20 + 0.75x (blue, short dash line) for RD computed using VB and GVB, respectively; the equation for RT is y = 0.20 + 0.75x (blue, solid line). See Table 3 for model parameter estimates and fit statistics

Full size image

In contrast, the shape of damaged parts in binary images, measured in terms of RD, was poorly depicted in sonic tomograms, and this was especially true for damaged parts selected using only VB. Among all geometric features examined in this study, r, ρ, and pc were the lowest for RD measured in tomograms and binary images, implying greater dissimilarity between the RD measured using the two images. Regression indicated a significant linear relationship only between RD measured in tomograms and binary images using GVB (p < 0.001); the associated coefficients of determination indicated that RD determined using GV (r2 = 0.05) and GVB (r2 = 0.25) in tomograms accounted for little variation in RD measured from binary images (Table 3).

Analysis of variance indicated that the mathematical methods and colors used to select damaged parts significantly affected the absolute difference (%) between ZLOSS determined using tomograms and binary images, but these two factors did not interact to affect the absolute difference between ZLOSS determined using the two image types (Table 4). Overall, the absolute difference (%) between ZLOSS determined using tomograms and binary images was significantly less for estimates using GVB to select damaged parts than for others using VB. Overall, the average absolute difference in ZLOSS was 6% less for estimates using GVB compared to others using only VB. Among mathematical methods, pairwise comparisons revealed that the absolute difference between ZLOSS determined using tomograms and binary images was significantly greater for analytical methods neglecting the position of damaged parts (i.e., Coder and Wagener). Overall, the error associated with these estimates was between 5% and 9% greater than for the other methods, which did not differ significantly from one another (Table 4).

Table 4 Analysis of variance of the effect of mathematical methods and colors used to select damaged parts on the absolute difference (%) between maximum ZLOSS determined using sonic tomograms and binary images of the destructively measured internal condition of trees
Full size table

In terms of the actual difference between ZLOSS determined using tomograms and binary images, all mathematical methods underestimated ZLOSS in most cases. For Coder and Wagener, respectively, ZLOSS determined using tomograms was, on average, 25% and 21% less than determined numerically using binary images; these two methods underestimated ZLOSS in 98% of all cases. For the remaining methods, the average actual difference was smaller, but the estimates determined using tomograms were still less than determined numerically using binary images in most cases. Among these methods, the average actual difference between ZLOSS determined using tomograms and binary images was, in decreasing order: Ciftci I(b), 14%; Ciftci II, 11%; Ciftci I(c), 9%; zloss, 9%; Ciftci I(a), 4%.

Among all tested covariates, LO (F = 26.72; df = 7, 658; p < 0.001) and AD (error) (F = 17.68; df = 7, 658; p < 0.001) were selected as the only variables showing a significant linear relationship with the absolute difference between ZLOSS determined using tomograms and binary images. Although the slopes describing the change in the absolute difference between ZLOSS determined using tomograms and binary images over a unit change in LO varied significantly among mathematical methods (F = 4.95; df = 6, 658; p < 0.001), the same was not true for the slopes describing the change in this difference over a unit change in AD (error) (F = 1.17; df = 6, 658; p = 0.322). As a result, a common slope was used to describe the relationship between AD (error) and the absolute difference between ZLOSS determined using tomograms and binary images for all mathematical methods, and unequal slopes were fit to describe the relationship between LO and the absolute difference between ZLOSS determined using tomograms and binary images for each mathematical method individually. Using this model, analysis of covariance revealed that mathematical methods significantly affected the absolute difference between ZLOSS determined using tomograms and binary images, after accounting for LO and AD (error). Except for Coder, the intercepts associated with each method were not significantly different from zero, indicating that the absolute difference between ZLOSS determined using tomograms and binary images is minimized to effectively zero for most mathematical methods when the largest damaged part is concentric and AD is depicted accurately in tomograms. Except for zloss, all the slopes describing the relationship between LO and the absolute difference between ZLOSS determined using tomograms and binary images were significantly different from zero, indicating that, among all methods, the numerical approach was the least sensitive to changes in LO (Table 5).

Table 5 Analysis of covariance of the effect of mathematical methods on the absolute difference (%) between maximum ZLOSS determined using sonic tomograms and binary images of the destructively measured internal condition of trees, after accounting for geometric features of the examined cross sections
Full size table

Mean separation, performed at six combinations of the two covariates selected to represent the observed range of AD (error) and LO, revealed that differences among mathematical methods existed only for LO > 0. At AD (error) = 0 and LO = 0, there were no significant differences in the absolute difference between ZLOSS determined using tomograms and binary images among the mathematical methods, and there were similarly no significant differences among methods at AD (error) = 0.4 and LO = 0, since a common slope was fit to all observations of AD (error) and the absolute difference between ZLOSS determined using tomograms and binary images. For all mathematical methods, the absolute difference between ZLOSS determined using tomograms and binary images increased by 46% over a unit change in AD (error) (note that the possible range for AD (error) is [0, 1]). However, consistent differences arose among mathematical methods for LO > 0, owing to the different slopes fit to observations of LO and the absolute difference between ZLOSS determined using tomograms and binary images for each method separately (Table 5). For these cases, the absolute difference between ZLOSS determined using tomograms and binary images was greatest for Coder and Wagener, since these methods neglected LO. The remaining methods, in decreasing order of the absolute difference between ZLOSS determined using tomograms and binary images, were: Ciftci I(b), Ciftci II, Ciftci I(c), Ciftci I(a), and zloss (Table 6).

Table 6 Mean separation for the analysis of covariance of the effect of mathematical methods on the absolute difference (%) between maximum ZLOSS determined using sonic tomograms and binary images of the destructively measured internal condition of trees, determined at six combinations of two covariates accounting for geometric features of the examined cross sections
Full size table

Discussion

For decayed sections, most authors similarly observed that AD was underestimated in sonic tomograms in a range of tree species (Deflorio et al. 2008; Gilbert and Smiley 2004; Liang et al. 2007; Liang and Fu 2012; Marra et al. 2018; Wang et al. 2007, 2009). In agreement with these findings, Wang et al. (2009) also reported that the average difference between AD determined using sonic tomograms and destructive measurements was greater when using VB (mean 14%) than GVB (mean 2%) to select damaged parts. In other reports, authors only used two colors to select damaged parts in sonic tomograms, and the reported average underestimation of AD ranged between < 1% (Ostrovsky et al. 2017) and 14% (Wang et al. 2009). However, some authors computed AD using coarse grid systems with cell dimensions ranging between 5 mm (Gilbert and Smiley 2004) and 12.5 mm (Ostrovsky et al. 2017), contributing unknown error to the approximation.

It is possible that the underestimation of AD arises from the reduced sensitivity of sonic tomography to low-velocity features (Li et al. 2012) that limits the detection of incipient decay (Deflorio et al. 2008), and practitioners should account for this limitation when interpreting tomograms, especially in light of the consensus among related studies. Others have reported, in agreement with this study, a strong linear relationship between AD determined using tomograms and destructive measurements (Gilbert and Smiley 2004; Liang and Fu 2012). In a sample of 15 decayed sections, Liang and Fu (2012) reported much better agreement between AD determined using sonic tomograms and destructive measurements; the slope of a linear model fit to these observations was much closer to one than in this study, with a high coefficient of determination (r2 = 0.94) despite using only VB to select damaged parts. Although Gilbert and Smiley (2004) also reported a strong linear relationship between the amount of decay depicted in tomograms and measured on the images of decayed cross sections (r2 = 0.94), the authors did not fit a linear regression model to the observations, precluding a comparison of model coefficients. Compared to existing reports, there was a greater underestimation of AD in sonic tomograms in this study. Still, practitioners should use caution when considering the use of regression models from this study to adjust tomographic estimates, because the underlying observations were limited to three species at a single site. Although our sample of decayed sections was relatively large, it will be important to examine further the relationship between AD determined using tomograms and destructive measurements across several sites and species in future work.

Conversely, most existing reports indicated that AD was overestimated in sonic tomograms for sections with internal cracks (Liang et al. 2007; Wang et al. 2009; Wang and Allison 2008). In this study, only one of the examined sections (SM05–100) contained a crack, but it occurred alongside internal decay, preventing a separate evaluation of this type of defect. Without adjustment, this means that ZLOSS determined using tomograms would tend to be liberal and conservative for cracks and decay, respectively, and practitioners should consider these trends when computing ZLOSS from tomograms. Future studies should examine the accuracy of tomograms, in terms of AD, for each type of defect separately, taking care to separate those cracks present during tomographic measurement from others created by drying after felling.

Among related studies, this is the first report of a repeated overestimation of LO in sonic tomograms. In a sample of 17 decayed sections, Gilbert and Smiley (2004) observed that, in terms of the location of damaged parts, 2% and 9% of AD were false-positive and -negative estimates that did not match the internal condition of sections. However, LO is arguably a better feature to examine, in terms of ZLOSS, because damaged parts decrease I proportional to the square of this distance (Eq. 18). The observed repeated overestimation of LO in sonic tomograms should contribute to an equivalent overestimation of ZLOSS, proportional to AD (Eq. 18). Like AD, the difference between LO determined using tomograms and binary images was greater when using VB than GVB to select damaged parts, further justifying the addition of color(s) representing intermediate acoustic transmission speeds when analyzing tomograms, despite its usual omission by the manufacturer’s software.

The accuracy of ZLOSS estimates improved when using GVB to select damaged parts, corroborating the direct comparisons between geometric attributes in this study and other reports that these colors should be used to select damaged parts (Marra et al. 2018; Wang et al. 2009). Among the evaluated methods, the difference between ZLOSS determined using tomograms and binary images for Coder and Wagener was significantly greater than all other methods. Considering this difference, practitioners should avoid using methods neglecting LO to estimate ZLOSS, in agreement with Kane and Ryan (2004). Although Liang and Fu (2012) reported a much smaller difference between strength-loss estimates determined using tomograms and destructive measurements, the reported difference was determined only by the accuracy of tomograms, because the same method was applied to tomograms and destructive measurements in each case. In this study, the methods used to estimate ZLOSS from tomograms were compared with an improved numerical method, zloss, applied to binary images.

The difference between ZLOSS determined using tomograms and binary images did not vary with RT or RD, supporting the use of circles to approximate irregular shapes by the existing analytical methods (Ciftci et al. 2014; Coder 1989; Smiley and Fraedrich 1992; Wagener 1963). However, some authors have reported that AD (error) ∝ R−1 (Gilbert et al. 2016; Rabe et al. 2004; Rust 2017) and the use of circles for highly irregular trunk shapes may be less appropriate in these situations. The selection of AD (error) and LO as covariates means that the accuracy of ZLOSS estimates was primarily affected by the underestimation of AD in tomograms and the actual LO of the largest damaged part. Based on this analysis, it is apparent that the value of a method, relative to others examined in this study, depends largely on its consideration and approach to LO; all methods were similarly affected by the underestimation of AD in sonic tomograms. After accounting for AD (error) and LO, the consistent ranking among methods used to estimate ZLOSS, caused by the unequal slopes fit to each method for LO, usefully revealed methods that should be considered for greater use by arborists. Uniquely, the slope fit to zloss was not significantly different from zero, and the absolute difference between ZLOSS determined using tomograms and binary images was lowest for this method at all selected values of the covariates. As a result, the accuracy of this method was mostly determined by the error in estimating AD, and this provides justification for using this method as a benchmark, since it was least sensitive to changes in LO.

Among the remaining analytical methods proposed by Ciftci et al. (2014), Ciftci I(a) and I(c) gave better estimates, in terms of the absolute difference between ZLOSS determined using tomograms and binary images, than Ciftci II and I(b). The former two methods relied, in whole or part, on circumscribed circles fit to the trunk and largest damaged part. Since RT > RD for the examined sections, the circumscribed circles enlarged the area of damaged parts (mean + 86%) more than trunks (mean + 19%), relative to their corresponding area in tomograms, resulting in an average increase to AD of 7.5% and 2.5%, respectively, for Ciftci I(a) and I(c). The increased AD usefully offset its underestimation in tomograms, explaining the improved estimates offered by these two methods. Notably, solutions were available in all cases using Ciftci I(a), but the same was not true for all cases using other methods. For example, ZLOSS could not be estimated using Ciftci I(b), I(c), and II for one sugar maple cross section 80 cm above ground (SM28–080), because the damaged part was completely outside and did not intersect the solid trunk. Although Ciftci I(a) offered relatively superior estimates among the analytical methods proposed by Ciftci et al. (2014), it is useful to note that these methods are not strictly analytical, because they require image processing techniques, limiting their usefulness to practitioners.

Despite considering only the largest damaged part, the analytical estimates differed modestly from the numerical estimate computed from binary images in most cases. On average, the percent of total area occupied by the largest damaged part was 11% (SD 16%) less than AD. Still, the analytical methods gave sizeable underestimates of ZLOSS in some cases, because they neglected to consider one or more additional damaged parts. In one American beech section 60 cm above ground (AB06–060), the largest damaged part was in the center of the section, but the analytical estimate omitted the contributions from the second largest damaged part at the trunk periphery, causing ZLOSS to be underestimated by, on average, 16% among the six analytical methods.

The PiCUS Q74 software, like other sonic tomography devices, provides a built-in function to give an approximate estimate of the percent residual load-bearing capacity (Gocke 2017) equal to:

$${I_{{\text{du}}}}/{I_{{\text{Du}}}} \times 100,$$
(27)

where Idu and IDu are the second moments of area computed about the section’s centroid using the diameter of the damaged part (d) and trunk (D). To determine these diameters, the software requires users to select the boundary between damaged and solid wood, and it computes the lengths along a radius formed by the centroid and user-selected location (A. Richter, personal communication). This excludes considerable information in the tomogram from the estimate. Since Eq. 27 corresponds to 1 − Eq. 2, its performance can be considered equivalent to that ascribed to Coder in this study. Practitioners are cautioned against using this built-in function when eccentric decay is present, because Kane and Ryan (2004) demonstrated that Eq. 2 performed poorly in these cases.

It is possible that the image binarization process used in this study introduced unknown error into the ZLOSS estimates derived from binary images. Although the existence of damaged wood was obvious in most of the examined sections, error may have occurred in determining the precise boundary between damaged and solid wood. In the future, authors should consider alternative methods to binarize images for ZLOSS estimates. Likewise, the assumption of material isotropy may have introduced negligible error into the ZLOSS estimates (Ciftci et al. 2014), and authors should consider these effects, when relevant material properties information is available, in future work.

Conclusion

Among the evaluated methods, ZLOSS was best estimated using sonic tomograms numerically with zloss or analytically with Ciftci I(a), and practitioners should consider using these methods to assess the severity of internal defects measured with sonic tomography. The numerical method zloss addressed the simplifying assumptions contained in many existing methods by accommodating more geometric detail in the associated calculations, including irregular shapes and multiple offset damaged parts. Still, the repeated under- and overestimation, respectively, of AD and LO in tomograms limits the accuracy of ZLOSS estimates based on tomography, and these limitations should be considered when interpreting estimates. It is important to note that ZLOSS only estimates the reduced load-bearing capacity of the measured tree part (not the entire tree). Even more, the methods described in this article do not estimate the probability of tree failure, which requires a more thorough accounting of the total applied and resistive forces acting on a tree. There is little scientific consensus on a threshold value associated with a change in the likelihood of failure (Gruber 2008), but Kane (2014) showed that failure at an area with existing or simulated decay was more likely when ILOSS > 30%.

Author contribution statement

DB and BK conceived and designed the study, NB and RM collected the data, DB analyzed data and wrote the manuscript, and all authors edited the manuscript.