Alternative integration algorithms for three-dimensional mortar contact

Abstract

In this paper, a new approach is proposed to improve efficiency of the integration procedure for mortar integrals within finite element mortar methods for contact. Appropriate approaches subdivide polygonal integration segments into triangular integration cells where well-established quadrature rules can be applied for numerical integration. Here, a subdivision of segments into quadrilateral integration cells is proposed and investigated in detail. By this procedure, the numerical effort is decreased because the number of integration cells is smaller and less quadrature points are needed. In all the aforementioned methods, necessary projections of integration points result in rational polynomials in the integrand. Thus, an exact numerical integration is impossible. Using quadrilateral integration cells additionally involves non-constant Jacobian determinants which further increases the polynomial degree of the integrand. Numerical experiments indicate, that the resulting increase in the error is small enough to be acceptable in consideration of the gained speed-up.

1 Introduction

The first finite element formulations for quasi-static and dynamic contact problems have been presented by Francavilla and Zienkiewicz [10] and Hughes et al. [16]. Since then it has been a very active research field. This paper addresses the area of mortar-based contact formulations. A modified numerical integration algorithm for the contact integrals is presented and its efficiency and accuracy is investigated.

One characteristic feature of any particular contact algorithm is the way contact is discretized. Prior to the first mortar contact methods, node-to-segment (NTS) methods were investigated. In these formulations contact conditions are collocated at discrete points. Simo et al. [30] proposed for the first time a contact formulation which can be seen as a so-called segment-to-segment (STS) approach. In contrast to NTS formulations STS formulations evaluate integral conditions resulting from contact by numerical integration instead of pointwise collocation. STS formulations are usually more robust than NTS formulations and pass the contact patch test [21]. This is not possible with standard one-pass NTS algorithms. Apart from early STS formulations [6, 36] almost all currently used STS contact formulations are based on a domain decomposition technique originally proposed by Bernardi et al. [3]. The so-called mortar method was introduced to couple spectral elements with finite elements which are used on different subdomains in order to combine the advantages of both methods. First mortar contact formulations were described by Ben Belgacem [1]. In the subsequent years those formulations have been extended to frictional contact [19] and to non-linear kinematics [8, 27, 28, 35].

The specific method to enforce the contact constraints, i.e. the non-penetration conditions, is the second main distinction of contact algorithms. Established methods are the penalty method, the Lagrange multiplier method and the augmented Lagrangian approach. Overviews of the mentioned approaches are given e.g. by Wriggers [33] and Laursen [18]. In this work the Lagrange multiplier method is used, thus the non-penetration condition as well as the tangential contact condition can be satisfied exactly. Usually the Lagrange multipliers are additional unknowns which increase the size of the global system of equations. If Lagrange multipliers are discretised with so-called dual shape functions they can be eliminated from the global system of equations [31]. Wohlmuth and Krause [32] used dual shape functions for two-dimensional contact problems. Hartmann et al. [13] extended the algorithm to three-dimensional contact problems. A 3d-mortar contact formulation based on dual shape functions with consistent linearisation was described by Popp et al. [23]. Boundaries can be treated consistently if the algorithms described by Cichosz and Bischoff [4] or Popp et al. [25] are used for two-dimensional or three-dimensional simulations, respectively.

One of the most demanding processes in contact mortar formulations is the evaluation of the so-called mortar integrals, especially in three-dimensional settings. The domain of integration is the contact surface itself. Due to the finite element discretisation the surface representation of the contacting bodies has kinks and therefore for general cases the two surfaces do not match exactly in the contact domain. Hence, the domain of integration has to be chosen as one of the two surface representations, an intermediate one or another simplified surface within the contact domain. Furthermore, the existing algorithms differ in the way they treat the discontinuities within the contact domain which result from the discontinuous finite element surface representation. Farah et al. [7] give a comprehensive overview of the general approach for the numerical integration of the mortar integrals. Advantages and disadvantages of methods which consider discontinuities or ignore them to a greater extent are discussed in detail.

Here, the numerical integration is performed on segments which are areas on the domain of integration which have a smooth integrand. This segment-based approach is more accurate than methods where the integration is performed without looking after smooth integrands, especially when elements at boundaries, friction or higher order elements are considered [7]. One drawback of this procedure is the relatively high computational effort, which mainly comes from the larger number of integration points needed and the associated projections.

Efficiency of numerical integration is therefore a crucial aspect of the algorithm. In this contribution different methods for evaluating integrals on a segment are discussed. An algorithm which uses quadrilateral integration cells instead of the commonly used triangular integration cells to subdivide the polygonal segment is investigated. To the best of the authors’ knowledge this is done in detail for the first time.

The remainder of this paper is structured as follows: in Sect. 2 the contact problem is described in a continuum mechanical manner. The strong form of the boundary value problem is given and subsequently transferred to a weak representation. The finite element discretisation is given in the following section. Therein, the mortar integrals are defined whose numerical integration is described in detail in Sect. 4. Several approaches are summarised and general ideas to increase the efficiency of the algorithm are stated. Section 5 is the main part of this contribution. Here, quadrilateral integration cells are presented, the benefits are identified and possible inaccuracies resulting from their non-constant Jacobian determinants are investigated. In Sect. 6 the accuracy of the numerical integration with quadrilateral integration cells is compared to commonly used numerical integration schemes. To this end, three numerical experiments are evaluated. Furthermore, the convergence behaviour is compared by a fourth example. Concluding remarks are given in Sect. 7.

2 Continuum mechanical problem description

2.1 Strong form

In this section the governing equations for frictional large deformation contact problems are provided. In order to distinguish between the equations of two contacting elastic bodies, related quantities are labeled by the indices ${\alpha }= 1,2$, respectively. ${\varOmega }_0^{({\alpha })}$ and ${\varOmega }^{({\alpha })}$ describe the spatial domains of the contacting bodies in the reference and current configuration, respectively. The parentheses ought to imply no summation on repeated indices, otherwise Einstein’s summation convention applies. Their surfaces are denoted by ${\partial }{\varOmega }_0^{({\alpha })}$ and ${\partial }{\varOmega }^{({\alpha })}$, respectively. They are often called slave and master surface. Both surfaces are divided into three non-overlapping sets. In the reference configuration these are

$$\begin{aligned}&{\varGamma }_{\mathrm {D}}^{({\alpha })}\cup {\varGamma }_{\mathrm {N}}^{({\alpha })}\cup {\varGamma }_{\mathrm {c}}^{({\alpha })}={\partial }{\varOmega }_0^{({\alpha })}, \end{aligned}$$

(1)

$$\begin{aligned}&{\varGamma }_{\mathrm {D}}^{({\alpha })}\cap {\varGamma }_{\mathrm {N}}^{({\alpha })}=\emptyset , \nonumber \\&{\varGamma }_{\mathrm {D}}^{({\alpha })}\cap {\varGamma }_{\mathrm {c}}^{({\alpha })}=\emptyset ,\nonumber \\&{\varGamma }_{\mathrm {N}}^{({\alpha })}\cap {\varGamma }_{\mathrm {c}}^{({\alpha })}=\emptyset , \end{aligned}$$

(2)

where ${\varGamma }_{\mathrm {D}}^{({\alpha })}$ are the boundaries with prescribed Dirichlet conditions, ${\varGamma }_{\mathrm {N}}^{({\alpha })}$ are the boundaries with prescribed Neumann conditions and ${\varGamma }_{\mathrm {c}}^{({\alpha })}$ are the boundaries with prescribed contact conditions. Their corresponding representations in the current configuration are given by ${\gamma }_{\mathrm {D}}^{({\alpha })}$, ${\gamma }_{\mathrm {N}}^{({\alpha })}$ and ${\gamma }_{\mathrm {c}}^{({\alpha })}$, respectively. The set ${\gamma }_{\mathrm {c}}^{({\alpha })}$ is not known a priori but has to be identified during the computation. The current position vector $\mathbf {x}^{({\alpha })}(\mathbf {X},t)$ of any material point can be expressed by its position in the reference configuration $\mathbf {X}^{({\alpha })}$ and its displacement $\mathbf {u}^{({\alpha })}(\mathbf {X},t)$:

$$\begin{aligned} \mathbf {x}^{({\alpha })}(\mathbf {X},t) = \mathbf {X}^{({\alpha })}+\mathbf {u}^{({\alpha })}(\mathbf {X},t). \end{aligned}$$

(3)

The evolution of this deformation is described by the process variable t (pseudo time for the quasi-static problems treated herein). From the deformation the material deformation gradient $\mathbf {F}^{({\alpha })} = \frac{\mathrm {d} \mathbf {x}^{({\alpha })}}{\mathrm {d} \mathbf {X}^{({\alpha })}}$ and the Green-Lagrange strain tensor $\mathbf {E}^{({\alpha })} = \frac{1}{2}(\mathbf {F}^{\mathrm {T}}\mathbf {F}-\mathbf {I})^{({\alpha })}$ can be found in the usual way. In this work, a hyperelastic material of neo-Hookean type is used to relate strains and stresses. From the stored energy potential ${\varPsi }$ the second Piola-Kirchhoff stress tensor $\mathbf {S}^{({\alpha })}$ and the elasticity tensor $\overset{4}{\mathbf {C}}{}^{({\alpha })}$ can be derived, see e.g. [2]:

$$\begin{aligned} \mathbf {S}^{({\alpha })} = \frac{{\partial }{\varPsi }^{({\alpha })}}{{\partial }\mathbf {E}^{({\alpha })}},\qquad \overset{4}{\mathbf {C}}{}^{({\alpha })} = \frac{{\partial }^2{\varPsi }^{({\alpha })}}{{\partial }\mathbf {E}^{({\alpha })}{\partial }\mathbf {E}^{({\alpha })}}. \end{aligned}$$

(4)

Along with the relation between the second and first Piola-Kirchhoff stress tensor $\mathbf {P}= \mathbf {F}\mathbf {S}$, the reference unit outward normal $\bar{\mathbf {n}}$, the body load $\mathbf {b}$, the prescribed displacements $\check{\mathbf {u}}$ and stresses $\check{\mathbf {t}}$ the boundary value problem reads

$$\begin{aligned}&{{\mathrm{Div}}}\mathbf {P}^{({\alpha })}+{\rho }_0^{({\alpha })}\mathbf {b}^{({\alpha })}={\mathbf {0}}\quad \text {in }{\varOmega }_0^{({\alpha })},\nonumber \\&\mathbf {u}^{({\alpha })}=\check{\mathbf {u}}^{({\alpha })}\quad \text {on }{\varGamma }_{\mathrm {D}}^{({\alpha })},\nonumber \\&\mathbf {P}^{({\alpha })}\bar{\mathbf {n}}^{({\alpha })}=\check{\mathbf {t}}^{({\alpha })}\quad \text {on }{\varGamma }_{\mathrm {N}}^{({\alpha })}. \end{aligned}$$

(5)

For the description of the contact kinematics for each point of the contact surface, given by the position vector $\mathbf {x}^{(1)}(\mathbf {X},t)$, the closest point $\hat{\mathbf {x}}^{(2)}(\mathbf {X},t)$ on the master surface is needed. It is found by minimising the distance between $\mathbf {x}^{(1)}(\mathbf {X},t)$ and $\mathbf {x}^{(2)}(\mathbf {X},t)$ via an orthonormal projection

$$\begin{aligned} \hat{\mathbf {x}}^{(2)}(\mathbf {x}^{(1)})=\underset{\mathbf {x}^{(2)}\in {\gamma }_{\mathrm {c}}^{(2)}}{\arg \min }\Vert \mathbf {x}^{(1)}-\mathbf {x}^{(2)}\Vert . \end{aligned}$$

(6)

With this projection point at hand, the normal gap between the bodies is

$$\begin{aligned} g_{\mathrm {n}}\left( \mathbf {x}^{(1)}\right) =-\mathbf {n}^{(1)}\cdot \left( \mathbf {x}^{(1)}-\hat{\mathbf {x}}^{(2)}\right) , \end{aligned}$$

(7)

where $\mathbf {n}$ is the outward oriented surface normal. If adhesion is ignored the contact constraints can be stated as classical Karush-Kuhn-Tucker (KKT) conditions in normal direction:

$$\begin{aligned} g_{\mathrm {n}}\ge 0,\qquad t_{{\mathrm {c}}{\mathrm {n}}}^{(1)} \le 0,\qquad t_{{\mathrm {c}}{\mathrm {n}}}^{(1)} g_{\mathrm {n}}= 0, \end{aligned}$$

(8)

where $t_{{\mathrm {c}}{\mathrm {n}}}^{(1)} = \mathbf {t}_{{\mathrm {c}}}^{(1)}\cdot \mathbf {n}$ is the normal component of the contact stress vector (traction vector) $\mathbf {t}_{\mathrm {c}}^{(1)}$. In order to formulate the contact constraints in the tangential direction the relative tangential velocity $\mathbf {v}_{{\tau },{\mathrm {r}}{\mathrm {e}}{\mathrm {l}}}$ is defined as

$$\begin{aligned} \mathbf {v}_{{\tau },{\mathrm {r}}{\mathrm {e}}{\mathrm {l}}}\left( \mathbf {x}^{(1)}\right) ={\varvec{\tau }}^{\mathrm {T}}\left( \dot{\mathbf {x}}^{(1)}-\dot{\hat{\mathbf {x}}}^{(2)}\right) , \end{aligned}$$

(9)

where ${\varvec{\tau }}= \begin{bmatrix} {\varvec{\tau }}^\xi&{\varvec{\tau }}^{\eta }\end{bmatrix}$. Herein, ${\varvec{\tau }}^\xi$ and ${\varvec{\tau }}^{\eta }$ are the tangential vectors on the slave surface, which form an orthonormal basis in $\mathbb {R}^3$ together with $\mathbf {n}$. With Eq. (9) the contact conditions for the tangential direction using Coloumb’s friction law can be stated as

$$\begin{aligned}&{\psi }:=\Vert \mathbf {t}_{{\mathrm {c}}\tau }^{(1)}\Vert -\mu \mid t^{(1)}_{{\mathrm {c}}{\mathrm {n}}}\mid \le 0,\nonumber \\&\mathbf {v}_{{\tau },{\mathrm {r}}{\mathrm {e}}{\mathrm {l}}}\left( \mathbf {x}^{(1)}\right) -{\beta }\mathbf {t}^{(1)}_{{\mathrm {c}}{\tau }}=0,\nonumber \\&{\beta }\ge 0,\nonumber \\&{\psi }{\beta }= 0. \end{aligned}$$

(10)

In Eq. (10) the vector $\mathbf {t}_{{\mathrm {c}}\tau }^{(1)} = \begin{pmatrix}t_{{\mathrm {c}}{\tau }}^\xi&\quad t_{{\mathrm {c}}{\tau }}^{\eta }\end{pmatrix}^{\mathrm {T}}$ contains the tangential components of the contact stress vector, which can be calculated as

$$\begin{aligned} t_{{\mathrm {c}}{\tau }}^\xi = \mathbf {t}_{{\mathrm {c}}}^{(1)}\cdot {\tau }^\xi ,\qquad t_{{\mathrm {c}}{\tau }}^{\eta }= \mathbf {t}_{{\mathrm {c}}}^{(1)}\cdot {\tau }^{\eta }. \end{aligned}$$

(11)

2.2 Weak form

The principle of virtual work is used to get the weak form of the traction boundary condition and the equilibrium condition as a prerequisite for the finite element formulation. In addition to the standard expressions for the internal and external virtual work ${\delta }{\varPi }_{\mathrm {int}}$, ${\delta }{\varPi }_{\mathrm {ext}}$, representing the boundary value problem (5), the relation between the contact traction of the slave and master side

$$\begin{aligned} \mathbf {t}_{\mathrm {c}}^{(1)}\,{\mathrm {d}}{\gamma }_{\mathrm {c}}^{(1)}=-\mathbf {t}_{\mathrm {c}}^{(2)}\,{\mathrm {d}}{\gamma }_{\mathrm {c}}^{(2)}, \end{aligned}$$

(12)

is needed, representing the momentum balance on the contact surface. The weak form of the virtual work due to contact reads

$$\begin{aligned} {\delta }{\varPi }_{\mathrm {c}}= & {} \int _{{\gamma }_{\mathrm {c}}^{(1)}}\left( {\delta }\mathbf {u}^{(1)}-{\delta }\mathbf {u}^{(2)}\right) ^{\mathrm {T}}\mathbf {t}_{\mathrm {c}}^{(1)} \,{\mathrm {d}}{\gamma }_{\mathrm {c}}^{(1)}\nonumber \\= & {} -\int _{{\gamma }_{\mathrm {c}}^{(1)}}\left( {\delta }\mathbf {u}^{(1)}-{\delta }\mathbf {u}^{(2)}\right) ^{\mathrm {T}}{\varvec{\lambda }}\,{\mathrm {d}}{\gamma }_{\mathrm {c}}^{(1)}. \end{aligned}$$

(13)

The second equality uses the physical identification of the Lagrange multiplier, introduced next, as the negative contact traction of the slave side ${\varvec{\lambda }}= -\mathbf {t}_{\mathrm {c}}^{(1)}$.

The Lagrange multiplier method is used to enforce the non-penetration condition (8) and the frictional contact constraints (10). The corresponding weak form for the normal direction can be found by integrating the product of the normal gap $g_{\mathrm {n}}$ with the trial force ${\delta }{\lambda }_{\mathrm {n}}$ over the contact boundary. In tangential direction the relative tangential velocity $\mathbf {v}_{{\tau },{\mathrm {r}}{\mathrm {e}}{\mathrm {l}}}$ is multiplied by the trial force ${\delta }{\varvec{\lambda }}_{\tau }$ before integration is performed. ${\delta }{\lambda }_{\mathrm {n}}$ and ${\delta }{\varvec{\lambda }}_{\tau }$ can be found by a decomposition of ${\varvec{\lambda }}$ similar to the decomposition of $\mathbf {t}_{{\mathrm {c}}}^{(1)}$ into $t_{{\mathrm {c}}{\mathrm {n}}}^{(1)}$ and $\mathbf {t}_{{\mathrm {c}}{\tau }}^{(1)}$. In a nutshell, the weak form of the contact problem appears as a saddle point problem of the form:

$$\begin{aligned}&\sum _{{\alpha }=1}^2\left( {\delta }{\varPi }_{\mathrm {int}}^{({\alpha })}-{\delta }{\varPi }_{\mathrm {ext}}^{({\alpha })}\right) + {\delta }{\varPi }_{\mathrm {c}}= 0 \quad \forall {\delta }\mathbf {u}^{({\alpha })}\in \mathscr {V}^{({\alpha })}, \end{aligned}$$

(14)

$$\begin{aligned}&\int _{{\gamma }_{\mathrm {c}}^{(1)}}{\delta }{\lambda }_{\mathrm {n}}g_{\mathrm {n}}\,{\mathrm {d}}{\gamma }_{\mathrm {c}}^{(1)} = 0 \quad \forall {\delta }{\lambda }_{{\mathrm {n}}} \in \mathscr {M}_{\mathrm {n}}^{+}, \end{aligned}$$

(15)

$$\begin{aligned}&\int _{{\gamma }_{\mathrm {c}}^{(1)}}\mathbf {v}_{{\tau },{\mathrm {r}}{\mathrm {e}}{\mathrm {l}}}\cdot {\delta }{\varvec{\lambda }}_{\tau }\,{\mathrm {d}}{\gamma }_{\mathrm {c}}^{(1)} = 0 \quad \forall {\delta }{\varvec{\lambda }}_{{\tau }} \in \mathscr {M}_{\mathrm {n}}^{+}. \end{aligned}$$

(16)

Stating Eqs. (15) and (16) as equality conditions requires the knowledge about the current active contact area ${\gamma }_{\mathrm {c}}$, see [14, 22, 23] for appropriate active set strategies. In Eqs. (14)–(16) the solution spaces of the displacement $\mathbf {u}$ and its variation ${\delta }\mathbf {u}$ need to meet the following requirements for hyperelastic materials [17]:

$$\begin{aligned}&\mathbf {u}^{({\alpha })}\in \mathscr {U}^{({\alpha })}\nonumber \\&\mathscr {U}^{({\alpha })}= \lbrace \mathbf {u}^{({\alpha })}:{\varOmega }_0^{({\alpha })}\rightarrow \mathbb {R}^{3}\vert \mathbf {u}^{({\alpha })}\in \mathbf {W}^{1,6}({\varOmega }_0) ,\nonumber \\&\mathbf {u}^{({\alpha })}=\check{\mathbf {u}} ^{({\alpha })} \text {on} {\gamma }_{\mathrm {D}}^{({\alpha })} \rbrace , \end{aligned}$$

(17)

$$\begin{aligned}&{\delta }\mathbf {u}^{({\alpha })}\in \mathscr {V}^{({\alpha })}\nonumber \\&\mathscr {V}^{({\alpha })}= \lbrace {\delta }\mathbf {u}^{({\alpha })}:{\varOmega }_0^{({\alpha })}\rightarrow \mathbb {R}^{3}\vert {\delta }\mathbf {u}^{({\alpha })}\in \mathbf {W}^{1,6}({\varOmega }_0) ,\nonumber \\&{\delta }\mathbf {u}^{({\alpha })}={\mathbf {0}}\text { on } {\gamma }_{\mathrm {D}}^{({\alpha })} \rbrace . \end{aligned}$$

(18)

Herein, $\mathbf {W}^{1,6}$ is a Sobolev space of order (1,6). Lagrange multipliers ${\varvec{\lambda }}$ and their variations ${\delta }{\varvec{\lambda }}$ have to be part of the dual space $\mathbf {Q}^\prime$, with $\mathbf {Q}=\mathbf {W}^{1/2,6/5}({\varGamma }_{\mathrm {c}})$ being the space where the contact conditions have to be satisfied. Thus, the Lagrange multipliers ${\varvec{\lambda }}$ and their variations ${\delta }{\varvec{\lambda }}$ have to meet the following requirements [17]:

$$\begin{aligned}&{\lambda }\in \mathscr {M}^{-}\quad \mathscr {M}^{-}= \lbrace {\lambda }:{\varGamma }_{\mathrm {c}}\rightarrow \mathbb {R}^{-}\vert {\lambda }\in \mathbf {Q}^\prime ({\varGamma }_{\mathrm {c}}) ,{\lambda }\le 0 \rbrace , \end{aligned}$$

(19)

$$\begin{aligned}&{\delta }{\lambda }\in \mathscr {M}^{+}\quad \mathscr {M}^{+}=\lbrace {\delta }{\lambda }:{\varGamma }_{\mathrm {c}}\rightarrow \mathbb {R}^{+}\vert {\delta }{\lambda }\in \mathbf {Q}^\prime ({\varGamma }_{\mathrm {c}}) ,{\delta }{\lambda }\le 0 \rbrace .\nonumber \\ \end{aligned}$$

(20)

3 Finite element discretisation

In order to solve the problem described in Sect. 2 the finite element method is used. An appropriate discretisation is briefly sketched in this section, more detailed descriptions for two-dimensional and three-dimensional case are given by Cichosz and Bischoff [4] and Popp et al. [23], respectively.

Following the isoparametric concept, first-order interpolations are used for all involved quantities. The geometry of the contacting bodies is discretised with standard trilinear shape functions, thus the two-dimensional contact interface is represented by bilinear shape functions, as shown in the following.

$$\begin{aligned}&\mathbf {x}\vert _{{\varGamma }_{\mathrm {c}}^{({\alpha })}}\approx \mathbf {x}^h\vert _{{\varGamma }_{\mathrm {c}}^{({\alpha })h}}=\sum _{i=1}^{n_{({\alpha })}} N_i^{({\alpha })}\mathbf {x}_i, \end{aligned}$$

(21)

$$\begin{aligned}&\mathbf {u}\vert _{{\varGamma }_{\mathrm {c}}^{({\alpha })}}\approx \mathbf {u}^h\vert _{{\varGamma }_{\mathrm {c}}^{({\alpha })h}}=\sum _{i=1}^{n_{({\alpha })}} N_i^{({\alpha })}\mathbf {u}_i, \end{aligned}$$

(22)

$$\begin{aligned}&{\varvec{\lambda }}\approx {\varvec{\lambda }}^h=\sum _{i=1}^{n_{(1)}}{\varPhi }_i^{(1)} \mathbf {z}_i. \end{aligned}$$

(23)

Herein, quantities with the superscript $(\cdot )^{(1)}$ or $(\cdot )^{(2)}$ are located on the slave or master side, respectively. Discrete nodal coordinates, displacements and Lagrange multipliers are given by $\mathbf {x}_i$, $\mathbf {d}_i$ and $\mathbf {z}_i$, respectively. $n_{({\alpha })}$ are the number of nodes on the contact boundaries, $N_i^{({\alpha })}$ are standard shape functions and ${\varPhi }_i^{({\alpha })}$ are dual shape functions used for the Lagrange multiplier field. The use of dual shape functions for mesh tying problems using the mortar method has been introduced by Wohlmuth [31]. Note, that the use of dual shape functions is not mandatory for the proposed numerical integration procedures. Nevertheless they are applied here to take advantage of their properties. The virtual displacements and the virtual contact stress can be discretised analogous to Eqs. (22) and (23).

By insertion of Eqs. (21)–(23) into the virtual contact work (13) the mortar integrals

$$\begin{aligned} \mathbf {D}_\mathscr {S}[k,k]= & {} \int \limits _{{\gamma }_c^{(1)h}} {\varPhi }_k^{(1)} N_i^{(1)} \,{\mathrm {d}}{\gamma }_c^{(1)} \mathbf {I}_3 \nonumber \\= & {} \int \limits _{{\gamma }_c^{(1)h}} N_k^{(1)} \,{\mathrm {d}}{\gamma }_c^{(1)} \mathbf {I}_3 = {D}_{kk} \mathbf {I}_3, \nonumber \\ \mathbf {M}_\mathscr {M}[k,j]= & {} \int \limits _{{\gamma }_c^{(1)h}} {\varPhi }_k^{(1)} N_j^{(2)} \,{\mathrm {d}}{\gamma }_c^{(1)} \mathbf {I}_3 = {M}_{kj} \mathbf {I}_3, \end{aligned}$$

(24)

can be identified. In Eq. (24) the mortar integrals $\mathbf {D}_\mathscr {S}\in \mathbb {R}^{3n_{(1)}\times 3n_{(1)}}$ and $\mathbf {M}_\mathscr {M}\in \mathbb {R}^{3n_{(1)}\times 3n_{(2)}}$ are given in nodal blocks of $3\times 3$ and $\mathbf {I}_3\in \mathbb {R}^{3\times 3}$ is the identity. Sect. 4 describes in detail how the numerical integration of mortar matrices defined in Eq. (24) can be performed. Discretisation of the weak non-penetration condition in Eq. (15) and the tangential contact condition in Eq. (16) follows the ideas of Gitterle et al. [11, 12]. The interested reader is referred to this references for a detailed description of the entire discretisation as well as the solution strategy which can be used in order to solve for the unknown displacements $\mathbf {u}$ and contact stresses $\mathbf {z}$.

Fig. 1

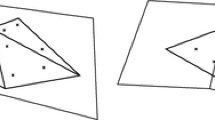
Procedure of finding integration cells (as proposed in [27]). a Initial Position of one slave and one master element, b Projection of slave and master element onto an auxiliary plane. Determine clip polygon (segment), c Division of segment into triangular integration cells and allocation of integration points within each integration cell, d Projection of integration points onto slave and master element (exemplarily shown for one integration point)

4 Evaluation of mortar integrals

In this section the numerical evaluation of the mortar integrals $\mathbf {D}_\mathscr {S}$ and $\mathbf {M}_\mathscr {M}$ given in Eq. (24) is investigated in detail. A modified method is presented in Sect. 5. Numerical integration of Eq. (24) is not straightforward. It is thus one of the main challenges when mortar formulations are used for contact problems but at the same time it features great potential for improving efficiency.

First, the integration domain has to be approximated because the discretised contacting surfaces ${\gamma }^{(1)}_{\mathrm {c}}$ and ${\gamma }^{(2)}_{\mathrm {c}}$ do not match for general cases. Second, the integrand of the mortar integral $\mathbf {M}_\mathscr {M}$ contains the product of shape functions which are defined on contact surfaces ${\gamma }^{(1)}_{\mathrm {c}}$ and ${\gamma }^{(2)}_{\mathrm {c}}$, respectively. Thus the integrand is not smooth whenever $C^0$-continuous shape functions are used on the contact interface.

Due to these reasons an exact evaluation is in general impossible in the three-dimensional case. In the literature mainly two approaches exist for a numerical approximation. Simo et al. [30] introduced an intermediate contact surface and suggested a subdivision into segments. A contact segment is defined as the overlap of one master and one slave element, projected onto the intermediate contact surface. The main characteristics of those segments is that the integrand of $\mathbf {M}_\mathscr {M}$ is smooth within each segment. Numerical integration is applied within the segments, using a small number of integration points. Puso and Laursen [26] use a similar approach for 3d-mesh tying and also apply the idea to three-dimensional contact problems [27, 28].

A second, widely used evaluation procedure is proposed by Fischer and Wriggers [8, 9]. The contact surface is defined to be identical to the slave surface and the suggested numerical integration is directly performed on the slave elements without any explicit segmentation. This approach uses high-order integration rules to reduce the errors introduced by ignoring potential discontinuities of the integrands within the individual elements.

Following the suggestion given by Farah et al. [7], the integration method originally proposed by Simo et al. [30] is denoted as segment-based and the method proposed by Fischer and Wriggers [8, 9] as element-based in this paper. The conclusion from a comparative study in [7] is that the element-based method is more efficient compared to the segment-based method but less accurate, especially for boundary problems, higher-order interpolations and frictional contact. Thus the segment-based integration may be recommendable whenever such problems are computed.

The underlying procedure is described in more detail in the remainder and afterwards alternative methods are presented. In Sect. 5 a new approach for numerical integration is described.

4.1 Segment-based approach

The main steps of the segment-based approach are illustrated in Fig. 1. In order to simplify the integration, a piecewise flat approximation of the contact region ${\gamma }_{(1)}$ is used. From the projected slave and master elements shown in Fig. 1, the overlap can be found by applying a clipping algorithm. An efficient and robust implementation is available in the Clipper Library by Angus Johnson.

The determined segment is a flat polygon with up to eight vertices. Puso and Laursen [27] suggest a subdivision of the segment into triangles in order to evaluate the mortar integrals numerically. The edges of the triangles connect the centre of gravity of the segment with its vertices. This way the number of triangles corresponds to the number of vertices of the segment. The triangles are also called integration cells and within each of them a set of integration points is allocated for numerical quadrature. In a subsequent step the integration points are projected onto the discretised slave and master surfaces. With the local coordinates of the projected integration points the mortar integrals $\mathbf {M}_\mathscr {M}$ and $\mathbf {D}_\mathscr {S}$ can be evaluated. The integrals of Eq. (24) can be expressed as the sum over all integration cells and all integration points within each of them.

$$\begin{aligned} \mathbf {D}_\mathscr {S}[k,k]= & {} \sum \limits _{i = 1}^{n_\text {intcell}} \sum \limits _{j = 1}^{n_\text {ip}} w_{j} N_k^{(1)}\left( {\varvec{\xi }}^{(1)}({\varvec{\eta }}_{j,i})\right) J_{i} \mathbf {I}_3,\nonumber \\ \mathbf {M}_\mathscr {M}[j,k]= & {} \sum \limits _{i = 1}^{n_\text {intcell}} \sum \limits _{j = 1}^{n_\text {ip}} w_{j} {\varPhi }_j^{(1)}\left( {\varvec{\xi }}^{(1)}({\varvec{\eta }}_{j,i})\right) \nonumber \\&\times \,N_k^{(2)}\left( {\varvec{\xi }}^{(2)}({\varvec{\eta }}_{j,i})\right) J_{i} \mathbf {I}_3. \end{aligned}$$

(25)

Here, $n_\text {intcell}$ is the number of integration cells, $n_\text {ip}$ is the number of integration points of integration cell i, J its Jacobian determinant and $w_j$ is the weight of integration point j. The local coordinates of integration point j within integration cell i are given by ${\varvec{\eta }}_{j,i}$. The integration point is located on the auxiliary plane. For evaluating shape functions $N_k$ and ${\varPhi }_j$ at the integration point, the local coordinates of the corresponding slave or master element have to be determined. Hence, the integration points are projected onto the contact interfaces. The local coordinates of the slave and master element are denoted as ${\varvec{\xi }}^{({\alpha })}$ in Eq. (25).

4.2 General ideas to increase efficiency

Integration points can be projected from the auxiliary plane onto slave and master elements as follows

$$\begin{aligned} \sum \limits _{k=1}^{n_{({\alpha })}^{\mathrm {e}}}\left( N_k^{({\alpha })}\left( {\varvec{\xi }}_{j}^{({\alpha })}\right) \mathbf {x}_k^{({\alpha })}\right) -\bar{{\alpha }}\mathbf {n}_0-\mathbf {x}({\varvec{\eta }}_{j})=0. \end{aligned}$$

(26)

Herein, the position vector $\mathbf {x}({\varvec{\eta }}_{j})$ contains the global coordinates of the integration point, $\bar{{\alpha }}$ is the distance between the integration point and its projection, ${\varvec{\xi }}_{j}^{({\alpha })}$ are the sought after local coordinates on the slave or master element and ${n_{({\alpha })}^{\mathrm {e}}}$ is the number of nodes of one slave or master element.

This is a computationally expensive procedure, because bilinearity of shape functions $N_k^{({\alpha })}$ makes Eq. (26) non-linear in the general case of distorted and warped surfaces, requiring an iterative solution. Hence, approaches for numerical integration, which reduce the number of integration points and consequently the number of projections needed, may significantly improve efficiency of the contact algorithm. Mainly two different approach are considered here:

• changing the shape of integration cells and

• utilizing alternative quadrature rules.

Due to the non-linearity of Eq. (26), the integrands of $\mathbf {M}_\mathscr {M}$ and $\mathbf {D}_\mathscr {S}$ can be rational polynomials. Therefore, numerical integration is not exact in general. Puso and Laursen [27], however, observed that a numerical integration, which integrates polynomials up to degree five exactly, is sufficiently accurate and robust for most problems. Following this supposition, the approaches discussed in the following are tailored to exactly integrate polynomials up to degree five.

4.3 Arbitrarily shaped integration cells

Performing numerical integration directly on segments, without subdivision into integration cells, is one possible approach. For its realisation, quadrature rules for arbitrarily shaped polygons are needed, because within a large-sliding contact problem all kinds of segments can appear. Mousavi et al. [20] and Xiao and Gimbutas [34] describe an appropriate algorithm to find feasible quadrature points for arbitrary polygons. It is briefly summarised in the following.

The algorithm starts with identifying a quadrature rule as reference which is exact up to the desired accuracy. It can be found by subdividing the domain of integration (the segment) into triangles, as described in Sect. 4.1. Integration points are allocated within the triangles such that a pre-selected set of functions $\{{\phi }_1,\ldots ,{\phi }_m\}$, e.g. Legendre polynomials up to the desired accuracy, can be integrated exactly in the domain of integration ${\varOmega }$ (i.e. a segment in our case). The solution is written to the left hand side of Eq. (27) and it remains unchanged during the algorithm.

The unknown locations $\mathbf {x}_i$ and weights ${\omega }_i$ of the quadrature rule can be computed from the condition

$$\begin{aligned} \begin{pmatrix} \displaystyle {\int }_{{\varOmega }}{\phi }_1(\mathbf {x})\,{\mathrm {d}}x\\ \displaystyle {\int }_{{\varOmega }}{\phi }_2(\mathbf {x})\,{\mathrm {d}}x\\ \cdots \\ \displaystyle {\int }_{{\varOmega }}{\phi }_m(\mathbf {x})\,{\mathrm {d}}x\\ \end{pmatrix} =\begin{pmatrix} {\phi }_1(\mathbf {x}_1) &{} \cdots &{} {\phi }_1(\mathbf {x}_n)\\ {\phi }_2(\mathbf {x}_1) &{} \cdots &{} {\phi }_2(\mathbf {x}_n)\\ \vdots &{} &{} \\ {\phi }_m(\mathbf {x}_1) &{} \cdots &{} {\phi }_m(\mathbf {x}_n) \end{pmatrix} \begin{pmatrix} {\omega }_1\\ {\omega }_2\\ \vdots \\ {\omega }_n \end{pmatrix}. \end{aligned}$$

(27)

It can be formulated as a non-linear least squares problem and it is solved iteratively using a Newton algorithm.

A main idea in the described algorithm is the successive elimination of integration points. In each step, a row of the matrix on the right hand side of (27) is eliminated, thus reducing n by 1. Afterwards, new positions and weights of integration points are calculated with a least squares Newton’s method such that the desired accuracy is retained. This can be continued as long as Newton’s method converges.

With this approach the number of integration points can be decreased tremendously. Quadrature rules for non-symmetric octagons with only seven integration points can be found [20]. Using the procedure described in Sect. 4.1 needs 56 integration points in order to be accurate up to degree five. Note, that the algorithms described in this section uses least squares Newton’s method to solve (27), therefore the gained quadratures are not exact. The error ${\varepsilon }$ can be kept small by choosing a small convergence tolerance in the Newton’s method, e.g. ${\varepsilon }< 10^{-11}$.

However, the algorithm needs to run for each segment in each iteration step. Every time a series of non-linear problems have to be solved in order to finally obtain an optimal quadrature rule and thus this method is not efficient for the problems at hand. We conclude that this approach is not a recommendable choice for numerical integration of mortar integrals.

4.4 Delaunay triangulation

In Sect. 4.1 a method is described where segments are subdivided into triangular integration cells. Within this algorithm, well-known and deformation independent quadrature rules can be applied. The method originally presented by Puso and Laursen [27] uses the centre of gravity to subdivide the segment into triangles. Popp [24] presents a subdivision using a constrained Delaunay triangulation. The constraint is that only the vertices of the segments are used for the triangulation. Due to the constraint some edges of triangulation do not satisfy the Delaunay condition. For a given number of integration points for each triangular integration cell $n_{\text {ip, intcell}}$, Delaunay triangulation decreases the number of integration points compared to the procedure presented by Puso and Laursen [27]. With v being the number of vertices of a segment, the number of integration points for a segment $n_{\text {ip, seg}}$ is

$$\begin{aligned} n_{\text {ip, seg}} = vn_{\text {ip, intcell}}, \end{aligned}$$

(28)

for the method proposed by Puso and Laursen [27] and only

$$\begin{aligned} n_{\text {ip, seg}} = (v-2)n_{\text {ip, intcell}}, \end{aligned}$$

(29)

if the approach of Popp [24] is applied. Another advantage of Delaunay based triangles is the fact that no linearisation of the expression determining the centre of gravity is needed, which saves computational time.

5 Quadrilateral integration cells

In this section, a new integration procedure is presented. The main idea is to subdivide polygonal segments into quadrilateral integration cells whenever possible. For quadrilateral integration cells well-known quadrature rules can be used which are deformation independent due to the local coordinate system applied. For segments with an odd number of vertices a combination of triangular and quadrilateral integration cells is applied.

The process of subdividing a polygon into quadrilaterals is usually called quadrangulation. It can be performed easily by directly assigning vertices of the segment by a given pattern to the quadrilaterals and triangles. The approach is straightforward and easy to implement. However, for a given geometry the outcome depends on the numbering of the vertices. As a result, integration cells with small sizes and very small angles can appear. This is demonstrated for a pentagonal segment in Fig. 2 a, b. Two possible subdivision patterns can be seen. For case a vertices 1–4 are used to build the quadrilateral whereas in case b vertices 5, 1, 2 and 3 are used. For case b the quadrangulation ends up with a triangle which has two very small angles.

Fig. 2

Quadrangulation. a using pattern, b using pattern, c with shape control

Small angles can be avoided by applying a constrained Delaunay triangulation (see Sect. 4.4 for details) to the segment before quadrilaterals are built. Subsequent to the constrained Delaunay triangulation adjacent triangles are merged to a quadrilateral integration cell. The sequence of the described shape control is illustrated in Fig. 2 c. Whether the additional effort of controlling the shape of integration cells is worthwhile is discussed in Sect. 6.

For quadrilateral integration cells the Jacobian determinant $J_i$ given in Eq. (25) is non-constant in general. The influence on the accuracy is discussed in Sect. 5.3.

5.1 Quadrature rule

As a second main approach to improve the efficiency of numerical integration, different quadrature rules are investigated. In order to retain the degree of accuracy up to five, seven integration points are needed for triangular integrations cells.

For quadrilaterals a standard Gauss-Legendre quadrature with nine integration points can be used. This already reduces the number of integration points for a segment, compared to triangulation methods, as can be seen in the next section. Note, that reduction of integration points also indirectly reduces computational effort because less projections are needed.

Further reduction can be achieved by applying a quadrature rule with less integration points which is still accurate to the degree five. Dunavant [5], for instance, presented a quadrature rule with eight integration points.

Using the procedure by Xiao and Gimbutas [34], described in Sect. 4.3, a quadrature rule with only seven integration points can be derived, which is still accurate up to order five. It is important to note that for the special case of quadrilaterals, integration points can be expressed in local coordinates, independently of the element shape. The previously mentioned drawback of repeated solving of a non-linear problem is thus obsolete in this particular situation. For a square with vertices ($-1, -1$), ($1, -1$), (1, 1) and ($-1, 1$) the coordinates of the integration points of the investigated quadrature are given in Table 1. This quadrature rule integrates polynomials of order five with an error ${\varepsilon }< 10^{-11}$.

Table 1 Quadrature of degree 5 for a unit-square, using the algorithm given in [34]

5.2 Benefits of presented approaches

In this section, the benefits of the proposed approach in terms of saving computational cost are investigated. For the time being, accuracy of the results is not considered. This is investigated later by numerical examples in Sect. 6.

Figure 3 shows the number of integration points needed depending on the number of the vertices of a segment. The different procedures are named as follows.

• Tri. triangulation as proposed by Puso and Laursen [27], 7 integration points.

• Tri. (Del.) constrained Delaunay triangulation as presented by Popp [24], 7 integration points.

• Quad. (9 IP) quadrangulation as described in Sect. 5, Gauss-Legendre integration with 9 integration points.

• Quad. (9 IP, Del.) similar to Quad. (9 IP) but with shape control, as described in Sect. 5.

• Quad. (7 IP) quadrangulation with 7 integration points according to Table 1.

Fig. 3

Number of integration points needed for one n-gon for integrating polynomials of degree 5

Figure 3 shows that, compared to standard triangulation, all alternative methods use less integration points. Tri. (Del.) always uses 14 integration points less for the same segment compared to Tri.. Applying the presented quadrangulation approaches decreases the number of necessary integration points even more. More than 50 % of the integration points can be saved using Quad. (9 IP). Depending on the number of vertices, the effort is further reduced by Quad. (7 IP). Quad. (9 IP, Del.) uses the same number of integration points as Quad. (9 IP) and is therefore not explicitly shown in the graph.

5.3 Influence of non-constant Jacobian determinants

In contrast to the case of triangular integration cells, the Jacobian determinants of quadrilateral integration cells are not constant in general. For flat, distorted quadrilateral integration cells the Jacobian determinant is bilinear in $\xi$ and ${\eta }$. Thus the degree of the integrand is increased. To investigate this potentially disadvantageous aspect, a representative setting of one pair of slave and master elements, as shown in Fig. 4, is considered. In the initial position the segment, which can be found from the overlapping of the slave and master element, is rectangular. Therefore, the Jacobian determinant is constant even if a quadrilateral cell is used. Subsequently, the setting is changed little by little in two ways (cf. case a and b in Fig. 4).

Fig. 4

Influence of Jacobian determinant of quadrilateral integration cells investigated for a distorted segments and b distorted slave elements

In order to investigate the influence of the non-constant Jacobian determinant on the accuracy of the mortar integrals the problem shown in Fig. 4 is computed with the procedures Tri., Tri. (Del.), Quad. (9 IP) and Quad. (7 IP). All mentioned procedures integrate polynomials of degree five exactly. The results are compared to an analytical reference solution. To quantify the error of the numerical integration procedures, the error in mortar integral $\mathbf {M}_\mathscr {M}$[3, 7] is investigated here exemplarily.

The first setting which is investigated is shown in Fig. 4 case a. The master element is rotated by an angle ${\beta }$ and thus the segment becomes distorted. When a quadrangulation is applied, the Jacobian determinant is not constant anymore and hence the degree of the integrand is increased. At the same time the projection given in Eq. (26) is trivial due to the rectangular shape of the master and slave element. The integrand of the mortar integrals does not contain rational polynomials.

Fig. 5

Relative error for case a of mortar integral $\mathbf {M}_\mathscr {M}$[3,7] for different subdivision schemes for segments

In Fig. 5 the relative error in the mortar integral $\mathbf {M}_\mathscr {M}$[3,7] is shown for case a for angles between 0 and 90 degrees. It can be seen that the triangulation schemes and the quadrangulation with 9 integration points integrate the mortar integral accurately, independent of the angle. Applying Quad. (7 IP) results in large errors for distorted segments and thus distorted quadrilateral integration cells. The reason for this poor results is that due to the non-constant Jacobian determinant and the projection the integrand exceeds the polynomial degree of five for the quadrilateral integration cell. With Quad. (9 IP) the integration can still be performed satisfactorily, which is not the case for Quad. (7 IP).

For setting b shown in Fig. 4 the slave element is distorted by moving one point by an amount u. Here, the segment retains its rectangular shape and therefore the Jacobian determinant remains constant even for a quadrilateral integration cell. However, numerical integration becomes more demanding because the projection of the integration points given in Eq. (26) yields rational polynomials in the integrand, independently of the shape of the integration cell.

Fig. 6

Relative error for case b of mortar integral $\mathbf {M}_\mathscr {M}$[3,7] for different subdivision schemes for segments

The relative errors in mortar integral $\mathbf {M}_\mathscr {M}$[3,7] for case b are shown in Fig. 6. Delaunay triangulation exhibits the largest error and the result differs noticeably from the result of the standard triangulation, although the integration scheme of both procedures has the same accuracy. The deviation results from the fact that the standard triangulation compared to the Delaunay triangulation yields more triangular integration cells and therefore more integration points which are necessary to integrate rational polynomials more accurate.

The errors of the procedures using quadrilateral integration points are only a little larger than for the standard triangulation. They can integrate rational polynomials almost as accurate as the standard triangulation although they use much less integration points. A significant difference can only be seen for an highly distorted slave element.

From the considered cases it can be summarised that the non-constant Jacobian determinant does not negatively affect the results of Quad. (9 IP). Only for distorted elements the errors are bigger than for Tri.. This can be avoided by using well-shaped finite elements. This is not possible to avoid distorted segments as in case a). The error of Quad. (7 IP) shown in Fig. 5 is therefore more serious.

5.4 Behavior of quadrangulation for finite deformation problems

During the incremental computation of non-linear contact problems subdivision of segments into integration cells might change considerably. As an example the setup of Fig. 4 case a can be considered. For ${\beta }= 44^\circ$ the segment is quadrilateral and thus a quadrilateral integration cell can be used. When, due to the load applied, ${\beta }= 45^\circ$ a triangular segment is found by the clipping algorithm and a triangular integration cell is used for the numerical integration. Beside this academic setting there exist a lot of cases where a small perturbation in the displacements results in a considerable change of the subdivision. This is also true if Tri. (Del.) is used. For the standard Tri., however, the change is smooth because the centre of gravity only moves a little when the topology is only changed a bit.

This aspect might negatively influence the robustness of the algorithm. So far the authors did not observe any problems with this aspect. A very challenging numerical problem where this issue comes up very often is computed and discussed in Sect. 6.2. Note, that the position of integration points themselves is not of great importance in the contact algorithm used herein. All decisions whether a point is in contact, sliding or sticking are made at slave node level as described in Gitterle et al. [11, 12] and depend on integrated quantities.

6 Examples

In this section the presented quadrature rules and integration cell subdivision procedures are tested. All examples are computed using trilinear 8-node hexahedral finite elements and are subjected to large deformations. Thus, for all examples except the patch test a variety of differently shaped segments are obtained during computation. A hyperelastic neo-Hookean material is always used. When not given explicitly, the parameters $c_{\mathrm {n}}$ and $c_{\mathrm {t}}$ used in the complementarity function (compare Eq. (7.1) in [15]) coincide with the Young’s modulus E. With the exception of the first example, friction is ignored.

For the first and second example the accuracy of the presented quadrature rules is compared to a numerical reference solution. In order to observe only the errors from the numerical integration in the contact area the reference solution is computed with the same finite element mesh. Only the contact integrals are computed more accurately by using a more accurate numerical integration for them. For the reference solution only triangular integration cells are used, each being integrated with 453 integration points [34]. This procedure exactly integrates polynomials of degree 49 and may therefore be considered as quasi “exact” integration within the numerical examples investigated herein.

6.1 Ironing problem

With this and the following example the accuracy of the numerical integration of mortar integrals $\mathbf {D}_{\mathscr {S}}$ and $\mathbf {M}_{\mathscr {M}}$ as well as the computing time are investigated. First, a frictional ironing problem which was also studied by Gitterle [12] is considered. A half-cylinder is pressed against an elastic block and then slides along the block. Problem setup, geometry and material data for the neo-Hookean material model used are given in Fig. 7. As stated in the reference, all quantities are given in a consistent unit system. The friction coefficient for Coulomb friction is taken to be $\mu = 0.2$. Areas with prescribed displacements are marked in red. The complementarity parameters $c_{\mathrm {n}}$ and $c_{\tau }$ are assumed to be 10. At first a vertical displacement in z-direction of $w=1.4$ is prescribed within 10 load steps. Then, a horizontal displacement in x-direction of $u=4.0$ is applied within 65 load steps.

Fig. 7

Ironing problem—geometry, finite element mesh, material data and final deformation

The problem is computed with the integration procedures described in Sect. 4 and 5. In order to compare the computational results obtained with the different integration procedures, the total reaction forces in global x- and z-direction of the half-cylindric die are evaluated. In Fig. 8 the results are plotted versus the load steps. There is hardly any difference visible. All curves show the typical load-displacement behaviour for frictional ironing problems: during the first ten load steps the reaction force in z-direction increases because the die indents the elastic block. As soon as the maximum vertical displacement is reached and the half-cylindric die is pushed horizontally, the reaction force remains more or less constant. The reaction force in x-direction is close to zero until the horizontal movement starts at load step ten. Afterwards the reaction force increases because some parts of the contact surface stick to each other due to friction. At load step 22 the entire contact surface slides and the horizontal reaction force remains more or less constant. At the end of the simulation the die approaches the edge of the elastic block. The resistance of the elastic block decreases and therefore the curves in Fig. 8 decrease as well.

Fig. 8

Ironing problem—reaction force of half-cylindric die in global x- and z-direction

In order to gain a more detailed insight into the differences, next the relative errors compared to the reference solution are investigated. Figure 9 exemplarily shows the relative error of the total reaction force in z-direction of the half-cylindric die. It can be seen that all procedures result in very small errors. Quad. (7 IP) shows a significantly bigger deviation from the reference solution than all other procedures. Their curves can hardly be distinguished from the x-axis. Investigation of contact stresses and other quantities provides similar results which are not shown here.

Fig. 9

Ironing problem—relative error of the reaction force

In Table 2 the number of integration point projections needed for the evaluation of the mortar integrals for each integration procedure is given relatively to the originally proposed approach by Puso and Laursen [27]. The number of integration points and therefore projections can be reduced by using the methods described in Sect. 4.4 and 5. By using quadrilateral integration cells up to 74 % of the integration points can be saved. Table 2 also shows the relative saving in computing time. It can be seen that the computing time also reduces a lot when applying the suggested quadrangulation. Of course, this speed-up depends on the implementation but due to the significant reduction of the number of integration points and, consequently, projections it can be expected that it is noticeable in any implementation.

Table 2 Ironing problem—number of integration point evaluations, i.e. projections and computing time for different integration procedures relative to Tri.

In Sect. 5.4 the potential drawback of abruptly changing integration point positions was discussed. We want to emphasize that even in this simple setup the integration point positions and quadratures change abruptly. This is mainly due to non-zero Poisson’s ratio and the resulting non-conforming distortion of the finite element meshes. Still, even for this frictional contact problem no disadvantageous behaviour can be observed when the quadrangulation is applied.

6.2 Rotating ironing problem

All segments which are generated during the calculation of the example from Sect. 6.1 are almost rectangular and flat. In order to demonstrate that the presented quadrangulation also works for a geometric variety of segments and therefore a variety of integration cells, the example from Sect. 6.1 is modified. Geometry and element data as well as the finite element mesh can be seen in Fig. 10. Friction is neglected here and the complementarity parameter is $c_\mathrm{n}$ = 100. Besides the geometry data, the most substantial difference to the example from Sect. 6.1 is the prescribed displacement. Similar to the first example within 10 load steps a vertical displacement in z-direction of $w=0.5$ is prescribed, followed by a horizontal displacement in x-direction of $u=3.0$ within 200 load steps. In addition to the horizontal displacement the die rotates about an axis which is parallel to the z-axis and passes the centre of gravity of the die. The total prescribed rotation is 180$^{\circ }.$

Fig. 10

Rotating ironing problem—geometry, finite element mesh and deformation at load step 100

Figure 11 shows the integration cells which have to be evaluated at load step 100, illustrating exemplarily that during the entire computation differently shaped integration cells show up and that the resulting quadrilaterals are not rectangular in general.

Fig. 11

Rotating ironing problem—integration cells at load step 100 for the rotating ironing problem

Fig. 12

Rotating ironing problem—Relative error of the reaction force

Next, the evolution of the die’s reaction forces is compared. Aside from Quad. (7 IP) all integration procedures are able to simulate the entire prescribed displacement. With Quad. (7 IP) the simulation fails to converge at load step 56. Before this point is reached the deviation compared to the reference solution is up to two orders of magnitude larger than for the other integration procedures. The reason for this is probably the large error of this particular quadrature rule when quadrilateral integration cells are highly distorted. This source of inaccuracy was also observed in Sect. 5.3.

In Fig. 12 the relative error of the total reaction forces in z-direction for all converging integration algorithms is illustrated. The error of the originally proposed triangulation procedure Tri. is negligible during the entire computation and is the smallest for all compared integration schemes. Although Tri. (Del.) uses exactly the same quadrature within each integration cell as Tri. the errors are larger because less integration cells and therefore less integration points are used. This deteriorates the accuracy for rational polynomials.

Using quadrilateral integration cells results in larger errors than for triangular integration cells but the relative error is still very small. Even though some of the quadrilateral integration cells occurring during the calculation are very distorted, the benefit of controlling the shape of the integration cells, as it has been proposed in Sect. 5, is not identifiable at least in this example. The additional effort therefore does not seem to be justified.

In case quadrilateral integration cells are applied, computing time is saved for this example as well. Compared to Tri. over 60 % of the integration points can be saved. As shown in Table 3 this benefit is also visible in the computing time for computing the contact stiffness. Less than 50 % is needed for Quad. (9 IP) compared to Tri.

Table 3 Rotating ironing problem—number of integration point evaluations, i.e. projections and computing time for different integration procedures relative to Tri.

Fig. 13

Patch test—finite element mesh (topview shown for upper and lower surface separately) and material data

6.3 Patch test

With the patch test depicted in Fig. 13 the behaviour of the presented integration procedures is investigated for significantly distorted elements. The geometry and finite element mesh is in the style of the patch test shown in Puso and Laursen [27]. The non-conforming mesh is shown in Fig. 13 and the coordinates for the x-y-plane are given in Table 4. Columns 1 and 2 belong to the upper block, the remaining columns are the coordinates of the lower block.

The lowermost surface is fixed against displacements in z-direction. On the topmost surface a prescribed displacement of $w=-1$ in z-direction is applied. Both blocks are retained against rigid body motions in the x-y-plane. With the given boundary conditions a uniaxial compression is simulated and thus a constant Cauchy stress ${\sigma }_{zz}$ can be expected. All presented integration procedures are able to represent the constant stress exactly (up to machine precision) when undistorted cubic elements are used. For the distorted elements used here the patch test cannot be passed exactly because the rational polynomials in the integrand of the mortar integrals cannot be integrated exactly by the numerical integration procedures used. The relative errors in ${\sigma }_{zz}$ for the integration procedures investigated are given in Table 5. The more integration points are used the better the integral of the rational polynomials can be approximated.

Table 4 Patch test—coordinates of finite element nodes

Table 5 Patch test—relative errors in Cauchy stress ${\sigma }_{zz}$

If Quad. (7 IP) is used the global Newton-Raphson was unable to converge below the given tolerance for the error in the residual forces of ${\varepsilon }_{{\mathrm {r}}{\mathrm {e}}{\mathrm {s}}} = 1 \times 10^{-6}$. The reason for this is probably the poor behaviour of this quadrature when distorted segments and integration cells are used. This property was already detected in Sect. 5.3.

For the remaining integration procedures convergence problems, meaning non-quadratic convergence, was observed as well when quadratures of degree five were used. This can be avoided by using quadratures with higher accuracy, i.e. quadratures of degree seven which use 13 integration points for triangular integration cells or 16 integration points for quadrilateral integration cells. For contact surfaces with distorted elements a large number of integration points seem to be necessary when accuracy is needed. The way the segment is subdivided into integration cells, i.e. triangulation or quadrangulation, seems to be less important.

6.4 Two cantilever beams

The third example is investigated in order to compare the different integration schemes with respect to their convergence behaviour when the finite element mesh is refined. The problem is taken from Cichosz and Bischoff [4] and its geometry, material properties, loading and support conditions are shown in Fig. 14. Being originally proposed as a 2d-problem, it is considered here as a three-dimensional one, with the width of the beam being $1\,\mathrm {mm}$.

Fig. 14

Two cantilever beams—geometry, mesh, material, loading, support conditions and deformation at load step 90

The two contacting parallel beams are computed using load control. The total load is applied in 175 increments. The relative error of the strain energy in measured after 90 load steps for different meshes. A reference solution is computed with 14,500 elements and a mesh size of $0.2\,\mathrm {mm}$. For the reference solution only triangular integration cells with seven integration points are used. In Fig. 15 the relative error of the strain energy is plotted versus the element size for a computation using triangular integration cells with seven integration points and quadrilateral integration cells with nine integration points, respectively. The error of both integration schemes is in the same magnitude and both integration procedures converge at the same rate when the mesh is refined. The convergence rate is approximately 2 and thus complies with the theoretically optimal value.

Fig. 15

Two cantilever beams—convergence of strain energy with mesh refinement, evaluated at load step 90

7 Conclusions and discussion

The necessity to solve a non-linear equation for mapping the integration point coordinates onto the slave and master surface makes the mortar contact algorithm expensive. Here, different approaches for reducing the number of integration points and at the same time retaining the degree of integration are investigated and compared. Using the polygonal segment itself without subdivision into integration cells is not worthwhile because existing quadratures are deformation dependent and finding new ones is cumbersome.

A subdivision into quadrilateral integration cells allows the application of well-established deformation independent quadrature rules. The number of integration points and thus numerical expense can be reduced considerably while the degree of integration remains of order five.

Quadrilateral integration cells have a non-constant Jacobian determinant for general geometries unlike triangular integration cells where the Jacobian determinant is constant. Numerical experiments in Sects. 5.3 and 6 show that this drawback is hardly noticeable in the overall performance when results gained by triangular integration cells are compared to results gained by quadrilateral integration cells. Only if the error is explicitly isolated, small differences become apparent. In Sect. 5.3 it is shown, that the differences in the results are mainly due to the rational polynomials emanating from the projection of the integration point coordinates and not from the non-constant Jacobian determinant.

A larger number of integration points is generally helpful to integrate rational polynomials more accurately. In Sect. 5.1 a quadrature rule with less integration points than a comparable Gauss-Legendre quadrature is applied to quadrilateral integration cells. However, the integration error in the case of distorted segments and rational polynomials is significantly larger. Moreover, application of this integration procedure caused failure of convergence in two investigated numerical examples. Thus, this approach does not seem to be recommendable in the given context. Furthermore the patch test performed in Sect. 6.3 demonstrates that distorted contact surfaces should be avoided or more accurate quadratures should be used when accuracy and robustness is an issue.

Using standard Gauss-Legendre quadratures for quadrilateral integration cells not only yields very good results but also a remarkable reduction of computational effort and thus gain in efficiency. Furthermore, with the example given in Sect. 6.4 it is shown that the rate of convergence is retained for the standard triangular integration cells.

The presented quadrangulation should also be applicable if quadratic elements are used because usually the quadratic surface elements are each subdivided into four linear elements [29]. The numerical integration is then performed as for linear elements.