A mixed element based on Lagrange multiplier method for modified couple stress theory

Abstract

A 2D mixed element is proposed for the modified couple stress theory. The $C^{1}$ continuity for the displacement field is required because of the second derivatives of displacement in the energy form of the theory. The $C^{1}$ continuity is satisfied in a weak sense with the Lagrange multiplier method. A supplementary rotation is introduced as an independent variable and the kinematic relation between the physical rotation and the supplementary rotation is constrained with Lagrange multipliers. Convergence criteria and a stability condition are derived, and the number and the positions of nodes for each independent variable are determined. Internal degrees of freedom are condensed out, so the element has only 21 degrees of freedom. The proposed element passes the $C^{0-1}$ patch test. Numerical results show that the principle of limitation is applied to the element and the element is robust to mesh distortion. Furthermore, the size effects are captured well with the element.

1 Introduction

Size effects are observed on the micro-nano scale where material properties are size dependent. Numerous experiments demonstrate these phenomena including copper wire torsion tests by Fleck et al. [12], micro-bending tests by Stolken et al. [31], and micro-indentation tests by Stelmashenko et al. [30] and Nix et al. [23]. Poole et al. [27] examined size effects in plasticity. Lam et al. [16] and McFarland et al. [19] showed the variation in the bending rigidity of a micro epoxy beam and a micro polypropylene beam, respectively. Cuenot et al. [6] and Li et al. [17] found that the Young’s modulus became larger as the size of a solid body is reduced.

Since classical continuum theory cannot capture the size effect, the higher order theories have been used to explain it. Many higher order theories have been developed since the pioneering work by Cosserat brothers [5]. Eringen et al. proposed a nonlocal elasticity theory [9] and a micromorphic theory [10]. Mindlin developed a microstructure theory [20] which has 18 material constants (two Lam’e constants and 16 additional constants) for isotropic materials, assuming that the deformation energy depends on the strain, the micro deformation gradient, and the relative deformation. The microstructure theory was then reduced to a first-strain gradient theory [21] by removing the relative deformation, resulting in only five additional material constants. Fleck et al. [11] reformulated the first-strain gradient theory, naming it the strain gradient theory, and extended it to a plastic strain gradient theory. A couple stress theory, which was developed by Mindlin et al. [22], Toupin [32] and Koiter [15], contains two additional constants by eliminating the difference between micro-rotation and macro-rotation in the Cosserat theory. Mindlin et al. [21] showed that the couple stress theory is a special case of the strain gradient theory.

Various efforts to reduce the number of additional constants have been carried out for practical applications. On the basis of the nonlocal theory, Aifantis [1] proposed a gradient elasticity theory that contains one additional constant, and Altan et al. [2] demonstrated that this theory is a special case of the strain gradient theory. Yang et al. [33] derived higher order equilibrium equations by considering the equilibrium of moments of couples, and then concluded that the components contributing to the deformation energy are only the symmetric part of the rotation gradient, while both the symmetric and antisymmetric parts contribute in the classical couple stress theory. This theory, the so called modified couple stress theory [33], has one additional constant as a result. Lam et al. [16] proposed a modified strain gradient theory by reducing the five additional constants in the strain gradient theory to three and verified the theory though micro epoxy beam experiments. The modified couple stress theory is a special case of the modified strain gradient theory. Both theories have been widely used in recent years because of their practicality and verifiability.

The finite element formulation for the higher order theories has a significant difficulty, in that the displacement field should satisfy at least the $C^{1}$ continuity because of the second derivatives of displacement in the energy forms of those theories. It is, however, complex to construct strict $C^{1}$ elements for various reasons; e.g. the nodal degrees of freedom (DOF) should include the second derivatives of displacement at least. Zervos et al. [35] and Papanicolopulos et al. [24] developed strict $C^{1}$ elements for the strain gradient theory, but too many DOF and the drawback that the elements can only be used in restricted cases make these elements almost impractical.

The mixed formulation can be an alternative that satisfies the $C^{1}$ continuity in a weak sense. For the strain gradient theory, Shu et al. [28] developed plane elements by constraining the relation between displacement and its derivatives with Lagrange multipliers and Zybell et al. [38] extended one of these elements into 3D continuum. Zervos [34] imposed the constraint between displacement and the micro deformation by considering the material parameter related to the relative deformation, which is in the microstructure theory, as a penalty parameter. Imatani et al. [14] constructed a mixed element based on the Hu-Washizu principle. In the case of the gradient elasticity theory, Amanatidou et al. [3] used a mixed form and Zhao et al. [36] combined the thin plate element with the nonconforming element.

For a couple stress theory suggested in [39], Ma et al. [18] established a plane element where weak $C^{1}$ continuity is satisfied by introducing displacement derivatives as nodal DOF. This resulted in 24 DOF for the element, which is a comparatively large number of DOF. For the modified couple stress theory, Garg et al. [13] added rotations to nodes as independent DOF and constrained the kinematic relation between the rotations and displacements using the penalty method. The proper penalty parameter for obtaining a reliable solution, however, depends on the size of the model, the number of elements, the scale of material properties, etc.

In this study, we propose a mixed element that can avoid the problems mentioned above with the Lagrange multiplier method for the modified couple stress theory. In Sect. 2 the modified couple stress theory is summarized. In Sect. 3 a total potential energy and a weak form with Lagrange multiplier for plane problems are introduced, and an element satisfying proper requirements is proposed. The element is assessed by a patch test and numerical examples with related discussions in Sect. 4 and conclusions are given in Sect. 5.

The sub(or super)-script index used in this paper follows the tensor notation.

2 Modified couple stress theory

In the classical couple stress theory [15, 22, 32], strain and rotation gradient contribute to the deformation energy with two additional constants; material length scale parameters. In the modified couple stress theory [33], the equilibrium of moments of couples is considered, and hence the couple stress tensor would be symmetric. As a result, strain and only the symmetric part of the rotation gradient tensor contribute to the energy, and then the number of material length scale parameters is reduced to one. Moreover, the modified couple stress theory was verified experimentally [16] and numerically [7], and many researchers have adopted this theory. The theory is summarized in the following for the completeness of the present paper.

The strain tensor $\varepsilon _{ij}$ and the rotation vector $\omega _k$ are related to the displacement vector $u_i$

$$\begin{aligned} \varepsilon _{ij} =\frac{1}{2}\left( {u_{i,j} +u_{j,i} } \right) \quad \hbox {and}\quad \omega _k =\frac{1}{2}e_{kij} u_{j,i} \end{aligned}$$

(1)

The symmetric curvature tensor $\chi _{ij}$ is defined using the symmetric part of rotation gradient as follows:

$$\begin{aligned} \chi _{ij} =\frac{1}{2}\left( {\omega _{i,j} +\omega _{j,i} } \right) \end{aligned}$$

(2)

And the deformation energy density w for isotropic materials is given by [33]

$$\begin{aligned} w=\frac{1}{2}\sigma _{ij} \varepsilon _{ij} +\frac{1}{2}m_{ij} \chi _{ij} \end{aligned}$$

(3)

where $\sigma _{ij}$ and $m_{ij}$ are the Cauchy stress tensor and the deviatoric part of the couple stress tensor, which are the work conjugate of $\varepsilon _{ij}$ and $\chi _{ij}$, respectively.

The constitutive equations for the theory are written as

$$\begin{aligned} \sigma _{ij} =\frac{\partial w}{\partial \varepsilon _{ij} }=D_{ijkl} \varepsilon _{kl} \quad \hbox { and} \quad m_{ij} =\frac{\partial w}{\partial \chi _{ij} }=2~\upmu l^{2}\chi _{ij} \end{aligned}$$

(4)

where $D_{ijkl}$ is the elasticity tensor, $\upmu$ is the shear modulus, and l is the material length scale parameter. The above equations yield symmetric $m_{ij}$, and the physical meaning of $m_{ij}$ is given schematically in Fig. 1.

Fig. 1

Physical meaning of couple stress tensor $m_{ij}$

The total potential energy can be expressed as

$$\begin{aligned} \Pi= & {} \int _\Omega {\frac{1}{2}\sigma _{ij} \varepsilon _{ij} d\Omega } + \int _\Omega {\frac{1}{2} m_{ij} \chi _{ij} d} \Omega \nonumber \\&- \int _\Omega {f_i u_i d} \Omega - \int _\Omega ^ {y_i \omega _i d} \Omega \nonumber \\&- \int _{\Gamma ^{t}}{t_i u_i d\Gamma } - \int _{\Gamma ^{q}}{q_i \omega _i d\Gamma } \end{aligned}$$

(5)

where $f_i$, $y_i$, $t_i$, and $q_i$ are the body force vector, the body couple vector, the traction vector, and the surface couple vector, respectively. By using the variational principle $\delta \Pi =0$, the equilibrium equation and boundary conditions are derived as follows [26]:

$$\begin{aligned}&\sigma _{ji,j} +\frac{1}{2}e_{jki} \left( {m_{lj,lk} +y_{k,j} } \right) +f_i =0 \quad \hbox {in} \quad \Omega \end{aligned}$$

(6a)

$$\begin{aligned}&n_j \sigma _{ji} +\frac{1}{2}e_{ijk} n_j \left( {m_{lk,l} -\left( {m_{pq} n_p n_q } \right) _{,k} +y_k } \right) \nonumber \\&\quad =\bar{{t}}_i -\frac{1}{2}e_{ijk} n_j \left( {\bar{{q}}_l n_l } \right) _{,k} \,or \,u_i =\bar{{u}}_i ,\quad \end{aligned}$$

(6b)

$$\begin{aligned} m_{ij} n_j -m_{pq} n_p n_q n_i =\bar{{q}}_i -\bar{{q}}_l n_l n_i \, or \, \omega _i =\bar{{\omega }}_i \quad \hbox {on }\quad \Gamma \end{aligned}$$

where $\bar{{t}}_i$, $\bar{{q}}_i$, $\bar{{u}}_i$, and $\bar{{\omega }}_i$ are prescribed boundary values.

3 A mixed finite element based on the Lagrange multiplier method

It is very difficult to satisfy the strict $C^{1}$ continuity as mentioned above, and therefore a great deal of effort has been devoted to developing weak $C^{1}$ finite elements. The mixed finite element method, where two or more independent variables are used for formulation and the relations between them are constrained with weaker conditions, has been considered a good approach to the present problem [3, 14, 28, 34, 38]. Garg et al. [13] constructed mixed finite elements by introducing a supplementary rotation vector $\phi _k$ as an independent variable and giving a kinematic constraint between the supplementary rotation vector $\phi _k$ and the physical rotation vector $\omega _k$ with the penalty method. The element, however, requires an appropriate penalty parameter, which depends on the size of the model, material parameter values, and the number of elements, so the element is not very useful. This can be overcome by introducing Lagrange multipliers.

3.1 Weak form for plane problems

The kinematic constraint between the supplementary rotation vector $\phi _k$ and the physical rotation vector $\omega _k$ is as follows:

$$\begin{aligned} \phi _i -\omega _i =0 \end{aligned}$$

(7)

The total potential energy form satisfying the kinematic constraint in a weak sense (or integral sense) with Lagrange multipliers in two dimensional problems can be derived by adding the constraint term to Eq.(5).

$$\begin{aligned} \Pi ^{L}\left( {u_i ,\phi _i ,\lambda _i } \right)= & {} \int _\Omega {\frac{1}{2}\sigma _{ij} \varepsilon _{ij} d\Omega } + \int _\Omega {\frac{1}{2} m_{ij} \chi _{ij} d} \Omega \nonumber \\&+ \int _\Omega {\lambda _i \left( {\phi _i -\omega _i } \right) } d\Omega \nonumber \\&- \int _\Omega {f_i u_i d} \Omega - \int _\Omega {y_i \phi _i d} \Omega \nonumber \\&-\int _{\Gamma ^{t}}{t_i u_i d\Gamma } - \int _{\Gamma ^{q}}{q_i \phi _i d\Gamma } \end{aligned}$$

(8)

where $\lambda _i$ is a Lagrange multiplier vector.

The constraint term on the surface, $\int _\Gamma {\lambda _i \left( {\phi _i -\omega _i } \right) } d\Gamma$, can be reduced to zero by mesh refinement, as analyzed in [13], so that the term is eliminated in the above equation.

The variational principle gives

$$\begin{aligned} \delta \Pi ^{L}= & {} \int _\Omega {\sigma _{ij} \delta \varepsilon _{ij} } d\Omega + \int _\Omega {m_{ij} \delta \chi _{ij} } d\Omega \nonumber \\&+ \int _\Omega {\left( {\phi _i -\omega _i } \right) \delta \lambda _i d\Omega } \nonumber \\&+ \int _\Omega {\lambda _i \delta \phi _i d\Omega } - \int _\Omega {\lambda _i \delta \omega _i d\Omega } \nonumber \\&- \int _\Omega {f_i \delta u_i d} \Omega - \int _\Omega {y_i \delta \phi _i d} \Omega \nonumber \\&-\int _{\Gamma ^{t}}{t_i \delta u_i d\Gamma } - \int _{\Gamma ^{q}}{{q}_i \delta \phi _i d\Gamma } \nonumber \\= & {} 0. \end{aligned}$$

(9)

The vector or matrix forms of Eqs. (1, 2, 4) can be expressed for 2D isotropic problems as

$$\begin{aligned} {{\varvec{\sigma }} }= & {} \mathbf{D}{{\varvec{\varepsilon }} } \,\hbox { or } \,\left\{ {{\begin{array}{l} {\sigma _{11} } \\ {\sigma _{22} } \\ {\tau _{12} } \\ \end{array} }} \right\} =\mathbf{D}\left\{ {{\begin{array}{l} {\varepsilon _{11} } \\ {\varepsilon _{22} } \\ {2\varepsilon _{12} } \\ \end{array} }} \right\} \end{aligned}$$

(10a)

$$\begin{aligned} \mathbf{m}= & {} \left( {2~\upmu l^{2}} \right) {{\varvec{\chi }} }\, \hbox {or} \,\left\{ {{\begin{array}{l} {m_{13} } \\ {m_{23} } \\ \end{array} }} \right\} =\left( {2~\upmu l^{2}} \right) \left\{ {{\begin{array}{l} {\chi _{13} } \\ {\chi _{23} } \\ \end{array} }} \right\} \end{aligned}$$

(10b)

$$\begin{aligned} {{\varvec{\upvarepsilon }}}= & {} \mathbf{Su}\, \hbox {or } \,\left\{ {{\begin{array}{l} {\varepsilon _{11} } \\ {\varepsilon _{22} } \\ {2\varepsilon _{12} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{ll} {\frac{\partial }{\partial x_1 }}&{} 0 \\ 0&{} {\frac{\partial }{\partial x_2 }} \\ {\frac{\partial }{\partial x_2 }}&{} {\frac{\partial }{\partial x_1 }} \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {u_1 } \\ {u_2 } \\ \end{array} }} \right\} \end{aligned}$$

(10c)

$$\begin{aligned} {{\varvec{\upchi }} }= & {} \mathbf{P}\varvec{\phi } \,\hbox {or}\, \left\{ {{\begin{array}{l} {\chi _{13} } \\ {\chi _{23} } \\ \end{array} }} \right\} =\frac{1}{2}\left[ {{\begin{array}{l} {\frac{\partial }{\partial x_1 }} \\ {\frac{\partial }{\partial x_2 }} \\ \end{array} }} \right] \phi _3 \end{aligned}$$

(10d)

$$\begin{aligned} {{\varvec{\upomega }}}= & {} \mathbf{Lu} \,\hbox {or} \,\omega _3 =\frac{1}{2}\left[ {{\begin{array}{ll} {-\frac{\partial }{\partial x_2 }}&{} {\frac{\partial }{\partial x_1 }} \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {u_1 } \\ {u_2 } \\ \end{array} }} \right\} \end{aligned}$$

(10e)

where

$$\begin{aligned} D=\left\{ \begin{array}{ll} \frac{E}{1-\nu ^{2}}\left[ \begin{array}{ccc} 1&{} \nu &{} 0 \\ \nu &{} 1&{} 0 \\ 0&{} 0&{} \left( {1-\nu } \right) /2 \\ \end{array} \right] &{}\quad { for} \,{ plane}\, { stress} \\ \frac{E}{\left( {1+\nu } \right) \left( {1-2\nu } \right) }\left[ \begin{array}{ccc} {\left( {1-\nu } \right) }&{} \nu &{} 0 \\ \nu &{} {\left( {1-\nu } \right) }&{} 0 \\ 0&{} 0&{} {\left( {1-2\nu } \right) /2} \\ \end{array} \right] &{}\quad { for}\, { plane} \,{ strain} \\ \end{array} \right. \end{aligned}$$

while E is the Young’s modulus and $\nu$ is the Poisson’s ratio.

Equation (9) then can be rewritten as

$$\begin{aligned}&\int _\Omega {\left( {\mathbf{S}\left( {\delta \mathbf{u}} \right) } \right) ^{T}{} \mathbf{D}\left( {\mathbf{Su}} \right) } d\Omega - \int _\Omega {\left( {\mathbf{L}\left( {\delta \mathbf{u}} \right) } \right) ^{T} { {\varvec{\lambda }} } d\Omega } \nonumber \\&\quad =\int _\Omega {\left( {\delta \mathbf{u}} \right) ^{T}{} \mathbf{f}\, d} \Omega +\int _{\Gamma ^{t}}{\left( {\delta \mathbf{u}} \right) ^{T}{} \mathbf{t}\, d\Gamma } , \nonumber \\&\int _\Omega {\left( {2~\upmu l^{2}} \right) \left( {\mathbf{P}\left( {\delta \varvec{\phi } } \right) } \right) ^{T}\left( {\mathbf{P}\varvec{\phi } } \right) } d\Omega + \int _\Omega {\left( {\delta \varvec{\phi } } \right) ^{T} {{\varvec{\lambda }} } d\Omega } \nonumber \\&\quad = \int _\Omega {\left( {\delta \varvec{\phi } } \right) ^{T}{} \mathbf{y}\, d} \Omega +\int _{\Gamma ^{q}} {\left( {\delta \varvec{\phi } } \right) ^{T}{} \mathbf{q}\, d\Gamma } , \nonumber \\&\int _\Omega {\left( {\delta {{\varvec{\lambda }} }} \right) ^{T}\left( {\varvec{\phi } -\mathbf{Lu}} \right) }\, d \Omega = 0. \end{aligned}$$

(11)

The Lagrange multiplier vector is another independent variable and the physical meaning of the Lagrange multiplier vector can be given as the couple moment vector from Eq. (11).

3.2 Finite element formulation

Each field of the independent variables can be discretized as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \mathbf{u}=\mathbf{N}_u {{{\varvec{\tilde{\mathrm{u}}}}}} \\ \varvec{\phi } =\mathbf{N}_{\varvec{\phi }} {\tilde{\varvec{\phi }}} \\ {{\varvec{\lambda }}}=\mathbf{N}_\lambda {{\varvec{{\tilde{\lambda }}}}} \\ \end{array}} \right. \end{aligned}$$

(12)

where $\mathbf{N}_\mathbf{u}$, $\mathbf{N}_{\varvec{\phi }}$ and $\mathbf{N}_{{\varvec{ \lambda }}}$ are shape function matrices for nodal DOF vectors ${{\varvec{ {\tilde{\mathrm{u}}}}}}$, $\varvec{\tilde{\phi }}$, and ${{\varvec{{\tilde{\lambda }}}}}$, respectively.

Equation (11) then can be written in matrix form as

$$\begin{aligned} \left[ {{\begin{array}{ccc} {\mathbf{K}_\mathbf{A} }&{} \mathbf{0}&{} {\mathbf{K}_\mathbf{B} } \\ \mathbf{0}&{} {\mathbf{K}_\mathbf{D} }&{} {\mathbf{K}_\mathbf{C} } \\ {\mathbf{K}_\mathbf{B}^\mathbf{T} }&{} {\mathbf{K}_\mathbf{C}^\mathbf{T} }&{} \mathbf{0} \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\varvec{{{{\tilde{\mathrm{u}}}}}}} \\ {{\tilde{\varvec{\phi }}}} \\ {{{\varvec{{\tilde{\lambda }}}}}} \\ \end{array} }} \right\} =\left\{ {{\begin{array}{ccc} {\mathbf{f}_\mathbf{1} } \\ {\mathbf{f}_\mathbf{2} } \\ \mathbf{0} \\ \end{array} }} \right\} \end{aligned}$$

(13)

where

$$\begin{aligned} \mathbf{K}_\mathbf{A}= & {} \int _\Omega {\left( {\mathbf{SN}_\mathbf{u} } \right) ^{T}{} \mathbf{D}\left( {\mathbf{SN}_\mathbf{u} } \right) d\Omega } , \\ \mathbf{K}_\mathbf{B}= & {} \int _\Omega {-\left( {\mathbf{LN}_\mathbf{u} } \right) ^{T}{} \mathbf{N}_{{\varvec{\lambda }} } d\Omega } , \\ \mathbf{K}_\mathbf{C}= & {} \int _\Omega {\mathbf{N}_\phi ^T \mathbf{N}_{{\varvec{\lambda }} } d\Omega } , \\ \mathbf{K}_\mathbf{D}= & {} \int _\Omega {2~\upmu l^{2}\left( {\mathbf{PN}_\phi } \right) ^{T}\left( {\mathbf{PN}_\phi } \right) d\Omega } ,\\ \mathbf{f}_\mathbf{1}= & {} \int _\Omega {\mathbf{N}_\mathbf{u}^T \mathbf{f}\, d\Omega } +\int _{\Gamma ^{t}}{\mathbf{N}_\mathbf{u}^T \mathbf{t}\, d\Gamma } , \\ \mathbf{f}_\mathbf{2}= & {} \int _\Omega {\mathbf{N}_\phi ^T \mathbf{y}\, d\Omega } +\int _{\Gamma ^{q}}{\mathbf{N}_\phi ^T \mathbf{q}\, d\Gamma } . \end{aligned}$$

3.2.1 Criteria for convergence

Both continuity and completeness conditions should be satisfied for convergence [4]. The continuity condition have been satisfied weakly with the Lagrange multipliers as mentioned above. In the classical theory, the completeness condition means that an element must represent rigid body modes and constant strain modes. In the modified couple stress theory, however, the curvature term is included in the variational form, Eq. (9), and thereby constant curvature states must also be represented in the element. Therefore, constant curvature modes should be added to the completeness condition for the modified couple stress theory. The minimum field of the supplementary rotation vector for constant curvature is linear. To represent the constant curvature exactly, the field of the supplementary rotation vector must be exactly the same as that of the physical rotation vector, which is derived from the displacement vector, and this means that the constraint Eq. (7) are satisfied not in the weak but in the strong sense (i.e., the Lagrange multiplier vector is zero). Therefore, the derivatives of displacement must be able to represent a linear field at least. The Q8 element (8 node serendipity element) and the Q9 element (9 node Lagrangian element) have a complete linear field of the derivatives of displacement in natural coordinates. However, only the Q9 element has a complete linear field of the derivatives of displacement in physical coordinates when the element shape is general [36]. Therefore, the number of displacement nodes should be 9 at least.

3.2.2 Static condensation

When the 9 nodes are chosen for the displacement field, the internal DOF can be condensed out.

Equation (13) can be partitioned as

(14)

where ${{\varvec{{\tilde{\mathrm{u}}}}}}_1$ are the displacement DOF of the nodes corresponding to the Q8 element, ${{\varvec{ {\tilde{\mathrm{u}}}}}}_2$ are those of the internal node, $\mathbf{f}_{1,1}$ is the part of $\mathbf{f}_1$ corresponding to ${{\varvec{{\tilde{\mathrm{u}}}}}}_1$, and $\mathbf{f}_{1,2}$ is that corresponding to ${{\varvec{ {\tilde{\mathrm{u}}}}}}_2$.

Equation (14) can be rewritten as

$$\begin{aligned}&\mathbf{K}_{A,11} {{\varvec{ {\tilde{\mathrm{u}}}}}}_1 +\mathbf{K}_{A,12} {{\varvec{ {\tilde{\mathrm{u}}}}}}_2 +\mathbf{K}_{B,1} {{\varvec{{\tilde{\lambda }}}}}=\mathbf{f}_{1,1}, \end{aligned}$$

(15a)

$$\begin{aligned}&{} \mathbf{K}_{A,12}^T {{\varvec{ {\tilde{\mathrm{u}}}}}}_1 +\mathbf{K}_{A,22} {{\varvec{ {\tilde{\mathrm{u}}}}}}_2 +\mathbf{K}_{B,2} {{\varvec{{\tilde{\lambda }}}}}=\mathbf{f}_{1,2}, \end{aligned}$$

(15b)

$$\begin{aligned}&{} \mathbf{K}_D {\tilde{\varvec{\phi }}}+\mathbf{K}_C {{\varvec{{\tilde{\lambda }}}}}=\mathbf{f}_2 , \end{aligned}$$

(15c)

$$\begin{aligned}&{} \mathbf{K}_{B,1}^T {{\varvec{ {\tilde{\mathrm{u}}}}}}_1 +\mathbf{K}_{B,2}^T {{\varvec{ {\tilde{\mathrm{u}}}}}}_2 +\mathbf{K}_C^T {\tilde{\varvec{\phi }}}=0. \end{aligned}$$

(15d)

After rearranging Eq. (15b) in terms of ${{\varvec{ {\tilde{\mathrm{u}}}}}}_2$ as

$$\begin{aligned} {{\varvec{ {\tilde{\mathrm{u}}}}}}_2 =-\mathbf{K}_{A,22}^{-1} \left( {\mathbf{K}_{A,12}^T {{\varvec{ {\tilde{\mathrm{u}}}}}}_1 +\mathbf{K}_{B,2} {{\varvec{{\tilde{\lambda }}}}-\mathbf{f}_{1,2}}} \right) , \end{aligned}$$

(16)

substituting Eq. (16) into Eqs. (15a, 15d) then gives

$$\begin{aligned}&\left( {\mathbf{K}_{A,11} -\mathbf{K}_{A,12} \mathbf{K}_{A,22}^{-1} \mathbf{K}_{A,12}^T } \right) {{\varvec{ {\tilde{\mathrm{u}}}}}}_1 \nonumber \\&\quad +\left( {\mathbf{K}_{B,1} -\mathbf{K}_{A,12} \mathbf{K}_{A,22}^{-1} \mathbf{K}_{B,2} } \right) {{\varvec{{\tilde{\lambda }}}}}=\mathbf{f}^{*}_1, \end{aligned}$$

(17a)

$$\begin{aligned}&{} \mathbf{K}_D {\tilde{\varvec{\phi }}}+\mathbf{K}_C {{\varvec{{\tilde{\lambda }}}}}=\mathbf{f}_2 , \end{aligned}$$

(17b)

$$\begin{aligned}&\left( {\mathbf{K}_{B,1}^T -\mathbf{K}_{B,2}^T \mathbf{K}_{A,22}^{-1} \mathbf{K}_{A,12}^T } \right) {{\varvec{ {\tilde{\mathrm{u}}}}}}_1 \nonumber \\&\quad +\mathbf{K}_C^T {\tilde{\varvec{\phi }}}-\left( {\mathbf{K}_{B,2}^T \mathbf{K}_{A,22}^{-1} \mathbf{K}_{B,2} } \right) {{\varvec{{\tilde{\lambda }}}}}=0. \end{aligned}$$

(17c)

where

$$\begin{aligned} \mathbf{f}_1^*=\mathbf{f}_{1,1} -\mathbf{K}_{A,12} \mathbf{K}_{A,22}^{-1} \mathbf{f}_{1,2} . \end{aligned}$$

Equation (17) can be expressed in matrix form as follows:

(18)

The computational advantage of the static condensation can be found in [40].

3.3 Stability condition

Solvability requirements for the element should be determined to avoid spurious zero energy modes (or locking).

In Eq. (13), adding the third row multiplied by $\gamma \mathbf{K}_B$ and $\gamma \mathbf{K}_C$, with an arbitrary constant $\gamma$, to the first row and the second row respectively leads to

$$\begin{aligned} \left[ {{\begin{array}{ccc} {\mathbf{K}_A +\gamma \mathbf{K}_B \mathbf{K}_B^T }&{} {\gamma \mathbf{K}_B \mathbf{K}_C^T }&{} {\mathbf{K}_B } \\ {\gamma \mathbf{K}_C \mathbf{K}_B^T }&{} {\mathbf{K}_D +\gamma \mathbf{K}_C \mathbf{K}_C^T }&{} {\mathbf{K}_C } \\ {\mathbf{K}_B^T }&{} {\mathbf{K}_C^T }&{} 0 \\ \end{array} }} \right] \left\{ {{\begin{array}{ccc} {{{\varvec{ {\tilde{\mathrm{u}}}}}}} \\ {{\tilde{\varvec{\phi }}}} \\ {{{\varvec{{\tilde{\lambda }}}}}} \\ \end{array} }} \right\} =\left\{ {{\begin{array}{ccc} {\mathbf{f}_1 } \\ {\mathbf{f}_2 } \\ 0 \\ \end{array} }} \right\} .\nonumber \\ \end{aligned}$$

(19)

The following condition should be satisfied to avoid singularity of the above matrix according to the explanation on pages 360–373 in [37].

$$\begin{aligned} n_u +n_\phi \ge n_\lambda \end{aligned}$$

(20)

where

$$\begin{aligned} n_u= & {} \hbox {the} \, \hbox {number} \, \hbox {of} \, \hbox {DOF} \, \hbox {of} \, {{\varvec{ {\tilde{\mathrm{u}}}}}}\\&-\,\hbox {the} \, \hbox {number} \, \hbox {of} \, \hbox {rigid} \, \hbox {body} \, \hbox {modes} \, \hbox {for }\, \hbox {displacement},\\ n_{\varvec{\phi }}= & {} \hbox {the} \, \hbox {number} \, \hbox {of} \, \hbox {DOF} \, \hbox {of}\, {\tilde{\varvec{\phi }}}\\&-\,\hbox {the} \, \hbox {number} \, \hbox {of} \, \hbox {rigid} \, \hbox {body} \, \hbox {modes} \, \hbox {for} \, \hbox {rotation},\\ n_{\lambda }= & {} \hbox { the} \, \hbox {number} \, \hbox {of} \, \hbox {DOF} \, \hbox {of} \,{{\varvec{{\tilde{\lambda }}}}}. \end{aligned}$$

3.4 Element design

The number and the positions of the nodes for each independent variable can be determined as in Fig. 2 according to the requirements described in Sects. 3.2 and 3.3.

Fig. 2

Element form

The requirements in Sect. 3.2 lead to 9 nodes approximation for displacement DOF. The supplementary rotation vector must satisfy the $C^{0}$ continuity at least because the first derivatives of the rotation vector appear in the functional$\Pi ^{L}$. Furthermore, the minimal field of the supplementary rotation vector should be linear, as described in Sect. 3.2, and a 4 nodes bilinear field is chosen for the rotational DOF. A function in the Lebesgue space $L_2 \left( \Omega \right)$ is enough for the Lagrange multiplier since no derivatives of the variable are in the functional, and a constant field is adopted at the center node of the element. This design also satisfy the stablilty condition.

Rewriting Eq. (17) for simplicity gives

$$\begin{aligned}&\mathbf{M}_A {{\varvec{ {\tilde{\mathrm{u}}}}}}_1 +\mathbf{M}_B {{\varvec{{\tilde{\lambda }}}}}=\mathbf{f}^{*}_1 \end{aligned}$$

(21a)

$$\begin{aligned}&{} \mathbf{M}_D {\tilde{\varvec{\phi }}}+\mathbf{M}_C {{\varvec{{\tilde{\lambda }}}}}=\mathbf{f}_2 \end{aligned}$$

(21b)

$$\begin{aligned}&{} \mathbf{M}_B^T {{\varvec{ {\tilde{\mathrm{u}}}}}}_1 +\mathbf{M}_C^T {\tilde{\varvec{\phi }}}+\mathbf{M}_E {{\varvec{{\tilde{\lambda }}}}}=0 \end{aligned}$$

(21c)

where

$$\begin{aligned} \mathbf{M}_A= & {} \mathbf{K}_{A,11} -\mathbf{K}_{A,12} \mathbf{K}_{A,22}^{-1} \mathbf{K}_{A,12}^T ,\\ \mathbf{M}_B= & {} \mathbf{K}_{B,1} -\mathbf{K}_{A,12} \mathbf{K}_{A,22}^{-1} \mathbf{K}_{B,2} ,\\ \mathbf{M}_C= & {} \mathbf{K}_C ,\\ \mathbf{M}_D= & {} \mathbf{K}_D ,\\ \mathbf{M}_E= & {} -\mathbf{K}_{B,2}^T \mathbf{K}_{A,22}^{-1} \mathbf{K}_{B,2} \end{aligned}$$

Note that ${{\varvec{{\tilde{\lambda }}}}}$ DOF are internal DOF but cannot be condensed out. The shape function corresponding to the internal displacement node in natural coordinates is as follows:

$$\begin{aligned} N_9 =\left( {1-\xi ^{2}} \right) \left( {1-\eta ^{2}} \right) \end{aligned}$$

(22)

The integration of the first derivatives of $N_9$ in the natural domain is always zero (i.e., $\int _{-1}^1 \int _{-1}^1 {\frac{\partial N_9 }{\partial \xi } d\xi d\eta } =\int _{-1}^1 {\int _{-1}^1 { \frac{\partial N_9 }{\partial \eta } d\xi d\eta } =0} )$. And the submatrix $K_{B,2}$ can be expressed as follows:

$$\begin{aligned} K_{B,2}= & {} \int _\Omega {-\frac{1}{2}\left[ {{\begin{array}{cc} {-\frac{\partial N_9 }{\partial x_2 }}&{} {\frac{\partial N_9 }{\partial x_1 }} \\ \end{array} }} \right] {}^{T}N_\lambda d\Omega } \nonumber \\= & {} \int _\Omega {-\frac{1}{2}\left[ {{\begin{array}{cc} {-\frac{\partial N_9 }{\partial x_2 }}&{} {\frac{\partial N_9 }{\partial x_1 }} \\ \end{array} }} \right] {} ^{T}N_\lambda J d\xi d\eta } \end{aligned}$$

(23)

where $\left\{ {{\begin{array}{l} {\frac{\partial N_9 }{\partial x_1 }} \\ {\frac{\partial N_9 }{\partial x_2 }} \\ \end{array} }} \right\} =\mathbf{J}^{-1}\left\{ {{\begin{array}{l} {\frac{\partial N_9 }{\partial \xi }} \\ {\frac{\partial N_9 }{\partial \eta }} \\ \end{array} }} \right\} , \quad \mathbf{J}^{-1}$ is the inverse Jacobian matrix and J is the Jacobian.

$N_\lambda =1$ due to the constant field approximation for the Lagrange multiplier.

When the shape of the mesh is regular, J is constant and $\mathbf{J}^{-1}$ can be expressed as $\mathbf{J}^{-1}=\left[ {{\begin{array}{ll} {c_{11} }&{} {c_{12} } \\ {c_{21} }&{} {c_{22} } \\ \end{array} }} \right]$, where $c_{11}$, $c_{12}$, $c_{21}$ and $c_{22}$ are constant, and $K_{B,2}$ is always zero, with the result being that $M_E$ is also zero. Therefore, $M_E$ is singular when the shape of the mesh is regular so that ${{\varvec{{\tilde{\lambda }}}}}$ cannot be condensed out, and the number of total DOF for the proposed element is 21.

Full integration (3$\times$3 Gauss quadrature for displacement, 2$\times$2 for rotation) is used for the calculation of each submatrix.

4 Numerical examples

4.1 $C^{0-1}$ patch test

The convergence of the proposed element can be ascertained through the $C^{0-1}$ patch test proposed by Soh et al. [29]. The test checks whether an element can reproduce not only linear strain modes but also constant curvature modes correctly.

The following quadratic polynomials satisfying the equilibrium equation in displacement form without body forces are tested, in contrast to the case of the traditional $C^{0}$ patch test.

$$\begin{aligned} u_1= & {} a_1 +a_2 x_1 +a_3 x_2 +a_4 x_1^2 \nonumber \\&-2\left[ {\left( {1-2\nu } \right) b_4 +2\left( {1-\nu } \right) b_6 } \right] x_1 x_2 +a_6 x_2^2 \nonumber \\ u_2= & {} b_1 +b_2 x_1 +b_3 x_2 +b_4 x_1^2 \nonumber \\&-2\left[ {2\left( {1-\nu } \right) a_4 +\left( {1-2\nu } \right) a_6 } \right] x_1 x_2 +b_6 x_2^2 \end{aligned}$$

(24)

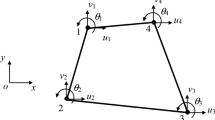
The proposed element is tested for the patch and the coefficients in [29], which are represented in Fig. 3 and Table 1.

Fig. 3

Patch test model

Table 1 The coefficient for patch test

Table 2 Results of patch test (at point(0.04,0.02))

Fig. 4

Micro epoxy cantilever beam problem

The essential boundary conditions are specified at each of the boundary nodes as the values calculated by Eq. (24).

As shown in Table 2, the element passes the test.

4.2 Cantilever beam

4.2.1 Length scale parameter

Lam et al. [16] measured the bending rigidity through the bending experiments of a micro epoxy beam and obtained the value of a bending parameter for the modified strain gradient stress theory. Based on the bending parameter value, Park et al. [25] determined the value of the length scale parameter for the modified couple stress theory as $l=17.6~\upmu \hbox {m}$. The results were verified by Dehrouyeh-Semnani et al. [8]

4.2.2 Comparison with experiments

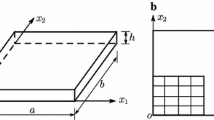
The FE model for the epoxy beam bending problem [16] is illustrated in Fig. 4.

The plane strain condition is assumed according to [16] for 160 continuum elements. An arbitrary concentrated force F is applied at point $\left( {L,0} \right)$ and the essential boundary conditions are imposed as follows:

$$\begin{aligned} \left. {u_1 } \right| _{x_1 =0} =0, \quad \left. {u_2 } \right| _{x_1 =0,x_2 =0} =0, \quad \left. {\phi _3 } \right| _{x_1 =0} =0 \end{aligned}$$

(25)

The material properties of the epoxy are as follows [25]:

$$\begin{aligned} E=1.44GPa, \quad \nu =0.38 \end{aligned}$$

The length scale parameter $l=17.6~\upmu m$ in the above section is used for the length scale parameter.

As in [16], the bending rigidity is expressed as

$$\begin{aligned} D^{{\prime }}\approx \frac{1}{3}\frac{FL^{3}}{w_0 h^{3}} \end{aligned}$$

(26)

where $w_0$ is the vertical displacement under the shear force F, while the bending rigidity in classical theory is independent of the beam thickness, as delineated in the following equation: $D_0^{\prime } =\frac{E}{12\left( {1-\nu ^{2}} \right) }$.

Different h values of 20, 38, 75 and 115 $\upmu \hbox {m}$ and $L=10h$ is considered as in the experiments. The bending rigidity of each case is obtained through FE simulations with the proposed element.

Fig. 5

Bending rigidity versus beam thickness

The results in Fig. 5 show that the bending rigidity resulted from the FE simulation with the proposed element is in good agreement with that of the experiments.

Fig. 6

FE model for testing the robustness to mesh distortion

4.2.3 Robustness to mesh distortion

The effect of mesh distortion is checked using the FE model in Fig. 6. The case of $h=20~\upmu \hbox {m}$ is chosen and the boundary conditions are the same as those in Sect. 4.2.2.

Defining a distortion ratio e as

$$\begin{aligned} e=\frac{a}{b}, \end{aligned}$$

(27)

Five different e values of 0, 0.2, 0.4, 0.6, and 0.8 are considered and the bending rigidity obtained through FE simulations are normalized by 0.3327, which is the average value of the experiments. The results of the proposed element are compared with that of the 8 nodes element, which is developed by Garg et al. [13] based on the penalty method, with a penalty parameter value of $10^{6}\upmu l^{2}$, as in [13].

The results in Fig. 7 show that the proposed element is more robust to the mesh distortion.

Fig. 7

Normalized bending rigidity versus distortion ratio

4.3 Simple shear

An analytic solution for the simple shear problem of the modified couple stress theory was derived by Park et al. [26]. In this section, the proposed element is assessed by comparing the results with the analytic solution.

The problem domain described in Fig. 8 is modeled as an infinite plate where L, w are much larger than h. The plane strain condition is assumed with $h=100~\upmu \hbox {m}$ and $L=1000~\upmu \hbox {m}$. The boundary conditions for the analytic solution are given as follows:

$$\begin{aligned}&u_1 =u_2 = \phi _3 = 0~at \quad x_2 =0 \\&u_1 =1~\upmu \hbox {m}, u_2 =\phi _3 = 0\quad \, at~x_2 =h \end{aligned}$$

The FE model and material properties are shown in Fig. 9.

Fig. 8

Simple shear problem

Fig. 9

FE model for simple shear problem

Figures 10 and  11 shows the displacement results with three different length scale parameters, 17.6, 8.8 and 1.76 $\upmu ~m$, and the error by normalizing the displacement with the analytic solution in the case of $l=17.6~\upmu ~m$, respectively, at the nodes along the center line depicted in Fig. 9.

The source of the error is as follows: the field of the rotational DOF is chosen as bilinear (see Sect. 3.4); hence, the maximum field of the curvature tensor, as expressed in Eq. (10d), is constant. The analytic solution for the curvature field is as follows:

$$\begin{aligned} \chi _{13} =0, \quad \chi _{23} =-\frac{2}{l^{2}}\left( {C_3 e^{\frac{2}{l}x_{2}}+C_4 e^{-\frac{2}{l}x_{2}}} \right) \end{aligned}$$

(28)

where $C_3$ and $C_4$ are constants (refer to [26]). The analytic field of $\chi _{23}$ in the above equation is not constant, which accounts for the error in Fig. 11. Considering this, the results follow the analytic solutions fairly well.

Fig. 10

Results of simple shear problem

4.3.1 Principle of limitation

The principle of limitation [37], which is applied to mixed elements in classical theory, explains that using higher approximation for a primary variable will not improve the performance of the elements. It is thus necessary to consider the limitation of the element that 8 nodes are approximated for $\phi _3$ as in Fig. 12. This element, which passes the $C^{0-1}$ patch test, is compared with the proposed element for the same FE model and the same material properties as in the previous example.

Fig. 11

Normalized displacement in the case of $l=17.6~\upmu ~m$

The results in Fig. 13 reveal that no improvement is observed by raising the order of the rotation field and the principle of limitation appears to be valid for the proposed element.

4.3.2 Performance variation owing to mesh distortion

A FE model with 228 elements, as in Fig. 14, is constructed with the material properties used in the previous model to take the effect of mesh distortion into consideration.

Fig. 12

Element form with 8 nodes for $\phi _3$

The performance of the proposed element is also compared with that of the penalty element used in Sect. 4.2.3.

Fig. 13

Results of the test for principle of limitation

Fig. 14

FE model for simple shear problem (distorted mesh)

The relative error norm in Table 3 is introduced to represent the error quantitatively as

$$\begin{aligned} \left\| {u_{FEM} -u_{analytic} } \right\| _2 /\left\| {u_{analytic} } \right\| _2 \end{aligned}$$

(29)

where $\left\| x \right\| _2 =\left( {\sum _i^ {\left| {x_i } \right| ^{2}} } \right) ^{1/2}$.

As shown in Fig. 15 and Table 3, the results of the proposed element follow the analytic solutions more accurately.

4.4 Plate with a hole

In this example, an infinite plate containing a circular hole under simple tension, as shown in Fig. 16, is considered to check the size effect.

A quarter FE model for the problem with the material properties is shown in Fig. 17, and symmetric boundary conditions are specified and $p=1000$ $Pa$ is imposed.

Table 3 Relative error norm for the simple shear problem (distorted mesh)

Fig. 15

Results of simple shear problem (distorted mesh)

The stress concentration factor at point$\left( {0,r} \right)$, which is constant in classical theory, is defined as

$$\begin{aligned} S.F.=\frac{\sigma _{\theta \theta } }{p}=\frac{\sigma _{11} }{p} \end{aligned}$$

(30)

FE analyses with the proposed element were conducted with 9 different ratios of length scale parameter to radius, l / r=1/100, 1/10, 1/8, 1/6, 1/4, 1/3, 1/2, 3/4, and 1.

The size effect is simulated well, as shown in Fig. 18, indicating that the stress concentration factor decreases as the length scale parameter approaches r. Furthermore, one can observe that the stress concentration factor approaches 3, which is the solution in the classical theory, with the decreasing length scale parameter.

Fig. 16

Plate with a hole problem

Fig. 17

FE model for plate with a hole problem

Fig. 18

Stress concentration factor versus l / r at point $\left( {0,r} \right)$

5 Conclusions

A 2D mixed element based on the Lagrange multiplier method for the modified couple stress theory has been proposed. Weak $C^{1}$continuity was satisfied by introducing a supplementary rotation as an independent variable and constraining the kinematic relation between the physical rotation and the supplementary rotation in a weak sense. The criteria for convergence to represent constant curvature modes and the stability condition for the element to contain no zero energy modes were derived. The number and the positions of the nodes for each independent variable were chosen according to these requirements. The internal DOF were removed by static condensation, so the element has only 21 DOF.

The proposed element passed the $C^{0-1}$ patch test. The results of micro epoxy beam bending with this element were in excellent agreement with the experiments. Through the simple shear problem, it was found that the principle of limitation is applied to the proposed element and the element is robust to mesh distortion. A plate with a hole problem showed the size effect well in that the stress concentration factor decreases as the length scale parameter increases.