Numerical integration of homogeneous functions on convex and nonconvex polygons and polyhedra

Abstract

We present a method for the numerical integration of homogeneous functions over convex and nonconvex polygons and polyhedra. On applying Stokes’s theorem and using the property of homogeneous functions, we show that it suffices to integrate these functions on the boundary facets of the polytope. For homogeneous polynomials, this approach is used to further reduce the integration to just function evaluations at the vertices of the polytope. This results in an exact cubature rule for a homogeneous polynomial f, where the integration points are only the vertices of the polytope and the function f and its partial derivatives are evaluated at these vertices. Numerical integration of homogeneous functions in polar coordinates and on curved domains are also presented. Along with an efficient algorithm for its implementation, we showcase several illustrative examples in two and three dimensions that demonstrate the accuracy of the proposed method.

1 Introduction

Integration of polynomial functions over arbitrarily-shaped polygons and polyhedra is required in computational methods such as extended finite elements [1], embedded interface methods [2–4], virtual element method [5], and weak Galerkin method [6], just to name a few. In these applications, accurate and efficient numerical integration techniques are needed.

For integrating functions over arbitrary polytopes, three general approaches have been employed: (i) tessellation of the domain into simplices; (ii) application of generalized Stokes’s theorem to reduce the volume integral to a surface integral; and (iii) use of moment fitting methods. Tessellation requires partitioning the domain into smaller subdomains (usually simplices) and then performing numerical integration over the subdomains. The generalized Stokes’s theorem (Gauss’s divergence theorem) converts integration over the domain into integration over the boundary of the domain, but often requires the integrand to be predefined or requires symbolic computations. Moment fitting methods solve a linear system of equations to build a cubature rule over the domain to integrate a given set of basis functions. For further details on these three approaches, the interested reader can refer to Sudhakar et al. [3].

Mousavi and Sukumar [7] presented a technique for integrating arbitrary polynomial functions over polygons in ${\mathbb {R}}^2$ and bounded polyhedra in ${\mathbb {R}}^3$. This method uses the properties of homogeneous functions to simplify integration over a d-dimensional polytope to integration over the $(d-1)$-dimensional faces of the polytope. In Mousavi and Sukumar [7], cubature rules for polygons and polyhedra are constructed. However, these rules were only applied to convex polytopes, a limitation that was noted in Sudhakar et al. [2]. Cubature rules that are applicable to both convex and nonconvex polytopes are desirable, and in this contribution we extend Lasserre’s approach to nonconvex polytopes.

In this paper, we demonstrate that the method developed by Lasserre [8] for integrating homogeneous polynomials is also valid for nonconvex polytopes, provided a precise definition of the polytope is given. This definition of the domain of the polytope in fact broadens the utility of the method and we provide examples that illustrate its use to integrate homogeneous functions over a range of convex and nonconvex polygons and polyhedra. Through recursive application of Lasserre’s method, we show that exact integration of homogeneous polynomials over arbitrary polytopes can be reduced to evaluation of the polynomial and its partial derivatives at the vertices of the polytope. The methods developed in this paper can be used to devise cubature rules, such as the ones constructed in Mousavi and Sukumar [7] and also elsewhere.

The remainder of this paper is organized as follows. In the following section, we establish the validity of the method described in Lasserre [8] for nonconvex polytopes. In Sect. 3, we discuss three particular extensions of this method. Specifically, in Sect. 3.1, we extend the method to reduce integration to function evaluation at vertices; in Sect. 3.2, we consider the integration of homogeneous functions over domains bounded by polar curves; and in Sect. 3.3, we treat the integration of weakly singular integrands and discontinuous integrands in polar coordinates over polygons. In Sect. 4, we provide an efficient algorithm to implement the above methods. Several numerical examples that demonstrate the accuracy and versatility of the new method are presented in Sect. 5 and we close with some final remarks in Sect. 6.

2 Integration of polynomials over arbitrary polytopes

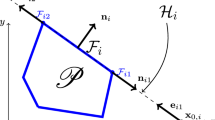
Consider a closed polytope $P \subset {\mathbb {R}}^d$ on an orientable manifold whose boundary is denoted by $\partial P$. The boundary $\partial P$ is defined by m $(d-1)$-dimensional boundary facets $F_i$, where $F_i \subset \varvec{a}_i^T \varvec{x} = b_i$ for some vectors $\varvec{a}_i$ and $\varvec{b}$. This definition is broader than the one used in Lasserre [8], since it now includes nonconvex polytopes. In comparison, a convex polytope is defined by $\varvec{A} \varvec{x} \le \varvec{b}$ for a matrix $\varvec{A}$ of dimensions $m \times d$, and a vector $\varvec{b}$ of length m. As illustrated in Fig. 1, this definition is no longer valid for nonconvex polytopes, since it will erroneously include or exclude parts of the polytope P.

Fig. 1

The cross-hatched region is defined by $\varvec{A}\varvec{x}\le \varvec{b}$, whereas the actual polygon is P—the grey, shaded area bounded by $\partial P$

We wish to integrate a polynomial function, $g(\varvec{x})$, over a polytope P, i.e.,

$$\begin{aligned} I = \int _P g(\varvec{x}) \, d \varvec{x} . \end{aligned}$$

(1)

For this purpose, we introduce the generalized Stokes’s theorem, which can be stated as (see Taylor [9]):

$$\begin{aligned}&\int _P \left( \nabla \cdot \varvec{X} \right) f( \varvec{x} ) \, d \varvec{x} + \int _P \left\langle \varvec{X}, \nabla f( \varvec{x} ) \right\rangle d \varvec{x} \nonumber \\&\quad = \int _{\partial P} \left\langle \varvec{X}, \mathbf {n} \right\rangle f( \varvec{x} ) \, d \sigma . \end{aligned}$$

(2)

In (2), $\left\langle \cdot , \cdot \right\rangle$ denotes the inner product of vectors and $d\sigma$ is the Lebesgue measure on $\partial P$. Choosing $f(\varvec{x}) := 1$ and the vector field $\varvec{X} := \varvec{x}$, one obtains

$$\begin{aligned} d \int _P d \varvec{x}= & {} \sum _{i=1}^m \int _{F_i} \left\langle \varvec{x}, \frac{\varvec{a}_i}{\Vert \varvec{a}_i\Vert } \right\rangle d \sigma \nonumber \\= & {} \sum _{i=1}^m \frac{b_i}{\Vert \varvec{a}_i\Vert } \int _{F_i} \, d\sigma , \end{aligned}$$

(3)

where $d \sigma$ is the Lebesgue measure on the $(d-1)$-dimensional affine variety¹ that contains the facet $F_{i}$. The formula (3), which first appeared in Lasserre [10], relates the volume of a polytope to the $(d-1)$-dimensional volume of its boundary, the collection of all boundary facets $F_i$, $i=1,\cdots ,m$. Geometrically, each term of the summation can be thought of as the volume of a simplex emanating from the origin to the boundary facet, $F_i$. In (3), $b_i$ and $\varvec{a}_i$ are related by $\varvec{a}_i^T\varvec{x} = b_i$, the hyperplane ${\mathcal {H}}_i$ in which $F_i$ lies. Furthermore, the normal to the hyperplane is: $\varvec{n} = \varvec{a}_i / \Vert \varvec{a}_i \Vert$. This is readily verified by normalizing the gradient of $\varvec{a}_i^T \varvec{x}$, which is in the direction that is perpendicular to the isocontours of $\varvec{a}_i^T \varvec{x}$.

Let $f(\varvec{x})$ be a positively homogeneous function of degree q that is continuously differentiable:

$$\begin{aligned} f(\lambda \varvec{x}) = \lambda ^q f(\varvec{x}) \quad (\lambda > 0), \end{aligned}$$

(4)

which satisfies Euler’s homogeneous function theorem:

$$\begin{aligned} q f(\varvec{x}) = \left\langle \nabla f(\varvec{x}), \varvec{x}\right\rangle \quad \forall \varvec{x}\in {\mathbb {R}}^d. \end{aligned}$$

(5)

Note that for functions with degree of homogeneity $q < 0$, the validity of (5) is for $\varvec{x}\in {\mathbb {R}}^d\backslash \{\varvec{0}\}$. For a homogeneous function f and $\varvec{X} := \varvec{x}$, (2) yields

$$\begin{aligned}&d \int _P f(\varvec{x}) \, d \varvec{x} + \int _P \left\langle \nabla f( \varvec{x} ), \varvec{x} \right\rangle d \varvec{x}\nonumber \\&\quad = \sum _{i=1}^m \frac{b_i}{\Vert \varvec{a}_i\Vert } \int _{F_i} f(\varvec{x}) \,d \sigma . \end{aligned}$$

(6)

On invoking Euler’s theorem given in (5), (6) simplifies to

$$\begin{aligned} \int _P f(\varvec{x}) \, d \varvec{x} = \frac{1}{d + q} \sum _{i=1}^m \frac{b_i}{\Vert \varvec{a}_i\Vert } \int _{F_i} f(\varvec{x}) \, d \sigma . \end{aligned}$$

(7)

Equation (7) relates integration of a positively homogeneous, continuously differentiable function $f(\varvec{x})$ over a polytope in ${\mathbb {R}}^d$ to integration of the same function over the polytope’s $\left( d - 1\right)$-dimensional boundary, $\partial P$. This equation appears in Lasserre [8]; however, the proof therein was only valid for convex polytopes. Here, the equation applies for both convex and nonconvex polytopes, provided P is defined by its boundary facets.

This method can be extended to arbitrary polynomial functions by decomposing such a function as a sum of homogeneous polynomials, then integrating each one. More formally, consider $g (\varvec{x})$ to be a polynomial of highest degree p, i.e., $g (\varvec{x}) := \sum _{j=0}^{p} \hat{f}_j (\varvec{x}) = \hat{f}_0 (\varvec{x}) + \cdots + \hat{f}_{p} (\varvec{x})$, where $\hat{f}_j (\varvec{x})$ is a homogeneous polynomial of degree j. If a polynomial contains no terms of degree j, we simply have $\hat{f}_j (\varvec{x}) = 0$. Now, selecting $X := \varvec{x}$ and $f( \varvec{x} ) := g( \varvec{x} )$, (2) becomes

$$\begin{aligned} \int _P g(\varvec{x}) \, d \varvec{x} = \sum _{j=0}^{p} \frac{1}{d + j} \sum _{i=1}^m \frac{b_i}{\Vert \varvec{a}_i\Vert } \int _{F_i} \hat{f}_j(\varvec{x}) \, d \sigma . \end{aligned}$$

(8)

3 Extensions of Lasserre’s method

3.1 Integration on facets of lower dimensions

We further reduce the integration of $\int _{F_i} f (\varvec{x}) \, d \sigma$ through application of Stokes’s theorem. We define $F_{ij} := F_{i} \cap F_j$ for $j \ne i$. $\mathcal {H}_{ij}$ is the $(d - 2)$-dimensional variety that is the intersection of ${\mathcal {H}}_i$ and ${\mathcal {H}}_j$, and $\varvec{n}_{ij}$ is the d-dimensional unit vector that lies in $\mathcal {H}_i$ and is normal to $F_{ij}$. Now,

$$\begin{aligned} \varvec{x}:= \varvec{x}_0 + \sum _{i=1}^{d-1} x_i^{\prime } \varvec{e}_i^{\prime } \end{aligned}$$

(9)

is a point in ${\mathbb {R}}^d$ that lies in $\mathcal {H}_i$. In (9), $\varvec{x}_0 \in {\mathcal {H}}_i$ is an arbitrary point (serves as the origin) that satisfies $\varvec{a}_i^T \varvec{x}_0 = b_i$, and $\{\varvec{e_i^\prime }\}_{i=1}^{d-1}$ form an orthonormal basis on the $(d-1)$-dimensional subspace ${\mathcal {H}}_i$. Note that the divergence of $\varvec{x}$ (restricted to ${\mathcal {H}}_i$) is $d-1$. For a homogeneous function $f(\varvec{x})$ and choosing the vector field $\varvec{X} := \varvec{x}- \varvec{x}_0 = \sum _{i=1}^{d-1} x_i^\prime \varvec{e}_i^\prime$, (2) becomes

$$\begin{aligned}&( d - 1 ) \int _{F_i} f ( \varvec{x} ) \, d \sigma + q \int _{F_i} f ( \varvec{x} ) \, d \sigma \nonumber \\&\quad = \sum _{j \ne i} \int _{F_{ij}} \left\langle \varvec{x} - \varvec{x}_0, \varvec{n}_{ij} \right\rangle f ( \varvec{x} ) \, d \nu + \int _{F_i} \left\langle \nabla f ( \varvec{x} ), \varvec{x}_0 \right\rangle d \sigma . \end{aligned}$$

Let $d_{ij} := \left\langle \varvec{x} - \varvec{x}_0 , \varvec{n}_{ij} \right\rangle$ be the algebraic distance from $\varvec{x}_0$ to ${\mathcal {H}}_{ij}$. Then, the above equation simplifies to

$$\begin{aligned} \int _{F_i} f ( \varvec{x} ) \, d \sigma =&\, \frac{1}{d + q - 1} \Biggl [ \sum _{j \ne i} \int _{F_{ij}} d_{ij} f ( \varvec{x} ) \, d \nu \nonumber \\&+ \int _{F_i} \left\langle \nabla f ( \varvec{x} ), \varvec{x}_0 \right\rangle d \sigma \Biggr ] . \end{aligned}$$

(10)

Equation (10) appears in Lasserre [8]; however, here it is shown to hold for both convex and nonconvex polytopes. When $f(\varvec{x})$ is a polynomial, (10) can be applied recursively to reduce integration over the polytope to evaluations of $f (\varvec{x})$ and its partial derivatives at the vertices. A simple example demonstrating this reduction is provided in Sect. 5.

In (10), the choice of $\varvec{x}_0 \in {\mathcal {H}}_i$ is arbitrary. However, careful selection of $\varvec{x}_0$ can reduce the number of function evaluations that are required. For example, consider the function $f ( \varvec{x} ) = x^{100} y$ defined in ${\mathbb {R}}^2$. If $F_i$ is not parallel to the y-axis, choosing $\varvec{x}_0$ such that it lies at the intersection of $\mathcal {H}_i$ and $x = 0$ greatly reduces the number of partial derivatives that need to be taken.

Combining (10) with (7), we can write down an explicit formula for the volume of a polytope in terms of the locations of its vertices. In 2D, this formula is:

$$\begin{aligned} \int _P d \varvec{x}= \frac{1}{2} \sum _{i=1}^m \frac{b_i}{\Vert \varvec{a}_i \Vert } \sum _{j \ne i} d_{ij} . \end{aligned}$$

(11)

Geometrically, $\sum _{j \ne i} d_{ij}$ is the length of the boundary edge, $F_i$, and $b_i / \Vert \varvec{a}_i \Vert$ is the algebraic distance (can be positive or negative) from the origin to $\mathcal {H}_i$. Therefore, the summation can be thought of as a set of triangles, of positive and negative areas, emanating from the origin to the boundary edges.

In 3D, the volume formula is:

$$\begin{aligned} \int _P d \varvec{x}= \frac{1}{3} \sum _{i=1}^m \frac{b_i}{\Vert \varvec{a}_i \Vert } \frac{1}{2} \sum _{j \ne i} d_{ij} \sum _{k \ne i, k \ne j} d_{ijk}, \end{aligned}$$

(12)

where

$$\begin{aligned}&\sum _{k \ne i, k \ne j} d_{ijk} = \text{ length } \text{ of } F_{ij} , \\&\frac{1}{2} \sum _{j \ne i} d_{ij} \sum _{k \ne i, k \ne j} d_{ijk} = \text{ area } \text{ of } F_i . \end{aligned}$$

Equation (12) can be viewed as the sum of volumes of tetrahedrons, of positive and negative volumes, emanating from the origin to the boundary facets.

In addition to computing the volume of polytopes, we can also use (10) with (7) to generate a closed-form expression for the integral of a homogeneous polynomial over P. Let $\alpha = (\alpha _1,\alpha _2)$ be a 2-tuple of nonnegative integers with absolute value $|\alpha | = \alpha _1 + \alpha _2$ and $\alpha ! = \alpha _1! \, \alpha _2!$. Let D be the differential operator in multi-index notation. Then, we have the following formula in 2D:

$$\begin{aligned} \int _P f ( \varvec{x}) \, d \varvec{x}&= \frac{ \sum \nolimits _{i=1}^m \dfrac{b_i}{\Vert \varvec{a}_i \Vert } \sum \nolimits _{j \ne i} d_{ij} I(\varvec{v}_{ij}) }{(q+2)(q+1)}, \end{aligned}$$

(13a)

where

$$\begin{aligned}&I(\varvec{v}_{ij}) := \sum _{k=0}^q \dfrac{ Q_k (\varvec{v}_{ij}) }{\left( {\begin{array}{c}q\\ k\end{array}}\right) }, \end{aligned}$$

(13b)

$$\begin{aligned}&Q_k (\varvec{v}_{ij}) := \sum _{|\alpha | = q-k} \dfrac{ D^{| \alpha |} f(\varvec{v}_{ij}) }{\alpha !} \prod _{\ell =1}^{2} (\varvec{x}_{0\ell })^{\alpha _\ell }. \end{aligned}$$

(13c)

In (13), $\varvec{x}_{0\ell }$ is the $\ell$-th component of $\varvec{x}_0 \in {\mathcal {H}}_i$ and $\varvec{v}_{ij}$ is the location of the vertex of the polygon that coincides with $\mathcal {H}_{ij}$. Also, when $k = q$, the final summation reduces to just the evaluation of the function $f(\varvec{x})$ at $\varvec{v}_{ij}$. Equation (13) is an exact cubature rule for a homogeneous polynomial f, where the integration points are the vertices of the polygon. Additionally, we can also use (13) as a cubature rule to integrate nonpolynomial homogeneous functions of degree q that are at least q times differentiable. Such a cubature is canonical in the sense that it only requires evaluations at vertices of the polygon, whereas cubature rules for polygons are typically specific to each particular polygon.

While the method described here provides a simple and appealing route to reduce integration to lower-dimensional facets, it is not the only way to accomplish this task. An alternative geometric method to reduce integration to point-evaluations at the vertices of the polytope is presented in the Appendix.

3.2 Integration of homogeneous functions over domains bounded by polar curves

In Lasserre [11], a formula is derived that reduces integration of a homogeneous function over a d-dimensional region to an integral over its $(d-1)$-dimensional boundary surfaces, where the surfaces are described by homogeneous functions. Here, we provide a few extensions of this approach for polar curves and for homogeneous functions in polar form.

Consider a closed region $V \subset {\mathbb {R}}^d$ bounded by m $(d-1)$-dimensional surfaces, $A_i$, which are described by the functions $h_i(\varvec{x}) = b_i$, with $h_i(\varvec{x})$ being a homogeneous function of degree $q_i$. We wish to integrate $f(\varvec{x})$, a homogeneous function of degree q, over V. Applying (2) to the integral with $\varvec{X} := \varvec{x}$, we obtain [11]

$$\begin{aligned} \int _V f(\varvec{x}) \, d \varvec{x} = \frac{1}{d + q} \sum _{i=1}^m \int _{A_i} \left\langle \frac{\nabla h_i }{\Vert \nabla h_i \Vert }, \varvec{x}\right\rangle f(\varvec{x}) \, d \sigma . \end{aligned}$$

(14)

Using the homogeneity of $h_i(\varvec{x})$, we can simplify this to

$$\begin{aligned} \int _V f(\varvec{x}) \, d \varvec{x} = \frac{1}{d + q} \sum _{i=1}^m q_i b_i \int _{A_i} \Vert \nabla h_i \Vert ^{-1} f(\varvec{x}) \, d \sigma . \end{aligned}$$

(15)

This result can be extended to a region bounded by curves, each of which can be expressed as a linear combination of homogeneous functions (for example, polynomials). First, we define $\hat{h}_i (\varvec{x}) = \sum _{j = 1}^n h^{(j)}_i (\varvec{x}) = b_i$, where $\hat{h}_i (\varvec{x})$ is a linear combination of n homogeneous polynomials, $h^{(j)}_i (\varvec{x})$. The function $h^{(j)}_i (\varvec{x})$ is homogeneous with degree $q_i^{(j)}$. Now, the result in (15) can be generalized to

$$\begin{aligned}&\int _V f(\varvec{x}) \, d \varvec{x} \nonumber \\&\quad = \frac{1}{d + q} \sum _{i=1}^m \int _{A_i} \Vert \nabla \hat{h}_i \Vert ^{-1} f(\varvec{x}) \sum _{j = 1}^n q_i^{(j)} h_i^{(j)} (\varvec{x}) \, d \sigma .\nonumber \\ \end{aligned}$$

(16)

In ${\mathbb {R}}^2$, it may be the case that $f ( \varvec{x} )$ is more conveniently represented in polar coordinates. An example in fracture mechanics is when $f(\varvec{x})$ represents elastic stresses in the vicinity of a crack-tip – stresses are proportional to $1 / \sqrt{r}$, where $r = \sqrt{x^2 + y^2}$ represents the distance from the crack-tip. Note that the function $f(\varvec{x})$ is homogeneous with degree $q = -\frac{1}{2}$. Even though the function is homogeneous, the method described in Sect. 3.1 is not exact since the partial derivatives of the function do not eventually vanish. As a result, we compute the one-dimensional line integrals in (7) using Gauss quadrature. In this section, we present a method to convert line integrals of this type to polar coordinates. After applying this transformation, the convergence rate is shown to improve for weakly singular integrands when compared to using quadrature on the Cartesian integral.

Fig. 2

The region $A := \bigl \{ r \in [0,1], \theta \in [0, \pi /2] \bigr \}$

Consider a region $A \subset {\mathbb {R}}^2$ that is enclosed by the polar curves $r = H_i (\theta )$. Each curve is represented as a linear combination of two homogeneous functions:

$$\begin{aligned} \hat{h}_i (r, \theta ) = r - H_i ( \theta ) = 0 . \end{aligned}$$

The gradient (in polar coordinates) of this function is

$$\begin{aligned} \nabla \hat{h}_i (r, \theta ) = \left\langle 1, - \frac{1}{r} \frac{ d H_i (\theta ) }{ d \theta } \right\rangle . \end{aligned}$$

On setting $h_i^{(1)} := r$ and $h_i^{(2)} := - H (\theta )$ with $q_i^{(1)} = 1$ and $q_i^{(2)} = 0$, respectively, one can use (16) to obtain

$$\begin{aligned} \int _A f(\varvec{x}) \, d \varvec{x} = \frac{1}{2+q} \sum _{i=1}^m \int _{\alpha _i}^{\beta _i} \frac{ r f\bigl (\varvec{x}(\theta )\bigr ) \left\| \bigl < r, \frac{ d H_i (\theta ) }{ d \theta } \bigr > \right\| }{ \frac{1}{r} \left\| \bigl < r, - \frac{ d H_i (\theta ) }{ d \theta } \bigr > \right\| } \, d \theta , \end{aligned}$$

where $ds := ||\left\langle r, dH_i(\theta )/d\theta \right\rangle || d \theta$ is the differential of the arc length and $\theta \in [\alpha _i, \beta _i]$ defines the limits for the polar curve. Since $r = H_i (\theta )$, the above equation simplifies to

$$\begin{aligned} \int _A f(\varvec{x}) \, d \varvec{x} = \frac{1}{2+q} \sum _{i=1}^m \int _{\alpha _i}^{\beta _i} H_i^2 ( \theta ) f \bigl ( \varvec{x} (\theta ) \bigr ) \, d \theta . \end{aligned}$$

(17)

Equation (17) allows very accurate integration over regions whose boundary curves are described by equations of the form $r = H_i (\theta )$ where $H_i (\theta )$ can be any function given in terms of $\theta$. The utility of (17) is demonstrated with the evaluation of the following integral:

$$\begin{aligned} I&:= \int _{A} f(r,\theta ) \, d\varvec{x}, \quad f(r,\theta ) = \dfrac{1}{\sqrt{r}}, \end{aligned}$$

(18a)

where the region A (see Fig. 2) is given by

$$\begin{aligned} A&:= \bigl \{ r \in [0,1], \theta \in [0, \pi /2] \bigr \}. \end{aligned}$$

(18b)

Direct integration yields the exact value: $I = \frac{\pi }{3}$. Note that the function $f (r, \theta )$ becomes singular at one of the vertices of the region A. On applying (17) to evaluate the integral in (18), we obtain:

$$\begin{aligned} I := \int _A \dfrac{d\varvec{x}}{\sqrt{r}} = \frac{2}{3} \int _{0}^{\pi / 2}\, d \theta . \end{aligned}$$

Since the integrand only contains a constant, one-point Gauss quadrature yields the exact result.

The previous example, while illustrative, yields a rather trivial result. Therefore, we will also consider an example over a more complex polar region. We integrate

$$\begin{aligned} I&:= \int _{A} f(r,\theta ) \, d\varvec{x}, \quad f(r,\theta ) = \dfrac{1}{r} \end{aligned}$$

(19a)

over the region A (see Fig. 3), which is given by

$$\begin{aligned} A&:= \{ r \in [0,1], \theta \in [\pi /4, \pi /2] : \nonumber \\&\qquad r \ge \cos \theta , r \le \sin \theta , \theta \le \pi /2 \}. \end{aligned}$$

(19b)

Direct integration yields $I = \sqrt{2} - 1$. The function 1 / r is homogeneous with degree $q = -1$. As with the previous example, a singularity is present at one of the vertices of the domain. On applying (17), the integration simplifies to

$$\begin{aligned} I := \int _A \dfrac{d\varvec{x}}{r} = \int _{\pi / 4}^{\pi / 2} (\sin \theta - \cos \theta ) \, d \theta . \end{aligned}$$

Using a six-point Gauss rule to compute the one-dimensional integral on the right-hand side results in a relative error that is close to machine precision. In Fig. 3, the plot of the relative error as a function of the number of Gauss points is shown.

Fig. 3

Numerical integration of 1 / r. a Domain of integration, which is defined in (19b); and b Relative error

3.3 Integration of homogeneous functions in polar form on polygons

In the previous section, we considered the boundary of polar regions to be defined by $r = H_i (\theta )$. At first glance, this may seem to limit the utility of (17). However, we demonstrate in this section that this representation for the boundary of a polar region can describe any polygon in ${\mathbb {R}}^2$.

The equation $\varvec{a}_i^T \varvec{x}= b_i$ gives the general equation of a line. Substituting $x = r \cos \theta$ and $y = r \sin \theta$ in the general equation of a line gives

$$\begin{aligned} r = \frac{b_i}{\left\langle \varvec{a}_i, \{\cos \theta , \sin \theta \} \right\rangle } = \frac{b_i}{\hat{H}_i ( \theta )} , \end{aligned}$$

(20)

where $\hat{H}_i ( \theta ) = \left\langle \varvec{a}_i, \{\cos \theta , \sin \theta \} \right\rangle$. This polar representation of a line is of the form introduced in Sect. 3.2, namely $r = H_i (\theta )$. Replacing (20) in (17), one obtains

$$\begin{aligned} \int _{P} f(\varvec{x}) \, d\varvec{x}= \frac{1}{2 + q} \sum _{i=1}^m b_i^2 \int _{\alpha _i}^{\beta _i} \frac{f \bigl ( \varvec{x}( \theta ) \bigr )}{\hat{H}_i^2 ( \theta )} d \theta , \end{aligned}$$

(21)

where $\beta = \tan ^{-1} \frac{y_1}{x_1}$, $\alpha = \tan ^{-1} \frac{y_2}{x_2}$, and $(x_1,y_1)$ and $(x_2,y_2)$ are the vertex coordinates of the boundary edge. Note that $f ( r ) = r^q$ becomes $\hat{f}(\theta ) = \bigl ( b_i / \hat{H}_i ( \theta ) \bigr )^q$ with $q > -2$ in ${\mathbb {R}}^2$, and then (21) simplifies to

$$\begin{aligned} \int _{P} f(\varvec{x}) \, d\varvec{x}= \frac{1}{2 + q} \sum _{i=1}^m b_i^{q+2} \int _{\alpha _i}^{\beta _i} \frac{1}{\hat{H}_i^{q+2} (\theta )} \, d \theta . \end{aligned}$$

(22)

For this technique, numerical integration is tested for three different functions. In the first two cases, the weakly singular integrands $f( r ) = r^{-1}$ and $f(r) = r^{-1/2}$ are integrated over hexagonal and square domains. In the third case, we consider the discontinuous, weakly singular function $f(r,\theta ) = \frac{1}{\sqrt{r}} \sin \frac{\theta }{2}$. For all cases, results using one-dimensional quadrature on the transformed polar integral in (22) are compared to quadrature on the untransformed Cartesian integral in (7) and to tensor-product Gauss cubature, where possible.

First, we use (22) to integrate $f ( r ) = r^{-1}$ and $f ( r ) = r^{-1/2}$ over a regular hexagon inscribed inside a unit circle centered at the origin. These functions are unbounded at the origin, but the integrals are finite and continuous, and are referred to as being weakly singular. Results are compared to those obtained using Gauss quadrature on (7). From Fig. 4, we observe that Gauss quadrature on the transformed polar integral converges faster than when it is used directly on the Cartesian integral in (7).

Next, we compute cubature on these integrals for a biunit square centered at the origin. We compare numerical integration using the techniques presented in this paper to tensor-product Gauss cubature. For both cases, Gauss quadrature on the polar integral delivers accuracy to $\mathcal{O}(10^{-14})$ with about 55 integration points, whereas quadrature on the Cartesian integral requires up to 75 integration points to realize the same accuracy. The domain is subdivided into four squares and tensor-product Gauss cubature is applied over each square: a total of $10^4$ integration points provide accuracy to only $\mathcal{O}(10^{-3})$ for $f ( r) = 1/r$. Results are presented in Fig. 5.

Finally, numerical integration of the weakly singular, discontinuous function $f(r,\theta ) = \frac{1}{\sqrt{r}} \sin \frac{\theta }{2}$ is demonstrated over the biunit square centered at (0.5, 0.5). The discontinuity in the function is treated as two additional boundary facets, and therefore, the entire domain is viewed as a nonconvex polygon with seven sides. This decomposition is demonstrated in Fig. 6a. For this case, since the tensor-product cubature points do not coincide with the location of the singularity, the domain does not require subdivision. As with the previous two cases, integration of the transformed polar version of the integral is the most accurate. A complete set of results for this example are plotted in Fig. 6b.

Fig. 4

Relative error in the numerical integration of weakly singular functions over a regular hexagon that is inscribed within the unit circle. The functions are: a $f ( r ) = r^{-1}$ and b $f ( r ) = r^{-1/2}$. The dashed line with triangular markers represents integration error with the Cartesian integral, whereas the solid line with circular markers represents integration error for the polar integral

Fig. 5

Relative error in the numerical integration of weakly singular functions over a biunit square centered at the origin. The functions are: a $f ( r ) = r^{-1}$ and b $f ( r ) = r^{-1/2}$. The polar and Cartesian integrals are displayed as in Fig. 4. Tensor-product cubature on the square is shown as a thick line

Fig. 6

Numerical integration of $f(r,\theta ) = \frac{1}{\sqrt{r}} \sin \frac{\theta }{2}$ over a biunit square centered at (0.5, 0.5). The polygon P, its edges $F_i$, and $f (r, \theta )$ (shaded in grey) are plotted in (a) and the relative error in the numerical integration from three different methods (see Fig. 5 for a description) is shown in (b). Note in (a) that $f (r, \theta )$ is discontinuous along $y = 0 \cap x < 0$ and becomes unbounded at the origin

4 Numerical implementation

In this section, we describe an algorithm to implement the methods detailed in Sects. 2 and 3.1. The assumed inputs of this algorithm are the vertices of a polytope (given in Cartesian coordinates), the connectivity of the vertices in the polytope that define the boundary facets, and the polynomial function to integrate. The output is the integral of the polynomial function over the polytope.

Algorithms 1 and 2 contain pseudocode that implements the methods and equations presented in Sects. 2 and 3.1, respectively. Lines of pseudocode without an explicit assignment operator refer to functions that carry out the calculations described. Since the implementation of most of these functions is straightforward, they are not provided in this paper.

One function whose implementation is not obvious is the function to calculate $\varvec{a}_i$ and $b_i$ from the vertices of the hyperplane. These quantities must be calculated such that the normal is oriented outward from the polytope. A simple method to do this is to order the vertices of a polygon in clockwise orientation and the vertices that belong to a face of a polyhedron in counterclockwise orientation when standing outside the polyhedron. Then, we calculate $\varvec{a}_i$ and $b_i$ using the equation

$$\begin{aligned} \det \left| \begin{array}{ccccc} x_1 &{}\quad x_2 &{}\quad \ldots &{}\quad x_d &{}\quad 1\\ x_{11} &{}\quad x_{12} &{}\quad \ldots &{}\quad x_{1 d} &{}\quad 1\\ x_{21} &{}\quad x_{22} &{}\quad \ldots &{}\quad x_{2 d} &{}\quad 1\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ x_{d 1} &{}\quad x_{d 2} &{}\quad \ldots &{}\quad x_{d d} &{}\quad 1 \end{array}\right| = 0, \end{aligned}$$

(23)

where $x_{ij}$ is the j-th coordinate of the i-th vertex of d linearly independent vertices that lie in the hyperplane of interest. The determinant gives $a_{i1} x_1 + a_{i2} x_2 \dots + a_{id} x_d - b_i = 0$ with the proper orientation. For example, given the vertices (1, 0) and (0, 1) of the i-th hyperplane in ${\mathbb {R}}^2$, (23) yields

$$\begin{aligned} \det \left| \begin{array}{ccc} x_1 &{}\quad x_2 &{}\quad 1\\ 1 &{}\quad 0 &{}\quad 1\\ 0 &{}\quad 1 &{}\quad 1 \end{array}\right| = 0, \end{aligned}$$

which simplifies to $-x_1 - x_2 = -1$, and hence we obtain $\varvec{a}_i = \{-1,-1\}$ and $b_i = -1$.

5 Results

The implementation described in Sect. 4 is applied to several test problems to demonstrate its versatility and ability to accurately and efficiently integrate polynomial functions. We present a selection of these test problems in this section. First, we demonstrate the method in Sect. 3 for a simple convex polygon. Then, we apply our algorithm to more complicated shapes in Sects. 5.3 through 5.5. Results are verified with LattE integrale 1.7.2 [12], a code capable of generating exact, fractional expressions for integrals of polynomials over convex polytopes [13, 14].

5.1 Illustrative example

First, we apply our method to the integration of a homogeneous polynomial over a two-dimensional triangle. In this simple case, direct integration is carried out and compared to the result from our approach.

Consider the evaluation of the following two-dimensional integral:

$$\begin{aligned} I&= \int _{P} xy \, dx dy \end{aligned}$$

(24a)

over the triangle described by

$$\begin{aligned} P&:= \left\{ (x,y) \in {\mathbb {R}}^2 | x+y \le 2, x \ge y, x \ge 0 \right\} . \end{aligned}$$

(24b)

Direct integration gives the exact result: $I = 1/3$.

On setting $F_1 := P \cap \left\{ x+y \le 2\right\}$, we have

$$\begin{aligned} \frac{b_1}{\Vert \varvec{a}_1 \Vert } \int _{F_1} xy \, d\mu = \sqrt{2} \int _{F_1} xy \, d\mu . \end{aligned}$$

Selecting $\varvec{x}_0 = (2,0)$ and using (10), the integration over $F_1$ reduces to

$$\begin{aligned} \sqrt{2} \int _{F_1} xy \, d\mu = \frac{\sqrt{2}}{2+2-1} \left( \sqrt{2} + 2 \int _{F_i} y \, d\mu \right) . \end{aligned}$$

On reapplying (10), we obtain

$$\begin{aligned} \sqrt{2} \int _{F_1} xy \, d\mu = \frac{\sqrt{2}}{3} \left( \sqrt{2} + \frac{2}{2+2-2} \left( \sqrt{2} \right) \right) = \frac{4}{3}. \end{aligned}$$

Now, set $F_2 := P \cap \left\{ x \ge y\right\}$ and $F_3 := P \cap \left\{ x \ge 0\right\}$. For both of these hyperplanes, $b_i / \Vert \varvec{a}_i \Vert = 0$. Therefore, on applying (7), we get

$$\begin{aligned} I = \frac{1}{2 + 2} \left( \frac{4}{3} \right) = \frac{1}{3} , \end{aligned}$$

which matches the exact value of the integral.

5.2 Application to convex polygons

We apply our algorithm to a variety of convex polygons, and compare our numerical results to exact results from LattE. Polygons with randomized vertex coordinates are constructed using a random number generator. The number of facets is first decided by generating a random integer between 3 and 10, with the random points selected in $(- 5, 5)^2 \subset {\mathbb {R}}^2$. These random points are truncated at the thousandth decimal place to allow for fractional representation in LattE. The points are verified to form a convex polygon, then Algorithms 1 and 2 are executed for the homogeneous polynomial $x^2 + x y + y^2$. We provide results for two different polygons, which are shown in Fig. 7c, d. The vertices of the polygons are listed in Table 1.

To verify the accuracy of our method, we invoke the Symbolic Math Toolbox as part of MATLAB R2014a™, which allows for exact calculation of these integrals using our algorithm. Results from integrating these polygons are listed in Table 3, along with exact results from LattE. For both test cases, our results exactly match those obtained using LattE.

5.3 Application to simple nonconvex polygons

Next, we apply our algorithm to a variety of simple (non-intersecting) nonconvex polygons, and compare our numerical results to exact results from LattE. Polygons that are random, simple, and nonconvex are generated in a similar manner to those in Sect. 5.2, and then Algorithms 1 and 2 are executed for the homogeneous polynomial $x^2 + x y + y^2$. Results are computed for two different polygons that are illustrated in Fig. 7c, d. The vertices of the polygons are listed in Table 1.

Results from integration using the MATLAB Symbolic Math Toolbox and exact integration from LattE are listed in Table 3. Since LattE is only capable of integration on convex polytopes, the nonconvex polygons that we consider are integrated in LattE by decomposing them into a collection of convex polygons, performing integration over each polygon, and then summing the results. No error is introduced by this decomposition since results from LattE are exact. For both test cases, our results exactly match those obtained using LattE.

Fig. 7

Tests on polygons and polyhedra. a, b Convex polygons; cToulouse, d Simple nonconvex polygons; e, f Non-simple nonconvex polygons; and g, h, i Polyhedra. Positive and negative areas in (e) and (f) are represented by the (+) and ($-$) symbols, respectively. h, i are nonconvex polyhedra. The homogeneous polynomial $x^2 + x y + y^2$ is integrated over the polygons (a)–(f). The homogeneous polynomial $x^2 + x y + y^2 + z^2$ is integrated over the polyhedra (g)–(i)

Table 1 Vertices of polygons used as test cases

5.4 Application to nonsimple nonconvex polygons

Our approach is also able to handle integration of nonconvex polygons where the boundary facets are intersecting, provided we define positive and negative areas of the polygon. These definitions arise naturally from the sign of the determinant used to calculate $\varvec{a}_i$ and $b_i$ for each hyperplane. The function f of interest is integrated over triangles emanating from the origin O with the sign determined by $b_i$. If the two vertices and the point O have a clockwise orientation, then the sign of the integral is positive and vice versa. How this ultimately affects the calculated result over the polygon in Fig. 7f is depicted in Fig. 8. Triangles that are associated with positive area contribute to the integral of f over the triangle, whereas those with negative area give the negative of the integral of f over the triangle. Regions that are covered by triangles with both positive and negative areas cancel out and the integral over these regions is zero.

Fig. 8

Decomposition of positive and negative areas to calculate the integral over the nonsimple nonconvex polygon in Fig. 7f. The origin is indicated by O

The polygons in Fig. 7e, f are used to verify the ability of our method to calculate integrals over nonsimple nonconvex polygons. In Fig. 7e, f, portions of the polygon with positive area are denoted with a $(+)$ and portions with a negative area are denoted with a $(-)$. The vertices of these polygons are listed in Table 1. The exact results using LattE are computed by decomposing the nonsimple polygon into convex polygons as described in the previous section. As was the case with the convex polygons and the simple nonconvex polygons, our results (listed in Table 3) exactly match those obtained using LattE.

5.5 Application to nonconvex polyhedra

Finally, our algorithm was applied to a range of different convex and nonconvex polyhedra. The test cases presented here include a cube, a nonconvex polyhedron consisting of a cube with a notch removed from it, and a tetrahedron with a tetrahedron carved from a face to make the polyhedron nonconvex. Rather than selecting random vertices and boundary facets as was done in Sects. 5.3 and 5.4, we choose to manually select the vertices of this polyhedron. The vertices of these polyhedra are listed in Table 2 and illustrations are provided in Fig. 7g–i. The homogeneous polynomial $x^2 + x y + y^2 + z^2$ is integrated over the polyhedra. As demonstrated in Table 3, our results exactly match those produced using LattE.

Table 2 Vertices of polyhedra used as test cases

Table 3 Results of integrating a homogeneous polynomial over the polytopes shown in Figure 7 using LattE [12] and the present method

5.6 Integration of arbitrary polynomials

While the methods introduced in the previous sections are of great utility when the integrand is known explicitly, often times the integrand is not known, and can only be evaluated at points within the domain. To handle this situation, Mousavi and Sukumar [7] developed a method to integrate arbitrary, unknown polynomials up to degree p by taking advantage of the properties of homogeneous functions and solving a small system of linear equations. We demonstrate that the method is equally valid for both convex and nonconvex polytopes.

Integrating a polynomial using (8) requires the polynomial to be known a priori. However, simple manipulation of (8) leads to

$$\begin{aligned}&\sum _{j=0}^{p} (d + j) \int _P \hat{f}_j (\varvec{x}) \, d \varvec{x}\nonumber \\&\quad = \sum _{i=1}^m \frac{b_i}{\Vert \varvec{a}_i\Vert } \int _{F_i} \sum _{j=0}^{p} \hat{f}_j (\varvec{x} ) \, d \sigma . \end{aligned}$$

(25)

Note that

$$\begin{aligned} \int _P g (\varvec{x}) \, d \varvec{x} = \sum _{j=0}^{p} \int _P \hat{f}_j (\varvec{x}) \, d \varvec{x} \end{aligned}$$

(26)

gives the quantity of interest. The integral $\int _{F_i} \sum _{j=0}^{p} \hat{f}_j (\varvec{x}) \, d \sigma$ can be computed without explicitly knowing the integrand if a quadrature (or cubature) rule is available to integrate a polynomial on $F_i$. Noting that homogeneous functions of degree q have the property $f ( \lambda \varvec{x} ) = \lambda ^ q f ( \varvec{x} )$, we can manipulate (25) to obtain

$$\begin{aligned} \sum _{j=0}^{p} \lambda ^j (d + j) I_j&= Q(\lambda ), \end{aligned}$$

(27a)

where

$$\begin{aligned}&I_j := \int _P \hat{f}_j (\varvec{x}) \, d \varvec{x}, \end{aligned}$$

(27b)

$$\begin{aligned}&Q(\lambda ) := \sum _{i=1}^m \frac{b_i}{\Vert \varvec{a}_i\Vert } \int _{F_i} \sum _{j=0}^{p} \hat{f}_j (\lambda \varvec{x}) \, d \sigma . \end{aligned}$$

(27c)

This provides an arbitrary number of equations that are formed by varying the value of $\lambda$. Note that the right-hand side of the equation can be evaluated by sampling points within ${\mathcal {H}}_i$. Choosing $p + 1$ values of $\lambda$ results in a $(p + 1) \times (p + 1)$ system of equations that can be used to solve each term of (26), without explicitly knowing each homogeneous polynomial, $\hat{f}_j ( x )$. On choosing $p + 1$ distinct values for $\lambda$, we can write (27) as

$$\begin{aligned} \sum _{j=0}^{p} \lambda _k^j (d + j) I_j = Q (\lambda _k) \end{aligned}$$

(28)

for $k = 1, \cdots , p+1$.

This approach is used to integrate the bivariate polynomial $f(x) = x^3 + xy^2 + y^2 + x$ over the polygons shown in Figure 7a, c. The polynomial f(x) contains monomials up to degree three. Therefore, the integral of each monomial can be determined through the solution of a $4 \times 4$ linear system, which is defined by (28). We choose $\lambda = (0.25, 0.5, 0.75, 1)$ to compute the $4 \times 4$ system matrix and to determine the location of the quadrature points within the domain of the boundary facets.

With this choice of $\lambda$ for the polygon shown in Figure 7a, (28) becomes

$$\begin{aligned} \left[ \begin{array}{cccc} 2 &{}\quad \frac{3}{4} &{}\quad \frac{1}{4} &{}\quad \frac{5}{64} \\ 2 &{}\quad \frac{3}{2} &{}\quad 1 &{}\quad \frac{5}{8} \\ 2 &{}\quad \frac{9}{4} &{}\quad \frac{9}{4} &{}\quad \frac{135}{64} \\ 2 &{}\quad 3 &{}\quad 4 &{}\quad 5 \end{array} \right] \quad \left[ \begin{array}{c} I_1 \\ I_2 \\ I_3 \\ I_4 \end{array} \right] =\left[ \begin{array}{l} -\frac{11550135635909446173}{256000000000000000} \\ -\frac{9080398944401774173}{32000000000000000} \\ -\frac{251474206771886854671}{256000000000000000} \\ -\frac{9628722192185938173}{4000000000000000} \end{array} \right] . \end{aligned}$$

Solving for $I_1, \cdots , I_4$, we obtain

$$\begin{aligned} \left[ \begin{array}{c} I_1 \\ I_2 \\ I_3 \\ I_4 \end{array} \right] =\left[ \begin{array}{l} 0 \\ -\frac{99066199641}{2000000000} \\ \frac{582878710330541}{4000000000000} \\ -\frac{11365839835662102173}{20000000000000000}\end{array} \right] . \end{aligned}$$

Using (26), we calculate $\int _P g(\varvec{x}) \, d \varvec{x} \approx -472.105$. This result exactly matches integration of the monomials using (8).

For the polygon in Figure 7c, the linear system that is obtained from (28) is:

$$\begin{aligned} \left[ \begin{array}{cccc} 2 &{}\quad \frac{3}{4} &{}\quad \frac{1}{4} &{}\quad \frac{5}{64} \\ 2 &{}\quad \frac{3}{2} &{}\quad 1 &{}\quad \frac{5}{8} \\ 2 &{}\quad \frac{9}{4} &{} \frac{9}{4} &{}\quad \frac{135}{64} \\ 2 &{}\quad 3 &{}\quad 4 &{}\quad 5 \end{array} \right] \quad \left[ \begin{array}{c} I_1 \\ I_2 \\ I_3 \\ I_4 \end{array} \right] =\left[ \begin{array}{l} -\frac{1005647136056845793}{256000000000000000} \\ -\frac{659018727981237793}{32000000000000000} \\ -\frac{16790442429180948411}{256000000000000000} \\ -\frac{617991551841433793}{4000000000000000} \end{array} \right] . \end{aligned}$$

Again, solving for $I_1, \cdots , I_4$ gives

$$\begin{aligned} \left[ \begin{array}{c} I_1 \\ I_2 \\ I_3 \\ I_4 \end{array} \right] =\left[ \begin{array}{l} 0\\ -\frac{22047837983}{6000000000}\\ \frac{22814962939549}{4000000000000} \\ -\frac{665155727633629793}{20000000000000000}\end{array} \right] . \end{aligned}$$

Summing each $I_k$, we obtain $\int _P g(\varvec{x}) \, d \varvec{x} \approx -31.229$. As was the case for the convex polygon, this result exactly matches integration of the monomials using (8).

6 Concluding remarks

In this paper, we applied Euler’s homogeneous function theorem and Stokes’s theorem to devise a method for reducing integration of homogeneous polynomials over arbitrary convex and nonconvex polytopes to integration over the boundary facets of the polytope. Additionally, we also demonstrated that the same tools could be used to further reduce the integration if partial derivatives of the homogeneous function exist. For homogeneous polynomials, integration can ultimately be reduced to function evaluation at the vertices of the polytope.

We implemented our method and presented several numerical examples that showcased its capabilities. In addition to integrating homogeneous polynomials over convex and nonconvex polygons and polyhedra, we also demonstrated how the method could be applied to nonsimple polygons. Furthermore, we also successfully tested the approach for the integration of weakly singular functions in two dimensions over polygons with straight and curved facets. For all cases involving homogeneous polynomials that we tested, our results exactly matched the results obtained using the code LattE [12]. As part of future work, we plan to assess the proposed integration scheme in applications of the extended and embedded finite element methods, as well as Galerkin methods on polygons and polyhedra.

Appendix

In this appendix, we describe an alternative method for reducing integration of homogeneous polynomials over polygons and polyhedra to lower-dimensional facets. Rather than using partial derivatives, as was done in Sect. 3, this method uses rotations to simplify integration over lower-dimensional facets. As with the method in Sect. 3, this method can be used to reduce integration to function evaluations at the vertices of the polytope.

To integrate the expression $f(\varvec{x})$ in (7) $\bigl ($or $\hat{f}_j(\varvec{x}$ in (8)$\bigr )$ over the boundary facets, $F_i$, the integral over ${\mathbb {R}}^d$ must first be transformed to an integral over $\mathcal {H}_i$, the hyperplane in which $F_i$ lies. This can be accomplished by applying an affine transformation of the boundary facet such that it lies normal to one of the orthonormal coordinate axes in ${\mathbb {R}}^d$. In ${\mathbb {R}}^2$ and ${\mathbb {R}}^3$, this transformation is completed with a simple rotation matrix applied to both the vertices of the boundary facet and to the variables in the expression $f(\varvec{x})$. Calculation of this rotation matrix in ${\mathbb {R}}^3$ is expedited by using Rodrigues’s finite rotation formula [15]:

$$\begin{aligned} \varvec{R} = \varvec{I} + \hat{\varvec{\omega }} \sin \theta + \hat{\varvec{\omega }}^2 ( 1 - \cos \theta ), \end{aligned}$$

(29)

where $\theta$ is the desired angle of rotation, $\varvec{I}$ is the $3 \times 3$ identity matrix, and $\hat{\varvec{\omega }}$ is a skew-symmetric matrix whose components are:

$$\begin{aligned} \hat{\varvec{\omega }} = \left( \begin{array}{ccc} 0 &{}\quad -\omega _z &{}\quad \omega _y \\ \omega _z &{}\quad 0 &{}\quad -\omega _x \\ -\omega _y &{}\quad \omega _x &{}\quad 0 \end{array} \right) , \end{aligned}$$

(30)

where $\varvec{\omega } \equiv (\omega _x,\omega _y,\omega _z)$ is the unit vector about which the rotation occurs. This vector can be constructed for each $F_i$ by the vector cross product

$$\begin{aligned} \varvec{\omega } = \varvec{a}_i / \Vert \varvec{a}_i \Vert \times \varvec{e}_z , \end{aligned}$$

(31)

where $\varvec{e}_z$ is a unit vector in the z-direction. When the transformation is applied to $f(\varvec{x})$, it is likely that the resulting equation will no longer be a homogeneous function. Instead, it will become a polynomial that can be integrated using (8). Applying this procedure d times to a d-dimensional polytope reduces integration to simple evaluation at the vertices of the polytope. Algorithm 3 describes an implementation of this method. The examples in Sect. 5 were calculated using this method, and were found to exactly match results using the method of Sect. 3. An example that illustrates this method follows.

1.1 Numerical example

We demonstrate the geometric method of degree-reduction using the example considered in Sect. 5.1: we evaluate the two-dimensional integral $I = \int _{P} x y \, dxdy$, where P is the triangle defined in (24b). Direct integration gives $I = 1/3$.

On setting $F_1 := P \cap \left\{ x+y \le 2\right\}$, we have

$$\begin{aligned} \frac{b_1}{\Vert \varvec{a}_1 \Vert } \int _{F_1} x y \, d\mu = \sqrt{2} \int _{F_1} x y \, d\mu . \end{aligned}$$

Next, we apply the rotation matrix

$$\begin{aligned} \varvec{R} = \frac{1}{\sqrt{2}} \left[ \begin{array}{cc} 1 &{}\quad -1 \\ 1 &{}\quad 1 \end{array} \right] , \end{aligned}$$

which aligns the hyperplane parallel to the x-axis (see Algorithm 3). The resulting transformed integral is:

$$\begin{aligned} \sqrt{2} \int _{F_1} x y \, d\mu = \sqrt{2} \int _{0}^{\sqrt{2}} \left( 1 - \frac{(x')^2}{2} \right) dx' . \end{aligned}$$

Applying (8) yields

$$\begin{aligned} \sqrt{2} \int _{0}^{\sqrt{2}} \left( 1 - \frac{(x')^2}{2} \right) dx' = \sqrt{2} \left[ \sqrt{2} - \frac{\sqrt{2}}{3} \right] = \frac{4}{3}. \end{aligned}$$

Now, set $F_2 := P \cap \left\{ x \ge y\right\}$ and $F_3 := P \cap \left\{ x \ge 0\right\}$. For both these hyperplanes, $b_i / \Vert \varvec{a}_i \Vert = 0$. Therefore, on applying (7), we get

$$\begin{aligned} I = \frac{1}{2 + 2} \left( \frac{4}{3} \right) = \frac{1}{3}, \end{aligned}$$

which exactly matches the result from direct integration.