1 Introduction

The aim of this work is to propose a formulation to solve contact problems in the context of large and small deformations using the finite element method. We consider both standard finite elements and the so called immersed boundary elements in which an underlying Cartesian grid made of regular hexahedral elements is cut by the real geometry and integration is performed only in the internal part of the elements. In recent years segment-to-segment formulations like the mortar method [8] have been successfully applied to solving a wide variety of contact problems in 2D [27, 35, 55] and 3D [38, 39], with linear and quadratic elements [28, 53], in large and small deformations including Coulomb friction [17, 18, 20, 40–42, 50] and dynamic problems [24]. The theoretical basis of the mortar method is well known [15, 28, 30–32]. The compatibility of the displacement field and the contact stresses allows the Brezzi–Babuska-InfSup condition to be fulfilled, so the optimal convergence rate of the finite element solution can be achieved. The above references are only a part of the bibliography on the mortar method applied to contact problems.

In the case of immersed boundaries it is more difficult to find finite element spaces that fulfill the InfSup condition. To our knowledge only the Vital Vertex method, first proposed by Bechet et al. [7], can satisfy the compatibility between displacements and multipliers. This method has been used for imposing Dirichlet boundary conditions in 2D and 3D [2] immersed boundaries. However, its applicability to deal with large deformation contact problems is more involved, although there are some works in 2D [37]. For this reason, other techniques based on stabilized formulations have recently been proposed to solve contact problems. In these techniques the finite element spaces can be freely chosen at the price of adding new stabilizing terms to the formulation. Modifications of the Nitsche method have been applied to standard FEM [13, 26, 29, 57], X-FEM [3, 4, 21] and interface problems [1, 2, 12, 23, 45]. Other techniques use different stabilized formulations. For example [34] uses a polynomial stabilization valid for linear elements or [11] penalizes the jump in the multiplier linear elements. In other works the idea of extending the solution of internal elements to the intersected elements was explored [14, 25]. In [19] the idea of condensing the Lagrange multipliers to obtain a simplified method for immersed boundaries was introduced. It was also used in [51] using the quadrature points. The same ideas were applied in [5] using a stabilizing field defined in the volume of the element instead of its surface. For Navier–Stokes equations in [46] a stabilization term that takes into account the jump in the derivative in the internal elements edges is used to overcome limitations of the Nitsche method in immersed boundaries.

In this work we propose a formulation derived from the stabilized Nitsche method. With the choice of finite element spaces, after simplifying the formulation, we obtain a formulation of the perturbed Lagrangian formulation proposed in [47]. From our analysis, an extra term due to contact is introduced to obtain a consistent formulation. The correction term can be iteratively computed using a smooth stress field. The same idea is used in [52] to impose the Dirichlet boundary conditions in immersed boundaries. It is demonstrated that the optimal convergence rate of the finite element solution can be achieved for linear and quadratic elements. This paper is organized as follows: Section 2 describes the formulation of the contact problem using Lagrange multipliers. In Sect. 3 we propose a stabilized formulation based on the Nitsche method. We propose an iterative method to solve the problem. In Sect. 4, the convergence of the iterative method is analyzed. In Sect. 5 the formulation is simplified and expressed as a modified penalty formulation with a suitable choice of the Lagrange multiplier field. We provide some details of the linearization for solving large deformation problems. In the last section some numerical examples are solved.

2 Contact problem formulation

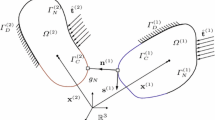
In this part we introduce the contact problem formulation for small deformations. In Sect. 5 we will extend the formulation to deal with large deformations and large sliding problems. Figure 1 shows a schematic representation of two deformable bodies labeled \(^{\scriptscriptstyle {(1)}}\) and \(^{\scriptscriptstyle {(2)}}\) that occupy volumes \(\varOmega ^{\scriptscriptstyle {(1)}}\) and \(\varOmega ^{\scriptscriptstyle {(2)}}\), respectively. The boundary of each body \({\varGamma }^{\scriptscriptstyle {(i)}}\) is divided into three non-overlapping surfaces, \({\varGamma }_{\scriptscriptstyle {D}}^{\scriptscriptstyle {(i)}}\) on which Dirichlet boundary conditions are imposed, \({\varGamma }_{\scriptscriptstyle {N}}^{\scriptscriptstyle {(i)}}\), the Neumann boundary, and \({\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(i)}}\) the surface of the bodies on which contact can occur. We assume a linear elastic behavior of the materials and small deformations. With this setting, the contact problem can be formulated as a minimization of a functional [33, 54], the total potential energy, under the contact constraints, i.e.:

$$\begin{aligned} \begin{aligned}&\min \left\{ \varPi _\text {p}(\mathbf u ) \!=\! \sum _{i=1,2} \left( \int _{\varOmega ^{\scriptscriptstyle {(i)}}} \varvec{\sigma }(\mathbf u ) : \varvec{\epsilon }(\mathbf u ) \; d\varOmega \!-\! \int _{{\varGamma }_{\scriptscriptstyle {N}}^{\scriptscriptstyle {(i)}}} \mathbf u \cdot {\hat{\mathbf{t }}}\;d{\varGamma }\right) \right\} \\&\quad \text { subject to } \quad g_{\scriptscriptstyle {N}}\ge 0 \qquad \text {in } {\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}} \end{aligned} \end{aligned}$$
(1)

where \(\varvec{\sigma }\) is the stress tensor, \(\varvec{\epsilon }\) linear strain tensor and \({\hat{\mathbf{t }}}\) are the tractions imposed at the Neumann boundary. The normal gap between the two contact surfaces is \(g_{\scriptscriptstyle {N}}\). Here we assume that the contact constraint is satisfied for surface \({\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}\). The gap is computed as the distance between the surface point \(\mathbf x ^{\scriptscriptstyle {(1)}}\) and the intersection of the other contact surface \({\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(2)}}\) with the line emanating from the first point in the direction of the normal vector \(\mathbf n ^{\scriptscriptstyle {(1)}}\),

$$\begin{aligned} g_{\scriptscriptstyle {N}}= \left( \mathbf x ^{\scriptscriptstyle {(2)}}\left( \varvec{\xi }^{\scriptscriptstyle {(2)}}\right) - \mathbf x ^{\scriptscriptstyle {(1)}} \right) \cdot \mathbf n ^{\scriptscriptstyle {(1)}} \end{aligned}$$
(2)

where \(\varvec{\xi }^{\scriptscriptstyle {(2)}}\) is the local coordinate of the intersection point on surface \({\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(2)}}\) (in 3D it has 2 components). The position can be written as the sum of the initial position and the displacement, i.e. \(\mathbf x ^{\scriptscriptstyle {(i)}} = \mathbf x ^{\scriptscriptstyle {(i)}}_0 + \mathbf u ^{\scriptscriptstyle {(i)}}\). In small deformations we assume that the contact point denoted by the surface coordinate \(\varvec{\xi }^{\scriptscriptstyle {(2)}}\) remains the same despite the deformation of the solids, i.e. it can be computed for the initial undeformed position. We can therefore write:

$$\begin{aligned} \begin{aligned} g_{\scriptscriptstyle {N}}=&\left( \mathbf u ^{\scriptscriptstyle {(2)}}\left( \varvec{\xi }^{\scriptscriptstyle {(2)}}\right) - \mathbf u ^{\scriptscriptstyle {(1)}} \right) \cdot \mathbf n ^{\scriptscriptstyle {(1)}} + \left( \mathbf x ^{\scriptscriptstyle {(2)}}_0\left( \varvec{\xi }^{\scriptscriptstyle {(2)}}\right) - \mathbf x ^{\scriptscriptstyle {(1)}}_0 \right) \cdot \mathbf n ^{\scriptscriptstyle {(1)}} \\ =&\left( \mathbf u ^{\scriptscriptstyle {(2)}}\left( \varvec{\xi }^{\scriptscriptstyle {(2)}}\right) - \mathbf u ^{\scriptscriptstyle {(1)}} \right) \cdot \mathbf n ^{\scriptscriptstyle {(1)}} + {g_{\scriptscriptstyle {N}}}_0 \end{aligned} \end{aligned}$$
(3)

The minimization problem under inequality constraints (1) can be solved using the Lagrange multiplier method, which is the basis of many finite element formulations for contact problems. A new variable, the Lagrange multiplier field \(\lambda _{\scriptscriptstyle {N}}\) is introduced and the following functional must be minimized with respect to the displacements and maximized with respect to the multipliers

$$\begin{aligned} \begin{aligned}&\text {opt} \left\{ \sum _{i=1,2} \int _{\varOmega ^{\scriptscriptstyle {(i)}}} \varvec{\sigma }(\mathbf u ): \varvec{\epsilon }(\mathbf u ) \; d\varOmega \!-\! \int _{{\varGamma }_{\scriptscriptstyle {N}}^{\scriptscriptstyle {(i)}}} \mathbf u \cdot {\hat{\mathbf{t }}}\;d{\varGamma }\!+\! \int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} \lambda _{\scriptscriptstyle {N}}g_{\scriptscriptstyle {N}}\; d{\varGamma }\right\} \\&\quad \text { subject to } \quad \lambda _{\scriptscriptstyle {N}}\le 0 \qquad \end{aligned} \end{aligned}$$
(4)

With this formulation the inequality constraint affects the multiplier \(\lambda _{\scriptscriptstyle {N}}\). This restriction can be resolved by an active set strategy, assuming that the real contact surface is known, solving the problem and modifying the contact surface. From now onwards, for the analysis of convergence, we assume that the real contact surface is known and denoted as \({\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}\). In Sect. 5 we provide details of the algorithm used to update the real contact surface.

Fig. 1
figure 1

Scheme of two deformable bodies in contact

Full size image

As pointed out above, Eq. (4) can be used to obtain a finite element formulation of the contact problem. The displacement and multiplier fields are replaced by a suitable finite element approximation \(\mathbf u ^{h}\in {\fancyscript{U}}^{h}\) and \(\lambda _{\scriptscriptstyle {N}}^{h}\in {\fancyscript{M}}^{h}\).

In this work we use both 3D standard hexahedral finite elements and the so-called immersed boundary method with 8-node linear elements \({\fancyscript{H}}_8\) and 20-node quadratic elements \({\fancyscript{H}}_{20}\). Here we only describe the basic aspects of the immersed boundary method. A more detailed description can be found in [36, 49], for example. In the immersed boundary method, sometimes referred to as the Cartesian grid method, the underlying mesh consists of regular hexahedra, and this will be used in this work. Figure 2 schematically shows the Cartesian grids of two bodies that can come into contact. The thick lines represent the contact surface, which in general does not coincide with the edges of the elements. The shaded area represents the real domain of the bodies. For the boundary elements (elements cut by the real geometry of the problem) the integration is performed only in the part of the elements lying within the problem domain. Thus, a linear sub-triangulation of the internal part of the elements is defined only for integration purposes and the contact surface is approximately represented with straight segments, as depicted in Fig. 2. Analogously, in the 3D case, the boundary elements are subdivided into tetrahedra for integration and the contact surface is approximately represented by linear triangles.

Fig. 2
figure 2

Cartesian grid finite elements in contact. The thick lines are the contact surfaces that follow the deformation of the boundary elements. Thin lines represent the subtriangulation of the boundary elements performed only for integration purposes

Full size image

The contact interaction between Cartesian meshes follows the same definition as the gap given in Eq. (2) using the local coordinate in the contact surface \(\varvec{\xi }^{\scriptscriptstyle {(1)}}\) and normal vector \(\mathbf n ^{\scriptscriptstyle {(1)}}\). The position of the contact surface in the deformed configuration is defined by standard finite element interpolation using all the nodes of the boundary elements and not only the boundary nodes.

It is well known that in mixed formulations such as that of Eq. 4 a careful choice must be made of the discretization spaces for displacements and multipliers to achieve the optimal convergence rate. There are two conditions [9, 10] the ElKer and the InfSup. As a solution for the compatibility of the spaces of Lagrange multipliers and displacements we find the mortar method, which has been successfully applied to 2D and 3D, large and small deformation contact problems using linear or quadratic elements, as pointed out in the Introduction. For immersed boundary methods the Vital Vertex method has been defined to fulfill the InfSup condition in the case of a Dirichlet boundary in 2D [7] and 3D [2].

The InfSup condition introduces many constraints in the case of immersed boundaries and it is by no means straightforward to derive a contact formulation that fulfills this condition. Stabilized methods can be used obtain greater freedom to choose the Lagrange multiplier space. This will be introduced in the following section and will form the basis of the proposed formulation.

3 Stabilized formulation

The difficulty in solving Eq. 4 by finite elements usually arises when the space of the multipliers is too rich, i.e. there are too many constraints in relation to the displacement degrees of freedom as the mesh is refined. Even though the problem can be solved, the convergence rate of the solution may be compromised. As the number of constraints increases, the constraint equations become more dependent and the value of the multiplier is unbounded. The idea of the stabilized formulations is to add a new term to the functional 4 that would prevent the multiplier from taking unbounded values.

In order to simplify the notation, from now on, we assume that the finite element variables are denoted without superscript \(h\), i.e. \(\mathbf u =\mathbf u ^{h}\) and \(\lambda _{\scriptscriptstyle {N}}=\lambda _{\scriptscriptstyle {N}}^{h}\).

The ideas of stabilizing the solution were used in [47]. Simo, Wriggers and Taylor proposed a perturbed Lagrangian formulation to solve contact problems as the optimization of the following functional

$$\begin{aligned} \text {opt} \left\{ \varPi _\text {p}(\mathbf u ) + \int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} \lambda _{\scriptscriptstyle {N}}g_{\scriptscriptstyle {N}}\; d{\varGamma }- \dfrac{1}{2 k}\int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} \lambda _{\scriptscriptstyle {N}}^2 \; d{\varGamma }\right\} \end{aligned}$$
(5)

The last integral in the functional is a penalty stabilizing term that allows the values of the multipliers to be bounded. As pointed out in [47], this penalized method is not consistent, in the sense that the exact solution of the contact problem is a solution of the above functional only at the limit, when the parameter \(k\rightarrow \infty \), which is impossible in practice. In [47], after some simplifications, a structure of the problem as a pure penalty method was obtained in which the contact constraints are imposed in an average sense.

In this work we propose a new method that includes a modification of the perturbed Lagrangian formulation to make the formulation consistent, i.e. the finite element solution converges to the exact solution as the mesh is refined for a wide range of bounded values of the penalty parameter \(k\).

In what follows, we first introduce (Sect. 3.1) the modified functional used to stabilize the problem and analyze the similarities of the proposed formulation with the Nitsche method. In Sect. 3.2 we introduce the stabilization field used in this work and show that the proposed field overcomes some limitations of the Nitsche method, particularly for immersed boundary meshes. The proof of convergence of the proposed formulation will be analyzed in Sect. 5 after introducing the iterative solution method.

3.1 Proposed stabilized functional

The proposed formulation can be derived from a modified version of the Barbosa–Hughes stabilization [6] in which the stabilizing term is replaced by a smooth stress field. Stenberg [48] demonstrated that the Barbosa–Hughes stabilization was equivalent to the Nitsche method, so that the proposed formulation can also be considered as a modified version of the Nitsche method. The functional reads as:

$$\begin{aligned}&\text {opt} \left\{ \varPi _\text {p}(\mathbf u ) + \int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} \lambda _{\scriptscriptstyle {N}}g_{\scriptscriptstyle {N}}\; d{\varGamma }\right. \nonumber \\&\qquad \left. - \sum _{\forall e} \dfrac{h}{2 E\kappa }\int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} \left( \lambda _{\scriptscriptstyle {N}}- {p_{\scriptscriptstyle {N}}}\right) ^2 \; d{\varGamma }\right\} \end{aligned}$$
(6)

where \(E\) is the Young modulus, \(\kappa \) a user-defined penalty parameter that will be defined in the following sections and \({p_{\scriptscriptstyle {N}}}\) is the stabilizing stress. The difference is found in the definition of the stabilizing stress \({p_{\scriptscriptstyle {N}}}\).

The last integral in Eq. 6 is computed for each contact segment, as defined in the following section. The constant multiplying the stabilizing term includes \(E\) and a representative measure of the element size \(h\). The former is needed to obtain a physical meaning of energy, since we have the product of stress multiplied by stress in the integral. Thus, dividing by \(E\) transforms the term into energy. The latter, \(h\), is included to give the stabilizing term the same order of magnitude as the strain energy. As the element size is reduced, the variation of the element strains and stresses inside the element is also reduced. We can think on the limit as being constant in the entire element. Thus, the strain energy will be proportional to \(h^3\), as it is a volume integral. The stabilizing term is a surface integral so it will be proportional to \(h^2\). The additional \(h\) constant is introduced to have the same order of magnitude, as we need to bound the stabilizing term with the strain energy to achieve the convergence of the method (see the following Section).

In the case of the Nitsche method \({p_{\scriptscriptstyle {N}}}\) is the contact traction computed from the finite element solution, i.e. \({p_{\scriptscriptstyle {N}}}= \mathbf n \cdot \varvec{\sigma }(\mathbf u ) \mathbf n \). This has been applied in [26, 29] to derive the formulations to solve contact problems. With the same choice for \({p_{\scriptscriptstyle {N}}}\), the value of the constant can be adapted to deal with X-FEM problems [1, 3, 4, 45].

The negative sign before the last integral is necessary, as the optimization of the functional is a maximization with respect to the multipliers. However, as the problem is a minimization with respect to the displacements and \(\mathbf n \cdot \varvec{\sigma }(\mathbf u ) \mathbf n \) linearly depends on this field, the negative sign may cause a non desired behavior of the stabilization term. A possible solution with standard finite elements is to bound this term by taking a sufficiently large value for \(\kappa \) so that this integral can be bounded by the strain energy [51]. In the case of immersed boundary elements there are some difficulties involved in bounding this term, particularly in meshes with cut elements that have a very small volume/surface ratio, as pointed out in [25].

To illustrate this problem two boundary elements with small internal volumes are shown in Fig. 3. In general the \(L^2\) norm of the stress on the boundary cannot be bounded by the energy norm of the element as its volume depends on distance \(d\) which can be very close to zero. Therefore, the stress \(\mathbf n \cdot \varvec{\sigma }(\mathbf u ) \mathbf n \) can only be bounded with very large values of the constant \(\kappa \) up to a geometric tolerance (see also [2, 45]). This can affect the convergence of the Nitsche method in this context, although from the engineering point of view, the results obtained using the tolerance seem to be acceptable. Appropriate choices for the stabilizing constant are proposed in the \(\gamma -\)Nitsche method [1, 45] for X-FEM applications. Schott and Wall [46] recently proposed an additional stabilization term that penalizes the jump in the derivative along internal element edges for fluid problems.

Fig. 3
figure 3

Patch of elements for computing the smooth stress field of node \(i\). The internal volume of the boundary elements depends on distance \(d\)

Full size image

3.2 Smooth stress field

In this work we propose to define \({p_{\scriptscriptstyle {N}}}\) as a smooth stress field obtained from the finite element solution, following the ideas introduced in [52] to apply Dirichlet boundary conditions in immersed boundaries. This choice is motivated from the observation that any variable having good convergence properties to the exact contact traction can be used as stabilizing term \({p_{\scriptscriptstyle {N}}}\) in Eq. 6. The smooth stress field depends not only on the solution of the boundary elements but also on the internal elements, where stresses are better estimated. The idea is close to that used in [14, 25], where the displacements of the internal elements are extended to the boundary cut elements. In [46] the solution of the internal elements is also used to stabilize the variables in the boundary elements.

The smooth stress field is based on the SPR (Superconvergent Patch Recovery) first proposed in [59] and improved in [43] to include constraint equations that must be fulfilled by the exact solution. Here we recall the main features of the smooth stress field calculation. The smooth stress field \(\mathbf S _i = \left\{ 1 \, x \, y \, xy \, \ldots \right\} \mathbf a _i\) is defined as a polynomial associated to each node \(i\) whose coefficients \(\mathbf a _i\) are computed solving the following minimization problem:

$$\begin{aligned} \mathbf a _i = \text {argmin} \left\{ \int _{\varOmega _i^{\text {patch}}} \left( \varvec{\sigma }(\mathbf u )-\mathbf S _i \right) \cdot \left( \varvec{\sigma }(\mathbf u )-\mathbf S _i \right) \; d\varOmega \right\} \end{aligned}$$
(7)

where \(\varvec{\sigma }(\mathbf u )\) is the stress field computed from the finite element solution. The integral is extended in the volume of a so-called nodal patch \({\varOmega _i^{\text {patch}}}\). This volume includes all internal elements that contain node \(i\) and the internal volume of boundary elements that contain this node. For example, Fig. 3 shows the patch of node \(i\) in a 2D case, that contains two internal and two boundary elements. With this choice, small-volume boundary elements (\(d\) close to zero, in which the finite element stress is poorly estimated, i.e. it has a large error) contribute less than the internal elements to the computation of the smooth stress field.

The stabilization term is computed as the normal traction of the smooth stress in the contact surface \({p_{\scriptscriptstyle {N}}}= \mathbf n \cdot \mathbf S \mathbf n \). With this definition it can be proved that the \(L^2\) norm of \({p_{\scriptscriptstyle {N}}}\) in the contact surface can be bounded with the energy norm [52], with a bounded positive constant \(C\) as follows

$$\begin{aligned} \displaystyle \Vert \mathbf S \Vert ^2_{L^2({\varGamma }_{\scriptscriptstyle {C}})} \le \dfrac{EC}{h} \Vert \mathbf u \Vert ^2_{E} \end{aligned}$$
(8)

where \(h\) is a representative measure of the element size and \(\Vert \cdot \Vert _E\) is the energy norm in the volume. The value of \(C\) depends on the order of the interpolation and the nodal patches. For immersed boundaries the worst case appears for nodes whose elements are cut and have very small volume. Even in that case, as the smooth stress field depends on the solution of the internal elements, the constant \(C\) is bounded. In practice we found that we can use \(C\ge 10\) for linear and quadratic elements.

4 Iterative solution method

The stabilization term \({p_{\scriptscriptstyle {N}}}\) depends on the finite element solution \(\mathbf u \). However, it is somewhat cumbersome to obtain an explicit formula for it, as its computation derives from Eq. (7). Following the ideas presented in [52], we propose an iterative process to solve the optimization problem 6 in which the stabilization term \({p_{\scriptscriptstyle {N}}}\) is assumed to be constant. After solving the problem, \({p_{\scriptscriptstyle {N}}}\) is updated from the finite element solution, and problem 6 is solved again. The process begins with \({p_{\scriptscriptstyle {N}}}=0\) and runs until convergence is achieved.

Assuming that the stabilization term \({p_{\scriptscriptstyle {N}}}\) is known, we solve problem (6) taking variations with respect to the displacements and the multipliers to obtain a following variational equation. We have to find the iteration \(k\) solution, \([\mathbf u ^k,\lambda _{\scriptscriptstyle {N}}^k]\), solving the following system

$$\begin{aligned} \displaystyle \begin{aligned}&\sum _{i=1,2} G^{\scriptscriptstyle {(i)}}_{int}(\mathbf u ^k,\delta \mathbf u ) + \int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} \lambda _{\scriptscriptstyle {N}}\delta g_{\scriptscriptstyle {N}}(\mathbf u ^k) \; d{\varGamma }\\&\quad = \sum _{i=1,2} G^{\scriptscriptstyle {(i)}}_{ext}(\delta \mathbf u ) \qquad \forall \delta \mathbf u \\&\int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} \delta \lambda _{\scriptscriptstyle {N}}^k \, g_{\scriptscriptstyle {N}}(\mathbf u ^k) \; d{\varGamma }- \dfrac{h}{E\kappa }\int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} \delta \lambda _{\scriptscriptstyle {N}}\, \lambda _{\scriptscriptstyle {N}}^k \; d{\varGamma }\\&\quad = - \dfrac{h}{E\kappa }\int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} \delta \lambda _{\scriptscriptstyle {N}}\, {p_{\scriptscriptstyle {N}}}(\mathbf u ^{k-1}) \; d{\varGamma }\qquad \forall \delta \lambda _{\scriptscriptstyle {N}}\end{aligned} \end{aligned}$$
(9)

\(G^{\scriptscriptstyle {(i)}}_{int}\) and \(G^{\scriptscriptstyle {(i)}}_{ext}\) are the virtual work of internal and external forces of body \(i\), respectively. The contact integral in the first equation is the virtual work of contact forces, and \(\delta g_{\scriptscriptstyle {N}}\) is the virtual gap computed by taking variations in Eq. (3). The smooth pressure is written as \({p_{\scriptscriptstyle {N}}}(\mathbf u ^{k-1})\) to emphasize the dependence of this variable on the solution of a previous iteration \(k-1\). In the second equation, the first integral contains the constraints imposed to fulfill the non-penetrability condition of contact. The other two integral terms in the second equation prevent the contact constraints from being exactly fulfilled but tend to compensate each other as the mesh is refined. At the limit, when the element size tends to zero, \(\lambda _{\scriptscriptstyle {N}}={p_{\scriptscriptstyle {N}}}\) and the exact constraint will be enforced.

Note that, compared with the Nitsche method used in [26], the proposed formulation has a lower number of integrals that need to be evaluate to obtain the tangent matrix of the system. In particular, all the terms of the Nitsche method that derive from the variation of the stabilization term \({p_{\scriptscriptstyle {N}}}\) (which is here a function of \(\mathbf u \)) are avoided in the proposed formulation, at the cost of an iterative solution process. It is necessary to verify the conditions under which the iterative method converges to the solution and to check the stability of the system. This is done in the following Section after defining the Lagrange multiplier finite element space.

5 Lagrange multiplier interpolation: Penalty method

The stabilized formulation (9) gives greater freedom than the Lagrange formulation to choose the Lagrange multiplier finite element space. The displacement field is defined in \(\mathbf u ^{h}\in H^1(\varOmega )\) and the multiplier space \(\lambda _{\scriptscriptstyle {N}}^{h}\in L^2({\varGamma }_{\scriptscriptstyle {C}})\). We choose for the displacement field linear 8-node \({\fancyscript{H}}_8\) or quadratic 20-node \({\fancyscript{H}}_{20}\) hexahedral elements, having degree of interpolation \(p=1\) and \(p=2\), respectively. As pointed out above, we deal with standard or cut (immersed boundary) elements.

The only requirement for the Lagrange multiplier space is that it must have adequate approximation properties. Stenberg [48] analyzes the approximation properties of the multiplier space used to impose the Dirichlet boundary conditions using the Nitsche method. From this analysis, if the solution is regular enough, the optimal convergence rate can be achieved [52] if the Lagrange multiplier space is at least a piecewise constant, not necessarily continuous, interpolation for linear elements \({\fancyscript{H}}_8\) and a piecewise linear, not necessarily continuous, interpolation for quadratic elements \({\fancyscript{H}}_{20}\).

In [51] an implicit definition of the multiplier field was introduced for 2D elements, based on the value of the multiplier at the quadrature points of the surface used to numerically evaluate the boundary integrals. The Dirichlet boundary conditions in immersed boundary elements problem was analyzed in this work. For 2D problems, the Dirichlet boundary was divided into segments defined in each cut element. It has been stated that \(n_{pg}=2\) quadrature points for linear elements define a piecewise linear interpolation for the multiplier \(q=1\) and can exactly integrate polynomials of degree 3. As the product of the multiplier and the displacement has degree 2, it is enough to exactly evaluate integrals with constant Jacobian. Similarly, in 2D for quadratic elements \(n_{pg}=3\) allows exact integration and good approximation properties of the multiplier field.

In the case of contact problems, the boundary integrals on the contact surface are more complex because they involve functions defined in the two bodies in contact. Exact evaluation of the contact surface integrals would need a segmentation of the surface, as proposed for the mortar method in [39, 40, 56]. Instead of looking for exact integration, in this work we use the same strategy proposed in [18, 22, 50] and depicted in Fig. 4. The approximate integration is performed evaluating the integrand at the quadrature points defined on the surface \({\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}\) regardless of whether the integrand belongs to one or other body. Despite the inexact integration, this method has certain advantages. First, the evaluation has a lower computational cost and is easy to implement. Also, the optimal convergence rate of the finite element solution error can be achieved for linear elements if a uniform refinement is performed. The reason is that the error in the contact integral computation will decrease linearly as the mesh is refined.

Fig. 4
figure 4

Concentrated inexact numerical integration. The integrands are only evaluated at the quadrature points (shown as multiplication) defined in each contact slave surface segment. The circles are the nodes and the squares are the corresponding contact points on the master surface. Normal vectors are independently defined for each slave segment

Full size image

The main drawback of this integration is that for quadratic elements the theoretical rate of convergence \(p+1\) in energy norm is lost when the mesh is refined. The problem can be alleviated by increasing the number of quadrature points, so that the level of the integration error is reduced. Even though the rate is not improved, the optimal rates of convergence of the finite element error could be achieved for the first meshes when the discretization error is much higher than the integration error. Therefore, from the engineering point of view, the method is suitable for achieving an accurate finite element solution with a reasonable amount of degrees of freedom. It must be pointed out that in some contact problems the regularity of the solution itself limits the theoretical rate of convergence that could be achieved with quadratic elements.

Another alternative that is explored in the numerical examples in the present paper is to impose the contact constraints on both contact boundaries \({\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}, {\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(2)}}\) at the same time, which is possible due to the stabilized formulation. It can be seen as the double pass strategy defined in the classical penalty method. As the stabilization stresses \({p_{\scriptscriptstyle {N}}}^{\scriptscriptstyle {(1)}}\) and \({p_{\scriptscriptstyle {N}}}^{\scriptscriptstyle {(2)}}\) are acting at the same time on both bodies, \(\lambda _{\scriptscriptstyle {N}}= {p_{\scriptscriptstyle {N}}}^{\scriptscriptstyle {(1)}} + {p_{\scriptscriptstyle {N}}}^{\scriptscriptstyle {(2)}}\) must be fulfilled. Any weight factor can be defined between 0 and 1 for the two pressures. In the examples we choose \({p_{\scriptscriptstyle {N}}}^{\scriptscriptstyle {(1)}} = {p_{\scriptscriptstyle {N}}}^{\scriptscriptstyle {(2)}} = \lambda _{\scriptscriptstyle {N}}/ 2\).

5.1 Penalty method

Once the Lagrange multiplier field is defined, the iterative method of Eq. (9) can be simplified by eliminating the Lagrange multipliers. As the interpolation is defined as a piecewise discontinuous function, the multiplier can be condensed element by element before the assembly. Indeed, due to the concentrated numerical integration, they can also be eliminated for every quadrature point. The value of the Lagrange multiplier at each quadrature point is:

$$\begin{aligned} {\lambda _{\scriptscriptstyle {N}}^k}_g = {p_{\scriptscriptstyle {N}}}(\mathbf u ^{k-1}) + \dfrac{E\kappa }{h} {g_{\scriptscriptstyle {N}}}_g \end{aligned}$$
(10)

where the subindex \(g\) is used to denote the value of the variable at the quadrature point.

Formally, we proceed as in [48, 52] to obtain a simplified stabilized problem. We can take the variation of the multiplier as the projection in \(L^2\) of an appropriate displacement field in the second equation of the problem (9) to condense the multiplier and then substitute in the first equation to obtain:

$$\begin{aligned} \displaystyle&\sum _{i=1,2} G^{\scriptscriptstyle {(i)}}_{int}(\mathbf u ^k,\delta \mathbf u ) + \dfrac{E\kappa }{h}\int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} g_{\scriptscriptstyle {N}}(\mathbf u ^k) \, \delta g_{\scriptscriptstyle {N}}\; d{\varGamma }\nonumber \\&\quad = \sum _{i=1,2} G^{\scriptscriptstyle {(i)}}_{ext}(\delta \mathbf u ) - \int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} \delta g_{\scriptscriptstyle {N}}\, {p_{\scriptscriptstyle {N}}}(\mathbf u ^{k-1}) \; d{\varGamma } \end{aligned}$$
(11)

Here we find a close similarity between the proposed formulation and the perturbed Lagrangian formulation [47]. In the first iteration, when \({p_{\scriptscriptstyle {N}}}=0\), the formulation is a pure penalty method, but computed in a distributed sense. This coincides with the formulation in [47]. As far as the integral can be exactly evaluated, the penalty term in Eq. (11) is like a distributed spring that joins the two bodies in contact. As it has been pointed out above, the number of quadrature points can be freely chosen, provided that they define a suitable interpolation of sufficient degree. Increasing the number of points only affects the numerical integration error. Although the number of constraints in the formulation (9) is increased, as we condense the Lagrange multipliers, the number of equations remains the same for the simplified formulation (11). On the right hand side of Eq. (11) the smooth stress field has the effect of compensating the error introduced by the penalty method. This term is computed iteratively from the finite element solution (see Sect. 5.3). Another alternative followed in the literature in order to find stable contact formulations using springs without stabilizing terms (penalty formulation) is to properly choose the number of quadrature points and define a distributed integration [16, 58].

The system of Eq. (11) can be written in matrix form using the standard finite element procedure to define the following residual:

$$\begin{aligned} \mathbf r ^{k} = \left( \mathbf K + \dfrac{E\kappa }{h} \mathbf M \right) \mathbf d ^{k} - \mathbf f - \mathbf S \, \mathbf d ^{k-1} = 0 \end{aligned}$$
(12)

where \(\mathbf d ^{k}\) is the nodal displacements vector in the iteration \(k, \mathbf K \) is the stiffness matrix and \(\mathbf f \) is the external force vector. For clarity of presentation we assume that the initial gap \({g_{\scriptscriptstyle {N}}}_0\) is zero. Matrix \(\mathbf M \) is computed from the second integral of Eq. (11) using the numerical integration presented above and the gap definition. Although, in general, \(h\) is included in the integral of each element for meshes with different element sizes, here we leave the factor to emphasize the dependence of this term on the element size. Matrix \(\mathbf S \) is derived from the last integral of Eq. (11) and points out the linear dependence of the smooth stress field with respect to the displacement field. In practice, this term is computed as the additional contact force vector \(\mathbf f ^{k-1}_{N}\) depending on the previous displacement field and \(\mathbf S \) is not explicitly obtained.

5.2 Large deformations

The formulation proposed above for small deformations can be extended to deal with large deformations and large sliding problems. The virtual work of internal and external forces can be evaluated in the standard way for all type of material behavior, including hyper-elasticity and plasticity. In addition to the contact iterations, another non-linear behavior due to contact has to be considered, i.e. the change of the contact point as the bodies deform. This makes the gap and the virtual gap to be non-linear functions of the displacements. Equation (11) is now the residual of a non-linear equation that can be solved using a semi-smooth Newton method. After numerical integration the residual can be expressed as:

$$\begin{aligned} \displaystyle \delta \mathbf u \cdot \mathbf r ^{k}= & {} \delta \mathbf u \cdot \left( \mathbf f _{int}(\mathbf u ^k) - \mathbf f _{ext} \right) \nonumber \\&\quad + \sum _{\forall g} H_g \left( \dfrac{E\kappa }{h}{g_{\scriptscriptstyle {N}}}_g(\mathbf u ^k) \! \,+\, \! {{p_{\scriptscriptstyle {N}}}}_g(\mathbf u ^{k-1}) \right) \delta {g_{\scriptscriptstyle {N}}}_g J_g \nonumber \\ \end{aligned}$$
(13)

where \(H_g\) is the weight of the quadrature point and \(J_g\) the Jacobian of the transformation. Here the sum is extended to the active quadrature points that will be discussed in the following subsection.

Here any definition found in the literature of the contact variables \(g_{\scriptscriptstyle {N}}\) and \(\delta {g_{\scriptscriptstyle {N}}}\) at the quadrature points could be used (based on closest point projection [33, 54] for example) although the aim of this paper is not to deal with the computation details of these contact variables for large deformation problems. We have chosen the definition given in a previous paper [50], to which we refer for details of linearizations. Also, we neglect the linearization of the Jacobian because it leads to a non-symmetric tangent matrix. An additional term could be included in the functional of the formulation to recover symmetry [17] and perform a consistent linearization. In practice, the convergence obtained without consistent linearization in the numerical problems analyzed seems to be acceptable.

We use the definition of the gap based on the ray tracing, so we follow the formulation proposed in [50] also used in [24] for 2D problems, but extended to 3D. We recall here the main steps of the derivation. Taking variations in expression (2), we have

$$\begin{aligned} \displaystyle \delta {g_{\scriptscriptstyle {N}}} = \left( \delta \mathbf u ^{\scriptscriptstyle {(2)}} - \delta \mathbf u ^{\scriptscriptstyle {(1)}} \right) \cdot \mathbf n ^{\scriptscriptstyle {(1)}} + \mathbf s ^{\scriptscriptstyle {(2)}}_\xi \cdot \mathbf n ^{\scriptscriptstyle {(1)}} \, \delta \xi + \mathbf s ^{\scriptscriptstyle {(2)}}_\eta \cdot \mathbf n ^{\scriptscriptstyle {(1)}} \, \delta \eta \nonumber \\ \end{aligned}$$
(14)

where \(\delta \xi \) and \(\delta \eta \) are the variations of the contact point local coordinates and \(\mathbf s ^{\scriptscriptstyle {(2)}}_\xi \) and \(\mathbf s ^{\scriptscriptstyle {(2)}}_\eta \) are the tangent vectors. The variations of the contact point can be computed using the same procedure as in [50] to obtain the following system (2), we have

$$\begin{aligned}&\displaystyle \left[ \begin{array}{c@{\quad }c} \mathbf s ^{\scriptscriptstyle {(1)}}_\xi \cdot \mathbf s ^{\scriptscriptstyle {(2)}}_\xi &{} \mathbf s ^{\scriptscriptstyle {(1)}}_\xi \cdot \mathbf s ^{\scriptscriptstyle {(2)}}_\eta \\ \mathbf s ^{\scriptscriptstyle {(1)}}_\eta \cdot \mathbf s ^{\scriptscriptstyle {(2)}}_\xi &{} \mathbf s ^{\scriptscriptstyle {(1)}}_\eta \cdot \mathbf s ^{\scriptscriptstyle {(2)}}_\eta \\ \end{array} \right] \left\{ \begin{array}{c} \delta \xi \\ \delta \eta \end{array} \right\} \nonumber \\&\quad = \left\{ \begin{array}{c} \left( \delta \mathbf x ^{\scriptscriptstyle {(2)}} - \delta \mathbf x ^{\scriptscriptstyle {(1)}}\right) \cdot \mathbf s ^{\scriptscriptstyle {(1)}}_\xi + g_{\scriptscriptstyle {N}}\delta \mathbf n ^{\scriptscriptstyle {(1)}} \cdot \mathbf s ^{\scriptscriptstyle {(1)}}_\xi \\ \left( \delta \mathbf x ^{\scriptscriptstyle {(2)}} - \delta \mathbf x ^{\scriptscriptstyle {(1)}}\right) \cdot \mathbf s ^{\scriptscriptstyle {(1)}}_\eta + g_{\scriptscriptstyle {N}}\delta \mathbf n ^{\scriptscriptstyle {(1)}} \cdot \mathbf s ^{\scriptscriptstyle {(1)}}_\eta \end{array} \right\} \end{aligned}$$
(15)

The tangent matrix is obtained taking the derivative with respect to the displacements. As pointed out above, we neglect the derivative of the Jacobian. The tangent matrix used in the numerical examples is:

$$\begin{aligned} \displaystyle \mathbf K _T= & {} \mathbf K + \sum _{\forall g} H_g \dfrac{E\kappa }{h} {\Delta }{g_{\scriptscriptstyle {N}}}_g(\mathbf u ^k) \, \delta {g_{\scriptscriptstyle {N}}}_g J_g \nonumber \\&\quad + \sum _{\forall g} H_g \left( \dfrac{E\kappa }{h}{g_{\scriptscriptstyle {N}}}_g(\mathbf u ^k) + {{p_{\scriptscriptstyle {N}}}}_g(\mathbf u ^{k-1}) \right) {\Delta }\delta {g_{\scriptscriptstyle {N}}}_g J_g \nonumber \\ \end{aligned}$$
(16)

where \(\mathbf K \) is the directional derivative of the work of internal forces with respect to the displacements. For the derivative of the virtual gap \({\Delta }\delta g_{\scriptscriptstyle {N}}\) the procedure described above can be followed.

5.3 Solution algorithm

figure a

The proposed method has certain similarities with the Uzawa algorithm used in the augmented Lagrangian formulation, in which updating the Lagrange multiplier is called augmentation. We use the same term for the updating performed in (10), using the smooth stress field. It also resembles the method used in [1] to solve contact problems. The algorithm for small deformation problems is shown in Algorithm 5.1. For every load step, the smooth stress field \({{p_{\scriptscriptstyle {N}}}}_g\) and the gap \({g_{\scriptscriptstyle {N}}}_g\) are first obtained for each quadrature contact point from the previous solution.

In addition to the augmentation iterations, another iterative process is defined to resolve the contact surface, i.e. to determine which part of the potential contact surface is active and will be used to impose the impenetrability constraints. The contact check is performed at each quadrature point, using the value of the multiplier defined in Eq. (10), so that \({\lambda _{\scriptscriptstyle {N}}}_g \le 0\). It can be seen that the contact iterations are performed with a constant value of the smooth stress \({p_{\scriptscriptstyle {N}}}\), which acts as an external pressure on the contact surface, so that the contact iterations are similar to a pure penalty method. The contact iterations run until the active contact points are unchanged. In this work this is directly checked with the residual of Eq. (12).

For large deformation problems, the structure of the algorithm is the same, the only changes being the computation of the residual, which is now defined in Eq. (13), and the solution of the system of equations by a Newton method.

In terms of computational cost, the proposed method is equivalent to an augmented Lagrange formulation implemented by the Uzawa algorithm. The advantage of the proposed method is the freedom to choose the number of quadrature points at which the contact constraints are imposed as the method is stabilized. Compared with the Lagrange multiplier formulation (or augmented Lagrange in which the multipliers remain as variables of the system), in the proposed method the system of equations to be solved in each iteration is smaller in size. Another advantage is that the system matrix is positive definite, which usually reduces the resolution time. On the other hand, the number of iterations is in general greater as there is a nested loop.

5.4 Convergence of the iterative method

The iterative process for augmentations defined above in Eq. (12) can be viewed as the Richardson method of solving a system of equations. This system can be rewritten as:

$$\begin{aligned} \left( \mathbf K + \dfrac{E\kappa }{h} \mathbf M \right) \mathbf d ^{k} = \mathbf S \, \mathbf d ^{k-1} + \mathbf f \end{aligned}$$
(17)

The convergence [44, 52] is then verified if the spectral radius of the iteration matrix \(\left( \mathbf K + \dfrac{E\kappa }{h} \mathbf M \right) ^{-1} \mathbf S \) is lower than 1 (equivalently, the modulus of any eigenvalue \(\alpha \) is lower than 1), even if the set of active quadrature points changes from one iteration to another.

To prove this, we start with the definition of the eigenvalue problem. Any eigenvector \(\mathbf v ^{*}\) associated with an eigenvalue \(\alpha \) of the iteration matrix fulfils

$$\begin{aligned} \mathbf S \, \mathbf v ^{*} = \alpha \, \left( \mathbf K + \dfrac{E\kappa }{h} \mathbf M \right) \mathbf v ^{*} \end{aligned}$$
(18)

On the other hand, if the following equation is satisfied for any nodal displacement vector \(\mathbf v \):

$$\begin{aligned} \mathbf v ^{T} \mathbf S \, \mathbf v < \mathbf v ^{T} \left( \mathbf K + \dfrac{E\kappa }{h} \mathbf M \right) \mathbf v \qquad \forall \mathbf v \end{aligned}$$
(19)

then the modulus of \(\alpha \) is necessarily lower than 1 and the convergence is proven.

To check Eq. (19), we use the definition of the stabilization term \(\mathbf S \, \mathbf v \):

$$\begin{aligned} \left| \mathbf v ^{T} \mathbf S \, \mathbf v \right| = \left| \int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} g_{\scriptscriptstyle {N}}(\mathbf v ) \, {p_{\scriptscriptstyle {N}}}(\mathbf v ) \; d{\varGamma }\right| . \end{aligned}$$

Applying the Cauchy-Schwarz inequality, using Eq. (8), and taking into account that for two positive numbers \(x, y\) , it holds that \(2\,x \, y \le x^2 + y^2\), we have:

$$\begin{aligned} \left| \mathbf v ^{T} \mathbf S \, \mathbf v \right|= & {} \left| \int _{{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} g_{\scriptscriptstyle {N}}(\mathbf v ) \, {p_{\scriptscriptstyle {N}}}(\mathbf v ) \; d{\varGamma }\right| \le \Vert g_{\scriptscriptstyle {N}}(\mathbf v ) \Vert _{L^2,{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}}\nonumber \\&\times \Vert {p_{\scriptscriptstyle {N}}}(\mathbf v ) \Vert _{L^2,{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}}\le \Vert g_{\scriptscriptstyle {N}}(\mathbf v ) \Vert _{L^2,{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} \sqrt{\dfrac{EC}{h}} \Vert \mathbf v \Vert _{E}\nonumber \\\le & {} {\dfrac{EC}{4 h}} \Vert g_{\scriptscriptstyle {N}}(\mathbf v ) \Vert ^2_{L^2,{\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}} + \Vert \mathbf v \Vert ^2_{E} \end{aligned}$$
(20)

Now, taking \(\kappa > C / 4\) we obtain the bound of the stabilization term and the iterative process will converge.

Remark The stabilization term is only computed on the active contact zone of the current iteration, even if the size of the contact surface \({\varGamma }_{\scriptscriptstyle {C}}^{\scriptscriptstyle {(1)}}\) has been modified. This ensures that Eq. 20 is verified even in this case.

6 Numerical examples

Some academic examples have been solved to test the performance of the proposed formulation. We used standard finite elements and immersed boundary elements with linear \({\fancyscript{H}}_8\) and quadratic \({\fancyscript{H}}_{20}\) interpolation and different number of quadrature points. In the case of standard linear elements we tried \(n_{pg}=2\times 2, n_{pg}=3\times 3\) and \(n_{pg}=16\times 16\). For quadratic elements we tried \(n_{pg}=3x3\) and \(n_{pg}=16\times 16\). For immersed boundary elements the number of quadrature points is based on the triangulation of the surface due to the intersection of the real geometry with the element. For integration purposes, we divide the hexahedra into tetrahedra and use the quadrature formulas for the surface triangles of the tetrahedra whose face coincides approximately with the contact surface.

6.1 Hollow sphere under internal pressure

The first example to be tested is a problem with an exact solution, so that the discretization error can be exactly computed. The problem is a hollow sphere under internal pressure. We define two volumes that are discretized using non-conforming meshes as depicted in Fig. 5. A sequence of uniformly refined meshes is obtained by element subdivision. In this problem all the quadrature points of the potential contact surface are in contact, so there are no iterations due to changes in contact conditions.

Fig. 5
figure 5

First two meshes of the sequence used to solve the problem of a hollow sphere under internal pressure. The hollow sphere is discretized into two volumes using non-conforming meshes

Full size image

The first test was performed to check the influence of the constant \(\kappa \) in the finite element solution using standard linear (L) and quadratic (Q) elements. In Figs. 6 and 7 the energy norm error and the \(L^2\) norm error of the finite element solution are plotted as a function of a representative element size. The triangles show the theoretical convergence rate that can be achieved in every case. These test were performed using \(n_{pg}=16x16\) quadrature points both for \({\fancyscript{H}}_8\) and \({\fancyscript{H}}_{20}\) elements to keep the integration error as small as possible. The theoretical convergence rate is obtained in all cases, at least for this level of error. The results show that the influence of the parameter \(\kappa \) is negligible in this example, as the curves for different values of \(\kappa \) perfectly overlap.

Fig. 6
figure 6

Energy norm error of the solution as a function of the element size for the hollow sphere under internal pressure problem. Analysis of the influence of parameter \(\kappa \)

Full size image
Fig. 7
figure 7

\(L^2\) norm error of the solution as a function of the element size for the hollow sphere under internal pressure problem. Analysis of the influence of parameter \(\kappa \)

Full size image

As pointed out above, it is not expected that the quadratic elements can achieve the theoretical rate of convergence of the finite element solution because of the integration error. However, if the meshes are not very refined (for example, the meshes shown in Fig. 5), the level of the discretization error is much higher than the integration error. Despite the lower rate of convergence of the latter, the optimal convergence rate can be achieved. To test the influence of the integration error we solved the same problem using different number of quadrature points and different types of integration. For \({\fancyscript{H}}_8\) linear elements we used \(n_{pg}=2\times 2, n_{pg}=3\times 3\) and \(n_{pg}=16\times 16\). For \({\fancyscript{H}}_{20}\) quadratic elements we used \(n_{pg}=3\times 3, n_{pg}=3\times 3\) with double pass integration (i.e. the surfaces of both bodies are considered at the same time as contact surfaces where the numerical integration is performed), and \(n_{pg}=16\times 16\). The discretization error is shown in Figs. 8 and 9, in energy and \(L^2\) norms, respectively. The triangles show the theoretical rate of convergence. Optimal convergence is achieved for linear elements. However, for quadratic elements using \(n_{pg}=3\times 3\) quadrature points, the integration error seems to affect the solution for the more refined meshes and the convergence rate is reduced. To alleviate this effect, using both a double pass strategy and more quadrature points seems to reduce the integration error and allows the optimal rate to be recovered in this case and for these element sizes.

Fig. 8
figure 8

Energy norm error of the solution as a function of the element size for the hollow sphere under internal pressure problem. Analysis of the influence of the integration error

Full size image
Fig. 9
figure 9

\(L^2\) norm error of the solution as a function of the element size for the hollow sphere under internal pressure problem. Analysis of the influence of the integration error

Full size image

This linear example was used to test the convergence of the Richardson iterations of the system and the influence of parameter \(\kappa \). In Fig. 10 the normalized norm of the residual (Eq. (11)) is shown as a function of the number of iterations. The results are shown for linear \({\fancyscript{H}}_8\) and quadratic \({\fancyscript{H}}_{20}\) elements and different values of the parameter \(\kappa \). Convergence is achieved between 4 and 6 iterations. This behavior is representative of all the tests ran for other numerical examples. In this case, the best convergence is achieved with a double pass strategy and \(\kappa =100\).

Fig. 10
figure 10

Hollow sphere under internal pressure problem. Convergence of the Richardson iteration of the system. The normalized norm of the residual is shown for linear and quadratic elements

Full size image

6.2 Rigid sphere in contact with a deformable block

In the second example a contact problem between a rigid sphere and an elastic solid is solved using an immersed boundary mesh. The geometry of the elastic solid is shown in Fig. 11. It is a modified block with dimensions \(2\times 2\times 2\) units of length, in which the upper face is a parabolic surface. The highest point of the parabolic surface is at \(2.5\) units of length. As it can be observed the elastic solid geometry is embedded in a uniform Cartesian Grid. The boundary elements are cut by the geometry and integration is only performed in the internal part of these elements. A sub-triangulation of the boundary elements using linear tetrahedra is performed only for integration purposes. The number of quadrature points on the contact surface also depends on this sub-triangulation (7 quadrature points for each triangle).

Fig. 11
figure 11

Model of the rigid sphere contact with an immersed boundary mesh

Full size image

The sphere is located above the curved surface of the block, and contact occurs at this curved face (see Fig. 12). A rigid body motion towards the elastic solid is applied to the sphere causing a maximum theoretical penetration of \(Dz=0.15\) or \(Dz=0.3\) units of length. The radius of the sphere is \(2\) units of length. Figure 12 shows the deformed configuration of the elastic block. The colormap values are related to the modulus of the displacement field. The contact traction at each quadrature point of the surface is also shown in the same figure. The convergence of the contact iterations and the augmentations is shown in Table 1 for different initial penetration \(Dz\) and penalty parameter \(\kappa \) values. We use a tolerance of \(10^{-8}\) to determine if the solution has converged, both for the contact and Richardson iterations.

Fig. 12
figure 12

Contact traction of the rigid sphere contact with an immersed boundary mesh

Full size image
Table 1 Rigid sphere in contact with an immersed boundary mesh
Full size table

6.3 Deformable ring in contact with a deformable block

The third example is a large deformation and large sliding contact problem. A scheme of the example is shown in Fig. 13. The upper body consists of two joined rings of equal thickness but different Neo-Hookean hyperelastic material properties. The material parameters are \(E=10^5\) and \(\upsilon =0.3\) for the inner ring and \(E=10^3\) and \(\upsilon =0.3\) for the outer ring. The problem is 3D, with symmetry boundary condition applied to the frontal plane. The ring thickness is 40 units of length and the block thickness is 50 units of length. The block is linear elastic with material parameters \(E=10^3\) and \(\upsilon =0.3\). We solved the problem assuming two materials for the block: a pure elastic behavior and plasticity with yielding limit \(S_y=50\) and plastic hardening \(H=50\). A downward displacement of \(Dy=90\) is applied to the elastic ring. The displacement is applied in 20 steps in the elastic case and 40 steps in the plastic case, with the time ranging from \(t = 0\) to \(t = 1\). Linear elements were used in the simulation and the number of quadrature points was \(n_{pg}=4\times 4\). The block contact surface was taken as slave surface where the integration is performed.

Fig. 13
figure 13

Initial configuration of the elastic ring contact problem

Full size image

Figures 14 and 15 shown some snapshots of the deformed configuration and contact pressure with elastic and plastic behavior of the block. In the first time steps, the deformation of the block is pure elastic and both examples show the same deformed configuration. From \(t=0.65\) plastic deformation occurs in the second case that causes a different deformation of the ring and contact pressure distribution. This effect can also be noticed in Fig. 16, where the reaction force is plotted versus the time step for both cases (elastic and elasto-plastic).

Fig. 14
figure 14

Deformable ring in contact with an elastic block. Deformation and contact pressure for different time steps of the simulation

Full size image
Fig. 15
figure 15

Deformable ring in contact with an elasto-plastic block. Deformation and contact pressure for different time steps of the simulation

Full size image
Fig. 16
figure 16

Elastic ring in contact with a block. Reaction force in the ring as a function of the time step

Full size image

In Table 2 we show the convergence of the contact and Richardson iterations for different time steps and both elastic (EL) and elasto-plastic (PL) behavior of the block. The normalized norm of the residual (Eq. 13) is shown as a function of the iterations. A mark is shown when an augmentation is performed, i.e. the stabilizing stress \({p_{\scriptscriptstyle {N}}}\) is updated. The tolerance of the relative error of the residual is set at \(10^{-8}\). As in the linear Example 1 shown above, after 3 or 4 Richardson’s iterations the solution has almost converged and the changes in the displacement or contact stresses are very small.

Table 2 Elastic rings in contact with a block
Full size table

6.4 Bicycle inner tube

The last example is depicted in Fig. 17 and shows a quarter of the inner tube of a bicycle tire that is submitted to increasing internal pressure. As the tube deforms, contact occurs between the tire and the rim. The rim is an elastic material with properties \(E=10^8\) and \(\upsilon =0.3\), the inner tube and the casing are hyper-elastic materials with \(E=1000\) and \(\upsilon =0.3\). The pressure is increased from 0 to \(p=40\) units of pressure. A variable time step increment is applied from \(t=0\) to \(t=1\) in 40 steps. In the front plane of the casing there is a crack that allows the inner tube to escape. The number of elements in the casing at this plane is \(65\). The casing is subdivided in 65 equal segments corresponding to the element edge and the crack ranges as depicted in Fig. 17.

Fig. 17
figure 17

Model of the bicycle tire contact problem. The inner tube is shown in yellow (light grey), the rim in blue (dark grey) and the casing in white. (Color figure online)

Full size image

The value of the penalty constant was \(\kappa =10\). The problem was solved using both a double pass and single pass strategies. The deformed configuration is shown in Fig. 18 for different time steps using the double pass contact. In Table 3 a comparison of the residual convergence is shown. In this example, similar behavior is found for both strategies.

Fig. 18
figure 18

Inner tube contact problem. Comparison of the deformed configuration for different time steps. The colormap is proportional to the modulus of the displacement

Full size image
Table 3 Inner tube contact problem
Full size table

7 Conclusions

This paper proposes a new method for solving contact problems. The formulation is based on the stabilized Nitsche method and after simplifying the equations by condensing the multipliers, a modified penalty formulation is obtained. The method has similarities with the perturbed Lagrangian formulation [47], but with the addition of an extra term that can be computed iteratively and makes the formulation consistent. The proposed method was effectively applied to solving large and small deformation problems implemented with 3D standard 8-node linear and 20-node quadratic elements and with immersed boundary elements in which a Cartesian grid is cut by the real geometry. The method was also tested for materials with elastic, elasto-plastic and hyperelastic behavior. The formulation is robust and simple and can converge to the exact solution with optimal convergence rates.

The results show an optimal convergence rate of the finite element solution for linear elements. For quadratic elements, the integration error can reduce the optimal convergence rate. To overcome this problem, the use of more quadrature points or a double pass strategy has been shown to be effective from the engineering point of view. The method has a user-dependent parameter \(\kappa \) to be defined. In the numerical examples we analyzed a wide range of variation of \(\kappa \) from 10 to 1000 and similar discretization errors and convergence of the iterations were obtained.

A double iterative process is defined to solve contact problems. The first loop is the contact iteration in which the stabilization stress is kept constant and the formulation is a pure penalty method, with \(\kappa \) as penalty constant. The convergence analysis of the method show that a relatively high value of the penalty parameter is needed to guarantee convergence. This value prevents the use of very large time step increments in which the initial penetration of the unconverged solution is very large, and can be considered as a limitation of the method.