On Densities of Lattice Arrangements Intersecting Every i-Dimensional Affine Subspace

Abstract

In 1978, Makai Jr. established a remarkable connection between the volume-product of a convex body, its maximal lattice packing density and the minimal density of a lattice arrangement of its polar body intersecting every affine hyperplane. Consequently, he formulated a conjecture that can be seen as a dual analog of Minkowski’s fundamental theorem, and which is strongly linked to the well-known Mahler-conjecture. Based on the covering minima of Kannan and Lovász and a problem posed by Fejes Tóth, we arrange Makai Jr.’s conjecture into a wider context and investigate densities of lattice arrangements of convex bodies intersecting every i-dimensional affine subspace. Then it becomes natural also to formulate and study a dual analog to Minkowski’s second fundamental theorem. As our main results, we derive meaningful asymptotic lower bounds for the densities of such arrangements, and furthermore, we solve the problems exactly for the special, yet important, class of unconditional convex bodies.

1 Introduction

A convex body is a compact convex full-dimensional set in the Euclidean space ${\mathbb {R}}^n$. We denote by ${\mathcal {K}}^n$ the family of all convex bodies in ${\mathbb {R}}^n$, and we write ${\mathcal {K}}^n_o$ for the subfamily of o-symmetric convex bodies $K\in {\mathcal {K}}^n$, that is, $K=-K$. Let ${\mathcal {L}}^n$ denote the set of full-dimensional lattices in ${\mathbb {R}}^n$, that is, discrete subgroups of ${\mathbb {R}}^n$ of full rank. Every lattice $\Lambda \in {\mathcal {L}}^n$ can be written as $\Lambda =A{\mathbb {Z}}^n$ for some invertible matrix $A\in {\mathrm {GL}}_n({\mathbb {R}})$. Let ${\mathcal {A}}_i({\mathbb {R}}^n)$ be the family of i-dimensional affine subspaces of ${\mathbb {R}}^n$. Given a subset $S\subseteq {\mathbb {R}}^n$ and a lattice $\Lambda \in {\mathcal {L}}^n$, we call $S+\Lambda =\bigcup _{z\in \Lambda }(S+z)$ a lattice arrangement. For more basic notation and background information on convex bodies and lattices, we refer to the textbooks by Gruber [18] and Martinet [29], respectively.

Our main interest in this paper concerns the so-called covering minima and their relation to the volume of a convex body. Motivated by a number of applications, for instance, to flatness theorems and to inhomogeneous simultaneous Diophantine approximation, these numbers have been formally introduced by Kannan and Lovász [22]¹: For a convex body $K\in {\mathcal {K}}^n$, a lattice $\Lambda \in {\mathcal {L}}^n$, and $i=1,\ldots ,n$, the i-th covering minimum (of K with respect to $\Lambda$) is defined as

$$\begin{aligned} \mu _i(K,\Lambda )=\inf \big \{\mu >0:\left( \mu K+\Lambda \right) \cap L\ne \emptyset \text { for all }L\in {\mathcal {A}}_{n-i}({\mathbb {R}}^n)\big \}. \end{aligned}$$

These numbers extend the classical notion of the covering radius $\mu _n(K,\Lambda )=\inf \{\mu >0:\mu K+\Lambda ={\mathbb {R}}^n\}$, which is also known as the inhomogeneous minimum (see [19, Sect. 13]).

The concept of lattice arrangements that intersect every $(n-i)$-dimensional affine subspace has been studied already before the work of Kannan and Lovász. In fact, generalizing the sphere covering problem, Fejes Tóth [12] proposed to determine the density of the thinnest lattice arrangement of solid spheres with this property (more on this in Sect. 2).

A basic result on lattice coverings, meaning lattice arrangements covering the whole space, is that their density is at least one. More precisely, for any $K\in {\mathcal {K}}^n$ and $\Lambda \in {\mathcal {L}}^n$, the density of $K+\Lambda$ is defined as

$$\begin{aligned} \delta (K,\Lambda )=\frac{{\mathrm {vol}}(K)}{\det (\Lambda )}, \end{aligned}$$

where ${\mathrm {vol}}(K)$ denotes the volume (Lebesgue-measure) of K and the determinant of the lattice $\Lambda =A{\mathbb {Z}}^n$. Now, if $K+\Lambda ={\mathbb {R}}^n$, then $\delta (K,\Lambda )\ge 1$, which can be equivalently formulated in the language of the covering radius as (cf. [19, Sect. 13.5])

$$\begin{aligned} \mu _n(K,\Lambda )^n\,{\mathrm {vol}}(K)&\ge \det (\Lambda ). \end{aligned}$$

(1)

The corresponding result for lattice packings, that is, lattice arrangements $K+\Lambda$ with the property that $({\mathrm {int}}(K)+x)\cap ({\mathrm {int}}(K)+y)=\emptyset$, for every $x,y\in \Lambda$, $x\ne y$, is the intuitively clear statement that their density is $\delta (K,\Lambda )\le 1$. In order to give an equivalent formulation that corresponds to (1), we introduce Minkowski’s successive minima, which are defined for any o-symmetric $K\in {\mathcal {K}}^n_o$ and any $\Lambda \in {\mathcal {L}}^n$ as

$$\begin{aligned} \lambda _i(K,\Lambda )=\min \big \{\lambda \ge 0:\dim (\lambda K\cap \Lambda )\ge i\big \},\quad \text {for }i=1,\ldots ,n. \end{aligned}$$

Here, $\dim (S)$ denotes the dimension of the affine hull of the set $S\subseteq {\mathbb {R}}^n$. For general $K\in {\mathcal {K}}^n$, one usually extends this definition by setting $\lambda _i(K,\Lambda ):=\lambda _i(\frac{1}{2}{\mathcal {D}}K,\Lambda )$, where ${\mathcal {D}}K=K-K$ is the difference body of K. Based on the fact that $K+\Lambda$ is a lattice packing if and only if $\lambda _1(K,\Lambda )\ge 2$ (cf. [18, Sect. 30]), one can reformulate the density statement for lattice packings as

$$\begin{aligned} \lambda _1(K,\Lambda )^n\,{\mathrm {vol}}(K)&\le 2^n\det (\Lambda ). \end{aligned}$$

(2)

In the case that K is o-symmetric, this inequality is known as Minkowski’s first fundamental theorem (cf. [18, Sect. 22] and [31, Sect. 30]). Minkowski strengthened his fundamental theorem by taking the whole sequence of successive minima into account. He formulated his result for o-symmetric convex bodies, but analogously to (2) it naturally extends to arbitrary $K\in {\mathcal {K}}^n$ and $\Lambda \in {\mathcal {L}}^n$, and reads as follows (cf. [18, Sect. 23] and [27]):

$$\begin{aligned} \lambda _1(K,\Lambda )\cdot \ldots \cdot \lambda _n(K,\Lambda ){\mathrm {vol}}(K)&\le 2^n\det (\Lambda ). \end{aligned}$$

(3)

The main motivation for our studies is a conjecture of Makai Jr. which is an analog of (1) for the first covering minimum and at the same time a polar version of Minkowski’s Theorem (2).

Conjecture 1.1

(Makai Jr. [25]) Let $K\in {\mathcal {K}}^n$ and let $\Lambda \in {\mathcal {L}}^n$. Then

$$\begin{aligned} \mu _1(K,\Lambda )^n\,{\mathrm {vol}}(K)&\ge \frac{n+1}{2^nn!}\det (\Lambda ), \end{aligned}$$

(4)

and equality can only hold if K is a simplex.

Moreover, if K is o-symmetric, then

$$\begin{aligned} \mu _1(K,\Lambda )^n\,{\mathrm {vol}}(K)&\ge \frac{1}{n!}\det (\Lambda ), \end{aligned}$$

(5)

and equality can only hold if K is a crosspolytope.

Makai Jr. showed that for the standard lattice $\Lambda ={\mathbb {Z}}^n$, equality in (4) holds for the simplex $T_n={\mathrm {conv}}\{e_1,\ldots ,e_n,-\mathbf{1}_n\}$ and in (5) for the crosspolytope $C_n^\star ={\mathrm {conv}}\{\pm e_1,\ldots ,\pm e_n\}$. Here, $e_i$ denotes the i-th coordinate unit vector and $\mathbf{1}_n=(1,\ldots ,1)^\intercal \in {\mathbb {R}}^n$ the all-one vector; we omit the subscript and only write $\mathbf{1}$ if the dimension is clear from the context.

Note that Makai Jr. did not state his conjecture in terms of $\mu _1(K,\Lambda )$ but rather in terms of what he calls non-separable arrangements, which are lattice arrangements that intersect every affine hyperplane. In order to explain why Makai Jr.’s conjecture would be a polar Minkowski theorem, we make use of an identity of Kannan and Lovász [21, Lem. (2.3)] that says that the first successive minimum is strongly dual to the first covering minimum. More precisely, for any $K\in {\mathcal {K}}^n_o$ and $\Lambda \in {\mathcal {L}}^n$, we have

$$\begin{aligned} \lambda _1(K,\Lambda )\mu _1(K^\star ,\Lambda ^\star )&=\frac{1}{2}, \end{aligned}$$

(6)

where $K^\star =\{x\in {\mathbb {R}}^n:x^\intercal y\le 1,\text { for all }y\in K\}$ is the polar body of K, and $\Lambda ^\star =\{x\in {\mathbb {R}}^n:x^\intercal y\in {\mathbb {Z}},\text { for all }y\in \Lambda \}$ is the polar lattice of $\Lambda$. By the definition of the first successive minimum, we have for any $K\in {\mathcal {K}}^n_o$,

$$\begin{aligned} \lambda _1(K,\Lambda )\ge 1\quad \text { if and only if }\quad {\mathrm {int}}(K)\cap \Lambda =\{0\}. \end{aligned}$$

Therefore, based on (6) we see that under the condition ${\mathrm {int}}(K)\cap \Lambda =\{0\}$, Minkowski’s Theorem (2) states that ${\mathrm {vol}}(K)\le 2^n\det (\Lambda )$, whereas the o-symmetric part of Conjecture 1.1 claims that

$$\begin{aligned} {\mathrm {vol}}(K^\star )&\ge \frac{2^n}{n!}\det (\Lambda ^\star ) \quad \text {for any }K\in {\mathcal {K}}^n_o\text { with }{\mathrm {int}}(K)\cap \Lambda =\{0\}. \end{aligned}$$

(7)

Yet another interpretation of Makai Jr.’s conjecture can be given in terms of the lattice width $\omega _\Lambda (K)=\min _{v\in \Lambda ^\star \setminus \{0\}}\omega (K,v)$ of K with respect to $\Lambda$, where $\omega (K,v)=\max _{x\in K}x^\intercal v-\min _{x\in K}x^\intercal v$ is the width of K in direction v. The identity (6) shows that $\mu _1(K,\Lambda )$ is reciprocal to $\omega _\Lambda (K)$ and hence (5) can be seen as a discrete analog to the obvious inequality ${\mathrm {vol}}(K)\ge \frac{\kappa _n}{2^n}\omega (K)^n$, for $K\in {\mathcal {K}}^n_o$, where $\omega (K)=\min _{u\in S^{n-1}}\omega (K,u)$ is the usual width of K and $\kappa _n=\pi ^{n/2}/\Gamma (n/2+1)$ is the volume of the Euclidean unit ball $B_n$.

Rather than attacking Conjecture 1.1 directly, our main objective is to embed Makai Jr.’s problem into a wider context that strengthens the analogy to the covering inequality (1) and the duality to Minkowski’s classical results. In the spirit of Fejes Tóth [12], we are interested in minimal densities of lattice arrangements with the more refined covering property captured by the i-th covering minimum. In particular, we investigate the following problem.

Problem 1.2

Find optimal constants $c_{1,n},\ldots ,c_{n,n}>0$ and $c_n>0$ that depend only on their indices, such that for any $K\in {\mathcal {K}}^n$ and $\Lambda \in {\mathcal {L}}^n$, one has

$$\begin{aligned} \mu _i(K,\Lambda )^n\,{\mathrm {vol}}(K)&\ge c_{i,n}\det (\Lambda ) \end{aligned}$$

(8)

for $i=1,\ldots ,n$, and

$$\begin{aligned} \mu _1(K,\Lambda )\cdot \ldots \cdot \mu _n(K,\Lambda ){\mathrm {vol}}(K)&\ge c_n\det (\Lambda ). \end{aligned}$$

(9)

Observe that the inequalities in Problem 1.2 are invariant under simultaneous transformations of K and $\Lambda$ by an invertible linear mapping. Therefore, we usually restrict our attention to the standard lattice $\Lambda ={\mathbb {Z}}^n$. The question (9) involving the whole sequence of covering minima was already posed by Betke et al. [8] and in the case $n=2$ answered by Schnell [33] (cf. Theorem 4.1). This inequality can be seen as a dual inequality to Minkowski’s second fundamental Theorem (3). For convenience, we call $\mu _1(K,\Lambda )\cdot \ldots \cdot \mu _n(K,\Lambda ){\mathrm {vol}}(K)/\det (\Lambda )$ the covering product of K (with respect to $\Lambda$).

Our contributions to Problem 1.2 focus on the one hand on determining meaningful first bounds on the optimal constants $c_{i,n}$ and $c_n$, and on the other hand, on solving it for a particular family of convex bodies. To be more precise, in Theorem 3.1 we obtain lower bounds of the type (8) that support the natural guess that $c_{i,n}$ is in order much bigger than $c_{j,n}$ for any $i>j$. Regarding the covering product, we prove in Theorem 4.3 that $c_n\ge 1/n!$, which is a necessary condition for (5), since the covering minima form a non-decreasing sequence, that is, $\mu _1(K,\Lambda )\le \ldots \le \mu _n(K,\Lambda )$. For the family of standard unconditional convex bodies, which are convex bodies that are symmetric with respect to every coordinate hyperplane, we derive the best possible bounds in (8) and (9), and characterize the extremal convex bodies (see Theorems 3.4 and 4.5). Finally, we argue in Sect. 4 that for general convex bodies the optimal constant in (9) is most likely given by $c_n=(n+1)/2^n$, and we exhibit a concrete example that has exponentially smaller covering product than any standard unconditional body. All these results show that, unlike for Minkowski’s inequalities (2) and (3), the problems (8) and (9) are independent from each other.

Before we discuss the details of the aforementioned findings, we survey known results and various connections of Makai Jr.’s conjecture to some notoriously difficult problems in convex and discrete geometry. Moreover, we illustrate the applicability of the polar Minkowski inequality by deriving a variant of a linear form theorem from a known case of Conjecture 1.1.

2 A Review of the Literature Around Makai Jr.’s Conjecture and an Application to Linear Forms

For the ease of presentation, we mostly restrict the discussion to the case of o-symmetric convex bodies in this section. There are analogous “non-symmetric” versions of the relations elaborated on below, which can easily be found in the cited literature. Specifically, Álvarez Paiva et al. [2, Sect. 3] provide detailed information for the general case.

There is a strong connection of Makai Jr.’s conjecture to a well-known problem regarding the volume-product of a convex body. Still an unsolved question today, Mahler conjectured in 1939 that for o-symmetric convex bodies $K\in {\mathcal {K}}^n_o$ the volume-product ${\mathrm {M}}(K)={\mathrm {vol}}(K){\mathrm {vol}}(K^\star )$ is minimized by the cube $C_n=[-1,1]^n$. In symbols,

$$\begin{aligned} {\mathrm {M}}(K)\ge {\mathrm {M}}(C_n)=\frac{4^n}{n!}. \end{aligned}$$

(10)

We refer the reader to [10] for a historical account of Mahler’s conjecture, an overview of the state of the art, and references to the original literature on partial results concerning (10) that we mention below.

Now, Makai Jr. [25, Thm. 1] proved the remarkable identity

$$\begin{aligned} {\mathrm {M}}(K)&=4^{n}\delta (K)\theta _1(K^\star ) \quad \text {for}\quad K\in {\mathcal {K}}^n_o, \end{aligned}$$

(11)

where $\delta (K)=\max \{\delta (K,\Lambda ):\Lambda \in {\mathcal {L}}^n, K+\Lambda \text { a packing}\}$ denotes the maximum density of a lattice packing of K, and $\theta _i(K)=\inf _{\Lambda \in {\mathcal {L}}^n}\delta (\mu _i(K,\Lambda )K,\Lambda )$ the infimum of the densities of lattice arrangements of K that intersect every $(n-i)$-dimensional affine subspace.² This relation shows that Mahler’s conjecture (10) is equivalent to $\delta (K)\theta _1(K^\star )\ge 1/n!$, a statement on densities of lattice arrangements.

In view of $\delta (K)\le 1$, for $K\in {\mathcal {K}}^n_o$, we see that Makai Jr.’s conjecture (5), which reformulates as $\theta _1(K)\ge 1/n!$, is a necessary condition for Mahler’s conjecture (10). In particular, partial results for the latter problem transfer to the former. For example, Conjecture 1.1 holds for $n=2$ (cf. [16, 25]). Moreover, its o-symmetric version (5), and hence the polar Minkowski inequality (7), hold for unconditional convex bodies, ellipsoids, zonotopes, and the respective polar bodies.

While the exact conjectured lower bound in (10) remains elusive, the asymptotic growth rate of the dimensional constant is well understood. The strongest result is due to Kuperberg [23], who showed that ${\mathrm {M}}(K)\ge \pi ^n/n!$, for any $K\in {\mathcal {K}}^n_o$. As a consequence one obtains the following asymptotic estimates in Makai Jr.’s problem. For any $K\in {\mathcal {K}}^n$ hold

$$\begin{aligned} \theta _1(K)&\ge \bigg (\frac{\pi }{8}\bigg )^n\frac{n+1}{2^nn!} \qquad \text {and}\qquad \theta _1(K)\ge \bigg (\frac{\pi }{4}\bigg )^n\frac{1}{n!} \quad \text {if }K\in {\mathcal {K}}^n_o. \end{aligned}$$

(12)

The first of these inequalities appears in Álvarez Paiva et al. [2, Thm. 2]. Note also that already Mahler [24] studied asymptotic estimates of this kind.

Conversely, it turns out that an affirmative answer to Makai Jr.’s conjecture implies good asymptotic results for Mahler’s problem, so that the two conjectures (5) and (10) are asymptotically equivalent. More precisely, one can use the famous Minkowski–Hlawka theorem (cf. [19, p. 202]), which is a reverse statement of Minkowski’s fundamental theorem (2), and obtain the bound ${\mathrm {M}}(K)\ge 2^n/n!$, under the assumption $\theta _1(K)\ge 1/n!$. Details on this relation have been discussed in [2].

Finally, we survey the very limited knowledge on the densities $\theta _i(K)$ for particular convex bodies K. The original problem of Fejes Tóth [12] concerns the densities $\theta _i(B_n)$. Since the volume-product ${\mathrm {M}}(B_n)$ is known explicitly, Makai Jr.’s identity (11) shows that determining $\theta _1(B_n)$ is equivalent to determining $\delta (B_n)$. This is the lattice sphere packing problem which is solved in dimension $n\le 8$ and $n=24$ (see [13] and [18, Sect. 29]). On the other hand, the lattice sphere covering problem is exactly the question on $\theta _n(B_n)$, being solved for $n\le 5$ (see [13]). The only known value of $\theta _i(B_n)$ for $i\notin \{1,n\}$ is $\theta _2(B_3)$ due to Bambah and Woods [4]; see Table 1.

Table 1 Densities of lattice arrangements of $B_n$ in small dimensions

Since the cube admits a lattice packing that covers the whole space, we have $\delta (C_n)=\theta _n(C_n)=1$ and hence via (11) and ${\mathrm {M}}(C_n)=4^n/n!$, we find $\theta _1(C_n^\star )=1/n!$. Exchanging the roles of $C_n$ and $C_n^\star$ leads to a difficult problem for which only recently the first non-trivial results were proven. In [14] it was shown that there is an absolute constant $c>0$ such that $\delta (C_n^\star )\le c\cdot 0.8685^n$, and hence $\theta _1(C_n)\ge c \cdot 1.1514^n/n!$.

We end this discussion by posing a concrete and probably managable problem on these densities:

$$\begin{aligned} \text {Is it true that }\theta _{n-1}(C_n)=1/2\text { for every }n\ge 2\,? \end{aligned}$$

The conjectured value 1 / 2 would be realized by the chessboard lattice $\Lambda _o=\{x\in {\mathbb {Z}}^n:x_1+\cdots +x_n \equiv 0 \text { mod }2\}$ that also appears at the end of Sect. 3. A closely related problem is the chessboard conjecture of Fejes Tóth, which was proved by Böröczky et al. [9]. It states that the density of $K+\Lambda$ is at least 1 / 2 provided that every connected component of ${\mathbb {R}}^n\setminus (K+\Lambda )$ is bounded. Furthermore, it suggests that $\theta _{n-1}(K)\ge 1/2$, for every o-symmetric convex body $K\in {\mathcal {K}}^n_o$.

2.1 An Application to Linear Forms

Minkowski successfully applied his fundamental theorem (2) to questions concerning solutions of inequalities involving linear forms; a benchmark example is his “linear form theorem” (cf. [18, Cor. 22.2]). It works best in situations where the volume of the underlying convex body that describes the problem at hand, can be explicitly computed. It should come as no surprise that an affirmative answer to Makai Jr.’s conjecture (5) would be equally useful to solve questions in which the volume of the polar body can be controlled. An illustrating example is the following.

Theorem 2.1

Consider n linear homogeneous forms $\ell _i(x)=a_i^\intercal x$, for some $a_1,\ldots ,a_n\in {\mathbb {R}}^n$, of determinant $\det (A)=\det (a_1,\ldots ,a_n)\ne 0$. Then, there exists a non-zero integral vector $x\in {\mathbb {Z}}^n\setminus \{0\}$ such that

For small dimensions one can provide sharp bounds:

If $n=2$, there exists a non-zero integral vector $x\in {\mathbb {Z}}^n\setminus \{0\}$ such that

The forms $\ell _1(x)=x_1-2x_2$, $\ell _2(x)=x_1+x_2$ show that the constant on the right hand side cannot be improved.

If $n=3$, there exists a non-zero integral vector $x\in {\mathbb {Z}}^n\setminus \{0\}$ such that

The forms $\ell _1(x)=3x_1+3x_2-4x_3$, $\ell _2(x)=3x_1-4x_2+3x_3$, and $\ell _3(x)=-4x_1+3x_2+3x_3$ show the minimality of the constant.

Proof

Consider the zonotope $Z_n=[-1,1]^n+[-\mathbf{1},\mathbf{1}]$. This is an o-symmetric convex body whose volume can be computed by dissecting $Z_n$ into $n+1$ parallelepipeds, and which is given by ${\mathrm {vol}}(Z_n)=(n+1)2^n$ (see [6, Chap. 9]). Denoting the norm function of $K\in {\mathcal {K}}^n_o$ by $\Vert y\Vert _K=\min \{\lambda \ge 0:y\in \lambda K\}$, we have

where $h_{Z_n}(x)=\max _{y\in Z_n}x^\intercal y$, $x\in {\mathbb {R}}^n$, is the support function of  $Z_n$ (see [18]). Therefore, for any $\tau \ge 0$, we have

By the formulation of (5) as a polar Minkowski’s Theorem (7) and its validity for polars of zonotopes, we get that $\tau A^{-1} Z_n^\star$ contains a non-zero integral vector $x\in {\mathbb {Z}}^n$, if

This holds if and only if , implying the claim for arbitrary n.

For $n\in \{2,3\}$, the density of a densest lattice packing of $Z_n^\star$ is known, and moreover, we can compute the volume of $Z_n^\star$ explicitly. These facts enable us to use Minkowski’s fundamental theorem instead of (7) and they lead to the sharp bounds stated in the theorem. By definition of the density $\delta (Z_n^\star )$ one can introduce it as a parameter in (2) and obtain that $\lambda _1(Z_n^\star ,{\mathbb {Z}}^n)^n{\mathrm {vol}}(Z_n^\star )\le 2^n\delta (Z_n^\star )$ (cf. [19, Sect. 20.1]). Since the density $\delta (Z_n^\star )$ is invariant under invertible linear transformations, this inequality guarantees the existence of a non-zero integral vector in $\tau A^{-1}Z_n^\star$ as long as

(13)

Now, $Z_2^\star$ is a hexagon of volume ${\mathrm {vol}}(Z_2^\star )=3/4$ which tiles the plane by translations of the lattice $\frac{1}{2}\big ({\begin{matrix}1&{}-2\\ 1&{}1\end{matrix}}\big ){\mathbb {Z}}^2$. Hence, $\delta (Z_2^\star )=1$, and (13) gives the condition . This implies the claimed bound, for $n=2$. The extremal example can be read off from the lattice that realizes $\delta (Z_2^\star )$.

In the case $n=3$, we find that $Z_3^\star$ is the cubeoctahedron, which is an Archimedean polytope with 12 vertices and volume ${\mathrm {vol}}(Z_3^\star )=5/12$. A densest lattice packing of $Z_3^\star$ has been computed by Betke and Henk [7, Sect. 5]. After a linear transformation of our coordinates of the cubeoctahedron, their result shows that $\delta (Z_3^\star )=45/49$, and this density is realized by the lattice with basis $(1/6)\cdot \big \{(3,3,-4)^\intercal ,(3,-4,3)^\intercal ,(-4,3,3)^\intercal \big \}$. Analogously to the case $n=2$, we use this information together with (13) in order to obtain the desired bound and an extremal example. $\square$

3 Results Concerning Inequalities of the Form (8)

In this section, we are concerned with the study of lower bounds on the functionals $\mu _i(K,\Lambda )^n\,{\mathrm {vol}}(K) / \det (\Lambda )$. Before we state and prove our results, we discuss some fundamental facts on covering minima.

It is clear that, by compactness of $K\in {\mathcal {K}}^n$, we can replace the infimum in the definition of the covering radius $\mu _n(K,\Lambda )$ by a minimum. However, the fact that this is possible for every covering minimum $\mu _i(K,\Lambda )$, $i=1,\ldots ,n$, is not immediate to see and needs a subtle argument³. The proof of Kannan and Lovász [22, Lem. 2.2] moreover shows that the i-th covering minimum admits an equivalent description via projections: For a lattice $\Lambda \in {\mathcal {L}}^n$ we denote by ${\mathcal {L}}_i(\Lambda )$ the family of i-dimensional lattice planes of $\Lambda$, that is, linear subspaces of ${\mathbb {R}}^n$ that are spanned by vectors of $\Lambda$. Denoting by S|L the orthogonal projection of $S\subseteq {\mathbb {R}}^n$ onto a linear subspace L, they prove in [22, Rem. 1] that

$$\begin{aligned} \mu _i(K,\Lambda )&=\max \big \{\mu _i(K|L, \Lambda |L):L\in {\mathcal {L}}_i(\Lambda )\big \}. \end{aligned}$$

(14)

Note that $\Lambda |L$ is a lattice in the subspace $L\in {\mathcal {L}}_i(\Lambda )$, so that it makes sense to compute the covering radius of K|L with respect to this lattice.

As explained in the introduction, there is no loss of generality in restricting the consideration to the standard lattice ${\mathbb {Z}}^n$ in Problem 1.2. For the sake of brevity, we write $\mu _i(K)=\mu _i(K,{\mathbb {Z}}^n)$, and also $\lambda _i(K)=\lambda _i(K,{\mathbb {Z}}^n)$, in this case, for any $K\in {\mathcal {K}}^n$ and any $i\in [n]:=\{1,\ldots ,n\}$. We start our discussion with first general bounds of the form (8).

Theorem 3.1

• (i) Let $K\in {\mathcal {K}}^n_o$. There exists a constant ${\mathrm {Flt}}(n)$ only depending on n such that, for any $i\in [n]$,

  $$\begin{aligned} \mu _i(K)^n{\mathrm {vol}}(K)\ge \frac{i!}{n!}\,{\mathrm {Flt}}(n)^{-(n-i)}. \end{aligned}$$

  In particular, we can choose ${\mathrm {Flt}}(n)=c\,n(1+\log {n})$, for some $c>0$.

• (ii) Let $K\in {\mathcal {K}}^n$ be such that $\mu _i(K)K+{\mathbb {Z}}^n$ contains every i-dimensional coordinate plane. Then

  $$\begin{aligned} \mu _i(K)^n{\mathrm {vol}}(K)\ge \frac{i!^{{n}/{i}}}{n!}. \end{aligned}$$

Proof

(i) First of all, Jarník’s inequality [20] (cf. [22, Lem. (2.4)]) claims that $\lambda _n(K)/2\le \mu _n(K)$. In view of the flatness theorem there is a constant ${\mathrm {Flt}}(n)$ only depending on n such that $\mu _n(K)\le {\mathrm {Flt}}(n)\mu _1(K)$ (cf. [22, Thm. (2.7)]). Therefore, $\lambda _n(K)\le 2{\mathrm {Flt}}(n)\mu _1(K)$, and since $\lambda _i(K)$ and $\mu _i(K)$ form non-decreasing sequences with respect to $i\in [n]$, we get $\lambda _{n-i}(K)\le 2{\mathrm {Flt}}(n)\mu _i(K)$. This means that there is an $(n-i)$-dimensional lattice plane $L\in {\mathcal {L}}_{n-i}({\mathbb {Z}}^n)$ and linearly independent vectors $a_1,\ldots ,a_{n-i}\in {\mathbb {Z}}^n\cap L$, such that the crosspolytope ${\mathrm {conv}}\{\pm a_1,\ldots ,\pm a_{n-i}\}$ is contained in the body $2{\mathrm {Flt}}(n)\mu _i(K) K\cap L$. Thus,

$$\begin{aligned} {\mathrm {vol}}_{n-i}(K\cap L)&\ge \bigg (\frac{1}{2{\mathrm {Flt}}(n)\mu _i(K)} \bigg )^{n-i}\frac{2^{n-i}}{(n-i)!}\det ({\mathbb {Z}}^n\cap L), \end{aligned}$$

(15)

where, for any Lebesgue-measurable set $S\subseteq {\mathbb {R}}^n$ with $\dim (S)=i$, we denote by ${\mathrm {vol}}_i(S)$ the volume of S computed in its affine hull. Let $L^\perp$ be the orthogonal complement of L. By (14), we have $\mu _i(K)\ge \mu _i(K|L^\perp ,{\mathbb {Z}}^n|L^\perp )$, and applying inequality (1) to the projected body $K|L^\perp$ and the projected lattice ${\mathbb {Z}}^n|L^\perp$, we obtain

$$\begin{aligned} \mu _i(K)^i\,{\mathrm {vol}}_i(K|L^\perp )&\ge \det ({\mathbb {Z}}^n|L^\perp ). \end{aligned}$$

(16)

Finally, we utilize an inequality of Rogers and Shephard [32, Thm. 1], which states that

$$\begin{aligned} {\mathrm {vol}}_{n-i}(K\cap L){\mathrm {vol}}_i(K|L^\perp )\le \left( {\begin{array}{c}n\\ i\end{array}}\right) {\mathrm {vol}}(K). \end{aligned}$$

(17)

Putting together (15), (16), and (17), and using $\det ({\mathbb {Z}}^n\cap L)\det ({\mathbb {Z}}^n|L^\perp )=\det ({\mathbb {Z}}^n)=1$ (see [29, Prop. 1.9.7]), we arrive at

$$\begin{aligned} \mu _i(K)^n\,{\mathrm {vol}}(K)&\ge \frac{\mu _i(K)^n\,{\mathrm {vol}}_i(K|L^\perp ) {\mathrm {vol}}_{n-i}(K\cap L)}{\left( {\begin{array}{c}n\\ i\end{array}}\right) \det ({\mathbb {Z}}^n|L^\perp )\det ({\mathbb {Z}}^n\cap L)}\\&\ge \frac{\mu _i(K)^{n-i}}{\left( {\begin{array}{c}n\\ i\end{array}}\right) }\,\frac{1}{\big ({\mathrm {Flt}}(n) \mu _i(K)\big )^{n-i}(n-i)!}=\frac{i!}{n!}\,{\mathrm {Flt}}(n)^{-(n-i)}. \end{aligned}$$

Due to a result of Banaszczyk [5], we can choose ${\mathrm {Flt}}(n)=c\,n(1+\log {n})$, for some absolute constant $c>0$.

(ii) For $J\subseteq [n]$, let $L_J={\mathrm {lin}}\{e_j:j\in J\}$ be the linear subspace spanned by $e_j$, $j\in J$. An inequality of Meyer [30] states that, for all $i\in [n]$, we have

$$\begin{aligned} \big (n!{\mathrm {vol}}(K)\big )^{{i}/{n}}\ge i!\Bigg (\prod _{J \subseteq [n], |J|=i}{\mathrm {vol}}_i(K\cap L_J)\Bigg )^{1/{\left( {\begin{array}{c}n\\ i\end{array}}\right) }}. \end{aligned}$$

By assumption, every i-dimensional coordinate hyperplane $L_J$, $J \subseteq [n]$, $|J|=i$, is covered by the translates $\mu _i(K)K+{\mathbb {Z}}^n$. Therefore, by (1) we have that ${\mathrm {vol}}_i\big (\mu _i(K)K\cap L_J\big )\ge 1$. Hence, Meyer’s inequality gives us

$$\begin{aligned} \mu _i(K)^n\,{\mathrm {vol}}(K)&={\mathrm {vol}}(\mu _i(K)K)\ge \frac{i!^{{n}/{i}}}{n!}, \end{aligned}$$

as desired. $\square$

Remark 3.2

• (i) For $k\in {\mathbb {N}}$ a constant, Theorem 3.1 (i) yields a lower bound of the type $\mu _{n-k}(K)^n\,{\mathrm {vol}}(K)\ge c/(n^{2k}(\log {n})^k)$ which dramatically improves upon the bound that follows from the monotonicity of the $\mu _i(K)$ and the known asymptotic bounds (12) on $\mu _1(K)^n\,{\mathrm {vol}}(K)$.

• (ii) The case $i=1$ in Theorem 3.1 (ii) is included in the more general setting that $\mu _1(K)K+{\mathbb {Z}}^n$ is connected, which has been studied in [15, 17].

Our next goal is to derive sharp lower bounds on $\mu _i(K)^n\,{\mathrm {vol}}(K)$ on a particular family of convex bodies K. Before we state our result, we introduce and investigate a family of polytopes that interpolates between the cube and the crosspolytope. For every $i\in [n]$, let

$$\begin{aligned} P_{n,i}={\mathrm {conv}}\left\{ \pm e_{j_1}\pm \cdots \pm e_{j_i}:1\le j_1<\cdots <j_i\le n\right\} =C_n\cap iC_n^\star . \end{aligned}$$

Note that $P_{n,n}=C_n$ and $P_{n,1}=C_n^\star$. Moreover, $P_{3,2}$ is the cubeoctahedron and $P_{4,2}$ is the 24-cell. The facet $P_{n,i}\cap \{x\in {\mathbb {R}}^n:x_1+\cdots +x_n=i\}$ of $P_{n,i}$ is known as the i-th hypersimplex and usually denoted by $\Delta _{n-1}(i)$ (see [35, Ex. 0.11] for more information and the origin of these interesting polytopes). We may therefore think of the $P_{n,i}$ as the symmetric cousins of the hypersimplices. The covering minima and the volume of these special polytopes can be computed explicitly as follows.

Proposition 3.3

• (i) For $i\in [n]$, we have

  $$\begin{aligned} \mu _j(P_{n,i})=\frac{1}{2} \,\,\text { for }j\le i \quad \text {and}\quad \mu _j(P_{n,i})=\frac{j}{2i}\,\, \text { for }j>i. \end{aligned}$$

  In particular, $\mu _i(C_n)=1/2$ and $\mu _i(C_n^\star )=i/2$, for all $i\in [n]$.

• (ii) For $i\in [n]$, we have⁴

  $$\begin{aligned} {\mathrm {vol}}(P_{n,i})=\frac{2^n}{n!}\sum _{k=0}^i(-1)^k\left( {\begin{array}{c}n\\ k\end{array}}\right) (i-k)^n. \end{aligned}$$

Proof

(i) Let $j\in \{1,\ldots ,i\}$ and let $L_j$ be a j-dimensional coordinate subspace. Then, $P_{n,i}|L_j=P_{n,i}\cap L_j=C_j$, where we identify $L_j$ with ${\mathbb {R}}^j$. Since also $L_j\subseteq \frac{1}{2} P_{n,i}+{\mathbb {Z}}^n$, we get $\mu _j(P_{n,i})=1/2$. For the case $j\in \{i+1,\ldots ,n\}$, we first note that since $P_{n,i}\subseteq C_n$ and $(i/n,\ldots ,i/n)$ lies in the boundary of $P_{n,i}$, we have $\mu _n(P_{n,i})=n/(2i)$. Using that $P_{n,i}|L_j=P_{j,i}$, for all j-dimensional coordinate subspaces $L_j$, this implies $\mu _j(P_{n,i})=j/(2i)$.

(ii) It is known that (see [34] for instance), for any $k\in [n]$,

$$\begin{aligned} {\mathrm {vol}}\Big ([0,1]^n\cap \Big \{x\in {\mathbb {R}}^n:k-1\le \sum _{i=1}^nx_i\le k\Big \}\Big )=\frac{1}{n!}\,A_{n,k}, \end{aligned}$$

where $A_{n,k}$ denotes the Eulerian numbers. Therefore,

$$\begin{aligned} {\mathrm {vol}}(P_{n,i})&=2^n{\mathrm {vol}}\Big ([0,1]^n\cap \Big \{x\in {\mathbb {R}}^n:0\le \sum _{i=1}^nx_i\le i\Big \}\Big )=\frac{2^n}{n!}\sum _{k=1}^iA_{n,k}, \end{aligned}$$

(18)

which implies the desired formula in view of the identity (cf. [6, Chap. 2])

$$\begin{aligned} A_{n,k}=\sum _{j=0}^k(-1)^j\left( {\begin{array}{c}n+1\\ j\end{array}}\right) (k-j)^n \end{aligned}$$

and routine algebraic manipulations. $\square$

Now, recall that a convex body $K\in {\mathcal {K}}^n_o$ is called standard unconditional if for every $x\in K$, we have $(\pm x_1,\ldots ,\pm x_n)\in K$, that is, K is symmetric with respect to every coordinate hyperplane. Observe that by construction the polytopes $P_{n,i}$ are standard unconditional.

Theorem 3.4

Let $K\in {\mathcal {K}}^n_o$ be standard unconditional and let $i\in [n]$. Then,

$$\begin{aligned} \mu _i(K)^n\,{\mathrm {vol}}(K)\ge \mu _i(P_{n,i})^n\,{\mathrm {vol}}(P_{n,i}). \end{aligned}$$

Equality holds if and only if K is a dilate of $P_{n,i}$.

Proof

As before, for $i\in [n]$ and $J \subseteq [n]$, $|J|=i$, we let $L_J={\mathrm {lin}}\{e_j:j\in J\}$. By the unconditionality of K, we get $K|L_J=K\cap L_J$, and furthermore ${\mathbb {Z}}^n|L_J={\mathbb {Z}}^n\cap L_J={\mathbb {Z}}^i$, where we identify $L_J$ with ${\mathbb {R}}^i$. Since the claimed inequality is invariant under scalings of K, we may assume that

$$\begin{aligned} \mu _i(K)=\max \left\{ \mu _i(K|L,{\mathbb {Z}}^n|L):L\in {\mathcal {L}}_i({\mathbb {Z}}^n)\right\} =1. \end{aligned}$$

Then, clearly $\mu _i(K|L_J,{\mathbb {Z}}^n|L_J)\le 1$, which, by the above observations, means that $(K\cap L_J)+({\mathbb {Z}}^n\cap L_J)$ covers $L_J$, for all $J \subseteq [n]$, $|J|=i$. The body $K\cap L_J$ is a standard unconditional body in $L_J$. Therefore, the covering property yields that $\frac{1}{2}\sum _{j\in J}e_j\in K\cap L_J\subseteq K$, for all $J \subseteq [n]$, $|J|=i$. By the definition of $P_{n,i}$, we see that $\frac{1}{2} P_{n,i}\subseteq K$, and hence, using Proposition 3.3  (i), ${\mathrm {vol}}(K)\ge {\mathrm {vol}}(\frac{1}{2} P_{n,i})=\mu _i(P_{n,i})^n\,{\mathrm {vol}}(P_{n,i})$ as desired.

Equality holds if and only if $K=\frac{1}{2} P_{n,i}$ which implies the claimed equality case characterization because we assumed that $\mu _i(K)=1$. $\square$

Since the cases $i=n$ and $i=1$ of Theorem 3.4 correspond exactly to (1) and (5), respectively, it is tempting to conjecture that the polytopes $P_{n,i}$ minimize the functional $\mu _i(K)^n\,{\mathrm {vol}}(K)$ on the whole class ${\mathcal {K}}^n_o$ of o-symmetric convex bodies. However, the following examples show that this is not the case in general: Consider the chessboard lattice

$$\begin{aligned} \Lambda _o=\big \{x\in {\mathbb {Z}}^n:x_1+\cdots +x_n\equiv 0\text { mod }2\big \}, \end{aligned}$$

which is a sublattice of ${\mathbb {Z}}^n$ of determinant $\det (\Lambda _o)=2$ (see [29, Chap. 4]). We leave it to the reader to check that $\frac{1}{2}C_n+\Lambda _o$ intersects every line and $C_n^\star +\Lambda _o$ intersects every $(n-2)$-dimensional affine subspace (cf. [22, p. 588]). Moreover, we cannot shrink $\frac{1}{2}C_n$ or $C_n^\star$ in order to maintain the corresponding intersection property, and hence $\mu _{n-1}(C_n,\Lambda _o)=1/2$ and $\mu _2(C_n^\star ,\Lambda _o)=1$. In view of Proposition 3.3, equation (18) and $\sum _{k=1}^nA_{n,k}=n!$, we obtain

$$\begin{aligned} \mu _{n-1}(P_{n,n-1})^n\,{\mathrm {vol}}(P_{n,n-1})=\frac{n!-1}{n!} >\frac{1}{2}=\mu _{n-1}(C_n,\Lambda _o)^n\,\frac{{\mathrm {vol}}(C_n)}{\det (\Lambda _o)}, \end{aligned}$$

and

$$\begin{aligned} \mu _2(P_{n,2})^n\,{\mathrm {vol}}(P_{n,2})=\frac{2^n-n}{n!}>\frac{2^{n-1}}{n!} =\mu _2(C_n^\star ,\Lambda _o)^n\,\frac{{\mathrm {vol}}(C_n^\star )}{\det (\Lambda _o)}, \end{aligned}$$

for every $n\ge 3$.

4 Results Concerning the Covering Product

In this section, we are interested in the dual version of Minkowski’s inequality (3), that is, in lower bounds on the covering product (9) in Problem 1.2. For the case of planar convex bodies this was completely solved by Schnell [33]. His result shows that, unlike Conjecture 1.1, the covering product does not distinguish between o-symmetric and general convex bodies.

Theorem 4.1

(Schnell [33]) For any $K\in {\mathcal {K}}^2$, one has

$$\begin{aligned} \mu _1(K)\mu _2(K){\mathrm {vol}}(K)\ge \frac{3}{4}. \end{aligned}$$

Equality holds, up to transformations that do not change the covering product, exactly for one triangle, one parallelogram, one trapezoid, one pentagon, and one hexagon.

In the proof of [22, Lem. (2.5)], the authors derive the following very useful property. Because the arguments are somewhat implicitly given in [22], we provide the reader with a short proof.

Lemma 4.2

Let $K\in {\mathcal {K}}^n$ and let $j\in [n]$. Then

$$\begin{aligned} \mu _j(K)\ge \mu _j(K|L,{\mathbb {Z}}^n|L) \end{aligned}$$

for every lattice plane $L\in {\mathcal {L}}_i({\mathbb {Z}}^n)$ of dimension $i\ge j$.

Proof

Let $i\ge j$ and let $L\in {\mathcal {L}}_i({\mathbb {Z}}^n)$. Assume that $\mu _j(K)=1$, that is, every $(n-j)$-dimensional affine subspace intersects $K+{\mathbb {Z}}^n$. Now, let M be an $(i-j)$-dimensional affine subspace in L. Consider the subspace $M'$ that is the preimage of M under the projection onto L, in symbols, $M'=M\oplus L^\perp$. Clearly, $M'$ is an $(n-j)$-dimensional subspace in ${\mathbb {R}}^n$. By assumption it must intersect $K+{\mathbb {Z}}^n$, and hence $M\cap (K|L+{\mathbb {Z}}^n|L)=(M'\cap (K+{\mathbb {Z}}^n))|L\ne \emptyset$. Therefore, $\mu _j(K)=1\ge \mu _j(K|L,{\mathbb {Z}}^n|L)$ as desired. $\square$

With the help of this lemma we can give a lower bound on the covering product of an arbitrary convex body $K\in {\mathcal {K}}^n$, which, in view of the monotonicity of the sequence of covering minima, is a necessary inequality for Conjecture 1.1 (5) to hold.

Theorem 4.3

Let $K\in {\mathcal {K}}^n$. Then

$$\begin{aligned} \mu _1(K)\cdot \ldots \cdot \mu _n(K){\mathrm {vol}}(K)\ge \frac{1}{n!}. \end{aligned}$$

Proof

Recall that ${\mathcal {D}}K=K-K$ denotes the difference body of K. From Jarník’s inequality [20, 22] we know that $\mu _n(K)\ge \lambda _n({\mathcal {D}}K) \ge \lambda _1({\mathcal {D}}K)$. In particular, there exists a vector $z\in \mu _n(K){\mathcal {D}}K\cap ({\mathbb {Z}}^n\setminus \{0\})$. This means that there are points $x,y\in K$ such that $z=\mu _n(K)(x-y)$. Hence, putting $L_z={\mathrm {lin}}\{z\}$, the line $L=y+L_z$ passing through x and y satisfies

$$\begin{aligned} {\mathrm {vol}}_1(K\cap L)\ge \Vert x-y\Vert =\frac{\Vert z\Vert }{\mu _n(K)}\ge \frac{\det ({\mathbb {Z}}^n\cap L_z)}{\mu _n(K)}. \end{aligned}$$

By Lemma 4.2, it holds $\mu _j(K)\ge \mu _j(K|L_z^\perp ,{\mathbb {Z}}^n|L_z^\perp )$, for every $j=1,\ldots ,n-1$. Based on these observations and the inequality (17) of Rogers and Shephard with respect to the line L, we obtain inductively, that

$$\begin{aligned} \mu _1(K)&\cdot \ldots \cdot \mu _n(K){\mathrm {vol}}(K)\\&\ge \frac{1}{n}\,\frac{\mu _1(K)\cdot \ldots \cdot \mu _{n-1}(K) {\mathrm {vol}}_{n-1}(K|L^\perp )}{\det ({\mathbb {Z}}^n|L_z^\perp )}\,\frac{\mu _n(K) {\mathrm {vol}}_1(K\cap L)}{\det ({\mathbb {Z}}^n\cap L_z)}\\&\ge \frac{1}{n}\,\frac{\mu _1(K|L_z^\perp ,{\mathbb {Z}}^n|L_z^\perp )\cdot \ldots \cdot \mu _{n-1}(K|L_z^\perp ,{\mathbb {Z}}^n|L_z^\perp ){\mathrm {vol}}_{n-1}(K|L_z^\perp )}{\det ({\mathbb {Z}}^n|L_z^\perp )}\\&\ge \frac{1}{n}\,\frac{1}{(n-1)!}=\frac{1}{n!}. \end{aligned}$$

We also used the identity $\det ({\mathbb {Z}}^n\cap L_z)\det ({\mathbb {Z}}^n|L_z^\perp )=\det ({\mathbb {Z}}^n)=1$ again. $\square$

Remark 4.4

Based on Theorem 3.1 (i) (cf. Remark 3.2) one can slightly improve the lower bound 1 / n! in Theorem 4.3 to roughly $(1/n!)^{(n-k)/n}$, for any o-symmetric $K\in {\mathcal {K}}^n_o$ and any fixed constant $k\in {\mathbb {N}}$.

This is meaningful because it shows that (for o-symmetric convex bodies) Makai Jr.’s conjecture Conjecture 1.1 is independent from Problem 1.2 (9).

The lower bound in Theorem 4.3 improves drastically on the family of standard unconditional bodies. Indeed, we prove a sharp bound on this class and illustrate that there are infinitely many non-equivalent extremal examples. Before we can state and prove our result, we need to recall the concept of the barycentric subdivision of the cube which is a standard way to obtain a triangulation. We refer to [35] for basic notions on convex polytopes. Let

$$\begin{aligned} {\mathcal {F}}_n=\big \{(F_0,F_1,\ldots ,F_{n-1}):F_j\text { a }j\text {-face of } C_n, F_0\subseteq F_1\subseteq \cdots \subseteq F_{n-1}\big \} \end{aligned}$$

be the set of flags of $C_n$. There are exactly $n!\,2^n$ flags of the cube. The barycenter ${\mathrm {b}}(F_j)$ of a j-face of $C_n$ has the form ${\mathrm {b}}(F_j)=\pm e_{i_1} \pm \cdots \pm e_{i_{n-j}}$, for some $1\le i_1< i_2< \cdots < i_{n-j} \le n$. The barycentric subdivision of $C_n$ is the triangulation induced by the simplices $S_F={\mathrm {conv}}\{0,{\mathrm {b}}(F_0),{\mathrm {b}}(F_1),\ldots ,{\mathrm {b}}(F_{n-1})\}$, $F=(F_0,F_1,\ldots ,F_{n-1})\in {\mathcal {F}}_n$.

Theorem 4.5

Let $K\in {\mathcal {K}}^n_o$ be a standard unconditional body. Then,

$$\begin{aligned} \mu _1(K)\cdot \ldots \cdot \mu _n(K){\mathrm {vol}}(K)\ge 1. \end{aligned}$$

Equality holds if and only if

$$\begin{aligned} K=\bigcup _{F\in {\mathcal {F}}_n}S_F(K), \end{aligned}$$

where $S_F(K)={\mathrm {conv}}\big \{0,\frac{1}{2\mu _n(K)}\,{\mathrm {b}}(F_0),\frac{1}{2\mu _{n-1}(K)}\,{\mathrm {b}}(F_1),\ldots ,\frac{1}{2\mu _1(K)}\,{\mathrm {b}}(F_{n-1})\big \}$, for every $F=(F_0,F_1,\ldots ,F_{n-1})\in {\mathcal {F}}_n$.

Proof

For the sake of brevity, for any $i\in [n]$, we write $\mu _i=\mu _i(K)$. From the proof of Theorem 3.4, we infer $\frac{1}{2} P_{n,i}\subseteq \mu _i\cdot K$, for $i\in [n]$. In view of the vertex description $P_{n,i}={\mathrm {conv}}\{\pm e_{j_1}\pm \cdots \pm e_{j_i}:1\le j_1<\cdots <j_i\le n\}$, every point $\frac{1}{2\mu _i}(\pm e_{j_1}\pm \cdots \pm e_{j_i})$, for $1\le j_1<\cdots <j_i\le n$ and $i\in [n]$, belongs to K. Therefore, using the notation introduced above, the simplex

$$\begin{aligned} S_F(K)={\mathrm {conv}}\bigg \{0,\frac{1}{2\mu _n}\,{\mathrm {b}}(F_0),\frac{1}{2\mu _{n-1}} \,{\mathrm {b}}(F_1),\ldots ,\frac{1}{2\mu _1}\,{\mathrm {b}}(F_{n-1})\bigg \} \subseteq K, \end{aligned}$$

for every flag $F=(F_0,F_1,\ldots ,F_{n-1})\in {\mathcal {F}}_n$ of $C_n$. Since these simplices arise from the simplices $S_F$ of the barycentric subdivision of $C_n$ by dilating vertices, they are pairwise non-overlapping. Moreover, by the symmetry of the cube and the barycentric subdivision, all the simplices $S_F(K)$, $F\in {\mathcal {F}}_n$, are congruent.

Let $F'\in {\mathcal {F}}_n$ be the flag corresponding to the faces of $C_n$ whose barycenters are given by $e_1,e_1+e_2,\ldots ,e_1+\cdots +e_n$. A simple volume computation shows that the simplex $S_{F'}(K)={\mathrm {conv}}\big \{0,\frac{1}{2\mu _1}\,e_1,\frac{1}{2\mu _2}\,(e_1+e_2),\ldots ,\frac{1}{2\mu _n}\,(e_1+\cdots +e_n)\big \}$ has volume $(n!\,2^n\mu _1\cdot \ldots \cdot \mu _n)^{-1}$. Thus, defining $Q_K=\bigcup _{F\in {\mathcal {F}}_n}S_F(K)\subseteq K$, we arrive at the claimed inequality

$$\begin{aligned} {\mathrm {vol}}(K)\ge {\mathrm {vol}}(Q_K)=n!\,2^n\,{\mathrm {vol}}(S_{F'}(K))=\frac{1}{\mu _1\cdot \ldots \cdot \mu _n}. \end{aligned}$$

Since the only step where we could lose volume is in the inclusion $Q_K\subseteq K$, we immediately see that equality holds if and only if $K=Q_K$. $\square$

Remark 4.6

The cube $C_n=P_{n,n}$ and the crosspolytope $C_n^\star =P_{n,1}$ are the only bodies among the $P_{n,i}$ that attain equality in Theorem 4.5. This is due to the fact that for $i\notin \{1,n\}$ the points $\frac{1}{2\mu _1(P_{n,i})}\,e_1=e_1$ and $\frac{1}{2\mu _n(P_{n,i})}\,(e_1+\cdots +e_n)=\frac{i}{n}\,(e_1+\cdots +e_n)$ are contained in different facets of $P_{n,i}$. Hence, the line segment connecting these two points is not contained in the boundary of $P_{n,i}$, so that the simplices $S_F(P_{n,i})$, $F\in {\mathcal {F}}_n$, do not cover $P_{n,i}$ completely.

Corollary 4.7

Let $S\in {\mathcal {K}}^n$ be such that $S=K\cap {\mathbb {R}}^n_{\ge 0}$ for some standard unconditional body $K\in {\mathcal {K}}^n_o$. Then

$$\begin{aligned} \mu _1(S)\cdot \ldots \cdot \mu _n(S){\mathrm {vol}}(S)\ge 1, \end{aligned}$$

with equality if and only if K attains equality in Theorem 4.5.

Proof

By the unconditionality of K, we get that $2^n{\mathrm {vol}}(S)={\mathrm {vol}}(K)$. In order for a dilate of S to induce a lattice covering of the whole space it needs to contain the unit cube $[0,1]^n$. On the other hand, for K it suffices to cover half of it, that is, $[0,1/2]^n$. By similar considerations as in the proof of Proposition 3.3 this shows that $\mu _i(S)=2\mu _i(K)$, for all $i\in [n]$. In view of these identities, the claimed inequality together with its equality case characterization follow from Theorem 4.5. $\square$

The obtained constants in Theorems 4.3 and 4.5 are of course far off from each other. We conjecture that the truth lies somehow in between and that the biggest possible lower bound on the covering product decreases exponentially with the dimension.

Conjecture 4.8

For every $K\in {\mathcal {K}}^n$, we have

$$\begin{aligned} \mu _1(K)\cdot \ldots \cdot \mu _n(K){\mathrm {vol}}(K)\ge \frac{n+1}{2^n}, \end{aligned}$$

with equality, for example, for $K={\mathrm {conv}}\{e_1,\ldots ,e_n,-\mathbf{1}\}$.

For $n=2$, this conjecture reduces to Schnell’s inequality (Theorem 4.1). In analogy to Schnell’s result, we expect that there are many more extremal examples minimizing the covering product, and that there are also o-symmetric bodies among them. These extremal examples, even for $n=3$, can be seen as interesting variants of the so-called parallelohedra, which are convex bodies that are extremal in (1) (cf. [18, Sect. 32]).

In the sequel, we consider the simplex $T_n={\mathrm {conv}}\{e_1,\ldots ,e_n,-\mathbf{1}\}$ in more detail. It turns out that the determination of the whole sequence of covering minima of $T_n$ is a highly non-trivial task. In general, an upper bound on the covering minima for simplices with integral vertices is the following: For any simplex $T={\mathrm {conv}}\{v_0,v_1,\ldots ,v_n\}$, with vertices $v_j\in {\mathbb {Z}}^n$, we have

$$\begin{aligned} \mu _i(T)\le \mu _i(S_\mathbf{1})=i \quad \text {for all }i\in [n], \end{aligned}$$

(19)

where $S_\mathbf{1}={\mathrm {conv}}\{0,e_1,\ldots ,e_n\}$ is the standard simplex. Indeed, if we let $V\in {\mathbb {Z}}^{n\times n}$ be the matrix with columns $v_i-v_0$, $i\in [n]$, then $T=VS_\mathbf{1}+v_0$. Moreover, $V{\mathbb {Z}}^n\subseteq {\mathbb {Z}}^n$, because V has only integral entries, and thus $VS_\mathbf{1}+V{\mathbb {Z}}^n\subseteq VS_\mathbf{1}+{\mathbb {Z}}^n$. The definition of the covering minima then implies that $\mu _i(S_\mathbf{1})=\mu _i(VS_\mathbf{1},V{\mathbb {Z}}^n)\ge \mu _i(VS_\mathbf{1})=\mu _i(T)$. The fact that $\mu _i(S_\mathbf{1})=i$, for all $i\in [n]$, is easy to see, for instance, by similar arguments as in the proof of Proposition 3.3.

Now, we concentrate on determining the exact value of $\mu _n(T_n)$ in arbitrary dimension. This will be enough to show that the covering product of $T_n$ decreases exponentially with n, and thus motivates Conjecture 4.8.

Proposition 4.9

For the simplex $T_n={\mathrm {conv}}\{e_1,\ldots ,e_n,-\mathbf{1}\}$, we have

• (i) $\mu _n(T_n)=\frac{n}{2}$, and

• (ii) $\mu _1(T_n)\cdot \ldots \cdot \mu _n(T_n){\mathrm {vol}}(T_n)\le \frac{n+1}{n!}\big \lfloor \frac{n}{2}\big \rfloor !\big (\frac{n}{2}\big )^{\lceil {n}/2\rceil }\approx \frac{n+1}{(2/\sqrt{e})^n}$.

Remark 4.10

For the i-dimensional coordinate subspace $L_i=\{e_1,\ldots ,e_i\}$ holds $T_n|L_i=T_i\times \{0\}^{n-i}$ and ${\mathbb {Z}}^n|L_i={\mathbb {Z}}^i\times \{0\}^{n-i}$. Hence by (14), we have $\mu _i(T_n)\ge \mu _i(T_i)=i/2$. We conjecture that this is actually an identity for every $i\in [n]$, which, in view of ${\mathrm {vol}}(T_n)=(n+1)/n!$, explains the claimed lower bound in Conjecture 4.8.

The proof of Proposition 4.9 needs a bit of preparation. The covering radius of simplices has appeared in various contexts in the literature. For instance, a celebrated result of Kannan [21] establishes a relation to the Frobenius coin problem, and more recently, Marklof and Strömbergsson [28] (cf. [1]) made a connection to diameters of so-called quotient lattice graphs. The latter interpretation suits our purposes well, so we introduce the necessary notation following [28]. We use basic concepts from graph theory, for which the reader may consult the textbook of Diestel [11].

Let ${\mathrm {LG}}_n^+$ be the standard lattice graph, that is, the directed graph with vertex set ${\mathbb {Z}}^n$ and a directed edge $(x,x+e_i)$, for every $x\in {\mathbb {Z}}^n$ and $i\in [n]$. For a full-dimensional sublattice $\Lambda \subseteq {\mathbb {Z}}^n$ the quotient lattice graph ${\mathrm {LG}}_n^+/\Lambda$ is defined as the directed graph with vertex set ${\mathbb {Z}}^n/\Lambda$ and edges $(x+\Lambda ,x+e_i+\Lambda )$, for $x\in {\mathbb {Z}}^n$ and $i\in [n]$. For fixed $v\in {\mathbb {R}}^n_{>0}$, a distance in ${\mathrm {LG}}_n^+/\Lambda$ is defined by

$$\begin{aligned} {\mathrm {d}}_v(x+\Lambda ,y+\Lambda )=\min _{z\in (y-x+\Lambda )\cap {\mathbb {Z}}^n_{\ge 0}}v^\intercal z \quad \text {for any}\quad x,y\in {\mathbb {Z}}^n. \end{aligned}$$

In other words, ${\mathrm {d}}_v(x+\Lambda ,y+\Lambda )$ is the length of the shortest directed path from $x+\Lambda$ to $y+\Lambda$ in ${\mathrm {LG}}_n^+/\Lambda$, where additionally each edge $(x+\Lambda ,x+e_i+\Lambda )$ is given the weight $v_i$, for $i\in [n]$. The diameter of ${\mathrm {LG}}_n^+/\Lambda$ (with respect to v) can now be defined as

$$\begin{aligned} {\mathrm {diam}}_v({\mathrm {LG}}_n^+/\Lambda )=\max _{y\in {\mathbb {Z}}^n/\Lambda }{\mathrm {d}}_v(0+\Lambda ,y+\Lambda ). \end{aligned}$$

Note that, by definition, the distance ${\mathrm {d}}_v$ is translation invariant, that is, ${\mathrm {d}}_v(x+w+\Lambda ,y+w+\Lambda )={\mathrm {d}}_v(x+\Lambda ,y+\Lambda )$, for all $x,y,w\in {\mathbb {Z}}^n$, and hence it suffices to consider paths starting from the vertex $0+\Lambda$ in the definition of ${\mathrm {diam}}_v({\mathrm {LG}}_n^+/\Lambda )$. Finally, we define the simplex $S_v=\{x\in {\mathbb {R}}^n_{\ge 0}:v^\intercal x\le 1\}$.

The following expression for the covering radius of $S_v$ with respect to $\Lambda$ is a combination of Lemmas 3 and 4 of [28, Sect. 2].

Theorem 4.11

(Marklof and Strömbergsson [28]) Let $v=(v_1,\ldots ,v_n)\in {\mathbb {R}}^n_{>0}$ and let $\Lambda \subseteq {\mathbb {Z}}^n$ be a full-dimensional sublattice. Then,

$$\begin{aligned} \mu _n(S_v,\Lambda )={\mathrm {diam}}_v({\mathrm {LG}}_n^+/\Lambda )+v_1+\cdots +v_n. \end{aligned}$$

Before we can proceed to prove Proposition 4.9, we need an auxiliary statement from elementary number theory. For $k\in {\mathbb {Z}}$ and $m\in {\mathbb {N}}$, we let $[k]_m$ be the representative of k modulo m that lies in $\{0,1,\ldots ,m-1\}$. More precisely, $[k]_m=k-m\lfloor k/m \rfloor$.

Lemma 4.12

Let $n\ge 2$ be an integer. For $w=(w_1,\ldots ,w_{n-1})\in {\mathbb {Z}}^{n-1}$ and $r\in {\mathbb {Z}}$, let $\sigma _w(r)=\sum _{i=1}^{n-1}[w_i+r]_{n+1}$.

• (i) If n is even, then $|\{\sigma _w(r):r\in \{0,1,\ldots ,n\}\}|=n+1$.

• (ii) If n is odd, then no three of the numbers $\sigma _w(r)$, $r\in \{0,1,\ldots ,n\}$, are pairwise equal, and for $r,r'\in {\mathbb {Z}}$, the difference $|\sigma _w(r)-\sigma _w(r')|$ is even.

Proof

For $j\in {\mathbb {Z}}$, denote $s_w(j)=|\{i\in [n-1]:[w_i+j]_{n+1}=0\}|$. With this notation, we find that

$$\begin{aligned} \sigma _w(0)&=\sum _{i=1}^{n-1}[w_i]_{n+1}=\sum _{i=1}^{n-1}[w_i+1]_{n+1} -(n-1-s_w(1))+ns_w(1)\\&=\sigma _w(1)+(n+1)s_w(1)-(n-1). \end{aligned}$$

Therefore, we have

$$\begin{aligned} \sigma _w(k)=\sigma _w(0)-(n+1)\sum _{j=1}^ks_w(j)+k(n-1),\quad \text {for}\quad k=1,\ldots ,n. \end{aligned}$$

(20)

This implies that, for $k,\ell \in \{0,1,\ldots ,n\}$ with $k<\ell$, we have $\sigma _w(k)=\sigma _w(\ell )$ if and only if

$$\begin{aligned} (\ell -k)(n-1)=(n+1)\sum _{j=k+1}^\ell s_w(j). \end{aligned}$$

(21)

This number lies in $\{1,\ldots ,n(n-1)\}$ and is a common multiple of $n-1$ and $n+1$. Now, if n is even, then $\gcd (n-1,n+1)=1$, and hence there is no $k<\ell$ satisfying (21), which proves (i).

So, let $n\ge 3$ be odd. Then $\gcd (n-1,n+1)=2$, and hence $(n-1)(n+1)/2$ is the only common multiple of $n-1$ and $n+1$ in $\{1,\ldots ,n(n-1)\}$. Assume that there are $k,l,m\in \{0,1,\ldots ,n\}$ with $k<\ell <m$ and $\sigma _w(k)=\sigma _w(\ell )=\sigma _w(m)$. It follows that $\ell -k=m-k=m-\ell =(n+1)/2$ and hence $k=\ell =m$. This contradiction proves the first claim of (ii). Moreover, $n-1$ and $n+1$ are even so that by (20), we see that the difference between any $\sigma _w(r)$ and $\sigma _w(r')$ is an even number. $\square$

Proof of Proposition 4.9

(i) For the computation of the covering radius $\mu _n(T_n)$ it turns out to be more convenient to transform $T_n$ to a multiple of the standard simplex $S_\mathbf{1}={\mathrm {conv}}\{0,e_1,\ldots ,e_n\}$. To this end, let $A=(a_{ij})\in {\mathbb {Z}}^{n\times n}$ be the matrix with entries $a_{ii}=n$, for $i\in [n]$, and $a_{ij}=-1$, for $i,j\in [n]$ with $i\ne j$. Then, we have $AT_n=(n+1)S_\mathbf{1}-\mathbf{1}$ and writing $\Lambda _n=A{\mathbb {Z}}^n$, we thus get

$$\begin{aligned} \mu _n(T_n)=\mu _n(S_\mathbf{1},\Lambda _n)/(n+1). \end{aligned}$$

Based on this identity and Theorem 4.11, we infer that

$$\begin{aligned} \mu _n(T_n)&=\frac{n}{2}\quad \text { if and only if }\quad {\mathrm {diam}}_\mathbf{1}({\mathrm {LG}}_n^+/\Lambda _n)=\left( {\begin{array}{c}n\\ 2\end{array}}\right) . \end{aligned}$$

(22)

The sublattice $\Lambda _n\subseteq {\mathbb {Z}}^n$ has a nice structure. For instance, we have

$$\begin{aligned} \Lambda _n=\bigcup _{i=0}^n\big (i\cdot \mathbf{1}+(n+1){\mathbb {Z}}^n\big )\quad \text {and}\quad \det (\Lambda _n)=(n+1)^{n-1}. \end{aligned}$$

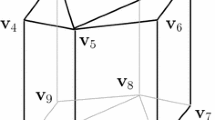
Considering the fundamental cell of $\Lambda _n$ that has vertices $\{0,n+1\}^{n-1}\times \{0\}$ and $\mathbf{1}+\{0,n+1\}^{n-1}\times \{0\}$, we see that the quotient lattice graph ${\mathrm {LG}}_n^+/\Lambda _n$ can be described as follows. Its vertex set is given by $\{0,1,\ldots ,n\}^{n-1}$ and (x, y) is a directed edge if and only if $y-x\in \{e_1,\ldots ,e_{n-1},-\mathbf{1}_{n-1}\}$ modulo $(n+1){\mathbb {Z}}^{n-1}$ (see Fig. 1). Notice that $e_1,\ldots ,e_{n-1}$ and $\mathbf{1}_{n-1}$ are points in ${\mathbb {R}}^{n-1}$ here. We now prove that the diameter of ${\mathrm {LG}}_n^+/\Lambda _n$ is as stated in (22).

Fig. 1

The quotient lattice graph ${\mathrm {LG}}_3^+/\Lambda _3$

We first argue that ${\mathrm {diam}}_\mathbf{1}({\mathrm {LG}}_n^+/\Lambda _n)\le \left( {\begin{array}{c}n\\ 2\end{array}}\right)$. For this to be true we need to show that there is a directed path in ${\mathrm {LG}}_n^+/\Lambda _n$ from $0+\Lambda _n$ to $w+\Lambda _n$ of length at most $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$, for every $w\in \{0,1,\ldots ,n\}^{n-1}$. By the definition of ${\mathrm {LG}}_n^+/\Lambda _n$ this amounts to finding a representation

$$\begin{aligned} w&=r_1e_1+\cdots +r_{n-1}e_{n-1}-r_n\mathbf{1}_{n-1}, \end{aligned}$$

(23)

for some $r_1,\ldots ,r_n\in {\mathbb {Z}}$ such that $\sum _{i=1}^n[r_i]_{n+1}\le \left( {\begin{array}{c}n\\ 2\end{array}}\right)$. Observe that once we fix $r_n\in \{0,1,\ldots ,n\}$, we have $r_i=w_i+r_n$, for $i\in [n-1]$. Hence, there exists such a representation of w if and only if there is an $r\in \{0,1,\ldots ,n\}$ such that

$$\begin{aligned} \sigma _w(r)&=\sum _{i=1}^{n-1}[w_i+r]_{n+1}\le \left( {\begin{array}{c}n\\ 2\end{array}}\right) -r. \end{aligned}$$

(24)

For the sake of contradiction, we assume that for every $r\in \{0,1,\ldots ,n\}$ the inequality (24) does not hold. Notice that, by definition of $[k]_m$, we have

$$\begin{aligned} \sum _{r=0}^n\sigma _w(r)&=\sum _{i=1}^{n-1}\sum _{r=0}^n[w_i+r]_{n+1} =\sum _{i=1}^{n-1}\sum _{j=0}^n j=(n+1)\left( {\begin{array}{c}n\\ 2\end{array}}\right) . \end{aligned}$$

(25)

Now, in the case that n is even, Lemma 4.12 (i) shows that the numbers $\sigma _w(r)$, $r\in \{0,1,\ldots ,n\}$, are pairwise different, and hence by our assumption

$$\begin{aligned} \sum _{r=0}^n\sigma _w(r)&>\sum _{r=0}^n\bigg (\left( {\begin{array}{c}n\\ 2\end{array}}\right) -r\bigg ) +\sum _{r=0}^n r=(n+1)\left( {\begin{array}{c}n\\ 2\end{array}}\right) , \end{aligned}$$

contradicting (25). The case that n is odd is similar. By Lemma 4.12 (ii), no three of the numbers $\sigma _w(r)$, $r\in \{0,1,\ldots ,n\}$, are pairwise equal, and moreover, any two different ones of these numbers differ by at least two. Therefore,

$$\begin{aligned} \sum _{r=0}^n\sigma _w(r)&\ge \sum _{r=0}^n\bigg (\left( {\begin{array}{c}n\\ 2\end{array}}\right) -r+1\bigg ) +2\sum _{j=0}^{({n-1})/{2}}(2j)=(n+1)\left( {\begin{array}{c}n\\ 2\end{array}}\right) +\frac{1}{2}\,(n+1), \end{aligned}$$

contradicting (25) again. In conclusion, there must be an $r\in \{0,1,\ldots ,n\}$ satisfying (24), and hence the diameter of ${\mathrm {LG}}_n^+/\Lambda _n$ is at most $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ as claimed.

In order to see that this bound is best possible, we consider the vertex $w=(2,3,\ldots ,n)\in \{0,1,\ldots ,n\}^{n-1}$ of ${\mathrm {LG}}_n^+/\Lambda _n$. In any representation of w of the form (23) with $r=r_n\in \{0,1,\ldots ,n\}$, we have $r_i=w_i+r=i+1+r$, for $i\in [n-1]$. Therefore, if $r=n$, then $\sum _{i=1}^{n-1}[r_i]_{n+1}=\sum _{i=1}^{n-1}i=\left( {\begin{array}{c}n\\ 2\end{array}}\right) >\left( {\begin{array}{c}n\\ 2\end{array}}\right) -r$, and if $r<n$, then

$$\begin{aligned} \sum _{i=1}^{n-1}[r_i]_{n+1}&=\sum _{i=1}^{n-r-1}(i+1+r)+\sum _{i=n-r}^{n-1}(i+r-n)\\&=\left( {\begin{array}{c}n\\ 2\end{array}}\right) -r+(n-r-1)\ge \left( {\begin{array}{c}n\\ 2\end{array}}\right) -r, \end{aligned}$$

with equality only for $r=n-1$. This means, that there is no path from $0+\Lambda _n$ to $w+\Lambda _n$ of length less than $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$, and thus ${\mathrm {diam}}_\mathbf{1}({\mathrm {LG}}_n^+/\Lambda _n)=\left( {\begin{array}{c}n\\ 2\end{array}}\right)$. In view of (22), we have thus proven that $\mu _n(T_n)=n/2$.

(ii) The claimed exponential upper bound on the covering product of $T_n$ follows directly from the inequalities (19), that is, $\mu _i(T_n)\le i$ for $i\in [n]$, and $\mu _n(T_n)\le n/2$. Indeed, using Stirling approximation, we get

$$\begin{aligned} \mu _1(T_n)\cdot \ldots \cdot \mu _n(T_n){\mathrm {vol}}(T_n)&\le 1\cdot 2\cdot \ldots \cdot \biggl \lfloor \frac{n}{2}\biggl \rfloor \bigg (\frac{n}{2}\bigg )^{n-\lfloor {n}/{2} \rfloor }\frac{n+1}{n!}\\&=\frac{n+1}{n!}\biggl \lfloor \frac{n}{2}\biggl \rfloor !\bigg (\frac{n}{2} \bigg )^{\lceil {n}/2\rceil }\\&\approx (n+1)\frac{\sqrt{\pi n}({n}/({2e}))^{{n}/{2}}({n}/{2})^{{n}/{2}}}{\sqrt{2\pi n}({n}/{e})^n}\approx \frac{n+1}{(2/\sqrt{e})^n}. \end{aligned}$$

Observe that $2/\sqrt{e}\approx 1.21306$, so that the derived upper bound on the covering product of $T_n$ is indeed decreasing exponentially with the dimension. $\square$