The Maximum Number of Faces of the Minkowski Sum of Two Convex Polytopes

Abstract

We derive tight bounds for the maximum number of k-faces, $0\le k\le d-1$, of the Minkowski sum, $P_1+P_2$, of two d-dimensional convex polytopes $P_1$ and $P_2$, as a function of the number of vertices of the polytopes. For even dimensions $d\ge 2$, the maximum values are attained when $P_1$ and $P_2$ are cyclic d-polytopes with disjoint vertex sets. For odd dimensions $d\ge 3$, the maximum values are attained when $P_1$ and $P_2$ are $\lfloor \frac{d}{2}\rfloor$-neighborly d-polytopes, whose vertex sets are chosen appropriately from two distinct d-dimensional moment-like curves.

1 Introduction

Let P, Q be two d-dimensional polytopes, or simply d-polytopes, in the Euclidean d-dimensional space ${\mathbb {E}}^d$. Their Minkowski sum, $P+Q$, which is again a d-polytope in ${\mathbb {E}}^d$, is defined as the set $\{p+q\,\,|\,\,p\in P, q\in Q\}$. Minkowski sums are fundamental structures in both Mathematics and Computer Science. They appear in a variety of different subjects including Combinatorial Geometry, Computational Geometry, Computer Algebra, Computer-Aided Design & Solid Modeling, Motion Planning, Assembly Planning, Robotics (see [6, 25] and the references therein), and, more recently, Game Theory [22], Computational Biology [21], and Operations Research [27].

Despite their apparent importance, little is known about the worst-case combinatorial complexity, i.e., the total number of faces, of Minkowski sums in dimensions four and higher. In two dimensions, the worst-case complexity of Minkowski sums is well understood. Given two convex polygons P and Q with n and m vertices, respectively, the maximum number of vertices and edges of $P+Q$ is $n+m$ [4]. This result can be immediately generalized (e.g., by induction) to any number of summands. If P is convex and Q is non-convex (or vice versa), the worst-case complexity of $P+Q$ is $\varTheta (nm)$, while if both P and Q are non-convex the complexity of their Minkowski sum can be as high as $\varTheta (n^2m^2)$ [4]. When P and Q are 3-polytopes (embedded in the 3-dimensional Euclidean space), the worst-case complexity of $P+Q$ is $\varTheta (nm)$, if both P and Q are convex, and $\varTheta (n^3m^3)$, if both P and Q are non-convex (e.g., see [5]). For the intermediate cases, i.e., if only one of P and Q is convex, see [24].

Given two convex d-polytopes $P_1$ and $P_2$ in ${\mathbb {E}}^d$, $d\ge 2$, with $n_1$ and $n_2$ vertices, respectively, we can easily get a straightforward upper bound of $O((n_1+n_2)^{\lfloor \frac{d+1}{2}\rfloor })$ on the complexity of $P_1+P_2$ by means of the following reduction: embed $P_1$ and $P_2$ in the hyperplanes $\{x_1=0\}$ and $\{x_1=1\}$ of ${\mathbb {E}}^{d+1}$, respectively; then the weighted Minkowski sum $(1-\lambda )P_1+\lambda P_2= \{(1-\lambda )p_1+\lambda p_2\,\,|\,\,p_1\in P_1,p_2\in P_2\}$, $\lambda \in (0,1)$, of $P_1$ and $P_2$ is the intersection of the convex hull P of $P_1$ and $P_2$ with the hyperplane $\{x_1=\lambda \}$. The embedding and reduction described above are essentially what are known as the Cayley embedding and Cayley trick, respectively, whereas the $(d+1)$-polytope P is called the Cayley polytope of $P_1$ and $P_2$ [11]. From this reduction it is obvious that the worst-case complexity of $(1-\lambda )P_1+\lambda P_2$ is bounded from above by the complexity of the Cayley polytope, which is in $O((n_1+n_2)^{\lfloor \frac{d+1}{2}\rfloor })$. Furthermore, the complexity of the weighted Minkowski sum of $P_1$ and $P_2$ is independent of $\lambda$, in the sense that, for any value of $\lambda \in (0,1)$, the polytopes we get by intersecting P with $\{x_1=\lambda \}$ are combinatorially equivalent. In fact, since $P_1+P_2$ is nothing but $\frac{1}{2}P_1+\frac{1}{2}P_2$ scaled by a factor of 2, the complexity of the weighted Minkowski sum of two convex polytopes is the same as the complexity of their unweighted Minkowski sum. The “obvious” upper bound for the complexity of the Minkowski sum stemming from the complexity of the Cayley polytope is tight in even dimensions. In odd dimensions, $d\ge 3$, however, this upper bound may not be tight; in this case, the worst-case complexity of $P_1+P_2$ is in $\varTheta (n_{1}n_2^{\lfloor \frac{d}{2}\rfloor }+n_{2}n_1^{\lfloor \frac{d}{2}\rfloor })$ (cf. [13]), which is a refinement over of the “obvious” upper bound when $n_1$ and $n_2$ asymptotically differ. In terms of exact bounds on the number of faces of the Minkowski sum of two polytopes, results are known only when the two summands are convex. Besides the trivial bound for convex polygons (2-polytopes), mentioned in the previous paragraph, the first result of this nature was shown by Gritzmann and Sturmfels [10]: given r polytopes $P_1,P_2,\ldots ,P_r$ in ${\mathbb {E}}^d$, with a total of n non-parallel edges, the number of l-faces $f_l(P_1+P_2+\cdots +P_r)$ of $P_1+P_2+\cdots +P_r$ is bounded from above by $2\left( {\begin{array}{c}n\\ l\end{array}}\right) \sum _{j=0}^{d-1-l}\left( {\begin{array}{c}n-l-1\\ j\end{array}}\right)$. This bound is attained when the polytopes $P_i$ are zonotopes, and their generating edges are in general position.

Regarding bounds as a function of the number of vertices or facets of the summands, Fukuda and Weibel [7] have shown that, given two 3-polytopes $P_1$ and $P_2$ in ${\mathbb {E}}^3$, the number of k-faces of $P_1+P_2$, $0\le k\le 2$, is bounded from above as follows:

$$\begin{aligned} \begin{aligned} f_0(P_1+P_2)&\le n_1 n_2,\\ f_1(P_1+P_2)&\le 2n_1 n_2+n_1+n_2-8,\\ f_2(P_1+P_2)&\le n_1 n_2+n_1+n_2-6, \end{aligned} \end{aligned}$$

(1)

where $n_j$ is the number of vertices of $P_j$, $j=1,2$. Weibel [25] has also derived similar expressions in terms of the number of facets $m_j$ of $P_j$, $j=1,2$, namely

$$\begin{aligned} f_0(P_1+P_2)&\le 4m_1 m_2-8m_1-8m_2+16,\\ f_1(P_1+P_2)&\le 8m_1 m_2-17m_1-17m_2+40,\\ f_2(P_1+P_2)&\le 4m_1 m_2-9m_1-9m_2+26. \end{aligned}$$

All these bounds are tight. Fogel et al. [5] have further generalized some of these bounds in the case of r summands. More precisely, they have shown that given r 3-polytopes $P_1,P_2,\ldots ,P_r$ in ${\mathbb {E}}^3$, where $P_j$ has $m_j\ge d+1$ facets, the number of facets of the Minkowski sum $P_1+P_2+\cdots +P_r$ is bounded from above by

$$\begin{aligned} \sum _{1\le i<j\le r}(2m_i-5)(2m_j-5)+\sum _{i=1}^r m_i+\left( {\begin{array}{c}r\\ 2\end{array}}\right) , \end{aligned}$$

and this bound is tight.

In dimensions four and higher, there are no results that relate the worst-case number of k-faces of the Minkowski sum of two or more convex polytopes with the number of facets of the summands. There are, however, bounds on the number of k-faces of the Minkowski sum of convex polytopes, as a function of the number of vertices of the summands. Fukuda and Weibel [7] have shown that the number of vertices of the Minkowski sum of r d-polytopes $P_1,\ldots ,P_r$, where $r\le d-1$ and $d\ge 2$, is bounded from above by $\prod _{i=1}^{r}n_i$, where $n_i$ is the number of vertices of $P_i$, and this bound is tight. On the other hand, for $r\ge d$, this bound cannot be attained: Sanyal [23] has shown that for $r\ge d$, $f_0(P_1+\cdots +P_r)$ is bounded from above by $(1-\frac{1}{(d+1)^d})\prod _{i=1}^{r}n_i$, which is, clearly, strictly smaller than $\prod _{i=1}^{r}n_i$. For higher-dimensional faces, i.e., for $k\ge 1$, Fukuda and Weibel [7] have proven what they call the trivial upper bound, namely that the number of k-faces of the Minkowski sum of r d-polytopes is bounded as follows:

$$\begin{aligned} f_k(P_1+P_2+\cdots +P_r)\le \sum _{\begin{array}{c} 1\le s_i\le n_i\\ s_1+\ldots +s_r=k+r \end{array}}\prod _{i=1}^r\left( {\begin{array}{c}n_i\\ s_i\end{array}}\right) , \qquad 0\le k\le d-1, \end{aligned}$$

(2)

where $n_i$ is the number of vertices of $P_i$, and the $s_i$’s take integral values. Furthermore, it is shown in [7] that these bounds are tight for $d\ge 4$, $r\le \lfloor \frac{d}{2}\rfloor$, and for all k with $0\le k\le \lfloor \frac{d}{2}\rfloor -r$, i.e., for the cases where both the number of summands and the dimension of the faces considered are small. The above-mentioned ranges for the parameters d, r, and k for which the trivial upper bound is tight are not the best possible: Karavelas and Tzanaki [15] have shown that the trivial upper bound is tight for $d\ge 3$, $2\le r\le d-1$ and for all $0\le k\le \lfloor \frac{d+r-1}{2}\rfloor -r$, and these ranges are maximal. This result immediately implies a tight worst-case asymptotic bound on the complexity of the Minkowski sum of r n-vertex d-polytopes, namely $\varTheta (n^{\lfloor \frac{d+r-1}{2}\rfloor })$.

We end our discussion of the previous work related to this paper by some results presented in Weibel [26]. In this paper, Weibel considers the case where the number of summands r is at least as big as the dimension of the polytopes. In this setting, he gives a relation between the number of k-faces of the Minkowski sum of r polytopes, $r\ge d\ge 2$, and the number of k-faces of the Minkowski sum of subsets of the original set of r polytopes that are of size at most $d-1$. In more detail, if we have r d-polytopes $P_1,P_2,\ldots ,P_r$ in ${\mathbb {E}}^d$, where $r\ge d$, that are in general position, then the following relation holds for any k with $0\le k\le d-1$:

$$\begin{aligned} f_k(P_1+P_2+\cdots +P_r)= & {} \alpha +\sum _{j=1}^{d-1}(-1)^{d-1-j}\left( {\begin{array}{c}r-1-j\\ d-1-j\end{array}}\right) \sum _{S\in {\mathcal {C}}_j^r}(f_k(P_S)-\alpha )\nonumber \\\le & {} \sum _{S\in {\mathcal {C}}_{d-1}^r}f_k(P_S), \end{aligned}$$

(3)

where ${\mathcal {C}}_j^r$ is the family of subsets of $\{1,2,\ldots ,r\}$ of cardinality j, $P_S$ is the Minkowski sum of the polytopes in S, and, finally, $\alpha =2$ if $k=0$ and d is odd, $\alpha =0$, otherwise. Weibel used this relation to derive tight upper bounds on the number of vertices of the Minkowski sum of r d-polytopes in ${\mathbb {E}}^d$, when $r\ge d$. In particular, the following tight upper bound holds (cf. [26, Thm. 3]):

$$\begin{aligned} f_0(P_1+P_2+\cdots +P_r)\le \alpha +\sum _{j=1}^{d-1}(-1)^{d-1-j}\left( {\begin{array}{c}r-1-j\\ d-1-j\end{array}}\right) \sum _{S\in {\mathcal {C}}_j^r} \Big (\prod _{i\in S}f_0(P_i)-\alpha \Big ), \end{aligned}$$

where ${\mathcal {C}}_j^r$ and $\alpha$ are defined as for relation (3).

In this paper, we extend previous results on the exact maximum number of faces of the Minkowski sum of two convex d-polytopes.¹ More precisely, we show that given two d-polytopes $P_1$ and $P_2$ in ${\mathbb {E}}^d$ with $n_1\ge d+1$ and $n_2\ge d+1$ vertices, respectively, the maximum number of k-faces of the Minkowski sum $P_1+P_2$ is bounded from above as follows:

$$\begin{aligned} f_{k-1}(P_1+P_2)\le & {} f_k(C_{d+1}(n_1+n_2)) \\&-\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\left( {\begin{array}{c}d+1-i\\ k+1-i\end{array}}\right) \Bigg ( \left( {\begin{array}{c}n_1-d-2+i\\ i\end{array}}\right) +\left( {\begin{array}{c}n_2-d-2+i\\ i\end{array}}\right) \Bigg ), \end{aligned}$$

where $1\le k\le d$, and $C_d(n)$ stands for the cyclic d-polytope with n vertices. The expressions above are shown to be tight for any $d\ge 2$ and for all $1\le k\le d$, and match with the corresponding expressions for two and three dimensions (cf. rel. (1)), as well as the expressions in (2) for $r=2$ and for all $0\le k\le \lfloor \frac{d}{2}\rfloor -2$.

To prove the upper bounds, we use the Cayley embedding already described above. Given the d-polytopes $P_1$ and $P_2$ in ${\mathbb {E}}^d$, we embed $P_1$ and $P_2$ in the hyperplanes $\{x_1=0\}$ and $\{x_1=1\}$ of ${\mathbb {E}}^{d+1}$. We consider the Cayley polytope $P=CH_{d+1}(P_1,P_2)$ of $P_1$ and $P_2$ and argue that, for the purposes of the worst-case upper bounds, it suffices to consider the case where P is simplicial, except possibly for its two facets $P_1$ and $P_2$. We concentrate on the set ${\mathcal {F}}$ of faces of P that are neither faces of $P_1$ nor faces of $P_2$. The reason that we focus on ${\mathcal {F}}$ is that there is a bijection between the k-faces of ${\mathcal {F}}$ and the $(k-1)$-faces of $P_1+P_2$, $1\le k\le d$, and, thus, deriving upper bounds of the number of $(k-1)$-faces of $P_1+P_2$ reduces to deriving upper bounds for the number of k-faces of ${\mathcal {F}}$. We then proceed in a manner analogous to that used by McMullen [20] to prove the Upper Bound Theorem for polytopes.

We consider the f-vector ${\varvec{f}}({\mathcal {F}})$ of ${\mathcal {F}}$, and from this we define the h-vector ${\varvec{h}}({\mathcal {F}})$ of ${\mathcal {F}}$ and continue by

• (i) deriving Dehn–Sommerville-like equations for ${\mathcal {F}}$, expressed in terms of the elements of ${\varvec{h}}({\mathcal {F}})$ and the g-vectors of the boundary complexes of $P_1$ and $P_2$, and

• (ii) establishing a recurrence relation for the elements of ${\varvec{h}}({\mathcal {F}})$.

From the latter, we inductively compute upper bounds on the elements of ${\varvec{h}}({\mathcal {F}})$, which we combine with the Dehn–Sommerville-like equations for ${\mathcal {F}}$, to get refined upper bounds for the “left-most half” of the elements of ${\varvec{h}}({\mathcal {F}})$, i.e., for the values $h_k({\mathcal {F}})$ with $k>\lfloor \frac{d+1}{2}\rfloor$. We then establish our upper bounds by computing ${\varvec{f}}({\mathcal {F}})$ from ${\varvec{h}}({\mathcal {F}})$.

To prove the tightness of our upper bounds, we distinguish between even and odd dimensions. In even dimensions $d\ge 2$, we show that the k-faces of the Minkowski sum of any two cyclic d-polytopes with $n_1$ and $n_2$ vertices, respectively, whose vertex sets are distinct, attain the upper bounds we have proved. In odd dimensions $d\ge 3$, the construction that establishes the tightness of our bounds is more intricate. We consider the $(d-1)$-dimensional moment curve ${\varvec{\gamma }}(t)=(t,t^2,t^3,\ldots ,t^{d-1})$, $t>0$, and define two vertex sets $V_1$ and $V_2$ with $n_1$ and $n_2$ vertices on ${\varvec{\gamma }}(t)$, respectively. For $i=1,2$, we define $P_i$ as the convex hull in ${\mathbb {E}}^d$ of the vertices in $V_i.$ We embed $P_1,P_2$ in ${\mathbb {E}}^{d+1}$ so that they lie in two affinely independent hyperplanes of ${\mathbb {E}}^{d+1}$ and then appropriately perturb their vertices so that they become combinatorially equivalent to d-dimensional cyclic polytopes. We next argue that, by the way we have chosen $V_1$ and $V_2$, the number of k-faces of the Minkowski sum $P_1+P_2$ attains its maximum possible value. At a very high/qualitative level, the appropriate choice we refer to above amounts to choosing $V_1$ and $V_2$ so that the parameter values on ${\varvec{\gamma }}(t)$ of the vertices in $V_1$ and $V_2$ lie within two disjoint intervals of ${\mathbb {R}}$ that are sufficiently away from each other.

The structure of the rest of the paper is as follows: In Sect. 2 we formally give various definitions and recall a version of the Upper Bound Theorem for polytopes that will be useful later in the paper. In Sect. 3 we define what we call bineighborly polytopal complexes and prove some properties associated with them. The reason why we introduce this new notion is the fact that the tightness of our upper bounds is shown to be equivalent to requiring that the Cayley polytope of $P_1$ and $P_2$ is bineighborly. In Sect. 4 we prove our upper bounds on the number of faces of the Minkowski sum of two polytopes. In Sect. 5 we describe our worst-case constructions and show that these constructions attain the upper bounds proved in Sect. 4. We conclude the paper with Sect. 6, where we summarize our results, and state open problems and directions for future work.

2 Definitions and Preliminaries

A convex polytope, or simply polytope, P in ${\mathbb {E}}^d$ is the convex hull of a finite set of points V in ${\mathbb {E}}^d$. The minimal subset $V'$ of V for which the convex hull of $V'$ is P is called the vertex set of P. A polytope P can equivalently be described as the intersection of all the closed halfspaces containing V. A face of P is the intersection of P with a hyperplane H for which the polytope is contained in one of the two closed halfspaces delimited by H. Such a hyperplane is called a supporting hyperplane of P. The dimension of a face of P is the dimension of its affine hull. A k-face of P is a k-dimensional face of P. We consider the polytope itself as a trivial d-dimensional face; all the other faces are called proper faces. We use the term d-polytope to refer to a polytope the trivial face of which is d-dimensional. For a d-polytope P, the 0-faces of P are its vertices, the 1-faces of P are its edges, the $(d-2)$-faces of P are called ridges, while the $(d-1)$-faces are called facets. For $0\le k\le d$ we denote by $f_k(P)$ the number of k-faces of P. Note that every k-face F of P is also a k-polytope whose faces are all the faces of P contained in F. A k-simplex in ${\mathbb {E}}^d$, $k\le d$, is the convex hull of any $k+1$ affinely independent points in ${\mathbb {E}}^d$. A polytope is called simplicial if all its proper faces are simplices. Equivalently, P is simplicial if for every vertex v of P and every face $F\subset P$, v does not belong to the affine hull of the vertices in $F\setminus \{v\}$.

A polytopal complex ${\mathcal {C}}$ is a finite collection of polytopes in ${\mathbb {E}}^d$ such that (i) $\emptyset \in {\mathcal {C}}$; (ii) if $P\in {\mathcal {C}}$, then all the faces of P are also in ${\mathcal {C}}$; and (iii) the intersection $P\cap Q$ for two polytopes P and Q in ${\mathcal {C}}$ is a face of both P and Q. The dimension $\dim ({\mathcal {C}})$ of ${\mathcal {C}}$ is the largest dimension of a polytope in ${\mathcal {C}}$. A polytopal complex is called pure if all its maximal (with respect to inclusion) faces have the same dimension. In this case the maximal faces are called the facets of ${\mathcal {C}}$. We use the term d-complex to refer to a polytopal complex whose maximal faces are d-dimensional (i.e., the dimension of ${\mathcal {C}}$ is d). A polytopal complex is called simplicial if all its faces are simplices. Finally, a polytopal complex ${\mathcal {C}}'$ is called a subcomplex of a polytopal complex ${\mathcal {C}}$ if all faces of ${\mathcal {C}}'$ are also faces of ${\mathcal {C}}$.

One important class of polytopal complexes arises from polytopes. More precisely, a d-polytope P, together with all its faces, including the empty face, forms a d-complex, denoted by ${\mathcal {C}}(P)$. The only maximal face of ${\mathcal {C}}(P)$, which is clearly the only facet of ${\mathcal {C}}(P)$, is the polytope P itself. Moreover, all proper faces of P form a pure $(d-1)$-complex, called the boundary complex ${\mathcal {C}}(\partial {P})$, or simply $\partial {P}$ of P. The facets of $\partial {P}$ are just the facets of P,  and the dimension of $\partial {P}$ is clearly $\dim (\partial {P})=\dim (P)-1=d-1$.

Given a d-polytope P in ${\mathbb {E}}^d$, consider a facet F of P and call H the supporting hyperplane of F (with respect to P). For an arbitrary point p in ${\mathbb {E}}^d$, we say that p is beyond (resp., beneath) the facet F of P, if p lies in the open halfspace of H that does not contain P (resp., contains the interior of P). Furthermore, we say that an arbitrary point $v'$ is beyond the vertex v of P if for every facet F of P containing v, $v'$ is beyond F, while for every facet F of P not containing v, $v'$ is beneath F. For a vertex v of P, the star of v, denoted by ${\text {star}}(v,P)$, is the polytopal complex of all faces of P that contain v, and their faces. The link of v, denoted by $\text {link}(v,P)$ or ${P}/{v}$, is the subcomplex of ${\text {star}}(v,P)$ consisting of all the faces of ${\text {star}}(v,P)$ that do not contain v.

Definition 1

([28, Rem. 8.3]) Let ${\mathcal {C}}$ be a pure simplicial polytopal d-complex. A shelling ${\mathbb {S}}({\mathcal {C}})$ of ${\mathcal {C}}$ is a linear ordering $F_1,F_2,\ldots ,F_s$ of the facets of ${\mathcal {C}}$ such that, for all $1<j\le s$, the intersection $F_j\cap (\bigcup _{i=1}^{j-1}F_i)$ of the facet $F_j$ with the previous facets is non-empty and pure $(d-1)$-dimensional. In other words, for every $i<j$, there exists some $\ell <j$ such that the intersection $F_i\cap F_j$ is contained in $F_\ell \cap F_j$ and such that $F_\ell \cap F_j$ is a facet of $F_j$.

The shelling definition above is the specialization, to simplicial complexes, of the shelling definition for general polytopal complexes (cf. [28, Def. 8.1]). We refrained from stating the general definition, as in the sequel of the paper we will only consider shellings of simplicial polytopal complexes. A polytopal complex that has a shelling is called shellable, while not all polytopal complexes are shellable. It was a major result in polytopal theory that the boundary complex of a polytope is always shellable (cf. [2]).

Consider a pure shellable simplicial polytopal complex ${\mathcal {C}}$ and let ${\mathbb {S}}({\mathcal {C}})=\{F_1,\ldots ,F_s\}$ be a shelling order of its facets. The restriction $R(F_j)$ of a facet $F_j$ is the set of all vertices $v\in F_j$ such that $F_j\setminus \{v\}$ is contained in one of the earlier facets.² The main observation here is that when we construct ${\mathcal {C}}$ according to the shelling ${\mathbb {S}}({\mathcal {C}})$, the new faces at the j-th step of the shelling are exactly the vertex sets G with $R(F_j)\subseteq G\subseteq F_j$ (cf. [28, Sect. 8.3]). Moreover, notice that $R(F_1)=\emptyset$ and $R(F_i)\ne R(F_j)$ for all $i\ne j$.

The f-vector ${\varvec{f}}(P)=(f_{-1}(P),f_0(P),\ldots ,f_{d-1}(P))$ of a d-polytope P (or its boundary complex $\partial {P}$) is defined as the $(d+1)$-dimensional vector consisting of the numbers $f_k(P)$ of k-faces of P, $-1\le k\le d-1$, where $f_{-1}(P)=1$ refers to the empty set. The h-vector ${\varvec{h}}(P)=(h_0(P),h_1(P),\ldots ,h_d(P))$ of a d-polytope P (or its boundary complex $\partial {P}$) is defined as the $(d+1)$-dimensional vector, where

$$\begin{aligned} h_k(P):=\sum _{i=0}^{k}(-1)^{k-i}\left( {\begin{array}{c}d-i\\ d-k\end{array}}\right) f_{i-1}(P), \qquad 0\le k\le d. \end{aligned}$$

(4)

It is easy to verify from the defining equations of the $h_k(P)$’s that the elements of ${\varvec{f}}(P)$ determine the elements of ${\varvec{h}}(P)$ and vice versa (see also [28, Sect. 8.3] and below). In particular, the elements of ${\varvec{f}}(P)$ can be written in terms of the elements of ${\varvec{h}}(P)$ as follows:

$$\begin{aligned} f_{k-1}(P)=\sum _{i=0}^{k}\left( {\begin{array}{c}d-i\\ k-i\end{array}}\right) h_i(P), \qquad 0\le k\le d. \end{aligned}$$

(5)

For simplicial polytopes, the number $h_k(P)$ counts the number of facets of P in a shelling of $\partial {P}$, whose restriction has size k; this number is independent of the particular shelling chosen (cf. [28, Thm. 8.19]). Moreover, the elements of ${\varvec{f}}(P)$ (or, equivalently, ${\varvec{h}}(P)$) are not linearly independent; they satisfy the so-called Dehn–Sommerville equations, which can be written in a very concise form as $h_k(P)=h_{d-k}(P)$, $0\le k\le d$. An important implication of the existence of the Dehn–Sommerville equations is that if we know the face numbers $f_k(P)$ for all $0\le k\le \lfloor \frac{d}{2}\rfloor -1$, we can determine the remaining face numbers $f_k(P)$ for all $\lfloor \frac{d}{2}\rfloor \le k\le d-1$ (cf. relations (4) and (5)).

Both the f-vector and h-vector of a simplicial d-polytope are related to the so-called g-vector. For a simplicial d-polytope P, its g-vector is the $(\lfloor \frac{d}{2}\rfloor +1)$-dimensional vector ${\varvec{g}}(P)=(g_0(P),g_1(P),\ldots ,$ $g_{\lfloor \frac{d}{2}\rfloor }(P))$, where $g_0(P)=1$ and $g_k(P)=h_k(P)-h_{k-1}(P)$, $1\le k\le \lfloor \frac{d}{2}\rfloor$ (see also [28, Sect. 8.6]). Using the convention that $h_{d+1}(P)=0$, we can actually extend the definition of $g_k(P)$ for all $0\le k\le d+1$, while using the Dehn–Sommerville equations for P yields $g_{d+1-k}(P)=-g_k(P)$, $0\le k\le d+1$. We can then express ${\varvec{f}}(P)$ in terms of ${\varvec{g}}(P)$ as follows:

$$\begin{aligned} f_{k-1}(P)=\sum _{j=0}^{\lfloor \frac{d}{2}\rfloor }g_j(P) \Bigg (\left( {\begin{array}{c}d+1-j\\ d+1-k\end{array}}\right) -\left( {\begin{array}{c}j\\ d+1-k\end{array}}\right) \Bigg ),\quad 0\le k\le d+1. \end{aligned}$$

As a final note for this section, the Upper Bound Theorem for polytopes can be expressed in terms of their g-vector:

Corollary 2

[28, Cor. 8.38] We consider simplicial d-polytopes P of fixed dimension d and fixed number of vertices $n=g_1(P)+d+1$. ${\varvec{f}}(P)$ is component-wise maximal if and only if all the components of ${\varvec{g}}(P)$ are maximal, with

$$\begin{aligned} g_k(P)=\left( {\begin{array}{c}g_1(P)+k-1\\ k\end{array}}\right) =\left( {\begin{array}{c}n-d-2+k\\ k\end{array}}\right) , \end{aligned}$$

(6)

for $0\le k\le \lfloor \frac{d}{2}\rfloor$. Also, $f_{k-1}(P)$ is maximal if and only if $g_i(P)$ is maximal for all i with $i\le \min \{k,\lfloor \frac{d}{2}\rfloor \}$.

The relation between the f-vector and h-vector of a polytopal complex is better manipulated using generating functions. For a pure simplicial $(d-1)$-complex ${\mathcal {C}}$, its $f$-polynomial and $h$-polynomial, respectively, are defined as

$$\begin{aligned} {\mathtt {f}}({{\mathcal {C}}};t)&= \sum _{i=0}^d f_{i-1} t^{d-i} = f_d +f_{d-1}t+\cdots +f_{-1} t^d, \end{aligned}$$

(7)

$$\begin{aligned} {\mathtt {h}}({{\mathcal {C}}};t)&= \sum _{i=0}^d h_{i} t^{d-i} = h_d +h_{d-1}t+\cdots + h_0 t^d. \end{aligned}$$

(8)

The relation between the f-vector and h-vector (cf. relations (4) and (5)) can then be expressed as

$$\begin{aligned} {\mathtt {f}}({{\mathcal {C}}};t) = {\mathtt {h}}({{\mathcal {C}}};t+1) \end{aligned}$$

(9)

or equivalently as

$$\begin{aligned} {\mathtt {h}}({{\mathcal {C}}};t) = {\mathtt {f}}({{\mathcal {C}}};t-1). \end{aligned}$$

(10)

If P is a simplicial d-polytope, then its boundary complex $\partial {P}$ is a simplicial $(d-1)$-complex. We can therefore use relations (9) and (10) to define ${\mathtt {f}}({\partial {P}};t)$ and ${\mathtt {h}}({\partial {P}};t)$. Furthermore, we may define the g-polynomial ${\mathtt {g}}({\partial {P}};t)$ of P as

$$\begin{aligned} {\mathtt {g}}({\partial {P}};t) := \sum _{i=0}^d g_{i}t^{d+1-i} = g_d t +g_{d-1}t^2+\cdots + g_0 t^{d+1}. \end{aligned}$$

(11)

The relation between the g- and h-vector of $\partial {P}$ can be expressed in terms of generating polynomials as

$$\begin{aligned} {\mathtt {g}}({\partial {P}};t)= (t-1) {\mathtt {h}}({\partial {P}};t). \end{aligned}$$

(12)

Furthermore, the Dehn–Sommerville equations for a simplicial d-polytope are captured in the following reciprocal relation:

$$\begin{aligned} t^d\,{\mathtt {h}}({\partial {P}};\tfrac{1}{t}) = {\mathtt {h}}({\partial {P}};t). \end{aligned}$$

(13)

We end this section with a technical lemma. Its proof may be found in Appendix.

Lemma 3

For any d-polytope P

$$\begin{aligned} d\, {\mathtt {h}}({\partial {P}};t)+(1- t)\,{\mathtt {h'}}({\partial {P}};t) = \sum _{v\in \,{\mathrm{vert}}(P)} {\mathtt {h}}({{\partial {P}}/{v}};t), \end{aligned}$$

(14)

where $\,{\mathrm{vert}}(P)$ is the vertex set of P (or $\partial {P}$), and ${\mathtt {h'}}({\cdot };t)$ denotes the derivative of ${\mathtt {h}}({\cdot };t)$ with respect to t.

3 Bineighborly Polytopal Complexes

Let ${\mathcal {C}}$ be a d-complex with vertex set V. Let $\{V_1,V_2\}$ be a partition of V and define ${\mathcal {C}}_1$ (resp., ${\mathcal {C}}_2$) to be the subcomplex of ${\mathcal {C}}$ consisting of all the faces of ${\mathcal {C}}$ whose vertices are vertices in $V_1$ (resp., $V_2$). We start with a useful definition:

Definition 4

Let ${\mathcal {C}}$ be a d-complex. We say that ${\mathcal {C}}$ is $(k,V_1)$-bineighborly if we can partition the vertex set V of ${\mathcal {C}}$ into two non-empty subsets $V_1$ and $V_2=V\setminus V_1$ such that for every $\emptyset \subset S_j\subseteq V_j$, $j=1,2$, with $|S_1|+|S_2|\le k$, the union $S_1\cup S_2$ is the vertex set of a $(|S_1|+|S_2|-1)$-face of ${\mathcal {C}}$.

We introduce the notion of bineighborly polytopal complexes because they play an important role when considering the maximum complexity of the Minkowski sum of two d-polytopes $P_1$ and $P_2$. As we will see in the upcoming section, the number of $(k-1)$-faces of $P_1+P_2$ is maximal for all $1\le k\le l$, $l\le \lfloor \frac{d-1}{2}\rfloor$, if and only if the Cayley polytope P of $P_1$ and $P_2$ is $(l+1,V_1)$-bineighborly, where $V_1$ stands for the vertex set of $P_1$. Even more interestingly, in any odd dimension $d\ge 3$, the number of k-faces of $P_1+P_2$ is maximized for all $0\le k\le d-1$, if and only if P is $(\lfloor \frac{d+1}{2}\rfloor ,V_1)$-bineighborly. In the rest of this section we highlight some properties of bineighborly polytopal complexes that will be useful in the upcoming sections.

A direct consequence of our definition is the following: suppose that ${\mathcal {C}}$ is a $(l,V_1)$-bineighborly polytopal complex, and let F be a k-face of ${\mathcal {C}}$, $1\le k<l$, such that at least one vertex of F is in $V_1$ and at least one vertex of F is in $V_2$; then F is a k-simplex. Another immediate consequence of Definition 4 is that a k-neighborly d-complex is also $(k,V')$-bineighborly for every non-empty subset $V'$ of its vertex set:

Corollary 5

Let ${\mathcal {C}}$ be a k-neighborly d-complex, with vertex set V. Then, for every $V'$, with $\emptyset \subset V'\subset V$, ${\mathcal {C}}$ is $(k,V')$-bineighborly.

It is easy to see that if a d-complex ${\mathcal {C}}$ is $(k,V_1)$-bineighborly, then it is $(k-1)$-neighborly, as the following straightforward lemma suggests.

Lemma 6

Let ${\mathcal {C}}$ be a $(k,V_1)$-bineighborly d-complex, $k\ge 2.$ Then ${\mathcal {C}}$ is $(k-1)$-neighborly.

Proof

Let $S\subseteq V$ be of size $k-1$. Choose $v \in V \setminus S$ such that $(S \cup \{v\}) \cap V_i\ne \emptyset$ for $i=1,2$, and let $S'=S\cup \{v\}$. Since ${\mathcal {C}}$ is $(k,V_1)$-bineighborly, $S'$ is the vertex set of a $(k-1)$-face of ${\mathcal {C}}$ and, as argued above, a $(k-1)$-simplex. Clearly, S is the vertex set of a $(k-2)$-face of $S'$ and hence an element of ${\mathcal {C}}$. $\square$

The following lemma is in some sense the converse of Lemma 6.

Lemma 7

Let ${\mathcal {C}}$ be a $(k,V_1)$-bineighborly d-complex and let its two subcomplexes ${\mathcal {C}}_1$ and ${\mathcal {C}}_2$ be k-neighborly. Then ${\mathcal {C}}$ is also k-neighborly.

Proof

Let S be a non-empty subset of V of size k. Consider the following, mutually exclusive cases:

• (i) S consists of vertices of both $V_1$ and $V_2$. Then, since ${\mathcal {C}}$ is $(k,V_1)$-bineighborly, S defines a $(k-1)$-face of ${\mathcal {C}}$.

• (ii) S consists of vertices of $V_j$ only, $j=1,2$. Since ${\mathcal {C}}_j$ is k-neighborly, S defines a $(k-1)$-face of ${\mathcal {C}}_j$. However, ${\mathcal {C}}_j$ is a subcomplex of ${\mathcal {C}}$, which further implies that S is also a face of ${\mathcal {C}}$.

Hence, for every vertex subset S of V of size k, S defines a $(k-1)$-face of ${\mathcal {C}}$, i.e., ${\mathcal {C}}$ is k-neighborly. $\square$

Consider again a d-complex ${\mathcal {C}}$ with vertex set $V=V_1\cup V_2$, where $V_1\cap V_2=\emptyset$. Let ${\mathcal {B}}$ be the set of faces of ${\mathcal {C}}$ that are not faces of either ${\mathcal {C}}_1$ or ${\mathcal {C}}_2$. The following lemma gives tight upper bounds for the number of faces in ${\mathcal {B}}$. In what follows, we denote by $n_j$ the cardinality of $V_j$, $j=1,2$.

Lemma 8

The number of $(k-1)$-faces of ${\mathcal {B}}$ is bounded from above as follows:

$$\begin{aligned} f_{k-1}({\mathcal {B}})\le \sum _{j=1}^{k-1} \Big (\begin{array}{cc}{n_1}\\ {j}\end{array}\Big )\Big (\begin{array}{cc}{n_2}\\ {k-j}\end{array}\Big ) =\Big (\begin{array}{cc}{n_1+n_2}\\ {k}\end{array}\Big )-\Big (\begin{array}{cc}{n_1}\\ {k}\end{array}\Big )-\Big (\begin{array}{cc}{n_2}\\ {k}\end{array}\Big ), \quad 1\le k\le d, \end{aligned}$$

(15)

where equality holds if and only if ${\mathcal {C}}$ is $(k,V_1)$-bineighborly.

Proof

For the purposes of proving an upper bound for elements of the f-vector of ${\mathcal {B}}$, it suffices to consider the case where ${\mathcal {C}}_1$ and ${\mathcal {C}}_2$ are in general position with respect to each other, in which case ${\mathcal {B}}$ is simplicial.

Under the assumption that ${\mathcal {B}}$ is simplicial, we can identify each face of ${\mathcal {B}}$ with its uniquely defined vertex set. Consider a $(k-1)$-face F of ${\mathcal {B}}$. The face F is a $(k-1)$-simplex and, seen as a vertex set, it is neither a subset of $V_1$ nor $V_2$. Clearly, the number $\#_k{\mathcal {B}}$ of vertex sets of cardinality k of ${\mathcal {B}}$, which are neither subsets of $V_1$ nor $V_2$, is bounded by above by the number $\#_k(V_1,V_2)$ of k-element subsets of V not fully contained in either $V_1$ or $V_2$; this is precisely the right-hand side of (15). Finally, notice that $\#_k{\mathcal {B}}$ is equal to $\#_k(V_1,V_2)$ if and only if for every non-empty subset $S_1$ of $V_1$ and every non-empty subset $S_2$ of $V_2$, where $|S_1|+|S_2|=k$, the set $S_1\cup S_2$ is the vertex set of a $(k-1)$-face of ${\mathcal {C}}$. In other words, equality in (15) can only hold if and only if ${\mathcal {C}}$ is $(k,V_1)$-bineighborly. $\square$

4 Upper Bounds

Fig. 1

The d-polytopes $P_1$ and $P_2$ are embedded in the hyperplanes $\Pi _1=\{x_1=0\}$ and $\Pi _2=\{x_1=1\}$ of ${\mathbb {E}}^{d+1}$. The polytope $\tilde{P}$ is the intersection of the Cayley polytope of $P_1$ and $P_2$ with the hyperplane $\tilde{\Pi }=\{x_1=\frac{1}{2}\}$

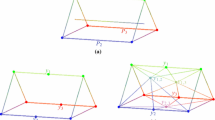
Let $P_1$ and $P_2$ be two d-polytopes in ${\mathbb {E}}^d$, with $n_1$ and $n_2$ vertices, respectively. Let us consider the Cayley embedding of $P_1$ and $P_2$, i.e., we embed $P_1$ (resp., $P_2$) in the hyperplane $\Pi _1$ (resp., $\Pi _2$) of ${\mathbb {E}}^{d+1}$ with equation $\{x_1=0\}$ (resp., $\{x_1=1\}$). Then the Minkowski sum $P_1+P_2$ (scaled by a factor of 2) is the d-polytope we get when intersecting the Cayley polytope $P=CH_{d+1}(P_1,P_2)$ of $P_1$ and $P_2$ with the hyperplane $\tilde{\Pi }$ with equation $\{x_1=\frac{1}{2}\}$ (see Fig. 1). This immediately implies that the k-faces of the Minkowski sum $P_1+P_2$ correspond bijectively to the $(k+1)$-faces of P not contained in either $P_1$ or $P_2$.

Karavelas and Tzanaki [13, Lem. 2] have shown that the vertices of $P_1$ and $P_2$ can be perturbed in such a way that

• (i) the vertices of $P_1'$ and $P_2'$ remain in $\Pi _1$ and $\Pi _2$, respectively, and both $P_1'$ and $P_2'$ are simplicial;

• (ii) the Cayley polytope $P'$ of $P_1'$ and $P_2'$ is also simplicial, except possibly the facets $P_1'$ and $P_2'$; and

• (iii) the number of vertices of $P_1'$ and $P_2'$ is the same as the number of vertices of $P_1$ and $P_2$, respectively, whereas $f_k(P)\le f_k(P')$ for all $k\ge 1$,

where $P_1'$ and $P_2'$ are the polytopes in $\Pi _1$ and $\Pi _2$ we get after perturbing the vertices of $P_1$ and $P_2$, respectively. In view of this result, it suffices to consider the case where both $P_1$, $P_2$, as well as their Cayley polytope P, are simplicial complexes, except possibly the facets $P_1$ and $P_2$ of P.

In the rest of this section, we consider that this is the case: P is considered simplicial, with the possible exception of its two facets $P_1$ and $P_2$. Let ${\mathcal {F}}$ be the set of proper faces of P having non-empty intersection with $\tilde{\Pi }$. Note that $\tilde{P}=P\cap \tilde{\Pi }$ is a d-polytope, which is, in general, non-simplicial, and whose proper non-trivial faces are intersections of the form $F\cap \tilde{\Pi }$ where $F\in {\mathcal {F}}$. As we have already observed above, $\tilde{P}$ is combinatorially equivalent to the Minkowski sum $P_1+P_2$. Furthermore,

$$\begin{aligned} f_{k-1}(P_1+P_2)=f_{k-1}(\tilde{P})=f_k({\mathcal {F}}), \qquad 1\le k\le d. \end{aligned}$$

(16)

The remainder of this section is devoted to deriving upper bounds for $f_k({\mathcal {F}})$, which, by relation (16), become upper bounds for $f_{k-1}(P_1+P_2)$.

Let ${\mathcal {K}}$ be the polytopal complex whose faces are all the faces of ${\mathcal {F}}$, as well as the faces of P that are subfaces of faces in ${\mathcal {F}}$. Clearly, the d-faces of ${\mathcal {K}}$ are exactly the d-faces of ${\mathcal {F}}$, and thus, ${\mathcal {K}}$ is a pure simplicial d-complex, with the d-faces of ${\mathcal {F}}$ being the facets of ${\mathcal {K}}$. Moreover, the set of k-faces of ${\mathcal {K}}$ is the disjoint union of the sets of k-faces of ${\mathcal {F}}$, $\partial {P}_1$ and $\partial {P}_2$. This implies

$$\begin{aligned} f_k({\mathcal {K}})=f_k({\mathcal {F}})+f_k(\partial {P}_1)+f_k(\partial {P}_2),\qquad -1\le k\le d, \end{aligned}$$

(17)

where $f_d(\partial {P}_j)=0$, $j=1,2$. Since ${\mathcal {K}}$, $\partial {P}_1$, and $\partial {P}_2$ are complexes, we have, by definition, that $f_{-1}({\mathcal {K}})=f_{-1}(\partial {P}_1)=f_{-1}(\partial {P}_2)=1$. In order for relation (17) to be valid for $k=-1$, we conventionally set $f_{-1}({\mathcal {F}})=-1$. We next express (17) in terms of generating functions:

$$\begin{aligned} {\mathtt {f}}({{\mathcal {K}}};t)&=\sum _{i=0}^{d+1} f_{i-1}({\mathcal {K}}) t^{d+1-i} \nonumber \\&=\sum _{i=0}^{d+1} f_{i-1}({\mathcal {F}})t^{d+1-i} + \sum _{i=0}^{d+1} f_{i-1}(\partial {P}_1)t^{d+1-i} +\sum _{i=0}^{d+1} f_{i-1}(\partial {P}_2) t^{d+1-i} \nonumber \\&= {\mathtt {f}}({{\mathcal {F}}};t) + t \sum _{i=0}^{d} f_{i-1}(\partial {P}_1)t^{d-i} + t\sum _{i=0}^{d} f_i(\partial {P}_2) t^{d-i} \nonumber \\&= {\mathtt {f}}({{\mathcal {F}}};t) + t\,{\mathtt {f}}({\partial {P}_1};t)+ t\,{\mathtt {f}}({\partial {P}_2};t), \end{aligned}$$

(18)

where we used that $\dim ({\mathcal {K}})=\dim ({\mathcal {F}})=d$, $\dim (\partial {P}_i)=d-1$, and $f_d(\partial {P}_1)=f_d(\partial {P}_2)=0$.

Fig. 2

The polytope Q is created by adding two vertices $y_1$ and $y_2$. The vertex $y_1$ (resp., $y_2$) is below $P_1$ (resp., above $P_2$) and is visible by the vertices of $P_1$ (resp., $P_2$) only

For $i=1,2$, let $y_i$ be a point beyond the facet $P_i$ of P, and beneath every other facet of P (see Fig. 2). We call Q the $(d+1)$-polytope we get by taking the stellar subdivisions of P with $y_1$ and $y_2$, respectively (cf. [28, Problem 3.0]). Notice that since the facets $P_1$ and $P_2$ are disjoint, the order in which we perform the stellar subdivisions does not matter. The boundary complex $\partial {Q}$ is then the disjoint union of the set of

• (i) faces in the star ${\mathcal {S}}_1$ of $y_1$, faces in the star ${\mathcal {S}}_2$ of $y_2$, and

• (ii) faces in ${\mathcal {F}}$.

This implies that

$$\begin{aligned} f_k(\partial {Q})=f_k({\mathcal {F}})+f_k({\mathcal {S}}_1)+f_k({\mathcal {S}}_2),\quad 0\le k\le d, \end{aligned}$$

(19)

where $f_0({\mathcal {F}})=0$. Since ${\mathcal {S}}_i = {\text {star}}(y_i,\partial {P}_i)$, we can further write

$$\begin{aligned} f_k({\mathcal {S}}_j)=f_k(\partial {P}_j)+f_{k-1}(\partial {P}_j),\quad 0\le k\le d, \qquad i=1,2, \end{aligned}$$

(20)

where $f_{-1}(\partial {P}_j)=1$ and $f_d(\partial {P}_j)=0$. Combining relations (19) and (20), we get

$$\begin{aligned} f_k(\partial {Q})=f_k({\mathcal {F}})+f_k(\partial {P}_1)+f_{k-1}(\partial {P}_1)+ f_k(\partial {P}_2)+f_{k-1}(\partial {P}_2),\quad 0\le k\le d. \end{aligned}$$

(21)

As for (17), we now express (21) in terms of generating functions (recall that $\dim ({\mathcal {F}})= \dim (\partial {Q}) = d$ and $\dim (\partial {P}_i) = d-1$):

$$\begin{aligned} {\mathtt {f}}({\partial {Q}};t)={\mathtt {f}}({{\mathcal {F}}};t)+(t+1){\mathtt {f}}({\partial {P}_1};t)+(t+1){\mathtt {f}}({\partial {P}_1};t). \end{aligned}$$

(22)

We call ${\mathcal {K}}_j$, $j=1,2$, the subcomplex of $\partial {Q}$ consisting of faces of ${\mathcal {K}}$ or faces of ${\mathcal {S}}_j$. ${\mathcal {K}}_j$ is a pure simplicial d-complex, the facets of which are either facets of ${\mathcal {S}}_j$ or ${\mathcal {K}}$. Furthermore, ${\mathcal {K}}_j$ is shellable. To see this, first notice that $\partial {Q}$ is shellable (Q is a polytope). Consider a line shelling (cf. [28, Sect. 8.2]) $F_1,F_2,\ldots ,F_s$ of $\partial {Q}$ that shells ${\text {star}}(y_2,\partial {Q})$ last, and let $F_{\lambda +1},F_{\lambda +2},\ldots ,F_s$ be the facets of $\partial {Q}$ that correspond to ${\mathcal {S}}_2$. Trivially, the subcomplex of $\partial {Q}$, the facets of which are $F_1,F_2,\ldots ,F_\lambda$, is shellable; however, this subcomplex is nothing but ${\mathcal {K}}_1$. The argument for ${\mathcal {K}}_2$ is analogous.

The k-faces of ${\mathcal {K}}_j$, $j=1,2$, are either k-faces of ${\mathcal {K}}$ or k-faces of the star ${\mathcal {S}}_j$ of $y_j$ that contain $y_j$. The latter faces are in one-to-one correspondence with the $(k-1)$-faces of $\partial {P}_j$, i.e., we get

$$\begin{aligned} f_k({\mathcal {K}}_j)=f_k({\mathcal {K}})+f_{k-1}(\partial {P}_j). \end{aligned}$$

(23)

Expressing (23) in terms of generating functions, we get

$$\begin{aligned} {\mathtt {f}}({{\mathcal {K}}_j};t) = {\mathtt {f}}({{\mathcal {K}}};t)+ {\mathtt {f}}({\partial {P}_j};t). \end{aligned}$$

(24)

Notice that Q is a simplicial $(d+1)$-polytope, while ${\mathcal {K}}$, ${\mathcal {K}}_1$, and ${\mathcal {K}}_2$ are simplicial d-complexes; hence their h-vectors are well defined. We define the f-vector of ${\mathcal {F}}$ to be the $(d+2)$-vector ${\varvec{f}}({\mathcal {F}})=(f_{-1}({\mathcal {F}}),f_0({\mathcal {F}}),\ldots ,f_d({\mathcal {F}}))$, recalling that $f_{-1}({\mathcal {F}})=-1$. From ${\varvec{f}}({\mathcal {F}})$ we can also define the $(d+2)$-vector ${\varvec{h}}({\mathcal {F}})=(h_0({\mathcal {F}}),h_1({\mathcal {F}}),\ldots ,$ $h_{d+1}({\mathcal {F}}))$, where

$$\begin{aligned} h_k({\mathcal {F}}) =\sum _{i=0}^{k}(-1)^{k-i}\left( {\begin{array}{c}d+1-i\\ d+1-k\end{array}}\right) f_{i-1}({\mathcal {F}}), \quad 0\le k\le d+1. \end{aligned}$$

(25)

We naturally call this vector the h-vector of ${\mathcal {F}}$ (see also relation (4)). As for polytopal complexes and polytopes, the f-vector of ${\mathcal {F}}$ defines the h-vector of ${\mathcal {F}}$ and vice versa (cf. (4) and (5)).

The next lemma associates the elements of ${\varvec{h}}(\partial {Q})$, ${\varvec{h}}({\mathcal {K}})$, ${\varvec{h}}({\mathcal {K}}_1)$, ${\varvec{h}}({\mathcal {K}}_2)$, ${\varvec{h}}({\mathcal {F}})$, ${\varvec{h}}(\partial {P}_1)$, and ${\varvec{h}}(\partial {P}_2)$ via generating functions. The last among the relations in the lemma can be thought of as the analogue of the Dehn–Sommerville equations for ${\mathcal {F}}$.

Lemma 9

$$\begin{aligned} {\mathtt {h}}({Q};t)&= {\mathtt {h}}({{\mathcal {F}}};t) +t {\mathtt {h}}({P_1};t) + t {\mathtt {h}}({P_2};t), \end{aligned}$$

(26)

$$\begin{aligned} {\mathtt {h}}({{\mathcal {K}}};t)&= {\mathtt {h}}({{\mathcal {F}}};t) + {\mathtt {g}}({P_1};t) + {\mathtt {g}}({P_2};t), \end{aligned}$$

(27)

$$\begin{aligned} {\mathtt {h}}({{\mathcal {K}}_j};t)&= {\mathtt {h}}({{\mathcal {K}}};t)+{\mathtt {h}}({P_j};t), \qquad j=1,2, \end{aligned}$$

(28)

$$\begin{aligned} t^{d+1} {\mathtt {h}}({{\mathcal {F}}};\tfrac{1}{t})&= {\mathtt {h}}({{\mathcal {F}}};t)+{\mathtt {g}}({\partial {P}_1};t)+{\mathtt {g}}({\partial {P}_2};t). \end{aligned}$$

(29)

Proof

Using (22) we have

$$\begin{aligned} {\mathtt {h}}({\partial {Q}};t)&={\mathtt {f}}({\partial {Q}};t-1)\\&= {\mathtt {f}}({{\mathcal {F}}};t-1) + t{\mathtt {f}}({\partial {P}_1};t-1) + t{\mathtt {f}}({\partial {P}_1};t-1)\\&={\mathtt {h}}({{\mathcal {F}}};t) + t{\mathtt {h}}({\partial {P}_1};t) + t{\mathtt {h}}({\partial {P}_1};t). \end{aligned}$$

Using (12) and (18), we arrive at the following:

$$\begin{aligned} {\mathtt {h}}({{\mathcal {K}}};t)&={\mathtt {f}}({{\mathcal {K}}};t-1)\\&={\mathtt {f}}({{\mathcal {F}}};t-1) + (t-1){\mathtt {f}}({\partial {P}_1};t-1) + (t-1) {\mathtt {f}}({\partial {P}_2};t-1)\\&= {\mathtt {h}}({{\mathcal {F}}};t) + (t-1){\mathtt {h}}({\partial {P}_1};t)+ (t-1) {\mathtt {h}}({\partial {P}_2};t)\\&= {\mathtt {h}}({{\mathcal {F}}};t) + {\mathtt {g}}({\partial {P}_1};t)+ {\mathtt {g}}({\partial {P}_2};t). \end{aligned}$$

Similarly, from (24) we get

$$\begin{aligned} {\mathtt {h}}({{\mathcal {K}}_j};t)={\mathtt {f}}({{\mathcal {K}}_j};t-1) = {\mathtt {f}}({{\mathcal {K}}};t-1)+ {\mathtt {f}}({\partial {P}_j};t-1) ={\mathtt {h}}({{\mathcal {K}}};t)+ {\mathtt {h}}({\partial {P}_j};t). \end{aligned}$$

To prove (29) recall the Dehn–Sommerville equations (13) for the $(d+1)$-polytope $\partial {Q}$ and the d-polytopes $\partial {P}_i, i = 1,2$:

$$\begin{aligned} t^{d+1}{\mathtt {h}}({\partial {Q}};\tfrac{1}{t}) = {\mathtt {h}}({\partial {Q}};t) \end{aligned}$$

(30)

and

$$\begin{aligned} t^d {\mathtt {h}}({\partial {P}_i};\tfrac{1}{t}) = {\mathtt {h}}({\partial {P}_i};t). \end{aligned}$$

Substituting $\frac{1}{t}$ for t in (26) and multiplying both sides with $t^{d+1}$, we get

$$\begin{aligned} t^{d+1} {\mathtt {h}}({\partial {Q}};\tfrac{1}{t})&= t^{d+1} {\mathtt {h}}({{\mathcal {F}}};\tfrac{1}{t}) +\tfrac{t^{d+1}}{t} {\mathtt {h}}({\partial {P}_1};\tfrac{1}{t})+ \tfrac{t^{d+1}}{t} {\mathtt {h}}({\partial {P}_2};\tfrac{1}{t}) \nonumber \\&= t^{d+1} {\mathtt {h}}({{\mathcal {F}}};\tfrac{1}{t}) +t^{d} {\mathtt {h}}({\partial {P}_1};\tfrac{1}{t}) + t^d {\mathtt {h}}({\partial {P}_2};\tfrac{1}{t}) \nonumber \\&= t^{d+1} {\mathtt {h}}({{\mathcal {F}}};\tfrac{1}{t}) + {\mathtt {h}}({\partial {P}_1};t) + {\mathtt {h}}({\partial {P}_2};t). \end{aligned}$$

(31)

Using (26) and (30), relation (31) becomes

$$\begin{aligned} t^{d+1} {\mathtt {h}}({{\mathcal {F}}};\tfrac{1}{t}) + {\mathtt {h}}({\partial {P}_1};t) + {\mathtt {h}}({\partial {P}_2};t) = {\mathtt {h}}({{\mathcal {F}}};t)+t\,{\mathtt {h}}({\partial {P}_1};t) + t\,{\mathtt {h}}({\partial {P}_2};t), \end{aligned}$$

or equivalently

$$\begin{aligned} t^{d+1} {\mathtt {h}}({{\mathcal {F}}};\tfrac{1}{t})&= {\mathtt {h}}({{\mathcal {F}}};t) + (t-1){\mathtt {h}}({\partial {P}_1};t) + (t-1){\mathtt {h}}({\partial {P}_2};t)\\&= {\mathtt {h}}({{\mathcal {F}}};t) +{\mathtt {g}}({\partial {P}_1};t) + {\mathtt {g}}({\partial {P}_2};t), \end{aligned}$$

which completes our proof. $\square$

Definition 10

Let $p(t)= \sum _{i=0}^d p_i t^i$ and $q(t)= \sum _{i=0}^d q_i t^i$ be two polynomial functions of degree at most d. We will write $p(t) \preccurlyeq q(t)$ if and only if p(t) is coefficient-wise lesser than or equal to q(t), i.e., $p_i \le q_i$, $0 \le i \le d$.

Lemma 11

For $j=1,2$ and all $v\in V_j$, we have

$$\begin{aligned} t\,{\mathtt {h}}({{\mathcal {K}}/v};t) - t\,{\mathtt {g}}({\partial {P}_j/v};t) \preccurlyeq {\mathtt {h}}({{\mathcal {K}}};t)-{\mathtt {g}}({\partial {P}_j};t). \end{aligned}$$

(32)

Proof

We are going to prove our claim for $j=1$; the case $j=2$ is entirely analogous. To prove relation (32), we rewrite it in terms of the elements of the h- and g-vectors involved. More precisely, it suffices to show that, for all $0\le k\le d+1$,

$$\begin{aligned} h_k({{\mathcal {K}}}/{v})-g_k({\partial {P}_1}/{v})\le h_k({\mathcal {K}})-g_k(\partial {P}_1). \end{aligned}$$

(33)

First, notice that for $k=0$ the statement of lemma is trivial since ${{\mathcal {K}}}/{v}, {\partial {P}_1}/{v}, {\mathcal {K}}$ and $\partial {P}_1$ are simplicial complexes and, thus, $h_0({{\mathcal {K}}}/{v})=g_0({\partial {P}_1}/{v})=h_0({\mathcal {K}})=g_0(\partial {P}_1)=1$. Thus, in what follows we will assume that $k>0$.

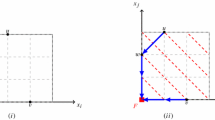
Fix a vertex $v\in V_1$. Call ${\mathcal {X}}_1$ the set of faces of ${\mathcal {K}}$ that are not faces of $\partial {P}_1$, i.e., ${\mathcal {X}}_1={\mathcal {K}}\setminus \partial {P}_1$. It is easy to verify that ${\mathcal {X}}_1$ is also the set of faces of ${\mathcal {K}}_1$ that are not faces of ${\mathcal {S}}_1$, i.e., ${\mathcal {X}}_1={\mathcal {K}}_1\setminus {\mathcal {S}}_1$. Similarly, the faces in ${{\mathcal {X}}_1}/{v}$ is the set of faces ${{\mathcal {K}}}/{v}$ which are not faces in ${\partial {P}_1}/{v}$, or, equivalently, the set of faces of ${{\mathcal {K}}_1}/{v}$ that are not faces of ${{\mathcal {S}}_1}/{v}$, i.e., ${{\mathcal {X}}_1}/{v}=({{\mathcal {K}}_1}/{v})\setminus ({{\mathcal {S}}_1}/{v})$ (see also the left two subfigures in Fig. 3). Hence we have

$$\begin{aligned} f_k({\mathcal {X}}_1)=f_k({\mathcal {K}})-f_k(\partial {P}_1)=f_k({\mathcal {K}}_1)-f_k({\mathcal {S}}_1), \qquad -1\le k\le d-1, \end{aligned}$$

and

$$\begin{aligned} f_k({{\mathcal {X}}_1}/{v})=f_k({{\mathcal {K}}}/{v})-f_k({\partial {P}_1}/{v}) =f_k({{\mathcal {K}}_1}/{v})-f_k({{\mathcal {S}}_1}/{v}), \qquad -1\le k\le d-2. \end{aligned}$$

Rewriting these equations in terms of generating functions, we obtain

$$\begin{aligned} {\mathtt {f}}({{\mathcal {X}}_1};t) = {\mathtt {f}}({{\mathcal {K}}};t)-t\,{\mathtt {f}}({\partial {P}_1};t) = {\mathtt {f}}({{\mathcal {K}}_1};t)-{\mathtt {f}}({{\mathcal {S}}_1};t) \end{aligned}$$

and

$$\begin{aligned} {\mathtt {f}}({{{\mathcal {X}}_1}/{v}};t) = {\mathtt {f}}({{{\mathcal {K}}}/{v}};t)-t\,{\mathtt {f}}({{\partial {P}_1}/{v}};t) = {\mathtt {f}}({{{\mathcal {K}}_1}/{v}};t)-{\mathtt {f}}({{{\mathcal {S}}_1}/{v}};t). \end{aligned}$$

Using (10), we further deduce that

$$\begin{aligned} {\mathtt {h}}({{\mathcal {X}}_1};t)= & {} {\mathtt {h}}({{\mathcal {K}}};t)-(t-1) {\mathtt {h}}({\partial {P}_1};t) = {\mathtt {h}}({{\mathcal {K}}};t)-{\mathtt {g}}({\partial {P}_1};t) \nonumber \\= & {} {\mathtt {h}}({{\mathcal {K}}_1};t)-{\mathtt {h}}({{\mathcal {S}}_1};t) \end{aligned}$$

(34)

and

$$\begin{aligned} {\mathtt {h}}({{{\mathcal {X}}_1}/{v}};t)= & {} {\mathtt {h}}({{{\mathcal {K}}}/{v}};t)-(t-1) {\mathtt {h}}({{\partial {P}_1}/{v}};t) = {\mathtt {h}}({{{\mathcal {K}}}/{v}};t)-{\mathtt {g}}({{\partial {P}_1}/{v}};t) \\= & {} {\mathtt {h}}({{{\mathcal {K}}_1}/{v}};t)-{\mathtt {h}}({{{\mathcal {S}}_1}/{v}};t). \end{aligned}$$

Consider now a shelling ${\mathbb {S}}(\partial {Q})$ of $\partial {Q}$ that shells the star of $y_1$ first and the star of $y_2$ last. Such a shelling does exist since $y_1$ and $y_2$ are not visible from each other: $y_j$ is beyond the facet $P_j$ of ${\mathcal {C}}$, $j=1,2$, while $P_1$ and $P_2$ are parallel to each other (the purple numbers in the top-left subfigure of Fig. 3 indicate such a shelling). The shelling ${\mathbb {S}}(\partial {Q})$ gives a shelling ${\mathbb {S}}({\mathcal {K}}_1)$ for ${\mathcal {K}}_1$ (we just have to discard the facets at the end of ${\mathbb {S}}(\partial {Q})$ that are facets in ${\mathcal {S}}_2$), which shells the star of $y_1$ in $\partial {Q}$ first. In turn, ${\mathbb {S}}({\mathcal {K}}_1)$ induces a shelling ${\mathbb {S}}({{\mathcal {K}}_1}/{v})$ for ${{\mathcal {K}}_1}/{v}$, which shells the star of $y_1$ in ${{\mathcal {K}}_1}/{v}$ first (this induced shelling is shown for the star of v in $\partial {Q}$ in the top-right subfigure of Fig. 3).³

Fig. 3

Top left The complex $\partial {Q}$ from Fig. 2, cut along the edges $y_1a_1$–$a_1b_1$–$b_1y_2$ and embedded in the plane. The colored edges are identified. The vertex v is shown in orange. The purple numbers refer to a shelling of $\partial {Q}$ that shells ${\text {star}}(y_1,\partial {Q})$ first and ${\text {star}}(y_2,\partial {Q})$ last. The directed graph in red is the dual graph $G^{\Delta }(\partial {Q})$ of $\partial {Q}$ whose edge orientations correspond to the shelling of $\partial {Q}$ indicated in the figure. Top right The complex ${\text {star}}(v,\partial {Q})$. The purple numbers refer to the shelling order of ${\text {star}}(v,\partial {Q})$ induced by the shelling in the figure to the left (with the numbers in parenthesis being the order of the corresponding facets in the shelling of $\partial {Q}$). The directed graph in red is the dual graph $G^{\Delta }({\text {star}}(v,\partial {Q}))$ of ${\text {star}}(v,\partial {Q})$ that corresponds to the shelling of ${\text {star}}(v,\partial {Q})$ shown in the figure; observe that $G^{\Delta }({\partial {Q}}/{v})$ is the subgraph of $G^{\Delta }(\partial {Q})$ corresponding to the vertices of $G^{\Delta }({\text {star}}(v,\partial {Q}))$ that are duals of facets in ${\text {star}}(v,\partial {Q})$. Bottom left The set of faces ${\mathcal {X}}_1$ of $\partial {Q}$, along with the portion of $G^{\Delta }(\partial {Q})$ that corresponds to the vertices that are duals of facets of ${\mathcal {X}}_1$. Bottom right The set of faces ${\text {star}}(v,{\mathcal {X}}_1)$ of ${\text {star}}(v,\partial {Q})$, along with the portion of $G^{\Delta }({\text {star}}(v,\partial {Q}))$ that corresponds to the vertices that are duals of facets of ${\text {star}}(v,{\mathcal {X}}_1)$. For the particular example shown: ${\varvec{h}}(\partial {Q})=(1,16,16,1)$, ${\varvec{h}}({\partial {Q}}/{v})=(1,4,1)$, ${\varvec{h}}({\mathcal {X}}_1)=(0,8,9,0)$, and ${\varvec{h}}({{\mathcal {X}}_1}/{v})=(0,3,1)$

Let us now consider the dual graph $G^\Delta (\partial {Q})$ of $\partial {Q}$, oriented⁴ according to the shelling ${\mathbb {S}}(\partial {Q})$, as well as the dual graph $G^\Delta ({\partial {Q}}/{v})$ of ${\partial {Q}}/{v}$, also oriented according to the shelling ${\mathbb {S}}({\partial {Q}}/{v})$ (these graphs are shown in red in the top two subfigures of Fig. 3). We will denote by $V^\Delta ({\mathcal {Y}})$ the vertices of $G^\Delta (\partial {Q})$ that are the duals of the facets in $\partial {Q}$ that belong to ${\mathcal {Y}}$, where ${\mathcal {Y}}$ stands for a subset of the set of proper faces of $\partial {Q}$; for simplicity we will abbreviate $V^\Delta (\partial {Q})$ to $V^\Delta$.

Since ${\mathbb {S}}({\partial {Q}}/{v})$ is induced from ${\mathbb {S}}(\partial {Q})$, $G^\Delta ({\partial {Q}}/{v})$ is isomorphic to the subgraph of $G^\Delta (\partial {Q})$ defined over $V^\Delta ({\text {star}}(v,\partial {Q}))$. Moreover, $h_k(\partial {Q})$ counts the number of vertices of $V^\Delta$ of in-degree equal to k [12], while $h_k({\mathcal {S}}_1)$ counts the number of vertices of $V^\Delta ({\mathcal {S}}_1)$ of in-degree k in $G^\Delta (\partial {Q})$ (for the particular shelling ${\mathbb {S}}(\partial {Q})$ of $\partial {Q}$ that we have chosen). Consequently, $h_k({\mathcal {X}}_1)$ counts the number of vertices of $V^\Delta ({\mathcal {X}}_1)$ of in-degree k in $G^\Delta (\partial {Q})$; in an analogous manner, we can conclude that $h_k({{\mathcal {X}}_1}/{v})$ counts the number of vertices of $V^\Delta ({\text {star}}(v,{\mathcal {X}}_1))$ with in-degree k in $G^\Delta ({\partial {Q}}/{v})$ (refer to the bottom two subfigures of Fig. 3 to verify these facts for the particular example shown in the figure). Since, however, $G^\Delta ({\partial {Q}}/{v})$ is a subgraph of $G^\Delta (\partial {Q})$, the number of vertices of $V^\Delta ({\text {star}}(v,{\mathcal {X}}_1))$ with in-degree k cannot exceed the number of vertices of $V^{\Delta }({\mathcal {X}}_1)$ with in-degree k. Hence, $h_k({{\mathcal {X}}_1}/{v})\le h_k({\mathcal {X}}_1)$, which is precisely relation (33). $\square$

Using Lemma 11, we can now derive the following generating function inequality, which is essential in our upper bound proof.

Lemma 12

The following inequality holds:

$$\begin{aligned} t(1-t)\,{\mathtt {h'}}({{\mathcal {F}}};t) \preccurlyeq [n_1+n_2-t(d+1)]\,{\mathtt {h}}({{\mathcal {F}}};t) + n_1\,{\mathtt {g}}({\partial {P}_2};t) + n_2\,{\mathtt {g}}({\partial {P}_1};t). \end{aligned}$$

(35)

Proof

Let us denote by V the vertex set of $\partial {Q}$ and by $V_j$ the vertex set of $\partial {P_j}$, $j=1,2$.

Applying Lemma 3 to Q, $P_1$, and $P_2$, we get the following relations:

$$\begin{aligned} (d+1){\mathtt {h}}({\partial {Q}};t)+(1-t){\mathtt {h'}}({\partial {Q}};t)&=\sum _{v\in V}{\mathtt {h}}({{\partial {Q}}/{v}};t), \end{aligned}$$

(36)

$$\begin{aligned} d\,{\mathtt {h}}({\partial {P_j}};t)+(1-t){\mathtt {h'}}({\partial {P_j}};t)&=\sum _{v\in V_j}{\mathtt {h}}({{\partial {P_j}}/{v}};t),\qquad j=1,2. \end{aligned}$$

(37)

Recall that the link of $y_j$ in $\partial {Q}$ is $\partial {P_j}$, $j=1,2$, and observe that the link of $v\in V_j$ in $\partial {Q}$ coincides with ${{\mathcal {K}}_j}/{v}$. Expanding relation (36) by means of relation (26), we deduce

$$\begin{aligned} \begin{aligned}&(d+1)\Big [{\mathtt {h}}({{\mathcal {F}}};t)+t\sum _{j=1}^{2}{\mathtt {h}}({\partial {P_j}};t)\Big ]\\&\qquad +(1-t)\Big [{\mathtt {h'}}({{\mathcal {F}}};t)+\sum _{j=1}^{2}[{\mathtt {h}}({\partial {P_j}};t)+t{\mathtt {h'}}({\partial {P}_j};t)]\Big ]\\&\quad =(d+1){\mathtt {h}}({{\mathcal {F}}};t)+(1-t){\mathtt {h'}}({{\mathcal {F}}};t) +t[d\,{\mathtt {h}}({\partial {P_1}};t)+(1-t){\mathtt {h'}}({\partial {P_1}};t)]\\&\qquad +t[d\,{\mathtt {h}}({\partial {P_2}};t)+(1-t){\mathtt {h'}}({\partial {P_2}};t)] +{\mathtt {h}}({\partial {P_1}};t)+{\mathtt {h}}({\partial {P_2}};t)\\&\quad =\sum _{v\in V}{\mathtt {h}}({{\partial {Q}}/{v}};t) ={\mathtt {h}}({{\partial {Q}}/{y_1}};t)+{\mathtt {h}}({{\partial {Q}}/{y_2}};t) +\sum _{v\in V_1\cup V_2}{\mathtt {h}}({{\partial {Q}}/{v}};t)\\&\quad ={\mathtt {h}}({\partial {P_1}};t)+{\mathtt {h}}({\partial {P_2}};t) +\sum _{v\in V_1}{\mathtt {h}}({{{\mathcal {K}}_1}/{v}};t)+\sum _{v\in V_2}{\mathtt {h}}({{{\mathcal {K}}_2}/{v}};t). \end{aligned} \end{aligned}$$

Utilizing relations (37), the above equation is equivalent to

$$\begin{aligned} (d+1){\mathtt {h}}({{\mathcal {F}}};t)+(1-t){\mathtt {h'}}({{\mathcal {F}}};t) =\sum _{j=1}^{2}\sum _{v\in V_j}[{\mathtt {h}}({{{\mathcal {K}}_j}/{v}};t)-t\,{\mathtt {h}}({{\partial {P}_j}/{v}};t)]. \end{aligned}$$

(38)

Using an analogous argumentation to that used for deriving relation (24), we deduce that, for any $v\in V_j$, $j=1,2$, we have

$$\begin{aligned} {\mathtt {f}}({{{\mathcal {K}}_j}/{v}};t)={\mathtt {f}}({{{\mathcal {K}}}/{v}};t)+{\mathtt {f}}({{\partial {P}_j}/{v}};t). \end{aligned}$$

Using relation (10), we readily get

$$\begin{aligned} {\mathtt {h}}({{{\mathcal {K}}_j}/{v}};t)={\mathtt {h}}({{{\mathcal {K}}}/{v}};t)+{\mathtt {h}}({{\partial {P}_j}/{v}};t). \end{aligned}$$

Substituting in (38), we finally get

$$\begin{aligned}&(d+1){\mathtt {h}}({{\mathcal {F}}};t)+(1-t){\mathtt {h'}}({{\mathcal {F}}};t)\nonumber \\&\quad =\sum _{j=1}^{2}\sum _{v\in V_j}[{\mathtt {h}}({{{\mathcal {K}}}/{v}};t)+{\mathtt {h}}({{\partial {P}_j}/{v}};t)-\,t{\mathtt {h}}({{\partial {P}_j}/{v}};t)]\nonumber \\&\quad =\sum _{j=1}^{2}\sum _{v\in V_j}[{\mathtt {h}}({{{\mathcal {K}}}/{v}};t)-{\mathtt {g}}({{\partial {P}_j}/{v}};t)]. \end{aligned}$$

(39)

Thus, by applying Lemma 11 and using relation (28), we get for every vertex $v\in V_1$

Similarly, by applying Lemma 11 and using relation (28), we get for every vertex $v\in V_2$

We thus arrive at the following inequality, for $0\le k\le d$,

$$\begin{aligned}&t(d+1){\mathtt {h}}({{\mathcal {F}}};t)+t(1-t){\mathtt {h'}}({{\mathcal {F}}};t)\nonumber \\&\quad \preccurlyeq (n_1+n_2)\,{\mathtt {h}}({{\mathcal {F}}};t) +n_1\,{\mathtt {g}}({\partial {P_2}};t)+n_2\,{\mathtt {g}}({\partial {P_1}};t), \end{aligned}$$

(40)

which gives the inequality in the statement of the lemma. $\square$

Corollary 13

For all $0\le k\le d$,

$$\begin{aligned} h_{k+1}({\mathcal {F}})\le \frac{n_1+n_2-d-1+k}{k+1}\,h_k({\mathcal {F}}) +\frac{n_1}{k+1}\,g_k(\partial {P_2})+\frac{n_2}{k+1}\,g_k(\partial {P_1}). \end{aligned}$$

(41)

Proof

Expanding the generating functions in relation (40), we have

$$\begin{aligned}&t\sum _{k=0}^{d+1}(d+1) h_k({\mathcal {F}})\,t^{d+1-k} +t(1-t)\sum _{k=0}^{d+1}(d+1-k)h_k({\mathcal {F}})\,t^{d-k}\\&\quad \preccurlyeq (n_1+n_2)\sum _{k=0}^{d+1}h_k({\mathcal {F}})\,t^{d+1-k} +n_1\sum _{k=0}^{d+1}g_k(\partial {P}_2)\,t^{d+1-k} + n_2\sum _{k=0}^{d+1}g_k(\partial {P}_1)\,t^{d+1-k}, \end{aligned}$$

or, equivalently,

$$\begin{aligned}&\sum _{k=0}^{d+1}(d+1-k) h_k({\mathcal {F}})\,t^{d+1-k} +\sum _{k=0}^{d+1}k h_k({\mathcal {F}})\,t^{d+2-k}\\&\quad \preccurlyeq (n_1+n_2)\sum _{k=0}^{d+1}h_k({\mathcal {F}})\,t^{d+1-k} +n_1\sum _{k=0}^{d+1}g_k(\partial {P}_2)\,t^{d+1-k}+n_2\sum _{k=0}^{d+1}g_k(\partial {P}_1)\,t^{d+1-k}. \end{aligned}$$

Setting $\lambda = k-1$ in the second sum of the left-hand side, we get

$$\begin{aligned} \sum _{\lambda =-1}^{d}(\lambda +1) h_{\lambda +1}({\mathcal {F}})\,t^{d+1-\lambda } \preccurlyeq \,&(n_1+n_2-d-1+k)\sum _{k=0}^{d+1}h_k({\mathcal {F}})\,t^{d+1-k}\\&+n_1\sum _{k=0}^{d+1}g_k(\partial {P}_2)\,t^{d+1-k} +n_2\sum _{k=0}^{d+1}g_k(\partial {P}_1)\,t^{d+1-k}. \end{aligned}$$

Equating terms of equal power of t, we get the following relation for all $0\le k\le d$:

$$\begin{aligned} (k+1) h_{k+1}({\mathcal {F}})\le (n_1+n_2-d-1+k)h_k({\mathcal {F}})+n_1g_k(\partial {P}_2)+n_2g_k(\partial {P}_1), \end{aligned}$$

which gives relation (41). $\square$

Using the recurrence relation from Corollary 13, we get the following bounds on the elements of ${\varvec{h}}({\mathcal {F}})$.

Lemma 14

For all $0\le k\le d+1$,

$$\begin{aligned} h_k({\mathcal {F}})\le \left( {\begin{array}{c}n_1+n_2-d-2+k\\ k\end{array}}\right) -\left( {\begin{array}{c}n_1-d-2+k\\ k\end{array}}\right) -\left( {\begin{array}{c}n_2-d-2+k\\ k\end{array}}\right) . \end{aligned}$$

(42)

Equality holds for all k with $0\le k\le l$ if and only if $l\le \lfloor \frac{d+1}{2}\rfloor$ and P is $(l,V_1)$-bineighborly.

Proof

We show the desired bound by induction on k. Clearly, the bound holds (as equality) for $k=0$, since

$$\begin{aligned} h_0({\mathcal {F}})= & {} -1=1-1-1\nonumber \\ {}= & {} \left( {\begin{array}{c}n_1+n_2-d-2+0\\ 0\end{array}}\right) -\left( {\begin{array}{c}n_1-d-2+0\\ 0\end{array}}\right) -\left( {\begin{array}{c}n_2-d-2+0\\ 0\end{array}}\right) .\nonumber \\ \end{aligned}$$

(43)

Suppose now that the bound holds for $h_k({\mathcal {F}})$, where $k\ge 0$. Using the recurrence relation (41), in conjunction with the upper bounds for the elements of the g-vector of a polytope from Corollary 2, and since for $k\ge 0$, $n_1+n_2-d-1+k\ge d+1>0$, we have

$$\begin{aligned}&h_{k+1}({\mathcal {F}})\nonumber \\&\quad \le \frac{n_1+n_2-d-1+k}{k+1}\,h_k({\mathcal {F}})+\,\frac{n_1}{k+1}\,g_k(\partial {P_2}) +\frac{n_2}{k+1}\,g_k(\partial {P_1})\nonumber \\&\quad \le \frac{n_1+n_2-d-1+k}{k+1}\nonumber \\&\qquad \times \,\Big [\Big (\begin{array}{cc}{n_1+n_2-d-2+k}\nonumber \\ {k}\end{array}\Big ) -\Big (\begin{array}{cc}{n_1-d-2+k}\\ {k}\end{array}\Big )-\Big (\begin{array}{cc}{n_2-d-2+k}\\ {k}\end{array}\Big )\Big ]\nonumber \\&\qquad +\,\frac{n_1}{k+1}\Big (\begin{array}{cc}{n_2-d-2+k}\\ {k}\end{array}\Big ) +\frac{n_2}{k+1}\Big (\begin{array}{cc}{n_1-d-2+k}\\ {k}\end{array}\Big )\nonumber \\\quad&\quad =\frac{n_1+n_2-d-1+k}{k+1}\Big (\begin{array}{cc}{n_1+n_2-d-2+k}\\ {k}\end{array}\Big )\nonumber \\&\qquad -\,\frac{n_1-d-1+k}{k+1}\Big (\begin{array}{cc}{n_1-d-2+k}\\ {k}\end{array}\Big )-\frac{n_2-d-1+k}{k+1}\Big (\begin{array}{cc}{n_2-d-2+k}\\ {k}\end{array}\Big )\nonumber \\&\quad =\Big (\begin{array}{cc}{n_1+n_2-d-1+k}\\ {k+1}\end{array}\Big )-\Big (\begin{array}{cc}{n_1-d-1+k}\\ {k+1}\end{array}\Big ) -\Big (\begin{array}{cc}{n_2-d-1+k}\\ {k+1}\end{array}\Big ). \end{aligned}$$

(44)

Let us now turn to our equality claim. The claim for $l=0$ is obvious (cf. (43)), so we assume below that $l\ge 1$.

Suppose first that P is $(l,V_1)$-bineighborly. Then, we have

$$\begin{aligned} f_{i-1}({\mathcal {F}})=\left( {\begin{array}{c}n_1+n_2\\ i\end{array}}\right) -\left( {\begin{array}{c}n_1\\ i\end{array}}\right) -\left( {\begin{array}{c}n_2\\ i\end{array}}\right) , \qquad 0\le i\le l. \end{aligned}$$

(45)

Substituting $f_{i-1}({\mathcal {F}})$ from (45) in the defining (25) for ${\varvec{h}}({\mathcal {F}})$, we get, for all $0\le k\le l$

$$\begin{aligned} h_k({\mathcal {F}})= & {} \sum _{i=0}^{k}(-1)^{k-i}\left( {\begin{array}{c}d+1-i\\ d+1-k\end{array}}\right) f_{i-1}({\mathcal {F}})\\= & {} \sum _{i=0}^{k}(-1)^{k-i}\left( {\begin{array}{c}d+1-i\\ d+1-k\end{array}}\right) \Bigg (\left( {\begin{array}{c}n_1+n_2\\ i\end{array}}\right) -\left( {\begin{array}{c}n_1\\ i\end{array}}\right) -\left( {\begin{array}{c}n_2\\ i\end{array}}\right) \Bigg )\\= & {} \sum _{i=0}^{k}(-1)^{k-i}\left( {\begin{array}{c}d+1-i\\ d+1-k\end{array}}\right) \left( {\begin{array}{c}n_1+n_2\\ i\end{array}}\right) -\sum _{i=0}^{k}(-1)^{k-i}\left( {\begin{array}{c}d+1-i\\ d+1-k\end{array}}\right) \left( {\begin{array}{c}n_1\\ i\end{array}}\right) \\&-\sum _{i=0}^{k}(-1)^{k-i}\left( {\begin{array}{c}d+1-i\\ d+1-k\end{array}}\right) \left( {\begin{array}{c}n_2\\ i\end{array}}\right) \\= & {} \,\left( {\begin{array}{c}n_1+n_2-d-2+k\\ k\end{array}}\right) -\left( {\begin{array}{c}n_2-d-2+k\\ k\end{array}}\right) -\left( {\begin{array}{c}n_2-d-2+k\\ k\end{array}}\right) , \end{aligned}$$

where for the last equality we used the fact that $\left( {\begin{array}{c}d+1-i\\ d+1-k\end{array}}\right) =0$ for $i>k$, in conjunction with the following combinatorial identity (cf. [9, Eq. (5.25)], [28, Exer. 8.20]):

$$\begin{aligned} \sum _{0\le k\le l}\left( {\begin{array}{c}l-k\\ m\end{array}}\right) \left( {\begin{array}{c}s\\ k-n\end{array}}\right) (-1)^k =(-1)^{l+m}\left( {\begin{array}{c}s-m-1\\ l-m-n\end{array}}\right) . \end{aligned}$$

In the equation above we set $k\leftarrow i$, $l\leftarrow d+1$, $m\leftarrow d+1-k$, $n\leftarrow 0$, while s stands for either $n_1+n_2$, $n_1$ or $n_2$. We thus conclude that (42) holds as equality for all $0\le k\le l$.

Suppose now that inequality (42) holds as equality for all $0\le k\le l$. Solving (25) in terms of ${\varvec{f}}({\mathcal {F}})$ (cf. also (5)) and substituting $h_i({\mathcal {F}})$, $0\le i\le l$, from (42), we get

$$\begin{aligned}&f_{l-1}({\mathcal {F}})\nonumber \\&\quad =\sum _{i=0}^{d+1}\left( {\begin{array}{c}d+1-i\\ l-i\end{array}}\right) h_i({\mathcal {F}})\nonumber \\&\quad =\sum _{i=0}^{d+1}\left( {\begin{array}{c}d+1-i\\ l-i\end{array}}\right) \Bigg (\left( {\begin{array}{c}n_1+n_2-d-2+i\\ i\end{array}}\right) -\left( {\begin{array}{c}n_1-d-2+i\\ i\end{array}}\right) -\left( {\begin{array}{c}n_2-d-2+i\\ i\end{array}}\right) \Bigg )\nonumber \\&\quad =\sum _{i=0}^{d+1}\left( {\begin{array}{c}d+1-i\\ l-i\end{array}}\right) \left( {\begin{array}{c}n_1+n_2-d-2+i\\ i\end{array}}\right) -\sum _{i=0}^{d+1}\left( {\begin{array}{c}d+1-i\\ l-i\end{array}}\right) \left( {\begin{array}{c}n_1-d-2+i\\ i\end{array}}\right) \nonumber \\&\qquad -\sum _{i=0}^{d+1}\left( {\begin{array}{c}d+1-i\\ l-i\end{array}}\right) \left( {\begin{array}{c}n_2-d-2+i\\ i\end{array}}\right) \nonumber \\&\quad =\sum _{i=0}^{d+1}\left( {\begin{array}{c}d+1-i\\ d+1-l\end{array}}\right) \left( {\begin{array}{c}n_1+n_2-d-2+i\\ n_1+n_2-d-2\end{array}}\right) -\sum _{i=0}^{d+1}\left( {\begin{array}{c}d+1-i\\ d+1-l\end{array}}\right) \left( {\begin{array}{c}n_1-d-2+i\\ n_1-d-2\end{array}}\right) \nonumber \\&\qquad -\sum _{i=0}^{d+1}\left( {\begin{array}{c}d+1-i\\ d+1-l\end{array}}\right) \left( {\begin{array}{c}n_2-d-2+i\\ n_2-d-2\end{array}}\right) \end{aligned}$$

(46)

$$\begin{aligned}&\quad = \Big (\begin{array}{cc}{(d+1)+(n_1+n_2-d-2)+1}\\ {(d+1-l)+(n_1+n_2-d-2)+1}\end{array}\Big )\nonumber \\&\qquad -\Big (\begin{array}{cc}{(d\,{+}\,1)\,{+}\,(n_1\,{-}\,d\,{-}\,2)\,{+}\,1}\\ {(d\,{+}\,1\,{-}\,l)\,{+}\,(n_1\,{-}\,d\,{-}\,2)\,{+}\,1}\end{array}\Big ) \,{-}\,\Big (\begin{array}{cc}{(d\,{+}\,1)\,{+}\,(n_2\,{-}\,d\,{-}\,2)\,{+}\,1}\\ {(d\,{+}\,1\,{-}\,l)\,{+}\,(n_2\,{-}\,d\,{-}\,2)\,{+}\,1}\end{array}\Big ) \qquad \qquad \end{aligned}$$

(47)

$$\begin{aligned}&=\Big (\begin{array}{cc}{n_1+n_2}\\ {n_1+n_2-l}\end{array}\Big )- \Big (\begin{array}{cc}{n_1}\\ {n_1-l}\end{array}\Big )-\Big (\begin{array}{cc}{n_2}\\ {n_2-l}\end{array}\Big )\\&=\Big (\begin{array}{cc}{n_1+n_2}\\ {l}\end{array}\Big )-\Big (\begin{array}{cc}{n_1}\\ {l}\end{array}\Big )-\Big (\begin{array}{cc}{n_2}\\ {l}\end{array}\Big ), \end{aligned}$$

where, in order to get from (46) to (47), we used the combinatorial identity (cf. [9, Eq. (5.26)]):

$$\begin{aligned} \sum _{0\le k\le l}\Big (\begin{array}{cc}{l-k}\\ {m}\end{array}\Big )\Big (\begin{array}{cc}{q+k}\\ {n}\end{array}\Big ) =\Big (\begin{array}{cc}{l+q+1}\\ {m+n+1} \end{array}\Big ), \end{aligned}$$

with $k\leftarrow i$, $l\leftarrow d+1$, $m\leftarrow d+1-k$, $q\leftarrow s-d-2$, $n\leftarrow s-d-2$, and s stands for either $n_1+n_2$, $n_1$ or $n_2$. Hence, P is $(l,V_1)$-bineighborly. $\square$

Using the Dehn–Sommerville-like relations (49), in conjunction with the bounds from the previous lemma, we derive alternative bounds for $h_k({\mathcal {F}})$, which are of interest since they refine the bounds for $h_k({\mathcal {F}})$ from Lemma 14 for large values of k, namely for $k>\lfloor \frac{d+1}{2}\rfloor$. More precisely:

Lemma 15

For all $0\le k\le d+1$,

$$\begin{aligned} h_{d+1-k}({\mathcal {F}})\le \Big (\begin{array}{cc}{n_1+n_2-d-2+k}\\ {k}\end{array}\Big ). \end{aligned}$$

(48)

Equality holds for all k with $0\le k\le l$ if and only if $l\le \lfloor \frac{d}{2}\rfloor$ and P is l-neighborly.

Proof

The Dehn–Sommerville-like relation (29) corresponds to the following equalities for the elements of ${\varvec{h}}({\mathcal {F}})$:

$$\begin{aligned} h_{d+1-k}({\mathcal {F}})=h_k({\mathcal {F}})+g_k(\partial {P}_1)+g_k(\partial {P}_2), \qquad 0\le k\le d+1. \end{aligned}$$

(49)

The upper bound claim in (48) is then a direct consequence of relation (49), the upper bounds from Lemma 14, and the Upper Bound Theorem for polytopes as stated in Corollary 2.

The rest of the proof deals with the equality claim. In view of the Dehn–Sommerville-like equations $h_{d+1-k}({\mathcal {F}})=h_k({\mathcal {F}})+g_k(\partial {P}_1)+g_k(\partial {P}_2),$ the inequality (48) holds as equality for all $0\le k\le l$, where $l\le \lfloor \frac{d}{2}\rfloor$, if and only if the following two conditions hold:

• (i) inequality (42) holds as equality for all $0\le k\le l\le \lfloor \frac{d}{2}\rfloor$,

• (ii) for $j=1,2$ and all $0\le k\le l\le \lfloor \frac{d}{2}\rfloor$, we have $g_k(\partial {P}_j)=\left( {\begin{array}{c}n_j-d-2+k\\ k\end{array}}\right)$.

The first condition holds true if and only if P is $(l,V_1)$-bineighborly, while the second condition holds true if and only if $P_j$, $j=1,2$, is l-neighborly. Therefore, inequality (48) holds as equality for all $0\le k\le l$ if and only if $l\le \lfloor \frac{d}{2}\rfloor$, P is $(l,V_1)$-bineighborly and both $P_1$, $P_2$ are l-neighborly. In view of Lemma 7, we conclude that equality in (48) holds for all $0\le k\le l$ if and only if $l\le \lfloor \frac{d}{2}\rfloor$ and P is l-neighborly. $\square$

We are now ready to compute upper bounds for the face numbers of ${\mathcal {F}}$. Using relation (9) , in conjunction with the bounds on the elements of ${\varvec{h}}({\mathcal {F}})$ from Lemmas 14 and 15, we get, for $0\le k\le d+1$:

$$\begin{aligned}&f_{k-1}({\mathcal {F}}) \nonumber \\&\quad =\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big )h_i({\mathcal {F}}) +\sum _{i=\lfloor \frac{d+1}{2}\rfloor +1}^{d+1}\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big )h_i({\mathcal {F}})\nonumber \\&\quad =\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big )h_i({\mathcal {F}}) +\sum _{i=0}^{\lfloor \frac{d}{2}\rfloor }\Big (\begin{array}{cc}{i}\\ {k-d-1+i}\end{array}\Big )h_{d+1-i}({\mathcal {F}})\nonumber \\&\quad \le \sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor } \left( {\begin{array}{c}d+1-i\\ k-i\end{array}}\right) \Bigg ( \left( {\begin{array}{c}n_1+n_2-d-2+i\\ i\end{array}}\right) -\sum _{j=1}^2\left( {\begin{array}{c}n_j-d-2+i\\ i\end{array}}\right) \Bigg )\nonumber \\&\qquad +\sum _{i=0}^{\lfloor \frac{d}{2}\rfloor }\Big (\begin{array}{cc}{i}\\ {k-d-1+i}\end{array}\Big ) \Big (\begin{array}{cc}{n_1+n_2-d-2+i}\\ {i}\end{array}\Big )\nonumber \\&\quad =\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big )\Big (\begin{array}{cc}{n_1+n_2-d-2+i}\\ {i}\end{array}\Big ) \nonumber \\&\qquad +\sum _{i=0}^{\lfloor \frac{d}{2}\rfloor }\Big (\begin{array}{cc}{i}\\ {k-d-1+i}\end{array}\Big ) \Big (\begin{array}{cc}{n_1+n_2-d-2+i}\\ {i}\end{array}\Big )\nonumber \\&\qquad -\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big ) \sum _{j=1}^2\Big (\begin{array}{cc}{n_j-d-2+i}\\ {i}\end{array}\Big ) \end{aligned}$$

(50)

$$\begin{aligned}&\quad =\sum \limits _{i=0}^{\frac{d+1}{2}}{^{^{*}}} \Bigg (\left( {\begin{array}{c}d+1-i\\ k-i\end{array}}\right) +\left( {\begin{array}{c}i\\ k-d-1+i\end{array}}\right) \Bigg ) \left( {\begin{array}{c}n_1+n_2-d-2+i\\ i\end{array}}\right) \nonumber \\&\qquad -\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big ) \sum _{j=1}^2\Big (\begin{array}{cc}{n_j-d-2+i}\\ {i}\end{array}\Big )\\&\quad =f_{k-1}(C_{d+1}(n_1+n_2))-\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big ) \sum _{j=1}^2\Big (\begin{array}{cc}{n_j-d-2+i}\\ {i}\end{array}\Big )\nonumber , \end{aligned}$$

(51)

where $C_d(n)$ stands for the cyclic d-polytope with n vertices, and ${\sum \nolimits _{i=0}^{\frac{\delta }{2}}{^{^{*}}}T_{i}}$ denotes the sum of the elements $T_0, T_1,\ldots ,T_{\lfloor \frac{\delta }{2}\rfloor }$ where the last term is halved if $\delta$ is even; in order to get from (50) to (51), we used an identity proved in Appendix. The following lemma summarizes our results.

Lemma 16

For all $0\le k\le d+1$

$$\begin{aligned} f_{k-1}({\mathcal {F}})\le & {} f_{k-1}(C_{d+1}(n_1+n_2)) \\&\, -\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\left( {\begin{array}{c}d+1-i\\ k-i\end{array}}\right) \Bigg (\left( {\begin{array}{c}n_1-d-2+i\\ i\end{array}}\right) +\left( {\begin{array}{c}n_2-d-2+i\\ i\end{array}}\right) \Bigg ), \end{aligned}$$

where $C_d(n)$ stands for the cyclic d-polytope with n vertices. Furthermore:

• (i) Equality holds for all $0\le k\le l$ if and only if $l\le \lfloor \frac{d+1}{2}\rfloor$ and P is $(l,V_1)$-bineighborly.

• (ii) For $d\ge 2$ even, equality holds for all $0\le k\le d+1$ if and only if P is $\lfloor \frac{d}{2}\rfloor$-neighborly.

• (iii) For $d\ge 3$ odd, equality holds for all $0\le k\le d+1$ if and only if P is $(\lfloor \frac{d+1}{2}\rfloor ,V_1)$-bineighborly.

Since $f_{k-1}(P_1+P_2)=f_k({\mathcal {F}})$ for all $1\le k\le d$, we arrive at the central theorem of this section, stating upper bounds for the face numbers of the Minkowski sum of two d-polytopes.

Theorem 17

Let $P_1$ and $P_2$ be two d-polytopes in ${\mathbb {E}}^d$, $d\ge 2$, with $n_1\ge d+1$ and $n_2\ge d+1$ vertices, respectively. Let also P be the Cayley polytope of $P_1$ and $P_2$ in ${\mathbb {E}}^{d+1}$. Then, for $1\le k\le d$, we have

$$\begin{aligned} f_{k-1}(P_1+P_2)\le & {} f_k(C_{d+1}(n_1+n_2))\\&-\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\left( {\begin{array}{c}d+1-i\\ k+1-i\end{array}}\right) \Bigg (\left( {\begin{array}{c}n_1-d-2+i\\ i\end{array}}\right) +\left( {\begin{array}{c}n_2-d-2+i\\ i\end{array}}\right) \Bigg ). \end{aligned}$$

Furthermore:

• (i) Equality holds for all $1\le k\le l$ if and only if $l\le \lfloor \frac{d-1}{2}\rfloor$ and P is $(l+1,V_1)$-bineighborly.

• (ii) For $d\ge 2$ even, equality holds for all $1\le k\le d$ if and only if P is $\lfloor \frac{d}{2}\rfloor$-neighborly.

• (iii) For $d\ge 3$ odd, equality holds for all $1\le k\le d$ if and only if P is $(\lfloor \frac{d+1}{2}\rfloor ,V_1)$-bineighborly.

5 Tightness of the Upper Bounds

In the previous section we proved upper bounds on the face numbers of the Minkowski sum $P_1+P_2$ of two polytopes $P_1$ and $P_2$, and we provided necessary and sufficient conditions for these bounds to hold. However, there is one remaining important question: Are these bounds tight? In this section we give a positive answer to this question.

We recall, from the introductory section, the already known results, and discuss how they are related to the results in this paper. It is already known (e.g., cf. [4]) that the maximum number of vertices/edges of the Minkowski sum of two polygons (i.e., 2-polytopes) is the sum of the vertices/edges of the summands. These match our expressions for $d=2$ in Theorem 17. Fukuda and Weibel [7] have shown tight expressions for the number of k-faces, $0\le k\le 2$, of the Minkowski sum of two 3-polytopes $P_1$ and $P_2$, as a function of the number of vertices of $P_1$ and $P_2$. These maximal values are given in relations (1) and match our expressions for $d=3$ in Theorem 17. In the same paper, Fukuda and Weibel have shown that given r d-polytopes $P_1,P_2,\ldots ,P_r$, the number of k-faces of $P_1+P_2+\ldots +P_r$ is bounded from above as per relation (2). These bounds have been shown to be tight for $d\ge 4$, $r\le \lfloor \frac{d}{2}\rfloor$, and for all k with $0\le k\le \lfloor \frac{d}{2}\rfloor -r$. For $r=2$, the upper bounds in (2) reduce to

$$\begin{aligned} f_k(P_1+P_2)\le \sum _{j=1}^{k+1}\Big (\begin{array}{cc}{n_1}\\ {j} \end{array}\Big )\Big (\begin{array}{cc}{n_2}\\ {k+2-j} \end{array}\Big ), \qquad 0\le k\le d-1, \end{aligned}$$

(52)

and are tight for all k, with $0\le k\le \lfloor \frac{d}{2}\rfloor -2$. According to Fukuda and Weibel [7], these upper bounds are attained when considering two cyclic d-polytopes $P_1$ and $P_2$, with $n_1$ and $n_2$ vertices, respectively, with disjoint vertex sets. As we show below, this construction gives, in fact, tight bounds on the number of k-faces of the Minkowski sum for all $0\le k\le d-1$, when the dimension d is even.

Theorem 18

Let $d\ge 2$ and d is even. Consider two cyclic d-polytopes $P_1$ and $P_2$ with disjoint vertex sets on the d-dimensional moment curve, and let $n_j$ be the number of vertices of $P_j$, $j=1,2$. Then, for all $1\le k\le d$,

$$\begin{aligned} f_{k-1}(P_1+P_2)= & {} f_k(C_{d+1}(n_1+n_2))\\&-\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\left( {\begin{array}{c}d+1-i\\ k+1-i\end{array}}\right) \Bigg (\left( {\begin{array}{c}n_1-d-2+i\\ i\end{array}}\right) +\left( {\begin{array}{c}n_2-d-2+i\\ i\end{array}}\right) \Bigg ), \end{aligned}$$

where $C_d(n)$ stands for the cyclic d-polytope with n vertices.

Proof

Let $V_1$ and $V_2$ be two disjoint sets of points on the d-dimensional moment curve of cardinality $n_1$ and $n_2$, respectively. Let $P_1$ and $P_2$ be the corresponding cyclic d-polytopes, and call P their Cayley polytope in ${\mathbb {E}}^{d+1}$. As in the previous section, we define ${\mathcal {F}}$ as the set of proper faces of P whose vertex set has non-empty intersection with both $V_1$ and $V_2$. We then get

$$\begin{aligned} f_{\lfloor \frac{d}{2}\rfloor -1}({\mathcal {F}})= & {} f_{\lfloor \frac{d}{2}\rfloor -2}(P_1+P_2) =\sum _{j=1}^{\lfloor \frac{d}{2}\rfloor -1}\Big (\begin{array}{cc}{n_1}\\ {j}\end{array}\Big )\Big (\begin{array}{cc}{n_2}\\ {\lfloor \frac{d}{2}\rfloor -j}\end{array}\Big )\\= & {} \Big (\begin{array}{cc}{n_1+n_2}\\ {\lfloor \frac{d}{2}\rfloor }\end{array}\Big )-\Big (\begin{array}{cc}{n_1}\\ {\lfloor \frac{d}{2}\rfloor }\end{array}\Big ) -\Big (\begin{array}{cc}{n_2}\\ {\lfloor \frac{d}{2}\rfloor }\end{array}\Big ), \end{aligned}$$

which, by Lemma 8, implies that P is $(\lfloor \frac{d}{2}\rfloor ,V_1)$-bineighborly. Using Lemma 7, in conjunction with the fact that both $P_1$ and $P_2$ are $\lfloor \frac{d}{2}\rfloor$-neighborly, we further conclude that P is $\lfloor \frac{d}{2}\rfloor$-neighborly. Hence, by Theorem 17, our upper bounds in Theorem 17 are attained for all face numbers of $P_1+P_2$. $\square$

If $d\ge 5$ and d is odd, however, the construction in [7] gives tight bounds for $f_k(P_1+P_2)$ for all $0\le k\le \lfloor \frac{d}{2}\rfloor -2$, which according to Theorem 17 are not sufficient to establish that the bounds are tight for the face numbers of all dimensions. To establish the tightness of the bounds in Theorem 17 for all the face numbers of all dimensions, we need to construct two d-polytopes $P_1$ and $P_2$, with $n_1$ and $n_2$ vertices, respectively, such that

$$\begin{aligned} f_{\lfloor \frac{d}{2}\rfloor }({\mathcal {F}})=f_{\lfloor \frac{d}{2}\rfloor -1}(P_1+P_2)= \Big (\begin{array}{cc}{n_1+n_2}\\ {\lfloor \frac{d+1}{2}\rfloor }\end{array}\Big ) -\Big (\begin{array}{cc}{n_1}\\ {\lfloor \frac{d+1}{2}\rfloor }\end{array}\Big )- \Big (\begin{array}{cc}{n_2}\\ {\lfloor \frac{d+1}{2}\rfloor }\end{array}\Big ), \end{aligned}$$

or, equivalently, construct two d-polytopes $P_1$ and $P_2$ such that P is $(\lfloor \frac{d+1}{2}\rfloor ,V_1)$-bineighborly.

The rest of this section is devoted to this construction. Before getting into the technical details, we outline our approach. In what follows $d\ge 3$ and d is odd. We denote by ${\varvec{\gamma }}(t)$, $t>0$, the $(d-1)$-dimensional moment curve, i.e., ${\varvec{\gamma }}(t)=(t,t^2,\ldots ,t^{d-1})$, and we define two additional curves ${\varvec{\gamma }}_{1}(t;\zeta )$ and ${\varvec{\gamma }}_{2}(t;\zeta )$ in ${\mathbb {E}}^{d+1}$, as follows:

$$\begin{aligned} \begin{aligned} {\varvec{\gamma }}_{1}(t;\zeta )&=(0,t,\zeta t^d,t^2,t^3,\ldots ,t^{d-1}),\\ {\varvec{\gamma }}_{2}(t;\zeta )&=(1,\zeta t^d,t,t^2,t^3,\ldots ,t^{d-1}), \end{aligned} \qquad t>0,\qquad \zeta \ge 0. \end{aligned}$$

(53)

Notice that ${\varvec{\gamma }}_{1}(t;\zeta )$ and ${\varvec{\gamma }}_{2}(t;\zeta )$, with $\zeta >0$, are d-dimensional moment-like curves,⁵ embedded in the hyperplanes $\{x_1=0\}$ and $\{x_1=1\}$, respectively. Choose $n_1+n_2$ real numbers $\alpha _i$, $i=1,\ldots ,n_1$, and $\beta _i$, $i=1,\ldots ,n_2$, such that $0<\alpha _1<\alpha _2<\cdots <\alpha _{n_1}$ and $0<\beta _1<\beta _2<\cdots <\beta _{n_2}$. Let $\tau$ be a strictly positive parameter determined below, and let $U_1$ and $U_2$ be the $(d-1)$-dimensional point sets:

$$\begin{aligned} \begin{aligned} U_1&=\{{\varvec{\gamma }}_{1}(\alpha _1\tau ),{\varvec{\gamma }}_{1}(\alpha _2\tau ),\ldots , {\varvec{\gamma }}_{1}(\alpha _{n_1}\tau )\},\\ U_2&=\{{\varvec{\gamma }}_{2}(\beta _1),{\varvec{\gamma }}_{2}(\beta _2),\ldots ,{\varvec{\gamma }}_{2}(\beta _{n_2})\}, \end{aligned} \end{aligned}$$

(54)

where ${\varvec{\gamma }}_j(\cdot )$ is used to denote ${\varvec{\gamma }}_j(\cdot ;0)$, for simplicity. Notice that $U_1$ and $U_2$ consist of points on the moment curve ${\varvec{\gamma }}(t)$, embedded in the $(d-1)$-subspaces $\{x_1=0,x_3=0\}$ and $\{x_1=1,x_2=0\}$ of ${\mathbb {E}}^{d+1}$, respectively. Call $Q_j$ the cyclic $(d-1)$-polytope defined as the convex hull of the points in $U_j$, $j=1,2$. We first show that, for sufficiently small $\tau$, any subset U of $\lfloor \frac{d+1}{2}\rfloor$ vertices of $U_1\cup U_2$ such that $U\cap U_j\ne \emptyset$, $j=1,2$, defines a $\lfloor \frac{d}{2}\rfloor$-face of $Q=CH_{d+1}(\{Q_1,Q_2\})$; in other words, we show that, for sufficiently small $\tau$, the $(d+1)$-polytope Q is $(\lfloor \frac{d+1}{2}\rfloor ,U_1)$-bineighborly. We then appropriately perturb $U_1$ and $U_2$ (by considering a positive value for $\zeta$) so that they become d-dimensional. Let $V_1$, $V_2$ be the perturbed vertex sets, and $P_1$, $P_2$ be the resulting d-polytopes ($V_j$ is the vertex set of $P_j$). The final step of our construction amounts to considering the Cayley polytope P of $P_1$ and $P_2$, and arguing that, if the perturbation parameter $\zeta$ is sufficiently small, then P is $(\lfloor \frac{d+1}{2}\rfloor ,V_1)$-bineighborly. In view of Theorem 17, this establishes the tightness of our bounds for all face numbers of $P_1+P_2$.

We start off with a technical lemma. Its proof may be found in Appendix.

Lemma 19

Fix two integers $k,\ell \ge 2$. Let $D_{k,\ell }(\tau )$ be the $(k+\ell )\times (k+\ell )$ determinant:

$$\begin{aligned} D_{k,\ell }(\tau )= \begin{vmatrix} 1&\,\,1&\cdots&1&\,\, 0&\,\,0&\cdots&0\\ x_1\tau&\,\,x_2\tau&\cdots&x_k\tau&\,\,0&\,\,0&\cdots&0\\ 0&\,\,0&\cdots&0&\,\, 1&\,\,1&\cdots&1\\ 0&\,\,0&\cdots&0&\,\,y_1&\,\,y_2&\cdots&y_\ell \\ x_1^2\tau ^2&\,\,x_2^2\tau ^2&\cdots&x_k^2\tau ^2&\,\, y_1^2&\,\,y_2^2&\cdots&y_\ell ^2\\ x_1^3\tau ^3&\,\,x_2^3\tau ^3&\cdots&x_k^3\tau ^3&\,\, y_1^3&\,\,y_2^3&\cdots&y_\ell ^3\\ \vdots&\vdots&\vdots&\,\,\vdots&\vdots&\vdots \\ x_1^m\tau ^m&\,\,x_2^m\tau ^m&\cdots&x_k^m\tau ^m&\,\, y_1^m&\,\,y_2^m&\cdots&y_\ell ^m \end{vmatrix},\qquad m=k+\ell -3, \end{aligned}$$

where $0<x_1<x_2<\cdots <x_k$, $0<y_1<y_2<\cdots <y_\ell$, and $\tau >0$. Then, there exists some $\tau _0>0$ (that depends on the $x_i$’s, the $y_i$’s, k, and $\ell$) such that for all $\tau \in (0,\tau _0)$, the determinant $D_{k,\ell }(\tau )$ is strictly positive.

We now formally proceed with our construction. As described above, consider the vertex sets $U_1$ and $U_2$ (cf. (54)) and call $Q_j$ the cyclic $(d-1)$-polytope with vertex set $U_j$, $j=1,2$. As in the previous section, call $\tilde{\Pi }$ the hyperplane of ${\mathbb {E}}^{d+1}$ with equation $\{x_1=\lambda \}$, $\lambda \in (0,1)$. Let $Q=CH_{d+1}(\{Q_1,Q_2\})$, and let ${\mathcal {F}}_{Q}$ be the set of proper faces of Q with non-empty intersection with $\tilde{\Pi }$, i.e., ${\mathcal {F}}_{Q}$ consists of all the proper faces of Q, the vertex set of which has non-empty intersection with both $U_1$ and $U_2$. The following lemma establishes the first step toward our construction.

Lemma 20

There exists a sufficiently small positive value $\tau ^\star$ for $\tau$ such that the $(d+1)$-polytope Q is $(\lfloor \frac{d+1}{2}\rfloor ,U_1)$-bineighborly.

Proof

Let $t_i=\alpha _i\tau$, $t_i^\varepsilon =(\alpha _i+\varepsilon )\tau$, $1\le i\le n_1$, and $s_i=\beta _i$, $s_i^\varepsilon =\beta _i+\varepsilon$, $1\le i\le n_2$, where $\varepsilon >0$ is chosen such that $\alpha _i+\varepsilon <\alpha _{i+1}$, for all $1\le i<n_1$, and $\beta _i+\varepsilon <\beta _{i+1}$, for all $1\le i<n_2$.

Choose a subset U of $U_1\cup U_2$ of size $\lfloor \frac{d+1}{2}\rfloor$ such that $U\cap U_j\ne \emptyset$, $j=1,2$. We denote by $\mu$ (resp., $\nu$) the cardinality of $U\cap U_1$ (resp., $U\cap U_2$), and, clearly, $\mu +\nu =\lfloor \frac{d+1}{2}\rfloor$. Let ${\varvec{\gamma }}_{1}(t_{i_1}),{\varvec{\gamma }}_{1}(t_{i_2}),\ldots ,{\varvec{\gamma }}_{1}(t_{i_\mu })$ be the vertices in $U\cap U_1$, where $i_1<i_2<\ldots <i_\mu$, and analogously, let ${\varvec{\gamma }}_{2}(s_{j_1}),{\varvec{\gamma }}_{2}(s_{j_2}),\ldots ,{\varvec{\gamma }}_{2}(s_{j_\nu })$ be the vertices in $U\cap U_2$, where $j_1<j_2<\cdots <j_\nu$. Let ${\varvec{x}}=(x_1,x_2,\ldots ,x_{d+1})$ and define the $(d+2)\times (d+2)$ determinant $H_U({\varvec{x}})$ as follows:

$$\begin{aligned}&H_U({\varvec{x}})\nonumber \\&\quad =-\left| \begin{array}{ccccccccccc} 1&{}\quad 1&{}1&{}\cdots &{}1&{}1&{}1&{}1&{}\cdots &{}1&{}1\\ {\varvec{x}}&{}{\varvec{\gamma }}_{1}(t_{i_1})&{}{\varvec{\gamma }}_{1}(t_{i_1}^\varepsilon )&{}\cdots &{}{\varvec{\gamma }}_{1}(t_{i_\mu })&{}{\varvec{\gamma }}_{1}(t_{i_\mu }^\varepsilon ) &{}{\varvec{\gamma }}_{2}(s_{j_1})&{}{\varvec{\gamma }}_{2}(s_{j_1}^\varepsilon )&{}\cdots &{}{\varvec{\gamma }}_{2}(s_{j_\nu })&{}{\varvec{\gamma }}_{2}(s_{j_\nu }^\varepsilon ) \end{array} \right| .\qquad \,\, \end{aligned}$$

(55)

The equation $H_U({\varvec{x}})=0$ is the equation of a hyperplane in ${\mathbb {E}}^{d+1}$ that passes through the points in U.

Consider first the case ${\varvec{u}}\in U_1\setminus U$. Then, ${\varvec{u}}={\varvec{\gamma }}_{1}(t)=(0,t,0,t^2,t^3,\ldots ,t^{d-1})$, $t=\alpha \tau$, for some $\alpha \not \in \{\alpha _{i_1},\alpha _{i_2},\ldots ,\alpha _{i_\mu }\}$, in which case $H_U({\varvec{u}})$ becomes

$$\begin{aligned}&H_U({\varvec{u}})\\&\quad =-\left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1&{}1&{}1&{}\cdots &{}1&{}1&{}1&{}1&{}\cdots &{}1&{}1\\ {\varvec{\gamma }}_{1}(t)&{}{\varvec{\gamma }}_{1}(t_{i_1})&{}{\varvec{\gamma }}_{1}(t_{i_1}^\varepsilon )&{}\cdots &{}{\varvec{\gamma }}_{1}(t_{i_\mu })&{}{\varvec{\gamma }}_{1}(t_{i_\mu }^\varepsilon ) &{}{\varvec{\gamma }}_{2}(s_{j_1})&{}{\varvec{\gamma }}_{2}(s_{j_1}^\varepsilon )&{}\cdots &{}{\varvec{\gamma }}_{2}(s_{j_\nu })&{}{\varvec{\gamma }}_{2}(s_{j_\nu }^\varepsilon ) \end{array} \right| \\&\quad =\left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1&{}1&{}1&{}\cdots &{}1&{}1&{}1&{}1&{}\cdots &{}1&{}1\\ t&{}t_{i_1}&{}t_{i_1}^\varepsilon &{}\cdots &{}t_{i_\mu }&{}t_{i_\mu }^\varepsilon &{}0&{}0&{}\cdots &{}0&{}0\\ 0&{}0&{}0&{}\cdots &{}0&{}0&{}1&{}1&{}\cdots &{}1&{}1\\ 0&{}0&{}0&{}\cdots &{}0&{}0&{}s_{j_1}&{}s_{j_1}^\varepsilon &{}\cdots &{}s_{j_\nu }&{}s_{j_\nu }^\varepsilon \\ t^2&{}t_{i_1}^2&{}(t_{i_1}^\varepsilon )^2&{}\cdots &{}t_{i_\mu }^2&{}(t_{i_\mu }^\varepsilon )^2 &{}s_{j_1}^2&{}(s_{j_1}^\varepsilon )^2 &{}\cdots &{}s_{j_\nu }^2&{}(s_{j_\nu }^\varepsilon )^2\\ t^3&{}t_{i_1}^3&{}(t_{i_1}^\varepsilon )^3&{}\cdots &{}t_{i_\mu }^3&{}(t_{i_\mu }^\varepsilon )^3 &{}s_{j_1}^3&{}(s_{j_1}^\varepsilon )^3 &{}\cdots &{}s_{j_\nu }^3&{}(s_{j_\nu }^\varepsilon )^3\\ \vdots &{}\vdots &{}\vdots &{}&{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}&{}\vdots &{}\vdots \\ t^{d-1}&{}t_{i_1}^{d-1}&{}(t_{i_1}^\varepsilon )^{d-1}&{}\cdots &{}t_{i_\mu }^{d-1}&{} (t_{i_\mu }^\varepsilon )^{d-1}&{} s_{j_1}^{d-1}&{}(s_{j_1}^\varepsilon )^{d-1}&{}\cdots &{}s_{j_\nu }^{d-1} &{}(s_{j_\nu }^\varepsilon )^{d-1} \end{array}\right| . \end{aligned}$$

Observe now that we can transform $H_U({\varvec{u}})$ in the form of the determinant $D_{k,\ell }(\tau )$ of Lemma 19, where $k=2\mu +1$ and $\ell =2\nu$, by means of the following determinant transformations:

• (i) Subtract the third row of $H_U({\varvec{u}})$ from the first.

• (ii) Shift the first column of $H_U({\varvec{u}})$ to the right so that all columns of $H_U({\varvec{u}})$ are arranged in increasing order according to their parameter. Clearly, this can be done with an even number of column swaps.

The case ${\varvec{u}}\in U_2\setminus U$ is entirely analogous.

We thus conclude that, for any specific choice of U, and for any specific point ${\varvec{u}}\in (U_1\cup U_2)\setminus U$, there exists some $\tau _0>0$ (cf. Lemma 19) that depends on ${\varvec{u}}$ and U and such that for all $\tau \in (0,\tau _0)$, $H_U({\varvec{u}})>0$. Since the number of all such choices is finite, it suffices to consider a value $\tau ^\star$ for $\tau$ that is small enough so that all possible determinants $H_U({\varvec{u}})$ are strictly positive. For this specific choice of $\tau$, every subset of U of $U_1\cup U_2$, where $|U|=\lfloor \frac{d+1}{2}\rfloor$, $U\cap U_j\ne \emptyset$, $j=1,2$, defines a $\lfloor \frac{d}{2}\rfloor$-face of Q, which means that Q is $(\lfloor \frac{d+1}{2}\rfloor ,U_1)$-bineighborly. $\square$

We are now ready to perform the last step of our construction. In the remainder of this section we assume that $\tau$ is equal to $\tau ^\star$ so that the polytopes $Q_1, Q_2$ constructed above have all the properties mentioned in the proof of Lemma 20. We consider the vertex sets $U_1, U_2$ of the polytopes $Q_1, Q_2$, respectively, and perturb them to get the vertex sets $V_1$ and $V_2$. We do this by considering vertices on the curves ${\varvec{\gamma }}_{1}(t;\zeta )$ and ${\varvec{\gamma }}_{2}(t;\zeta )$, with $\zeta >0$ instead of the curves ${\varvec{\gamma }}_{1}(t)$ and ${\varvec{\gamma }}_{2}(t)$ (cf. (53)). More precisely, define the sets $V_1$ and $V_2$ as

$$\begin{aligned} \begin{aligned} V_1&=\{{\varvec{\gamma }}_{1}(\alpha _1\tau ^\star ;\zeta ),{\varvec{\gamma }}_{1}(\alpha _2\tau ^\star ;\zeta ), \ldots ,{\varvec{\gamma }}_{1}(\alpha _{n_1}\tau ^\star ;\zeta )\},\quad \text {and}\\ V_2&=\{{\varvec{\gamma }}_{2}(\beta _1;\zeta ),{\varvec{\gamma }}_{2}(\beta _2;\zeta ),\ldots , {\varvec{\gamma }}_{2}(\beta _{n_2};\zeta )\}, \end{aligned} \end{aligned}$$

(56)

where $\zeta >0$. Let $P_j$ be the convex hull of the vertices in $V_j$, $j=1,2$, and notice that $P_j$ is a $\lfloor \frac{d}{2}\rfloor$-neighborly d-polytope. Let P be the Cayley polytope of $P_1$ and $P_2$, and let ${\mathcal {F}}_P$ be the set of proper faces of P, the vertex set of which has non-empty intersection with both $V_1$ and $V_2$. The following lemma establishes the final step of our construction. In view of Theorem 17, it also establishes the tightness of our bounds for all face numbers of $P_1+P_2$.

Lemma 21

There exists a sufficiently small positive value $\zeta ^\star$ for $\zeta$ such that the $(d+1)$-polytope P is $(\lfloor \frac{d+1}{2}\rfloor ,V_1)$-bineighborly.

Proof

Similarly to what we have done in the proof of Lemma 20, let $t_i=\alpha _i\tau ^\star$, $t_i^\varepsilon =(\alpha _i+\varepsilon )\tau ^\star$, $1\le i\le n_1$, and $s_i=\beta _i$, $s_i^\varepsilon =\beta _i+\varepsilon$, $1\le i\le n_2$, where $\varepsilon >0$ is chosen such that $\alpha _i+\varepsilon <\alpha _{i+1}$, for all $1\le i<n_1$, and $\beta _i+\varepsilon <\beta _{i+1}$, for all $1\le i<n_2$.

Choose V, a subset of $V_1\cup V_2$ of size $\lfloor \frac{d+1}{2}\rfloor$, such that $V\cap V_j\ne \emptyset$, $j=1,2$. Denote by $\mu$ (resp., $\nu$) the cardinality of $V\cap V_1$ (resp., $V\cap V_2$). Considering $\zeta$ as a small positive parameter, let ${\varvec{\gamma }}_{1}(t_{i_1};\zeta ),{\varvec{\gamma }}_{1}(t_{i_2};\zeta ),\ldots ,{\varvec{\gamma }}_{1}(t_{i_\mu };\zeta )$ be the vertices in $V\cap V_1$, where $i_1<i_2<\cdots <i_\mu$, and analogously, let ${\varvec{\gamma }}_{2}(s_{j_1};\zeta ),{\varvec{\gamma }}_{2}(s_{j_2};\zeta ),\ldots ,{\varvec{\gamma }}_{2}(s_{j_\nu };\zeta )$ be the vertices in $V\cap V_2$, where $j_1<j_2<\cdots <j_\nu$. Let ${\varvec{x}}=(x_1,x_2,\ldots ,x_{d+1})$ and define the $(d+2)\times (d+2)$ determinant $F_V({\varvec{x}};\zeta )$ as

$$\begin{aligned} F_V({\varvec{x}};\zeta )=- \left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1&{}1&{}1&{}\cdots &{}1&{}1&{}1&{}\cdots &{}1\\ {\varvec{x}}&{}{\varvec{\gamma }}_{1}(t_{i_1};\zeta )&{}{\varvec{\gamma }}_{1}(t_{i_1}^\varepsilon ;\zeta )&{}\cdots &{}{\varvec{\gamma }}_{1}(t_{i_\mu }^\varepsilon ;\zeta ) &{}{\varvec{\gamma }}_{2}(s_{j_1};\zeta )&{}{\varvec{\gamma }}_{2}(s_{j_1}^\varepsilon ;\zeta )&{}\cdots &{}{\varvec{\gamma }}_{2}(s_{j_\nu }^\varepsilon ;\zeta ) \end{array} \right| . \end{aligned}$$

(57)

The equation $F_V({\varvec{x}};\zeta )=0$ is the equation of a hyperplane in ${\mathbb {E}}^{d+1}$ that passes through the points in V. We claim that for all vertices ${\varvec{v}}\in (V_1\cup V_2)\setminus V$, we have $F_V({\varvec{v}};\zeta )>0$ for sufficiently small $\zeta$.

To prove our claim, observe that

$$\begin{aligned} \lim _{\zeta \rightarrow 0^+}F_V({\varvec{v}};\zeta )=F_{U}({\varvec{u}};0) =H_{U}({\varvec{u}}), \end{aligned}$$

(58)

where ${\varvec{u}}=\lim _{\zeta \rightarrow 0^+}{\varvec{v}}$ is the projection of ${\varvec{v}}\in V_i\setminus V$ on the curve ${\varvec{\gamma }}_i(t;0), i=1,2,$ and $H_{U}({\varvec{u}})$ is the determinant in relation (55) in the proof of Lemma 20, which is positive due to the way we have chosen $\tau ^\star$. Clearly, $F_V({\varvec{v}};\zeta )$ is a polynomial function in $\zeta$. Since $H_{U}({\varvec{u}})>0,$ relation (58) implies that there exists some $\zeta _0>0$ depending on ${\varvec{v}}$ and V such that, for all $\zeta \in (0,\zeta _0)$, $F_V({\varvec{v}};\zeta )>0$.

We choose a value $\zeta ^{\star }$ for $\zeta$ that is small enough so that, for any $V\subseteq V_1\cup V_2$ with $V\cap V_j\ne \emptyset$, $j=1,2$, and for all $v\in (V_1\cup V_2)\setminus V$, the determinant $F_V({\varvec{v}};\zeta ^{\star })$ is strictly positive. Since the number of such determinants is finite, we conclude that for $\zeta$ equal to $\zeta ^{\star }$, every subset V of $V_1\cup V_2$, where $|V|=\lfloor \frac{d+1}{2}\rfloor$ and $V\cap V_j\ne \emptyset$, $j=1,2$, defines a face of P; this means that P is $(\lfloor \frac{d+1}{2}\rfloor ,V_1)$-bineighborly. $\square$

We are now ready to state the second main theorem of this section that concerns the tightness of our upper bounds on the number of k-faces of the Minkowski sum of two d-polytopes for all $0\le k\le d-1$ and for all odd dimensions $d\ge 3$.

Theorem 22

Let $d\ge 3$ and d is odd. There exist two $\lfloor \frac{d}{2}\rfloor$-neighborly d-polytopes $P_1$ and $P_2$ with $n_1$ and $n_2$ vertices, respectively, such that, for all $1\le k\le d$,

$$\begin{aligned} f_{k-1}(P_1+P_2)= & {} f_k(C_{d+1}(n_1+n_2))\\&-\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\left( {\begin{array}{c}d+1-i\\ k+1-i\end{array}}\right) \Bigg (\left( {\begin{array}{c}n_1-d-2+i\\ i\end{array}}\right) +\,\left( {\begin{array}{c}n_2-d-2+i\\ i\end{array}}\right) \Bigg ), \end{aligned}$$

where $C_d(n)$ stands for the cyclic d-polytope with n vertices.

6 Summary and Open Problems

In this paper we have computed the maximum number of k-faces, $f_k(P_1+P_2)$, $0\le k\le d-1$, of the Minkowski sum of two d-polytopes $P_1$ and $P_2$ as a function of the number of vertices $n_1$ and $n_2$ of these two polytopes. In even dimensions $d\ge 2$, these maximal values are attained if $P_1$ and $P_2$ are cyclic d-polytopes with disjoint vertex sets. In odd dimensions $d\ge 3$, the construction that achieves the upper bounds is more intricate. Denoting by ${\varvec{\gamma }}_{1}(t;\zeta )$ and ${\varvec{\gamma }}_{2}(t;\zeta )$ the d-dimensional moment-like curves $(t,\zeta t^d,t^2,t^3,\ldots ,t^{d-1})$ and $(\zeta t^d,t,t^2,t^3,\ldots ,t^{d-1})$, where $t>0$ and $\zeta >0$, we have shown that these maximum values are attained if $P_1$ and $P_2$ are the d-polytopes with vertex sets $V_1=\{{\varvec{\gamma }}_{1}(\alpha _i\tau ^\star ;\zeta ^\star )\,\,|\,\,i=1,\ldots ,n_1\}$ and $V_2=\{{\varvec{\gamma }}_{2}(\beta _j;\zeta ^\star )\,\,|\,\,j=1,\ldots ,n_2\}$, respectively, where $0<\alpha _1<\alpha _2<\cdots <\alpha _{n_1}$, $0<\beta _1<\beta _2<\cdots <\beta _{n_2}$, and $\tau ^\star$, $\zeta ^\star$ are appropriately chosen, sufficiently small, positive parameters.

The obvious next step is to extend the results in this paper for the Minkowski sum of r d-polytopes in ${\mathbb {E}}^d$ for $r\ge 3$ and $d\ge 4$. The case $r=3$ and $d\ge 2$ has already been resolved by the authors of this paper in collaboration with Konaxis [18, 19], while recently Adiprasito and Sanyal [1] have resolved the general problem for any $r,d\ge 2$, as well as for summands of different dimensions. The Adiprasito and Sanyal approach uses tools from Combinatorial Commutative Algebra, through a newly developed powerful theory called the relative Reisner–Stanley theory for simplicial complexes. An alternative proof for the case $r<d$ that is based on geometric arguments has very recently been proposed by the authors of this paper in [16, 17].

A related problem is to express the number of k-faces of the Minkowski sum of r d-polytopes in terms of the number of facets of these polytopes. Results in this direction are known for $d=2$ and $d=3$ only (see the introductory section and [5] for the 3-dimensional case). We would like to derive such expressions for any $d\ge 4$ and any number r of summands.

Appendix

1.1 Proof of Lemma 3

Proof

McMullen [20] in his original proof of the Upper Bound Theorem for polytopes proved that for any d-polytope P the following relation holds:

$$\begin{aligned} (k+1)h_{k+1}(\partial {P})+(d-k)h_k(\partial {P}) =\sum _{v\in \,{\mathrm{vert}}(P)}h_k({\partial {P}}/{v}),\qquad 0\le k\le d-1. \end{aligned}$$

(59)

Multiplying both sides of (59) by $t^{d-k-1}$ and summing over all $0 \le k \le d$, we get

$$\begin{aligned}&\sum _{k=0}^{d} (k+1)h_{k+1}(\partial {P}) t^{d-k-1} + \sum _{k=0}^{d} (d-k)h_k(\partial {P})t^{d-k-1} \nonumber \\&\quad = \sum _{k=0}^{d} \sum _{v\in \,{\mathrm{vert}}(P)}h_k({\partial {P}}/{v})t^{d-k-1}. \end{aligned}$$

(60)

For the right-hand side of (60), we have

$$\begin{aligned} \sum _{k=0}^{d} \sum _{v\in \,{\mathrm{vert}}(P)}h_k({\partial {P}}/{v})t^{d-k-1}= & {} \sum _{v\in \,{\mathrm{vert}}(P)}\sum _{k=0}^{d}h_k({\partial {P}}/{v}) t^{d-1-k}\nonumber \\= & {} \sum _{v\in \,{\mathrm{vert}}(P)} {\mathtt {h}}({{\partial {P}}/{v}};t), \end{aligned}$$

(61)

whereas for the left-hand side of (60), we get

$$\begin{aligned}&\sum _{k=0}^{d} (k+1)h_{k+1}(\partial {P}) t^{d-k-1} + \sum _{k=0}^{d} (d-k)h_k(\partial {P})t^{d-k-1} \nonumber \\&\quad =\sum _{k=0}^{d} k h_{k}(\partial {P}) t^{d-k} + \sum _{k=0}^{d} (d-k)h_k(\partial {P})t^{d-k-1}\nonumber \\&\quad = d \sum _{k=0}^{d} h_{k}(\partial {P}) t^{d-k} +(1-t)\sum _{k=0}^{d} (d-k) h_{k}(\partial {P}) t^{d-k-1}\nonumber \\&\quad =d\, {\mathtt {h}}({\partial {P}};t)+(1- t)\, {\mathtt {h'}}({\partial {P}};t). \end{aligned}$$

(62)

Substituting in (60), from (61) and (62), we recover the relation in the statement of the lemma. $\square$

1.2 Proof of an Identity

In this section we prove the following identity, used in Sect. 4, to prove the upper bound for $f_{k-1}({\mathcal {F}})$ (see relations (50) and (51)).

Lemma 23

For any $d\ge 2$ and any sequence of numbers $\alpha _i$, where $0\le i\le \lfloor \frac{d+1}{2}\rfloor$, we have

$$\begin{aligned}&\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{d+1-i}\\ {k-i} \end{array}\Big )\alpha _i +\sum _{i=0}^{\lfloor \frac{d}{2}\rfloor }\Big (\begin{array}{cc}{i}\\ {k-d-1+i} \end{array}\Big )\alpha _i\\&\quad = \sum \limits _{i=0}^{\frac{d+1}{2}}{^{^{*}}} \Big (\Big (\begin{array}{cc}{d+1-i}\\ {k-i} \end{array}\Big ) +\Big (\begin{array}{cc}{i}\\ {k-d-1+i} \end{array}\Big )\Big )\alpha _i. \end{aligned}$$

Proof

We start by recalling the definition of the symbol $\sum \nolimits _{i=0}^{\frac{\delta }{2}}{^{^{*}}}T_i$. This symbol denotes the sum of the elements $T_0,T_1,\ldots ,T_{\lfloor \frac{\delta }{2}\rfloor }$, where the last term is halved if $\delta$ is even. More precisely:

$$\begin{aligned} \sum \limits _{i=0}^{\frac{\delta }{2}}{^{^{*}}}T_i= {\left\{ \begin{array}{ll} T_0+T_1+\cdots +T_{\lfloor \frac{\delta }{2}\rfloor -1}+\frac{1}{2}T_{\lfloor \frac{\delta }{2}\rfloor } &{}\text {if }\delta \text { is even},\\ T_0+T_1+\cdots +T_{\lfloor \frac{\delta }{2}\rfloor -1}+T_{\lfloor \frac{\delta }{2}\rfloor } &{}\text {if }\delta \text { is odd}. \end{array}\right. } \end{aligned}$$

Let us now first consider the case d odd. In this case $d+1$ is even, and we have

$$\begin{aligned}&\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big )\alpha _i +\sum _{i=0}^{\lfloor \frac{d}{2}\rfloor }\Big (\begin{array}{cc}{i}\\ {k-d-1+i}\end{array}\Big )\alpha _i\\&\quad =\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big )\alpha _i +\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor -1}\Big (\begin{array}{cc}{i}\\ {k-d-1+i}\end{array}\Big )\alpha _i\\&\quad =\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor -1}\Bigg (\left( {\begin{array}{c}d+1-i\\ k-i\end{array}}\right) +\left( {\begin{array}{c}i\\ k-d-1+i\end{array}}\right) \Bigg )\alpha _i +\left( {\begin{array}{c}d+1-\lfloor \frac{d+1}{2}\rfloor \\ k-\lfloor \frac{d+1}{2}\rfloor \end{array}}\right) \alpha _{\lfloor \frac{d+1}{2}\rfloor }\\&\quad = \sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor -1}\Bigg (\left( {\begin{array}{c}d+1-i\\ k-i\end{array}}\right) +\left( {\begin{array}{c}i\\ k-d-1+i\end{array}}\right) \Bigg )\alpha _i\\&\qquad \,\, +{\textstyle \frac{1}{2}}\Bigg (\left( {\begin{array}{c}d+1-\lfloor \frac{d+1}{2}\rfloor \\ k-\lfloor \frac{d+1}{2}\rfloor \end{array}}\right) +\left( {\begin{array}{c}\lfloor \frac{d+1}{2}\rfloor \\ k-d-1+\lfloor \frac{d+1}{2}\rfloor \end{array}}\right) \Bigg )\alpha _{\lfloor \frac{d+1}{2}\rfloor }\\&\quad =\sum \limits _{i=0}^{\frac{d+1}{2}}{^{^{*}}} \Bigg (\left( {\begin{array}{c}d+1-i\\ k-i\end{array}}\right) +\left( {\begin{array}{c}i\\ k-d-1+i\end{array}}\right) \Bigg )\alpha _i. \end{aligned}$$

The case d even is even simpler to prove. In this case $d+1$ is odd; hence

$$\begin{aligned}&\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big )\alpha _i +\sum _{i=0}^{\lfloor \frac{d}{2}\rfloor }\Big (\begin{array}{cc}{i}\\ {k-d-1+i}\end{array}\Big )\alpha _i\\&\quad =\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big )\alpha _i +\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\begin{array}{cc}{i}\\ {k-d-1+i}\end{array}\Big )\alpha _i\\&\quad =\sum _{i=0}^{\lfloor \frac{d+1}{2}\rfloor }\Big (\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big ) +\Big (\begin{array}{cc}{i}\\ {k-d-1+i}\end{array}\Big )\Big )\alpha _i\\&\quad =\sum \limits _{i=0}^{\frac{d+1}{2}}{^{^{*}}} \Big (\Big (\begin{array}{cc}{d+1-i}\\ {k-i}\end{array}\Big )+\Big (\begin{array}{cc}{i}\\ {k-d-1+i}\end{array}\Big )\Big )\alpha _i \end{aligned}$$

This completes the proof. $\square$

1.3 Proof of Lemma 19

Before proceeding with the proof of Lemma 19, we need to introduce Vandermonde and generalized Vandermonde determinants. Given a vector of $n\ge 2$ real numbers ${\varvec{x}}=(x_1,x_2,\ldots ,x_n)$, the Vandermonde determinant $\text {VD}({\varvec{x}})$ of ${\varvec{x}}$ is the $n\times n$ determinant

$$\begin{aligned} \text {VD}({\varvec{x}})=\left| \begin{array}{ccccc} 1&{}1&{}\cdots &{}1\\ x_1&{}x_2&{}\cdots &{}x_n\\ x_1^2&{}x_2^2&{}\cdots &{}x_n^2\\ \vdots &{}\vdots &{}&{}\vdots \\ x_1^{n-1}&{}x_2^{n-1}&{}\cdots &{}x_n^{n-1}\\ \end{array} \right| =\prod _{1\le i<j\le n}(x_j-x_i). \end{aligned}$$

From the above expression, it is readily seen that if the elements of ${\varvec{x}}$ are in strictly increasing order, then $\text {VD}({\varvec{x}})>0$. A generalization of the Vandermonde determinant is the generalized Vandermonde determinant: if, in addition to ${\varvec{x}}$, we specify a vector of exponents ${\varvec{\mu }}=(\mu _1,\mu _2,\ldots ,\mu _n)$, where we require that $0\le \mu _1<\mu _2<\cdots <\mu _n$, we can define the generalized Vandermonde determinant $\text {GVD}({\varvec{x}};{\varvec{\mu }})$ as the $n\times n$ determinant:

$$\begin{aligned} \text {GVD}({\varvec{x}};{\varvec{\mu }})=\left| \begin{array}{ccccc} x_1^{\mu _1}&{}\quad x_2^{\mu _1}&{}\cdots &{}x_n^{\mu _1}\\ x_1^{\mu _2}&{}\quad x_2^{\mu _2}&{}\cdots &{}x_n^{\mu _2}\\ x_1^{\mu _3}&{}\quad x_2^{\mu _3}&{}\cdots &{}x_n^{\mu _3}\\ \vdots &{}\vdots &{}&{}\vdots \\ x_1^{\mu _n}&{}\quad x_2^{\mu _n}&{}\cdots &{}x_n^{\mu _n}\\ \end{array} \right| . \end{aligned}$$

It is a well-known fact that, if the elements of ${\varvec{x}}$ are in strictly increasing order, then $\text {GVD}({\varvec{x}};{\varvec{\mu }})>0$ (for example, see [8] for a proof of this fact).

To prove Lemma 19 we exploit the Cauchy–Binet formula (cf. [3]). Let M be a $n\times n$ square matrix factorized into a product LR of an $n \times m$ and an $m \times n$ matrix L and R respectively, with $m \ge n$. If J is a subset of $\{1,2,\ldots , m \}$ of size n, we denote by $L_{[n],J}$ the $n \times n$ matrix whose columns are the columns of L at indices from J and by $R_{J,[n]}$ the $n \times n$ matrix whose rows are the rows of R at indices from J. The Cauchy–Binet theorem states that

$$\begin{aligned} \det (M) = \det (L R) = \sum \limits _{J\in \left( {\begin{array}{c}[m]\\ n\end{array}}\right) } \det (L_{[n],J}) \det (R_{J,[n]}), \end{aligned}$$

(63)

where $\left( {\begin{array}{c}[m]\\ n\end{array}}\right)$ denotes the set of subsets of [m] of size n.

Proof

The determinant $D_{k,l}(\tau )$ is clearly a polynomial function of $\tau$. To prove our lemma, it suffices to show that the coefficient of the minimum exponent of $\tau$ in $D_{k,l}(\tau )$ is strictly positive.

In order to apply the Cauchy–Binet formula in our case, we factorize the matrix $\Delta _{k,l}(\tau )$, corresponding to the determinant $D_{k,l}(\tau )$, into the product of an $(m+3)\times 2(m+1)$ and a $2(m+1) \times (k+l)$ matrix L and R, respectively, as follows (recall that $m+3=k+l$):

The numbers over and sideways of L indicate the column and row indices, respectively, with $\hat{k} := k+m+1$. We partition the index set J into $J_1 \cup J_2$ where $J_1 \subseteq \{1,\ldots ,m+1\}$ and $J_2\subseteq \{\widehat{1}, \widehat{2},\ldots ,\widehat{m+1} \}.$ Notice that a term $\det (L_{[m+3],J}) \det (R_{J,[k+l]})$ in the Cauchy–Binet expansion of $D_{k,l}(\tau )$ vanishes in the following two cases:

• (i) $i \in J_1$ and $\hat{\imath }\in J_2$ for some $3 \le i \le m+1$; in this case the i-th and $\hat{\imath }$-th columns of $L_{[m+3],J}$ are identical, and thus $\det (L_{[m+3],J})=0$.

• (ii) $|J_1| \ne k$ or $|J_2| \ne l$; in this case $R_{J,[k+l]}$ is a block-diagonal square matrix with non-square non-zero blocks. The determinant of such a matrix is always zero.⁶

Furthermore, notice that for any non-vanishing term in the Cauchy–Binet expansion of $D_{k,l}(\tau )$, we have

$$\begin{aligned} \det (R_{J,[k+l]})= & {} \text {GVD}(\tau {\varvec{x}};{\varvec{\mu }}_1)\,\text {GVD}({\varvec{y}};{\varvec{\mu }}_2),\\ \tau {{\varvec{x}}}= & {} (\tau x_1,\ldots ,\tau x_k),\\ {\varvec{y}}= & {} (y_1,\ldots ,y_l), \end{aligned}$$

where ${\varvec{\mu }}_1$ (resp., ${\varvec{\mu }}_2$) is the vector consisting of the elements in $\{i-1\mid i\in J_1\}$ (resp., $\{i-(m+1)-1\mid i\in J_2\}$) ordered increasingly. The parameter $\tau$ appears only in $\text {GVD}(\tau {\varvec{x}};{\varvec{\mu }}_1)$ and can be factored out (see 64). We thus have

$$\begin{aligned} \det (R_{J,[k+l]} ) =\tau ^{M(J)}\,\text {GVD}({\varvec{x}};{\varvec{\mu }}_1)\,\text {GVD}({\varvec{y}};{\varvec{\mu }}_2)>0, \qquad M(J) = \sum _{i \in J_1}(i-1), \end{aligned}$$

since $\text {GVD}({\varvec{x}};{\varvec{\mu }}_1)$ and $\text {GVD}({\varvec{y}};{\varvec{\mu }}_2)$ are positive due to the way we have chosen ${\varvec{x}}$ and ${\varvec{y}}$.

Among all possible index sets $J=J_1\cup J_2$ for which the product $\det (L_{[m+3],J})\det (R_{J,[k+l]})$ does not vanish, we have to find the index set that gives the minimum exponent for $\tau$. Recall that, in view of condition (ii), the size of $J_1$ is k and the size of $J_2$ is l. The minimum exponent M(J) is then attained when $J_1=J_1^\star :=\{1,\ldots ,k \}$. In view of condition (i), we have $J_2 \subseteq \{\widehat{1}, \widehat{2},\ldots ,\widehat{m+1}\}\setminus \{\widehat{3},\ldots ,\widehat{k} \},$ which leaves no other choice but $J_2=J_2^\star :=\{ \widehat{1}, \widehat{2}, \widehat{k+1},\ldots ,\widehat{m+1} \}$.

For $J^\star =J_1^\star \cup J_2^\star$, the matrix $L_{[m+3],J}$ is

$$\begin{aligned} L_{[m+3],J^\star } = \left( \begin{array}{cccc} \mathrm{I}_2&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \mathrm{I}_2&{}\quad 0\\ 0&{}\quad \mathrm{I}_k&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad \mathrm{I}_l \end{array}\right) . \end{aligned}$$

Clearly, $L_{[m+3],J^\star }$ becomes the identity matrix after 2k row swaps. Hence $\det (L_{[m+3],J^\star })=1$, which further implies that

$$\begin{aligned} \text {sign}(D_{k,l}(\tau ))=\text {sign}(R_{J^\star ,[k+l]}) > 0. \end{aligned}$$

$\square$